Glycerol–Water Solution-Assisted Mach–Zehnder Temperature Sensor in Specialty Fiber with Two Cores and One Channel
Abstract
:1. Introduction
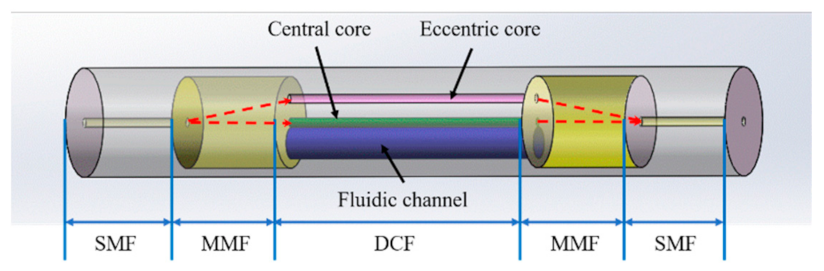
2. Fabrication of DCF
3. Operation Principle of the Sensor
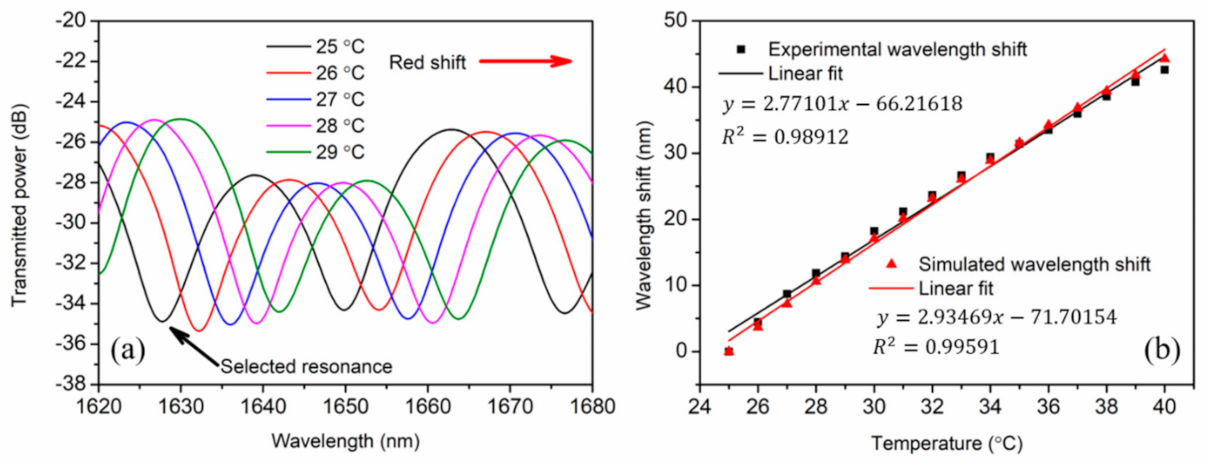
4. Experimental and Numerical Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Dong, Y.; Xiao, S.; Wu, B.; Xiao, H.; Jian, S. Refractive index and temperature sensor based on D-Shaped fiber combined with a fiber Bragg grating. IEEE Sens. J. 2019, 19, 1362–1367. [Google Scholar] [CrossRef]
- Hirayama, N.; Sano, Y. Fiber Bragg grating temperature sensor for practical use. ISA Trans. 2000, 39, 169–173. [Google Scholar] [CrossRef]
- Zhang, B.; Kahrizi, M. High-temperature resistance fiber Bragg grating temperature sensor fabrication. IEEE Sens. J. 2007, 7, 586–591. [Google Scholar] [CrossRef]
- Hu, X.; Pun, C.F.J.; Tam, H.Y.; Mégret, P.; Caucheteur, C. Highly reflective Bragg gratings in slightly etched step-index polymer optical fiber. Opt. Express 2014, 22, 18807–18817. [Google Scholar] [CrossRef]
- Qu, H.; Lan, X.; Huang, J.; Kaur, A.; Wei, T.; Gao, Z.; Xiao, H. Long-period grating inscribed on concatenated double-clad and single-clad fiber for simultaneous measurement of temperature and refractive index. IEEE Photon. Technol. Lett. 2012, 24, 1130–1132. [Google Scholar]
- Theodosiou, A.; Min, R.; Leal-Junior, A.; Ioannou, A.; Frizera, A.; Pontes, M.; Marques, C.; Kalli, K. Long period grating in a multimode cyclic transparent optical polymer fiber inscribed using a femtosecond laser. Opt. Lett. 2019, 44, 5346–5349. [Google Scholar] [CrossRef]
- Shu, X.; Allsop, T.; Gwandu, B.; Zhang, L.; Bennion, I. High-temperature sensitivity of long-period gratings in B-Ge codoped fiber. IEEE Photon. Technol. Lett. 2001, 13, 818–820. [Google Scholar]
- Colaço, C.; Caldas, P.; Villar, I.D.; Chibante, R.; Rego, G. Arc-induced long-period fiber gratings in the dispersion turning points. J. Light. Technol. 2016, 34, 4584–4590. [Google Scholar] [CrossRef]
- Wang, B.; Niu, Y.; Zheng, S.; Yin, Y.; Ding, M. A High temperature sensor based on sapphire fiber Fabry-Perot interferometer. IEEE Photonics Technol. Lett. 2020, 32, 89–92. [Google Scholar] [CrossRef]
- Li, J.; Li, Z.; Yang, J.; Zhang, Y.; Ren, C. Microfiber Fabry-Perot interferometer used as a temperature sensor and an optical modulator. Opt. Laser. Technol. 2020, 129, 106296. [Google Scholar] [CrossRef]
- Zhao, L.; Zhang, Y.; Chen, Y.; Wang, J. Composite cavity fiber tip Fabry-Perot interferometer for high temperature sensing. Opt. Fiber Technol. 2019, 50, 31–35. [Google Scholar] [CrossRef]
- Domínguez-Flores, C.E.; Monzón-Hernández, D.; Moreno-Basulto, J.I.; Rodríguez-Quiroz, O.; Minkovich, V.P.; López-Cortés, D.; Hernández-Romano, I. Real-time temperature sensor based on in-fiber Fabry–Perot interferometer embedded in a resin. J. Light. Technol. 2019, 37, 1084–1090. [Google Scholar] [CrossRef]
- Geng, Y.; Li, X.; Tan, X.; Deng, Y.; Yu, Y. High-sensitivity Mach–Zehnder interferometric temperature fiber sensor based on a waist-enlarged fusion bitaper. IEEE Sens. J. 2011, 11, 2891–2894. [Google Scholar] [CrossRef]
- Gao, S.; Ji, C.; Ning, Q.; Chen, W.; Li, J. High-sensitive Mach-Zehnder interferometric temperature fiber-optic sensor based on core-offset splicing technique. Opt. Fiber Technol. 2020, 56, 102202. [Google Scholar] [CrossRef]
- Zhao, Z.; Tang, M.; Fu, S.; Liu, S.; Wei, H.; Cheng, Y.; Tong, W.; Shum, P.P.; Liu, D. All-solid multi-core fiber-based multipath Mach–Zehnder interferometer for temperature sensing. Appl. Phys. B 2013, 112, 491–497. [Google Scholar] [CrossRef]
- Ma, J.; Yu, H.H.; Jiang, X.; Jiang, D.S. High-performance temperature sensing using a selectively filled solid-core photonic crystal fiber with a central air-bore. Opt. Express 2017, 25, 9406–9415. [Google Scholar] [CrossRef]
- Cao, Z.; Jiang, L.; Wang, S.; Wang, M.; Liu, D.; Wang, P.; Zhang, F.; Lu, Y. All-glass extrinsic Fabry–Perot interferometer thermo-optic coefficient sensor based on a capillary bridged two fiber ends. Appl. Opt. 2015, 54, 2371–2375. [Google Scholar] [CrossRef]
- Chang, S.; Hsu, C.C.; Huang, T.H.; Chuang, W.C.; Tsai, Y.S.; Shieh, J.Y.; Leung, C.Y. Heterodyne interferometric measurement of the thermo-optic coefficient of single mode fiber. Chin. J. Phys. 2000, 38, 437–442. [Google Scholar]
- Bauld, R.; Choi, D.Y.W.; Bazylewski, P.; Divigalpitiya, R.; Fanchini, G. Thermo-optical characterization and thermal properties of graphene–polymer composites: A review. J. Mater. Chem. C 2017, 6, 2901–2904. [Google Scholar] [CrossRef]
- Qu, H.; Skorobogatiy, M. Resonant bio- and chemical sensors using low-refractive-index-contrast liquid-core Bragg fibers. Sens. Actuators B Chem. 2012, 161, 261–268. [Google Scholar] [CrossRef]
- Rodney, W.S.; Spindler, R.J. Index of refraction of fused quartz glass for ultraviolet, visible, and infrared wavelengths. J. Opt. Soc. Am. 1954, 44, 677–679. [Google Scholar] [CrossRef]
- Rheims, J.; Köser, J.; Wriedt, T. Refractive-index measurements in the near-IR using an Abbe refractometer. Meas. Sci. Technol. 1997, 8, 601–605. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qiu, H.; Zhao, C.; Hu, X.; Chen, H.; Yu, Q.; Lian, Z.; Qu, H. Glycerol–Water Solution-Assisted Mach–Zehnder Temperature Sensor in Specialty Fiber with Two Cores and One Channel. Photonics 2021, 8, 103. https://doi.org/10.3390/photonics8040103
Qiu H, Zhao C, Hu X, Chen H, Yu Q, Lian Z, Qu H. Glycerol–Water Solution-Assisted Mach–Zehnder Temperature Sensor in Specialty Fiber with Two Cores and One Channel. Photonics. 2021; 8(4):103. https://doi.org/10.3390/photonics8040103
Chicago/Turabian StyleQiu, Haiming, Chunyu Zhao, Xuehao Hu, Haijin Chen, Qianqing Yu, Zhenggang Lian, and Hang Qu. 2021. "Glycerol–Water Solution-Assisted Mach–Zehnder Temperature Sensor in Specialty Fiber with Two Cores and One Channel" Photonics 8, no. 4: 103. https://doi.org/10.3390/photonics8040103
APA StyleQiu, H., Zhao, C., Hu, X., Chen, H., Yu, Q., Lian, Z., & Qu, H. (2021). Glycerol–Water Solution-Assisted Mach–Zehnder Temperature Sensor in Specialty Fiber with Two Cores and One Channel. Photonics, 8(4), 103. https://doi.org/10.3390/photonics8040103





