Abstract
Greatly improving the energy of a single mode-locked pulse while ensuring the acquisition of the width of short pulses will contribute to the application of mode-locked pulse in basic research, such as precision machining. This report has investigated a Q-switched and mode-locked (QML) erbium doped ring fiber laser based on the nonlinear polarization rotation (NPR) technology and a mechanical Q-switched device. Without the working of the mechanical Q-switched device, the fiber laser exported the continuous-wave mode-locked (CWML) pulse, with a width of 212.5 ps, and a repetition frequency of 81.97 MHz. For the CWML operation, the maximum output average power is 25.7 mW, and the energy is only 0.31 nJ. For the QML operation, 18.03 mW average power is achieved at the Q-switching frequency of 100 Hz. The energy of the QML pulse is increased by over 1100 times to 360.6 nJ. The width of the QML pulse is 203.1 ps measured by an autocorrelation curve, with the time-band product (TBP) being 0.598. The power instability is 0.5% (RMS) and 0.7% (RMS), respectively, for CWML and QML operation within 120 min. Furthermore, the spectral signal-to-noise ratio is about 60 dB. For the QML operation, the power instability is 0.48% (RMS) within 60 s and 0.37% (RMS) within 10 s. After frequency stabilization, the frequency fluctuation is ±100 Hz in the long-term of 1200 s, with the frequency stability (FS) calculated to be 2.44 × 10−6. It indicates that the QML fiber laser has good power stability and frequency stability.
1. Introduction
The introduction should briefly place the study in a broad context and highlight why it is important. As an ideal ultra-fast light source, ultrashort pulse fiber laser has the advantages of small volume and stable performance compared with solid-state laser. Narrow pulse fiber lasers of hundreds of picoseconds have been widely used in many important fields, such as optical fiber sensing [1], atmospheric optics [2,3], micro-machining [4,5], ultra-fast spectroscopy [6], optical fiber communication [7,8], and medicine [9,10]. Based on the nonlinear polarization rotation characteristics, the self-started mode-locked fiber lasers have been extensively investigated, attributed to their advantages of in-line all-fiber structures, low repetition frequencies, ultra-broadband spectra, and high energies [11,12,13,14]. The fiber nonlinear Kerr effect and the formation of fiber dissipative solitons are the intrinsic mechanisms for the self-started nonlinear polarization rotation mode-locked lasers [15,16]. With respect to mode-locked fiber lasers, Q-switched fiber lasers have higher energy optical pulses, but a larger pulse width [17,18,19]. Combining the advantages of both Q-switched and mode-locked laser technology, the fiber laser can have the superior performance of higher pulse energy and narrower pulse width, compared to ordinary QML fiber lasers [20,21].
Usually, the repetition frequency of a continuous mode-locked pulse sequence is too large, resulting in a too small single pulse energy and low peak power. However, the improvement of ultrashort pulse energy and peak power can be achieved by using Q-switching technology combined with mode-locking technology. In 2021, Sun et al. obtained a QML Er-doped fiber laser based on a MAX phase Ti2AlC saturable absorber [22]. The maximum single pulse energy of the Q-switched laser was 92.8 nJ, and the pulse width of mode-locked laser was 680 fs. Nizamani B. et al. reported a QML fiber laser based on aluminum zinc oxide as a saturable absorber [23]. The same technique was used to obtain a nanosecond pulse mode-locked operation, with a pulse width and repetition rate of 470 ns and 0.97 MHz, respectively. In 2020, Xinxin Shang et al. surveyed a QML Er-doped fiber laser of 1531.69 nm with a minimum pulse width of 2.36 ps, using titanium disulfide (TiS2) as a saturable absorber [24]. A maximum pulse energy and a minimum pulse width of 67.2 nJ and 2.34 µs were obtained.
Due to the limited damage threshold of a saturable absorber, it is usually difficult to obtain the higher QML pulse. In addition, the long-term stability of the laser is affected because of its complex preparation technology and the structure of all non-fiber. The fiber laser studied in this paper adopts an all-optical fiber structure. A quick response mechanical Q-switched device is used to achieve Q-switched and mode-locked working by pressing a segment of fiber to change the polarization state of an oscillating laser in a cavity. The energy and peak power of the QML pulse are increased by three orders of magnitude compared with those of the CWML pulse. The structure is simple and compact, and the structural stability and repetition stability can be guaranteed. By measuring, we found that the power instability is 0.7% and the signal-to-noise ratio of frequency spectral line is 50–60 dB, both on their way to a better level.
2. Experimental Setup
The setup of a passively Q-switched and mode-locked Er3+-doped all-fiber laser is as shown in Figure 1. It is composed of a single-mode 976 nm LD as the pump source, a 980/1550 wavelength division multiplexer (WDM), a section of Er3+-doped fiber as gain medium, two polarization controllers (PC1 and PC2), a polarization dependent isolator (PDISO), a mechanical Q-switched device, and a 40/60 coupling output. The pump 976 nm LD has a maximal output power of 280 mW. In the experiment, the LD pump source is equipped with a precise temperature control and feedback functions. The temperature control accuracy is up to 0.1 °C, and the wavelength is stable within 976 ± 0.2 nm in the whole process. The model of Er3+-doped fiber is EDFL-980-H-125, with a length of 1.2 m, a numerical aperture (NA) of 0.22, and an absorption coefficient of 5–10 dB/m at 980 ± 5 nm. The mode field diameter (MFD), cladding diameter, and coating diameter of EDFL-980-H-125 at 1550 nm is 6.5 μm, 125 μm, and 245 μm, respectively. The other fibers used in the cavity are SMF-28e single-mode fibers. The typical parameters of a SMF-28e single-mode fiber are shown in Table 1. Both the Er3+-doped gain fiber and single-mode fiber are placed in a cooling device with temperature control at a range of 20 ± 0.1 °C. The temperature control of LD and fiber is to prevent the fluctuation of wavelength and refractive index with temperature, which affects the stability of the laser output spectrum. This is an active frequency stabilization method. PC1 and PC2 are both mechanical polarization controllers with three rings. As we know, a quarter wave plate can be formed by winding two turns of optical fiber in the ring, and a half wave plate can be formed by winding four turns of optical fiber in the ring. The PDISO can control the propagation direction of the laser in the ring cavity. As shown in Figure 1, the direction indicated by the arrow is the propagation direction of the laser. The output efficiency of the coupled ring is 40.6%.
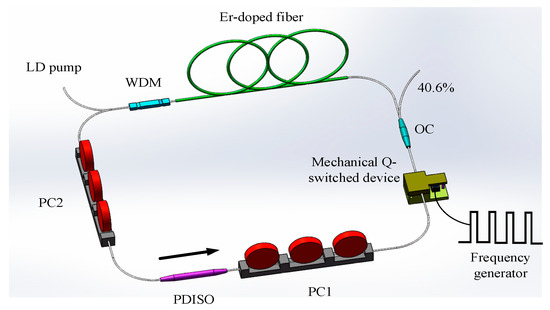
Figure 1.
Schematic of the passively Q-switched and mode-locked Er3+-doped fiber laser.

Table 1.
The typical parameters of SMF-28e single-mode fiber.
In the experiment, we achieve self-started mode-locked laser pulses through controlling the polarization state of the oscillating laser in the cavity. In order to change the polarization state of the laser transporting in the optical fiber, it needs to wound in different turns in the polarization controllers. Whatever this Er-doped fiber laser operates in the CWML or QML state, the state of the two polarization controllers is noted as in Figure 1; for PC1 there are two turns, four turns, and two turns of optical fibers in the three rings in turn, meaning that they will form a quarter-wave plate, a half wave plate, and a quarter-wave plate in proper order. PC2 is then winded in two turns, zero turn, and four turns of optical fibers in the first ring and second ring, meaning that they will form a quarter-wave plate and a half wave plate, respectively.
The scheme of the mechanical Q-switched device is shown in Figure 2. The mechanical extrusion structure is divided into two parts: a movable pressing block and base. The upper surface of the base is provided with a groove, and a section of the optical fiber passes through the groove. One side of the extrusion structure is provided with an electric control telescopic rod, and one end of the telescopic rod is connected with a frequency generator. When the telescopic rod receives a signal from the frequency generator, the telescopic rod compresses rapidly so as to drive the pressure block to squeeze the optical fiber in the groove. The compressed optical fiber has high polarization loss. At this time, the cavity loss is greater than the gain, and there is no laser to output. Photons oscillate continuously in the cavity, and the number of inversion particles accumulates continuously. When the frequency generator does not work or sends a low-level signal, the telescopic rod extends to the original position rapidly, and the optical fiber in the groove will not be squeezed. At this time, the loss disappears, and the accumulated large number of inverted particles avalanche output with forming a Q-switched giant pulse. In addition, a finite position column is set to prevent excessive compression from causing stress damage to the optical fiber.
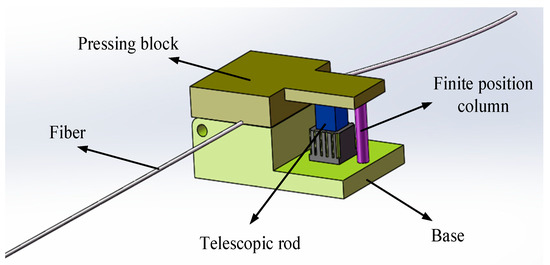
Figure 2.
Schematic diagram of the mechanical Q-switched device.
3. Results
The continuous-wave mode-locked experiment is carried out on the premise that the mechanical Q-switched device does not work. Under the maximum pump power of 280 mW, the two PCs are accurately adjusted to produce a nonlinear polarization rotation effect in the cavity to realize mode locking. The output pulse trains wave-form of the CWML operation is shown in Figure 3. Figure 3a shows the pulse trains wave-form with a time scale of 10 ns, and Figure 3b shows the wave-form of single continuous-wave mode-locked pulse. The result is measured by a TDS7254b oscillograph from the Tektronix company. The oscilloscope bandwidth is 2.5 GHz and the sampling rate is 20 GHz, while the photodetector used is model 14,151 produced by the Newfocus company with the response time of 18.5 ps. As shown in Figure 3a, the time interval between adjacent CWML pulses is 12.2 ns, corresponding to the repetition frequency of the CWML pulse trains is 81.97 MHz. The results of expanding the CWML pulse trains at a time scale of 100 ps is shown in Figure 3b. As shown in Figure 3b, the full wave at half maximum (FWHM) of the CWML pulse is 212.5 ps. As calculated, the single energy of the mode-locked pulse is about 0.31 nJ with a peak power of only 1.41 W.
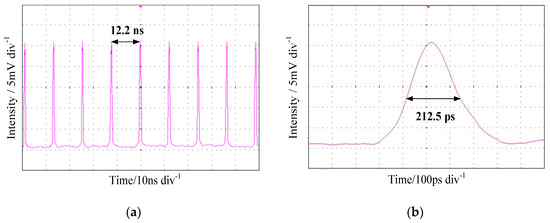
Figure 3.
Pulse trains wave-form of the CWML Er3+-doped fiber laser: (a) pulse trains; (b) wave-form of single CWML pulse.
The mechanical extrusion structure presses a piece of passive fiber in the circular cavity. The pulse signal with a frequency is transmitted by the frequency generator, which can drive the telescopic rod to run quickly and realize the function of the Q-switched device. The maximum displacement of the telescopic rod used in the experiment is 15 microns. In the experiment, the modulation frequency is set to 100 Hz. When the quick response telescopic rod starts to work, the Q-switched pulse output is as shown in Figure 4a. As shown, the time interval between adjacent Q-switched giant pulses is 10 ms, matching the modulation frequency of frequency generator. As shown in Figure 4b, we expand the Q-switched envelope and observe it at a time scale of 10 us. It can be found that each Q-switched envelope contains hundreds of small mode-locked pulses. The width of the whole envelope of the Q-switched giant pulse is about 6 us.
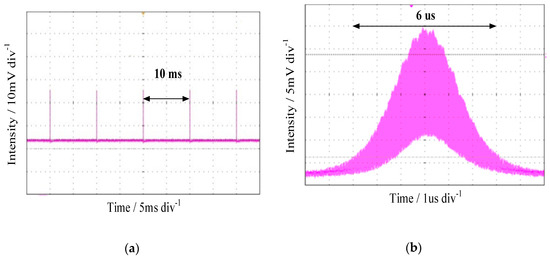
Figure 4.
Pulse waveform of the QML Er3+-doped fiber laser: (a) pulse sequence of Q-switched; (b) envelope of single Q-switched giant pulse.
The waveform of every mode-locked small pulse in the Q-switched envelope within the time scale of 5 ns is shown in Figure 5. For the Q-switched and mode-locked operations, the FWHM of the mode-locked pulse is 220.3 ps and the QML pulse interval is about 12.2 ns.
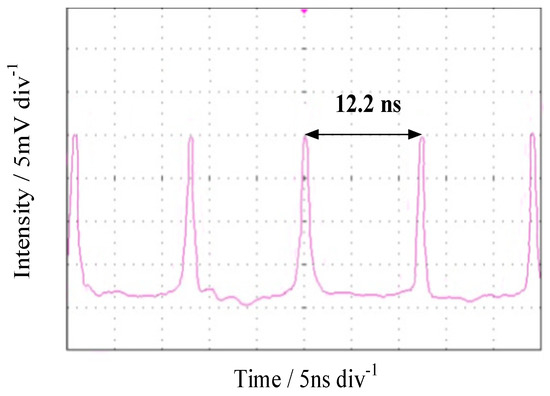
Figure 5.
Pulse sequence wave-form of QML fiber laser.
In the experiment, a spectrum analyzer is used to analyze the spectrum of the fiber laser under different working modes. Figure 6a,b shows the spectrum of this Er3+-doped fiber laser under a continuous-wave mode-locked operation state and Q-switched mode-locked operation state, respectively. Figure 6a shows the laser’s spectrum within the ±500 kHz bandwidth near 81.98 MHz. The automatic resolution bandwidth (RBW) is 10.0 kHz. It is obvious that there is only one large peak in the whole bandwidth, and the frequency of the peak is 81.97 MHz. It indicates that the laser has been working in the continuous-wave mode-locked operation state, and that the working state is very stable. We then reduce the RBW of the spectrometer to 100 Hz, matching the frequency of Q-switched device. Figure 6b shows the measured result of laser’s spectrum within the ±150 kHz bandwidth near 81.97 MHz. It is obvious that there is one large peak in the whole bandwidth, and that the frequency of the peak is 81.97 MHz. However, there are two spikes in the range of about ±3 kHz near the center frequency, corresponding exactly to the frequency of the Q-switched envelope.
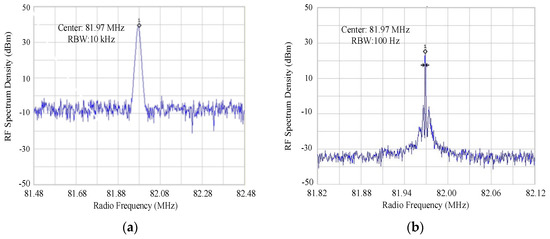
Figure 6.
Measurement results of spectrometer in two states: (a) CWML operation state; (b) QML operation state.
The short-term and long-term working stability of the spectrum is studied, and the result is shown in Figure 7. When the fiber laser is working on QML mode, Figure 7a records the drift of the frequency spectrum of this laser in the short-term at free running and frequency stabilization case, respectively. Without frequency stabilization, the laser operates in free-running mode. The illustration shows the fluctuation curve of laser output frequency after frequency stabilization. As can be seen from Figure 7a, the frequency shifts significantly during free-running operation. This is because the LD wavelength shifts, and the change of temperature affects the refractive index of the fiber. The drift reaches about 690 kHz in the term of 100 s. After the frequency stabilization design, the frequency stability has been significantly improved, and there is no one-way drift of frequency. The frequency fluctuates up and down along the central frequency, and the fluctuation range is about ±90 Hz. Figure 7b shows the long-term frequency fluctuation diagram under frequency stabilization. The frequency fluctuates up and down along the central frequency, and the fluctuation range is about ±100 Hz.
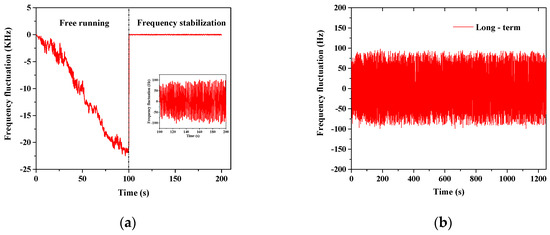
Figure 7.
Frequency fluctuation diagrams of QML operation state: (a) short-term frequency fluctuation for the free running and frequency stabilization case; (b) long-term frequency fluctuation.
The output average power versus the pump power of LD is shown as in Figure 8. The highest output average power is 25.7 mW for CWML operating under the pump power of 280 mW, corresponding to a slope efficiency of 37.7%. Compared, the highest output average power is 18.03 mW for QML operating, corresponding to a slope efficiency of 28.2%.
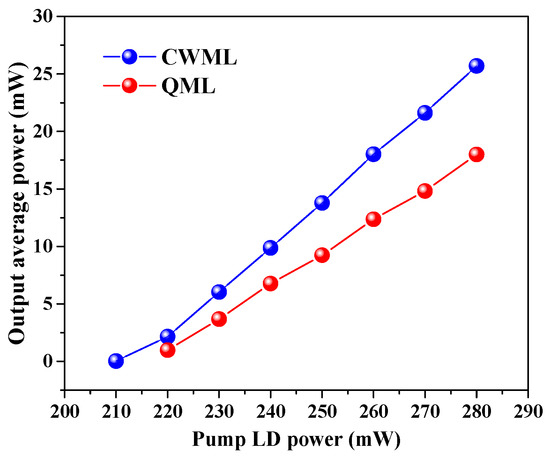
Figure 8.
Output average power versus the pump at CWML and QML operation state.
Figure 9 shows the average energy of single mode-locked pulse versus the pump power of LD. It is calculated that the single pulse energy is only 0.31 nJ in CWML operating with a peak power is only 1.41 W. However, the energy of Q-switched envelope is 180.03 uJ with a Q-switching frequency of 100 Hz. As shown in Figure 4b, a Q-switched envelope contains about hundreds of small mode-locked pulses. The average energy and peak power of single mode-locked pulse is increased to 360.6 nJ and 1.64 KW, respectively. Obviously, the energy and peak power of the mode-locked pulse are increased by three orders of magnitude compared with those of CWML operating.
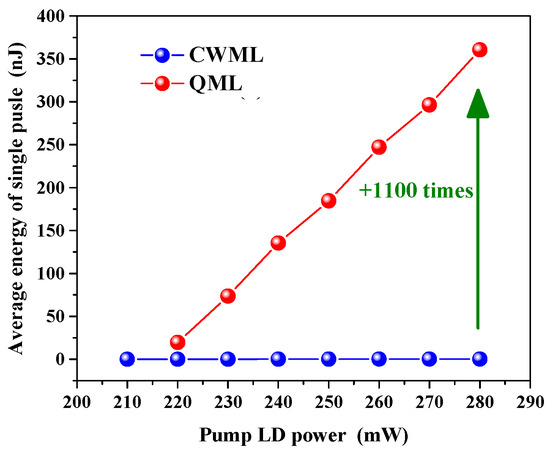
Figure 9.
Average energy of single mode-locked pulse versus the pump at CWML and QML operation state.
Under the two different states, we measured the output power, and the results are shown in Figure 10. Similarly, the measurement duration is 120 min. During this time period, the minimum power is 24.94 mW, the maximum is 26.30 mW, and the average power is 25.73 mW of the CWML operation state, according to the results of Figure 10a. In addition, the minimum power is 17.65 mW, the maximum is 18.50 mW, and the average power is 18.03 mW of the QML operation state, according to the results of Figure 10b.
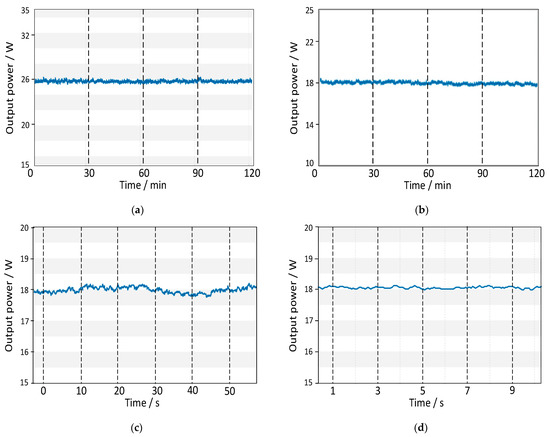
Figure 10.
Stability test results of output power of two different states: (a) power long-terms fluctuation of CWML operation state; (b) power long-terms fluctuation of QML operation state; (c) power short-terms fluctuation of CWML operation state; (d) power short-terms fluctuation of QML operation state.
In addition, the autocorrelation measurement curve is shown in Figure 11 below. In Figure 11, black dots are the measured relative intensity data of the second harmonic, and the red line is the Gaussian fitting curve. The full wave at half maximum (FWHM) obtained from the autocorrelation curve divided by the conversion coefficient is equal to the mode-locked pulse width. For Gaussian curve fitting, the conversion coefficient is 1.414 [25]. As shown in Figure 11, the FWHM of the autocorrelation curve is 287.3 ps, so the width corresponding to the mode-locked pulse is about 203.1 ps.
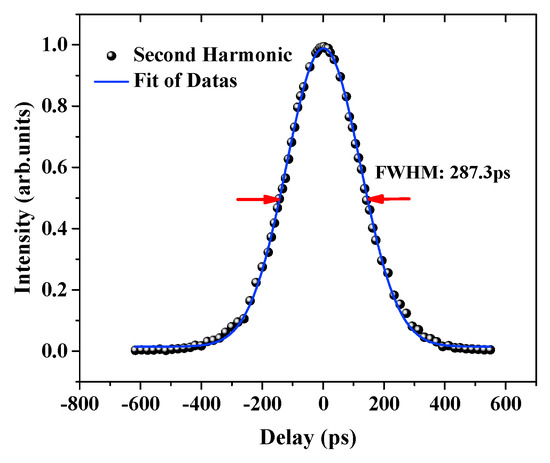
Figure 11.
Autocorrelation curve of the QML operation.
The output wavelength of the passively Q-switched and mode-locked Er3+-doped fiber laser is shown in Figure 12, measured by a Co. EXFO 1500 laser wavemeter (1 pm resolution). The emission spectra is guided by an InGaAs detector with a SRS830 lock-in amplifier for signal extraction. As shown, the center wavelength is 1562.8 nm with a FWHM line-width of about 24 pm, and there are no other emission oscillates with it simultaneously.
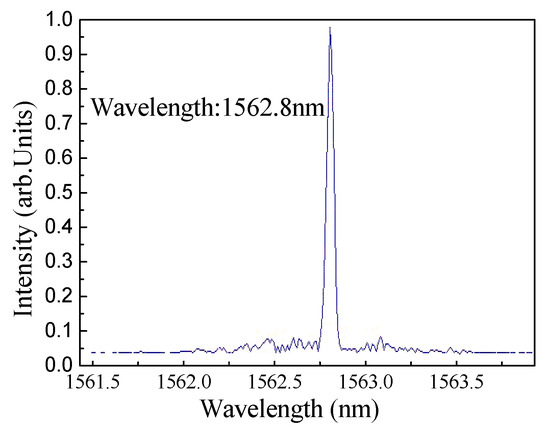
Figure 12.
Output spectra of the QML fiber laser.
4. Discussion
Because of the Q-switching effect, the mode-locked pulse is modulated, and an avalanches-like release forms a Q-switching giant envelope. The energy of a single Q-switched giant envelope pulse is up to 0.18 mJ. At the same time, the energy of a mode-locked pulse existing in the Q-switched giant envelope avalanches-like growth. The interval between two adjacent mode-locked pulses is 12.2 ns, so there are about 500 narrow pulses in the Q-switched giant envelope with a width of 6 us. After calculation, the average energy of single Q-switched mode-locked pulse is about 360 nJ. Compared with the continuous-wave mode-locked pulse of only 0.31 nJ, the method improves by 1100 times. Therefore, we have found a method to effectively obtain the narrow pulse width and high energy mode-locked pulse.
As shown in Figure 6, if the intensity ratio is 40 dB, the intensity ratio of the QML pulse energy to background noise is 104. After modulation, the QML pulse energy is about 360 nJ. Accordingly, the background noise is 0.036 nJ, which is equivalent to the mode-locked pulse energy of 0.31 nJ in CWML working mode. Reference proposes that the intensity ratio of the QML laser for stable operation is 50–70 dB [26,27]. Large fluctuation will affect the stability of the output power and frequency of QML laser. In fact, from Figure 6, we find that the ratio of the center frequency intensity to the background noise intensity is about 60 dB, within the range of 50–70 dB, which indicates that the QML fiber laser is in stable operation. The oscillating optical power is much greater than the noise. Theoretically, this fiber laser has relatively good stability and strong anti-interference ability. It should be that the low relaxation oscillation of pump source LD laser improves the anti-interference ability of the mode-locked laser. Moreover, these noises do not exist in a certain frequency, but in the whole spectrum of measured bandwidth. This shows that these noises may be random fluctuations caused by external mechanical vibration or acoustic interference, and the laser is still in the mode-locked operation. In addition to Figure 6b, there are two small spikes near the center frequency. The two small spikes are caused by the Q-switching frequency of 100 Hz, which is consistent with the set RBW of 100 Hz.
The parameters affecting power stability include pump stability and fiber temperature. The stability of the pump depends on the temperature. Long term operation causes the temperature to rise, which will cause the wavelength shift of LD pump source. According to the absorption spectrum of erbium-doped fiber, the change of pump wavelength affects the absorption efficiency of erbium ion. In the experiment, the LD pump source is equipped with a precise temperature control and feedback functions. The temperature control accuracy is up to 0.1 °C, and the wavelength is stable within 976 ± 0.2 nm in the whole process. The parameters affecting frequency stability are cavity length and the refractive index of the optical fiber. The length of the resonant cavity and the refractive index of the optical fiber material are also related to the temperature. The change of temperature can change the refractive index. Both the Er3+-doped gain fiber and single-mode fiber are placed in a cooling device with temperature control at a range of 20 ± 0.1 °C. The temperature control of LD and fiber is to prevent the fluctuation of wavelength and refractive index with temperature, which affects the stability of the laser output and spectrum output power. This is an active frequency stabilization method. This active frequency stabilization design through temperature regulation not only stabilizes the laser output spectrum, but also ensures the stability of output power.
Without frequency stabilization, parameters such as the wavelength of the pump source and the refractive index of the fiber change unrestricted with the change of temperature. At this time, the laser is in a free running state. Obviously, the laser output frequency will drift. After the improvement of frequency stabilization, the parameters affecting the spectrum drift are controlled, and the laser output frequency will not drift significantly. At this time, the main parameter affecting the frequency fluctuation is the length of the resonant cavity. Of course, due to the interference of the mechanical Q-switching method, its stability will be affected to a certain extent. The mechanical Q-switching device will change the resonant cavity length at the micron level. With the expansion and contraction of the telescopic rod, the expansion and contraction variation of this section of optical fiber is about 6 μm. As shown in Figure 7, the long-term and short-term frequency drift is about ±95 Hz and ±100 Hz, respectively. It fluctuates periodically along the central frequency. This corresponds to the periodic resonant cavity length expansion. Figure 7b shows the long-term frequency fluctuation diagram under frequency stabilization. The frequency fluctuates up and down along the central frequency, and the fluctuation range is about ± 100 kHz. By using the following equation, the frequency stability (FS) is calculated to be 2.44 × 10−6. Here, = 200 Hz ps, = 81.97 MHz.
For Figure 9, it is measured that the root mean square (RMS) is 128.5 uw and 123.8 uw, corresponding to CWML and QML operating modes respectively. Finally, the result calculated shows that the power instability is 0.5% (RMS) and 0.7% (RMS), respectively. In contrast, the instability of the QML operating mode is a little worse. The result is in good agreement with the spectrum comparison in Figure 6. However, its value is less than 1%. For short-term, the root mean square (RMS) is 86.97 uW within 60 s and 68.03 uw within 10 s. The instability is 0.48% (RMS) and 0.37% (RMS), respectively. It can be seen that instability increases over time, but this increase is very slow. This is caused by fatigue of the heat dissipation structure and temperature control system. Generally, it can be considered that the whole is still at a relatively stable level. Furthermore, the stability of this QML fiber laser is proved.
There is a certain deviation between the Autocorrelation curve fitting of 203.1 ps and that measured of 220.3 ps by fast photodetector. However, the two results are similar and belong to a reasonable error range. The deviation may be caused by the mismatch between the response speed of the photodetector and oscilloscope, or by the experimental error and fitting error of autocorrelation measurement. As shown in Figure 12, the FWHM of the spectral is 24 pm, and the central wavelength is 1562.8 nm. By using the following equation, the time-band product (TBP) was calculated to be 0.598. Here, TFWHM = 203.1 ps, = 24 pm, = 1562.8 nm, and C = 3.0 × 108 m/s.
The TBP is not close to the limit TBP value of 0.315, which indicates that the mode-locked pulse contains a certain chirp [28]. This is due to the group velocity dispersion (GVD) and self-phase modulation (SPM) effect in the optical fiber. The dispersion coefficient of the SMF-28e single-mode fiber at 1550 nm is about 18.0 ps/(nm.km), and the GVD is about −22.958 fs2/km. The experiment does not introduce enough positive dispersion to neutralize the negative dispersion produced by the single-mode fiber. It is well known that large GVD in optical fiber will cause pulse broadening. However, the purpose of this experiment is to find a method to improve the energy of picosecond mode-locked pulse and obtain stable power and frequency output. Obtaining the bandwidth limit pulse is not the main content of this experiment.
5. Conclusions
In summary, based on the combination of the nonlinear polarization rotation effect and mechanical Q-switched device, two output operations of CWML and QML are realized in this paper. The polarization state in the ring cavity is adjusted by PC1 and PC2 to realize continuous-wave mode-locked output. When at the CWML operation, the maximum average power is 25.73 mW, and the width of the model-locked pulse is 212.5 ps under the 976 nm LD pump power of 280 mW. At this time, the pulse frequency is 81.97 MHz and the energy of a single mode-locked pulse is only 0.31 nJ. Furthermore, the mechanical Q-switched device changes the polarization state of the oscillating laser in the ring cavity by pressing a piece of fiber so as to modulate the insertion loss regularly. This fiber laser then works in the state of QML. Firstly, this is an effective method to greatly improve the energy of mode-locked pulse. When the mechanical Q-switched device works at a frequency of 100 Hz, the maximum output average power is 18.03 mW under the same pump power. The Q-switching giant envelope contains hundreds of small QML pulses, with the width of the QML pulse being 203.1 ps measured by an autocorrelation curve, with the TBP at about 0.598. Most important of all, the average energy and the peak power of the QML pulse improves to 360.6 nJ and 1.64 KW, respectively. They both increase by three orders of magnitude compared with that of the CWML operation. Therefore, the QML pulses can improve the energy of single mode-locked pulse greatly while ensuring the acquisition of the width of short pulses. Secondly, the power instability is 0.5% (RMS) and 0.7% (RMS), respectively, for the different operation, within a measurement time period of 120 min. For the QML operation, the power instability is 0.48% (RMS) within 60 s, and 0.37% (RMS) within 10 s. The spectral signal-to-noise ratio reaches 60 dB. In the case of frequency stabilization, the frequency fluctuation is 200 Hz in the long-term of 1200 s, with the frequency stability (FS) calculated to be 2.44 × 10−6. It indicates that this QML fiber laser has good power stability and frequency stability.
Author Contributions
Conceptualization, J.W.; investigation, J.W.; methodology, J.W. and T.Z.; validation, J.W. and T.Z.; funding acquisition, W.Z.; supervision, W.Z.; writing—original draft, J.W.; writing—review and editing, J.W. All authors have read and agreed to the published version of the manuscript.
Funding
Please add: This research was funded by the Key Deployment Projects of the Chinese Academy of Sciences (Grant No.ZDRW-CN-2019-01), excellent projects in Zhejiang Province (Grant No. 2020C01036), and the National Natural Science Foundation of China under (Grant No.51805525).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Acknowledgments
In this section, you can acknowledge any support given which is not covered by the author contribution or funding sections. This may include administrative and technical support, or donations in kind (e.g., materials used for experiments).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Nicholson, J.W.; Ramachandran, S.; Ghalmi, S. A passively mode-locked, Yb-doped, figure-eight, fiber laser utilizing anomalous-dispersion higher-order-mode fiber. Opt. Express 2007, 15, 6623–6628. [Google Scholar] [CrossRef]
- Abramov, P.I.; Kuznetsov, E.V.; Skvortsov, L.A. Prospects of using quantum-cascade lasers in optoelectronic countermeasure systems. J. Opt. Technol. 2017, 84, 331–341. [Google Scholar] [CrossRef]
- Bloss, R. Lasers, radar, acoustics and magnetic sensors come to the aid of unmanned vehicles. Sens. Rev. 2013, 33, 197–201. [Google Scholar] [CrossRef]
- D’Amico, C.; Martin, G.; Troles, J.; Cheng, G.; Stoian, R. Multiscale Laser Written Photonic Structures in Bulk Chalcogenide Glasses for Infrared Light Transport and Extraction. Photonics 2021, 8, 211. [Google Scholar] [CrossRef]
- Jing, L.; Wenjiang, T.; Jinhai, S.; Zhen, K.; Xun, H. Generation of Ultrabroad and Intense Supercontinuum in Mixed Multiple Thin Plates. Photonics 2021, 8, 311. [Google Scholar]
- Niu, S.; Wang, S.; Ababaike, M.; Yusufu, T.; Miyamoto, K.; Omatsu, T. Tunable near- and mid-infrared (1.36–1.63 µm and 3.07–4.81 µm) optical vortex laser source. Laser Phys. Lett. 2020, 17, 45402. [Google Scholar] [CrossRef]
- Yuting, H.; Jiangbing, D.; Yufeng, C.; Ke, X.; Zuyuan, H. Machine Learning Assisted Inverse Design for Ultrafine, Dynamic and Arbitrary Gain Spectrum Shaping of Raman Amplification. Photonics 2021, 8, 260. [Google Scholar]
- Georg, R.; Benjamin, P.J.; Ruben, L.S.; Tobias, E.A.; Nicolas, F.K.; Mikael, M.; Haoshuo, C.; Roland, R.; David, N.T.; Pierre, S.; et al. Peta-bit-per-second optical communications system using a standard cladding diameter 15-mode fiber. Nat. Commun. 2021, 12, 4238. [Google Scholar]
- Wu, X.; Tang, D.Y.; Zhang, H.; Zhao, L.M. Dissipative soliton resonance in an all-normal-dispersion erbium-doped fiber laser. Opt. Express 2009, 17, 5580–5584. [Google Scholar] [CrossRef] [PubMed]
- Traxer, O.; Keller, E.X. Thulium fiber laser: The new player for kidney stone treatment A comparison with Holmium: YAG laser. World J. Urol. 2020, 38, 1883–1894. [Google Scholar] [CrossRef] [Green Version]
- Zhao, L.M.; Tang, D.Y.; Wu, J. Gain-guided soliton in a positive group-dispersion fiber laser. Opt. Lett. 2004, 31, 1788–1790. [Google Scholar] [CrossRef]
- Wang, L.R.; Liu, X.M.; Gong, Y.K.; Mao, D.; Feng, H. Ultra-broadband high-energy pulse generation and evolution in a compact erbium-doped all-fiber laser. Laser Phys. Lett. 2011, 8, 376–381. [Google Scholar] [CrossRef]
- Jingcheng, S.; Yizhou, L.; Shengzhi, Z.; Yuefeng, Z.; Yuzhi, S.; Tao, L.; Tianli, F. The Investigation on Ultrafast Pulse Formation in a Tm–Ho-Codoped Mode-Locking Fiber Oscillator. Molecules 2021, 26, 3460. [Google Scholar]
- Armas-Rivera, I.; Rodriguez-Morales, L.A.; Durán-Sánchez, M.; Ibarra-Escamilla, B. Dual-wavelength mode-locked Er-doped fiber laser in a spectral filter free cavity. Opt. Laser Technol. 2021, 142, 10722. [Google Scholar] [CrossRef]
- Tianhao, D.; Jiaqiang, L.; Yong, Z.; Chun, G.; Peijun, Y.; Lixin, X. Noise-like square pulses in a linear-cavity NPR mode-locked Yb-doped fiber laser. Opt. Laser Technol. 2021, 136, 18–21. [Google Scholar]
- Jingcheng, S.; Jianshu, F.; Tao, L.; Tianli, F.; Yizhou, L.; Shengzhi, Z.; Yuefeng, Z.; Yuzhi, S. A Watt-level noise-like Tm-doped fiber oscillator by nonlinear polarization rotation. Appl. Phys. Express 2021, 14, 52201. [Google Scholar]
- Pérez-Millán, P.; Díez, A.; Andrés, M.V.; Zalvidea, D.; Duchowicz, R. Q-switched all-fiber laser based on magnetostriction modulation of a Bragg grating. Opt. Express 2005, 13, 5046–5051. [Google Scholar] [CrossRef] [PubMed]
- Fu, B.; Wang, P.; Li, Y.; Condorelli, M.; Fazio, E.; Sun, J.; Xu, L.; Scardaci, V.; Compagnini, G. Passively Q-switched Yb-doped all-fiber laser based on Ag nanoplates as saturable absorber. Nanophotonics 2020, 9, 3873–3880. [Google Scholar] [CrossRef]
- Chunxiang, Z.; Yu, C.; Taojian, F.; Yanqi, G.; Chujun, Z.; Han, Z.; Shuangchun, W. Sub-hundred nanosecond pulse generation from a black phosphorus Q-switched Er-doped fiber laser. Opt. Express 2020, 28, 4807–4816. [Google Scholar]
- Cuadrado-Laborde, C.; Díez, A.; Cruz, J.L.; Andrés, M.V. Doubly active Q switching and mode locking of an all-fiber laser. Opt. Lett. 2009, 34, 2709–2711. [Google Scholar] [CrossRef]
- Cuadrado-Laborde, C.; Diez, A.; Cruz, J.L.; Andr´es, M.V. Actively Q-switched and mode locked all-fiber lasers. Laser Phys. Lett. 2010, 7, 870–875. [Google Scholar] [CrossRef]
- Guoqing, S.; Ming, F.; Kang, Z.; Tianhao, W.; Yuanhao, L.; Dongdong, H.; Yigang, L.; Feng, S. Q-Switched and Mode-Locked Er-doped fiber laser based on MAX phase Ti2AlC saturable absorber. Results Phys. 2021, 26, 104451. [Google Scholar]
- Nizamani, B.; Abdul Khudus, M.I.M.; Sameer, S.; Mustafa, M.N.; Jafry, A.A.A.; Hanafi, E.; Yasin, M.; Harun, S.W. Q-switched and mode-locked laser based on aluminium zinc oxide deposited onto D-shape fiber as a saturable absorber. Results Opt. 2021, 3, 100057. [Google Scholar] [CrossRef]
- Xinxin, S.; Linguang, G.; Huanian, Z.; Dengwang, L.; Qingyang, Y. Titanium Disulfide Based Saturable Absorber for Generating Passively Mode-Locked and Q-Switched Ultra-Fast Fiber Lasers. Nanomaterials 2020, 10, 1922. [Google Scholar]
- Honninger, C.; Paschotta, R.; Morier-Genoud, F.; Moser, M.; Keller, U. Q-switching stability limits of continuous-wave passive mode locking. J. Opt. Soc. Am. B Opt. Phys. 1999, 16, 46–56. [Google Scholar] [CrossRef]
- Yusoff, R.A.M.; Jafry, A.A.A.; Kasim, N.; Zulkipli, N.F.; Samsamnun, F.S.M.; Yasin, M.; Harun, S.W. Q-switched and mode-locked erbium-doped fiber laser using gadolinium oxide as saturable absorber. Opt. Fiber Technol. 2020, 57, 102209–102216. [Google Scholar] [CrossRef]
- Diels, J.M.; Fontaine, J.J.; McMichanel, I.C.; Simoni, F. Control and measurement of ultrashort pulse shapes (in amplitude and phase) with femtosecond accuracy. Appl. Opt. 1985, 24, 1270–1282. [Google Scholar] [CrossRef] [PubMed]
- Li, D.; Jussila, H.; Wang, Y.; Hu, G.; Albrow-Owen, T.; Howe, R.C.T.; Ren, Z.; Bai, J.; Hasan, T.; Su, Z. Wavelength and pulse duration tunable ultrafast fifiber laser modelocked with carbon nanotubes. Sci. Rep. 2018, 8, 2738–2745. [Google Scholar] [CrossRef] [PubMed] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).