Collective Lattice Resonances in All-Dielectric Nanostructures under Oblique Incidence

Abstract

Collective lattice resonances (CLRs) emerging under oblique incidence in 2D finite-size arrays of Si nanospheres have been studied with the coupled dipole model. We show that hybridization between the Mie resonances localized on a single nanoparticle and angle-dependent grating Wood–Rayleigh anomalies allows for the efficient tuning of CLRs across the visible spectrum. Complex nature of CLRs in arrays of dielectric particles with both electric dipole (ED) and magnetic dipole (MD) resonances paves a way for a selective and flexible tuning of either ED or MD CLR by an appropriate variation of the angle of incidence. The importance of the finite-size effects, which are especially pronounced for CLRs emerging for high diffraction orders under an oblique incidence has been also discussed.

1. Introduction

All-dielectric nanophotonics, being a rapidly emerging field of modern physics [1], provides a low-loss platform for an impressive number of applications. Well-developed state-of-the-art methods for synthesis of different all-dielectric materials [2] enable their successful implementation in color printing [3,4,5,6,7], biosensing [8,9,10], lasing [11,12], waveguiding [13,14,15], optical filtering [16,17,18], and nonlinear [19,20,21,22,23] optics. Among a rich variety of electromagnetic phenomena arising in all-dielectric nanostructures, collective effects in regular arrays of nanoparticles (NPs) have attracted a lot of attention recently [24,25,26,27,28,29,30,31,32,33,34,35,36,37], which is justified by the appearance of non-trivial lattice-mediated phenomena—for example, suppression of the back-scattering (Kerker effect) [38,39,40,41].

Collective lattice resonances (CLRs) arising in arrays of NPs originate from the strong interaction between NPs composing the lattice, which usually occurs under the illumination with a wavelength close to Wood–Rayleigh anomalies (WRAs) [42,43] of the array. In this case, a majority of NPs are excited with the same phase, which results in ultra-narrow high-Q spectral features. CLRs have been well studied for nanostructures from plasmonic NPs for a long time [44,45,46,47,48,49,50,51,52,53,54,55,56], while the all-dielectric analogues have gained attention only a decade ago [57]. In contrast to plasmonic NPs (in most of the cases characterized by weak magnetic and strong electric responses), all-dielectric NPs with pronounced electric and magnetic optical resonances [58] give rise to a rich variety of tunable CLRs that emerge even in regular rectangular-shaped arrays [32]. Moreover, 2D structures from all-dielectric NPs with two distinct electric dipole (ED) and magnetic dipole (MD) resonances exhibit inherently more sophisticated and intriguing behavior compared to the respective situations in purely ED-responsive plasmonic arrays, for example, in disordered [36,59] and finite-size [37,38,60,61,62] lattices.

Most of the numerical and theoretical studies of CLRs deal with infinitely large arrays of NPs under a normal incidence; however, it can be easily anticipated that, under oblique incidence, all-dielectric arrays may exhibit a plethora of properties overlooked in the literature. Our expectations are well justified by the reported results for plasmonic arrays [63,64] (with only ED response), which imply that, for all-dielectric NPs with ED and MD resonances, one may expect to observe even more effects. Thus, in this work, we address this problem and study electromagnetic properties of 2D arrays of all-dielectric NPs under oblique illumination. Moreover, we focus on finite-size arrays and reveal a role of the array size (in terms of a total number of NPs composing the lattice) on CLRs emerged under such conditions, which is more relevant to the experimental setups than infinite-array approximation.

2. Model

2.1. Coupled Dipole Approximation

Consider an array from $N_{\mathrm{tot}}$ spherical NPs embedded in a vacuum and illuminated by a plane wave, which, at any location $\mathbf{r}$, reads as

$${\mathbf{E}}_{\mathrm{inc}}\left(\mathbf{r}\right)={\mathbf{E}}_{0}exp(i\mathbf{k}·\mathbf{r}),{\mathbf{H}}_{\mathrm{inc}}\left(\mathbf{r}\right)={\mathbf{H}}_{0}exp(i\mathbf{k}·\mathbf{r}),$$

where ${\mathbf{E}}_0=\left(E_{0x},E_{0y},E_{0z}\right)$ and ${\mathbf{H}}_0=\left(H_{0x},H_{0y},H_{0z}\right)$ are amplitudes of the electric and magnetic fields, and $\mathbf{k}$ is a wave vector. The time dependence $exp(-i\omega t)$ is assumed and suppressed throughout a paper. In the framework of point-dipole approximation, electric, ${\mathbf{d}}_i$, and magnetic, ${\mathbf{m}}_i$, dipole moments induced on a given i-th NP under such an incidence are coupled to the respective dipoles on other $j\ne i$ NPs and to the external field as [57,65,66] (unlike these works, we use Gauss units)

$${\mathbf{d}}_i={\alpha }^e\left({\mathbf{E}}_{\mathrm{inc}}\left({\mathbf{r}}_i\right)+\sum _{j\ne i}^{N_{\mathrm{tot}}}{G}_{ij}{\mathbf{d}}_j-\sum _{j\ne i}^{N_{\mathrm{tot}}}{C}_{ij}{\mathbf{m}}_j\right),{\mathbf{m}}_i={\alpha }^m\left({\mathbf{H}}_{\mathrm{inc}}\left({\mathbf{r}}_i\right)+\sum _{j\ne i}^{N_{\mathrm{tot}}}{G}_{ij}{\mathbf{m}}_j+\sum _{j\ne i}^{N_{\mathrm{tot}}}{C}_{ij}{\mathbf{d}}_j\right),$$

(1)

where ${\mathbf{r}}_i$ is the position of the i-th NP center, ${\alpha }^e=3i{a}_1/2k^3$ and ${\alpha }^m=3i{b}_1/2k^3$ are electric and magnetic dipole polarizabilities, where $a_1$ and $b_1$ are scattering coefficients [67], $k=\left|\mathbf{k}\right|=2\pi /\lambda$, and $\lambda$ is a wavelength. Tensors $G_{ij}$ and $C_{ij}$ describe the interaction between dipoles induced on i-th and j-th NPs:

$$G_{ij}={\displaystyle \frac{\exp \left(ik{r}_{ij}\right)}{r_{ij}}}\left[\left(k^2-{\displaystyle \frac{1}{r_{ij}^2}}+{\displaystyle \frac{ik}{r_{ij}}}\right)\mathbb{I}+\left(-k^2+{\displaystyle \frac{3}{r_{ij}^2}}-{\displaystyle \frac{3ik}{r_{ij}}}\right){\displaystyle \frac{{\mathbf{r}}_{ij}\otimes {\mathbf{r}}_{ij}}{r_{ij}^2}}\right],$$

$${\left(C_{ij}\right)}_{\alpha \beta }=\sum _{\gamma }{\epsilon }_{\alpha \gamma \beta }{\left({\mathbf{g}}_{ij}\right)}_{\gamma },{\mathbf{g}}_{ij}={\displaystyle \frac{\exp \left(ik{r}_{ij}\right)}{r_{ij}}}\left(k^2+{\displaystyle \frac{ik}{r_{ij}}}\right){\displaystyle \frac{{\mathbf{r}}_{ij}}{r_{ij}}},$$

where $\mathbb{I}$ is a $3\times 3$ unit tensor, ⊗ denotes a tensor product, $r_{ij}=|{\mathbf{r}}_{ij}|=|{\mathbf{r}}_i-{\mathbf{r}}_j|$ is center-to-center distance between i-th and j-th NPs, and ${\epsilon }_{\alpha \gamma \beta }$ is Levi–Civita symbol with $\alpha$, $\beta$, $\gamma$ denoting Cartesian components of the tensors.

For an array with a given geometry and composition of NPs, the solution of the linear system of Equations (1) yields ${\mathbf{d}}_i$ and ${\mathbf{m}}_i$ induced on each i-th NP; thus, the electromagnetic response of the array to the incident excitation can be explicitly found. Particularly, in this work, we consider the total amount of the electromagnetic energy scattered and absorbed by the array normalized to the sum of the cross sectional area of all NPs, i.e., the extinction efficiency [57,66]:

$$Q_{\mathrm{ext}}=\frac{4k}{|{\mathbf{E}}_0{|}^2{N}_{\mathrm{tot}}{R}^2}\Im \sum _{i=1}^{N_{\mathrm{tot}}}\left[{\mathbf{d}}_i·{\mathbf{E}}_{\mathrm{inc}}^{\ast }\left({\mathbf{r}}_i\right)+{\mathbf{m}}_i·{\mathbf{H}}_{\mathrm{inc}}^{\ast }\left({\mathbf{r}}_i\right)\right],$$

(2)

where the asterisk denotes a complex conjugate, R is the radius of the NP, and ℑ takes the imaginary part.

2.2. Wood–Rayleigh Anomalies

CLRs emerge at wavelengths close (slightly red-shifted) to WRAs, which for a general case of a regular 2D lattice (with pitches $h_x$ and $h_y$ along x and y axes, as shown in Figure 1a) takes place if

$${\mathbf{k}}_{\Vert }={\mathbf{k}}_{\sigma }+p{\mathbf{K}}_x+q{\mathbf{K}}_y,$$

(3)

where ${\mathbf{K}}_x=(2\pi /h_x)\widehat{x}$ and ${\mathbf{K}}_y=(2\pi /h_y)\widehat{y}$ are reciprocal lattice vectors, ${\mathbf{k}}_{\Vert }=(k_{\Vert x},k_{\Vert y})$ is wave vector of a wave propagating in the lattice plane, ${\mathbf{k}}_{\sigma }$ is projection of the incident wave vector on the lattice plane, $[p,q]$ is a pair of integers which denotes the order of the anomaly, and symbol$\widehat{}$denotes a unit vector. Explicitly, x and y components in Equation (3) read as

$$k_{\Vert x}={\displaystyle \frac{2\pi }{\lambda }}sin{\theta }_x+{\displaystyle \frac{2\pi }{h_x}}p,k_{\Vert y}={\displaystyle \frac{2\pi }{\lambda }}sin{\theta }_y+{\displaystyle \frac{2\pi }{h_y}}q,$$

(4)

where ${\theta }_x$ and ${\theta }_y$ are angles between the z-axis and projections of $\mathbf{k}$ to $XOZ$ and $YOZ$ planes (see Figure 1a and Figure 2a, respectively).

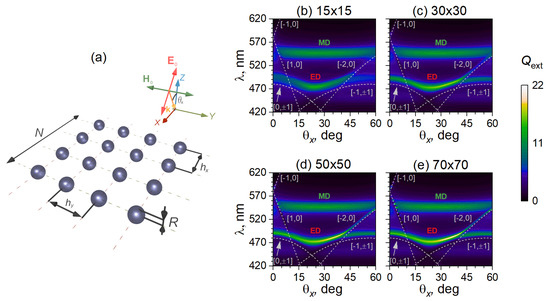
Figure 1. (a) Schematic representation of a regular 2D array from $N_{\mathrm{tot}}=N\times N$ NPs with radius R and pitches $h_x$ and $h_y$ along the x and y axes. The incident wave vector $\mathbf{k}$ lies within $XOZ$ plane, and the angle ${\theta }_x$ is varied, while ${\theta }_y=0$; (b–e) corresponding extinction efficiency $Q_{\mathrm{ext}}$ for arrays from NPs with $R=65$ nm, $h_x=580$ nm, $h_y=480$ nm and for a different number of NPs: (b) $15\times 15$; (c) $30\times 30$; (d) $50\times 50$; (e) $70\times 70$. The dashed lines show spectral positions of WRAs of $[p,q]$ order, as labeled in plots. Data from Ref. [68] have been used for the refractive index of Si.

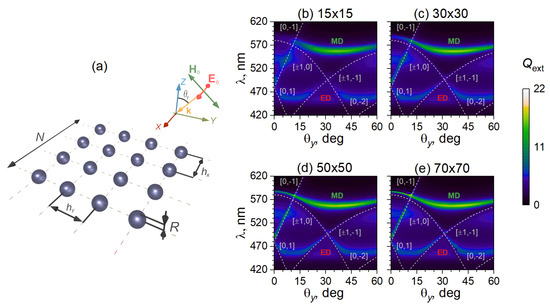
Figure 2. The same as in Figure 1, but with varying ${\theta }_y$ and constant ${\theta }_x=0$. The incident wave vector $\mathbf{k}\in YOZ$.

In a homogeneous environment, the wave vector of a wave propagating in the lattice plane is $|{\mathbf{k}}_{\Vert }{|}^2=k_{\Vert x}^2+k_{\Vert y}^2={(2\pi /\lambda )}^2$, which along with Equation (4) provide the quadratic equation in $\lambda$:

$$\left({\displaystyle \frac{p^2}{h_x^2}}+{\displaystyle \frac{q^2}{h_y^2}}\right){\lambda }^2+2\left({\displaystyle \frac{psin{\theta }_x}{h_x}}+{\displaystyle \frac{qsin{\theta }_y}{h_y}}\right)\lambda +\left({sin}^2{\theta }_x+{sin}^2{\theta }_y-1\right)=0,$$

(5)

where, for a given combination of integers $[p,q]$, one can get a corresponding spectral position ${\lambda }_{p,q}$ of WRA of $[p,q]$ order.

We emphasize that the hybridization between localized Mie resonances and $[\pm 1,0]$ or $[0,\pm 1]$ WRAs is usually considered in a solid body of the literature [32,36,37,57]. For a special case of normal incidence (${\theta }_x={\theta }_y=0$), these WRAs are simply ${\lambda }_{\pm 1,0}=h_x$ and ${\lambda }_{0,\pm 1}=h_y$. However, Equation (5) immediately implies that the broad variation of ${\theta }_x$ and/or ${\theta }_y$ may result in CLRs emerging from the hybridization with WRAs of higher order (i.e., $\left|p\right|,\left|q\right|>1$), which are studied below.

3. Results

We consider regular arrays from Si NPs with $R=65$ nm, arranged in a 2D rectangular lattice with $h_y=480$ nm and $h_x=580$ nm. A direct comparison with full-field simulations ([31] Figure 1) ([38] Figure 3) has confirmed a reliability of the coupled dipole approximation (1) for arrays with similar pitches and the same R. Under a normal incidence with ${\mathbf{E}}_0=\left(E_{0x},0,0\right)$ and ${\mathbf{H}}_0=\left(0,H_{0y},0\right)$, arrays with these geometrical parameters exhibit ED and MD CLRs ([37] Figure 2b) at $\lambda \approx 490$ nm and $\lambda \approx 586$ nm, respectively, which is the result of a hybridization between ED ($\lambda \approx 450$ nm) and MD ($\lambda \approx 550$ nm) resonances of a single NP ([57] Figure 3b) with $[0,\pm 1]$ and $[\pm 1,0]$ WRAs ([37] Figure 2a), correspondingly. Since the efficient tuning of ED and MD CLRs occurs if $h_{y,x}$ are changed in a direction perpendicular with respect to the polarization of ${\mathbf{E}}_0$ or ${\mathbf{H}}_0$ ([32] Figures 2 and 4), ([36] Figure 2), it is insightful to consider an incidence with only one ${\theta }_{x,y}$ varied keeping the other ${\theta }_{y,x}=0$. Following this approach, it is possible to study separately ED and MD CLRs, while, for any other oblique incidence with ${\theta }_x\ne 0$ and ${\theta }_y\ne 0$, one can expect the optical response to be a superposition of the studied examples.

Figure 1b–e show the extinction efficiency for arrays with different $N_{\mathrm{tot}}=N\times N$ under incidence with $0^{\circ }\le {\theta }_x\le {60}^{\circ }$ and ${\theta }_y=0$. Dashed $[p,q]$ lines show corresponding angle-dependent ${\lambda }_{p,q}$ for WRA which fall within a visible range for a geometry considered. It can be seen that, apart from common $[0,\pm 1]$ and $[\pm 1,0]$, WRAs of $[-2,0]$ and $[-1,\pm 1]$ orders have emerged. This leads to the appearance of additional ED CLRs for $[-1,\pm 1]$ WRA under ${\theta }_x>{25}^{\circ }$ illumination, and for $[-2,0]$ WRA under ${\theta }_x>{40}^{\circ }$ incidence. Moreover, even for ${\theta }_y=0$, variation of ${\theta }_x$ implies gradual blue-shift of $[0,\pm 1]$ WRA, which allows for fine-tuning of ED CLRs for ${\theta }_x<{25}^{\circ }$. Such angle-dependent hybridization between Mie resonances on single NP and WRAs paves a way for the efficient tuning of ED CLRs in the 450–540 nm range. It is noteworthy that MD CLR vanishes quite rapidly with a slight change of ${\theta }_x$, since ${\lambda }_{\pm 1,0}$ strongly depends on ${\theta }_x$ (cf. Equation (5)); thus, for ${\theta }_x>5^{\circ }$, only an MD resonance of a single NP is observed. As it might be expected from Ref. [37], the extinction efficiency at the CLR regime grows with $N_{\mathrm{tot}}$; thus, the CLRs that have emerged from the interaction with high-order WRAs are more pronounced for larger arrays, which can be clearly seen by the following Figure 1b for the array from $15\times 15$ NPs to Figure 1e for $70\times 70$ NPs.

On the contrary, by changing ${\theta }_y$ and keeping ${\theta }_x=0$ constant, one can control the spectral position of MD CLRs, as clearly shown in Figure 2. In this case, however, ED CLR does not vanish so rapidly for $0<{\theta }_y<5^{\circ }$ (as it does MD CLR from Figure 1 for the opposite case of $0^{\circ }<{\theta }_x<5^{\circ }$). ED resonance on a single NP efficiently couples to $[0,-1]$ WRA and thus corresponding ED CLR can be tuned all the way up to $\approx 570$ nm, and, finally, overlap with $[\pm 1,0]$ MD CLR around 580 nm under ${\theta }_y\approx {12}^{\circ }$ incidence. MD CLR, however, can be efficiently tuned only for $[\pm 1,0]$ WRA, while, wavelengths of high-order WRAs appear to be quite far away from MD resonance, and only $[\pm 1,-1]$ efficiently interacts with MD resonance, but for quite large angles of incidence.

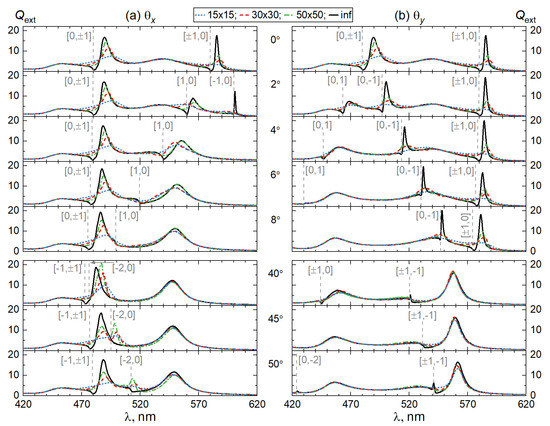
Figure 3 further elaborates on discussed effects and shows several extinction spectra for the clearer presentation. Indeed, under oblique incidence, one can observe efficient tuning of the optical properties of the 2D lattice from Si NPs. The “gradual” quadratic ${\lambda }_{p,q}\left({\theta }^2\right)$ and “rapid” linear ${\lambda }_{p,q}\left(\theta \right)$ dependence with one of the ${\theta }_x,y$ being zero (see Equation (5)) allows for a flexible control of ED and MD CLRs. For a strong coupling of single-particle resonance with WRAs (i.e., for spectral regions where they almost overlap), the finite size effects are of particular importance, while, for a weakly coupled case (i.e., for spectral regions where they are sufficiently far from each other), these effects have a minor impact. For example, from Figure 3a, one can see that $Q_{\mathrm{ext}}$ rapidly grows with increasing $N\times N$ for ED CLR strongly coupled to $[0,\pm 1]$ around $\lambda \approx 490$ nm, while MD CLR for $[1,0]$ WRA becomes almost independent on $N_{\mathrm{tot}}$ with increasing ${\theta }_x$.

Figure 3. Extinction spectra for arrays from (a) Figure 1 and (b) Figure 2 for selected ${\theta }_{x,y}$ and for arrays from $15\times 15$, $30\times 30$, and $50\times 50$ NPs. Spectra of infinite (inf) arrays are shown for comparison. Vertical dashed lines show the spectral positions of $[p,q]$ WRAs.

Finally, Figure 4 demonstrates angle-dependent Q-factors of ED CLRs from Figure 1, for arrays with different $N\times N$. As it might be expected, the Q-factor is generally larger for arrays with larger $N\times N$. Interestingly, for $0^{\circ }\le {\theta }_x\le {24}^{\circ }$ incidence, with increasing ${\theta }_x$, i.e., weakening coupling between single-particle resonance and $[0,\pm 1]$ WRA, Q-factor gradually converges to $\approx 30$ value for any array size at ${\theta }_x\approx {24}^{\circ }$. It is noteworthy that for CLRs that have emerged from the hybridization with high-order $[-2,0]$ WRA, Q-factor is about two times larger than that of commonly considered CLRs that have emerged from the interaction with $[0,\pm 1]$ WRA.

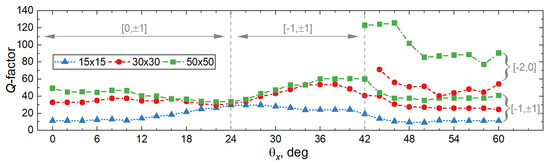
Figure 4. Q-factor of ED CLRs from Figure 1 as a function of ${\theta }_x$ for arrays with different number $N\times N$ of NPs. Vertical dashed lines separate regions where the ED of a single NP hybridizes with different WRAs: $[0,\pm 1]$ for $0^{\circ }\le {\theta }_x\le {24}^{\circ }$, $[-1,\pm 1]$ for ${24}^{\circ }\le {\theta }_x\le {42}^{\circ }$, $[-2,0]$ and $[-1,\pm 1]$ for ${42}^{\circ }\le {\theta }_x\le {60}^{\circ }$. Note that $15\times 15$ arrays do not exhibit ED CLRs for $[-2,0]$ WRA, as may be clearly seen from Figure 3a.

4. Conclusions

To conclude, we have considered the features of collective lattice resonances emerging in regular 2D arrays of all-dielectric nanoparticles under an oblique incidence. For a particular case of Si constituents with fixed pitches $h_{x,y}$, we have shown that high-order Wood–Rayleigh anomalies appear to be within a visible range and close to the optical resonances of a single Si nanoparticle. Under such conditions, an efficient hybridization between either electric dipole or magnetic dipole resonance of a single nanoparticle with, for instance, $[-1,\pm 1]$, $[-2,0]$ or $[\pm 1,-1]$ Wood–Rayleigh anomalies leads to the appearance of collective lattice resonances, which can only be observed under an oblique incidence. Moreover, by adjusting the angle of illumination, one can efficiently tune the spectral position of such collective lattice resonances across the whole visible spectrum. We emphasize that all the results presented in this work correspond to a single lattice (with given $N\times N$). It means that the optical response of a considered nanostructure can be tuned to a variety of scenarios by simply inclining the array with the respect to the incident illumination, which, in some cases, might be more preferable compared to other strategies used to tune the wavelength of the collective lattice resonances [69,70]. Finally, we show that the total number of nanoparticles composing arrays may play a crucial role for collective lattice resonances under an oblique incidence, depending on the coupling strength between Wood–Rayleigh anomalies and single-particle resonance. Thus, results reported in this manuscript might be used in the design of photonic devices where the tuning of the resonant response can be achieved without complex technologies.