Orbital Instability of Chaotic Laser Diode with Optical Injection and Electronically Applied Chaotic Signal

Abstract

We numerically studied the chaotic dynamics of a laser diode (LD) system with optical injection, where a chaotic signal, which is generated by an LD with optical feedback, is applied to the drive current of the master LD. To quantify the orbital instability of the slave LD, the Lyapunov exponent was calculated as a function of the optical injection ratio between the master and slave LDs and the optical feedback ratio of the applied signal. We found that the Lyapunov exponent was increased and the orbital instability was enhanced by applying a chaotic signal when the inherent system without the applied signal was in a “window”. Next, we investigated the orbital instability of the slave LD in terms of statistical and dynamical quantities of the applied chaotic signal. The maximal value of the Lyapunov exponent for a certain range of the injection ratio was calculated and we showed that a chaotic pulsation is suitable for enhancing the orbital instability of the LD system. We then investigated chaos synchronization between the LDs. It is concluded that the orbital instability of an LD with optical injection can be enhanced by applying chaotic pulsation without chaos synchronization.

1. Introduction

Since the chaotic oscillation of a laser diode (LD) [1,2,3,4,5,6,7] has a high frequency and broad bandwidth, its potential applications, such as physical random bit generation [8,9,10,11], reservoir computing [12,13,14], decision-making [15], and chaotic communication [16,17,18,19], have been widely studied. In these applications, more chaotic oscillation can contribute to increasing the performance, for example, randomness in random bit generation, a high bit rate in security in chaotic communication. Various methods of generating chaotic oscillation with a broad bandwidth and large chaotic property have been studied, for example, using a master–slave LD system with frequency detuning [20,21], an external feedback system with dual feedback [22], or an external feedback system with random feedback [23].

We previously proposed a method using a master–slave LD system with a random signal applied to the drive current of the LDs [24]. In the optical injection system, which consists of master and slave LDs, various dynamics of the slave LD appear. For a small optical injection ratio, the slave laser oscillates stably, periodically or quasi-periodically. Then, the dynamics develop into a chaotic state with increasing optical injection ratio, and periodic oscillation is observed between chaotic states, which is called a “window”. In a window, the chaotic dynamics are concealed. We have shown numerically that the chaotic dynamics are revealed by applying a pseudorandom signal to the drive current of the master LD, and the chaotic property, that is, the orbital instability of the slave LD, is enhanced by increasing the standard deviation of the applied random signal. The orbital instability of a chaotic system can be controlled by applying a statistical random signal to a deterministic chaotic system.

In this work, a deterministic chaotic signal is adopted as the applied signal. We numerically investigate an optical injection system with unidirectional coupling from a master LD to a slave LD by applying a signal, which is generated by the chaos source LD with external optical feedback, to the drive current of the master LD. First, we compare the system with an applied chaotic signal and the system with an applied random signal having the same mean and standard deviation as the chaotic signal. It is shown that, in the window, the chaotic dynamics of the slave LD are revealed by the applied chaotic signal as well as the applied pseudorandom signal. Moreover, the applied chaotic signal more greatly enhances the orbital instability of the slave LD than the applied pseudorandom signal. Next, to explore the factor causing the enhanced orbital instability of the slave LD, we estimate the orbital instability of the slave LD in terms of statistical and dynamical quantities of the applied chaotic signal. Then, we discuss the suitable conditions of the applied chaotic signal for enhancing the orbital instability of the LD system, and the chaos synchronization between the applied signal and LD system.

2. Chaotic Laser System and Lyapunov Exponent

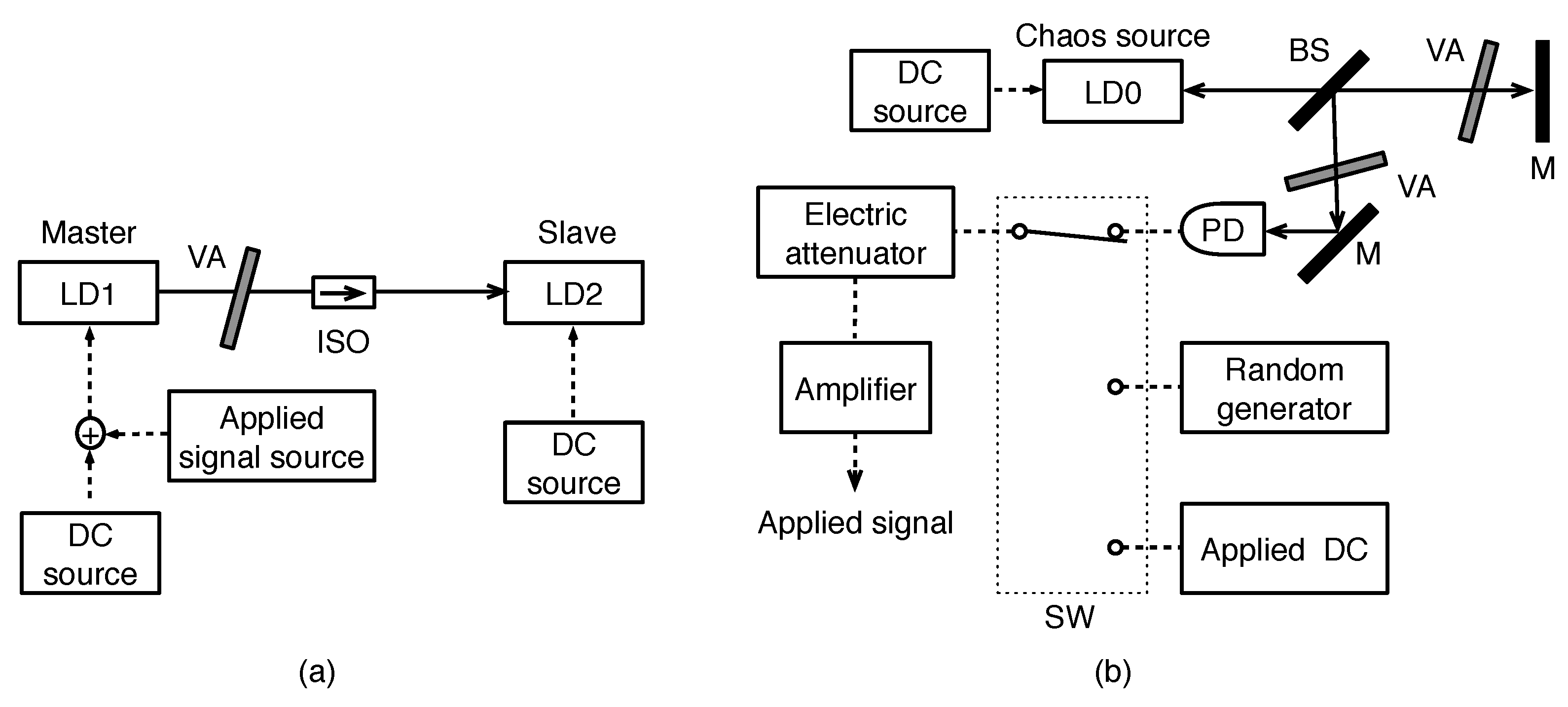
We consider the optical injection system consisting of two laser diodes (LDs), that is, a master LD (LD1) and a slave LD (LD2) in Figure 1a, which are driven by a DC source. The optical coupling from LD2 to LD1 is restricted by an optical isolator (ISO) and the coupling ratio is controlled by a variable attenuator (VA). An external signal is electronically applied to the drive current of LD1, which is generated by an external applied signal source, and the amplification of the applied signal is controlled by a variable electric attenuator and an amplifier. In the following sections, we consider three kinds of applied signals, that is, a chaotic signal, a pseudorandom signal and a DC. The applied pseudorandom signal, and applied DC are generated by a signal generator, and the chaotic signal is generated by an external chaos source LD (LD0) with optical feedback whose ratio is controlled by VA (Figure 1b). The chaotic signal is detected and converted into electric signal by a photo detector (PD). Since actual electric circuits have a frequency response and a cutoff frequency, impacts of the frequency band of the applied signal are needed to consider like Refs. [24,25]. In this work, we ignore the frequency response of the electric circuit to focus on the impacts of chaotic signal. The dynamics of LD0, LD1 and LD2 are described by the following rate equations [26,27]:

$$\begin{array}{cc}\hfill & \frac{\mathrm{d}{A}_1(t)}{\mathrm{d}t}=\frac{1}{2}{G}_N{n}_1(t)A_1(t),\hfill \end{array}$$

(1)

$$\begin{array}{cc}\hfill & \frac{\mathrm{d}{\varphi }_1(t)}{\mathrm{d}t}=\frac{1}{2}\alpha G_N{n}_1(t),\hfill \end{array}$$

(2)

$$\begin{array}{cc}\hfill & \frac{\mathrm{d}{n}_1(t)}{\mathrm{d}t}=[1+g·C(t)](p-1)J_{\mathrm{th}}-\gamma n_1(t)-[\Gamma +G_N{n}_1(t)]A_1^2(t),\hfill \end{array}$$

(3)

$$\begin{array}{cc}\hfill & \frac{\mathrm{d}{A}_2(t)}{\mathrm{d}t}=\frac{1}{2}{G}_N{n}_2(t)A_2(t)+{\kappa }_{\mathrm{inj}}{A}_1(t-{\tau }_{\mathrm{inj}})cos[\omega {\tau }_{\mathrm{inj}}+{\varphi }_2(t)-{\varphi }_1(t-{\tau }_{\mathrm{inj}})],\hfill \end{array}$$

(4)

$$\begin{array}{cc}\hfill & \frac{\mathrm{d}{\varphi }_2(t)}{\mathrm{d}t}=\frac{1}{2}\alpha G_N{n}_2(t)-{\kappa }_{\mathrm{inj}}\frac{A_1(t-{\tau }_{\mathrm{inj}})}{A_2(t)}sin[\omega {\tau }_{\mathrm{inj}}+{\varphi }_2(t)-{\varphi }_1(t-{\tau }_{\mathrm{inj}})],\hfill \end{array}$$

(5)

$$\begin{array}{cc}\hfill & \frac{\mathrm{d}{n}_2(t)}{\mathrm{d}t}=(p-1)J_{\mathrm{th}2}-\gamma n_2(t)-[\Gamma +G_N{n}_2(t)]A_2^2(t),\hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill & \frac{\mathrm{d}{A}_0(t)}{\mathrm{d}t}=\frac{1}{2}{G}_N{n}_0(t)A_0(t)+{\kappa }_{\mathrm{fb}}{A}_0(t-{\tau }_{\mathrm{fb}})cos[\omega {\tau }_{\mathrm{fb}}+{\varphi }_0(t)-{\varphi }_0(t-{\tau }_{\mathrm{fb}})],\hfill \end{array}$$

(7)

$$\begin{array}{cc}\hfill & \frac{\mathrm{d}{\varphi }_0(t)}{\mathrm{d}t}=\frac{1}{2}\alpha G_N{n}_0(t)-{\kappa }_{\mathrm{fb}}\frac{A_0(t-{\tau }_{\mathrm{fb}})}{A_0(t)}sin[\omega {\tau }_{\mathrm{fb}}+{\varphi }_0(t)-{\varphi }_0(t-{\tau }_{\mathrm{fb}})],\hfill \end{array}$$

(8)

$$\begin{array}{cc}\hfill & \frac{\mathrm{d}{n}_0(t)}{\mathrm{d}t}=(p-1)J_{\mathrm{th}}-\gamma n_0(t)-[\Gamma +G_N{n}_0(t)]A_0^2(t),\hfill \end{array}$$

(9)

where $A(t)$, $\varphi (t)$, and $n(t)$ are the amplitude, the phase of the laser field, and the carrier number above the value for the solitary LD, respectively. The subscripts 1, 2, and 0 denote LD1, LD2, and LD0, respectively. $G_N$ is the differential optical gain, $\alpha$ is the linewidth enhancement factor, $\gamma$ is the carrier decay rate, and $\Gamma$ is the cavity decay rate. The angular frequency of the solitary LD is described as $\omega =2\pi c/\lambda$, where c is the velocity of light and $\lambda$ is the wavelength. The drive current of the system without an applied signal is expressed as $p{J}_{\mathrm{th}}$.

Equations (1)–(3) describe the dynamics of LD1. The external signal is applied to ensure that the drive current of LD1 is above the threshold $[1+g·C(t)](p-1)J_{\mathrm{th}}$, where $A_0$ is the amplitude of LD0, g is the amplification coefficient, and $C(t)=a·A_0{(t)}^2$ represents the applied signal for LD1, which is normalized by the parameter a. Equations (4)–(6) describe the dynamics of LD2, which has the optical injection from LD1. The second terms on the right side of Equations (4) and (5) describe the optical injection from LD1 to LD2. $A_1(t-{\tau }_{\mathrm{inj}})$ and ${\varphi }_1(t-{\tau }_{\mathrm{inj}})$ are the amplitude and phase of the laser field injected into LD2 from LD1, respectively. Equations (7)–(9) describe the dynamics of LD0, which has the optical feedback. The second terms on the right side of Equations (7) and (9) describe the optical feedback for LD0. $A_0(t-{\tau }_{\mathrm{fb}})$ and ${\varphi }_0(t-{\tau }_{\mathrm{fb}})$ are the amplitude and phase of the laser field fed back from the external cavity to LD0, respectively. ${\tau }_{\mathrm{inj}}$ is the injection time from LD1 to LD2, and ${\tau }_{\mathrm{fb}}$ is the round-trip time of the external cavity for LD0. The injection and feedback coefficients are expressed as ${\kappa }_{\mathrm{inj}}=(1-r_0^2)r_{\mathrm{inj}}/r_0{\tau }_{\mathrm{in}}$ and ${\kappa }_{\mathrm{fb}}=(1-r_0^2)r_{\mathrm{fb}}/r_0{\tau }_{\mathrm{in}}$, respectively, where $r_{\mathrm{inj}}$ is the injection ratio of the output injected into LD2 to the output of LD1, $r_{\mathrm{fb}}$ is the feedback ratio of the output fed back from the external cavity to LD0, and ${\tau }_{\mathrm{in}}$ is the round-trip time in the inner cavity. In our simulation using the Runge–Kutta method, where the step size is $1\mathrm{ps}$, the following values are assigned to the parameters, which are taken from Ref. [26]: $G_N=2.142\times {10}^4[{\mathrm{s}}^{-1}]$, $\alpha =5.0$, $\lambda =635[\mathrm{nm}]$, $c=3.0\times {10}^8[\mathrm{m}/\mathrm{s}]$, $\gamma =0.909[{\mathrm{ns}}^{-1}]$, $\Gamma =0.357[{\mathrm{ps}}^{-1}]$, $r_0=0.556$, ${\tau }_{\mathrm{in}}=8.0[{\mathrm{ps}}^{-1}]$, $N_{\mathrm{sol}}=1.708\times {10}^8$, ${\tau }_{\mathrm{fb}}=5.0[\mathrm{ns}]$ and ${\tau }_{\mathrm{inj}}=5.0[\mathrm{ns}]$. The initial values $A(0)$ and $n(0)$ are the convergent values of the solitary LD, and $\varphi (0)=0$ is utilized. Then, the pseudorandom signal is generated by the Mersenne Twister random number generator [28] and Box–Muller transform [29].

In this study, the maximal Lyapunov exponent is estimated to quantify the orbital instability of the chaotic LD. We describe how to estimate the maximal Lyapunov exponent by linear stability analysis [30,31,32]. When we estimate the Lyapunov exponent of LD2, the small variations ${\delta }_{A2}(t)$, ${\delta }_{\varphi 2}(t)$ and ${\delta }_{n2}(t)$ of the dynamic variables of Equations (4)–(6) from the reference orbit, respectively written as $A_{s2}(t)$, $({\omega }_{s2}(t)-\omega )t$ and $n_{s2}(t)$, are considered. Since LD2 is the optical injection system, ${\delta }_{A2}(t)$, ${\delta }_{\varphi 2}(t)$, and ${\delta }_{n2}(t)$ for LD2 satisfy

$$\begin{array}{c}\hfill \left(\begin{array}{c}{\displaystyle \frac{\mathrm{d}{\delta }_{A2}(t)}{\mathrm{d}t}}\\ {\displaystyle \frac{\mathrm{d}{\delta }_{\varphi 2}(t)}{\mathrm{d}t}}\\ {\displaystyle \frac{\mathrm{d}{\delta }_{n2}(t)}{\mathrm{d}t}}\end{array}\right)=J_{\mathrm{inj}}\left(\begin{array}{c}{\delta }_{A2}(t)\\ {\delta }_{\varphi 2}(t)\\ {\delta }_{n2}(t)\end{array}\right).\end{array}$$

(10)

Here, $J_{\mathrm{inj}}$ is the Jacobian matrix of order $3\times 3$, and is given in the Appendix A. In this work, the time delay terms, $A_1(t-{\tau }_{\mathrm{inj}})$ and ${\varphi }_1(t-{\tau }_{\mathrm{inj}})$, are dealt with as external parameters since these parameters are not the dynamic variables of LD2 but those of LD1; in other words, the dynamics of LD2 is approximated using only three variables of LD2. On the other hand, when we estimate the Lyapunov exponent of LD0, since LD0 is the optical feedback system, the small variations ${\delta }_{A0}(t)$, ${\delta }_{\varphi 0}(t)$, ${\delta }_{n0}(t)$, $A_0(t-{\tau }_{\mathrm{fb}})$ and ${\varphi }_0(t-{\tau }_{\mathrm{fb}})$ of Equations (7)–(9) from the reference orbit, respectively written as $A_{s0}(t)$, $({\omega }_{s0}(t)-\omega )t$, $n_{s0}(t)$, $A_{s0}(t-{\tau }_{\mathrm{fb}})$ and $({\omega }_{s0}(t-{\tau }_{\mathrm{fb}})-\omega )(t-{\tau }_{\mathrm{fb}})$, are considered. Then, ${\delta }_{A0}(t)$, ${\delta }_{\varphi 0}(t)$, ${\delta }_{n0}(t)$, ${\delta }_{A0}(t-{\tau }_{\mathrm{fb}})$ and ${\delta }_{\varphi 0}(t-{\tau }_{\mathrm{fb}})$ satisfy

$$\begin{array}{c}\hfill \left(\begin{array}{c}{\displaystyle \frac{\mathrm{d}{\delta }_{A0}(t)}{\mathrm{d}t}}\\ {\displaystyle \frac{\mathrm{d}{\delta }_{\varphi 0}(t)}{\mathrm{d}t}}\\ {\displaystyle \frac{\mathrm{d}{\delta }_{n0}(t)}{\mathrm{d}t}}\end{array}\right)=J_{\mathrm{fb}}\left(\begin{array}{c}{\delta }_{A0}(t)\\ {\delta }_{\varphi 0}(t)\\ {\delta }_{n0}(t)\\ {\delta }_{A0}(t-{\tau }_{\mathrm{fb}})\\ {\delta }_{\varphi 0}(t-{\tau }_{\mathrm{fb}})\end{array}\right),\end{array}$$

(11)

where $J_{\mathrm{fb}}$ is the Jacobian matrix of order $3\times 5$, and is given in the Appendix A. These equations are calculated numerically using the Runge–Kutta method, where the step size is $1\mathrm{ps}$, and the norm $D_j=\sqrt{{\sum }_t\left({\delta }_{Ai}^2(t)+{\delta }_{\varphi i}^2(t)+{\delta }_{ni}^2(t)\right)}(i=0,2j=1,2,3,\cdots )$ is calculated by the method in Refs. [33,34]. The subscript j indicates the time section $[(j-1)\tau ,j\tau )$ and the term in the square root is the summation in the range of $[(j-1)\tau ,j\tau )$, where $\tau$ indicates the injection time ${\tau }_{\mathrm{inj}}$ for LD2 or the feedback time ${\tau }_{\mathrm{fb}}$ for LD0. Since the norm between the chaotic orbit and the reference orbit is gradually large and the local approximation can not be used, we initialize and replace the small variation ${\delta }_{Ai}(j\tau )$, ${\delta }_{\varphi i}(j\tau )$ and ${\delta }_{ni}(j\tau )$ with ${\delta }_{Ai}(j\tau )/D_j$, ${\delta }_{\varphi i}(j\tau )/D_j$ and ${\delta }_{ni}(j\tau )/D_j$, respectively, at intervals of $\tau$. The rate of increase in the norm is considered and the Lyapunov exponent is represented by

$${\lambda }_{\mathrm{LSA}}=\frac{1}{N\tau }\sum _{j=1}^{N}ln\frac{D_{j+1}}{D_j}.$$

(12)

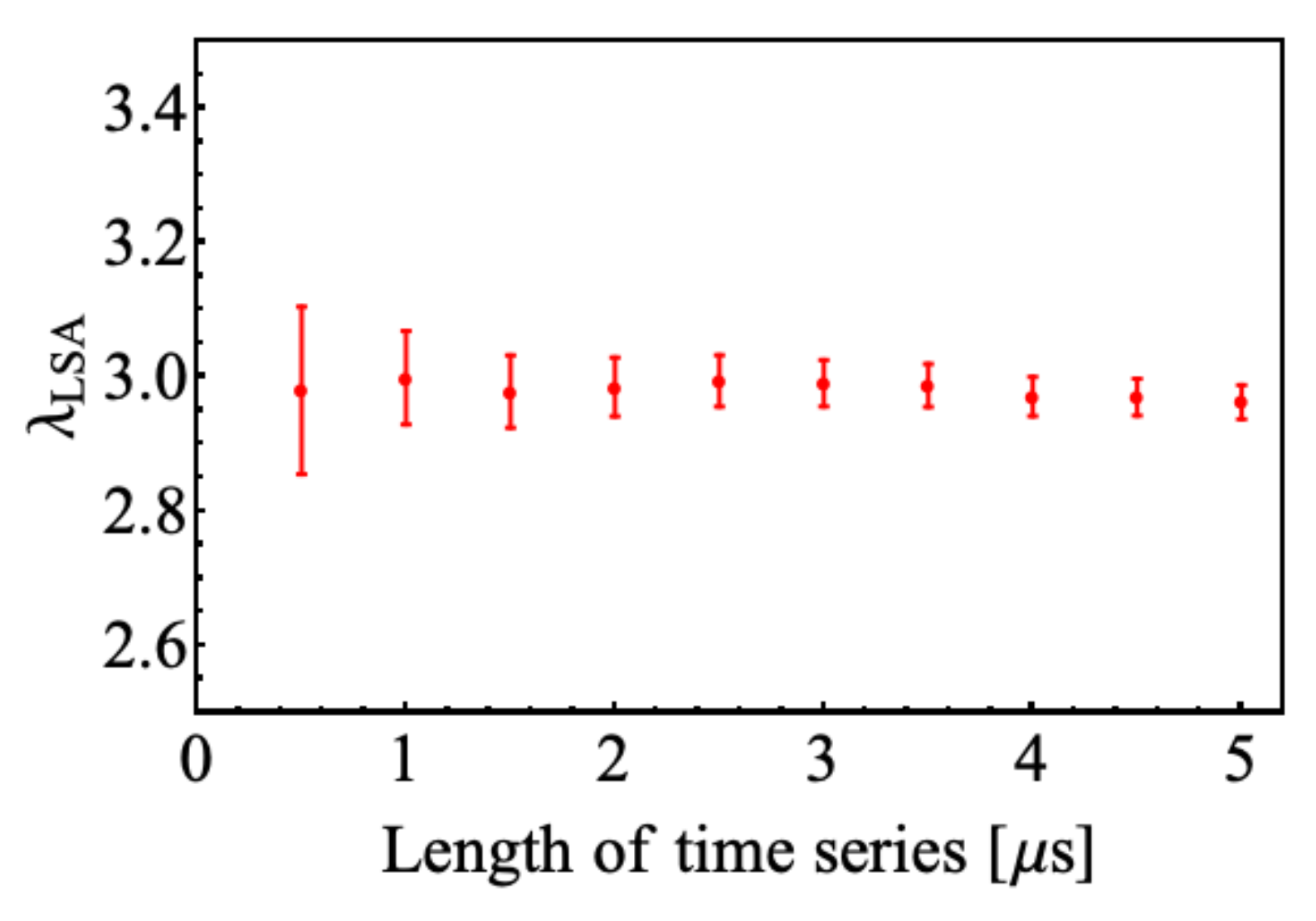
We use the discrete optical outputs $A_i(t)$, ${\varphi }_i(t)$ and $n_i(t)(i=0,1,2)$, which are sampled at intervals of 10 ps over 5 µs. Here, to show the robustness of ${\lambda }_{\mathrm{LSA}}$ against initial conditions, we investigate ${\lambda }_{\mathrm{LSA}}$ plotted against length of time series for the calculation of ${\lambda }_{\mathrm{LSA}}$. We consider the LD used in the figure of Section 3.2, which has the parameters $r_{\mathrm{inj}}=0.06$ and $r_{\mathrm{fb}}=0.10$ as a typical example, and show the mean of ${\lambda }_{\mathrm{LSA}}$ in Figure 2. The error bars represent the standard deviations. The number of this population is a thousand and the initial value of $A_2(t)$ are given randomly in the range of $[0.9\times A_2(0),1.1\times A_2(0)]$. As the length increases, ${\lambda }_{\mathrm{LSA}}$ converges and the standard deviation sufficiently becomes small; for example, the standard deviation for 5 µs is 0.025. In this work, we adopt 5 µs as the length of time series, and the results shown in the following figures are not means but values which are obtained by a single calculation. Then, in the following numerical simulations, some ${\lambda }_{\mathrm{LSA}}$ diverge when $A_2\to 0$ or $A_0\to 0$ and are not shown in the following figures.

3. Orbital Instability of Chaotic Laser Diode with Chaotic Applied Signal

3.1. Mean and Standard Deviation of Applied Signal

In this section, we investigate the orbital instability of LD2 by applying a chaotic signal to the drive current of LD1. The chaotic signal is normalized to a value of $[0,1]$ using the parameter a in Equation (3). The Lyapunov exponent ${\lambda }_{\mathrm{LSA}}$ is plotted against the optical injection ratio $r_{\mathrm{inj}}$ in Figure 3. In Figure 3a, the black circles and red squares indicate ${\lambda }_{\mathrm{LSA}}$ of LD2 without any applied signal and with an applied chaotic signal for $g=5.0$ and $r_{\mathrm{fb}}=0.05$, respectively. The mean and standard deviation of the applied chaotic signal are 0.113 and 0.080, respectively. The gray plots are the extrema of the intensity of LD2 without any applied signal, which shows the bifurcation diagram. When LD2 has no applied signal, for small $r_{\mathrm{inj}}$, LD2 oscillates stably or periodically and the corresponding ${\lambda }_{\mathrm{LSA}}$ is nonpositive. With increasing $r_{\mathrm{inj}}$, the intensity of LD2 has a large number of extrema and the dynamics are chaotic, with positive ${\lambda }_{\mathrm{LSA}}$. Then, a large window is observed between the chaotic states around $r_{\mathrm{inj}}\sim 0.10$ and small windows are observed for some other $r_{\mathrm{inj}}$, where LD2 oscillates periodically and the corresponding ${\lambda }_{\mathrm{LSA}}$ is nonpositive. However, chaotic dynamics appear upon applying a chaotic signal to the drive current of LD1, and ${\lambda }_{\mathrm{LSA}}>0$, as shown by the red squares in Figure 3a. This phenomenon is similar to that observed when by applying a pseudorandom signal in Ref. [24]. In addition, it seems that the red squares in Figure 3a shift slightly away from the black circles in the negative direction of $r_{\mathrm{inj}}$.

Next, we consider the applications of a pseudorandom signal with a mean of 0.113 and standard deviation of 0.080, which are the same values as those of the applied chaotic signal, and DC with $C(t)=0.113$. In Figure 3a, the blue diamonds and purple triangles indicate ${\lambda }_{\mathrm{LSA}}$ of LD2 with the pseudorandom signal and with the applied DC, respectively. Since the mean of the drive current increases by the applied signal for both plots, the chaotic dynamics of the injection system are enhanced and the plots are shifted away from the black circles in the negative direction of $r_{\mathrm{inj}}$. When the applied signal is a DC but not a pseudorandom signal, windows are observed.

In Figure 4, we confirm that the distribution of ${\lambda }_{\mathrm{LSA}}$ is shifted away from the intrinsic distribution in the negative direction of $r_{\mathrm{inj}}$ by applying a signal to the drive current of LD1, which is a DC and pseudorandom signal with a standard deviation of 0.10 in Figure 4a,b, respectively. The black circles, red squares, blue diamonds, and purple triangles indicate $\overline{g·C(t)}=0,0.10,0.50\mathrm{and}1.00$, respectively. The gray plots show the bifurcation diagram for the intrinsic system without the applied signal. With increasing applied signal, the shift of the plots increases. Thus, the orbital instability is sensitive to the mean of the applied signal for the DC or pseudorandom signal.

However, the orbital instability is not always sensitive to the mean of the applied signal for a chaotic signal. In Figure 3b, we show ${\lambda }_{\mathrm{LSA}}$ for the system with the chaotic applied signal of $r_{\mathrm{fb}}=0.20$, where the mean and standard deviation of the signal are 0.108 and 0.102, respectively. The black circles, red squares, blue diamonds, and purple triangles indicate the injection system without any applied signal, with the chaotic signal, with the pseudorandom signal with a mean of 0.108, and standard deviation of 0.102, and with DC with a mean of 0.108, respectively. The plots for the system with the applied pseudorandom signal and the applied DC are shifted away from the black circles in the negative direction of $r_{\mathrm{inj}}$. Since the mean of the applied signal is larger than that in Figure 3a, the shift of the plots is larger. On the other hand, when the chaotic signal is applied, the plots are shifted away from the black circles in the positive direction of $r_{\mathrm{inj}}$. Therefore, it is considered that the factor contributing to the enhanced orbital instability is not the mean or standard deviation but another factor.

3.2. Optical Feedback Ratio and Optical Injection Ratio

Here, to consider the effect of the applied chaotic signal, we show the orbital instability of the system with the applied chaotic signal as a function of the optical feedback ratio $r_{\mathrm{fb}}$ of LD0 and the optical injection ratio $r_{\mathrm{inj}}$ from LD1 to LD2. Figure 5 shows ${\lambda }_{\mathrm{LSA}}$ plotted against $r_{\mathrm{fb}}$ and $r_{\mathrm{inj}}$. According to the previous discussion, the mean of the applied signal may contribute to the orbital instability of LD2. Thus, all the applied signals in this subsection are normalized by the parameter a in Equation (3), and the mean of the applied signal is fixed as $\overline{g·C(t)}=0.5\mathrm{and}5.0$, shown in Figure 5a,b, respectively. When the amplitude of the applied chaotic signal is small, $r_{\mathrm{fb}}$ makes a small contribution to ${\lambda }_{\mathrm{LSA}}$ for small $r_{\mathrm{inj}}$ (Figure 5a). With increasing $r_{\mathrm{inj}}$, when $r_{\mathrm{fb}}$ is large, ${\lambda }_{\mathrm{LSA}}$ increases gradually. For larger $r_{\mathrm{fb}}$, ${\lambda }_{\mathrm{LSA}}$ has a peak around $r_{\mathrm{inj}}\sim 0.14$. On the other hand, when the amplitude of the applied chaotic signal is large, $r_{\mathrm{fb}}$ makes a larger contribution to ${\lambda }_{\mathrm{LSA}}$ (Figure 5b) than that in Figure 5a. The window around $r_{\mathrm{inj}}\sim 0.10$, which is observed in the inherent system without the applied signal, is not observed, the peak around $r_{\mathrm{inj}}\sim 0.05$ is shifted in the positive direction of $r_{\mathrm{inj}}$ and the peak around $r_{\mathrm{inj}}\sim 0.14$ gradually becomes large.

Figure 5c shows the maximal value of ${\lambda }_{\mathrm{LSA}}$ in the range of $0<r_{\mathrm{inj}}\le 0.20$ and the corresponding optical injection ratio $r_{\mathrm{inj}}^{\prime }$ plotted against $r_{\mathrm{fb}}$ for $\overline{g·C(t)}=0.5$. When $r_{\mathrm{fb}}\le 0.04$, ${\lambda }_{\mathrm{LSA}}$ has the maximal value at $r_{\mathrm{inj}}^{\prime }\sim 0.058$. On the other hand, when $r_{\mathrm{fb}}\ge 0.04$, ${\lambda }_{\mathrm{LSA}}$ depends on $r_{\mathrm{fb}}$, and $0.10\le r_{\mathrm{inj}}^{\prime }\le 0.15$, where the window is observed in the inherent system without the applied signal. Similarly, we shows the maximal value of ${\lambda }_{\mathrm{LSA}}$ in the range of $0<r_{\mathrm{inj}}\le 0.20$ and the corresponding optical injection ratio $r_{\mathrm{inj}}^{\prime }$ plotted against $r_{\mathrm{fb}}$ for $\overline{g·C(t)}=5.0$. When $r_{\mathrm{fb}}\le 0.03$, ${\lambda }_{\mathrm{LSA}}$ has the maximal value at $r_{\mathrm{inj}}^{\prime }\sim 0.037$. Then, the maximal value of ${\lambda }_{\mathrm{LSA}}$ depends on $r_{\mathrm{fb}}$. Since the maximal value of ${\lambda }_{\mathrm{LSA}}$ gradually increases and saturates with increasing $r_{\mathrm{fb}}$, it is controlled by $r_{\mathrm{fb}}$ of the applied chaotic signal. In the next section, we discuss some quantities of the applied signal to study the conditions of the applied signal that cause large orbital instability of LD2.

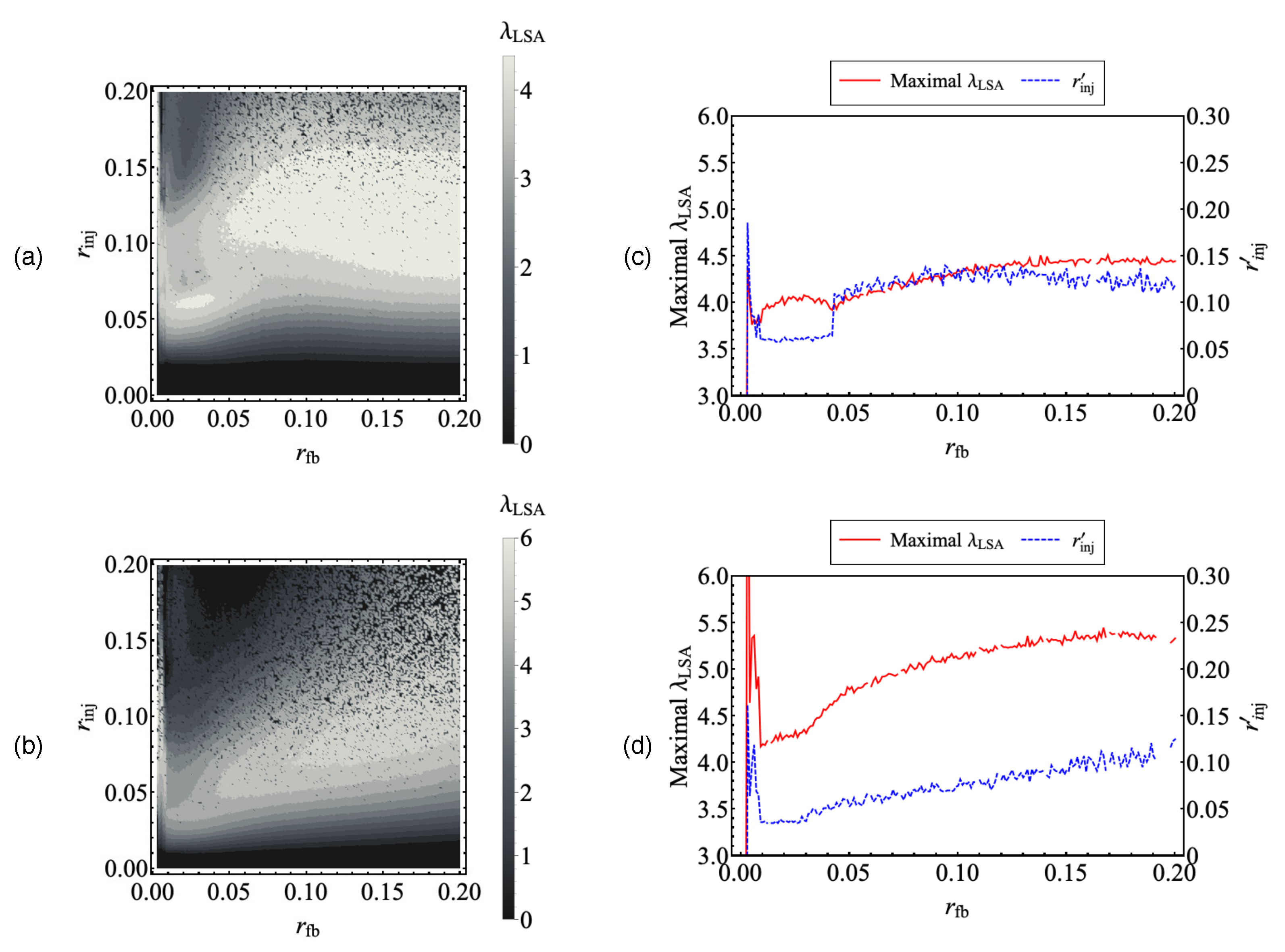
4. Orbital Instability against Statistical and Dynamical Quantities of Applied Signal

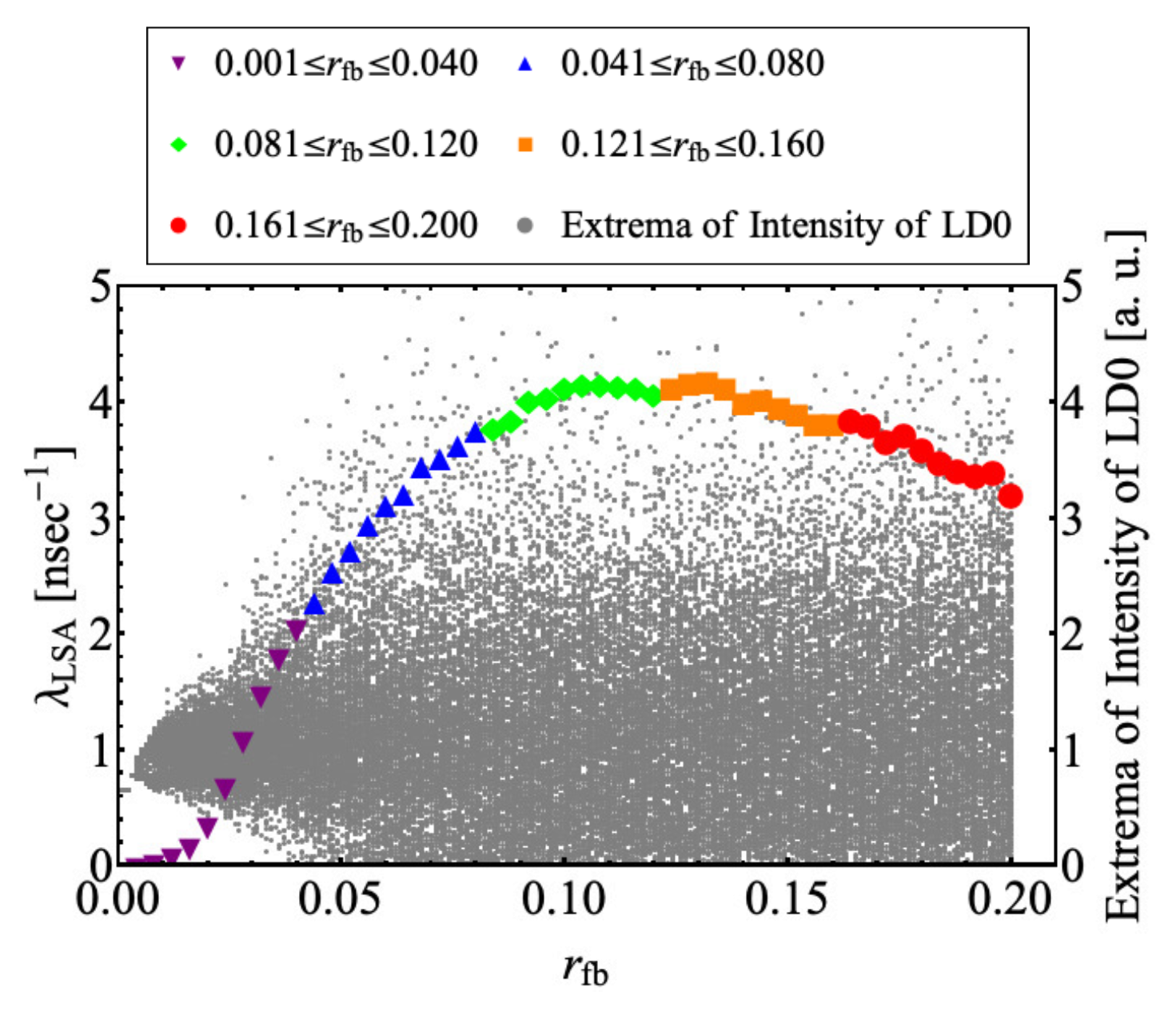
First, we study the applied chaotic signal, which is generated by LD0 with optical feedback. Figure 6 shows the extrema of the intensity of LD0 and the Lyapunov exponent ${\lambda }_{\mathrm{LSA}}$ plotted against the optical feedback ratio $r_{\mathrm{fb}}$. Different symbols are used for different ranges of $r_{\mathrm{fb}}$, that is, purple down-pointing triangles, blue up-pointing triangles, green diamonds, orange squares, and red circles indicate ${\lambda }_{\mathrm{LSA}}$ for $0<r_{\mathrm{fb}}\le 0.040$, $0.040<r_{\mathrm{fb}}\le 0.080$, $0.080<r_{\mathrm{fb}}\le 0.120$, $0.120<r_{\mathrm{fb}}\le 0.160$ and $0.160<r_{\mathrm{fb}}\le 0.200$, respectively. In the range of $0<r_{\mathrm{fb}}\le 0.040$, the fluctuation of the intensity is small and ${\lambda }_{\mathrm{LSA}}$ is small. With increasing $r_{\mathrm{fb}}$, ${\lambda }_{\mathrm{LSA}}$ inceases for $0.040<r_{\mathrm{fb}}\le 0.120$ and gradually decreases for $0.120<r_{\mathrm{fb}}$.

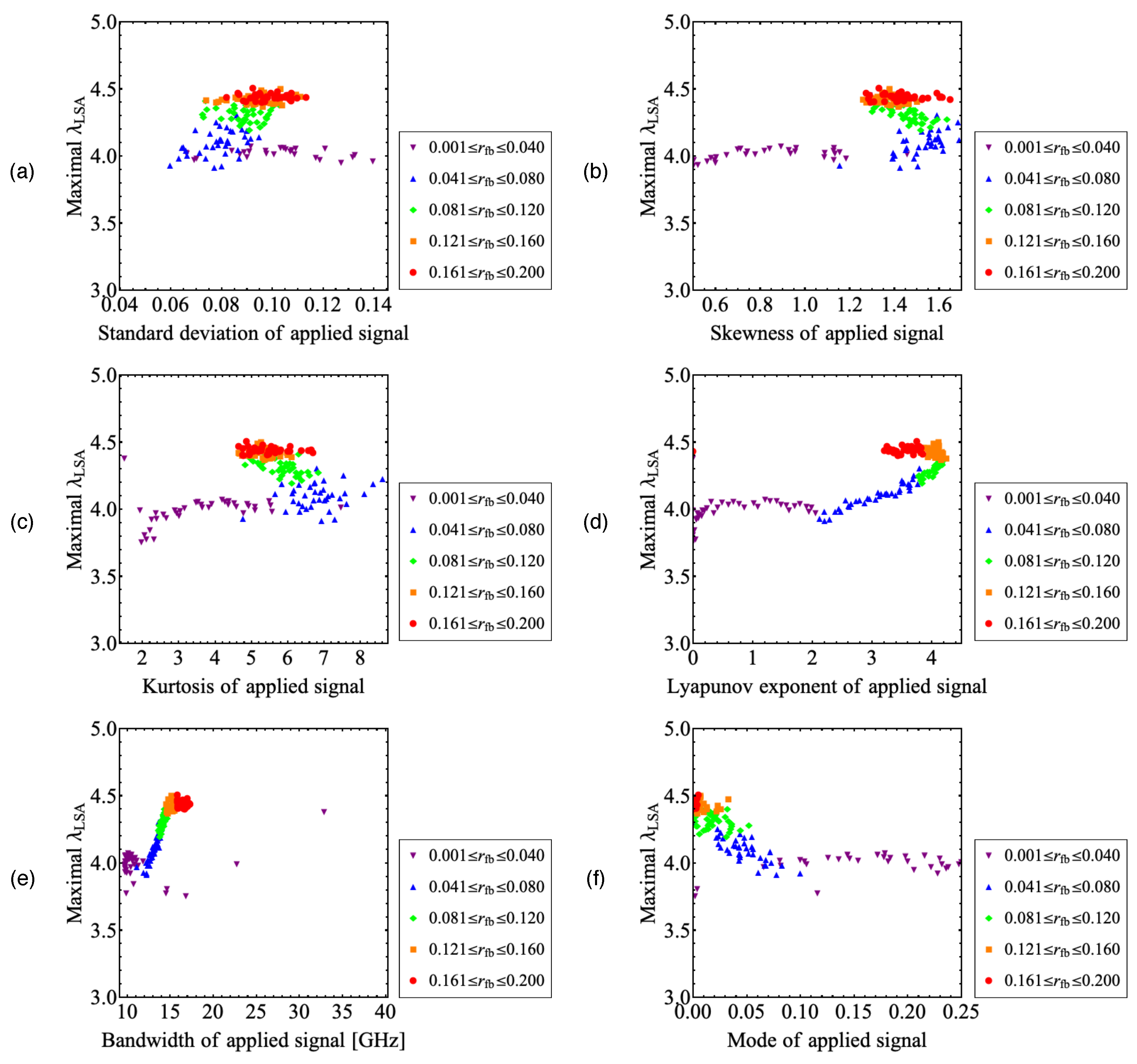
Next, we study the orbital instability of LD2 with the applied chaotic signal for statistical and dynamical quantities of the applied chaotic signal to show the characteristics of the applied chaotic signal that can control the orbital instability of LD2. The maximal values of ${\lambda }_{\mathrm{LSA}}$ of LD2 in the range of $0<r_{\mathrm{inj}}\le 0.20$ for certain $r_{\mathrm{fb}}$ of LD0 are calculated and plotted against the standard deviation, skewness, kurtosis, Lyapunov exponent, bandwidth, and mode of the histogram of LD0 in Figure 7. The symbols correspond to those in Figure 6. In the range where the orbital instability of the applied signal is small ($0<r_{\mathrm{fb}}\le 0.040$), the maximal value of ${\lambda }_{\mathrm{LSA}}$ does not vary with $r_{\mathrm{fb}}$ (purple down-pointing triangles in Figure 7). We then consider the range of $0.040<r_{\mathrm{fb}}\le 0.200$ where the orbital instability of the applied chaotic signal is sufficiently large. The correlation between the maximal value of ${\lambda }_{\mathrm{LSA}}$ and the standard deviation of the applied signal is low in Figure 7a. On the other hand, in Figure 7b–d, the maximal value of ${\lambda }_{\mathrm{LSA}}$ is nonlinear with the skewness, kurtosis, and Lyapunov exponent of the applied signal in the range of $0.040<r_{\mathrm{fb}}\le 0.200$, respectively. The plots for $0.040<r_{\mathrm{fb}}\le 0.160$ and $0.160<r_{\mathrm{fb}}\le 0.200$ have different gradients: thus, it is difficult to identify ${\lambda }_{\mathrm{LSA}}$ from the statistical quantities. However, in Figure 7e–f, the maximal value of ${\lambda }_{\mathrm{LSA}}$ is linear to the bandwidth and mode of the histogram of the applied signal in the range of $0.040<r_{\mathrm{fb}}\le 0.200$. Therefore, we can identify ${\lambda }_{\mathrm{LSA}}$ from these quantities. Since the large bandwidth and small mode of the histogram of the applied signal contribute to the large Lyapunov exponent, the orbital instability of LD2 can be enhanced by applying a chaotic pulsation having a broad bandwidth.

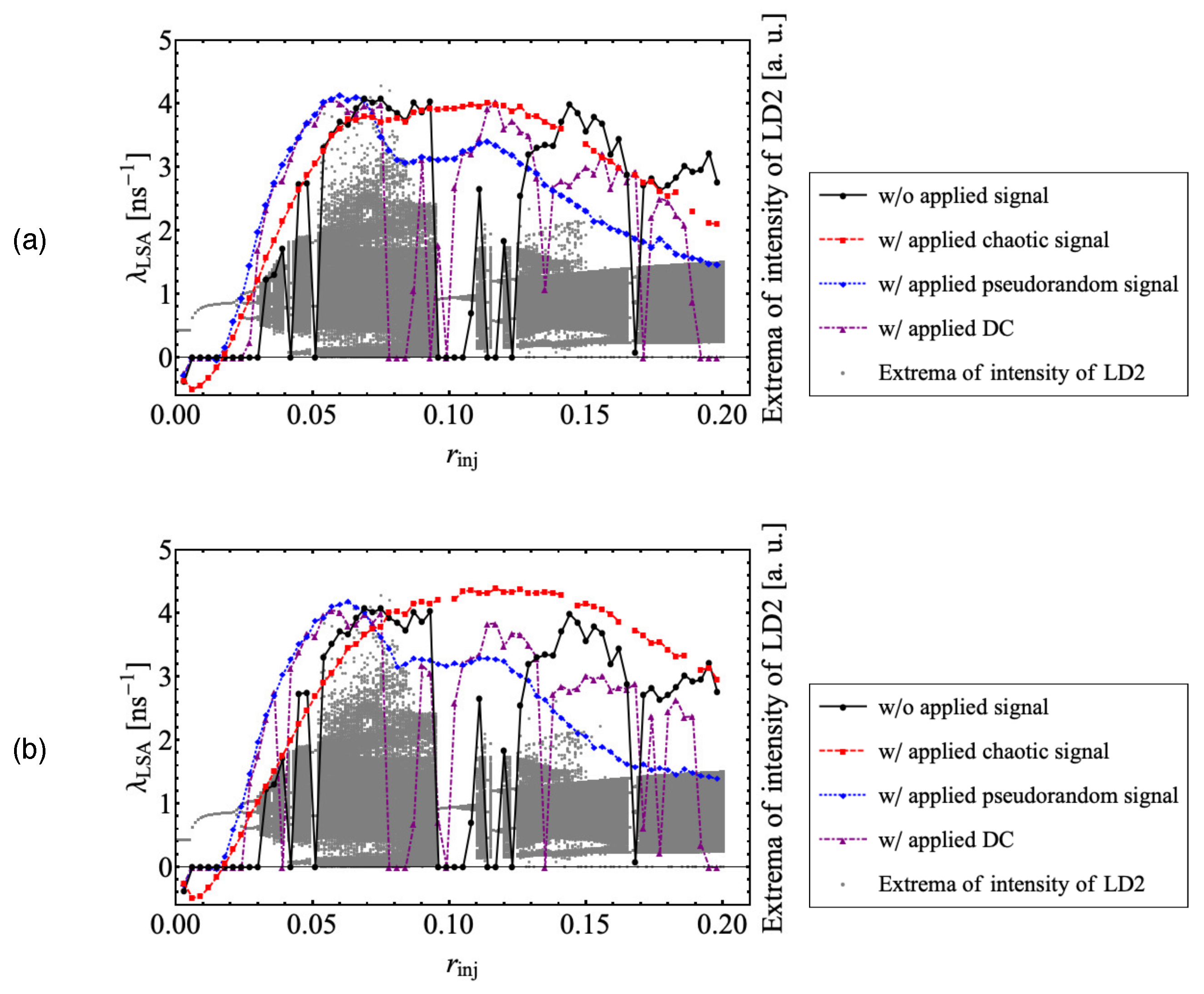
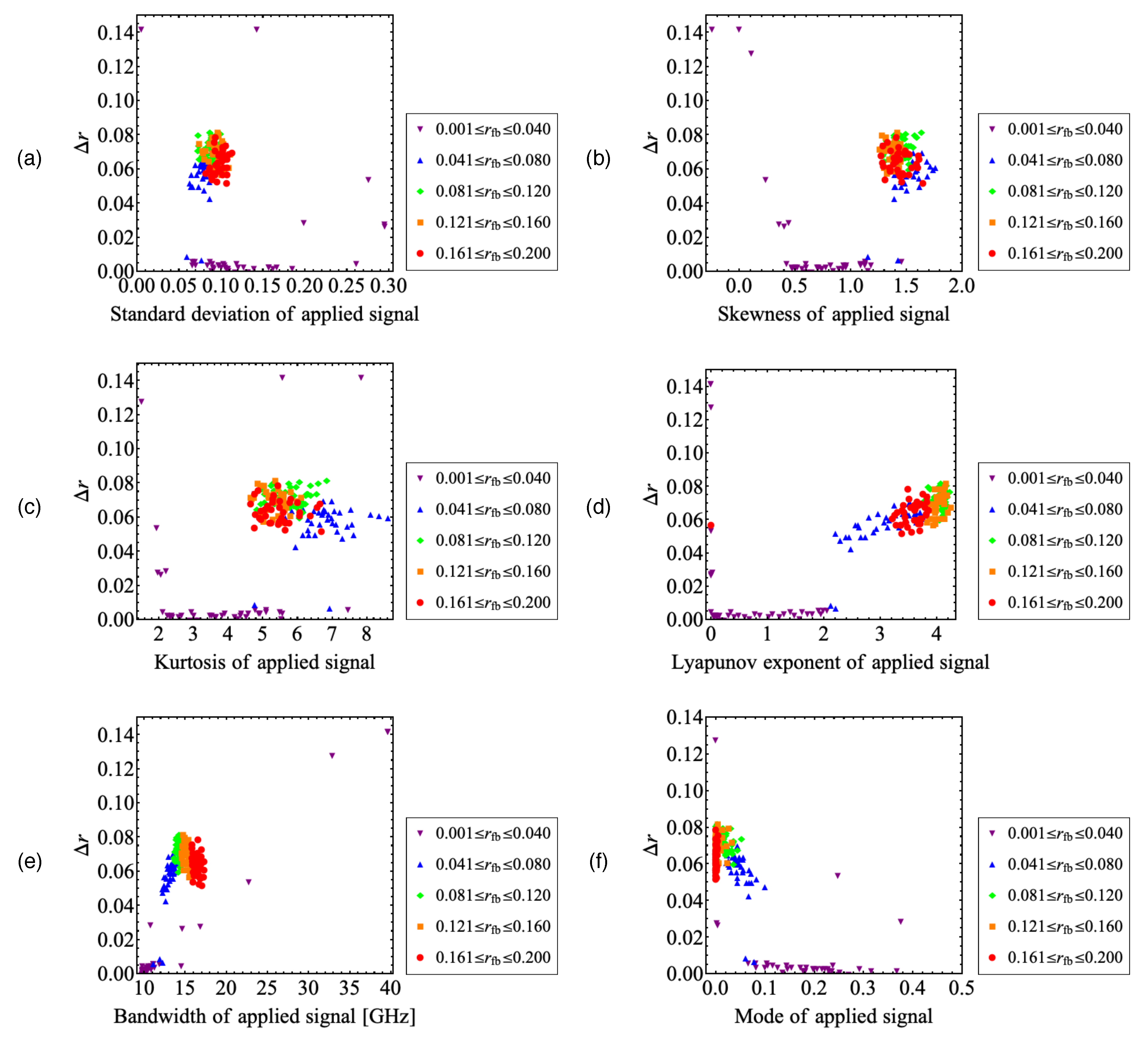
Next, we discuss the shift of the maximal value of ${\lambda }_{\mathrm{LSA}}$ upon applying the chaotic signal in Figure 5. We consider the optical injection ratio $r_{\mathrm{inj}0}^{\prime }$, which is $r_{\mathrm{inj}}^{\prime }$ for the inherent system without the applied signal, and introduce the difference $\Delta r=r_{\mathrm{inj}}^{\prime }-r_{\mathrm{inj}0}^{\prime }$. Figure 8 shows $\Delta r$ plotted against statistical and dynamical quantities of the applied chaotic signal, that is, the standard deviation, skewness, kurtosis, Lyapunov exponent, bandwidth, and mode of the histogram of LD0 as in Figure 7. In the range where the orbital instability of the applied signal is small ($0<r_{\mathrm{fb}}\le 0.040$), $\Delta r$ is small for most plots. However, in the range of $0<r_{\mathrm{fb}}\le 0.010$, the orbital instability of LD2 is reduced since LD0 oscillates periodically or quasi-periodically. Since an additional optical injection is needed to obtain similar orbital instability, $\Delta r$ becomes large. In the range of $0.040<r_{\mathrm{fb}}\le 0.160$, the orbital instability of LD2 is enhanced in the range of $0.09⪅r_{\mathrm{inj}}⪅0.13$, where a window can be observed in the inherent system, and the plots are concentrated around $\Delta r\sim 0.07$.

The correlation between $\Delta r$ and the standard deviation, skewness and kurtosis of the applied signal is low in Figure 8a–c, respectively. In Figure 8e,f, $\Delta r$ is nonlinear to the bandwidth and mode of the histogram of the applied signal in the range of $0.040<r_{\mathrm{fb}}\le 0.200$, respectively. The plots for $0.040<r_{\mathrm{fb}}\le 0.160$ and $0.160<r_{\mathrm{fb}}\le 0.200$ have different gradients. On the other hand, $\Delta r$ seems to depend on the Lyapunov exponent of the applied signal in the range of $0.040<r_{\mathrm{fb}}\le 0.200$ (Figure 8d).

Finally, we discuss the chaos synchronization between LDs. For example, we assume the application of the present system to chaotic secure communication that is a digital scheme by using a difference of the orbital instability of chaotic LD [18]. The scheme is hardware-dependent, where the key to communication is based on the parameter of the LD system. LD1 and LD2 act as the transmitter and receiver LDs, respectively. Then, LD0 is the driver used to control the dynamics of LD1 and the message is modulated by LD0 and applied to LD1. The orbital instability of LD2 is controlled by LD0 through LD1 and corresponds to the digit. The proper receiver quantifies from only the optical intensity of LD2 at a certain interval, for example, using the method in Ref. [32], and compares the quantified orbital instability with the predetermined threshold to decide the digit. Since the dynamics of LD2 are decided by the parameters of three LDs, it is difficult for eavesdroppers to decode the digit with only the transmitting signal. However, if LD2 synchronizes with the other LDs, the eavesdropper can estimate the digit from the transmitting signal. Thus, we investigate the chaos synchronization between LD2 and the other LDs. In Figure 9, we calculate the correlation coefficient between the LDs plotted against $r_{\mathrm{fb}}$ and $r_{\mathrm{inj}}$ to quantify the chaos synchronization. Figure 9a,b show the correlation coefficients between LD0 and LD2 and between LD1 and LD2, respectively. The correlation coefficient is expressed as

$$\begin{array}{c}\hfill {\rho }_{i2}=\underset{\Delta t}{max}\frac{〈(I_i(t)-\langle I_i\rangle )(I_2(t+\Delta t)-\langle I_2\rangle )〉}{\sqrt{〈{(I_i(t)-\langle I_i\rangle )}^2〉〈{(I_2(t+\Delta t)-\langle I_2\rangle )}^2〉}},\end{array}$$

(13)

where $I_i$ and $I_2$ indicate the optical outputs of LDi ($i=0,1$) and LD2, respectively, and $\langle ·\rangle$ indicates the ensemble average. The roundtrip time of the external cavity ${\tau }_{\mathrm{fb}}$ and the trip time of the injection light from LD1 to LD2 ${\tau }_{\mathrm{inj}}$, have the same value, and the correlation coefficient is calculated in the range $-10{\tau }_{\mathrm{fb}}\le \Delta t\le 10{\tau }_{\mathrm{fb}}$. Figure 9c,d show the maximal value of ${\rho }_{02}$ and ${\rho }_{12}$ in the range of $0<r_{\mathrm{inj}}\le 0.20$ and the corresponding optical injection ratio $r_{\mathrm{inj}}^{″}$ plotted against $r_{\mathrm{fb}}$. In Figure 9a,c, the correlation coefficient ${\rho }_{02}$ between LD0 and LD2 is small in the entire range and the maximum is 0.11, showing that LD2 does not synchronize with LD0. On the other hand, as shown in Figure 9b,d, the correlation coefficient ${\rho }_{12}$ between LD1 and LD2 is larger than that in Figure 9a. For all $r_{\mathrm{fb}}$, the correlation coefficient is small in the range of $r_{\mathrm{inj}}\le 0.05$. With increasing $r_{\mathrm{inj}}$, the correlation coefficient becomes larger since the orbital instability of LD2 is enhanced ($r_{\mathrm{inj}}\sim 0.05$). With further increase of $r_{\mathrm{inj}}$, the correlation coefficient becomes small again in the range of $r_{\mathrm{inj}}\ge 0.10$, where a window can be observed in the inherent system. Since the maximal correlation coefficient between LD1 and LD2 is 0.40, chaos synchronization between LD1 and LD2 is not achieved. Therefore, it is concluded that the orbital instability of LD2 can be controlled by varying the parameters of LD0, which generates the applied chaotic signal, without chaos synchronization between the LDs.

5. Conclusions

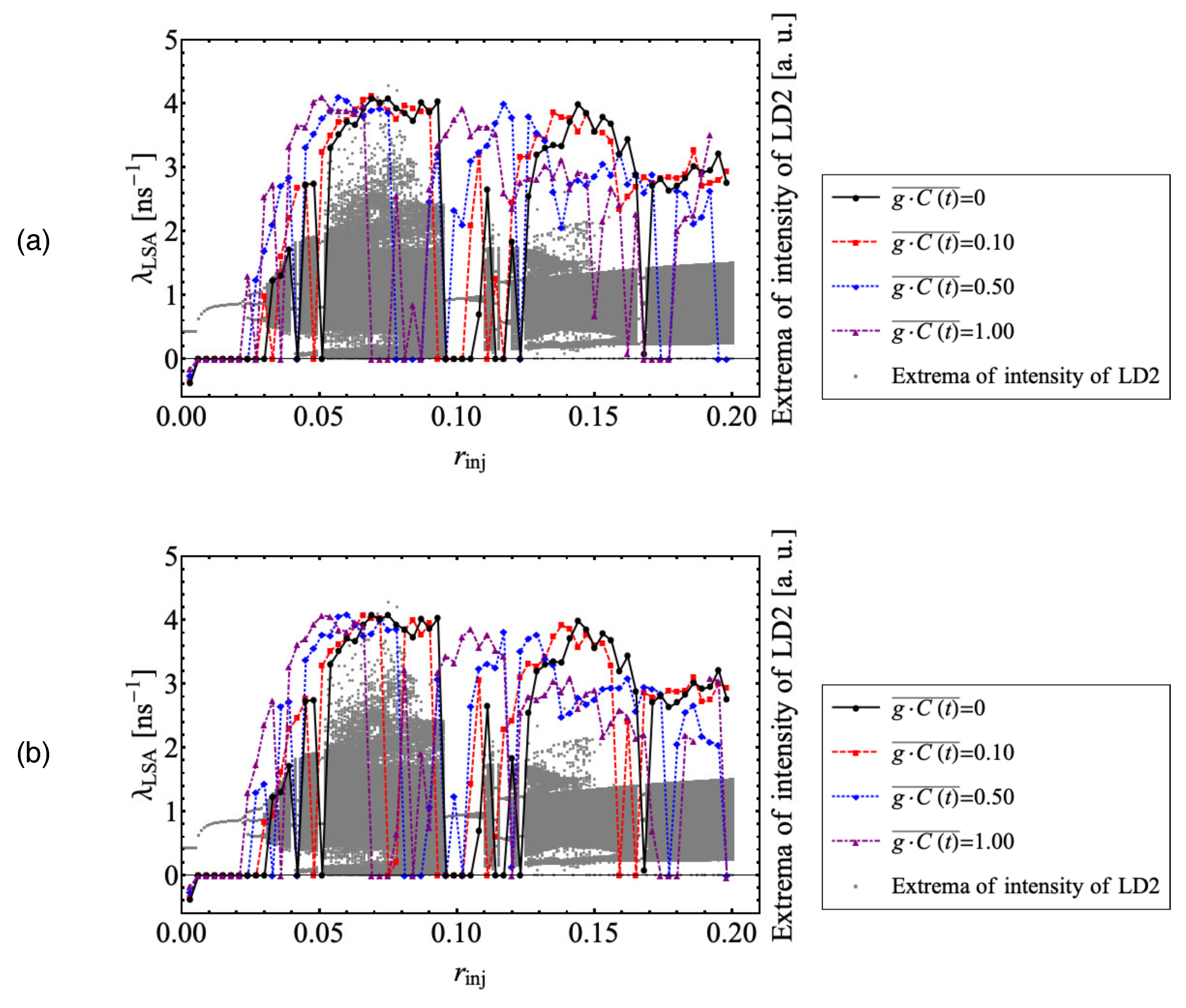
We numerically studied the orbital instability of a chaotic laser diode (LD) system with optical injection, which consists of the master LD (LD1) and slave LD (LD2). The drive current of LD1 is modulated by the chaotic applied signal, which is generated by LD0 with optical feedback. First, we showed that chaotic behavior in the window is actualized by applying the chaotic signal as well as a pseudorandom signal. The optical injection ratio required to oscillate LD2 chaotically is decreased by applying the pseudorandom signal or DC but increased by applying the chaotic signal.

Next, we investigated the maximal value of the Lyapunov exponent of LD2 in the range of $0<r_{\mathrm{inj}}\le 0.20$ as a function of the optical feedback ratio of LD0 and the optical injection ratio from LD1 to LD2. When the amplitude of the applied chaotic signal is sufficiently large and the inherent system without the applied chaotic signal is in the window, the Lyapunov exponent of LD2 can be controlled by varying the optical feedback ratio of LD0.

Then, we discussed the effect of statistical and dynamical quantities of the applied chaotic signal on the orbital instability of LD2. The bandwidth and mode of the histogram of the applied chaotic signal are linear to the maximal value of the Lyapunov exponent of LD2. It was shown that the orbital instability of LD2 can be enhanced efficiently by applying a chaotic pulsation having a broad bandwidth.

Finally, we investigate the chaos synchronization between LDs. The LDs do not synchronize with each other. It was shown that the orbital instability of the chaotic LD can be controlled without chaos synchronization. Since it is difficult to estimate the dynamics of LD0 from the optical intensity of LD1, the characteristics is useful to the application of chaotic LD like a secure communication.