An 850 nm Grating Coupler on Thin-Film Lithium Niobate Enabled by Topological Unidirectional Guided Resonance

Abstract

The inherently high-voltage-length product (V_πL) of thin-film lithium niobate (TFLN) modulators in the O-, C-, and L-telecom bands restricts further scaling of photonic integrated circuits’ bandwidth density, driving their migration toward shorter operating wavelengths. Nevertheless, the corresponding grating couplers, as critical optical input/outputs (optical I/Os) interfaces, remain largely undeveloped. Here, we demonstrate an 850 nm TFLN grating coupler designed based on topological unidirectional guided resonance (UGR). By breaking C₂ symmetry of the unit cell and precisely tailoring its geometry, we achieve unidirectional upward radiation with a 63.7 dB up/down intensity ratio. Subsequent apodization of groove widths and periods enables precise control of the electrical field distribution in both real and momentum spaces. This yields a vertical-cavity surface-emitting laser (VCSEL)-matched, highly fabrication-tolerant TFLN grating coupler that attains, to the best of our knowledge, the highest simulated coupling efficiency of −0.6 dB without mirrors or hybrid materials. This work delivers a high-efficiency, layout-flexible, and complementary metal oxide semiconductor (CMOS)-compatible optical I/Os solution for short-wavelength TFLN modulators with low V_πL. It offers substantial engineering value and broad applicability for on-chip light source integration and high-bandwidth-density short-reach optical interconnects.

1. Introduction

The training of ultra-large-scale models relies heavily on frequent data communications among chips within computing clusters. Establishing chip-to-chip interconnects with high bandwidths and low latency via optical interconnection is a critical pathway to scaling node capacity and achieving substantial gains in cluster computational efficiency [1,2,3,4,5]. Among various photonic integration platforms for optical interconnects, thin-film lithium niobate (TFLN) exhibits tremendous application potential due to its outstanding mechanical stability, broad transparency window, and superior electro-optic properties [6,7,8,9]. Grating couplers offer a layout-flexible, highly alignment-tolerant optical I/O approach that enable efficient light coupling between TFLN photonic waveguides and out-of-plane light sources/detectors [10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28]. Previously, extensive efforts have been devoted to enhancing the coupling efficiency (CE) of TFLN grating couplers in the O-, C-, and L-telecom bands. Approaches include introducing hybrid materials [29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45], incorporating mirrors [46,47,48,49,50,51,52,53,54], designing T-shaped gratings [45], or etching the buried oxide layer (BOX) [55] to improve upward radiation directionality. Based on these strategies, several studies have achieved sub-dB CE [29,46,47,48,49], with the highest reported simulated CE reaching −0.52 dB [48].

However, it should be noted that although long wavelengths exhibit lower losses than short wavelengths in long-reach communication scenarios, the inherently high V_πL of the corresponding TFLN modulators inevitably results in excessively large device footprints, thereby constraining the achievable bandwidth density in photonic integrated circuits [9]. Several studies have demonstrated that operating in shorter wavelengths can substantially suppress the V_πL [56,57,58,59,60,61,62,63]. This reduction originates from two fundamental effects: the increased wave vector, which enhances phase accumulation for a given interaction length, and the diminished optical mode profile, which permits narrower electrode gaps and, consequently, stronger field confinement [57,61]. The short-wavelength TFLN modulators featuring low-V_πL provide a high-bandwidth-density solution for short-reach optical interconnects within data centers (chip-to-chip, etc.). From the perspective of on-chip light source integration (VCSEL, etc.), this motivates application scenarios for short-wavelength TFLN grating couplers [64,65,66,67,68]. Nonetheless, investigations addressing such couplers are sparse and reported CEs remain low [11,14]. Consequently, substantial and rigorous investigations in this area are imperative. Compared with conventional solutions based on hybrid materials or mirrors, the unidirectional guided-resonance (UGR) principle, revealed from a radiative topology view, is more favorable for designing short-wavelength TFLN grating couplers that combine high CE with CMOS process compatibility. Studies show that breaking the grating C₂ symmetry or the up-down mirror symmetry can induce the merger of a pair of half-integer topological charges on one side of the grating while they remain separated on the other side, thereby yielding unidirectional radiation [69,70,71,72].

In this work, we present a dual-trapezoidal unit cell design founded on the UGR principle. Through systematic geometric refinement, we achieve precise control of the grating coupler’s real and momentum space electrical field distribution, resulting in an 850 nm, VCSEL-matched TFLN grating coupler that attains, to the best of our knowledge, the highest simulated CE of −0.6 dB without the use of mirrors or hybrid materials. This approach furnishes an effective solution for on-chip, light-source-integrated, short-reach optical interconnects that demand high bandwidth, low energy consumption, CMOS-compatible, and compact TFLN photonic integration circuits.

2. Device Structure and Design Methodology of the Unidirectional Radiation Grating Coupler

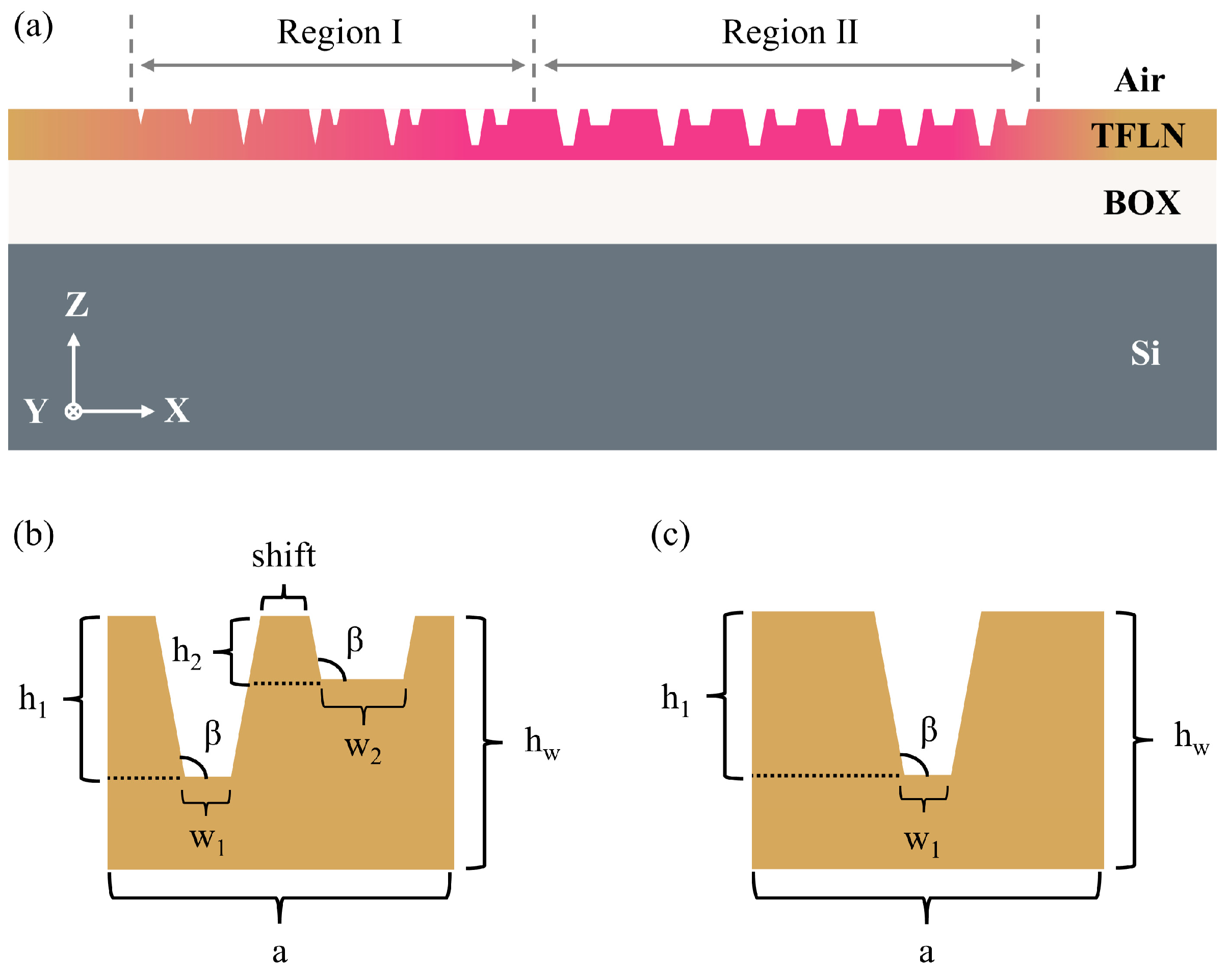
It has been reported that the conditions for realizing UGR—whether via breaking up-down mirror symmetry or C₂ symmetry—can be fulfilled within the two-dimensional parameter space defined by k_x and structural parameters (with k_y = 0) [69,70]. Accordingly, herein we adopt commercially manufacturable thin-film lithium niobate on insulator (LNOI) wafer parameters to propose a one-dimensional periodic grating coupler featuring air/TFLN (refractive index 2.17)/BOX (thickness 2 μm)/Si substrate, as shown in Figure 1a. A series of dual-trapezoidal gratings are defined in the TFLN layer. As illustrated in Figure 1b, the TFLN layer features a thickness of $h_w$ = 350 nm. The unit cell, with period $a$, comprises two grooves separated by a lateral offset “shift”, and the widths and depths of the grooves are denoted as $w_1$, $h_1$ and $w_2$, $h_2$, respectively. Considering the practical etching constraints of TFLN, the sidewall angle $\beta$ of the grooves is fixed at 97° [73].

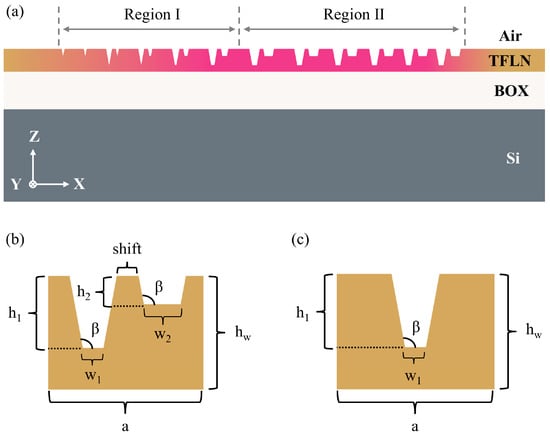
Figure 1. (a) Schematic of the unidirectional radiation grating coupler. Region I: unit cells with simultaneous variation of groove width and period. Region II: unit cells with period variation only. (b) Unit cell with C₂ asymmetry. (c) Unit cell with C₂ symmetry.

In this work, we exploit the integer topological charges carried by the bound state in the continuum (BIC) at the Brillouin-zone center—protected by C₂-symmetry—as the origin of half-integer topological charges [72,74]. By continuously varying the unit cell geometry, we control the splitting of the integer charges in momentum space and the subsequent evolution of the emergent half-integer charges, thereby realizing UGR (numerical simulation by COMSOL Multiphysics 6.2). All simulations in COMSOL were performed within the Radio Frequency Module under frequency domain analysis. The photonic band structure and quality factors were obtained using the eigenvalue solver. The asymmetry ratio was determined by employing two boundary probes positioned above and below the structure. To realize a grating coupler with low back-scatterings and a prescribed electrical field distribution, we arrayed UGR-enabled unit cells by chirping the groove widths and radiation angles to tailor their local radiative properties. Furthermore, invoking the phase-matching principle [75], the unit cell periods were varied according to the equation given below so that all unit cells radiate at the same wavelength into the specified angle with an isophase surface (numerical simulation by Lumerical, Finite-Difference Time-Domain (FDTD)). In the Lumerical FDTD simulations, a mode source is positioned on the left side of the waveguide to excite the grating coupler. The simulation domain is enclosed by perfectly matched layers (PML) on all boundaries. Four frequency-domain field and power monitors are employed to extract the upward radiation power (as well as the spatial/angular distribution), downward leakage power, back-reflection power, and tail-loss power, respectively. These monitors are positioned 2 μm above the grating coupler, 2 μm below it, 12 μm to the left, and 9 μm to the right.

$$a={\displaystyle \frac{\lambda +w_1\left({n_{wg}-n}_1\right)+w_2\left({n_{wg}-n}_2\right)}{n_{wg}-n_c\mathit{sin}\theta }}$$

(1)

where $\lambda$ is the wavelength; $n_c$ is the refractive index of the upper cladding, which is 1 in this work; $n_{wg}$, $n_1$, and $n_2$ are the effective indices of the waveguide modes in the unetched region, etched depth $h_1$, and etched depth $h_2$, respectively; $\theta$ is the radiation angle of each unit cell.

3. Results and Discussion

3.1. Implementation of UGR

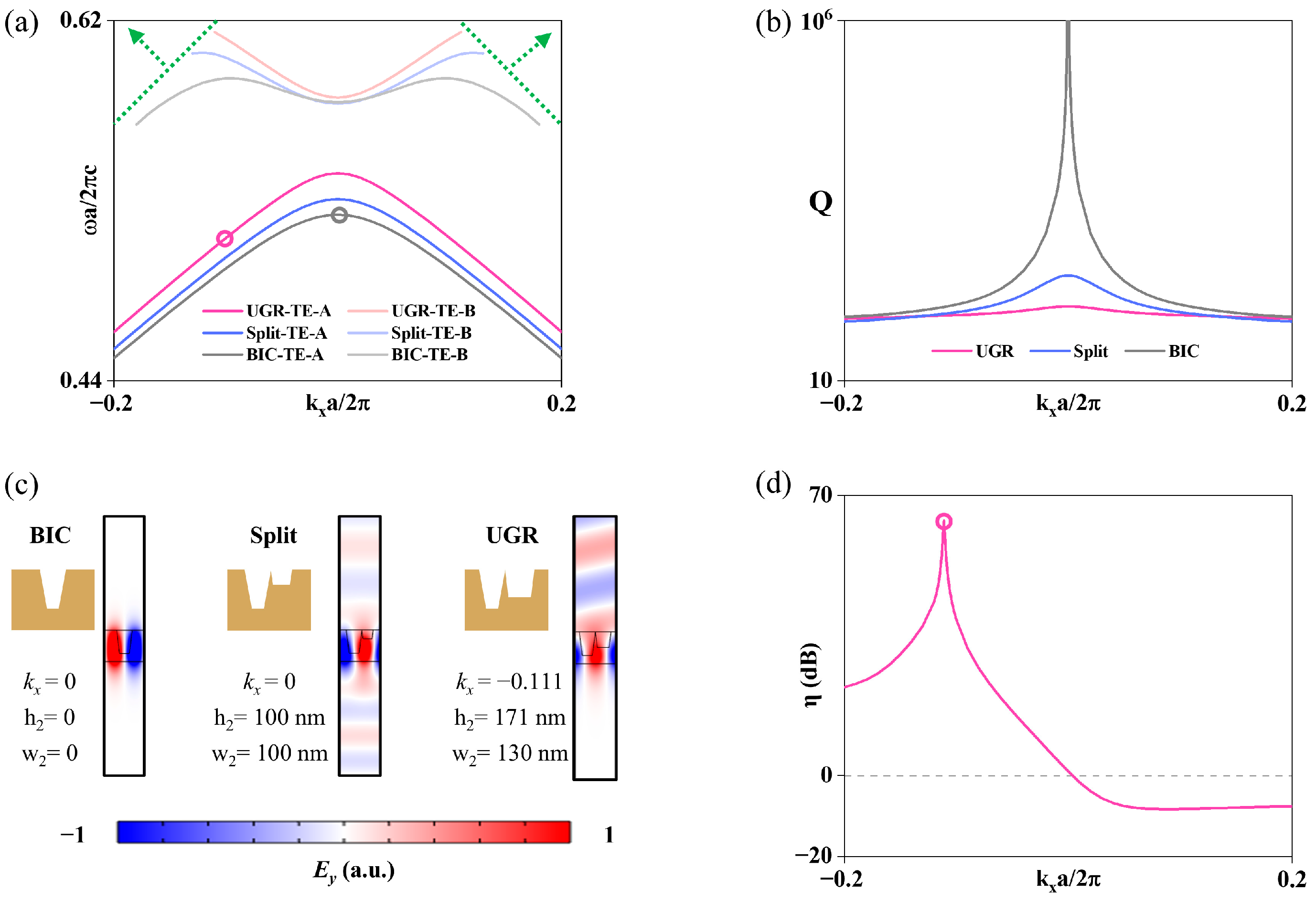
To obtain unit cells exhibiting UGR characteristics, we began with the C₂-symmetric structure shown in Figure 1c as the initial configuration. As a specific example, the period $a$ and lateral offset “shift” were fixed at 432 nm and 0, respectively, with $w_1$ = 110 nm, $h_1$ = 260 nm, and $w_2$ = $h_2$ = 0.

At the center of the Brillouin zone (Γ point, k_x = 0), the unit cell supports a BIC at the lowest, antisymmetric transverse electric (TE) band denoted as “TE-A” (Figure 2a, black circle), exhibiting an infinite quality factor “Q” (Figure 2b, black line). As a topological defect in the far-field polarization major axes, the mode does not radiate energy both upward toward the unit cell’s top side and downward toward its bottom side (Figure 2c, left). Subsequently, $w_2$ and $h_2$ were assigned random values unequal to $w_1$ and $h_1$ (for instance, $w_2$ = $h_2$ = 100 nm), respectively, and denoted this intermediate configuration as “Split.” The Qs of resonances in the vicinity of the Γ point degrade to 291 (Figure 2b, blue line), indicating that the BIC is eliminated by the breaking of C₂ symmetry. The E_y mode profile at k_x = 0 (Figure 2c, middle) confirms that, in this state, the mode radiates energy both upward and downward. Furthermore, by continuously adjusting the values of $w_2$ and $h_2$, we found that when $w_2$ = 130 nm and $h_2$ = 171 nm, the unit cell exhibits a UGR on the TE-A band at k_x = −0.111 (Figure 2a, red circle), with a corresponding quality factor of 80 (Figure 2b, red line), sufficient for use in grating-coupler applications. The E_y mode profile in the right panel of Figure 2c confirms that the unit cell radiates energy almost exclusively upward, achieving an upward-to-downward radiation intensity ratio of 63.7 dB (Figure 2d, red circle). From the perspective of radiation topology, the emergence of the UGR is ascribed to the breaking of the unit cell C₂-symmetry, which causes the integer topological charges carried by the BICs on the unit cell’s top and bottom sides to each split into pairs of half-integer topological charges carried by circularly polarized resonances. Under fine geometry tuning, the pair of half-integer charges on the unit cell’s top side remain separated during their evolution in momentum space, thereby destroying the BIC; Meanwhile, the pair on the bottom side merge into an integer topological charge, thus restoring a BIC. This asymmetry between the top and bottom evolutions yields upward unidirectional radiation [69,72].

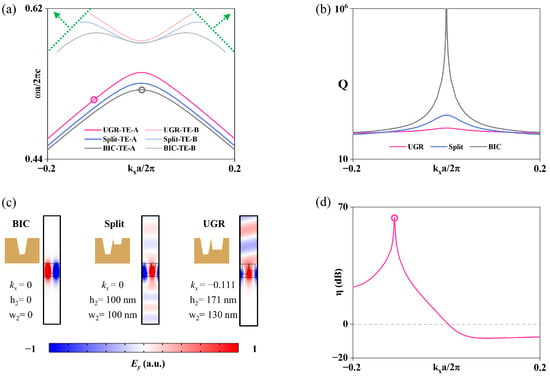
Figure 2. (a) Band structures with the BIC marked by a black circle for C₂ symmetric and the UGR marked by a red circle for C₂ asymmetric structures. (b) Quality factors and (c) E_y mode profiles of the unit cell under different geometries. By fine-tuning, the quality factor reduces from infinite to 108 (Γ point) and the radiation direction of the mode is precisely controlled. (d) The up/down radiation intensity ratio of the UGR configuration reaches 63.7 dB at k_x = −0.111.

It is noteworthy that an excessively thin film thickness or an overly large groove depth reduces the effective refractive index of the mode in the grating region. Since the refractive index contrast governs the extent of band expansion, gratings designed on low-index materials such as TFLN are more readily driven into higher-order diffraction regimes (indicated by the green arrow in Figure 2a), thereby rendering UGR unsuitable for grating couplers [64,71]. Nonetheless, on a 350 nm LNOI platform, we achieved an upward-to-downward radiation intensity ratio almost close to the 65.8 dB reported in Reference [72] for a 340 nm Silicon-On-Insulator (SOI) platform [72]. This result validates the scientific feasibility of realizing UGRs that operate in the short-wavelength band on low-refractive-index materials.

3.2. Assembly of a Unidirectionally Radiating Grating Coupler

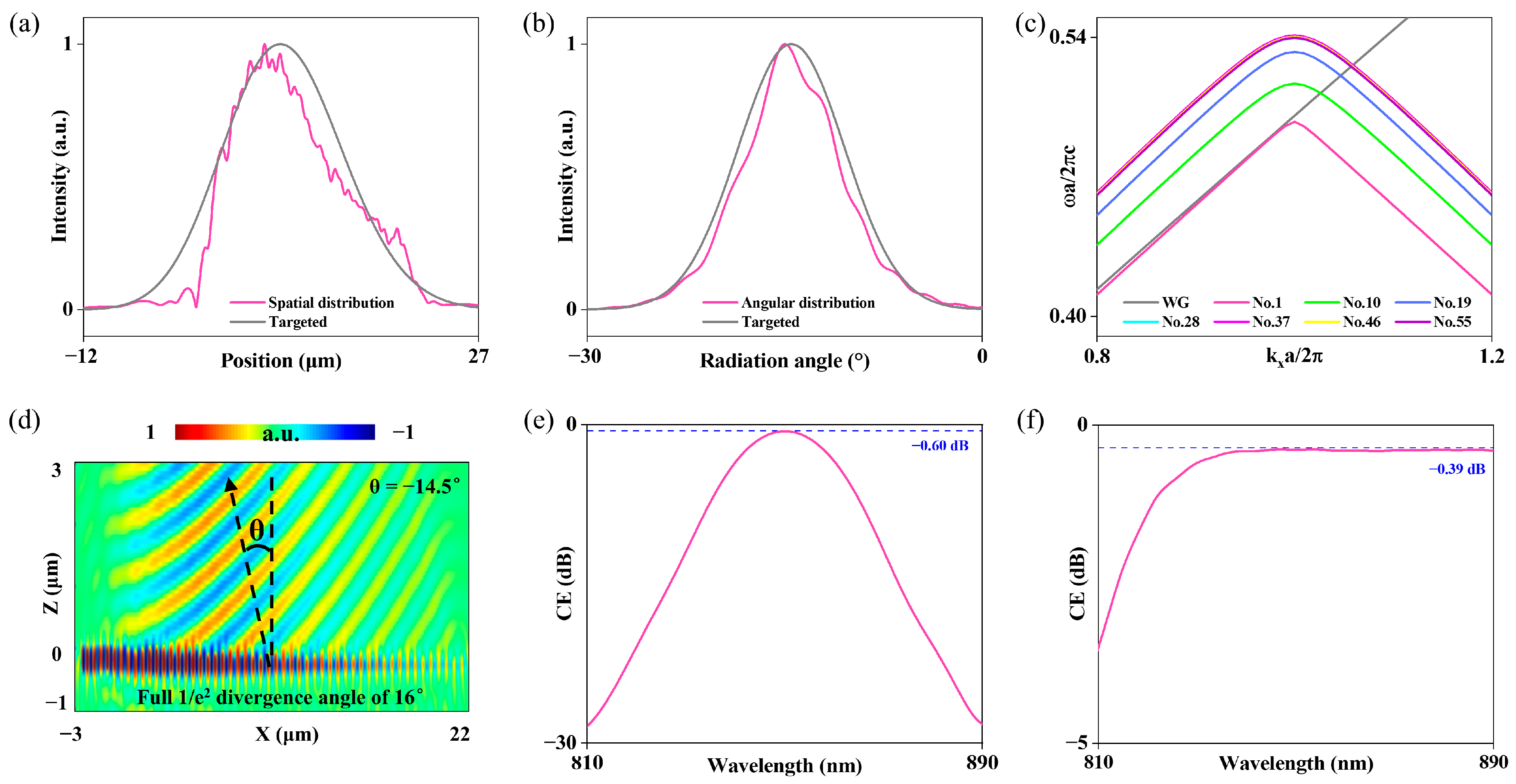
Taking the on-chip heterogeneous integration of the light source via tilted flip-chip bonding as an example, we arranged an array of 55 unit cells exhibiting UGR characteristics based on the phase-matching principle, thereby designing a tailored grating coupler (footprint of 22.3 μm × 22.5 μm) for an 850 nm VCSEL with a Gaussian beam featuring 1/e² beam waist diameter of 3.8 μm and full 1/e² divergence angle of 16° [65].

In detail, as illustrated in Figure 1a, the first 30 unit cells (region I) were specifically engineered with linearly increasing groove widths to serve two primary objectives: (i) to precisely modulate the local scattering strength of the gratings in real space, thereby achieving a near-Gaussian radiated electric field distribution, and (ii) to gradually reduce the effective refractive index step between the waveguide and the grating mode, which significantly suppresses back-scattering. To this end, the groove width $w_1$ and the groove width $w_2$ in region I were linearly ramped from 0 to 110 nm and from 0 to 130 nm, respectively. Furthermore, to match the large far-field divergence angle of the VCSEL in momentum space, the radiation angle of the unit cell was deliberately varied across the entire structure through a linear chirp from −4° to −22° (with the nominal radiation angle of the UGR unit cell in this work being −12.61°). In region II, where the groove widths $w_1$ and $w_2$ were held constant, satisfaction of the phase-matching condition necessarily resulted in a corresponding linear reduction of the grating period $a$ along the propagation direction. As a direct consequence of this precise geometric control, the designed grating coupler exhibits a radiated electric field profile that closely approximates a Gaussian distribution, as evidenced in Figure 3a,b. This design achieves excellent mode overlap with the target VCSEL in both real space (spatial domain) and momentum space (angular domain), thereby ensuring efficient coupling despite the source’s substantial divergence. The combined apodization (region I) and chirping (region II) strategy thus yields a highly adapted coupler that simultaneously suppresses back-scattering, shapes the near-field envelope, and tailors the far-field angular distribution to the specific emission characteristics of the tilted flip-chip bonded 850 nm VCSEL. The band dispersion relations for the waveguide (WG) mode and the grating modes in the 1st, 10th, 19th, 28th, 37th, 46th, and 55th unit cells were calculated and plotted in Figure 3c. These curves exhibit nearly identical slopes at the wavevector k_x = 0.889 (corresponding to the zone-folded point from k_x = −0.111 in the Brillouin zone), confirming excellent group velocity matching (v_g = dω/dk) and momentum conservation between the waveguide mode and the grating modes across the entire structure. Numerical simulations further verify that the vast majority of the radiated energy is emitted upward at a tilt angle of θ = −14.5° (Figure 3d). By setting the etch depth $h_1$ of the first three-unit cells to 0, back-scattering of the waveguide mode during propagation through the grating region is suppressed to only 1.5%.

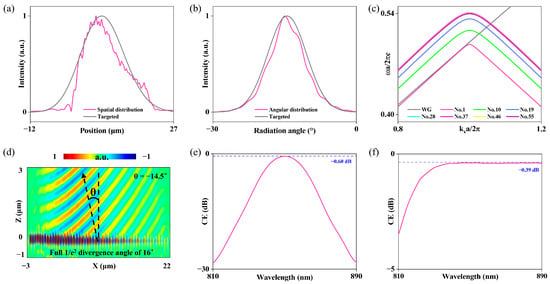
Figure 3. (a,b) The spatial and angular distributions of the upward radiation from this unidirectional radiative grating coupler, which aligns well with the VCSEL. (c) Band structures of the waveguide and local gratings. By apodizing the grating widths and periods, excellent momentum and group-velocity matching is achieved. (d) The electric field distribution (E_y) of the unidirectional radiative grating coupler at 850 nm, excited by a mode source. (e) CE from the VCSEL to the simulated coupler as a function of wavelength. (f) Detection efficiency from the simulated coupler to the detector as a function of wavelength.

When the VCSEL illuminates the coupler from a vertical distance of 55 μm, the UGR-based grating coupler achieves a simulated coupling efficiency of −0.6 dB at the 850 nm wavelength (Figure 3e). Conversely, when energy is launched from the waveguide and radiated outward through the same grating coupler, a simulated detection efficiency of −0.39 dB is obtained (Figure 3f). This performance represents not only an outstanding result for short-wavelength TFLN grating couplers, but also, to the best of our knowledge, the highest simulated efficiency reported to date among all TFLN-based grating couplers that refrain from incorporating mirrors or hybrid materials. The corresponding 3D-FDTD simulation results are detailed in Figure S3 of the Supplementary Information.

However, although we achieved a similar upward-to-downward radiation intensity ratio on the unit cell comparable to that on the SOI platform in Reference [72], the CE of the grating coupler at the device level is much lower than that reported there (−0.34 dB) [72]. This is primarily attributed to the apodization applied to all unit cells in our work to match the VCSEL’s large mode field, which degraded the performance of the UGR. When the VCSEL illuminates from above the grating coupler, 9% of the power leaks to the substrate. Another noteworthy aspect is that the −1 dB bandwidth and −3 dB bandwidth of the grating coupler demonstrated in this work are only 12 nm and 20 nm, respectively. Although these values meet the requirements for commercial VCSELs, they are significantly inferior compared to the UGR-based work in Reference [72], where the −1 dB bandwidth and −3 dB bandwidth are 28.9 nm and 57.6 nm, respectively. In the present work, to better match the large mode field of the VCSEL, we deliberately selected a UGR mode with a high Q of 80, which consequently imposes a limitation on the bandwidth. From another perspective, the low scattering strength of the grating under such a high-Q regime also results in a significantly extended overall device length. After the real-space to k-space Fourier transformation, this extended length leads to a certain degree of compression in the achievable operational bandwidth. Nevertheless, this design approach for an efficient short-wavelength grating coupler, achieved by combining the low-refractive-index material TFLN with UGR, exhibits originality, and the underlying concept also offers a degree of scalability. In the Supplementary Information (Figure S1), by proportionally scaling down the structural parameters of the original UGR unit cell, we identified a UGR on the TE-A band at k_x = −0.118, exhibiting an upward-to-downward radiation intensity ratio of 71.5 dB. The corresponding parameters are $w_1$ = 70 nm, $w_2$ = 84 nm, $h_1$ = 167 nm, $h_2$ = 110 nm, and $a$ = 277 nm. Based on this, we obtained a grating coupler with a simulated detection efficiency of −0.33 dB at 568 nm wavelength, reducing the overall device length to approximately 15 μm. This provides a prerequisite for the development of shorter-wavelength TFLN modulators. Furthermore, with the continuous advancements in industrial etching equipment and technologies, the TFLN etching process achieving perfectly vertical sidewalls may become commonplace in the near future. Accordingly, we conducted corresponding extension studies (See Figure S2 in the Supplementary Information). Through structural optimization, at $w_1$ = 136 nm, $w_2$ = 176 nm, $h_1$ = 236 nm, $h_2$ = 142 nm, and $a$ = 426 nm, we identified a UGR operating on the TE-A band (k_x = −0.113) in the unit cell with vertical sidewalls, exhibiting an upward-to-downward radiation intensity ratio of 65.2 dB. Based on this, we obtained a grating coupler operating at a wavelength of 850 nm, with a simulated detection efficiency of −0.35 dB.

3.3. Tolerance Analysis and Robustness to Fabrication Variations

In practical fabrication of photonic integrated circuits, the realized device geometry invariably deviates from the ideal theoretical design, owing to multiple non-idealities inherent in the manufacturing workflow. These deviations primarily arise from limitations in the electron-beam or deep-ultraviolet lithography systems, including finite minimum feature size, overlay alignment accuracy, and proximity effects that distort patterned features during exposure. Furthermore, material inhomogeneity and etching processes introduce additional variability through limited etch-uniformity, which directly impacts critical dimensions such as grating groove width, depth and sidewall roughness. Beyond chip processing, module-level integration, particularly the flip-chip bonding of the VCSEL, introduces further uncertainty due to mechanical placement precision, typically resulting in angular misalignments relative to the designed optimum, as well as lateral and vertical offsets. A rigorous tolerance analysis is, therefore, indispensable to quantify performance sensitivity to these realistic variations. In the following, we present tolerance analyses conducted at three hierarchical levels: the unit cell, device, and module.

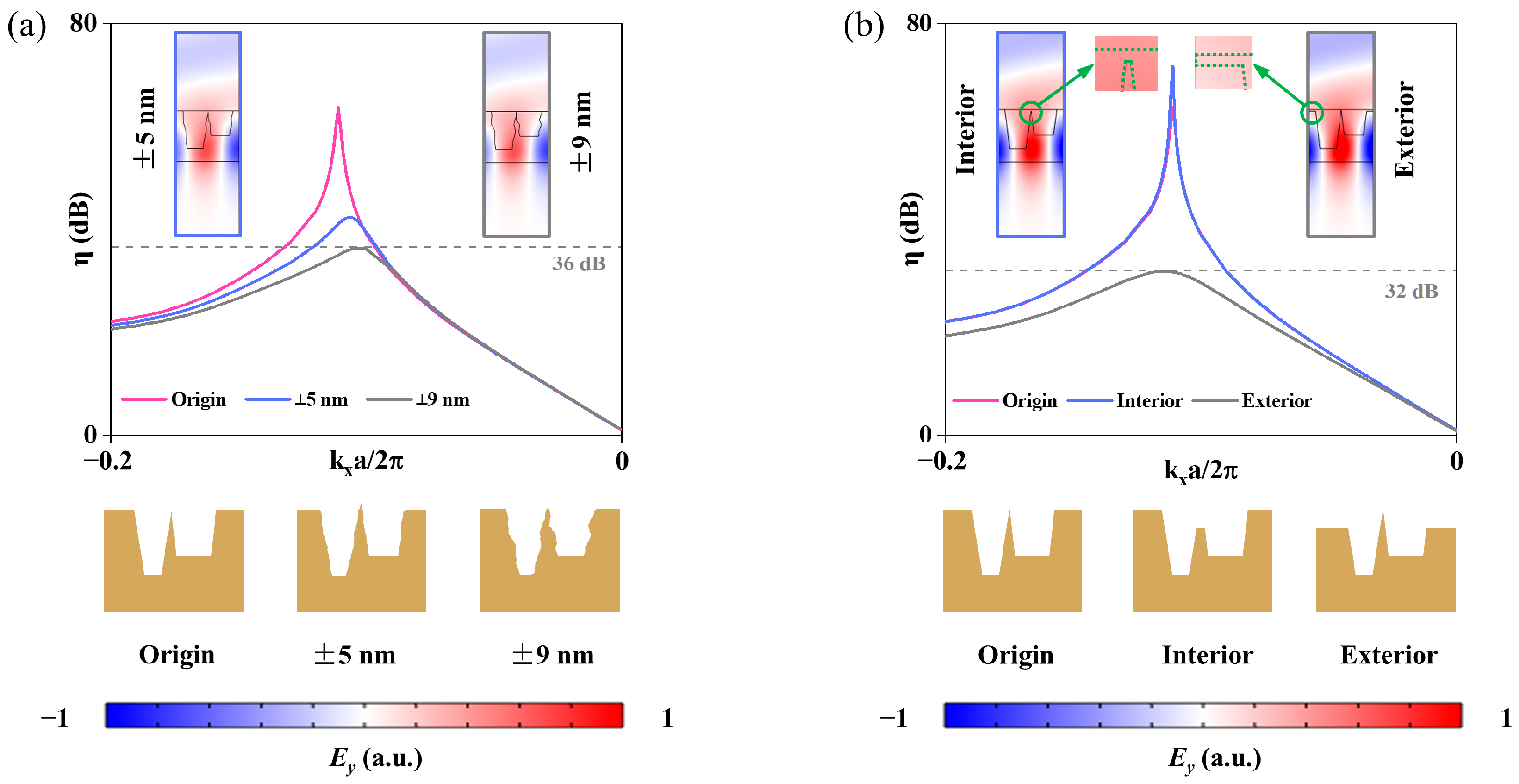
At the unit cell level, as two representative examples, we investigated the specific impact of sidewall roughness and material inhomogeneity on the stability of the topological state. Regarding sidewall roughness, we modeled the rough sidewalls by replacing the smooth sidewalls of the original UGR structure with parameterized curve. The parameterized curve was generated by combining random distribution functions with summation operators, thereby forming a random curve, whose expressions in the $x$ and $z$ directions are given by:

$$\begin{array}{c}x=A_x+\left(B_x-A_x\right)\ast s+\left(-{\displaystyle \frac{B_z-A_z}{sqrt\left({\left(B_x-A_x\right)}^2+{\left(B_z-A_z\right)}^2\right)}}\right)\ast \\ \left(R\ast s\ast \left(1-s\right)\ast sum\left(if\left(m!=0,{\left(m^2\right)}^{-{\displaystyle \frac{b}{2}}}\ast g1\left(m\right)\ast cos\left(2\ast pi\ast m\ast s+u1\left(m\right)\right),0\right),m,-N,N\right)\right)\end{array}$$

(2)

$$\begin{array}{c}z=A_z+\left(B_z-A_z\right)\ast s+\left({\displaystyle \frac{B_x-A_x}{sqrt\left({\left(B_x-A_x\right)}^2+{\left(B_z-A_z\right)}^2\right)}}\right)\ast \\ \left(R\ast s\ast \left(1-s\right)\ast sum\left(if\left(m!=0,{\left(m^2\right)}^{-{\displaystyle \frac{b}{2}}}\ast g1\left(m\right)\ast cos\left(2\ast pi\ast m\ast s+u1\left(m\right)\right),0\right),m,-N,N\right)\right)\end{array}$$

(3)

Here, (${\mathrm{A}}_{\mathrm{x}}$, ${\mathrm{A}}_{\mathrm{z}}$) and (${\mathrm{B}}_{\mathrm{x}}$, ${\mathrm{B}}_{\mathrm{z}}$) denote the upper and lower endpoints of the smooth sidewalls of the original UGR structure, respectively. The functions $g1$ and $u1$ are the built-in one-dimensional Gaussian random function and one-dimensional uniform random function in COMSOL Multiphysics, respectively. The variable $s$ denotes the spatial variable ranging from 0 to 1, $R$ is the scaling factor, $b$ is the spectral exponent parameter, $N$ is the maximum integer value of the spatial frequency, and m is the integer spatial frequency parameter. In this work, $N$ and $b$ are fixed at 20 and 1.3, respectively, and the sidewall roughness is controlled solely by varying $R$. When $R$ = 10, the maximum deviation (indentation and protrusion) of the rough sidewall relative to the smooth sidewall of the original UGR structure is approximately ±5 nm. The middle figure in the bottom panel of Figure 4a provides a schematic illustration of the unit cell morphology in this case, and this structure exhibits an upward-to-downward radiation intensity ratio of 42.4 dB at k_x = −0.106 (top panel of Figure 4a, blue line). When $R$ = 20, the maximum deviation increases to approximately ±9 nm. The right figure in the bottom panel of Figure 4a provides a schematic illustration of the unit cell morphology in this case, and this structure displays an upward-to-downward radiation intensity ratio of 36.4 dB at k_x = −0.103 (top panel of Figure 4a, black line). In both cases, the UGR operates on the TE-A band and maintains nearly the same Q (~80) as the original UGR structure. The E_y mode distribution inset in the top panel of Figure 4a demonstrates that even when the sidewall smoothness deviates from the ideal design, the asymmetry ratio remains at a high level. Regarding material inhomogeneity, we considered two scenarios. In the first scenario, the film thickness in the central region of the unit cell is 10 nm lower than that in the surrounding regions; we denote this structure as “Interior”. The middle figure in the bottom panel of Figure 4b provides a schematic illustration of the unit cell morphology in this case. In the second scenario, the film thickness in the surrounding regions of the unit cell is 10 nm lower than that in the central region; we denote this structure as “Exterior”. The right figure in the bottom panel of Figure 4b provides a schematic illustration of the unit cell morphology in this case. Simulation results indicate that the “Interior” structure achieves a higher upward-to-downward radiation intensity ratio than the ideal original UGR structure at k_x = −0.111, reaching 71.6 dB (top panel of Figure 4b, blue line). The “Exterior” structure also maintains a high asymmetry ratio of 31.9 dB at k_x = −0.115 (top panel of Figure 4b, black line). The E_y mode distribution inset in the top panel of Figure 4b corroborates the robustness of the UGR under material inhomogeneity. In both scenarios, the operating band and Q show no significant deviation relative to the ideal original UGR structure. In summary, considering typical process variations and material yield levels, the topological state of the unit cell in the double-trapezoidal structure can maintain high stability, thereby meeting the requirements for practical production and providing assurance for the fabrication of efficient grating couplers.

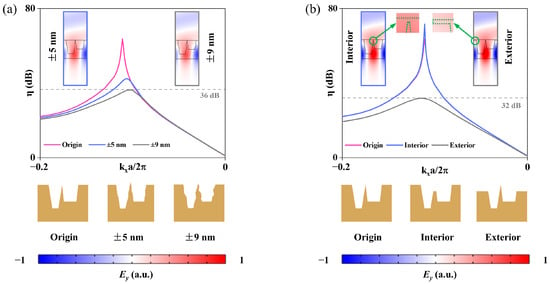
Figure 4. (a) When the sidewalls of the original UGR structure transition from smooth to exhibiting maximum deviations (dents and protrusions) of ±5 nm and ±9 nm, respectively, the unit cells achieve upward-to-downward radiation intensity ratios of 42.4 dB at the corresponding k_x = −0.106 and 36.4 dB at k_x = −0.103 (top panel). The insets of the top panel show E_y mode profiles for different sidewall roughness levels, while the bottom panel shows schematic unit-cell illustrations for those roughness levels. (b) For the original UGR structure with the central region 10 nm thinner than the surrounding, the unit cell exhibits an upward-to-downward radiation intensity ratio of 71.6 dB at k_x = −0.111; when the surrounding region is instead 10 nm thinner than the center, the ratio remains 31.9 dB at k_x = −0.115. The insets of the top panel show the corresponding E_y mode profiles for different relative thickness conditions. The bottom panel depicts schematic illustrations of the unit cell in those cases.

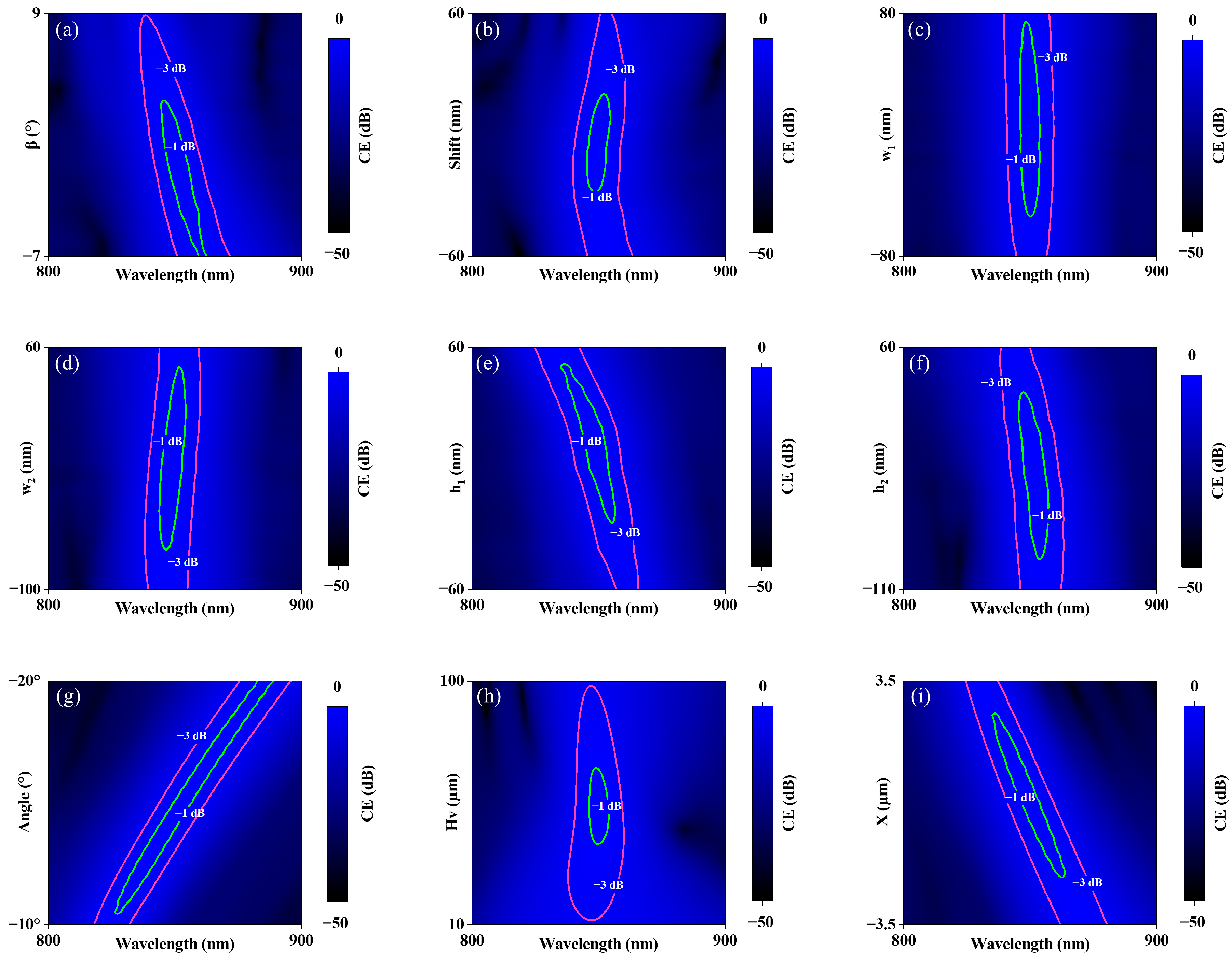
At the device level, Figure 5a–f (the vertical axis represents the deviation values) present contour plots of the CE as a function of key parameters—namely, the sidewall angle $\beta$, alignment errors (shift), etching widths $w_1$ and $w_2$, and etching depths $h_1$ and $h_2$—across the operating wavelength range. The green and red contours denote the −1 dB and −3 dB CE thresholds, respectively. Figure 5a–f reveal that, over the 850 ± 10 nm bandwidth, the −1 dB tolerance windows for $\beta$, shift, $w_1$, $w_2$, $h_1$ and $h_2$ are [−7, +3.5] °, [−32, +22] nm, [−56, +76] nm, [−76, +50] nm, [−30, +40] nm, and [−90, +30] nm, respectively. For the more relaxed −3 dB criterion, the tolerance window for $\beta$ is [−7, +8.5] ° and the tolerances for the other parameters exceed ±60 nm, which comfortably absorb the process variations typical of mass manufacturing. In particular, the case of −7° corresponds to perfectly vertical sidewalls.

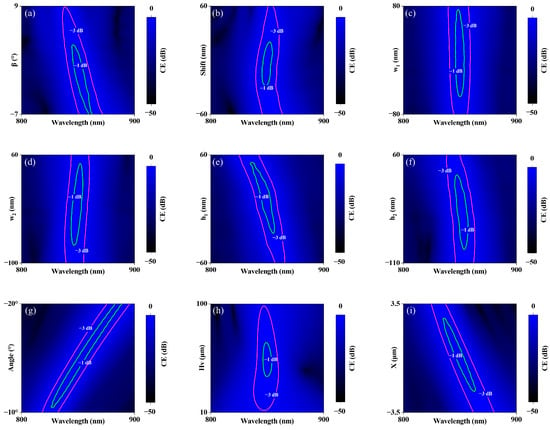
Figure 5. Coupling efficiency as a function of the process perturbations. (a) Sidewall angle $\beta$ , (b) alignment errors (shift), (c) groove width $w_1$, (d) groove width $w_2$, (e) groove depth $h_1$, and (f) groove depth $h_2$. Over the 850 ± 10 nm bandwidth, the −1 dB tolerance windows for $\beta$, shift, $w_1$, $w_2$, $h_1$, and $h_2$ are [−7, +3.5] °, [−32, +22] nm, [−56, +76] nm, [−76, +50] nm, [−30, +40] nm, and [−90, +30] nm, respectively. (g) Incident angle of the VCSEL angular tolerances of approximately 1° and 3° for the −1 dB and −3 dB thresholds at the 850 nm. (h) Vertical offset $Hv$ and (i) lateral offset $X$. Over the 850 ± 10 nm bandwidth, the −1 dB tolerance windows for $Hv$ and $X$ are ±15 μm and ±2 μm, respectively.

At the module level, Figure 5g–i present contour plots of the CE as a function of key parameters—namely, the VCSEL incidence angle, vertical offset $Hv$, and lateral offset $X$—across the operating wavelength range. To make the correspondence between the parameters and the actual assembly dimensions more intuitive, the vertical axes of the angle and $Hv$ plots represent the actual values (the vertical axis of the $X$ plot remains the deviation values). As shown in Figure 5g, the UGR-based unidirectional radiating grating coupler provides angular tolerances of approximately 1° and 3° for the −1 dB and −3 dB thresholds at the design wavelength of 850 nm. Figure 5h,i reveal that over the 850 ± 10 nm bandwidth, the −1 dB tolerance windows for $Hv$ and $X$ are ±15 μm and ±2 μm, respectively. For the more relaxed −3 dB criterion, $Hv$ exhibits tolerances exceeding ±40 μm, and $X$ exhibits tolerances exceeding ±3 μm. These values are fully compatible with state-of-the-art module-level packaging capabilities.

In conclusion, the proposed grating coupler, constructed from topologically protected UGR unit cells, displays outstanding robustness against fabrication imperfections and assembly errors. This resilience originates from the inherent topological nature of the UGR configuration, which preserves a high upward/downward radiation ratio, even in the presence of common uncontrollable perturbations, thereby sustaining near-optimal coupling and detection efficiencies across process corners.

Compared to the limited short-wavelength TFLN grating couplers currently reported in the literature, namely Reference [11] (−3 dB at 775 nm) and Reference [14] (−1.8 dB at 532 nm), our work (−0.6 dB at 850 nm) exhibits a significant advantage in simulated CE [11,14]. In terms of bandwidth, the −3 dB bandwidths reported in References [11,14] are 11 nm and 20 nm, respectively, which are comparable to those in the present work. Regarding fabrication tolerance, Reference [11] does not provide a detailed discussion, whereas Reference [14] reports that a 30 nm deviation in etching width results in a decrease in CE from −1.87 dB to −3.37 dB; in contrast, the present work maintains a CE of −1 dB under etching width fluctuations of ±50 nm. Overall, relative to existing studies, our short-wavelength TFLN grating coupler achieves a more favorable balance among CE, bandwidth, and fabrication tolerance. However, we do not hold an advantage in process complexity, as this design necessitates dual-etching—an aspect that we are currently actively optimizing. In future work, we plan to explore a broader array of single-etch structural schemes to further simplify the fabrication process.

4. Conclusions

In this work, we designed an 850 nm-band grating coupler on a thin-film lithium niobate platform based on the UGR principle. By breaking the C₂ symmetry of the unit cell and precisely controlling the evolution of the topological charge, unidirectional upward radiation was achieved at the unit-cell level (up/down radiation ratio of 63.7 dB) without requiring mirrors or hybrid materials. Through apodized variation of the groove widths and grating periods, excellent radiation distribution matching with the VCSEL was realized in both real and momentum space, yielding a simulated coupling efficiency of −0.6 dB from the VCSEL to the coupler and a simulated detection efficiency of −0.39 dB from the coupler to the detector. Fabrication tolerance analysis showed that, owing to the topological protection inherent in UGR, the unidirectional radiation grating coupler exhibits outstanding robustness against geometric perturbations and assembly deviations. The present design provides a high-efficiency, layout-flexible, CMOS-compatible optical I/Os solution for short-wavelength LNOI modulators with low V_πL. It offers substantial engineering value and strong potential for adoption in on-chip light-source integration and high-bandwidth-density short-reach optical interconnects.