Abstract
An ultrathin film capable of exhibiting material properties across and around two different dimensions by bridging two-dimensionality frameworks, called a trans-dimensional (TD) material, can be an exceptional tool to tune various electronic and optoplasmonic properties of a system that are unattainable from either dimension. Taking an example of the planar periodic arrangement of single-walled carbon nanotube (SWCNT) TD films, we semi-analytically calculated their dynamical conductivities and dielectric responses as a function of the incident photon frequency and the SWCNT’s radius using the many-particles Green’s function formalism within the Matsubara frequency technique. The periodic array of SWCNTs has an anisotropic dielectric response, which is almost a constant and the same as that of the host dielectric medium in the perpendicular direction of the alignment of the SWCNT array due to the depolarization effect that SWCNTs have. However, the dielectric response functions depend on the incident photon energy in addition to the film’s thickness, the SWCNT’s sparseness, inhomogeneity, and the SWCNT’s diameter. The energy difference between the resonant absorption peak and the plasmonic peak varies with the thickness of the film. Varying the length of the CNTs, we also observed that the exciton–plasmon coupling strength increases with the increase in length of the SWCNTs. The metallic SWCNT-containing films have comparatively pronounced plasmon resonance peaks at low photon energy than semiconducting SWCNT-containing films. Both metallic and semiconducting SWCNT-consisting films have negative refraction for a wide range of energy, making them good candidates for metamaterials.
1. Introduction
Since the first observation of a carbon nanotube (CNT) with a diameter of 50 nanometers in 1952 [1], many scientific studies have been conducted on the synthesis, characterization, and detailed investigation of the mechanical, thermal, electronic, optical, and plasmonic properties of carbon nanotubes. In 1975, Oberlin et al. observed a multi-walled CNT (MWCNT) as a hollow tube of rolled graphite in carbon fiber synthesis utilizing the chemical vapor deposition method decomposing benzene and hydrogen at high temperatures in the presence of a transition metal as a catalyst [2]. Dresselhaus et al. contributed to the theoretical investigation of carbon-based materials, namely carbon whiskers and graphite intercalation compounds, in the late 1970s [3,4]. The first evidence of CNT production as fiber in a carbon anode via the arc discharge technique was presented at the Biennial Conference of Carbon in 1978 [5]. MWCNTs were perceived as rolled graphene layers in a cylindrical geometry after Nesterenko et al.’s work on the thermoanalytical disproportionation of carbon monoxide to characterize carbon nanoparticles [6]. Howard Tennent received a US patent for producing cylindrical discrete carbon fibrils of diameters in the range of 3.5 to 70 nm [7]. The experimental discovery of MWCNTs by S. Iijima in arc-burned graphite rods and their imaging through a high-resolution electron beam technique of transmission electron microscopy has been considered a turning point of CNT research [8]. Within two years after the discovery, it was observed that some single-walled CNTs (SWCNTs) show exceptional conducting behavior [9,10]. Since then, CNTs have received significant attention among researchers in this field because of their high tensile strength (∼order of Pa for SWCNTs [11]), higher electrical and thermal conductivities, optoplasmonic properties, and chirality-dependent metallicity.
The plasmon spectrum of SWCNTs is rich in plasmon resonance peaks. Semiconducting SWCNTs have plasmon modes in the infrared and visible ranges of a few hundred to thousands of terahertz (THz), while metallic SWCNTs have plasmon modes and comparatively intense plasmon peaks in the low-frequency range of only a few THz besides the other plasmon modes in the infrared and visible ranges, like semiconducting SWCNTs [12,13]. For a thin film of CNTs, the film’s plasmonic behavior on its interaction with light results due to the collective excitons, which can be tuned by changing the radius, sparseness of CNTs, thickness of dielectric medium in which CNTs are immersed, and chirality of the SWCNTs [14,15,16,17].
Plasmonic interconnected circuits built from CNTs offer a new material platform for nanoscale electronic devices integrated with optoelectronic components as they offer high electrical conductivity, ballistic transportation, resistance to electromigration, and broadband response [18]. When target molecules are bound to a CNT’s surface, the CNT can be used for gas sensing, chemical sensing, and bio-sensing as the plasmonic properties of the CNT have become sensitive in the presence of target molecules [19,20]. SWCNT films’ optical transparency, excellent flexibility, and remarkable potency under mechanical stress make them good candidates for transparent conductive films for liquid crystal display and organic light-emitting diode displays, transparent electrodes in photovoltaic cells, and quantum dot light-emitting diodes [21,22]. The films can also be used in optical modulators and optoelectronic sensors. SWCNT films can be integrated into metamaterials for sub-wavelength imaging in super lenses, cloaking devices, beam-steering technologies, and electromagnetic interference shielding for aerospace and telecommunications [23]. Hybrid plasmonic–CNT structures obtained by incorporating one-dimensional (1D) CNT tubules with other 2D plasmonic materials such as MXenes and graphene are useful for fine-tuning various electrical, optical, thermal, and plasmonic properties as MXenes and graphene provide additional pathways for electron transport and enhance the coupling between MXenes’ or graphene’s localized surface plasmons and the electron-rich CNT network, amplifying the plasmonic response [24,25,26].
Various semi-analytical approaches such as ab initio calculations, density functional theory, molecular dynamics, and continuum mechanics have been reported as reliable methods for studying the structural property relation between SWCNTs and their electro-optical nature. One can also employ mathematically sophisticated analytical approaches such as fractional calculus calculations as presented in Ref. [27], where the authors show that the temporal dynamics of the heat conduction induced by light in SWCNT thin films present a nonlinear dependence on optical irradiance.
Any SWCNT of chiral indices can be thought of as being a hollow cylinder prepared by rolling a graphene sheet along the specific chiral vector given by , where and represent the graphene lattice vectors. and serve as translation vectors. A scheme of rolling a graphene sheet to obtain different types of SWCNTs is presented in Figure 1. The radius and chiral angle of any SWCNT can be calculated as [28,29,30]
and
where Å is the carbon-to-carbon distance in a graphene sheet. The chiral angle satisfies 0° 30°. equals 0° for a zigzag SWCNT with chiral indices and 30° for an armchair SWCNT with chiral indices . The chiral angle satisfies 0° < < 30° for chiral SWCNTs. All the armchair SWCNTs are metallic. However, the zigzag SWCNTs are metallic or small bandgap semiconductors based on whether the chiral index n is divisible by 3 or not, respectively. The chiral SWCNTs, whose chiral indices n and m are neither identical nor either one is zero, are quasi-metallic if the difference in chiral indices, , is divisible by 3. Otherwise, they are semiconductive. Statistically, 1/3 of SWCNTs are metallic, while the remaining 2/3 are semiconducting with a small bandgap. Depending on the technological requirement, one can synthesize SWCNTs of a specific chirality.
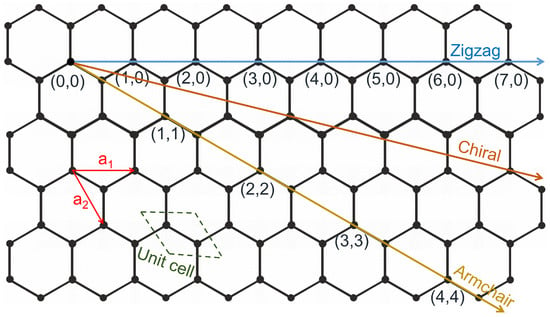
Figure 1.
A schematic diagram showing the rolling direction for the most general chiral with chirality vector and two special cases of achiral, namely zigzag for and armchair SWCNTs.
The literature is rich in the study of mechanical [31], electronic [32], optical [33,34,35], and plasmonic [36,37] behaviors of a single SWCNT. This paper extends our work to the thin and ultrathin films of homogeneous SWCNTs, which are oriented along the y-axis in periodic alignment. A schematic diagram of the theoretical model considered in this study is presented in Figure 2. Each SWCNT presented in the figure was plotted using Nanotube Modeler Software, Version 1.8 [38,39], which is a program to generate -coordinates and plot interactive graphics for capped and uncapped nanotubes and nanocones for a chosen chirality, tube length, and bond length. The SWCNT array is immersed in a dielectric medium of thickness d and constant effective relative permittivity . The substrate and superstate have relative permittivities of and , which are relatively much smaller in value than . Each SWCNT has a radius R and length L. The center-to-center inter-tube distance satisfies with the minimum ideal distance being the sum of the radii of the two closest tubes. determines the dispersiveness of SWCNTs in the film, with a larger signifying a highly dispersed SWCNT film. denotes the SWCNT film width. The SWCNTs have uniform electronic charge distribution throughout the surface of the tube.
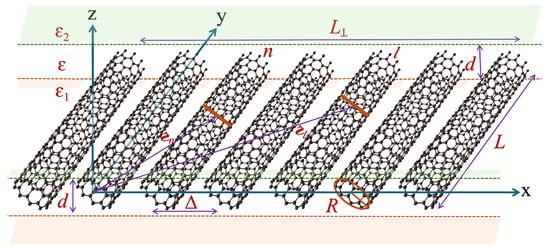
Figure 2.
A schematic diagram showing a planar periodic array of identical non-chiral SWCNTs taken in our theoretical model.
The carrier concentration, mobility, and conductivity can be enhanced, thereby decreasing sheet resistance by treating SWCNT films with inorganic acids such as nitric, sulfuric, and hydrochloric acid (for example, see Ref. [40]). Acid-treated SWCNT films maintain a p-type nature with enhanced carrier mobility and low resistance, making them good candidates for hole-transporting layers in solar cells. Atomic impurities can induce localized surface plasmon resonance, while a vacancy acts as a localized charge trap, increases plasmonic decoherence, and broadens plasmon resonance by increasing scattering. This study considers the pristine SWCNTs with no impurities or defects.
Taking rings in nth SWCNT at position vector and lth SWCNT at , the distance between the rings can be expressed as . For a thin film with a thickness smaller than the distance between rings denoting unit cells of different SWCNTs as shown in Figure 2, i.e., , the electrostatic (Coulomb) interaction between the rings of unit cells becomes so strong that it loses the dependency on its vertical component. As a result, the effective dimensionality of the SWCNT film decreases by one, making it a 2D problem retaining the vertical size, i.e., thickness, as a parameter [16,17]. Such a system with a relatively small thickness, better known as trans-dimensional material (TDM), offers an exceptional tool to tune various optoplasmonic properties that are unattainable from both 3D bulk and/or single-layered 2D counterparts.
To understand and utilize light–matter interactions in an SWCNT and its film at the nanoscale, evaluating and analyzing their dielectric response tensors are crucial, as dielectric response functions delineate collective oscillations of free electrons, excitons, and plasmons. The dielectric property-dependent surface plasmons and localized surface plasmon resonances occur on the film’s surface, creating strong electromagnetic fields when free electrons resonate with incident photon [41,42]. We derived closed-form mathematical expressions for the dynamical (as a function of photon frequency) dielectric response functions of the SWCNT array as presented in Figure 2 using the many-particle Green’s function technique by exploiting the Matsubara frequency approach, as discussed in Ref. [43].
We organize this paper as follows. We orient ourselves with a mathematical overview for dielectric responses for SWCNTs in Section 2. We first evaluate an SWCNT’s dynamic conductivity, which is then used to evaluate its polarizability and dielectric response functions. A comparative study of the dynamical conductivity of two different types of SWCNTs is presented, followed by the dynamical permittivities and dynamical conductivity of an SWCNT used in the SWCNT array. The dielectric response functions of an array of identical SWCNTs are presented in Section 3. Therein, we set up the Hamiltonian of the system, determine the interaction Hamiltonian for the SWCNT film, and present the closed-form expressions for dielectric responses. Taking two different films, one containing metallic (9,0) SWCNTs and the other containing semiconducting (10,0) SWCNTs, as references, we discuss our research findings in Section 4. We present conclusions in Section 5. We have used Gaussian units throughout this paper unless otherwise stated.
2. Dielectric Responses of an Isolated SWCNT
When light interacts with a valence electron of carbon in an SWCNT, the electron becomes excited to the conduction band, leaving a hole behind, thereby creating an electron–hole pair called exciton and inducing an anisotropic polarization. The induced polarization is dominant along the SWCNT axis and negligible in the directions perpendicular to the SWCNT alignment due to the weakening of the response to incident photon along the width of the tube called the transverse depolarization effect [44,45]. The photon frequency and SWCNT radius-dependent axial polarizability of an SWCNT can be expressed in terms of its axial surface conductivity as [46]
where is an infinitesimal frequency parameter. The dynamical conductivity of an SWCNT is estimated using the well-known method of band structure calculations [45,47]. The conducting behavior of SWCNTs significantly varies with the chirality and divisibility of the difference between chiral indices by 3. For example, (9,0) SWCNT is metallic, while (10,0) SWCNT is a semiconducting one. The exciton–plasmon spectrum for the conductivity of metallic SWCNT significantly differs from the semiconducting one, as shown in Figure 3.
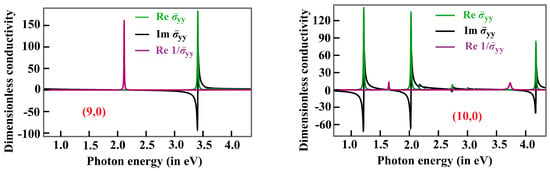
Figure 3.
Dimensionless conductivities of (9,0) (left panel) and (10,0) (right panel) SWCNTs along the corresponding CNT axis as a function of photon energy (expressed in eV).
One may ask how the plasmon spectrum for the conductivity of an isolated SWCNT, measured by , can have such intense resonance peaks. The quantity can be expressed as
where and denote the real and imaginary parts, respectively. At the energy value, in which the real part approaches zero, and the imaginary part switches the sign simultaneously, the quantity will have a significantly large value. As can be smaller than unity when the imaginary part becomes zero, the can be larger than unity. The plasmon resonance appears at a lower photon energy than that of the exciton for metallic (9,0) SWCNT. The same is not true for semiconducting (10,0) SWCNT. In the chosen window of the photon energy, i.e., 0.75−4.25 eV, (10,0) SWCNT has three intense exciton resonance peaks, while the (9,0) SWCNT has only one resonance peak in this energy range for each real, imaginary, and energy-loss parts of the spectrum.
Knowing the conductivity of a single SWCNT, one can easily evaluate its dielectric response functions using [13]
where denotes the surface area of an SWCNT in which the charge is uniformly distributed, and is the number of SWCNTs per unit volume. For an isolated SWCNT, . Consequently, . One can normalize the axial surface conductivity of an SWCNT as
such that is a dimensionless axial surface conductivity as a function of dimensionless energy and an infinitesimal dimensionless energy , where is the carbon atom’s nearest neighbor overlap integral in an SWCNT. Substituting the value of from Equation (6) to Equation (5), one obtains
One can resolve the complex quantity presented in Equation (7) as
for the real and imaginary parts of dielectric response. The loss function , determined from the plasmon spectra, is given by
For illustrative purposes, the dimensionless response functions, namely longitudinal conductivities and longitudinal dielectric functions for an (11,0) SWCNT, are presented in Figure 4. gives us the surface plasmon’s density of states, which is nonzero when the imaginary part of vanishes and the real part of also approaches zero. The quantity is nonzero only if the is zero and approaches zero at the same time.
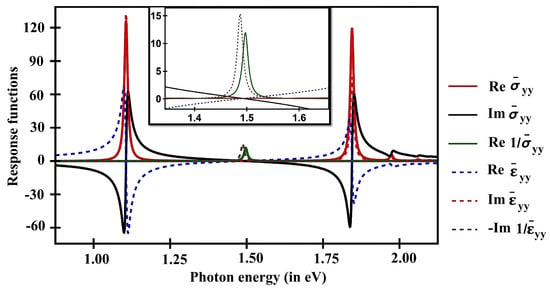
Figure 4.
Dimensionless conductivities and dimensionless dielectric functions of an (11,0) SWCNT along the SWCNT axis plotted as a function of photon energy (expressed in eV). Only the first two excitonic peaks and a plasmonic peak are shown. For better visibility, curves and are scaled by . In the inset, the magnified version of the curves near the resonances of and are shown.
3. Dielectric Responses of SWCNT Films
From the principle of the second quantization, one can write the Hamiltonian of free exciton on the surface of the SWCNT as
where is an exciton energy in its s-subband. is the electron’s quasimomentum in the plane, where is the quasimomentum component along the SWCNT alignment and is along the perpendicular direction to the plane. The exciton annihilation and creation operators follow boson statistics and satisfy the following identities:
A complication arises when we have not just a single SWCNT but an array of SWCNTs as they interact via dipole–dipole interaction. The Hamiltonian interaction can be written as [17]
where
is the interaction potential with being the transition dipole associated with s-subband excitation. , , a, and are the intraband plasma oscillation frequency, the surface electron density, the lattice translation period, and the Fourier transform of the SWCNTs’ dipole–dipole interaction, respectively. The total Hamiltonian of the system is the sum of Equations (10) and (12):
which can be analytically diagonalized using the Bogoliubov–Valatin transformation as presented in Ref. [48].
For the SWCNT array, the dielectric response is anisotropic, which, along the direction perpendicular to the SWCNT alignment, remains constant with the value of the dielectric constant of the host medium, while along the SWCNT alignment, it is given as [17]
where is the ratio of the SWCNTs’ volume to the volume of the film. measures the sparseness of SWCNTs and/or thickness of the SWCNT film. has a lower value for larger inter-tube distance and/or larger value of thickness. satisfies , implying that the screening of the host dielectric medium is always present in an SWCNT array even at the very tightly packed SWCNT array. The screening leads to broadening excitonic and plasmonic peaks and enhances exciton–plasmon coupling. and in Equation (15) are the zeroth-order modified cylindrical Bessel functions. The dielectric response of the SWCNT array is not only the function of photon energy and SWCNT radius similar to a single SWCNT, but it is also a function of the volumetric fraction , permittivities , , and of the substrate, superstrate, and the dielectric medium holding the SWCNT array and quasi-momentum along the SWCNT alignment. As the ratio of the physical quantities is the same as the dimensionality, the dielectric response function expressed in Equation (15) is a dimensionless quantity.
4. Discussion
For , the right side of Equation (15) equals unity, implying that the dielectric response of the SWCNT array equals the host dielectric medium’s permittivity, which makes the dielectric response function isotropic. For the nonzero value of or , the component of the dielectric response is a complex function. The for two different composite films, one consisting of a periodic array of (9,0) SWCNTs and the other consisting of (10,0) SWCNTs, are presented in Figure 5. The SWCNT layers are embedded in a dielectric medium of thickness and relative permittivity , where R is the radius of the respective film’s SWCNT. The fractional volume of the CNT in both these composites is . The real part represents the exciton refraction spectrum, the imaginary represents the exciton absorption spectrum, and represents the plasmon response. The plasmon mode has a resonance at the point in which changes sign from negative to positive, and approaches zero. The plasmon response is positive for the entire energy range, indicating that energy loss is unavoidable. Even in the wide range of energy window (up to ∼4.0 eV), only one resonance is present for the (9,0) SWCNT film. However, one witnesses two resonances for the (10,0) SWCNT film for photon energy up to ∼2.6 eV. The plasmon resonance appears at a lower energy than the excitonic resonance for the (9,0) SWCNT film. The same is not true for the (10,0) SWCNT film. The plasmon spectrum is comparatively more pronounced in the (9,0) than in the (10,0) SWCNT film.
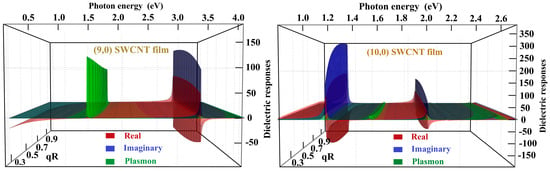
Figure 5.
Dimensionless dielectric responses of a periodic array of (9,0) SWCNTs (left panel) and (10,0) SWCNTs (right panel) along their CNT axis as a function of momentum times the radius of the respective CNT and the photon energy (expressed in eV). The relative permittivity of the substrate, superstrate, and dielectric medium are taken as 1, 1, and 20, respectively. Only the first resonances of the response functions are shown for the (9,0) SWCNT film, while the first two resonances of the response functions are shown for the (10,0) SWCNT film. The fractional density parameter is . The red-colored surface represents the , the blue-colored surface depicts the , and the negative of is shown by the green-colored surface.
The real part of the dielectric response function is negative for a large range of photon energy for both (9,0) and (10,0) SWCNT films, making both SWCNT films good candidates for hyperbolic metamaterials. The energy range, however, depends on the chirality of constituent SWCNTs. The semiconducting SWCNT films show hyperbolic metamaterial behavior in the near-infrared and visible spectrum. The metallic SWCNT films behave as hyperbolic metamaterials in low energy, including the microwave, in addition to the infrared and visible photon energy range as in semiconducting ones. The exciton–plasmon spectra of homogenous arrays of any metallic SWCNTs such as (12,0), (15,0), (18,0), etc. SWCNTs are expected to behave similarly to (9,0) SWCNT arrays. At the same time, resonance intensity and photon energy for resonances depend on the particular metallic SWCNT that the film consists of. The SWCNT films are made up of semiconducting SWCNT arrays such as (13,0), or (16,0), or (19,0), etc. SWCNTs have similar behavior to an array of (10,0) SWCNTs. The hyperbolic nature of the SWCNT array has been experimentally observed in various studies [49,50,51,52]. Pristine SWCNTs can be prepared in a controlled manner with desired chiral purity, density, and alignment as per their need in electronics [53,54]. This study opens new pathways for experimentalists to design and explore more on the SWCNT films discussed in this manuscript.
The exciton–plasmon coupling strength is stronger in the SWCNT array than in a single SWCNT. The inhomogeneity effect abruptly increases the exciton–plasmon coupling [15] for a mixture of SWCNTs of slightly different diameters. Comparing the dielectric responses for a single homogeneous array presented in Ref. [14], one can conclude that the SWCNT film containing more than a single array of identical SWCNTs has a more intense response function.
Substituting the expression of the volume of an isolated SWCNT and the composite volume, can be expressed as , which depends on the thickness of the film and SWCNT sparseness. Choosing a fixed value of , one can observe the effect of film thickness on the exciton–plasmon spectra, with varying values of . Note that is smaller for a larger value of d. Figure 6 shows a comparative study of dielectric responses for three different values of with fixed .
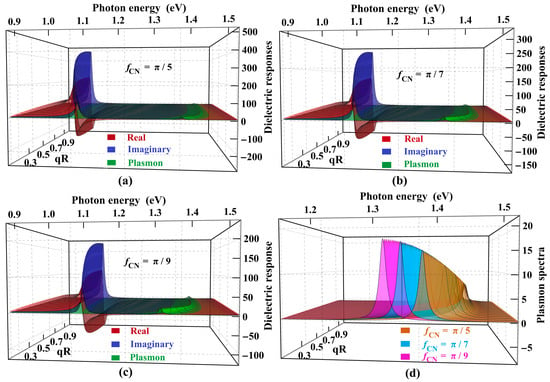
Figure 6.
Dimensionless dielectric functions of a periodic array of (11,0) CNTs along the CNT axis as a function of momentum times radius of (11,0) CNT and the photon energy (expressed in eV). The relative permittivities of the substrate, superstrate, and dielectric medium are taken as 1, 1, and 15, respectively. Only the first resonances of the response functions are shown. Three different scenarios if the values, namely (a), (b), and (c), are taken. Figure (d) shows the comparison of plasmon spectra only for the cases chosen in (a–c).
As shown in Equation (15), the dielectric response function of the SWCNT array is electron quasi-momentum q-dependent. The minimum nonzero value that q can take is , where L is the length of an SWCNT. One can further explore how the length of an SWCNT plays a role in the minimum value of q. For , the longitudinal component of the response functions reads
where is the length of an SWCNT in terms of its circumference. See Figure 7 for the dielectric response function at the minimum nonzero value of momentum . The major contribution to the dielectric response comes from the momentum. At the same time, one should not forget that with also has a nonzero contribution to the response function, which decays exponentially. The exciton and the plasmon resonances approach each other more closely for than for the larger q. However, the intensity of each of the resonance peaks for is smaller than the large q counterpart. Thus, the resonance intensity and exciton–plasmon coupling strength depend on the SWCNT length. The momentum has a lower value for a longer SWCNT than the shorter one. As the CNT length increases, the plasmon resonance comes closer to the exciton resonance, strengthening the exciton–plasmon coupling.
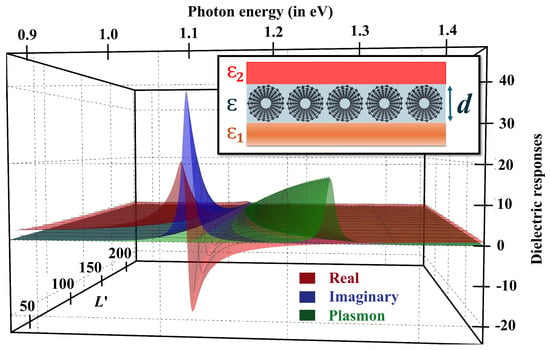
Figure 7.
Dimensionless dielectric responses of an ultrathin array of (11,0) CNTs along the CNT axis as a function of photon energy (expressed in eV) and length of a CNT (expressed in terms of the circumference of an (11,0) CNT) for the mimimum nonzero momentum . The CNTs are tightly packed, and the thickness of the film equals the diameter of an (11,0) CNT, resulting in . The inset shows the geometry related to the SWCNT film.
The resonance peaks become slightly less intense and appear at low photon energy with the increase in the radii of the SWCNTs, provided that the SWCNTs have the same chirality. For example, the film of the (10,0) SWCNT array has a more substantial resonance peak at higher photon energy than the film of the (13,0) SWCNT array. The theoretical model is based on an approximation that the host dielectric medium has larger relative permittivity than the substrate and superstrate. Thus, the substrate and superstrate should be chosen adequately based on the permittivity of the host dielectric material and vice versa. For example, if silicon or GaAs are taken as a host dielectric medium whose permittivities are, respectively, 11.7 and 13.1 [55], then the current study requires the substrate and superstrate to have relative permittivities of about 1 to 3, such as hexagonal boron nitride, fluorinated silica, etc. For high-dielectric host materials such as TiO2, Ti3C2, and Ti2C [56], one has a little more freedom of choice for the substrate and superstrate.
The SWCNT film is only a few nanometers thick, which warrants a brief discussion of its nanoscale effects and the advantages and disadvantages of such effects. At the nanoscale, conductivity can be tuned selectively with the chosen SWCNT of the desired chirality. One can use plasmonic resonance as a tool to enable surface plasmon-based sensing and optoelectronic applications. At the nanoscale, SWCNTs can sustain current densities much higher than copper. However, SWCNTs at the nanoscale have some limitations; as a result, using SWCNTs and their thin films in the current technology is not free from challenges. One of the significant challenges using the currently available synthesis methods is producing SWCNTs of a specific chirality and their scalability [57]. Although some claims on producing pure SWCNTs have been reported, some issues, such as removing amorphous carbon, washing out metallic catalysts after catalytic SWCNT synthesis, and yielding defect-free SWCNTs, remain [58]. As chirality control is usually an issue in SWCNT production, having a consistent film thickness, as this article proposed, needs extra work in the experimental setup, which may not only have an inhomogeneous mixing of SWCNTs of different chiralities, but also have tubular misalignment and inter-tube junction resistance due to phonon scattering. The phonon scattering at the inter-tube junction reduces the conductivity of the SWCNT film. In future studies, we will focus on the phonon scattering at inter-tube junctions and its effect on dielectric responses in the homogeneous SWCNT arrays and inhomogeneous arrays of SWCNTs of approximately the same diameters. Future work will concentrate on creating hybrid materials combining SWCNTs with other materials, such as graphene and polymers, in search of optoelectronic performance enhancements.
5. Conclusions
Using Green’s function theory for many-body systems within the Matsubara frequency approach, we derived a closed form of mathematical expression for the dielectric response function of a periodic array of identical SWCNTs embedded in a dielectric medium with comparatively higher permittivities than substrates and superstates. The dielectric response functions of SWCNTs and its array are both anisotropic. The conducting nature of SWCNTs depends on the chirality resulting from turning graphene sheets into tubules. The SWCNT’s photon energy and cylindrical tube’s radius-dependent dynamical conductivity are calculated using the method of the band structure theory. The dielectric response of the SWCNT film along the perpendicular direction of the SWCNT alignment is constant and matches the value of the host dielectric medium, while the same along the direction of SWCNT alignment takes a complex function, which depends on various parameters, namely photon energy, the radius of SWCNT, volumetric fraction of SWCNT , relative permittivity of the host medium of high dielectric constant, and the substrate and superstrate of low permittivities and dynamic conductivity of each SWCNT in the film. The expression we derived for the SWCNT film’s dielectric response functions links the SWCNT film dielectric responses to the individual SWCNT’s conductivity and the individual SWCNT’s plasma frequency. The screening of the host dielectric medium is inevitable in an SWCNT array primarily because of its geometry.
The excitonic and plasmonic peaks come closer in the periodic array of SWCNTs than in an SWCNT, increasing the exciton–plasmon coupling. The real part of the dielectric response function is negative for a vast range of photon energy in both cases of having an array of metallic and semiconducting SWCNTs, making them good candidates for hyperbolic metamaterials. This finding is consistent with a recent experimental observation of the hyperbolic metamaterial behavior for horizontally aligned films of SWCNTs. We revealed that the exciton–plasmon resonance peaks are closest to the minimum nonzero value of q, and the resonance intensity and exciton–plasmon coupling strength depend on the SWCNTs’ length.
Funding
This research was funded by the 2024 Ralph E. Powe Junior Faculty Enhancement Awards, provided by Oak Ridge Associated Universities (ORAU).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data obtained in this research are included in this paper. Any raw data will be available by the author upon request.
Acknowledgments
The author gratefully acknowledges the support of the 2024 Ralph E. Powe Junior Faculty Enhancement Awards, provided by Oak Ridge Associated Universities (ORAU).
Conflicts of Interest
The author declares no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| CNT | Carbon nanotube |
| SWCNT | Single-walled carbon nanotube |
| MWCNT | Multi-walled carbon nanotube |
| THz | Terahertz |
| 1D | One-dimensional |
| 2D | Two-dimensional |
| 3D | Three-dimensional |
| TD | Trans-dimensional |
| TDM | Trans-dimensional material |
| ORAU | Oak Ridge Associated Universities |
References
- Radushkevich, L.V.; Lukyanovich, V.M. On the structure of carbon produced at thermal decomposition of carbon monoxide on an ironcontact. J. Phys. Chem. 1952, 26, 88–95. [Google Scholar]
- Oberlin, A.; Endo, M.; Koyama, T. Filamentous growth of carbon through benzene decomposition. J. Cryst. Growth 1976, 32, 335–349. [Google Scholar] [CrossRef]
- Dresselhaus, M.S.; Dresselhaus, G.; Eklund, P.C.; Chung, D.D.L. Lattice vibrations in graphite and intercalation compounds of graphite. Mater. Sci. Eng. 1977, 31, 141–152. [Google Scholar] [CrossRef]
- Dresselhaus, M.S.; Dresselhaus, G.; Fischer, J.E. Graphite intercalation compounds: Electronic properties in the dilute limit. Phys. Rev. B 1977, 15, 3180. [Google Scholar]
- Abrahamson, J.; Wiles, P.G.; Rhoades, B.L. Structure of carbon fibres found on carbon arc anodes. Carbon 1999, 37, 1873–1874. [Google Scholar] [CrossRef]
- Nesterenko, A.M.; Kolesnik, N.F.; Akhmatov, Y.S.; Suhomlin, V.I.; Prilutskii, O.V. Osobennosti fazovogo sostava i struktury produktov vzaimodeistviya NiO i Fe2O3 s okis’yu ugleroda. Izv. Akad. Nauk SSSR Seriya Met. 1982, 3, 12–17, Chemical Abstracts, 1982, v. 97, 201884t. [Google Scholar]
- Tennent, H.G. Carbon Fibrils, Method for Producing Same and Compositions Containing Same. US Patent # 4663230, 5 May 1987. [Google Scholar]
- Iijima, S. Helical microtubules of graphitic carbon. Nature 1991, 354, 56–58. [Google Scholar] [CrossRef]
- Mintmire, J.W.; Dunlap, B.I.; White, C.T. Are fullerene tubules metallic? Phys. Rev. Lett. 1992, 68, 631–634. [Google Scholar] [CrossRef]
- Iijima, S.; Ichihashi, T. Single-shell carbon nanotubes of 1-nm diameter. Nature 1993, 363, 603–605. [Google Scholar] [CrossRef]
- Takakura, A.; Beppu, K.; Nishihara, T.; Fukui, A.; Kozeki, T.; Namazu, T.; Miyauchi, Y.; Itami, K. Strength of carbon nanotubes depends on their chemical structures. Nat. Commun. 2019, 10, 3040. [Google Scholar] [CrossRef]
- Kempa, K.; Chura, R. Plasmons in Carbon Nanotubes. In Low-Dimensional Systems: Theory, Preparation, and Some Applications; NATO Science Series; Liz-Marzán, L.M., Giersig, M., Eds.; Springer: Dordrecht, The Netherlands, 2003; Volume 91. [Google Scholar]
- Bondarev, I.V.; Meliksetyan, A.V. Possibility for exciton Bose-Einstein condensation in carbon nanotubes. Phys. Rev. B 2014, 89, 045414. [Google Scholar] [CrossRef]
- Adhikari, C.M.; Bondarev, I.V. Optical response of ultrathin periodically aligned single-wall carbon nanotube films. MRS Adv. 2020, 5, 2685. [Google Scholar] [CrossRef]
- Adhikari, C.M.; Bondarev, I.V. Controlled exciton–plasmon coupling in a mixture of ultrathin periodically aligned single-wall carbon nanotube arrays. J. Appl. Phys. 2021, 129, 015301. [Google Scholar] [CrossRef]
- Keldysh, L.V. Coulomb interaction in thin semiconductor and semimetal films. Engl. Transl. JETP Lett. 1980, 29, 658. [Google Scholar]
- Bondarev, I.V.; Adhikari, C.M. Collective Excitations and Optical Response of Ultrathin Carbon-Nanotube Films. Phys. Rev. Appl. 2021, 15, 034001. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, J.; Liu, H.; Wang, S.; Peng, L.M. Electrically driven monolithic subwavelength plasmonic interconnect circuits. Sci. Adv. 2017, 3, e1701456. [Google Scholar] [CrossRef]
- Gupta, B.D.; Pathak, A.; Semwal, V. Carbon-Based Nanomaterials for Plasmonic Sensors: A Review. Sensors 2019, 19, 3536. [Google Scholar] [CrossRef]
- Duan, Q.; Liu, Y.; Chang, S.; Chen, H.; Chen, J.-H. Surface Plasmonic Sensors: Sensing Mechanism and Recent Applications. Sensors 2021, 21, 5262. [Google Scholar] [CrossRef]
- Jiang, K. Chapter 4—Carbon Nanotubes for Displaying. In Micro and Nano Technologies, Industrial Applications of Carbon Nanotubes; Peng, H., Li, Q., Chen, T., Eds.; Elsevier: Amsterdam, The Netherlands, 2017; pp. 101–127. [Google Scholar] [CrossRef]
- Singh, B.P.; Sikarwar, S.; Pandey, K.K.; Manohar, R.; Depriester, M.; Singh, D.P. Carbon Nanotubes Blended Nematic Liquid Crystal for Display and Electro-Optical Applications. Electron. Mater. 2021, 2, 466–481. [Google Scholar] [CrossRef]
- Zecchi, S.; Cristoforo, G.; Piatti, E.; Torsello, D.; Ghigo, G.; Tagliaferro, A.; Rosso, C.; Bartoli, M. A Concise Review of Recent Advancements in Carbon Nanotubes for Aerospace Applications. Micromachines 2025, 16, 53. [Google Scholar] [CrossRef]
- Serafinelli, C.; Fantoni, A.; Alegria, E.C.B.A.; Vieira, M. Hybrid Nanocomposites of Plasmonic Metal Nanostructures and 2D Nanomaterials for Improved Colorimetric Detection. Chemosensors 2022, 10, 237. [Google Scholar] [CrossRef]
- Pyo, S.; Eun, Y.; Sim, J.; Kim, K.; Choi, J. Carbon nanotube-graphene hybrids for soft electronics, sensors, and actuators. Micro Nano Syst. Lett. 2022, 10, 9. [Google Scholar] [CrossRef]
- Chaudhuri, K.; Alhabeb, M.; Wang, Z.; Shalaev, V.; Gogotsi, Y.; Boltasseva, A. Highly Broadband Absorber Using Plasmonic Titanium Carbide (MXene). ACS Photonics 2018, 5, 10. [Google Scholar] [CrossRef]
- Hernández-Acosta, M.A.; Martines-Arano, H.; Soto-Ruvalcaba, L.; Martínez-González, C.L.; Martínez-Gutiérrez, H.; Torres-Torres, C. Fractional Thermal Transport and Twisted Light Induced by an Optical Two-Wave Mixing in Single-Wall Carbon Nanotubes. Int. J. Therm. Sci. 2020, 147, 106136. [Google Scholar] [CrossRef]
- Obitayo, W.; Liu, T. A Review: Carbon Nanotube-Based Piezoresistive Strain Sensors. J. Sens. 2012, 652438. [Google Scholar] [CrossRef]
- Kolahdouz, M.; Xu, B.; Nasiri, A.F.; Fathollahzadeh, M.; Manian, M.; Aghababa, H.; Wu, Y.; Radamson, H.H. Carbon-Related Materials: Graphene and Carbon Nanotubes in Semiconductor Applications and Design. Micromachines 2022, 13, 1257. [Google Scholar] [CrossRef]
- Ando, T. The electronic properties of graphene and carbon nanotubes. NPG Asia Mater. 2009, 1, 17–21. [Google Scholar] [CrossRef]
- Arash, B.; Wang, Q.; Varadan, V. Mechanical properties of carbon nanotube/polymer composites. Sci. Rep. 2014, 4, 6479. [Google Scholar] [CrossRef]
- Liu, J. The Electrical Properties of Single-Walled Carbon Nanotubes. J. Phys. Conf. Ser. 2021, 1748, 052005. [Google Scholar] [CrossRef]
- Nanot, S.; Hároz, E.H.; Kim, J.-H.; Hauge, R.H.; Kono, J. Optoelectronic Properties of Single-Wall Carbon Nanotubes. Adv. Mater. 2012, 24, 4977–4994. [Google Scholar] [CrossRef]
- Rai, D.P.; Singh, Y.T.; Chettri, B.; Houmad, M.; Patra, P.K. A theoretical investigation of electronic and optical properties of (6,1) single-wall carbon nanotube (SWCNT). Carbon Lett. 2021, 31, 441–448. [Google Scholar] [CrossRef]
- Preciado-Rivas, M.R.; Torres-Sánchez, V.A.; Mowbray, D.J. Optical absorption and energy loss spectroscopy of single-walled carbon nanotubes. Phys. Rev. B 2019, 100, 235429. [Google Scholar] [CrossRef]
- Itas, Y.S.; Suleiman, A.B.; Ndikilar, C.E.; Lawal, A.; Razali, R.; Idowu, I.I.; Khandaker, M.U.; Ahmad, P.; Tamam, N.; Sulieman, A.; et al. Computational Studies of the Excitonic and Optical Properties of Armchair SWCNT and SWBNNT for Optoelectronics Applications. Crystals 2022, 12, 870. [Google Scholar] [CrossRef]
- Nanot, S.; Thompson, N.A.; Kim, J.-H.; Wang, X.; Rice, W.D.; Hároz, E.H.; Ganesan, Y.; Pint, C.L.; Kono, J. Single-Walled Carbon Nanotubes. In Springer Handbook of Nanomaterials; Springer Handbooks; Vajtai, R., Ed.; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Melchor, S.; Dobado, J.A. An algorithm for connecting two arbitrary carbon nanotubes. J. Chem. Inf. Comput. Sci. 2004, 44, 1639–1646. [Google Scholar] [CrossRef] [PubMed]
- Johnson, J.E.; Speir, J.A. Quasi-equivalent Viruses: A Paradigm for Protein Assemblies. J. Mol. Biol. 1997, 269, 665–675. [Google Scholar] [CrossRef]
- Dolafi Rezaee, M.; Dahal, B.; Watt, J.; Abrar, M.; Hodges, D.R.; Li, W. Structural, Electrical, and Optical Properties of Single-Walled Carbon Nanotubes Synthesized through Floating Catalyst Chemical Vapor Deposition. Nanomaterials 2024, 14, 965. [Google Scholar] [CrossRef]
- Kosuda, K.; Bingham, J.; Wustholz, K.; Van Duyne, R.; Groarke, R. Nanostructures and surface-enhanced Raman Spectroscopy. In Comprehensive Nanoscience and Nanotechnology; Elsevier: Amsterdam, The Netherlands, 2016; pp. 117–152. [Google Scholar]
- Vaghasiya, H.; Miclea, P.-T. Investigating Laser-Induced Periodic Surface Structures (LIPSS) Formation in Silicon and Their Impact on Surface-Enhanced Raman Spectroscopy (SERS). Optics 2023, 4, 538–550. [Google Scholar] [CrossRef]
- Mahan, G.D. Many-Particle Physics, 3rd ed.; Kluwer Academic: New York, NY, USA, 2000. [Google Scholar]
- Tasaki, S.I.; Maekawa, K.; Yamabe, T. π-band contribution to the optical properties of carbon nanotubes: Effects of chirality. Phys. Rev. B 1998, 57, 9301. [Google Scholar] [CrossRef]
- Ando, T. Theory of Electronic States and Transport in Carbon Nanotubes. J. Phys. Soc. Jpn. 2005, 74, 777. [Google Scholar] [CrossRef]
- Bondarev, I.V.; Woods, L.M.; Tatur, K. Strong exciton-plasmon coupling in semiconducting carbon nanotubes. Phys. Rev. B 2009, 80, 085407. [Google Scholar] [CrossRef]
- Ando, T. Excitons in Carbon Nanotubes. J. Phys. Soc. Jpn. 1997, 66, 1066. [Google Scholar]
- Adhikari, C.M.; Morris, D.M.; Noonan, T.W.; Neupane, T.; Lamichhane, B.R.; Gautam, B.R. Dispersion in Single-Wall Carbon Nanotube Film: An Application of Bogoliubov–Valatin Transformation for Hamiltonian Diagonalization. Condens. Matter 2023, 8, 53. [Google Scholar] [CrossRef]
- Gao, W.; Doiron, C.F.; Li, X.; Kono, J.; Naik, G.V. Macroscopically Aligned Carbon Nanotubes as a Refractory Platform for Hyperbolic Thermal Emitters. ACS Photonics 2019, 6, 1602–1609. [Google Scholar]
- Roberts, J.A.; Yu, S.-J.; Ho, P.-H.; Schoeche, S.; Falk, A.L.; Fan, J.A. Tunable Hyperbolic Metamaterials Based on Self-Assembled Carbon Nanotubes. Nano Lett. 2019, 19, 3131–3137. [Google Scholar] [CrossRef] [PubMed]
- Schöche, S.; Ho, P.H.; Roberts, J.A.; Yu, S.J.; Fan, J.A.; Falk, A.L. Mid-IR and UV-Vis-NIR Mueller matrix ellipsometry characterization of tunable hyperbolic metamaterials based on self-assembled carbon nanotubes. J. Vac. Sci. Technol. B 2020, 38, 014015. [Google Scholar] [CrossRef]
- Jerome, B.; Prasad, C.S.; Doumani, J.; Dewey, O.S.; Baydin, A.; Pasquali, M.; Kono, J.; Gao, W.; Alabastri, A.; Naik, G.V. Outcoupling hyperbolic modes from aligned carbon nanotube films. In CLEO: QELS_Fundamental Science; Optica Publishing Group: Washington, DC, USA, 2022. [Google Scholar]
- Schlittler, R.R.; Seo, J.W.; Gimzewski, J.K.; Durkan, C.; Saifullah, M.S.M.; Welland, M.E. Single Crystals of Single-Walled Carbon Nanotubes Formed by Self-Assembly. Science 2001, 292, 1136–1139. [Google Scholar] [CrossRef]
- Chen, Y.; Lyu, M.; Zhang, Z.; Yang, F.; Li, Y. Controlled Preparation of Single-Walled Carbon Nanotubes as Materials for Electronics. ACS Cent. Sci. 2022, 8, 1490–1505. [Google Scholar] [CrossRef] [PubMed]
- Gao, J. Heterojunction Bipolar Transistors for Circuit Design: Microwave Modeling and Parameter Extraction; Wiley: Berlin, Germany, 2015. [Google Scholar]
- Adhikari, C.M.; Dahal, D.; Kunwar, S.; Gautam, B.R. Ti3C2 and Ti2C MXenes-Based Distributed Bragg Reflectors in Fabry Pérot Cavity’s Resonance Tuning. J. Electron. Mater. 2025, 1–10. [Google Scholar] [CrossRef]
- Sakurai, S.; Inaguma, M.; Futaba, D.N.; Yumura, M.; Hata, K. A Fundamental Limitation of Small Diameter Single-Walled Carbon Nanotube Synthesis-A Scaling Rule of the Carbon Nanotube Yield with Catalyst Volume. Materials 2013, 6, 2633–2641. [Google Scholar] [CrossRef]
- Daneshvar, F.; Chen, H.; Noh, K.; Sue, H.J. Critical challenges and advances in the carbon nanotube–metal interface for next-generation electronics. Nanoscale Adv. 2021, 3, 942–962. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).