Abstract
Kerr nonlinear effect extremely impacts both the spectral and the temporal evolutions of ultrashort pulses, although it is challenging to tailor over a broadened spectral region. In this work, we propose an on-chip Si3N4-organic hybrid waveguide with sophisticated non-monotonic nonlinear coefficient γ(ω). A chirp-free pulse can be broadened or compressed at different peak powers in the normal dispersion range. The impact of the second-order Kerr nonlinearity with respect to frequency can overbalance that of dispersion. This new method deepens the understanding of the high-order nonlinear effects and help exploit innovative nonlinearity-engineered on-chip platforms for pulse shaping in the immediate future.
1. Introduction
Ultrafast optics hold great promise for versatile applications including time-resolved spectroscopy [], imaging and microscopy [], optical communications [], and strong field physics []. The most common sources to generate pulses in the femtosecond and picosecond time scales are mode-locked lasers. Pulse shaping is complementary to ultrashort pulse generation and widely applied in temporal pulse compression in the cycle regime [,,,], and coherent laser control of quantum processes [,]. Among these, pulse compression through nonlinear effects in the anomalous dispersion regime has been widely used [,,]. Kerr nonlinearities not only play a critical role in generating new spectral components and shaping the spectrum but also act together with chromatic dispersion to affect the pulse waveform evolution [,].
The dispersion and Kerr nonlinearities are controlled by two parameters that are dependent on frequency, β(ω) and γ(ω), known as the propagation constant and the nonlinear coefficient, respectively. Traditionally, dispersion in nonlinear optical systems is crucial to manipulate an ultrashort pulse [,]. In fact, nonlinear effects also greatly influence the temporal evolution of ultrashort pulses. As an example, optical fibers typically have a nonlinear coefficient γ(ω) that decreases with wavelength, which leads to self-steepening during the pulse propagation, associated with the first-order term in the Taylor expansion of γ(ω) and responsible for the formation of an optical shock at the pulse falling edge.
In contrast with optical fibers, on-chip integrated waveguides have an advantage in engineering γ(ω) due to strong mode confinement and hybrid integration of novel materials. There have been some reports on the self-steepening in nonlinear integrated waveguides. An optical shock with several tens of femtoseconds has been studied in silicon waveguides [,]. It can even be as short as 3 fs in a Si3N4 waveguide, accompanied with an octave-spanning supercontinuum assisted by self-steepening []. This study focused on the role of self-steepening in silicon waveguides with a large first-order nonlinear term up to 4.2 × 10−7 s/m/W and a negligible 2nd-order nonlinear term. Anomalous self-steepening has influenced soliton self-compression in photonic crystal waveguides []. The group-velocity modulation leads to a self-steepening coefficient two orders of magnitude larger than traditional systems, which results in a temporal forward tilt and pulse advance in the time domain. Recently, a rectangle-wave-shaped pulse waveform with a steep rising pulse edge down to 13 fs has been studied in an organic hybrid waveguide with an increased nonlinearity with wavelength []. This work separates the first-order nonlinear term from the intensity-dependent group velocity term and considers their impacts separately. However, the 2nd-order Kerr nonlinear term in the γ(ω)’s Taylor expansion has been ignored in most past works. Little attention is paid to tailoring the higher-order (i.e., second order) nonlinearity and studying its influence. When high-order nonlinear terms (mainly up to the third-order term) are taken into account, second-order nonlinearity only slightly modifies the influence of first-order nonlinearity since the effect of the first-order term is much greater than that of the second-order term []. Compared with previous studies focused on first-order nonlinearity, we study how the second-order term dynamically changes the pulse in the time and spectral domains using a designed hybrid waveguide without the influence of first-order nonlinearity.
Here, we propose a Si3N4-organic hybrid slot waveguide with non-monotonic frequency-dependent nonlinearity to study the influence of the higher-order nonlinear term on pulse shaping. Due to second-order Kerr nonlinearity, a chirp-free pulse is compressed from 100 to 28 fs in the normal dispersion regime, accompanied by a supercontinuum generation from 745 to 2467 nm (>1.5 octaves). With a varied input peak power, the pulse can be broadened or compressed due to the competition between group-velocity dispersion and second-order Kerr nonlinearity, which provides greater insight into the physical mechanism of high-order nonlinearity.
2. Device Design and Modeling
Organic materials with large nonlinear susceptibilities make organic hybrid waveguides promising for nonlinear devices [,,]. 2-methoxy-5-(2-ethylhexyloxy)-1, 4-phenylenvinylene (MEH-PPV) is one of the most popular organic materials for Kerr nonlinearities. The nonlinear refractive index n2 is found to be 4.5 × 10−17 m2/W by z-scan measurements [], which is two orders of magnitude higher than that of stoichiometric Si3N4 []. This polymer can be spin-coated on a chip. As shown in Figure 1, the proposed waveguide consists of two Si3N4 strips coated with MEH-PPV, with strip widths W1 = 700 nm and W2 = 500 nm, gap G = 100 nm, strip height H = 600 nm, and sidewall angle θ = 85°.
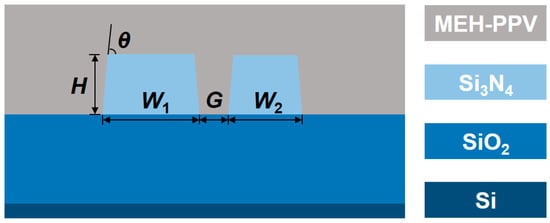
Figure 1.
The proposed Si3N4-organic slot hybrid waveguide with a non-monotonic γ over wavelength.
The two material dispersions are taken into account using Sellmeier equations. For Si3N4, we use the following Sellmeier equation []:
For MEH-PPV, we use the following Sellmeier equation []:
We also obtain the effective refractive index (neff) of the fundamental quasi-TE mode by employing a full-vectorial mode solver.
We obtain a non-monotonic frequency-dependent nonlinear coefficient in the proposed waveguide. The dispersion, D, is around −600 ps/nm/km from 1000 to 1450 nm as shown in Figure 2a. We obtain an all-normal dispersion profile with the dispersion coefficient β2 lower than 3 ps2/m over a 1610 nm-wide range from 600 nm to 2210 nm. The minimum β2 is 0.27 ps2/m at around 800 nm. Although on-chip waveguides are typically mm long, such a dispersion profile means a non-negligible group delay change over this spectral bandwidth. This is suitable to study the influences of the positive β2 and the second-order nonlinearity. Note that the dispersion is intentionally designed to be strong enough to achieve normal dispersion. In Figure 2b, the nonlinear coefficient γ increases from 6.4 to 51.5 /m/W, from 600 to 1400 nm, and then decreases to 9.7 /m/W until 2500 nm. The nonlinear coefficient is expressed by , where λ is the wavelength, Aeff is the effective mode area, and can be viewed as weighted by power confinement ratios in different waveguide materials []. The averaged can be rewritten as []
where k, , , and are the wave vector, the permittivity of vacuum, the permeability of vacuum, and the unit vector pointing in the positive z-direction, respectively. eν and hν are the electric and magnetic modal field distributions of propagating modes in the waveguide, respectively. The definition of can separate γ into two parts describing the linear (Aeff) and nonlinear () characteristics. When wavelength increases, the quasi-TE mode spreads from the Si3N4 strips to the MEH-PPV slot. As shown in Figure 2c, in the spectral range from 600 to 2500 nm, the power confinement factor in the strip Si3N4 (ΓSiN) decreases from 0.9 to 0.13, while the power confinement factor in the slot MEH-PPV (ΓMEH-PPV) increases from 0.1 to 0.8. The averaged increases linearly from 2.4 × 10−19 to 3.1 × 10−17 m2/W due to the different values of in MEH-PPV and Si3N4, while the Aeff changes slightly at a short wavelength and increases sharply over 2000 nm (see Figure 2d). Thus, peaking at 1400 nm, γ experiences a significant increase and decrease with wavelength, which provides an opportunity to study the high-order terms of γ(ω) over a broad band.
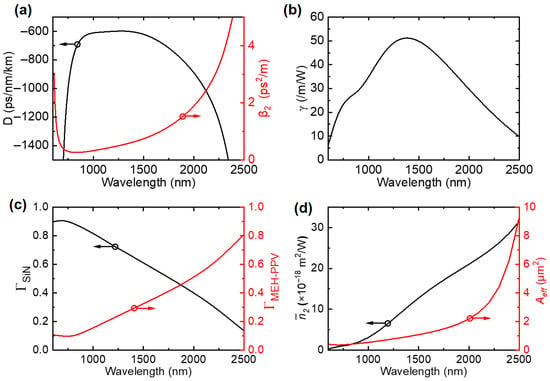
Figure 2.
(a) The calculated all-normal dispersion and (b) of the designed slot waveguide. (c) The power confinement factors in two materials of Si3N4 (ΓSiN) and MEH-PPV (ΓMEH-PPV). (d) The averaged nonlinear refractive index () and the effective mode area (Aeff) as a function of wavelength.
We consider all frequency-dependent linear and nonlinear effects governed by β(ω) and γ(ω). The Taylor expansion of β(ω) traditionally describes the frequency-dependent linear dispersion, but nonlinear effects introduce not only intensity-dependent but also frequency-dependent modifications. The linear and nonlinear effects can be explained as follows:
where n, ω, c, I, and P are the refractive index, the angular frequency, the speed of light in vacuum, the optical intensity, and the optical power, respectively. β(ω) is expanded in a Taylor series to define the high-order dispersion coefficients, and γ(ω) can be treated in the same way:
where (n = 0, 1, 2) is evaluated at . In most nonlinear schemes, all order terms of β(ω) are included, but only the first two terms are typically retained for γ(ω), i.e., γ1 is related to the self-steepening effect, while γ2 is always negligible.
It is useful to define the length scales associated with the high-order nonlinearity similar to the high-order dispersion lengths []. LNL1 and LNL2 are the first- and second-order nonlinear lengths, respectively. They are described as and , respectively, where T0 is the pulse width of the input pulse. γ1 is typically deemed to be responsible for the self-steepening effect in conventional schemes, in which , and thus can be written as []. In traditional nonlinear waveguides, the pulse without initial chirp broadens monotonically with distance in the normal dispersion regime. Nonlinear phase shifts significantly enhance pulse broadening due to a nearly linear positive chirp from self-phase modulation (SPM). In contrast, using the proposed waveguide with tailored γ(ω) that includes a negative γ2, we can study how the high-order nonlinearity entirely shapes the pulse even with a positive β2. More specifically, the effect of γ2 is the opposite to that of β2. With sufficiently high peak power, second-order nonlinearity can reshape the pulse and overbalance that of normal dispersion, causing pulse compression.
To study the influence of frequency-dependent nonlinear effects on the pulse propagation, we use a generalized nonlinear Schrödinger equation (GNLSE) [,] with frequency-dependent dispersion, propagation loss, and nonlinearity. We consider terms up to the sixth order in the expansion of γ(ω). The GNLSE also includes the Raman contribution to account for the Raman-induced frequency shift []. A chirp-free hyperbolic secant pulse centered at 1400 nm is launched into the proposed waveguide. The full width at half-maximum (FWHM) of the input pulse is set to be 100 fs. The Raman shock time τshockR is 0.23 fs. The Raman scattering properties of the two materials are given in [,]. The scattering loss is set to be 2 dB/cm. We neglect two-photon absorption in this band. Here, we set the carrier frequency at the point where the γ(ω) reaches its maximum value to have γ1 close to zero, and the influence of γ2 can be isolated. The β2, the γ0, and the γ2 at the pump wavelength are 6.28 × 10−25 s2/m, 51.5 /m/W, and −2.22 × 10−28 s2/m/W, respectively.
3. Evolution of Pulses in the Hybrid Waveguides
Figure 3 shows the FWHM as a function of distance at different input peak powers. As is the case in conventional waveguides, the chirp-free pulse broadens monotonically over propagation distance at a small peak power of 1 and 3 kW due to normal dispersion. When peak power increases from 1 to 3 kW, SPM enhances pulse broadening by inducing a larger positive chirp. However, the pulse no longer undergoes broadening but becomes rather slightly narrower in the initial stage when the peak power reaches 5 kW. This is because γ2P and β2 are roughly balanced. The FWHM of the pulse decreases to 91.4 fs at 0.106 mm and then increases back to 100 fs at 0.147 mm. The effect of the negative γ2 can almost balance that of the positive β2 initially, but afterwards due to propagation loss the nonlinearity-induced pulse narrowing becomes weaker, and the pulse becomes broadened again due to dispersion. When the peak power is larger than 5 kW, the pulses are compressed because the effect of the negative γ2 is larger than that of the positive β2. Although the positive chirp induced by SPM still exists, the combined effect of both the negative γ2 and the positive β2 is equivalent to anomalous dispersion. As the peak power continues to increase, the obtained pulse width decreases more quickly. The pulse is compressed to 51 fs with the peak power of 6 kW, while the FWHM can reach 35 fs with the peak power of 7 kW. The compressed pulse waveform can only maintain a very short propagation distance. Then, the pulse may undergo broadening or splitting. When the peak power is 8 kW, the pulse is nonlinearly compressed to 28 fs by a factor of 3.6 at a distance of 0.053 mm.
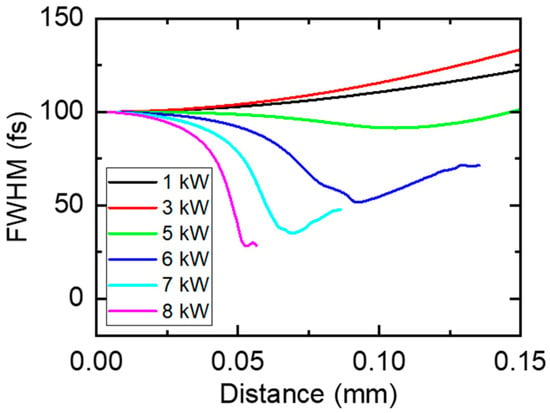
Figure 3.
The FWHM of the pulse as a function of distance at different input peak power.
As an example, we show the time and spectral evolutions of the pulse when the peak power is 8 kW. In this case, the dispersion length LD = 5.12 × 10−3 m, the first-order nonlinear length LNL1 approaches infinity, and the second-order nonlinear length LNL2 = 1.81 × 10−3 m, which means that, although the normal dispersion is designed to be relatively large, the effect of the second-order nonlinearity is still much stronger than that of the normal dispersion. To further highlight the role of γ2, we also show the case with only γ0 and no frequency dependence for comparison below.
The temporal evolutions, with up to sixth-order γ6 and only γ0, are shown in Figure 4a and Figure 4b, respectively. In both Figure 4a,b, the two pulses change slightly before 0.02 mm, because of relatively small nonlinearity accumulation. Additionally, the two pulses tilt backward slightly, associated with self-steepening caused by weak intensity-dependent group delay (i.e., in the GNLSE) []. When high-order γ(ω) terms in the GNLSE are considered (see Figure 4a), the pulse is compressed, and the intensity accumulates at the pulse peak after 0.04 mm. This is accompanied by spectral broadening, which is only observed in the anomalous dispersion regime before. In Figure 4b, the pulse is broadened, and the peak power decreases along the distance. Figure 4c and Figure 4d compare the pulse waveforms and chirps in the two cases at 0.053 mm, respectively. The FWHM of the pulse is compressed from 100 to 28 fs with the actual higher order γ terms (red curve). Unfortunately, the pulse pedestal is still large when compared with the input pulse (dashed curve), because nonlinear effects are weak at the pulse pedestal. In contrast, the pulse with the frequency-independent γ0 (blue curve) is broadened to 118 fs. In Figure 4d, the main difference between the two chirps exists at the pulse temporal center. The maximum chirp is enhanced from 54 to 93 THz, when we compare the actual frequency-dependent γ(ω) (red curve) with the constant γ0 (blue curve).
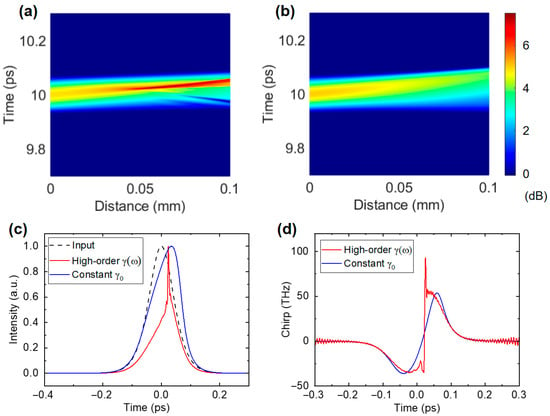
Figure 4.
Temporal evolutions of the pulse when considering (a) the all-order γ(ω) and (b) the constant γ0. (c) The output pulse waveforms (the dotted line indicates the input pulse) and (d) the chirps at 0.053 mm.
Figure 5a,b show the spectral evolutions along the waveguide in the two cases above. At the beginning of propagation before 0.045 mm, the pulse experiences nearly symmetric spectral broadening due to SPM, while the high-order nonlinearity induces more oscillatory peaks in Figure 5a. At a propagation distance of 0.055 mm, a supercontinuum including deeper blue and red components is formed from 745 to 2467 nm at −30 dB, covering more than 1.5 octaves. With a constant γ0, the spectrum spans from 1010 to 1870 nm (see Figure 5b), much narrower than that in Figure 5a.
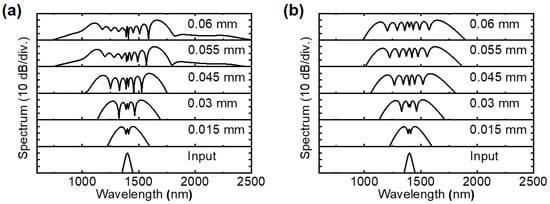
Figure 5.
Spectral evolutions of the pulse when considering (a) the high-order γ(ω) terms and (b) the constant γ0.
A better understanding is obtained by checking the spectrogram evolutions with the two different γ(ω) profiles in Figure 6 and Figure 7. The 2nd-order nonlinearity does not take effect before 0.02 mm, as shown in Figure 6b and Figure 7b. At 0.046 mm, the new frequency components are generated at the pulse peak when high-order γ terms are included (see Figure 6c), which does not occur when only considering γ0 in Figure 7c. Certain frequencies overlap temporally, and additional coherent four-wave mixing (FWM) between them occur. The second-order nonlinearity acts as an additional source [,] and affects phase-matching conditions given by the normal dispersion []. We also note that this effect also modifies the pulse waveform substantially (compare the black circles in Figure 6c and Figure 7c). Because the newly generated frequency components from the high-order nonlinearity have not yet walked off, the power increases at the center of the pulse. Then, the higher peak power induces deeper red and blue components at 0.053 mm, as shown in the white circle in Figure 6c. The pedestals at the leading and trailing pulse edges are still stable without interactions or walking off, as shown in the yellow circles in Figure 6d and Figure 7d. It is crucial to emphasize that the frequency dependence of the nonlinear effect plays a role in controlling both the main pulse waveform and the newly generated frequency components.
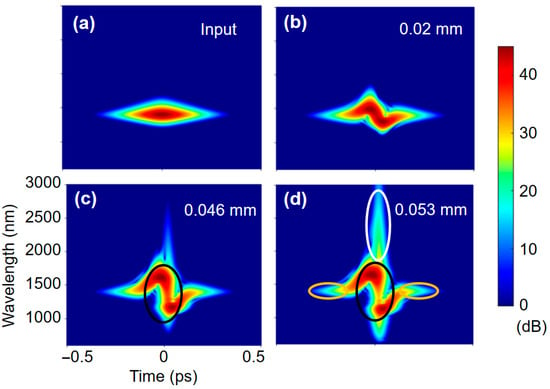
Figure 6.
Spectrogram evolution of the pulse at (a) 0 mm, (b) 0.02 mm, (c) 0.046 mm, and (d) 0.053 mm when considering the high-order γ(ω). The modified pulse waveforms, the pedestals, and the deeper red components are shown in the black circles, the yellow circles, and the white circles, respectively.
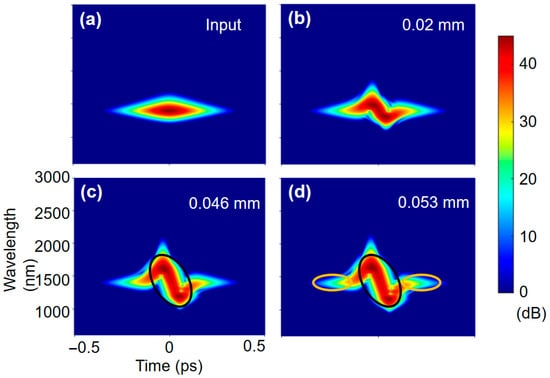
Figure 7.
Spectrogram evolution of the pulse at (a) 0 mm, (b) 0.02 mm, (c) 0.046 mm, and (d) 0.053 mm when considering the constant γ0. The almost unchanged pulse waveforms and the pedestals are shown in the black and the yellow circles, respectively.
Figure 8a,b illustrates the spectral and temporal properties when the input peak power increased from 5 to 9 kW. As peak power increases, a narrower compressed pulse with wider spectral broadening is generated at a shorter propagation distance. As shown in Figure 8a, the distance decreases from 0.104 to 0.045 mm, while the output peak power increases linearly. However, in Figure 8b, the spectral broadening and the temporal compression as a function of input peak power become saturated, when the peak power is larger than 7 kW, indicating that the impact of γ2 is ultimately discounted as the pulse spectrum greatly expands to the bands where chromatic dispersion becomes stronger and stronger. As shown in Figure 5a and Figure 6d, γ2 acts as an additional source to generate new spectral components from 745 to 2467 nm within the region with a relatively low dispersion. When the newly spectral components generate beyond the low-dispersion region, they walk away from each other under the influence of the accumulated dispersion. Therefore, the spectrum is no longer broadened, and the FWHM of the pulse is no longer compressed even as the input peak power increases. This can also be interpreted as the phase-matching condition given by the γ2P and normal dispersion no longer being satisfied beyond the low-dispersion region.
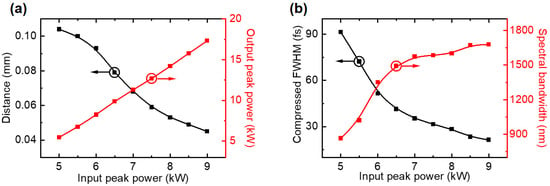
Figure 8.
(a) The optimal compressed distance, the spectral bandwidth at −30 dB level as input peak power increases from 5 to 9 kW, (b) the compressed FWHM, and the output peak power as a function of the input peak power with saturation behaviors beyond 7 kW.
4. Discussion
We also consider the practical feasibility of the Si3N4-polymer hybrid waveguide. A more in-depth discussion of the fabrication feasibility and structural tolerances is as follows. We change the W1, W2, G, and H within a range of 2% based on the actual fabrication error in Figure 9. The nonlinear coefficient is almost insensitive to the dimension variations. The second-order nonlinearity γ2 could be almost unchanged, which reduces the requirements for fabrication tolerances.
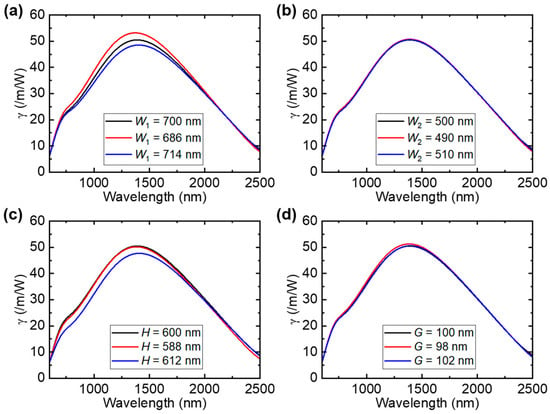
Figure 9.
Nonlinear coefficient profiles with (a) W1, (b) W2, (c) G, and (d) H changed within a range of 2%.
The device is fabricated on a standard Si wafer with a thermal oxide on the top wafer. A 600 nm-thick Si3N4 is deposited by using low-pressure chemical vapor deposition. The device pattern is transferred to the Si3N4 layer using electron beam lithography and inductively coupled plasma etching. After removing the remaining photoresist, the dissolved MEH-PPV is hybrid integrated on the chip by means of spin coating under vacuum to remove the air in the narrow slot [].
We find more degrees of freedom to engineer nonlinear phenomena and help engineer the nonlinearity in on-chip platforms. Our work provides a possible solution for the further applications of pulse compression and pulse shaping, such as all-optical switching [], communications based on spectral phase encoding and decoding [], multiphoton confocal microscopy [], and so on, which pose requirements for miniaturization and integration.
5. Conclusions
In summary, we have proposed a Si3N4-organic hybrid slot waveguide with engineered Kerr nonlinearity. A chirp-free pulse can be compressed in the normal dispersion range, which was observed in the anomalous dispersion regime before. Although we used the specific waveguide as an example to emphasize the role of the frequency-dependent γ(ω), these studies not only explain more physical mechanisms of high-order nonlinearity but also help exploit innovative chip-based platforms for engineering the nonlinearity to support pulse compression and pulse shaping.
Author Contributions
Conceptualization, methodology, and software, Y.Z. and L.Z.; validation, Y.L. and L.X.; investigation, Y.Z.; data curation, Y.Z. and L.X.; writing—original draft preparation, Y.Z.; writing—review and editing, Y.Z., Y.L. and L.Z.; supervision, L.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Acknowledgments
The authors gratefully acknowledge support by the Advanced Integrated Optoelectronics Facility at Tianjin University.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| MEH-PPV | 2-methoxy-5-(2-ethylhexyloxy)-1, 4-phenylenvinylene |
| GNLSE | generalized nonlinear Schrödinger equation |
| FWHM | full width at half-maximum |
| FWM | four-wave mixing |
References
- Allison, T.K.; Kunin, A.; Schönhense, G. Cavity-enhanced high-order harmonic generation for high-performance time-resolved photoemission experiments. APL Photonics 2025, 10, 010906. [Google Scholar] [CrossRef]
- Glerean, F.; Rigoni, E.M.; Jarc, G.; Mathengattil, S.Y.; Montanaro, A.; Giusti, F.; Mitrano, M.; Benatti, F.; Fausti, D. Ultrafast pump-probe phase-randomized tomography. Light. Sci. Appl. 2025, 14, 115. [Google Scholar] [CrossRef] [PubMed]
- Turitsyn, S.K.; Prilepsky, J.E.; Le, S.T.; Wahls, S.; Frumin, L.L.; Kamalian, M.; Derevyanko, S.A. Nonlinear Fourier transform for optical data processing and transmission: Advances and perspectives. Optica 2017, 4, 307–322. [Google Scholar] [CrossRef]
- Kang, Y.; Wang, X.; Tang, L.; Liu, X.; Gong, X. High Repetition Rate and High Energy Ultrashort Laser Pulse: The Next Light Source for Attosecond Spectroscopy. ACS Photonics 2025, 12, 2279–2290. [Google Scholar] [CrossRef]
- Tan, D.T.H.; Agarwal, A.M.; Kimerling, L.C. Nonlinear photonic waveguides for on-chip optical pulse compression. Laser Photonics Rev. 2015, 9, 294–308. [Google Scholar] [CrossRef]
- Balciunas, T.; Fourcade-Dutin, C.; Fan, G.; Witting, T.; Voronin, A.A.; Zheltikov, A.M.; Gerome, F.; Paulus, G.G.; Baltuska, A.; Benabid, F. A strong-field driver in the single-cycle regime based on self-compression in a kagome fibre. Nat. Commun. 2015, 6, 6117. [Google Scholar] [CrossRef]
- Travers, J.C.; Grigorova, T.F.; Brahms, C.; Belli, F. High-energy pulse self-compression and ultraviolet generation through soliton dynamics in hollow capillary fibres. Nat. Photonics 2019, 13, 547–554. [Google Scholar] [CrossRef]
- Nagy, T.; Simon, P.; Veisz, L. High-energy few-cycle pulses: Post-compression techniques. Adv. Phys. X 2021, 6, 1845795. [Google Scholar] [CrossRef]
- Nuernberger, P.; Vogt, G.; Brixner, T.; Gerber, G. Femtosecond quantum control of molecular dynamics in the condensed phase. Phys. Chem. Chem. Phys. 2007, 9, 2470–2497. [Google Scholar] [CrossRef]
- Weiner, A.M. Ultrafast optical pulse shaping: A tutorial review. Opt. Commun. 2011, 284, 3669–3692. [Google Scholar] [CrossRef]
- Dudley, J.M.; Genty, G.; Coen, S. Supercontinuum generation in photonic crystal fiber. Rev. Mod. Phys. 2006, 78, 1135–1184. [Google Scholar] [CrossRef]
- Dekker, R.; Usechak, N.; Först, M.; Driessen, A. Ultrafast nonlinear all-optical processes in silicon-on-insulator waveguides. J. Phys. D Appl. Phys. 2007, 40, R249. [Google Scholar] [CrossRef]
- Yue, Y.; Zhang, L.; Huang, H.; Beausoleil, R.G.; Willner, A.E. Silicon-on-Nitride Waveguide With Ultralow Dispersion Over an Octave-Spanning Mid-Infrared Wavelength Range. IEEE Photonics J. 2012, 4, 126–132. [Google Scholar] [CrossRef]
- Yang, M.; Xu, L.; Wang, J.; Liu, H.; Zhou, X.; Li, G.; Zhang, L. An octave-spanning optical parametric amplifier based on a low-dispersion silicon-rich nitride waveguide. IEEE J. Sel. Top. Quantum Electron. 2018, 24, 8300607. [Google Scholar] [CrossRef]
- Voronin, A.A.; Zheltikov, A.M. Soliton self-frequency shift decelerated by self-steepening. Opt. Lett. 2008, 33, 1723–1725. [Google Scholar] [CrossRef]
- Panoiu, N.C.; Liu, X.; Osgood, R.M. Self-steepening of ultrashort pulses in silicon photonic nanowires. Opt. Lett. 2009, 34, 947–949. [Google Scholar] [CrossRef]
- Zhang, L.; Yan, Y.; Yue, Y.; Lin, Q.; Painter, O.; Beausoleil, R.G.; Willner, A.E. On-chip two-octave supercontinuum generation by enhancing self-steepening of optical pulses. Opt. Express 2011, 19, 11584–11590. [Google Scholar] [CrossRef]
- Liao, J.; Tan, Y.; Gao, Y.; Wang, Z.; Sun, Y.; Ma, L.; Li, X. Giant anomalous self-steepening and temporal soliton compression in silicon photonic crystal waveguides. APL Photonics 2021, 6, 086107. [Google Scholar] [CrossRef]
- Zhai, Y.; Xu, L.; Ren, K.; Zhang, L. Reversed self-steepening in Si3N4-organic hybrid slot waveguides with engineered nonlinearity. J. Phys. D Appl. Phys. 2024, 57, 465105. [Google Scholar] [CrossRef]
- Bose, S.; Melchert, O.; Willms, S.; Babushkin, I.; Morgner, U.; Demircan, A.; Agrawal, G.P. Role of frequency dependence of the nonlinearity on a soliton’s evolution in photonic crystal fibers. Opt. Lett. 2021, 46, 3921–3924. [Google Scholar] [CrossRef]
- Nielsen, M.P.; Shi, X.; Dichtl, P.; Maier, S.A.; Oulton, R.F. Giant nonlinear response at a plasmonic nanofocus drives efficient four-wave mixing. Science 2017, 358, 1179–1181. [Google Scholar] [CrossRef]
- Das, S.; Wenner, B.R.; Allen, J.W.; Allen, M.S.; Vasilyev, M. Investigation of hybrid silicon-nitride/polymer waveguides for second-harmonic generation. IEEE Photonics J. 2019, 11, 4500509. [Google Scholar] [CrossRef]
- Wang, Y.; He, S.; Gao, X.; Ye, P.; Lei, L.; Dong, W.; Zhang, X.; Xu, P. Enhanced optical nonlinearity in a silicon-organic hybrid slot waveguide for all-optical signal processing. Photonics Res. 2022, 10, 50–58. [Google Scholar] [CrossRef]
- Ikeda, K.; Saperstein, R.E.; Alic, N.; Fainman, Y. Thermal and Kerr nonlinear properties of plasma-deposited silicon nitride/silicon dioxide waveguides. Opt. Express 2008, 16, 12987–12994. [Google Scholar] [CrossRef]
- Luke, K.; Okawachi, Y.; Lamont, M.R.; Gaeta, A.L.; Lipson, M. Broadband mid-infrared frequency comb generation in a Si3N4 microresonator. Opt. Lett. 2015, 40, 4823–4826. [Google Scholar] [CrossRef]
- Bader, M.A.; Marowsky, G.; Bahtiar, A.; Koynov, K.; Bubeck, C.; Tillmann, H.; Hörhold, H.-H.; Pereira, S. Poly (p-phenylenevinylene) derivatives: New promising materials for nonlinear all-optical waveguide switching. J. Opt. Soc. Am. B 2002, 19, 2250–2262. [Google Scholar] [CrossRef]
- Afshar, S.; Monro, T.M. A full vectorial model for pulse propagation in emerging waveguides with subwavelength structures part I: Kerr nonlinearity. Opt. Express 2009, 17, 2298–2318. [Google Scholar] [CrossRef]
- Lin, Q.; Painter, O.J.; Agrawal, G.P. Nonlinear optical phenomena in silicon waveguides: Modeling and applications. Opt. Express 2007, 15, 16604–16644. [Google Scholar] [CrossRef] [PubMed]
- Fang, Y.; Bao, C.; Li, S.A.; Wang, Z.; Geng, W.; Wang, Y.; Han, X.; Jiang, J.; Zhang, W.; Pan, Z. Recent progress of supercontinuum generation in nanophotonic waveguides. Laser Photonics Rev. 2023, 17, 2200205. [Google Scholar] [CrossRef]
- Wang, Y.; Yue, R.; Han, H.; Liao, X. Raman study of structural order of a-SiNx: H and its change upon thermal annealing. J. Non-Cryst. Solids 2001, 291, 107–112. [Google Scholar] [CrossRef]
- Zhao, P.; Ye, Z.; Karlsson, M.; Torres-Company, V.; Andrekson, P.A. Low-Noise Phase-sensitive Parametric Amplifiers Based on Integrated Silicon-Nitride-Waveguides for Optical Signal Processing. J. Lightwave Technol. 2022, 40, 1847–1854. [Google Scholar] [CrossRef]
- Weiner, A.M. Femtosecond pulse shaping using spatial light modulators. Rev. Sci. Instrum. 2000, 71, 1929–1960. [Google Scholar] [CrossRef]
- Efimov, A.; Reitze, D.H. Programmable dispersion compensation and pulse shaping in a 26-fs chirped-pulse amplifier. Opt. Lett. 1998, 23, 1612–1614. [Google Scholar] [CrossRef] [PubMed]
- Bardeen, C.J.; Yakovlev, V.V.; Squier, J.A.; Wilson, K.R.; Carpenter, S.D.; Weber, P.M. Effect of pulse shape on the efficiency of multiphoton processes: Implications for biological microscopy. J. Biomed. Opt. 1999, 4, 362–367. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).