You are currently viewing a new version of our website. To view the old version click .
MDPIMDPI
Search all articles
Mathematical and Computational Applications
Download PDF
  • Article
  • Open Access

19 August 2024

Comparison of Interval Type-3 Mamdani and Sugeno Models for Fuzzy Aggregation Applied to Ensemble Neural Networks for Mexican Stock Exchange Time Series Prediction

,
,
and
1
Tijuana Institute of Technology, Tecnologico Nacional de Mexico, Tijuana 29050, BC, Mexico
2
School of Engineering, Universidad Autonoma de Baja California, Tijuana 21100, BC, Mexico
*
Author to whom correspondence should be addressed.
Math. Comput. Appl.2024, 29(4), 67;https://doi.org/10.3390/mca29040067
This article belongs to the Section Engineering
Version Notes
Order Reprints

Abstract

In this work, interval type-2 and type-3 fuzzy systems were designed, of Mamdani and Sugeno types, for time series prediction. The aggregation performed by the type-2 and type-3 fuzzy systems was carried out by using the results of an optimized ensemble neural network (ENN) obtained with the particle swarm optimization algorithm. The time series data that were used were of the Mexican stock exchange. The method finds the best prediction error. This method consists of the aggregation of the responses of the ENN with type-2 and type-3 fuzzy systems. In this case, the systems consist of five inputs and one output. Each input is made up of two membership functions and there are 32 possible fuzzy if-then rules. The simulation results show that the approach with type-2 and type-3 fuzzy systems provides a good prediction of the Mexican stock exchange. Statistical tests of the comparison of type-1, type-2, and type-3 fuzzy systems are also presented.

1. Introduction

Time series prediction is important as it allows us to prevent future events and take preventive measures [1,2,3,4]. Fuzzy logic [5,6] has gained a lot of recognition due to the diversity of its applications, which range from the control of industrial processes to the design of automatic deduction devices, the construction of electronic devices for domestic use and medical diagnostic systems, and time series prediction [7,8].
ENNs comprise a set of neural networks (NNs) that are used to solve complex problems [9,10,11]. The main idea of ENNs is that the outputs of multiple NNs can be combined to enhance the final results [12,13,14].
In this paper, ENNs are used for time series prediction since, by combining multiple results, a good prediction can be achieved. ENNs have already been applied in many areas, such as medical diagnosis, image recognition, classification of seismic signals, and prediction of time series for different problems [14,15,16,17,18,19].
Fuzzy logic (of type-1) has been booming in the area of industrial control and in other areas, such as robotics and control [20,21,22,23]. Type-2 fuzzy systems have been able to surpass type-1 fuzzy systems since they handle uncertainty and, in this way, better results can be obtained when applying them in different areas [24,25,26,27,28]. Fuzzy systems can help solve complex problems. For this reason, we proposed the design of type-2 and type-3 fuzzy systems for enhancing prediction with respect to type 1 [29,30,31,32,33].
The contribution of this work is the design of type-3 fuzzy systems in ENN decision making, as type-3 fuzzy logic could provide a better ability in handling the uncertainty of combining the responses of the modules forming the ENN. In this case, this is done for the prediction of the Mexican stock exchange [34]. A type-3 fuzzy system is proposed as a model for ENN aggregation to enhance time series prediction. In previous work, we worked with type-1 and type-2 fuzzy systems. However, in this work, Mamdani and Sugeno type-3 fuzzy systems are proposed for the first time in this application. The systems are made up of five inputs and one output (called ‘prediction’) with 32 possible fuzzy rules. Also, a type-2 fuzzy system was designed to compare the results and verify whether the type-3 fuzzy systems can obtain better results for time series prediction.
The objective of this article is to design interval type-3 fuzzy inference systems for aggregating the results of the ensemble neural network, which was optimized with the PSO algorithm. In this work, type-3 Gaussian MFs are used in each input of the fuzzy inference system (FIS), and the design of these MFs is based on varying their LowerScale and LowerLag parameters in order to obtain the best prediction error for the Mexican stock market. In future work, the type-3 FIS design proposed in this work can be applied to other areas, such as the integration method applied to pattern recognition, edge detection in images, and control problems.
The rest of the paper is structured as follows. Section 2 describes the basic concepts of type-3 fuzzy systems. In Section 3, the methodology and model description are presented. Section 4 describes the simulations and comparison of results, and Section 5 presents the conclusions.

2. Type-3 Fuzzy Systems

Zadeh proposed fuzzy sets in 1965 [35,36], where an element partially belongs with a specific membership grade with a crisp number between 0 and 1 to a set. Later, type-1 fuzzy logic (FL) was also proposed. An improvement of this FL was later put forward, known as type-2 FL [25,27,37]. In type-2 FL, unlike type-1 FL, the elements do not have a precise membership in [0, 1].
In type-2 FL, the membership function (MF) of an element is defined by a fuzzy set (FS) in [0, 1]. A type-2 FS is defined as:
à = {((x, u), µÃ (x, u)) | ∀x ∈ X, ∀u ∈ Jx ⊆ [0, 1], µÃ(x, u) ∈ [0, 1]}
where X represents the domain of the fuzzy variable. In this case, there is a primary and a secondary membership. The first one is defined by Jx ⊆ [0, 1], and the second is a type-1 FS defined by µÃ(x, u). The footprint of uncertainty (FOU) is an uncertainty region. If µÃ (x, u) = 1, ∀u∈ Jx ⊆ [0, 1], an interval type-2 FS is defined as:
à = {((x, u), 1) |∀x ∈ X, ∀u∈ Jx ⊆ [0, 1]}
In type-3, we can potentially handle higher degrees of uncertainty with respect to type-2 due to the nature of the membership functions [38,39,40,41,42,43]. A type-3 fuzzy set (T3 FS) [29], represented by the notation A(3), is the graph of a trivariate function named the MF of A(3) in the Cartesian product defined by Equation (3), where the primary variable of A(3) has a universe X, x. The MF of A(3) is defined by A(3) (x, u, v) and is a type-3 MF of the T3 fuzzy set formulated by Equation (4):
A(3): X × [0, 1] × [0, 1] → [0, 1]
A ( 3 ) = { ( x , u ( x ) , v ( x , u ) , μ A ( 3 ) ( x , u , v ) |   x ∈ X , u ∈ U ⊆ [ 0 ,   1 ] , v ∈ V ⊆ [ 0 ,   1 ] }
where u is the secondary variable and has the universe U, and V is the universe for the tertiary variable v.

3. Model Description

The method consists of using ENNs, where the results are taken from previous work [23], and the outputs of these ENNs are combined with type-2 and type-3 fuzzy systems. Figure 1 illustrates the architecture of the proposed method, where the results of the ENNs for the time series of the Mexican stock exchange (MSE) are aggregated with a fuzzy system and, in this way, we obtain a final prediction to calculate the prediction error.
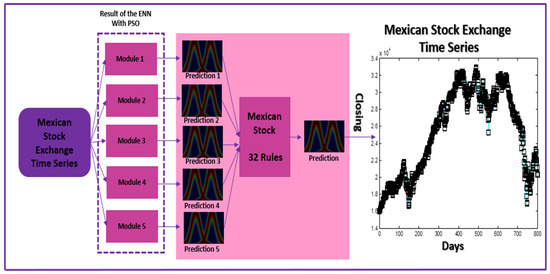
Figure 1. Proposed model.
Figure 1 represents the proposed model, where we have first the historical data as in [23]. Then, the results of the optimization algorithm based on swarms of particles determine the number of modules of the ENNs, which can be from one to five modules, as well as the number of layers that this module has, which could be from one to three layers, and the number of neurons by layer, which could be from one to three neurons. The responses of the ENN are combined by the aggregation method, where Mamdani and Sugeno type-2 and type-3 fuzzy systems are applied. The input and output linguistic variables of the fuzzy system have Gaussian MFs. The performance of the type-2 and type-3 fuzzy integrators was analyzed under different levels of the scale and lag parameters to determine the best design of the MFs for the rules of the fuzzy system. For the type-2 and type-3 fuzzy integrators, we used two MFs, which are called “low prediction” and “high prediction”. MFs are of the Gaussian type, and we used different lag and scale parameters, as shown in the results in the table headers, to obtain a better prediction of the time series.
If we consider five modules in the ENN, then the fuzzy system will have five input linguistic variables and the rules used will be determined according to the possible combinations according to the number of inputs and MFs of the fuzzy system. Considering that it has five inputs and two MFs for each of the inputs, then there are 32 possible combinations of fuzzy rules.
The following equation represents the objective function that we used with particle swarm optimization to minimize the prediction error of the time series.
E R M = ( ∑ i = 1 d | p   i     − x   i     | ) / d
P r e d i c t i o n   E r r o r = ( E R M   1   + E R M   2   + … + E R M   N   ) / N
where  p represents the prediction of the data for each of the modules of the ensemble recurrent network, X  corresponds to the real data of the time series, d  represents the number of data points used by the time series, E R M is the prediction error determined by module of the ERNN, N corresponds to the number of modules determined by the GA, and P r e d i c i o n   E r r o r corresponds to the average prediction error achieved by the ERNN.

3.1. Time Series Prediction

The MSE is a financial institution that operates by a grant from the Department of Finance and Public Credit, with the goal of following closely the Securities Market of Values in Mexico.
Derived from the monitoring of global trends and changes that have occurred in legislation, the MSE concluded with a conversion process, becoming a company whose shares are likely to be traded on the market stock exchange, with the initial public offering taking place on 13 June 2008 with its shares representing its capital [34].
In this work, two time periods were determined in order to evaluate the proposed method. For the first period, 800 data points were used. The data used were from the closing of the MSE and are daily data that correspond to the period from 9 November 2005 to 15 January 2009, where we plot on the x axis the historical data (in this case, the daily data) and on the y axis the closing of the MSE (illustrated in Figure 2). In the experiments, 70% of the data was used for training the ensemble neural network and 30% was used to test the network [34].
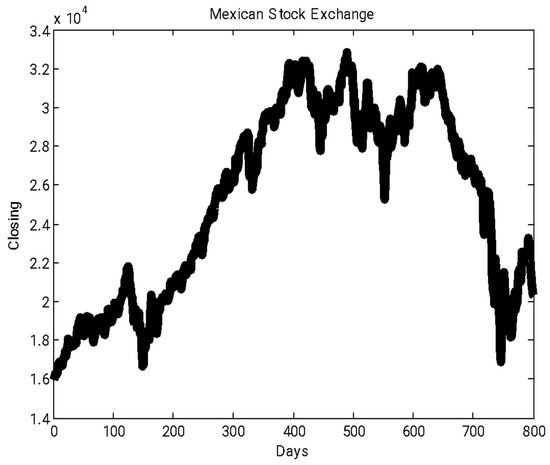
Figure 2. Mexican stock exchange time period #1.
The second time period corresponds to the period from 8 April 2008 to 9 May 2011. In Figure 3, the x axis shows the historical data (in days) and the y axis shows the closing of the MSE. Both time periods allow us to test the performance of the method.
Figure 3. MSE for time period #2.

3.2. Type-2 and Type-3 Fuzzy Systems

The Type-3 and Type-2 fuzzy systems that were used have five inputs (Prediction 1, Prediction 2, Prediction 3, Prediction 4, and Prediction 5) and one output (Prediction(Pd)), where the parameters range from 0 to 3.2 and the MFs are called “low” (Lw) and “high” (Hh), as shown in Figure 4.
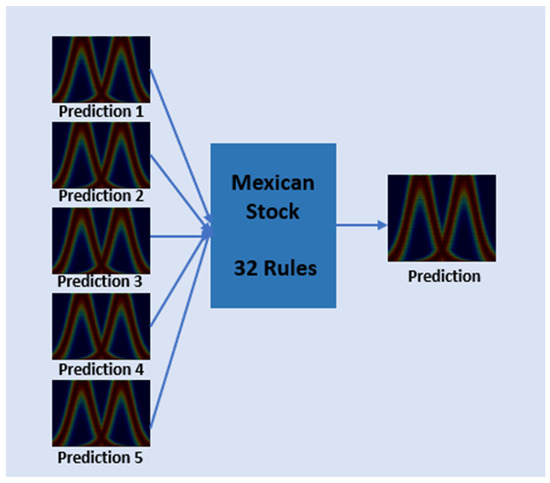
Figure 4. Type-3 fuzzy system for the MSE.
As the fuzzy system has five inputs and two MFs in each input, there are 32 possible fuzzy rules as shown in Figure 5. These rules were used for the type-2 and type-3 fuzzy systems. The general parameters of the MFs are presented in Table 1, which shows the center (m) and deviation (σ) of the particular linguistic values utilized in the variables. The values of the scale and lag parameters were changed for each case and are given in Section 4.
Figure 5. Type-3 fuzzy rules for predicting the MSE.
Table 1. Parameters of the MFs in the variables.

4. Simulations and Comparison of Results

This section presents the results of experiments and comparisons for the Mexican stock exchange with type-2 and type-3 fuzzy systems as the integration method. Comparisons were made between the Mamdani type-2 and type-3 fuzzy systems for the two-time series mentioned above. Also, comparisons were made between the Sugeno type-2 and type-3 fuzzy systems for the two-time series.
Table 2 shows the results of the optimization algorithm (PSO), for which 30 experiments were performed. However, this table only shows the 10 best results. The best result is shown in Row 7, where the prediction error is 0.0089454.
Table 2. Particle swarm results for the ENN.
The aggregation results of the Mamdani type-1 fuzzy system are presented in Table 3 for the time series of the MSE for time period #1. Different values for scale and lag were established for each ENN.
Table 3. Aggregation with the Mamdani type-1 fuzzy system for the MSE time series (time period #1).
The aggregation results of the Mamdani type-2 fuzzy system are presented in Table 4 for the time series of the MSE for time period #1. The different values for scale and lag that were established for each ENN are shown as well as the time of each experiment.
Table 4. Aggregation with the Mamdani type-2 fuzzy system for the MSE time series (time period #1).
The aggregation results of the Sugeno type-2 fuzzy system are presented in Table 5 for the time series of the MSE for time period #1. The different values for scale and lag that were established for each ENN are shown as well as the time of each experiment.
Table 5. Aggregation with the Sugeno type-2 fuzzy system for the MSE time series (time period #1).
The aggregation results of the Mamdani type-3 fuzzy system are presented in Table 6 for the time series of the MSE for time period #1. The different values for scale and lag that were established for each ENN are shown as well as the time of each experiment.
Table 6. Aggregation with the Mamdani type-3 fuzzy system for the MSE time series (time period #1).
The aggregation results of the Sugeno type-3 fuzzy system are presented in Table 7 for the time series of the MSE for time period #1. The different values for scale and lag that were established for each ENN are shown as well as the time of each experiment.
Table 7. Aggregation with the Sugeno type-3 fuzzy system for the MSE time series (time period #1).
Table 8 shows the results of the PSO algorithm, for which 30 experiments were performed. This table only shows the best 10 results, where the best result is shown in Row 9 and the prediction error is 0.0079875.
Table 8. PSO results for the ensemble neural network of the MSE for time series #2.
The aggregation results of the Mamdani type-1 fuzzy system are presented in Table 9 for the time series of the MSE for time period #2. Different values for scale and lag were established for each ENN.
Table 9. Aggregation with the Mamdani type-1 fuzzy system for the MSE time series (time period #2).
The aggregation results of the Mamdani type-2 fuzzy system are presented in Table 10 for the time series of the MSE for time period #2. The different values for scale and lag that were established for each ENN are shown as well as the time of each experiment.
Table 10. Aggregation with the Mamdani type-2 fuzzy system for the MSE time series (time period #2).
The aggregation results of the Sugeno type-2 fuzzy system are presented in Table 11 for the time series of the MSE for time period #2. The different values for scale and lag that were established for each ENN are shown as well as the time of each experiment.
Table 11. Aggregation with the Sugeno type-2 fuzzy system for the MSE time series (time period #2).
The aggregation results of the Mamdani type-3 fuzzy system are presented in Table 12 for the time series of the MSE for time period #2. The different values for scale and lag that were established for each ENN are shown as well as the time of each experiment.
Table 12. Aggregation with the Mamdani Type-3 fuzzy system for the MSE time series (time period #2).
The aggregation results of the Sugeno type-3 fuzzy system are presented in Table 13 for the time series of the MSE for time period #2. The different values for scale and lag that were established for each ENN are shown as well as the time of each experiment.
Table 13. Aggregation with the Sugeno Type-3 fuzzy system for the MSE time series (time period #2).

4.1. Comparison of Results

This subsection shows the comparison of the results of the type-2 and type-3 fuzzy systems using Student’s t statistical test. In this case, we compare type-2 fuzzy systems against type-3 systems for the Mamdani model and type-2 systems against type-3 systems for the Sugeno model for the two-time series considered in this paper.

4.1.1. Type-2 and Type-3 Mamdani Fuzzy Systems for the First Time Period

To compare the two fuzzy systems for MSE Series 1, the t statistical test was used. The results show that the type-3 system has better results on average, but there is not a sufficient statistical difference. The number of samples was 29, and a 95% confidence interval was used. This produced a p value of 0.6331 and a T value of 0.48. Table 14 shows the comparison of results between the Mamdani type-2 and type-3 systems for the first time period.
Table 14. T statistical test for MSE Series 1 for the Mamdani model.

4.1.2. Type-2 and Type-3 Sugeno Fuzzy Systems for the First Time Period

To compare the two fuzzy systems for MSE Series 1, the t statistical test was used. We can conclude that there is a significant difference between the Sugeno type-2 fuzzy system and the type-3 Sugeno fuzzy system. In other words, it can be said that the type-2 Sugeno fuzzy system is slightly better, but not significantly better. The number of samples was 29, and a 95% confidence interval was used. This produced a p value of 0.772 and a T value of −0.29. Table 15 shows the results for the Sugeno type-2 and type-3 systems for the first time period.
Table 15. T statistical test for MSE Series 1 for the Sugeno model.

4.1.3. Type-2 and Type-3 Mamdani Fuzzy Systems for the Second Time Period

To compare the two fuzzy systems for MSE Series 2, the t statistical test was used. We can conclude that, in this case, there is a significant difference between the Mamdani type-2 and type-3 fuzzy systems. In other words, it can be said that the Mamdani type-3 fuzzy system is better. The number of samples was 29, and a 95% confidence interval was used. This produced a p value of 0.000 and T value of 6.04. Table 16 shows the comparison of results between the type-2 and type-3 systems for MSE Series 2. We also illustrate in Figure 6 a plot with a comparison of the values obtained with type-2 and type-3 fuzzy aggregation, where it is clearly shown how the type 3 values are lower than those of type-2.
Table 16. T statistical test for MSE Series 2 for the Mamdani model.
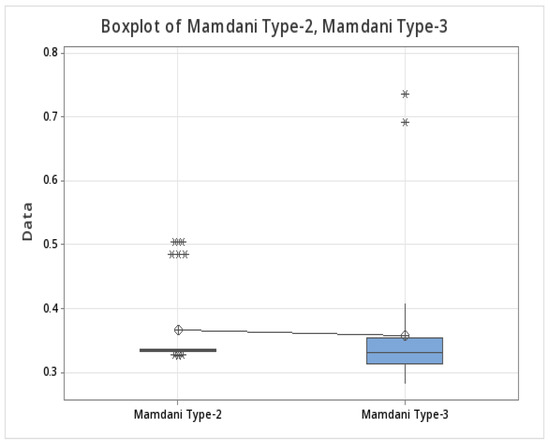
Figure 6. Box plot for the Mexican stock exchange series for Mamdani model (first time period).

4.1.4. Type-2 and Type-3 Sugeno Fuzzy Systems for the Second Time Period

To compare the two fuzzy systems for MSE Series 2, the t statistical test was used. The results show that the type 3 system provides better results, but there is not a sufficient statistical difference. The number of samples was 29, and a 95% confidence interval was used. This produced a p value of 0.511 and a T value of 0.66. Table 17 shows the comparison of results between the Sugeno type-2 and type-3 systems for the second time period. We also illustrate in Figure 7 a plot with a comparison of the values obtained with type-2 and type-3 fuzzy aggregation for the Sugeno model (first time period), where it is clearly shown how the type-3 values are lower than those of type 2. Figure 8 shows the comparison for the Mamdani models for second time period. Figure 9 shows the comparison for the Sugeno models for the second time period.
Table 17. T statistical test for MSE Series 2 for the Sugeno model.
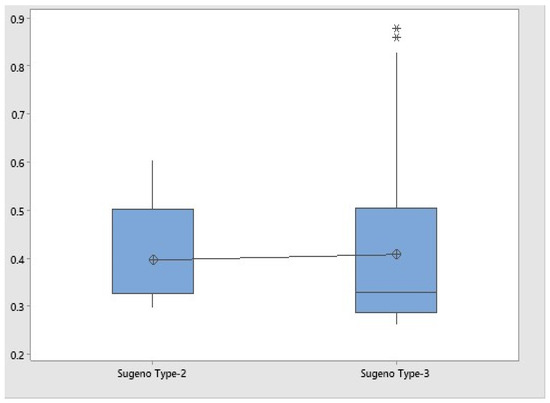
Figure 7. Box plot for the MSE Series for the Sugeno model (first time period).
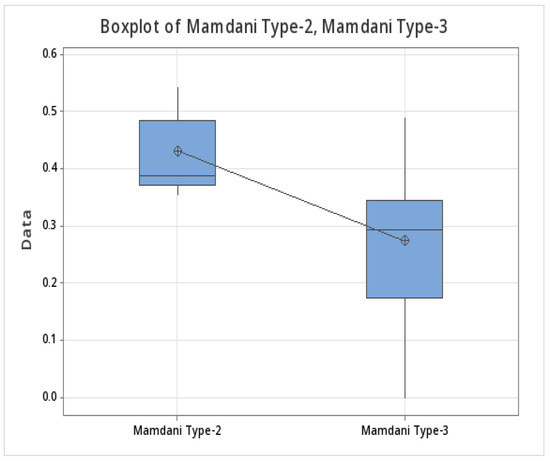
Figure 8. Box plot for MSE Series 2 for the Mamdani model (second time period).
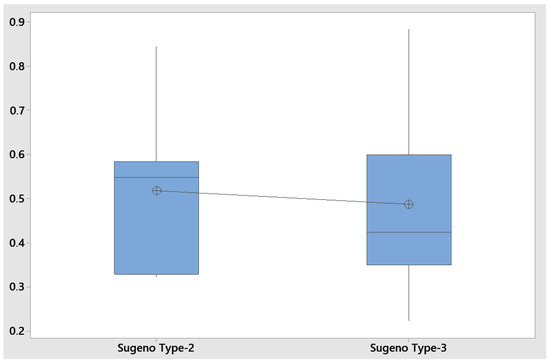
Figure 9. Box plot for the MSE series for the Sugeno model (second time period).
Table 18 shows the best 10 prediction errors for the ensemble neural network, the prediction error with type-1 fuzzy aggregation, and the prediction error with type-2 fuzzy aggregation and type-3 fuzzy aggregation for time period #1. The average obtained from 30 experiments on the Mamdani type-1 system was 0.55153, that obtained from 30 experiments on the Mandami type-2 system was 0.3666, that obtained from 30 experiments on the Sugeno type-2 system was 0.3962, that obtained from 30 experiments on the Mamdani type-3 system was 0.3557, and that obtained from 30 experiments on the Sugeno type-3 system was 0.4080.
Table 18. Results of the MSE for the time series (time period #1).
Table 19 shows the results of the prediction error for the ensemble neural network, the prediction error with type-1 fuzzy aggregation, and the prediction error with type-2 fuzzy aggregation and type-3 fuzzy aggregation for time period #2. The average obtained from 30 experiments for the Mamdani type-1 system was 0.64047, that obtained from 30 experiments for the Mamdani type-2 system was 0.4307, that obtained from 30 experiments for the Sugeno type-2 system was 0.5171, that obtained from 30 experiments for the Mamdani type-3 system was 0.2736, and that obtained from 30 experiments for the Sugeno type-3 system was 0.4864.
Table 19. Results of the MSE for the time series (time period #2).

4.2. Discussion of Results

In summary, we have considered four cases for the experiments because two periods of time were considered and two types of fuzzy models. The goal was to compare the performance of type-3 versus type-2 in the four cases. Based on the results, we can state that in three cases type-3 was able to surpass type-2, although the advantage was statistically significant in only one case. On the other hand, type-2 exhibited slightly better results, but not statistically significant results, in only one case. Finally, based on these results, we can say that type-3 fuzzy logic has potential in handling the uncertainty in prediction.
We have to mention that the proposed method has two extra parameters that make it more difficult to parameterize than type-2. However, at the same time, it has a higher capability for modeling real-world uncertainty because of the geometry of the footprint of uncertainty. Also, it requires a bit more computation, but it has been shown that the computational complexity remains linear, so it is actually not a significant increase in computation. Having said that, the main idea of type-3 is having the potential to handle higher levels of uncertainty (that some complex problems could require), but this has the disadvantage of higher computational complexity. In addition, in the design process of type-3 fuzzy systems, additional effort is required in order to find the parameter values, so this is what causes a greater degree of variation in the results. However, at the end, for practical applications, we would be required to use only one of the type-3 designs (the best one), and then we can achieve the best prediction. The utilization of the averages is to be able to establish whether, statistically speaking, we can say that type-3 is better (in general) and, in this sense, the greater degree of variation in type-3 does not affect the applicability of the proposed method.

5. Conclusions

In this paper, we considered Mamdani and Sugeno type-2 and type-3 fuzzy systems to integrate responses of the ENN to predict the time series of the Mexican stock exchange in two time periods. We were able to achieve good results, and we can say that the Mamdani type-3 systems produced good results in the prediction error for this case, but the response time is longer than that of the Sugeno type-3 fuzzy systems. In conclusion, the utilization of ENNs with type-3 fuzzy integration could be a good option to predict complex time series. In the future, the optimization of type-2 and type-3 (Mamdani and Sugeno) fuzzy system aggregators with other metaheuristics could be undertaken to possibly obtain an even better prediction error value. Type-2 and type-3 fuzzy systems could be optimized in terms of the parameter values of the MFs, the type of MF, and the number of rules.

Author Contributions

Conceptualization, M.P. and P.M.; methodology, P.M. and O.C.; software, M.P. and J.R.C.; validation, M.P. and P.M.; formal analysis, P.M. and O.C.; investigation, M.P. and J.R.C.; writing—original draft preparation, M.P. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

All data are contained within the article.

Acknowledgments

We acknowledge the support given by Tecnologico Nacional de Mexico (TecNM).

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Brockwell, P.D.; Davis, R.A. Introduction to Time Series and Forecasting; Springer: New York, NY, USA, 2002; pp. 1–219. [Google Scholar]
  2. Castillo, O.; Melin, P. Hybrid intelligent systems for time series prediction using neural networks, fuzzy logic, and fractal theory Neural Networks. IEEE Trans. Neural Netw. 2002, 13, 1395–1408. [Google Scholar] [CrossRef] [PubMed]
  3. Cowperthwaite, P.; Metcalfe, A. Introductory Time Series with R; Time Series; Springer: Dordrecht, The Netherlands; Heidelberg, Germany; London, UK; New York, NY, USA, 2009; pp. 2–5. [Google Scholar]
  4. Huarng, K. Effective lengths of intervals to improve forecasting in fuzzy time series. Fuzzy Sets Syst. 2001, 123, 3387–3394. [Google Scholar] [CrossRef]
  5. Jang, J.S.R.; Sun, C.T.; Mizutani, E. Neuro-Fuzzy and Soft Computing; Prentice Hall: Hoboken, NJ, USA, 1996. [Google Scholar]
  6. Zadeh, L. Some reflections on soft computing, granular computing and their roles in the conception, design and utilization of information/intelligent systems. Soft Comput. 1998, 2, 23–25. [Google Scholar] [CrossRef]
  7. Chang, J.R.; Wei, L.; Cheng, C.H. OWA-based ANFIS model for TAIEX forecasting. Econ. Model. 2013, 30, 442–448. [Google Scholar] [CrossRef]
  8. Cheng, C.H.; Chen, T.L.; Theo, H.J.; Chiang, C.H. Fuzzy time-series based on adaptive expectation model for TAIEX forecasting. Expert Syst. Appl. 2008, 34, 1126–1132. [Google Scholar] [CrossRef]
  9. Cunningham, P.; Carney, J.; Jacob, S. Stability problems with artificial neural networks and the ensemble solution. Artif. Intell. Med. 2000, 20, 217–225. [Google Scholar] [CrossRef]
  10. Jia, D.; Wu, Z. Seismic fragility analysis of RC frame-shear wall structure under multidimensional performance limit state based on ensemble neural network. Eng. Struct. 2021, 246, 112975–112985. [Google Scholar] [CrossRef]
  11. Sharkey, A. Combining Artificial Neural Nets: Ensemble and Modular Multi-Net Systems; Springer: London, UK, 1999. [Google Scholar]
  12. Gurney, K. An Introduction to Neural Networks, 1st ed.; CRC Press: Florida, FL, USA, 1997; pp. 3–10. [Google Scholar]
  13. Hansen, L.K.; Salomon, P. Neural network ensembles. IEEE Trans. Pattern Anal. Mach. Intell. 1990, 12, 993–1001. [Google Scholar] [CrossRef]
  14. Maclin, R.; Shavlik, J.W. Combining the predictions of multiple classifiers: Using competitive learning to initialize neural networks. In IJCAI-95; Morgan Kaufmann: Montreal, QC, Canada; San Mateo, CA, USA, 1995; pp. 524–530. [Google Scholar]
  15. Pulido, M.; Melin, P. Optimization of Ensemble Neural Networks with Type-2 Fuzzy Integration of Responses for the Dow Jones Time Series Prediction. Intell. Autom. Soft Comput. 2014, 20, 403–418. [Google Scholar]
  16. Wilkinson, I.; Bhattacharjee, R.; Shafer, J.; Osborne, A. Confidence estimation in the prediction of epithermal neutron resonance self-shielding factors in irradiation samples using an ensemble neural network. Energy AI 2022, 7, 100131–100149. [Google Scholar] [CrossRef]
  17. Peng, B.; Tong, L.D.; Huo, W. Experimental research and artificial neural network prediction of free piston expander-linear generator. Energy Rep. 2022, 8, 1966–1978. [Google Scholar] [CrossRef]
  18. Prakarsha, K.; Sharma, G. Time series signal forecasting using artificial neural networks: An application on ECG signal. Biomed. Signal. Process. Control 2022, 76, 103705–103720. [Google Scholar]
  19. Mao, J. A case study on bagging, boosting and basic ensembles of neural networks for OCR. In IJCNN-98; IEEE Computer Society Press: Anchorage, AK, USA; Los Alamitos, CA, USA, 1998; Volume 3, pp. 1828–1833. [Google Scholar]
  20. Melin, P.; Castillo, O. A review on type-2 fuzzy logic applications in clustering, classification and pattern recognition. Appl. Soft Comput. 2014, 21, 568–577. [Google Scholar] [CrossRef]
  21. Melin, P.; Monica, J.C.; Sánchez, D.; Castillo, O. Multiple Ensemble Neural Network Models with Fuzzy Response Aggregation for Predicting COVID-19 Time Series: The Case of Mexico. Healthcare 2020, 8, 181–190. [Google Scholar] [CrossRef]
  22. Pulido, M.; Castillo, O.; Melin, P. Genetic Optimization of Ensemble Neural Networks for Complex Time Series Prediction of the Mexican Exchange. Int. J. Innov. Comput. Inf. Control. 2013, 9, 4151–4166. [Google Scholar]
  23. Pulido, M.; Melin, P.; Castillo, O. Particle Swarm Optimization of Ensemble Neural Networks with Fuzzy Aggregation for Time Series Prediction of the Mexican Stock Exchange. Inf. Sci. 2014, 280, 188–204. [Google Scholar] [CrossRef]
  24. Karnik, N.; Mendel, J.M. Applications of type-2 fuzzy logic systems to forecasting of time-series. Inf. Sci. 1999, 120, 89–111. [Google Scholar] [CrossRef]
  25. Karnik, N.; Mendel, J.M. Introduction to type-2 fuzzy logic systems. IEEE Trans. Signal Process. 1998, 2, 915–920. [Google Scholar]
  26. Karnik, N.; Mendel, J.M. Operations on Type-2 Fuzzy Sets. Fuzzy Sets Syst. 2001, 122, 327–348. [Google Scholar] [CrossRef]
  27. Castillo, O.; Melin, P. Type-2 Fuzzy Logic: Theory and Applications; Springer: New York, NY, USA, 2008; pp. 29–40. [Google Scholar]
  28. Al-Jamimi, H.; Saleh, T. Transparent predictive modelling of catalytic hydrodesulfurization using an interval type-2 fuzzy logic. J. Clean. Prod. 2019, 231, 1079–1088. [Google Scholar] [CrossRef]
  29. Castillo, O.; Castro, J.R.; Melin, P. Interval Type-3 Fuzzy Systems: Theory and Design, 1st ed.; Springer: Cham, Switzerland, 2022; pp. 45–67. [Google Scholar]
  30. Cao, Y.; Raise, A.; Mohammadzadeh, A.; Rathinasamy, S.; Band, S.; Mousavi, A. Deep learned recurrent type-3 fuzzy system: Application for renewable energy modeling/prediction. Energy Rep. 2021, 7, 8115–8127. [Google Scholar] [CrossRef]
  31. Castorena, G.A.H.; Méndez, G.M.; López-Juárez, I.; García, M.A.A.; Martinez-Peon, D.C.; Montes-Dorantes, P.N. Parameter Prediction with Novel Enhanced Wagner Hagras Interval Type-3 Takagi–Sugeno–Kang Fuzzy System with Type-1 Non-Singleton Inputs. Mathematics 2024, 12, 1976–1986. [Google Scholar] [CrossRef]
  32. Qasem, S.; Ahmadian, A.; Mohammadzadeh, A.; Rathinasamy, S.; Pahlevanzadeh, B. A type-3 logic fuzzy system: Optimized by a correntropy based Kalman filter with adaptive fuzzy kernel size. Inf. Sci. 2021, 572, 424–443. [Google Scholar] [CrossRef]
  33. Mohammadzadeh, A.; Sabzalian, M.; Zhang, W. An Interval Type-3 Fuzzy System and a New Online Fractional-Order Learning Algorithm: Theory and Practice. IEEE Trans. Fuzzy Syst. 2020, 28, 1940–1950. [Google Scholar] [CrossRef]
  34. Mexico Bank Database. Available online: http://www.banxico.org.mx (accessed on 30 August 2011).
  35. Zadeh, L. Fuzzy sets. Inf. Control. 1965, 8, 338–353. [Google Scholar] [CrossRef]
  36. Zadeh, L. The concept of a linguistic variable and its application to approximate reasoning. Inf. Sci. 1975, 8, 199–249. [Google Scholar] [CrossRef]
  37. Rickard, J.; Aisbett, J.; Gibbon, G. Fuzzy subsethood for fuzzy sets of type-2 and generalized type-n. IEEE Trans. Fuzzy Syst. 2009, 17, 50–60. [Google Scholar] [CrossRef]
  38. Gheisarnejad, M.; Mohammadzadeh, A.; Farsizadeh, H.; Khooban, M.H. Stabilization of 5G telecom converter-based deep type-3 fuzzy machine learning control for telecom applications. IEEE Trans. Circuits Syst. II Express Briefs 2021, 69, 544–548. [Google Scholar] [CrossRef]
  39. Gheisarnejad, M.; Mohammadzadeh, A.; Khooban, M. Model Predictive Control-Based Type-3 Fuzzy Estimator for Voltage Stabilization of DC Power Converters. IEEE Trans. Ind. Electron. 2021, 69, 13849–13858. [Google Scholar] [CrossRef]
  40. Huang, H.; Xu, H.; Chen, F.; Zhang, C.; Mohammazadeh, A. An Applied Type-3 Fuzzy Logic System: Practical Matlab Simulink and M-Files for Robotic, Control, and Modeling Applications. Symmetry 2023, 15, 475–484. [Google Scholar] [CrossRef]
  41. Liu, Z.; Mohammadzadeh, A.; Turabieh, H.; Mafarja, M.; Band, S.; Mosavi, A. A New Online Learned Interval Type-3 Fuzzy Control System for Solar Energy Management Systems. IEEE Access 2021, 9, 10498–10508. [Google Scholar] [CrossRef]
  42. Singh, D.J.; Verma, N.K.; Ghosh, A.K.; Malagaudanavar, A. An approach towards the design of interval type-3 T-S fuzzy system. IEEE Trans. Fuzzy Syst. 2022, 30, 3880–3893. [Google Scholar] [CrossRef]
  43. Vafaie, R.H.; Mohammadzadeh, A.; Piran, M.J. A new type-3 fuzzy predictive controller for MEMS gyroscopes. Nonlinear Dynam. 2021, 106, 381–403. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Article Metrics

Citations

Article Access Statistics

Journal Statistics
Multiple requests from the same IP address are counted as one view.
Download PDF
Dynamical Properties of Perturbed Hill’s System
Previous
Estimation of Anthocyanins in Heterogeneous and Homogeneous Bean Landraces Using Probabilistic Colorimetric Representation with a Neuroevolutionary Approach
Next