New Lifetime Distribution for Modeling Data on the Unit Interval: Properties, Applications and Quantile Regression

Abstract

Probability distributions are very useful in modeling lifetime datasets. However, no specific distribution is suitable for all kinds of datasets. In this study, the bounded truncated Cauchy power exponential distribution is proposed for modeling datasets on the unit interval. The probability density function exhibits desirable shapes, such as left-skewed, right-skewed, reversed J, and bathtub shapes, whereas the hazard rate function displays J and bathtub shapes. For the purpose of modeling dependence between measures in a dataset, a bivariate extension of the proposed distribution is developed. The bivariate probability density function displays monotonic and non-monotonic shapes, making it suitable for modeling complex bivariate relations. Subsequently, the applications of the distribution are illustrated using COVID-19 data. The results revealed that the new distribution provides a better fit to the datasets compared to other existing distributions. Finally, a new quantile regression model is developed and its application demonstrated. The generated quantile regression model offers a decent fit to the data, according to the residual analysis.

1. Introduction

Disease modeling and prediction are primary tasks of epidemiologists and researchers interested in the estimation of disease occurrences. To perform these tasks, modeling the variability in disease occurrences using probability distributions is essential. With the emergence of the novel coronavirus disease in late 2019 (COVID-19) and its negative impact on humanity, many researchers have proposed new probability distributions (discrete or continuous) for modeling the number of infections, mortality rate, and recovery rates, among others. Some of the proposed probability distributions or families of distributions include: Marshall–Olkin reduced Kies distribution [1], modified inverse Weibull distribution [2], weighted Weibull distribution [3], type I half logistic Burr X-G family [4], unit power Weibull distribution [5], new extended exponentiated Weibull distribution [6], discrete extended odd Weibull exponential distribution [7], odd Weibull inverse Topp–Leone distribution [8], log-logistic tangent distribution [9], discrete-type half-logistic exponential distribution [10], and unit Johnson $S_U$ distribution [11].

Among these probability distributions used for modeling diseases, those defined on the unit interval play a major role due to their usefulness in areas such as health, psychology, and epidemiology, among others. For instance, researchers may be interested in modeling mortality or recovery rates. Observations measured on these variables are usually proportions, fractions, or rates, which are defined in the unit interval. Although the beta distribution is the oldest for modeling datasets measured on the unit interval, the intractability of its cumulative distribution function (CDF) and quantile function has called for the development of new distributions with tractable CDFs and quantile functions that are also capable of modeling data on the unit interval. Unit distributions proposed recently in literature include: unit Gamma/Gompertz distribution [12], bounded odd inverse Pareto exponential distribution [13], bounded shifted Gompertz distribution [14], unit modified Burr-III distribution [15], unit generalized half normal distribution [16], unit Lindley distribution [17], unit Gompertz distribution [18], logit slash distribution [19], unit Weibull distribution [20] and unit inverse Gaussian distribution [21].

Despite the existence of many unit distributions in the literature, no single distribution is capable of modeling all forms of data since the data generating process produces data with different characteristics such as symmetric, skewed, varied degrees of kurtosis, and monotonic and non-monotonic failure rates. This study thus proposes a new unit distribution called the bounded truncated Cauchy power exponential (BTCPE) distribution. The motivations for developing the new distribution are as follows: to provide a model capable of modeling complex data on unit interval that exhibits platykurtic, leptokurtic, reversed J, left-skewed, right-skewed, bathtub, and J shapes; to develop a bivariate distribution for modeling interdependence between random data on unit interval; and to develop a quantile regression model for understanding the relationship between a response variable and given covariates.

The remainder of the paper is organized in nine sections, described as follows: Section 2 presents the development of the BTCPE distribution, Section 3 describes some of its important properties, Section 4 focuses on a special bivariate extension of the BTCPE distribution, Section 5 is devoted to the parametric estimation methods, Section 6 presents the Monte Carlo simulation of nine frequentist estimation methods, Section 7 contains the univariate applications of the BTCPE distribution, Section 8 is about the quantile regression model and its application, and finally the conclusion of the paper is presented in Section 9.

2. Bounded Truncated Cauchy Power Exponential Distribution

A random variable $X$ follows the truncated Cauchy power exponential (TCPE) distribution if its CDF and probability density function (PDF), respectively, are defined as

$$F_X(x;\alpha ,\lambda )=\frac{4}{\pi }\arctan [{(1-e^{-\lambda x})}^{\alpha }],\alpha >0,\lambda >0,x>0,$$

(1)

and

$$f_X(x;\alpha ,\lambda )=\frac{4\alpha \lambda e^{-\lambda x}{(1-e^{-\lambda x})}^{\alpha -1}}{\pi [1+{(1-e^{-\lambda x})}^{2\alpha }]},x>0.$$

(2)

The TCPE distribution can be presented as a special case of the TCP Weibull distribution proposed by [22]. Now, we define a new unit distribution, called the BTCPE distribution, corresponding to the distribution of $Y=e^{-X}$. The associated CDF is obtained as follows:

$$\begin{array}{l}{F}_Y(y;\alpha ,\lambda )=\mathbb{P}(e^{-X}\le y)=\mathbb{P}(-X\le \log (y))\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=1-\mathbb{P}(X\le -\log (y))\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=1-F_X(-\log (y);\alpha ,\lambda ).\end{array}$$

Hence, the CDF of the BTCPE distribution is expressed as

$$F_Y(y;\alpha ,\lambda )=1-\frac{4}{\pi }\arctan [{(1-y^{\lambda })}^{\alpha }],0<y<1,$$

(3)

and $\alpha >0$ and $\lambda >0$ are the shape parameters that have to be estimated. The associated PDF of the BTCPE distribution is obtained by differentiating Equation (3), and it is given by

$$f_Y(y;\alpha ,\lambda )=\frac{4\alpha \lambda y^{\lambda -1}{(1-y^{\lambda })}^{\alpha -1}}{\pi [1+{(1-y^{\lambda })}^{2\alpha }]},0<y<1.$$

(4)

Often, the PDFs are expressed in expanded form for easy derivation of the statistical properties of the proposed distribution. The expanded form of the PDF of the BTCPE distribution is mainly obtained using the generalized binomial expansion, ${(y+a)}^{-n}={\displaystyle \sum _{k=0}^{\infty }\left(\begin{array}{c}-n\\ k\end{array}\right)}{y}^k{a}^{-n-k},|y|<a$, where $n$ is any real number. Thus, it is given by

$$f_Y(y;\alpha ,\lambda )=\frac{4\alpha \lambda }{\pi }{\displaystyle \sum _{i=0}^{\infty }{(-1)}^i{y}^{\lambda -1}{(1-y^{\lambda })}^{\alpha (2i+1)-1}},0<y<1.$$

(5)

The corresponding hazard rate function (HRF) is given by

$$h_Y(y;\alpha ,\lambda )=\frac{\alpha \lambda y^{\lambda -1}{(1-y^{\lambda })}^{\alpha -1}}{[1+{(1-y^{\lambda })}^{2\alpha }]\arctan [{(1-y^{\lambda })}^{\alpha }]},0<y<1.$$

(6)

The shapes of the PDF and HRF for some given parameter values are shown in Figure 1. The PDF exhibits symmetric, bathtub, left-skewed and right-skewed shapes for the given parameter values. The HRF displays bathtub and increasing failure rates.

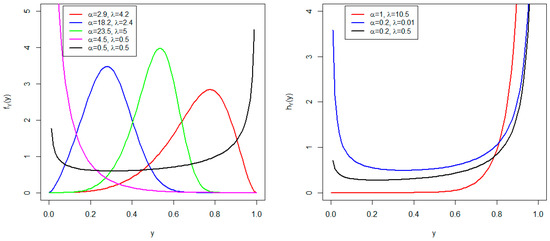
Figure 1. PDF (left) and HRF (right) of the BTCPE distribution.

3. Some Important Properties

This section presents some relevant properties of the BTCPE distribution.

3.1. Distribution Inequalities

This subsection investigates some desirable inequalities satisfied by the CDF of the BTCPE distribution. These inequalities are very essential in determining the first order stochastic dominance of random variables [23].

Proposition 1. 

The CDF of the BTCPE distribution is increasing with respect to the parameter$\alpha$. The CDF of the BTCPE distribution is decreasing with respect to the parameter$\lambda$.

Proof. 

For the first point, since ${(1-y^{\lambda })}^{\alpha }\log (1-y^{\lambda })<0$ , for $y\in (0,1)$, we have

$$\frac{\partial F_Y(y;\alpha ,\lambda )}{\partial \alpha }=-\frac{4{(1-y^{\lambda })}^{\alpha }\log (1-y^{\lambda })}{\pi [1+{(1-y^{\lambda })}^{2\alpha }]}\ge 0.$$

This means that $F_Y(y;\alpha ,\lambda )$ is increasing with respect to $\alpha$. For the second point, since $y^{\lambda }{(1-y^{\lambda })}^{\alpha -1}\log (y)<0$, for $y\in (0,1)$, we have

$$\frac{\partial F_Y(y;\alpha ,\lambda )}{\partial \lambda }=\frac{4\alpha y^{\lambda }{(1-y^{\lambda })}^{\alpha -1}\log (y)}{\pi [1+{(1-y^{\lambda })}^{2\alpha }]}\le 0.$$

This implies that $F_Y(y;\alpha ,\lambda )$ is decreasing with respect to $\lambda$. This completes the proof of the proposition. From Proposition 1, the following stochastic ordering property follows immediately: if ${\alpha }_1\le {\alpha }_2$ then $F_Y(y;{\alpha }_1,\lambda )\le F_Y(y;{\alpha }_2,\lambda )$. Also, if ${\lambda }_1\le {\lambda }_2$ then $F_Y(y;\alpha ,{\lambda }_2)\le F_Y(y;\alpha ,{\lambda }_1)$. ☐

3.2. Quantile Function

The quantile function or the inverse CDF is simply the solution $Q(u;\alpha ,\lambda )$ of the following nonlinear equation: $F_Y(Q(u;\alpha ,\lambda );\alpha ,\lambda )=u$, for all $u\in (0,1)$. Thus, after some algebraic manipulation, we have

$$Q(u;\alpha ,\lambda )={\left\{1-{\left(\tan \left[\frac{\pi }{4}(1-u)\right]\right)}^{1/\alpha }\right\}}^{1/\lambda },u\in (0,1).$$

(7)

The median is obtained by substituting $u=0.5$. The quantile function plays an important role in the generation of random observations from the BTCPE distribution. The quantile function values are also useful in computing measures of skewness and kurtosis. As a classical quantile measure, the MacGillivray measure of skewness [24] is given by

$$\rho (u;\alpha ,\lambda )=\frac{Q(1-u;\alpha ,\lambda )+Q(u;\alpha ,\lambda )-2Q(0.5;\alpha ,\lambda )}{Q(1-u;\alpha ,\lambda )-Q(u;\alpha ,\lambda )},u\in (0,1).$$

In particular, the MacGillivray measure of skewness can be used to efficiently describe the effect of the parameters $(\alpha ,\lambda )$ on the skewness. The more the shapes of $\rho (u;\alpha ,\lambda )$ vary according to the parameters, the more flexible the skewness is. Figure 2 shows the plot of this skewness measure for a fixed value of $\lambda$ while $\alpha$ varies and for a fixed value of $\alpha$ while $\lambda$ varies. From Figure 2, the wider variations seen imply that both parameters have a strong influence on the skewness of the BTCPE distribution. In addition, as the values of $\alpha$ or $\lambda$ increase, $\rho (u;\alpha ,\lambda )$ gets closer to the horizontal line. This shows that utilizing higher values of the parameter can result in a symmetrical distribution.

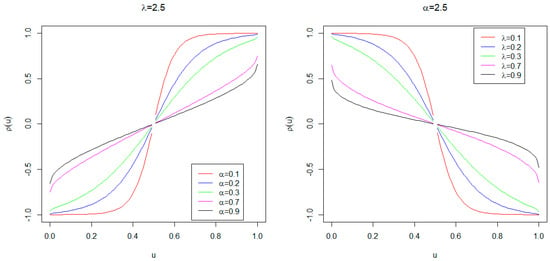
Figure 2. Plots of the MacGillivray skewness.

The kurtosis of the BTCPE distribution can be studied using the Moors kurtosis [25]. The Moors (coefficient of) kurtosis is usually given by

$$K(\alpha ,\lambda )=\frac{Q(7/8;\alpha ,\lambda )-Q(5/8;\alpha ,\lambda )+Q(3/8;\alpha ,\lambda )-Q(1/8;\alpha ,\lambda )}{Q(3/4;\alpha ,\lambda )-Q(1/4;\alpha ,\lambda )}.$$

Large values of the Moors kurtosis imply that the distribution has a heavy tail, and small values are indications of a light tail. Figure 3 displays the Moors kurtosis for the BTCPE distribution. It can be observed that the BTCPE distribution exhibits various degrees of kurtosis. When the parameters $\alpha$ and $\lambda$ are equal, the distribution displays a platykurtic shape. The overall shapes show how flexible the BTCPE distribution is with regards to modeling datasets having different degrees of kurtosis and skewness.

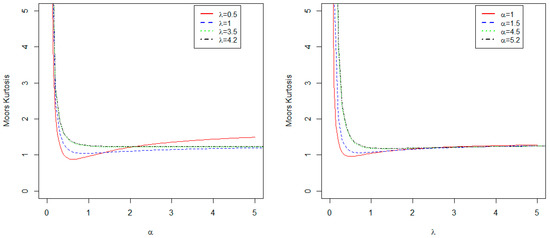
Figure 3. Plots of Moors kurtosis.

3.3. Moments and Moments Generating Function

The $r^{th}$ moments, incomplete moments and moment generating function of the BTCPE distribution are presented in this subsection.

Proposition 2. 

If$Y$is a BTCPE random variable, i.e., a random variable with the BTCPE distribution, then its$r^{th}$non-central moment is given by

$${{\mu }^{\prime }}_r=\frac{4\alpha }{\pi }{\displaystyle \sum _{i=0}^{\infty }{(-1)}^{i}B\left(\frac{r}{\lambda }+1,\alpha (1+2i)\right)},r=1,2,\dots ,$$

(8)

where$B(a,b)={\displaystyle \underset{0}{\overset{1}{\int }}{z}^{a-1}{(1-z)}^{b-1}dz}$is the beta integral function.

Proof. 

The $r^{th}$ non-central moment of the BTCPE random variable is defined as ${{\mu }^{\prime }}_r=E(Y^r)={\displaystyle \underset{0}{\overset{1}{\int }}{y}^r{f}_Y(y;\alpha ,\lambda )dy}$. Thus, substituting the expanded form of the PDF given in Equation (5) yields

$${{\mu }^{\prime }}_r=\frac{4\alpha \lambda }{\pi }{\displaystyle \sum _{i=0}^{\infty }{(-1)}^i{\displaystyle \underset{0}{\overset{1}{\int }}{y}^{r+\lambda -1}{(1-y^{\lambda })}^{\alpha (1+2i)-1}dy}.}$$

Letting $z=y^{\lambda },y\to 0,z\to 0;y\to 1,z\to 1$ and $dz=\lambda y^{\lambda -1}dy$ , we get

$${{\mu }^{\prime }}_r=\frac{4\alpha }{\pi }{\displaystyle \sum _{i=0}^{\infty }{(-1)}^i{\displaystyle \underset{0}{\overset{1}{\int }}{z}^{\frac{r}{\lambda }}{(1-z)}^{\alpha (1+2i)-1}dz}}.$$

Hence, several algebraic manipulation yield

$${{\mu }^{\prime }}_r=\frac{4\alpha }{\pi }{\displaystyle \sum _{i=0}^{\infty }{(-1)}^{i}B\left(\frac{r}{\lambda }+1,\alpha (1+2i)\right)}.$$

This completes the proof. ☐

The non-central moments can be used to derive other important characteristics of the BTCPE distribution such as estimating the variance, coefficient of skewness and kurtosis.

Proposition 3. 

The$r^{th}$incomplete moment of the BTCPE random variable is given by

$${\phi }_r=\frac{4\alpha }{\pi }{\displaystyle \sum _{i=0}^{\infty }{(-1)}^{i}B\left(y^{\lambda };\frac{r}{\lambda }+1,\alpha (1+2i)\right)},r=1,2,\dots ,$$

(9)

where$B(q;a,b)={\displaystyle \underset{0}{\overset{q}{\int }}{z}^{a-1}{(1-z)}^{b-1}dz}$is the incomplete beta integral function.

Proof. 

By definition, the $r^{th}$ incomplete moment is given by

$${\phi }_r=E(Y^{r}1\{Y<y\})={\displaystyle \underset{0}{\overset{y}{\int }}{x}^{r}f(x;\alpha ,\lambda )dx}.$$

Hence, substituting the expanded form of the PDF into the definition yields

$${\phi }_r=\frac{4\alpha \lambda }{\pi }{\displaystyle \sum _{i=0}^{\infty }{(-1)}^i{\displaystyle \underset{0}{\overset{y}{\int }}{x}^{r+\lambda -1}{(1-x^{\lambda })}^{\alpha (1+2i)-1}dx}}.$$

Letting $z=x^{\lambda },x\to 0,z\to 0;x\to y,z\to y^{\lambda }$ and $dz=\lambda x^{\lambda -1}dx$ . Hence, applying similar concepts for proving the incomplete moments yields

$${\phi }_r=\frac{4\alpha }{\pi }{\displaystyle \sum _{i=0}^{\infty }{(-1)}^{i}B\left(y^{\lambda };\frac{r}{\lambda }+1,\alpha (1+2i)\right)}.$$

This completes the proof. ☐

The moment generating function is useful for deriving the moments of a random variable if only the moment exists.

Proposition 4. 

The moment generating function of the BTCPE random variable is given by

$$M_Y(t)=\frac{4\alpha }{\pi }{\displaystyle \sum _{r=0}^{\infty }{\displaystyle \sum _{i=0}^{\infty }\frac{{(-1)}^i{t}^r}{r!}}}B\left(\frac{r}{\lambda }+1,\alpha (1+2i)\right).$$

(10)

Proof. 

By definition and a standard exponential expansion, we have $M_Y(t)=E(e^{tY})={\displaystyle \sum _{r=0}^{\infty }\frac{t^r}{r!}{{\mu }^{\prime }}_r}$. Hence, substituting the $r^{th}$non-central moment of the BTCPE distribution into the definition completes the proof. ☐

Table 1 shows the first six moments of the BTCPE distribution and other useful measures, such as the standard deviation (SD), coefficients of variation (CV), skewness (CS) and kurtosis (CK). The SD, CV, CS and CK are, respectively, given by

$$SD=\sqrt{{\mu }_2^{\prime }-{\mu }^2},$$

$$CV=\frac{\sigma }{\mu }=\sqrt{\frac{{\mu }_2^{\prime }}{{\mu }^2}-1},$$

$$CS=\frac{{\mu }_3^{\prime }-3\mu {\mu }_2^{\prime }+2{\mu }^3}{{({\mu }_2^{\prime }-{\mu }^2)}^{3/2}}$$

and

$$CK=\frac{{\mu }_4^{\prime }-4\mu {\mu }_3^{\prime }+6{\mu }^2{\mu }_2^{\prime }-3{\mu }^4}{{({\mu }_2^{\prime }-{\mu }^2)}^2}.$$

Table 1. Values of moment measures, including the SD, CV, CS and CK.

${\mathit{\mu }}_{\mathit{r}}^{\mathbf{\prime }}$	$\mathit{\alpha }\mathbf{=}\mathbf{0.4}\mathbf{,}\mathit{\lambda }\mathbf{=}\mathbf{2.5}$	$\mathit{\alpha }\mathbf{=}\mathbf{4.5}\mathbf{,}\mathit{\lambda }\mathbf{=}\mathbf{3.1}$	$\mathit{\alpha }\mathbf{=}\mathbf{20.0}\mathbf{,}\mathit{\lambda }\mathbf{=}\mathbf{1.5}$
${\mu }_1^{\prime }$	0.8799	0.5602	0.1339
${\mu }_2^{\prime }$	0.8021	0.3401	0.0242
${\mu }_3^{\prime }$	0.7457	0.2185	0.0053
${\mu }_4^{\prime }$	0.7020	0.1465	0.0013
${\mu }_5^{\prime }$	0.6667	0.1017	0.0004
${\mu }_6^{\prime }$	0.6373	0.0726	0.0001
SD	0.1668	0.1619	0.0794
CV	0.1896	0.2890	0.5931
CS	−1.9527	−0.3403	0.7713
CK	6.6850	2.7084	3.5390

From Table 1, the CS is negative for the given parameter values and positive for others. It can be seen that the BTCPE distribution can be leptokurtic or platykurtic depending on the parameter values, since the CK can be lower than 3 or greater than 3, respectively. The coefficient of skewness also reveals that the BTCPE distribution can model both left and right-skewed data.

3.4. Order Statistics

Order statistics play an imperative role in both statistics and industrial reliability analysis. They can be used to estimate the minimum, maximum, and range of observations. They are used in developing control charts that are useful in industrial quality control analyses. Let $Y_{1:n}\le Y_{2:n}\le \dots \le Y_{n:n}$ be $n$ order statistics from $n$ BTCPE random variables. Then, the PDF of $Y_{k:n}$ is given by

$$f_{k:n}(y;\alpha ,\lambda )={\mathsf{\Omega }}_{k:n}{[F_Y(y;\alpha ,\lambda )]}^{k-1}{[1-F_Y(y;\alpha ,\lambda )]}^{n-k}{f}_Y(y;\alpha ,\lambda ),$$

where

$${\mathsf{\Omega }}_{k:n}=\frac{n!}{(k-1)!(n-k)!}.$$

Using the binomial expansion ${(1-y)}^{\lambda -1}={\displaystyle \sum _{i=0}^{\infty }{(-1)}^i\left(\begin{array}{c}\lambda -1\\ i\end{array}\right)}{y}^i,|y|<1$, we can write

$$f_{k:n}(y;\alpha ,\lambda )={\mathsf{\Omega }}_{k:n}{\displaystyle \sum _{i=0}^{k-1}{(-1)}^i\left(\begin{array}{c}k-1\\ i\end{array}\right)}{[1-F_Y(y;\alpha ,\lambda )]}^{n-k+i}{f}_Y(y;\alpha ,\lambda ).$$

Thus, we have

$$f_{k:n}(y;\alpha ,\lambda )=\frac{{\mathsf{\Omega }}_{k:n}4\alpha \lambda y^{\lambda -1}{(1-y^{\lambda })}^{\alpha -1}}{\pi [1+{(1-y^{\lambda })}^{2\alpha }]}{\displaystyle \sum _{i=0}^{k-1}{(-1)}^i\left(\begin{array}{c}k-1\\ i\end{array}\right)}{\left[\frac{4}{\pi }\arctan [{(1-y^{\lambda })}^{\alpha }]\right]}^{n-k+i}.$$

(11)

On the other side, the CDF of $Y_{1:n}$ is simply given by

$$\begin{array}{l}{F}_{1:n}(y;\alpha ,\lambda )=1-{[1-F_Y(y;\alpha ,\lambda )]}^n\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=1-{\left[\frac{4}{\pi }\arctan [{(1-y^{\lambda })}^{\alpha }]\right]}^n,\end{array}$$

and the CDF of $Y_{n:n}$ is derived as

$$F_{n:n}(y;\alpha ,\lambda )={[F_Y(y;\alpha ,\lambda )]}^n={\left[1-\frac{4}{\pi }\arctan [{(1-y^{\lambda })}^{\alpha }]\right]}^n.$$

The distribution of the smallest order statistic represents the lifetime of a system connected in series, and that of the maximum order statistic denotes the lifetime of a system connected in parallel. Hence, they are vital in studying the minimum and maximum time to failure of components in engineering reliability. The minimum and maximum (min-max) plots of the order statistics can be used to investigate the distributional behavior of observations. The min–max plot captures not only the information in the tails but all the information about the whole distribution. The min–max plots shown in Figure 4 for some parameter values depend on $E(Y_{1:n})$ and $E(Y_{n:n})$. From the min–max plots, the distribution can exhibit symmetrical, left-skewed, and right-skewed shapes.

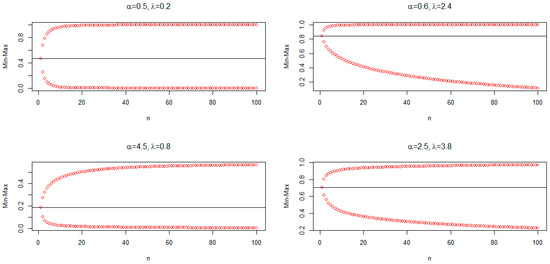
Figure 4. Min–max plots for some parameter values.

4. Bivariate Extension

Researchers may be interested in modeling the dependence between two (quantitative) measures in a dataset. For instance, one may be interested in modeling the relationship between age and the body mass index of individuals. Bivariate distributions have been used in reliability analysis, queuing theory, finance, and insurance risk analysis, among others, to study interdependency (see [26]). In this section, the bivariate extension of the BTCPE (BEBTCPE) distribution is proposed following the strategy developed in [26,27]. Given a bivariate continuous random vector $(X,Y)$, the CDF of the BEBTCPE distribution with parameters $\alpha ,\lambda ,{\delta }_1,{\delta }_2,{\delta }_3$, where $\alpha >0,\lambda >0,$ $-1<{\delta }_1+{\delta }_3<1$, $-1<{\delta }_2+{\delta }_3<1,0<x<1$ and $0<y<1$, is given by

$$F_{XY}(x,y;\mathit{\eta })=\frac{(1-\frac{4}{\pi }\arctan [{(1-x^{\lambda })}^{\alpha }])(1-\frac{4}{\pi }\arctan [{(1-y^{\lambda })}^{\alpha }])}{{\left\{1+({\delta }_1+{\delta }_3)\frac{4}{\pi }\arctan [{(1-x^{\lambda })}^{\alpha }]+({\delta }_2+{\delta }_3)\frac{4}{\pi }\arctan [{(1-y^{\lambda })}^{\alpha }]\right\}}^{-1}},$$

(12)

where $\mathit{\eta }={(\alpha ,\beta ,{\delta }_1,{\delta }_2,{\delta }_3)}^{\mathrm{T}}$. The parameters ${\delta }_1,{\delta }_2$ and ${\delta }_3$ quantify the dependence between the two variables of a BEBTCPE random vector. The plots of the CDF for the following parameter values are shown in Figure 5:

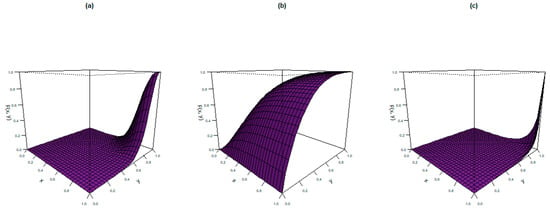
Figure 5. CDF plots of the BEBTCPE distribution.

(a)

$\alpha =3.5,\lambda =8.2,{\delta }_1=0.3,{\delta }_2=0.1,{\delta }_3=0.3$;

(b)

$\alpha =2.5,\lambda =0.8,{\delta }_1=0.5,{\delta }_2=0.4,{\delta }_3=0.2$ and

(c)

$\alpha =0.5,\lambda =4.8,{\delta }_1=-0.3,{\delta }_2=-0.7,{\delta }_3=-0.1$.

We notice various concave and convex shapes from these plots.

The corresponding bivariate PDF is given by

$$f_{XY}(x,y;\mathit{\eta })=\frac{{(4\alpha \lambda /\pi )}^2{(xy)}^{\lambda -1}{(1-x^{\lambda }-y^{\lambda }+{(xy)}^{\lambda })}^{\alpha -1}{[1+{(1-x^{\lambda })}^{2\alpha }]}^{-1}{[1+{(1-y^{\lambda })}^{2\alpha }]}^{-1}}{{\left\{1+({\delta }_1+{\delta }_3)\frac{8}{\pi }\arctan [{(1-x^{\lambda })}^{\alpha }]+({\delta }_2+{\delta }_3)\frac{8}{\pi }\arctan [{(1-y^{\lambda })}^{\alpha }]\right\}}^{-1}}.$$

(13)

Figure 6 shows the bivariate PDF plots of the BEBTCPE distribution for the following parameter values:

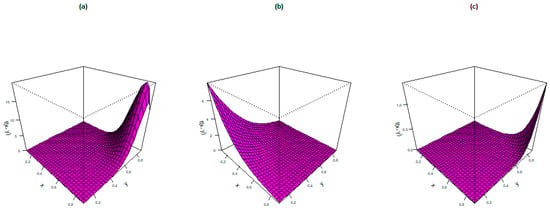
Figure 6. PDF plots of the BEBTCPE distribution.

(a)

$\alpha =3.5,\lambda =8.2,{\delta }_1=0.3,{\delta }_2=0.1,{\delta }_3=0.3$;

(b)

$\alpha =2.5,\lambda =0.8,{\delta }_1=0.5,{\delta }_2=0.4,{\delta }_3=0.2$ and

(c)

$\alpha =0.5,\lambda =4.8,{\delta }_1=-0.3,{\delta }_2=-0.7,{\delta }_3=-0.1$.

The first graph displays a non-monotonic shape whereas the other two exhibit monotonic shapes, illustrating the versatility in the bivariate modeling sense.

5. Parameter Estimation Methods

This section presents nine estimation methods for estimating the parameters of the BTCPE distribution. These include the maximum likelihood (ML) estimation (MLE), ordinary least squares (OLS), weighted least squares (WLS), Cramér–von Mises (CVM), percentile (PC) estimation, Anderson–Darling (AD) methods, and maximum and minimum product spacing methods.

5.1. Maximum Likelihood Estimation

One of the most common methods used for estimating the parameters of a developed model is the MLE method. Suppose that $Y$ follows the BTCPE distribution, with $\mathit{\vartheta }={(\alpha ,\lambda )}^{\mathrm{T}}$ as the parameter vector. For a single observation $y$ of $Y$, the log-likelihood function $\ell =\ell (\mathit{\vartheta })$ is

$$\ell =\log \left(\frac{4\alpha \lambda }{\pi }\right)+(\lambda -1)\log (y)+(\alpha -1)\log (1-y^{\lambda })-\log (1+{(1-y^{\lambda })}^{2\alpha }).$$

(14)

To obtain the estimates of the parameters for the single observation, the first partial derivative of Equation (14) with respect to the parameters needs to be derive. Here, we obtain

$$\frac{\partial \ell }{\partial \alpha }=\frac{1}{\alpha }+\log (1-y^{\lambda })-\frac{2{(1-y^{\lambda })}^{2\alpha }\log (1-y^{\lambda })}{1+{(1-y^{\lambda })}^{2\alpha }},$$

(15)

and

$$\frac{\partial \ell }{\partial \lambda }=\frac{1}{\lambda }+\log (y)-\frac{y^{\lambda }(\alpha -1)\log (y)}{1-y^{\lambda }}+\frac{2\alpha y^{\lambda }{(1-y^{\lambda })}^{2\alpha -1}\log (y)}{1+{(1-y^{\lambda })}^{2\alpha }}.$$

(16)

Given that $y_1,y_2,\dots ,y_n$ are (independent and identically) observations from $n$ BTCPE random variables, then the total log-likelihood function is given by ${\ell }_n^{*}={\displaystyle \sum _{i=1}^n{\ell }_i(\mathit{\vartheta })}$, where ${\ell }_i(\mathit{\vartheta }),i=1,2,\dots ,n$ is defined in Equation (14) with $y=y_i$. The estimates of the parameters can be obtained by maximizing the total log-likelihood function directly using MATLAB, MATHEMATICA and R software. In this study, the R software is used [28]. Alternatively, the estimates of the parameters can be obtained by equating the first partial derivatives with respect to the parameters to zero and solving the resulting system of equations simultaneously. However, since the resulting system of equations does not have a closed form, the nonlinear system of equations ${\left(\frac{\partial {\ell }_n^{*}}{\partial \alpha },\frac{\partial {\ell }_n^{*}}{\partial \lambda }\right)}^{\mathrm{T}}={(0,0)}^{\mathrm{T}}$ is solved numerically to obtain the estimates of the parameters.

5.2. Ordinary and Weighted Least Squares Estimation

Suppose that $y_{(1)},y_{(2)},\dots ,y_{(n)}$ are ordered observations from $n$ BTCPE random variables. The OLS estimates of the parameters ${\widehat{\alpha }}_{LSE}$ and ${\widehat{\lambda }}_{LSE}$ are obtained by minimizing the following function:

$$LSE(\alpha ,\lambda )={\displaystyle \sum _{i=1}^n{\left[\left(1-\frac{4}{\pi }\arctan [{(1-y_{(i)}^{\lambda })}^{\alpha }]\right)-\frac{i}{n+1}\right]}^2},$$

(17)

with respect to the parameters $\alpha$ and $\lambda$. On the other hand, the OLS estimates can be obtained by numerically solving the following nonlinear equations:

$${\displaystyle \sum _{i=1}^n\left[\left(1-\frac{4}{\pi }\arctan [{(1-y_{(i)}^{\lambda })}^{\alpha }]\right)-\frac{i}{n+1}\right]}{\Delta }_s(y_{(i)}|\alpha ,\lambda )=0,s=1,2,$$

(18)

where

$${\Delta }_1(y_{(i)}|\alpha ,\lambda )=-\frac{8{(1-y_{(i)}^{\lambda })}^{\alpha }\log (1-y_{(i)}^{\lambda })}{\pi [1+{(1-y_{(i)}^{\lambda })}^{2\alpha }]}$$

and

$${\Delta }_2(y_{(i)}|\alpha ,\lambda )=\frac{8\alpha y_{(i)}^{\lambda }{(1-y_{(i)}^{\lambda })}^{\alpha -1}\log (y_{(i)})}{\pi [1+{(1-y_{(i)}^{\lambda })}^{2\alpha }]}.$$

The WLS estimates ${\widehat{\alpha }}_{WLS}$ and ${\widehat{\lambda }}_{WLS}$ are obtained by minimizing the following function:

$$WLS(\alpha ,\lambda )={\displaystyle \sum _{i=1}^n\frac{{(n+1)}^2(n+2)}{i(n-i+1)}}{\left[\left(1-\frac{4}{\pi }\arctan [{(1-y_{(i)}^{\lambda })}^{\alpha }]\right)-\frac{i}{n+1}\right]}^2,$$

(19)

with respect to the parameters $\alpha$ and $\lambda$. Alternatively, the WLS estimates can be obtained by numerically solving the following nonlinear equations:

$${\displaystyle \sum _{i=1}^n\frac{{(n+1)}^2(n+2)}{i(n-i+1)}}\left[\left(1-\frac{4}{\pi }\arctan [{(1-y_{(i)}^{\lambda })}^{\alpha }]\right)-\frac{i}{n+1}\right]{\Delta }_s(y_{(i)}|\alpha ,\lambda )=0,s=1,2,$$

(20)

where ${\Delta }_s(x_{(i)}|\alpha ,\lambda ),s=1,2$ are defined above.

5.3. Cramér–Von Mises Estimation

Let $y_{(1)},y_{(2)},\dots ,y_{(n)}$ be ordered observations from $n$ BTCPE random variables. The CVM estimates of the parameters ${\widehat{\alpha }}_{CVM}$ and ${\widehat{\lambda }}_{CVM}$ are obtained by minimizing the following function:

$$CVM(\alpha ,\lambda )=\frac{1}{12n}+{\displaystyle \sum _{i=1}^n{\left[\left(1-\frac{4}{\pi }\arctan [{(1-y_{(i)}^{\lambda })}^{\alpha }]\right)-\frac{2i-1}{2n}\right]}^2},$$

(21)

with respect to the parameters $\alpha$ and $\lambda$. The estimates of the parameters can also be obtained by numerically solving the following equations:

$${\displaystyle \sum _{i=1}^n\left[\left(1-\frac{4}{\pi }\arctan [{(1-y_{(i)}^{\lambda })}^{\alpha }]\right)-\frac{2i-1}{2n}\right]{\Delta }_s(y_{(i)}|\alpha ,\lambda )=0},s=1,2,$$

(22)

where ${\Delta }_s(y_{(i)}|\alpha ,\lambda ),s=1,2$ are given above.

5.4. Anderson–Darling Estimation

Another minimum distance estimation method is the AD estimation technique. Let $y_{(1)},y_{(2)},\dots ,y_{(n)}$ be ordered observations from $n$ BTCPE random variables. The AD estimates for the parameters of the BTCPE distribution are obtained by minimizing the following function:

$$AD(\alpha ,\lambda )=-n-\frac{1}{n}{\displaystyle \sum _{i=1}^n(2i-1)\left[\log \left(1-\frac{4}{\pi }\arctan [(1-y_{(i)}^{\lambda })]\right)+\log \left(\frac{4}{\pi }\arctan [(1-y_{(i)}^{\lambda })]\right)\right]},$$

(23)

with respect to the parameters $\alpha$ and $\lambda$.

5.5. Percentile Estimation

The PC estimation approach is another method of estimating the parameters of a given model. Let $y_{(1)},y_{(2)},\dots ,y_{(n)}$ be ordered observations from $n$ BTCPE random variables and $u_i=i/(n+1)$ be an unbiased estimate of $F_Y(y_{(i)};\alpha ,\lambda )$. The PC estimates of the parameters of the BTCPE distribution are obtained by minimizing the following function:

$$PC(\alpha ,\lambda )={{\displaystyle \sum _{i=1}^n\left[y_{(i)}-{\left\{1-{\left(\tan \left[\frac{\pi }{4}(1-u_i)\right]\right)}^{1/\alpha }\right\}}^{1/\lambda }\right]}}^2,$$

(24)

with respect to the parameters $\alpha$ and $\lambda$.

5.6. Maximum and Minimum Product Spacing Estimation

An alternative parameter estimation technique which is based on the Kullback–Leibler information measure is the maximum product spacing (MPS). Let $y_{(1)},y_{(2)},\dots ,y_{(n)}$ be ordered observations from $n$ BTCPE random variables. Consider the uniform spacing

$$\begin{array}{l}{D}_i=F_Y(y_{(i)};\alpha ,\lambda )-F_Y(y_{(i-1)};\alpha ,\lambda )\\ \hspace{1em}=\frac{4}{\pi }\arctan [(1-y_{(i-1)}^{\lambda })]-\frac{4}{\pi }\arctan [(1-y_{(i)}^{\lambda })]\end{array}$$

where $F_Y(y_{(0)};\alpha ,\lambda )=0,F_Y(y_{(n+1)};\alpha ,\lambda )=1$ and $D_0(\alpha ,\lambda )+D_1(\alpha ,\lambda )+\dots +D_{n+1}(\alpha ,\lambda )=1$. The estimates of the parameters are obtained via the MPS approach by maximizing the logarithm of the geometric mean of the spacing defined by

$$MPS(\alpha ,\lambda )=\frac{1}{n+1}{\displaystyle \sum _{i=1}^{n+1}\log D_i(\alpha ,\lambda )},$$

(25)

with respect to the parameters $\alpha$ and $\lambda$.

Additionally, the minimum spacing distance (MSD) estimates for the parameters $\alpha$ and $\lambda$ are obtained by minimizing the following function:

$$MSD(\alpha ,\lambda )={\displaystyle \sum _{i=1}^{n+1}\vartheta (D_i(\alpha ,\lambda ),\frac{1}{n+1})},$$

(26)

where $\vartheta (x,y)$ is an appropriate distance, with respect to the parameters $\alpha$ and $\lambda$. Although different choices of $\vartheta (x,y)$ exist, in this study the absolute distance $|x-y|$ and the absolute-log distance $|\log x-\log y|$ are utilized. Thus, the minimum spacing absolute distance (MSAD) and minimum spacing absolute-log distance (MSALD) estimates are, respectively, obtained by minimizing the following functions:

$$MSAD(\alpha ,\lambda )={\displaystyle \sum _{i=1}^{n+1}|D_i(\alpha ,\lambda )-\frac{1}{n+1}|}$$

(27)

and

$$MSALD(\alpha ,\lambda )={\displaystyle \sum _{i=1}^{n+1}|\log D_i(\alpha ,\lambda )-\log \frac{1}{n+1}|},$$

(28)

where $D_i(\alpha ,\lambda )\ne \frac{1}{n+1}$ and $\log D_i(\alpha ,\lambda )\ne \log \frac{1}{n+1}$.

6. Simulation

In this section, simulation experiments are carried out to assess how well the proposed parameters of the BTCPE distribution have been estimated. The experiments are carried out with the following two different parameter combinations: $\alpha =4.1,\lambda =2.5$ and $\alpha =3.1,\lambda =8.5$. The experiments are replicated 5000 times with the following different sample sizes: $n=25,75,125,175$ and 225. The bias (AB) and root mean square error (RMSE) of the estimates are then computed and compared.

The AB and RMSE are, respectively, computed using

$$AB=\frac{1}{R}{\displaystyle \sum _{i=1}^R\left(\widehat{{\vartheta }_i}-\vartheta \right)}$$

and

$$RMSE=\sqrt{\frac{1}{R}{\displaystyle \sum _{i=1}^R{\left(\widehat{{\vartheta }_i}-\vartheta \right)}^2}},$$

where $\widehat{\vartheta }$ is either $\widehat{\alpha }$ or $\widehat{\lambda }$ and R = 5000 is used in this study.

From Table 2 and Table 3, most of the estimates have their ABs and RMSEs decreasing as the sample size increases. This is an indication that most of the estimates exhibit the consistency property. From Table 2, it can be observed that for sample sizes 25, 75 and 125 the PC estimate is the best for $\alpha$ and, for the sample sizes 175 and 225, the MLE is the best for $\alpha$. For the parameter $\lambda$, the PC estimate is the best for the sample size 25 and the MLE is the best for 75, 125, 175 and 225. In Table 3, for sample sizes 25 and 75 the AD estimate is the best for the parameter $\alpha$ and the MLE is the best for 125, 175 and 225. For the parameter $\lambda$, the MLE is the best for sample sizes 25, 125, 175 and 225. The AD estimate is best for $\lambda$ when the sample size is 75.

Table 2. AB and RMSE for $\alpha =4.1$ and $\lambda =2.5$.

Parameter	$\mathit{n}$	AB									RMSE
		MLE	MPS	MADS	MALDS	OLS	WLS	CVM	AD	PC	MLE	MPS	MADS	MALDS	OLS	WLS	CVM	AD	PC
$\alpha$	25	0.7980	2.2327	−2.3189	0.531	0.3530	−2.6423	1.1477	0.4713	−0.3155	2.2233	3.5728	2.9322	3.3391	2.4457	2.6729	3.5377	1.9964	1.4972
	75	0.2140	0.7443	−1.8442	0.0634	0.1365	−3.1632	0.3415	0.1180	−0.1694	0.9157	1.3139	2.4241	1.1330	1.1489	3.1657	1.2820	0.9535	0.8506
	125	0.1342	0.4372	−1.3088	−0.0031	0.0472	−3.3268	0.1337	0.0713	−0.0783	0.6843	0.8313	1.9860	0.7795	0.8149	3.3279	0.8159	0.7025	0.6641
	175	0.0914	0.2987	−0.8738	−0.0272	0.0460	−2.1721	0.1164	0.0657	−0.0484	0.5365	0.6791	1.5544	0.6323	0.6845	2.1990	0.6955	0.5941	0.5393
	225	0.0677	0.2509	−0.6976	0.0062	0.0301	3.0791	0.1096	0.0365	−0.0623	0.4841	0.5505	1.3266	0.5926	0.5906	3.3377	0.6147	0.5240	0.4860
$\lambda$	25	0.1871	0.5436	−1.1017	0.0300	−0.0075	−1.3344	0.2060	0.0670	−0.1737	0.6038	0.8201	1.3862	0.7382	0.6538	1.3687	0.7340	0.5749	0.5401
	75	0.0478	0.2197	−0.8939	−0.0079	0.0078	−2.0003	0.0802	0.1185	−0.0672	0.3089	0.4026	1.2090	0.3996	0.3692	2.0029	0.3886	0.3379	0.3175
	125	0.0378	0.1293	−0.6271	−0.0160	−0.0055	−2.1461	0.0305	0.0146	−0.0448	0.2407	0.2740	0.9681	0.2987	0.2752	2.1472	0.2798	0.2560	0.2466
	175	0.0233	0.0866	−0.3986	−0.0139	0.0034	−1.6394	0.0280	0.0114	−0.0267	0.1959	0.2314	0.7264	0.2315	0.2372	1.6455	0.2383	0.2134	0.2008
	225	0.0208	0.0820	−0.3101	0.0021	0.0003	0.1937	0.0230	0.0007	−0.0225	0.1810	0.1939	0.6057	0.2196	0.2079	0.3066	0.2124	0.1874	0.1835

Table 3. AB and RMSE for $\alpha =3.1$ and $\lambda =8.5$.

Parameter	$\mathit{n}$	AB									RMSE
		MLE	MPS	MADS	MALDS	OLS	WLS	CVM	AD	PC	MLE	MPS	MADS	MALDS	OLS	WLS	CVM	AD	PC
$\alpha$	25	0.5120	1.5281	−1.3158	0.3712	0.2359	−1.9121	0.7701	0.2725	−0.6748	1.4793	2.5597	2.0817	1.9689	1.6086	1.9366	2.4325	1.3231	1.4204
	75	0.2081	0.5190	−0.9456	0.0477	0.0264	−2.2924	0.1973	0.0989	−0.3302	0.6848	0.8671	1.5913	0.7865	0.7088	2.2949	0.8122	0.6294	0.8145
	125	0.0994	0.3218	−0.6895	0.0570	0.0153	−2.4255	0.1020	0.0757	−0.2704	0.4778	0.6228	1.2854	0.5657	0.5532	2.4266	0.5644	0.5109	0.6262
	175	0.0867	0.2259	−0.5478	0.0107	0.0240	−1.3857	0.0882	0.0554	−0.2187	0.4077	0.4554	1.0538	0.4821	0.4813	1.4810	0.4940	0.4163	0.5242
	225	0.0461	0.1719	−0.4192	0.0007	0.0195	2.2166	0.0555	0.0200	−0.1735	0.3331	0.3880	0.8460	0.4021	0.4133	2.3785	0.4184	0.3477	0.4768
$\lambda$	25	0.5725	1.9602	−3.5282	0.1675	0.1107	−4.6443	0.7293	0.2368	−1.6432	2.0951	3.1555	4.8358	2.6753	2.3883	4.7703	2.6517	2.1203	2.6346
	75	0.2957	0.8211	−2.4563	−0.0292	−0.0416	−6.9243	0.2449	0.0825	−0.7220	1.1627	1.4130	3.9050	1.3676	1.2655	6.9330	1.3246	1.1047	1.4877
	125	0.1098	0.4964	−1.6975	0.0128	−0.0435	−7.3960	0.1015	0.0784	−0.5259	0.8837	1.0321	3.0631	1.0694	0.9899	7.3994	0.9670	0.9327	1.1482
	175	0.1182	0.3504	−1.2348	−0.0232	0.0022	−5.5678	0.1061	0.0622	−0.4011	0.7361	0.7786	2.4368	0.8864	0.8608	5.5937	0.8687	0.7734	0.9365
	225	0.0631	0.2843	−0.9196	−0.0034	0.0015	0.6715	0.043	0.0249	−0.3171	0.6223	0.7091	1.9241	0.7604	0.7452	1.0898	0.7515	0.6590	0.8305

7. Applications

Three applications of the BTCPE distribution are illustrated in this section, and its performance is compared to other competitive distributions defined in the unit interval. The performance of the BTCPE distribution was compared with that of the beta, unit Burr-III (UBIII) [29], bounded M-O extended exponential (BMOEE) [30], unit Gompertz (UG) [18], unit Lindley (UL) [17], unit Weibull (UW) [20] and unit-improved second-degree Lindley (UISDL) [31] distributions. The Akaike information criterion (AIC), Bayesian information criterion (BIC), Anderson–Darling (AD) test, and Cramér–von Mises (CVM) are the model selection techniques employed in arriving at the best model. For these selection techniques, the best model is the one with the smallest test statistic. The datasets represent the mortality rate of COVID-19 patients in Canada and the United Kingdom (UK), and the recovery rate of COVID-19 patients in Spain. The first two datasets were recently reported by [8].

The first dataset is the mortality rate for UK from 1 December 2020 to 29 January 2021. The data are: 0.1292, 0.3805, 0.4049, 0.2564, 0.3091, 0.2413, 0.1390, 0.1127, 0.3547, 0.3126, 0.2991, 0.2428, 0.2942, 0.0807, 0.1285, 0.2775, 0.3311, 0.2825, 0.2559, 0.2756, 0.1652, 0.1072, 0.3383, 0.3575, 0.2708, 0.2649, 0.0961, 0.1565, 0.1580, 0.1981, 0.4154, 0.3990, 0.2483, 0.1762, 0.1760, 0.1543, 0.3238, 0.3771, 0.4132, 0.4602, 0.352, 0.1882, 0.1742, 0.4033, 0.4999, 0.3930, 0.3963, 0.3960, 0.2029, 0.1791, 0.4768, 0.5331, 0.3739, 0.4015, 0.3828, 0.1718, 0.1657, 0.4542, 0.4772, 0.3402.

The second dataset denotes the mortality rate for Canada from 1 November to 26 December 2020. The data are: 0.1622, 0.1159, 0.1897, 0.1260, 0.3025, 0.2190, 0.2075, 0.2241, 0.2163, 0.1262, 0.1627, 0.2591, 0.1989, 0.3053, 0.2170, 0.2241, 0.2174, 0.2541, 0.1997, 0.3333, 0.2594, 0.2230, 0.2290, 0.1536, 0.2024, 0.2931, 0.2739, 0.2607, 0.2736, 0.2323, 0.1563, 0.2677, 0.2181, 0.3019, 0.2136, 0.2281, 0.2346, 0.1888, 0.2729, 0.2162, 0.2746, 0.2936, 0.3259, 0.2242, 0.1810, 0.2679, 0.2296, 0.2992, 0.2464, 0.2576, 0.2338, 0.1499, 0.2075, 0.1834, 0.3347, 0.2362.

The third dataset constitutes the recovery rates of COVID-19 patients in Spain from 3 March to 7 May 2020. The dataset can be found in [1] and are: 0.6670, 0.5000, 0.5000, 0.4286, 0.7500, 0.6531, 0.5161, 0.7895, 0.7689, 0.6873, 0.5200, 0.7251, 0.6375, 0.6078, 0.6289, 0.5712, 0.5923, 0.6061, 0.5924, 0.5921, 0.5592, 0.5954, 0.6164, 0.6455, 0.6725, 0.6838, 0.6850, 0.6947, 0.7210, 0.7315, 0.7412, 0.7508, 0.7519, 0.7547, 0.7645, 0.7715, 0.7759, 0.7807, 0.7838, 0.7847, 0.7871, 0.7902, 0.7934, 0.7913, 0.7962, 0.7971, 0.7977, 0.8007, 0.8038, 0.8289, 0.8322, 0.8354, 0.8371, 0.8387, 0.8456, 0.8490,0.8535, 0.8547, 0.8564, 0.8580, 0.8604, 0.8628, 0.6586, 0.7070, 0.7963, 0.8516.

The ML estimates of the parameters are estimated using the bbmle package in R [32]. The initial values of the parameters of the fitted distributions used for the optimization are obtained using the GenSA package in R [33]. Table 4 displays the descriptive statistics for COVID-19 mortality for the UK and Canada, as well as the recovery rate for Spain. The datasets are platykurtic due to the negative excess kurtosis. The UK mortality is right-skewed and that of Canada is left-skewed. The recovery rate for Spain is also left-skewed. This is affirmed by the boxplot of the datasets shown in Figure 7.

Table 4. Descriptive statistics for datasets.

Country	Minimum	Maximum	Mean	Skewness	Kurtosis
UK	0.0807	0.5331	0.2888	0.0476	−1.1034
Canada	0.1159	0.3347	0.2305	−0.0850	−0.4402
Spain	0.4286	0.8628	0.7240	−0.6890	−0.4761

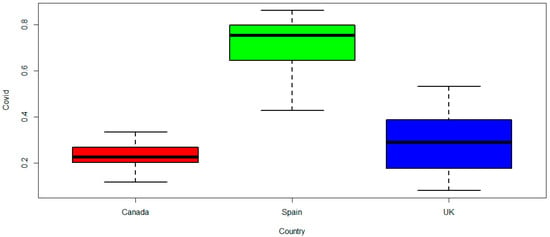
Figure 7. Boxplots of COVID-19 datasets.

7.1. UK COVID-19 Mortality

Table 5 presents ML estimates of the parameters and their corresponding standard errors in brackets, the log-likelihood ($\ell$), AIC, BIC, AD, and CVM for the fitted distributions. Given that it has the lowest values for the AIC, BIC, AD, and CVM and the maximum log-likelihood, the BTCPE distribution offers the best fit to the UK mortality dataset.

Table 5. Parameter estimates and model selection criteria for UK.

Model	Parameter	$\mathit{\ell }$	AIC	BIC	AD	CVM
BTCPE	$\alpha =16.6904(5.2798)$ $\lambda =2.3884(0.2865)$	45.4400	−86.8726	−82.6840	0.6494	0.1049
Beta	$\alpha =4.0502(0.7128)$ $\beta =10.0132(1.8287)$	45.4000	−86.7958	−82.6071	0.7356	0.1280
UBIII	$\alpha =0.0757(0.0383)$ $\beta =13.3804(6.5631)$	38.9000	−73.8075	−69.6188	2.8948	0.5248
BMOEE	$\alpha =105.2655(59.9004)$ $\beta =3.5949(0.4092)$	40.7200	−77.4396	−73.2509	1.1465	0.1698
UW	$\alpha =0.2834(0.0602)$ $\beta =3.1228(0.3047)$	42.5600	−81.1208	−76.9322	1.0656	0.1820
UG	$\alpha =686.3600(2.2295\times {10}^{-10})$ $\beta =0.0011(1.4051\times {10}^{-4})$	2.8400	−1.6760	2.5127	12.2290	2.4707
UL	$\alpha =2.8293(0.3029)$	32.3800	−62.7533	−60.6590	4.4878	0.7574
UISDL	$\alpha =3.4259(0.3151)$	33.6100	−65.2142	−63.1198	3.9972	0.6545

Figure 8 displays the empirical and fitted PDFs and CDFs of the various distributions used to model the UK mortality dataset. The figure gives an indication that the BTCPE distribution provides a good fit to the dataset compared to the other models.

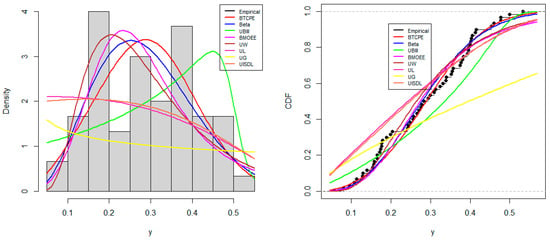
Figure 8. Empirical and fitted PDFs (left) and CDFs (right) of UK dataset.

Figure 9 is the probability–probability (P-P) plots of the fitted distributions. Figure 9 once more shows that the BTCPE distribution fits the UK drought mortality well because the points cluster along the diagonal.

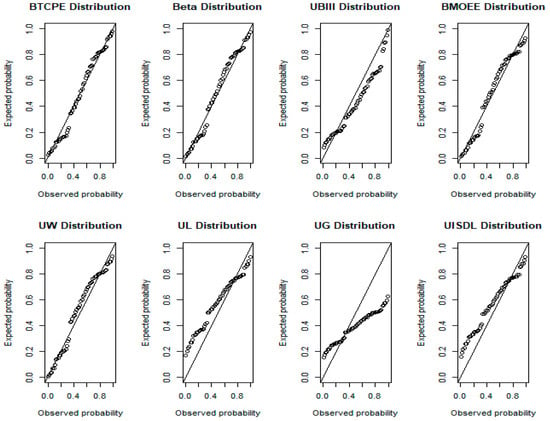
Figure 9. P-P plots for UK drought mortality.

The profile log-likelihood plots for the estimated parameter values of the BTCPE distribution for the UK mortality data are shown in Figure 10. From the plots, it can be observed that the estimated values are the true maxima.

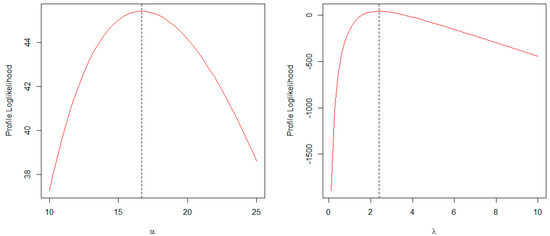
Figure 10. Profile log-likelihood plots for estimated parameters of BTCPE for UK.

7.2. Canada COVID-19 Mortality

Table 6 presents ML estimates of the parameters and their corresponding standard errors in brackets and model selection criteria for the fitted distributions. The BTCPE distribution again provides the best fit to the Canada mortality dataset since it has the highest log-likelihood and the lowest values of the AIC, BIC, AD, and CVM.

Table 6. Parameter estimates and model selection criteria for Canada.

Model	Parameter	$\mathit{\ell }$	AIC	BIC	AD	CVM
BTCPE	$\alpha =622.2064(399.8188)$ $\lambda =4.5085(0.4837)$	86.4400	−168.8806	−164.8299	0.3767	0.0689
Beta	$\alpha =14.5128(2.7128)$ $\beta =48.4900(9.1745)$	85.9400	−167.8800	−163.8293	0.4398	0.0692
UBIII	$\alpha =0.0080(0.0011)$ $\beta =101.7700(8.4127\times {10}^{-8})$	30.8900	−57.7749	−53.7242	14.8770	3.1113
BMOEE	$\alpha =2822.9776(3.3087\times {10}^{-5})$ $\beta =5.4444(0.1439)$	80.6700	−157.3394	−153.2887	1.5514	0.2327
UW	$\alpha =0.0552(0.0193)$ $\beta =6.1602(0.5868)$	79.9500	−155.9080	−151.8573	1.4890	0.2389
UG	$\alpha =628.3885(2.4072\times {10}^{-10})$ $\beta =0.0011(1.4212\times {10}^{-4})$	5.2500	−6.4901	−2.4393	18.5180	3.9712
UL	$\alpha =3.9381(0.4506)$	41.1400	−80.2707	−78.2453	12.7090	2.5936
UISDL	$\alpha =3.4259(0.3151)$	42.2000	−82.3913	−80.3660	12.3010	2.4925

Figure 11 shows the empirical and fitted PDFs and CDFs of the various distributions used to model the Canada drought mortality dataset. The figure gives an indication that the BTCPE distribution provides a better fit to the drought mortality for Canada than the other models, as it mimics the empirical PDF and CDF of the dataset better than the other models.

Figure 11. Empirical and fitted PDFs (left) and CDFs (right) of Canada dataset.

Figure 12 shows the P-P plots of the fitted models. Figure 12 gives an indication that the BTCPE distribution provides a good fit to the Canada mortality as the points cluster along the diagonal.

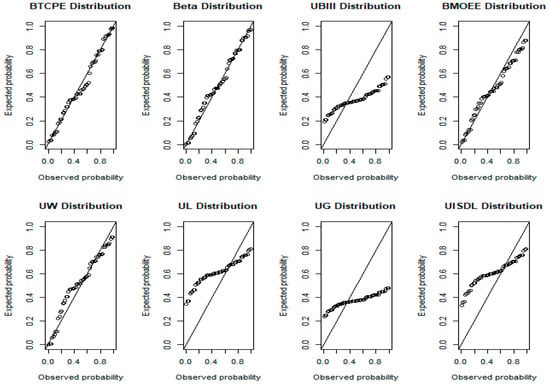
Figure 12. P-P plots for Canada mortality.

Figure 13 displays the profile log-likelihood plots for the estimated parameter values of the BTCPE distribution for the Canada mortality data. It can be observed from the plots that the estimates are unique and represent the true maxima.

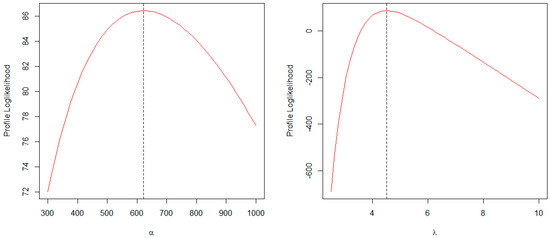
Figure 13. Profile log-likelihood plots for estimated parameters of BTCPE for Canada.

7.3. Spain COVID-19 Recovery Rate

The ML estimates of the parameters and their corresponding standard errors in brackets and model selection criteria for the fitted distributions are shown in Table 7. Because it has the lowest values for the AIC, BIC, AD, and CVM and the maximum log-likelihood, the BTCPE distribution again offers the best fit to the Spain recovery rate dataset.

Table 7. Parameter estimates and model selection criteria for Canada.

Model	Parameter	$\mathit{\ell }$	AIC	BIC	AD	CVM
BTCPE	$\alpha =7.1385(1.7764)$ $\lambda =7.1961(0.9033)$	58.7500	−113.4953	−109.1160	0.8770	0.1363
Beta	$\alpha =12.7943(2.2291)$ $\beta =4.8994(0.8270)$	57.5700	−111.1489	−106.7692	1.0520	0.1783
UBIII	$\alpha =5.4398(0.7948)$ $\beta =2.0613(0.1723)$	53.8000	−103.5927	−99.2134	1.3725	0.2209
BMOEE	$\alpha =22.1286(9.9041)$ $\beta =10.0043(1.2381)$	51.4600	−98.9276	−94.5483	1.4958	0.2100
UW	$\alpha =8.6445(1.6973)$ $\beta =2.2320(0.2036)$	53.9700	−103.9316	−99.5523	1.3830	0.2238
UG	$\alpha =0.2792(0.1059)$ $\beta =3.8482(0.6025)$	46.0300	−88.0569	−83.6776	2.4709	0.3691
UL	$\alpha =0.5200(0.0466)$	46.1100	−90.2298	−88.0402	4.2480	0.6736
UISDL	$\alpha =0.7403(0.0539)$	52.0400	−102.0717	−99.8820	2.3450	0.3194

The empirical and fitted PDFs and CDFs of the various distributions used to model the Spain recovery rate dataset are shown in Figure 14. It can be seen that the BTCPE distribution provides a better fit to the recovery rate data than the other models.

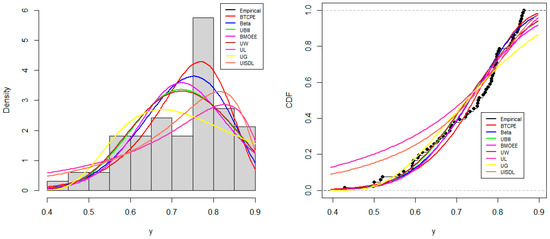
Figure 14. Empirical and fitted PDFs (left) and CDFs (right) of Spain dataset.

The P-P plots of the fitted models for the recovery rate data are displayed in Figure 15. The plots indicate that the BTCPE distribution provides a good fit to the recovery rate data as the points cluster along the diagonal.

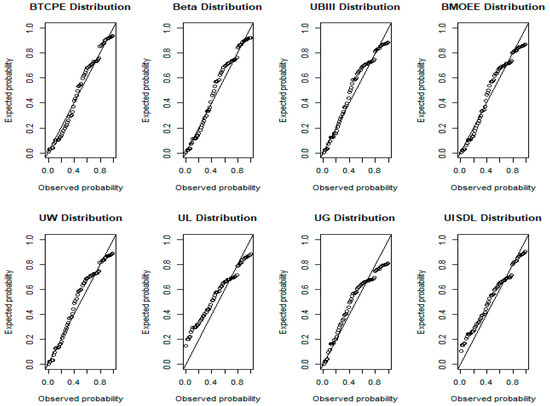
Figure 15. P-P plots for Spain recovery data.

The profile log-likelihood plots for the estimated parameter values of the BTCPE distribution for the recovery rate data are shown in Figure 16. The plots suggest that the estimates are unique and represent the true maxima.

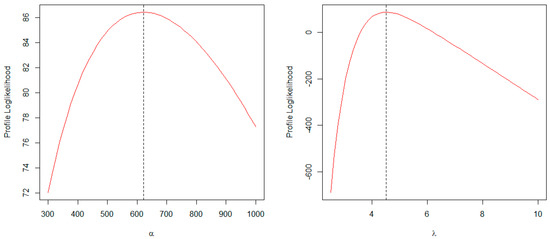
Figure 16. Profile log-likelihood plots for estimated parameters of BTCPE for Spain.

8. Quantile Regression

When the response variable defined in the unit interval is skewed or contaminated with outliers, the beta regression model, which models the conditional mean of the response variable, is no longer reliable. A robust regression model is needed to model the effects of the covariates on the response variable. In this study, a quantile regression model is proposed for modeling the conditional quantile of the response variable. Given the quantile function of the BTCPE distribution, the PDF of the BTCPE distribution can be re-parameterized in terms of its $u^{th}$ quantile as $\rho =Q(u;\alpha ,\lambda ),\rho \in [0,1]$. If $\lambda =\log (1-{(\tan [\pi (1-u)/4])}^{1/\alpha })/\log (\rho )$, then the re-parameterized PDF is

$$\begin{array}{l}{f}_Y(y;\alpha ,\lambda )=\\ \frac{4\alpha (\log (1-{(\tan [\pi (1-u)/4])}^{1/\alpha })/\log (\rho ))y^{(\log (1-{(\tan [\pi (1-u)/4])}^{1/\alpha })/\log (\rho ))-1}{(1-y^{(\log (1-{(\tan [\pi (1-u)/4])}^{1/\alpha })/\log (\rho ))})}^{\alpha -1}}{\pi [1+{(1-y^{(\log (1-{(\tan [\pi (1-u)/4])}^{1/\alpha })/\log (\rho ))})}^{2\alpha }]}.\end{array}$$

(29)

The parameter $\rho$ is the quantile parameter. The BTCPE quantile regression is defined as

$$g({\rho }_i)={z^{\prime }}_i\mathit{\theta },$$

where $\mathit{\theta }=({\theta }_0,{\theta }_1,\dots ,{\theta }_p{)}^{\prime }$ is the vector of unknown parameters, ${\rho }_i$ is the $i^{th}$ quantile parameter and ${z^{\prime }}_i=(1,z_{i1},z_{i2},\dots ,z_{ip})$ are the known $i^{th}$ vector of covariates. The link function $g(\cdot )$ is used to link the covariates to the conditional median of the dependent variable $Y$. The logit link function is used to link the covariates to the conditional quantile since $y\in (0,1)$. Hence, we have

$$g({\rho }_i)=\mathrm{logit}({\rho }_i)=\log (\frac{{\rho }_i}{1-{\rho }_i}).$$

Further, we can write

$${\rho }_i=\frac{\exp ({z^{\prime }}_i\mathit{\theta })}{1+\exp ({z^{\prime }}_i\mathit{\theta })}.$$

Substituting ${\rho }_i$ into the re-parameterized PDF, the log-likelihood for estimating the parameters of the BTCPE quantile regression is given by

$$\begin{array}{l}\ell ={\displaystyle \sum _{i=1}^n\log \left((4\alpha /\pi )(\log (1-{(\tan [\pi (1-u)/4])}^{1/\alpha })/\log ({\rho }_i))\right)}-{\displaystyle \sum _{i=1}^n\log (1+{(1-z_i)}^{2\alpha })}+\\ \hspace{1em}{\displaystyle \sum _{i=1}^n[(\log (1-{(\tan [\pi (1-u)/4])}^{1/\alpha })/\log ({\rho }_i))-1]\log (y_i)}+(\alpha -1){\displaystyle \sum _{i=1}^n\log (1-z_i)},\end{array}$$

(30)

where $z_i=y_i{}^{(\log (1-{(\tan [\pi (1-u)/4])}^{1/\alpha })/\log ({\rho }_i))}$. The estimates of the parameters of the regression equation are obtained by directly maximizing the log-likelihood function. They will be denoted as $\widehat{\alpha }$ and $\widehat{\mathit{\theta }}=({\widehat{\theta }}_0,\dots ,{\widehat{\theta }}_p{)}^{\prime }$ of $\alpha$ and $\mathit{\theta }$, respectively.

8.1. Residual Analysis

Model diagnostics are very essential when fitting a model to a dataset. Often, the behavior of the model residuals is examined to see if the model really provides a good fit to the data. In this study, the randomized quantile residuals are used to assess the adequacy of the regression model. The randomized quantile residuals are defined as

$$r_i={\mathsf{\Phi }}^{-1}(F_Y(y_i;\widehat{\alpha },\widehat{\mathit{\theta }})),i=1,2,\dots ,n,$$

where ${\mathsf{\Phi }}^{-1}(\cdot )$ is the quantile of the standard normal distribution. The randomized quantile residuals are expected to be distributed as the standard normal distribution if the models provide a good fit to the data.

8.2. Monte Carlo Simulation for Quantile Regression

Monte Carlo simulations are carried out in this section to examine the performance of the ML estimates of the parameters of the BTCPE regression model. The exercise is performed with two covariates. The following regression structure is adopted for the simulation:

$${\rho }_i=\frac{\exp ({\theta }_0+{\theta }_1{z}_{i1}+{\theta }_2{z}_{i2})}{1+\exp ({\theta }_0+{\theta }_1{z}_{i1}+{\theta }_2{z}_{i2})}.$$

The observations for the response variable are generated from the BTCPE distribution using sample sizes $n=50,100,250,350,500,600$ and 700. The experiments were repeated 5000 times for each sample size. The performance of the ML estimates is examined using AB and RMSE. The simulations were carried out using the median, $u=0.5$. The following parameter combinations were used in the simulation: $I:(\alpha ,{\theta }_0,{\theta }_1,{\theta }_2)=(0.7,0.2,0.8,0.3),$ $II:(\alpha ,{\theta }_0,{\theta }_1,{\theta }_2)=(0.6,0.5,0.4,1.8)$ and $III:(\alpha ,{\theta }_0,{\theta }_1,{\theta }_2)=(0.8,0.4,0.9,0.6)$. From the simulation results shown in Table 8, the ABs and RMSEs of the estimates’ decrease as the sample size increases. Hence, the ML estimates for the BTCPE regression parameters are consistent.

Table 8. Simulation results for the quantile regression.

		I		II		III
Parameter	n	AB	RMSE	AB	RMSE	AB	RMSE
${\theta }_0$	50	0.1949	0.2235	0.3599	0.3753	0.2609	0.2969
	100	0.1946	0.1961	0.3551	0.3726	0.2178	0.2579
	250	0.1919	0.1941	0.3465	0.3673	0.1525	0.1926
	350	0.1898	0.1928	0.3271	0.3544	0.1320	0.1700
	500	0.1838	0.1927	0.3109	0.3482	0.1101	0.1431
	600	0.1779	0.1886	0.3051	0.3434	0.0998	0.1318
	700	0.1761	0.1850	0.2908	0.3333	0.0908	0.1196
${\theta }_1$	50	0.2826	0.3067	0.3485	0.3807	0.8194	0.8276
	100	0.2605	0.2904	0.3181	0.3486	0.8142	0.8238
	250	0.2290	0.2651	0.3171	0.3363	0.8013	0.8134
	350	0.2176	0.2539	0.3138	0.3342	0.7872	0.8041
	500	0.2097	0.2454	0.3083	0.3305	0.7727	0.7945
	600	0.2079	0.2433	0.3020	0.3272	0.7188	0.7610
	700	0.2053	0.2389	0.2978	0.3253	0.6862	0.7447
${\theta }_2$	50	1.5889	1.5959	1.7104	1.7153	0.5212	0.5338
	100	1.5835	1.5913	1.7046	1.7102	0.5140	0.5291
	250	1.5818	1.5910	1.6938	1.7006	0.5073	0.5250
	350	1.5698	1.5815	1.6751	1.6845	0.4893	0.5130
	500	1.5566	1.5723	1.6432	1.6578	0.4753	0.5046
	600	1.4749	1.5132	1.5559	1.5917	0.4601	0.4999
	700	1.3803	1.4520	1.4593	1.5264	0.4535	0.4921
$\alpha$	50	0.0792	0.0998	0.0842	0.1110	0.1091	0.1520
	100	0.0577	0.0745	0.0570	0.0747	0.0872	0.1382
	250	0.0352	0.0463	0.0339	0.0437	0.0523	0.0859
	350	0.0295	0.0378	0.0287	0.0366	0.0427	0.0650
	500	0.0246	0.0316	0.0239	0.0317	0.0340	0.0467
	600	0.0227	0.0287	0.0217	0.0290	0.0317	0.0449
	700	0.0210	0.0267	0.0201	0.0259	0.0287	0.0375

8.3. Application

The application of the quantile regression model is demonstrated in this section using a real dataset. The data are taken from [34] and are also available at http://www.leg.ufpr.br/doku.php/publications:papercompanions:multquasibeta (accessed on 30 August 2022). The data consist of body fat percentage (response variable) measured in five regions: android, arms, gynoids, legs and trunk. The data are comprised of 298 observations and the independent variables are: age (in years), body mass index (in kg/m²), sex (female or male) and IPAQ (sedentary (S), insufficiently active (I), or active (A)). In this study, the response variable body fat percentage at arms is regressed on age ($z_{i1}$), body mass index ($z_{i2}$) and sex ($z_{i3}$, 0 for female and 1 for male). The response variable is regressed on the covariates using the relationship $\mathrm{logit}({\rho }_i)={\theta }_0+{\theta }_1{z}_{i1}+{\theta }_2{z}_{i2}+{\theta }_3{z}_{i3},i=1,2,\dots ,298$. Table 9 presents ML estimates, standard errors, and p-values for the parameters of the fitted models for the different quantiles. The estimates are all significant at the 5% level of significance.

Table 9. ML estimates for quantile regression.

$\mathit{u}$		${\widehat{\mathit{\theta }}}_0$	${\widehat{\mathit{\theta }}}_1$	${\widehat{\mathit{\theta }}}_2$	${\widehat{\mathit{\theta }}}_3$	$\widehat{\mathit{\alpha }}$
0.10	Estimates	−3.6699	0.0076	0.0905	−1.004	308.7724
	Standard error	0.1681	$1.1670\times {10}^{-3}$	$7.5355\times {10}^{-3}$	$4.3797\times {10}^{-2}$	$9.3305\times {10}^{-5}$
	p-value	$<0.0001$	$<0.0001$	$<0.0001$	$<0.0001$	$<0.0001$
0.25	Estimates	−3.2544	0.0071	0.0845	−0.9326	325.4705
	Standard error	0.1545	$1.0687\times {10}^{-3}$	$6.9379\times {10}^{-3}$	$4.0103\times {10}^{-2}$	$4.6137\times {10}^{-5}$
	p-value	$<0.0001$	$<0.0001$	$<0.0001$	$<0.0001$	$<0.0001$
0.50	Estimates	−2.8977	0.0067	0.0792	−0.8732	340.4285
	Standard error	0.1436	$9.9065\times {10}^4$	$6.4570\times {10}^{-3}$	$3.7166\times {10}^{-2}$	$1.3990\times {10}^{-5}$
	p-value	$<0.0001$	$<0.0001$	$<0.0001$	$<0.0001$	$<0.0001$
0.75	Estimates	−2.6424	0.0064	0.0766	−0.8384	281.1611
	Standard error	0.1405	$9.7128\times {10}^{-4}$	$6.3363\times {10}^{-3}$	$3.6303\times {10}^{-2}$	$6.4012\times {10}^{-6}$
	p-value	$<0.0001$	$<0.0001$	$<0.0001$	$<0.0001$	$<0.0001$
0.90	Estimates	−2.4030	0.0061	0.0731	−0.7987	273.9968
	Standard error	0.1353	$9.3470\times {10}^{-4}$	$6.1047\times {10}^{-3}$	$3.4900\times {10}^{-2}$	$2.9792\times {10}^{-5}$
	p-value	$<0.0001$	$<0.0001$	$<0.0001$	$<0.0001$	$<0.0001$

Table 10 presents the model selection criteria for the different quantiles. It is observed that the 0.90th quantile provides the best fit for the data as it has the least values of the model selection criteria.

Table 10. Model selection criteria for quantile regression.

$\mathit{u}$	$-2\mathit{\ell }$	AIC	BIC
0.10	−885.3517	−875.3517	−856.8663
0.25	−887.4067	−877.4067	−858.9212
0.50	−889.1990	−879.1990	−860.7136
0.75	−889.8634	−879.8634	−861.3779
0.90	−890.8307	−880.8307	−862.3453

Figure 17 shows the rate of change of the regression coefficients for the different quantile levels and the corresponding 95% confidence interval (CI). It can be observed that all the coefficients approach zero as the quantile level increases, suggesting that they are more important in explaining smaller quantiles.

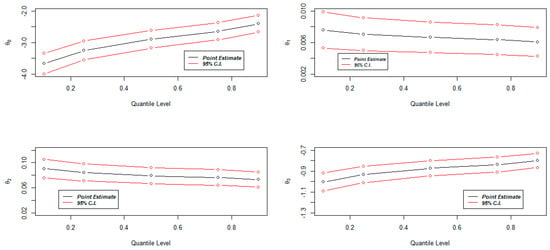
Figure 17. Rate of change of regression coefficients for different quantiles.

Figure 18 and Figure 19 show the P-P plots and half-normal plots with simulated envelopes, respectively, for the randomized quantile residuals. These figures display good fits of the BTCPE quantile regression model to the $u^{th}$ percentage of body fat in arms for $u\in (0.10,0.25,0.50,0.75,0.90)$.

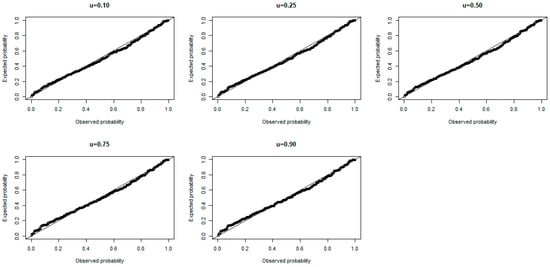
Figure 18. P-P plots for randomized quantile residuals.

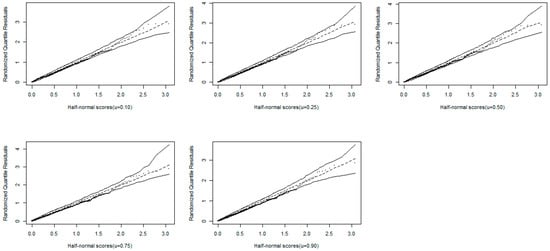
Figure 19. Half-normal plots with simulated envelopes for randomized quantile residuals.

9. Conclusions

In this study, the BTCPE distribution is proposed for modeling datasets that are defined on the unit interval. The PDF of this distribution exhibits left-skewed, right-skewed, reversed J, and approximately symmetric shapes. The HRF displays increasing and bathtub shapes. This makes the distribution a suitable candidate for modeling datasets that exhibit these traits. Nine estimation methods were proposed for estimating the parameters of the distribution, and simulation results revealed that most of these estimates were consistent when it came to the estimation of the parameters of the distribution. The applications of the BTCPE distribution were illustrated using datasets on the mortality rate and recovery rates of COVID-19. The results revealed that for the three datasets, the BTCPE model provided a better fit than the other competing models. A quantile regression model for studying the relationship between the conditional quantiles of a bounded response variable and a set of covariates was proposed. The application of the regression model was illustrated using real data. The study only defined the cumulative distribution and probability density functions of the bivariate distribution. Our future research will study the detailed properties of the bivariate distribution, estimate its parameters, and illustrate its applications.