Abstract
Current market requirements force manufacturing companies to face production changes more often than ever before. Reconfigurable manufacturing systems (RMS) are considered a key enabler in today’s manufacturing industry to cope with such dynamic and volatile markets. The literature confirms that the use of simulation-based multi-objective optimization offers a promising approach that leads to improvements in RMS. However, due to the dynamic behavior of real-world RMS, applying conventional optimization approaches can be very time-consuming, specifically when there is no general knowledge about the quality of solutions. Meanwhile, Pareto-optimal solutions may share some common design principles that can be discovered with data mining and machine learning methods and exploited by the optimization. In this study, the authors investigate a novel knowledge-driven optimization (KDO) approach to speed up the convergence in RMS applications. This approach generates generalized knowledge from previous scenarios, which is then applied to improve the efficiency of the optimization of new scenarios. This study applied the proposed approach to a multi-part flow line RMS that considers scalable capacities while addressing the tasks assignment to workstations and the buffer allocation problems. The results demonstrate how a KDO approach leads to convergence rate improvements in a real-world RMS case.
1. Introduction
Current trends in the manufacturing industry are challenging companies to cope with demand variations and fluctuating production volumes. Companies are required to rapidly adjust the functionalities of their manufacturing systems to critically manage the needs of this dynamic market to stay competitive [1]. By implementing Reconfigurable Manufacturing Systems (RMSs), companies can efficiently meet the requirements of the competitive market [2]. RMSs enable cost-effective means to meet dynamic market demands by reconfiguring, among other aspects, their resources (e.g., machines, operators, buffers, etc.) and the process plan of the manufacturing system [3].
Today’s manufacturing industry is affected by disruptions and shortages of components caused by extraordinary situations such as a global pandemic or war. These disruptions, combined with an increasingly shortened product life-cycle trend, mean that manufacturing organizations are required to ramp up and down products more frequently by modifying their production volumes more often than ever before [4]. Therefore, findings regarding how dynamic market demands of today can be addressed more efficiently constitutes a crucial research area in the RMS community.
Although an RMS may be able to meet the dynamic requirements in the market, designing and configuring the RMS is no trivial task. Simulation techniques, particularly discrete event simulation, have proven to be a powerful tool for the manufacturing industry to assess the capabilities of their production systems [5,6]. Often, several conflicting objectives are used to simultaneously measure the quality of the system. Combining simulation techniques with Multi-Objective Optimization (MOO), i.e., Simulation-based Multi-objective Optimization (SMO), has been a successful approach for optimizing RMSs in the literature [4,7,8]. A general Multi-Objective Optimization Problem (MOOP) can be defined as:
for M number of objective functions, in the constrained and feasible search space S, where is a vector of N decision variables. Due to the structure of MOOPs, a MOOP solution can be seen to inhabit two distinct spaces: the decision space and the objective space, and the objective functions can be seen as a mapping from the decision space to the objective space. The goal of MOO is to find a set of solutions that together represent the so-called Pareto-optimal front—the set of solutions that outperform or dominate all other solutions to the MOOP in S.
| Minimize: |
| Subject to: |
Due to complex aspects, such as the stochastic failures of resources and equipment that can be modeled using simulation techniques, exact methods are often omitted from consideration when optimizing SMO problems; instead, evolutionary algorithms are used. Multi-Objective Evolutionary Algorithms (MOEAs) are optimization techniques that are developed to mimic fundamental principles of evolution found in nature such as the well-known algorithm Non-dominated Sorting Genetic Algorithm II (NSGA-II) [9], which is inspired by Darwinian survival of the fittest and evolves a population of solutions over a number of generations to converge on the Pareto-optimal front.
Although MOEAs are a powerful tool to solve all kinds of MOOPs, they generate many non-optimal solutions during the optimization process. Since these are largely eliminated during optimization and rarely considered in the decision-making process, one can see the wasted computational effort in evaluating them, specifically given the very time-consuming simulations in SMO. After the observation that most of the analysis of MOOP solutions is focused solely on the objective space, and mostly disregarding the dominated solutions, the authors of [10] present Knowledge Driven Optimization (KDO), which is the idea to employ knowledge discovery methods to describe decision-makers (DMs) preferences in the objective space, in terms of knowledge about the solutions in the decision space, and then use this knowledge to drive the search towards faster convergence on more optimal solutions. This can be achieved in two ways, either offline where knowledge is generated related to a previous scenario or case, and used to improve the convergence in a future scenario, or online where knowledge discovery is integrated into the optimization process as part of the MOEA itself to drive the search towards better convergence in the current scenario. In this paper, we investigate an offline KDO approach.
In this work, we employ a knowledge-driven NSGA-II for a real-world Multi-Part Flow Line (MPFL) to optimize the RMS configuration by considering scalable capacities and fluctuating production volumes. The MOOP formulation addresses task allocation to workstations as well as buffer allocation while maximizing throughput (THP) and minimizing total buffer capacity (TBC). In Section 5, we show how the new approach is able to speed up the convergence towards non-dominated solutions for new scenarios by utilizing knowledge discovered from initial scenarios. The scope of the paper is limited to proposing and showcasing this knowledge-driven approach and comparing the effects of utilizing knowledge in the form of decision rules discovered from one variant of the considered RMS, to speed up the convergence rate of another variant of the same RMS.
2. Background
Simulation and optimization techniques have successfully been used in the context of manufacturing in the literature. However, the analysis of solutions is often limited to manual methods and mostly focus on the objective space. This section offers a background of simulation and optimization, knowledge discovery in MOO, and knowledge-driven optimization.
2.1. Simulation and Optimization in Manufacturing Systems
Regardless of the benefits of RMS compared to traditional manufacturing systems in achieving demand and capacity fluctuations, the design and management of these systems are considered a complex combinatorial NP-hard problem which therefore can be handled by the employment of simulation and optimization tools [7,11,12]. When it comes to RMS problems, meta-heuristic methods such as genetic algorithms have become very popular in the literature because they have shown better performance in generating near-optimal solutions [7]. In addition, simulation has been a satisfactory tool to support the modeling and analysis of manufacturing systems for many years [13]. Because of the complexity and dynamism inherent in manufacturing systems, engineers and DMs supported by simulation tools can perform better analysis and, therefore, obtain a better understanding of the real-world systems [14]. Concerning RMS, simulation has been identified in the literature as a supportive technique to handle the uncertainty found in these types of dynamic, evolving systems [15]. Still, considering that the complexity of today’s manufacturing systems is growing and that they need to consider a range of possible scenarios with a large number of variables to model and analyze, the use of simulation tools becomes nonfunctional. Alternatively, optimization methods could be employed to solve larger-scale NP-hard problems [7]. However, the majority of prior studies that applied optimization methods to RMS reduced the problem by excluding variability and stochasticity (e.g., machine failures) and therefore providing imprecise solutions. Therefore, studies that employed simulation and optimization separately have shown some of the above-mentioned shortcomings. Against these drawbacks, simulation-based optimization combines the benefits of simulation and optimization. In the literature, simulation-based optimization has successfully led to improvements in manufacturing systems. Consequently, SMO could lead to improvements in current RMSs [11,13].
RMSs need to address three main challenges, namely: (i) the system configuration, (ii) the process planning, and (iii) the components of the system [3]. The system configuration targets the physical arrangement of the resources (e.g., operators, machines, etc.) in the system [2]. This challenge is usually addressed by optimizing the resource assignment to workstations (WSs). The process planning targets the task allocation and balancing throughout the WSs [16]. This challenge is usually addressed by optimizing the work tasks allocation. Lastly, the components of the system address the appropriate number and type of components (e.g., buffers, operators, machines, etc.) in the system to reach the established capacity goal [13]. This challenge is usually addressed by optimizing the number of resources to perform the tasks. Although simulation-based optimization has been employed to address RMS problems previously in the literature, the use of SMO to address several or all of these challenges simultaneously is sporadic.
2.2. Knowledge Discovery in MOO
Methods for knowledge discovery in the decision space of MOO solutions are not conventional in the multi-criteria decision-making literature, which mostly focus on manual methods for analyzing the solutions in the objective space. However, Ref. [10] offers a survey of data mining and machine learning methods that have been employed for knowledge discovery to support decision-making in MOO. The process of innovization [17] was developed as a way of finding innovative design principles to describe the Pareto-optimal front. Innovization was initially described as a manual process of formulating relationships between correlated regions of the objective space using appropriate regression models; however, it has since been automated using genetic programming [18]. Simulation Based Innovization (SBI) is another method for knowledge discovery in MOO [19,20]. SBI trains a decision tree with the distance to a user-defined reference point (a point describing a DMs aspiration) in the objective space as the regression target. The DM then chooses a threshold for the distance to the reference point to find rules that describe the decision space for the solutions within this threshold. A further application of knowledge discovery methods used in the analysis of solutions is offered by [21] where the authors used clustering in both the objective and decision spaces, as well as association rule analysis in cantilever design optimization problems.
Flexible Pattern Mining
Although previous approaches have successfully utilized common data mining and machine learning methods for knowledge discovery, these methods were not developed specifically for the indented use in MOO, and may not fully be able to manage the typical characteristics of MOOP solutions, such as different variable types (continuous, discrete and ordinal, and nominal) [10]. However, a method that has been specifically developed for knowledge discovery in MOO is Flexible Pattern Mining (FPM) [22]. FPM was developed to extend sequential pattern mining [23] using the a priori algorithm [24] for finding decision rules. While sequential pattern mining finds rules of the form for a variable and constant value c, FPM is further able to find rules on the forms , , , and . To run FPM, the DM is required to supply a selected and an unselected set of solutions, and these selections are made in the objective space. With these selections as input, FPM then generates rules that separate the selected set from the unselected set in terms of the variables in the decision space. Typically, the DM may choose the non-dominated solutions as the selected set and the remaining solutions as the unselected set. Each rule generated by FPM has an associated significance or value, which is the fraction of solutions in the selected set that are covered by the rule, and a similar unselected significance or for the fraction of solutions in the unselected set. An interesting and meaningful FPM-rule would have a high while having a low , and thereby be describing only the solutions in the selected set. Rule interactions can also be considered by combining several FPM-rules and evaluating their combined and . The three individual rules , and can be combined into the three-level rule interaction .
2.3. Knowledge-Driven Optimization
Knowledge discovery methods can be a powerful tool in decision-making; however, in this manner, the knowledge is only used by the DMs. The term Knowledge-Driven Optimization (KDO) is used when knowledge discovered from good or preferred MOOP solutions is fed back into the optimization algorithm to affect the convergence behaviour, or used to update the MOOP formulation itself to make the search more efficient. The former is called online KDO, while the latter refers to offline KDO [10].
A key difference between online and offline KDO is that, since the knowledge used for the former is discovered during the search process from the best-so-far solutions, it does not necessarily describe the optimal solutions to the MOOP. On the other hand, with the assumption that an optimizer converges close to the Pareto-optimal front, offline KDO has access to “pure” knowledge directly describing the optimal (or preferred) solutions.
2.3.1. Online KDO
Online KDO in a MOEA involves a specific knowledge discovery step to generate knowledge from previous or current solutions, and is able to use this knowledge to affect the convergence behaviour and more effectively generate better or preferred solutions. Online KDO algorithms have been implemented to involve an additional step after the ordinary evolutionary process that finds knowledge for feeding into the evolutionary operators for the next generation. An example of an approach like this is shown in [25,26], where FPM rules are generated to build a distribution over the preferred solutions close to the reference point in preference-based MOO. This distribution is then sampled in a new mutation operator for the next generation of solutions. Another approach using FPM rules is presented in [27], where the rules are used as constraints in the decision space.
Approaches that train a classifier between good and bad solutions have also been proposed. In [28], a classifier was trained online to differentiate between dominated and non-dominated solutions, and in [29], a classifier is trained online to find constraint violating solutions. In both papers, the classifier was used before the solutions were evaluated, in order to save time by not evaluating poor solutions. Recently, approaches that use innovization online have also been proposed [30,31].
2.3.2. Offline KDO
Offline KDO refers to when knowledge about MOOP solutions is generated offline, after an optimization run has finished and is used to benefit future optimizations of the same or similar cases, or to give insights that can lead to an updated MOOP formulation. Only when DMs fully understand the MOOP and its solutions are they able to make an informed decision.
In [32], SBI was used to find decision rules about solutions close to a user-defined reference point, and then used as constraints in a second optimization run, to generate more non-dominated solutions. This method served both as a way to discover more preferred solutions, but also to validate the method and show that it generates actionable knowledge. Previously, it has also been found that leveraging domain knowledge can also greatly benefit the optimization [33,34]. This type of knowledge is not generated from previous optimizations, but from the experience and intuitions of veteran DMs. In [35], domain knowledge was used to develop specialized design heuristics to speed up the convergence of a multi-objective satellite design system problem.
Offline KDO is similar to the concept of transfer learning in the machine learning literature [36], where a model able to perform a specific task is also able to perform or jump-start the learning process of another related task. In this paper, we focus on using offline KDO in order to generate knowledge from an initial scenario that can be applied to benefit the search in a new scenario. In the next section, we present an illustration of how offline KDO can be implemented.
3. Illustration of Offline KDO
Knowledge generated from MOOP solutions obtained in one scenario may be beneficial for future scenarios of similar MOOPs. Preferred solutions in the objective space may have a certain structure in the decision space that can be exploited to ensure a faster convergence towards the Pareto-optimal front or a greater density of preferred solutions. In this paper, we consider the knowledge generated through the FPM procedure [22] and the openly available implementation in the web-based decision support system Mimer (Mimer: https://assar.his.se/mimer/, accessed on 6 October 2022).
In this section, we want to showcase an example of how simple knowledge about non-dominated solutions can help to speed up the convergence and generate even more non-dominated solutions. We show how knowledge in the form of FPM-rules can be applied as constraints in the decision space to focus the search for non-dominated solutions in different parts of the Pareto-front.
Illustrative Example
We showcase an example of offline KDO on the RE3-5-4 problem from the RE suite of real-world (inspired) test-problems [37]. We show how it is possible to use FPM to generate rules that describe non-dominated solutions, and then use these rules as box-constraints for the decision variables of the MOOP for a different optimization run. Without first generating knowledge about an initial solution set, this approach would not be possible. We also compare this offline approach with simply constraining the decision space to focus the search without relying on any knowledge.
The RE3-5-4 is a three-objective engineering problem with a mathematical formulation, based on the vehicle crash-worthiness design problem described in [38]. The objectives to RE3-5-4 are: () minimize the weight of the vehicle, () minimize the acceleration characteristics in the crash, and () minimize the toe-board intrusion during the crash, while the variables (–) each relate to the thickness of a different support member in the frontal structure in the vehicle.
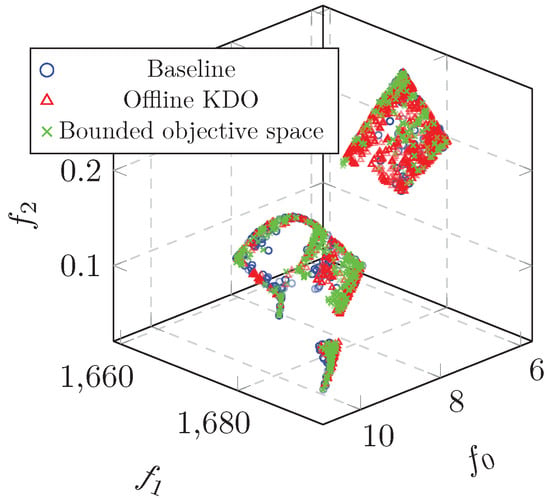
Figure 1 shows non-dominated solutions generated from a single run on the RE3-5-4 problem with a budget of 6000 function evaluations, which resulted in 2344 non-dominated solutions. The structure of the objective space clearly shows three distinct, disconnected clusters of solutions. A DM would not only be interested in what causes solutions to end up in these different clusters in terms of the decision space, but also how to focus the search to further saturate these regions with more trade-off solutions. We can use FPM for each of the clusters, to find knowledge for the respective solutions in terms of the decision space. The FPM procedure requires a selected and an unselected set of solutions. We run FPM three times using Mimer, each time with the non-dominated solutions from one of the clusters as the selected set and the remaining solutions from the entire solution set as the unselected set, thus finding rules that describe the non-dominated solutions in each cluster. The resulting FPM rules are shown in Table 1.
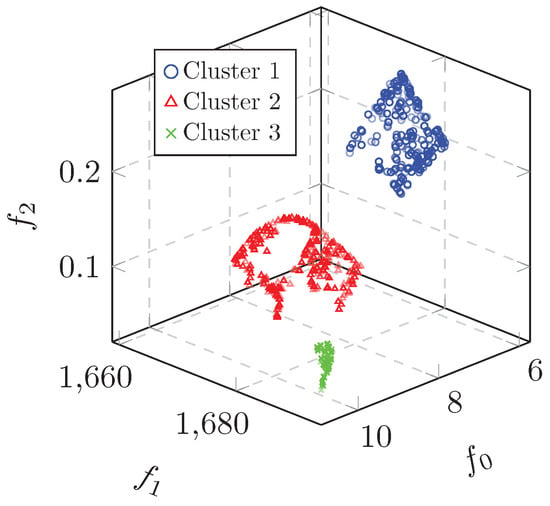
Figure 1.
Non-dominated solutions from RE3-5-4.

Table 1.
Rule interactions found by using FPM for each of the clusters shown in Figure 1.
FPM was run with a minimum significance of 100% in each case, meaning that all discovered rules completely covered the selected set, and the results still show that the rules discriminate between the selected and unselected set, given the low unselected significance. However, the rule interaction found for cluster 2 had an of 22.68%. This means that the rule interaction also describes 22.68% of the solutions in the unselected set, which would lead to a lower search pressure towards the non-dominated solutions within this cluster when used for offline KDO.
With this knowledge about the different clusters in hand, we run additional optimizations, focusing on each of these clusters separately. We used the rule interactions found using FPM as bounds to constrain the decision space, and ran an optimization with a total of 2000 function evaluations for each respective rule interaction. These three solution sets where then combined, and the non-dominated solutions from these combined runs are shown in Figure 2. This offline approach resulted in 3070 non-dominated solutions, with the same total function evaluations (6000) as the original run.
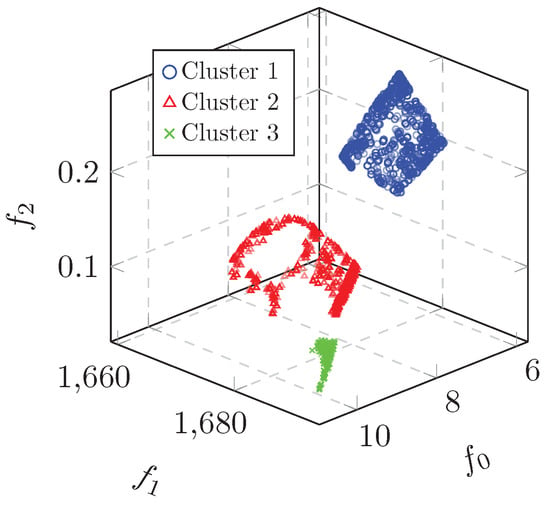
Figure 2.
Non-dominated solutions from RE3-5-4 using offline KDO.
We also compare this offline KDO approach with the crude method of simply constraining the objective space to focus the search on the three clusters. The clusters can be classified by the objective space bounds shown in Table 2. To be fair against the offline KDO approach, we gave this crude method a budget of 4000 function evaluations for each cluster since the offline KDO approach was able to utilize knowledge from an initial 6000 solutions. We combined the final solutions sets from each cluster into one. This approach resulted in 2858 total non-dominated solutions, which are shown in Figure 3.

Table 2.
Objective space bounds for each of the clusters as shown in Figure 1.
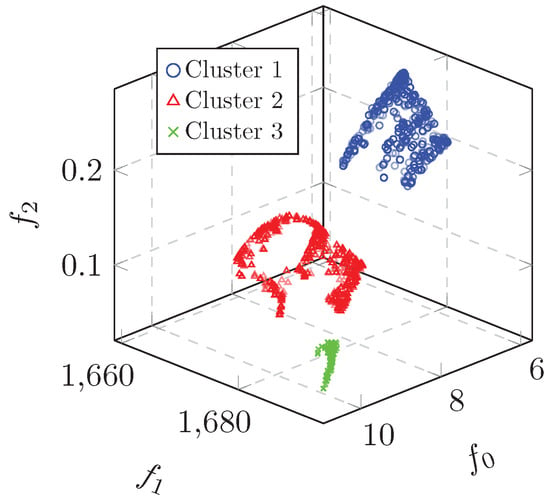
Figure 3.
Non-dominated solutions from RE3-5-4 using bounded objective space.
We compare the baseline run with the offline KDO approach and the bounded objective space approach, by using the hypervolume metric (HV) [39] and by counting the contribution of each run to the composite front produced by combining the solutions from the three approaches. The composite front is shown in Figure 4 and the resulting HV and contribution to the composite front is shown in Table 3. The offline KDO approach resulted in a slightly greater HV and a greater contribution to the composite front, meaning that this approach gives superior performance over the other approaches.

Table 3.
HV score and contribution to composite front of the three approaches.
Since the offline KDO approach is utilizing knowledge discovered from a previous run, it is expected to have a higher performance. However, this example demonstrates that simply adding knowledge as box constraints in the decision space is enough to greatly improve the performance of an optimization run. This example also highlighted that applying a similar approach, by constraining the objective space, is not as effective as this offline KDO approach. This example shows the potential of incorporating offline knowledge into a MOO pipeline by spending a portion of the function evaluation budget on generating solutions, then finding knowledge about high performing solutions, and then utilizing this knowledge offline, for the remaining function evaluation budget, to reach a faster convergence on more preferred solutions.
4. Real-World RMS Problem
The considered RMS comes from a MPFL setup implemented in a truck manufacturer in Sweden. The case is based on a pedal car production, where two product families are manufactured. The MPFL is composed of three reconfigurable WSs able to add, relocate, or remove operators from them in order to cope with production changes (e.g., volumes or capacity changes). Both products need to be produced at specific volumes. As the total production capacity or the production volumes fluctuate, the system configuration, the process plan, and the components of the systems change to meet the new scenario. The changes include the number of operators employed, the assignments of operators to the WSs, the tasks’ assignments to WSs, and the buffers’ capacities. The company was interested in different scenarios. Initially, they wanted to investigate the system’s capacity with seven operators for the specific production volumes, 70/30 and 30/70. These different proportions of production volumes determine the total proportion to be produced of the two product parts. For example, a proportion of 70/30 refers to the fact that 70% of the total parts produced should be of part A, and the remaining 30% should be of part B. Furthermore, the company also wanted to investigate how much capacity could be gained by adding one and two extra operators to the system, including the information regarding how to reconfigure the system, how to re-balance the tasks, and a re-assessment of the capacities of the buffers. Therefore, as the proportion and volume changes, the RMS evolve accordingly. The assumptions of the RMS are:
- A MPFL consisting of several WSs produce several products under different volumes;
- The resources of the RMS are subjected to disturbances, such as breakdowns, setup times, and variability of the tasks;
- Each WS has a number of parallel and identical resources that execute the same sequence of tasks;
- Each WS has reserved space for adding or reallocating resources;
- There are buffers with variable capacity in-between the WSs;
- The manufacturing tasks of the considered products are subjected to a precedence relationship and technological constraints that ensure a feasible sequence to be performed in each WS.
The mathematical problem formulation for the considered MPFL-RMS is detailed in [40].
In this paper, we consider an SMO problem using Throughput (THP) and Total Buffer Capacity (TBC) as objectives while striving for the optimal buffer and tasks allocation for the different scenarios. The total manufacturing time for the production is 336.38 s for part A and 293.38 s for part B divided into 29 and 24 tasks, respectively. The tasks precedence relations for both products are shown in Figure 5. Note that each task can be assigned to only one WS.
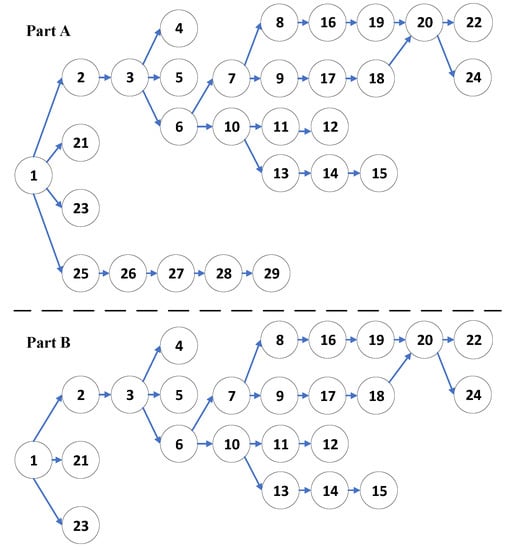
Figure 5.
Precedence relation of the tasks for both products.
SMO Approach
The architecture of the SMO approach used can be divided into two major components: the simulation engine and the optimization engine, which are tightly integrated. For the simulation engine, the discrete event simulation software FACTS Analyzer [41] was employed for modeling the production system and simulating the studied scenarios. The optimization engine was implemented in the well-known platform MATLAB. The integration between the simulation and optimization engines allows an accurate representation of a realistic production line involving many types of model variables regardless of their nature (e.g., failure, availability, mean time to repair, process time) while avoiding the simplification found in other production line optimization studies. The process begins in the optimization engine where custom-made encoding and decoding mechanisms generate feasible RMS solutions to, later on, be automatically mapped to the simulation engine. The simulation engine then uses the received combination of input variables to run the simulation on the model. The results from the simulation experiments are fed back to the optimization engine in order to be evaluated by the optimization algorithm in terms of the designated conflicting objectives. This process in which the optimization engine evaluates the output of the optimization for instructing a new combination of input parameters to be simulated is repeated until the results converge to a set of optimal solutions or the stopping criterion is reached (i.e., a predefined number of generations).
Due to the outstanding performance in handling up to three conflicting objectives and being known as an effective MOEA when handling complex combinatorial problems, a customized NSGA-II with specific encoding and decoding mechanisms for RMS was implemented within the optimization engine to generate feasible solutions [4,12]. There are three main factors behind the success of NSGA-II, the fast non-dominated sorting which establishes a dominance relationship between each pair of solutions, the elitism mechanism to keep the best solutions, and the crowding distance calculation that ensures that ranks the solutions of each individual front maintaining diversity. The general steps of the customized NSGA-II for RMS are shown in Algorithm 1.
| Algorithm 1 Enhanced SMO-NSGA-II |
Require: Generation limit ; Population size; Precedence relation; RMS inputs regarding WSs, buffers, resources and constraints
|
Due to the differences in how the considered RMS is encoded from a standard MOOP solved by NSGA-II, the variables for the number of WSs, and task- and buffer assignment are encoded as random keys in the enhanced algorithm, and on Line 4, they are decoded as feasible input for the simulation model. On Line 5, these decoded solutions are sent to and evaluated by the simulation engine, and the objective values are sent back to the algorithm. A complete description of the enhanced algorithm is provided in [40].
5. Experimental Results
In this section, we present the results from the initial optimizations, the knowledge we were able to discover from the solutions to these optimizations, and new results from an offline KDO study using this discovered knowledge. We investigate the improvement in convergence towards the Pareto-optimal front by applying FPM rules as constraints in the decision space. All optimizations refer to the real-world RMS problem described in Section 4. All knowledge discovery was performed using the openly available web-based decision-support system Mimer, enabling the knowledge discovery framework described in [42].
5.1. Optimization Results
We ran six optimizations initially, one scenario for each pair of number of operators (7, 8, 9) and proportion (70/30, 30/70). Each optimization run had a budget of 500 generations and a population size of 50. The resulting non-dominated solutions from these runs are shown in terms of their task allocation in Figure 6, where each row represents one solution and each column represents one task for either product A or B, and the color of the cell shows the WS it was assigned to. In total, 72 non-dominated solutions were found in these scenarios altogether.
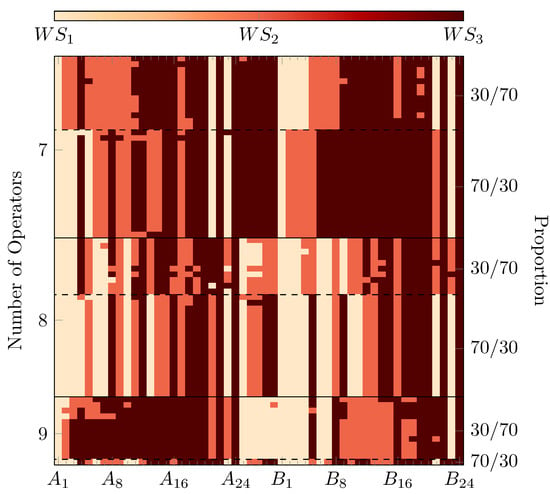
Figure 6.
Task allocations from the non-dominated solutions from all scenarios in the initial optimizations.
From the figure, it is clear that most of the non-dominated solutions in each scenario share common task allocations. However, all solutions shown in Figure 6 are distinct and have varying buffer allocations which are not shown here.
The number of non-dominated solutions from each scenario is shown in Table 4, where we can see that the number of non-dominated solutions in each scenario varies from 10–19, except for the scenario of nine operators with a proportion of 70/30 where only one non-dominated solution was found. The objective space of the non-dominated solutions from all scenarios is also shown in Figure 7, where it is very clear how increasing the number of operators, as expected, has a definite impact on the throughput.

Table 4.
Number of non-dominated solutions found for each scenario in the initial optimizations.
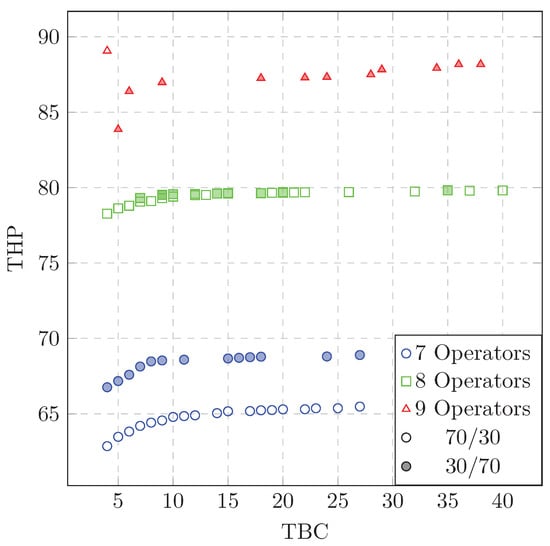
Figure 7.
Objective space of the non-dominated solutions from all scenarios in the initial optimizations.
5.2. Knowledge Discovery
Due to the ability of the system to both increase and decrease the number of operators and to change the proportion between the two parts, in this paper, we are interested in finding generalized knowledge about each of the different number of operators and the different proportions. In other words, if we can generate knowledge from the previous scenarios with seven operators that can be generalized to improve the optimization process for future scenarios with seven operators but new proportions, and if we can generate knowledge from the scenarios with a proportion of 30/70 and use it in future scenarios with different numbers of operators, and so on for each group of scenarios.
We generate knowledge in the form of decision rules using the FPM procedure. From the initial results, we are interested in five groups of scenarios to generate knowledge from. The scenarios wherein the numbers of operators equal 7, 8, and 9, and where the proportions equal 30/70 and 70/30. In order to run FPM, we merged the solutions from all optimization scenarios into one combined dataset so that the different scenarios can take all cases into account. For each group, we ran FPM with the non-dominated solutions from the scenarios in the group as the selected set, and all remaining solutions (dominated and non-dominated) from all scenarios as the unselected set. In this way, the generated knowledge is general between scenarios in the MOOP.
For this knowledge discovery, we only focus on the task allocation. Even so, the number of decision variables is high (53) which affects the run-time of the FPM procedure. For this reason, the maximum level of rule interactions was limited to 4, i.e., only interactions of four FPM-rules are considered. As we can see in Figure 6, many non-dominated solutions in one scenario share the same task allocations for many tasks. Therefore, FPM is expected to find many rules with high significance. However, it is the rules that have a high significance while simultaneously having a low unselected significance, which are descriptive, since these rules more accurately distinguish between the selected and unselected sets of solutions.
Table 5 shows the FPM rules discovered for each scenario, indicating the tasks that distinguish the non-dominated solutions in the groups of scenarios more from the other solutions. For all groups, the parameter for the minimum required significance was kept constant at 90% when running the FPM procedure. For the scenarios with seven operators, a rule interaction was found with a significance of 100% and an unselected significance of 10.13%, meaning that all non-dominated solutions in the scenarios support the rules, while only 10.13% of the solutions in the unselected set support the rules. The rule interaction with the highest ratio between significance and unselected significance was found in the scenarios with nine operators, perhaps indicating that the non-dominated solutions in these scenarios are easier to distinguish from the rest. The scenarios with the lowest ratio are where the proportion is 30/70, perhaps indicating that the non-dominated solutions in these scenarios are more difficult to distinguish.

Table 5.
Rule interactions found by using FPM for each of the scenarios from the initial optimization.
5.3. Offline Knowledge-Driven Optimization
The rules for the different groups were applied to ten new scenarios, using the proportions of 40/60 and 60/40 between parts A and B for 7, 8, and 9 operators, and using 6 and 10 operators with the proportions of 30/70 and 70/30. We compare standard optimization runs for the new scenarios versus runs using the offline KDO approach of applying the rules presented in Table 5 as constraints in the decision space. Due to the high computational cost involved in the evaluation of each solution, each scenario was given an evaluation budget of 2500 solutions (50 generations with a population size of 50).
We compare the rate of convergence of the standard MOO approach and the offline KDO approach in each separate scenario by plotting the Hypervolume (HV) [39] contribution at each generation. Figure 8 shows the convergence plots for all scenarios. We also consider the Area Under the Curve (AUC) of the convergence plots as a quantitative score for the convergence rate. The AUC scores for all scenarios are shown in Table 6.
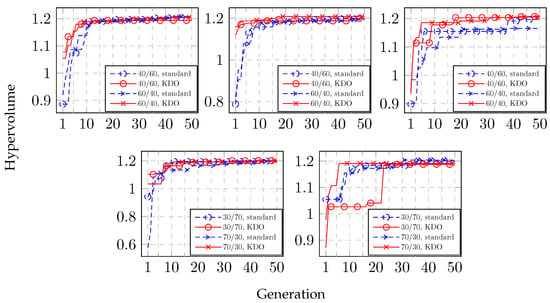
Figure 8.
Convergence plots of the scenarios with 7 operators (top left), 8 operators (top center), 9 operators (top right), 6 operators (lower left), and 10 operators (lower right).

Table 6.
Area Under the Curve (AUC) of the convergence plots shown in Figure 8 for the different cases of Number of Operators (NO), proportion, and optimization approach.
The results show that the offline KDO approach leads to faster convergence in all scenarios with operators equal to 7, 8, and 9 and the new proportions of 40/60 and 60/40 compared with the standard approach, and most of the scenarios using the proportions of 30/70 and 70/30 and the new numbers of operators of 6 and 10. In fact, only in the scenario with 10 operators and a proportion of 30/70 did the offline KDO approach not lead to faster convergence. However, the convergence plots for six operators are very similar for both approaches. This indicates that the offline KDO approach leads to an improved convergence rate for the current RMS MOOP when considering new proportions for the initial assignment of 7, 8, or 9 operators, but may be slightly less fruitful for scenarios with new numbers of operators and the original proportions.
6. Discussion
The initial results provided solutions found for six different scenarios from the same real-world RMS MOOP involving task allocation. The approach presented in this paper demonstrates the use of a knowledge discovery method to generate decision rules which are applied in future, different scenarios to help the optimization algorithm reach faster convergence on non-dominated solutions. We grouped scenarios where the numbers of operators were the same and proportions were different, in order to find if there is generalized knowledge that can be applied across scenarios with the same number of operators as well as the same for scenarios with the same proportions and different numbers of operators.
Although the initial optimization runs had a very high evaluation budget, they did not produce many non-dominated solutions in each scenario. In the scenario with nine operators and a proportion of 70/30, only a single non-dominated solution was found. This means that the optimization did not find a diverse set of solutions for this scenario, which might in turn means that the knowledge generated is not general enough. However, despite this, as shown in Figure 8 and Table 6, the offline KDO approach did result in faster convergence compared to the standard approach for both scenarios with nine operators.
To generate knowledge about the different scenarios, we used Flexible Pattern Mining (FPM) to find decision rules. However, the number of aspects in terms of decision variables considered by this study increases the complexity of the SMO and its knowledge discovery post-optimal analysis exponentially. For this reason, the number of rule interactions considered in each scenario was limited to four. Nonetheless, the rules extracted reveal knowledge regarding which tasks are more important and therefore need to be prioritized for finding competitive solutions with respect to different criteria. However, finding more complex rule interactions could potentially lead to more precise knowledge which might be of further benefit.
FPM is expected to identify the rules that are the most interesting to the decision-maker. Considering the rules discovered by FPM and shown in Table 5, we can see that, out of all groups of scenarios, some tasks are repeated in the rule interactions, namely , , , and . Indicating that these tasks have higher importance for more general scenarios, however, since no rules are common in all scenario groups, likely no rule describes a completely general scenario for the considered RMS MOOP. Only half of these tasks (, , ) have the same rule in the different scenario groups.
In the presented offline KDO approach, we applied the discovered rule as hard constraints in the decision space by limiting the values that the corresponding variables could take on. Although this approach did result in faster convergence in most cases, it does not guarantee that the solutions found are Pareto-optimal since it limits the search space. Secondly, the significance of the rule interactions used might also impact the quality of the final non-dominated solutions found. This point is driven further by the possibility that the solutions found in the initial optimization runs did not convergence close to the true Pareto-optimal front. However, in the case of SMO where each evaluation can take a very long time, decision-makers are more interested in finding good enough solutions fast rather than finding the true Pareto-optimal solutions.
We used knowledge found from six initial scenarios to drive the search for faster convergence in 10 new scenarios. The results show a bigger increase in the convergence rate in the scenarios with the initial numbers of operators and different proportions than the scenarios with the initial proportions and different numbers of operators, when using the offline KDO approach. This indicates that, for the considered MOOP, more general knowledge may be derived for the scenarios grouped by considering the different numbers of operators. The rule interactions also confirm this for the scenarios grouped by the proportion of 30/70, where the unselected significance is high compared to the rest of the scenario groups. This implies that it was more difficult to find rules that distinguish this group. One possible explanation for why the offline KDO approach did not lead to more of an improvement in a convergence rate for these scenarios is that no simple rule interaction is able to capture the distinguishing features regarding the proportions in the initial results. Tasks that are more important for changes in the proportion may be overshadowed by tasks more important for differences in the number of operators.
In this paper, we only considered the variables related for task allocation in the knowledge discovery and offline KDO approach. However, it would also be interesting to investigate the possible convergence rate improvement by generating knowledge also about the operators’ assignments to WSs and the capacities of the inter-station buffers.
7. Conclusions
In this paper, we propose the use of an offline KDO approach for increased convergence rates in a real-world reconfigurable manufacturing system simulation-based multi-objective optimization problem. We first showcase an offline KDO approach for populating non-dominated solutions in the real-world inspired test problem RE3-5-4, by dividing found solutions into different clusters and finding specific knowledge for each cluster. This knowledge was then used to constrain the decision space to guide the optimization to converge on more non-dominated solutions. This approach was also shown to outperform a crude approach of constraining the objective space. We use a similar offline KDO approach on the real-world RMS problem.
RMSs are considered a key enabler for manufacturing systems to produce the required capacity and volume when needed. However, prior research in real-scale industrial applications is sporadic and seemingly ignores the importance of post-optimal analysis on the combined decision-objective space for supporting decision-making about the requirements of the future system. The use of offline KDO on SMO data sets of RMS is a novel area that can support the RMS research community, and accordingly, this paper illustrates an example of how it can be achieved.
In this paper, we considered knowledge discovery through the FPM procedure to generate if-then decision rules about the decision variables in relation to selections made in the objective space of the solutions. We considered variables related to task assignment in workstations. The results show how the offline KDO approach was able to lead the optimization to faster convergence in the majority of tested scenarios of new proportions and numbers of operators; however, for the considered MOOP, the offline KDO approach leads to a greater improvement in scenarios based on new proportions.
In additional to offline KDO, rules discovered through the FPM procedure can also be used to inform the decision-maker about various aspects about the MOOP and the solutions. Actionable insights from a post-optimal analysis using FPM for knowledge discovery may lead to improvements in the MOOP formulation and be a tool in decision-making.
For the future work, we would like to further investigate how the qualities of the generated rules correlate with the convergence when using offline KDO on more real-world applications. In this study, only knowledge in the form of FPM-rules was considered for offline KDO. Future work should also be focused on finding other appropriate knowledge representations for RMS applications.
Author Contributions
Conceptualization, H.S., C.A.B.-D., S.B. and A.H.C.N.; methodology, H.S. and C.A.B.-D.; software, H.S., C.A.B.-D. and A.N.; validation, H.S. and C.A.B.-D.; formal analysis, H.S.; investigation, H.S. and C.A.B.-D.; data curation, H.S. and C.A.B.-D.; writing—original draft preparation, H.S. and C.A.B.-D.; writing—review and editing, H.S., C.A.B.-D., S.B., A.H.C.N. and A.N.; visualization, H.S.; supervision, S.B. and A.H.C.N.; project administration, H.S. and C.A.B.-D.; funding acquisition, A.H.C.N. All authors have read and agreed to the published version of the manuscript.
Funding
This work was funded by the Knowledge Foundation (KKS), Sweden, through the KKS Profile Virtual Factories with Knowledge-Driven Optimization, VF-KDO, Grant No. 2018-0011.
Data Availability Statement
All reported data will be made available upon acceptance for publication.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Koren, Y. The Global Manufacturing Revolution: Product-Process-Business Integration and Reconfigurable Systems; John Wiley & Sons: Hoboken, NJ, USA, 2010. [Google Scholar]
- Koren, Y.; Heisel, U.; Jovane, F.; Moriwaki, T.; Pritschow, G.; Ulsoy, G.; Van Brussel, H. Reconfigurable manufacturing systems. CIRP Ann. 1999, 48, 527–540. [Google Scholar] [CrossRef]
- Koren, Y.; Gu, X.; Guo, W. Reconfigurable manufacturing systems: Principles, design, and future trends. Front. Mech. Eng. 2018, 13, 121–136. [Google Scholar] [CrossRef]
- Diaz, C.A.B.; Aslam, T.; Ng, A.H. Optimizing Reconfigurable Manufacturing Systems for Fluctuating Production Volumes: A Simulation-Based Multi-Objective Approach. IEEE Access 2021, 9, 144195–144210. [Google Scholar] [CrossRef]
- Mourtzis, D.; Doukas, M.; Bernidaki, D. Simulation in manufacturing: Review and challenges. Procedia Cirp 2014, 25, 213–229. [Google Scholar] [CrossRef]
- Haddou Benderbal, H.; Dahane, M.; Benyoucef, L. Modularity assessment in reconfigurable manufacturing system (RMS) design: An Archived Multi-Objective Simulated Annealing-based approach. Int. J. Adv. Manuf. Technol. 2018, 94, 729–749. [Google Scholar] [CrossRef]
- Renzi, C.; Leali, F.; Cavazzuti, M.; Andrisano, A.O. A review on artificial intelligence applications to the optimal design of dedicated and reconfigurable manufacturing systems. Int. J. Adv. Manuf. Technol. 2014, 72, 403–418. [Google Scholar] [CrossRef]
- Delorme, X.; Malyutin, S.; Dolgui, A. A multi-objective approach for design of reconfigurable transfer lines. IFAC-PapersOnLine 2016, 49, 509–514. [Google Scholar] [CrossRef]
- Deb, K.; Agrawal, S.; Pratap, A.; Meyarivan, T. A fast elitist non-dominated sorting genetic algorithm for multi-objective optimization: NSGA-II. In Proceedings of the International Conference on Parallel Problem Solving from Nature, Paris, France, 3 September 2000; Springer: Berlin, Germany, 2000; pp. 849–858. [Google Scholar]
- Bandaru, S.; Ng, A.H.; Deb, K. Data mining methods for knowledge discovery in multi-objective optimization: Part A-Survey. Expert Syst. Appl. 2017, 70, 139–159. [Google Scholar] [CrossRef]
- Bortolini, M.; Galizia, F.G.; Mora, C. Reconfigurable manufacturing systems: Literature review and research trend. J. Manuf. Syst. 2018, 49, 93–106. [Google Scholar] [CrossRef]
- Michalos, G.; Makris, S.; Mourtzis, D. An intelligent search algorithm-based method to derive assembly line design alternatives. Int. J. Comput. Integr. Manuf. 2012, 25, 211–229. [Google Scholar] [CrossRef]
- Diaz, C.A.B.; Fathi, M.; Aslam, T.; Ng, A.H. Optimizing reconfigurable manufacturing systems: A Simulation-based Multi-objective Optimization approach. Procedia CIRP 2021, 104, 1837–1842. [Google Scholar] [CrossRef]
- Mourtzis, D. Simulation in the design and operation of manufacturing systems: State of the art and new trends. Int. J. Prod. Res. 2020, 58, 1927–1949. [Google Scholar] [CrossRef]
- Petroodi, S.E.H.; Eynaud, A.B.D.; Klement, N.; Tavakkoli-Moghaddam, R. Simulation-based optimization approach with scenario-based product sequence in a reconfigurable manufacturing system (RMS): A case study. IFAC-PapersOnLine 2019, 52, 2638–2643. [Google Scholar] [CrossRef]
- Koren, Y. The rapid responsiveness of RMS. Int. J. Prod. Res. 2013, 51, 6817–6827. [Google Scholar] [CrossRef]
- Deb, K.; Srinivasan, A. Innovization: Innovating design principles through optimization. In Proceedings of the 8th Annual Conference on Genetic and Evolutionary Computation, Seattle, WA, USA, 8–12 July 2006; pp. 1629–1636. [Google Scholar]
- Bandaru, S.; Deb, K. A dimensionally-aware genetic programming architecture for automated innovization. In Proceedings of the International Conference on Evolutionary Multi-Criterion Optimization, Sheffield, UK, 19–22 March 2013; Springer: Berlin, Germany, 2013; pp. 513–527. [Google Scholar]
- Ng, A.; Deb, K.; Dudas, C. Simulation-based innovization for production systems improvement: An industrial case study. In Proceedings of the International 3rd Swedish Production Symposium, SPS’09, Göteborg, Sweden, 2–3 December 2009; pp. 278–286. [Google Scholar]
- Dudas, C.; Ng, A.H.; Pehrsson, L.; Boström, H. Integration of data mining and multi-objective optimisation for decision support in production systems development. Int. J. Comput. Integr. Manuf. 2014, 27, 824–839. [Google Scholar] [CrossRef]
- Sato, Y.; Izui, K.; Yamada, T.; Nishiwaki, S. Data mining based on clustering and association rule analysis for knowledge discovery in multiobjective topology optimization. Expert Syst. Appl. 2019, 119, 247–261. [Google Scholar] [CrossRef]
- Bandaru, S.; Ng, A.H.; Deb, K. Data mining methods for knowledge discovery in multi-objective optimization: Part B-New developments and applications. Expert Syst. Appl. 2017, 100, 119–138. [Google Scholar] [CrossRef]
- Agrawal, R.; Srikant, R. Mining sequential patterns. In Proceedings of the Eleventh International Conference on Data Engineering, Taipei, Taiwan, 6–10 March 1995; pp. 3–14. [Google Scholar]
- Agrawal, R.; Srikant, R. Fast algorithms for mining association rules. In Proceedings of the 20th International Conference on Very Large Data Bases, VLDB, Santiago de Chile, Chile, 12–15 September 1994; Volume 1215, pp. 487–499. [Google Scholar]
- Smedberg, H. Knowledge-driven reference-point based multi-objective optimization: First results. In Proceedings of the Genetic and Evolutionary Computation Conference Companion, Prague, Czech Republic, 13–17 July 2019; pp. 2060–2063. [Google Scholar]
- Smedberg, H.; Bandaru, S. A Modular Knowledge-Driven Mutation Operator for Reference-Point Based Evolutionary Algorithms. In Proceedings of the 2022 IEEE Congress on Evolutionary Computation (CEC), Padua, Italy, 18–23 July 2022; pp. 1–8. [Google Scholar]
- Karlsson, I.; Bandaru, S.; Ng, A.H. Online Knowledge Extraction and Preference Guided Multi-Objective Optimization in Manufacturing. IEEE Access 2021, 9, 145382–145396. [Google Scholar] [CrossRef]
- Zhang, J.; Zhou, A.; Tang, K.; Zhang, G. Preselection via classification: A case study on evolutionary multiobjective optimization. Inf. Sci. 2018, 465, 388–403. [Google Scholar] [CrossRef]
- Nojima, Y.; Tanigaki, Y.; Masuyama, N.; Ishibuchi, H. Multiobjective Evolutionary Data Mining for Performance Improvement of Evolutionary Multiobjective Optimization. In Proceedings of the 2018 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Miyazaki, Japan, 7–10 October 2018; pp. 745–750. [Google Scholar]
- Mittal, S.; Saxena, D.K.; Deb, K.; Goodman, E.D. A learning-based innovized progress operator for faster convergence in evolutionary multi-objective optimization. ACM Trans. Evol. Learn. Optim. (TELO) 2021, 2, 1–29. [Google Scholar] [CrossRef]
- Mittal, S.; Saxena, D.K.; Deb, K.; Goodman, E.D. Enhanced Innovized Progress Operator for Evolutionary Multi-and Many-objective Optimization. IEEE Trans. Evol. Comput. 2021, 26, 961–975. [Google Scholar] [CrossRef]
- Dudas, C.; Ng, A.H.; Bostroem, H. Post-analysis of multi-objective optimization solutions using decision trees. Intell. Data Anal. 2015, 19, 259–278. [Google Scholar] [CrossRef]
- Bonissone, P.P.; Subbu, R.; Eklund, N.; Kiehl, T.R. Evolutionary algorithms+ domain knowledge= real-world evolutionary computation. IEEE Trans. Evol. Comput. 2006, 10, 256–280. [Google Scholar] [CrossRef]
- Mahbub, M.S.; Wagner, M.; Crema, L. Incorporating domain knowledge into the optimization of energy systems. Appl. Soft Comput. 2016, 47, 483–493. [Google Scholar] [CrossRef]
- Hitomi, N.; Selva, D. Incorporating expert knowledge into evolutionary algorithms with operators and constraints to design satellite systems. Appl. Soft Comput. 2018, 66, 330–345. [Google Scholar] [CrossRef]
- Weiss, K.; Khoshgoftaar, T.M.; Wang, D. A survey of transfer learning. J. Big Data 2016, 3, 1–40. [Google Scholar] [CrossRef]
- Tanabe, R.; Ishibuchi, H. An easy-to-use real-world multi-objective optimization problem suite. Appl. Soft Comput. 2020, 89, 106078. [Google Scholar] [CrossRef]
- Liao, X.; Li, Q.; Yang, X.; Zhang, W.; Li, W. Multiobjective optimization for crash safety design of vehicles using stepwise regression model. Struct. Multidiscip. Optim. 2008, 35, 561–569. [Google Scholar] [CrossRef]
- Zitzler, E.; Thiele, L. Multiobjective evolutionary algorithms: A comparative case study and the strength Pareto approach. IEEE Trans. Evol. Comput. 1999, 3, 257–271. [Google Scholar] [CrossRef]
- Barrera-Diaz, C.A.; Nourmohammdi, A.; Smedberg, H.; Aslam, T.; Ng, A.H.C. An enhanced simulation-based multi-objective optimization approach with knowledge discovery for reconfigurable manufacturing systems. arXiv 2022, arXiv:cs.SY/2212.00581. [Google Scholar]
- Ng, A.H.; Bernedixen, J.; Moris, M.U.; Jägstam, M. Factory flow design and analysis using internet-enabled simulation-based optimization and automatic model generation. In Proceedings of the 2011 Winter Simulation Conference (WSC), Phoenix, AZ, USA, 11–14 December 2011; pp. 2176–2188. [Google Scholar]
- Smedberg, H.; Bandaru, S. Interactive knowledge discovery and knowledge visualization for decision support in multi-objective optimization. Eur. J. Oper. Res. 2022. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).