The Local Antimagic Chromatic Numbers of Some Join Graphs

Abstract

Let $G=\left(V\right(G),E(G\left)\right)$ be a connected graph with n vertices and m edges. A bijection $f:E\left(G\right)\to \{1,2,\cdots ,m\}$ is an edge labeling of G. For any vertex x of G, we define $\omega \left(x\right)={\sum }_{e\in E\left(x\right)}f\left(e\right)$ as the vertex label or weight of x, where $E\left(x\right)$ is the set of edges incident to x, and f is called a local antimagic labeling of G, if $\omega \left(u\right)\ne \omega \left(v\right)$ for any two adjacent vertices $u,v\in V\left(G\right)$. It is clear that any local antimagic labelling of G induces a proper vertex coloring of G by assigning the vertex label $\omega \left(x\right)$ to any vertex x of G. The local antimagic chromatic number of G, denoted by ${\chi }_{la}\left(G\right)$, is the minimum number of different vertex labels taken over all colorings induced by local antimagic labelings of G. In this paper, we present explicit local antimagic chromatic numbers of $F_n\vee \overline{K_2}$ and $F_n-v$, where $F_n$ is the friendship graph with n triangles and v is any vertex of $F_n$. Moreover, we explicitly construct an infinite class of connected graphs G such that ${\chi }_{la}\left(G\right)={\chi }_{la}(G\vee \overline{K_2})$, where $G\vee \overline{K_2}$ is the join graph of G and the complement graph of complete graph $K_2$. This fact leads to a counterexample to a theorem of Arumugam et al. in 2017, and our result also provides a partial solution to Problem 3.19 in Lau et al. in 2021.

1. Introduction

Throughout, we only consider undirected connected simple graphs. Let $G=\left(V\right(G),E(G\left)\right)$ be a connected graph with n vertices and m edges. A bijection $f:E\left(G\right)\to \{1,2,\cdots ,m\}$ is an edge labeling of G. For any vertex x of G, we define $\omega \left(x\right)={\sum }_{e\in E\left(x\right)}f\left(e\right)$ as the vertex label or weight of x, where $E\left(x\right)$ is the set of edges incident to x, and f is called an antimagic labeling of G, if $\omega \left(u\right)\ne \omega \left(v\right)$ for any two distinct vertices $u,v\in V\left(G\right)$. A graph G is called antimagic if G has an antimagic labeling.

The antimagic labeling of a graph was initially introduced by Hartsfield and Ringel [1] in 1990. They conjectured that every connected graph except $K_2$ admits such an antimagic labeling, which remains open till today.

Recently, based on the concept of antimagic labeling, Arumugam et al. [2] and Bensmail et al. [3] independently introduced the notation local antimagic labeling of graphs in 2017, which is weaker than antimagic labeling of graphs. Let $G=\left(V\right(G),E(G\left)\right)$ be a connected graph of order n and size m. A bijection $f:E\left(G\right)\to \{1,2,\cdots ,m\}$ is called a local antimagic labeling of G if any two adjacent vertices u and v in G satisfy $\omega \left(u\right)\ne \omega \left(v\right)$. It is clear that assigning $\omega \left(x\right)$ to x for each $x\in V\left(G\right)$ naturally induced a proper vertex coloring of G, which is called a local antimagic vertex coloring of G. A graph G is called local antimagic if G has a local antimagic labeling. Haslegrave [4] showed that every connected graph with at least three vertices is local antimagic. The local antimagic chromatic number of G, denoted by ${\chi }_{la}\left(G\right)$, is the minimum number of different vertex labels taken over all colorings of G induced by local antimagic labelings of G. If f is a local antimagic labeling of G, the number of distinct induced vertex labels under f, denoted by $c\left(f\right)$, is called the color number of f.

A friendship graph, denoted by $F_n$, is a simple graph in which any two vertices have exactly one common neighbour, which consists of n triangles with a common vertex. In [2], Arumugam et al. gave the exact value of the local antimagic chromatic numbers of special graphs, such as $P_n,C_n,F_n,K_{m,n},K_{2,n},W_n$, and $L\left(n\right)$, where $P_n$ and $C_n$ are path and cycle with n vertices, respectively, $K_{m,n}$ is the complete bipartite graph ($m\equiv n(mod2)$), $W_n$ is the wheel graph ($n\not\equiv 0(mod4)$), and $L\left(n\right)$ is the graph obtained by inserting a vertex to each edge of the star $S_n$. Ref. [5] was used in [2] to determine local antimagic chromatic numbers of complete bipartite graphs. When the graph is the wheel graph for $n\equiv 0(mod4)$ or the join graph $G\vee \overline{K_2}$ for $\left|V\right(G\left)\right|\ge 4$, where $\overline{K_2}$ is the complement graph of complete graph $K_2$, they also provided the lower and upper bounds of the local antimagic chromatic numbers of these graphs.

In 2018, Lau et al. [6] gave counterexamples to the lower bound of ${\chi }_{la}(G\vee \overline{K_2})$ that was obtained in [2]. Another counterexample was independently found by Shaebani [7]. A sharp lower bound of ${\chi }_{la}(G\vee \overline{K_n})$ and sufficient conditions for the given lower bound were obtained. Moreover, they gave affirmative solutions on Problem 3.3 of [2] and settled Theorem 2.15 of [2]. They also completely determined the local antimagic chromatic number of complete bipartite graphs.

In [8], Lau et al. provided several sufficient conditions for ${\chi }_{la}\left(H\right)\le {\chi }_{la}\left(G\right)$, where H is obtained from G with a certain number of edge-deleted or -added operations. They then determined the exact values of the local antimagic chromatic numbers of many cycle-related join graphs.

In 2019, Lau et al. [9] gave the sharp lower bound of the local antimagic chromatic number of a graph with cut-vertices given by pendant edges and then solved Problem 3.3 in [2] affirmatively. In Section 2 of [9], Lau et al. gave sufficient conditions for the one-point union of cycles with ${\chi }_{la}\left(G\right)=2$. In Section 3 of [9], they determined the exact values of the local antimagic chromatic numbers of many families of graphs with pendant edges. Finally, in Section 4, they obtained a few families of graphs with ${\chi }_{la}\left(G\right)=n$. This partially answered Problem 3.1 in [2].

Based on some known results, in this paper, we present the exact local antimagic chromatic numbers of $F_n\vee \overline{K_2}$ and $F_n-v$, where v is any vertex of $F_n$. Moreover, we explicitly construct an infinite class of connected graphs G such that ${\chi }_{la}\left(G\right)={\chi }_{la}(G\vee \overline{K_2})=3$, where $G\vee \overline{K_2}$ is the join graph of G and the complement graph of $K_2$. This fact leads to a counterexample to a theorem of [2], and our result also provides a partial solution to Problem 3.19 in [8].

2. Main Results

In [2], the authors gave the local antimagic chromatic number of the friendship graph as shown in the following lemma.

Lemma 1

([2]). Let $F_n$ be a friendship graph, then we have ${\chi }_{la}\left(F_n\right)=3$.

For two vertex disjoint graphs $F_n$ and $\overline{K_2}$, let $F_n\vee \overline{K_2}$ denote the join graph obtained by joining every vertex of $F_n$ with every vertex of $\overline{K_2}$. In the proof of the local antimagic chromatic number of $F_n\vee \overline{K_2}$, we write $i\equiv t(mods)$ ($0\le t<s$) as $i\stackrel{s}{\equiv }t$ in the following formula. The following theorem gives an exact value of the local antimagic chromatic number of $F_n\vee \overline{K_2}$.

Theorem 1.

Let H be the join graph $F_n\vee \overline{K_2}$, then we have ${\chi }_{la}\left(H\right)=4.$

Proof. 

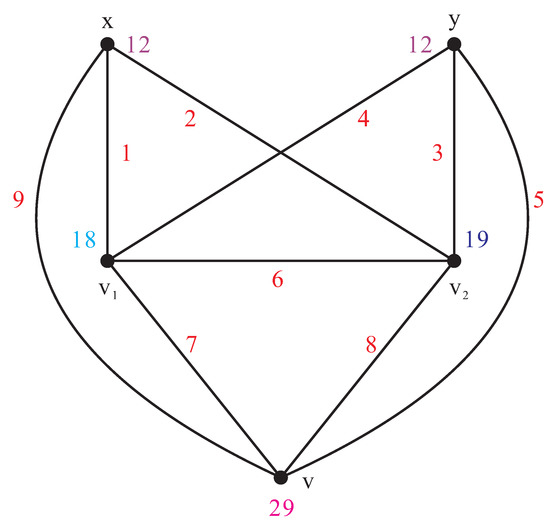
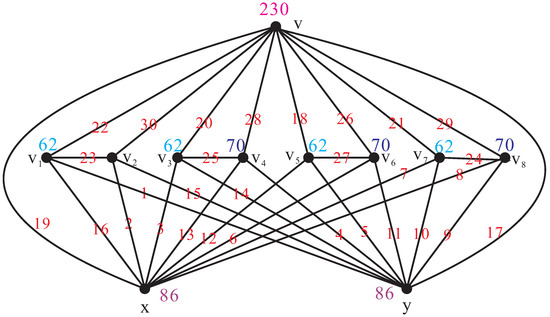
Let $\{v,v_1,v_2,\cdots ,v_{2n}\}$ be the vertex set of the friendship graph $F_n$, where v is its central vertex, and let $x,y$ be the two vertices of $K_2$. It is clear that there are $7n+2$ edges in H, namely, $\{v_i{v}_{i+1}:1\le i\le 2n\mathrm{and}i\equiv 1(mod2)\}\bigcup \{v{v}_i,x{v}_i,y{v}_i:1\le i\le 2n\}\bigcup \{xv,yv\}$. Since $K_4$ is an induced subgraph of H, we have ${\chi }_{la}\left(H\right)\ge \chi \left(H\right)\ge 4$. In order to prove ${\chi }_{la}\left(H\right)=4$, it suffices to provide a local antimagic labeling of H that induces a local antimagic vertex coloring using exactly four colors.

We suppose that there is a local antimagic labeling $f:E\left(H\right)\to \{1,2,3,\cdots ,7n+2\}$, such that $c\left(f\right)=4$. It means that $\omega \left(v_1\right)=\omega \left(v_3\right)=\cdots =\omega \left(v_{2n-1}\right)$, $\omega \left(v_2\right)=\omega \left(v_4\right)=\cdots =\omega \left(v_{2n}\right)$, and $\omega \left(x\right)=\omega \left(y\right)$, which are distinct with $\omega \left(v\right)$. In this regard, we first assign $f\left(x{v}_i\right)=i$ or $4n+1-i$ and $f\left(y{v}_i\right)=4n+1-i$ or i, for each $i\in \{1,2,\cdots ,2n\}$, then determine the exact value of remaining edges of H. Let us consider the following four cases.

Case 1.

$n\equiv 1(mod4)$

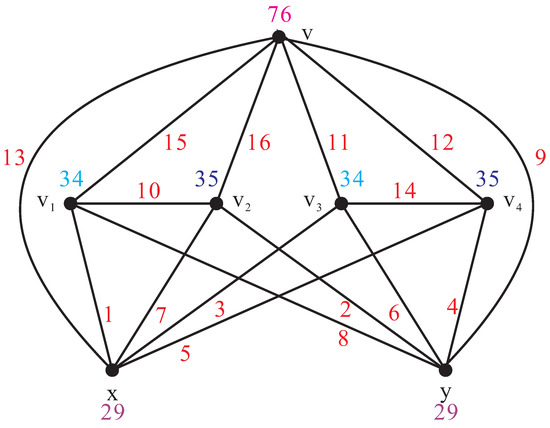
For $n=1$, the graph $H=F_1\vee \overline{K_2}$ admits a local antimagic labeling f with $c\left(f\right)=4$ as shown in Figure 1, which shows that ${\chi }_{la}\left(H\right)\le 4$, and so ${\chi }_{la}\left(H\right)=4$.

Figure 1. $F_1\vee \overline{K_2}$.

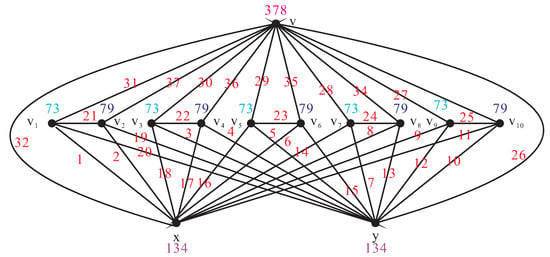
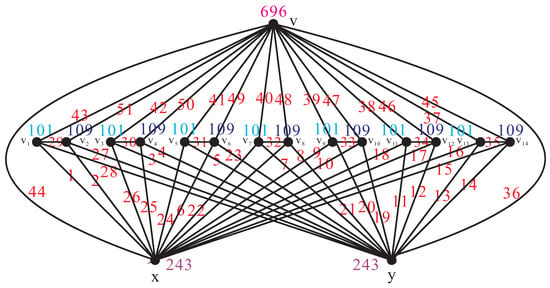
For $n=5$, we give the exact value of every edge label for the graph $H=F_5\vee \overline{K_2}$ as shown in Figure 2.

Figure 2. $F_5\vee \overline{K_2}$.

It is obvious that

$$\begin{array}{cc}\hfill \omega \left(x\right)& =\omega \left(y\right)=134,\hfill \\ \hfill \omega \left(v_1\right)& =\omega \left(v_3\right)=\omega \left(v_5\right)=\omega \left(v_7\right)=\omega \left(v_9\right)=73,\hfill \\ \hfill \omega \left(v_2\right)& =\omega \left(v_4\right)=\omega \left(v_6\right)=\omega \left(v_8\right)=\omega \left(v_{10}\right)=79,\hfill \\ \hfill \omega \left(v\right)& =378.\hfill \end{array}$$

From the above labeling, f is a local antimagic labeling of H that induces a local antimagic vertex coloring using exactly four colors. It means that ${\chi }_{la}\left(H\right)\le 4$, and so ${\chi }_{la}\left(H\right)=4$.

For $n\ge 9$, define $f:E\left(H\right)\to \{1,2,\cdots ,7n+2\}$ in the following way:

Let $f\left(xv\right)=6n+2,f\left(yv\right)=5n+1$, and determine the values of $f\left(x{v}_i\right)$ and $f\left(y{v}_i\right)$ for each $i\in \{1,2,3,4,5,2n-4,2n-3,2n-2,2n-1,2n\}$ as follows.

$$f\left(x{v}_i\right)=\left\{\begin{array}{cc}i,\hfill & \mathrm{if}i\in \{1,2,2n-4,2n-2,2n-1\},\hfill \\ 4n+1-i,\hfill & \mathrm{if}i\in \{3,4,5,2n-3,2n\}.\hfill \end{array}\right.$$

$$f\left(y{v}_i\right)=\left\{\begin{array}{cc}4n+1-i,\hfill & \mathrm{if}i\in \{1,2,2n-4,2n-2,2n-1\},\hfill \\ i,\hfill & \mathrm{if}i\in \{3,4,5,2n-3,2n\}.\hfill \end{array}\right.$$

Then label the edges $x{v}_i$ and $y{v}_i$ for $6\le i\le 2n-5$, respectively.

$$f\left(x{v}_i\right)=\left\{\begin{array}{cc}i,\hfill & \mathrm{if}i\stackrel{8}{\equiv }6,i\stackrel{8}{\equiv }0,i\stackrel{8}{\equiv }1\mathrm{or}i\stackrel{8}{\equiv }2,\hfill \\ 4n+1-i,\hfill & \mathrm{if}i\stackrel{8}{\equiv }7,i\stackrel{8}{\equiv }3,i\stackrel{8}{\equiv }4\mathrm{or}i\stackrel{8}{\equiv }5.\hfill \end{array}\right.$$

$$f\left(y{v}_i\right)=\left\{\begin{array}{cc}4n+1-i,\hfill & \mathrm{if}i\stackrel{8}{\equiv }6,i\stackrel{8}{\equiv }0,i\stackrel{8}{\equiv }1\mathrm{or}i\stackrel{8}{\equiv }2,\hfill \\ i,\hfill & \mathrm{if}i\stackrel{8}{\equiv }7,i\stackrel{8}{\equiv }3,i\stackrel{8}{\equiv }4\mathrm{or}i\stackrel{8}{\equiv }5.\hfill \end{array}\right.$$

Finally, we give the exact value of the remaining edges as follows.

$$\begin{array}{cc}f\left(v_i{v}_{i+1}\right)=4n+\frac{i+1}{2},\hfill & i\stackrel{2}{\equiv }1\mathrm{and}1\le i\le 2n,\hfill \\ f\left(v{v}_i\right)=6n+2-\frac{i+1}{2},\hfill & i\stackrel{2}{\equiv }1,\hfill \\ f\left(v{v}_i\right)=7n+3-\frac{i}{2},\hfill & i\stackrel{2}{\equiv }0.\hfill \end{array}$$

Since $n\equiv 1(mod4)$ and $n\ge 9$, we have $2n\equiv 2(mod8)$, and so the number of vertices in $\left\{v_i\right|6\le i\le 2n-5\}$ is divisible by 8.

If $\{i,i+1,i+2,\cdots ,i+7\}\subseteq \{6,7,\cdots ,2n-5\}$ and $i\equiv 6(mod8)$, then

$$\sum _{j=i}^{i+7}f\left(x{v}_j\right)=16n-6,\sum _{j=i}^{i+7}f\left(y{v}_j\right)=16n+14.$$

Accordingly, we have

$$\sum _{i=6}^{2n-5}f\left(x{v}_i\right)=4n^2-\frac{43n}{2}+\frac{15}{2},$$

$$\sum _{i=6}^{2n-5}f\left(y{v}_i\right)=4n^2-\frac{33n}{2}-\frac{35}{2}.$$

Since

$$\sum _{i=1}^{5}f\left(x{v}_i\right)=12n-6,\sum _{i=2n-4}^{2n}f\left(x{v}_i\right)=10n-2,$$

$$\sum _{i=1}^{5}f\left(y{v}_i\right)=8n+11,\sum _{i=2n-4}^{2n}f\left(x{v}_i\right)=10n+7.$$

It is clear that f is a local antimagic labeling of H and

$$\begin{array}{c}\omega \left(x\right)=\omega \left(y\right)=4n^2+\frac{13n}{2}+\frac{3}{2},\hfill \\ \omega \left(v_i\right)=14n+3,i\stackrel{2}{\equiv }1,\hfill \\ \omega \left(v_i\right)=15n+4,i\stackrel{2}{\equiv }0,\hfill \\ \omega \left(v\right)=12n^2+15n+3.\hfill \end{array}$$

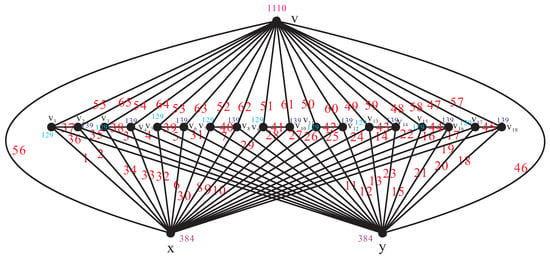
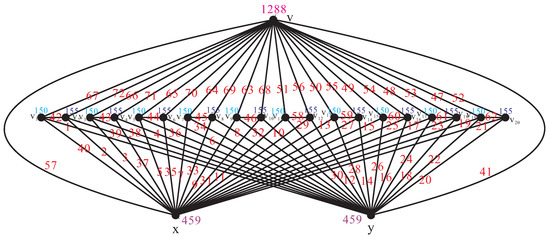
Hence, ${\chi }_{la}\left(H\right)\le 4$. The local antimagic labeling of the graph $F_9\vee \overline{K_2}$ is shown in Figure 3.

Figure 3. $F_9\vee \overline{K_2}$.

Case 2.

$n\equiv 3(mod4)$

For $n=3$ as shown in Figure 4, we obtain a local antimagic labeling of $F_3\vee \overline{K_2}$ with $c\left(f\right)=4$.

Figure 4. $F_3\vee \overline{K_2}$.

For $n\ge 7$, define $f:E\left(H\right)\to \{1,2,\cdots ,7n+2\}$ by the following

$$f\left(xv\right)=6n+2,f\left(yv\right)=5n+1.$$

Firstly, we set the following assignments of $x{v}_i$ and $y{v}_i$ for some special i, respectively.

$$f\left(x{v}_i\right)=\left\{\begin{array}{cc}i,\hfill & \mathrm{if}i\in \{1,2\},\hfill \\ 4n+1-i,\hfill & \mathrm{if}i\in \{3,4,5,2n\}.\hfill \end{array}\right.$$

$$f\left(y{v}_i\right)=\left\{\begin{array}{cc}4n+1-i,\hfill & \mathrm{if}i\in \{1,2\},\hfill \\ i,\hfill & \mathrm{if}i\in \{3,4,5,2n\}.\hfill \end{array}\right.$$

Secondly, considering the following assignments of the edges $x{v}_i$ and $y{v}_i$ for $6\le i\le 2n-1$,

$$f\left(x{v}_i\right)=\left\{\begin{array}{cc}i,\hfill & \mathrm{if}i\stackrel{8}{\equiv }6,i\stackrel{8}{\equiv }0,i\stackrel{8}{\equiv }1\mathrm{or}i\stackrel{8}{\equiv }2,\hfill \\ 4n+1-i,\hfill & \mathrm{if}i\stackrel{8}{\equiv }7,i\stackrel{8}{\equiv }3,i\stackrel{8}{\equiv }4\mathrm{or}i\stackrel{8}{\equiv }5.\hfill \end{array}\right.$$

$$f\left(y{v}_i\right)=\left\{\begin{array}{cc}4n+1-i,\hfill & \mathrm{if}i\stackrel{8}{\equiv }6,i\stackrel{8}{\equiv }0,i\stackrel{8}{\equiv }1\mathrm{or}i\stackrel{8}{\equiv }2,\hfill \\ i,\hfill & \mathrm{if}i\stackrel{8}{\equiv }7,i\stackrel{8}{\equiv }3,i\stackrel{8}{\equiv }4\mathrm{or}i\stackrel{8}{\equiv }5.\hfill \end{array}\right.$$

Finally, label the remaining edges as follows.

$$\begin{array}{cc}f\left(v_i{v}_{i+1}\right)=4n+\frac{i+1}{2},\hfill & i\stackrel{2}{\equiv }1\mathrm{and}1\le i\le 2n,\hfill \\ f\left(v{v}_i\right)=6n+2-\frac{i+1}{2},\hfill & i\stackrel{2}{\equiv }1,\hfill \\ f\left(v{v}_i\right)=7n+3-\frac{i}{2},\hfill & i\stackrel{2}{\equiv }0.\hfill \end{array}$$

Because $n\equiv 3(mod4)$ and $n\ge 7$, we have $2n\equiv 6(mod8)$, and so the number of vertices in $\left\{v_i\right|6\le i\le 2n-1\}$ is divisible by 8.

If $\{i,i+1,i+2,\cdots ,i+7\}\subseteq \{6,7,\cdots ,2n-1\}$ and $i\equiv 6(mod8)$, then

$$\sum _{j=i}^{i+7}f\left(x{v}_j\right)=16n-6,\sum _{j=i}^{i+7}f\left(y{v}_j\right)=16n+14.$$

We can obtain that

$$\sum _{i=6}^{2n-1}f\left(x{v}_i\right)=4n^2-\frac{27n}{2}+\frac{9}{2},$$

$$\sum _{i=6}^{2n-1}f\left(y{v}_i\right)=4n^2-\frac{17n}{2}-\frac{21}{2}.$$

Since

$$\sum _{i=1}^{5}f\left(x{v}_i\right)=12n-6,\sum _{i=1}^{5}f\left(y{v}_i\right)=8n+11,$$

$$f\left(x{v}_{2n}\right)=2n+1,f\left(y{v}_i\right)=2n.$$

For the vertex weights we have

$$\begin{array}{c}\omega \left(x\right)=\omega \left(y\right)=4n^2+\frac{13n}{2}+\frac{3}{2},\hfill \\ \omega \left(v_i\right)=14n+3,i\stackrel{2}{\equiv }1,\hfill \\ \omega \left(v_i\right)=15n+4,i\stackrel{2}{\equiv }0,\hfill \\ \omega \left(v\right)=12n^2+15n+3.\hfill \end{array}$$

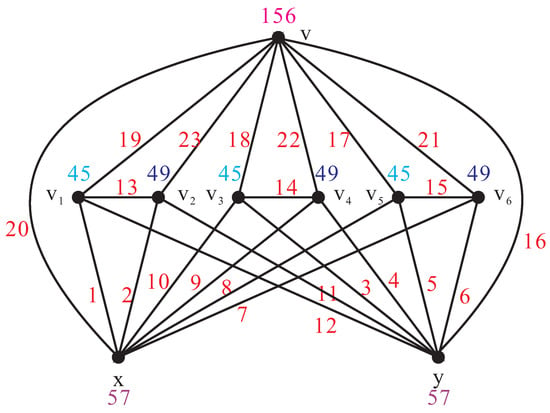
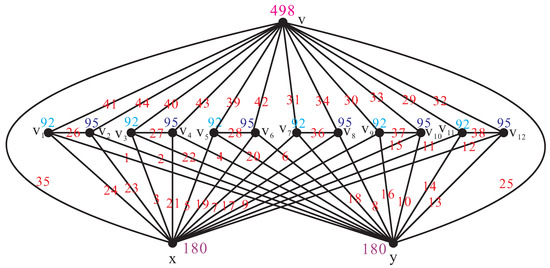
Hence, we can obtain that ${\chi }_{la}\left(H\right)=4$. For $n=7$, the exact values of each edge label of the graph $F_7\vee \overline{K_2}$ are given in Figure 5.

Figure 5. $F_7\vee \overline{K_2}$.

Case 3.

$n\equiv 2(mod4)$

In this case, we consider $n\equiv 2(mod8)$ and $n\equiv 6(mod8)$, respectively.

Subcase 3.1. $n\equiv 2(mod8)$

For $n=2$, there is a local antimagic labeling of the graph $H=F_2\vee \overline{K_2}$ in Figure 6. Hence, we have ${\chi }_{la}\left(H\right)=4$.

Figure 6. $F_2\vee \overline{K_2}$.

For $n\ge 10$, define the edge labeling $f:E\left(H\right)\to \{1,2,\cdots ,7n+2\}$ as follows:

$$f\left(xv\right)=\frac{11n}{2}+2,f\left(yv\right)=4n+1.$$

Assume that $n=8k+2,k=1,2,\cdots$, then we give the following exact values of $f\left(x{v}_i\right)$ and $f\left(y{v}_i\right)$ for $1\le i\le 2n$.

$$f\left(x{v}_i\right)=\left\{\begin{array}{cc}4n+1-i,\hfill & \mathrm{if}1\le i\le 2k\mathrm{and}i\stackrel{2}{\equiv }1,\hfill \\ i,\hfill & \mathrm{if}1\le i\le 2k\mathrm{and}i\stackrel{2}{\equiv }0,\hfill \\ i,\hfill & \mathrm{if}2k+1\le i\le 2n\mathrm{and}i\stackrel{2}{\equiv }1,\hfill \\ 4n+1-i,\hfill & \mathrm{if}2k+1\le i\le 2n\mathrm{and}i\stackrel{2}{\equiv }0.\hfill \end{array}\right.$$

$$f\left(y{v}_i\right)=\left\{\begin{array}{cc}i,\hfill & \mathrm{if}1\le i\le 2k\mathrm{and}i\stackrel{2}{\equiv }1,\hfill \\ 4n+1-i,\hfill & \mathrm{if}1\le i\le 2k\mathrm{and}i\stackrel{2}{\equiv }0,\hfill \\ 4n+1-i,\hfill & \mathrm{if}2k+1\le i\le 2n\mathrm{and}i\stackrel{2}{\equiv }1,\hfill \\ i,\hfill & \mathrm{if}2k+1\le i\le 2n\mathrm{and}i\stackrel{2}{\equiv }0.\hfill \end{array}\right.$$

Then label the remaining edges as follows:

$$f\left(v_i{v}_{i+1}\right)=\left\{\begin{array}{cc}4n+1+\frac{i+1}{2},\hfill & \mathrm{if}1\le i\le n\mathrm{and}i\stackrel{2}{\equiv }1,\hfill \\ 5n+2+\frac{i+1}{2},\hfill & \mathrm{if}n+1\le i\le 2n\mathrm{and}i\stackrel{2}{\equiv }1.\hfill \end{array}\right.$$

$$f\left(v{v}_i\right)=\left\{\begin{array}{cc}\frac{13n+4}{2}-\frac{i-1}{2},\hfill & \mathrm{if}1\le i\le n\mathrm{and}i\stackrel{2}{\equiv }1,\hfill \\ 7n+3-\frac{i}{2},\hfill & \mathrm{if}1\le i\le n\mathrm{and}i\stackrel{2}{\equiv }0,\hfill \\ \frac{11n+2}{2}-\frac{i-1}{2},\hfill & \mathrm{if}n+1\le i\le 2n\mathrm{and}i\stackrel{2}{\equiv }1,\hfill \\ 6n+2-\frac{i}{2},\hfill & \mathrm{if}n+1\le i\le 2n\mathrm{and}i\stackrel{2}{\equiv }0.\hfill \end{array}\right.$$

It is clear that f is a local antimagic labeling of H, and we have

$$\begin{array}{c}\omega \left(x\right)=\omega \left(y\right)=4n^2+\frac{23n}{4}+\frac{3}{2},\hfill \\ \omega \left(v_i\right)=\frac{29n}{2}+5,i\stackrel{2}{\equiv }1,\hfill \\ \omega \left(v_i\right)=15n+5,i\stackrel{2}{\equiv }0,\hfill \\ \omega \left(v\right)=\frac{23n^2}{2}+\frac{27n}{2}+3.\hfill \end{array}$$

So, we have ${\chi }_{la}(F_n\vee \overline{K_2})=4$ for $\mathrm{n}\stackrel{8}{\equiv }2$. The local antimagic labeling of the graph $F_{10}\vee \overline{K_2}$ is shown in Figure 7.

Figure 7. $F_{10}\vee \overline{K_2}$.

Subcase 3.2. $n\equiv 6(mod8)$

For $n\ge 6$, label the edges of H by the labeling $f:E\left(H\right)\to \{1,2,\cdots ,7n+2\}$ such that

$$f\left(xv\right)=\frac{11n}{2}+2,f\left(yv\right)=4n+1.$$

Assume $n=8k-2,k=1,2,\cdots$, then we label $f\left(x{v}_i\right)$ and $f\left(y{v}_i\right)$ for each i such that $1\le i\le 2n-1$.

$$f\left(x{v}_i\right)=\left\{\begin{array}{cc}4n+1-i,\hfill & \mathrm{if}1\le i\le 2k\mathrm{and}i\stackrel{2}{\equiv }1,\hfill \\ i,\hfill & \mathrm{if}1\le i\le 2k\mathrm{and}i\stackrel{2}{\equiv }0,\hfill \\ i,\hfill & \mathrm{if}2k+1\le i\le 2n-1\mathrm{and}i\stackrel{2}{\equiv }1,\hfill \\ 4n+1-i,\hfill & \mathrm{if}2k+1\le i\le 2n-1\mathrm{and}i\stackrel{2}{\equiv }0.\hfill \end{array}\right.$$

$$f\left(y{v}_i\right)=\left\{\begin{array}{cc}i,\hfill & \mathrm{if}1\le i\le 2k\mathrm{and}i\stackrel{2}{\equiv }1,\hfill \\ 4n+1-i,\hfill & \mathrm{if}1\le i\le 2k\mathrm{and}i\stackrel{2}{\equiv }0,\hfill \\ 4n+1-i,\hfill & \mathrm{if}2k+1\le i\le 2n-1\mathrm{and}i\stackrel{2}{\equiv }1,\hfill \\ i,\hfill & \mathrm{if}2k+1\le i\le 2n-1\mathrm{and}i\stackrel{2}{\equiv }0.\hfill \end{array}\right.$$

For the last vertex $v_{2n}$,

$$f\left(x{v}_{2n}\right)=2n,f\left(y{v}_{2n}\right)=2n+1.$$

Now, determine the exact value of $f\left(v{v}_i\right)$ for each i such that $1\le i\le 2n$.

$$f\left(v{v}_i\right)=\left\{\begin{array}{cc}\frac{13n+4}{2}-\frac{i-1}{2},\hfill & \mathrm{if}1\le i\le n\mathrm{and}i\stackrel{2}{\equiv }1,\hfill \\ 7n+3-\frac{i}{2},\hfill & \mathrm{if}1\le i\le n\mathrm{and}i\stackrel{2}{\equiv }0,\hfill \\ \frac{11n+2}{2}-\frac{i-1}{2},\hfill & \mathrm{if}n+1\le i\le 2n\mathrm{and}i\stackrel{2}{\equiv }1,\hfill \\ 6n+2-\frac{i}{2},\hfill & \mathrm{if}n+1\le i\le 2n\mathrm{and}i\stackrel{2}{\equiv }0.\hfill \end{array}\right.$$

When i is odd for $1\le i\le 2n$, we can label $f\left(v_i{v}_{i+1}\right)$ as follows.

$$f\left(v_i{v}_{i+1}\right)=\left\{\begin{array}{cc}4n+1+\frac{i+1}{2},\hfill & \mathrm{if}1\le i\le n\mathrm{and}i\stackrel{2}{\equiv }1,\hfill \\ 5n+2+\frac{i+1}{2},\hfill & \mathrm{if}n+1\le i\le 2n\mathrm{and}i\stackrel{2}{\equiv }1.\hfill \end{array}\right.$$

For the vertex weights under the labeling f, we have

$$\begin{array}{c}\omega \left(x\right)=\omega \left(y\right)=4n^2+\frac{23n}{4}+\frac{3}{2},\hfill \\ \omega \left(v_i\right)=\frac{29n}{2}+5,i\stackrel{2}{\equiv }1,\hfill \\ \omega \left(v_i\right)=15n+5,i\stackrel{2}{\equiv }0,\hfill \\ \omega \left(v\right)=\frac{23n^2}{2}+\frac{27n}{2}+3.\hfill \end{array}$$

This implies that ${\chi }_{la}\left(H\right)=4$. For $n=6$, we obtain the local antimagic labeling of the graph $F_6\vee \overline{K_2}$ under f as shown in Figure 8.

Figure 8. $F_6\vee \overline{K_2}$.

Case 4.

$n\equiv 0(mod4)$

We define $f:E\left(H\right)\to \{1,2,\cdots ,7n+2\}$ as follows:

$$f\left(xv\right)=4n+3,f\left(yv\right)=4n+1.$$

The following labeling has the desired properties:

$$f\left(x{v}_i\right)=\left\{\begin{array}{cc}4n+1-i,\hfill & \mathrm{if}i\stackrel{4}{\equiv }1\mathrm{or}i\stackrel{4}{\equiv }0,\mathrm{and}i\ne 2n,\hfill \\ i,\hfill & \mathrm{if}i\stackrel{4}{\equiv }3\mathrm{or}i\stackrel{4}{\equiv }2,\mathrm{or}i=2n.\hfill \end{array}\right.$$

$$f\left(y{v}_i\right)=\left\{\begin{array}{cc}i,\hfill & \mathrm{if}i\stackrel{4}{\equiv }1\mathrm{or}i\stackrel{4}{\equiv }0,\mathrm{and}i\ne 2n,\hfill \\ 4n+1-i,\hfill & \mathrm{if}i\stackrel{4}{\equiv }3\mathrm{or}i\stackrel{4}{\equiv }2,\mathrm{or}i=2n.\hfill \end{array}\right.$$

$$f\left(v_i{v}_{i+1}\right)=\left\{\begin{array}{cc}5n+2+i,\hfill & \mathrm{if}1\le i\le n+1\mathrm{and}i\stackrel{2}{\equiv }1,\hfill \\ 7n+3-i,\hfill & \mathrm{if}n+3\le i\le 2n\mathrm{and}i\stackrel{2}{\equiv }1.\hfill \end{array}\right.$$

$$f\left(v{v}_i\right)=\left\{\begin{array}{cc}5n+3-i,\hfill & \mathrm{if}1\le i\le n+2\mathrm{and}i\stackrel{2}{\equiv }1,\hfill \\ 7n+4-i,\hfill & \mathrm{if}1\le i\le n+2\mathrm{and}i\stackrel{2}{\equiv }0,\hfill \\ 3n+2+i,\hfill & \mathrm{if}n+3\le i\le 2n\mathrm{and}i\stackrel{2}{\equiv }1,\hfill \\ 5n+1+i,\hfill & \mathrm{if}n+3\le i\le 2n\mathrm{and}i\stackrel{2}{\equiv }0.\hfill \end{array}\right.$$

For the vertex weights under the labeling f, we have

$$\begin{array}{c}\omega \left(x\right)=\omega \left(y\right)=4n^2+5n+2,\hfill \\ \omega \left(v_i\right)=14n+6,i\stackrel{2}{\equiv }1,\hfill \\ \omega \left(v_i\right)=16n+6,i\stackrel{2}{\equiv }0.\hfill \\ \omega \left(v\right)=11n^2+13n+2.\hfill \end{array}$$

The above arguments indicate that f is a local antimagic labeling of H with four colors, and so ${\chi }_{la}\left(H\right)=4$. The exact values of each edge label of the graph $F_4\vee {\overline{K}}_2$ are given in Figure 9. The proof is completed. □

Figure 9. $F_4\vee \overline{K_2}$.

Let $H=F_n-v$ be a graph obtained from the friendship graph $F_n(n\ge 2)$ by deleting any vertex v of $F_n$. If the deleted vertex is its central vertex, then H does not have a local antimagic labeling. Thus, we only consider that the deleted vertex is a vertex with degree 2.

Theorem 2.

Let H be the graph $F_n-v$, where v is any vertex of $F_n(n\ge 2)$ with degree 2, then we have ${\chi }_{la}\left(H\right)=3.$

Proof. 

Let $V\left(F_n\right)=\{u_i:1\le i\le n\}\bigcup \{v_i:1\le i\le n\}\bigcup \left\{x\right\}$ and $E\left(F_n\right)=\{u_i{v}_i:1\le i\le n\}\bigcup \{x{u}_i:1\le i\le n\}\bigcup \{x{v}_i:1\le i\le n\}$. Without loss of generality, we assume that the deleted vertex is $v_n\in V\left(F_n\right)$, then define $h:E\left(H\right)\to \{1,2,\cdots ,3n-2\}$ by

$$\begin{array}{cc}h\left(u_i{v}_i\right)=i,\hfill & 1\le i\le n-1,\hfill \\ h\left(x{u}_i\right)=3n-2-i,\hfill & 1\le i\le n-1,\hfill \\ h\left(x{v}_i\right)=2n-1-i,\hfill & 1\le i\le n-1,\hfill \\ h\left(x{u}_n\right)=3n-2.\hfill \end{array}$$

Clearly, h is a local antimagic labeling of H and we have

$$\begin{array}{cc}\hfill \omega \left(v_i\right)& =2n-1,\mathrm{where}1\le i\le n-1,\hfill \\ \hfill \omega \left(u_i\right)& =3n-2,\mathrm{where}1\le i\le n,\hfill \\ \hfill \omega \left(x\right)& =4n^2-4n+1.\hfill \end{array}$$

Thus, ${\chi }_{la}\left(H\right)\le 3$. Since ${\chi }_{la}\left(H\right)\ge \chi \left(H\right)=3$; it follows that ${\chi }_{la}\left(H\right)=3$. □

Theorem 2.16 of [2] asserts that if a graph G has at least four vertices, then ${\chi }_{la}\left(G\right)+1={\chi }_{la}(G\vee \overline{K_2})$, when G is of even order n. In this section, we explicitly construct an infinite class of connected graphs G such that ${\chi }_{la}\left(G\right)=3$ and ${\chi }_{la}(G\vee \overline{K_2})=3$. Our procedure is to consider path $P_n$ that satisfies ${\chi }_{la}\left(P_n\right)=3$ for each positive integer $n\ge 3$. We show that if n is even, then ${\chi }_{la}(P_n\vee \overline{K_2})=3$. Our result provides partial solution to Problem 3.19 in [8].

Theorem 3.

If $P_n$ is a path of order n, then we have ${\chi }_{la}(P_n\vee \overline{K_2})=3$ for even n.

Proof. 

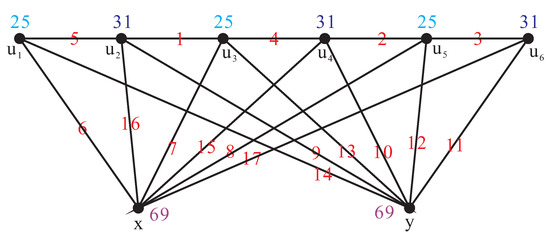
The lower bound of the local antimagic chromatic number of the join graph $P_n\vee \overline{K_2}$ even for n is clearly obtained. We have ${\chi }_{la}(P_n\vee \overline{K_2})\ge \chi (P_n\vee \overline{K_2})=3$ since $K_3$ is a induced subgraph of $P_n\vee \overline{K_2}$. We show that the upper bound of the chromatic number ${\chi }_{la}(P_n\vee \overline{K_2})$ is attainable.

Let $\{u_i:1\le i\le n\}$ and $\{x,y\}$ be the vertex set of the path $P_n$ and the complement graph of $K_2$, respectively. Then $E(P_n\vee \overline{K_2})=\{x{u}_i,y{u}_i:1\le i\le n\}\cup \{u_i{u}_{i+1}:1\le i\le n-1\}$, and $\left|E\right(P_n\vee \overline{K_2}\left)\right|=3n-1$.

Label the edges $u_i{u}_{i+1}$ as follows:

$$f\left(u_i{u}_{i+1}\right)=\left\{\begin{array}{cc}n-\frac{i+1}{2},\hfill & \mathrm{if}i\mathrm{is}\mathrm{odd},\hfill \\ \frac{i}{2},\hfill & \mathrm{if}i\mathrm{is}\mathrm{even}.\hfill \end{array}\right.$$

Then, label the edges $x{u}_i$ as follows:

$$f\left(x{u}_i\right)=\left\{\begin{array}{cc}n+\frac{i-1}{2},\hfill & \mathrm{if}i\mathrm{is}\mathrm{odd},\hfill \\ 3n-\frac{i+2}{2},\hfill & \mathrm{if}i\mathrm{is}\mathrm{even},i\ne n,\hfill \\ 3n-1,\hfill & i=n.\hfill \end{array}\right.$$

Finally, label the edges $y{u}_i$ as follows:

$$f\left(y{u}_i\right)=\left\{\begin{array}{cc}\frac{5n}{2}-\frac{i+1}{2},\hfill & \mathrm{if}i\mathrm{is}\mathrm{odd},\hfill \\ \frac{3n}{2}+\frac{i-2}{2},\hfill & \mathrm{if}i\mathrm{is}\mathrm{even}.\hfill \end{array}\right.$$

We can conclude that

$$\begin{array}{cc}\omega \left(u_i\right)=\frac{9n}{2}-2,\hfill & \mathrm{if}i\mathrm{is}\mathrm{odd};\hfill \\ \omega \left(u_i\right)=\frac{11n}{2}-2,\hfill & \mathrm{if}i\mathrm{is}\mathrm{even};\hfill \\ \omega \left(x\right)=\omega \left(y\right)=2n^2-\frac{n}{2}.\hfill \end{array}$$

Therefore, f is a local antimagic labeling of $P_n\vee \overline{K_2}$ that induces a local antimagic vertex coloring using exactly three colors. The local antimagic labeling of the graph $P_6\vee \overline{K_2}$ as an example is shown in Figure 10. □

Figure 10. $P_6\vee \overline{K_2}$.

3. Conclusions and Scope

In this paper, we obtain the exact values of the local antimagic chromatic number of the join graphs $F_n\vee \overline{K_2}$, $P_n\vee \overline{K_2}$ and the graph $F_n-v$. Hence, the following problem arises naturally.

Problem 1.

Find the local antimagic chromatic number of the cartesian product of simple graphs G and H.

Problem 2.

Find the local antimagic chromatic number of other operations of graphs.

Problem 3.

Characterize the class of a graph G for which ${\chi }_{la}(G\vee \overline{K_2})={\chi }_{la}\left(G\right)$.