The Local Antimagic Chromatic Numbers of Some Join Graphs
Abstract
:1. Introduction
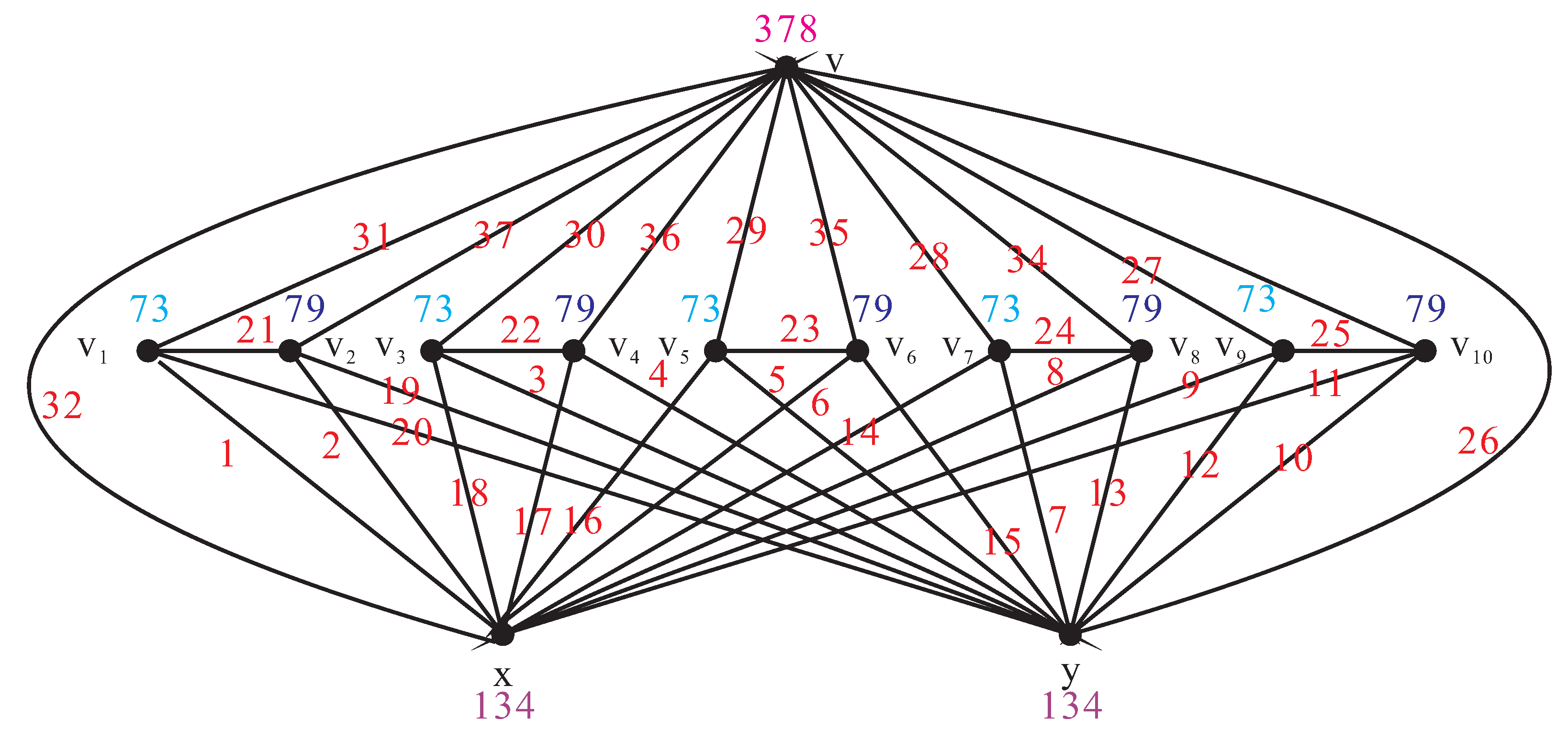
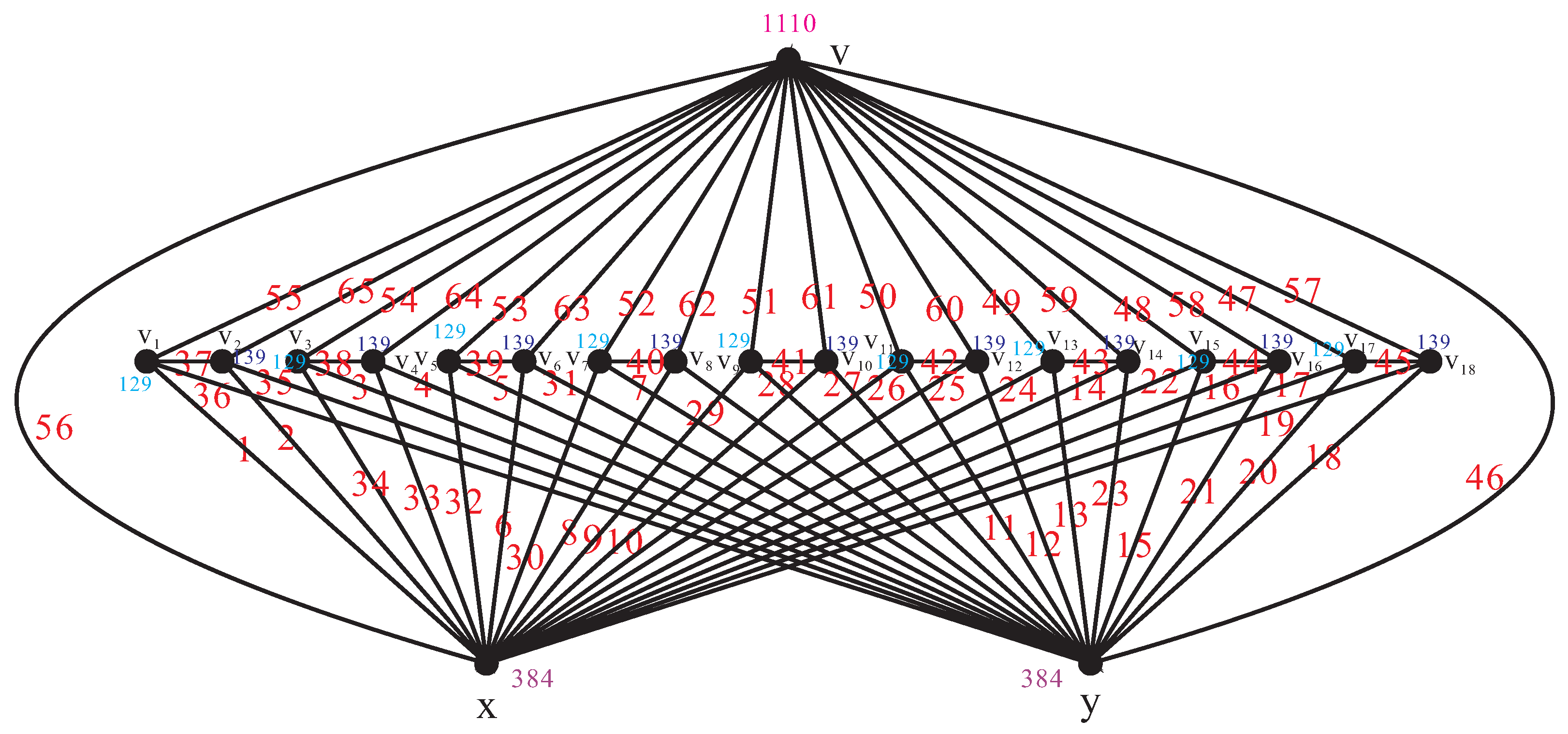
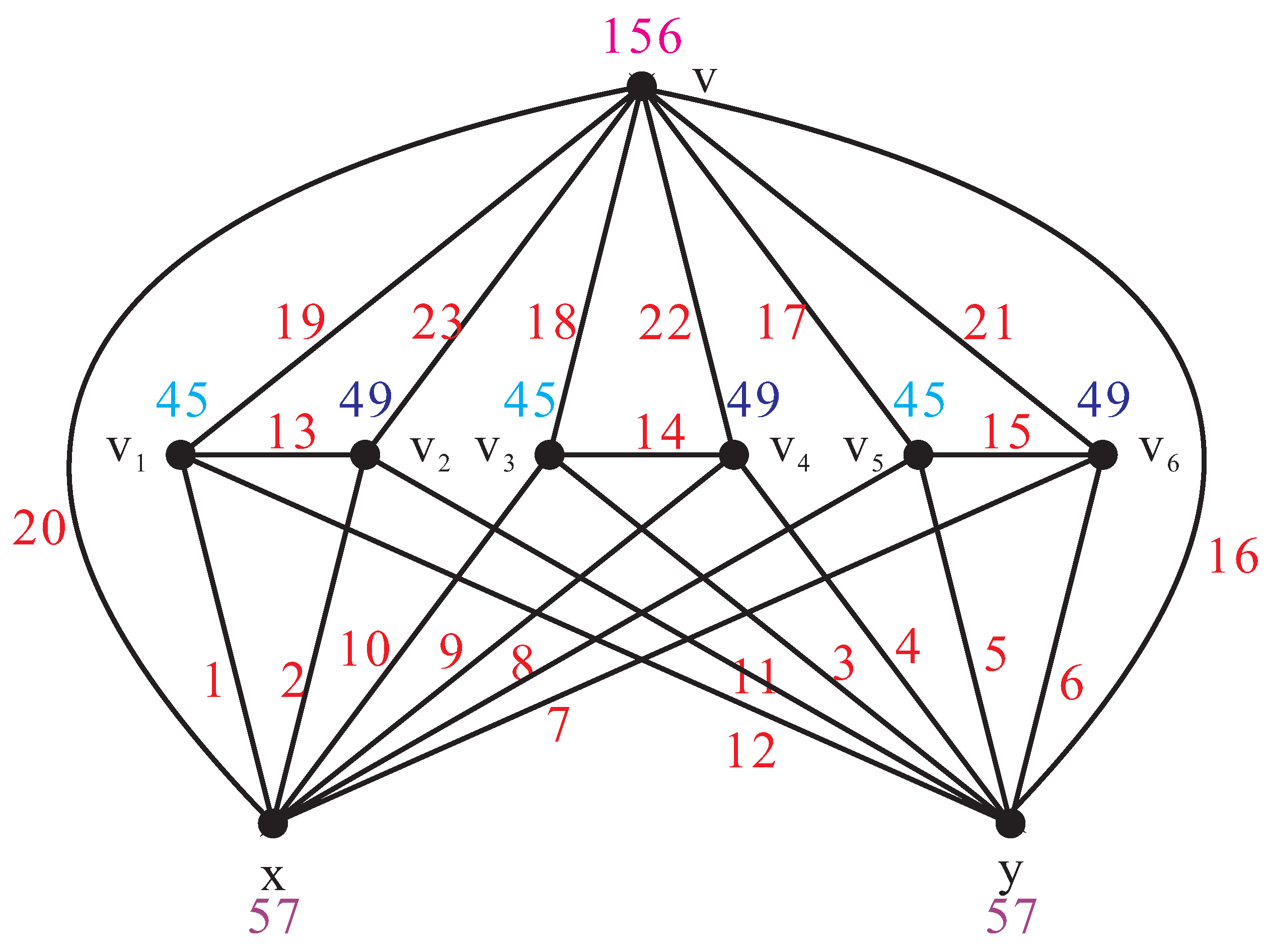
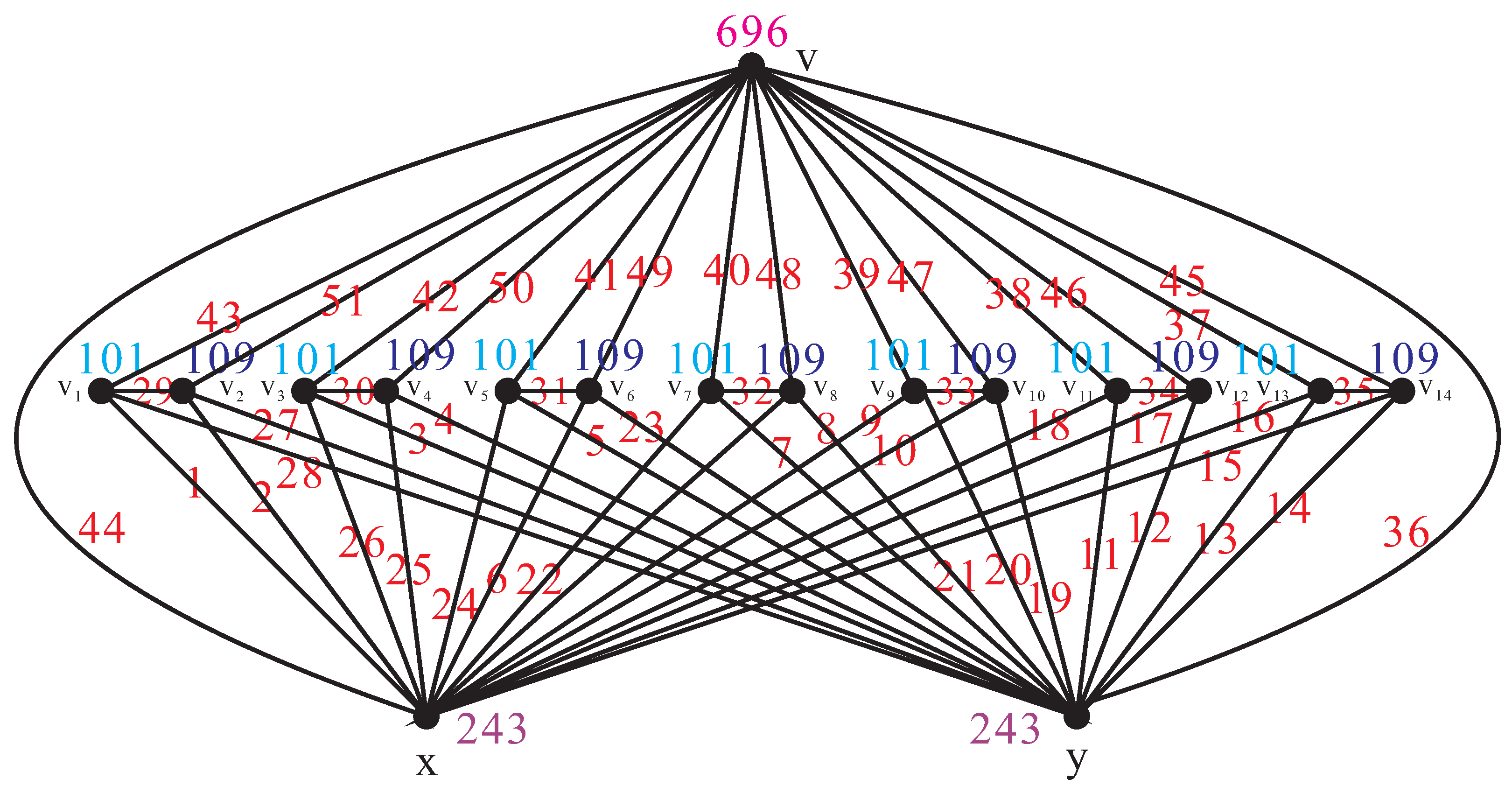
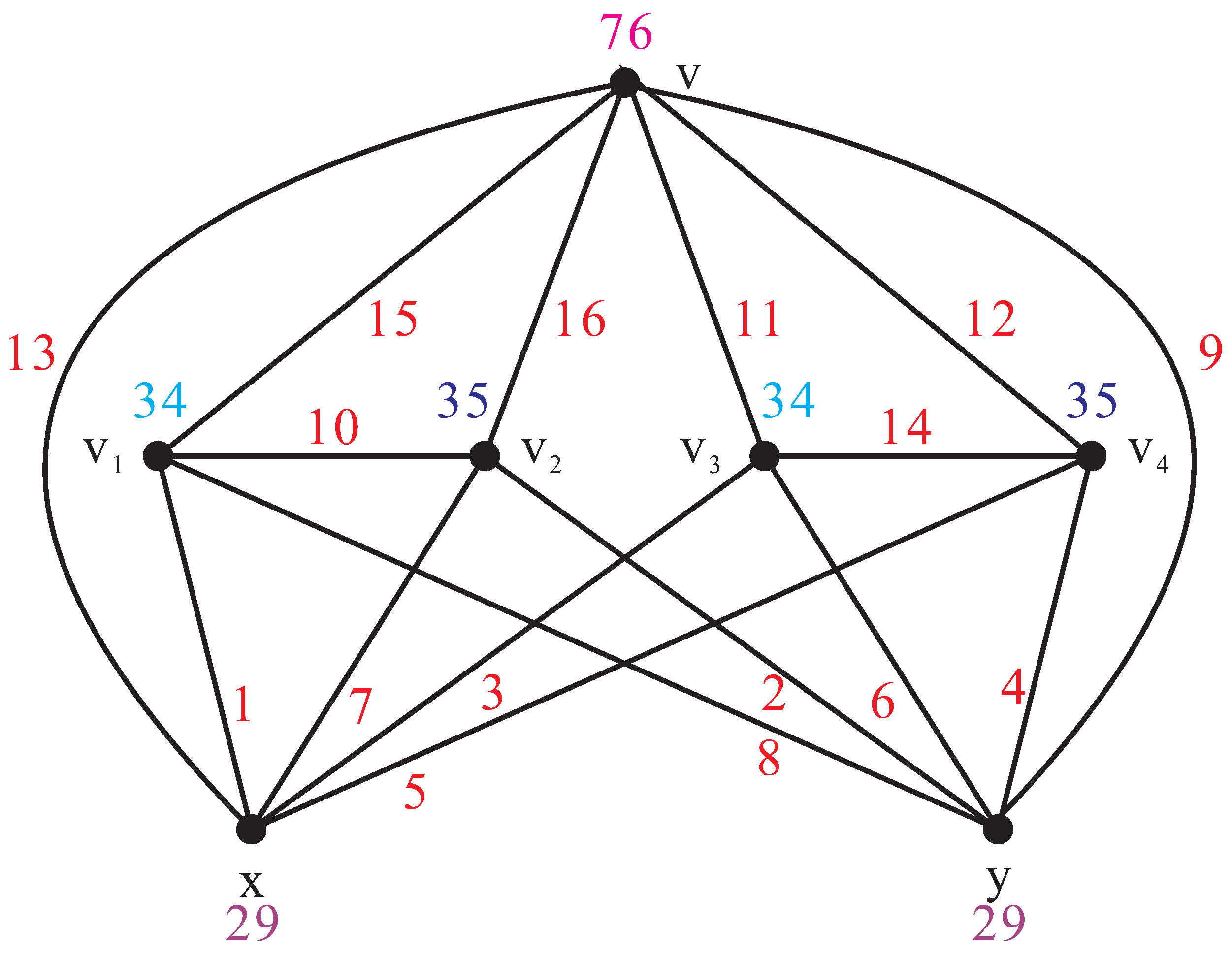
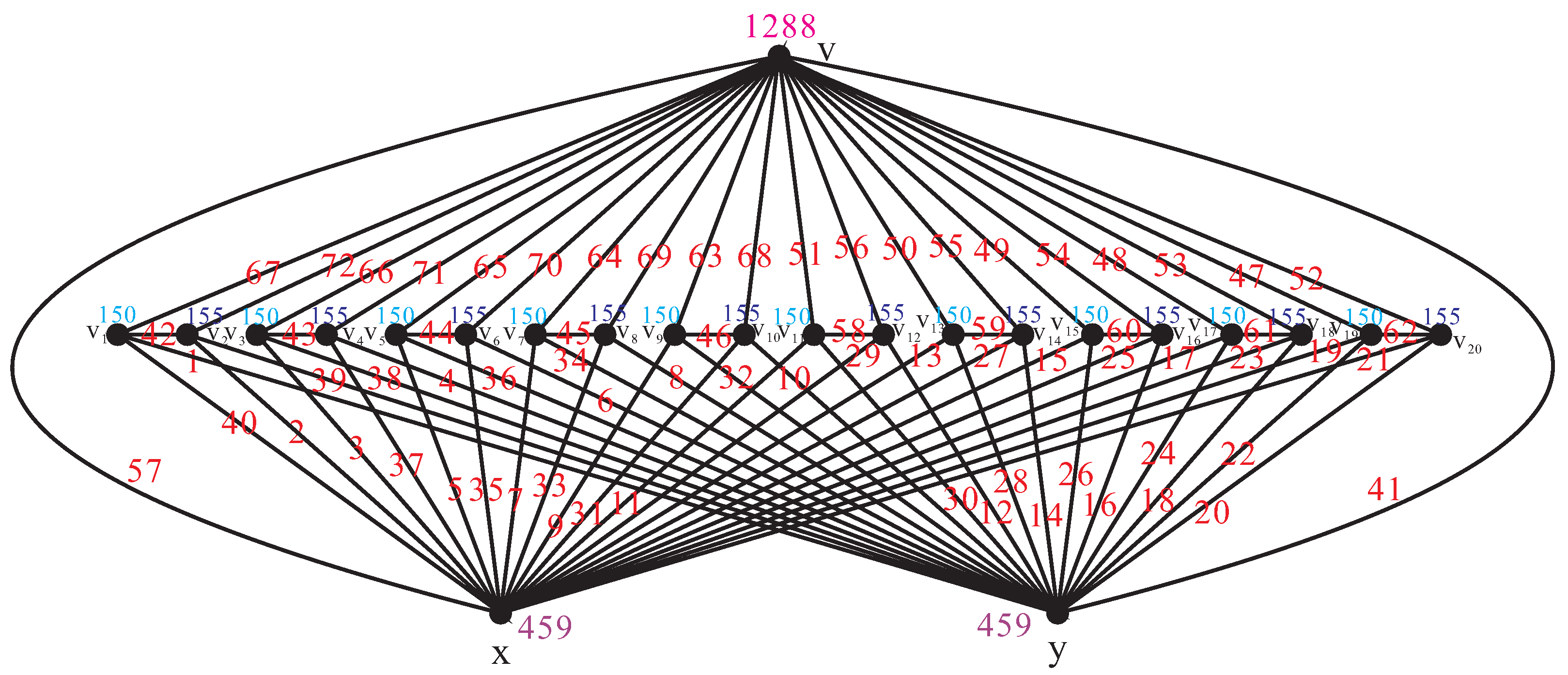
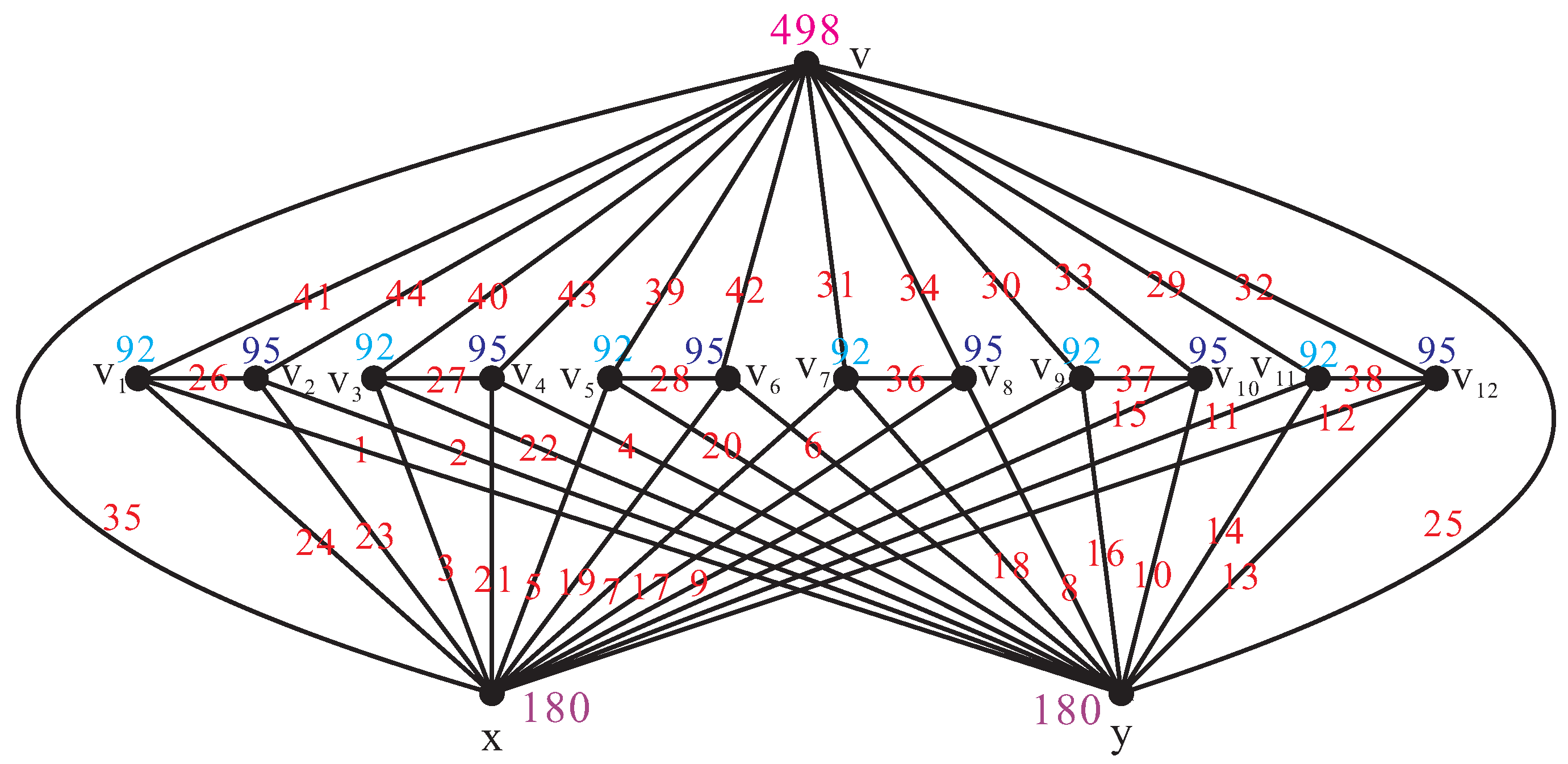
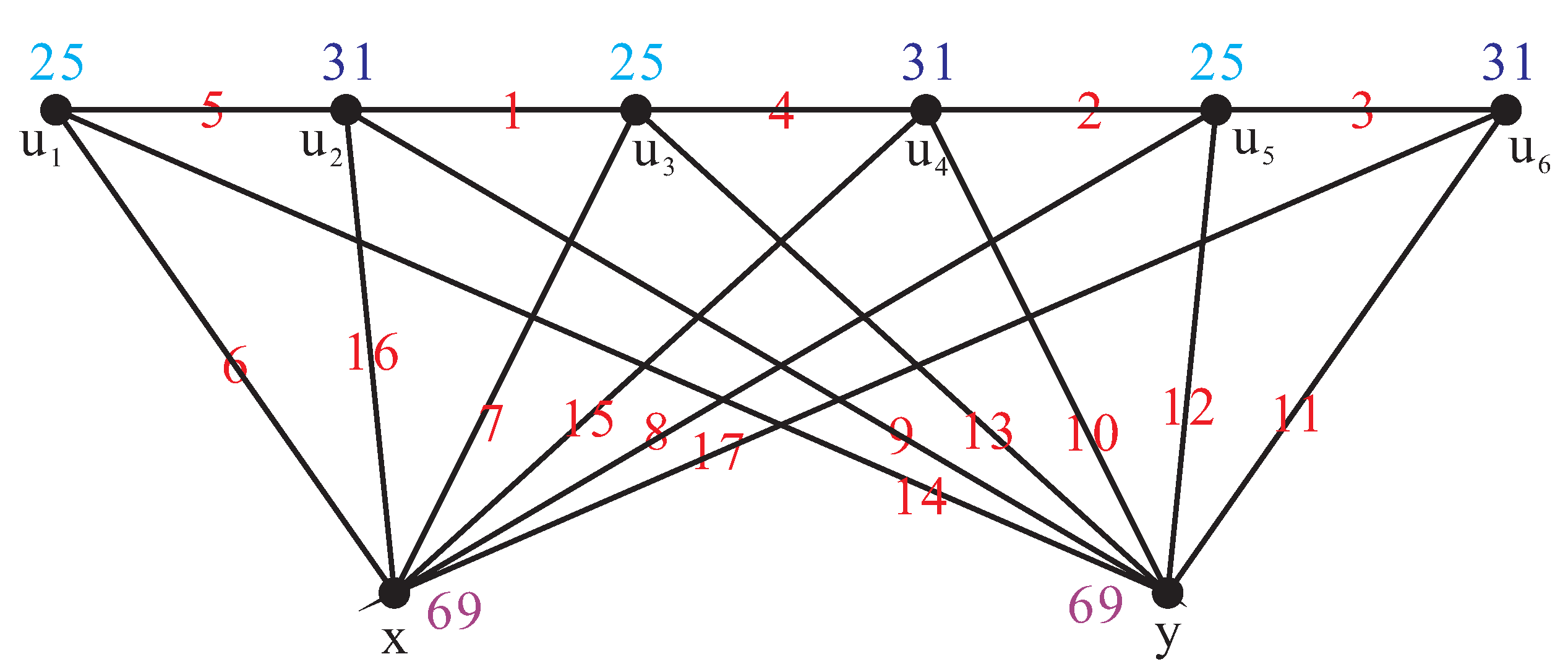
2. Main Results
3. Conclusions and Scope
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hartsfield, N.; Ringel, G. Pearls in Graph Theory; Academic Press Inc.: Boston, MA, USA, 1994. [Google Scholar]
- Arumugam, S.; Premalatha, K.; Bacǎ, M.; Semaničová-Feňovčíková, A. Local antimagic vertex coloring of a graph. Graphs Comb. 2017, 33, 275–285. [Google Scholar] [CrossRef]
- Bensmail, J.; Senhaji, M.; Lyngsie, K.S. On a combination of the 1-2-3 Conjecture and the Antimagic Labelling Conjecture. Discret. Math. Theor. Comput. Sci. 2017, 19, 1–17. [Google Scholar]
- Haslegrave, J. Proof of a local antimagic conjecture. Discr. Math. Theor. Comp. Sci. 2018, 20, 1–14. [Google Scholar]
- Hagedorn, T.R. Magic rectangles revisited. Discrete Math. 1990, 207, 65–72. [Google Scholar] [CrossRef] [Green Version]
- Lau, G.C.; Shiu, W.C.; Ng, H.K. Affirmative solutions on local antimagic chromatic number. Graphs Comb. 2020, 5, 69–78. [Google Scholar] [CrossRef]
- Shaebani, S. On local antimagic chromatic number of graphs. Algebr. Syst. 2020, 7, 245–256. [Google Scholar]
- Lau, G.C.; Shiu, W.C.; Ng, H.K. On local antimagic chromatic number of cycle-related join graphs. Discuss. Math. Graph Theory 2021, 41, 133–152. [Google Scholar] [CrossRef]
- Lau, G.C.; Shiu, W.C.; Ng, H.K. On local antimagic chromatic number of graphs with cut-vertices. arXiv 2018, arXiv:1805.04801v6. [Google Scholar]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, X.; Bian, H.; Yu, H.; Liu, D. The Local Antimagic Chromatic Numbers of Some Join Graphs. Math. Comput. Appl. 2021, 26, 80. https://doi.org/10.3390/mca26040080
Yang X, Bian H, Yu H, Liu D. The Local Antimagic Chromatic Numbers of Some Join Graphs. Mathematical and Computational Applications. 2021; 26(4):80. https://doi.org/10.3390/mca26040080
Chicago/Turabian StyleYang, Xue, Hong Bian, Haizheng Yu, and Dandan Liu. 2021. "The Local Antimagic Chromatic Numbers of Some Join Graphs" Mathematical and Computational Applications 26, no. 4: 80. https://doi.org/10.3390/mca26040080
APA StyleYang, X., Bian, H., Yu, H., & Liu, D. (2021). The Local Antimagic Chromatic Numbers of Some Join Graphs. Mathematical and Computational Applications, 26(4), 80. https://doi.org/10.3390/mca26040080




