The Limited Validity of the Conformable Euler Finite Difference Method and an Alternate Definition of the Conformable Fractional Derivative to Justify Modification of the Method

Abstract

A method recently advanced as the conformable Euler method (CEM) for the finite difference discretization of fractional initial value problem $D_t^{\alpha }y\left(t\right) = f\left(t;\mathrm{y}\left(t\right)\right), y\left(t_0\right) = y_0, a\le t\le b$, and used to describe hyperchaos in a financial market model, is shown to be valid only for $\alpha =1$. The property of the conformable fractional derivative (CFD) used to show this limitation of the method is used, together with the integer definition of the derivative, to derive a modified conformable Euler method for the initial value problem considered. A method of constructing generalized derivatives from the solution of the non-integer relaxation equation is used to motivate an alternate definition of the CFD and justify alternative generalizations of the Euler method to the CFD. The conformable relaxation equation is used in numerical experiments to assess the performance of the CEM in comparison to that of the alternative methods.

1. Introduction

Termed the conformable Euler method (CEM), a finite difference discretization method is adopted in [1] and justified by applying the fractional power series expansion. The method is proposed to solve equations of the form

$$T_t^{\alpha }y\left(t\right) = f\left(t;\mathrm{y}\left(t\right)\right), y\left(t_0\right) = y_0, a\le t\le b$$

(1)

where $T_t^{\alpha }y\left(t\right)$ denotes the conformable fractional derivative (CFD) of order $\alpha$ introduced in [2], since most differential equations using the CFD do not have exact analytic solutions, so that numerical approximation methods must be developed. The method has the following form:

$$\alpha \frac{y_{k+1}-y_k}{h^{\alpha }}=f\left(t_k,y_k\right), 0\le k\le N,\mathrm{where}h=\frac{b-a}{N}.$$

(2)

In [1], the method is used to solve conformable fractional differential equation systems with time delays and in [3], it is used to calculate numerical solutions for testing the hyperchaos of conformable derivative models for financial systems with market confidence and ethics risk. The purpose of the present article is to show that, while the CEM (2) clearly reduces to the ordinary Euler method, it is not valid as a generalization of the standard forward Euler method to the CFD for $0<\alpha <1$, and to propose alternative generalizations.

The CFD was introduced in [2] and is defined as

$$T_t^{\alpha }f\left(t\right)=\underset{\epsilon \to 0}{\lim }\frac{f\left(t+\epsilon t^{1-\alpha })-f\left(t\right)\right)}{\epsilon }, \alpha \in \left(0,1\right].$$

(3)

Among its basic properties given in [2] is that if both $T_t^{\alpha }f\left(t\right)$ and $\frac{d}{dt}f\left(t\right)$ exist, then the following identity holds:

$$T_t^{\alpha }f\left(t\right)=t^{1-\alpha }\frac{d}{dt}f\left(t\right).$$

(4)

As stated in [4], “there is a debate among contemporary mathematicians about what it really means by a fractional derivative… as a consequence of introducing” the CFD. While several mathematical reasons drive this debate, the main one is the identity Equation (4), which renders questionable the fractionality of the CFD. The following titles capture the main problem with fractional derivatives and enumerate some of the arguments against the fractionality of the CFD and its generalizations: What is a Fractional Derivative? [5], No violation of the Leibniz rule. No fractional derivative [6], Local Fractional Derivatives of Differentiable Functions are Integer-order Derivatives or Zero [7], No Nonlocality, No Fractional Derivative [8], The flaw in the conformable calculus: It is conformable because it is not fractional [9] (see also [10,11,12]). This has led to the conclusion that “from mathematical point of view the introduced conformable derivatives does not provide any real improvement to the theory of fractional calculus in compare with the classical fractional derivatives. Furthermore, they bring nothing new at least as mathematical advantages in the field of the ordinary differential equations with fractional derivatives” [10].

Such debate on its nature notwithstanding, the CFD appears to have removed a hurdle for the use of fractional derivatives, that of being very complex for applications and not easy to master or use (see [13]) and spurred brisk activity in studies of previously un-explored phenomena, as is evident from the number of references in for example [12,14]. While the debate about the “mathematical fractionality” of the CFD continues, the CFD is being used in applications to arrive at conclusions about, among others, systems with time delays [1], economic models of financial systems [3], classic games [15], electrical circuits [16,17], Newtonian [18] and quantum [19] mechanics, HIV therapeutic interventions [20], general biological modeling [21], and general sub-diffusion processes [14,22]. These continued uses of the CFD, because of its ease of implementation, to describe various phenomena considered important make necessary the development of tools for its use. A method has already been devised as a generalization of the Euler method for the CFD [1] and is being applied to problems of consequence (e.g., [1,3,15]): it is important therefore that, regardless of its classification as fractional or not, all methods being developed with such use of the CFD must be properly examined and benchmarked like any other for all derivative concepts. It is in this spirit that the work presented in this article offers an assessment of the CEM and suggests alternative methods for the generalization of the standard forward Euler method to the CFD.

Motivated in part by dismissals of the CFD as referenced above and the reality that phenomena are being described with methods employing the CFD, the exact spectral derivative discretization finite difference (ESDDFD) method was introduced in [23], wherein fractionality is determined by wave type behavior of processes under study and locality is defined by the relaxation pattern as follows:

• The Euler (ordinary) exponential function $e^z\equiv \sum _{k=0}^{\infty }\frac{z^k}{k!}$ is local, whereas the Mittag-Leffler generalized exponential function $E_{\alpha }\left(z\right)\equiv E_{\alpha ,1}\left(z\right)=\sum _{k=0}^{\infty }\frac{z^k}{\mathsf{\Gamma }\left(\alpha k+1\right)}$ is non-local (see, e.g., [24]).
• Debye exponential wave patterns, described by $\mathsf{\Phi }\left(t\right)=\mathsf{\Phi }\left(t_0\right)\exp \left(-ct\right)$ and are not fractional, whereas Kohlrausch–Williams–Watts (KWW) stretched exponential wave patterns, described by $\mathsf{\Phi }\left(t\right)=\mathsf{\Phi }\left(t_0\right)\exp \left(-c_{\alpha }{t}^{\alpha }\right)$ and $\mathsf{\Phi }\left(t\right)=\mathsf{\Phi }\left(t_0\right){\mathrm{E}}_{\alpha }\left(-c_{\alpha }{t}^{\alpha }\right)$ are fractional (see, e.g., [25]).

In that viewpoint, the generalized Caputo derivative can be expressed in terms of the generalized CFD, just as the Caputo derivative can be expressed in terms of the CFD (see, e.g., [26]). Further, the generalized RL derivative can be expressed in terms of the generalized Caputo derivative (which is parallel to the case for the classic Caputo and RL derivatives (see, e.g., [27]), as well as their Atangana–Baleanu extensions [28], and a parallel RL extension of the CFD can also be constructed [23]. The ESDDFD method of constructing generalized non-integer derivatives (NIDs) from the solution of the non-integer relaxation equation (NIRE), wherein fractionality is determined by wave type behavior as stated above and the CFD serves as a foundation for NIDs of both Caputo and RL types, is used in this article to motivate and justify the suggested alternatives for the generalization of the Euler method for the CFD.

The rest of this article is organized as follows. In the next section, the derivation of the CEM from [1] is recalled and it is shown that the CEM is valid only for $\alpha =1$. In Section 3, the relationship (4) is used to describe the ordinary Euler method (OEM) for the IVP (1) and to derive a modified CEM (MCEM). Section 4 recalls the ESDDFD method, and the exact discretization of the conformable relaxation equation (CRE) is used to justify the MCEM as well as to motivate an ESDDFD Euler method (EDM). Numerical experiments are presented in Section 5 assessing the accuracy, against the analytic solution of the CRE, of the CEM, MCEM, EDM, and OEM. A discussion in Section 6 of the theoretical and experimental results presented, as well as of recommendations based on those results, conclude the article.

2. The Conformable Euler’s Method

In this section, the derivation of the CEM is recalled and its validity is discussed.

2.1. Derivation of the Conformable Euler’s Method

The method (2), referred to in [1,3,15] as the conformable Euler’s method for (3), is obtained from truncation of a power series expansion as follows. Since $h=t_{k+1}-t_k$, it is assumed that there exist ${\theta }_k$ where $0<{\theta }_k<1$ is such that

$$y\left(t_{k+1}\right)-y\left(t_k\right)=\frac{1}{\alpha }{h}^{\alpha }\left(D_t^{\alpha }y\right)\left(t_k\right)+\frac{1}{2{\alpha }^2}{h}^{2\alpha }\left(D_t^{2\alpha }y\right)\left(t_k+{\theta }_{k}h\right).$$

(5)

Letting $y\left(t_{k+1}\right)-y\left(t_k\right)⟶y_{k+1}-y_k$ and substituting $\left(D_t^{\alpha }y\right)\left(t_k\right)=f\left(t_k,y_k\right)$ into (5) results in

$$y_{k+1}-y_k=\frac{1}{\alpha }{h}^{\alpha }f\left(t_k,y_k\right)+\frac{1}{2{\alpha }^2}{h}^{2\alpha }\left(D_t^{2\alpha }y\right)\left(t_k+{\theta }_{k}h\right),$$

or, equivalently

$$\alpha \frac{y_{k+1}-y_k}{h^{\alpha }}=f\left(t_k,y_k\right)+\frac{1}{2\alpha }{h}^{\alpha }\left(D_t^{2\alpha }y\right)\left(t_k+\theta h\right).$$

(6)

For small enough $h$, ignoring the second term on the right-hand side of (6) yields the conformable Euler’s method (2):

$$\alpha \frac{y_{k+1}-y_k}{h^{\alpha }}=f\left(t_k,y_k\right),$$

(7)

which reduces to the usual Euler’s method for $\alpha =1$.

2.2. Validity of the Conformable Euler’s Method

Since the CFD satisfies property (4), substituting $\left(D_t^{\alpha }y\right)\left(t_k\right)={\left(t_k\right)}^{1-\alpha }\frac{dy}{dt}\left(t_k\right)$ into (5) results in

$$y_{k+1}-y_k=\frac{1}{\alpha }{h}^{\alpha }{\left(t_k\right)}^{1-\alpha }\frac{dy}{dt}\left(t_k\right)+\frac{1}{2{\alpha }^2}{h}^{2\alpha }\left(D_t^{2\alpha }y\right)\left(t_k+{\theta }_{k}h\right),$$

or, equivalently

$$\alpha \frac{y_{k+1}-y_k}{h^{\alpha }}={\left(t_k\right)}^{1-\alpha }\frac{dy}{dt}\left(t_k\right)+\frac{1}{2\alpha }{h}^{\alpha }\left(D_t^{2\alpha }y\right)\left(t_k+\theta h\right).$$

(8)

For small enough $h$, ignoring the second term on the right-hand side of (8) yields

$$\alpha \frac{y_{k+1}-y_k}{h^{\alpha }}={\left(t_k\right)}^{1-\alpha }\frac{dy}{dt}\left(t_k\right),$$

and therefore

$$\frac{\alpha }{h^{\alpha -1}}\frac{y_{k+1}-y_k}{h}={\left(t_k\right)}^{1-\alpha }\frac{y_{k+1}-y_k}{h},$$

from which it follows that

$$\alpha h^{1-\alpha }={\left(t_k\right)}^{1-\alpha }.$$

(9)

Next, let us consider separately the cases of (9) (a) $t_0=0$ and (b) $t_0\ne 0$

(a)

If $t_0=0$, then $t_k=kh$, so that

$$\alpha h^{1-\alpha }={\left(t_k\right)}^{1-\alpha }={\left(kh\right)}^{1-\alpha }=k^{1-\alpha }{h}^{1-\alpha },$$

from which we conclude that

$$\alpha =k^{1-\alpha },$$

whose only constant solution is $\alpha =1$.

(b)

If $t_0\ne 0$, then $t_k=t_0+kh$, so that

$$\alpha h^{1-\alpha }={\left(t_k\right)}^{1-\alpha }={\left(t_0+kh\right)}^{1-\alpha }=h^{1-\alpha }{\left(\frac{t_0}{h}+k\right)}^{1-\alpha },$$

from which we conclude that

$$\alpha ={\left(\frac{t_0}{h}+k\right)}^{1-\alpha },$$

(10)

whose only constant solution is $\alpha =1$. Note that, if $\alpha <1$ is assumed on the right-hand side of (10), then for fixed $t_0, k$, and writing the left-hand side as $\alpha \left(h\right)$, results in $\alpha \left(h\right)\to \infty$ as $h\to 0$, a contradiction.

Since (9) holds if, and only if, both (2) and (4) hold, we conclude therefore that both (2) and (4) hold if, and only if, $\alpha =1$.

3. The Ordinary Euler’s and Modified Conformable Euler’s Methods

Next, the ordinary Euler method (OEM), obtained by re-writing the CFD in terms of the integer-order derivative, and a modified Euler method proposed in [29] are described.

3.1. The Ordinary, Integer-Order Euler’s Method

As mentioned in the introduction, one of the main reasons for the dismissal of the CFD as an NID is the property (4), which may be used to re-write Equation (1) in the following form,

$$\frac{d}{dt}y\left(t\right)=t^{\alpha -1}f\left(t;\mathrm{y}\left(t\right)\right), y\left(t_0\right)=y_0, a\le t\le b.$$

(11)

However, because of the singularity at $t=0$, the re-written problem (11) is ill-posed and its ordinary Euler method (OEM) representation,

$$\frac{y_{k+1}-y_k}{h}=t_k^{\alpha -1}f\left(t_k,y_k\right),\left(t_0,y_0\right),$$

(12)

cannot be implemented on any interval of the form $\left[0, b\right]$ without input additional to that of the given IVP (1). It can therefore be argued that the problem solved by implementing (12) with such additional information, such as

$$\frac{y_{k+1}-y_k}{h}=t_k^{\alpha -1}f\left(t_k,y_k\right),\left(t_0,y_0\right),\left(t_1,y_1\right),$$

(13)

which is used in Section 4, is not the same as (12).

3.2. The Modified Conformable Euler’s Method

In [29], a method consistent with the definition of the CFD and property (4) is obtained by rewriting $t^{1-\alpha }$ as a derivative and then using the $\alpha =1$ definition of the derivative as follows:

$$\begin{gathered} T_t^{\alpha }y\left(t\right)=t^{1-\alpha }\frac{d}{dt}y\left(t\right)=\left(\frac{d}{dt}y\left(t\right)\right)/\left(\frac{1}{\alpha }\frac{d}{dt}\left(t^{\alpha }\right)\right)=\underset{h\to 0}{\lim }\left(\frac{y\left(t+h\right)-y\left(t\right)}{h}\right)/ \\ \left(\frac{1}{\alpha }\frac{{\left(t+h\right)}^{\alpha }-t^{\alpha }}{h}\right)=\alpha \underset{h\to 0}{\lim }\left(\frac{y\left(t+h\right)-y\left(t\right)}{{\left(t+h\right)}^{\alpha }-t^{\alpha }}\right). \end{gathered}$$

(14)

For small enough $h$, therefore, and making the identifications

$$t⟶t_k, t+h⟶t_{k+1},y\left(t+h\right)⟶y_{k+1}, y\left(t\right)⟶y_k$$

(15)

in (14) result in the following discrete representation of ${}_0{}^{C}T_{}^{}{}_t^{\alpha }y\left(t\right)$:

$$T_t^{\alpha }y\left(t\right)=\alpha \underset{h\to 0}{\lim }\left(\frac{y\left(t+h\right)-y\left(t\right)}{{\left(t+h\right)}^{\alpha }-t^{\alpha }}\right)\to \alpha \frac{y_{k+1}-y_k}{{\left(t_{k+1}\right)}^{\alpha }-{\left(t_k\right)}^{\alpha }}.$$

Based on the above, it is claimed in [29] that the modified conformable Euler’s method for (1) is therefore given by

$$\alpha \frac{y_{k+1}-y_k}{{\left(t_{k+1}\right)}^{\alpha }-{\left(t_k\right)}^{\alpha }}=f\left(t_k,y_k\right),$$

(16)

valid for $0<\alpha \le 1$, which is also a generalization of the Euler method for $\alpha =1$.

4. Alternative Definition of the CFD and Justification of the MCEM

4.1. An Alternative Definition of the CFD from the ESDDFD Method

The second derivation of a modified CEM is based on the exact discretization of the initial value problem for the conformable relaxation equation, obtained from the following results from [23], in which it is generally assumed that the IVP (1) is being discretized on intervals of the form $\left[0, b\right]$.

Theorem 1.

For a given definition of an NID, let$\mho \left(t,\alpha ;y_0\right)$denote the analytic solution of initial value problem for the relaxation equation:

$$D_t^{\alpha }y\left(t\right)=-y\left(t\right), y\left(0\right)=y_0, 0\le t\le b; 0<\alpha \le 1.$$

(17)

Thus, a corresponding difference quotient representation (DQR) of Caputo type consistent with that derivative is

$${}_0{}^{GC}\Delta _{}^{}{}_t^{\alpha }y\left(t\right)=\frac{y\left(t+h\right)-y\left(t\right)}{\left(1-\mho \left(t+h,\alpha ;y_0\right)/\mho \left(t,\alpha ;y_0\right)\right)}.$$

(18)

Assuming $y_0=1$ and using the solution of (17) for the CFD,

$$\mho \left(t, \alpha \right)=\exp \left(-\frac{1}{\alpha }{t}^{\alpha }\right),$$

(19)

which describes behavior consistent with local, fractional, KWW wave patterns, in Equation (18) leads to the following DQR for the CFD:

$${}_0{}^{CFD}\Delta _{}^{}{}_t^{\alpha }y\left(t\right)=\frac{y\left(t+h\right)-y\left(t\right)}{\left(1-{\mathrm{e}}^{\frac{-1}{\alpha }\left({\left(t+h\right)}^{\alpha }-t^{\alpha }\right)}\right)}.$$

(20)

Taking the limit as $h\to 0$ in Equation (20) yields the following alternative definition of the CFD:

Definition 1.

Given a real-valued function on $\left[0,\infty \right)$, the conformable fractional derivative has the following alternative definition:

$$T_t^{\alpha }f\left(t\right)={}_0{}^{C}T_{}^{}{}_t^{\alpha }f\left(t\right)\equiv \underset{h\to 0}{\lim }{}_0{}^{CFD}\Delta _{}^{}{}_t^{\alpha }f\left(t\right)=\alpha \underset{h\to 0}{\lim }\frac{f\left(t+h\right)-f\left(t\right)}{{\left(t+h\right)}^{\alpha }-t^{\alpha }},$$

where ${}_0{}^{C}T_{}^{}{}_t^{\alpha }f\left(0\right)$ is understood to mean ${}_0{}^{C}T_{}^{}{}_t^{\alpha }f\left(0\right)=\underset{t\to 0^{+}}{lim}{}_0{}^{C}T_{}^{}{}_t^{\alpha }f\left(t\right)$.

The following result regarding the basic properties of ${}_0{}^{C}T_{}^{}{}_t^{\alpha }$ above has elementary proofs that follow directly from Definition 1 and are omitted here; it is the same as Theorem 2.2 of [2] and is a particular case of Theorem 2.1.6 of [23].

Theorem 2.

Let$\alpha \in \left(0, 1\right]$and the functions $f, g$be $\alpha$-differentiable at a point $t\in \left[0, \infty \right)$. Then, for all real-valued constants $A, B, K, p$, the following properties hold:

1. 

${}_0{}^{C}T_{}^{}{}_t^{\alpha }\left(Af+Bg\right)=A{}_0{}^{C}T_{}^{}{}_t^{\alpha }\left(f\right)+B{}_0{}^{C}T_{}^{}{}_t^{\alpha }\left(g\right)$

2. 

${}_0{}^{C}T_{}^{}{}_t^{\alpha }\left(fg\right)=g{}_0{}^{C}T_{}^{}{}_t^{\alpha }\left(f\right)+f{}_0{}^{C}T_{}^{}{}_t^{\alpha }\left(g\right)$

3. 

${}_0{}^{C}T_{}^{}{}_t^{\alpha }\left(\frac{f}{g}\right)=\frac{1}{g^2}\left(g{}_0{}^{C}T_{}^{}{}_t^{\alpha }\left(f\right)-f{}_0{}^{C}T_{}^{}{}_t^{\alpha }\left(g\right)\right)$

4. 

${}_0{}^{C}T_{}^{}{}_t^{\alpha }\left(t^p\right)=p{t}^{p-\alpha }$

5. 

${}_0{}^{C}T_{}^{}{}_t^{\alpha }\left(K\right)=0$

6. 

If$f\left(t\right)$is first order differentiable, then it also holds that${}_0{}^{C}T_{}^{}{}_t^{\alpha }\left(f\left(t\right)\right)=t^{1-\alpha }\frac{df\left(t\right)}{dt}$

Direct application of Definition 1 yields the following values for some common functions, which are identical to those obtained in [2], for $p,k\in ℝ$:

• ${}_0{}^{C}T_{}^{}{}_t^{\alpha }\left(t^p\right)=p{t}^{p-\alpha }$
• ${}_0{}^{C}T_{}^{}{}_t^{\alpha }\left(1\right)=0$
• ${}_0{}^{C}T_{}^{}{}_t^{\alpha }\left(e^{kt}\right)=k{t}^{1-\alpha }{e}^{kt}$
• ${}_0{}^{C}T_{}^{}{}_t^{\alpha }\left(sinkt\right)=k{t}^{1-\alpha }coskt$
• ${}_0{}^{C}T_{}^{}{}_t^{\alpha }\left(coskt\right)=-k{t}^{1-\alpha }sinkt$
• ${}_0{}^{C}T_{}^{}{}_t^{\alpha }\left(t^{\alpha }\right)=1$
• ${}_0{}^{C}T_{}^{}{}_t^{\alpha }\left(e^{\frac{1}{\alpha }{t}^{\alpha }}\right)=e^{\frac{1}{\alpha }{t}^{\alpha }}$
• ${}_0{}^{C}T_{}^{}{}_t^{\alpha }\left(sin\frac{1}{\alpha }{t}^{\alpha }\right)=cos\frac{1}{\alpha }{t}^{\alpha }$
• ${}_0{}^{C}T_{}^{}{}_t^{\alpha }\left(cos\frac{1}{\alpha }{t}^{\alpha }\right)=-sin\frac{1}{\alpha }{t}^{\alpha }$

Remark 1.

Since the alternative definition of the conformable fractional derivative, Definition 1, has the same basic properties and derivative values as the conformable fractional derivative, it is the same as the CFD, that is, ${}_{t_0}{}^{C}T_{}^{}{}_t^{\alpha }\left[f\left(t\right)\right]=T_{\alpha }^{t_0}\left(f\right)\left(t\right)$, where the right-hand side uses the notation in [9]. It should therefore be noted that, as recently pointed out in [30], the alternative definition shows that the conformable derivative for differentiable functions results from the integer-order derivative with the fractional change of variable$u={\left(t-t_0\right)}^{\alpha }/\alpha$, which can be easily seen. To see the equivalence of the CFD and this change of variable, assume $f$ is differentiable. Then, since ${}_{t_0}{}^{C}T_{}^{}{}_t^{\alpha }f\left(t\right)=T_{\alpha }^{t_0}f\left(t\right)\left(t\right)={\left(t-t_0\right)}^{1-\alpha }\frac{d}{dt}f\left(t\right)$and$\frac{du\left(t\right)}{dt}={\left(t-t_0\right)}^{\alpha -1}$, direct substitution in identity (4) and the chain rule yield

$$\begin{gathered} {}_{t_0}{}^{C}T_{}^{}{}_t^{\alpha }f\left(t\right)={\left(t-t_0\right)}^{1-\alpha }\frac{df\left(t\right)}{dt} \\ ={\left(t-t_0\right)}^{1-\alpha }\frac{df\left(u\right)}{du}\frac{du\left(t\right)}{dt} \\ ={\left(t-t_0\right)}^{1-\alpha }\frac{df\left(u\right)}{du}{\left(t-t_0\right)}^{\alpha -1} \\ =\frac{df\left(u\right)}{du} \end{gathered}$$

4.2. Justification of and an Alternative to the Modified Conformable Euler’s Method

The identifications (15) applied in Equation (18) yield the following discretization rule for $D_t^{\alpha }y\left(t\right)$ as a corollary to Theorem 1.

Corollary 1.

Let $\mho \left(t,\alpha ;y_0\right)$be as in Theorem 1. Then the following is a consistent discrete representation of $D_t^{\alpha }y\left(t\right)$:

$$D_t^{\alpha }y\left(t\right)⟶{}_0{}^{GC}\Delta _{}^{}{}_{t_k}^{\alpha }{y}_k\equiv \frac{y_{k+1}-y_k}{\left(1-\mho \left(t_{k+1},\alpha ;y_0\right)/\mho \left(t_k,\alpha ;y_0\right)\right)}.$$

The denominator is a complex function of both the step size, $h=t_{k+1}-t_k$, and lattice point, $t_k$, and is described in [23] as a generalization of the nonstandard finite difference (NSFD) denominator [31]. Similarly applying the identifications (15) in Definition 1 and using $\mho \left(t, \alpha \right)$ as given by Equation (19) in Corollary 1 therefore results in the following discrete representations of the CFD:

$$\mathrm{Modified}\mathrm{Conformable}\mathrm{Euler}:{}_0{}^{C}T_{}^{}{}_t^{\alpha }y\left(t\right)=\alpha \underset{h\to 0}{\lim }\left(\frac{y\left(t+h\right)-y\left(t\right)}{{\left(t+h\right)}^{\alpha }-t^{\alpha }}\right)\to \alpha \frac{y_{k+1}-y_k}{{\left(t_{k+1}\right)}^{\alpha }-{\left(t_k\right)}^{\alpha }}.$$

$$\mathrm{NSFD}\mathrm{Conformable}\mathrm{EDM}:{}_0{}^{C}T_{}^{}{}_t^{\alpha }y\left(t\right)=\alpha \underset{h\to 0}{\lim }\frac{y\left(t+h\right)-y\left(t\right)}{\left(1-{\mathrm{e}}^{-\frac{1}{\alpha }\left({\left(t+h\right)}^{\alpha }-t^{\alpha }\right)}\right)}\to \alpha \frac{y_{k+1}-y_k}{\left(1-{\mathrm{e}}^{-\frac{1}{\alpha }\left({\left(t_{k+1}\right)}^{\alpha }-{\left(t_k\right)}^{\alpha }\right)}\right)}.$$

A clear corollary to the foregoing are the following Euler discretization rules for the IVP (1), which provide justification of, and an alternative to, the MCEM as extensions of the Euler method to the CFD:

Corollary 2.

The following discrete representations are generalizations of the (forward) Euler method for the CFD valid for $\alpha \in \left(0, 1\right]$:

$$\mathrm{Modified}\mathrm{Conformable}\mathrm{Euler}:\alpha \frac{y_{k+1}-y_k}{{\left(t_{k+1}\right)}^{\alpha }-{\left(t_k\right)}^{\alpha }}=f\left(t_k,y_k\right)$$

$$\mathrm{ESDDFD}\text{-}\mathrm{based}\mathrm{Conformable}\mathrm{Euler}:\alpha \frac{y_{k+1}-y_k}{\left(1-{\mathrm{e}}^{-\frac{1}{\alpha }\left({\left(t_{k+1}\right)}^{\alpha }-{\left(t_k\right)}^{\alpha }\right)}\right)}=f\left(t_k,y_k\right).$$

5. Comparisons of Discrete Models of the Conformable Relaxation Equation

To demonstrate that the CEM is not a viable extension of the Euler method to the CFD for $\alpha \in \left(0,1\right)$ and to validate the suggested alternatives, comparisons against the analytic solution are presented in graphical and tabular form for the following discrete representations of the CRE obtained from the conformable Euler, ordinary Euler, modified conformable Euler, and ESDDFD-based Euler methods (respectively, CEM, OEM, MCEM, and EDM):

$$\begin{gathered} \mathrm{CEM}: y_{k+1}=y_k-\frac{1}{\alpha }{h}^{\alpha }{y}_k, \\ \mathrm{OEM}: y_{k+1}=y_k-h{t}_k^{\alpha -1}{y}_k, \\ \mathrm{MCEM}: y_{k+1}=y_k-\frac{1}{\alpha }\left({\left(t_{k+1}\right)}^{\alpha }-{\left(t_k\right)}^{\alpha }\right)y_k \\ \mathrm{EDM}: y_{k+1}=y_k-\frac{1}{\alpha }\left(1-{\mathrm{e}}^{-\frac{1}{\alpha }\left({\left(t_{k+1}\right)}^{\alpha }-{\left(t_k\right)}^{\alpha }\right)}\right)y_k \end{gathered}$$

5.1. Tabular Comparisons of Actual and Relative Errors

In Table 1 relative error comparisons are given for various values of $\alpha$ at $t_k=1.00$.

Table 1. % error by method compared to actual value at $t_k=1.00$.

$\mathit{\alpha }$	Exact Value	EDM	CEM	MCEM	OEM
0.99	0.36	0.00	5.06	1.29	1.30
0.98	0.36	0.00	8.93	1.32	1.38
0.97	0.36	0.00	12.90	1.34	1.46
0.96	0.35	0.00	16.80	1.37	1.54
0.95	0.35	0.00	20.80	1.40	1.62
0.62	0.20	0.00	99.60	4.56	7.31

It is clear from Table 1 that, for this simplest example, the CEM performs poorly compared to all other methods and yields significantly incorrect approximations for $\alpha <0.98$, with relative error reaching almost 100% at $\alpha =0.62$. While the OEM is almost comparable to the MCEM for $\alpha$ close to unity, its relative error is almost double that of the MCEM for $\alpha <0.62$. The EDM, as expected for this example, has the same values as the analytic solution.

5.2. Graphical Comparisons of Actual and Relative Errors

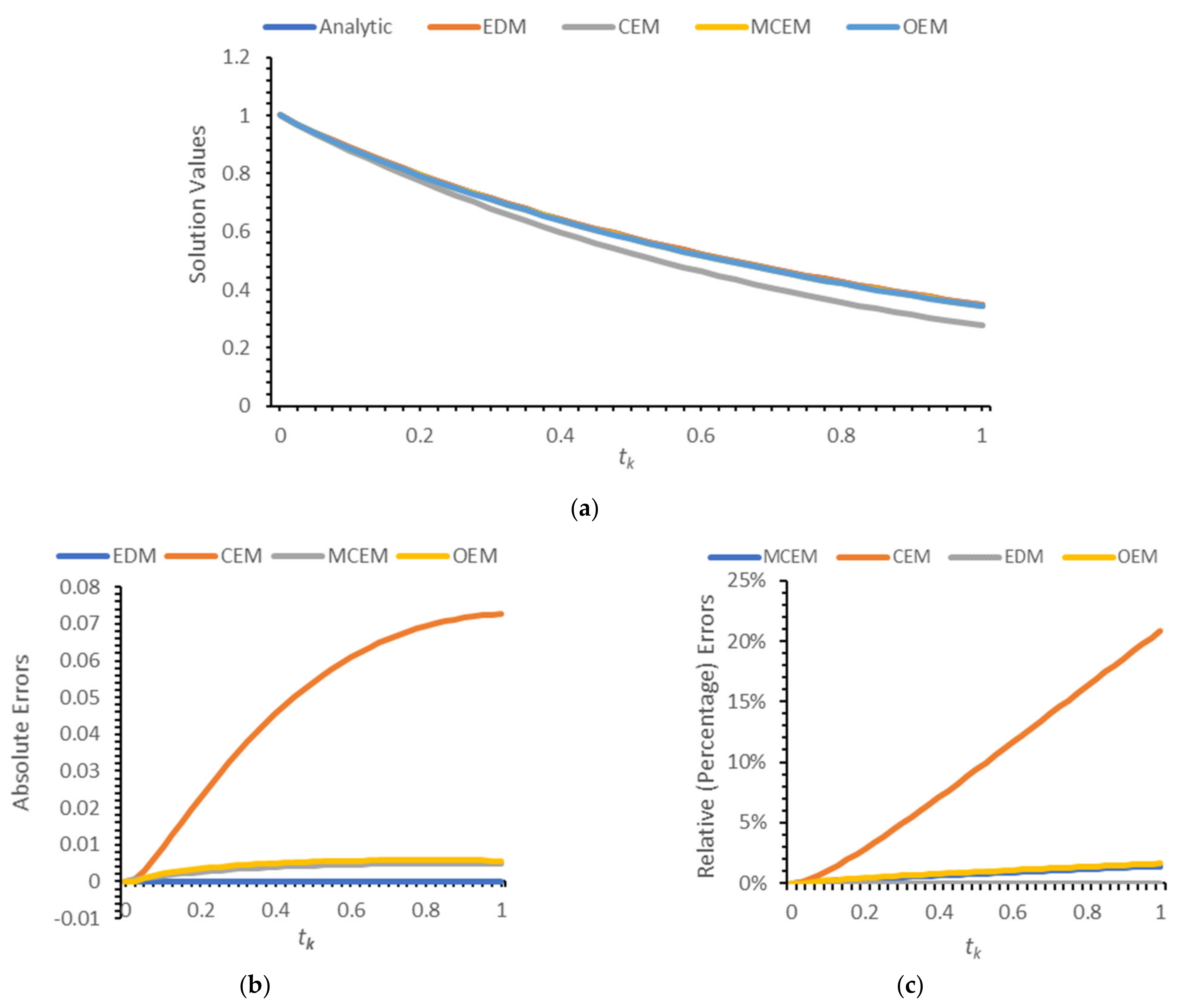
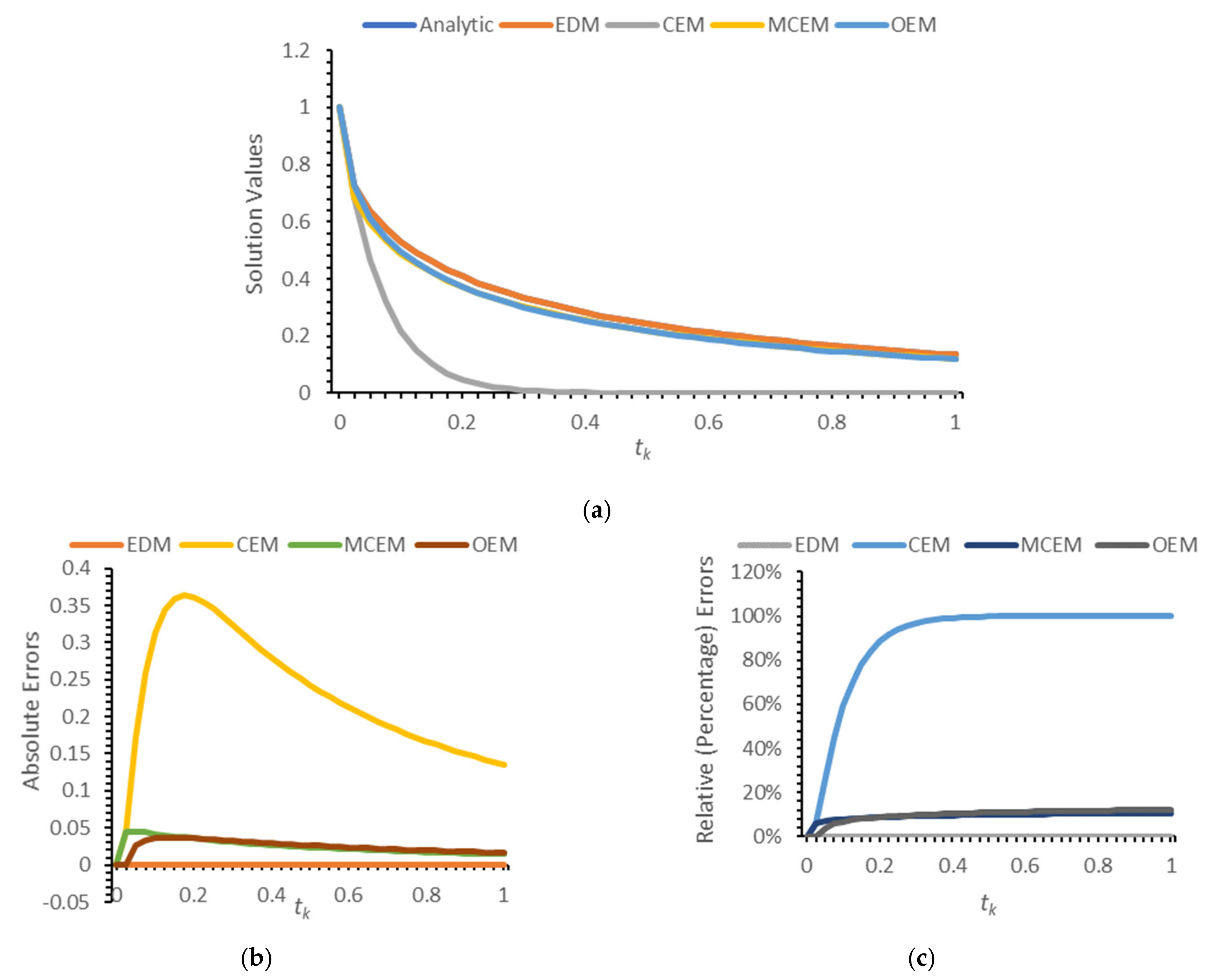
Comparisons are presented in terms of solution profiles as well as actual and relative errors for $\alpha =0.95$ in Figure 1a–c and for $\alpha =0.5$ in Figure 2a–c.

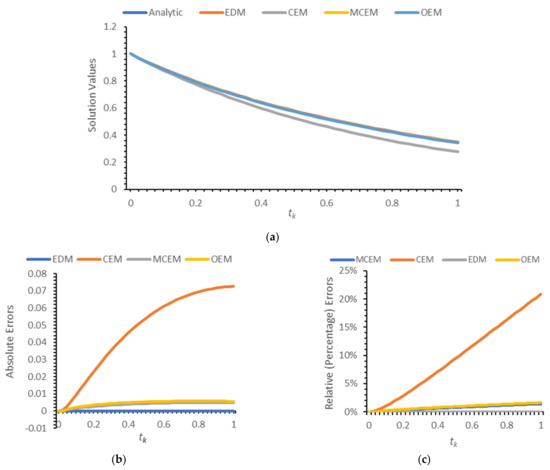
Figure 1. Analytic solution profile of (17) compared on $\left[0, 1\right]$ to approximations by the EDM, CEM, MCEM, and OEM at $\alpha =0.95$ with $h=0.025$: (a) solution values ($y_k$), (b) absolute errors ($\left|y\left(t_k\right)-y_k\right|$) and (c) relative (percentage) errors ($\frac{\left|y_k-y\left(t_k\right)\right|}{y\left(t_k\right)}\left(100\right)$).

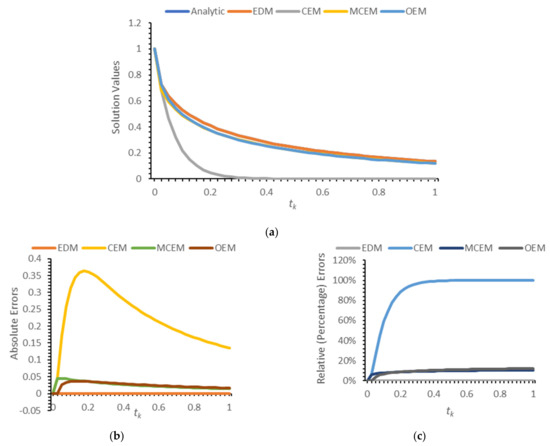
Figure 2. Analytic solution profile of (17) compared on $\left[0, 1\right]$ to approximations by the EDM, CEM, MCEM, and OEM at $\alpha =0.5$ with $h=0.025$: (a) solution values ($y_k$), (b) absolute errors ($\left|y\left(t_k\right)-y_k\right|$) and (c) relative (percentage) errors ($\frac{\left|y_k-y\left(t_k\right)\right|}{y\left(t_k\right)}\left(100\right)$).

6. Conclusions

A discretization method, termed the conformable Euler’s method, for the fractional initial value problem with the conformable fractional derivative has been considered that extends the integer Euler method to the conformable derivative. Its justification using a fractional series expansion is recalled and it is shown that the assumption ${}_0{}^{C}T_{}^{}{}_t^{\alpha }\left(f\right)\left(t\right)=t^{1-\alpha }\frac{d}{dt}f\left(t\right)$ leads to the conclusion that $\alpha =1$ in the method. The ordinary Euler method, obtained by rewriting the CFD in terms of the integer-ordered derivative, is described and its main implementation disadvantage briefly discussed. A modified conformable Euler’s method is proposed that is derived from rewriting the term of the right-hand side of the equation assumed above as a derivative quotient and then using the integer definition of the derivative.

To justify the proposed modification of the CEM, the ESDDFD method, wherein fractionality is determined by wave type behavior of processes under study, of generalized difference quotient derivative representation is recalled. An alternate definition of the CFD is presented that is derived from the analytic solution of the CRE, which describes fractional KWW wave behavior, and it is shown that it has the same basic properties and returns the same derivative values as the CFD. It is observed that the alternate definition shows that the CFD is a fractional change of variable rather that a fractional operator. The MCEM follows as a limit of, and is therefore consistent with, the exact ESDDFD representation of the CRE, whereas the CEM is not.

Numerical experiments are then presented to assess the accuracy of the CEM in approximating the solution of the CRE. The CEM model of the CRE is compared with three discrete models obtained from the ordinary Euler, modified conformable Euler, and conformable NSFD (or ESDDFD) methods. Results are presented for several values of $\alpha , 0.62\le \alpha \le 0.99$, showing errors for the four models relative to the analytic solution, as well as those of profile and error graphs for $\alpha =0.95, \alpha =0.5$. While comparisons are presented only for a few values of $\alpha$, the results displayed are typical and conclusively show that the CEM yields incorrect approximations, with respective relative errors of 5.06%, 20.80%, and 99.60% for $\alpha =0.99$, $\alpha =0.95$, and $\alpha =0.62$. In comparison, the relative errors at the same values of for the OEM and MCEM are, respectively, 1.30%, 1.62%, and 7.31% and 1.29%, 1.40%, and 4.56%; the EDM has no errors for the CRE since it is exact. Based on these numerical results, and with support of the theoretical arguments presented, it is concluded that the CEM is not a valid generalization of the standard forward Euler method to the CFD for $0<\alpha <1$, and that the MCEM and EDM offer more accurate alternative generalizations.