Platform Motions and Mooring System Coupled Solver for a Moored Floating Platform in a Wave

Abstract

In advance of building moored floating offshore platforms, in recent years, there has been a greater demand for two-way coupled simulations between a motion solver based on the viscous flow theory and a mooring line model, including cable dynamics. This paper introduces open-source libraries such as MoorDyn (the lumped-mass mooring line model) and OpenFOAM (the computational fluid dynamics libraries). It describes the methods by which they can be coupled bi-directionally. In each time step, the platform motions calculated by OpenFOAM are transferred to MoorDyn as the boundary conditions for the mooring system analysis. In contrast, MoorDyn calculates the restoring force and moment due to the mooring system and transfers them to OpenFOAM. The restoring force and moment act on the platform as the external force and moment for the platform motions in the next time step. The static tension and profile of the mooring system, dynamic tension of the mooring system, and free decay motions of the floating buoy in the still water were simulated to check the accuracy of OpenFOAM and MoorDyn. The coupled solver was used to produce simulations of the moored decay motions of the floating buoy in the still water and the moored motions with the Stokes 5th order wave. All simulation results were compared and showed good agreement with the numerical solution and experiment results. In addition, the characteristics of each solver were investigated.

1. Introduction

As land resources have become depleted, human efforts to develop new resources have turned to the oceans and have moved beyond the shallow and deep seas into the Arctic Ocean. This has led to the emergence of offshore structures such as Tension Leg Platform (TLP), SPAR, and Floating Production Storage Offloading (FPSO). Unlike ships intended to transport personnel and materials, these offshore structures are required to operate for an extended period at a fixed location. They must be capable of maintaining their positions to ensure global performance and stability even under various environmental loads such as waves, currents, winds, and so on. For the station-keeping of offshore structures, mooring systems of different types and materials can be used. As such, the proper design of the mooring system is very important and has a significant impact on global performance and stability.

Traditionally, numerical analyses based on the potential flow-based theory and quasi-static mooring models have been used to simulate the platform motions and mooring system. Though basing the numerical analyses on potential flow-based theory allows for a very fast computation speed, it cannot fully consider the viscous effects around the platform. A quasi-static mooring model does not consider the hydrodynamic forces, such as the added mass force and drag force, which cannot be neglected as the depth increases. These days, there is more interest in the viscous effects around the platform, and the mooring line model that includes the cable dynamics is more necessary as the environmental loads become increasingly severe, and the installation depths go deeper. Moreover, the two-way coupling of both solvers is also in higher demand for more accurate simulation results.

In research on the interaction between the platform motions and mooring system, the potential flow-based theory and the strip theory are still being widely used because of the fast computation speed. Masciola et al. [1] conducted a coupled simulation using Fatigue, Aerodynamics, Structures, and Turbulence (FAST) code developed by the National Renewable Energy Laboratory (FAST) and commercial mooring system analysis code OrcaFlex based on the lumped-mass model to investigate the effects of the mooring system on the motions of the semisubmersible floating offshore wind turbine (FOWT) model DeepCwind. Hall and Goupee [2] conducted the same research using FAST and a new lumped-mass mooring line model (later named MoorDyn). HydroDyn, which is FAST’s hydrodynamic analysis module, uses potential flow-based theory and strip theory to analyze the platform motions. Sirnivas et al. [3] investigated the interaction between the wave energy converter and the mooring system using Wave Energy Converter Simulator (WEC-Sim) and MoorDyn. WEC-Sim is the wave energy converter analysis code developed using MATLAB, and its hydrodynamic coefficients for platform motion analysis are obtained from the frequency-domain potential flow-based solver WADAM. Antonutti et al. [4] conducted the coupled simulation using CALcul HYdrodynamique Pour les Structures Offshore (CALHYPSO) and Code_Aster, both of which are developed by Electricé de France Research and Development (EDF R&D), to investigate the effects of the mooring model, including cable dynamics. CALHYPSO is a program that incorporates the aerodynamic, hydrostatic, hydrodynamic, inertial, and mooring forces acting on FOWT in the time-domain [5], and Code_Aster is the all-purpose structural analysis solver based on the finite element method.

Recently, analyses of the platform motions based on the viscous flow have been actively carried out by improving computational fluid dynamics (CFD) techniques and computing resources. Quallen et al. [6] investigated the interactions between the OC3-Hywind FOWT and the mooring system using CFDShip-Iowa code based on the finite difference method and quasi-static Crowfoot mooring model. Nicholls-Lee et al. [7] used the all-purpose commercial CFD code ANSYS CFX based on the finite volume method and Orcaflex to apply to the wave energy converter simulation. Tran and Kim [8] conducted a fully coupled analysis, including the aerodynamics of turbine rotor blades, hydrodynamics of semisubmersible turbine base, and mooring system for the DeepCwind FOWT model. They used the all-purpose commercial CFD code STAR-CCM+ based on the finite volume method and quasi-static catenary mooring model. Palm et al. [9]. carried out a coupled simulation for the wave energy converter using open-source CFD libraries called OpenFOAM and an in-house lumped-mass mooring cable solver called Moody based on the discontinuous Galerkin method.

This paper coupled the open-source libraries MoorDyn and OpenFOAM bi-directionally to enable a more accurate analysis for a moored platform. To couple both solvers, loose and delayed methods were selected. MoorDyn, OpenFOAM, and coupled solver were each studied individually.

This paper is organized as follows. Section 2 and Section 3 introduce a mooring system solver and a platform motion, respectively. Section 4 describes their coupling procedure. The results and discussion are presented in Section 5. Finally, some conclusions are drawn in Section 6.

2. Mooring System Solver

For mooring system analyses, MoorDyn [2] was selected. To discretize the mooring line, MoorDyn used the lumped-mass model [2]. Figure 1 shows the internal and external forces acting on the nodes. The internal forces include net buoyancy (W), tensile force (T), and internal damping force (C). The net buoyancy is the sum of the weight and buoyancy on the node, and the tensile and internal damping forces are only calculated in the axial direction. The compression forces are neglected for the tensile force, and the internal damping force plays an important role in the numerical stability. The external forces contain transverse and tangential hydrodynamic forces (D) by Morison’s equation and the seabed contact force (B). The hydrodynamic forces consist of the drag and added mass forces, and the seabed contact force was modeled as a vertical spring-damper system that acted only when the node touched down the seabed.

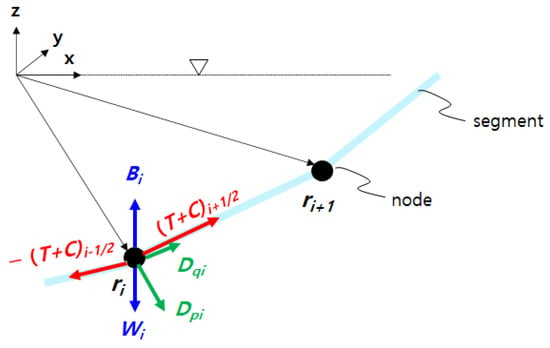
Figure 1. Internal and external forces acting on the nodes and segments.

MoorDyn has three core functions. LinesInit( ), LinesCalc( ), and LinesClose( ) are related with initialization, calculation and closing modules, respectively. Using these core functions, it can be coupled with other simulation tools easily.

3. Platform Motion Solver

To solve platform motions, open-source computational fluid dynamics libraries, called OpenFOAM version 4.1, were used.

3.1. Governing Equations

For the incompressible, multi-phase, and transient flow, the mass and momentum conservation equations can be written as

$$\nabla ·\overrightarrow{v_m}=0$$

(1)

$$\frac{\partial {\rho }_m\overrightarrow{v_m}}{\partial t}+\nabla ·({\rho }_m\overrightarrow{v_m}\overrightarrow{v_m})=-\nabla p+\nabla ·\stackrel{\overline{¯}}{\tau }+S$$

(2)

where the subscript $m$ means the mixture, and $\overrightarrow{v}$, $\rho$, and $p$ represent the velocity, density, and static pressure, respectively. $\stackrel{\overline{¯}}{\tau }$ is the viscous stress tensor, and $S$ is the source. The properties of the mixture can be represented as

$${\rho }_m=\left(1-\alpha \right){\rho }_{air}+{\alpha \rho }_{water}$$

(3)

$${\mu }_m=\left(1-\alpha \right){\mu }_{air}+\alpha {\mu }_{water}$$

(4)

where $\alpha$ and $\mu$ are the volume fraction of the water phase in the control volume and dynamic viscosity, respectively. The subscripts air and water indicate the air phase and water phase, respectively.

To detect the free surface and its motions, the volume of fluid (VOF) method was used, and the volume fraction can be calculated using the volume fraction transport equation as

$$\frac{\partial }{\partial t}\left({\alpha \rho }_m\right)+\nabla ·({\alpha \rho }_m\overrightarrow{v_m})+C_{ad}\nabla ·(\alpha \left(1-\alpha \right)\overrightarrow{v_r})=0$$

(5)

where $\alpha$ is 1 in the water phase, 0 in the air phase, and $0<\alpha <1$ in the interface region. The third term is an anti-diffusion source term that artificially reduces the solution smearing of the volume fraction transport equation [10,11,12]. In this study, the value of 0.5 was used. $\overrightarrow{v_r}$ is the artificial compression velocity for the interface.

3.2. Numerical Methods

To discretize the time derivative term, the Crank-Nicolson scheme, a second order implicit scheme, was used, and its off-centering coefficient was 0.9. For the diffusion and convection terms, the second order central differencing scheme and the total variation diminishing (TVD) scheme with a van Leer limiter were used, respectively.

The PIMPLE algorithm, which combines the Semi-Implicit Method for Pressure Linked Equation (SIMPLE) algorithm and the Pressure-Implicit with Splitting of Perators (PISO) algorithm, was used for the velocity and pressure coupling. The number of internal and external loops was 2 and 3, respectively. The renormalization group (RNG) k-ε model [13,14] with the wall function [15] was used for the turbulence closure, and the discretized algebraic equations were solved using a pointwise Gauss-Seidel iterative method with the algebraic multi-grid (AMG) solver.

3.3. Mesh Deformation

To solve the six-degrees-of-freedom motions, mesh deformation is needed, and it is calculated using a Laplace equation as

$$\nabla ·(\gamma \nabla \overrightarrow{v_p})=0$$

(6)

$$\gamma =\frac{1}{d^2}$$

(7)

where, γ is the diffusion coefficient that is quadratic inverse distance, $d$. is the distance from the wall boundaries to the center of moving meshes, and $\overrightarrow{v_p}$ is the moving velocity of a grid point that can be adjusted by the diffusion coefficient.

After the moving velocity was calculated, the mesh is deformed as

$$\overrightarrow{x_p}=\overrightarrow{x_{p0}}+\overrightarrow{v_p}\Delta t$$

(8)

where, $\overrightarrow{x_{p0}}$ and $\overrightarrow{x_p}$ are the previous and deformed positions, respectively. This method has the advantage of smoothly deforming the mesh while maintaining its orthogonality because it deforms the mesh while maintaining a constant distance ratio between the grid points.

3.4. Motion: SixDoFSolver Class

SixDoFSolvers class calculates six-degrees-of-freedom rigid body motions based on the acceleration and torque calculated for each sixDoFRigidBodyMotion class. It contains three solvers: symplectic, Crank-Nicolson, and Newmark [16] solvers.

The symplectic solver is an explicit motion solver using the second order accurate leapfrog scheme. The Crank–Nicolson and Newmark solvers are second order accurate implicit motion solvers. Free decay simulations for the heave motion were conducted to compare the characteristics of the explicit symplectic solver and the implicit Newmark solver. Figure 2 shows the accelerations of the two solvers for the heave motion. Though the accelerations of the two solvers are converged and identical after some time, their characteristics are quite different during the initial transient period. In the explicit symplectic solver, the acceleration changes monotonically in the same time step, but it oscillates between the time steps. In contrast, the acceleration of the Newmark solver oscillates in the same time step but changes monotonically between the time steps. The implicit Newmark solver is more reasonable physically, and it shows faster convergence (within the fifth time step) than the explicit symplectic solver (after the twentieth time step).

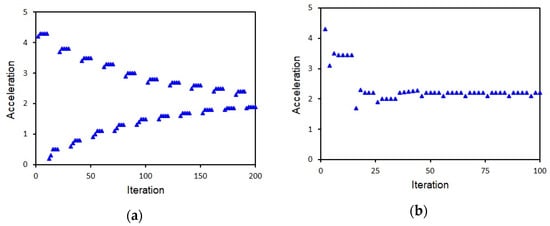
Figure 2. Convergence characteristics of explicit and implicit solvers: (a) Symplectic solver (explicit); (b) Newmark solver (implicit).

4. Two-Way Coupling Interface

The procedures of two-way coupling between the platform motions and mooring system are as follows. First, OpenFOAM transfers the six-degrees-of-freedom displacement and velocity, current time, and time step size to MoorDyn. MoorDyn calculates the fairleads’ positions, velocities, and accelerations, and all other nodes using displacement and velocity as the boundary conditions. Then, the mooring system’s tensile load and restoring force are calculated and transferred to OpenFOAM as the additional external forces acting on the platform. Finally, OpenFOAM calculates the acceleration, torque, and platform motions.

In the developed two-way coupled solver, MoorDyn was coupled to OpenFOAM as a secondary solver. Thus, the core functions in MoorDyn must be called in OpenFOAM, which is implemented by the dynamic loading of functions [17]. The core functions must be compiled into a shared library file to use the dynamic loading of the functions. As shown in Figure 3, three core functions were compiled into libmooring.so and called in OpenFOAM.

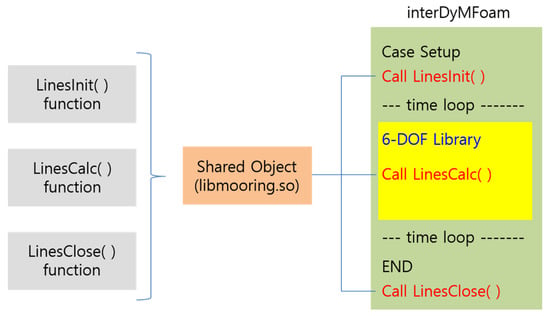
Figure 3. Dynamic loading and call of core functions in OpenFOAM.

For the two-way coupling between MoorDyn and OpenFOAM, a loose coupling method and a delayed coupling method were used in this study. Two coupling methods, loose coupling and tight coupling were generally used to couple two different solvers [18]. In the loose coupling method, all variables and data of each solver are calculated and saved in each one, and some variables are exchanged via the interface only at the coupling time, while the tight coupling method calculates and saves all variables and data in the common coupled solver, and each solver only composes its own governing equations. The loose coupling method can adopt different time step sizes for each solver for computational efficiency.

The Newmark motion solver of OpenFOAM, the implicit solver, calculates the body’s velocity first. The motions of the body later using the calculated velocity in a time step. In contrast, MoorDyn, the explicit solver, calculates the mooring tension using the velocity of the fairlead from its starting position in a time step. As such, OpenFOAM can only give MoorDyn the starting position of the fairlead in the same time step and not the velocity from the starting position when the function LinesCalc( ) is called. To resolve this problem, a delayed coupling method was used. In the delayed coupling method, as shown in Figure 4, MoorDyn uses the position (CoM) of the previous-previous time step and the velocity (V) of the previous time step to calculate the mooring system and transfers the restoring force and moment to the position of the previous time step while it works in the current time step. This resulted in a one-time-step delayed coupling, and the delayed time was 0.001 s.

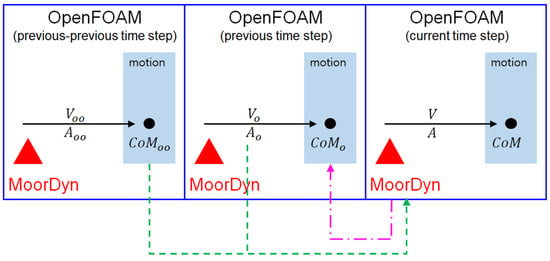
Figure 4. Concept of delayed coupling between OpenFOAM and MoorDyn: $V$ and $A$ are the velocity and the acceleration in the current timep step, respectively; The subscripts o and oo indicate the previous time step and the previous-previous time step, respectively.

5. Results and Discussion

5.1. Static Profile and Load of Mooring Line

To validate the accuracy of the static profile and a load of a mooring line, the static analysis by MoorDyn was conducted. The mooring line length, diameter, weight, and stiffness were 550 m, 0.01 m, 150 kg/m, and 5.0E6 N, respectively. The results compared with the commercial software ANSYS AQWA are presented in Figure 5. The mooring line profile of MoorDyn shows good agreement with ANSYS AQWA for the line length that is laid on the seabed and the positions of the internal nodes.

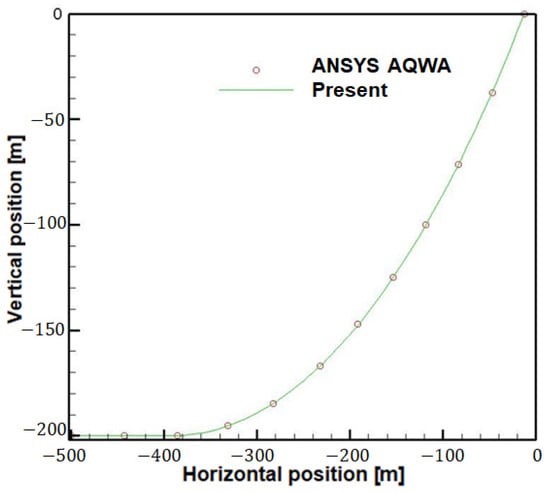
Figure 5. Static profile of mooring line.

5.2. Dynamic Load of Mooring Line

The dynamic analysis was conducted to validate the accuracy of the dynamic load of a mooring line, and the result was compared with the experimental data [19]. The experimental setup is illustrated in Figure 6, and the properties of the mooring line are summarized in Table 1. The experiments were performed in a tank with a depth of 3 m. The lower end of the mooring line was fixed on the bottom of the tank, and the upper end was fixed on the disk rotated by an electric motor. The center of rotation of the disk was located 0.3 m above the free surface. The experiments were performed while varying the distance from the center of rotation to the fixed point of the upper end of the mooring line and the disk’s rotation speed. For the validation case, the distance of 0.2 m and rotational period of 3.5 s was selected.

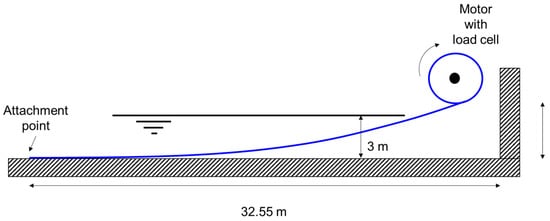
Figure 6. Experimental setup for a dynamic load test.

Table 1. Properties of mooring line for dynamic load.

Properties	Values	Properties	Values
Horizontal span (m)	32.554	Normal drag coefficient (-)	1.6
Vertical span (m)	3.1	Tangential drag coefficient (-)	0.1
Line length (m)	33	Normal added mass coefficient (-)	1.0
Line diameter (m)	3.65 × 10−3	Tangential added mass coefficient (-)	0.0
Line weight (kg/m)	8.18 × 10−2	Bottom stiffness (Pa/m)	3.0 × 106
Stiffness (N)	1.0 × 104	Bottom damping coefficient (Pa∙s/m)	3.0 × 105

Acomparison of the simulation result and the experimental data [19] is shown in Figure 7. The dynamic load’s period, magnitude, and pattern showed good agreement with the experiment results, which means that all dynamic effects are reflected well. The dynamic load tends to oscillate slightly in the slack mooring region, which may be due to the influence of the mooring line discretization.

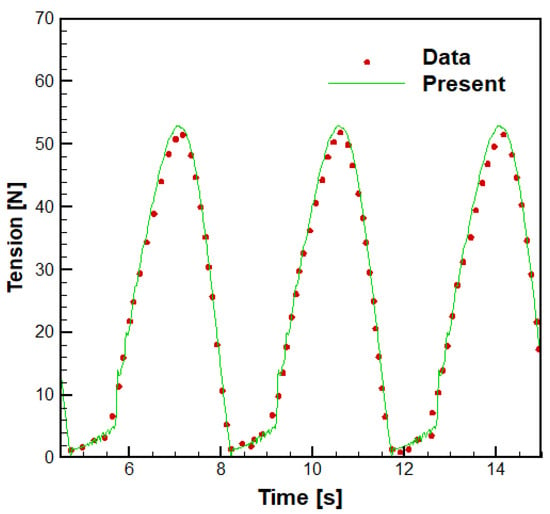
Figure 7. Dynamic load of the mooring line.

The seabed was modeled as a spring-damper system [2]. The seabed contact force of the node i ($B_i$) can be written as

$$B_i=dl\left[\left(z_{bottom}-z_i\right)k_b-{\dot{z}}_i{c}_b\right]{\widehat{e}}_z$$

(9)

where $d$ and $l$ represent the diameter and segment length of the mooring line, respectively. $z_{bottom}$ and $z_i$ are the vertical coordinates of the seabed and node i, respectively, and ${\dot{z}}_i$ means the vertical velocity of node i. $k_b$ and $c_b$ represent the stiffness and damping coefficients per unit area of the seabed, respectively. ${\widehat{e}}_z$ is the unit vector in the positive z-direction, so the seabed contact force acts in the upward direction only when the node i touches the seabed ($z_{bottom}\ge z_i)$. The stiffness coefficient supports the nodes so that they are located on the seabed. The positions of the nodes for various stiffnesses in the seabed model are shown in Figure 8. The stiffness of the seabed model must be sufficient to support the nodes at the seabed location against the net buoyancy, which is the sum of the weight and buoyancy of the node [20]. If the stiffness is not sufficient, the cable simply hangs in the air with two endpoints that are fixed; if the stiffness is sufficient, the nodes are located at the specified location as if the seabed is actually presented.

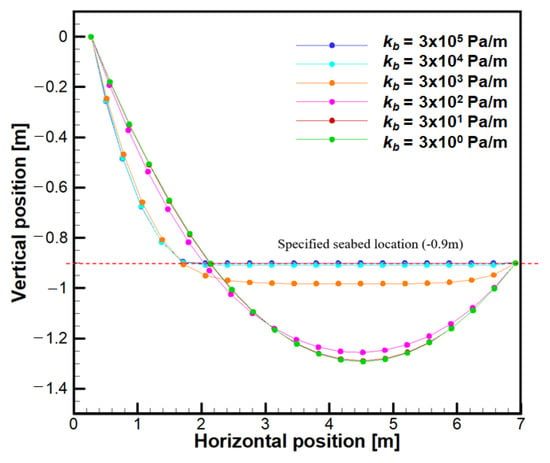
Figure 8. Node positions for various seabed stiffnesses.

The fairlead tensions for various damping coefficients in the seabed model are shown in Figure 9 when the fairlead rises at a constant velocity. The damping coefficient causes to dissipate the kinetic energy and the static friction when the node touches and is lifted from the seabed, respectively. When the damping coefficient is excessively large, a significant discontinuous region appears in the fairlead tension. This is because excessive frictional force is applied when the node is lifted from the seabed, which is quite different from what appears in a real mooring line. In contrast, when the damping coefficient is very small, the fairlead tension appears to oscillate. When the node is lifted from the seabed, there is a small dissipation for the kinetic energy delivered to the adjacent node.

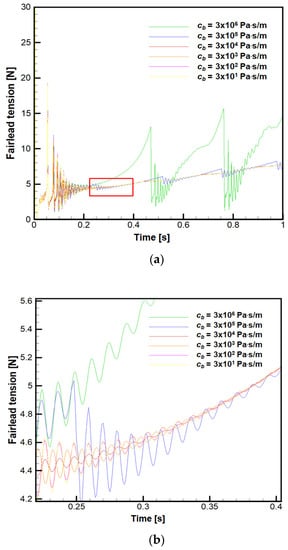
Figure 9. Fairlead tension for various seabed damping coefficients: (a) Global view for discontinuity of fairlead tension; (b) Local view for oscillation of fairlead tension.

5.3. Free Decay Motion in Still Water

To evaluate the motions of a floating body, free decay tests in still water were conducted and compared with the experimental data [9,21]. The experiments were conducted with the cylindrical buoy in the wave tank of 15 m length, 5 m width, and 1.8 m depth, and the water depth was 0.9 m. The mass, diameter, height, and moment of inertia of the buoy were 35.85 kg, 0.515 m, 0.401 m, and 0.9 kg∙m². The laminar flow condition was used because the velocity of the cylindrical buoy was very small. The analyses were performed until 4.5 s with the fixed time step size of 0.001 s, and the results compared with the experiment were shown in Figure 10. The heave motion showed good agreement with the experimental data. The period during four periods of 1.112 s. agreed well with the measured one of 1.110 s.

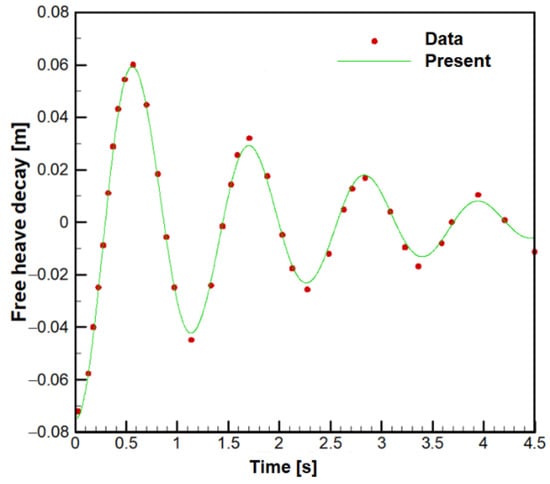
Figure 10. Free heave decay motions in still water.

5.4. Moored Decay Motion in Still Water

To evaluate the accuracy of the two-way coupled solver, moored decay tests were conducted in still water. The same conditions and properties used in the scenario of the free decay in still water were applied.

The mooring system consists of three catenary chain mooring lines, and each line was installed at 120-degree intervals. The fairleads were located at the water level and installed 0.015 m away from the surface of the buoy. Each chain was divided into 30 segments, and the calculational nodes of the mooring lines are shown in Figure 11. The properties of the mooring line were summarized in Table 2 [2,9,21].

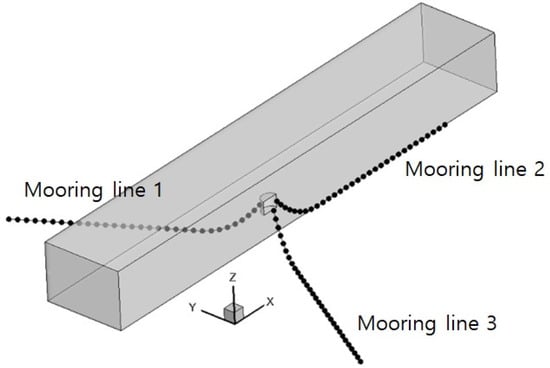
Figure 11. Calculational nodes of mooring lines.

Table 2. Mooring properties and environmental parameters for moored decay test.

Properties	Values	Properties	Values
Horizontal span (m)	6.66	Normal drag coefficient (-)	1.08
Vertical span (m)	0.9	Tangential drag coefficient (-)	0.213
Line length (m)	6.95	Normal added mass coefficient (-)	0.865
Line diameter (m)	4.786 × 10−3	Tangential added mass coefficient (-)	0.269
Line weight (kg/m)	0.1447	Bottom stiffness (Pa/m)	3.0 × 106
Stiffness (N)	1.6 × 106	Bottom damping coefficient (Pa∙s/m)	3.0 × 104

The analyses were performed until 4.5 s with the fixed time step size of 0.001 s for the heave motion. The results compared with the experiment [9,21] are shown in Figure 12. The moored heave motion showed good agreement with experimental data in the period and amplitude, but the equilibrium position of the motion tended to be slightly downward. It seems that the numerical conditions did not consider the increased draft caused by the addition of the mooring system. The average period during the four periods was 1.130 s, which was similar to the measured one of 1.114 s.

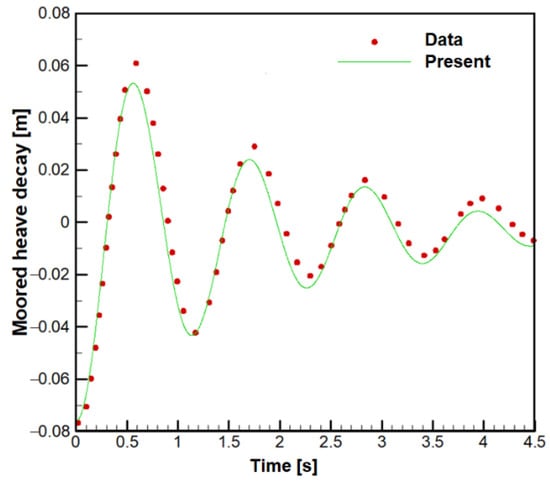
Figure 12. Moored heave decay motion in still water.

5.5. Moored Motion in Wave

To evaluate the two-way coupled solver’s accuracy, the moored motions’ simulation in a wave and tensile loads of the mooring system was conducted. The properties of the mooring line used were summarized in Table 2. The Stokes 5th order wave was generated, and its properties were listed in Table 3. All numerical methods were identical with the case of the moored decay motions only, except that the RNG k-ε model and wave generation condition on inlet were applied instead of the laminar flow and still water conditions, respectively. In addition to the inlet and outlet boundaries, the relaxation zones whose lengths were 3 m (one wavelength) and 6 m (two wavelengths) were set to generate and absorb the wave effectively, respectively. More than 140 and 22 meshes per wavelength and height were located in the wave region to detect the free surface accurately. These numbers exceed the International Towing Tank Conference [22] guideline, which specifies 80 and 20 meshes per wavelength and height, respectively.

Table 3. Description of Stokes 5th order wave.

Properties	Values
Period (s)	1.4
Wave height (m)	0.08
Wavelength (m)	2.94
Reynolds number (-)	0.925 × 105
Keulegan-Carpenter number (-)	0.488

The initial buoy position and free surface for the moored buoy in the wave are shown in Figure 13, and the wavefield was initialized with the wave profile to reduce the computation time. The initial buoy position was the equilibrium position in still water. The analysis was performed until 65 s (about 46 periods) with the fixed time step size of 0.001 s to eliminate transient features that may arise in the early stage of the simulation.

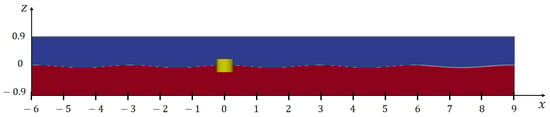
Figure 13. Initial buoy position and free surface for a moored buoy in wave.

Figure 14 shows the moored motions of the buoy in the wave. The heave motion shows good agreement with the experiment results [21] both in the amplitude and period of the motion, but the surge and pitch motions show good agreement only in the period. The overestimated viscous effect causes the small amplitude of the pitch motion at the cylinder edge. For the surge motion, the result shows a larger drift motion in the positive (leeward) direction than the experimental data. It seems that the non-zero Stokes drift velocity, which was defined in the wave parameter, generated additional drift force on the buoy.

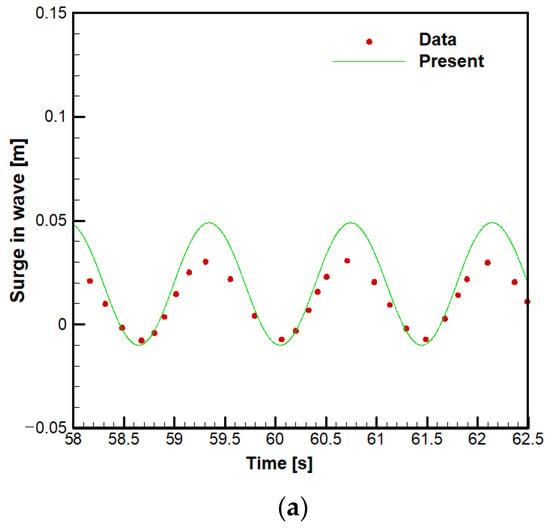
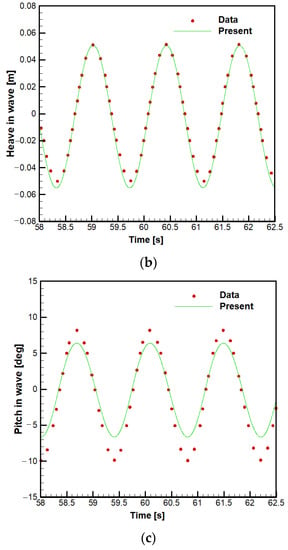
Figure 14. Moored motions in wave: (a) Moored surge motion in wave; (b) Moored heave motion in wave; (c) Moored pitch motion in wave.

The fairlead tensions in the mooring lines are shown in Figure 15. The fairlead tensions of mooring line 1 (symmetric with the mooring line 3) on the seaward side and mooring line 2 on the leeward side were compared with the experiment results. They show good agreement in the amplitude, period, and pattern of the tension. Mooring line 1 shows a larger fairlead tension than mooring line 2 because the drift motion was generated from the equilibrium position to the leeward side. The pattern of the fairlead tensions also shows good agreement with the experiment and the local humps of the tension shown in the region in which the fairlead tension increases were predicted very well. In addition, local humps of the fairlead tension appeared when the direction of the surge and pitch motions is changed, and then the velocity increases, which seemed to be due to the increase in the transverse drag force of the mooring line the angle of the mooring line changes.

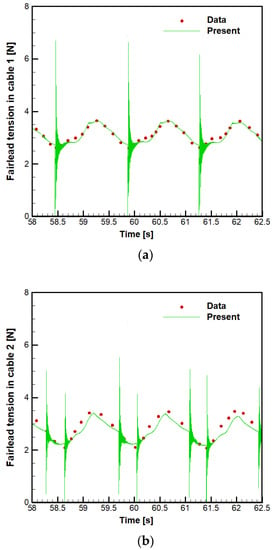
Figure 15. Fairlead tensions of moored buoy: (a) Fairlead tension in mooring line 1; (b) Fairlead tension in mooring line 2.

In the region with low fairlead tension, strange noises appeared. To analyze them, the fairlead tensions and vertical locations of the mooring line nodes were scaled and shown in Figure 16. It was found that these noises are generated when the mooring line nodes touch the seabed. In the case of mooring line 1, the noise appeared once during one period, and it appeared when the twenty-second node touched the seabed. During the same period, the twenty-third node never touched it. In the case of mooring line 2, the noises appeared twice during one period and appeared when the twenty-second and twenty-third nodes touched the seabed, alternatively. It seemed that the noises’ appearance is related to the mooring line discretization and the characteristics of MoorDyn, which ignores the bending moment and compression force acting on the mooring line. The noises can be minimized by properly selecting the stiffness and damping coefficients of the seabed model. Since these noises disappeared within a short time and the fairlead tension was immediately restored to the normal condition, the effect on the motions of the buoy seemed to be insignificant.

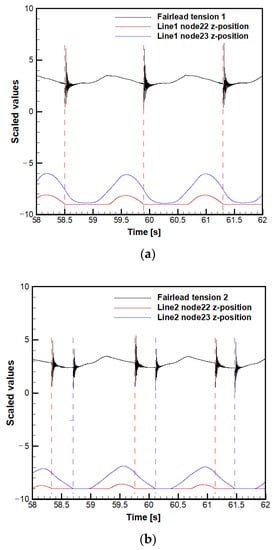
Figure 16. Noise analyses in tensions of moored buoy: (a) Mooring line 1; (b) Mooring line 2.

6. Conclusions

In this study, the two-way coupled solver between the platform motions and mooring system was developed using open-source libraries such as OpenFOAM and MoorDyn. For the coupling of the platform motions and the tensile load of the mooring system, the loose coupling method, which exchanges required data only at the coupling time step, was used. To ensure the consistency of the position and time synchronization between the two coupled solvers, the delayed coupling method was used because the manner of the time progressing of both solvers is different. In this method, the restoring force and moment of the current time step are calculated using the platform position of the previous-previous time step and the platform velocity of the previous time step; then, they act on the platform’s center of rotation of the previous time step.

Various simulations were conducted to validate the two solvers and coupled solver, and their results were compared with the numerical solution and experiment data. The accuracy of MoorDyn was validated through the simulations of the static tension and profile of the mooring system and the dynamic tension of the mooring system. The accuracy of OpenFOAM was validated through the simulations of the free decay motions of the floating buoy in the still water. In the simulation of the coupled solver, the accuracy was validated by the moored decay motions of the floating buoy in the still water and the moored motions and fairlead tensions in the Stokes 5th order wave.

In operating a two-way coupled solver, the time step size of MoorDyn should generally be smaller than a tenth of that of OpenFOAM, i.e., coupling time step, to eliminate the numerical instability due to its discretized mooring system model, which is treated explicitly. It should be adjusted according to the length of the mooring line, stiffness, number of nodes, and so on. In addition, to minimize the noise in the fairlead tension, the coefficients of the seabed model should be selected appropriately, so the nodes do not oscillate on the seabed and sink below it.