Optimum Design of Blank Dimensions Guided by a Business Compass in the Machining Process

Abstract

Blanks, an important raw material for the manufacturing industry, are semi-finished products for further processing. The energy consumption and processing efficiency in the process of blank production and use can be determined to a great extent in the blank design stage. The design of appropriate blank dimensions is an important means of realizing ecological civilization. Current blank designs seldom consider the production conditions of enterprises. In order to design energy-saving and efficient blanks on the basis of the actual conditions of an enterprise, this paper establishes the blank dimension optimization design model from the perspective of a business compass. With energy savings and efficiency as the goals, and the blank production and use-process equipment parameters as variables, the blank dimensions were optimized by an NSGA-II algorithm, and the results showed that the energy efficiency and processing efficiency of the designed blank dimensions were significantly better than for the existing blank dimensions in the process of enterprise operation.

1. Introduction

Nowadays, blank-dimension design is being given increasing expectations for achieving energy efficiency and emission reductions. According to statistics, 90% of energy consumption and release of 84% of CO₂ emissions in the industrial sector is attributable to the manufacturing industry [1,2]. Blank dimensions are the link between the production and use of blanks, and the energy consumption in the process of production and use of blanks accounts for more than 80% of the energy consumption in the manufacturing industry. It is worth mentioning that the blank design stage is very important, and can determine the energy consumption of more than 80% of the blank process [3,4]. The research of optimization of blank-dimension design has attracted extensive attention because it can determine the energy consumption and efficiency. To solve the problems, scholars have made many efforts, such as constructing a set of indicators and policies promoting various optimization methods [5]. The finite element method (FEM) is widely used for optimization of blank-dimension design, such as predicting deformation behavior and simulating the features of NURBS surfaces [6,7]. Through finite element analysis (FEA), Kuwabara et al. computer-program-optimized the shape of a blank [8]. Lee used a 3D multi-step backward AFE method to design a blank’s shape [9]. Qian presented four blank design results that provided a validated rectangular cross-section design in the experiment [10]. In addition, artificial neural networks (ANNs) and support vector regression (SVR) have been used to optimize the polygon blank shape [11,12]. Kitayama et al. optimized both the segmented VBHF trajectories and a blank’s shape [13]. Aminzadeh et al. applied multi-objective optimization (MOO) based on a genetic algorithm to optimize design input parameters using drawing depth, weld-line movement, and energy absorption as objective functions [14]. Mahmood et al. optimized the blank shape to provide flange-free micro-square products with a net shape and using FES with commercial code [15]. Zhu et al. developed a unified viscoplastic-Hosford-MK (UVH) model to optimize the initial blank shape through the analysis of the strain rate, evolutionary temperature, and loading path of failure regions [16]. Radonjic et al. applied a new method to significantly reduce the spring band using the alternation draw-in of a blank, and conducted hat channel part geometry using FEA with the simulation code [17]. Cheng et al. presented a multi-objective, reliability-based design optimization (MORBDO) method to optimize a blank design and combined it with NSGA-II to search for the optimal reliable program [18]. Clearly, each coin has two sides. Different methods of blank structure design have different advantages.

In addition, according to the blank production conditions for blank dimension optimization design, there is also the optimization of blank processing energy and time. Cai et al. promoted a set of policies and standards based on lean-type energy-saving measures and sustainable development [19,20,21]. Li et al., through a multi-objective optimization model, optimized processing speed and energy, which markedly saved processing energy and time [22]. A novel energy-saving method for ring parts was presented by Li et al. [23]. Wang et al. established a non-dominated genetic algorithm-II (NSGA-II) for a cutting process to achieve the goals of low energy consumption, low cost, and high quality [24]. Li et al. established an optimization mathematical model using a simulated annealing algorithm (SAA) to minimize the energy consumption of a blank’s processing [24]. Wei et al. minimized welding-energy consumption and maximized thermal efficiency using the fitness-sharing genetic algorithm (FSGA) compared with the general genetic algorithm solution [25]. Lu et al. established a multi-objective backtracking search algorithm (MOBSA) to minimize energy consumption while keeping high processing quality [26]. Meanwhile, Kant et al. applied grey correlation analysis (GCA), principal component analysis (PCA), and RSM to decrease the solution energy consumption and maintain high surface quality [27]. Wang et al. proposed an intelligent generation algorithm of a working step chain and combined it with a particle-swarm optimization algorithm to solve the optimization model aimed at solving today’s sustainable development concept [28]. Hong et al. established the empirical parametric models of different machining phases to optimize parameters and machining allowance distribution with full consideration of energy-saving strategies and other multi-objectives [29]. Wang reported an energy-consumption calculation method by traversing the feature parameter of NC code [30]. Xiao et al. found that the appropriate blank dimension could be better ensured after the consideration of minimum energy, cost, and time with the comparison of the optimization of energy consumption and cost [31]. Duan et al. established a mathematical model of double-resource constraint (DRC) and multi-objective optimal scheduling (MOS) with minimum machine processing energy consumption, maximum completion time, and overhead traveling crane energy consumption as the optimization objectives [32].

In general, various optimized methods have been promoted by many scholars to analyze blank dimension design and then select the blank’s dimensions to reduce energy consumption and the time of blank production and processing. Blanks are objects in need of further processing, and blank dimension is a transition parameter, so a lot of blank energy-saving research chooses the appropriate blank dimension from a good blank to optimize the next processing parameters. However, it is difficult to match the blank dimension with the actual situation of the enterprise. At present, the traditional blank dimensions are a series of standard dimensions given according to the relevant national regulations. These dimensions are used for the selection of a blank’s use process. The selected blank dimensions cannot guarantee the minimum energy consumption in the blank’s processing. In the process of blank-dimension design, few studies take into account the actual situation of the enterprises using the blank, and the design of the blank’s dimensions to meet energy-saving needs to the greatest extent is difficult.

Based on the above discussion, this paper proposes an improved optimum design method of blank dimensions guided by a business compass in the machining process. In this method, energy consumption and time are set as optimization objectives, and the processing parameters of the equipment are variables. This model was optimized by NSGA-II. The blank dimensions that best met the actual production requirements of the enterprise were optimized and calculated.

2. Blank-Dimension Design and the Business Compass

2.1. Blank-Dimension Design

A blank is a semi-finished product designed to be processed into a work piece. The dimensions of the blank appear in the production process and disappear after it is used. The dimensions of the blank are an important link between the production process and the use process. The dimensions of the blank determines the operation process of the blank production and use enterprise, including processing technology, the selection of processing equipment, the establishment of processing procedures, and the optimization of processing parameters. Blank-dimension design is a complex system, not only for the blank production and use process’s equipment, participation, and determination of production goals, but also for the enterprise’s overall planning, department planning, operator technology, and many other factors; the relationship is shown in Figure 1. It involves coordinating with related departments, arranging personnel and equipment according to production quantities, and the general target of the enterprise. Blank-dimension optimization based on enterprise is a complex system engineering pursuit that needs to strengthen the top-level design and overall planning of enterprise, and strengthen the connection of relevance, systematism, and feasibility studies. Based on the determination of the blank-dimension design’s objective, the relationship between each factor and the coupling relationship between each factor are studied in order to promote each other in the implementation process and obtain the best actual effect.

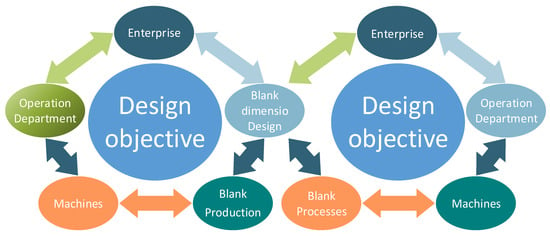
Figure 1. Blank-dimension design and enterprise operation.

2.2. Business Compass

A business compass is a people-oriented business thinking system based on all-new perspectives. It serves as a corporate tool of top-level design. The five dimensions of the business compass, which connote the five elements in ancient Chinese philosophy, are at the core of management theory and practice; Figure 2 shows the relationship. These elements, wood, fire, earth, metal and water, comprise a systemic worldview typical of Taoist philosophy. Joseph Needham believed that Taoist philosophy developed many of the most important features of the scientific attitude [33]. Chen explained that “Tao” is the cause of all things, but is itself not subject to any cause [34]. Regarded as fundamental elements of all things in the world, the five elements theory looks at the world’s temporal–spatial structure with insights, and depicts how things are generated and come into being as a relationship of coexistence and inter-restriction as well, which is shown in Table 1 and Table 2. The five dimensions; namely, trend, law, measure, implement, and interest, are symbolic of corporate management in that they constitute the five elements of a business activity and define the genesis and operation of an enterprise in the temporal and spatial dimensions. The five dimensions can be adopted to depict the specific problem and provide solutions for it in corporate management. When identified, the relationship of coexistence, coordination and inter-restraining can be used to cope with more systematic problems when it comes to competition and cooperation [35]. Business compass and blank-dimension design in enterprise operation is shown in Figure 3.

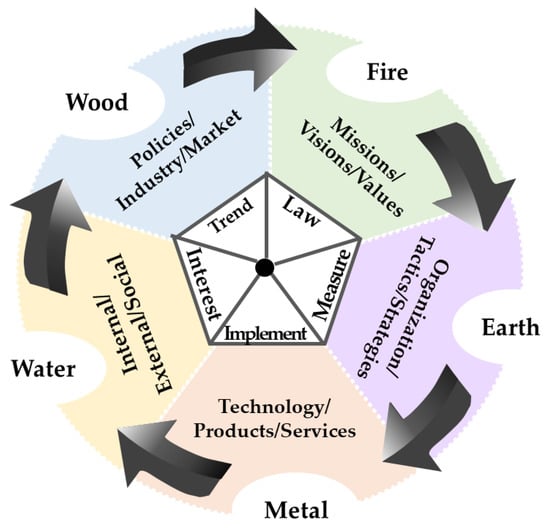
Figure 2. The five dimensions of the business compass.

Table 1. The coexisting relationship among the five dimensions of the business compass.

Five Dimensions of the Business Compass: Interest→Law→Implement→Trend→Measure		Five Elements of Ancient Chinese Philosophy: Water→Fire→Metal→Wood→Earth
Trend can generate law	When conditions emerge, call partners with lofty ideals to create career together. New trend will produce new class and new class will have new dreams.	Wood can generate fire
Law can generate measure	Missions, visions and values are like a massive stone against invasion of temptation. They serve as the guiding ideology, action program, operation guideline and conduct standard of an enterprise.	Fire can generate earth
Measure can generate implement	Strategies, tactics and organization are the guarantee for an enterprise to release new products or services with competitiveness to the market. They change with the market.	Earth can generate metal
Implement can generate interest	Products or services with strong competitiveness is the base of interest maximization. They are the start and result of corporative business activities which strive for fame and interest.	Metal can generate water
Interest can generate trend	Interest obtainer incurs interest contender. Rebirth generates new trend. New trend results in interest changes. Such conditions circulate without end.	Water can generate wood

Table 2. The restricting relationship among the five dimensions of the business compass (BC model).

Five Dimensions of the Business Compass: Interest→Law→Implement→Trend→Measure		Five Elements of Ancient Chinese Philosophy: Water→Fire→Metal→Wood→Earth
Interest can restrain law	A rational interest allocation mechanism and an incentive mechanism against improper interests will keep an enterprise to its course and true to its values.	Water can restrict fire
Law can restrain implement	Missions, visions and values of an enterprise restrain the enterprise from deviating from its predetermined technical and product development routes.	Fire can restrict metal
Implement can restrain trend	Technical and product innovation capability and market competitiveness guides the trend and market needs.	Metal can restrict wood
Trend can restrain measure	The external environment (institutional policy trend, industrial business trend, market trend) can restrict the strategic correctness, tactic power and organizational execution of an enterprise.	Wood can restrict earth
Measure can restrain interest	Strategic correctness, tactical effectiveness and organizational fitness directly affect revenue level and contain profitability of an enterprise.	Earth can restrict water

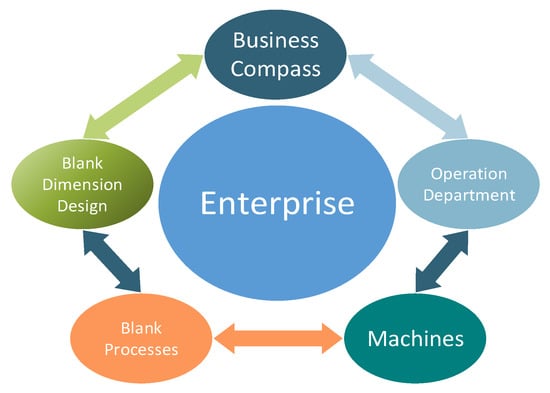
Figure 3. Business compass and blank-dimension design in enterprise operation.

2.3. Overall Research Framework

Based on the above review, blank-dimension design is related to many factors of two kinds of enterprises, and the relationship between them is complex and difficult to coordinate. The business compass is taken as the guide to coordinate the process elements to achieve the optimal design of blank dimensions. Figure 4 shows the framework of this study.

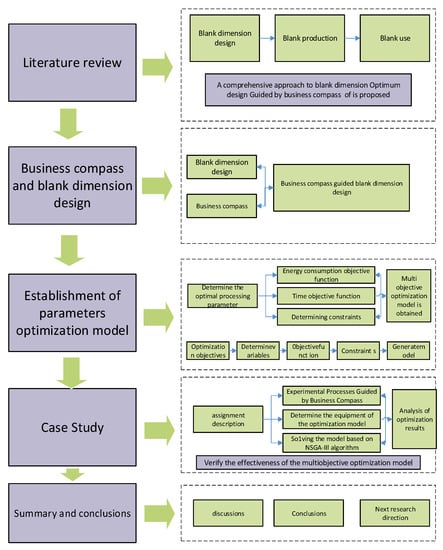
Figure 4. Overall research framework.

3. Establishment of Blank-Dimension Design Model

Blank dimensions are parameters related to objective of the production process. The blank dimensions can be calculated by optimizing the production process.

3.1. The Energy Objective

Energy, including blank production stage rolling energy consumption $E_Z$ and further processing energy consumption $E_M$ is shown in Equation (1):

$$E=E_Z+E_M$$

(1)

According to Zhang et al. [36], $E_Z$ can be expressed as:

$$E_Z={{\displaystyle \sum }}_{t=1}^n{q}_t={{\displaystyle \sum }}_{t=1}^n{M}_t{v}_t{\tau }_t/D_t$$

(2)

where t of the rolling pass moment, rolling speed, rolling time, and rolling energy consumption are respectively represented as $M_t$, $v_t$, ${\tau }_t$, and $q_t$. $D_t$ is the roll working diameter, a is the coefficient, and n is the rolling pass. The total rolling energy consumption should be minimized by rolling passes from raw material to finished product. This can achieve the purpose of saving energy and reducing production time. Rolling passes are variables related to total elongation coefficient and average elongation coefficient, in which total elongation coefficient is an average elongation coefficient.

$$n=\frac{log\left(u_z\right)}{log\left(u_p\right)}$$

(3)

$$u_z=\frac{F_0}{F_n}=\frac{{\left(a_t{A}_t\right)}^2-0.86\times {\left(0.1\times a_t{A}_t\right)}^2}{\pi \times {\left(D{a}_t\right)}^2/4}$$

(4)

The thermal expansion coefficient is $a_t$, the billet side length is $A_t$, the blank diameter is $D,$ and the section area of the red billet and finished product $\mathrm{is}{F}_0$ and $F_n$, respectively.

According to Xiao et al. [31,37], turning energy consumption can be written as Equation (5):

$$\begin{array}{l}{E}_M={\mathrm{p}}_0{t}_1+\left(p_0+(1+a_1)\frac{C_{Fc}{(\frac{D-d}{2})}^{x_{Fc}}{f}^{y_{Fc}}{v}_c^{n_{Fc}}{K}_{Fc}{v}_c}{6\times {10}^4}+a_2{(\frac{C_{Fc}{(\frac{D-d}{2})}^{x_{Fc}}{f}^{y_{Fc}}{v}_c^{n_{Fc}}{K}_{Fc}{v}_c}{6\times {10}^4})}^2\right)t_2+{\mathrm{p}}_0{t}_3(\frac{t_2}{T})+y_E(\frac{t_2}{T})\\ \end{array}$$

(5)

Total energy consumption can be represented as Equation (6):

$$E={{\displaystyle \sum }}_{t=1}^n\frac{M_t{v}_t{\tau }_t}{D_t}+E_M$$

(6)

3.2. The Time Objective

Time objective is expressed as:

$$T_{}=T_U+T_P$$

(7)

where $T_U$ is the total blank production time and $T_P$ is the blank production time.

$$T_p=t_m+t_d\frac{t_m}{T}+t_0$$

(8)

$$T_p=\frac{60l}{nf}(1+\frac{t_d}{T})+t_0$$

(9)

where $t_m$ is the processing time and $t_m=\frac{60L}{nf}$, L is the workpiece length. T is the tool durability, v is the cutting speed, D is the cutting diameter, $t_d$ is the tool adjustment time, $\frac{t_m}{T}$ is the integer minimum in machining, and $t_0$ is the auxiliary time. The time objective is:

$$T=T_U+\frac{60l}{nf}(1+\frac{t_d}{T})+t_0$$

(10)

4. Constraints

The constraints to be considered in the blank-design process are as follows:

$$\alpha \le {\alpha }_{max}$$

(11)

The actual bite angle is $\alpha$ is and ${\alpha }_{max}$ is the maximum bite angle

$${\beta }_{min}<\beta <{\beta }_{max}$$

(12)

$$\frac{\pi \times d_0\times n_{min}}{1000}\le v\le \frac{\pi \times d_0\times n_{max}}{1000}$$

(13)

The extreme values for the machine tool spindle are $n_{min}$ and $n_{max}$.

$$f_{min}<f<f_{max}$$

(14)

The extreme values of the machine feed are $f_{min}$ and $f_{max}$.

$$F<F_{max}$$

(15)

The maximum cutting force is $F_{\max }$.

$$P\le \mu P_{max}$$

(16)

The power effective coefficient is μ and the maximum effective cutting power is $P_{max}$.

$$R\le R_{max}$$

(17)

The maximum allowable surface roughness is $R_{max}$.

5. Case Study

5.1. Background of the Optimization Problem

The number of required shafts is 100,000, and the shaft dimensions are shown in Figure 5. We designed the blank dimension according to the situation of the factory.

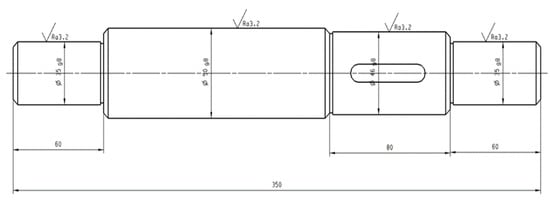
Figure 5. Work dimensions.

5.2. Experimental Processes Guided by a Business Compass

Blank-dimension design needs to coordinate various factors of blank production and blank use, including people, equipment, material environment, etc. of the two enterprises. The business-compass model is the top management mode of the enterprise, and can coordinate the total profit cooperation of relevant personnel, equipment, etc. of the two enterprises in blank-dimension design. Only the top support can ensure the actual effect of blank-dimension design.

The factory equipment is the basis of enterprise operation and management, and also the premise of blank-dimension design. The factory blank-processing equipment was a CNC lathe. According to the existing situation of machine tools, we chose the most suitable one. The entire experimental environment of blank-dimension design is shown in Figure 6.

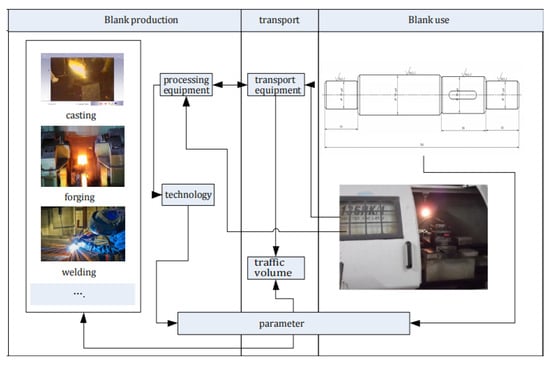
Figure 6. Requirements of blank-dimension design.

From the point of view of the processing task, it belongs to batch production with loading and unloading materials, and the processing procedures are the same as the processing requirements. Experience-based processing of this type of ladder shaft is generally not less than 5 min, and the problem of material loading and unloading exists in the process of parts processing; according to experience, the manual loading time is usually less than 20 s. An experienced employee can control 5–8 machines at the same time. According to the human-oriented idea of the business compass, to avoid overwork, one person should control three machines at the same time. The enterprise intended to dedicate nine lathes to the use of blanks, of which every three were arranged in a zigzag pattern, as shown in Figure 7. The workshop adopted a double-shift mode; each shift had 11 h of working time and one hour for adjustment [38,39].

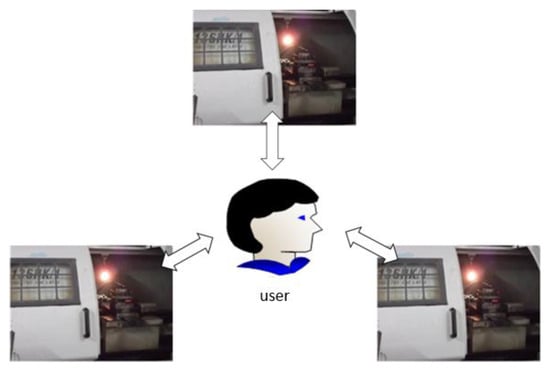
Figure 7. Machine controlled by an operator.

In the blank-production stage, the former work of steel forming was basically the same, so no adjustment was made here. The most important forming process of dimensions was the use of 22 rolling mills, which were divided into roughing, neutralizing, and finishing. The billet used was 45 steel with 165 mm in length and width, and the rolling mill was composed of 4-6-6-6.

5.3. NSGA-II Algorithm Simulation for the Optimization Model

The NSGA-II algorithm is widely used in solving multi-objective optimization problems in engineering practice. Generally, the population dimension and generation can be selected according to the experiment. After thousands of experiments, the population selected had 100 dimensions. Algebra is generally between 10 and 500. After thousands of tests, 100 was selected as the code. In addition, the cross-pass probability was C = 1, the number of individuals. The NSGA-II algorithm was implemented in MATLAB 2014 to optimize the compromise parameters. For the NSGA-II algorithm, the initial point and final point were determined in advance.

5.4. Simulation Results

The energy-consumption and time-objective diagram simulated by the NSGA-II algorithm was similar to an exponential function and shown in Figure 8. The designed blank dimension could be calculated by the workpiece dimension and back-cutting amount. The optimal energy consumption and time were 458.6 and 6.3, respectively. The designed optimal blank dimension was 53.62.

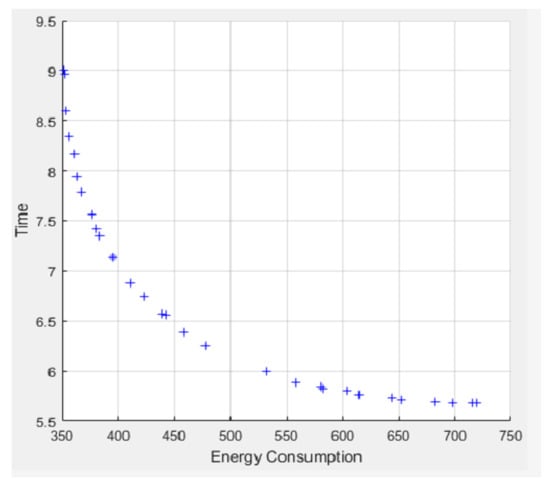
Figure 8. Optimizing results.

6. Discussion

In this paper, a method of blank-dimension design was presented that was based on the inverse calculation of the machining process parameters under the given production conditions guided by a business compass. The designed blank dimensions could meet the requirements of energy consumption and efficiency of the enterprise under given conditions. Some questions relating to the results of the proposed methodology require further discussion.

6.1. Comparison to Selected Blank Dimension

This paper presents a method to optimize the design of blank dimensions guided by a business compass. The optimal energy consumption and efficiency can be obtained by coordinating and optimizing the factors in the process of blank production and use. The blank dimension to be designed can be calculated according to the workpiece dimension and the back-cutting amount in the further processing of the blank, which can realize better energy consumption and efficiency under the assumed production conditions.

Contrasting the selected blank dimensions 53 and 55 with the designed blank, the optimal energy consumption and time of the selected blank dimension in this paper were 483.9 and 6.8, and 507.5 and 6.98 respectively, which is shown in Table 3. Through data comparison, it was found that the designed blank dimension had obvious advantages in energy saving and efficiency convenience. Compared with the available selected blank dimensions of 53 and 55, and considering enterprise conditions, the optimal designed blank dimension’s energy consumption was only close to 94.7% and 90.3% of the selected blank dimensions, respectively, and the time was 92.6% and 90.2% of the selected dimensions, respectively. Therefore, the designed blank dimension can achieve high efficiency and save energy.

Table 3. Comparison of different blank dimensions and optimization objectives.

Scheme	Blank Dimension	Energy Consumption	Time
1	53.62	458.6	6.3
2	53	483.9	6.8
3	55	507.5	6.98

From the perspective of the enterprise business compass, this method provides energy-saving and highly efficient blank-dimension design for enterprises in the actual production process. In the blank-dimension-design process, the equipment, materials, and other aspects are optimized and coordinated on the basis of the enterprise’s current operation and management. It provides suggestions for enterprises to design blank dimensions according to their own situation. This method has been verified in theory and practice, and it is an effective measure for the manufacturing industry to achieve energy conservation and emission reductions.

6.2. Compared with Previous Works

Different studies have different emphases and corresponding advantages, and the methods in the references can meet their needs. Nevertheless, blank production and blank use are processes with large energy consumption. These methods only select the designed blank dimensions, and the selected blank dimensions can only ensure the energy consumption and efficiency of the later processing. In this study, the optimal choice was to consider the blank dimensions designed by the actual situation of the enterprise from the perspective of blank production and blank use of the enterprise operating compass.

7. Conclusions

Guided by the people-oriented thinking of the business compass, the machine tool was arranged on the basis of the operator’s convenience of loading and unloading, and the loading and unloading time was reasonably arranged. On this basis, the machining-process equipment parameters were optimized, and the optimization calculation was completed by the NSGA-II algorithm. According to the optimized result, the blank dimensions were calculated by the inverse method, which can meet the requirements of enterprises accurately.

From the point of view of the blank-using enterprise, the reverse design of the blank dimensions is carried out on the basis of the evaluation of the enterprise’s own resources, so the designed blank dimensions can guarantee all the resource and environmental requirements of the production and use process. During the optimization design of blank dimensions, the business compass was used to set up the production process, and the multi-objective optimization algorithm was used to optimize the process, which provided theoretical support for the design of blank dimensions. Then we just set up a type of enterprise production; in a follow-up study, we will verify the different types of production.