A Review on the Hydrodynamics of Taylor Flow in Microchannels: Experimental and Computational Studies

Abstract

Taylor flow is a strategy-aimed flow to transfer conventional single-phase into a more efficient two-phase flow resulting in an enhanced momentum/heat/mass transfer rate, as well as a multitude of other advantages. To date, Taylor flow has focused on the processes involving gas–liquid and liquid–liquid two-phase systems in microchannels over a wide range of applications in biomedical, pharmaceutical, industrial, and commercial sectors. Appropriately micro-structured design is, therefore, a key consideration for equipment dealing with transport phenomena. This review paper highlights the hydrodynamic aspects of gas–liquid and liquid–liquid two-phase flows in microchannels. It covers state-of-the-art experimental and numerical methods in the literature for analyzing and simulating slug flows in circular and non-circular microchannels. The review’s main objective is to identify the considerable opportunity for further development of microflows and provide suggestions for researchers in the field. Available correlations proposed for the transition of flow patterns are presented. A review of the literature of flow regime, slug length, and pressure drop is also carried out.

1. Introduction

Multiphase flow in micro-sized structures refers to a microflow in which two or more distinct phases are recognizable, i.e., a carrying or continuous phase and one or more dispersed phases. A two-phase flow denotes a combination of two distinct phases, including gas, liquid, and solid particles. Gas–liquid (GL) and liquid–liquid (LL) are two common types of multiphase flows in microchannels encountered in various practical applications, such as biomedical, pharmacological, engineering, and commercial purposes. Immiscible LL two-phase flows can also be observed in many industrial applications, where the dispersive liquid flow is introduced as droplets into the carrying liquid flow. Intensified liquid–liquid extraction as a separation process is another application for two-phase flow in oil and gas industries. The gas bubbles with equivalent diameters of the microchannel diameter in a GL Taylor flow are surrounded by a thin liquid film of the continuous flow and separated by the liquid slugs [1]. The interaction between the different phases, flow rates, thermophysical properties, and geometrical details of the channel characterizes the flow pattern, liquid film thickness, gas bubble or droplet shape, pressure drop, heat, and mass transfer rates. Knowledge of two-phase flow characteristics enables researchers and designers to optimize channel size and operating conditions. Minimizing the pressure drop can reduce corrosion and erosion while providing a high heat transfer rate [1,2]. An essential feature of Taylor flow is the flow pattern in the liquid slug, which can also be classified in recirculation flow and bypass flow [2,3]. Therefore, knowledge of hydrodynamic properties of Taylor flow is certainly required to understand transport phenomena characteristics for improving the performance of microchannels and enabling operational conditions to be optimized.

A review on the hydrodynamic characteristics of Taylor flow was conducted by Angeli and Gavriilidis [1] for circular and non-circular small channels. Correlations for film thickness measurements were summarized and the key effects of Capillary number (Ca) on film thickness were discussed in detail. Recently, Etminan et al. [4] presented all of the correlations proposed for film thickness measuring in the literature. They found the best-fitted correlation between some experimental data and a wide range of Ca. It can be concluded that there is still a lack of certainties for the gradient of surface tension at the interfacial region resulting in discrepancies between experimental predictions and numerical/theoretical findings. Moreover, more attempts should be devoted to finding specific flow and operational conditions for enhancing the performance of microchannels.

For multiphase flows, it is necessary to predict the transport phenomena in terms of flow parameters, i.e., superficial flow velocity components, slug length, liquid film thickness, and the flow rates of each phase. Multiphase flow is valid as long as the separation between phases is recognizable at a scale greater than the molecular level. The ability to describe the behavior of multiphase flow requires a set of basic definitions and assumptions. The following subsections have been designed to represent the importance of these basic definitions and the role of dimensionless groups in describing the two-phase flows’ behavior. This paper is aimed to review two-phase flows in microchannels, with a particular focus on the hydrodynamic aspects. Fundamentals of multiphase flows, such as basic definitions and dimensionless parameters are studied. Identification of flow pattern and bubble/droplet formation are discussed in experimental investigations, numerical simulations, and flow regime transitions. Correlations of slug lengths and pressure drop are presented and classified in terms of cross-sectional areas of microchannels.

2. Basic Definitions in Two-Phase Flows

The capillary length has been used to identify the compaction in micro-sized applications, such as microchannels in heat exchangers. A micro-sized channel can be adequately assumed when the hydraulic diameter of the channel is less than the capillary length. In contrast, for large-diameter channels, the Laplace number (La) can be properly considered as a suitable length scale for calculations instead of the bubble or droplet diameter. Many other definitions have been developed to describe the characteristics of multiphase flows, including fluid flow, and heat and mass transfers, which are presented in Table 1. It should be noted that due to the presence of more than one phase and the interaction between all phases involved in multiphase flow, the thermophysical properties have been expressed differently compared to those of a single-phase flow [3,4,5].

Table 1. Important definitions for multiphase flows.

Name	Symbol	Definition	Description
Total mass flow rate	${\dot{\mathrm{m}}}_{\mathrm{t}}$	${\dot{\mathrm{m}}}_1+{\dot{\mathrm{m}}}_{\mathrm{g}}$	The sum of mass flow rate of the liquid and the gas phases
Total volumetric flow rate	${\mathrm{Q}}_{\mathrm{t}}$	${\mathrm{Q}}_{\mathrm{l}}{+\mathrm{Q}}_{\mathrm{g}}$	The sum of volumetric flow rate of the liquid and gas phases
Total mass flux	${\mathrm{G}}_{\mathrm{t}}$	${\dot{\mathrm{m}}}_{\mathrm{t}}/\mathrm{A}$	The total mass flow rate by cross-sectional area of the tube
Capillary length	Lca	${\left[\frac{\mathsf{\sigma }}{\mathrm{g}\left({\mathsf{\rho }}_{\mathrm{l}}{-\mathsf{\rho }}_{\mathrm{g}}\right)}\right]}^{0.5}$	The ratio between interfacial and gravitational (buoyancy) effects
Slip ratio	S	${\mathrm{U}}_{\mathrm{g}}{/\mathrm{U}}_{\mathrm{l}}$	The ratio of average real velocity of the gas and liquid phases
Average velocity of gas phase	Ug	$\frac{{\mathrm{Q}}_{\mathrm{g}}}{{\mathrm{A}}_{\mathrm{g}}}=\frac{{\mathrm{Q}}_{\mathrm{g}}}{\mathsf{\alpha }\mathrm{A}}=\frac{{\mathrm{V}}_{\mathrm{g}}}{\mathsf{\alpha }}$	The ratio of volumetric flow rate of the gas phase to tube cross-sectional area occupied by the gas phase flow
Average velocity of liquid phase	Ul	$\frac{{\mathrm{Q}}_{\mathrm{l}}}{{\mathrm{A}}_{\mathrm{l}}}=\frac{{\mathrm{Q}}_{\mathrm{l}}}{(1-\mathsf{\alpha })\mathrm{A}}=\frac{{\mathrm{V}}_{\mathrm{l}}}{(1-\mathsf{\alpha })}$	The ratio of volumetric flow rate of the liquid phase to tube cross-sectional area occupied by the liquid phase flow
Superficial velocity of gas phase	Vg	${\mathrm{Q}}_{\mathrm{g}}/\mathrm{A}$	The velocity of the gas phase if it flows alone in the tube or the ratio of the volumetric flow rate of the gas phase and the cross-sectional area of the tube
Superficial velocity of liquid phase	Vl	${\mathrm{Q}}_{\mathrm{l}}/\mathrm{A}$	The velocity of the liquid phase if it flows alone in the tube or the ratio of the volumetric flow rate of the liquid phase and the cross-sectional area of the tube
Mixture velocity	Vm	$\frac{{\mathrm{Q}}_{\mathrm{t}}}{\mathrm{A}}{=\mathrm{V}}_{\mathrm{l}}{+\mathrm{V}}_{\mathrm{g}}$	The sum of the superficial velocities of two phases
Quality or dryness fraction	x	${\dot{\mathrm{m}}}_{\mathrm{g}}/{\dot{\mathrm{m}}}_{\mathrm{t}}$	The ratio of the mass flow rate of the gas phase to the total mass flow rate
Void fraction	α	${\mathrm{A}}_{\mathrm{g}}/\mathrm{A}$	The ratio of the tube cross-sectional area (or volume) occupied by the gas phase to the tube cross-sectional area (or volume)
Volumetric quality (dynamic holdup)	β	${\mathrm{Q}}_{\mathrm{g}}{/\mathrm{Q}}_{\mathrm{t}}$	The ratio of the volumetric flow rate of the gas phase to the total volumetric flow rate
Two-phase friction multiplier	φ	${\left(1+\frac{\mathrm{C}}{\mathrm{X}}+\frac{1}{{\mathrm{X}}^2}\right)}^{0.5}$	A function of the Lockhart–Martinelli parameter (X) and the Chisholm constant (C)

3. Dimensionless Parameters

A dimensionless number can represent the ratio of two different forces or physical quantities, which play a significant role in the flow pattern and interaction between phases (see Table 2). The length scale of a channel, which appears for the majority of dimensionless numbers, is often defined as the diameter of tubes or the hydraulic diameter of ducts.

Table 2. Some of the most common non-dimensional numbers in multiphase flow.

Name	Symbol	Definition	Description
Archimedes	Ar	$\frac{{\mathsf{\rho }}_{\mathrm{l}}\left({\mathsf{\rho }}_{\mathrm{l}}{-\mathsf{\rho }}_{\mathrm{g}}\right){\mathrm{gd}}^3}{{\mathsf{\mu }}_{\mathrm{l}}{}^2}$	The ratio of the gravitational to the viscous effects
Bond or Eötvös	Bo Eo	$\frac{{\mathrm{gd}}^2\left({\mathsf{\rho }}_{\mathrm{l}}{-\mathsf{\rho }}_{\mathrm{g}}\right)}{4\mathsf{\sigma }}$	The ratio of the gravitational (buoyancy) and the capillary force scales
Cahn	Cn	$\mathsf{\xi }/\mathrm{d}$	The ratio of the interface width and the tube diameter or any other length scale
Capillary	Ca	$\mathsf{\mu }\mathrm{U}/\mathsf{\sigma }$	The ratio of the viscous forces and the capillary forces
Ca/Re	Ca/Re	${\mathsf{\mu }}^2/\left(\mathsf{\rho }\mathrm{d}\mathsf{\sigma }\right)$	(N/A)
Froude	Fr	$\mathrm{U}/\sqrt{\mathrm{gd}}$	The ratio between the flow inertia and the external field
Laplace	La	${\left[\frac{\mathsf{\sigma }}{{\mathrm{gd}}^2\left({\mathsf{\rho }}_{\mathrm{l}}{-\mathsf{\rho }}_{\mathrm{g}}\right)}\right]}^{0.5}$	The ratio of the capillary and the gravitational (buoyancy) effects
Ohnesorge	Oh	$\frac{\sqrt{\mathrm{We}}}{\mathrm{Re}}=\frac{\mathsf{\mu }}{\sqrt{\mathsf{\sigma }\mathsf{\rho }\mathrm{d}}}$	The ratio of the viscous force to the inertia and the surface tension forces
Reynolds	Re	$\mathsf{\rho }\mathrm{Ud}/\mathsf{\mu }$	The ratio between the inertia and the viscous forces
Suratman	Su	$\frac{{\mathrm{Re}}^2}{\mathrm{We}}=\frac{1}{{\mathrm{Oh}}^2}=\frac{\mathsf{\sigma }\mathsf{\rho }\mathrm{d}}{{\mathsf{\mu }}^2}$	The ratio of the surface tension to the viscous forces
Weber	We	$\mathrm{CaRe}=\frac{{\mathsf{\rho }\mathrm{U}}^2\mathrm{d}}{\mathsf{\sigma }}$	The ratio of the inertial forces to the interfacial forces

The relation of gravitational to viscous forces is Archimedes number (Ar) that the formal definition is given in Table 2. This number frequently appears in tube-shaped chemical process reactor designs, which describe the motion of fluids caused by the difference in densities. The Ar was linked to the Reynolds number (Re) as an explicit-iterative correlation [6]:

$$\mathrm{Re}=\frac{\mathrm{Ar}}{18}{\left(1+{0.579\mathrm{Ar}}^{0.412}\right)}^{-1.214}$$

(1)

Hua et al. [7] found that ellipsoidal gas bubbles were produced as the Ar and Bond (Bo) numbers were gradually increased. In solid particle multiphase flows, the Ar has also been related to the drag force coefficient and the Re [8,9,10] and the wind threshold velocities of particles in GL flow [11]. The Ar number was also correlated with the inverse viscosity number (N) by Quan [12] in an upward or downward co-current Taylor flow,

$${\mathrm{N}=\mathrm{Ar}}^{0.5}= {\left(\frac{{\mathsf{\rho }}_{\mathrm{l}} \left({\mathsf{\rho }}_{\mathrm{l}}{-\mathsf{\rho }}_{\mathrm{g}}\right){\mathrm{gd}}^3}{{\mathsf{\mu }}_{\mathrm{l}}{}^2}\right)}^{0.5}$$

(2)

For a large N, the elongated tail of the bubbles oscillated for upward flow, and the shortened tail was only observed for downward flow.

The Bond number (Bo), also called Eötvös number (Eo), is the inverse of the Ar number and denotes the ratio between the gravitational and capillary effects. Since the Bond number varies with the square of length–scale, each change, even small, in channel diameter causes significant variation in the Bo. For air–water two-phase flow in channels of a diameter less than 1 mm, which are very common in micro-sized applications, the Bo number is approximately in the order of 0.1 and the importance of viscous effects is predominant. Therefore, the gravitational effects can be negligible in most GL flows in microchannels. Hua et al. [7] and Uno and Kintner [13] showed that the gas bubble velocity was significantly impacted by the wall effects for high Bond numbers. They showed that bubble shape was significantly affected by the Bo number: elongated bubbles with spherical caps at both ends appeared for $\mathrm{Bo}>50$. Some other specific regions of Bo and ${\mathrm{BoRe}}_{\mathrm{l}}^{0.5}$ numbers have been proposed by investigators to categorize the behavior of multiphase flows, for example, dominant surface tension for $\mathrm{Bo}\le 1.5$, non-negligible inertia, surface tension, and viscous effects for $1.5<\mathrm{Bo}\le 11$, and negligible surface tension effects for $\mathrm{Bo}>11$ [14,15,16,17]. The absorption of CO₂ in micro-scale reactors where the Chisholm parameter was correlated with the Bo number was studied by Ganapathy et al. [18]. Prajapati and Bhandari [19] quantified the instability increase of boiling flow in a microchannel for the region of $\mathrm{Bo}<1$.

The Cahn number (Cn) is defined as the ratio of the interface width (ξ) and the tube diameter or any other length scale (d),

$$\mathrm{Cn}=\mathsf{\xi }/\mathrm{d}$$

(3)

Cahn and Hilliard [20,21] and Cahn [22] focused their studies on the free energy of the volume of an isotropic system, where the densities of components involved are non-uniform. The concept of the Cahn number was introduced by them when they found an increase in the thickness with temperature. Soon after, the efforts to obtain the governing equation in a non-equilibrium situation led to a well-known Cahn–Hilliard equation involving the Cahn number for the first time [23,24,25,26]. For example, Choi and Anderson [27] coupled the Cahn–Hilliard theory with the Extended Finite Volume Method (XFVM) for the dynamic modeling of suspended particles in two-phase flows.

The importance of viscous and capillary effects in two-phase flow in microchannels has been correlated by the capillary number based on the liquid slug velocity,

$$\mathrm{Ca}=\mathsf{\mu }\mathrm{U}/\mathsf{\sigma }$$

(4)

The capillary number is a dimensionless group to explain how viscous and surface tension forces affect the interface between the gas and liquid phases, and also between two immiscible liquids. Although, the length-scale does not appear in the capillary number, surface tension forces become more significant relative to gravity as the cross-sectional area of the channel is decreased. For most microflow applications, the approximate values of superficial velocity range from 10 μms⁻¹ to 1 ms⁻¹, when the viscosity is 10⁻³ kg m⁻¹ s⁻¹, and the surface tension can be reasonably considered at 0.05 N m⁻¹. These flow conditions cause the Ca to range from 2 × 10⁻⁷ to 2 × 10⁻². For high viscosity liquids, such as silicone oil at a mixture velocity of 1 ms⁻¹, the Ca becomes ~1. The Ca frequently appears in correlations measuring liquid film thickness [28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52], pressure drop [30,35,44,48,53,54,55,56,57], and slug length [58,59,60,61] in multiphase flows. Recently, the poor accuracy of classical pressure drop correlations with an increase of the Ca was emphasized by Ni et al. [51]. This was due to the presence of waves around the tail of the bubble, change of the semi-spherical head of the bubble, and powerful circulation inside the liquid slugs. Patel et al. [52] indicated that the film thickness at the corner of a square microchannel decreased with an increase of Ca, where a linear expression was derived for the film thickness in terms of Ca. Several other researchers showed an increasing trend in film thickness with Ca. These hydrodynamic features will be discussed in the following sections.

The Re expresses the ratio of inertial to viscous effects and predicts the flow pattern in different situations:

$$\mathrm{Re}=\mathsf{\rho }\mathrm{Ud}/\mathsf{\mu }$$

(5)

where ρ, μ, and U are the density, dynamic viscosity of the continuous phase fluid, and the velocity of flow, respectively. The thermophysical properties of a multiphase flow are different from a single-phase flow, which has been discussed by Awad [5] in detail. Regarding the value of the inertia forces, the flow regime remained laminar for the Re numbers less than ~2300 [62,63]. Since the cross-sectional area of a microchannel often has a diameter of 1 mm or smaller and the liquid velocity is less than 1 m s⁻¹, the Re for water as the continuous phase is ~1000 or less. This means that the flow regime in the microchannel applications is normally laminar and the predominant effects of the viscous forces must be taken into account. Because more than one phase is involved, different approaches have been used by researchers to determine the value of Re and the thermophysical properties in the multiphase flows. To realize the importance of the Re definition, consider two following cases: first, the inertia effects of the gas phase are insignificant, when the gas and the liquid superficial velocities are in the same order. For instance, the air to water density ratio in two-phase flow is around $1.225\times {10}^{-3}$, which indicates the dominant role of the liquid phase density in defining the Re. This situation can be recognized in a bubbly flow pattern. Second, the inertia effects of both phases are important when the gas superficial velocity is relatively high compared with the liquid superficial velocity. The friction factor is necessarily calculated for the pressure drop calculation, while the Re appears in other correlations of hydrodynamic concepts, see Section 6 for further information. The Re is in the correlations for liquid film thickness and pressure drop obtained by Heiszwolf et al. [39] and Han and Shikazono [46]. The product of the Re and the We numbers was introduced as a transition criterion from slug to slug-bubbly regimes by Suo and Griffith [64]. Jayawardena et al. [65] proposed the ratio of liquid phase to gas phase the Re numbers to identify the transitions from bubbly to slug and from slug to annular patterns. Several other non-dimensional numbers in multiphase flows have been gathered and discussed by Awad [5].

As the diameter of the channel and the velocity of flow decrease, the inertial, and gravitational effects become negligible, while the surface tension becomes a predominant factor. The knowledge of the hydrodynamics of multiphase flow is strictly intertwined with the dimensionless numbers presented in Table 3. According to this table, an accurate description of the flow map, bubble or droplet formation, and transition from one flow regime to another are highly depended on Bo or Eo, Ca, Re, We, Su, and Fr. While, Bo, Ca, and Re have appeared in the pressure drop correlations so far, the friction factor is only governed by the Re. The liquid film thickness has been correlated or described with Re, Ca, and We numbers. Finally, the slug length has only included the Re and the Ca numbers.

Table 3. Dependency of hydrodynamic aspects and the dimensionless numbers.

	Dimensionless Numbers
Hydrodynamic Aspects	Bo (Eo)	Ca	Fr	Re	Su	We
film thickness
pressure drop
slug length
friction factor
flow map, slug profile
flow regime transition

A graphical flow map, which displays the specific region for each flow regime along with their transition lines, uses a few important characteristics of multiphase flow, such as superficial velocity, Re, Ca, and We. Table 4 summarizes the non-dimensional numbers and other flow parameters that use the x- and y-axis coordinates for quantitative-based flow map diagrams.

Table 4. Some non-dimensional numbers and thermophysical properties selected by authors for displaying flow maps.

		Dispersed Liquid or Gas Phase, #2
		V	Re	Ca	Re2/Re1	We	We Oh	Ql/(Ql + Qg)	ρV2	G/λ	X	Quality
Continuous Liquid Phase, #1	V	(1)
	Re		(13)
	Ca			(11)		(15)		(6)
	Re/Ca		(3)
	We			(15)		(2)	(14)
	Su		(9)		(10)
	We Oh					(14)	(4)
	ρV2								(7)
	Bλψ/G									(5)
	Flow Rate											(8)
	Force										(12)

The list of authors: (1) Ganapathy et al. [18], Patel et al. [52], Hewitt and Roberts [66], Fukano and Kariyasaki [67], Triplett et al. [68], Zhao and Bi [69], Akbar et al. [70], Kawaji and Chung [71], Cubaud and Ho [72], Günther et al. [73], Yue et al. [74], Kirpalani et al. [75], Yue et al. [76], Dessimoz et al. [77], Roudet et al. [78], Deendarlianto et al. [79], Wu and Sundén [80], Farokhpoor et al. [81] (2) Akbar et al. [70], Yue et al. [76], Zhao et al. [82], Yagodnitsyna et al. [83], (3) Jayawardena et al. [65], Dessimoz et al. [77], (4) Wu and Sundén [80], Yagodnitsyna et al. [83], (5) Baker [84], (6) Suo and Griffith [64], (7) Hewitt and Roberts [66], (8) Sato et al. [85], (9) Jayawardena et al. [65], (10) Jayawardena et al. [65], (11) Cubaud and Mason [86], (12) Kirpalani et al. [75], (13) Dessimoz et al. [77], (14) Yagodnitsyna et al. [83], (15) Wu and Sundén [80].

As a guide to reading this table; the kinetic energy of flow (ρV²) was used by the author’s group of 7 which its row and column are colored red. The first effort to display a flow pattern diagram dates back to 1953 when Baker [84] computed the mass velocity of each phase and two other expressions involving the viscosity and densities (G/λ and Bλψ/G) of both phases (see ‘5’ in Table 4). These dimensional terms were not chosen by others afterward. In contrast, it is the interfacial velocities of the phases that have frequently been selected by scholars for more than half a century (see ‘1’ in Table 4). After velocity, it seems that Re, We, and Ca numbers have the highest use by researchers for showing the flow pattern clearly and more understandably.

4. Identification of Flow Patterns and Bubble/Slug Formation

The first step of transport phenomena analysis of multiphase flows is to explain the flow characteristics in a phase-mapped diagram. The transition lines in such maps specify the criterion of a transition from one flow regime to another. A two-phase flow usually consists of a train of dispersed bubbles or droplets carried by a continuous phase, which potentially enhances the rates of heat and mass transfers in industrial applications. Although the flow patterns in microchannels and large-diameter channels show similarities, there are several differences. As the channel diameter increases, the laminar flow regime starts to be unstable due to the inertial effects. Kawaji and Chung [71] and Akbar et al. [70,87] indicated flow patterns in micro and minichannels, where the stratified flow regime was not present for larger channels. The effects of increasing the Reynolds number on the bubble profile were numerically and experimentally discussed by Kreutzer et al. [88]. Their results indicated a more elongated nose and flattened tail due to the lack of large enough interfacial forces to keep the hemispherical shape of the bubble caps as Reynolds number increased.

Figure 1 presents a schematic of GL flow patterns in capillaries. The geometrical details of the channel, configuration of the channel, properties of phases, superficial velocities of phases, and types of junctions are the predominant factors to determine flow patterns in microchannels. The wetting or drainage effects of each phase are responsible for at least part of the flow maps in multiphase flows. In a bubbly flow regime, the individual bubbles move through the continuous liquid phase at very low liquid superficial velocities. When the bubble size is small, the interaction between bubbles is negligible. Conversely, increasing the gas-to-liquid volumetric flow rate causes the bubbles to coalesce and a breakup occurs (Figure 1). Bubble coalescence becomes stronger as the gas-to-liquid volumetric flow rate is increased, to make large long bubbles with a rounded front that spans the cross-sectional area of the channel. Characteristics of the bullet-shaped bubbles most often called Taylor or slug flow in which the Taylor bubbles are surrounded by a thin layer of the carrier liquid phase, Figure 1. Some small dispersed bubbles are between the Taylor bubbles as the gas-to-liquid volumetric flow rate is enhanced to make a transition from slug to churn patterns (Figure 1e). In a churn flow pattern, neither dispersed nor carrier phases are continuous and irregular plugs of gas flow through the liquid phase and a wide variety of bubble lengths can be observed. This chaotic flow pattern occurs when the velocity is increased (Figure 1f). In large-diameter tubes, an oscillating chaotic flow is much more remarkable than that in small-diameter tubes. This flow regime is also named a semi-annular or unstable-slug flow pattern. In an annular flow pattern, a very thin thickness of the liquid phase remains on the walls of the channel for two flow conditions: the gas-to-liquid volumetric flow rate increases and the velocities of phases rise at low liquid volume fraction (Figure 1g). While very small-diameter droplets of the liquid phase are in the core of the gas phase, the flow pattern is mist (Figure 1h).

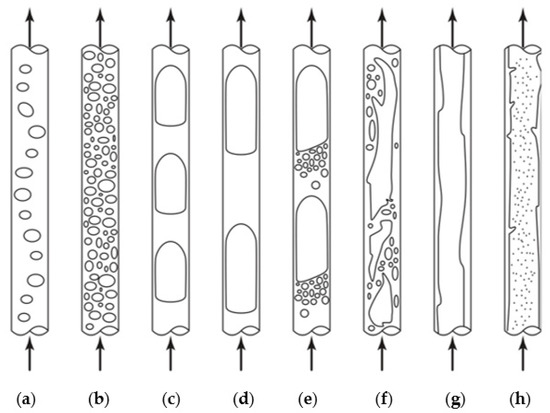
Figure 1. The schematic of observed flow regimes in the vertical microchannels; (a,b) bubbly flow, (c,d) Taylor or segmented flow, (e) transitional flow from slug to churn, (f) churn flow, (g) annular-film flow, (h) mist-annular or wispy-annular flow [44]. Reproduced by permission from Kreutzer, M.T.; Kapteijn, F.; Moulijn, J.A.; Heiszwolf, J.J., Chemical Engineering Science; published by Elsevier, 2005.

An experimental study of a hydrophobic ionic/water two-phase flow in two T and Y inlet junctions on the flow patterns was carried out by Tsaoulidis et al. [89], resulting in a negligible impact of the inlet configuration. They also investigated the effects of capillaries’ materials made of glass, Fluorinated Ethylene Propylene (FEP), and Tefzel on flow patterns illustrated in Figure 2. Although the boundaries of the FEP and Tefzel are similar, the plug flow regime occupies a larger area in the flow map compared to the FEP capillary, and an annular pattern is observed in higher mixture velocities and lower ionic volume fraction. They did not observe annular and drop patterns in the glass capillary when the continuous phase was water.

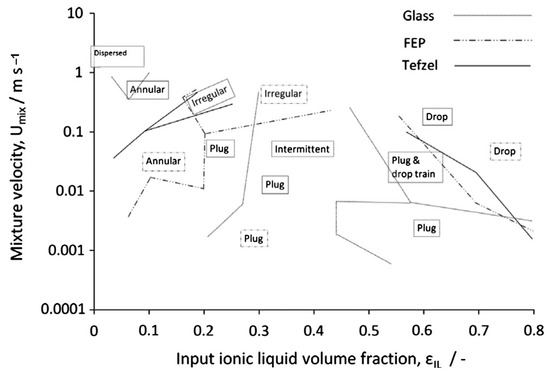
Figure 2. Flow map boundaries observed in three different glass, FEP, and Tefzel microchannels with a T-junction [89]. Reproduced by permission from Tsaoulidis, D.; Dore, V.; Angeli, P.; Plechkova, N.V.; Seddon, K.R., International Journal of Multiphase Flow; published by Elsevier, 2013.

4.1. Experimental Investigations

Transport phenomena for multiphase flows in capillary passages involve the behavior of each phase individually, the mutual interactions of phases, and the interactions between phases and solid boundaries. The presence of gas bubbles in a multiphase flow can be considered as an obstacle to the liquid phase flow, which is known as the Jamin effect [90]. This phenomenon is prominent enough to decrease the productions of the petroleum industry due to the high-pressure drop and the flow pattern transition. At the interface between two components of a GL two-phase flow, the surface tension gradient is substantial, which affects the interaction between phases and other transport phenomena. Historically, this effect is known as the Marangoni effect, which pushes the liquid phase to flow away from low surface tension regions and was first explained by Gibbs [91].

A comprehensive experimental study on the flow maps by means of high-speed X-ray photography and flash methods simultaneously was reported by Hewitt and Roberts [66], which recognized the previous correlations for each flow pattern proposed by Baker [84] and Wallis [92]. A rough sketch of streamlines in the slug region of a GL flow was experimentally obtained by Taylor [31], where a stagnation point on the vortex and a stagnation ring on the curvature of the bubble were observed for two extreme cases of velocity fraction, (V_g − V_m)/V_g, greater and less than 0.5. The high-speed photography was compared with X-ray technology to provide clear images of air–water flow regimes through a capillary [66]. Irandoust and Andersson [34] experimentally depicted Taylor’s bubble profile, where the film thickness remained constant in the middle of the gas bubble. They also confirmed that the gas bubble was elongated in the front and squeezed in the rear parts. A review study on the flow maps was conducted by Akbar et al. [70] to show the dominant effects in each flow regime using available experimental data. They proposed a hydraulic diameter of 1 mm as a criterion for classifying the previous studies into the five regions: bubbly, plug or slug (surface tension dominated), annular (inertia dominated), dispersed, and transition zones regarding the amounts of superficial velocities and the Weber numbers. Micro-particle image velocimetry (μ-PIV) and fluorescence microscopy techniques were used by Günther et al. [73] to recognize a micro-segmented GL flow in a rectangular cross-section area channel. They showed that the roughness of the inner side of the channel and compressibility of the gas bubbles induce an imbalance into the flow field and accelerate the mixing rate accordingly. The periodic switching of recirculation regions in the liquid slugs caused a higher mixing rate in a meandering channel compared with a straight channel (Figure 3). Dore et al. [93] investigated the dynamics of water/ionic two-phase flow by exploring slug formation and recirculation flow in fluid segments at T-junction, straight and curved microchannel employing μ-PIV. As shown in Figure 4, the circulation patterns in water plug consisted of two main mirrored and counter rotating vortices for low mixture velocity. As the mixture velocity increased, two secondary vortices arose at the nose cap of water plug.

Figure 3. The sketch of fluorescent micrographs for, (a) straight channel, and (b) meandering channel [73]. Reproduced with permission from Günther, A.; Khan, S.A.; Thalmann, M.; Trachsel, F.; Jensen, K.F., Lab on a Chip; published by Royal Society of Chemistry, 2001.

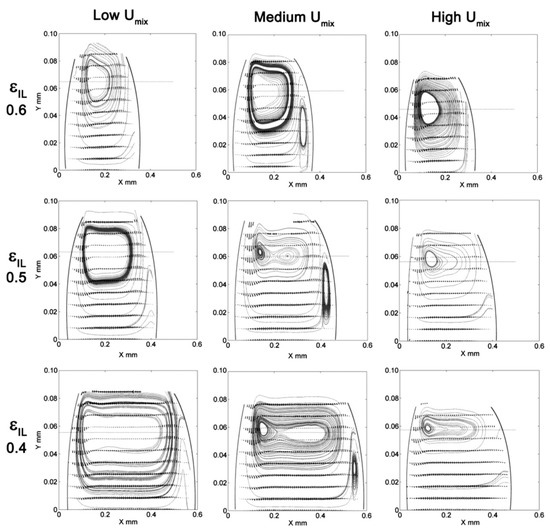
Figure 4. Schematic representative of circulation patterns within water plugs for three different water holdups and mixture velocities [93]. Reproduced with permission from V Dore, D Tsaoulidis, P Angeli., Chemical engineering science; published by Elsevier, 2012.

The flow patterns of an LL two-phase flow in a rectangular cross-section duct were experimentally investigated by Zhao et al. [82]. The flow maps and the flow transitions were correlated by the inertia forces of each phase and the interfacial forces. They realized six distinctive flow maps in terms of dispersed phase droplet formation process at a T-junction as follows:

• Slug regime; when the interfacial tension is greater than inertial forces, and the Weber numbers are ${7.61\times 10}^{-6}{<\mathrm{We}}_{\mathrm{ws}}<{4.87\times 10}^{-2}$ and ${5.94\times 10}^{-6}{<\mathrm{We}}_{\mathrm{ks}}<{5.94\times 10}^{-4}$.
• Monodispersed droplet regime; when the carrier phase flow rate is increased, and the Weber numbers.
• The droplet population regime; when ${1.07<\mathrm{We}}_{\mathrm{ws}}<30.43$ and ${3.8\times 10}^{-4}{<\mathrm{We}}_{\mathrm{ks}}<{2.38\times 10}^{-1}$. This flow regime is observed at the center of the channel where the inertial effects of the continuous phase are significantly greater than the interfacial tension.
• Chaotic thin striations regime; when both flow rates are increased the We numbers are in a range of ${0.17<\mathrm{We}}_{\mathrm{ws}}<30.43$ and ${4.29<\mathrm{We}}_{\mathrm{ks}}<53.5$. This flow map will be eventually changed into annular due to the instability of the flow.

A combination of experimental observations and numerical simulations was employed by Meyer et al. [94] to show velocity profile, flow patterns in a $2\mathrm{mm}\times 2\mathrm{mm}$ vertical channel, Figure 5. Both methods predicted a Couette velocity distribution within the liquid film region, a mirrored main recirculating region, and two small vortices in the nose and rear caps with a direction of opposite. They also realized some differences between the results of the two methods as shown previously by [95].

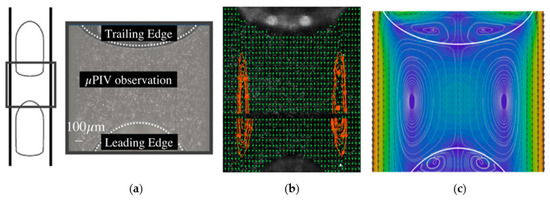
Figure 5. Flow patterns and streamlines within the Taylor bubble and liquid plug predicted by (a,b) μ-PIV, and (c) numerical simulation [94]. Reproduced with permission from Meyer, C.; Hoffmann, M.; Schlüter, M., International Journal of Multiphase Flow; published by Elsevier, 2014.

Experimental analysis by Zhao et al. [82] revealed that the volume of dispersed flow was significantly affected by interfacial forces, inertia force, and the volumetric ratio of dispersed phase, which correlated by the multivariable least squares method,

$$\frac{\mathrm{R}}{{\mathrm{d}}_{\mathrm{H}}}=-0.1276\ln \left[\frac{{\mathrm{We}}_{\mathrm{ws}} \left(1-\mathsf{\epsilon }\right)}{{\left({\mathrm{We}}_{\mathrm{ks}}\mathsf{\epsilon }\right)}^{0.15}}\right]+0.5595$$

(6)

where the dynamic hold-up fraction (ε) and equivalent radius (R) in terms of the volume of dispersed phase (V_d) are,

$${\mathsf{\epsilon }=\mathrm{Q}}_{\mathrm{k}}/\left({\mathrm{Q}}_{\mathrm{w}}{+\mathrm{Q}}_{\mathrm{k}}\right)$$

(7)

$$\mathrm{R}=\sqrt[3]{3{\forall }_{\mathrm{d}}/4\mathsf{\pi }}{\times 10}^{-3}$$

(8)

The diameter of the channel has a major role in the measured void fraction and a flow pattern which is shown in Figure 6 for the small diameter tube of 38.1 mm (upper row) and large diameter tube of 101.6 mm (lower row). An increase in tube diameter resulted in more compressed gas bubbles toward the top wall and occupied a smaller region of the cross-sectional area [96]. The measurement also showed that a further increase in superficial velocity ratio makes a more uniform gas phase distribution realized by a smaller portion of gas volume in the top region of the tube. As a consequence, the bubbly to plug/slug transition occurs at lower superficial velocity as the channel’s diameter increases (i.e., $j_{\mathrm{g}}=0.51\mathrm{m}/\mathrm{s}$ for the smaller pipe and $j_{\mathrm{g}}=0.25\mathrm{m}/\mathrm{s}$ for the larger pipe).

Figure 6. Snapshot images to highlight the effects of channel’s diameter increase on bubbly to plug/slug transition regimes for different superficial velocities [96]. Reproduced with permission from Kong, R.; Kim, S.; Bajorek, S.; Tien, K.; Hoxie, C., Experimental Thermal and Fluid Science; published by Elsevier, 2018.

A critical Reynolds number of ~300 was found by Butler et al. [97], where the time-averaged gas phase volume fraction showed a significant difference by means of the PIV measurements in capillaries with a T-junction. As shown in Figure 7, a large mirrored recirculation region was observed between two consecutive O₂ bubbles with a relative velocity of ${2\mathrm{V}}_{\mathrm{tp}}–{\mathrm{V}}_{\mathrm{g}}$ resulting in the most efficient convective transport (regimes 1, 2, 11, and 13 in Figure 7). They also revealed the key role of the recirculating motion in the liquid plug on the dynamics of mass transfer and its dependency on the bubble velocity.

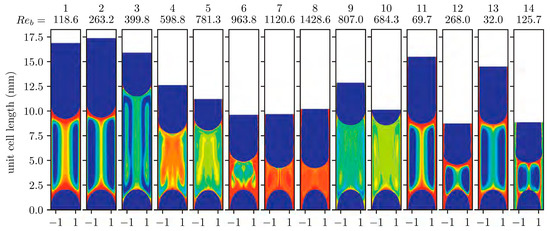
Figure 7. Time-averaged O₂ volume fraction plots for 14 different flow regimes in terms of ${\mathrm{Re}}_{\mathrm{b}}$ in the liquid plug regions between two consecutive gas bubbles [97]. Reproduced with permission from Butler, C.; Lalanne, B.; Sandmann, K.; Cid, E.; Billet, A.M., International Journal of Multiphase Flow; published by Elsevier, 2018.

Two different structures named high-concentrated and low-concentrated were observed by Yao et al. [98] to characterize the mass transfer and flow patterns of liquid–liquid slug flow at the bend region of a rectangular meandering microchannel. As is shown in Figure 8a, smaller flow rates created a non-crossing evolution pattern where the red filaments occupied the outer and inner layers when moving through the bend. Conversely, when the flow rates were increased, Figure 8b, the outer red filament was shifted to the central region of the bend.

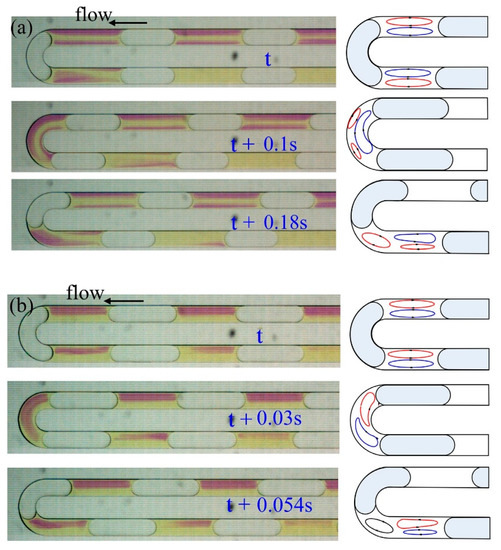
Figure 8. The evolution patterns of a typical water/toluene two-phase flow at the bend of microchannel for (a) non-crossing pattern and (b) crossing pattern [98]. Reproduced with permission from Yao, C.; Ma, H.; Zhao, Q.; Liu, Y.; Zhao, Y.; Chen, G., Chemical Engineering Science; published by Elsevier, 2020.

Table 5 presents selected experimental studies on the flow patterns of two-phase flows in tubular and non-tubular microchannels and gas bubble or droplet formation.

Table 5. The literature of selected experimental studies on the flow pattern maps and bubble or droplet formation.

Comment(s)	Cross-Section	Phases	Reference
Several correlations as the function of velocity and pressure drop in each phase were suggested for different flow regimes	Circular	GL	[84]
Combination of X-ray and high speed flash photography technique High liquid flow rates	Circular	GL	[66]
Recognizing a novel flow map using Su number for microgravity two-phase flow	Circular	GL	[65]
Boiling heat transfer of R141b Heat transfer coefficient correlations Different flow regime in small- and large-diameter tubes Observation of local dry-out on the channel wall	Circular	GL (single phase)	[99]
Using particle image velocimetry Recirculation flow pattern with a high degree of mixing Counter-rotating vortices were observed inside the liquid slugs Velocity profile inside the slugs	Circular Square	GL	[37]
Increasing gas superficial velocity led to the development of the slug flow Low liquid superficial velocity made longer bubbles, shorter liquid slugs profile Slug and annular patterns At high liquid superficial velocity, churn flow was established	Circular Semi-Triangular	GL	[68]
Five flow regimes were observed including bubbly, wedging, slug, bubbly, and dry flow for moderate void fraction The classification of patterns regarding liquid fraction The effect of a sharp return of the channel Void fraction measurement The gravitational effects were taken into account for a bubbly pattern with a spherical gas bubble Liquid droplets may be observable on the walls in wedging pattern	Square	GL	[72]
Using μ-PIV and fluorescent microscopy imaging The liquid phase segments were attached at the corners of the cross-section Gas phase flow improved the mixing and the residence time features	Rectangular	GL	[73]
The hemispherical ends of gas bubbles were not maintained as the Ca increases The nose and the tail of the bubble elongated and flattened as the Re increased The Marangoni effect was observed in experiment efforts and was not taken into account in the numerical simulations	Circular	GL	[44]
Surface modifications Contact angle measurements Meandering microchannel When the length of the bubble was equal to the channel diameter, the flow map was annular At low void fraction when the surface energy was low, the isolated symmetric bubble patterns were observed At moderate void fractions, the flow pattern was asymmetric	Square	GL	[100]
Discussed in the text	Rectangular	LL	[82]
An increase in Ca changes the droplet profile Development of droplet formation with the increase in Ca The significant deviation between the measured film thickness and the Bretherton and Taylor predictions	Circular	LL	[45]
At relatively low flow rates, the slug pattern was established with the length equal to the inner diameter of the tube At high volumetric flow rate, the deformed interface regime was made with long water slugs and small cyclohexane droplets	Circular	LL	[101,102]
Using a μ-PIV technique to capture bubble formation in a T-junction About 25% of the liquid phase passed the gas bubble The gas bubble formation process was included in three steps: Gas bubble growing until occupied the junction Gas bubble developing was decreased as the liquid phase passes the bubbles and the bubble neck was tightened Gas bubble neck was rapidly decreased until approached one-quarter of the diameter before breaking up	Square	GL	[103]
An empirical correlation for a transition from Taylor to unstable slug flow regimes At lower superficial velocities, the Taylor regime was established At higher superficial velocities, the Taylor flow was transited into the dripping flow pattern	Circular	GL	[74,76]
Boiling heat transfer of Fluorinert FC-77 As the heat flux enhanced, the bubble generation rate increased along with an increase of bubble length At moderate heat flux, flow pattern went back and forth between churn and wispy-annular flow regimes	Rectangular	GL (single phase)	[104]
Bubbly flow regime was found at a low gas superficial velocity and a high liquid superficial velocity An increase in gas superficial velocity generated slug regime, where the gas-bubble length was longer than the diameter High liquid velocity and moderated gas superficial velocity produced churn flow map Low liquid superficial velocity and high gas superficial velocity transited the churn to the slug-annular	Circular	GL	[105]
PIV measurements were taken into account Backflow around the liquid slugs were observed The liquid slugs moved faster than that of average flow due to the lubricating effects	Circular	LL	[106]
Using a µ-PIV technique to capture flow structure Slug or Taylor pattern was observed for low superficial velocities As the superficial velocities increased, the lengths of bubbles, and slugs became more variable At high enough gas velocity, the gas phase penetrates the liquid and the length of slugs became shorter	Circular	GL	[107]
Using a laser signal system to provide flow pattern images The channel diameter affects the flow pattern and transition conditions In the bubbly flow regime, the size of the bubbles was approximately was the same as channel diameter	Circular	GL	[108]
A model of mass and momentum balance Stratified flow regime was observed for low oil to gas superficial velocity ratios An increase in the velocity of the gas phase makes the interface to be wavy	Circular	GL	[109]
The number of small bubbles in liquid plug/slug was significantly increased with increasing Vg The size of small bubbles was decreased with increasing Vg or increasing Vl Increasing Vg or decreasing Vl slightly increased the depth of the plug/slug bubble Increasing pipe size enhanced the contribution from large bubbles to a total void fraction Large bubble was accelerated due to small bubble coalescence as flow developed, leading to α decreases	Circular	GL	[96]
Indicating of wave growth and coalescence during slug flow formation For low superficial velocities, the flow pattern remained stratified smooth By an increase of superficial gas velocity, the flow pattern was changed to wavy	Circular	GL	[79]

4.2. Numerical Simulations

Numerical modeling methods can be categorized into four main groups; electronic, atomistic, mesoscale, and continuum [110]. In the following, we only review some of the widely-used numerical methods in the modeling of Taylor flows, and more in-depth reviews on the rest of numerical studies can be found in literature, i.e., [111].

Two different methods may be considered in numerical analysis when describing the motions of fluids in two-phase flows: continuous fluid (Eulerian) and discrete particle (Lagrangian). The first method solves the governing partial differential equations to predict the motion of the continuum-based fluid flow, while the second method follows the movement of fluid particles or molecules to predict fluid flow and heat transfer. The interaction between different phases is calculated by both methods to determine the coalescence and interference of interfacial forces [112]. Hashim et al. [113] simulated transport phenomena and biological components, such as proteins, DNA, and cells using the Eulerian method. The innovative aspect of their simulation was to describe the mixing concentration distribution at the interaction of biological components. Apte et al. [114] numerically investigated the liquid fuel spray from a nozzle using the Eulerian-Lagrangian approach with a point-particle approximation for the liquid droplets. Ni et al. [51] investigated numerical study of the GL and LL Taylor flows on an Arbitrary Lagrangian–Eulerian (ALE) formulation to track interfacial and curvatures of slugs. They showed the predominant roles of the viscosity ratio and density ratio of continuous phase to the disperse phase for quite large Ca causing a non-stagnant liquid film region. The Lagrangian approach was also used by [115,116,117,118,119], but not limited to. Therefore, these methods can be widely employed in applications concerning fluid motion.

The Lattice Boltzmann Method (LBM) is a Computational Fluid Dynamics (CFD) method that simulates a fluid density on a lattice framework with streaming and collision (relaxation) processes instead of solving the Navier-Stokes equation directly [120]. This method is an efficient tool for modeling complex fluid systems that include complex boundaries, microscopic interactions, propagations, and the collusions of particles [121,122,123,124,125,126,127,128]. The LBM in a GL two-phase flow modeling was proposed by Seta and Kono [129], based on a particle velocity-dependent forcing scheme. Their results revealed that the effects of high potential caused instability in a three-dimensional model. A diffuse interface free energy LBM was utilized by Komrakova et al. [130] to study the behavior of a single liquid-droplet suspended in another liquid. They found that for droplets with a radius of less than 30 lattice units, a smaller interface thickness is required. Li et al. [131] comprehensively reviewed different uses of LBM proposed by others for simulating thermal boundary treatments, interaction forces between two different phases, mechanical stability conditions, liquid-vapor phase changes, fuel cells, droplet collisions, and energy storage systems. Recently, Fei et al. [132] developed a three-dimensional, multiple-relaxation-time LBM based on a set of non-orthogonal vectors for modeling realistic multiphase flows. Some other uses of the LBM have also been developed by many investigators, e.g., [133,134,135].

Another widely used method for modeling two-phase flows is the Volume of Fluid (VoF), which is a numerical technique that determines the location of a free surface, GL, and LL interface by following the Eulerian approach. This numerical method is a powerful tool for modeling the interfaces of incompressible and immiscible two-phase flows because it is able to predict the interface between two phases even though the interface is becoming too weak to capture the curvature of the interfacial line [136]. Ketabdari [137] discussed VoF regarding the governing equations, as well as its advantages and capabilities predicting the interface line between two phases with large deformation. Osher and Sethian [138] devised a new numerical algorithm to realize and determine the propagation of curvature-dependent speed, which can be combined with VoF. This algorithm approximates the equations of motion by using hyperbolic conversation laws. Many investigators employed this method when simulating a two-phase flow’s interface, e.g., [139,140,141,142]. The general applications of this method and a comprehensive review were conducted by Osher and Fedkiw [143], which discusses the variants and extension methods, such as fast methods for steady-state problems, diffusion generated motion and the variation level set approach. The growth of liquid film thickness was governed by one equation [144]. They assumed a constant pressure gradient in the channel direction and a linear velocity distribution over the liquid film thickness, emphasizing that the model was valid only for a film thickness less than near-wall grid size.

An effort to predict the bubble profile was analytically conducted by Bretherton [30], where he found that considering gravitation as a buoyancy force produced nonsensical results in the vertical configuration of a capillary tube. A critical value $\left({\mathsf{\rho }\mathrm{gR}}^2/\mathsf{\sigma }\right)$of 0.842 was introduced to show no upward movement of the bubble for the amount less than the critical value. Kolb and Cerro [145] found an axisymmetric bubble profile for the Ca greater than 0.1, where the lubrication’s law predicts the interface profiles and the flow patterns adequately. The effects of bubble and slug lengths on the mass transfer in a GL flow was experimentally studied by Berčič and Pintar [146]. Their results revealed that the amount of nitrite transported was independent of the gas bubble length and primarily depended on the liquid slug length. The flow field predictions were numerically obtained by Giavedoni and Saita [36], who illustrate the streamlines for showing the bubble profiles and the slug region. They found that with an increase in the Ca, the recirculation flow disconnected the GL interface and moved downstream. Brauner et al. [147] followed an exact analytical solution to model the interface curvature of two-dimensional stratified flow. Heil [43] numerically simulated the influence of fluid inertia, Re, on the flow patterns and the propagation of an air bubble on two flexible and rigid walls of a GL flow in a two-dimensional channel. Fujioka and Grotberg [148] numerically analyzed the propagation of liquid plugs inside a two-dimensional channel using a finite volume method. They showed that as the liquid plug grew, the frontal part swept the interfacial surfactant from the precursor liquid film. A pair of recirculation regions was found inside the liquid plug shortening as the magnitude of the velocity decreased. They also noted that micelle production and its transport process must be added to the numerical model when plug propagation occurs with a much higher concentration. Their results revealed that as the Re increases, a recirculation flow appears inside the plug core and is then skewed toward the rear part of the bubble. Kreutzer et al. [44] denoted that the inertia effects due to an increase in the Reynolds number elongated the nose and flattened the rear menisci of the gas bubble profile.

The influence of pressure gradient on the flow patterns and bubble profile were illustrated in Figure 9. According to this figure, as the pressure gradient increases, the elongated gas bubble is stretched along the tube axis and the impact of the no-slip conditions at the walls becomes weaker on the bubble shape. Strong, and clockwise circulation is predicted next to the head cap of the bubble resulted in bubble elongation when the pressure is intermediate. Falconi et al. [149] numerically and experimentally studied a vertical-upward three-dimensional Taylor flow in a square mili-channel using the VoF in-house finite volume code and μ-PIV measurements, respectively, Figure 10a. Instantaneous streamlines in Figure 10b show three vortices within the bubble; a large central vortex, two small toroidal vortices at the caps of the bubble. The main central vortex represents the highest z-component velocity next to the channel axis with the direction of rotation of opposite to the smaller vortices. Valizadeh et al. [150] conducted a numerical parametric study of non-Newtonian turbulent flow in a spiral duct by investigating the effects of geometry, consistency index, and power-law index values of viscosity. Since their study was dealt with a wide range of large Reynolds numbers in mili-channel, we do not discuss their findings anymore.

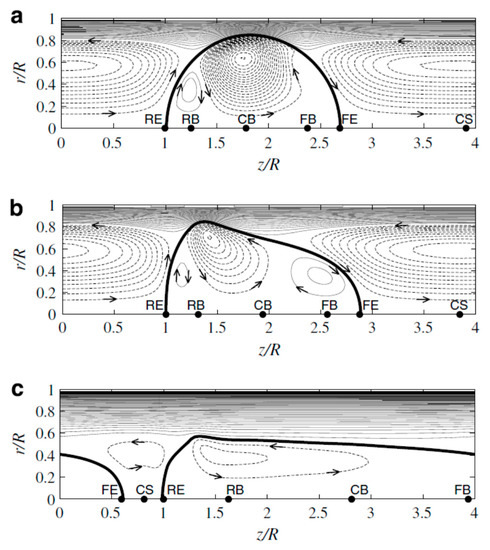
Figure 9. The streamlines inside and outside the bubbles for different pressure gradients (a) 85 M Pam⁻¹, (b) 850 M Pam⁻¹, and (c) 3000 M Pam⁻¹ [139]. Reproduced with permission from Fukagata, K.; Kasagi, N.; Ua-arayaporn, P.; Himeno, T., International Journal of Heat and Fluid Flow; published by Elsevier, 2007.

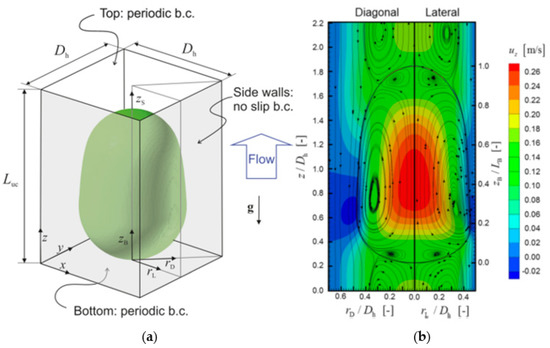
Figure 10. (a) The schematic of computational setup and coordinate system, and (b) instantaneous streamlines in the moving frame with the bubble and z-component velocity contour-plot in a fixed frame of reference [149]. Reproduced with permission from Falconi, C.J.; Lehrenfeld, C.; Marschall, H.; Meyer, C.; Abiev, R.; Bothe, D.; Reusken, A.; Schlüter, M.; Wörner, M., Physics of Fluids, published by AIP Publishing, 2016.

Both experimental and 3D numerical simulations were carried out by Abdollahi et al. [151] for liquid–liquid Taylor flow in a square channel with hydraulic diameters of 1 and 2 mm. Figure 11 displays the non-dimensional contour of the radial velocity component highlighting its key effects on heat transfer enhancement and recirculating flow within the slugs and the carrying phase. The highest radial velocity occurred at the nose and rear of the slug to make two vortices rotating in the opposite direction of the main recirculation zone in the middle of the slugs as observed by [139,149]. In a constant length unit cell, as the dispersed phase volume fraction increased, the liquid film thickness remained constant. The large recirculating zone in the middle of the slug show less axial flow and more radial flow as the droplet length was decreased. Their results also showed a huge increase of heat transfer rate up to 700% compared to single-phase flow indicating more effectiveness of short slugs on the heat transfer rate.

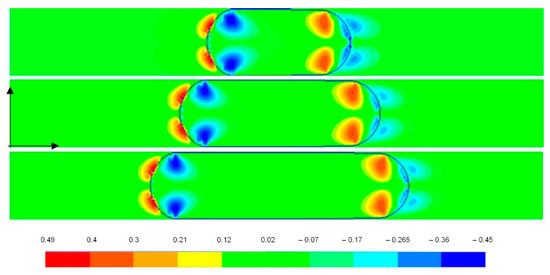
Figure 11. Radial velocity component contours with different dispersed phase volume fraction in a fixed unit cell length [151]. Reproduced with permission from Abdollahi, A.; Norris, S.E.; Sharma, R.N., Applied Thermal Engineering; published by Elsevier, 2020.

Xu et al. [152] numerically simulated 3D Taylor flow in a microchannel with a square cross-section under ultrasonic oscillation. A harmonic, vertical, and ultrasonic oscillating applied to microreactor as,

$${\mathrm{d}}_{\mathrm{y}}=\mathrm{A}\cos \left({\mathsf{\omega }}_0\mathrm{t}\right)$$

(9)

where the amplitude of the microreactor oscillation (A) is in the order of 2–8 microns and the angular frequency as a function of a constant vibrating frequency of $f_0=20\mathrm{kHz}$ is

$${\mathsf{\omega }}_0{=2\mathsf{\pi }f}_0$$

(10)

They found the channel oscillation affected the flow pattern and hydrodynamic characteristics in both liquid slugs and bubbles as shown in Figure 12 for Taylor flow in bends and oscillating bubbly flows, for example. Twisted flow structure in the liquid slugs improved mixing rate and transport phenomena. Wavy interface of bubble enhanced the interfacial area accelerating the mass transfer rate across the channel and improved the performance of microreactor. The sub-harmonic bubble surface wave was also created by the pressure pulsation in the parallel direction of the oscillation.

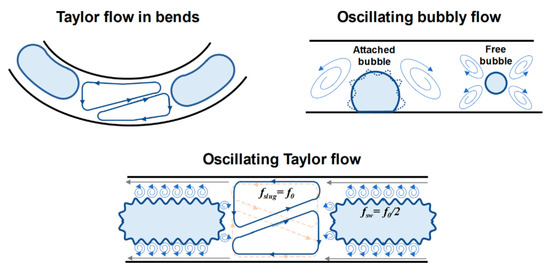
Figure 12. Schematic of different gas–liquid Taylor flow in microchannel; Taylor flow in bends, oscillating bubbly flow, and oscillating Taylor flow observed by [152]. Reproduced with permission from Xu, F.; Yang, L.; Liu, Z.; Chen, G., Chemical Engineering Science; published by Elsevier, 2021.

A summary of analytical and numerical investigations on the flow patterns and the formations of the gas/liquid slugs is presented in Table 6.

Table 6. Selected numerical and analytical studies on the flow patterns and the bubble or the droplet formation.

Comment(s)	Cross-Section	Phases	Reference
The film thickness at the advance of the rear meniscus oscillated The front and rear menisci were slightly different in curvatures Equilibrium bubble profile under surface tension and gravitational effects in a vertical tube	Circular	GL	[30]
The film thickness The profiles of front and rear film thickness The film thickness for very elongated gas bubbles	Circular and Square	GL	[35]
Bubble profile Flow fields around and between bubbles The motion of a bubble	Square	GL	[145]
The influence of velocity on the mass transport phenomenon The effects of liquid slug lengths on flow parameters	Circular	GL	[146]
Stronger recirculating flow region as the Ca decreased A liquid backflow was appeared at non-dimensional liquid thickness less than 1/3 Single stagnation point at the vertex of bubble curvature for no-recirculating flow conditions A decrease in the Ca made recirculating flow and moved the stagnation point further the vertex	Parallel plates and Circular	GL	[36]
The effects of flow rates on the interface curvature The influence of Eo and wall adhesion on the interface curvature	Circular	Two-phase (parametric)	[147]
The rear profile of bubble meniscus versus Ca and Re The effect of Re on the free surface undulations Gas bubble profile The curvature of the gas bubble	Circular	GL	[38]
The flow inertia effect was more significant even for deformable wall channels Flexible wall channels were more sensitive than rigid wall channels to the propagation of air bubbles into the walls at low Re and Re/Ca situations The pressure gradient in faraway positions of the tip of the air bubble was generated by Poiseuille flow	2D	GL	[43]
The propagation of liquid plug The adsorption/desorption process of the surfactant was modeled The Marangoni stress results in nearly zero surface velocity at the front meniscus	2D	GL	[148]
Refer to Table 5	Circular	GL	[44]
Slug flow development with time Either uniform or parabolic inlet velocity profile made the same-sized slugs The inlet mixing level influence on the slug lengths	2D	GL	[58]
Bubble shape in slug flow regime The effects of pressure gradient on the bubble profile The presence of gas bubbles made the circulating regions stronger causing a higher momentum transport	2D	GL	[139]
Curved vertical microchannel Slug flow development with time The gas bubbles moved faster than liquid slugs The impact of inlet geometry on the slug development	Circular	GL	[153]
The VoF and level-set methods The lack of enough adhesion on wall deformed the rear interface of the slugs	2D	LL	[106]
The VoF method Bubble shapes and formation The effects of superficial velocities on the bubble profiles The influence of nozzle diameter on the bubble formation and shapes	2D and 3D	GL	[154]
Structured-square grid minimizes inaccuracies in the surface tension calculation The process of bubble formation was happened periodically	2D	GL	[155]
The VoF and level set techniques Two commercial simulating software; Ansys and TransAT Bubble formation and development The effect of mixture velocity on the flow pattern and the bubble shapes	2D	GL	[156]
Bubble curvature in slug flow The characteristics of flow were dominantly determined by adherent liquid film thickness An optimized model to minimize the pressure drop and maximize the heat transfer rate	2D	GL	[26]

5. Flow Regime Transitions

A transition from one flow regime to another often occurs when the flow or boundary conditions are changed. The actual flow maps and the transition conditions specifically depend on a group of effective features during an experiment or the assumptions in numerical simulations [157,158,159,160]. For example, Bottin et al. [161] experimentally obtained various flow regimes for a horizontal two-phase flow in a pipe with an inner diameter of 0.1 m. They attempted to describe different flow regimes regarding the values of superficial velocities of the gas and liquid phases in the earlier experiments [162,163,164,165,166,167]. Some of the transition criteria from a flow regime to another in microchannels are presented in Table 7.

Table 7. Summary of proposed criteria for the transition of flow pattern.

Comment(s)	Criterion	Mechanism	Cross-Section	Phases	Reference
Bubbly to slug transition The collision frequency was so low when the void fraction was smaller than 10% The collision frequency was rapidly increased at a void fraction above 25% so that transition to slug flow was rapid even in a strongly liquid	When the rate of coalescence was much more than that of break-up and at a void fraction of 0.25 − 0.3	Bubble coalescence and void fraction	Circular	GL	[168]
Churn to annular happens at a value of	$\frac{{\mathrm{V}}_{\mathrm{g}}{\mathsf{\rho }}_{\mathrm{g}}^{0.5}}{{\left[\mathrm{gd}\left({\mathsf{\rho }}_{\mathrm{l}}{-\mathsf{\rho }}_{\mathrm{g}}\right)\right]}^{0.5}}$	Minimum gas and liquid superficial velocities	Circular	GL	[92]
Slug to slug-bubbly transition No stratified flow pattern was observed in channels with diameter less than 1 mm (it was also verified by [67])	$\mathrm{ReWe}={2.8\times 10}^5$ where, ${\mathrm{Re}=\mathsf{\rho }}_{\mathrm{l}}{\mathrm{dV}}_{\mathrm{g}}{/2\mathsf{\mu }}_{\mathrm{l}}$ ${\mathrm{We}=\mathsf{\rho }}_{\mathrm{l}}{\mathrm{dV}}_{\mathrm{g}}^2/2$	The production of Re and the We numbers	Rectangular	GL	[64]
The churn to annular transition occurred at lower in comparison to the flow reversal transition	the same as [92]	The same as [92]	Circular	GL	[66]
Bubbly to slug transition	0.25	Void fraction	Circular	GL	[163]
The transition from stratified to slug regimes	$\mathrm{H}\ge \left(1-\frac{\mathsf{\pi }}{4}\right)\mathrm{d}$ ${\mathrm{Bo}}_{\mathrm{cr}}=4.7$	Kelvin-Helmholtz instability and critical Bond number	Circular	GL	[164]
Upward and vertical flow For several transitions The flowing quality was more suitable than the thermal equilibrium quality to correlate the flow-regime transitions	For bubbly to slug: ~0.3	Void fraction	Circular	GL	[169]
Concentric and eccentric annuli (eccentricity 50%) Upward and vertical flow Mathematical modeling Insignificant effect of eccentricity on transitions for many transitions	$\frac{\mathrm{V}}{{\mathrm{V}}_{\max }}$ and ${\displaystyle \int }\mathrm{PDF}\mathrm{dv}$	Probability Density Function (PDF)	Circular	GL	[170]
The dominant surface tension in stratified flow regime	$\mathrm{o}=\frac{{\left(2\mathsf{\pi }\right)}^2\mathsf{\sigma }}{\left({\mathsf{\rho }}_{\mathrm{l}}{-\mathsf{\rho }}_{\mathrm{g}}\right){\mathrm{d}}^2\mathrm{g}}$	Linear stability analysis	Circular	GL	[171]
Bubble to slug transition Upward and vertical flow Turbulence-dependent rate processes controlled the transition at a high flow rate	$~34\%$	Average void fraction	Circular	GL	[172]
Discussed in the text	$\frac{{\mathrm{Re}}_{\mathrm{g}}}{{\mathrm{Re}}_{\mathrm{l}}}={464.16\mathrm{Su}}^{-\frac{2}{3}}$ $\{\begin{array}{c}\frac{{\mathrm{Re}}_{\mathrm{g}}}{{\mathrm{Re}}_{\mathrm{l}}}={4641.6\mathrm{Su}}^{-\frac{2}{3}}\\ {\mathrm{Re}}_{\mathrm{g}}{=2\times 10}^{-9}{\mathrm{Su}}^2\end{array}$	Suratman number	Circular	GL	[65]
Bubble to slug transition Upward and vertical flow	(N/A)	Void fraction	Circular	GL	[173]
Bubbly to slug transition The formulation of interfacial transport equations The classification of bubble interactions The categorization of basic mechanisms of bubble coalescence and breakup	(N/A)	Interfacial area concentrations	Circular	GL	[174]
Upward and vertical flow for a bubble to slug transition	for ${\mathrm{s}<\mathrm{d}}_{\mathrm{b}}$ $\mathsf{\alpha }=0.2$ for ${\mathrm{d}}_{\mathrm{b}}\le \mathrm{s}\le {3\mathrm{d}}_{\mathrm{b}}$ $\mathsf{\alpha }=\frac{\mathrm{s}}{{20\mathrm{d}}_{\mathrm{b}}}+0.15$ for ${\mathrm{s}>3\mathrm{d}}_{\mathrm{b}}$ $\mathsf{\alpha }=0.3$	Void fraction	Rectangular	GL	[175]
Discussed in the text	Discussed in the text	Liquid fraction	Square	GL	[72,100]
The bubble size distribution played a crucial role in the flow regime transition and flow patterns	(N/A)	Population Balance Model (PBM)	Circular	GL	[176]
Slug into parallel transition happened at small flow rates and large superficial flow ratio By increasing the flow rate, the chaotic flow was changed into annular Equivalent radius was correlated to the We numbers and holdup fraction	Specific range of We for each flow pattern	Weber number	Rectangular	LL	[82]
Slug to deformed interface occurred for ${2.5<\mathrm{Q}}_{\mathrm{c}} /{\mathrm{Q}}_{\mathrm{d}}<5$ Slug to drop transition happened in the ${3<\mathrm{Q}}_{\mathrm{d}} /{\mathrm{Q}}_{\mathrm{c}}<6$	$\frac{{\mathrm{Q}}_{\mathrm{c}}}{{\mathrm{Q}}_{\mathrm{d}}}$	Volumetric flow rate ratio	Circular	LL	[45]
Bubbly to slug transition Vertical and upward configuration Effect of bubble size and diameter on the transition	Maximum bubble size	PBM	Circular	LL	[101]
Bubbly to slug transition The influence of the bubble population at the inlet region on the regime transition An increase in bubble diameter transits the flow map from bubbly to slug A decrease in tube diameter changed the flow patterns from slug to bubbly regimes	Bubble diameter	PBM	Circular	GL	[177,178]
Stable slug regime in the square duct at ${\mathrm{Re}}_{\mathrm{g}}<24$ Stable slug regime in the circular duct at ${\mathrm{Re}}_{\mathrm{g}}<36$ Stable slug regime in the rectangular duct at ${\mathrm{Re}}_{\mathrm{g}}<40$ Stable slug regime in the trapezoidal duct at ${\mathrm{Re}}_{\mathrm{g}}<72$ Annular flow regime at $\frac{{\mathrm{Re}}_{\mathrm{l}}}{{\mathrm{Ca}}_{\mathrm{l}}}\le {24\mathrm{Re}}_{\mathrm{g}}-7638$	$\frac{{\mathsf{\rho }}_{\mathrm{g}}{\mathrm{V}}_{\mathrm{g}}{\mathrm{d}}_{\mathrm{H}}}{{\mathsf{\mu }}_{\mathrm{g}}}$	Reynolds number of gas phase	Square and Trapezoidal	GL	[77]
Slug to churn transition and flow map identification	$\mathsf{\alpha }\ge f_{\alpha }$	Void fraction	Circular	GL	[179]
A transition on the slug producing from squeezing to dripping occurred at the junction	${\mathrm{Q}}_{\mathrm{g}}>20$	Gas volumetric flow rate	Rectangular	GL	[180]
Above the transition value of Ca, an elliptic or oval cross-section area of the gas bubble was observed, and viscous shear overcame the interfacial tension	0.01	Capillary number	Quasi-trapezoidal	GL	[80]

Jayawardena et al. [65] showed the ratio of gas to liquid Reynolds numbers as a function of the Suratman number for recognizing the flow maps. An accurate transitional value of the Su occurs between 10⁴ and 10⁷ from a bubble to a slug transition. However, the transition from a slug regime to an annular regime has two different criteria regarding the value of Su, greater and less than 10⁶. The motion of the gas bubble through a microchannel with a square cross-sectional area was experimentally studied by Cubaud and Ho [72] and Cubaud et al. [100]. Regarding the liquid fraction, Q_l / (Q_l + Q_g), they classified the flow patterns into several categories: bubbly, wedging, slug, annular, and dry, which are illustrated in Figure 13. Their experiments specified some critical liquid fractions for a transition from one flow regime to another, which are ~0.75 from bubbly to wedging, ~0.20 from wedging to slug, ~0.04 from slug to annular, and ~0.005 from annular to dry transitions. They also found that at low liquid velocity, the gas bubbles clogged at the sharp corner of the channel bend before merging and eventually passing the bend. The corner of the channel bend trapped a gas bubble to merge into another upcoming bubble, producing a single larger bubble.

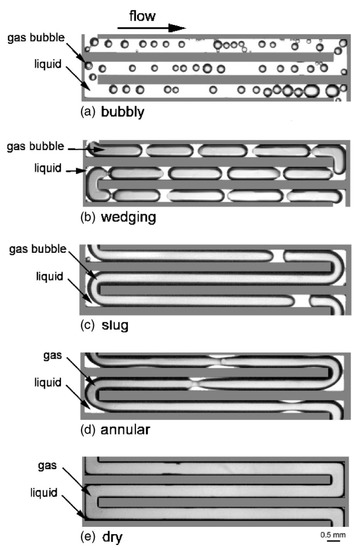
Figure 13. The different flow patterns from high to low liquid fraction [100] (Reproduced with permission from Cubaud, T.; Ulmanella U.; Ho, C.M., Fluid Dynamics Research; published by Elsevier, 2006).

6. Slug Length

The hydrodynamic characteristics of slug flows are highly dependent on the profile and length of the liquid slug. Bubble length measuring was experimentally conducted by Marchessault and Mason [29], where the change in the shape of the liquid film thickness around short bubbles was likely caused by end effects, buoyancy, and cylindrical model assumption. According to Schwartz et al. [32], the liquid film thickness left behind a gas bubble in a capillary was adequately close to the predictions of lubrication theory when the length of bubbles was short. They also found that for the length of bubbles shorter than the tube diameter, the thin film layer region was no longer observed. According to Kashid and Agar [101] and Kashid et al. [102], slug length is significantly affected by the capillary number and the junction dimensions. In a slug flow regime, the lengths of slugs of both phases are greater than their diameters, but at relatively low volumetric flow rates the slug pattern is established with the length equal to the inner diameter of the tube. In the case of a high volumetric flow rate and surrounded water slugs by cyclohexane, the deformed interface regime is made with long water slugs and small cyclohexane droplets. A few simple linear equations to compute the stable slug lengths were reported by [163,170,181,182], which indicated that the ratio of the liquid slug length to the tube diameter remained at a constant value of 16, 20.7, 7.5, and 21.5, respectively.

Table 8 presents the correlations for measuring the length of liquid slugs of two-phase flow in a microchannel including the void fractions. Beyond the data provided in Table 8, two other recent studies, Han and Chen [183] and Qian et al. [184], are concerned with the slug length and its formation, but the correlations of slug length were not proposed by the authors. The first study numerically simulated the droplet formation at a T-junction in a microchannel. The effective diameter of droplets was studied in terms of contact angle, continuous phase viscosity, flow rate ratio, and interfacial tension. The latter experimental investigation considered the influence of flow rate on the liquid slug generation in a microchannel with a square cross-sectional area. They found the slug lengths vary from 0.923 to 1.186 mm based on different flow rates of the continuous and dispersed phases. The distance between subsequent water slugs was also measured.

Table 8. The literature on the correlation of the slug length in two-phase flows in circular and non-circular cross-section area microchannels.

Correlation	Comment(s)	Flow Parameter	Cross-Section	Phases	Method	Reference
$\frac{{\mathrm{L}}_{\mathrm{g}}}{\mathrm{d}}= {\left(\frac{\mathrm{Re}}{{\mathrm{Eo}}^2}\right)}^{0.63}=0.0878{\left(\frac{{\mathrm{V}}_{\mathrm{s}}{\mathsf{\rho }}_{\mathrm{l}}{\mathsf{\sigma }}^2}{{\mathsf{\mu }}_{\mathrm{l}}{\left({\mathsf{\rho }}_{\mathrm{l}}{-\mathsf{\rho }}_{\mathrm{g}}\right)}^2{\mathrm{d}}^3{\mathrm{g}}^2}\right)}^{0.63}$ $\frac{{\mathrm{L}}_{\mathrm{l}}}{\mathrm{d}}={\left(\frac{1}{\mathrm{Re}\mathrm{Eo}}\right)}^{1.2688}=3451{\left(\frac{{\mathsf{\mu }}_{\mathrm{l}}\mathsf{\sigma }}{\left({\mathsf{\rho }}_{\mathrm{l}}{-\mathsf{\rho }}_{\mathrm{g}}\right){\mathsf{\rho }}_{\mathrm{l}}{\mathrm{V}}_{\mathrm{g}}{\mathrm{d}}^3\mathrm{g}}\right)}^{1.2688}$	The gas and liquid slug lengths versus dimensionless numbers The effect of gas superficial velocity on slug lengths	$\mathrm{d}\le 4\mathrm{mm}$ $55\le \mathrm{Re}\le 2000$ $0.0015\le \mathrm{Ca}\le 0.1$	Circular	GL	Experimental	[185]
${\mathrm{L}}_{\mathrm{l}}=\frac{{1-\mathsf{\epsilon }}_{\mathrm{g}}}{{\mathsf{\epsilon }}_{\mathrm{g}}}\frac{\mathsf{\pi }}{6}\frac{{\mathrm{d}}_{\mathrm{g}}^3}{{\mathrm{d}}^2}$	The slug length was extensively depended on physical means of the experiment, operational conditions, and delivering system	$\mathrm{d}=50\mathrm{mm}$ ${0.07\mathrm{ms}}^{-1}\le {\mathrm{V}}_{\mathrm{g}}\le {0.27\mathrm{ms}}^{-1}$ ${0.07\mathrm{ms}}^{-1}\le {\mathrm{V}}_{\mathrm{l}}\le {0.27\mathrm{ms}}^{-1}$	Circular	GL	Experimental	[186]
$\frac{\mathrm{L}}{\mathrm{w}}=1+\mathsf{\alpha }\frac{{\mathrm{Q}}_{\mathrm{d}}}{{\mathrm{Q}}_{\mathrm{c}}}$	The squeezing mechanism affected the size of droplets or bubbles	$\mathrm{w}=0.1\mathrm{mm}$ $\mathrm{h}=0.033\mathrm{mm}$ $10\mathrm{mPas}\le {\mathsf{\mu }}_{\mathrm{c}}\le 100\mathrm{mPas}$ $10\mathrm{mPas}\le {\mathsf{\mu }}_{\mathrm{d}}\le 100\mathrm{mPas}$ ${\mathrm{Q}}_{\mathrm{c}}=0.00278,0.0278,{0.278\mathsf{\mu }\mathrm{Ls}}^{-1}$	Rectangular	LL GL	Experimental	[187]
$\frac{{\mathrm{L}}_{\mathrm{uc}}}{\mathrm{d}}={1.637\mathsf{\epsilon }}^{-0.893}{\left(1-\mathsf{\epsilon }\right)}^{-1.05}{\mathrm{Re}}^{-0.075}{\mathrm{Ca}}^{-0.0687}$ $\frac{{\mathrm{L}}_{\mathrm{g}}}{\mathrm{d}}={1.637\mathsf{\epsilon }}^{0.107}{\left(1-\mathsf{\epsilon }\right)}^{-1.05}{\mathrm{Re}}^{-0.075}{\mathrm{Ca}}^{-0.0687}$ $\frac{{\mathrm{L}}_{\mathrm{l}}}{\mathrm{d}}={1.637\mathsf{\epsilon }}^{-0.893}{\left(1-\mathsf{\epsilon }\right)}^{-0.05}{\mathrm{Re}}^{-0.075}{\mathrm{Ca}}^{-0.0687}$	A decrease in superficial liquid velocity increased the gas slug length An increase in superficial gas velocity enhanced the gas slug length Both slug lengths were moderately affected by the surface tension and wall surface adhesion The gravitational effects on the slug lengths can be ignored	$\mathrm{d}=0.25,0.5,0.75,1,2,3\mathrm{mm}$ $15\le \mathrm{Re}\le 1500$ ${2.78\times 10}^{-4}\le \mathrm{Ca}\le 0.01$ $0.09\le \mathsf{\epsilon }\le 0.91$	2D and Circular	GL	Numerical	[58]
$\frac{{\mathrm{L}}_{\mathrm{d}}}{\mathrm{w}}=1.59{\left(\frac{{\mathrm{Q}}_{\mathrm{c}}}{{\mathrm{Q}}_{\mathrm{d}}}\right)}^{-0.2}{\mathrm{Ca}}^{-0.2}$	The effects of wettability and the shape of the interface as the volumetric flow rates ratio on the plug length The equilibrium of the shear force and interfacial tension in the form of Ca on the plug length	$\mathrm{w}=0.4\mathrm{mm}$ $\mathrm{Ca}<0.1$ $\frac{{\mathrm{Q}}_{\mathrm{c}}}{{\mathrm{Q}}_{\mathrm{d}}}>1$	Square	GL	Experimental	[59]
$\frac{{\mathrm{L}}_{\mathrm{l}}}{\mathrm{w}}=0.369\ln \left[{\left(\frac{\mathrm{Re}}{\mathrm{Ca}}\right)}^{0.33}\frac{\frac{{\mathrm{V}}_{\mathrm{l}}}{{\mathrm{V}}_{\mathrm{l}}{+\mathrm{V}}_{\mathrm{g}}}}{509.12}\right]+3.15$	An increase in superficial velocities enhanced the slug length Larger bend diameter of the meandering channel made longer slugs	$0.2\mathrm{mm}\le \mathrm{w}\le 0.4\mathrm{mm}$ $\mathrm{h}=0.15\mathrm{mm}$ ${4.7\times 10}^{-3}\le \mathrm{Ca}\le {7.4\times 10}^{-3}$ $11.6\le \mathrm{Re}\le 22.6$ ${20.4\times 10}^3\le \mathrm{Pe}\le {39.6\times 10}^3$ ${0.01\mathrm{ms}}^{-1}\le {\mathrm{V}}_{\mathrm{l}}\le {0.07\mathrm{ms}}^{-1}$ ${\mathrm{V}}_{\mathrm{g}}={0.08\mathrm{ms}}^{-1}$	Rectangular	GL	Experimental and Numerical	[60]
$\frac{{\mathrm{L}}_{\mathrm{g}}}{\mathrm{d}}=2$ $\frac{{\mathrm{L}}_{\mathrm{s}}}{\mathrm{d}}=1.3$	The inlet conditions affect the bubble length significantly The lengths were computed at the centerline of the channel	$\mathrm{d}=0.5\mathrm{mm}$ ${\mathrm{V}}_{\mathrm{g}}={0.245\mathrm{ms}}^{-1}$ ${\mathrm{V}}_{\mathrm{l}}={0.255\mathrm{ms}}^{-1}$ $\mathrm{Re}=280$ $\mathrm{Ca}=0.006$	2D	GL	Numerical	[155]
$\frac{{\mathrm{d}}_{3\mathrm{D}}}{\mathrm{h}}=0.334{\left(\frac{\frac{\mathrm{w}}{\mathrm{h}}-0.89}{\frac{\mathrm{w}}{\mathrm{h}}+0.79}\right)}^{0.5}{\mathrm{Ca}}_{\mathrm{c}}^{-0.5}$ and at $\frac{\mathrm{w}}{\mathrm{h}}>4.5$: $\frac{{\mathrm{d}}_{3\mathrm{D}}}{\mathrm{h}}={0.334\mathrm{Ca}}_{\mathrm{c}}^{-0.5}$	Droplet size at the junction The dependency of droplet diameter on the channel width was insignificant at large width to height ratio	$\mathrm{w}=22.6\mathrm{and}23.7\mathsf{\mu }\mathrm{m}$ $\mathrm{h}=5\mathsf{\mu }\mathrm{m}$ $0.008\le {\mathrm{Ca}}_{\mathrm{c}}\le 0.2$	Rectangular	LL	Experimental	[61]
$\frac{{\mathrm{L}}_{\mathrm{g}}}{{\mathrm{d}}_{\mathrm{H}}}={1.3\mathsf{\epsilon }}^{0.07}{\left(1-\mathsf{\epsilon }\right)}^{-1.01}{\mathrm{We}}^{-0.1}$	Variation of slug length with volumetric gas and liquid flow rates	${\mathrm{d}}_{\mathrm{H}}=0.15,0.29,\mathrm{and}0.4\mathrm{mm}$ $0.1\le \mathrm{We}\le 26$ ${0.02\mathrm{ms}}^{-1}\le {\mathrm{V}}_{\mathrm{g}}\le {1.2\mathrm{ms}}^{-1}$ ${0.004\mathrm{ms}}^{-1}\le {\mathrm{V}}_{\mathrm{l}}\le {0.7\mathrm{ms}}^{-1}$ $0.06\le \mathsf{\epsilon }\le 0.85$	Square	GL	Experimental	[188]
$\frac{{\mathrm{L}}_{\mathrm{g}}}{\mathrm{w}}=\frac{{\mathrm{V}}_{\mathrm{g}}}{{\mathrm{V}}_{\mathrm{l}}}\left(1+{1.37\mathrm{We}}^{-0.349}\right)$ $\frac{{\mathrm{L}}_{\mathrm{l}}}{\mathrm{w}}=1.157{\left(\frac{{\mathrm{V}}_{\mathrm{g}}}{{\mathrm{V}}_{\mathrm{l}}{+\mathrm{V}}_{\mathrm{g}}}\right)}^{-0.365}{\left(\frac{{\mathrm{V}}_{\mathrm{l}}}{{\mathrm{V}}_{\mathrm{l}}{+\mathrm{V}}_{\mathrm{g}}}\right)}^{-0.373}{\mathrm{We}}^{-0.208}$	The effects of flow rates on the slug lengths	$\mathrm{w}=0.75\mathrm{mm}$ $\mathrm{h}=0.28\mathrm{mm}$ ${0.08\mathrm{ms}}^{-1}\le {\mathrm{V}}_{\mathrm{l}}\le {0.5\mathrm{ms}}^{-1}$ ${0.155\mathrm{ms}}^{-1}\le {\mathrm{V}}_{\mathrm{g}}\le {0.952\mathrm{ms}}^{-1}$	Rectangular	GL	Experimental	[189]
${\mathrm{L}}_{\mathrm{d}}=\frac{1\text{±}\sqrt{1-4\mathrm{w}\left(0.96{\left(\frac{{\mathrm{Q}}_{\mathrm{d}}}{{\mathrm{Q}}_{\mathrm{c}}}\right)}^{-1.5}\right)}}{2\left(0.96{\left(\frac{{\mathrm{Q}}_{\mathrm{d}}}{{\mathrm{Q}}_{\mathrm{c}}}\right)}^{-1.5}\right)}$ ${\mathrm{L}}_{\mathrm{c}}=\frac{0.73\mathrm{w}{\left(\frac{{\mathrm{Q}}_{\mathrm{d}}}{{\mathrm{Q}}_{\mathrm{c}}}\right)}^{-1.1}}{{\mathrm{L}}_{\mathrm{d}}}$	The slug lengths of dispersed and continuous phases The slug formation process was not affected by pressure fluctuations Varying slug lengths	$\mathrm{w}=0.1\mathrm{mm}$ $\mathrm{h}=0.095\mathrm{mm}$ ${4\mathsf{\mu }\mathrm{Lmin}}^{-1}\le {\mathrm{V}}_{\mathrm{l}}\le {44\mathsf{\mu }\mathrm{Lmin}}^{-1}$ $0.6\le \frac{{\mathrm{Q}}_{\mathrm{d}}}{{\mathrm{Q}}_{\mathrm{c}}}\le 3$ ${\mathsf{\mu }}_{\mathrm{d}}=1\mathrm{cs}$	Rectangular	LL	Experimental	[190]
${\mathrm{L}}_{\mathrm{d}}={0.0116\mathrm{V}}_{\mathrm{uc}}^{-0.32}{\mathrm{d}}^{1.25}{\left(\frac{{\mathrm{Q}}_{\mathrm{a}}}{{\mathrm{Q}}_{\mathrm{o}}}\right)}^{0.89}$	The length of dispersed slugs The effects of operational conditions on the slug lengths The influence of slug velocity and flow rate on the slug length	$\mathrm{d}=0.6,0.8,1\mathrm{mm}$ $0.5\le \frac{{\mathrm{Q}}_{\mathrm{a}}}{{\mathrm{Q}}_{\mathrm{o}}}\le 3$ ${0.01\mathrm{ms}}^{-1}\le {\mathrm{V}}_{\mathrm{l}}\le {0.03\mathrm{ms}}^{-1}$	Circular	LL	Experimental	[191]
${\mathrm{L}}_{\mathrm{l}}=\frac{1}{2}\left({\mathrm{t}}_{\mathrm{CH}1}{+\mathrm{t}}_{\mathrm{CH}2}\right){\mathrm{V}}_{\mathrm{l}}$	A slug flow in superhydrophobic microchannel An increase in gas flow rate decreased the slug length	$\mathrm{w}=0.8\mathrm{mm}$ $\mathrm{h}=0.9\mathrm{mm}$ $6<\mathrm{Re}<40$ ${5\mathrm{mLmin}}^{-1}\le {\mathrm{Q}}_{\mathrm{g}}\le {30\mathrm{mLmin}}^{-1}$ $2\le \frac{{\mathrm{Q}}_{\mathrm{g}}}{{\mathrm{Q}}_{\mathrm{l}}}\le 300$	Rectangular	GL	Experimental	[180]

7. Pressure Drop

The interactive structure of different phases and between phases and solid walls represent the predominant parameters to describe the flow pattern of multiphase flow and pressure loss through the channel. Two homogenous and separated flow models have been employed by researchers to predict the frictional pressure drop [62]. The first model postulates the same velocity for both gas and liquid phases, which implies that the slip ratio at the interactive boundaries is equal to one. This model considers two or more different phases as a single phase. The values of the flow properties are dependent on the quality, while the frictional pressure drop can be obtained by single-phase theory [63]:

$$\mathrm{f}=\left(\frac{1}{2}\frac{\mathrm{d}}{{\mathsf{\rho }\mathrm{V}}^2}\right){\left(\frac{\mathrm{dp}}{\mathrm{d}z}\right)}_{\mathrm{l}}$$

(11)

where z indicates the axial direction of the channel.

The Hagen–Poiseuille equation is a physical law to compute the pressure drop of a Newtonian and incompressible flow through a long and circular tube with a constant cross-section area [63]. The flow regime remained laminar due to the Reynolds number of the microflows, where the friction factor becomes $\mathrm{f}=16/\mathrm{Re}$ for round tubes and the equation above can be rearranged as:

$$\Delta \mathrm{p}=\frac{16}{\mathrm{Re}}\left(\frac{1}{2}{\mathsf{\rho }\mathrm{V}}^2\right)\frac{4\mathrm{L}}{\mathrm{d}}$$

(12)

where L and d are the length and the diameter of the tube, respectively.

The presence of the second phase in two-phase flow causes an additional term to the pressure loss of a single-phase flow and does not satisfy Poiseuille’s law anymore. Therefore, the total pressure drop $(\Delta {\mathrm{p}}_{\mathrm{t}})$ is the sum of the single-phase pressure drop $(\Delta {\mathrm{p}}_{\mathrm{s}})$ and the interaction pressure drop $(\Delta {\mathrm{p}}_{\mathrm{int}})$ caused by introducing the secondary phase. These pressure drop components can be shown together as follows:

$${\mathrm{fRe}}_{\mathrm{t}}=16+\frac{\Delta {\mathrm{p}}_{\mathrm{int}}^{*}}{{2\mathrm{L}}^{*}}$$

(13)

The non-dimensional pressure drop and length scale in Equation (12) were proposed by Walsh et al. [54], as below:

$$\Delta {\mathrm{p}}_{\mathrm{int}}^{*}=\frac{\Delta {\mathrm{p}}_{\mathrm{int}}\mathrm{d}}{\mathsf{\mu }\mathrm{V}}$$

(14)

$${\mathrm{L}}^{*}=\frac{{\mathrm{L}}_{\mathrm{s}}}{\mathrm{d}}$$

(15)

where μ and L_s denote the dynamic viscosity of the continuous phase and the length of liquid slugs, respectively.

The pressure drop over a unit cell can also be described by three components [51,88,107]:

$$\Delta {\mathrm{p}}_{\mathrm{uc}}=\Delta {\mathrm{p}}_{\mathrm{s}}+\Delta {\mathrm{p}}_{\mathrm{f}}+\Delta {\mathrm{p}}_{\mathrm{cap}}$$

(16)

Furthermore, Abiev [192] assumed the total pressure losses in the capillary tubes were a summation of two components, named the formation of a new surface during the motion of bubble and the arrangement of a velocity profile in liquid slugs as below (refer to Table 9 for further details):

$$\Delta {\mathrm{p}}_{\mathrm{t}}=\Delta {\mathrm{p}}_{\Delta \mathrm{F}}+\Delta {\mathrm{p}}_{\mathrm{trans}}$$

(17)

Table 9. The literature on pressure drop correlations of the two-phase flow in the microchannels.

Correlation	Comment(s)	Flow Parameter	Cross-Section	Phases	Method	Reference
Across a bubble $\Delta \mathrm{p}=14.894\frac{\mathsf{\sigma }}{\mathrm{d}}{\mathrm{Ca}}^{\frac{2}{3}}$	Dynamic pressure component was dominantly greater than the static value (lubrication approximation) for small Ca The main pressure drop caused by a slight difference between the head and rear curvatures of the bubble	$\mathrm{d}=1\mathrm{mm}$ ${1\times 10}^{-3}\le \mathrm{Ca}\le 0.01$	Circular	GL	Experimental and Analytical	[30]
$\Delta \mathrm{p}=\frac{{2\mathsf{\mu }}_{\mathrm{l}}{\mathrm{V}}_{\mathrm{g}}}{\mathrm{d}}\left[\frac{64\mathsf{\nu }}{{\mathsf{\pi }\mathrm{d}}^3}+\mathrm{K}\right]$	The end effect (K) of the bubble was shown by a constant value of 45 for $0<\mathrm{Re}<270$ a function of the Re of ${0.163(\mathsf{\rho }}_{\mathrm{l}}{\mathrm{V}}_{\mathrm{g}}{\mathrm{D})/2\mathsf{\mu }}_{\mathrm{l}}$ for $270<\mathrm{Re}<360$	$0.5\mathrm{mm}\le \mathrm{d}\le 0.8\mathrm{mm}$ $0.5\le {\mathrm{U}}_{\mathrm{s}}/{\mathrm{U}}_{\mathrm{b}}\le 1$ $\frac{23\le {\mathsf{\mu }}_{\mathrm{l}}}{{\mathsf{\mu }}_{\mathrm{b}}\le 58}$	Circular	GL	Experimental	[64]
For circular tube: $\Delta \mathrm{p}={9.4\mathrm{Ca}}^{\frac{2}{3}}-{12.6\mathrm{Ca}}^{0.95}$ For Square tube: axisymmetric bubbles, $\Delta \mathrm{p}={3.14\mathrm{Ca}}^{0.14}$ non-axisymmetric bubbles, $\Delta \mathrm{p}={12.2\mathrm{Ca}}^{0.55}$	Matched Asymptotic Analysis Infinite bubbles, $\mathrm{L}>\mathrm{d}$ Finite bubbles, $\mathrm{L}<\mathrm{d}$	${3\times 10}^{-3}\le \mathrm{Ca}\le 0.01$ ${\mathrm{Bo}=4\times 10}^{-4}$	Circular and Square	GL	Numerical and Analytical	[35]
$\Delta \mathrm{p}=\Delta {\mathrm{p}}_{\mathrm{l}}{\mathsf{\epsilon }}_{\mathrm{l}}\left[1+0.065{\left(\frac{{\mathrm{L}}_{\mathrm{s}}}{{\mathrm{d}\mathrm{Re}}_{\mathrm{l}}}\right)}^{-0.66}\right]$	An entry region friction model	(N/A)	Circular	GL	Numerical and Analytical	[39]
In uniform film thickness region: $\Delta \mathrm{p}=-\frac{1}{{\mathrm{R}}_{\mathrm{s}\infty }}$	Bubble profiles For $0.1<\mathrm{Ca}<0.54:$axisymmetric bubbles, For $\mathrm{Ca}>0.54:$ bubbles moved faster than liquid and complete by-pass was realized For $\mathrm{Ca}<0.54:$bubbles moved slower than liquid and reverse flow occurred For $\mathrm{Ca}=0.54:$ bubbles traveled as the same velocity as the liquid and no stagnation pressure	$\mathrm{Ca}=0.16,0.54,\mathrm{and}1$ $\mathrm{We}\ll 1.0$	Square	GL	Numerical and Analytical	[145]
$\Delta \mathrm{p}=\Delta {\mathrm{p}}_{\mathrm{l}}{\mathsf{\alpha }}_{\mathrm{l}}^{-\frac{1}{2}}$	The pressure drop of two-phase flow was greater than single-phase flow The Lockhart and Martinelli model did not adequately predict the pressure drop for the laminar flow regime [193] The viscosity of the liquid phase had a key role in the frictional part of the pressure loss	${\mathrm{d}}_{\mathrm{H}}=0.2\mathrm{and}0.525\mathrm{mm}$ $0.001\le \mathrm{Ca}\le 0.2$ $0.004\le {\mathrm{V}}_{\mathrm{g}}\le 11$ $0.001\le {\mathrm{V}}_{\mathrm{l}}\le 0.2$	Square	GL	Experimental	[72]
$\Delta \mathrm{p}=16\left(1+0.17\frac{\mathrm{d}}{{\mathrm{L}}_{\mathrm{s}}}{\left(\frac{\mathrm{Re}}{\mathrm{Ca}}\right)}^{\frac{1}{3}}\right)$ $\Delta \mathrm{p}=14.2\left(1+0.17\frac{\mathrm{d}}{{\mathrm{L}}_{\mathrm{s}}}{\left(\frac{\mathrm{Re}}{\mathrm{Ca}}\right)}^{\frac{1}{3}}\right)$	Pressure drop over the slugs	$\mathrm{d}=2\mathrm{mm}$ $0.002\le \mathrm{Ca}\le 0.04$ $0.04\le {\mathrm{V}}_{\mathrm{l}}\le 0.3$ $\mathrm{Re}\le 900$	Circular and Square	GL	Experimental and Numerical	[44,53]
$\Delta \mathrm{p}=32\frac{{\mathrm{Q}}_{\mathrm{l}}{\mathsf{\mu }}_{\mathrm{l}}{\mathrm{L}}_{\mathrm{g}}}{{\mathrm{hf}}^3}$	A decrease in the channel curve radius enhanced the pressure drop An increase in vorticity enhanced the pressure linearly Pressure drop was decreased with	$0.2\mathrm{mm}\le \mathrm{w}\le 0.4\mathrm{mm}$ $\mathrm{h}=0.15\mathrm{mm}$ ${4.7\times 10}^{-3}\le \mathrm{Ca}\le {7.4\times 10}^{-3}$ $11.6\le \mathrm{Re}\le 22.6$ ${20.4\times 10}^3\le \mathrm{Pe}\le {39.6\times 10}^3$ ${0.01\mathrm{ms}}^{-1}\le {\mathrm{V}}_{\mathrm{l}}\le {0.07\mathrm{ms}}^{-1}$ ${\mathrm{V}}_{\mathrm{g}}={0.08\mathrm{ms}}^{-1}$	Rectangular	GL	Experimental and Numerical	[60,183]
$\Delta {\mathrm{p}=\mathsf{\epsilon }}_{\mathrm{l}}\mathrm{f}\left(\frac{4\mathrm{L}}{\mathrm{d}}\right)\left[\frac{1}{2}{\mathsf{\rho }}_{\mathrm{l}}{\left({\mathrm{V}}_{\mathrm{l}}{+\mathrm{V}}_{\mathrm{g}}\right)}^2\right]$	The pressure distribution in liquid slug and gas bubble was significantly different due to the interfacial effects The interfacial pressure difference at the nose was greater than the tail of the gas bubble	$\mathrm{d}=0.5\mathrm{mm}$ ${\mathrm{V}}_{\mathrm{g}}={0.245\mathrm{ms}}^{-1}$ ${\mathrm{V}}_{\mathrm{l}}={0.255\mathrm{ms}}^{-1}$ $\mathrm{Re}=280$ $\mathrm{Ca}=0.006$	2D	GL	Numerical	[152]
Total pressure drop $\Delta \mathrm{p}=16+\frac{7.16{\left(3\mathrm{Ca}\right)}^{\frac{2}{3}}}{{2\mathrm{L}}^{*}\mathrm{Ca}}$ Curve fitting after scaled using ${\left(\frac{\mathrm{Ca}}{\mathrm{Re}}\right)}^{\frac{1}{3}}$ $\Delta \mathrm{p}=16+\frac{1.92}{{\mathrm{L}}^{*}}{\left(\frac{\mathrm{Re}}{\mathrm{Ca}}\right)}^{\frac{1}{3}}$	The pressure drop behavior with ${\mathrm{L}}^{*}{\left(\mathrm{Ca}/\mathrm{Re}\right)}^{\frac{1}{3}}$ was approximated by two asymptotes The total pressure drop was a summation of Poiseuille flow and Taylor components Poiseuille flow was dominant when ${\mathrm{L}}^{*}{\left(\mathrm{Ca}/\mathrm{Re}\right)}^{\frac{1}{3}}$ was greater than 0.1 and Taylor flow was dominant for ${\mathrm{L}}^{*}{\left(\mathrm{Ca}/\mathrm{Re}\right)}^{\frac{1}{3}}$ less than 0.1	$\mathrm{d}=1\mathrm{mm}$ $1.58\le \mathrm{Re}\le 1024$ $0.0023\le \mathrm{Ca}\le 0.2$ $0.034\le \mathrm{Bo}\le 0.28$	Circular	GL	Experimental	[54]
$\Delta \mathrm{p}=56.9\left[1+0.07\left(\frac{{\mathrm{d}}_{\mathrm{H}}}{{\mathrm{L}}_{\mathrm{s}}}\right){\left(\frac{{\mathsf{\rho }}_{\mathrm{l}}\mathrm{d}\mathsf{\sigma }}{{\mathsf{\mu }}_{\mathrm{l}}^2}\right)}^{\frac{1}{3}}+{5.5\times 10}^{-5}{\left(\frac{{\mathrm{L}}_{\mathrm{s}}}{{\mathrm{d}}_{\mathrm{H}}\mathrm{Re}}\right)}^{-1.6}\right]$	Shorter liquid slugs and higher inertia force empowered the inner recirculation region At $\frac{{\mathrm{L}}_{\mathrm{s}}}{{\mathrm{D}}_{\mathrm{h}}}\le 3$, and Re=200, the pressure drop approached to that proposed by Kreutzer et al. [44]	${\mathrm{d}}_{\mathrm{H}}=0.4\mathrm{mm}$ $0.05\le \mathrm{We}\le 5.5$	Square	GL	Experimental	[184]
$\Delta \mathrm{p}=16\left[1+0.931\frac{\mathrm{R}\mathrm{F}}{{\mathrm{V}}_{\mathrm{l}}}\frac{1}{{\mathrm{Ca}}^{\frac{1}{3}}+3.34\mathrm{Ca}}\right]$	Pressure drop was assumed as a summation of frictional and interfacial components The accuracy of the proposed pressure drop model increased for Re greater than 150	$\mathrm{d}=0.25\mathrm{mm}$ $0.0023\le \mathrm{Ca}\le 0.0088$ $41\le \mathrm{Re}\le 159$	Circular	GL	Experimental	[55]
$\Delta {\mathrm{p}}_{\mathrm{sf}}=\frac{{4\mathrm{V}}_{\mathrm{s}}\mathsf{\alpha }\mathrm{L}}{\frac{0.5{\left(\mathrm{R}-\mathsf{\delta }\right)}^2}{{\mathsf{\mu }}_{\mathrm{d}}}}+\frac{{4\mathrm{V}}_{\mathrm{m}}{\mathsf{\mu }}_{\mathrm{c}}(1-\mathsf{\alpha })\mathrm{L}}{{0.5\mathrm{R}}^2}+\frac{\mathrm{L}}{{\mathrm{L}}_{\mathrm{uc}}}7.446\frac{\mathsf{\sigma }}{\mathrm{R}}{\mathrm{Ca}}^{\frac{2}{3}}$ $\Delta {\mathrm{p}}_{\mathrm{mf}}=\frac{{4\mathrm{V}}_{\mathrm{s}}\mathsf{\alpha }\mathrm{L}}{\frac{{\mathrm{R}}^2-{\left(\mathrm{R}-\mathsf{\delta }\right)}^2}{{\mathsf{\mu }}_{\mathrm{c}}}+\frac{0.5{\left(\mathrm{R}-\mathsf{\delta }\right)}^2}{{\mathsf{\mu }}_{\mathrm{d}}}}+\frac{{4\mathrm{V}}_{\mathrm{m}}{\mathsf{\mu }}_{\mathrm{c}}(1-\mathsf{\alpha })\mathrm{L}}{{0.5\mathrm{R}}^2}+\frac{\mathrm{L}}{{\mathrm{L}}_{\mathrm{uc}}}7.446\frac{\mathsf{\sigma }}{\mathrm{R}}{\mathrm{Ca}}^{\frac{2}{3}}$	Pressure drop was assumed as a summation of frictional and interfacial components Stagnant film (sf) reduced the channel diameter effectively Moving film (mf) considered the dispersed phase frictional drop	$0.248\mathrm{mm}\le \mathrm{d}\le 0.498\mathrm{mm}$ ${0.03\mathrm{ms}}^{-1}\le {\mathrm{V}}_{\mathrm{s}}\le {0.5\mathrm{ms}}^{-1}$ $0.1\le \frac{{\mathrm{Q}}_{\mathrm{o}}}{{\mathrm{Q}}_{\mathrm{a}}}\le 4$	Circular	LL	Experimental	[56]
$\Delta {\mathrm{p}}_{\Delta \mathrm{F}}=\frac{{2\mathrm{R}}_{\mathrm{b}}}{{\mathrm{R}}^2}\frac{\mathrm{w}}{{\mathrm{U}}_{\mathrm{s}}}\frac{{\mathrm{L}}_{\mathrm{c}}}{{\mathrm{L}}_{\mathrm{uc}}}\mathsf{\sigma }$ $\Delta {\mathrm{p}}_{\mathrm{trans}}{=-\mathrm{aN}}_{\mathrm{uc}}{\mathrm{L}}_{\mathrm{s}}$ $\left\{1+\frac{1}{{2\mathrm{bL}}_{\mathrm{s}}}\left[1-\exp \left({-\mathrm{bL}}_{\mathrm{s}}\right)\right]\right\}$	The dominant role of the number of bubbles compared the gas holdup on the pressure losses	${3.04\times 10}^{-4}<\mathrm{Ca}<{9.6\times 10}^{-3}$ ${0.053<\mathsf{\epsilon }}_{\mathrm{l}}<0.917$	Circular	GL and LL	Analytical and Experimental	[183]
$\Delta {\mathrm{p}}_{\mathrm{uc}}=\frac{{4\mathsf{\mu }}_{\mathrm{c}}{\mathrm{V}}_{\mathrm{m}}{\mathrm{L}}_{\mathrm{s}}}{{0.5\mathrm{R}}^2}\frac{\mathrm{L}}{{\mathrm{L}}_{\mathrm{uc}}}+$ $\frac{{4\mathrm{V}}_{\mathrm{m}}{\mathsf{\mu }}_{\mathrm{c}}{\mathrm{L}}_{\mathrm{f}}}{{0.5\mathrm{R}}^2\left[\left(1+{\left(\frac{{\mathrm{R}}_{\mathrm{i}}}{\mathrm{R}}\right)}^4\right)\left(\frac{1}{\mathsf{\gamma }}-1\right)\right]}\frac{\mathrm{L}}{{\mathrm{L}}_{\mathrm{uc}}}$ $+\frac{\mathrm{L}}{{\mathrm{L}}_{\mathrm{uc}}}9.402\frac{\mathsf{\sigma }}{\mathrm{R}}{\mathrm{Ca}}^{\frac{2}{3}}$	The pressure drop prediction was only valid for long droplets The interfacial pressure drop increased as the diameter decreases The interfacial pressure drop was negligible for very long slugs and droplets	$\mathrm{d}=1.06\mathrm{mm}$ $0.0045\le \mathrm{Ca}\le 0.0089$ $21\le \mathrm{Re}\le 41$	Circular	LL	Experimental and Numerical	[48]
$\Delta \mathrm{p}=16\left[1+1.061\frac{\mathrm{R}\mathrm{F}}{{\mathrm{V}}_{\mathrm{l}}}\frac{1}{{\mathrm{Ca}}^{\frac{1}{3}}+3.34\mathrm{Ca}}{\left(1-\frac{{\mathrm{Q}}_{\mathrm{d}}}{{\mathrm{Q}}_{\mathrm{t}}}\right)}^{\frac{1}{3}}\right]$	Total pressure drop was increased as the total volumetric flow rate enhances The total pressure drop approaches to an asymptotic value of 16 for single-phase flow for $\frac{{\mathrm{L}}_{\mathrm{c}}}{\mathrm{d}}{\left(\mathrm{Ca}/\mathrm{Re}\right)}^{\frac{1}{3}}$ greater than 0.12	$\mathrm{d}=1.59\mathrm{mm}$ $1.45\le \mathrm{Re}\le 567.59$ ${4.49\times 10}^{-5}\le \mathrm{Ca}\le 0.067$ $1.5\le \frac{{\mathsf{\mu }}_{\mathrm{c}}}{{\mathsf{\mu }}_{\mathrm{d}}}\le 953$	Circular	GL LL	Experimental	[57]

Besides, Song et al. [180] expressed the total pressure drop considering the total number of water slugs (n), including the pinching off slug,

$$\Delta {\mathrm{p}}_{\mathrm{t}}=\Delta {\mathrm{p}}_{\mathrm{g}}+\Delta {\mathrm{p}}_{\mathrm{cr}}+\left(\mathrm{n}-1\right)\Delta {\mathrm{p}}_{\mathrm{s}}$$

(18)

where the first term indicates the pressure drop of single-phase flow of gas, the second term is the critical pressure drop to break up the water slugs, and the last term denotes the pressure drop due to the moving slugs through the capillary.

According to the literature, a circular cross-sectional area has been assumed for the gas bubble, where the velocity gradient is limited to the confined liquid region surrounding the bubbles, not inside the bubbles [29]. However, the linear ratio between the pressure and velocity fields is valid for a straight tube, independent of the diameter of the channel. Introducing gas bubbles into the continuous phase flow changes the relation to be nonlinear. The moving bubbles in a tube leave a backfill of liquid left behind the bubble, where the volumetric flow rate of this backflow can be calculated by ${\mathsf{\pi }\mathrm{r}\mathsf{\delta }\mathrm{V}}_{\mathrm{g}}$. Marchessault and Mason [29] also showed the pressure gradient as a function of surface tension, film thickness, and the radius of the tube. They experimentally determined that at high velocities the liquid film thickness increases in the direction of the gas-bubble movement, when the profile of the bubble shows a tendency to be conic at the front.

Table 9 presents the correlations to calculate the pressure drop created by bubble/droplet in a microflow. One of the first empirical correlations of pressure loss in a capillary tube for horizontal and vertical configurations was experimentally and analytically obtained by Bretherton [30]. He discovered that the pressure drop was enhanced from a coefficient of 14.894 at the leading to 18.804 at the trailing regions due to the slight difference between the frontal and rear menisci of the bubble. Ratulowski and Chang [35] proposed a correlation for pressure drop over a finite gas bubble approaching Bretherton’s law for low Ca along with two other correlations for a square tube. Using a Finite Element Method (FVM), Giavedoni and Saita [36] determined the pressure gradient between two specific points; the first at the stagnation point of the gas bubble, and the second in the uniform film thickness region. Their results revealed an increasing trend in pressure gradient with the capillary number. They also found that the backflow region disappears when the capillary number is sufficiently high. Interfacial pressure along the free surface on the rear half of the gas bubble was found by them two years later, where the pressure was significantly decreased because of leaving liquid phase from the uniform film thickness region [38]. Kawaji and Chung [71] found that the shape of the ducts had an impact on the frictional pressure loss or the void fraction. They showed that the total pressure drop was a summation of pressure loss in the single-phase part and the two-phase part of a unit cell. The size impact of the cross-section area of a rectangular microchannel was experimentally carried out by Harirchian and Garimella [104] for a boiling heat transfer situation. A slight decrease in pressure drop was found with a heat flux increase caused by liquid viscosity reduction as the liquid phase temperature increased. They also observed an increase in pressure loss as the cross-sectional area decreased. Niu et al. [105] showed the total pressure drop in a two-phase microflow was the summation of the wall friction and the sudden expansion components showing good agreement when compared with homogenous and separated models.

8. Conclusions

In this review paper, the literature of GL and LL two-phase flows through microchannels with different cross-sectional areas were discussed. Key results can be summarized in the following way.

• The maps of Taylor flow and the transition boundaries between each flow regime have been explained by x-y graphs, where the axes are defined by the superficial phase velocities, dimensionless numbers, and volumetric flow rates.
• Most often the gas bubbles and dispersed liquid droplets are surrounded by a thin film of carrying phase, except in non-circular tubes with very high void fraction where the dry-out at the inner surface of the tube has been observed.
• There is still no universal agreement to classify all flow regimes due to the experimental apparatus and capturing equipment, which force investigators to name the flow regimes differently.
• As more efficient numerical solutions and supercomputers emerge, they are used to solve interesting microflow problems with acceptable accuracy. Since the hydrodynamic of the film thickness is crucial and informative, high-resolution images can be produced via CFD. Meanwhile, there is still room to pay more attention to this region because of the important effect of film thickness on the frictional pressure drop, bubble or droplet profile, and heat and mass transfer.
• Contact angle can play a major role in the flow pattern as long as two phases are in contact with the inner surface of the tube, except for Taylor flow is, i.e., gas bubbles or dispersed liquid droplets surrounded by a liquid film.
• The transition criterion from one flow regime into another one has been investigated by many researchers, resulting in numerous criteria based on the nature of the flow, experimental approach, and key parameters.
• The quantitative attempts to correlate slug length, liquid film thickness (recently summarized by [4] in a comprehensive review paper), and pressure drop have been compared. These correlations include non-dimensional numbers, superficial velocity ratios, volumetric flow rate ratios, void fraction, and other thermophysical characteristics of phases.