Influencing Factors on the Accuracy of Soil Calibration Models by EDG

Abstract

Compaction is an important standard in evaluating the quality of earth filling work. The EDG, an electrical density gauge, is a new type of fast and nondestructive compaction detection equipment. It is used to test the dry density and water content of the soil by establishing a soil calibration model while the accuracy of measurement is mainly based on the precision of equation of calibration model. In this paper, the factors affecting the accuracy of the soil calibration model were studied by an indoor calibration test, and soil samples were prepared to verify the accuracy of the soil calibration model. The test results showed that the dry density range, water content range, and sample quantity 13 samples of soil had a significant influence on the correlation coefficient (R2) of the equation of the soil calibration model. In addition, when using the calibration model with different sample numbers and sample combinations but similar correlation coefficients to test multiple groups of density and moisture content, there are also differences in the expected value and standard deviation of the error probability curve of the test results. In the engineering practice, the reasonable sample quantity was determined by the applicable range of dry density and water content obtained from the measurement error analysis of the soil calibration model.

1. Introduction

Compaction, an important standard in evaluating earth filling works, is calculated by testing the dry density of soil obtained from the conversion of the wet density and water content. Traditional soil density test methods include the cutting ring method and the sand replacement method; the traditional soil water content test methods aregenerally the drying method or alcohol burning method. The results of these test methods areaccurate and easy to understand, but they are time-consuming and arduous. In addition, these destructive testing methods will affect the construction progress of earthwork. Therefore, scholars from China and other countries invented nuclear density gauges and non-nuclear density gauges to solve these problems. Nuclear density gauges test the density and water content of soil by using radioactive elements, but their radiological limitations hold back their application [1,2].

Non-nuclear density gauges, including MDI, EDG, SDG, and PQI, test the density and water content of soil based on the electrical principles [3,4,5]. The EDG (electrical density gauge), a commonly used gauge in the world, has been listed in the American Society for Testing Materials (ASTM) as the standard test method [6]. By associating the measured electrical parameters of the soil with the density and water content of the soil measured by the cutting ring method, sand replacement method, and drying method, a soil model was established for field measurement [7,8]. Establishing a high-accuracy soil model is the key to ensure the precision of measurement results. The eigenvalue characterizing the accuracy of the soil model is the correlation coefficient (R²) of the equation of the soil model. Recent research results showed that the factors affecting the accuracy of the soil model include the uniformity, density, water content, and sample quantity of soil samples [9,10,11]. Some scholars carried out a compaction test by the static pressure method and put forward technical parameters related to compaction through static pressure to effectively improve the uniformity of soil samples with a large diameter [12,13]. Some scholars studied the calibration range of the soil model by EDG and proposed the calibration range of effective water content and density of the soil [14].

This paper took low-ductility clay as the experimental object. Based on the test result of density and water content of the soil using EDG, the cutting ring method, and drying method, the influence of the density range, water content range, and sample quantity of soil samples on the R² was studied. The applicable conditions of EDG were proposed to provide reference for field testing and application of EDG.

2. Test Principle

The conductive physical properties of soil, namely the composite impedance of soil, are determined by conductivity and dielectricity. Specifically, conductivity determines the real part of composite impedance, and dielectricity determines the imaginary part of composite impedance. An ideal soil model can be physically designed as the parallel circuit of capacitance (C) and resistance (R). In this way, the actual resistance (R) and capacitance (C) of soil can be analyzed by testing the circuit composed of the parallel resistance and capacitor. When the density and water content of soil change, the capacitance, resistance, and composite impedance of the soil change, too. Figure 1 is the system configuration of EDG. A radio-frequency voltage of 3.0MHz was applied to the soil with an EDG to measure the voltage and current across the electrode as well as their phase difference. Based on this, the composite impedance|Z|, equivalent resistance (R), and capacitance (C) of the soil were calculated, and the correlations between dry density (ρ) and composite impedance |Z|, between volumetric water content (θ_v) and thecapacitance resistance ratio (C/R) were established. Equations (1)–(5) were established through multiple sets of measurements:

$$\rho =a\left|Z\right|+b$$

(1)

$${\theta }_v=c\frac{C}{R}+d$$

(2)

$${\rho }_d=\rho -{\theta }_v{\rho }_w$$

(3)

$$K=\frac{{\rho }_d}{{\rho }_{\max }}$$

(4)

where: $\rho$—wet density of soil; ${\theta }_v$—volumetric water content; ${\rho }_d$—dry density of soil; ${\rho }_w$—density of water, generally take 1.00 g/cm³; K—compaction of soil; ${\rho }_{\max }$—maximum dry density of soil, obtained by the indoor compaction test; and a, b, c, d were the coefficients of the soil model.

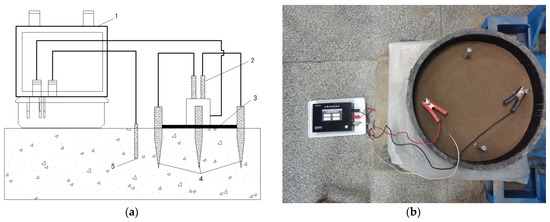
Figure 1. Composition of EDG. (a) Instrument connection diagram. (b) Instrument test diagram.1—main host; 2—electric cable clip connecting the host; 3—standard guide; 4—metal conductive probe (steel chisel); 5—temperature sensor.

The fitting of the established equation was characterized by R², whose maximum was 1. The closer the R² was to 1, the better the fitting and the more accurate the soil model. The measurement of density and water content of the soil by EDG was a two-stage process: soil model establishment and the field test. By associating the measured electrical parameters of the soil with the density and water content of the soil measured by the cutting ring method, sand replacement method, and drying method, a soil calibration model was established for calculation of a, b, c, d.

3. Calibration and Verification

3.1. Soil Sample Properties and Test Method

The soil samples in this paper were silty clay collected in the suburb of Jinan City, Shandong Province. The physical indicators are shown in Table 1.

Table 1. Physical and mechanical parameters of soil samples.

Indicator	GS	ρmax (g/cm3)	wop (%)	Cu	Cc	Ip
Value	2.71	1.79	15.9	3.8	1.96	12.3

Note: G_S—specific gravity of soil particles; w_op—optimummoisturecontent; C_u—coefficient of non-uniformity; C_c—coefficient of curvature; and I_p—plasticity index.

According to the indoor compaction test of soil samples, the experimental soil was prepared in consideration of possible compaction and water content ranges during earth filling. In the testing by EDG, the spacing between two probes was 35 cm, and the depth was 15 cm; there were no conductors within the test range. To meet the test requirements and reduce the impact of the soil sample size on the test results, a sample mold with an internal diameter of 45 cm and a height of 30 cm was made to compact the soil samples into three layers by a static pressure method. See Figure 2 for the preparation of soil samples.

Figure 2. Preparation of soil samples. (a) Compaction in layers. (b) Compaction thickness control.

3.2. Effect of Density and Water Content Ranges of Soil Samples

The soil calibration model included a density-composite impedance and volumetric water content–capacitance resistance ratio. Therefore, the valid range test of the soil calibration model also included the valid range test of density and the water content of the soil.

3.2.1. Effect of Soil Density Range

Compaction is a key control index of earth filling quality. According to the type and grade of engineering in China, the minimum compaction is 0.90–0.96 ρ_max [15,16], and the theoretical maximum compaction is 1.00, that is, the measured dry density is equal to the maximum dry density. However, in the actual construction, the error of the indoor compaction test may result in a measured compaction exceeding 1.00 [17,18]. Based on the above, the dry density range was controlled by the compaction so as to test the valid range of the soil density. In order to meet the actual needs of compaction testing, the compaction range was set to 0.85–1.00, and the water content range was determined according to the optimal water content obtained by the indoor compaction test. Thus, the test scheme designed included seven groups of dry density and seven groups of water content, which were 0.85, 0.87, 0.89, 0.91, 0.94, 0.97, and 1.00 of maximum dry density, and 9.9%, 10.9%, 11.9%, 12.9%, 13.9%, 14.9%, and 15.9%, respectively. The soil samples were divided into seven groups for a test of the valid range of the soil density according to the different compaction designed, as shown in Table 2.

Table 2. Groups of soil samples for test of valid range of soil density.

No.	1	2	3	4	5	6	7
Control value of compaction	0.85	0.87	0.89	0.91	0.94	0.97	1.00
Design value of dry density (g/cm3)	1.522	1.557	1.593	1.629	1.683	1.736	1.790
Water content (%)	9.9	10.9	11.9	12.9	13.9	14.9	15.9

Note: Each soil sample group included 7 samples with different water contents. The density and water content of actual samples will deviate, subject to the measurements by cutting ring method and drying method.

The soil samples were measured using an EDG. The wet density of each soil sample was measured by the cutting ring method. In addition, the correlation between wet density and composite impedance was established. See Table 3 for the correlation coefficients of calibration equations for soil sample groups with different densities. See Figure 3 and Figure 4 for the wet density-composite impedance calibration equation.

Table 3. Correlation coefficients of calibration equations for soil sample groups with different densities.

Group No.	A1	A2	A3	A4	A5	A6	A7
Compaction range	0.85–1.00	0.85–0.97	0.85–0.94	0.87–1.00	0.87–0.97	0.89–0.97	0.89–1.00
Correlation coefficient R2	0.584	0.596	0.613	0.750	0.766	0.869	0.880

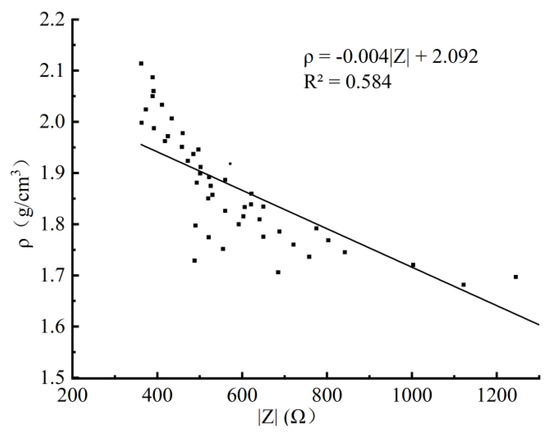
Figure 3. ρ-|Z|calibration equation (A1 group).

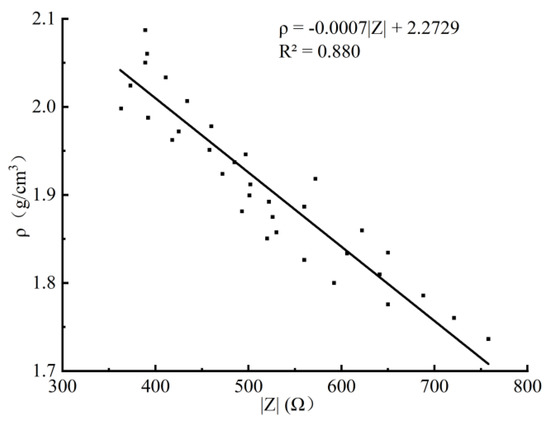
Figure 4. ρ-|Z| calibration equation (A7 group).

According to Table 3, the density ranges of the soil samples had a significant influence on the R² of calibration equations. This is because with the decrease of soil density, the increase of soil porosity will lead to the conductivity of the soil, which will affect the accuracy of the dielectric constant test results and further affect the correlation coefficient of the calibration equation.For example, when the compaction range of the soil samples was 0.87–1.00, R² ≥ 0.75; when the compaction range of soil samples was 0.89–1.00, R² ≥ 0.85.

3.2.2. Effect of Soil Water Content Range

During earth filling, theoretically, the soil samples with optimal water content can be compacted to realize the maximum dry density. However, water evaporation in construction led to lower measured water content than optimal water content during compaction testing. Based on the above considerations, with the optimal water content as a benchmark and a floating range of 4–8%, the valid range of water content of the soil was set to 7.9–19.9%. Thus, 13 groups of water content were designed, each corresponding with three groups of dry density, which were 91%, 94%, and 97% of the maximum dry density, respectively. The soil samples were divided into 13 groups according to different design values of water content, as shown in Table 4.

Table 4. Groups of soil samples for the test of valid range of water content of soil.

No.	1	2	3	4	5	6	7	8	9	10	11	12	13
Water content (%)	7.9	8.9	9.9	10.9	11.9	12.9	13.9	14.9	15.9	16.9	17.9	18.9	19.9

Note: Each soil sample group included 3 samples with different densities. The density and water content of soil samples will deviate, subject to the measurements by cutting ring method and drying method.

The capacitance resistance ratio of the soil samples was measured using an EDG. The density and water content of soil samples were measured by the cutting ring method and drying method to obtain the volumetric water content converted by Equation (5).

$${\theta }_v=\frac{\rho w}{\left(1+\mathrm{w}\right){\rho }_w}$$

(5)

where: θ_v—volumetric water content; $\rho$—wet density of soil; $w$—water content of soil; and ${\rho }_w$—density of water.

The correlation between the volumetric water content and capacitance resistance ratio was established. See Table 5 for the correlation coefficients of calibration equations for the soil sample groups with different water contents. See Figure 5 and Figure 6 for the volumetric water content-capacitance resistance ratio calibration equation.

Table 5. Correlation coefficients of calibration equations for soil sample groups with different water contents.

Group No.	B1	B2	B3	B4	B5	B6	B7
Water content range (%)	7.9–19.9	7.9–18.9	8.9–18.9	9.9–18.9	9.9–17.9	9.9–16.9	10.9–16.9
Difference with optimum water content	−8.0/+4.0	−8.0/+3.0	−7.0/+3.0	−6.0/+3.0	−6.0/+2.0	−6.0/+1.0	−5.0/+1.0
Correlation coefficient R2	0.729	0.733	0.757	0.796	0.857	0.901	0.915

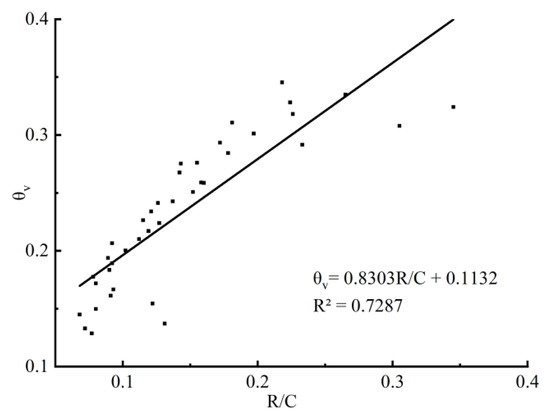
Figure 5. θ_v-R/C calibration equation (B1 group).

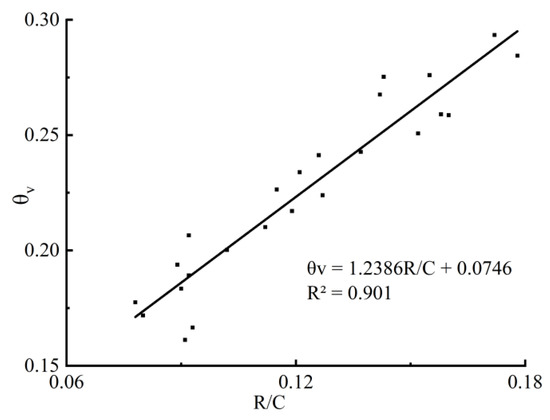
Figure 6. θ_v-R/C calibration equation (B6 group).

According to Table 5, the water content of soil samples had a significant influence on the R² of calibration equations. This is because with the increase of soil moisture content, the conductivity of the soil gradually strengthens, and the correlation coefficient of the established calibration equation between volume moisture content and the capacitance resistance ratio gradually increases. However, after reaching the optimal moisture content, the soil is completely saturated, and the increase of moisture content will no longer indicate the conductivity, and even water will be squeezed out during compaction;to some extent, it will reduce the correlation coefficient of the established calibration equation. When the difference between the water content of soil samples and the optimal water content was −7.0%/+3.0%, R² ≥ 0.75; when the difference was −6.0%/+2.0%, R² ≥ 0.85; and when the difference was −6.0%/+1.0%, R² ≥ 0.90.

3.3. Effect of SamplingSizeon the Accuracy of Soil Calibration Model

Research has shown that the soil calibration model is generated by the data matrix of n × m (n ≥ 2, m ≥ 2). The n and m stand for n groups of different soil densities and m groups of different water contents, respectively, and their increase improves the precision of the soil calibration model [6,14]. As the preparation of soil samples is complicated and time-consuming, it is very necessary to determine a reasonable amount of samples and reduce the workload of establishing the soil calibration model.

With the dry density range and the water content range being set to 1.593 g/cm³–1.790 g/cm³ (0.89–1.00${\rho }_{\max }$) and 9.9–16.9% (w_op−6.0%–w_op +1.0%), respectively, four sample data points (2*2), six sample data points (2*3, 3*2), nine sample data points (3*3), twelve sample data points (3*4, 4*3), and sixteen sample data points (4*4) were selected to establish the soil calibration model. See Table 6 for the measurement results.

Table 6. Correlation coefficients of soil calibration models for different sample quantities.

No.	Number of Sample Data Point Groups	Sample Data Combination		Number of Measurements	Average R2 of ρ-|Z| Calibration Equation	Average R2 of θv-R/C Calibration Equation
		Number of Density Groups (n)	Number of Water Content Groups (m)
1	4	2	2	3	0.793	0.848
2	6	2	3		0.887	0.913
3		3	2		0.893	0.902
4	9	3	3		0.907	0.929
5	12	3	4		0.894	0.913
6		4	3		0.916	0.924
7	16	4	4		0.913	0.910

According to Table 6, the average R² of $\rho$-$\left|Z\right|$ and ${\theta }_v$-R/C calibration equations generated by four sample data points was 0.793 and 0.83, respectively, significantly lower than that generated by the six sample data points. The average R² of the density-composite impedance calibration equation and water content–capacitance resistance ratio generated by six sample data points was greater than 0.85 and 0.90, respectively. The average R² of $\rho$-$\left|Z\right|$ calibration equation generated by the sixteen sample data points increased slightly, but the average R² of ${\theta }_v$-R/C calibration equation did not significantly change. Therefore, while ensuring the minimum workload in modeling, the soil calibration models generated by six or nine sample data points were believed to meet the accuracy requirements.

4. Verification and Comparison of the Accuracy of Soil Calibration Model

The soil samples with different water contents and densities were configured to verify whether the soil calibration model was accurate. First, within the range of sample data points of the soil calibration model, the ranges of density and water content of the soil samples and the measurement errors of EDG were measured; second, outside the range of sample data points of the soil calibration model, the ranges of density and water content of the soil samples and measurement errors of EDG were measured. The verifications were completed indoors, and the samples used had a different density and water content.

Five soil calibration models, selected from the five models identified by the sample data points of 2*3, 3*2, 3*3, 3*4, and 4*3 were used to verify the accuracy of the soil calibration model. The correlation coefficients of their calibration equations were close. The dry density range and water content range of the sample data corresponding to the models were 1.593 g/cm³–1.790 g/cm³ (0.89 ${\rho }_{\max }$–1.00 ρ_max) and 9.9–16.9% (w_op−6.0%–w_op +1.0%), respectively. See Table 7 for the models to verify the accuracy of the soil calibration model.

Table 7. Models to verify the accuracy of soil calibration model.

Model No.	Sample Data Combination			$\mathit{\rho }$$-\left|\mathit{Z}\right| \mathbf{Calibration} \mathbf{Equation}$		${\mathit{\theta }}_{\mathit{v}}-\mathbf{R}/\mathbf{C} \mathbf{Calibration} \mathbf{Equation}$
	n*m	Dry Density (g/cm3)	Water Content (%)	Calibration Equation	R2	Calibration Equation	R2
M1	2*3	1.593/1.736	9.9/12.9/16.9	$\rho$ = −0.0007$\left|Z\right|$ + 2.268	0.892	${\theta }_v$ = 1.4350$\frac{C}{R}$ + 0.044	0.920
M2	3*2	1.593/1.683/1.790	10.9/15.9	$\rho$ = −0.0008$\left|Z\right|$ + 2.349	0.902	${\theta }_v$ = 1.3765$\frac{C}{R}$ + 0.051	0.912
M3	3*3	1.593/1.683/1.36	9.9/13.9/16.9	$\rho$ = −0.0008$\left|Z\right|$ + 2.345	0.898	${\theta }_v$ = 1.5011$\frac{C}{R}$ + 0.037	0.928
M4	3*4	1.593/1.683/1.790	9.9/11.9/13.9/15.9	$\rho$ = −0.0008$\left|Z\right|$ + 2.356	0.907	${\theta }_v$ = 1.3782$\frac{C}{R}$ + 0.060	0.907
M5	4*3	1.593/1.629/1.736/1.790	9.9/12.9/15.9	$\rho$ = −0.0008$\left|Z\right|$ + 2.342	0.913	${\theta }_v$ = 1.3951$\frac{C}{R}$ + 0.058	0.901

Note: n*m stands for the sample combination mode. n is the number of density groups and m is the number of water content groups.

There was a total of 65 soil sample groups configured. The dry density ${\rho }_d$ and water content $w$, measured by the cutting ring method and drying method, were used as the true values in the error statistical analysis. The models M1–M5 were selected for measurement of ${\rho }_d^{\prime }$ and $w\prime$. The relative error of the measurements was calculated by Equations (6) and (7).

$$\Delta {\rho }_d\%=\frac{{\rho }_d-{\rho }_d^{\prime }}{{\rho }_d}$$

(6)

$$\Delta w\%=\frac{w-w\prime }{w}$$

(7)

A statistical analysis of the relative errors among different models for the dry density and water content of 65 soil sample groups according to the normal distribution method was conducted, and the frequency curves of the relative error of dry density and water content were drawn. Figure 7 and Figure 8 are the statistical result charts of the relative error frequencies of dry density and water content of M1. Table 8 is the statistical results of the relative error frequencies of dry density and water content of M1. Considering that the frequency distribution curve approximately matched the normal distribution, the expected value μ and the standard deviation σ were counted through normal distribution fitting. Table 9 shows the statistical analysis of the normal distribution fitting of the relative error frequencies of dry density and water content of M1–M5.

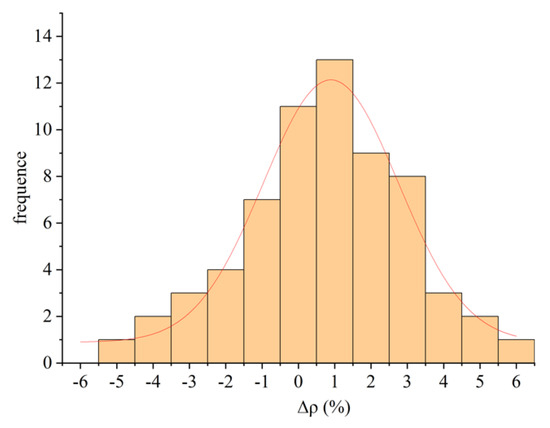
Figure 7. Statistical result chart of the relative error frequency of density of M1.

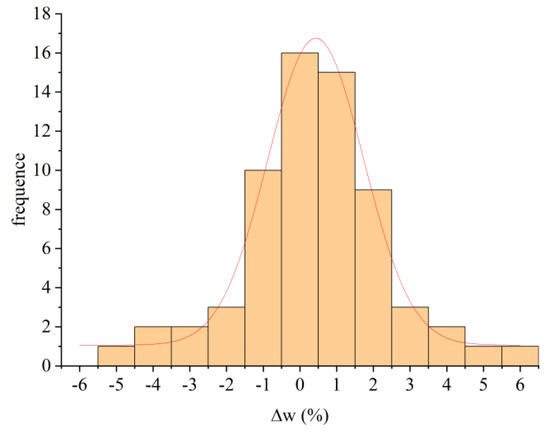
Figure 8. Statistical result chart of the relative error frequency of water content of M1.

Table 8. Statistical results of the relative error frequencies of dry density and water content of M1.

Model No.	Sample Data Combination	Relative Error Frequency of Dry Density		Relative Error Frequency of Water Content
		μ	σ	μ	σ
M1	2*3	1.02	2.79	0.73	1.68
M2	3*2	0.68	2.42	0.62	1.57
M3	3*3	0.77	2.51	−0.42	1.83
M4	3*4	−0.68	2.60	−0.50	1.41
M5	4*3	0.55	2.48	0.48	1.56

Table 9. Statistical analysis of the normal distribution fitting of the relative error frequencies of dry density and water content of M1–M5.

Model No.	Sample Data Combination	Probability Curve of the Relative Error Frequency of Dry Density		Probability Curve of the Relative Error Frequency of Water Content
		μ	σ	μ	σ
M1	2*3	0.97	3.59	0.73	1.68
M2	3*2	0.68	3.12	0.62	1.57
M3	3*3	0.77	3.06	−0.42	1.83
M4	3*4	−0.62	2.92	−0.50	1.41
M5	4*3	0.55	2.72	0.48	1.56

The statistical results in Table 8 and Table 9 are as follows:

(1)

When the number of samples used to establish the ρ-|Z| calibration equation increased, the relative error of dry density measurements decreased, the frequency of −2–2% increased, and the expected value μ decreased, suggesting that the central tendency position of the measurements was close to the point 0; the standard deviation σ also decreased, indicating that the dispersion of the measurements was decreasing.

(2)

When the number of samples used to establish the θ_v-R/C calibration equation increased, the relative error of water content measurements did not significantly change, and the expected value μ decreased, suggesting that the central tendency position of the measurements was close to the point 0; the standard deviation σ did not significantly change, indicating that the dispersion of the measurements had little change.

(3)

When the number of samples used to establish the ρ-|Z| calibration equation was equal, namely 6 sample data and 12 sample data, the number of dry density groups was greater than the number of water content groups; both the expected value μ and the standard deviation σ were small, suggesting that this calibration equation was more advantageous for dry density measurements.

(4)

The accuracy of water content measurements was significantly higher than those of dry density measurements, which was consistent with the case where the R² of θ_v-R/C calibration equation was higher than that of the ρ-|Z| calibration equation.

5. Conclusions

In this paper, through the indoor calibration test with an EDG and the verification by the cutting ring method and drying method, the influence of the compaction range (dry density range), water content range, and sample quantity of soil samples on the accuracy of calibration equations was studied, and the soil calibration models composed of different sample combinations were verified; the precision of the soil calibration models were analyzed, reaching the following conclusions:

(1)

The dry density and water content ranges of soil samples, whose setting was closely related to the maximum dry density (ρ_max) and optimal water content (w_op) of the soil samples, had a significant influence on the R² of calibration equations. When the compaction (K) of the soil samples was 0.89–1.00 and the water content range (w) was w_op − 6.0%–w_op +1.0%, R² ≥ 0.85 (R² of ρ-|Z| and θ_v-R/C calibration equations).

(2)

The number of samples had a significant influence on the R² of ρ-|Z| and θ_v-R/C calibration equations. The average R² of ρ-|Z| and θ_v-R/C calibration equations generated by four sample data points was significantly lower than that generated by the six sample data points. The average R² of ρ-|Z| calibration equation generated by the sixteen sample data points increased slightly, but the average R² of θ_v-R/C calibration equation did not significantly change. Therefore, while ensuring the minimum workload in modeling, the soil calibration models generated by six or nine sample data points were believed to meet the accuracy requirements.

(3)

The frequency curves of the relative errors of dry density and water content measurements showed a normal distribution. Both the expected value μ and the standard deviation σ deviated from 0, and the accuracy of the water content measurements was significantly higher than that of dry density measurements. When the number of samples used to establish the ρ-|Z| calibration equation increased, both the expected value μ and the standard deviation σ decreased slightly, suggesting that the central tendency position of the measurements was close to the point 0 and the dispersion of the measurements was decreasing. When the number of samples used to establish the θ_v ‒ R/C calibration equation increased, the expected value μ decreased, and the standard deviation σ did not significantly change.

(4)

When the number of samples used to establish the ρ-|Z| calibration equation wasequal, namely 6 sample data and 12 sample data, and the number of dry density groups was greater than the number of water content groups, both the expected value μ and the standard deviation σ were small, suggesting that this calibration equation was more advantageous for dry density measurements.