Numerical Simulation of Axial Vortex in a Centrifugal Pump as Turbine with S-Blade Impeller
Abstract
1. Introduction
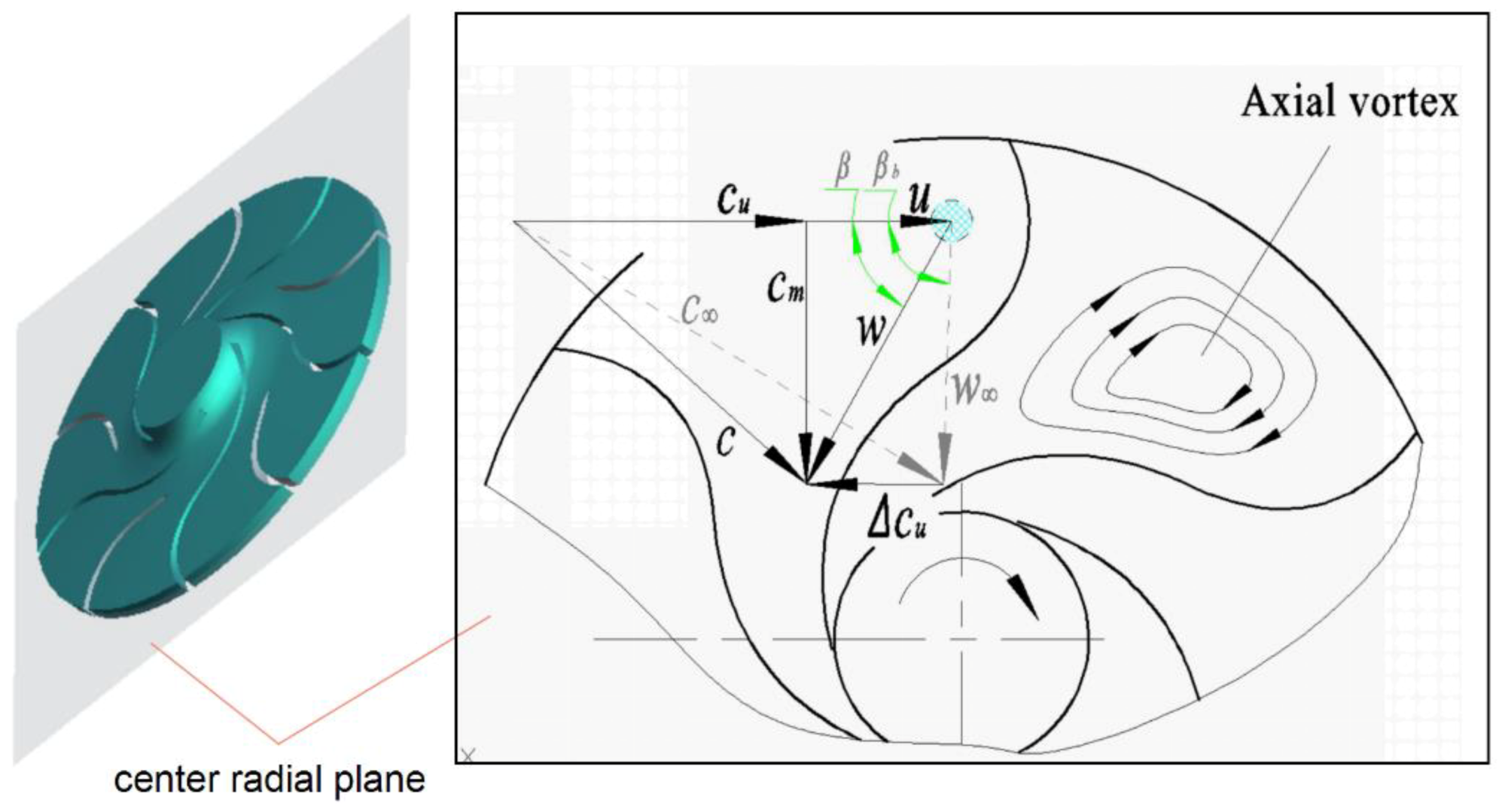
2. Theoretical Model of Vortex
3. Numerical Simulation
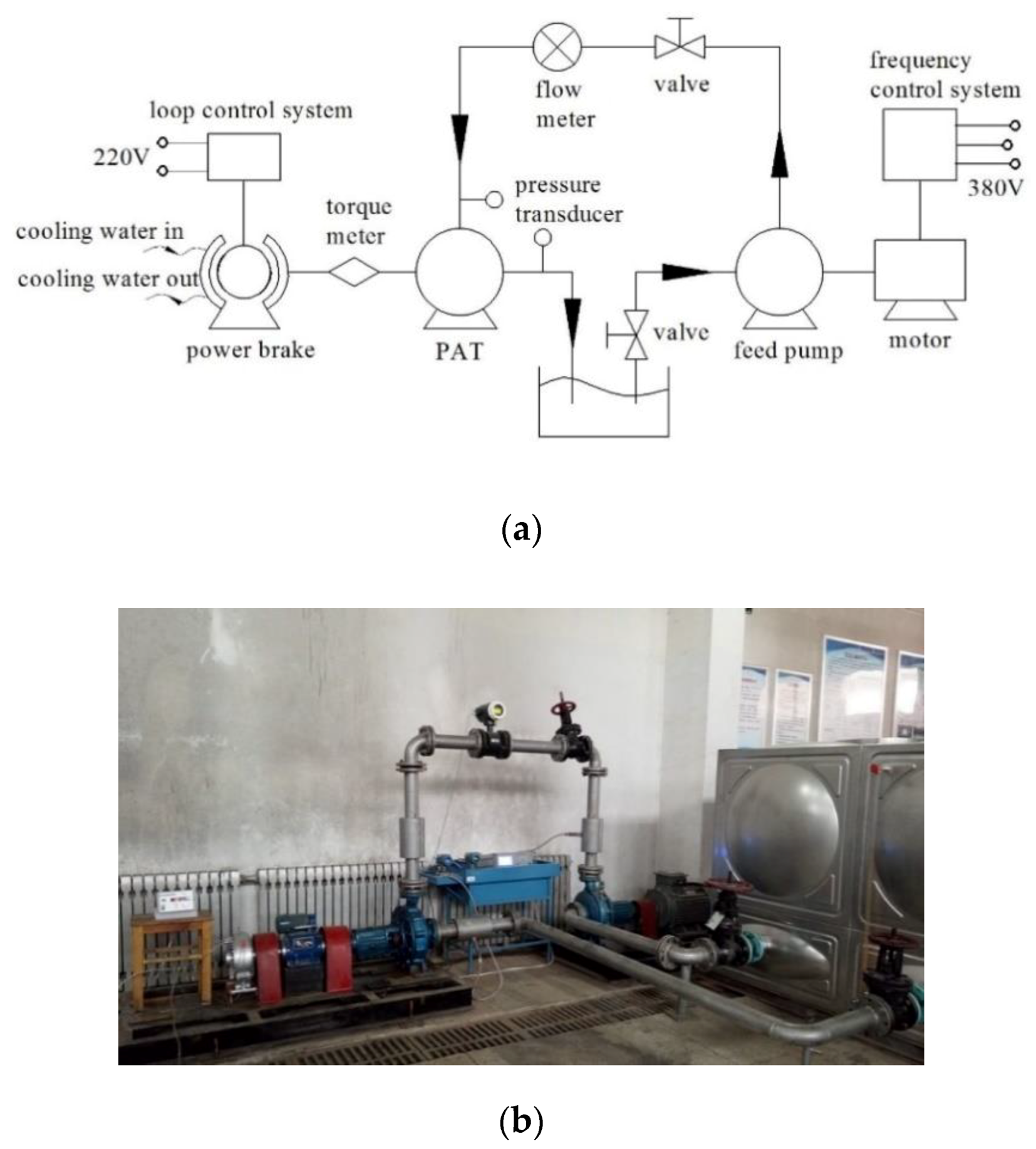
3.1. Numerical Method
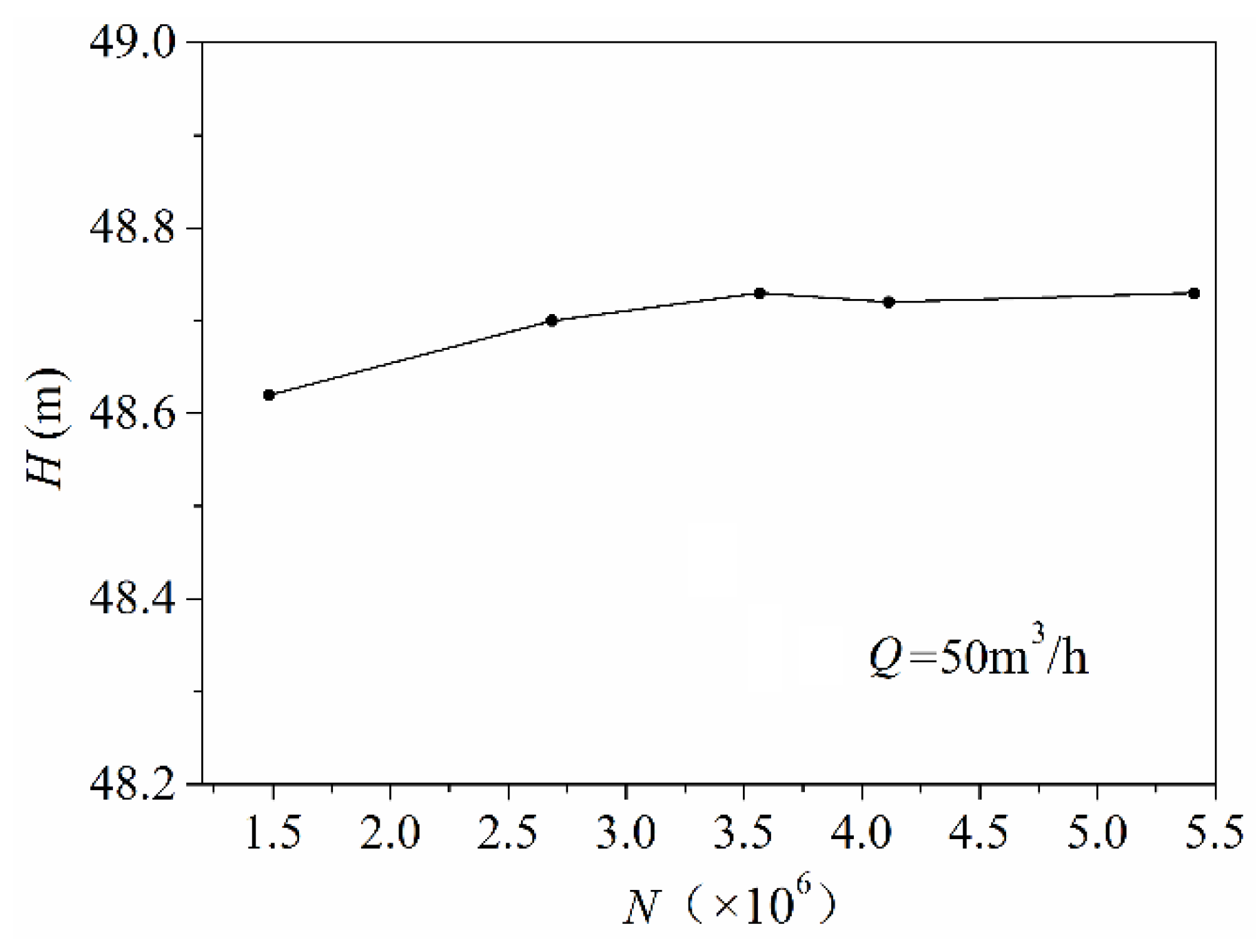
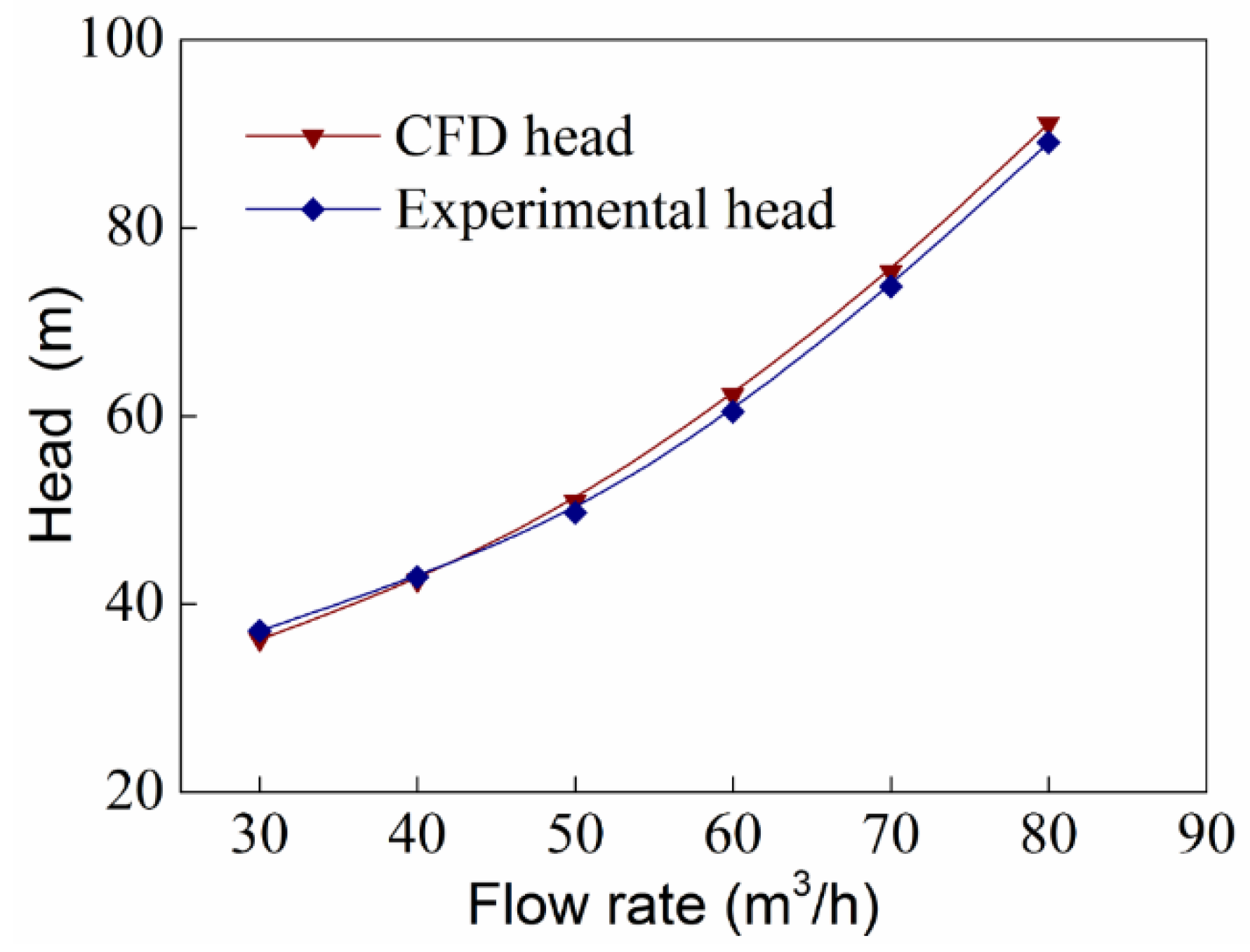
3.2. Verification of Numerical Method
4. Results and Discussion
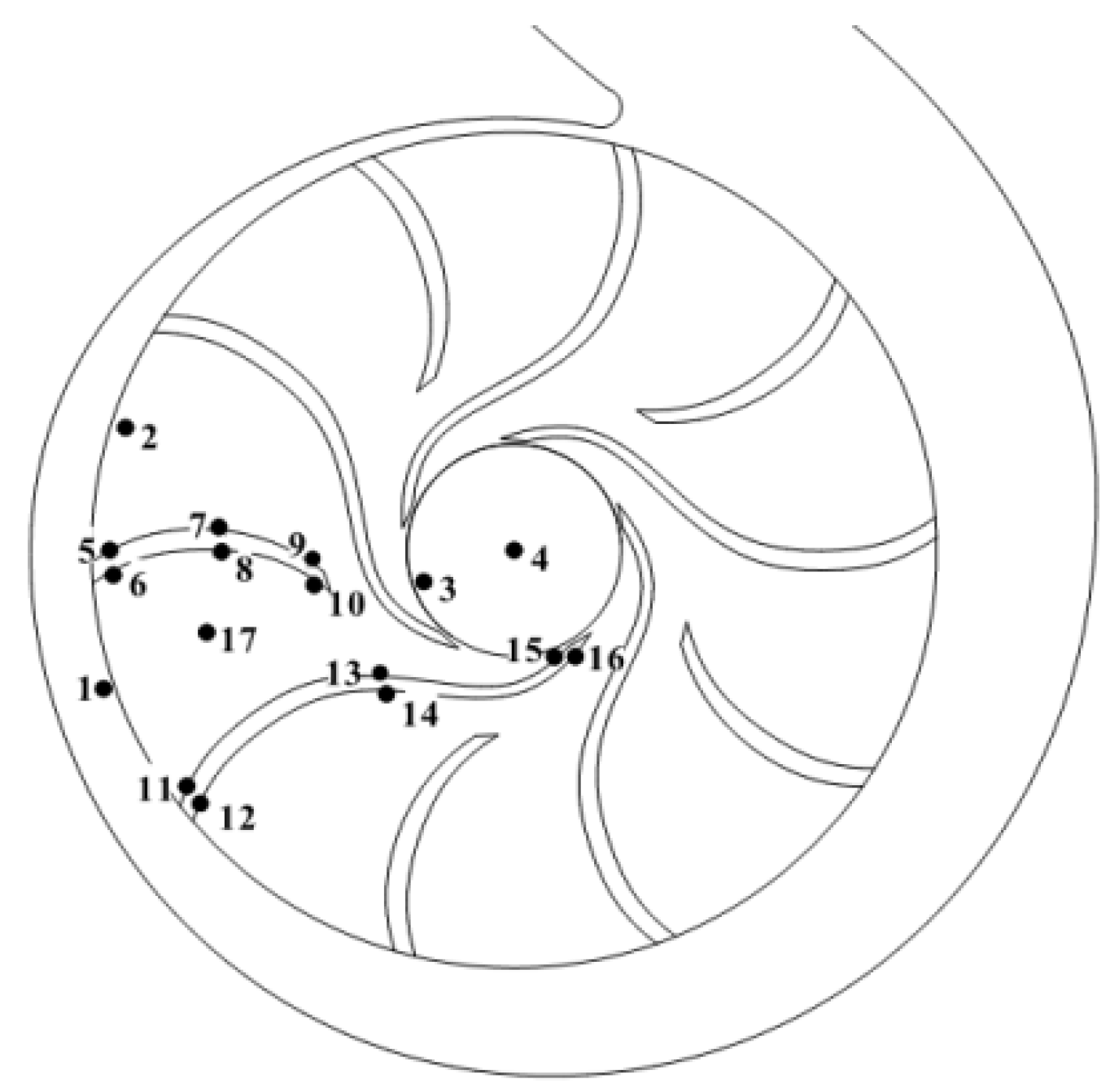
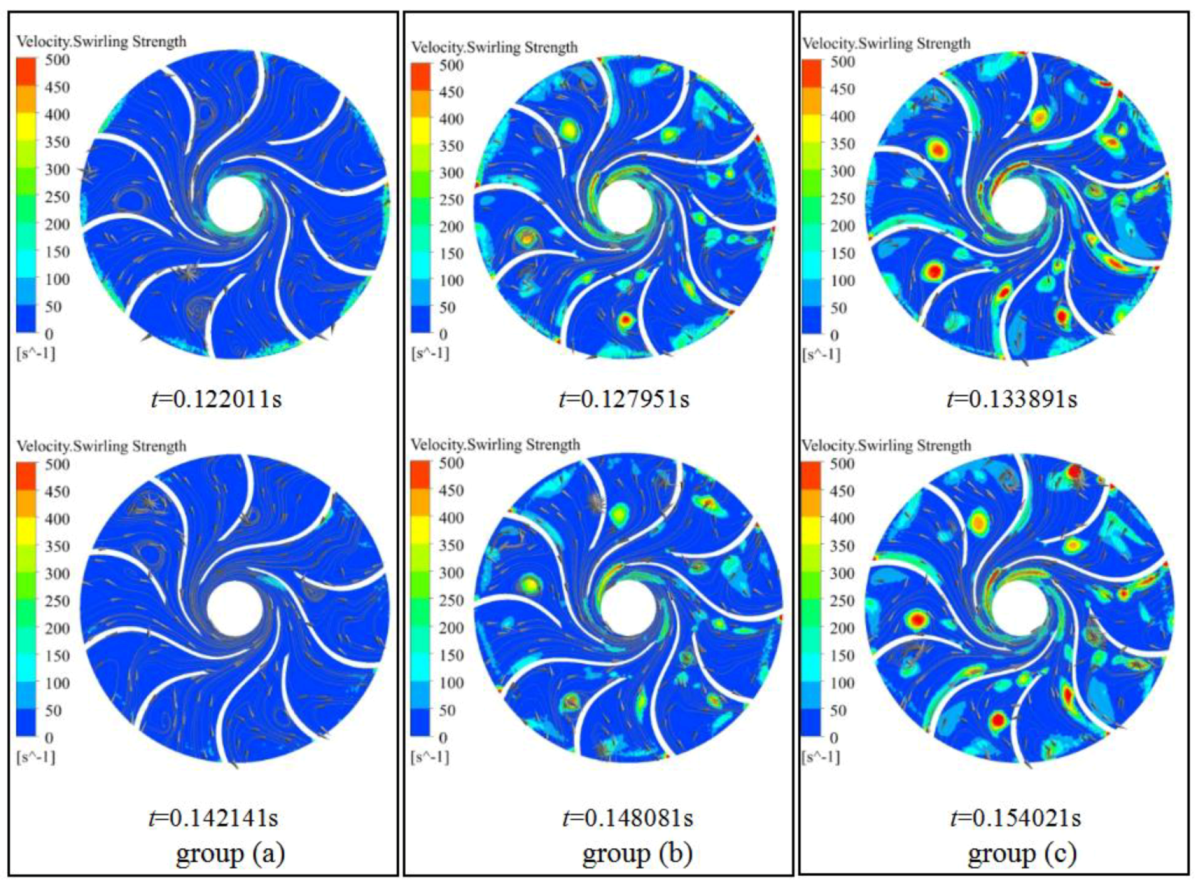
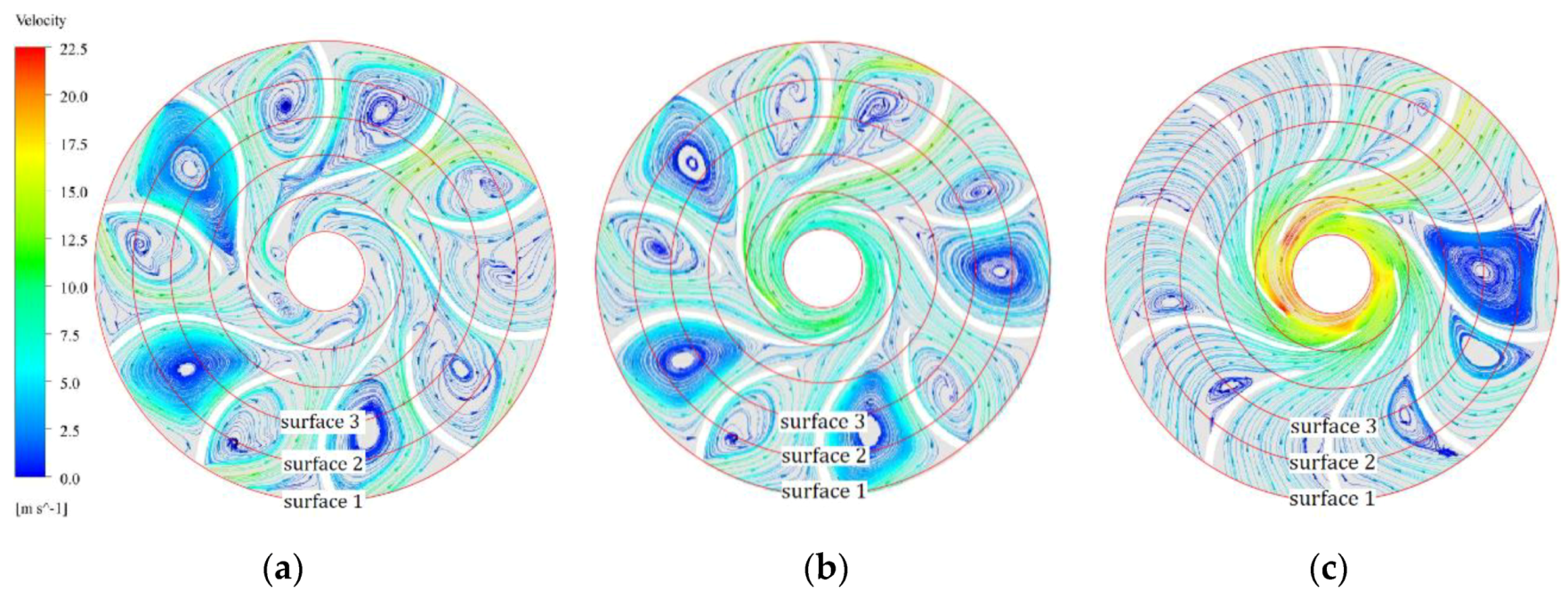
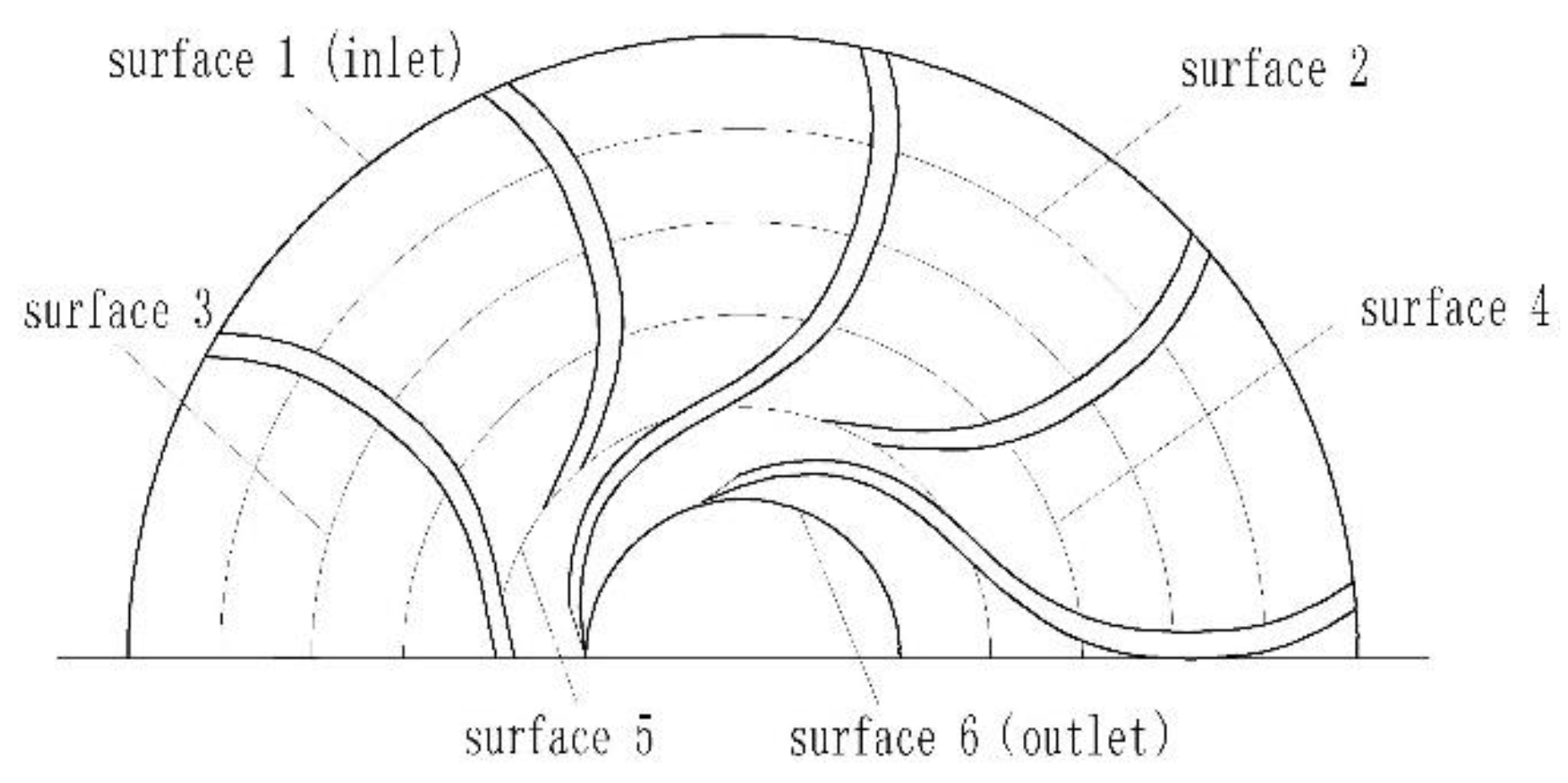
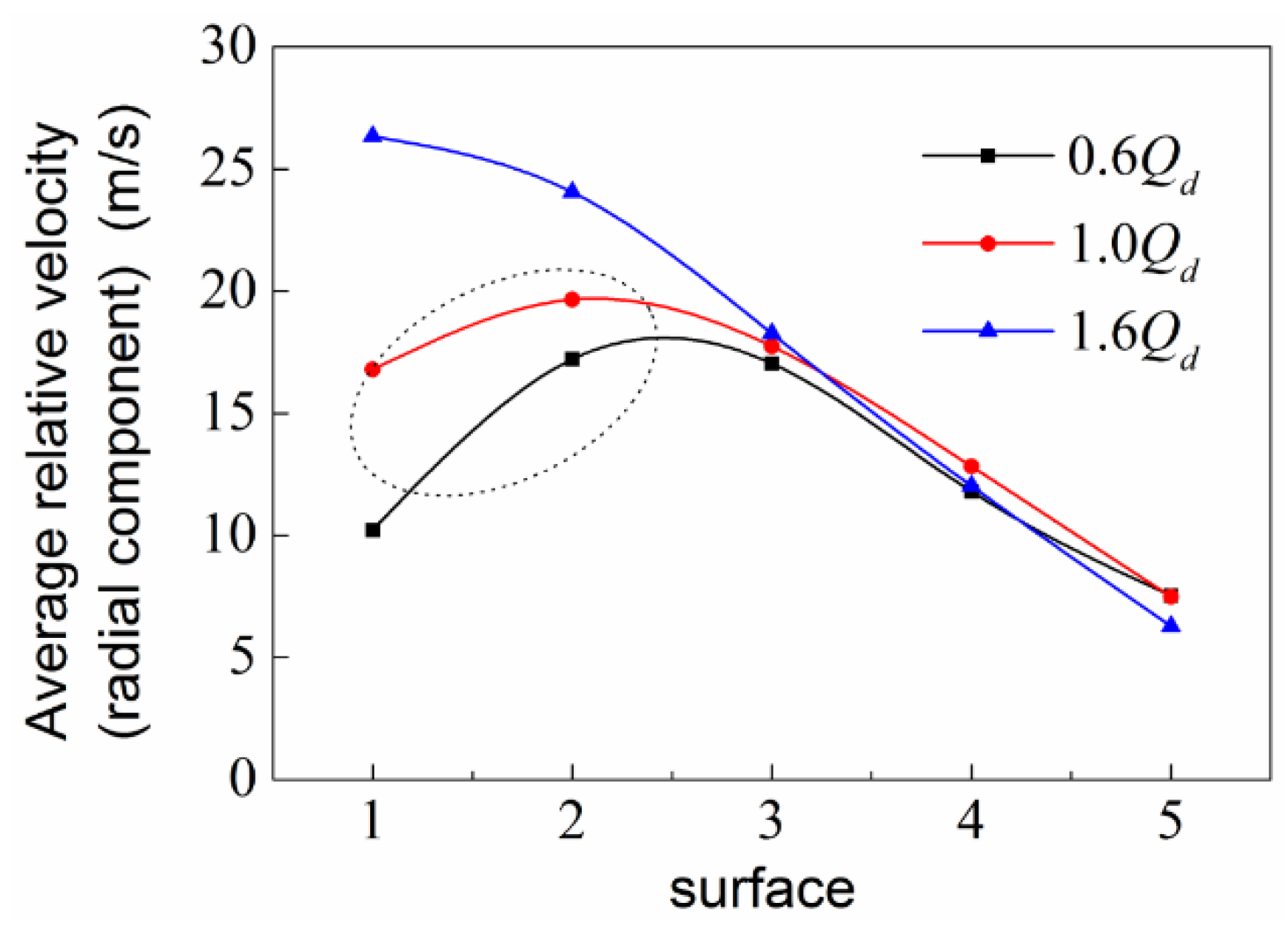
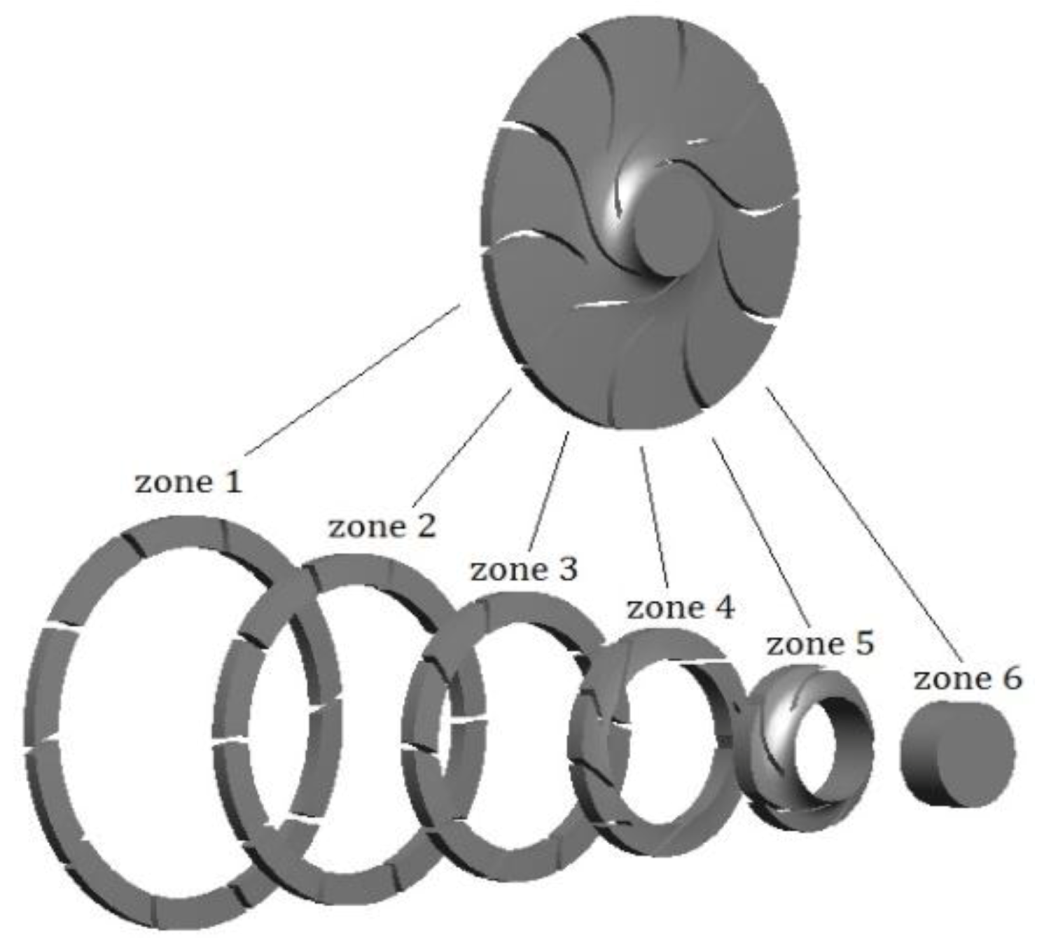
4.1. Vortex Information in Flow Channels
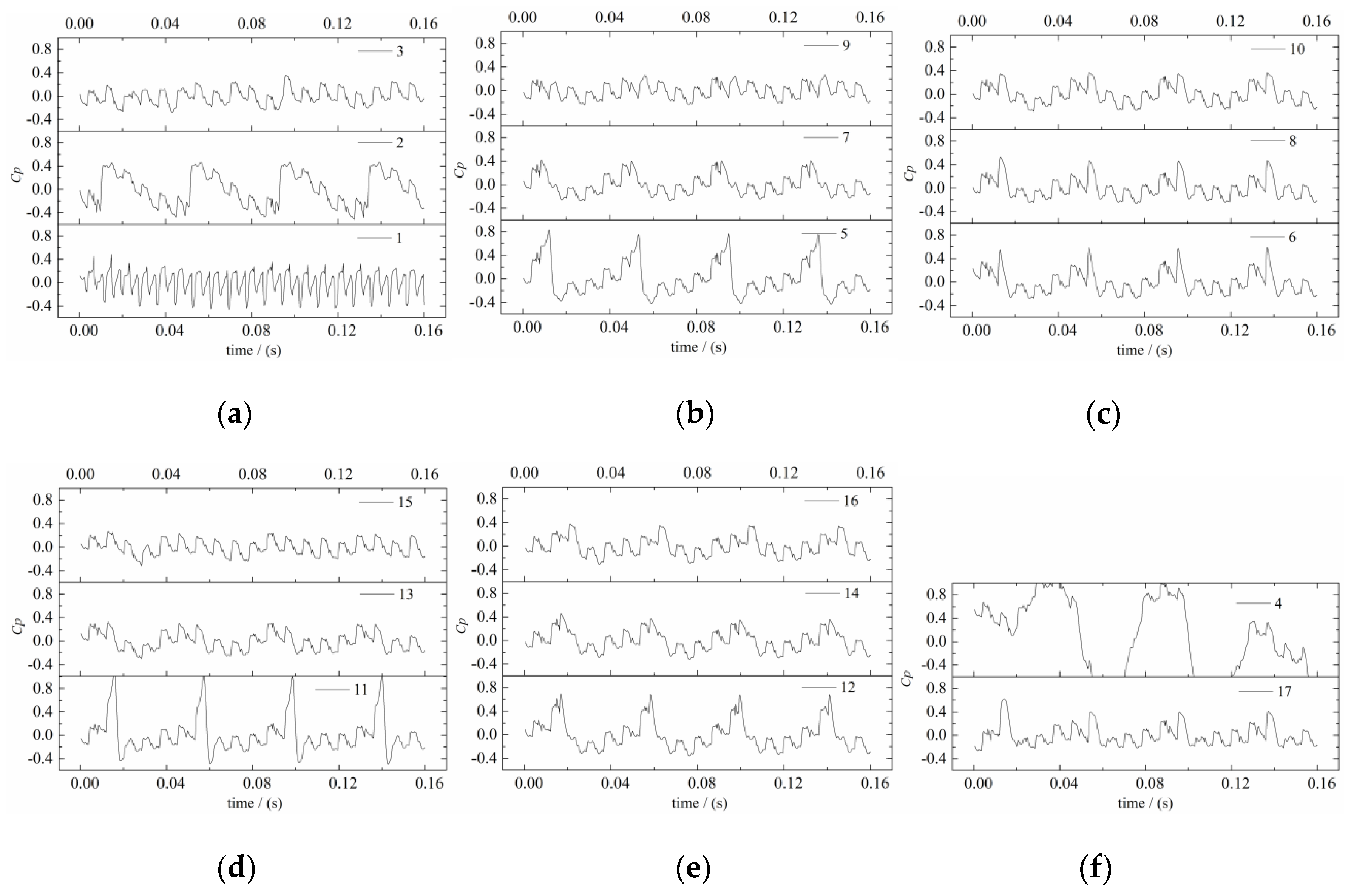
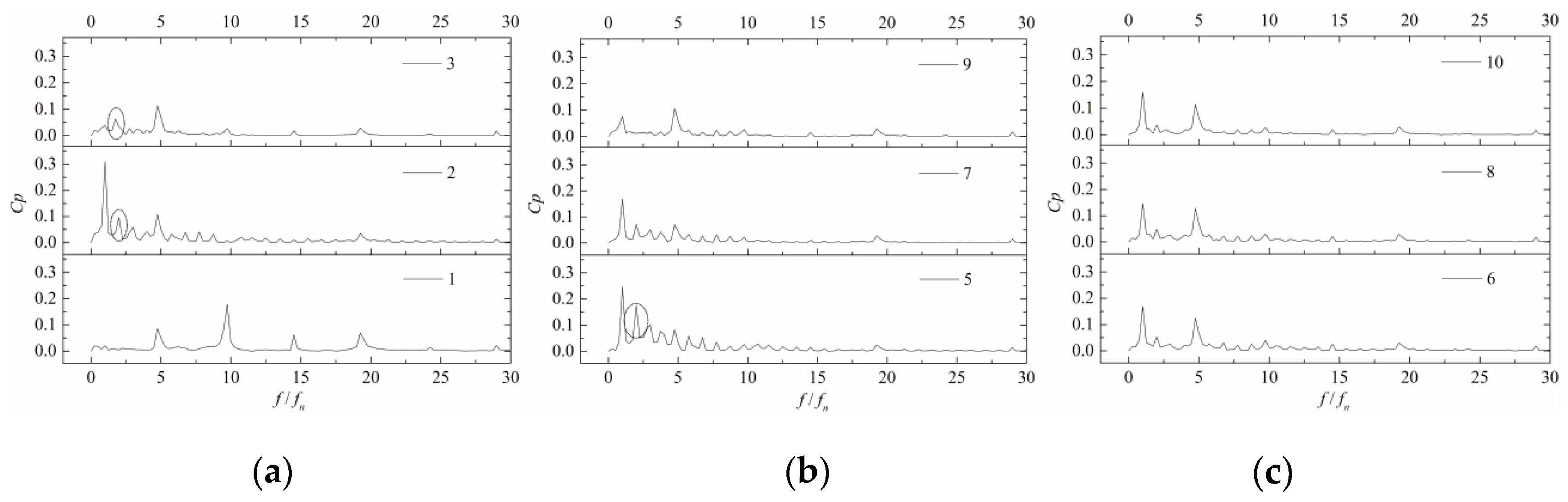
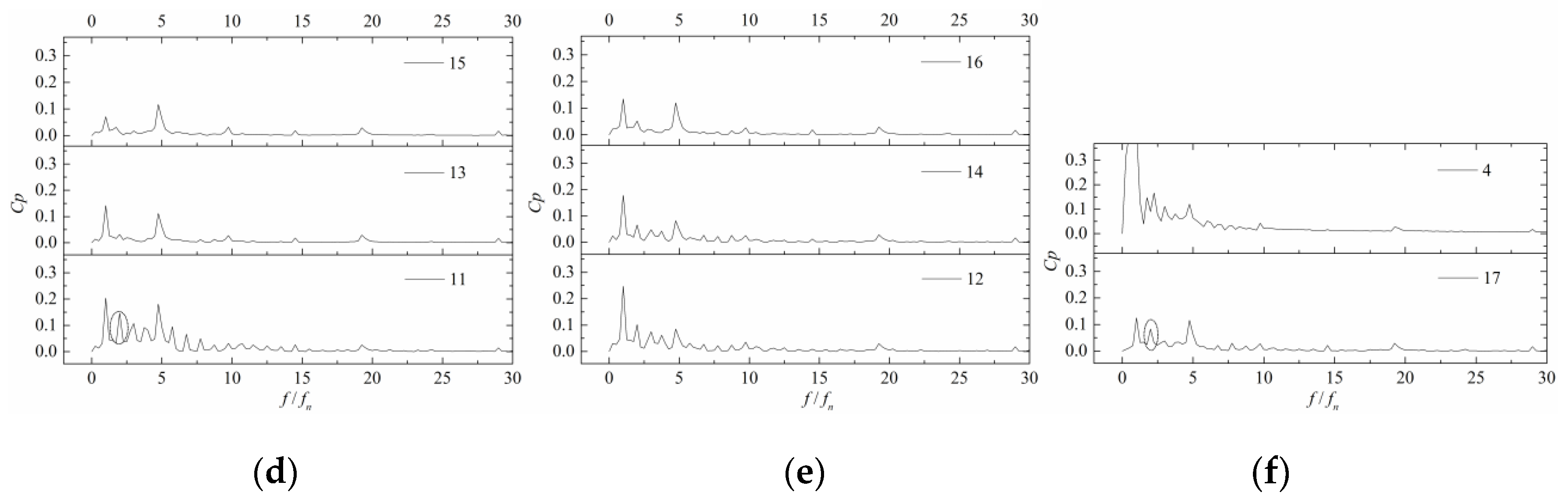
4.2. Pressure Fluctuation of Vortex
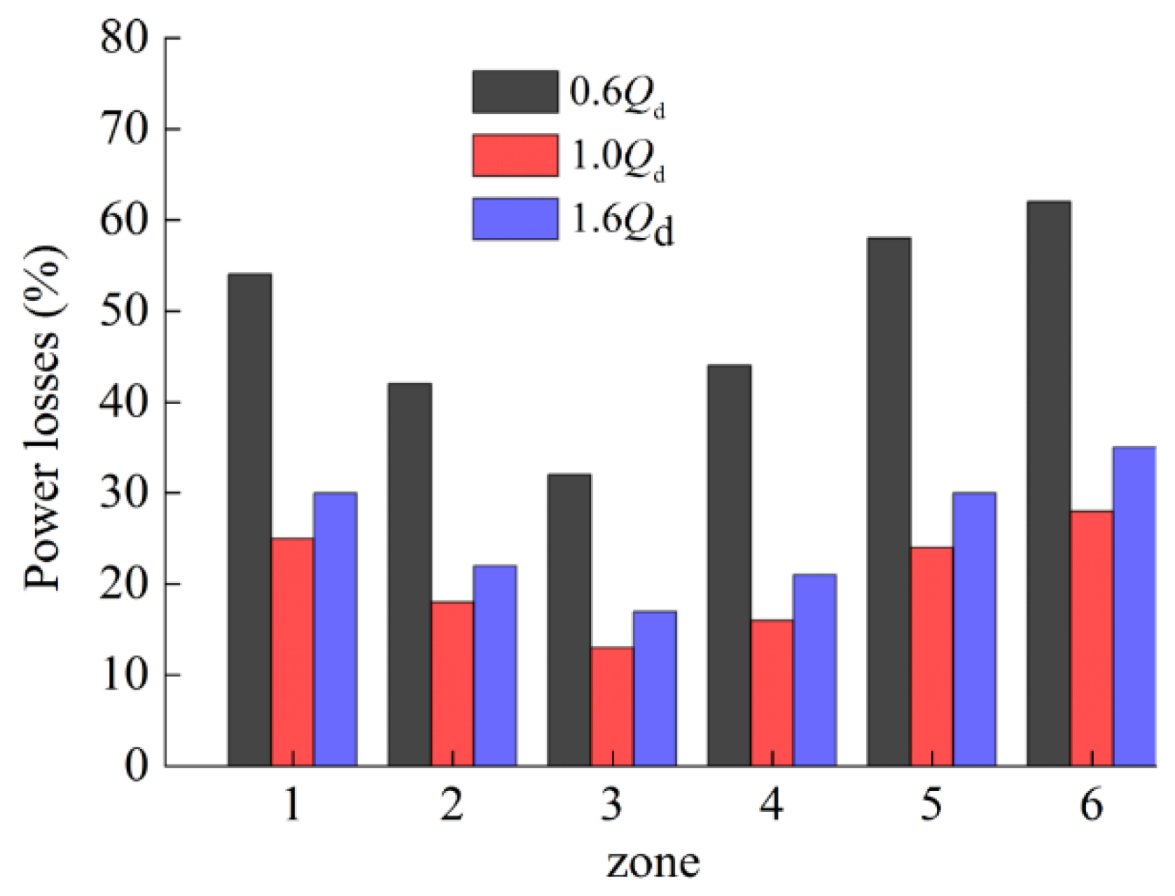
4.3. Power Losses Caused by Vortex
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Giosio, D.R.; Henderson, A.D.; Waiker, J.M.; Brandner, P.A.; Sargison, J.E.; Gautam, P. Design and performance evaluation of pump-as-turbine micro-hydro test facility with incorporated inlet flow control. Renew. Energy 2015, 78, 1–6. [Google Scholar] [CrossRef]
- Lydon, T.; Coughlan, P.; McNabola, A. Pump-as-turbine: Characterization as an energy recovery device for the water distribution network. J. Hydraul. Eng. 2017, 143, 04017020.1–04017020.10. [Google Scholar] [CrossRef]
- Ramos, H.; Borga, A. Pumps as turbines: An unconventional solution to energy production. Urban Water 1999, 1, 261–263. [Google Scholar] [CrossRef]
- Rossi, M.; Nigro, A.; Pisaturo, G.R.; Renzi, M. Technical and economic analysis of Pumps-as-Turbines (PaTs) used in an Italian Water Distribution Network (WDN) for electrical energy production. Energy Procedia 2019, 158, 117–122. [Google Scholar] [CrossRef]
- Alberizzi, J.C.; Renzi, M.; Righetti, M.; Pisaturo, G.R.; Rossi, M. Speed and pressure controls of pumps-as-turbines installed in branch of water-distribution network subjected to highly variable flow rates. Energies 2019, 12, 4738. [Google Scholar] [CrossRef]
- Mohameda, E.S.; Papakakisa, G.; Mathioulakisb, E. The effect of hydraulic energy recovery in a small sea water reverse osmosis desalination system; experimental and economical evaluation. Desalination 2005, 184, 241–246. [Google Scholar] [CrossRef]
- Van Antwerpen, H.J.; Greyvenstein, G.P. Use of turbines for simultaneous pressure regulation and recovery in secondary cooling water systems in deep mines. Energy Convers. Manag. 2005, 46, 563–575. [Google Scholar] [CrossRef]
- Wang, X.H.; Yang, J.H.; Xia, Z.T.; Hao, Y.; Cheng, X.R. Effect of Velocity Slip on Head Prediction for Centrifugal Pumps as Turbines. Math. Probl. Eng. 2019, 2019, 5431047. [Google Scholar] [CrossRef]
- Singh, P.; Nestmann, F. An optimization routine on a prediction and selection model for the turbine. Exp. Therm. Fluid Sci. 2010, 34, 152–164. [Google Scholar] [CrossRef]
- Su, X.H.; Huang, S.; Zhang, X.J.; Yang, S.S. Numerical research on unsteady flow rate characteristics of pump as turbine. Renew. Energy 2016, 94, 488–495. [Google Scholar] [CrossRef]
- Ardizzon, G.; Pavesi, G. Optimum incidence angle in centrifugal pumps and radial inflow turbines. Proc. Inst. Mech. Eng. Part A J. Power Energy 1998, 212, 97–107. [Google Scholar] [CrossRef]
- Singh, P. Optimization of Internal Hydraulics and of System Design for Pumps as Turbines with Field Implementation and Evaluation. Ph.D. Thesis, University of Karlsruhe, Karlsruhe, Germany, 2005. [Google Scholar]
- Pascoa, J.C.; Silva, F.J.; Pinheiro, J.S.; Martins, D.J. Accuracy details in realistic CFD modeling of an industrial centrifugal pump in direct and reverse modes. J. Therm. Sci. 2010 19, 491–499. [CrossRef]
- Singh, P.; Nestmann, F. Internal hydraulic analysis of impeller rounding in centrifugal pumps as turbines. Exp. Therm. Fluid Sci. 2011, 35, 121–134. [Google Scholar] [CrossRef]
- Yang, S.S.; Kong, F.Y.; Chen, H.; Su, X.H. Effects of blade wrap angle influencing a pump as turbine. J. Fluids Eng. 2012, 134, 061102–061109. [Google Scholar] [CrossRef]
- Zhang, S.; Shi, Q.; Zhang, K. Flow behavior analysis of reversible pump-turbine in “S” characteristic operating zone. In Proceedings of the IOP Conferences Series: Earth and Environmental Science, Beijing, China, 19–23 August 2012; Volume 15, p. 032045. [Google Scholar]
- Staubli, T.; Senn, F.; Sallaberger, M. Instability of Pump-Turbines during Start-up in Turbine Mode. 2008. Available online: http://xueshu.baidu.com/usercenter/paper/show?paperid=97f4d4701a82fd4c1510fe74f46d3c6c&site=xueshu_se (accessed on 13 February 2020).
- Zobeiri, A.; Kueny, J.L.; Farhat, M.; Avellan, F. Pump-turbine rotor-stator interactions in generating mode: Pressure fluctuation in distributor channel. In Proceedings of the 23rd IAHR Symposium on Hydraulic Machinery and Systems, Yokohama, Japan, 17–21 October 2006. [Google Scholar]
- Simão, M.; Pérez-Sanchez, M.; Carravetta, A.; Ramos, H.M. Flow Conditions for PATs Operating in Parallel: Experimental and Numerical Analyses. Energies 2019, 12, 901. [Google Scholar] [CrossRef]
- Simão, M.; Pérez-Sanchez, M.; Carravetta, A.; Lopez-Jimenez, P.; Ramos, H.M. Velocities in a Centrifugal PAT Operation: Experiments and CFD Analyses. Fluids 2018, 3, 3. [Google Scholar] [CrossRef]
- Barrio, R.; Fernandez, J.; Blanco, E. Performance characteristics and internal flow patterns in a reverse-running pump-turbine. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2012, 226, 695–708. [Google Scholar] [CrossRef]
- Shi, F.; Tsukamoto, H. Numerical study of pressure fluctuations caused by impeller-diffuser interaction in s diffuser pump stage. J. Fluids Eng. 2001, 123, 466–474. [Google Scholar] [CrossRef]
- Zang, Z.P.; Gao, F.P.; Cui, J.S. Physical modeling and swirling strength analysis of vortex shedding from near-bed piggyback pipelines. Appl. Ocean Res. 2013, 40, 50–59. [Google Scholar] [CrossRef]
- Krappel, T.; Kuhlmann, H.; Kirschner, O. Validation of an IDDES-type turbulence model and application to a Francis pump turbine flow simulation in comparison with experimental results. Int. J. Heat Fluid Flow 2015, 55, 167–179. [Google Scholar] [CrossRef]
- Magnoli, M.V.; Schilling, R. Numerical simulation of pressure pulsations in Francis turbines. In Advances in Hydroinformatics. Springer Hydrogeology; Gourbesville, P., Cunge, J., Caignaert, G., Eds.; Springer: Singapore, 2013; pp. 389–403. [Google Scholar]
- Masterov, M.V.; Baltussen, W.M.; Kuipers, J. Numerical simulation of a square bubble column using Detached Eddy Simulation and Euler–Lagrange approach. Int. J. Multiph. Flow 2018, 107, 275–288. [Google Scholar] [CrossRef]
- Tu, S.Z.; Aliabadi, S.; Patel, R.; Watts, M. An implementation of the Spalart-Allmaras DESmodel in an implicit unstructured hydrid finite volume/element solver for incompressible turbulent flow. Int. J. Numer. Methods Fluids 2009, 59, 1051–1062. [Google Scholar] [CrossRef]
- Trivedi, C.; Gandhi, B.; Michel, C.J. Effect of transients on Francis turbine runner life: A review. J. Hydraul. Res. 2013, 51, 121–132. [Google Scholar] [CrossRef]




| Categories | Parameters | |
|---|---|---|
| Impeller | Inlet diameter D1 (mm) | 312 |
| Outlet diameter D2 (mm) | 80 | |
| Hub diameter dh (mm) | 0 | |
| Inlet width b1 (mm) | 10 | |
| Blade inlet angle β1 (°) | 120 | |
| Blade number Z | 10 | |
| Blade outlet angle β1 (°) | 30 | |
| Volute | Inlet diameter Ds (mm) | 50 |
| Outlet width b0 (mm) | 24 | |
| Basic circle diameter D0 (mm) | 320 | |
| Draft tube | Length Ld (mm) | 120 |
| Exit diameter Dd (mm) | 80 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Kuang, K.; Wu, Z.; Yang, J. Numerical Simulation of Axial Vortex in a Centrifugal Pump as Turbine with S-Blade Impeller. Processes 2020, 8, 1192. https://doi.org/10.3390/pr8091192
Wang X, Kuang K, Wu Z, Yang J. Numerical Simulation of Axial Vortex in a Centrifugal Pump as Turbine with S-Blade Impeller. Processes. 2020; 8(9):1192. https://doi.org/10.3390/pr8091192
Chicago/Turabian StyleWang, Xiaohui, Kailin Kuang, Zanxiu Wu, and Junhu Yang. 2020. "Numerical Simulation of Axial Vortex in a Centrifugal Pump as Turbine with S-Blade Impeller" Processes 8, no. 9: 1192. https://doi.org/10.3390/pr8091192
APA StyleWang, X., Kuang, K., Wu, Z., & Yang, J. (2020). Numerical Simulation of Axial Vortex in a Centrifugal Pump as Turbine with S-Blade Impeller. Processes, 8(9), 1192. https://doi.org/10.3390/pr8091192




