Numerical Simulation of Water Based Ferrofluid Flows along Moving Surfaces

Abstract

The steady two-dimensional boundary layer flow past a stretching flat sheet in a water-based ferrofluid is investigated. The spatially varying magnetic field is created by two line currents. The similarity method is applied to transform the governing equations into a system of coupled ordinary differential equations. Numerical investigations are performed for ferrofluids, the suspensions of water, and three types of ferroparticles (magnetite, cobalt ferrite, and Mn-Zn ferrite). The impact of the solid volume fraction, the surface stretching parameter, and the ferromagnetic coefficient on the dimensionless velocity and temperature profiles, the skin friction coefficient, and the local Nusselt number are analysed for the three types of ferrofluid.

1. Introduction

The motivation for studying the flow of nanofluids is their significance in widespread industrial applications. The industrial intensification has a demand on the development of more efficient heat transfer systems.

Nanofluids are used as energy saving cooling liquids instead of traditional coolants. First, Choi [1] introduced the term nanofluid for a liquid when nanosized (1–100 nm) solid particles are dispersed in a base solution. Nanoparticles can be, e.g., metals, metal oxides, and carbide ceramics, which increase heat conduction and convection. Due to their thermophysical properties and heat transfer performance, these fluids can improve the heating or cooling efficiency [2,3,4].

Ferrofluids are nanofluids in which magnetic particles (magnetite, cobalt or iron) are suspended in the base fluid. The studies on ferrofluids have shown that the addition of these particles improves significantly the heat transfer in the fluid flow [5,6]. Ferrites (magnetite (Fe₃O₄), cobalt ferrite (CoFe₂O₄) and Mn–Zn ferrite (Mn-ZnFe₂O₄)) incorporated within the base fluid (water) have a wide range of industrial applications in biomedical applications (for example, therapeutic applications in hyperthermia, in cancer treatment, drug delivery) and in diagnostic applications (nuclear magnetic resonance imaging) [7,8,9,10]. Ferroparticles have a high capacity to remove high concentrations of organic compounds. Its industrial application is the removal of dyes that appear in wastewater as a result of manufacturing processes (e.g., paint manufacturing, textile manufacturing, or tanning) [11,12,13,14,15,16].

Boundary layer theory was introduced by Prandtl [17] in order to understand the flow behaviour of a viscous fluid above the boundary. One of the classic applications of this theory is the flow of the boundary layer over a moving plate. Sakiadis [18,19] and Tsou et al. [20] examined the flow behaviour when the plate moves at a constant speed. This problem can be applied during extrusion processes. In the case of linear stretching, Crane [21] provided a solution to the Sakiadis problem for heat and mass transfer in a closed form with exponential function. Linear stretching was extended by Chakrabarti and Gupta for the flow over a linearly stretched surface through a transverse magnetic field [22].

Similarity solutions for the boundary layer equations have been given by Banks [23] when the surface velocity is not constant, when it is stretching with power law velocity. The similarity method was applied to find solutions for non-Newtonian power-law fluid flows along moving surfaces (see e.g., [24,25,26]). The flow caused by a magnetic field having a special power function form is discussed by Chiam [27].

The boundary layer flow and heat characteristics along stretching sheet have been examined by many researchers, for example, for fluids with variable physical properties, Andersson and Aarseth [28], Takhar et al. [29], Pop et al. [30], and Elbashbeshy and Bazid [31]. The flow governed by the Darcy–Brinkman model is taken into account for stretching and shrinking sheet with first- and second-order slip coefficients and mass transpiration in [32].

The magnetohydrodynamic (MHD) flow of different fluids is studied over a linearly or nonlinearly stretching sheet in the literature. Andersson [33] reported the effect of a uniform transverse magnetic field on the movement of electrically conductive Walters’ B fluid along a stretching surface. For quadratically stretching sheet, the boundary layer problem for Walters’ B fluid was studied by Siddheshwar et al. [34]. The boundary layer equations through a porous medium over a stretching sheet with superlinear stretching speed were investigated by Singh et al. [35]. The influence of the slip conditions on the Casson fluid flow over the nonlinearly stretching sheet has been reported by Ullah et al. in [36].

The ferrofluid flow occurs in many industrial processes. Neuringer and Rosensweig [5] pointed out that ferrohydrodynamics require the existence of a spatially varying magnetic field. The flow past an impermeable elastic sheet in a uniform transverse magnetic field was investigated by Andersson [37]. Neuringer [38] investigated the effect of the spatially varying magnetic field on the magneto-thermo-mechanical interaction. Khan et al. [39] examined the effect of uniform heat flux and slip velocity on ferrofluids containing Fe₃O₄, CoFe₂O₄, Mn-ZnFe₂O₄ magnetic particles in water or in kerosene and concluded that the velocity of the ferrofluid increases and the temperature decreases compared to the non-magnetic case.

Our motivation is to study the nanofluid flow and heat transfer over a stretching sheet in a spatially varying magnetic field for nanofluids of water solution with three different ferromagnetic particles: Fe₃O₄, CoFe₂O₄, Mn-ZnFe₂O₄. We investigate the effects of nanoparticle volume fraction, nonlinear stretching, and ferromagnetic property on the flow properties, skin friction, and local Nusselt number.

2. Formulation of the Problem

We investigate the steady boundary layer flow of a viscous, electrically nonconducting, and incompressible nanofluid over an impermeable flat surface placed in the horizontal direction.

Cartesian coordinates are chosen so that the $x$-axis is along the flow direction while $y$-axis is perpendicular to the surface. The nanofluid is confined above the surface. The ambient fluid has a constant temperature $T_{\infty }$, the temperature of the surface is a decreasing function of $x$ and is given by $T_w=T_C-A{x}^{m+1}$, where $A$ and $m$ are real parameters and $T_c$ denotes the Curie temperature. The horizontally stretching surface is placed at $y=0$ and the nanofluid flow is above the surface. The sheet is being stretched at speed $u_w=U_w{x}^m$ with a power function of distance $x$. The ambient fluid temperature is $T_{\infty }=T_c$, and the exterior streaming speed is zero.

The magnetic field is generated by currents perpendicular to the flow plane and generated by two wires, which are equidistant from the flat surface [40]. The direction of magnetization of the suspension’s element is taken into account in the direction of the local magnetic field, and the scalar potential function can be described by

$$\varphi \left(x,y\right)=-\frac{I_0}{2\pi }\left(ta{n}^{-1}\frac{y+a}{x}+ta{n}^{-1}\frac{y-a}{x}\right)$$

(1)

where $I_0$ is the dipole moment per unit length and $a$ denotes the distance of the line current from the origin. The ferrofluid flow is affected by the magnetic field created by the magnetic dipole. In this case, the magnetic field can be expressed as a linear function of the temperature

$$M\left(T\right)=K\left(T_C-T\right)$$

(2)

where $K$ is the pyromagnetic coefficient [5].

The governing equations in two-dimensions can be formulated as follows [41]

$$\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0$$

(3)

$$u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}=-\frac{I_0{\mu }_{0}K}{\pi {\rho }_{nf}}\left(T_C-T\right)\frac{1}{x^2}+\frac{{\mu }_{nf}}{{\rho }_{nf}}\frac{{\partial }^{2}u}{\partial y^2}$$

(4)

$$u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}={\alpha }_{nf}\frac{{\partial }^{2}T}{\partial y^2}$$

(5)

where $u$ and $v$ are the parallel and normal velocity components to the plate, respectively, ${\mu }_{nf}$ is the dynamic viscosity, ${\rho }_{nf}$ denotes the density, ${\alpha }_{nf}$ is the thermal diffusivity of the nanofluid, which will be assumed constant, and ${\mu }_0$ is the magnetic permeability.

Equations (3)–(5) are subjected to the boundary conditions on the sheet $\left(y=0\right)$

$$u\left(x,0\right)=u_w, v\left(x,0\right)=0, T\left(x,0\right)=T_w$$

(6)

with $u_w=U_w{x}^m,T_w=T_C-A{x}^{m+1}$ and far from the surface:

$$u\left(x,y\right)\to 0, T\left(x,y\right)\to T_{\infty }$$

(7)

The parameter $m$ controls the stretching of the surface and the behaviour of boundary layers.

Three types of nanofluids will be investigated. Different volume fractions of the nanoparticles Fe₃O₄, CoFe₂O₄, and Mn-ZnFe₂O₄ dispersed in water are considered. In this work, nanofluids are considered as single-phase fluids. The thermophysical properties of the nanofluids can be expressed in term of the properties of the base fluid, nanoparticles and nanoparticle concentration $\varphi$ in the base fluid as follows:

$${\mu }_{nf}=\frac{{\mu }_b}{{(1-\varphi )}^{2.5}}$$

(8)

where ${\mu }_{nf}$ is the viscosity of the nanofluid and ${\mu }_b$ is the viscosity of the base fluid water,

$${\rho }_{nf}=\left(1-\varphi \right){\rho }_b+\varphi {\rho }_{p }$$

(9)

where ${\rho }_b$ and ${\rho }_p$ denote the density of the base fluid and nanoparticles, respectively, and the heat capacity of the nanofluid ${(C_p)}_{nf}$ is assumed as

$${(C_p)}_{nf}=\frac{\varphi {(\rho C_p)}_p+\left(1-\varphi \right){(\rho C_p)}_b}{{\rho }_{nf}}$$

(10)

The thermal conductivity $k_{nf}$ of the nanofluid is calculated with the thermal conductivity $k_b$ of base fluid and the thermal conductivity $k_p$ of the particles with the formula

$$k_{nf}=k_b\frac{k_p+2k_b-2\varphi \left(k_b-k_p\right)}{k_p+2k_b+\varphi \left(k_b-k_p\right)}$$

(11)

Table 1 shows the thermo-physical properties for water, Fe₃O₄, CoFe₂O₄, and Mn-ZnFe₂O₄ particles [29].

Table 1. The thermo-physical properties of water, Fe₃O₄, CoFe₂O₄, and Mn-ZnFe₂O₄ particles.

Parameter	Fe3O4	CoFe2O4	Mn-ZnFe2O4	H2O
$\rho \left(\mathrm{k}\mathrm{g}/{\mathrm{m}}^3\right)$	5180	4907	4900	997.1
${\mathrm{C}}_{\mathrm{p}}\left(\mathrm{J}/\mathrm{k}\mathrm{g}·\mathrm{K}\right)$	670	700	800	4179
k $\left(\mathrm{W}/\mathrm{m}·\mathrm{K}\right)$	9.7	3.7	5	0.613
$\mathsf{\mu }\left(\mathrm{Pa}·\mathrm{s}\right)$	-	-	-	0.001

The similarity functions and similarity variable are introduced as follows:

$$\eta =\sqrt{\frac{{\rho }_{nf}{U}_w}{{\mu }_{nf}}}{x}^{\frac{m-1}{2}}y, \psi \left(x,y\right)=\sqrt{\frac{{\mu }_{nf}{U}_w}{{\rho }_{nf}}}{x}^{\frac{m+1}{2}}f\left(\eta \right), T=T_C-A{x}^{m+1}\Theta \left(\eta \right)$$

(12)

Equation (3) is automatically satisfied with stream function $\psi \left(x, y\right)$ choosing such as $u=\partial \psi ∕\partial y$ and $v=-\partial \psi ∕\partial x$. Applying the similarity transformations (12), the governing Equations (3)–(5) can be rewritten as follows:

$$f^{‴}+\frac{m+1}{2}f{f}^{″}-m{f^{\prime }}^2-\beta \Theta =0,$$

(13)

$${\Theta }^{″}+\mathrm{Pr}\left[\frac{m+1}{2}f{\Theta }^{\prime }-\left(m+1\right)\Theta f^{\prime }\right]=0,$$

(14)

where the Prandtl number for the nanofluid is defined by $\mathrm{Pr}={\left(\mu \rho ∕\alpha \right)}_{nf}$ and $\beta =I_0{\mu }_{0}KA∕\pi {\rho }_{nf}{U}_w^2$ is the ferromagnetic parameter. The primes denote differentiation with respect to $\eta .$ Also, boundary conditions (6) and (7) are converted to

$$f\left(0\right)=0, f^{’}\left(0\right)=1, \Theta \left(0\right)=1$$

(15)

$$f^{\prime }\left(\eta \right)=0, \Theta \left(\eta \right)=0 as \eta \to \infty$$

(16)

Based on the above quantities, the skin friction coefficient $C_f$ and the local Nusselt number $N{u}_x$ can be given as follows

$$C_f=-\frac{2 {\tau }_w}{{\rho }_b U_w^2} ,$$

(17)

$$N{u}_x=\frac{x q_w}{k_b\left(T_w-T_{\infty }\right)} ,$$

(18)

where the wall shear stress ${\tau }_w$ and the wall heat flux $q_w$ are

$${\tau }_w={\mu }_{nf}{\left(\frac{\partial u}{\partial y}\right)}_{y=0}, q_w=-k_{nf} {\left(\frac{\partial T}{\partial y}\right)}_{y=0}$$

(19)

Using the above equations, we get

$$R{e}_x^{\frac{1}{2}}{C}_f{x}^{-\frac{3m}{2}}=\sqrt{\frac{1-\varphi +\varphi \frac{{\rho }_p}{{\rho }_b}}{{\left(1-\varphi \right)}^{2.5}}} f^{″}\left(0\right) ,$$

(20)

$$R{e}_x^{-\frac{1}{2}}N{u}_x x^{-\frac{m}{2}}=-\frac{k_{nf }}{k_{b }}\sqrt{\left(1-\varphi +\varphi \frac{{\rho }_p}{{\rho }_b}\right){\left(1-\varphi \right)}^{2.5}} {\theta }^{\prime }\left(0\right) ,$$

(21)

where the local Reynolds number $R{e}_x$ is defined by ${Re}_x=\frac{{\rho }_{nf} U_w x}{{\mu }_{nf}}$.

We remark that the exact solution to Equation (13) with boundary conditions $f\left(0\right)=0, f^{\prime }\left(0\right)=1,$ $f^{\prime }(\infty )=0 \mathrm{for} m=1 \mathrm{and} \beta =0$ can be given in the closed form

$$f\left(\eta \right)=1-e^{-\eta }$$

(22)

then, the corresponding stream function is

$$\psi \left(x,y\right)=\sqrt{\frac{{\mu }_{nf}{U}_w}{{\rho }_{nf}}}x \left(1-e^{-\sqrt{\frac{{\rho }_{nf }{U}_w}{{\mu }_{nf}}}y}\right)$$

(23)

and the velocity components are

$$u\left(x,y\right)=U_{w}x e^{-\sqrt{\frac{{\rho }_{nf }{U}_w}{{\mu }_{nf}}}y} ,$$

(24)

$$v\left(x,y\right)=-\sqrt{\frac{{\mu }_{nf}{U}_w}{{\rho }_{nf}}} \left(1-e^{-\sqrt{\frac{{\rho }_{nf }{U}_w}{{\mu }_{nf}}}y}\right) .$$

(25)

These solutions are equivalent to those obtained by Crane [11].

3. Results and Discussion

The coupled transformed system of differential Equations (13)–(14) subjected to boundary conditions (15) and (16) are solved numerically by employing the fourth-order method (bvp4c) in MATLAB. The influence of several physical parameters, namely the stretching exponent $m$, the ferromagnetic interaction parameter $\beta$, the Prandtl number Pr of the three types of nanofluids on the boundary layer flow and heat transfer in ferromagnetic viscoelastic fluid are investigated numerically. The system of Equations (13)–(14) are solved in the interval $0 \le \eta \le 10$, the solutions at infinity converge to the boundary conditions. The physical parameters are taken from Table 1 for the nanoparticles Fe₃O₄, CoFe₂O₄, and Mn-ZnFe₂O₄ and for the water base fluid. The two differential equations are converted into a system of first order differential equations and solved.

The influence of the nanoparticle concentration on the Prandtl number for Fe₃O₄- water ferrofluid is depicted in Figure 1. It can be noticed that the addition of nanoparticles will cause a significant decrease in the Prandtl number of the ferrofluid.

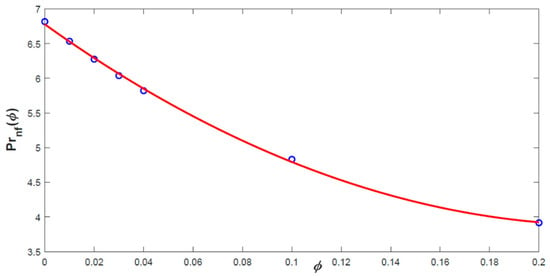
Figure 1. Variation of ${\mathrm{Pr}}_{nf}$ with $\varphi$ for Fe₃O₄.

Figure 2 demonstrates the impact of the ferromagnetic solid particles on the nondimensional velocity distribution when the volume fraction is $\varphi =0.02,$ the ferromagnetic parameter is fixed as $\beta =0.05$ and the stretching parameter is $m=0.05$. This plot shows that the velocity is the smallest and the boundary layer thickness is the shortest one for Fe₃O₄- water solution. For the same parameters, the thermal distribution is shown in Figure 3. It can be observed that the temperature gradient is also the largest for CoFe₂O₄. Based on the figures, the thickness of the momentum and the thermal boundary layer for the variable $\eta$ are around 8 and 2, respectively.

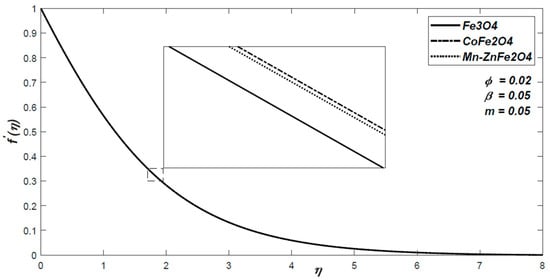
Figure 2. The variation of the nondimensional velocity for three types of nanoparticles with volume fraction $\varphi =0.02$.

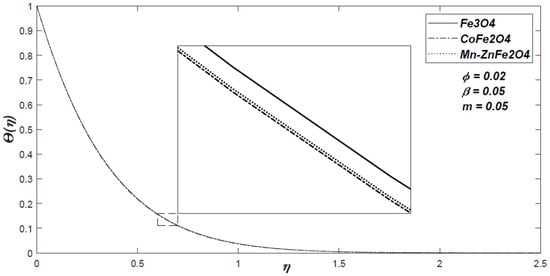
Figure 3. The variation of the nondimensional temperature for three types of nanoparticles with volume fraction $\varphi =0.02$.

Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10 and Figure 11 are presented for the nanofluid made of Fe₃O₄. The influence of the external magnetic field induced by the two line currents on the velocity and temperature distribution is shown in Figure 4 and Figure 5. It is highlighted that the ferromagnetic parameter $\beta$ decelerates the fluid flow and the temperature gradient decreases with an increase in the value $\beta .$

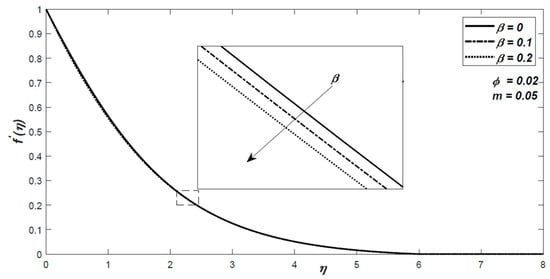
Figure 4. The variation of the nondimensional velocity for different values of the ferromagnetic parameter $\beta$.

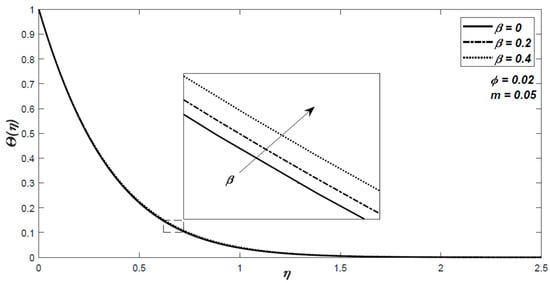
Figure 5. The variation of the nondimensional temperature for different values of the ferromagnetic parameter $\beta$.

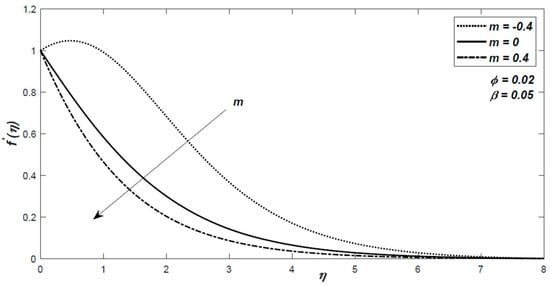
Figure 6. The variation of the nondimensional velocity for different values of the stretching parameter $m$.

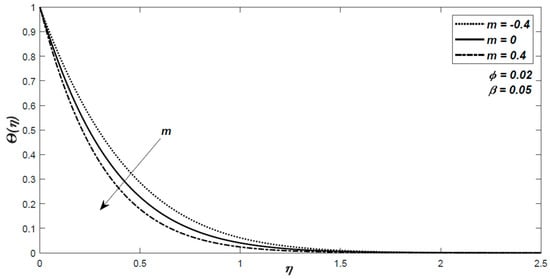
Figure 7. The variation of the nondimensional temperature for different values of the stretching parameter $m$.

Figure 8. The variation of the nondimensional velocity for different values of volume fraction $\varphi$.

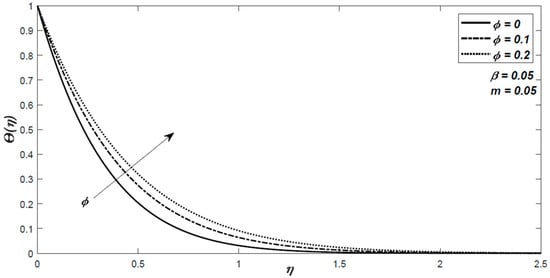
Figure 9. The variation of the nondimensional temperature for different values of volume fraction $\varphi$.

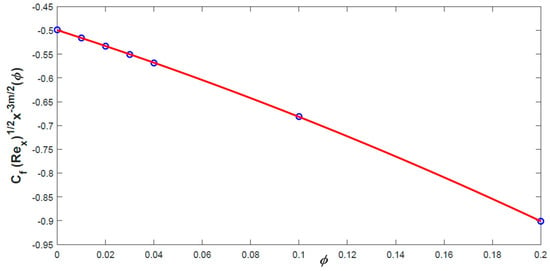
Figure 10. Variation of ${\mathrm{Re}}_x^{1/2}{C}_f$ with $\varphi$ (Fe₃O₄).

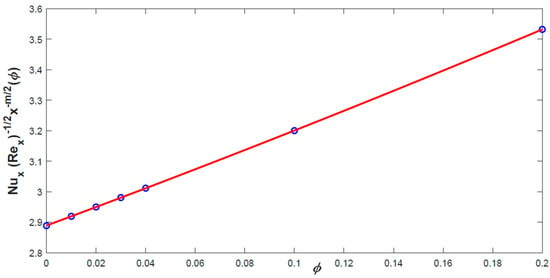
Figure 11. Variation of ${\mathrm{Re}}_x^{-1/2}Nu$ with $\varphi$ (Fe₃O₄).

Figure 6 and Figure 7 highlight the effect of stretching parameter $m$ on the dynamics of the fluid. It is observed that the velocity decreases with an increase in positive $m.$ Figure 6 shows that, for a negative value of $m$, the velocity initially shows an increasing trend and then decreases monotonically to zero. For $m=0$ or $m>0$, this phenomenon cannot be observed. In addition, for $m$ negative values, the boundary layer is thicker.

For the temperature distribution we see a decrease of the temperature with increasing $m$ for both positive and negative values of $m$.

The effect of nanoparticle’s volume fraction on dimensionless velocity and temperature are shown in Figure 8 and Figure 9 for the ferrofluid water-Fe₃O₄. From these figures, it is noted that velocity decreases for increasing values of volume fraction $\varphi$. The influence of increasing nanoparticle concentration is the opposite in the temperature profiles.

Quantities important for technical practice are the skin coefficient of friction $C_f$ and the local Nusselt number $Nu$ given by (17) and (18). For the ferrofluid with different nanoparticle concentration, the variation of the $R{e}_x^{\frac{1}{2}}{C}_f{x}^{-\frac{3m}{2}}$ and $R{e}_x^{-\frac{1}{2}}N{u}_x x^{-\frac{m}{2}}$ are depicted on Figure 10 and Figure 11 for Fe₃O₄ with $\beta =0.05$, $m=0.05$. It is observed that the variation of the skin friction with the volume fraction of solid particles is decreasing in the interval $0\le \varphi \le 0.2$. However, the local Nusselt number is increasing with values of the volume fraction $\varphi$.

Table 2, Table 3 and Table 4 give the variation of $-f^{″}\left(0\right)$ and $-{\theta }^{\prime }\left(0\right)$ depending on the volume fraction $\varphi$, the ferromagnetic parameter $\beta$, and the stretching parameter $m$. These values have a great influence on the wall shear stress and on the wall heat flux.

Table 2. The variation of the component of $C_f$ and $Nu$ with $\varphi$ ($m=0.05$, $\beta =0.05$).

$\mathit{\varphi }$	$-{\mathbf{f}}^{\mathbf{″}}\mathbf{\left(}\mathbf{0}\mathbf{\right)}$	$\mathbf{-}{\mathsf{\theta }}^{\mathbf{\prime }}\mathbf{\left(}\mathbf{0}\mathbf{\right)}$
0	0.49878	2.88860
0.01	0.49905	2.82487
0.02	0.49931	2.76548
0.03	0.49957	2.71004
0.04	0.49981	2.65821
0.1	0.50114	2.40859
0.2	0.50279	2.15356

Table 3. The variation of the component of $C_f$ and $Nu$ with $\beta$ ($\mathsf{\varphi }=0.02$, $m=0.05$).

$\mathit{\beta }$	$\mathbf{-}{\mathit{f}}^{\mathbf{″}}\mathbf{\left(}\mathbf{0}\mathbf{\right)}$	$-{\mathit{\theta }}^{\mathbf{\prime }}\mathbf{\left(}\mathbf{0}\mathbf{\right)}$
0	0.48568	2.76777
0.1	0.51299	2.76318
0.2	0.54350	2.75758
0.3	0.57565	2.75144
0.4	0.61388	2.74333

Table 4. The variation of the component of ${\mathrm{C}}_{\mathrm{f}}$ and $\mathrm{Nu}$ with $\mathrm{m}$ ($\mathsf{\varphi }=0.02$, $\mathsf{\beta }=0.05$).

$\mathit{m}$	$\mathbf{-}{\mathit{f}}^{\mathbf{″}}\mathbf{\left(}\mathbf{0}\mathbf{\right)}$	$\mathbf{-}{\mathit{\theta }}^{\mathbf{\prime }}\left(0\right)$
−0.4	−0.19087	2.21520
−0.2	0.25261	2.45502
0	0.45861	2.70528
0.1	0.53734	2.82465
0.2	0.60697	2.93399
0.3	0.69944	3.10580
0.4	0.72781	3.15931

4. Conclusions

The effects of volume fraction of solid ferroparticles and the non-uniform magnetic field on the dimensionless velocity and temperature and on the skin friction coefficient and local Nusselt number are investigated in ferrofluid flows along nonlinearly stretched sheets for three selected ferroparticles (magnetite, cobalt ferrite and Mn-Zn ferrite) in water base fluid. It has been shown that a very small amount of ferro particle affects the velocity and temperature of a ferrofluid in a non-constant magnetic field. The effect of the concentration of solid particles in the base fluid is examined in the range 0 ≤ ϕ ≤ 0.2, $\varphi =0$ means the case when only the base fluid is considered. The thermophysical properties of the base fluid and the applied nanoparticles are given in Table 1. The density and thermal conductivity of the suspension of solid particles and the water are increasing with the increase of the concentration of Fe₃O₄, CoFe₂O₄, and Mn-ZnFe₂O₄ particles. The values of Prandtl number for each ferrofluid is decreasing with $\varphi$ in the interval 3.91 … 6.81 as it is shown for Fe₃O₄ particles in Figure 1.

We considered the impacts provided by the varying values of the pertinent parameters (stretching parameter, volume fraction, and ferromagnetic parameter) on the dimensional velocity, dimensional temperature, the skin friction, and local Nusselt number. Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8 and Figure 9 illustrate the variation in the velocity and temperature. We observed that the increase in the volume fraction slows down the flow and increases the temperature. The increase in the magnetic effect has the same impact on the velocity and temperature profiles. An increase in the stretching parameter will decrease both the velocity and the temperature. The Nusselt number and the skin friction for different values of the volume fraction are also analysed in Figure 10 and Figure 11. The Nusselt number is increasing and the skin friction is decreasing with an increasing value of $\varphi .$