Modeling the Municipal Waste Collection Using Genetic Algorithms

Abstract

Calculating adequate vehicle routes for collecting municipal waste is still an unsolved issue, even though many solutions for this process can be found in the literature. A gap still exists between academics and practitioners in the field. One of the apparent reasons why this rift exists is that academic tools often are not easy to handle and maintain by actual users. In this work, the problem of municipal waste collection is modeled using a simple but efficient and especially easy to maintain solution. Real data have been used, and it has been solved using a Genetic Algorithm (GA). Computations have been done in two different ways: using a complete random initial population, and including a seed in this initial population. In order to guarantee that the solution is efficient, the performance of the genetic algorithm has been compared with another well-performing algorithm, the Variable Neighborhood Search (VNS). Three problems of different sizes have been solved and, in all cases, a significant improvement has been obtained. A total reduction of 40% of itineraries is attained with the subsequent reduction of emissions and costs.

1. Introduction

The improvement of the waste collection process can be considered aligned with the 11th Sustainable Development Goal (SDG) “Sustainable cities and communities” [1]. Nevertheless, this process is still far from being in an optimal status. As experts state [2], inadequate vehicle routes are among the problems the process should tackle. The optimization of the routes for waste collection vehicles with time window is known as the Waste Collection Vehicle Routing Problem (WCVRP).

As indicated by Caria, Todde, and Pazzona [3], the WCVRP is a specific case of the whole class of problems, known as the Vehicle Routing Problem (VRP). The oldest VRP type problem in the transport history is the Travelling Salesman Problem (TSP), solved for the first time by Lin [4], where the aim is to find the shortest route visiting each member of a collection of locations and returning to the starting point. The TSP has evolved towards solving similar problems with different and additional restrictions and objectives, including the WCVRP presented herein.

The WCVRP needs to organize routes, vehicles, and customers, while respecting the constraints that are imposed by the system. VRP allows for reaching the goals that are referred to as transport logistics, as well as the minimization of costs and carbon dioxide (CO${}_2$) emissions [3]. On top of the overall VRP considerations, WCVRP is concerned with finding cost optimal routes for garbage trucks such that all garbage bins are emptied and the waste is driven to disposal sites while respecting customer time windows and ensuring that drivers are given the breaks that the law requires. The first waste collection problem was probably presented by Beltrami and Bodin [5]. Since then, the problem has evolved into the herein presented WCVRP. Many relevant references have studied this problem so far, offering different approaches for solving the same challenge (or similar ones). Concerning the most relevant and recent ones, Buhrkal, Larsen, and Ropke [6] propose an adaptive large neighborhood search algorithm for solving the problem. Babaee Tirkolaee, Mahdavi, and Seyyed Esfahani [7] apply an improved hybrid simulated annealing algorithm (SA) for optimizing the mathematical model developed. Hannan et al. [8] propose a particle swarm optimization algorithm to optimize a model that considers not only typical distance, total waste, collection efficiency, etc. parameters but also Threshold Waste Level (TWL) tightness factors. De Bruecker et al. [9] present an enhanced model for the WCVRP that models distinct labor cost types and collecting speeds; thus, they differentiate between cheaper regular shifts during traffic peak hours, against higher collection speeds but with expensive, non-regular shift-rates. Rodrigues Pereira Ramos, Soares de Moraisa, and Barbosa-Póvoa [10] study three operational management approaches to define dynamic optimal routes based on sensoring, Radio Frequency Identification (RFID), and considering the access to real-time information on the bins’ fill-levels. Benjamin and Beasley [11] develop a model for the waste collection vehicle routing problem with time windows, driver rest period, and multiple disposal facilities as a differential aspect.

It is worth mentioning that the sometimes explicit, but always present idea of this optimization problem is the reduction of CO${}_2$ emissions, as the current logistic methods used in this routing problems depend strongly on fossils fuels [12].

The fact of not having generalized optimized routes for the WCVRP is striking, as many solutions for this process can be found in the literature. When analyzing the potential causes of this breach between the practitioners and the academia, it could be stated that generic routing tools are considered incomplete for this variant of the traveling salesman problem [13], whereas more specific tools (such as [14,15]) have a related cost that often entities are not willing to afford. Additionally, many researchers developed their solutions to the problem, but normally they are more focused on publishing them than in offering them to entities that manage the waste collection. Thus, even though the problem has been deeply studied from a theoretical point of view, its application to real-world problems is scarce.

Within this context, the aim of this work has been to show the development and implementation of a procedure for the optimization for a local commonwealth for tackling the WCVRP of a region.

In the final solutions, Genetic Algorithms (GAs) have been applied. GAs belong to the more general classification of evolutionary optimization techniques or evolutionary programs and they are surely the most widely known type of Evolutionary Algorithms. They are based on selection, crossover, and mutation principles of Darwin’s theory of evolution. In the last few years, there has been a growing effort to apply GAs to general constrained optimization problems as most of engineering optimization problems often see their solution constrained by a number of restrictions imposed on the decision variables [16].

The research method had three major steps: first, we performed a literature review of optimization algorithms applied to this case that is detailed in Section 1. The aim of this study was to analyze how this problem was modeled in the past, and to pre-select which types of algorithms could fit best to the end user requirements in terms of user friendliness, cost, and quality of results. Second, the characteristics of this specific optimization case (detailed in Section 2) were analyzed to offer the company a selection of the algorithm fitting best to its requirements. Finally, the designed solution was successfully implemented and tested with the pre-selected types of algorithms, to choose the one performing best, as it is detailed in Section 3 Methodology, Section 4 Algorithm, and Section 5 Results, remarking that the obtained results raised the interest of the surrounding communities.

2. Optimization Problems

Combinatorial optimization problems can be written mathematically as:

$$\begin{array}{cc}\hfill & \mathrm{minimize}f\left(x\right),\hfill \end{array}$$

(1)

$$\begin{array}{cc}\hfill & \mathrm{subject}\mathrm{to}{h}_i\left(x\right)\ge a_i,i=1,\dots ,m,\hfill \end{array}$$

(2)

$$\begin{array}{c}{f}_j\left(x\right)=b_j,j=1,\dots ,s,\hfill \end{array}$$

(3)

where $f:{\mathbb{R}}^n\to \mathbb{R}$ is the objective function, and $h_i:{\mathbb{R}}^n\to \mathbb{R}$, $i=1,\dots ,m$ and $f_j:{\mathbb{R}}^n\to \mathbb{R}$, $j=1,\dots ,s$ are the constraints.

The optimization problem has been written as a minimization problem, but after some modifications it can be written as a maximization problem:

$$ming\left(x\right)=max-g\left(x\right).$$

(4)

In the same way, the equality constraints $f_j\left(x\right)=b_j$ can be written as inequalities:

$$f_j\left(x\right)\ge b_j\mathrm{and}{f}_j\left(x\right)\le b_j.$$

(5)

The simplest constrained optimization problem arises when the objective function $f\left(x\right)$ and the restrictions are linear functions. This type of problem is a linear programming problem, and it can be solved quite efficiently by the simplex algorithm. However, in the majority of the optimization problems, neither the objective function nor the restrictions are linear functions. The vast majority of these problems are NP-complete problems, which means that there is no any solving algorithm that can be executed in polynomial time in relation to the size of the problem. In complexity theory, NP-complete denotes the set of problems that are not solvable by a deterministic polynomial time algorithm. The feasible solutions’ space is so large that the computation of the exact solution requires a lot of time. NP-complete problems can be solved by a restricted class of brute force search algorithms and they can be used to simulate any other problem with a similar algorithm. Genetic algorithms are also a good and efficient choice to find an approximate solution of these problems [17]. A classical NP-complete problem is the Travelling Salesman Problem (TSP), in which the shortest route for a traveling salesman starting and finishing in the same point and visiting every city once has to be found.

An efficient way to solve these types of problems is using genetic algorithms. The basic principles of genetic algorithms were established by Holland [18], and they are well described in several texts [19,20,21,22,23]. Owing to their simplicity, flexibility, ease of implementation, minimal requirements, fast convergence towards close-to-optimal solutions, and global perspective, GAs are successfully used in a wide variety of problems [16]. As these characteristics are essential for practitioners to have a utilizable solution, and as the performed literature review did not bring better solutions, the chosen option was to implement the simple GA (SGA) presented herein.

Traveling Salesman Problem

In the TSP problem, a collection of n cities are given. The objective is to determine the shortest route that a salesman has to follow, in which each city is visited once and then the salesman returns to the starting point of the route. This problem can be defined mathematically as follows:

Given an integer n and an $n\times n$ matrix $D=\left(d_{ij}\right)$ in which each $d_{ij}$ is the distance between two cities, the cyclic permutation $\pi$ of the integers $i=1$, 2, …, n that minimizes the distances has to be determined. As a first approximation, the feasible search space is formed by all cyclic permutations of the numbers $\left\{1,2,\dots ,n\right\}$:

$$F=\left\{\left.\left({\pi }_1{\pi }_2\dots {\pi }_n\right)\right|{\pi }_i\in \left\{1,2,\dots ,n\right\}and{\pi }_i\ne {\pi }_j\forall i\ne j\right\}.$$

(6)

The number of elements of this space is $n!$, being n the number of cities. In this way, the length of a permutation $\pi =\left({\pi }_1,{\pi }_2,\dots ,{\pi }_n\right)$ can be expressed as:

$$\sum _{i=2}^n{d}_{{\pi }_{i-1},{\pi }_i}+d_{{\pi }_n,{\pi }_1}.$$

(7)

For each permutation $\pi$, there are $(n-1)$ permutations that starting in a different city are similar to the given one. That is to say, the distance of these n permutations is the same. Taking into account this consideration, the size of the feasible space is $n!/n=(n-1)!$. Moreover, if the distance matrix D is symmetric, the distance of each permutation in both directions is the same, and the size of the feasible space is reduced to $(n-1)!/2$. As it can be observed, the main difficulty of this problem is the huge number of possible tours.

3. Methodology

The objective of this work is to find an optimal itinerary for the waste collection. This methodology will be applied to the data of Sopelana, a municipality in the province of Biscay, autonomous community of the Basque Country (Spain). Sopelana is located in the region of Plencia-Munguia or Uribe, and it is part of the Commonwealth of Services of Uribe Coast. It has an extension of 8.40 km${}^2$ and a population of 13,510 inhabitants, a figure that in summer is usually multiplied by four due to summer visitors.

It is the responsibility of the commonwealth everything related to waste management. There are various trash cans to collect waste:

• Restwaste: 317 trash cans. They are distributed in three routes. There are 186 trash cans in the first route, 72 trash cans in the second route, and 59 in the third one. The trash of the first route is collected everyday. The second route is done four days per week and the third route three days per week.
• Organic waste: 29 trash cans. This waste is collected once per week.
• Small recipients of plastic and metal: 85 trash cans. This waste is collected twice per week.
• Glass: 69 trash cans. Glass is collected once per month.
• Paper: 62 trash cans. These trash cans are divided in two groups depending on their filling frequency. Paper is collected everyday, but not all the containers are emptied everyday.
• Oil: 4 trash cans. This waste is collected twice per month.
• Reusable waste: 7 trash cans. From September to June, it is collected once per week, and in July and August twice per week.
• Batteries: 31 trash cans. They are collected twice per month.

Other types of waste such as big volume wastes are collected once per week following the same route as for the restwaste; there are eight points to collect lamps and fluorescent lightings and they are collected when the container is full; there are some locations in which CDs are collected when the containers are full. All the aforementioned data were given by the local government.

In this work, three problems of different sizes will be analyzed. In the three cases, the aim is to improve the waste collection itinerary in the sense of obtaining a shorter route than the one followed nowadays. A small problem of reusable waste with seven trash cans, a medium problem of organic waste consisting of 29 trash cans, and a big problem consisting of the first route of restwaste with a total of 186 trash cans will be considered. In the case of restwaste, there are several trash cans in the same location. Specifically, the 186 trash cans are distributed in 147 different locations; thus, these locations will be considered in the problem. The data of these problems can be seen in Table 1.

Table 1. Three problems analyzed.

Waste-Type	Number of Locations	Collecting Frequency
Reusable waste	7	September to June once per week,
		July and August twice per week
Organic waste	29	Once per week
Restwaste	147	Everyday

According to the data given by the enterprise in charge of restwaste collection, between 8000 kg and 13,000 kg of restwaste are collected everyday in Sopelana. A truck is enough to carry out this collection. The truck used has a load of 13 tons, and it has a compaction mechanism. Each container has $1.1$ m${}^3$, which is reduced to $0.183$ m${}^3$ after compaction. This means that the volume of 125 trash cans that are full can fit in the truck (125 × 0.183 m${}^3$ = 22.875 m${}^3$). In the event that the truck was filled during the collection of the 186 containers (147 location points), it would be emptied in the dump intended for it and, after that, it would continue with the route. However, this event is not very probable as it means that 125 trash cans out of 186 are full up (which is the $67.20$%).

4. Algorithms

For the three problems, the coordinates of the locations and the distance matrices have been calculated using Google Maps (https://www.google.com/maps, data from October and November 2019). The coordinates of all locations and the distance matrices can be found in Appendix A. The smallest distance between two locations has been considered in the distance matrices. The distance matrices are not symmetric, as the way back and forth from a location to another may be different.

The three problems have been solved using a VNS and a GA. The smallest problem (reusable waste, seven locations) has also been solved using the brute force algorithm. These two algorithms were chosen among all the set of alternatives for developing the final solution for maintainability reasons. The developers of the solutions are academic institutions, so we cannot provide maintenance services. As both literature [24] and the news [25] state, there is a lack of availability of computer science technicians. Because of this fact, the final user of the solution wanted a competitive but mainly easy to maintain algorithm. These algorithms being two of the most frequently applied when developing the syllabuses of subjects related to programming, the research team decided to compare them and offer the most effective possible solution. The distances that correspond to all the permutations of $n=7$ elements have been calculated that is $7!=5040$. The process has been implemented as it is explained in Algorithm 1.

Algorithm 1 Algorithm to determine solutions using brute force.

1: procedureBruteForce( distance matrix of $n=7$ problem ) 2:     Create all the permutations of $n=7$ elements 3:     for i=1:7! do 4:         Calculate the distance of the permutation 5:     end for 6:     Calculate the shortest distance among all the permutations 7: end procedure

We have started by trying the VNS algorithm [26] for all the problems. The VNS consists of applying a local search method repeatedly in the neighborhood ${\mathcal{N}}_k$ of the actual solution. When a local optimal is reached, the algorithm changes the system of neighborhood with the aim of escaping from local optima and reaching a better one. For this reason, it can be said that the VNS performs well both when searching local and global optima. In Algorithm 2, the process followed is explained. We have implemented two systems of neighborhoods: the 2-opt neighborhood and a swap-based neighborhood. The neighborhood structure 2-opt consists of changing a pair of edges between cities [27]. The swap-based neighborhood that we have created swaps the first element of the permutation with all the rest.

Algorithm 2 Algorithm to determine solutions using VNS.

1: procedureVariable neighborhood search(distance matrix) 2:     Choose a set of neighborhood structures ${\mathcal{N}}_k$ for $k=1,2,\dots ,k_{max}$ 3:     Generate the initial solution 4:     Consider the initial solution as the best one 5:     $k\leftarrow 1$ 6:     while $k\le k_{max}$ do 7:         while There is an improvement do 8:            Choose the neighborhood system that corresponds to k 9:            Find the best solution among all the neighbors 10:            if The solution is improved then 11:                Update the best solution and its evaluation function value 12:                Continue to search with $k\leftarrow 1$ 13:            else 14:                Continue to search with $k\leftarrow k+1$ 15:            end if 16:         end while 17:     end while 18:     Output the shortest distance and the corresponding route of the overall process 19: end procedure

Additionally, for all the problems $n=7$, $n=129$, and $n=147$, another two algorithms have been implemented. In Algorithm 3, an initial population of m different individuals (permutations) has been created. The evaluation function (distance of the route) of each individual has been calculated. In each generation, the process of selecting two parents randomly, the crossover operator, the posterior correction of the individual in order to be a permutation, and the mutation process have been performed $m/2$ times. If the new descendants are different from the individuals of the population and if their evaluation function (fitness function) is smaller than the worst (the largest) of the population, the worst individuals are replaced by these new descendants. The fourth algorithm implemented only differs from the third in the fact that the routes followed nowadays in the trash collection (one route in each problem) are inserted as a seed in the initial population.

Algorithm 3 Algorithm to determine solutions using SGA.

1: procedureSimple genetic algorithm(distance matrix, generations, population size, probabilities) 2:     Create an initial population of m different permutations randomly 3:     Compute the evaluation function of each permutation 4:     for i=1:generations do 5:         for j=1:m/2 do 6:            Select two parents randomly from the population 7:            Cross with a certain probability to produce two descendants 8:            Correct the descendants to be permutations 9:            Mutate each individual with a certain probability 10:            Compute the evaluation function of each descendant 11:            if evaluation function of the descendants smaller than the largest evaluation then 12:                if the descendants are not repeated in the population then 13:                    Replace the descendants by the permutations with largest evaluation 14:                end if 15:            end if 16:         end for 17:         Output the shortest distance and the corresponding route of each generation 18:     end for 19:     Output the shortest distance and the corresponding route of the overall process 20: end procedure

The crossover operator used is the classical one [18]. A crossover point is selected randomly from which the two strings of the parents are broken into separate parts. The new descendants are formed by recombination of these parts. For example, consider $n=7$ and the routes:

$$\begin{array}{c}\hfill \left(1234567\right)\\ \hfill \left(2453716\right)\end{array}$$

Randomly, a crossover point in which the strings are broken into separate parts is selected. Suppose that the crossover point is chosen between the third and the fourth bit:

$$\begin{array}{c}\hfill \left(123\left|4567\right.\right)\\ \hfill \left(245\left|3716\right.\right)\end{array}$$

Combining the head of the first route with the tail of the second route and vice versa, the result is the following:

$$\begin{array}{c}\hfill \left(123\left|3716\right.\right)\\ \hfill \left(245\left|4567\right.\right)\end{array}$$

If the resulting descendants are not permutations, then a correction algorithm is applied in order to obtain two individuals that belong to the feasible space. Each resulting individual is repaired, by calculating the repeated values and their positions, and by inserting the missing values randomly on the positions where the repeated values are located.

The exchange mutation operator, also called the swap mutation operator, has been applied, in which two positions of the route are selected randomly and the cities on those positions are exchanged [28]—for example, if we consider the route:

$$\left(123\mathbf{5}74\mathbf{6}\right),$$

and if we choose the fourth and seventh positions, the cities on those positions are interchanged:

$$\left(123\mathbf{6}74\mathbf{5}\right)$$

5. Results

In this section, the results obtained for each of the problems are presented.

For $n=7$, the brute force algorithm has been applied first. The shortest itinerary has $7.67$ km and the longest $13.2$ km. In Figure 1, the distances of all permutations ($7!=5040$) are shown. All the permutations are represented in the horizontal axis (that is, $7!=5040$), and the distance that corresponds to each of them is plotted in the vertical axis.

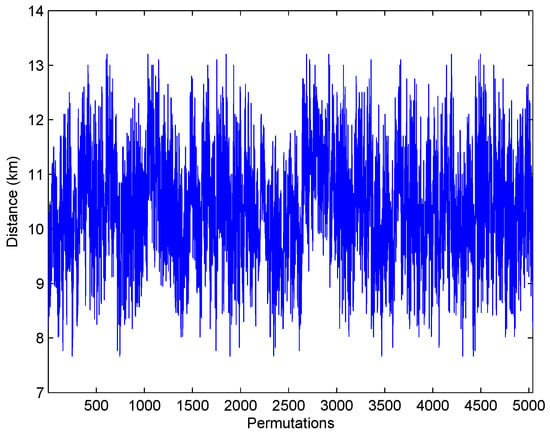
Figure 1. Brute force application, problem $n=7$.

For the three problems, the VNS algorithm has been applied next. Ten executions have been done for each problem. The best, the worst, the mean, and the median distances of this executions are presented in Table 2, Table 3 and Table 4. In all the executions, an initial solution has been generated randomly.

Table 2. Results of 10 executions $n=7$ problem, VNS.

$\mathit{n}=7$	VNS
Best distance (km)	$7.6700$
Worst distance (km)	$8.4000$
Mean distance (km)	$7.7690$
Median distance (km)	$7.6700$

Table 3. Results of 10 executions $n=29$ problem, VNS.

$\mathit{n}=29$	VNS
Best distance (km)	$19.4170$
Worst distance (km)	$25.5570$
Mean distance (km)	$22.5475$
Median distance (km)	$21.9450$

Table 4. Results of 10 executions $n=147$ problem, VNS.

$\mathit{n}=147$	VNS
Best distance (km)	$61.5470$
Worst distance (km)	$71.3560$
Mean distance (km)	$66.8944$
Median distance (km)	$66.9507$

In addition, finally, the SGA (without and with a seed) has been performed. For $n=7$, taking into account that the average of the shortest and the longest route is $10.4350$ km, the route $(6,7,3,4,2,5,1)$ of $10.45$ km has been chosen as seed. In the cases of $n=29$ and $n=147$, the actual itineraries have been chosen as seed. These data are available in Table 5. Notice that, if the VNS algorithm is started, taking the actual itinerary as initial solution, all the executions have the same performance. In this case, for $n=7$, a route of $8.2500$ km is obtained; for $n=29$, a route of $18.7670$ km; and, for $n=147$, a route of $34.4280$ km.

Table 5. Average distance route ($n=7$) and actual routes ($n=29$, $n=147$).

	$\mathit{n}=7$	$\mathit{n}=29$	$\mathit{n}=147$
Route	$(6,7,3,4,2,5,1)$	$(26,24,23,18,15,11,12,13,16,-$	$(135,136,140,141,139,138,137,107,142,147,-$
		$17,20,21,22,19,9,7,27,28,-$	$110,42,40,44,101,102,104,146,105,103,-$
		$14,25,10,8,6,2,3,4,5,29,1)$	$108,109,144,143,106,145,111,112,115,113,-$
			$41,114,116,121,126,127,132,131,133,134,-$
			$130,129,128,125,120,118,119,117,124,122,-$
			$123,58,57,69,70,96,97,100,99,98,-$
			$68,67,66,49,48,47,45,46,55,56,-$
			$65,64,62,95,94,77,76,75,74,73,-$
			$61,60,59,36,35,37,84,85,88,89,-$
			$86,7,10,9,8,3,2,1,4,6,-$
			$5,11,14,13,15,16,18,17,12,90,-$
			$91,92,93,78,79,80,81,87,19,83,-$
			$82,71,29,27,26,28,23,22,21,20,-$
			$24,25,72,30,31,32,34,33,38,43,-$
			$50,52,63,54,53,51,39)$
Distance (km)	$10.4500$	$22.9170$	$46.2890$

An execution for each problem has been performed. Parameters have been chosen according to [29]: a relatively high crossover rate ($\ge 0.6$), small mutation rate (range $[0.001,0.1]$) and a moderate population size. Data and results are presented in Table 6, Table 7 and Table 8. In all the cases, the execution in which the seed is considered obtains better solutions.

Table 6. Results of the $n=7$ problem.

$\mathit{n}=7$	SGA without Seed	SGA with Seed
Generations	20	20
Population size	30	30
Crossover probability	0.8	0.8
Mutation probability	0.01	0.01
Best route	$(3,2,1,6,7,4,5)$	$(7,4,5,3,2,1,6)$
Best distance (km)	$7.6700$	$7.6700$

Table 7. Results of the $n=29$ problem.

$\mathit{n}=29$	SGA without Seed	SGA with Seed
Generations	4000	4000
Population size	200	200
Crossover probability	0.8	0.8
Mutation probability	0.01	0.01
Best route	$(18,16,28,27,14,25,13,12,11,9,-$	$(10,12,13,17,23,24,26,22,19,21,-$
	$7,4,3,2,5,8,6,10,17,20,-$	$20,18,15,11,9,7,28,27,14,25,-$
	$21,23,24,26,22,19,1,29,15)$	$(16,1,29,5,4,3,2,8,6)$
Best distance (km)	$18.0270$	$17.6570$

Table 8. Results of the $n=147$ problem.

$\mathit{n}=147$	SGA without Seed	SGA with Seed
Generations	4000	4000
Population size	400	400
Crossover probability	0.8	0.8
Mutation probability	0.01	0.01
Best route	$(102,103,142,113,114,125,130,134,133,132,-$	$(141,140,135,136,107,138,137,139,142,147,-$
	$124,117,75,61,79,82,87,21,18,19,-$	$41,42,40,101,44,102,104,146,105,108,-$
	$53,139,141,52,36,85,8,7,10,9,-$	$145,109,144,143,106,103,111,112,110,113,-$
	$88,76,48,46,57,50,49,47,45,121,-$	$115,114,116,51,126,121,125,129,130,134,-$
	$120,119,116,56,64,62,99,98,69,67,-$	$133,131,128,127,119,132,124,117,120,122,-$
	$66,122,123,129,131,128,126,55,39,71,-$	$123,50,118,69,64,62,68,100,99,98,-$
	$73,97,68,65,63,104,146,105,137,138,-$	$97,67,66,49,48,47,45,46,55,43,-$
	$54,20,28,32,34,41,42,33,38,31,-$	$56,70,96,95,94,77,78,73,75,74,-$
	$29,24,25,30,35,44,106,107,143,147,-$	$61,60,59,39,31,37,76,84,88,86,-$
	$111,112,115,144,108,127,118,95,77,83,-$	$90,10,9,8,7,3,2,4,1,6,-$
	$3,4,2,1,14,80,110,43,51,100,-$	$5,12,11,13,15,17,18,16,14,89,-$
	$70,74,59,58,27,26,12,17,6,5,-$	$91,92,93,85,87,80,79,81,19,82,-$
	$22,23,72,78,86,11,13,15,16,81,-$	$83,71,29,27,25,26,23,22,21,20,-$
	$37,96,94,84,89,90,91,93,92,60,-$	$24,28,72,30,32,35,34,33,38,57,-$
	$40,101,145,140,135,136,109)$	$58,65,63,54,53,52,36)$
Best distance (km)	$48.3510$	$30.4510$

The longest, the shortest, and the average-distance itineraries for $n=7$ can be seen in Figure 2. The limit of the municipality of Sopelana is marked using a thick red line.

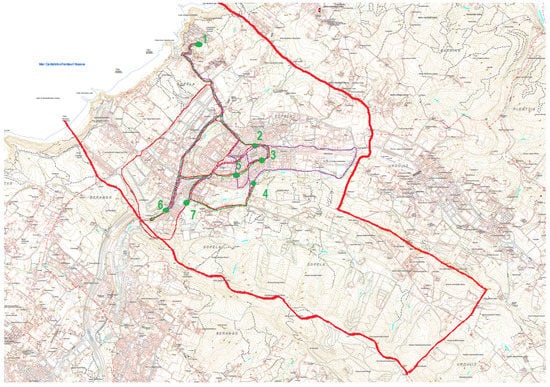
Figure 2. Routes of problem $n=7$, longest in red, shortest in green, “average” in purple.

Additionally, several executions have been performed for each of the problems ($n=7,29,147$). The best, the worst, the mean, and the median distance of this performance are presented in Table 9, Table 10 and Table 11. The values of these tables are acquired after performing 10 executions for each version of each problem.

Table 9. Results of 10 executions $n=7$ problem, SGA.

$\mathit{n}=7$	SGA without Seed	SGA with Seed
Generations	20	20
Population size	30	30
Crossover probability	0.8	0.8
Mutation probability	0.01	0.01
Best distance (km)	$7.6700$	$7.6700$
Worst distance (km)	$8.0200$	$7.7700$
Mean distance (km)	$7.7050$	$7.6900$
Median distance (km)	$7.6700$	$7.6700$

Table 10. Results of 10 executions $n=29$ problem, SGA.

$\mathit{n}=29$	SGA without Seed	SGA with Seed
Generations	4000	4000
Population size	200	200
Crossover probability	0.8	0.8
Mutation probability	0.01	0.01
Best distance (km)	$17.3770$	$17.1870$
Worst distance (km)	$19.0170$	$18.3670$
Mean distance (km)	$18.1910$	$17.8530$
Median distance (km)	$17.9420$	$17.7420$

Table 11. Results of 10 executions $n=147$ problem, SGA.

$\mathit{n}=147$	SGA without Seed	SGA with Seed
Generations	4000	4000
Population size	400	400
Crossover probability	0.8	0.8
Mutation probability	0.01	0.01
Best distance (km)	$48.4740$	$29.6310$
Worst distance (km)	$54.6080$	$32.7670$
Mean distance (km)	$50.9096$	$31.7165$
Median distance (km)	$50.3485$	$31.9552$

For the largest problems, $n=29$ and $n=147$, computation has been repeated choosing different parameters in order to obtain better results. The most important change is that a larger population size has been used, i.e., 4000 individuals. Execution data and results can be seen in Table 12 and Table 13.

Table 12. Results of the $n=29$ problem.

$\mathit{n}=29$	SGA without Seed	SGA with Seed
Generations	800	800
Population size	4000	4000
Crossover probability	0.8	0.8
Mutation probability	0.8	0.8
Best route	$(16,17,23,24,26,22,19,21,20,18,-$	$(15,11,10,13,16,17,23,24,26,22,-$
	$15,11,10,12,2,1,29,5,4,3-$	$19,21,20,18,14,25,28,27,12,9,-$
	$8,6,9,7,28,27,14)$	$(-,7,4,8,6,3,5,2,1,29)$
Best distance (km)	$17.1700$	$16.9370$

Table 13. Results of the $n=147$ problem.

$\mathit{n}=147$	SGA without Seed	SGA with Seed
Generations	1800	1800
Population size	4000	4000
Crossover probability	0.8	0.8
Mutation probability	0.8	0.8
Best route	$(107,142,53,37,73,60,59,50,58,67,-$	$(141,140,135,136,107,138,137,139,142,112,-$
	$66,29,26,25,24,28,30,51,121,116,-$	$41,42,40,101,44,102,104,146,105,106,-$
	$114,115,56,36,35,33,34,46,122,124,-$	$103,108,144,143,145,109,147,110,43,113,-$
	$117,120,126,127,132,119,19,80,17,16,-$	$115,114,116,123,127,126,129,130,134,133,-$
	$77,78,71,76,94,82,88,85,84,39,-$	$132,125,128,131,121,122,124,117,120,119,-$
	$31,32,38,57,143,105,146,104,103,108,-$	$52,118,100,69,70,94,73,97,99,98,-$
	$147,136,135,112,111,79,87,81,22,23,-$	$68,67,66,49,48,47,45,46,55,56,-$
	$72,48,45,145,144,139,138,137,123,128,-$	$58,64,62,96,95,77,78,71,61,75,-$
	$134,133,110,43,113,41,40,42,141,140,-$	$74,60,59,36,35,37,76,84,88,86,-$
	$64,62,68,69,70,96,95,93,92,91,-$	$90,10,9,8,7,3,1,2,4,6,-$
	$10,3,1,2,4,83,97,65,63,61,-$	$5,11,12,13,15,17,16,18,14,89,-$
	$75,74,118,100,99,98,49,47,55,125,-$	$91,92,93,85,79,87,80,81,19,83,-$
	$129,130,131,54,27,20,21,18,12,11,-$	$82,30,29,27,25,26,23,22,21,20,-$
	$6,5,7,8,9,89,90,86,14,13,-$	$24,28,72,39,31,32,34,33,38,57,-$
	$15,52,109,44,101,102,106)$	$50,65,63,54,53,51,111)$
Best distance (km)	$40.3460$	$27.0950$

The actual itineraries are presented in Figure 3 and Figure 4, and the improved itineraries of Table 12 and Table 13 obtained with the new parameters in Figure 5 and Figure 6. In the case of problem $n=147$, Figure 4 and Figure 6, the first and the last location of the route are marked in red.

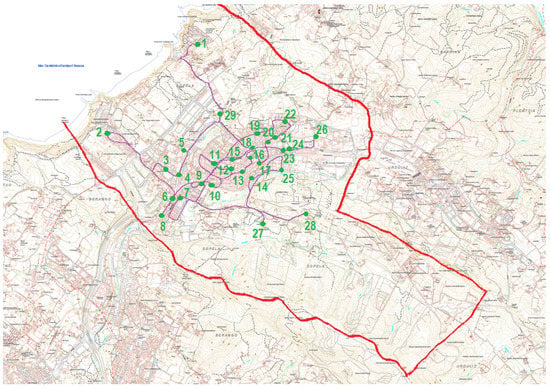
Figure 3. Actual route of problem $n=29$.

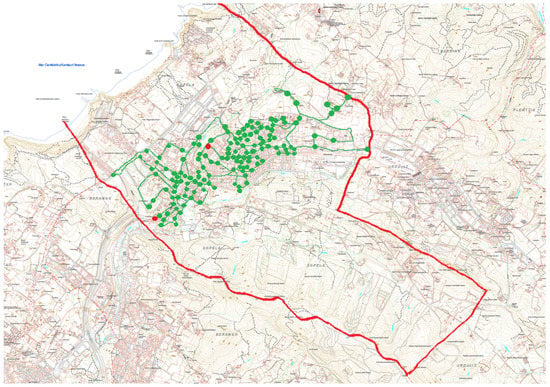
Figure 4. Actual route of problem $n=147$.

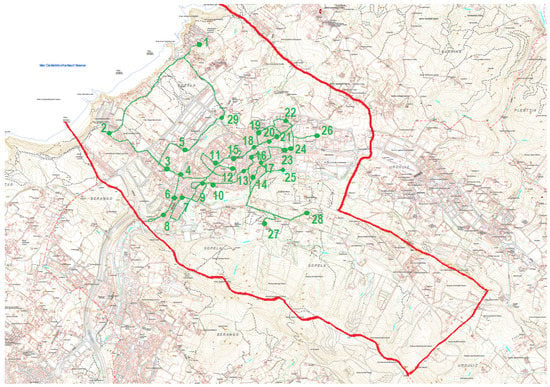
Figure 5. Smallest route obtained for problem $n=29$.

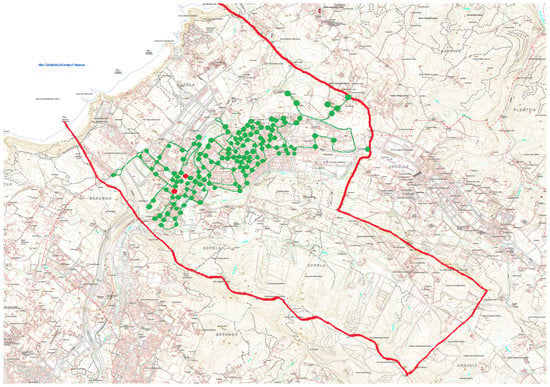
Figure 6. Smallest route obtained for problem $n=147$.

6. Conclusions

In this work, three waste collection itineraries have been improved in a municipality of Biscay (Spain). The average itinerary of the reusable waste ($n=7$ problem) has had a reduction of $2.78$ km; and the actual itineraries of organic waste ($n=29$ problem) and restwaste ($n=147$ problem) have been reduced $5.98$ km and $19.194$ km, respectively. Taking into account the collection frequencies of these three itineraries, this makes a total reduction of 7400 km per year, that is to say, a reduction of the 40% of the total actual itineraries.

The truck has a continent of 13 tons and it has a compaction mechanism. Considering the following average data for the truck: vehicle of 26 Tn, speed limit 30 km/h, with 270 CV minimum engine power (1 CV = 735.39, 875 W= 0.986 HP) and diesel fuel type and 29 L/100 km consumption [30]. This implies a reduction of $5.85$ Tn of CO${}_2$ emissions, $0.43$ Kg of CO, and $13.95$ Kg of NOx per year. In addition to these improvements, a direct cost savings of 7294€ was obtained (considering the direct cost per kilometer calculation model recommended by the Ministry of Transportation, Logistics and Urban Agenda of Spain [31]).

It is worth mentioning that the research team performed an additional validation for the developed model. Specifically, the actual consumptions versus the ones proposed by the model were analyzed at the two comparable routes (the ones the truck made before and after the optimization), obtaining negligible differences. This double check on the results and the easiness of the solution have raised the interest of other commonwealths, such as the one of Lea-Artibai. Thus, the short and midterm future steps would be oriented to the application of the same procedure to other local communities, incorporating other parameters such as the elevation information of the routes.