Thermal Stress and Deformation of Hollow Paddle-Shaft Components with Internal High Temperature Molten Salt Flow

Abstract

Excessive thermal stress and deformation are important reasons causing disservice of high temperature heat exchangers. This paper presents thermal stress and expansion analysis of single-leaf type hollow paddle-shaft components with internal high temperature molten salt flow based on three-dimensional numerical simulations. The results show that the hollow paddles enhance the heat transfer and decrease the maximum thermal stress simultaneously with the expense of a much higher pressure drop than that of solid paddles. The cumulative von Mises stress distribution curve shows that the stress distribution of the component with hollow paddles is more uniform than that with solid paddles. The radial and axial deformations do not differ much for the components with hollow and solid paddles. A larger volume of the fluid space in the hollow paddles leads to stronger heat transfer, smaller maximum thermal stress, and more uniform stress distribution. The effects of the paddle height, the diameter and number of flow holes, the molten salt flow rate, and the material-side heat transfer coefficient are identified. The advantages of hollow paddle designs in both heat transfer and thermal stress (local and overall) performance are revealed. The work in this study can provide a reference for the design and optimization of hollow paddle heat exchangers with high temperature molten salt as working fluid.

1. Introduction

High temperature heat exchangers (HTHEs) are widely used in many areas, including traditional industrial sectors and recently developed renewable energy fields (solar energy, biomass energy, etc.) [1,2,3,4,5]. The structures of HTHEs involve conventional shell-and-tube, fin-and-tube, and many new designs. Besides the thermo-hydraulic performance, thermal stress and deformation are critical in the design of HTHEs. Excessive thermal stress and thermal expansion may cause disservices of HTHEs.

As a traditional topic, thermal stress and deformation have been studied by many researchers for different heat exchanger structures. One important progress in thermal stress and deformation evaluation in recent years is the broad application of the finite element method (FEM) for solid mechanics combined with computational fluid dynamics (CFD) simulation of flow and heat transfer [6,7]. Some examples are given, as follows. In a recent study, Islamoglu [8,9] numerically investigated the temperature and thermal stress fields of ceramic heat exchanger tubes with circular fins. The results show that the significant parameters that affect the temperature and stress distributions are the fin diameter and non-uniform heat transfer coefficient. Using the CFD technique combined with response surface methodology and structural analysis, James [10] studied the optimization and thermal stress of an Yttria-Stabilized Zirconia heat exchanger. This study determined the safety of the environment of the extreme regions of the heat exchanger for the design purpose. Ceramic shell-and-plate high temperature heat exchangers were numerically investigated in References [11,12]. The authors studied the fluid flow, heat transfer, chemical reaction, and thermal stress, aiming to improve the heat transfer performance of the heat exchanger. Based on the results, methods of improving the design of the heat exchanger were recommended. Wang and his cooperators [13,14] investigated the heat transfer, fluid flow, stress, and deformation of a novel bayonet heat exchanger made by INCONEL 625. The stress performance of the internally finned bayonet tube of the heat exchanger under different conditions (thermal loads, geometrical parameters) was presented, and a Z-shape lateral fin profile was recommended for applications. Du et al. [15] analyzed the thermal stress and fatigue fracture of a single tube (made by 316L stainless steel) for the solar tower receiver. Their work identifies the key factors that affect thermal stress and fatigue fracture. González-Gómeza et al. [16] presented a methodology based on coupling transient thermodynamic and stress models, and studied a few TEMA heat exchangers (F, H, and X). The start-up performance (e.g., time) and thermal stress (e.g., the maximum stress) for three heat exchangers were documented and compared.

Paddle heat exchangers (also called screw heat exchangers) are a kind of heat exchangers with rotating heat transfer surfaces, which have widely been used in materials heating (like drying) with steam or heat transfer oil as working fluid [17,18,19,20]. Recently, paddle heat exchangers with high temperature molten salt as working fluid were studied. Zimpf et al. [21,22] presented their design of high temperature latent heat storage with a double screw heat exchanger. With Hitec salt as the working fluid, Zhang et al. [23] and Rajeh et al. [24] investigated the thermo-hydraulic characteristics of paddle heat exchangers: Double-leaf type and single-leaf type, respectively. The results in References [23,24] show that hollow paddle structures transfer more heat and consume more pumping power than solid paddle structures with the same constraints (e.g., outer shape).

In this paper, based on Reference [24], we further study the thermal stress and deformation of single-leaf type hollow paddle-shaft components with high temperature molten salt as working fluid and compare them with solid paddle-shaft components. The present work aims to provide theoretical support to further product design, manufacture, and operation.

2. Geometry

Figure 1 shows the scheme of the single-leaf type paddle heat exchanger used in the present study. For simplicity, only three paddles are considered. The number of paddles of a real heat exchanger may be much more. As in potential applications, molten salt does not change its temperature along its flow path significantly, the simplification is acceptable. Figure 1a shows the outer shape of the paddle-shaft component. Figure 1b corresponds to solid paddles, where molten salt only flows in the hollow shaft. Figure 1c,d correspond to hollow paddles with two flow holes and four flow holes, respectively. The flow holes connect the hollow paddle space and the hollow shaft space. Under steady conditions with constant rotating speed, the molten salt first flows into the distribution half of the hollow shaft (i.e., ① in Figure 1c,d), and then is distributed into the hollow paddle space through the inlet flow hole(s). Through the outlet flow hole(s), the molten salt flow into the collection half of the hollow shaft (i.e., ② in Figure 1c,d), and then finally leaves the component. The external material flow is driven by inclined paddles, and is heated by outer surfaces of the hot shaft and paddles. In this study, we only consider that the paddle-shaft component rotates at low speed (<10 rpm). The effects of rotating speed on flow, heat transfer, thermal stress, and deformation are neglected. In Figure 1c,d, the dashed lines only depict the flow direction schematically, not meaning real flow lines. In Figure 1, the following sizes are assumed constant: L = 180 mm, L₁ = 6 mm, L₂ = 26 mm, L₃ = 60 mm, D = 60 mm, t_s = 4 mm, and β = 4°.

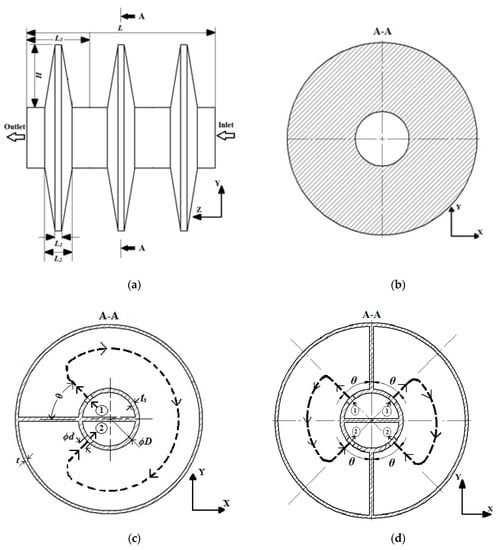
Figure 1. Single-leaf type paddle-shaft components: (a) Outer shape, (b) solid paddle, (c) hollow paddle with two flow holes, and (d) hollow paddle with four flow holes.

In the hollow paddles, the fluid volume determines the relative importance of heat conduction and convection [24]. We define dimensionless fluid volume ratio, as follows,

$$\varphi =\frac{V_f}{V_p}$$

(1)

where ϕ = 0 corresponds to the solid paddles. Table 1 shows the simulated cases with different ϕ in this paper. In Table 1, ϕ = 0.53 corresponds to the design of a prototype in the authors’ lab regarding the requirement of mechanical strength [24]. Other values of ϕ are used as case studies for understanding the effects of ϕ.

Table 1. Hollow paddles with different ϕ (m = 2, H = 62 mm, d = 8 mm).

ϕ	Paddle Type	Geometry Description
0	Solid	no fluid space in the paddles
0.04	Hollow	The fluid space is a tubular duct with 8 mm diameter in each paddle.
0.22	Hollow	t = 20 mm
0.46	Hollow	t = 6 mm
0.53	Hollow	t = 3 mm (standard hollow paddles)

3. Numerical Modeling

3.1. Fluid Flow and Heat Transfer Modeling

For simulating the molten salt flow and heat transfer in the domain illustrated in Figure 1, we use three dimensional CFD model with the following assumptions: Zero radiation of the outer surfaces of the paddles because of the material’s covering; constant properties of molten salt and the solid; constant temperature and convective heat transfer coefficient of the external material; negligible rotation effect; Newtonian fluid [24,25]; and single-phase steady turbulent forced flow for molten salt.

For the turbulent flow of molten salt, k-ε model is used. The equations have been documented in many textbooks (e.g., [26]) or in our previous study [24], which are not repeated here. For the solid region, the energy equation is

$$\frac{\partial }{\partial x_i}\left(\lambda \frac{\partial T}{\partial x_i}\right)=0$$

(2)

where T (x, y, z) represents the temperature field of the solid, which will be loaded to the solid part of the paddle-shaft component for calculating the thermal stress and deformation. In flow and heat transfer simulations, the boundary conditions are shown in Table 2, and the properties of molten salt are given in Table 3.

Table 2. Boundary conditions for flow and heat transfer.

Paddle Structure		Boundary Condition
Fluid	Inlet	$\dot{m}$ Ti
	Outlet	P = 0 Pa (gauge)
Material-side material	External material	To, ho
	End-wall surfaces of shaft	Adiabatic

Table 3. Properties of molten salt (Hitec) [25].

Property	Density (kg/m3)	Specific Heat At Constant Pressure J/(kgK)	Thermal Conductivity W/(mK)	Dynamic Viscosity kg/(ms)
Molten salt	1944	1559.886	0.908	0.0012

A commercial software (ANSYS: Canonsburg, PA, USA, Version 15.0) [27] is used to solve the above model. Pressure-based solver and SIMPLE algorithm for pressure-velocity coupling are adopted. The second-order upwind scheme is adopted for momentum and energy equations. For mass, momentum, turbulent kinetic energy, and dissipation rate equations, the residuals are 10⁻⁴, and for the energy equations, the residuals are 10⁻⁶. Less than 1% changes in pressure drop and heat transfer rate between successive grid sizes are considered acceptable results. The number of grids varies from case to case, from a few million to more than 15 million. An example of the grid independence checking is given in Table 4. In this paper, ΔT = 100 °C is defaulted as T_i = 500 °C and T_o = 400 °C based on the background of biomass pyrolysis heating [2]. In Table 4, for 10,206,999 and 12,156,322 elements, the differences of the pressure drops (43,397 Pa and 43,404 Pa) and the heat transfer rates (3595 W and 3570 W) are both less than 1%, which show the overall performance and are acceptable for engineering applications. In this case, 10,206,999 elements are selected in the following simulations. In fact, we used non-uniform meshes. For 10,206,999 elements, the thickness of the boundary layers is 0.009 mm, and the number of mesh layers is five. For 12,156,322 elements, the number of mesh layers is seven for the fixed thickness of the boundary layers. Also, we obtained the minimum value of y⁺ ≈ 1.8 in the near-wall regions and the maximum value y⁺ ≈ 37 in the log-law regions. This agrees with previous studies, like Reference [28].

Table 4. Grid independence of flow and heat transfer [h_o = 250 W/(m²K), $\dot{m}$ = 1 kg/s, H = 62 mm, ΔT = 100 °C, d = 8 mm, ϕ = 0.53, m = 2].

Number of Elements	12,156,322	10,206,999	7,448,980	5,262,150
$\dot{Q}$ (W)	3570	3595	3580	3624
ΔP (Pa)	43,404	43,397	43,339	43,505

3.2. Thermal Stress and Deformation Modeling

The solid temperature field T (x, y, z), obtained in Section 3.1, is applied as a body load in the thermal stress and deformation model. To calculate the thermal stress and deformation, a three-dimensional thermo-elastic finite element model is established based on small deformation assumption. The effects of the weight of the paddle-shaft component, the internal fluid pressure, and the external material pressure are neglected.

The equations of the thermo-elasticity mechanics are given, as follows. The equilibrium equations are,

$$\begin{array}{l}\frac{\partial {\sigma }_x}{\partial x}+\frac{\partial {\tau }_{yx}}{\partial y}+\frac{\partial {\tau }_{zx}}{\partial z}=0\\ \frac{\partial {\tau }_{xy}}{\partial x}+\frac{\partial {\sigma }_y}{\partial y}+\frac{\partial {\tau }_{zy}}{\partial z}=0\\ \frac{\partial {\tau }_{xz}}{\partial x}+\frac{\partial {\tau }_{yz}}{\partial y}+\frac{\partial {\sigma }_z}{\partial z}=0\end{array}\}$$

(3)

The normal strain ${\epsilon }_x$,${\epsilon }_y$,${\epsilon }_z$ and the shear strain ${\gamma }_{xy}$, ${\gamma }_{yz}$, ${\gamma }_{zx}$ are defined, as follows:

$$\begin{array}{l}{\epsilon }_x=\frac{\partial u_x}{\partial x}\\ {\epsilon }_y=\frac{\partial u_y}{\partial y}\\ {\epsilon }_z=\frac{\partial u_z}{\partial z}\\ {\gamma }_{xy}=\frac{\partial u_y}{\partial x}+\frac{\partial u_x}{\partial y}\\ {\gamma }_{yz}=\frac{\partial u_z}{\partial y}+\frac{\partial u_y}{\partial z}\\ {\gamma }_{zx}=\frac{\partial u_x}{\partial z}+\frac{\partial u_z}{\partial x}\end{array}\}$$

(4)

The compatibility equations are given by,

$$\begin{array}{l}\frac{{\partial }^2{\epsilon }_x}{\partial y^2}+\frac{{\partial }^2{\epsilon }_y}{\partial x^2}-\frac{{\partial }^2{\gamma }_{xy}}{\partial x\partial y}=0\\ \frac{{\partial }^2{\epsilon }_y}{\partial z^2}+\frac{{\partial }^2{\epsilon }_z}{\partial y^2}-\frac{{\partial }^2{\gamma }_{yz}}{\partial y\partial z}=0\\ \frac{{\partial }^2{\epsilon }_z}{\partial x^2}+\frac{{\partial }^2{\epsilon }_x}{\partial z^2}-\frac{{\partial }^2{\gamma }_{zx}}{\partial z\partial x}=0\\ \frac{\partial }{\partial x}\left(\frac{\partial {\gamma }_{zx}}{\partial y}+\frac{\partial {\gamma }_{xy}}{\partial z}-\frac{\partial {\gamma }_{yz}}{\partial x}\right)-2\frac{{\partial }^2{\epsilon }_x}{\partial y\partial z}=0\\ \frac{\partial }{\partial y}\left(\frac{\partial {\gamma }_{xy}}{\partial z}+\frac{\partial {\gamma }_{yz}}{\partial x}-\frac{\partial {\gamma }_{zx}}{\partial y}\right)-2\frac{{\partial }^2{\epsilon }_y}{\partial z\partial x}=0\\ \frac{\partial }{\partial z}\left(\frac{\partial {\gamma }_{yz}}{\partial x}+\frac{\partial {\gamma }_{zx}}{\partial y}-\frac{\partial {\gamma }_{xy}}{\partial z}\right)-2\frac{{\partial }^2{\epsilon }_z}{\partial x\partial y}=0\end{array}\}$$

(5)

The constitutive equations are, as follows,

$$\begin{array}{l}{\sigma }_x=\frac{E}{1-2\omega }\left[\frac{1-\omega }{1+\omega }{\epsilon }_x+\frac{\omega }{1+\omega }\left({\epsilon }_y+{\epsilon }_z\right)-\alpha \Delta T_l\right]\\ {\sigma }_y=\frac{E}{1-2\omega }\left[\frac{1-\omega }{1+\omega }{\epsilon }_y+\frac{\omega }{1+\omega }\left({\epsilon }_x+{\epsilon }_z\right)-\alpha \Delta T_l\right]\\ {\sigma }_z=\frac{E}{1-2\omega }\left[\frac{1-\omega }{1+\omega }{\epsilon }_z+\frac{\omega }{1+\omega }\left({\epsilon }_y+{\epsilon }_x\right)-\alpha \Delta T_l\right]\\ {\gamma }_{xy}=\frac{2\left(1+\omega \right)}{E}{\tau }_{xy}\\ {\gamma }_{xz}=\frac{2\left(1+\omega \right)}{E}{\tau }_{xz}\\ {\gamma }_{yz}=\frac{2\left(1+\omega \right)}{E}{\tau }_{yz}\end{array}\}$$

(6)

where ΔT_l is the local temperature change dependent on coordinates (x, y, z), E is the Young’s modulus, and ω is the Poisson’s ratio. The von Mises stress (equivalent stress) is used in evaluating the stress characteristics:

$$\sigma ={\left\{\frac{1}{2}\left[{\left({\sigma }_x-{\sigma }_y\right)}^2+{\left({\sigma }_y-{\sigma }_z\right)}^2+{\left({\sigma }_z-{\sigma }_x\right)}^2+6\left({\tau }_{xy}^2+{\tau }_{yz}^2+{\tau }_{xz}^2\right)\right]\right\}}^{\frac{1}{2}}$$

(7)

The maximum von Mises stress σ_max represents the local safety of the design, and the less, the better. In the thermal stress and deformation simulations, the right end in Figure 1a (or the inlet end of the fluid flow) is assumed fixed, and the left end is free to move. The properties of the solid (INCONEL 625) are shown in Table 5.

Table 5. Properties of the solid (INCONEL 625) [30].

T (°C)	P (kg/m3)	cp J/(kgK)	λ W/(mK)	E (GPa)		ω	$\mathit{\alpha }$ (1/K) × 10−6
				Tension	Shear
204	8440	456	12.5	197.9	76.5	0.286	12.5
316	8440	481	14.1	191.7	74.5	0.29	14.1
427	8440	511	15.7	185.5	71.7	0.295	15.7
538	8440	536	17.5	178.6	68.3	0.305	17.5
649	8440	565	19	170.3	64.8	0.321	19
760	8440	590	20.8	160.6	60	0.34	20.8
871	8440	620	22.8	147.5	55.2	0.336	22.8

Note: The Yield Strength σ_o = 414 MPa.

To analyze the cumulative von Mises stress distribution in the solid for a specific design, we incorporate an indicator of the uniformity of the thermal stress distribution, as follows [29]:

$$\psi =\frac{V_{\sigma \le {\sigma }_o}}{V}$$

(8)

Here, steeper ψ-σ₀ curve corresponds to a more uniform stress distribution, and the range of the stress distribution also represents the overall safety of the design (or the design redundancy).

The thermal stress and deformation are obtained by solving the above equations by ANSYS Workbench [27]. For grid independence checking, less than 1% changes in the maximum stress and the deformation between successive grids sizes are considered as acceptable results. An example of the grid independence checking is given in Table 6. For 6,764,457 and 4,726,844 elements, the differences of the maximum stress (68.532 MPa and 68.657 MPa), the radial deformation (0.53565 mm and 0.53908 mm), and the axial deformation (0.53392 mm and 0.53173 mm) are all less than 1%. In this case, 4,726,844 elements are selected in the following simulations.

Table 6. Grid independence of thermal stress and deformation [h_o = 250 W/(m²K), $\dot{m}$ = 1 kg/s, H = 62 mm, ΔT = 100 °C, d = 8 mm, ϕ = 0.53, m = 2].

Number of Elements	6,764,457	4,726,844	3,595,218	1,352,140
σmax (MPa)	68.532	68.657	68.51	68.606
δy (mm)	0.53565	0.53908	0.53476	0.5337
δz (mm)	0.53392	0.53173	0.5363	0.53462

It should be mentioned that to our best knowledge, up to now, there are no published related experimental or numerical results for the above topic, except our group work in flow and heat transfer simulations in Reference [24] (but no thermal stress and deformation in Reference [24]). As the above models of single phase flow and thermal stress simulations are mature and reliable, and the computational treatment is appropriate, so the above models-based results are acceptable from the viewpoint of engineering.

4. Results and Discussion

4.1. Effects of Geometrical Parameters

One of the critical parameters in designing the paddle-shaft component is the fluid volume ratio ϕ, which represents the relative importance of heat conduction and convection in the paddles. Figure 2 shows the effects of ϕ. In Figure 2a,b, when ϕ increases, both ΔP and $\dot{Q}$ increase. The result in Figure 2b illustrates the advantage of replacing the share of heat conduction by heat convection via enlarging the fluid space inside the paddles. Furthermore, in Figure 2c, with the increases of ϕ, the maximum thermal stress σ_max is reduced. This observation reveals how stronger heat transfer weakens local stress concentration. We can also notice that when ϕ ˃ 0.46, the increasing in $\dot{Q}$, and the decreasing in σ_max becomes slower. That is because with the increase of ϕ, the fluid speed decreases, and the heat transfer improvement will slow down. Figure 2d shows the directional deformation of the hollow paddles in the specified range of ϕ. The deformation δ_y increases weakly with the increasing of ϕ, while δ_z is approximately unchanged.

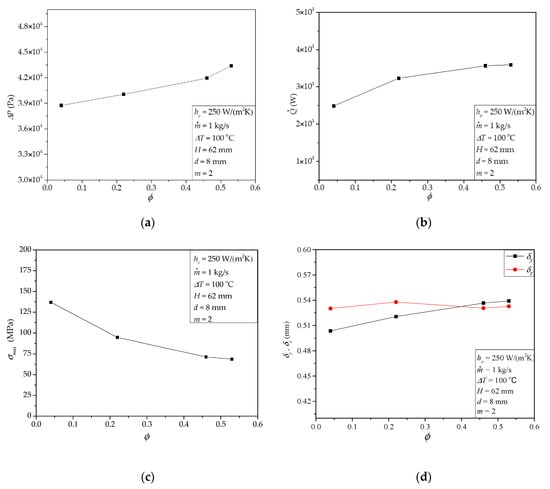
Figure 2. Effects of fluid volume ratio ϕ: (a) ΔP, (b) $\dot{Q}$, (c) σ_max, (d) δ_y, δ_z.

In References [24,31], the temperature distribution features of the hollow paddles with internal molten salt turbulent flow and laminar oil flow have been revealed, which have shown that the temperature distribution for hollow paddles is more uniform than that of solid paddles and are not repeated here. Figure 3 shows the von Mises stress distribution of the paddle designs with ϕ = 0.46 and 0.04. From Figure 3, we see that the high-stress region is located near the edge of the separating plate. It is clear that larger ϕ leads to more uniform temperature and stress distribution in the paddle, due to stronger convective heat transfer inside the paddles, and therefore, avoids extremely large local temperature gradient (or σ_max). This temperature smoothing effect is the mechanism of less maximum von Mises stress.

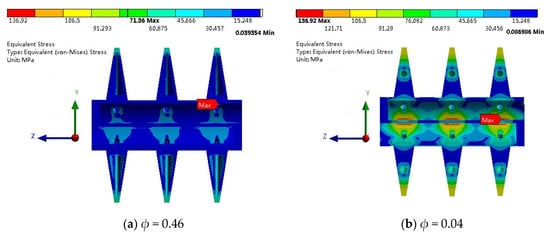
Figure 3. Von Misses stress distribution for different fluid volume ratio ϕ: h_o = 250 W/(m²K), $\dot{m}$ = 1 kg/s, ΔT = 100 °C, H = 62 mm, d = 8 mm, m = 2.

Figure 4 shows the cumulative von Mises stress distribution indicator for two designs with ϕ = 0.46 and 0.04, respectively. The steeper ψ curve with ϕ = 0.46 means more uniform stress distribution. From Figure 4, we also see that the volume of the high-stress region (e.g., σ > 50 MPa) with ϕ = 0.46 is less than that with ϕ = 0.04. Both the local stress performance (σ_max) and the overall stress performance (ψ) are improved.

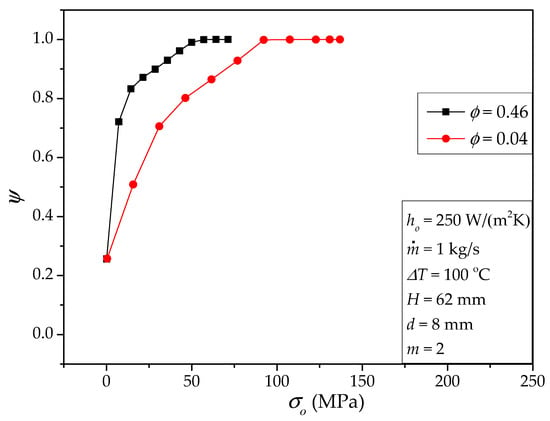
Figure 4. Cumulative von Mises stress distribution for different fluid volume ratio ϕ.

Figure 5 shows the directional deformations of the paddle designs with ϕ = 0.46 and 0.04. Basically, there is small difference in both the directional deformations for the two designs. That is because the deformations depend on the overall temperature gradient and the original size of the paddles. The overall temperature gradient does not differ very much. Different from δ_y and δ_Z, the maximum stress σ_max is affected by the local temperature gradient, not an overall feature.

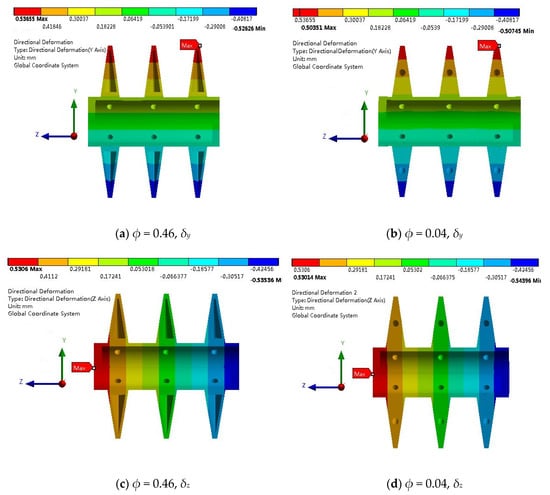
Figure 5. Directional deformations of different fluid volume ratio ϕ: h_o = 250 W/(m²K), $\dot{m}$ = 1 kg/s, ΔT = 100 °C, H = 62 mm, d = 8 mm, m = 2.

We know that too large directional deformations (i.e., axial and radial) may cause damages in the moving parts of the paddle heat exchangers, e.g., molten salt leakage from the rotary joints. For example, for the ϕ = 0.46 design in Figure 5c, δ_Z = 0.5306 mm, which is only for three paddles of a lab-scale prototype in this paper, but a real paddle heat exchanger may have much more paddles (e.g., more than twenty). For instance, if we assume that δ_Z is proportional to the number of the paddles, δ_Z = 4.068 mm for twenty-three elements (a prototype in the authors’ lab). This value is detrimental to the design of rotary joints, and cannot be neglected. For industry-scale paddle heat exchangers with higher molten salt temperatures, the deformation problem will be more serious.

Another important parameter in designing the paddle-shaft component is the paddle height (H), which corresponds to the heat transfer area. Table 7 shows that with the increase of H, ΔP increases slightly for hollow paddle structures. For example, ΔP increases 6.68% when H varies from 31 mm to 124 mm, while for the solid paddles ΔP is constant. Note that here we keep the thickness of paddles (t) constant for different H. For the hollow paddle designs, $\dot{Q}$ increases significantly, due to the increase of the heat transfer area. For the solid paddle designs, $\dot{Q}$ also increases with the increases of H, but the improvement degree is weaker than that of HP. The heat transfer enhancement by increasing H has price in the maximum thermal stress. For example, for the hollow paddle designs, σ_max for H = 124 mm is about three times of that for H = 31 mm, and for the solid paddle designs, σ_max for H = 124 mm is about two times of that for H = 31 mm. Nevertheless, for the same paddle height, σ_max for HP is always lower than that of SP. For the directional deformations, increasing H has a large impact on δ_y for both HP and SP, mainly because of the larger radial size. Lager H corresponds to greater δ_y. Here, for same H, the difference of δ_y between HP and SP is limited. In addition, the longitudinal deformation δ_z is approximately irrelevant to H, and for HP and SP, δ_z is very close.

Table 7. Effects of height of paddles: h_o = 250 W/(m²K), $\dot{m}$ = 1 kg/s, ΔT = 100 °C, d = 8 mm, t = 3 mm, m = 2.

Paddle Type	H (mm)	ΔP	$\dot{\mathit{Q}}$	σmax	δy	δz
HP	31	41,717	1822	39.613	0.35936	0.5312
	62	43,397	3595	68.657	0.5391	0.5327
	124	44,503	8332	120.48	0.8855	0.5345
SP	31	6.9	858	69.98	0.3234	0.5226
	62	6.9	1050	112.91	0.4494	0.5208
	124	6.9	1080	146.33	0.7333	0.5265

Figure 6 shows the corresponding stress distribution for the designs with two paddle heights for HP and SP. It is obvious that the stress distribution for HP is more uniform than that for SP for the two paddle heights. For HP, when H = 124 mm in Figure 6a, the maximum stress is located near one inlet flow hole, and when H = 31 mm in Figure 6c, the maximum stress is located near one outlet flow hole. Clearly, the distribution in Figure 6c is more uniform than that in Figure 6a. The observation reminds us that the region near the flow holes is the most dangerous from the viewpoint of stress (i.e., stress concentration). For SP in Figure 6b,d, high stress occurs at the center regions that correspond to the paddles’ bases, e.g., the red parts in Figure 6b. In Figure 6d, the maximum stress is not located in this cross-section, which is therefore not shown.

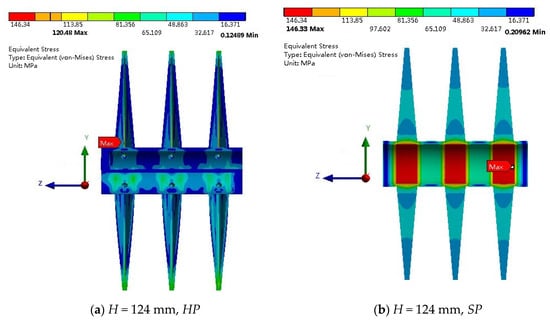
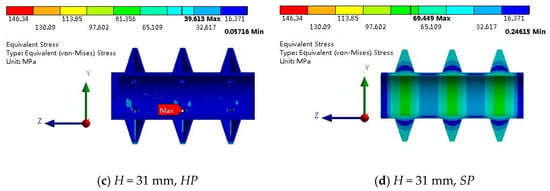
Figure 6. Stress distribution for two paddle heights: h_o = 250 W/(m²K), $\dot{m}$ = 1 kg/s, ΔT = 100 °C, d = 8 mm, t = 3 mm, m = 2.

Figure 7 summarizes the cumulative von Mises stress distribution with different paddle heights. For all the three paddle heights, the ψ curve of HP is steeper than that of SP with the same H, meaning the von Mises stress distribution of the hollow paddles is more uniform, and the volume with high stress is less. For HP, a smaller paddle height corresponds to better stress uniformity. For SP, it is similar that for smaller paddle height, and the volume of the high-stress region is less.

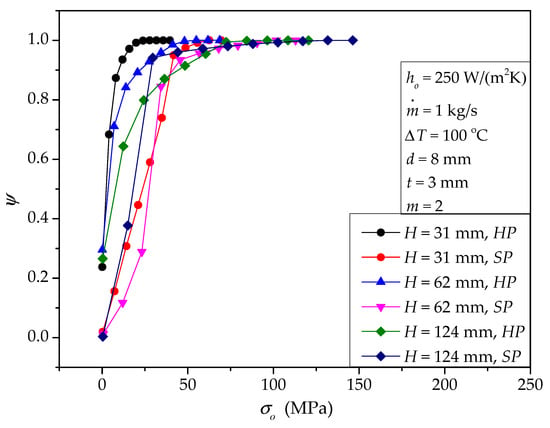
Figure 7. Cumulative von Mises stress distribution for different paddle heights.

Figure 8 shows the directional deformations for the designs with two different paddle heights. For the three paddles of one paddle-shaft component, the δ_y distribution is nearly the same for either HP or SP, but the δ_z distribution is different from the right (dead end) to left (free end). Larger paddle height affects δ_y significantly, but does not affect the distribution features of both δ_y and δ_z. For industry-scale components with large paddle height and long shaft, both δ_y and δ_z are important.

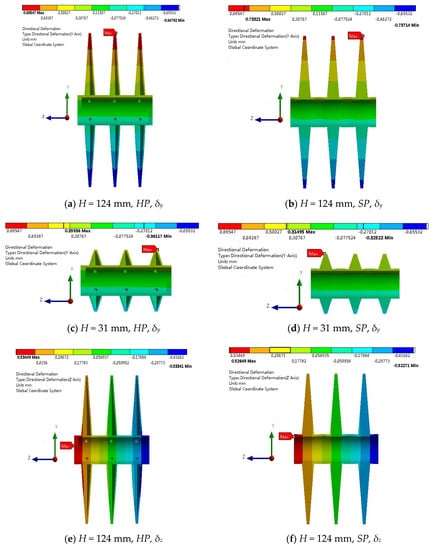
Figure 8. Directional deformations for two paddle heights: h_o = 250 W/(m²K), $\dot{m}$ = 1 kg/s, ΔT = 100 °C, d = 8 mm, t = 3 mm, m = 2.

Figure 9 shows the effects of the diameter (d) and number (m) of the flow holes, where d8-m2 represents d = 8 mm and m = 2. Similarly, d8-m4, d9-m2 and d9-m4 represent (d = 8 mm, m = 4), (d = 9 mm, m = 2), and (d = 9 mm, m = 4), respectively. It can be seen that from Figure 9a, ΔP drops rapidly with the increase of d and m. According to Figure 9b, there is a little effect on $\dot{Q}$ when d and m change. This attributes to the constant mass flow rate and heat transfer area. Figure 9c,d show that the effects of d and m on the thermal stress and corresponding deformations are weak. Here, we should remind that the above observation only holds for the specified conditions in this paper. As a general principle of mechanical design, more holes will influence the mechanical strength of a shaft. As a consequence, increasing m and d here has a significant advantage in decreasing ΔP, i.e., reducing the pumping power for driving the molten salt flow.

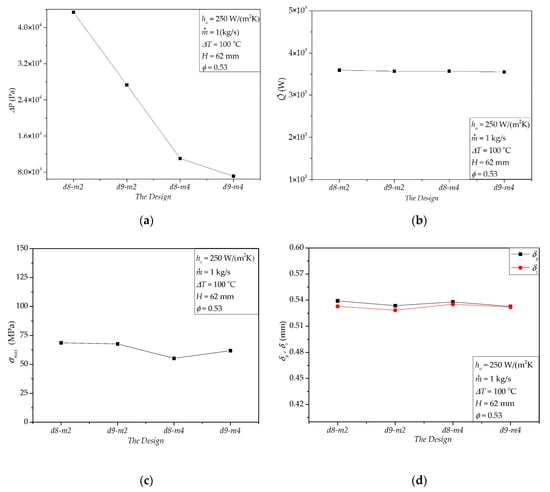
Figure 9. Effects of d and m: (a) ΔP, (b) $\dot{Q}$, (c) σ_max, (d) δ_y, δ_z.

4.2. Effects of Operation Conditions

For specified molten salt inlet temperature and material temperature (or ΔT), the variable operation parameters include the mass flow rate of the molten salt ($\dot{m}$) and the material-side heat transfer coefficient (h_o). Here, h_o expresses the material’s properties and flow features, e.g., the mass flow rate of the material. Table 8 documents two cases with different molten salt mass flow rates. Apparently, higher flow rate leads to a much larger pressure drop, which is a critical disadvantage of the hollow paddles. For $\dot{m}$ = 2 kg/s, $\dot{Q}$ increases about 6% and σ_max drops about 19% than that for $\dot{m}$ = 1 kg/s. The directional deformations δ_y and δ_z are nearly constant for the two cases.

Table 8. Two cases with different $\dot{m}$: h_o = 250 W/(m²K), ΔT = 100 °C, H = 62 mm, d = 8 mm, ϕ = 0.53, m = 2.

Paddle Type	$\dot{\mathit{m}}$	ΔP	$\dot{\mathit{Q}}$	σmax	δy	δz
HP	1	43,397	3595	68.657	0.5391	0.5327
	2	17,1589	3809	55.432	0.5394	0.5343
SP	1	6.9	1050	112.91	0.4494	0.5208
	2	26	1169	128.45	0.4487	0.5254

Figure 10 summarizes the cumulative von Mises stress distribution with different mass flow rates. For HP, the ψ curve for $\dot{m}$ = 2 kg/s is slightly steeper than that for $\dot{m}$ = 1 kg/s, meaning the von Mises stress distribution for the larger flow rate is more uniform and the volume with high stress is less. For SP, the two ψ curves for $\dot{m}$ = 1 kg/s and $\dot{m}$ = 2 kg/s are nearly the same.

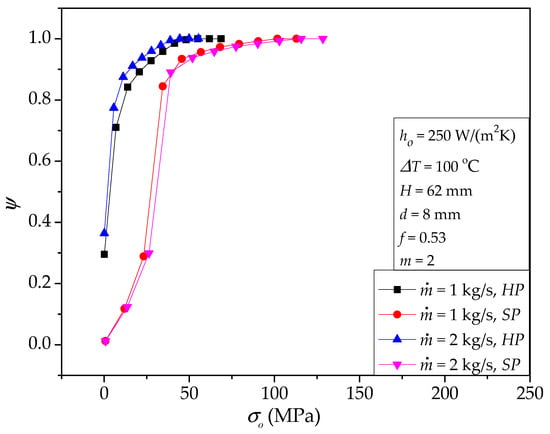
Figure 10. Cumulative von Mises stress distribution for different flow rates: h_o = 250 W/(m²K), ΔT = 100 °C, H = 62 mm, d = 8 mm, ϕ = 0.53, m = 2.

Table 9 documents two cases with different material-side material heat transfer coefficient (h_o). Since the properties of the molten salt are assumed constant, h_o does not affect the pressure drop of the molten salt flow, which is not shown here. Theoretically, when h_o increases, the overall thermal resistance will decrease, resulting in greater heat transfer rate, shown in Table 9. When h_o drops, the outer surface temperature of the paddles moves toward the molten salt side, which leads to a smaller temperature difference in the solid wall of the paddles, and therefore, lowers the stress σ_max. According to Table 9, σ_max for h_o = 50 W/(m²K) is only about 30% of that for h_o = 250 W/(m²K). This is the penalty of enhancing the material-side material heat transfer. The directional deformations δ_y and δ_z are nearly constant for the two heat transfer coefficients. Figure 11 summarizes the cumulative von Mises stress distribution for the two cases with different h_o. For HP, the ψ curve for h_o = 50 W/(m²K) is steeper than that for h_o = 250 W/(m²K), meaning the von Mises stress distribution for poorer material-side heat transfer is more uniform, and the volume with high stress is less. For SP, the slopes of the two ψ curves for h_o = 50 W/(m²K) and h_o = 250 W/(m²K) are close, but the maximum stress is different.

Table 9. Two cases with different h_o: ΔT = 100 °C, $\dot{m}$ = 1 kg/s, H = 62 mm, d = 8 mm, ϕ = 0.53, m = 2.

Paddle Type	ho W/(m2K)	$\dot{\mathit{Q}}$	σmax	δy	δz
HP	50	831	20.315	0.54751	0.53579
	250	3595	68.657	0.5391	0.5327
SP	50	468.76	75.548	0.49173	0.53367
	250	1050	112.91	0.4494	0.5208

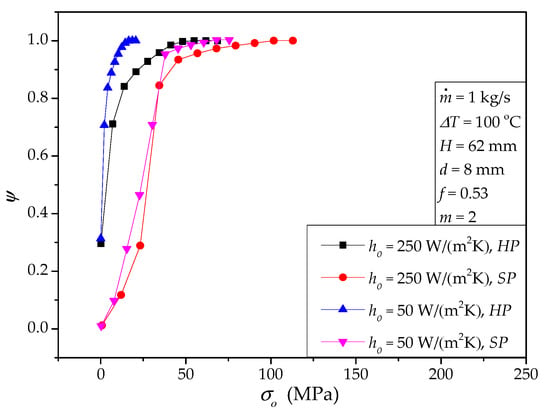
Figure 11. Cumulative von Mises stress distribution for different heat transfer coefficient h_o: $\dot{m}$ = 1 kg/s, ΔT = 100 °C, H = 62 mm, d = 8 mm, ϕ = 0.53, m = 2.

4.3. Further Discussion

Usually, the temperature difference between the molten salt inlet temperature (T_i) and the material temperature (T_o) is fixed by users or designers. If it is changeable, we can use the same method presented in Section 4.1 and Section 4.2 to evaluate its effects. Since the properties of the molten salt are assumed constant, ΔP is independent of ΔT. Theoretically, in general, for normal solid structures, larger ΔT will produce higher heat transfer rate, thermal stress, and deformation. Here, we only provide an example for HP to emphasize this common knowledge, shown in Table 10. According to Table 10, both $\dot{Q}$ and σ_max are significantly larger for ΔT = 200 °C than that for ΔT = 100 °C. The deformations δ_y and δ_z also increase with the increase of ΔT. Figure 12 summarizes the cumulative von Mises stress distribution for the temperature difference effect. Obviously, the ψ curve for smaller ΔT is steeper. Actually, a larger temperature difference proposes a more serious challenge in both σ_max (local feature) and stress uniformity (overall feature).

Table 10. Effects of ΔT for HP: h_o = 250 W/(m²K), $\dot{m}$ = 1 kg/s, H = 62 mm, d = 8 mm, ϕ = 0.53, m = 2.

Ti (°C)	To (°C)	ΔT (°C)	$\dot{\mathit{Q}}$	σmax	δy	δz
500	400	100	3595	68.657	0.5391	0.5327
550	350	200	7154	131.71	0.5848	0.6050

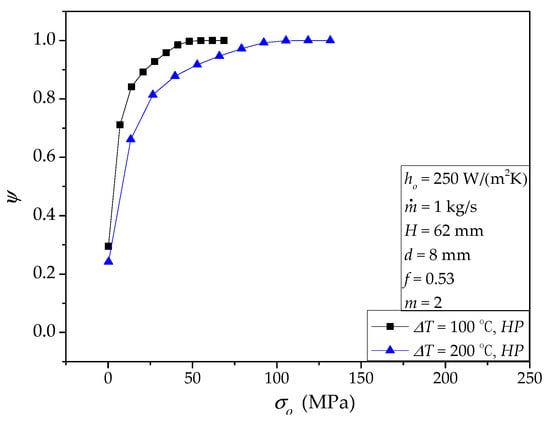
Figure 12. Cumulative von Mises stress distribution for two temperature differences: h_o = 250 W/(m²K), $\dot{m}$ = 1 kg/s, H = 62 mm, d = 8 mm, ϕ = 0.53, m = 2.

From the above discussion, we identified the maximum thermal stress and stress distribution, which can help us select proper solid material and improve the mechanical design. For instance, based on the fourth strength theory, the material could be safe on the condition that the maximum von Mises stress is less than the yield limit. The tensile yield strength of INCONEL 625 is 414 Mpa, larger than all the cases simulated in this paper. So, the material is in the elastic deformation range, meaning the material is safe under the present design conditions. In addition, the ψ curve reveals how much volume has high thermal stress that is close to the maximum, which is a kind of risk indicator (or safety indicator, or design redundancy). The ψ curve and the distribution images of the thermal stress and deformation simulations together provide us useful tools in thermal/mechanical design of the paddle-shaft components and paddle heat exchangers.

In this paper, we use molten salt as the heating fluid, which usually works under normal ambient pressure. For applications with high temperature/pressure steam as the working fluid, the fluid-side pressure load exerted on the solid structure should be considering in the stress analysis. Additionally, for large industry-scale devices, the weight of the paddle-shaft itself is also important and should be included in the loads.

5. Conclusions

In this paper, we investigated the thermal stress and deformation characteristics of single-leaf type hollow paddle-shaft components by three-dimensional simulations. The maximum von Mises stress, the deformation, and the cumulative von Mises stress distribution were evaluated. Hollow paddles provide greater heat transfer, lower maximum thermal stress, more uniform stress distribution than solid paddles. The deformation does not differ much for hollow and solid paddles. The penalty of the component with hollow paddles is a larger pressure drop or pumping power than that with solid paddles. The effects of geometrical parameters, including the fluid volume ratio, the paddle height, and the diameter and number of the flow holes, were also documented.

For the component with hollow paddles, although a higher molten salt flow rate increases the pressure drop significantly, it improves the heat transfer and thermal stress performance, and does not influence the deformation very much. Material-side heat transfer coefficient affects both the heat transfer and thermal stress characteristics. For specified material temperature, a higher material-side heat transfer coefficient means higher risk in the thermal stress aspect. One case with temperature variances between the molten salt and the material was also presented.

To summarize, the work in this paper identified the basic features and influencing factors of the pressure drop, the heat transfer rate, and the thermal stress and deformation for lab-scale single-leaf type hollow paddle-shaft components. The information may help us improve the design of high temperature molten salt paddle heat exchangers.