Abstract
Tire cord steel is widely used in the tire production process of the vehicle manufacturing industry due to its excellent strength and toughness. Titanium nitride (TiN) inclusion, existing in tire rod, has a seriously detrimental effect on the fatigue and drawing performances of the tire steel. In order to control its amount and morphology, the precipitation behavior of TiN during solidification in SWRH 92A tire cord steel was analyzed by selected thermodynamic models. The calculated results showed that TiN cannot precipitate in the liquid phase region regardless of the selected models. However, the precipitation of TiN in the mushy zone would occur at the final stage during the solidification process (at solid fractions greater than 0.98) if the LRSM (Lever-rule model was applied for the N and Scheil model for Ti) or Ohnaka models (without considering the effect of carbon on secondary dendrite arm spacing (SDAS)) were adopted. For the Ohnaka model, in the case when the effect of carbon on SDAS was considered, TiN would probably precipitate in the solid phase zone rather than precipitate in the liquid phase region or mushy zone.
1. Introduction
Tire cord steel is a kind of high-carbon steel and thus possesses high strength and toughness. Therefore, it is widely used in the production of tires for cars and airplanes []. With the development of lightweight materials, the strength level of tire cord steel has become a significant factor to be considered. The main types of tire cord steel were SWRH 62A and SWRH 67A (about 1750 MPa) before the 1990s, and then after that SWRH 72A (about 1870 MPa). In the 21st century, the hypereutectoid tire cord steel (SWRH 82A) dominated the market due to its higher strength level [,]. Nowadays, the research on ultra-high strength level steel, such as SWRH 92A tire cord steel, has been drawing the increasing attention of manufacturing engineers.
Non-metallic inclusions, such as oxide-or Ti-bearing inclusions, existing in tire cord steel have serious detrimental effects on the drawing performance and fatigue properties. Furthermore, the properties of inclusions, such as size, composition, amount, and morphology, play a key role on the quality of steel [,]. At present, the damage problems of brittle oxide inclusions for steel can be better controlled by morphology-controlling technology. Nevertheless, for Ti-bearing inclusions, due to their non-deformable characteristic, they could cause a serious detrimental effect on the drawing performance, which would reduce the life of high-carbon steels, especially for the SWRH 82A and SWRH 92A tire cord steels. Titanium nitride (TiN), with high hardness and melting point, would cause filament breaks during wire drawing and rope stranding or deteriorate the fatigue properties of steels. Furthermore, TiN inclusion has more harmful effects on the material processing than those of oxide inclusions. For example, a TiN inclusion of 6 μm would cause a similar fatigue performance to an oxide inclusion of 25 μm []. Titanium carbonitride (TiCxN1-x, x represents the molar ratio of TiC in TiCxN1-x), a continuous solid solution formed via replacing partial moles of N in TiN crystal with C has similar properties to those of TiN. It also has a detrimental effect on the fatigue performance and, as a result, leads to wire breaking during the drawing and stranding processes []. It has been reported [] that the molar ratio of TiC increases with increasing strength of tire core steel, which would cause a more seriously destructive effect. However, the value of x in TiCxN1-x is still very small []. In other words, the main composition of Ti-bearing inclusion precipitated in tire cord steel is still TiN. Thus, it is important to control TiN inclusion to improve the performance of SWRH 92A tire cord steel.
Many researchers [,,,,,,,,] have reported the precipitation behaviors of TiN inclusion in different types of steels over the decades. Jiang et al. [] found that the solidification segregation ratio of Ti was far greater than that of N, and reported that TiN inclusion would not precipitate until the solid fraction reached 0.9 when using SWRH 82A tire cord steel. Cai et al. [] showed that the precipitation of TiN could only occur in the solid–liquid two-phase region where the solid fraction was greater than 0.95, and the particle size of TiN decreased with increasing cooling rate. Similar results were also reported in other references [,,]. However, Liu et al. [] demonstrated that TiN would not precipitate in the liquid phase or mushy zone, but in austenite (γ-Fe). The precipitation temperature of 1598 K (below the solidus temperature in this reference) was calculated. Nowadays, in the industrial production of SWRH 92A tire cord steel, TiN inclusion always appears in samples even though the concentration of N and Ti are controlled at extremely low levels (0.0043 mass% and 0.0005 mass% for N and Ti, respectively). Therefore, the precipitation behavior of TiN in SWRH 92A tire cord steel remains a hard problem to be solved. In order to make the mechanism of TiN precipitation clearer, a series of relevant studies were initiated in this paper, to show guidance for the development of ultra-high strength grade steels.
2. Material and Equilibrium Solubility Product
The chemical composition of SWRH 92A tire cord steel studied (from a Chinese steel mill) is shown in Table 1. Elements O and N were analyzed by the ONH analyzer (TC500C, LECO Corporation, St. Joseph, MI, American), elements C and S were analyzed by the CS Analyzer (Model EMIA-820V), and the contents of other elements were analyzed by ICP technology (IRIS Advantage ER/S, Thermo Elemental Corporation, Waltham, MA, American). Content of C was about 0.9203 mass%.

Table 1.
Chemical composition of studied SWRH 92A tire cord steel (mass%).
To evaluate the stage (liquid phase, mushy zone, or solid phase) at which the TiN inclusion would precipitate in the steel, the liquidus temperature (TL) and solidus temperature (TS) as well as the equilibrium solubility product of N and Ti were first calculated.
Equations (1) and (2) were employed to estimate TL and TS [], respectively,
where TFe was the melting point of pure Fe, 1811 K; and were the reduced temperature values for element i when the mass fraction was 1 mass%, K, the corresponding values can be acquired from Table 2 []; w[i] represented the mass fraction of element i, 1 mass% was considered as the unit. Combining Table 1, Table 2, Equations (1) and (2), the values of TL and TS can be calculated, i.e., TL = 1748 K, TS = 1636 K.

Table 2.
Values of and in Equations (1) and (2) [], respectively.
The chemical reaction for the formation of TiN in molten steel can be expressed by Equation (3),
Standard Gibbs free energy change for Equation (3) can be derived from Equations (4)–(7) [,],
Therefore, the expression of can be obtained,
The reaction equilibrium constant for Equation (3) is shown as follows:
where , , and denote the activities of TiN, Ti, and N in molten steel, respectively, herein, ; and denote the mass fractions of Ti and N in molten steel, respectively; and denote the activity coefficients of Ti and N, which can be estimated by Equations (10) and (11) [], respectively.
where and are the interaction coefficients of Ti and N at 1873 K, which can be calculated by Equations (12) and (13) [,,], respectively:
Due to the fact that the mass fraction of Fe is more than 90 mass% in molten steel, then the impact of second-order interaction coefficients can be ignored. Thus, the first-order interaction coefficients (as shown in Table 3) are used only during the calculation process [,].

Table 3.
First-order interaction coefficients of solute elements in molten steel at 1873 K [,].
According to Equations (10)–(13), one can obtain,
For Equation (9), take the logarithm of 10 on both sides at the same time,
Taking the equilibrium solubility product of Ti and N as (), and combining Equations (14)–(16), one can obtain,
By substituting T = 1636 K and T = 1748 K into Equation (17), respectively, the relationship between and can be obtained, as shown in Figure 1. Figure 1 shows that concentrations of N and Ti in the sample, see Point A in this figure, are much lower than those at the liquidus phase and solidus phase temperatures, which indicates that TiN will not precipitate in the liquid phase or mushy zone.
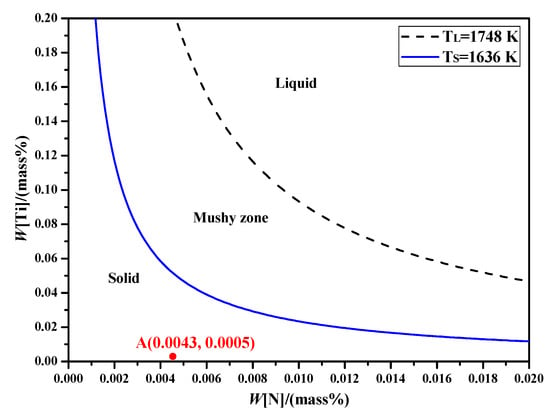
Figure 1.
Required solubility product of N and Ti for the precipitation of TiN inclusion in SWRH 92A tire cord steel.
3. Thermodynamic Analysis
3.1. Segregation Models
The above results shown in Figure 1 are based on the uniform distributions for elements N and Ti in molten steel without considering micro-segregation. However, due to the decrease in solubility of solute elements N and Ti during the solidification process, micro-segregation will occur inevitability, which will further lead to the precipitation of TiN. With respect to this issue, several micro-segregation models were proposed to describe the concentration changes of solute elements as a function of the solid fraction, as listed in Table 4 [].

Table 4.
Micro segregation models for solute elements during the solidification process [].
where and denote the instantaneous and initial concentration of solute elements (N and Ti) in the liquid phase zone during the solidification process, respectively; is the equilibrium distribution coefficient between liquid and γ-Fe phase, herein kC = 0.34, kN = 0.48, and kTi = 0.30 [,,]; g represents the solid fraction; ϕ (in the range of 0–1) denotes the inverse diffusion coefficient and α is the Fourier parameter.
3.2. Usage of the LRSM Model
As shown in Table 4, it can be seen that the Lever-rule model is obtained based on the assumption that solute elements are completely diffused in both liquid and γ-Fe phases; however, the Scheil model neglects such diffusion in the γ-Fe phase, which means the solute elements are completely diffused in liquid and have no diffusion in the γ-Fe phase. Due to the fact that the diffusion coefficient of N is much larger than that of Ti in the γ-Fe phase, as comparison of Equations (18) and (19) indicates [,], and more obviously supported by Figure 2, so, it is reasonable to assume that solute element N is completely diffused in the γ-Fe phase and the diffusion in the γ-Fe phase for Ti is neglected. That is to say, the Lever-rule model is applied for the N and Scheil model for Ti. In the current paper, this model combination was named as the LRSM model. Then the corresponding concentration expressions of solute elements N and Ti can be described by Equations (20) and (21), respectively.
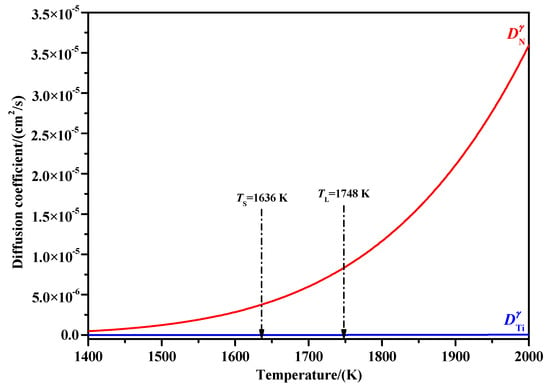
Figure 2.
Diffusion coefficients of solute elements N and Ti in the γ-Fe phase at different temperatures.
Prior to analyzing the solidification process of molten steel, the actual solubility products of N and Ti should be calculated, which can be considered as (), as shown by Equation (22),
In addition, the relationship between solidification front temperature (TL-S) and solid fraction (g) can be expressed by Equation (23) [],
At the same time, by substituting Equation (23) into Equation (17), the relationship between and solid fraction (g) can also be obtained. As is well known, if the actual solubility product reaches the equilibrium value (or ), TiN will precipitate. The values of and (calculated by LRSM model) are depicted in Figure 3, from which it can be easily seen that TiN will only precipitate at the very late stage of the solidification process, with a solid fraction bigger than 0.9966. When substituting 0.9966 into Equation (23), the solidification front temperature (TL-S = 1637 K) can be easily deduced, which is almost the same as the theoretical solidus temperature (TS = 1636 K) of the studied tire cord steel. This result suggests that TiN will not precipitate in the mushy zone until nearly close to complete solidification.
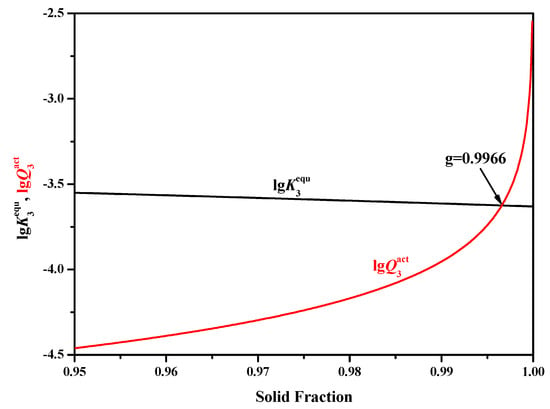
Figure 3.
Comparison of equilibrium solubility product with the calculated value obtained by the LRSM (Lever-rule model was applied for the N and Scheil model for Ti) model.
3.3. Usage of Ohnaka Model on Considering the Effect of Carbon on SDAS L
The above analytical results (Figure 3) were obtained based on the assumption that N is completely diffused and Ti has no diffusion in the γ-Fe phase. In fact, both N and Ti would diffuse to some extent in the γ-Fe phase, as shown in Equations (18) and (19), respectively.
In order to achieve a more realistic representation on the precipitation of TiN in SWRH 92A tire cord steel, the finite diffusion of the solute elements in the γ-Fe phase are now considered. The basic concentration expression is shown in Equation (24)). Herein, it can be easily found that if ϕ equals to zero, Equation (24) will change into the Scheil model; while if ϕ equals to one, Equation (24) will change into the Lever-rule model, instead. Furthermore, if the Brody–Fleming model [] is adopted (as seen in Equation (25)), ϕ will be not physically reasonable when the Fourier parameter α is bigger than 0.5; the Clyne–Kurz model [] lacks the actual physical meaning for ϕ if Equation (26) is used. In order to solve those problems, Ohnaka [] presented a simple modification of ϕ based on comparison with the approximate solution of the diffusion equation, as shown in Equation (27) [], which showed better agreement with the experimental data of Matsumiya et al. [] than did predictions using Equation (25). Therefore, the Ohnaka model was used in this paper. The Fourier parameter α involves the diffusion coefficient (cm2/s), SDAS L [cm, the unit of L was converted from μm (calculated by Equations (29) and (31)) to cm for the calculation in Equation (28), corresponding to the unit of ], and the local solidification time τ (s), as seen in Equation (28) [],
The expressions of for solute elements N and Ti are shown in Equations (18) and (19), respectively; SDAS L (herein, the unit of L calculated by Equation (29) was μm) is related with the cooling rate RC (K/s) and the carbon concentration , as expressed by Equation (29) []; the local solidification time τ (s) was calculated by Equation (30) [,].
By substituting Equations (27)–(30) and the equilibrium distribution coefficients and diffusion coefficients of different solute elements into Equation (24), the corresponding segregation ratio of different solute elements during the solidification process can be calculated, as shown in Figure 4. From Figure 4 it can be seen that the segregation ratio of both N and Ti increased with the increasing solid fraction, and the final segregation ratios almost equaled each other although the cooling rates were different, which suggests that the effect of the cooling rate can be ignored. However, it can also be seen that the cooling rate has a certain effect on the intermediate segregation process for Ti, the faster the cooling rate, the larger the segregation ratio would be. As for N, however, the effect can be ignored.
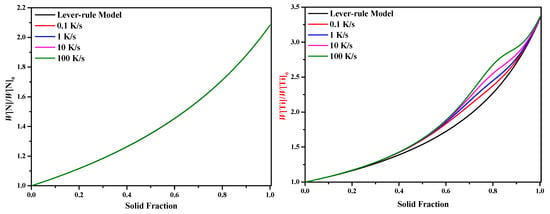
Figure 4.
Effects of cooling rates on the segregation ratios of solute elements N and Ti during the solidification process (the results obtained by the Lever-rule model are given as a reference).
What is more, when comparing with the results obtained by the Lever-rule model, it is surprising to find that the final segregation ratio almost kept the same for both N and Ti. The possible reasons may be explained as follows. When the segregation of solute element carbon was considered, the concentration of carbon would increase during the solidification process (the plot was not given in this paper), then the value of SDAS L would decrease (according to Equation (29) in the current condition), which may accelerate the diffusion velocity of solute elements between the liquid and the γ-Fe phases and even arrive complete. Besides, when the cooling rate became slower, the diffusion of solute element between liquid and γ-Fe phases would be more complete due to the adequate time, as shown in Figure 5, which makes the inverse diffusion coefficient closer to one and the results are similar to the case obtained by the Lever-rule model. In addition, it can also be seen from Figure 5 that the inverse diffusion coefficients of N almost equaled one during the total solidification process at the different cooling rates, so the results were almost the same as those obtained by the Lever-rule model. As for Ti, the inverse diffusion coefficients gradually increased with increasing solid fraction. The slower the cooling rate, the larger the inverse diffusion coefficients would be. However, the final values almost equaled one for the four different cooling rates (0.1, 1, 10, and 100 K/s). That is to say, the Ohnaka model applied will change into the Lever-rule model at the end of the solidification process.
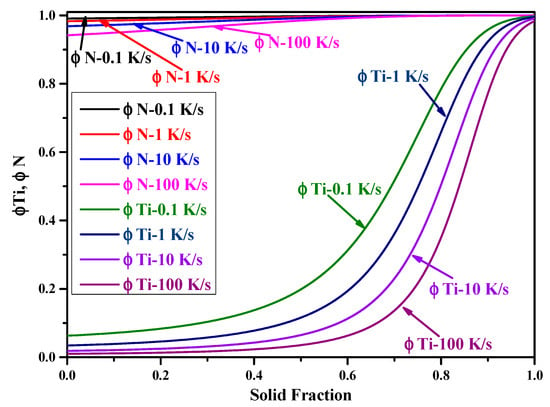
Figure 5.
Inverse diffusion coefficients of solute elements N and Ti with different cooling rates.
In addition, when the current Ohnaka model (considering the effect of carbon on SDAS L) was applied, precipitation of TiN during the solidification process would not happen because the value of the actual solubility product was much smaller than that of the equilibrium value , as can be seen in Figure 6. The current results clearly indicate that TiN cannot precipitate in the solid–liquid two-phase region (mushy zone).
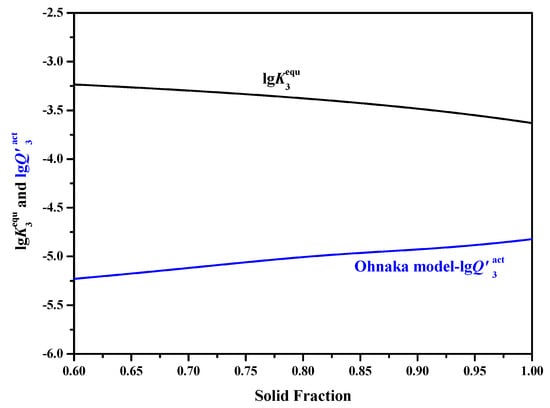
Figure 6.
Comparisons of equilibrium solubility product with the calculated value obtained by the Ohnaka model (considering the effect of carbon on SDAS L).
3.4. Use of the Ohnaka Model without Considering the Effect of Carbon on SDAS L
As mentioned above, when considering the effect of carbon on SDAS L, TiN will not precipitate during the solidification process. However, in other references [,,] on analyzing the segregation ratio of different solute elements, the SDAS L (herein, the unit of L calculated by Equation (31) is μm) was calculated as a function of the cooling rate RC (K/s) only, see Equation (31),
Similarly, by substituting Equations (27), (28), (30), and (31) and the equilibrium distribution coefficients and diffusion coefficients of different solute elements into Equation (24), the corresponding segregation ratios of the solute elements N and Ti during the solidification process can be obtained, as shown in Figure 7. From Figure 7 it can be seen that both N and Ti show a strong segregation tendency especially in the latter period and in comparison, the segregation ratio of Ti is much bigger than that of N. In addition, the effect of cooling rate on the segregation ratio can be nearly ignored (the plot is not given in the current paper). Therefore, it is possible for TiN to precipitate even though the initial concentrations of N and Ti are very low, as shown in Figure 8, and in which the critical solid fraction is a little smaller than that obtained by the LRSM model (0.98 vs. 0.9966). That is to say, TiN can precipitate a little earlier. Anyhow, TiN is only generated at the very late stage closing to the complete solidification of the molten steel.
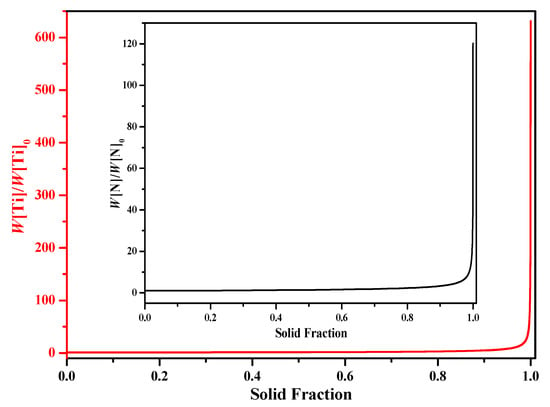
Figure 7.
Segregation ratio of solute elements N and Ti during the solidification process when Equation (31) was used with a cooling rate of 10 K/s.
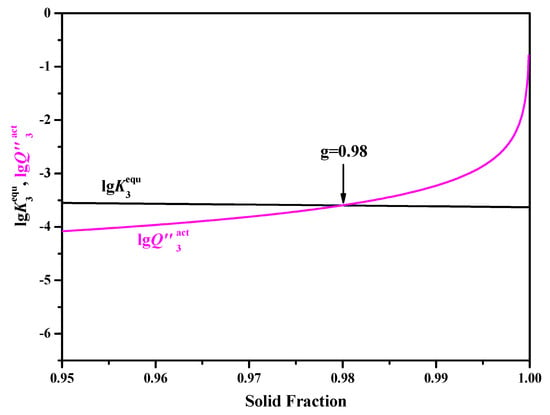
Figure 8.
Comparison of equilibrium solubility product with the calculated values obtained by the Ohnaka model (without considering the effect of carbon on SDAS L).
Similar to the previous calculation, another surprising phenomenon is also found in this case. The segregation ratios of solute elements N and Ti are nearly the same as those obtained by the Scheil model, as shown in Figure 9. As mentioned above, when the inverse diffusion coefficient ϕ equals zero, Equation (24) will turn into the Scheil model. In the current discussion, ϕ nearly equals zero for both N and Ti, as seen in Figure 10. That is to say, both N and Ti almost completely diffuse in the liquid and have no diffusion in the γ-Fe phase in this situation. The possible reason for this result may be due to characteristics of the microstructure (mostly likely due to the much larger SDAS L) between the liquid and solid phases, which makes the inverse diffusion of solute elements insufficient.
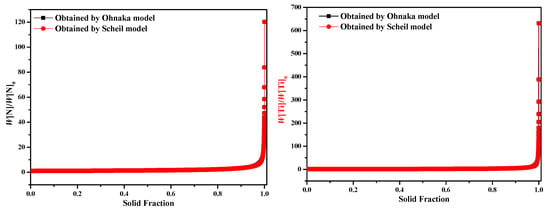
Figure 9.
Comparison of segregation ratio of solute elements N and Ti when adopting the Ohnaka (without considering the effect of carbon on SDAS L) and Scheil models.
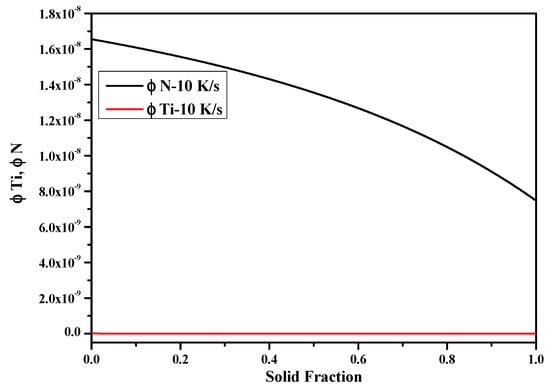
Figure 10.
Inverse diffusion coefficients of solute elements N and Ti when adopting the Ohnaka model (without considering the effect of carbon on SDAS L).
4. Conclusions
According to the calculated results, it is possible to summarize the precipitation behavior of TiN inclusion in SWRH 92A tire cord steel during the whole solidification process, as follows:
- (1)
- Precipitation of TiN will not occur in the liquid phase region regardless of the selected micro- segregation models.
- (2)
- When adopting the LRSM and Ohnaka (without considering the effect of carbon on secondary dendrite arm spacing (SDAS L)) models, TiN will precipitate in the mushy zone at the very late stage of the solidification process, with solid fractions larger than 0.9966 and 0.98, respectively. When considering the effect of carbon on SDAS L for the Ohnaka model, TiN will not precipitate in both the liquid phase and mushy zone.
- (3)
- Results of different segregation models show that the Ohnaka model (considering the effect of carbon on SDAS L) is similar to the Lever-rule model at the very late stage during the solidification process; however, for the case without considering the effect of carbon on SDAS L, the result is similar to the Scheil model.
- (4)
- Due to the fact that different segregation models may lead to different results, more attention should be paid to selecting the appropriate model or developing new models to analyze the actual segregation phenomena. Besides, further experimental work and theoretical analysis to understand in depth the precipitation behavior of TiN in SWRH 92A tire cord steel will be required in the future.
Author Contributions
Writing-original draft, methodology and review, L.W.; Methodology, visualisation and investigation, Z.-L.X.; Formal analysis, Y.-L.C.; Writing-review and editing, X.-G.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
The authors gratefully acknowledge the financial support from the National Natural Science Foundation of China, and the Special Project of Central Government for Local Science and Technology Development of Hubei Province (51874214 and 2019ZYYD076, respectively).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Yu, C.F.; Xue, Z.L.; Jin, W.T. Precipitation and Solid Solution of Titanium Carbonitride Inclusions in Hypereutectoid Tire Cord Steel. J. Iron Steel Res. Int. 2016, 23, 338–343. [Google Scholar] [CrossRef]
- Jiang, Y.D.; Lei, J.L.; Zhang, J.; Xiong, R.; Zou, F.; Xue, Z.L. Effect of carbon content on Ti inclusion precipitated in tire cord steel. J. Surf. Eng. Mater. Adv. Technol. 2013, 3, 283–286. [Google Scholar] [CrossRef][Green Version]
- Lei, J.L.; Xue, Z.L.; Jiang, Y.D.; Zhang, J.; Zhu, T. Study on TiN precipitation during solidification for hypereutectoid tire crod steel. Metal. Int. 2012, 17, 10–16. [Google Scholar]
- Jiang, Y.D.; Xue, Z.L.; Zhang, J. Genetic analysis for large TiN inclusions in wire rod for tire cord steel of SWRH82A. J. Iron Steel Res. Int. 2014, 21, 91–94. [Google Scholar] [CrossRef]
- Zou, X.; Zhao, D.; Sun, J.; Wang, C.; Matsuura, H. An integrated study on the evolution of inclusions in EH36 shipbuilding steel with Mg addition: From casting to welding. Metall. Mater. Trans. B 2018, 49, 481–489. [Google Scholar] [CrossRef]
- Yin, X.; Sun, Y.; Yang, Y.; Deng, X.; Barati, M.; McLean, A. Effect of alloy addition on inclusion evolution in stainless steels. Ironmak. Steelmak. 2017, 44, 152–158. [Google Scholar] [CrossRef]
- Ma, W.J.; Bao, Y.P.; Zhao, L.H.; Wang, M. Control of the precipitation of TiN inclusions in gear steels. Int. J. Miner. Metal. Mater. 2014, 21, 234–239. [Google Scholar] [CrossRef]
- Wang, L.; Xue, Z.L.; Zhu, H.Y.; Lei, J.L. Thermodynamic analysis of precipitation behavior of Ti-bearing inclusions in SWRH 92A tire cord steel. Results Phys. 2019. [Google Scholar] [CrossRef]
- Cai, X.F.; Bao, Y.P.; Wang, M.; Lin, L.; Dai, D.C.; Gu, C. Investigation of precipitation and growth behavior of Ti inclusions in tire cord steel. Metall. Res. Technol. 2015, 112, 407–418. [Google Scholar] [CrossRef]
- Zhang, J.; Xue, Z.L.; Jiang, Y.D.; Lei, J.L.; Zou, F.; Xiong, R. Research on precipitation of Ti inclusions during solidification of tire cord steel SWRH82A. Metal. Int. 2014, 19, 34–38. [Google Scholar]
- Jin, Y.; Du, S. Precipitation behaviour and control of TiN inclusions in rail steels. Ironmak. Steelmak. 2018, 45, 224–229. [Google Scholar] [CrossRef]
- Liu, T.; Chen, D.; He, W.; Long, M.; Gui, L.; Duan, H.; Cao, J. Study on the Formation and Control of TiN Inclusion in Mushy Zone for High Ti Microalloyed Steel. In TMS 2018 147th Annual Meeting & Exhibition Supplemetal Proceedings; Springer: Cham, Switzerland, 2018; pp. 605–615. [Google Scholar]
- Liu, H.; Wang, H.; Li, L.; Zheng, J.; Li, Y.; Zeng, X. Investigation of Ti inclusions in wire cord steel. Ironmak. Steelmak. 2011, 38, 53–58. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, L.F.; Duan, H.; Zhang, Y.; Luo, Y.; Conejo, A.N. Extraction, thermodynamic analysis, and precipitation mechanism of MnS-TiN complex inclusions in low-sulfur steels. Metall. Mater. Trans. A 2016, 47, 3015–3025. [Google Scholar] [CrossRef]
- Chen, J. Manual of Chart and Data in Common Use of Steel Making; Metallurgical Industry Press: Beijing, China, 2010. [Google Scholar]
- Fu, J.; Zhu, J.; Di, L.; Tong, F.S.; Liu, D.L.; Wang, L.Y. Study on the precipitation behavior of TiN in the microalloyed steels. Acta Metall. Sin. 2000, 36, 801–804. [Google Scholar]
- Tian, Q.; Wang, G.C.; Zhao, Y.; Li, J.; Wang, Q. Precipitation Behaviors of TiN Inclusion in GCr15 Bearing Steel Billet. Metall. Mater. Trans. B 2018, 49, 1149–1164. [Google Scholar] [CrossRef]
- Pa, M.; Dp, D.; Chandra, T.; Cr, K. Grain growth predictions in microalloyed steels. ISIJ. Int. 1996, 36, 194–200. [Google Scholar]
- Luo, S.; Wang, B.; Wang, Z.; Jiang, D.; Wang, W.; Zhu, M. Morphology of Solidification Structure and MnS Inclusion in High Carbon Steel Continuously Cast Bloom. ISIJ Int. 2017, 57, 2000–2009. [Google Scholar] [CrossRef]
- Suzuki, S.; Weatherly, G.; Houghton, D. The response of carbo-nitride particles in hsla steels to weld thermal cycles. Acta Metall. 1987, 35, 341–352. [Google Scholar] [CrossRef]
- Tian, Q.; Wang, G.C.; Shang, D.; Lei, H.; Yuan, X.; Wang, Q.; Li, J. In Situ Observation of the Precipitation, Aggregation, and Dissolution Behaviors of TiN Inclusion on the Surface of Liquid GCr15 Bearing Steel. Metall. Mater. Trans. B 2018, 49, 3137–3150. [Google Scholar] [CrossRef]
- Ma, Z.; Janke, D. Characteristics of oxide precipitation and growth during solidification of deoxidized steel. ISIJ Int. 1998, 38, 46–52. [Google Scholar] [CrossRef]
- Bower, T.F.; Brody, H.; Flemings, M.C. Measurements of solute redistribution in dendritic solidification. Trans. Metall. Soc. AIME 1966, 236, 624–634. [Google Scholar]
- Clyne, T.; Kurz, W. Solute redistribution during solidification with rapid solid state diffusion. Metall. Trans. A 1981, 12, 965–971. [Google Scholar] [CrossRef]
- Ohnaka, I. Mathematical analysis of solute redistribution during solidification with diffusion in solid phase. Trans. Iron Steel Inst. Jpn. 1986, 26, 1045–1051. [Google Scholar] [CrossRef]
- Matsumiya, T.; Kajioka, H.; Mizoguchi, S.; Ueshima, Y.; Esaka, H. Mathematical analysis of segregations in continuously-cast slabs. Trans. Iron Steel Inst. Jpn. 1984, 24, 873–882. [Google Scholar] [CrossRef]
- Lee, M.H.; Park, J.H. Synergistic effect of nitrogen and refractory material on TiN formation and equiaxed grain structure of ferritic stainless steel. Metall. Mater. Trans. B 2018, 49, 877–893. [Google Scholar] [CrossRef]
- Won, Y.M.; Thomas, B.G. Simple model of microsegregation during solidification of steels. Metall. Mater. Trans. A 2001, 32, 1755–1767. [Google Scholar] [CrossRef]
- Zhang, X.; Ma, G.J.; Liu, M.K. Micro-segregation model calculation of residual tin in boiler and pressure vessel steel. Philos. Mag. 2019, 99, 1041–1056. [Google Scholar] [CrossRef]
- Goto, H.; Miyazawa, K.I.; Yamada, W.; Tanaka, K. Effect of cooling rate on composition of oxides precipitated during solidification of steels. ISIJ Int. 1995, 35, 708–714. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).