Abstract
The effectiveness of model-based multivariable controllers depends on the quality of the model used. In addition to satisfying standard accuracy requirements for model structure and parameter estimates, a model to be used in a controller must also satisfy control-relevant requirements, such as integral controllability. Design of experiments (DOE), which produce data from which control-relevant models can be accurately estimated, may differ from standard DOE. The purpose of this paper is to emphasize this basic principle and to summarize some fundamental results obtained in recent years for DOE in two important cases: Accurate estimation of the order of a multivariable model and efficient identification of a model that satisfies integral controllability; both important for the design of robust model-based controllers. For both cases, we provide an overview of recent results that can be easily incorporated by the final user in related DOE. Computer simulations illustrate outcomes to be anticipated. Finally, opportunities for further development are discussed.
1. Introduction
The overarching themes in controller design are closed-loop performance and robustness. Both properties depend on the model of the controlled process, in whatever form that model may come. Therefore, a model used in controller design, whether implicitly or explicitly, must possess certain characteristics for good closed-loop performance and robustness. A process model may typically be identified from data obtained by performing process identification experiments or from standard operating data, as long as such data contain enough information. In an identification experiment, a process is excited by inputs with particular attributes, and output responses are recorded. The approach of designing such inputs in an identification experiment is studied in the realm of control-relevant design of experiments (DOE). Since the early days of automatic control, classical controller design methods (e.g., Ziegler–Nichols or Bode) have been associated with a model-building experimental procedure (DOE in the parlance of this paper), the outcome of which would subsequently be used in robust controller design. For multivariable controllers, the issue of model-building poses additional complications compared to single-input-single-output controllers. Multivariable process identification has received much attention in recent decades, and by extension, the properties of multivariable models crucial for multivariable controller design have been brought to the forefront. Of these properties, two that may have a significant effect on controller design are integral controllability (IC) and the structure (dimension of state space) of a multivariable model. DOE that generates data allowing the efficient identification of multivariable models which satisfy these two crucial properties has been the focus of substantial work in recent years [1,2,3,4,5,6,7,8,9,10,11]. Among these publications, the works in [1,2] and [9,10,11] offer rigorous guidelines for addressing the two multivariable model properties mentioned above. Possibly because of the complexity involved in developing the results generated by that work, it appears that these results have remained largely inaccessible to the control community, despite the relative simplicity of corresponding recipes. Regarding a common pattern that appears in these results, namely the use of rotated pseudo random binary sequence (PRBS) inputs in DOE, there are certainly empirical studies that do discuss heuristic aspects of designing such inputs, but this is where most publications of this nature stop, without providing a rigorous foundation for treating many important practical cases involving inputs and/or output constraints explicitly. To wit, in one of the many papers that Häggblom has co-authored on the subject [12], he mentions the following, citing a key publication by the corresponding author’s group [9]:
(underlining added in quotation) where “detuning factor” refers to the optimal ratio of rotated PRBS input variances when input constraints are present in DOE. While the case of control-relevant DOE subject to input constrains is common and even though the result for the optimal rotated PRBS input variances shown above is both explicit and simple, it has remained largely unnoticed. In another instance, Featherstone and Braatz [13] state that, unfortunately, incorporating the integral controllability conditions (Equation (11) below below) directly in DOE is problematic, as the eigenvalue inequalities’.“Using quite advanced theoretical considerations, Darby and Nikolaou (2009) derived the detuning factor for the -th gain direction.”
“main weakness is that they consist of a coupling between the process model and the true process, which is highly cumbersome.”
Finally, there are many more cases of control-relevant DOE (e.g., when individual input and/or output variance constraints are present) for which no rigorous results are available, the only exception being the framework initiated in [9] and further developed in [10,11]. Publications referring in passing to these results include [12,14,15,16,17,18]. However, no publications mention use, let alone further development, of these results. It is this void that this review paper purports to address. That is, after outlining the conceptual framework of control-relevant DOE (for integral controllability and subspace MIMO identification), the manuscript provides recipes for a non-expert user to easily formulate and solve control-relevant DOE problems. For each of the proposed designs, the paper.
- presents the mathematical problem formulation in a concise and clear manner;
- provides simple recipes to solve the problem either analytically or numerically; and
- illustrates the entire problem formulation/solution process through simulations on both textbook-level and realistic cases, to further help the user grasp the subject.
The rest of the paper is structured as follows: After a brief context given on control-relevant DOE for multivariable dynamic system identification, there are two basic tracks, one focusing on DOE for subspace identification and one on IC-compliant model identification. In each track, we provide a brief overview of the basic background, summarize recent results and present a number of illustrative computer simulation examples. Finally, we provide suggestions for further development.
2. Control-Relevant DOE
Starting with the momentum generated by Fisher’s seminal work [19] in the beginning of the 20th Century, design of experiments is at least a century old and has seen application in a large array of domains. Reviewing all of this work is well outside the scope of this manuscript. For the uninitiated reader, there is a wealth of books that cover the topic of DOE from various perspectives, including [20,21,22,23,24]. Beyond generalities, DOE ideas for control-relevant dynamic system identification started with the seminal paper by Mehra [25] and have branched out in different directions. Of particular interest is control-relevant DOE for multivariable systems, particularly ill-conditioned ones. It is noted here that there are several issues associated with control-relevant DOE. Among those, two key issues, focused on in this paper, are DOE for identification of multivariable models that: (a) have an accurate structure (dimension of state space); and (b) satisfy the integral controllability condition, as already mentioned in the Introduction. We elaborate on these two issues next.
3. DOE for Estimation of System Order in Subspace Identification
Identification of multivariable models uses a variety of model structures, including finite impulse response (FIR), autoregressive with exogenous input (ARX), state-space, and others [26,27]. Model parameters are estimated by some sort of squared-error minimization in a number of approaches, such as the prediction error method (PEM) [26], maximum likelihood method [28] and subspace identification (SI) method [29]. In all approaches, the system order, representing the number of states in the state-space representation of the system, is a crucial parameter that needs to be estimated accurately before the accuracy of parameter estimates is addressed. The quality of available data from which model order is estimated affects the accuracy of that estimate. Therefore, DOE is important for the generation of data that allow accurate estimates of model order. The determination of model order is particularly challenging for ill-conditioned systems [1,3]. Because many real processes are ill-conditioned, it is all the more necessary to develop a DOE framework for accurate estimation of the order of such systems. Such a framework has been developed in a number of papers in recent years. We present a user-oriented summary of these developments below, after a brief overview of the relevant background.
3.1. Relevant Background on Subspace Identification
The order, , of a system is equal to the dimension of the state vector in the state-space model:
where is the state, is the input, is the output and is white noise. Subspace identification (SI) methods [29,30,31,32] estimate the order of a system as in Equation (1) by:
- (a)
- constructing certain matrices directly from input and output data;
- (b)
- performing a projection operation [33] on these matrices and, finally;
- (c)
- performing a singular value decomposition (SVD) of the resulting matrix.
There is a number of SI variants, such as numerical algorithms for subspace state space system identification (N4SID), multivariable output-error state-space (MOESP) and canonical variate analysis (CVA) [29,31]. The essence of these variants is the same, that is they all perform reduced-rank squared-error minimization on input/output data [34,35]. For the MOESP SI variant, focused on in this paper, system order is determined by the dimension of the diagonal matrix that contains “large” singular values in an SVD of the matrix:
as:
where the diagonal matrix contains “small” singular values that are due to noise and would be identically equal to zero if there were no noise in Equation (1). The matrices that appear in Equation (2) are constructed from input and output data, as summarized in Appendix A.
3.2. Pitfalls in Model-Order Estimation from Ordinary Experimental Data
To estimate , as already mentioned, the singular values of are separated into two categories: “large” and “small”, lined up on the diagonals of and , respectively. Then, an estimate of is simply equal to the number of “large” singular values (i.e., the dimension of the square matrix ).
The underlying rationale for the separation of the singular values of into “large” and “small” is that some of these singular values are due to signal (the “large” ones, ending up in ), while the rest are due to noise and would be identically zero if there were no noise (the “small” ones, ending up in ).
Unfortunately, the pattern of singular values of may not allow reliable separation between “large” and “small” singular values. In fact, for well-conditioned systems, separation is typically clear-cut when data for model identification are generated from standard experiments with PRBS inputs exciting the process to be identified. However, for ill-conditioned systems, such experiments do not produce an accurate separation between “large” and “small” singular values. This, in turn, leads to poor estimates of system order. We illustrate this below by summarizing computer simulations on two cases, one where the cut-off point is clearly inaccurate and one where the cut-off point is not discernible at all.
The first case is a distillation column with:
and system order equal to two. The singular value pattern of shown in Figure 1 suggests just one non-zero (“large”) singular value of in the matrix , with all remaining singular values in being essentially zero (“small”). The resulting estimate of one for system order is clearly wrong and creates a singular input-output matrix, with obvious limitations for use of that model in effective controller design.
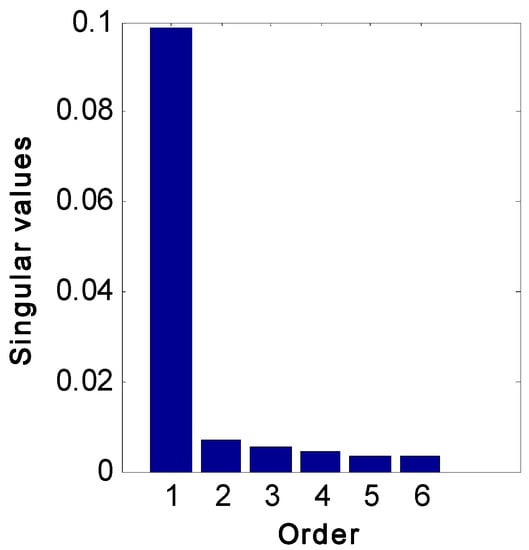
Figure 1.
Singular values of the matrix , Equation (3), resulting from input/output data collected for a distillation column excited by pseudo random binary sequence (PRBS) inputs.
The second system is taken from an industrial fluidized catalytic cracking (FCC) reactor-regenerator system with order equal to 15 and steady-state gain matrix:
(see Misra and Nikolaou [2] for the full model). Figure 2 shows that there is not even a hint as to where the right cut-off is between non-zero (“large”) and zero (“small”) singular values, thus leading to an entirely uncertain estimate of system order. Incidentally, possible hints in Figure 2 that the cut-off point is at two or four are grossly inaccurate, as the correct system order is 15, as stated above.
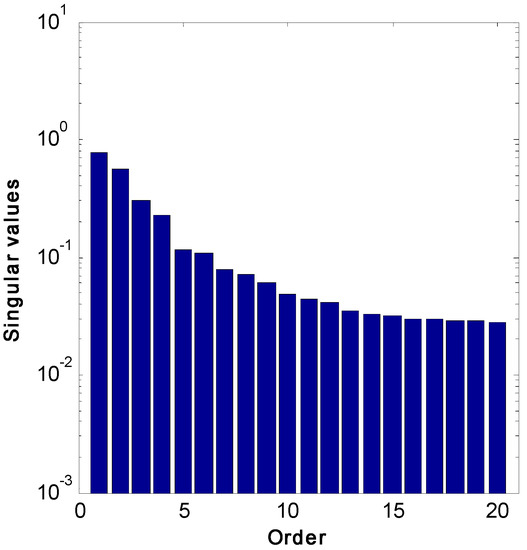
Figure 2.
Singular values of the matrix , Equation (3), resulting from input/output data collected for a fluidized catalytic cracking (FCC) system excited by PRBS inputs.
The underlying reasons for the problems on accurately estimating model order illustrated above are briefly discussed next.
3.3. Why Ordinary Data May Easily Lead to the Wrong Order of an MIMO Model
The underlying reason for poor estimates of system order for ill-conditioned systems is that data obtained from standard experiments using PRBS inputs produce highly correlated outputs, which in turn, lead to ill-conditioning of , Equation (3), and thus shape the smaller of the “large” singular values in close to the “small” singular values in (corresponding to noise). A rigorous justification for this argument is provided by Misra and Nikolaou [2].
3.4. DOE for Accurate Estimation of Model Order: The Case for Rotated Inputs
A direct insight from the preceding discussion on the above illustrative examples is that to accurately estimate the order of an ill-conditioned system, the identification experiment must be designed in such a way that the outputs produced are as uncorrelated as possible.
It turns out [2] that such an experiment can be designed by using appropriately scaled rotated PRBS inputs, an outgrowth of an idea originally proposed by Koung and MacGregor [36] in a different context and first applied to DOE for accurate model-order estimation by Misra and Nikolaou [1].
According to the analysis in [2], for a system with steady-state relationship , the singular values of the matrix are separated into “large” and “small”, following the system order, if input/output data are generated by an experiment with inputs:
where the entries of the rotated input vector are independent PRBS signals proportioned as:
and the rotation (orthonormal) matrix and singular values are obtained from SVD of the matrix with .
For the special case of a system, the rotation matrix can be parametrized in terms of a single rotation angle as:
Similar parametrizations can be obtained for higher-dimensional systems in terms of multiple rotation angles or equivalent Euler parameters [2,37].
3.5. What Could Go Wrong with Rotated Inputs
The input rotation matrix and singular values used to characterize the rotated PRBS inputs in Equations (6) and (7) are by default never known before the experiment; otherwise, the experiment would not be needed in the first place. An incorrect choice of or may easily lead to wrong estimates of model order. For example, using , instead of the true for the system described in Equation (4), yields an input design that produces experimental data from which the system order is estimated to be one, rather than the correct value of two (Figure 3). This problem of sensitivity of order estimate to the rotation angle used in experiment design has been pointed in the past by a number of authors [1,3]. To remedy this problem, Misra and Nikolaou [2] proposed an adaptive strategy for the design of experiments. In this strategy, input design and model estimates (hence and ) alternate for a number of cycles, until the procedure converges.
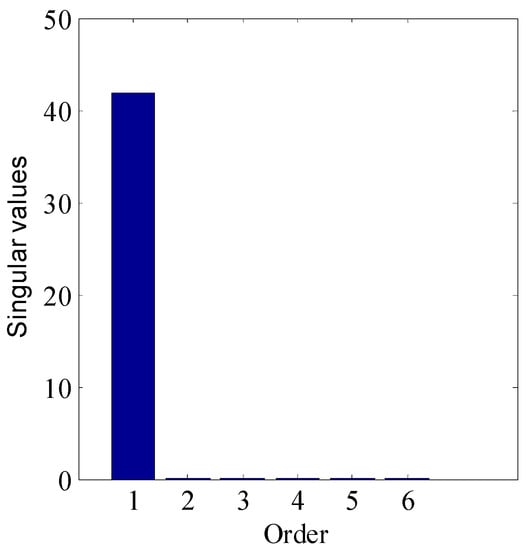
Figure 3.
Model order estimation for distillation column using experimental data from a process excited by rotated PRBS inputs at the wrong rotation angle of in place of the correct rotation angle of .
3.6. Adaptive DOE Employing Rotated Inputs
Adaptive design of experiments [2] is initiated with a preliminary model for , estimated either by performing a short identification experiment with PRBS inputs or from prior knowledge in the case of process revamp. This preliminary model is used to design the first sequence of rotated inputs. These inputs are used in the next experiment to estimate an updated model. As the cycle experiment/identification is repeated, model information improves with improved quality of data, i.e., the cut-off between singular values of and in Equation (3) becomes increasingly clear, ultimately yielding the correct order estimate. A step-by-step summary of the adaptive design employing rotated PRBS inputs is provided in Box 1 below.
Box 1. Adaptive DOE for estimation of multivariable model order.
- Use standard PRBS inputs and generate data to obtain a preliminary model estimate with steady-state gain matrix .
- Obtain an SVD .
- Design an input based on a rotated PRBS input , Equations (6) and (7), and perform an identification experiment.
- Using data of the latest experiment, perform an SVD of the resulting matrix (Equation (2)) and choose the system order (select the matrices and , Equation (3)) by checking where the singular values of demonstrate an abrupt transition from “large” to “small”.
- Using all experimental data collected, obtain matrix estimates of a state-space model using standard SI formulas (e.g., taking Steps 4–6 in combined Algorithm 1 or 2 outlined in [30], p. 121 and p. 124, respectively), and estimate the new steady-state gain matrix .
- If has satisfactorily converged, stop; else go to Step 2.
3.7. Illustration of Adaptive DOE with Rotated Inputs for Accurate Model-Order Estimation
We present here a summary of the computer simulation studies on the order estimate for the two cases mentioned above, namely a high-purity distillation column and a FCC system (Equations (4) and (5), respectively). The exposition is based on [2]. For both cases, order estimates improve with each experiment and quickly reach their correct values of two and 15, as shown in Figure 4 and Figure 5, respectively. Additional details can be found in the original publication [2].
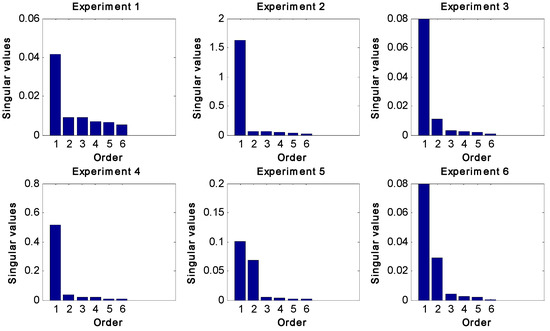
Figure 4.
Order estimation for distillation column using adaptive DOE with rotated PRBS inputs. A cut-off point is evident at two.
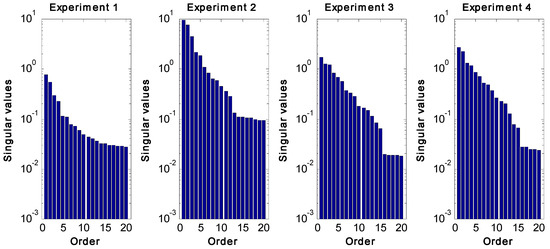
Figure 5.
Order estimation for a FCC system using adaptive DOE with rotated PRBS inputs. A cut-off point is evident at 15.
3.8. Adaptive DOE in Comparison to Other DOE Approaches
As mentioned previously, uncorrelated outputs, which greatly facilitate accurate order estimation for ill-conditioned systems, can be produced through process excitation by inputs designed on the basis of appropriately proportioned rotated PRBS signals. An alternative strategy to producing uncorrelated outputs could be a closed-loop experiment [1,3] with appropriate set point changes. For example, a decoupling multivariable controller with PRBS changes to set points can be used. However, the design of such a controller requires a number of controller design-related decisions and, most importantly, requires a useable process model. However, such a model is, by default, not available (otherwise, an identification experiment would not be needed in the first place). To illustrate the difficulty in MIMO model identification via closed-loop experiments, Misra and Nikolaou [2] used three different controllers with the distillation column in Equation (4), namely: (a) two decentralized PI controllers; (b) model predictive control (MPC); and (c) internal model control (IMC). All three failed to estimate the correct order of the system. Therefore, while closed-loop experiments cannot be excluded, they have their own design difficulties, mainly stemming from the unavailability of a reasonable model for controller design, compounded by decisions that have to be made for controller design, as well.
3.9. Summary: DOE for MIMO Model Order Estimation
For a multivariable system, particularly an ill-conditioned one, experiments with commonly-used PRBS inputs are not effective for estimation of the system order, a crucial first step before parameter estimation for complete model identification. Experiments that produce uncorrelated outputs are preferable. Such experiments may be open- or closed-loop. Adaptively designed open-loop experiments offer a straightforward approach towards generating data from which system order can be accurately estimated and a complete model identified.
Interestingly enough, the same concept of experiments with rotated inputs emerges when models satisfying the integral controllability condition must be identified, for the models to be usable in robust controller design. A review of this subject and guidelines for the design of experiments are presented next.
4. DOE for Identification of Models Satisfying Integral Controllability
Standard DOE targets minimization of some sort of model estimation error [24,25]. However, for a model to be useful in the control of a multivariable system, small error between controlled process and the estimated model alone is not enough. An associated property that must be satisfied in order to ensure robust closed-loop stability when the controller is detuned is integral controllability (IC) [38]. A number of recipes for DOE have been developed recently that focus on generating data for obtaining IC-compliant models. We motivate the discussion by first explaining how even very accurate models cannot be used in robust control if they are not IC-compliant.
4.1. Why Model Proximity to the Real Process Is Not Enough for Controller Design
Consider a high-purity distillation column [39] with steady-state transfer matrix:
Two models and with respective transfer matrices:
are used in a decoupling controller design using the standard multivariable IMC approach [39]. The relative errors for and compared to are approximately 1% and 20%, respectively, making much more accurate than , hence, one might expect, preferable for use in a decoupling controller. However, the controller using model results in an unstable closed-loop. On the other hand, the same controller using model stabilizes the controlled system (Figure 6).
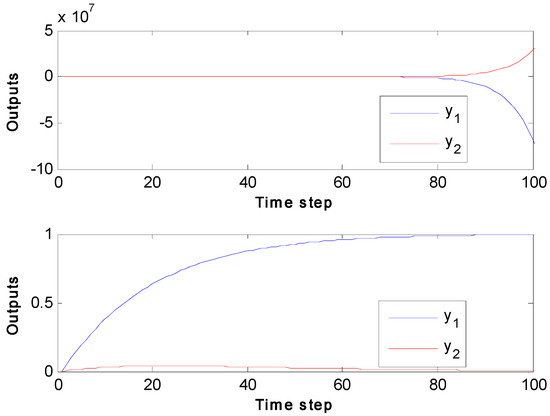
Figure 6.
Closed-loop output response for step change in the set point of Output-1 () and no change in the set point of Output-2 () using controllers based on model (top) and (bottom), respectively.
This example indicates that proximity of an estimated model to a true process is not synonymous with model quality for control purposes. As mentioned in the Introduction, among properties that capture the suitability of a model for controller design is integral controllability. The next section quickly summarizes this concept, and the subsequent discussion presents a general framework for DOE that produces data from which models satisfying integral controllability can be quickly identified.
4.2. Integral Controllability: A Measure of Multivariable Controller Robustness
The precise formulation of the result on integral controllability proven by Garcia and Morari [38] is as follows: assume that multivariable IMC with a diagonal (decoupling) filter matrix is used to control an stable, linear, time-invariant system with steady-state input-output behavior , , . Then, there exists an such that the closed loop remains stable for all if and only if the matrix (where and are the actual and estimated steady-state gain matrices, respectively) has eigenvalues satisfying the IC condition:
This result connects the achievable robustness of decoupling multivariable controllers that include integral action with the kind and magnitude of associated model uncertainty. Therefore, in order to design a robust model-based decoupling multivariable controller, the model used must satisfy the IC condition in Equation (11). Consequently, model identification experiments must be designed in a way that explicitly incorporates Equation (11). Unfortunately, incorporating Equation (11) directly in DOE is problematic, as the eigenvalue inequalities’ “main weakness is that they consist of a coupling between the process model and the true process, which is highly cumbersome” [13]. To remedy the difficulties posed by using Equation (11) directly, Darby and Nikolaou [9] developed an alternative inequality whose satisfaction guarantees the satisfaction of Equation (11), but is much more direct, hence usable in DOE, in that it contains explicitly the very inputs to be used in a corresponding identification experiment. As a result, that alternative inequality can be directly incorporated in DOE. We elaborate on this next, after a quick overview of relevant elements of the standard approach to the design of experiments.
4.3. Standard Approach to DOE for Multivariable Model Identification
As mentioned previously, standard DOE focuses on solving an optimization problem that minimizes errors in model parameter estimates, which is considered a benchmark for model quality. To be more specific, the optimization problem for the identification of a static model can be formulated as follows.
Consider an multivariable system with steady state relationship:
where indexes experiments; ; is the input vector used in experiment ; is the output vector in experiment ; is a Gaussian noise vector with zero mean and constant . The least-squares estimate of is:
or:
where:
for an experiment of length . The associated uncertainty ellipsoid for is:
for confidence level , where:
and the information matrix in Equations (13), (14), and (18) can be approximated [40] in terms of input covariance, , and length of experiment, , as:
From Equations (17)–(19), it is clear that the error in gain estimates can be reduced by selecting inputs in such a way that can be as large as possible, or alternatively, as small as possible. Given that input amplitudes have clear upper bounds, the interesting option that remains, in order to make small, is how to shape these inputs. This gives rise to an “alphabet soup” of standard DOE alternatives, such as the following [25].
- (1)
- D-optimal: minimize , equivalent to minimizing the volume of the uncertainty ellipsoids.
- (2)
- E-optimal: minimize , equivalent to minimizing the maximum variance amongst all parameters.
- (3)
- A-optimal: minimize , equivalent to minimizing average variance of the parameters.
Other criteria, such as C-, G-, T-, I-, or V- optimality [24], may also be used. Again, while these designs focus on accurate parameter estimates or predictions, they do not address IC, thus potentially making the resulting models not suitable for use in multivariable control.
4.4. Making IC-Compliant DOE Feasible
To simplify DOE for IC, Darby and Nikolaou [9] showed that Equation (11) is satisfied for and all in the standard ellipsoidal uncertainty set:
if
where are obtained from the SVD .
The ellipsoidal uncertainty set in the above Equation (20) typically arises in least-squares parameter estimation, with .
The advantage of Equation (21) over Equation (11) in DOE is that Equation (21) involves inputs directly (in or, equivalently, , Equation (19)). Therefore, Equation (21) can be combined as either a constraint or objective with whatever additional criterion is used in DOE, to characterize optimal inputs. For example, DOE could be cast as finding:
subject to whatever constraints are present. Alternatively, DOE could be cast as minimization of , or subject to Equation (21), in the spirit of D-, E- or A-optimality.
Interestingly enough, for a number of important practical cases, explicit recipes for the design of optimal inputs emerge, some of which were not known before the preceding approach appeared. In other cases of practical importance, optimal inputs are obtained through numerical solution of a corresponding optimization problem. These ideas are discussed in the next three subsections.
4.4.1. IC-Compliant DOE Subject to the Upper Bound on the Total Input/Output Variance: Analytical Solution
When an upper bound on the total input and output variance exists, DOE for IC can be cast as:
subject to:
The above Equation (24) places an upper bound on the combined weighted variance of inputs and outputs, where is the relative weight of output versus input variance.
It can be shown [9] that the resulting optimal solution is:
where is a vector whose components are uncorrelated PRBS signals with relative variance ratios:
with .
Equation (26) suggests that for , namely with a constraint placed on total output variance alone, the optimal solution satisfies:
which is the DOE prescription presented in Koung and MacGregor [36]. However, for , new optimal DOE prescriptions emerge, as introduced by Darby and Nikolaou [9]. For example, with a constraint placed on total input variance alone, the optimal rotated inputs should satisfy:
a simple recipe that differs markedly from Equation (27).
4.4.2. IC-Compliant DOE for Minimizing Total Input/Output Variance Subject to IC: Analytical Solution
When the least possible total input and output variance is desired, DOE for IC can be cast as:
subject to:
Interestingly enough, the resulting optimal solution for the above problem can be shown [9] to be the same as in the previous case, namely Equations (25) and (26).The preceding discussion in Section 4.4.1 and Section 4.4.2 provided analytical solutions. However, for a number of important formulations of IC-compliant DOE, an analytical solution is not possible, and a numerical solution is needed as presented next.
4.4.3. IC-Compliant DOE Subject to Bounds on Individual Input and/or Output Variances: Numerical Solution
When upper bounds on individual input and output variances exist, DOE for IC can be cast as:
subject to:
In the above problem of Equations (31) and (32), can be parameterized in terms of a triangular matrix using Cholesky factorization as . It can be shown [9] that the resulting optimal input is:
where is zero-mean PRBS with and is the numerically-obtained optimal solution of the problem of Equations (31) and (32).
The DOE problem in Equation (31) is a non-convex one, and thus, it is not easy to find the optimal numerical solution to this problem. For example, an arbitrary initial choice of may result in a solution that is a local minimum rather than the global minimum. To avoid this problem, Darby and Nikolaou [10] suggested to include as the initial guess for the optimal solution of a D-optimal or other standard convex DOE problem.
4.5. DOE for the Identification of IC-Compliant Dynamic Models
Design of experiments discussed so far dealt with identification of IC-compliant static models. Darby and Nikolaou [10] extended the IC-relevant DOE to the case of IC-compliant dynamic model identification. Their approach is applicable to stable systems. To formulate the corresponding DOE problem, some notation and assumptions are necessary, as follows.
For stable systems, a finite-impulse response (FIR) model structure is:
where is the matrix of impulse response coefficients, with the steady-state gain matrix . These authors have shown that IC is satisfied if:
where:
and:
is an auto-correlation matrix with . Two important assumptions made in the development of the IC condition (Equation (35)) are the following.
- (a)
- The components of are not correlated with each other, i.e., , , for all time lags .
- (b)
- The auto-correlation function (equivalently, frequency spectrum) is the same for all , i.e., .
Using the above notations, DOE for identification of an IC-compliant dynamic model can be cast as:
subject to constraints as discussed before, e.g., a bound on the total variance of inputs and outputs, Equation (24), or bounds on individual input and/or output variances, Equation (32). Cholesky parametrization of as is used again, as above.
The optimal solution to Equation (39) can be obtained numerically in the same manner as that obtained for DOE for the steady-state model identification discussed above. The problem associated with non-convex optimization (Equation (39)) can be addressed as discussed above.
4.6. DOE for Identification of Partially-Known IC-Compliant Models
It is intuitively expected that incorporating partial knowledge about a system in DOE may yield a desired IC-compliant model in reduced experimentation time. This intuition is indeed correct, as established rigorously by Panjwani and Nikolaou [11].
Partial knowledge about a system may be available in the form of constraints on the parameters of the model of that system. Such constraints may include linear or nonlinear constraints on elements of a steady-state gain matrix or similar constraints on a full dynamic model. We will focus here on linear equality constraints on elements of the steady-state gain matrix of a system. For example, for inputs known to have no effect on outputs, the associated elements of a gain matrix are exactly zero. As another example, relations between individual elements are known at the outset from fundamental balance equations.
From a mathematical viewpoint, we use different techniques for DOE subject to two different kinds of model parameter constraints that capture partial knowledge, namely for constraints involving a single row or multiple rows of a steady-state gain matrix. The corresponding DOE problems subject to these constraints are discussed next.
4.6.1. DOE for the Identification of an IC-Compliant Model Subject to Linear Equality Constraints on Each Row of the Steady-State Gain Matrix
A system with steady-state gain matrix may be partially known before an experiment is conducted, if for each row of , there are linear equalities of the form:
where , , with equal to the number of equality constraints for a given row, . Panjwani and Nikolaou [11] have shown that a model identified via least squares subject to the constraints in Equation (40) satisfies IC if:
where , and is the information matrix, which can be expressed in terms of the input covariance matrix as shown in Appendix B.
Based on Equation (41), DOE for IC when a static model is identified given partial knowledge (Equation (40)) can be cast as:
subject to constraints as discussed before, e.g., a bound on the total variance of inputs and outputs, Equation (24), or bounds on individual input and/or output variances, Equation (32). Cholesky parametrization of as is used again, similar to previous cases.
4.6.2. DOE for the Identification of an IC-Compliant Model Subject to Linear Equality Constraints Involving Multiple Rows of the Steady-State Gain Matrix
A system with steady-state gain matrix may be partially known before an experiment is conducted, if all rows of , stacked as a single vector , satisfy linear equalities of the form:
where , , with equal to the total number of linear equality constraints. Panjwani and Nikolaou [11] have shown that a static model for the system identified via least squares subject to the constraints in Equation (43) satisfies IC if:
where , , is the largest eigenvalue of the matrix and is the information matrix, which can be expressed in terms of the input covariance matrix as shown in Appendix C.
Based on Equation (44), DOE for IC when a static model is identified given partial knowledge (Equation (43)) can be cast as:
subject to constraints as discussed before, e.g., a bound on the total variance of inputs and outputs, Equation (24), or bounds on individual input and/or output variances, Equation (32). Cholesky parametrization of as is used again, similar to previous cases.
4.6.3. Numerical Solution to the DOE Problem for the Identification of an IC-Compliant Model of a Partially-Known System
The resulting optimal input for DOE framed in Equation (42) (or Equation (45)) is:
where is zero-mean PRBS with and is the numerically-obtained optimal solution of the problem of Equation 42 (or Equation (45)) subject to constraints on the input and output of the form in Equation (24) or (32).
Again, as discussed above, the problem is associated with non-convex optimization (Equations (42) and (45)).
4.7. Overview of DOE for the Identification of IC-Compliant Models
A step-by-step summary for obtaining the results for various DOEs discussed above using an adaptive approach is provided in Box 2 below.
Box 2. Adaptive DOE for identification of IC-compliant models.
- Obtain a preliminary model estimate with steady-state gain matrix , from input-output data using standard PRBS inputs for limited time.
- Based on , solve the minimization problem associated with the relevant DOE subject to input and/or output constraints, as follows.
- Equations (31) and (32) for identification of a steady-state multivariable model.
- Equations (32) and (39) for identification of a dynamic multivariable model.
- Equations (42) and (40) (or (45) and (43)) for identification of a multivariable model of a partially-known system.
- Implement the inputs determined in Step 2 for limited time, and collect input-output data, to update .
- If the updated model does not satisfy IC, i.e., Equation (30) for Case a, Equation (35) for Case b and Equation (41) (or (44)) for Case c, respectively, go to Step 2. Else, stop.
4.8. Illustrations of IC-Relevant DOE via Computer Simulations
The IC-optimal designs presented above will be illustrated next via computer simulations on various systems.
4.8.1. DOE for Minimization of Total Input/Output Variance Subject to IC
DOE targeting IC subject to total input plus output variance (Equations (29) and (30)) was simulated on a high-purity distillation column [41] with steady-state gain matrix:
and condition number , for the cases and in Equation (29). The resulting optimal inputs for this DOE were obtained analytically, via Equations (25) and (27) for and via Equations(25) and (28) for . Figure 7 and Figure 8 show the results of a typical simulated experiment following the preceding DOE. One hundred such experiments were simulated. Table 1 shows averages of correlation coefficients, and , and information content, , over all 100 experiments. As expected, the two cases (for and for ) differ in and most notably in and , as anticipated by the theory. Additional details can be found in Darby and Nikolaou [9].
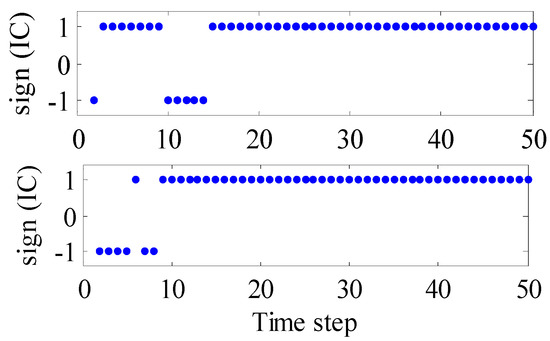
Figure 7.
Satisfaction (+1) or violation (−1) of IC for the identified model when (top row) and (bottom row). Integral controllability (IC) checked via Equation (11) for both cases.
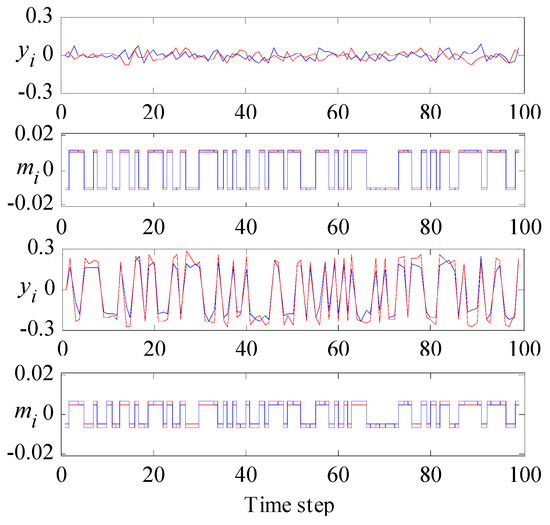
Figure 8.
Outputs, , and inputs, (), for IC optimal design when (top two rows) and (bottom two rows).

Table 1.
100-experiment averages for the design via Equation (26) on ; .
4.8.2. DOE for IC Subject to Constraints on Individual Input and/or Output Variances
DOE targeting IC subject to individual input and/or output variance constraints (Equations (31) and (32)) was simulated on two systems, namely an ill-conditioned distillation column [41] and a well-conditioned distillation column [42], described by steady-state gain matrices:
with condition number and , respectively. Optimal inputs for these two DOEs were obtained numerically. To show the efficiency of the IC-optimal design over other designs, DOEs with objectives different from IC were also simulated on the above two systems. These DOEs along with their objective functions and constraints are summarized in Table 2. Among these, Dmax is a convex constrained D-optimal design that targets maximization of . PRBSmax and are similar to Dmax, except that they design PRBS input and rotated PRBS input , respectively.

Table 2.
Summary of designs tested on and .
Relevant simulation results for designs summarized in Table 2 are provided in Table 3 for and . Important observations are derived from significant differences in values of , and input and output correlations as summarized below.

Table 3.
Summary of results for experiment designs on and . Corresponding variance value at its bound (active constraint in Equation (32)) is shown in bold and italics. Notation: , , : covariance matrices of , , , respectively; ; : Equation (31).
- IC-optimal rotated inputs, , are not necessarily uncorrelated as indicated by values for ICmin design.
- IC-optimal inputs, , are not necessarily highly correlated as indicated by Case #9 in Table 3.
- The optimal ratio, , may be quite smaller or larger than for ICmin design.
- Large values of and small values of for PRBSmax design indicate that PRBS inputs are neither IC-optimal nor D-optimal.
- The respective values of and for ICmin and Dmax designs are quite close to each other. These values indicate a trade-off between ICmin and Dmax designs for and , supporting the claim that ICmin design sacrifices some accuracy in parameter estimates (lower value of for ICmin compared to that for Dmax) to achieve IC.
Additional details can be found in Darby and Nikolaou [9].
4.8.3. DOE for the Identification of IC-Compliant Dynamic Models Subject to Constraints on Individual Input and/or Output Variances
DOE targeting IC directly linked to a dynamic model to be identified subject to constraints on individual input and output variances (Equations (32) and (39)) was simulated on three systems, namely,
- (a)
- a ill-conditioned, high-purity distillation column;
- (b)
- a well-conditioned distillation column;
- (c)
- a fluidized catalytic cracking (FCC) reactor-regenerator system.
Variants of D-optimal DOE were also simulated on the above systems for comparison purposes. All DOEs are enumerated below.
- (D1)
- Constrained D-optimal DOE, which seeks to maximize using a convex objective function, .
- (D2)
- Constrained IC-optimal DOE, which seeks to minimize (Equation (39)).
- (D3)
- DOE based on generalized binary noise (GBN) input [43], , with only adjusted to satisfy input and/or output constraints, Equation (32). (this design for model identification is widely followed in industry).
- (D4)
- DOE based on GBN rotated input , with only adjusted to satisfy input and/or output constraints, Equation (32).
Solutions (i.e., ) for all DOE problems posed above were obtained numerically.
The three cases are discussed next.
Case 1: ill-conditioned, high-purity distillation column:
DOEs D1–D4 were simulated on an ill-conditioned, high-purity distillation column [44] described by:
with condition number . The following constraints on outputs were placed.
Relevant results for DOEs D1–D4 are provided in Table 4. The values of in Table 4 indicate the time required by various designs to achieve IC (this follows from Equation (35); . Thus, the time required by uncorrelated GBN input design D3 to achieve IC is about 3100-times that required by designs that use correlated inputs, i.e., D1, D2 and D4. Furthermore, designs D1, D2 and D4 produce highly correlated outputs, whereas design D3 produces completely uncorrelated outputs (indicated by values in Table 4).

Table 4.
Skogestad and Morari column, . Results for different experiment designs. Generalized binary noise (GBN) signals in D3 and D4 are based on switching probability, , and mean switching time, . Active constraints are shown in bold italics.
Additional details can be found in Darby and Nikolaou [10].
Case 2: well-conditioned distillation column:
DOEs D1–D4 were simulated on a well-conditioned distillation column [42] described by:
with steady-state condition number . The following constraints on outputs were placed.
Relevant results for DOEs D1–D4 are provided in Table 5. The values of β in Table 5 indicate that the time required by uncorrelated GBN input design D3 to achieve IC is about six-times that required by designs that use correlated inputs, i.e., D1, D2 and D4. Furthermore, designs D1, D2 and D4 produce correlated outputs, whereas design D3 produces completely uncorrelated outputs (indicated by values in Table 5).

Table 5.
Wood and Berry column, . Results for different experiment designs. GBN signals in D3 and D4 are based on switching probability, , and mean switching time, . Active constraints are shown in bold italics.
Additional details can be found in Darby and Nikolaou [10].
Case 3: fluidized catalytic cracking (FCC) reactor-regenerator:
DOEs D1–D3 were simulated on a FCC reactor-regenerator system [10] having a steady-state gain matrix:
with condition number . The full state-space model of this system is provided in Darby [45]. The following constraints on outputs and inputs were placed.
Relevant results for DOEs D1–D3 are provided in Table 6. Again, values of β in Table 6 indicate that it takes about 2.5-times longer to achieve IC in a model identified from experimental data following designs D1 and D2 rather than the uncorrelated GBN input design D3. Furthermore, designs D1 and D2 produce fairly correlated outputs, whereas design D3 produces completely uncorrelated outputs (indicated by values in Table 6).

Table 6.
FCC reactor-regenerator system. Results for different experiment designs. GBN signals in D3 are based on switching probability, , and mean switching time, . Active constraints are shown in bold italics.
Additional details can be found in Darby and Nikolaou [10].
4.8.4. DOE for the Identification of IC-Compliant Models of Partially-Known Systems
DOE targeting IC using Equation (42) (or (45)) and following constraints as in Equation (40) (or (43)) were simulated on two partially known systems,
- (a)
- fluidized catalytic cracking (FCC) reactor-regenerator system;
- (b)
- two-stage absorber, respectively,
subject to constraints on individual input and output variances (Equation (32)). Variants of D-optimal DOE were also simulated on the above systems for comparison purposes. All of these DOEs are enumerated below.
- (D1)
- IC-optimal DOE based on Equation (42) (or (45)), taking partial knowledge into account, Equation (40) (or (43)), and subject to input-output variance constraints, Equation (32).
- (D2)
- IC-optimal DOE based on Equation (22), without taking partial knowledge into account, and subject to input-output variance constraints, Equation (32).
- (D3)
- D-optimal DOE based on:taking partial knowledge into account, Equation (40) (or (43)), and subject to input-output variance constraints, Equation (32).
- (D4)
- D-optimal DOE based on:without taking partial knowledge into account, and subject to input-output variance constraints, Equation (32).
Solutions for all DOE problems posed above were obtained numerically.
The two cases mentioned above are discussed next.
Case 1: FCC reactor-regenerator system with partial knowledge available in terms of linear equality constraints on individual rows of :
DOEs D1–D4 were simulated on a FCC reactor-regenerator system corresponding to the steady-state gain matrix:
with condition number . The following constraints on outputs and inputs were placed.
For this system, some of the elements in are known to be exactly zero (Equation (57) above), and therefore linear equality constraints of the form Equation (40) can be formulated for DOE. Thus, designs D1 and D3, which use partial knowledge, are based on Equation (42).
Figure 9 provides a comparison of designs D1–D4 in terms of time required for satisfaction of IC. Clearly, designs D1 and D3, which take into account partial knowledge, produce models that satisfy IC much earlier than designs D2 and D4, which do not take partial knowledge into account.
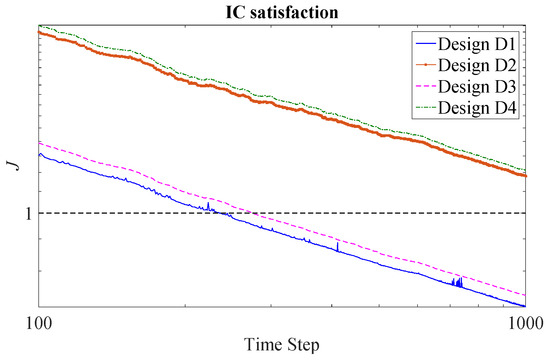
Figure 9.
Identification time required for satisfaction of IC for an FCC reactor-regenerator system when inputs are produced from designs D1–D4. (Equation (41)) for D1 and D3; (Equation (21)) for D2 and D4.
Furthermore, Table 7 and Table 8 provide values of design-relevant parameters, from which the following important observations are made.

Table 7.
Characterization of inputs and outputs for designs D1–D4 for a FCC unit; active constraints are in bold.

Table 8.
Input and output correlations matrices for designs D1–D4 for a FCC unit.
- Since in Equation (42) is the information matrix, and larger values of , indicate more accurate parameter estimates. The value of for D-optimal design D4, which specifically targets maximization of via maximization of , is larger than for design D2, which is IC-optimal. This shows that earlier IC satisfaction by IC-optimal designs is achieved at the cost of loss in accuracy of parameter estimates.
- The input and output pairs in experiments based on all of the above designs range from highly correlated to fairly uncorrelated. Therefore, the commonly used rule of thumb for control-relevant DOE to produce uncorrelated outputs is not always applicable when constraints are present.
Additional details can be found in Panjwani and Nikolaou [11].
Case 2: two-stage absorber with partial knowledge available in terms of linear equality constraints involving multiple rows of :
DOEs D1–D4 were simulated on a two-stage absorber described by the steady-state gain matrix:
The following constraints on outputs and inputs were placed.
For this system, partial knowledge is available in the form of relationships involving both rows as:
Therefore, designs D1 and D3, which use partial knowledge, are based on Equation (45).
Figure 10 provides a comparison of designs D1–D4 in terms of time required for satisfaction of IC. Again, similar to Case 1, designs D1 and D3, which take partial knowledge into account, satisfy IC much earlier than the other two designs, D2 and D4, which do not take partial knowledge into account. A close agreement is also observed between IC-optimal design D1 and D-optimal design D3 from their overlapping profiles, which can be investigated further in future research.
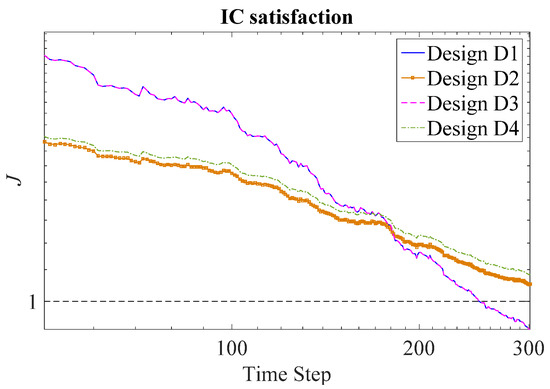
Figure 10.
Identification time required for satisfaction of IC for a two-stage absorber when inputs are produced from designs D1–D4. (Equation (44)) for D1 and D3; (Equation (21)) for D2 and D4.
Furthermore, as in Case 1, it can be observed from Table 9 that the value of (a measure of parameter estimation accuracy) is larger for design D4 than for design D2. This, again, illustrates the fact that earlier IC satisfaction by IC-optimal designs is achieved at the cost of loss in the accuracy of parameter estimates.

Table 9.
Characterization of inputs and outputs designs D1–D4 for a two-stage absorber; active constraints are in bold.
Additional details can be found in Panjwani and Nikolaou [11].
4.9. Summary: DOE for IC-Compliant Model Identification
To be useful in robust model-based control, a model can benefit from satisfaction of the IC condition. To identify such a model from experimental data, the IC condition must be directly incorporated into DOE. A number of DOE problems for the identification of IC-compliant models have been formulated and solved in recent years, as summarized here. These problems cover a number of cases and vary in rigor and complexity. Optimal inputs from these DOE problems can be obtained analytically or numerically, depending on the kind of constraints imposed on the inputs and outputs of the process to be identified.
5. Conclusions
In this paper, we summarized the formulation and solution of several DOE problems for the identification of models directly useful in model-based controller design. Specifically, the DOE problems focused on addressing two important control-relevant modeling issues, namely accurate estimation of multivariable model order and identification of an IC-compliant multivariable model.
For accurate multivariable model order estimation, a crucial first step before model parameter estimation, an adaptive DOE was presented. This DOE results in appropriately proportioned rotated PRBS inputs and is particularly useful for identification of ill-conditioned systems for which data from ordinary identification experiments with PRBS inputs fail to estimate model-order accurately.
For the identification of an IC-compliant multivariable model, a number of DOEs was presented that directly incorporated IC in the formulation of the problem. These IC-optimal designs address a number of cases of practical importance, depending on the kind of input and/or output constraints to be satisfied during an experiment and on prior knowledge about a process available before experimentation.
Solutions of corresponding DOE problems can be obtained either analytically or numerically, depending on the problem formulation for each case.
6. Future Work
Additional features to the DOE problems presented in this paper can be investigated, including the following.
- Design of rotated PRBS inputs using a multivariable dynamic model rather than steady-state gain matrix for adaptive rotated DOE (cf. Section 3.8).
- Extension of the adaptive DOE framework to incorporate various chance constraints on outputs (cf. Section 3.8).
- Extension of IC-optimal design framework to incorporate constraints on inputs and/or outputs in the time domain (cf. Section 4.4, Section 4.5 and Section 4.6).
- Extend the MPCI framework of simultaneous model predictive control and identification [46] by incorporating the IC condition directly in the closed-loop objective function.
- Investigate the underlying theoretical reasons for agreement or disagreement between IC-optimal and D-optimal designs (cf. Section 4.4, Section 4.5 and Section 4.6).
- Extension of the IC-optimal DOE framework to other dynamic model forms such as state-space identified by the prediction-error or and SI method (cf. Section 4.5).
- Extension of IC-optimal design framework to incorporate partial knowledge in the form of inequality constraints (cf. Section 4.6).
- Extension of IC-optimal DOE to other kinds of IC, such as decentralized integral controllability (DIC) [39].
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Matrices in Equation (2) are defined as follows:
with:
and the indices in Equations (A1), (A3), (A6) and (A7) being any integers that satisfy:
where is the length of experiment. The pseudoinverse of a matrix , which appears in Equation (A2), is defined as:
Appendix B
Matrix in Equation (41) appears in uncertainty ellipsoid of as:
where is the least squares estimate of in presence of linear equality constraint of the form in Equation (40) and is equal to:
Matrices that appear in Equations (A10) and (A11) are defined as follows:
is the unconstrained least-squares estimate of ,
In Equation (A16), is the diagonal matrix of non-zero singular values, and is the matrix of corresponding singular vectors in the singular value decomposition of the matrix:
In terms of the input covariance matrix and total experimentation time , Equation (A17) can be rewritten as:
Appendix C
Matrix in Equation (44) appears in uncertainty ellipsoid of as:
where is the least squares estimate of in the presence of the linear equality constraint of the form in Equation (43) and is equal to:
Matrices that appear in Equations (A19) and (A20) are defined as follows:
is the unconstrained least-squares estimate of ,
In Equation (A26), , are the diagonal matrix of non-zero singular values and matrix of corresponding singular vectors, respectively, obtained from singular value decomposition of the symmetric matrix:
with the identity matrix of dimensions .
Equation (A27) can be rewritten in terms of the input covariance matrix and total experimentation time as:
References
- Misra, P.; Nikolaou, M. Input design for model order determination in subspace identification. AIChE J. 2003, 49, 2124–2132. [Google Scholar] [CrossRef]
- Misra, S.; Nikolaou, M. Adaptive design of experiments for model order estimation in subspace identification. Comput. Chem. Eng. 2017, 100, 119–138. [Google Scholar] [CrossRef]
- Micchi, A.; Pannocchia, G. Comparison of input signals in subspace identification of multivariable ill-conditioned systems. J. Process Control 2008, 18, 582–593. [Google Scholar] [CrossRef]
- Featherstone, A.P.; Braatz, R.D. Input Design for Large-Scale Sheet and Film Processes. Ind. Eng. Chem. Res. 1998, 37, 449–454. [Google Scholar] [CrossRef]
- Bruwer, M.J.; MacGregor, J.F. Robust multi-variable identification: Optimal experimental design with constraints. J. Process Control 2006, 16, 581–600. [Google Scholar] [CrossRef]
- Zhu, Y.; Stec, P. Simple control-relevant identification test methods for a class of ill-conditioned processes. J. Process Control 2006, 16, 1113–1120. [Google Scholar] [CrossRef]
- Zhan, Q.; Li, T.; Georgakis, C. Steady state optimal test signal design for multivariable model based control. Ind. Eng. Chem. Res. 2006, 45, 8514–8527. [Google Scholar] [CrossRef]
- Li, T.; Georgakis, C. Dynamic input signal design for the identification of constrained systems. J. Process Control 2008, 18, 332–346. [Google Scholar] [CrossRef]
- Darby, M.L.; Nikolaou, M. Multivariable system identification for integral controllability. Automatica 2009, 45, 2194–2204. [Google Scholar] [CrossRef]
- Darby, M.L.; Nikolaou, M. Identification test design for multivariable model-based control: An industrial perspective. Control Eng. Pract. 2014, 22, 165–180. [Google Scholar] [CrossRef]
- Panjwani, S.; Nikolaou, M. Experiment design for control-relevant identification of partially known stable multivariable systems. AIChE J. 2016, 62, 2986–3001. [Google Scholar] [CrossRef]
- Häggblom, K.E. On experiment design for identification of Ill-conditioned systems. IFAC Proc. Vol. (IFAC-PapersOnline). 2014, 47, 1428–1433. [Google Scholar] [CrossRef]
- Featherstone, A.P.; Braatz, R.D. Integrated Robust Identification and Control of Large-Scale Processes. Ind. Eng. Chem. Res. 1998, 37, 97–106. [Google Scholar] [CrossRef]
- Vaillant, O.R.; Kuramoto, A.S.R.; Garcia, C. Effectiveness of signal excitation design methods for identification of ill-conditioned and highly interactive processes. Ind. Eng. Chem. Res. 2013, 52, 5120–5135. [Google Scholar] [CrossRef]
- Aghito, M.; Bjørkevoll, K.S.; Nybø, R.; Eaton, A.; Hedengren, J. Automatic Model Calibration for Drilling Automation. In SPE Bergen One Day Seminar; Society of Petroleum Engineers: Bergen, Norway, 2017. [Google Scholar]
- Patwardhan, R.S.; Goapluni, R.B. A moving horizon approach to input design for closed loop identification. J. Process Control 2014, 24, 188–202. [Google Scholar] [CrossRef]
- Meidanshahi, V.; Corbett, B.; Adams, T.A.; Mhaskar, P. Subspace model identification and model predictive control based cost analysis of a semicontinuous distillation process. Comput. Chem. Eng. 2017, 103, 39–57. [Google Scholar] [CrossRef]
- Ashari, A.E.; Aevel, L. Auxiliary input design for stochastic subspace-based structural damage detection. Mech. Syst. Signal Process. 2013, 34, 241–258. [Google Scholar] [CrossRef]
- Fisher, R.A. The Design of Experiments, 9th ed.; Macmillan Pub Co.: Landon, UK, 1971. [Google Scholar]
- Montgomery, D.C. Design and Analysis of Experiments, 8th ed.; John Wiley & Sons, Inc.: Somerset, NJ, USA, 2013. [Google Scholar]
- Box, G.E. The Design and Analysis of Industrial Experiments, 2nd ed.; ICI-Longman Group: London, UK, 1956. [Google Scholar]
- Hicks, C.R.; Turner, K.V. Fundamental Concepts in the Design of Experiments, 5th ed.; Oxford University Press: Oxford, UK, 1999. [Google Scholar]
- Cox, D.R.; Reid, N. The Theory of the Design of Experiments; Chapman and Hall/CRC: Boca Raton, FL, USA, 2000. [Google Scholar]
- Pukelsheim, F. Optimal Design of Experiments; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2006. [Google Scholar]
- Mehra, R.K. Optimal Input signals for Parameter Estimation in Dynamic Systems—Survey and New Results. IEEE Trans. Autom. Control 1974, 19, 753–768. [Google Scholar] [CrossRef]
- Ljung, L. System Identification: Theory for the User; Prentice-Hall, Inc.: Saddle River, NJ, USA, 1987; pp. 69–106. [Google Scholar]
- Soderstrom, T.; Ttoica, P. System Identification; Prentice Hall International (UK) Ltd.: Belfast, UK, 1989. [Google Scholar]
- Astrom, K.J. Maximum likelihood and prediction error methods. Automatica 1980, 16, 551–574. [Google Scholar] [CrossRef]
- Van Overschee, P.; De Moor, B. Subspace Identification for Linear Systems: Theory—Implementation—Applications; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1996. [Google Scholar]
- Larimore, W.E. Cannonical Variate Analysis in Identification, Filtering, and Adaptive-control. In Proceedings of the 29th IEEE Conference on Decision and Control, Honolulu, HI, USA, 5–7 December 1990; Volumes 1–6, pp. 596–604. [Google Scholar]
- Van Overschee, P.; De Moor, B. N4SID: Subspace algorithms for the identification of combined deterministic-stochastic systems. Automatica 1994, 30, 75–93. [Google Scholar] [CrossRef]
- Verhaegen, M. Identification of the deterministic part of MIMO state space models given in innovations form from input-output data. Automatica 1994, 30, 61–74. [Google Scholar] [CrossRef]
- Yanai, H.; Takeuchi, K.; Takane, Y. Projection Matrices, Generalized Inverse Matrices, and Singular Value Decomposition; Springer: New York, NY, USA, 2011. [Google Scholar]
- Van Overschee, P.; De Moor, B. A unifying theorem for three subspace system identification algorithms. Automatica 1995, 31, 1853–1864. [Google Scholar] [CrossRef]
- Shi, R.; MacGregor, J.F. Modeling of dynamic systems using latent variable and subspace methods. J. Chemom. 2000, 14, 423–439. [Google Scholar] [CrossRef]
- Koung, C.W.; Macgregor, J.F. Design of Identification Experiments for Robust-Control—A Geometric Approach for Bivariate Processes. Ind. Eng. Chem. Res. 1993, 32, 1658–1666. [Google Scholar] [CrossRef]
- Schaub, H.; Tsiotras, P.; Junkins, J.L. Principal Rotation Representations of Proper Nxn Orthogonal Matrices. Int. J. Eng. Sci. 1995, 33, 2277–2295. [Google Scholar] [CrossRef]
- Garcia, C.E.; Morari, M. Internal Model Control. 2. Design Procedure For Multivariable Systems. Ind. Eng. Chem. Process Des. Dev. 1985, 24, 472–484. [Google Scholar] [CrossRef]
- Morari, M.; Zafiriou, E. Robust Process Control; Prentice Hall, Inc.: Saddle River, NJ, USA, 1989. [Google Scholar]
- Goodwin, G.C.; Payne, R.L. Dynamic System Identification: Experimental Design and Data Analysis; Academic Press, Inc.: Amsterdam, The Netherlands, 1977. [Google Scholar]
- Skogestad, S.; Morari, M. Control configuration selection for distillation columns. AIChE J. 1987, 33, 1620–1635. [Google Scholar] [CrossRef]
- Wood, R.K.; Berry, M.W. Terminal composition control of a binary distillation column. Chem. Eng. Sci. 1973, 28, 1707–1717. [Google Scholar] [CrossRef]
- Tulleken, H.J. Generalized binary noise test-signal concept for improved identification-experiment design. Automatica 1990, 26, 37–49. [Google Scholar] [CrossRef]
- Skogestad, S.; Morari, M.; Doyles, J.C. Robust Control of Ill-Conditioned Plants: High-Purity Distillation. IEEE Trans. Autom. Control 1988, 33, 1092–1105. [Google Scholar] [CrossRef]
- Darby, M.L. Studies of online optimization methods for experimental test design and state estimation. In Chemical and Biomolecular Engineering; University of Houston: Houston, TX, USA, 2008; pp. 152–153. [Google Scholar]
- Genceli, H.; Nikolaou, M. New Approach to Constrained Predictive Control with Simultaneous Model Identification. AIChE J. 1996, 42, 2857–2866. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).