Computer-Aided Framework for the Design of Freeze-Drying Cycles: Optimization of the Operating Conditions of the Primary Drying Stage

Abstract

This paper deals with the freeze-drying process and, in particular, with the optimization of the operating conditions of the primary drying stage. When designing a freeze-drying cycle, process control aims at obtaining the values of the operating conditions (temperature of the heating fluid and pressure in the drying chamber) resulting in a product temperature lower than the limit value of the product, and in the shortest drying time. This is particularly challenging, mainly due to the intrinsic nonlinearity of the system. In this framework, deep process knowledge is required for deriving a suitable process dynamic model that can be used to calculate the design space for the primary drying stage. The design space can then be used to properly design (and optimize) the process, preserving product quality. The case of a product whose dried layer resistance, one of the key model parameters, is affected by the operating conditions is addressed in this paper, and a simple and effective method to calculate the design space in this case is presented and discussed.

1. Introduction

The freeze-drying process is commonly used to remove water (or, more rarely, an organic solvent) from a product, aiming at increasing its shelf life. At first, the product is loaded onto the shelves of the chamber of the freeze-dryer and, then, product temperature is decreased, usually to values ranging from −40 to −50 °C, in order to freeze the water. A cold fluid flows inside the shelves to get this result. Afterwards, the temperature of the shelves is increased and the pressure in the drying chamber is lowered in such a way that ice sublimation occurs (primary drying). The drying chamber is connected to a condenser, where the solvent vapor desublimates onto cold surfaces. A vacuum pump is used to get the desired level of vacuum, and it frequently operates with a “controlled leakage” of an inert gas in the chamber to get a better pressure control. Finally, when the ice sublimation is completed, it is necessary to remove the water bound to the dried product (secondary drying): product temperature is increased to cause water desorption, thus obtaining the target value of residual humidity in the final product [1,2,3,4,5]. The process is particularly indicated for water removal in case of products that are damaged by the higher temperatures of other drying processes, and it is widespread in the pharmaceutical industry where the high value of the manufactured products justifies the cost (and the duration) of a freeze-drying process.

During a freeze-drying process care must be paid to keep product temperature below a limit value that is a characteristic of the product being processed. The goal is to avoid product degradation, in particular in case of pharmaceutical and biopharmaceutical formulations, and also the collapse (or the shrinkage) of the dried product (the so called “cake”) in case aqueous solutions containing amorphous products are processed, as this threaten the elegance of the cake and the product could show a higher reconstitution time and a higher amount of residual humidity. In case aqueous solutions containing crystalline products are processed, the limit value is the eutectic temperature, in order to prevent product melting [6,7,8,9,10,11,12,13,14].

Therefore, a careful process control is required to set the values of the operating conditions of the freeze-drying process, i.e., the temperature of the heating fluid (T_fluid) and the pressure in the drying chamber (P_c). This is particularly true in the primary drying stage, which is the most risky part of the process because of the lower value of the limit temperature (due to the higher water content). In this framework mathematical modeling can support freeze-drying practitioners, avoiding the extended experimental investigation based on trial-and-error approaches. For example, mathematical modeling (coupled with few experiments) can be used to calculate the design space of the process, i.e., the “the multidimensional combination of input variables and process parameters that have been demonstrated to provide assurance of quality” as defined in Ref. [15]. Using mathematical modeling product quality can be obtained by design (and it is no longer tested at the end of the manufacturing process), following the guidelines of the Guidance for Industry PAT issued by the US-FDA in 2004 and encouraging the pharmaceutical industry to take advantage of the various Process Analytical Technologies (PAT) that can be used to monitor a manufacturing process, thus moving from a quality-by-testing to a quality-by-design approach.

In order to assess the effect of T_fluid and P_c on product temperature in the primary drying stage a one-dimensional model can be used [16,17,18,19,20,21]. The heat flux to the product (J_q) is proportional to the temperature difference between the heating fluid and the product at the bottom of the container (T_B):

$$J_q=K_v\left(T_{fluid}-T_B\right)$$

(1)

while the vapor flux from the interface of sublimation to the drying chamber (J_w) is proportional to the difference between the vapor pressure at the interface of sublimation (p_w,i) and the water vapor partial pressure in the drying chamber (p_w,c):

$$J_w=\frac{1}{R_p}\left(p_{w,i}-p_{w,c}\right)$$

(2)

where p_w,i is a function of product temperature at the interface of sublimation (T_i), and p_w,c can be considered equal to P_c as the composition of the gas in the chamber is about 100% water vapor.

In Equations (1) and (2) two parameters appear: K_v, the overall heat transfer coefficient between the heating fluid and the product in the container, and R_p, the resistance of the dried product to vapor flux. Various experimental methods were developed in the past to evaluate K_v and R_p, e.g., the test of pressure rise: the drying chamber is isolated from the condenser for a short time interval (usually ranging from 5–10 to 30 s) closing a valve in the duct connecting the chamber to the condenser and the pressure variation in the chamber, due to water vapor accumulation, is measured. Then, model parameters (K_v and R_p), as well as other variables like product temperature and the residual amount of ice, are estimated looking for the best fit between the values of chamber pressure measured and those calculated using a mathematical model of the process [22,23,24,25,26,27]. As an alternative to this method, it is possible to use Tunable Diode Laser Absorption Spectroscopy (TDLAS) to estimate K_v and R_p, beside product temperature and the residual amount of ice [28,29,30]. Moreover, a soft-sensor based on the measurement of product temperature, on a mathematical model of the process and on the Extended Kalman Filter algorithm was also proposed to get the values of K_v and R_p [31,32,33,34,35,36,37].

The mass balance for the dried cake allows describing the evolution of the thickness of the dried cake (L_dried):

$$\frac{d{L}_{dried}}{dt}=\frac{1}{{\rho }_{frozen}-{\rho }_{dried}}{J}_w\hspace{1em}{ L_{dried}|}_{t=0}=0$$

(3)

where ρ_frozen and ρ_dried are, respectively, the density of the frozen product and the effective density of the dried cake. As already described in Velardi and Barresi [21] the energy balance at the interface of sublimation gives:

$$J_q=\Delta H_s{J}_w$$

(4)

where ∆H_s is the heat of sublimation. Substituting Equations (1) and (2) into Equation (4), we obtain an expression that relates the temperature of the product at the interface of sublimation to that close to the bottom of the container. This last temperature (T_B) can then be calculated from the energy balance for the frozen product, assuming steady-state conditions:

$$T_B=T_{fluid}-\frac{1}{K_v}{\left(\frac{1}{K_v}+\frac{L_{frozen}}{k_{frozen}}\right)}^{-1}\left(T_{fluid}-T_i\right)$$

(5)

where L_frozen is the thickness of the frozen product, whose thermal conductivity is k_frozen. By solving Equations (3)–(5) it is possible to calculate the evolution of the product and, thus, to evaluate if the selected values of T_fluid and P_c belong to the design space (or not), and also the drying time.

Refs. [38,39,40,41,42] shows various methods, using simple one-dimensional models, to calculate the design space of the primary drying stage of a freeze-drying process. This paper aims at developing a model-based approach to calculate the design space of the primary drying in case the product processed is characterized by a dried cake resistance dependent on the operating conditions of the process. This is a particularly challenging task, never addressed previously in the literature, although there are many formulations characterized by such behavior of R_p. The paper is thus organized as follows: at first the method used to describe the dependence of R_p on the operating conditions is described. Then, details of the experimental investigations required to identify model parameters are given, as well as the application of this method to the calculation of the design space. Finally, results are presented and discussed, proving the effectiveness of the proposed method.

2. Materials and Methods

2.1. Modeling of the Effect of the Operating Conditions on Dried Cake Resistance

The sublimation flux in the dried product is due to Knudsen diffusion (free molecular flow) as the Knudsen number is usually greater than 3 [43]. Therefore, the sublimation flux can be expressed by means of the following equation:

$$J_w=D_e\frac{c_{w,i}-c_{w,c}}{L_{dried}}$$

(6)

where D_e is the effective Knudsen diffusivity and c_w,i and c_w,c are, respectively, the water vapor concentrations at the interface of sublimation and in the drying chamber. Using the ideal gas law, Equation (6) can be written as:

$$J_w=\frac{M_w{D}_e}{RT}\frac{p_{w,i}-p_{w,c}}{L_{dried}}$$

(7)

where M_w is the water molecular weight, R is the ideal gas constant and T is the “mean” temperature of the dried product. With this respect it has to be pointed out that T usually ranges in a narrow interval, e.g., from −35 to −20 °C, i.e., from 238 to 253 K: this means that the percentage effect of a variation of T on J_w is small. As T can be hardly known, it can be replaced by T_i without significantly affecting the accuracy of the results. Taking into account Equation (2) it comes that:

$$R_p=\frac{R{T}_i}{M_w{D}_e}{L}_{dried}$$

(8)

The effective diffusivity is related to the Knudsen diffusivity (D_k) by means of the following equation:

$$D_e=\frac{\epsilon }{\tau }{D}_k$$

(9)

where ε is the void fraction and τ is the tortuosity of the solid matrix. The Knudsen diffusivity is a function of the effective pore radius (r_e) and of the dried cake temperature (assumed equal to T_i in these calculations, as previously discussed) [43]:

$$D_k=K{r}_e{T}_i^{0.5}$$

(10)

where K is equal to 22.9 m/s K^0.5. Replacing Equation (10) into Equation (9) we get:

$$D_e=\frac{r_e}{\tau }K\epsilon T_i^{0.5}$$

(11)

The structure of the dried cake can be uniform, and in this case r_e/τ is not a function of the axial position. In this case, Equation (8) becomes:

$$R_p=\frac{R{T}_i^{0.5}}{M_w\frac{r_e}{\tau }K\epsilon }{L}_{dried}$$

(12)

corresponding to a linear dependence of R_p on L_dried. In various cases (e.g., with sucrose-based formulations), the structure of the cake is not uniform, and the following equation was demonstrated to be effective to fit the experimental values of dried cake resistance vs. cake thickness in a wide range of formulations and operating conditions [30]:

$$\frac{r_e}{\tau }=a_0+a_1{L}_{dried}$$

(13)

In this case, Equation (8) becomes:

$$R_p=\frac{A{L}_{dried}}{1+B{L}_{dried}}$$

(14)

where:

$$A=\frac{R{T}_i^{0.5}}{a_0{M}_{w}K\epsilon }\text{, }B=\text{}\frac{a_1}{a_0}$$

(15)

A non-zero intercept is then added to previous equation, accounting for a non null resistance of the top layer, often due to the formation of a surface crust:

$$R_p=R_{p,0}+\frac{A{L}_{dried}}{1+B{L}_{dried}}$$

(16)

Finally, it has to be taken into account that not only the structure of the dried cake can vary in the axial direction, but also the operating conditions can affect cake resistance. In particular, cake resistance can vary with product temperature due to the occurrence of micro-collapse: the higher is the temperature of the product, the lower is the resistance of the cake to vapor flow [30,37]. This means that the parameters a₀ and a₁ (and, thus A and B) can change with product temperature.

2.2. Experimental Investigation

The freeze-drying of a 5% w/w sucrose solution has been investigated as this formulation is representative of those products whose R_p is significantly affected by the operating conditions. Differential Scanning Calorimetry (DSC type Q200, TA Instruments, New Castle, DE, USA) was used to detect the glass transition temperature: the samples were frozen at −60 °C and heated up to room temperature at 10 °C·min⁻¹ (the analysis was carried out in inert atmosphere). A cryo-microscope (type BX51, Olympus Europa, Hamburg, Germany; temperature controller: PE95-T95, Linkam, Scientific Instruments, Tadworth, Surrey, UK) was used to detect the collapse temperature of the dried cake.

Freeze-drying runs were carried out in a LyoBeta 25 freeze-dryer (Telstar, Terrassa, Spain), a pilot-scale equipment with a chamber of 0.2 m³ and four shelves (the total area available is 0.5 m²), with an external condenser (the maximum ice capacity is 40 kg). Controlled leakage of inert gas was used to regulate chamber pressure. The system was equipped with T type thermocouples (Tersid, Milano, Italy) and a capacitance gauge (Baratron type 626A, MKS Instruments, Andover, MA, USA).

Tubular glass vials ISO 8362-1 6R (external diameter = 16 ± 0.2 mm, wall thickness = 1 ± 0.04 mm) were used in the freeze-drying tests: they were filled in with 1.5 mL of solution containing sucrose (Riedel de Haën) and ultra-pure water as solvent (Milli-Q RG, Millipore, Billerica, MA, USA). The filling volume produced a 10-mm-thick frozen layer. Vials were placed on the shelves of the freeze-dryer according to a hexagonal arrangement (a metal frame was used to keep vials in place). In all the cycles, solutions were frozen using the standard shelf-ramp method, from room temperature to −45 °C. At the beginning of the drying, the product temperature was between −40 and −43 °C.

The pressure rise test (coupled with DPE+ algorithm) was used to estimate K_v and R_p as a function of the operating conditions [27]. In order to determine the parameters a₀ and a₁ (and, thus, A and B), the values of R_p vs. L_dried were fitted with Equation (16), thus obtaining the three parameters R_p0, A and B. Then, a₀ and a₁ were calculated using Equation (15).

A Scanning Electron Microscope (FEI, Quanta Inspect 200, Eindhoven, The Netherlands), working at 15 kV and under high vacuum, was used to assess the morphology of freeze-dried cakes; all the samples were fixed on aluminum circular stubs and sputtered with chrome.

2.3. Calculation of the Design Space

The mathematical model constituted by Equations (3) and (5) is solved for a given set of operating conditions (T_fluid and P_c) to calculate the temperature of the product at the interface of sublimation: if this temperature remains below the limit value, than the couple of values of T_fluid and P_c belongs to the design space. When performing these calculations care has to be paid to the variation of the parameters A and B describing the effect of product temperature on the resistance of the dried cake to the water vapor flux. The detailed procedure is summarized in the following:

• Selection of the minimum and maximum values of the fluid temperature (T_fluid,min and T_fluid,max) and of the pressure in the chamber (P_c,min and P_c,max) to be considered in the design space.
• Calculation of the arrays of values of T_fluid and P_c:

  $$T_{fluid}\left(k\right)=T_{fluid,min}+\left(k-1\right)\Delta T_{fluid}\hspace{1em}\text{with }k=\left[1, n_T\right]$$

  (17)

  $$P_c\left(j\right)=P_{c,\min }+\left(j-1\right)\Delta P_c\hspace{1em}\text{with }k=\left[1, n_P\right]$$

  (18)

  where ∆T_fluid and ∆P_c are, respectively, the sampling intervals for T_fluid and P_c in the design space, and n_T and n_P are the length of the two arrays:

  $$n_T=\frac{T_{fluid,max}-T_{fluid,min}}{\Delta T_{fluid}}+1,\hspace{1em}{n}_P=\frac{P_{c,max}-P_{c,min}}{\Delta P_c}+1$$

  (19)
  A grid of n_T x n_P points with coordinates (T_fluid,k, P_c,j) is thus defined.
• Given a couple of values of T_fluid and P_c, the evolution of the product is simulated, as previously described, thus calculating the maximum value of its temperature. If this value is lower than the limit temperature, then the selected values of T_fluid and P_c belongs to the design space.

3. Results and Discussion

At first the limit temperature for the product considered in this study has been determined using both DSC and the cryo-microscope. Results are shown in Figure 1 and Figure 2, evidencing a glass transition temperature at −34.8 °C and a collapse temperature at −33.4 °C, in agreement with the fact that the collapse temperature is usually 1–2 °C higher than the glass transition temperature.

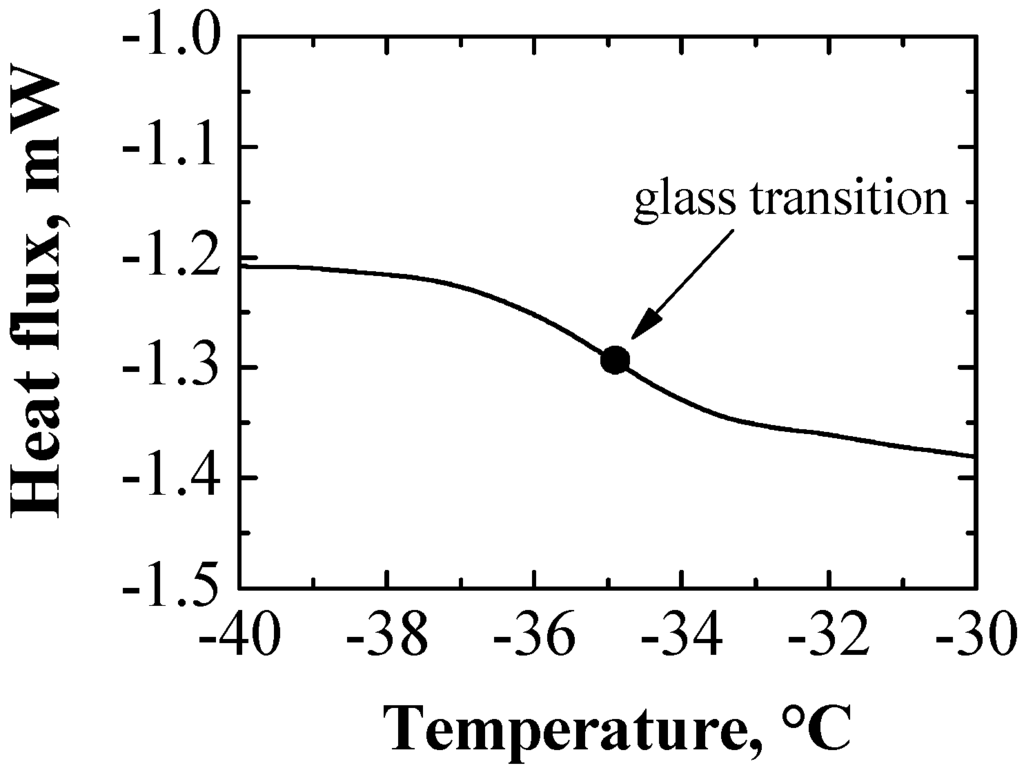
Figure 1. DSC thermogram for the 5% w/w sucrose formulation used in this study (the glass transition temperature is evidenced).

Figure 1. DSC thermogram for the 5% w/w sucrose formulation used in this study (the glass transition temperature is evidenced).

Figure 2. Images obtained at the cryo-microscope, showing the onset of the cake collapse at −33.4 °C.

Figure 2. Images obtained at the cryo-microscope, showing the onset of the cake collapse at −33.4 °C.

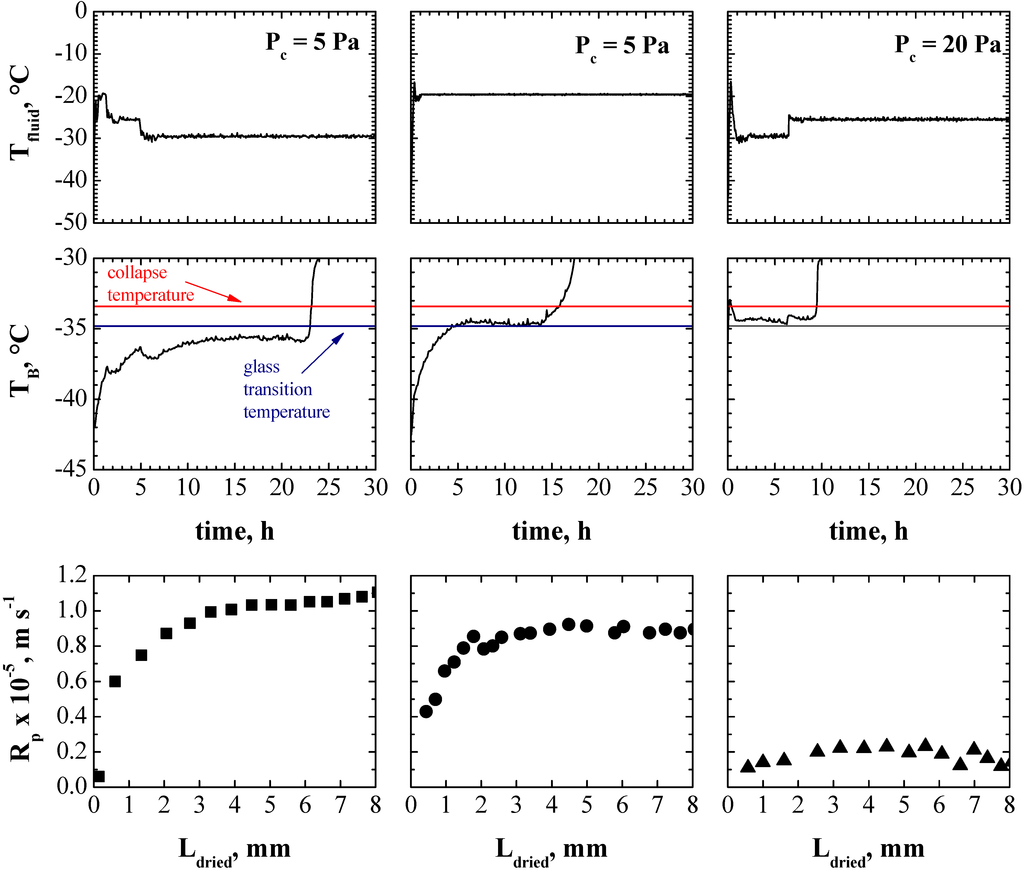
Figure 3. Comparison between the values of heating fluid temperature (upper graphs), product temperature at the bottom of the container (middle graphs) and dried cake resistance (lower graphs) in three different cycles for a 5% w/w sucrose solution.

Figure 3. Comparison between the values of heating fluid temperature (upper graphs), product temperature at the bottom of the container (middle graphs) and dried cake resistance (lower graphs) in three different cycles for a 5% w/w sucrose solution.

Various cycles were then performed to evaluate the effect of the temperature of the product on the resistance of the dried cake. Three representative cycles are shown in Figure 3. With respect to the temperature profiles, it has to be pointed out that at the beginning of the primary drying stage the temperature of the product started to increase from the value reached in the freezing stage and, then, a sort of steady-state value is obtained. When drying is completed, there is a sharp rise in product temperature, up to that of the heating fluid, but this does not mean that collapse occurs in the monitored vial, as ice sublimation does not occur any more.

In type-I runs, an example of which is shown in the left hand graphs of Figure 3, product temperature remains below the glass transition value. In type-II runs, as shown in the middle graphs of Figure 3, product temperature appears very close (or slightly higher) than the glass transition value. In type-III runs product temperature exceeds the glass transition value, while remaining below the collapse value.

This study evidenced, at first, that the resistance of the dried cake is not a linear function of L_dried, as shown in the bottom graphs of Figure 3, thus indicating a non-uniform cake structure in the axial direction, but also that the temperature of the product strongly influences the values of R_p, as dried cake resistance strongly decreases when the glass transition temperature is trespassed. This is due to micro-collapse phenomena, resulting in the formation of larger holes in the dried cake, as shown in Figure 4. This behavior was different to that shown in Overcashier et al. [44] where holes in the dried structure were observed. From this analysis, it is not however clear which is the maximum temperature reached by product during the drying process. We can hypothesize that the formation of these holes was due to the fact that the product temperature was very close to, or slightly higher than, the collapse temperature, thus promoting a more marked mobility of the freeze-concentrate.

Figure 4. Cake structures at 1 mm from the top obtained by Scanning Electron Microscope in the run I (A); run II (B); and in the run III (C).

Figure 4. Cake structures at 1 mm from the top obtained by Scanning Electron Microscope in the run I (A); run II (B); and in the run III (C).

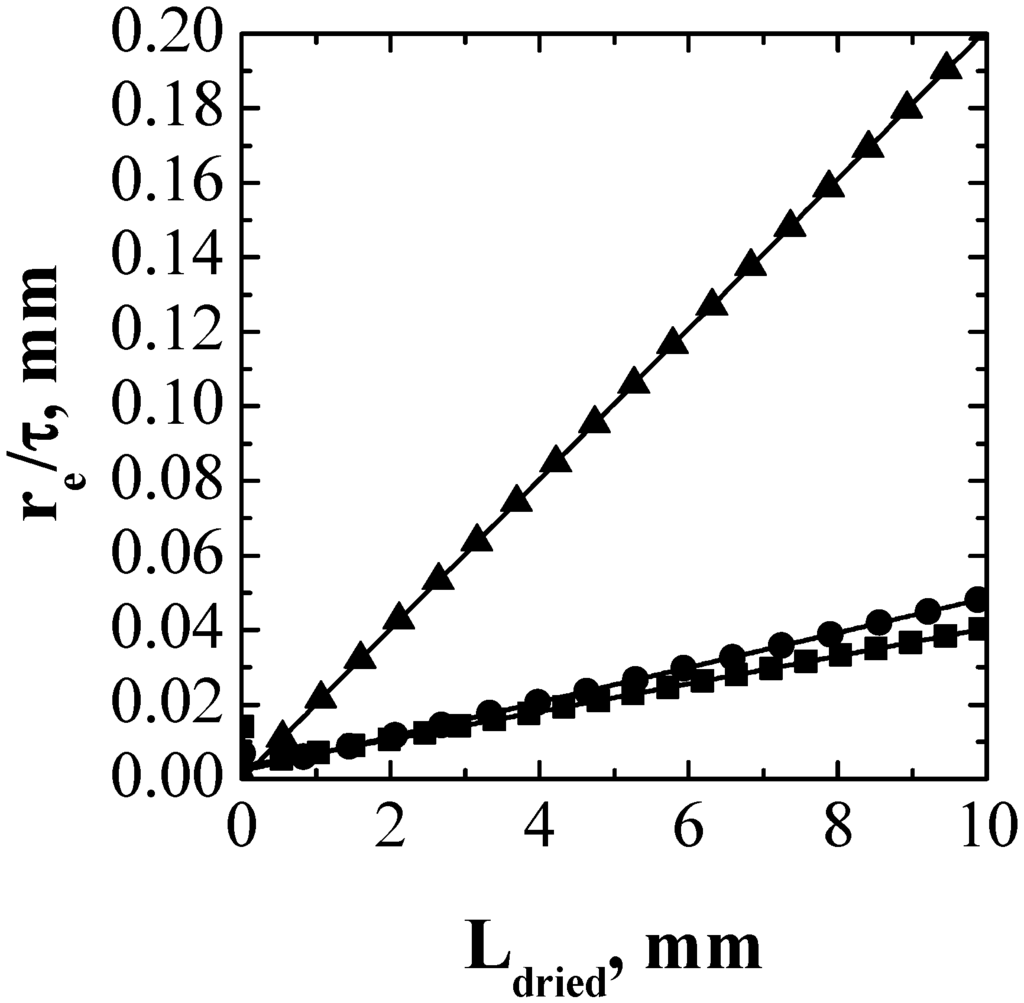
Figure 5. Values of r_e/τ as a function of L_dried calculated for type-I (■), type-II (●), and type-III (▲) runs.

Figure 5. Values of r_e/τ as a function of L_dried calculated for type-I (■), type-II (●), and type-III (▲) runs.

The values of r_e/τ as a function of L_dried calculated for the three types of runs are shown in Figure 5, evidencing that Equation (13) is suitable for describing the “structure” of the drying cake at different temperatures, providing that the values of the parameters a₀ and a₁ are modified. It appears that the structure of the cake, i.e., the values of r_e/τ, are different depending on the temperature of the product, and two sets of values of a₀ and a₁ (and, thus A and B) can be calculated depending on the fact that product temperature is higher or lower than the glass transition temperature.

Figure 6. Results obtained in a run where the values T_fluid and P_c are modified during the primary drying (as shown in the top graph). Values of product temperature measured using a thermocouple and of the dried cake resistance estimated using the pressure rise test are shown in the middle and in the bottom graph respectively.

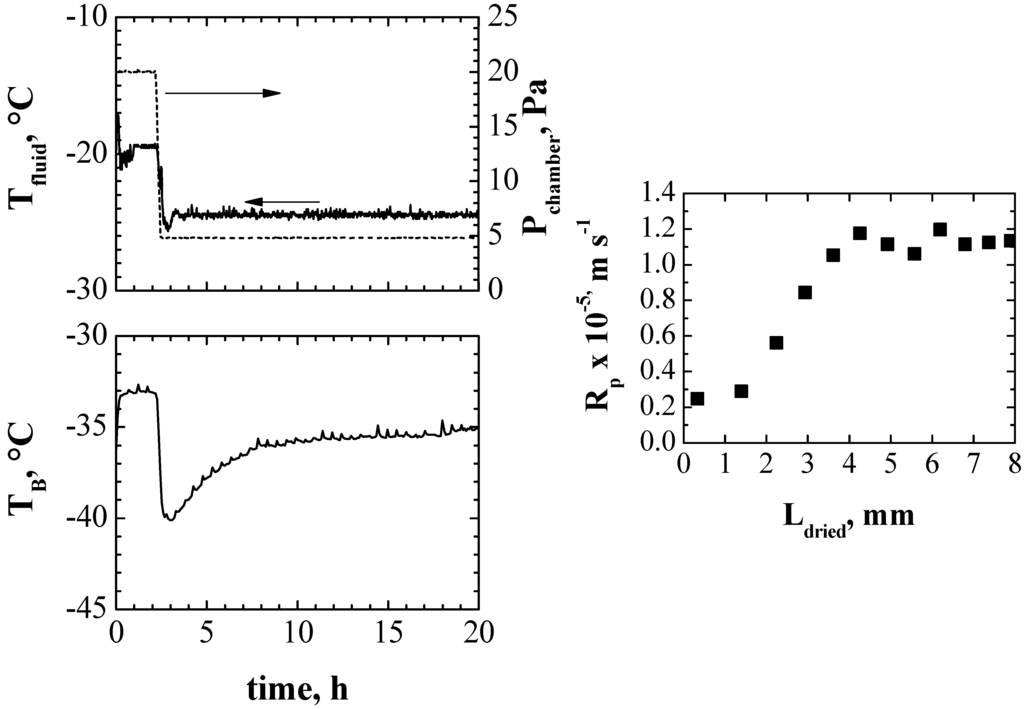
Figure 6. Results obtained in a run where the values T_fluid and P_c are modified during the primary drying (as shown in the top graph). Values of product temperature measured using a thermocouple and of the dried cake resistance estimated using the pressure rise test are shown in the middle and in the bottom graph respectively.

In order to confirm previous conclusions, a further cycle has been carried out using aggressive heating conditions (high pressure and high temperature) only during the first part of drying (see Figure 6, top graph). The selected value of T_fluid and P_c are shown in the upper graph, as well as product temperature (where a sharp decrease appears in the measured values when T_fluid and P_c are decreased) and the dried cake resistance in the middle and bottom graphs respectively. The higher pressure and temperature gave smaller resistance to vapor flow (bottom graph), because the product temperature was higher than the glass transition value in the first part of the drying and, thus, it promoted the formation of larger pores within the upper part of the lyophilized cake (see Figure 6, middle graph).

As can be seen in Figure 6 (bottom graph), in the first part of the primary drying the values of R_p were close to those obtained in a type-III run, where product temperature trespasses the glass transition value, and it appeared to be almost unaffected by the dried cake thickness. In the second part of the drying R_p increased with a trend similar to a type-I run, where product temperature remains below the glass transition value and, thus, micro-collapse did not occur and R_p increased to higher values as dried cake thickness increased.

These observations are confirmed when plotting r_e/τ as a function of L_dried, as shown in Figure 7: in the first part of the drying the values of r_e/τ are similar to those obtained in a type-III run and when product temperature decreases, the values of r_e/τ are close to those obtained in a type-I run, thus proving the adequacy of the proposed model to account for variations of R_p vs. L_dried as a function of product temperature.

In the previous part we showed that the resistance to vapor flow can dramatically decrease if the product temperature overcomes the glass transition value during drying. If, on the one side, it is true that the resistance to vapor flow might vary with the difference between the glass transition temperature and the collapse one, it is also true that this temperature range is so small, less than 2 °C, that it is difficult to evaluate this potential variation in the value of R_p. Therefore, in this study we hypothesized that the variation in R_p occurred only if the product temperature is higher than the glass transition value, independently of how much higher this difference is.

Figure 7. Values of r_e/τ as a function of L_dried calculated for the run shown in Figure 6 (symbols). The values obtained in type-I and type-III runs are shown for comparison (lines).

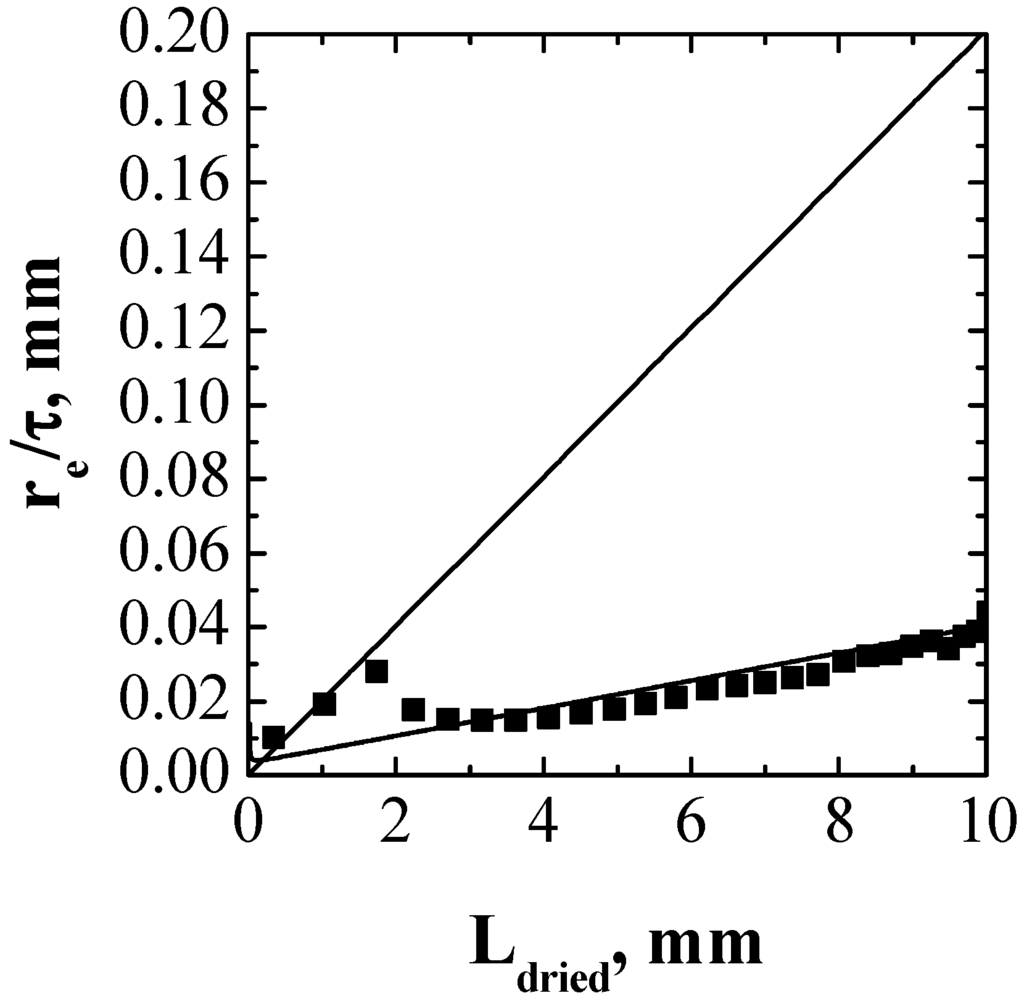
Figure 7. Values of r_e/τ as a function of L_dried calculated for the run shown in Figure 6 (symbols). The values obtained in type-I and type-III runs are shown for comparison (lines).

The variation in the value of R_p can have important effects on the design space of the primary drying stage. Figure 8 shows the maximum value of the temperature of the heating fluid as a function of chamber pressure. Dashed line corresponds to the values calculated assuming that the limit value is the glass transition temperature and, thus, the parameters corresponding to a type-I run are used to calculate R_p. This approach can be too precautionary, as higher values of product temperature (below the collapse value) are allowed. Therefore, for each value of P_c product dynamics has been simulated for higher values of T_fluid. Taking into account results shown in Figure 4, the resistance of the dried cake to vapor flux was described by two sets of values, one in case micro-collapse does not occur (when the temperature is below the glass transition temperature), and one in case of micro-collapse (when the temperature is above the glass transition temperature, and below the collapse temperature). Therefore, according to the algorithm described in Section 2.3, product dynamics has been simulated, thus resulting in the determination of the new maximum values of T_fluid, represented in Figure 8 by the solid line.

Figure 8. Design space of the primary drying stage calculated in case product temperature remains below the glass transition value (dashed line) and below the collapse value (solid line) for the 5% w/w sucrose solution investigated in this study.

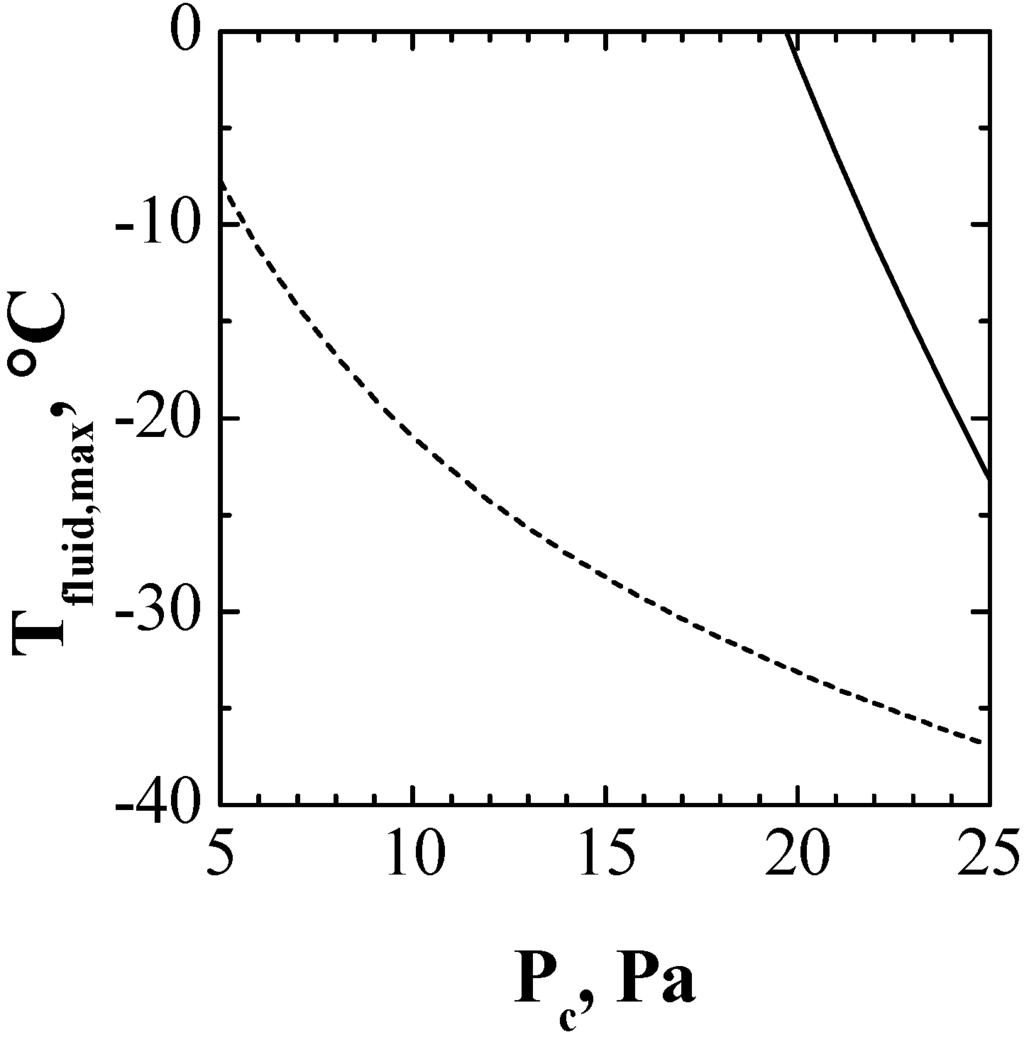
Figure 8. Design space of the primary drying stage calculated in case product temperature remains below the glass transition value (dashed line) and below the collapse value (solid line) for the 5% w/w sucrose solution investigated in this study.

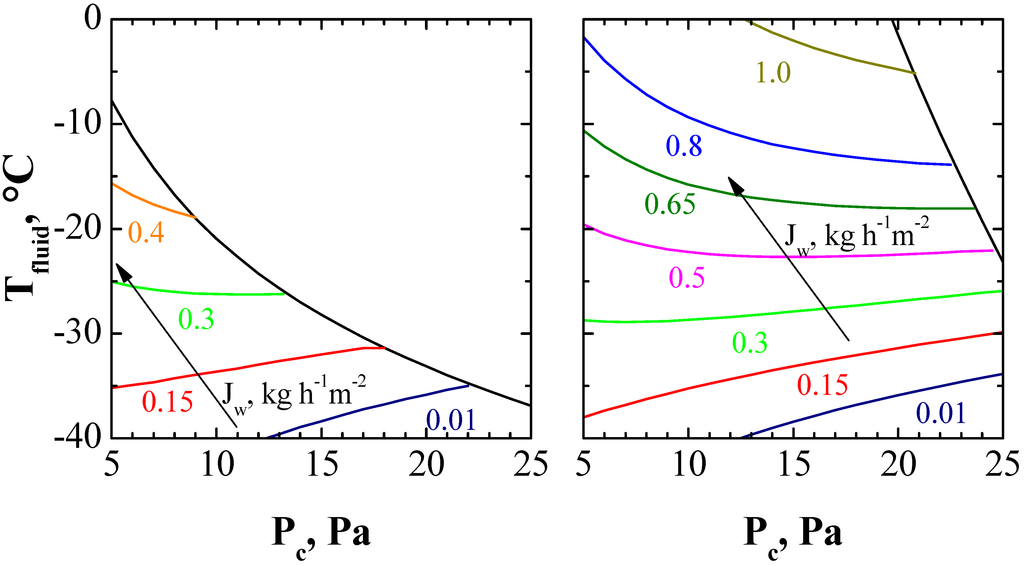
Figure 9. Values of the sublimation flux (colored lines) as a function of the operating conditions, in case the product has to be maintained below the glass transition temperature, or in case micro-collapse is allowed. Black line corresponds to the maximum allowed fluid temperature.

Figure 9. Values of the sublimation flux (colored lines) as a function of the operating conditions, in case the product has to be maintained below the glass transition temperature, or in case micro-collapse is allowed. Black line corresponds to the maximum allowed fluid temperature.

When simulating product evolution it is also possible to calculate the sublimation flux, allowing one to identify which of the operating conditions of the design space allows maximizing the sublimation flux and, thus, minimizing the drying time, thus truly optimizing the freeze-drying process. As a consequence of the variation of product temperature and of the thickness of the dried layer with time, also the sublimation flux changes with time. Figure 9 compares the values of sublimation flux as observed for a cycle carried out at temperature below the glass transition value (left graph) and for a similar cycle but in presence of micro-collapse of the lyophilized cake (right graph).

Even if the results shown in Figure 9 refer to the product when it nears the completion of ice sublimation, these results can still be considered representative of the system state through the entire primary drying stage. In fact, if it is true that the sublimation flux increases in the first part of the primary drying (when product temperature sharply increases from the freezing temperature to the drying one), then J_w reaches a steady-state value, remaining almost constant until the end of the process. In order to optimize the process, if the product has to remain below the glass transition temperature, a suitable value of T_fluid appears to be −10 °C and that of P_c appears to be 5 Pa; the sublimation flux obtained in this case is slightly higher than 0.4 kg h⁻¹m⁻². In case micro-collapse is allowed, it is possible to use T_fluid = −5 °C and P_c = 20 Pa, thus obtaining a sublimation flux higher than 1.0 kg·h⁻¹m⁻², that significantly reduced the duration of the primary drying stage.

4. Conclusions

The use of mathematical modeling allows a quick and reliable calculation of the design space of the primary drying stage of a freeze-drying process, provided that accurate values of model parameters are used. In this framework, the paper addressed the case of a particular, and widespread, class of products characterized by the variation of the dried cake resistance with the temperature and, in particular, by the occurrence of micro-collapse when the temperature trespass the glass transition temperature. A simple method was proposed to account for this effect using few experimental measurements to characterize the product, and the impact on the design space was assessed by means of mathematical simulation, thus evidencing the significant acceleration of the process when increasing product temperature.