Abstract
Recent advancements in photovoltaic (PV) and battery technologies, combined with improvements in power electronic converters, have accelerated the adoption of rooftop PV systems and electric vehicles (EVs) in distribution networks, while these technologies offer economic and environmental benefits and support the transition to sustainable energy systems, they also introduce operational challenges, including voltage fluctuations, increased system losses, and voltage regulation issues under high penetration levels. Traditional Voltage and Var Control (VVC) strategies, which rely on substation on-load tap changers, voltage regulators, and shunt capacitors, are insufficient to fully manage these challenges. This study proposes a novel Voltage, Var, and Watt Control (VVWC) framework that coordinates the operation of PV and EV resources, conventional devices, and demand responsive loads. A mixed-integer nonlinear multi-objective optimization model is developed, applying a Chebyshev goal programming approach to balance objectives that include minimizing PV curtailment, reducing system losses, flattening voltage profile, and minimizing demand not met. Unserved demand has, in particular, been modeled while incorporating the concepts of distributional and recognition energy justice. The proposed method is validated using a modified version of the IEEE 123-bus test distribution system. The results indicate that the proposed framework allows for high levels of PV and EV integration in the grid, while ensuring that EV demand is met and PV curtailment is negligible. This demonstrates an equitable access to energy, while maximizing renewable energy usage.
1. Introduction
The widespread deployment of renewable energy technologies, particularly rooftop photovoltaic (PV) systems, is viewed as a key solution for reducing greenhouse gas emissions from the power sector. Declining PV costs have led to exponential growth in rooftop installations since 2010, supporting global sustainability goals [1]. However, reducing emissions from electricity alone is insufficient, as transportation accounts for approximately 23% of global carbon dioxide emissions. This has motivated a transition toward electric vehicles (EVs), which offer significantly higher energy conversion efficiencies compared to internal combustion engine vehicles [2]. Together, PV and EV technologies present substantial benefits for society by promoting environmental sustainability, energy security, and economic development.
PV systems enable clean electricity generation without harmful emissions, while EVs provide zero tailpipe emission transportation, particularly when charged with a power grid predominantly supplied by renewable energy [3,4]. Financial incentives, falling technology costs, and supportive policies have further accelerated the adoption of both technologies. In addition, local energy generation and storage from PVs and EVs can improve energy resilience by reducing dependence on fossil fuel imports and mitigating exposure to price volatility. Advanced control strategies allow PV and EV integration to support grid flexibility by enabling services such as peak shaving, frequency regulation, and voltage support, particularly when vehicle-to-grid (V2G) technologies are employed [5,6].
Despite these benefits, high PV and EV penetration introduces operational challenges, which may include voltage fluctuations in the form of localized undervoltage or overvoltage instances, increased system losses, localized congestion, and localized stresses on grid infrastructure. The variability of solar generation and EV charging demand complicates voltage regulation and supply–demand balancing in distribution systems [7]. Without adequate management, these dynamics may lead to stability issues and, in extreme cases, localized outages, particularly during rapid changes in solar irradiance or simultaneous EV charging events. Furthermore, the charging demand for EVs, which can far exceed typical residential loads, raises concerns about peak load increases and localized circuit overloads. Upgrading grid infrastructure is a potential solution; however, it involves high costs and long timelines.
A more sustainable and cost-effective approach is to coordinate the operation of PVs and EVs with distribution grid management. In this context, demand response (DR) emerges as a critical tool [8]. DR programs enable dynamic adjustments of electricity demand in response to grid conditions, enhancing grid flexibility, reducing peak loads, and improving system resilience. By encouraging customers to shift or reduce electricity usage during critical periods, DR alleviates stress on the grid assets, mitigates voltage and frequency deviations, and facilitates greater renewable integration [9,10]. Specifically, DR can address evening peak challenges when solar production declines but EV charging demand likely increases, thereby reducing the need for expensive infrastructure reinforcements.
However, the implementation of DR raises important energy justice considerations. Energy justice is often viewed in terms of the three tenets of distributional justice, recognition justice, and procedural justice [11], which focus on the equitable distribution of benefits and burdens, recognition of diverse community needs and capabilities, and inclusive decision making, respectively. Load curtailment strategies, if not designed carefully, risk disproportionately affecting vulnerable populations that are less able to cope with the consequences of power outages [12]. Further, they may lead to a lopsided approach in implementing interruptions, for instance, when curtailing power from certain areas is more beneficial to the power grid compared to other neighborhoods, which means certain areas will likely experience the burdens (demand curtailment), while others enjoy the benefits (improved grid performance). On the other hand, if guided by energy justice principles, DR can be implemented in a way that the impacts of power disruptions are fairly shared, while considering the need to protect socially vulnerable groups, such as low-income households, elderly residents, and those with limited access to resources [13].
This paper puts forth a novel approach for controlling active and reactive power resources in a distribution power grid in such a way that technical objectives such as power losses, voltage quality, and meeting demand are balanced against environmental objectives such as utilization of renewable energy resources as well as energy justice objectives for promoting equitable grid performance.
2. Literature Review
Many researchers have studied the challenges associated with high PV penetration in power distribution systems and have proposed various mitigating solutions. The authors in [14] discussed the impacts of PV penetration on voltage regulation, voltage imbalance, and line losses, using a realistic distribution feeder modeled in CYMDIST. They concluded that around 50% PV penetration could enhance voltage profiles and reduce power losses. In [15], the effects of single-phase PV systems on unbalanced low-voltage networks were investigated, showing improvements in heavily loaded phases but risks of overvoltage in lightly loaded phases. Similar challenges, particularly stemming from utility-scale PV resources, were addressed in [16], where the authors examined the effects of PV locations and loading conditions. The study in [17] analyzed the impact of PV penetration on 12.47 kV distribution feeders of American Electric Power using OpenDSS simulations, emphasizing the critical role of PV size and placement on overall grid performance.
To optimize PV integration, researchers have often modeled the control of PV systems as an optimization problem. Heuristic methods are widely used due to their ability to handle nonlinear characteristics of the models. In [18], a quantum-inspired evolutionary algorithm was proposed to optimize real and reactive power dispatch of PV systems. Similarly, ref. [19] applied an evolutionary strategy to solve a multi-objective optimization problem for distributed generation, balancing active power production and system losses. Mathematical programming methods were also explored, such as the linear programming approach in [20], which aimed to optimize the voltage profile by coordinating distributed generation dispatch levels. Coordinated voltage control strategies for networks with multiple distributed energy resources were also discussed in [21], highlighting advanced methods for improving grid operation with high PV integration.
Regarding EV integration, significant challenges have been noted. An agent-based modeling study in [22] demonstrated that feeders with high R/X ratios are particularly vulnerable to EV charging loads. In [23], the authors found that a 60% EV penetration level could increase grid investment costs by 15% and system losses by 40%. Further analyses such as those in [24,25] identified problems such as voltage violations and main substation overloading in grids with high EV adoption, while ref. [26] focused on undervoltage issues at remote nodes.
To mitigate these challenges, researchers have proposed optimized EV charging strategies. In [27], a comparison between coordinated and uncoordinated EV charging showed that the former significantly mitigates voltage imbalance and overload problems. Similarly, ref. [28] demonstrated that smart charging strategies facilitate a much higher EV penetration without violating grid constraints. Optimal placement and sizing of EV charging stations (EVCS) were explored in [29], considering V2G capabilities, while ref. [30] focused on fast charging stations for public transportation networks. In [31], an optimal allocation approach was introduced to minimize power losses and enhance voltage stability, and in [32], strategies for maximizing load hosting capacity in unbalanced networks were discussed. Recent meta-heuristic approaches for EVCS siting and sizing, aiming to optimize network performance and minimize investment costs, were presented in [33]. Another study employed an adaptive integrated planning framework that dynamically updates investment decisions for charging stations and network upgrades over time, addressing uncertainties in EV adoption and spatial demand [34].
In parallel, integrated control of PV and EV systems has been explored to support grid stability. The study in [35] proposed VVC combined with energy storage to better coordinate EV charging in unbalanced distribution networks. Similarly, ref. [36] developed a coordinated energy management framework between home and grid energy systems to optimize EV charging and PV curtailment. An advanced model predictive control approach for decentralized voltage control of PV-EV integrated systems was presented in [37], while ref. [38] proposed a dual-stage model predictive control solution for volt-var management. In another study, a hierarchical control strategy was introduced in [39] to coordinate EV charging and regulate voltage levels across the grid, showing improved power quality and mitigation of voltage dips under high penetration scenarios. A study in [40] proposed a distributed optimization model for EV fleets and DER coordination that successfully balanced voltage profiles and minimized operational costs in low-voltage feeders. These studies validate the need for integrated strategies to maintain grid stability in the presence of large-scale distributed resources. The authors in [41] focused on optimizing EV charging station locations integrated with PV and energy storage using a fuzzy inference system. Their proposed model considers factors such as grid capacity, renewable energy availability, and traffic density, and it emphasizes the synergy between solar energy and EV demand.
In conjunction with increased penetration levels of PVs and EVs, demand response (DR) has been increasingly recognized as a critical strategy for modern grid operation. The authors in [42] proposed an optimal residential DR control model formulated as a convex-relaxed optimal power flow, coordinating household energy management systems with load-serving entities to reduce peak demand and maintain voltage stability. In [43], real-world DR behavior was modeled using price elasticity metrics, highlighting the importance of responsive consumer types in improving voltage profiles and reducing losses. Simulation studies in [44] explored the control of residential hot water systems as flexible DR loads, demonstrating significant cost savings and ramping reductions in solar-dominant grids. At the planning level, ref. [45] developed system-wide DR models for long-term cost reduction in the Dutch power system. Industrial DR applications were studied in [46,47], where MILP and Markov Decision Process frameworks, respectively, enabled intelligent real-time scheduling of energy-intensive tasks, achieving cost savings and supporting grid flexibility without productivity loss. These studies underline the growing role of DR not only for operational support but also for strategic grid resilience and planning.
Most existing studies in the literature about PV and EV integration rely on simplified representations of power distribution systems, often overlooking critical features such as system asymmetries, unbalanced operation, and the presence of voltage control devices. In terms of methodology, many studies adopt either linearized models that sacrifice accuracy or heuristic optimization techniques that cannot guarantee global optimality. Furthermore, the common use of weighted sum multi-objective formulations introduces subjectivity and risks biasing outcomes, as one objective may dominate others depending on subjective weight assignments. Moreover, social equity considerations are typically absent from DR and load curtailment strategies during grid stress events. These limitations negatively impact the ability to achieve the robust, equitable, and technically optimal integration of distributed resources within the power distribution grid.
To address these gaps, this paper proposes a comprehensive optimization framework that leverages PV, EV, and DR flexibility to enhance grid efficiency while systematically incorporating equity and justice into operational decision making. The main contributions of the current study are as follows:
- The proposed model balances technical performance efficiency (loss minimization and voltage quality), environmental goals (maximizing the utilization of PV resources), and energy justice (supplying EV demand while taking into account social vulnerabilities and equitable distribution of burdens and benefits).
- Demand curtailment is utilized as a flexibility tool guided by distributional and recognition justice to protect vulnerable communities and ensure fairness in power delivery.
- The model developed uses a realistic and comprehensive problem formulation in which power grid features such as asymmetries, imbalance, and the presence of legacy voltage control devices are considered.
- The proposed model considers nonlinearities in power grid models and operational constraints.
- The multi-objective optimization model is solved using a goal programming approach to ensure that no objective functions dominate others and that the Pareto-optimal solution is reached.
3. Problem Formulation
3.1. Objective Functions
The proposed optimization model consists of several objective functions that are to be simultaneously optimized. These include minimizing unmet demand considering both recognition and distributional justice, minimizing system losses, minimizing the curtailment of PV power generation, minimizing curtailment of EV charging demand at charging stations, and minimizing node voltage deviations from the desired values.
3.1.1. Unmet Demand Minimization
Under periods of high demand and low generation, the utility may be forced to implement load curtailment to ensure that the balance between generation and demand is maintained at all times. In this study, we model load curtailment as a voluntary reduction in demand in the form of DR. However, this resource must be used sparingly. Hence, the corresponding objective function is modeled as minimizing the energy not served as shown in (1). To ensure recognition justice, in Equation (1), demand at each node is weighted based on the social vulnerability level of the node, so that the more vulnerable populations experience fewer instances of demand reduction. Another important aspect of energy justice is known as distributional justice, which requires that the benefits and burdens associated with power grid operation are distributed equally across the grid. In this study, to ensure that the burdens, i.e., demand curtailment, are equally distributed across the grid, we minimize the variance of normalized unmet demand for all nodes, as shown in (2). It should be noted that, in this case, different nodes are no longer weighted based on their levels of social vulnerability and are given the same weight (importance). This is essential to ensure that all customers are viewed on equal terms.
3.1.2. System Loss Minimization
This objective function ensures that power losses across the system are minimized over the dispatch period by optimally delivering power to the loads via the most appropriate routes and using local PV resources as much as needed and/or possible. This objective function is modeled as in (3), and it includes both active and reactive power losses.
3.1.3. Minimization of PV Active Power Curtailment
In an effort to operate the grid in a sustainable fashion, another operational goal here is to minimize the total amount of active power curtailed from rooftop PV resources over the dispatch period and maximize their local generation, as expressed in (4).
3.1.4. Minimization of EVCS Demand Curtailment
It is assumed here that at any point in time, several EVs are present at each charging station, waiting or continuing to be charged. However, the amount of charge provided to the EVs must be coordinated with the operational constraints of the grid. The objective function in (5) intends to achieve the target EV charge levels (in terms of the energy provided) as much as technically possible. This has been considered as the EV demand at the station level, and not for individual EVs. It should be noted that this objective function does not consider residential EVs and their associated demand curtailment. However, that portion of demand can be viewed as a subset of the demand at individual nodes, which is to be supplied as much as possible, as denoted in Equations (1) and (2).
3.1.5. Improvement of Voltage Profile
If not coordinated, high PV and EV penetration levels can cause voltage rises and drops across the system, respectively. This objective function intends to improve (flatten) the voltage profile by getting node voltages as close to the rated 1.0 per unit as possible. It can be easily seen that in certain cases, this objective may become at odds with objective (3), e.g., when reducing node voltages, for instance, through conservation voltage reduction (CVR), it may help with reducing losses (especially in networks dominated by constant impedance loads). There are several methods to flatten the voltage profile across the grid, e.g., curtailing active power from PVs, coordinating EV charging levels, and injecting/absorbing reactive power through smart inverters. The objective function is shown in (6).
3.2. Constraints
The above objective functions are optimized, subject to the following operational constraints.
3.2.1. Power Flow Constraints
Equations (7)–(10) represent the real and imaginary parts of line currents and node voltages in the system. These equations provide means to represent the network model and power flow equations in the problem formulation. The benefit of using this approach is that the usage of phasors (and hence, the nonlinear sine and cosine functions) can be avoided. This significantly reduces the complexity of the model and enhances convergence while ensuring system performance is accurately modeled.
3.2.2. Power Constraints
Active and reactive powers for node demands, EVCS, and PV resources are all expressed in Cartesian form, expressed in Equations (11)–(16) as follows:
3.2.3. Constraint on Power Delivered from the Main Substation
Power provided by the main substation, i.e., the point of common coupling (PCC), may be limited due to operational or budgetary constraints. In this study, this has been modeled in the form of an inequality constraint, as shown in (17)–(19). Without loss of generality, the main substation has been denoted as node 1.
3.2.4. PV Power Constraints
Equations (20) and (21) represent the upper and lower limits for the active and reactive powers of rooftop PV resources. It is assumed here that PVs, equipped with smart inverters, can either absorb or inject reactive power based upon need.
3.2.5. Demand Constraints
Equation (22) denotes that the power provided to a node can be less than the desired amount. Equations (23) and (24) represent the active and reactive power constraints for EVCS. In this study, an EVCS is assumed to only be able to absorb reactive power from the grid, as shown in (25). The total energy delivered to each EVCS is equal to the sum of the energies delivered in each hour during the dispatch period, as shown in (26). Note that due to the time step of analysis, i.e., one hour, powers are equal to energies in value. The amount of energy delivered to each EVCS is less than or equal to the desired level, as shown in (27), but must be as close to it as possible, as ensured by (5).
3.2.6. Voltage Regulator Constraints
Voltage regulators in this study are assumed to be ideal transformers, capable of providing voltage regulation through a total of 32 steps (16 steps in each direction), which means that each step will provide a regulation of 0.00625 per unit. Equations (28)–(31) represent relationships between primary and secondary voltages and currents, which are simply based on the turn ratio of the transformer. In all these equations, bus j is assumed to be the secondary of the VR. Equation (32) denotes the limit on tap positions.
3.2.7. Node Voltage and Line Flow Constraints
To ensure stable and secure operation, node voltages must be within ANSI limits at all times, as shown in (33) and (34). Further, currents flowing through lines must be within the line’s rating, as denoted in (35) and (36).
The problem formulation also includes all the relevant non-negativity and integrality constraints that are omitted here for brevity.
3.3. Solution Methodology
3.3.1. Goal Programming
The multi-objective formulation is modeled here using Chebyshev goal programming for all cases except the cost-only case (see below), where all objectives are combined into a single aggregate objective. The overall problem can then be formulated as follows:
Subject to the following:
Equation (37) denotes the linear objective function, i.e., minimizing the maximum deviation of the six objectives from their target values. Constraint (38) forces each objective function to be less than the target value defined by the user. However, since this may not be possible within a multi-objective framework, a deficiency variable has been added for each objective function to change the constraints from hard constraints to soft ones. Since the unit for each of the objectives is different, the deficiency variables are all normalized based on their corresponding target values, and a variable L has then been defined as the upper bound for the normalized deficiency variables, as shown in Equation (39), which is then to be minimized.
3.3.2. Aggregate Multi-Objective Problem
To provide a comparison between the proposed multi-objective model (considering various technical, social, and environmental objectives) with the more commonly adopted practice in which costs are considered as the only objective function, a new aggregate objective function is considered, which consists only of the terms related to the powers provided by the utility (and hence, the revenue made by the utility). It is therefore assumed that a utility may prefer to only minimize the energy not served and the EV demand curtailment, both of which may lead to financial losses (or lost revenue). Because both objective functions have the same units, an aggregate function is defined as the sum of the corresponding individual objective functions as expressed in (41) as follows:
Note that denotes a modified version of , in which the SV values for all buses are set to 1.0 so that the value of the objective function is in pure kW (and not a weighted kW based on social vulnerability).
4. Case Study
4.1. Test System
The proposed model is applied to a modified version of the IEEE 123-bus test distribution system, which is mapped onto an arbitrarily chosen location in the State of Colorado, which offers high diversity in SV values, as shown in Figure 1. This area is chosen for proof of concept purposes only and does not impact the generality of the proposed model. The system base values are considered to be 5 MVA and 4.16 kV for power and voltage, respectively. The load profile is assumed to follow a typical daily residential pattern, as illustrated in Figure 2, where the highest peak, reaching approximately 0.698 p.u., occurs in the evening between hours of 9:00 and 10:00 p.m. A total of 42 PV resources have been added to the system, with a total rated power of 1750 kW (0.358 p.u.), representing a 50% penetration level. Although these represent rooftop PV, they are modeled in this work as aggregate resources at the node level. The locations of PV resources are shown in Figure 1. Without loss of generality, PV generation is modeled under ideal clear sky conditions, with sunrise beginning around 5:00 a.m. and sunset occurring at approximately 8:00 p.m. This results in a well-defined generation profile, with power production steadily increasing in the morning, reaching its peak of around 0.358 p.u. at midday, and gradually declining towards the evening hours, as illustrated in Figure 2.
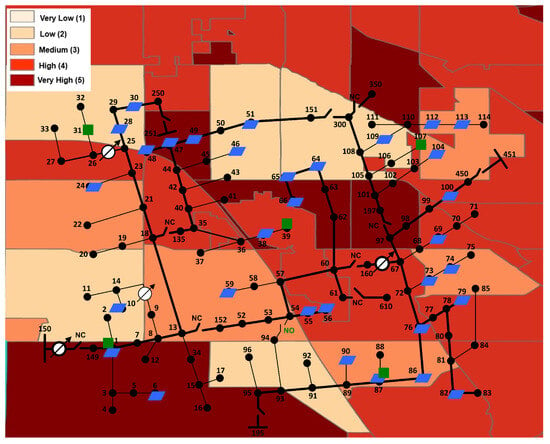
Figure 1.
Modified IEEE 123-bus test distribution system overlaid on an arbitrary area in the State of Colorado with the corresponding social vulnerability levels (darker colors indicate higher social vulnerability values. In this case study, no areas existed with ’very low’ vulnerability levels).
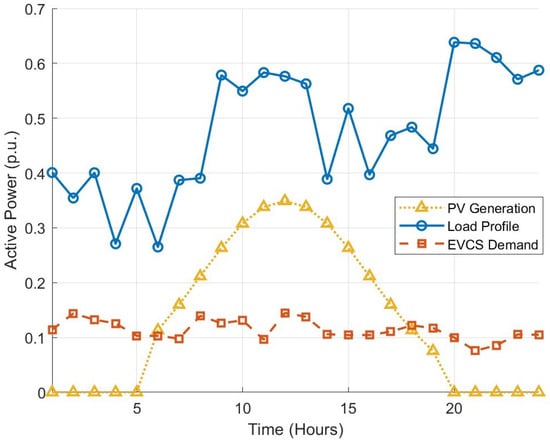
Figure 2.
Load profile, EVCS demand, and PV generation over a 24 h period.
In addition, five EVCSs have been added to the network, with a total of 96 level 2 chargers allocated to different stations. The maximum power of each charging point is considered to be 7.7 kW. To ensure a balanced representation of EVCS demand throughout the day, the EVCS load was modeled as a relatively constant load over the dispatch period, as shown in Figure 2. Moreover, there are two fixed capacitors in the system that can inject up to 750 kvar (0.15 p.u.) of reactive power. The PCC is assumed to be the reference bus, and as such, its voltage is set to be 1.0 per unit. To better regulate the voltage, the system is equipped with four voltage regulators and an OLTC, each modeled with 32 tap positions (16 positions in each direction, as indicated in Equation (32)). The optimization problem proposed in this paper, i.e., minimize (37) subject to (7)–(36) and (38)–(40), is modeled in GAMS (General Algebraic Modeling System) software version 24.2 and solved using the BONMIN (Basic Open source Nonlinear Mixed Integer programming) solver. On a computer with 13th Gen Intel(R) CoreTM i9-13900H @ 2.60 GHz, each case converges in approximately 18 min. The following case studies are considered here:
- Case 0: Base case, with no PV or EVCS.
- Case 1: EVCSs only.
- Case 2: PVs only.
- Case 3: Considering both PVs and EVCSs in the system.
- Case 4: Cost-only objective function.
4.2. Simulation Results
The base case represents the fundamental operation of the grid without any additional energy resources or extra loads introduced by PV or EVCS. It serves as a reference point for evaluating system performance under normal conditions, where only the existing demand is supplied by the grid, i.e., the main substation, and system losses and voltage profile are assessed without external influences. The EVCS-only case introduces EVCS demand to the system, but without any local PV generation support. This case assesses the impact of increased EV charging demand on system losses, voltage fluctuations, and demand curtailment, highlighting the challenges associated with integrating EVCS into the grid when the entire demand must be met by the main substation. In contrast, the PV-only case examines the effects of distributed renewable generation without flexible loads such as EV charging, While PV generation reduces reliance on the power supplied from the main grid and mitigates system losses during daylight hours, it may introduce challenges such as rising node voltages. As a result, PV curtailment may occur due to the lack of sufficient demand to absorb the excess energy. When both PV and EVCS are integrated, the system experiences a dynamic interplay between renewable energy supply and fluctuating charging demand. PV generation helps reduce grid dependency during the day, but in the evening, when solar power is unavailable, the increased demand and lack of local generation lead to demand curtailment. This case illustrates both the benefits and limitations of combining renewable energy with electric mobility. Finally, the cost-only case optimizes grid operation with the sole objective of maximizing revenue for the electric utility. This case prioritizes minimizing residential and EVCS demand curtailment over other operational constraints such as the power provided by the PVs or node voltage variations. It represents an approach that considers both operational stability and financial viability without considering the impact of such decisions on environmental sustainability and/or energy justice.
4.2.1. Active Power from PCC
The active power drawn from the PCC reflects the total energy supplied by the main substation to meet consumer demand across different cases. As shown in Figure 3, in the base case, where no PV generation or EVCS is present, the entire demand is met by the main grid, leading to high dependency on the centralized source of power. With the integration of EVCS, the grid experiences an increased burden, particularly during peak charging periods. The addition of PV generation reduces grid reliance during daylight hours by supplying local demand, significantly lowering PCC active power requirements. However, in the evening, when PV generation is absent, demand on the grid increases sharply, particularly in cases where EVCS demand remains high, while this general observation remains valid, different PV penetration levels may lead to various curves, especially in terms of the ramp up rate of the power provided by the PCC as solar irradiance decreases. The cost-only case appears to follow a similar trajectory to the PV and EVCS case but with noticeably higher active power drawn from the PCC, particularly between 6:00 a.m. and 8:00 p.m. This indicates that prioritizing the unserved demand over other objectives forces the model to draw more power from the PCC to be able to supply as much of the demand as technically possible. PV power is also used for this purpose, but due to the removal of the objective function associated with minimizing PV curtailment, this resource is only used when it can benefit the main objective function, i.e., reducing unmet demand.
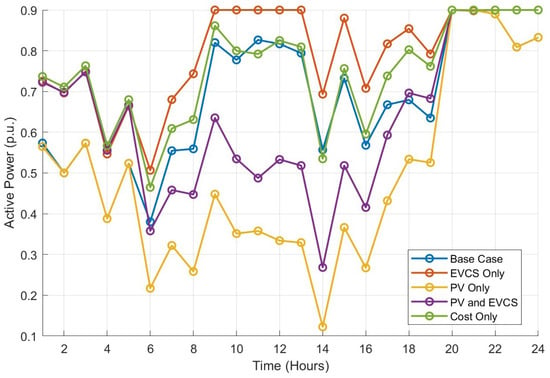
Figure 3.
PCC active power across different cases over a 24 h period for different cases, namely, base case (Case 0), PV-only (Case 1), EVCS-only (Case 2), PV and EVCS (Case 3), and cost-only (Case 4).
4.2.2. System Losses
System losses vary significantly across cases, largely influenced by the presence of distributed generation and additional loads, as observed in Figure 4. In the base case, losses are moderate but increase during peak load periods due to the flow of power over long distances. With EVCS integration, system losses rise considerably, as all charging demand must now be met by the PCC, increasing congestion and system losses. In contrast, PV integration helps mitigate system losses by supplying energy locally and reducing reliance on the main substation. However, excess PV generation can also introduce overvoltage issues, as well as system losses due to reverse power flow thus the curtailment of this resource may occur to maintain a balance. The combined PV and EVCS case present a mixed impact, i.e., while PV reduces daytime losses, EV charging in the evening leads to higher losses. On the other hand, the cost-only case shows the highest loss levels during much of the day, particularly from 8:00 a.m. to 4:00 p.m. This is expected since the loss minimization objective function is no longer included in this case, allowing the system to prioritize demand over system losses. This, in conjunction with the higher usage of the PCC power to meet the demand and less reliance on PV power, leads to the patterns observed in Figure 4.
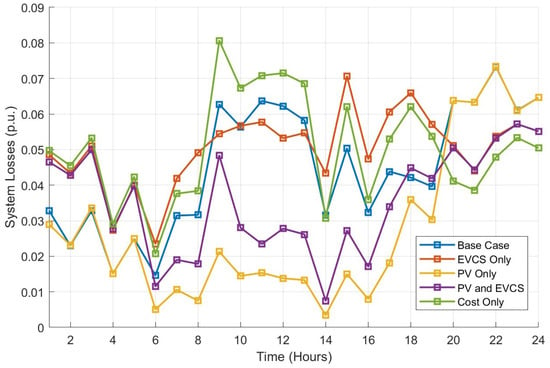
Figure 4.
System losses over a 24 h period for different cases, namely, base case (Case 0), PV-only (Case 1), EVCS-only (Case 2), PV and EVCS (Case 3), and cost-only (Case 4).
4.2.3. Residential Demand Curtailment
Load curtailment represents the demand that cannot be supplied due to grid constraints. In the base case, curtailment remains significantly low throughout most of the day, with only a minimal spike peaking at 0.02 p.u. around 8:00 p.m. due to the evening congestion, as shown in Figure 5. With EVCS integration, load curtailment follows a similar trend, as household and EV charging demand compete for available grid capacity. The absence of PV generation exacerbates this situation, forcing more load shedding to maintain stability during the daylight hours. Unlike the EVCS-only case, the PV-only case shows no visible load curtailment across the entire day. This is because the residential demand is relatively low and can be met effectively by both the grid and local PV generation. A similar pattern is observed in the combined PV and EVCS case, where load curtailment is minimized during daylight hours, as PV generation meets all demand (residential and EVCS demand). However, in the evening hours, especially around 8:00 p.m., curtailment rises sharply, reaching about 0.07 p.u., due to the drop in solar output and the continued high demand.
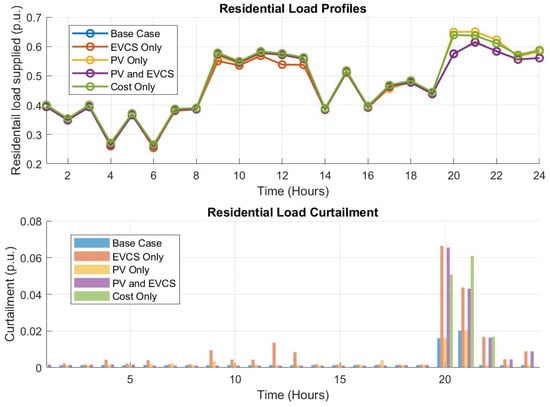
Figure 5.
Residential demand (top) and residential demand curtailment (bottom) over a 24 h period for different cases, namely, base case (Case 0), PV-only (Case 1), EVCS-only (Case 2), PV and EVCS (Case 3), and cost-only (Case 4).
The cost-only case prioritizes minimizing load curtailment, as it is one of the key objectives for maximizing utility revenues. As shown in Figure 5, no load curtailment occurs throughout most of the day, indicating the system’s capability to efficiently balance demand and generation. Around hour 20:00 (8:00 p.m.), a noticeable spike in curtailment occurs peaking near 0.06 p.u., corresponding to the evening demand surge driven by both residential and EVCS loads. Following this peak, curtailment drops sharply, reaching approximately 0.02 p.u. around hour 22:00 (10:00 p.m.). This reduction reflects the influence of setting all SV values to 1.0 across the network nodes, which enables more load to be served compared to the PV and EVCS case. Overall, the cost-only case quickly recovers, with curtailment levels rapidly declining and following an improved pattern compared to the PV and EVCS case.
4.2.4. PV Active Power Curtailment
PV integration significantly influences system performance, reducing reliance on power supplied from the main grid and lowering losses. In both PV-only and PV and EVCS cases, PV generation follows a typical bell-shaped curve, peaking around 12:00 p.m. In the PV-only case, despite high PV generation potential, minimal curtailment is observed. This indicates that in this case, the grid was generally capable of accommodating most of the solar energy. Any minor PV curtailment observed likely results from localized overvoltage conditions or loss minimization strategies during peak PV output periods. The PV and EVCS case demonstrates zero visible curtailment, indicating that the integration of EVCS successfully absorbs surplus PV energy, especially during midday when solar output is the highest. This highlights the value of flexible demand resources like EV charging, which help improve PV utilization and minimize the need for curtailment. The cost-only case exhibits a markedly different behavior. Instead of utilizing the full potential of available PV generation, the system curtails a significant portion of this resource, not entirely due to grid constraints, but because PV curtailment minimization was not factored into the cost optimization model. Since loss minimization was not included in the model, the solution may seek additional help from the PCC, making the PV resource unnecessary at times. Any usage of PV power may likely be due to localized voltage constraints (Figure 6).
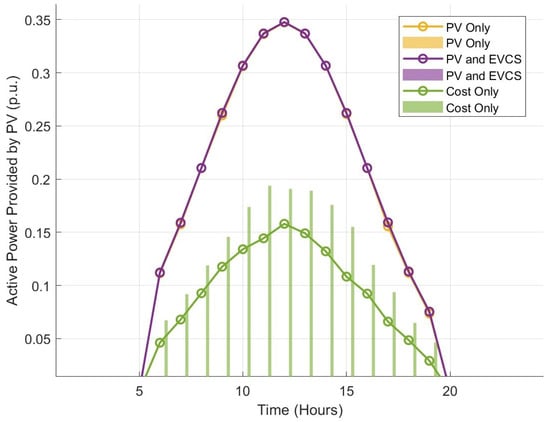
Figure 6.
PV generation over a 24 h period, with PV curtailment represented by bar plots for different cases, namely, PV-only (Case 1), PV and EVCS (Case 3), and cost-only (Case 4).
4.2.5. EVCS Demand Curtailment
EVCS demand adds significant stress to the grid, particularly in the absence of local generation by PV resources. As shown in Figure 7, curtailment occurs more frequently throughout the day in the EVCS-only case, where charging demand depends entirely on grid supply. The peak curtailment occurs around hour 21:00 (9:00 p.m.), reaching nearly 0.05 p.u., highlighting the grid’s inability to fully meet charging requirements. With PV integration, EVCS curtailment effectively reduced or even eliminated between hours 7:00 a.m. and 5:00 p.m., demonstrating the positive impact of PV integration on EV charging efficiency, unlike in the EVCS-only case, where charging depends solely on grid power. However, despite these improvements, the system once again becomes constrained, leading to visible curtailment spikes, although these remain slightly lower than in the EVCS-only case, as shown in Figure 7. The cost-only case exhibits a zero EVCS curtailment throughout most of the day, up until approximately hour 20:00 (8:00 p.m.). However, a noticeable increase in EVCS curtailment occurs around hour 21:00 (9:00 p.m.), where the cost-only case shows higher curtailment compared to the PV and EVCS case. This elevated curtailment during the evening peak is primarily due to grid capacity constraints caused by increased residential demand, which is also prioritized in the objective function. All three cases show a rapid drop in EVCS curtailment after the hour 22:00 (10:00 p.m.), suggesting that the system regains capacity to support EV charging once residential demand subsides.
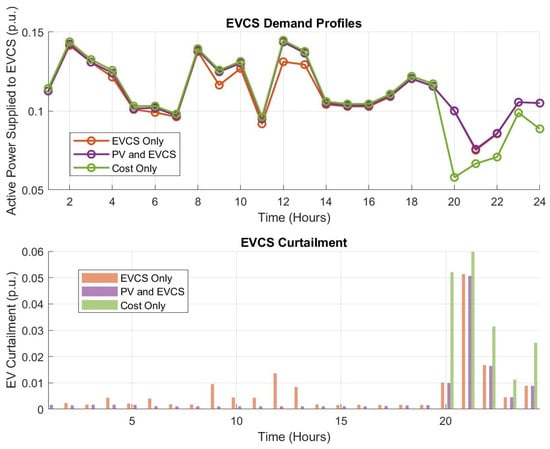
Figure 7.
EVCS demand (top) and curtailment (bottom) over a 24 h period, for different cases, namely, EVCS-only (Case 2), PV and EVCS (Case 3), and cost-only (Case 4).
4.2.6. Voltage Profile
Voltage stability is a key performance metric influenced by demand and generation. In the base case, voltage levels remain close to 1.0 p.u. throughout the day, as no additional sources or loads introduce fluctuations, as seen in Figure 8a. With EVCS integration, voltage deviations become more pronounced due to high-power drawing by charging stations. Although average voltage remains within permissible limits, localized voltage drops occur during peak charging hours, as observed in Figure 8b. In the PV-only case, voltage levels remain relatively steady but the case exhibits some variations due to fluctuating PV output. Under normal circumstances, voltage levels tend to rise during peak solar hours, potentially leading to overvoltage issues in certain parts of the network. However, this issue is mitigated here due to PV curtailment, which helps maintain voltage stability by preventing excessive power injection into the grid, as observed in Figure 8c. Additionally, the integration of PV and EVCS significantly influences the voltage profile of the system. As observed in Figure 8d, voltage fluctuations occur due to the intermittent nature of solar power and the varying demand from EVCSs, while PV generation generally supports voltage stability and mitigates drops caused by increasing EVCS demand. Although solar irradiance drops off in the evening, PV systems can still contribute to grid stability by injecting reactive power, which helps maintain voltage levels within acceptable limits, particularly during peak demand periods when the grid is more vulnerable to voltage drops. However, if reactive power is not properly absorbed or coordinated with system needs, it can also lead to voltage fluctuations or localized overvoltage instances. This dual effect is reflected in the voltage surface plot, where certain nodes exhibit elevated voltages despite the absence of active PV generation (Table 1).
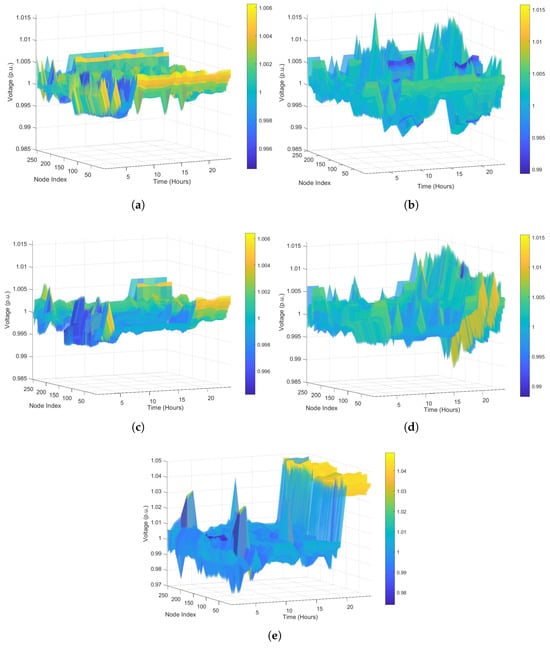
Figure 8.
Voltage profile across different node indices over time for different cases: (a) base case; (b) EVCS-only; (c) PV-only; (d) PV and EVCS; and (e) cost-only.

Table 1.
Voltage performance across case studies. All values are in per unit (p.u.).
In the cost-only case, most node voltage values remain clustered between 0.98 and 1.04 p.u., well within the acceptable operating range, as shown in Figure 8e. This behavior is primarily due to the absence of a dedicated voltage regulation objective within the optimization model for this case. Instead, the focus is directed toward minimizing demand curtailment, which can lead to elevated voltage levels across the network. Additionally, In the evening, particularly after hour 20:00 (8:00 p.m.), localized voltage rises are observed at certain nodes, with values reaching 1.03 p.u. This behavior is likely driven by a combination of reduced demand, and uneven distribution of EVCS loads. These conditions can lead to reverse reactive power flows which in turn push node voltages upward.
4.3. Discussion
The integration of both PV generation and EVCS into the distribution grid presents a complex interplay between renewable generation and charging demand, significantly impacting grid performance. The presence of PV generation helps mitigate system losses by supplying energy locally, reducing reliance on centralized power sources, particularly during daylight hours. However, the high energy demand from EVCS increases power flow through the network, leading to higher system losses during peak charging periods, especially in the evening when PV generation is unavailable. This dual effect underscores the importance of balancing renewable integration with demand-side management to optimize grid performance. One of the primary advantages of incorporating PV and EVCS together is the improved utilization of solar energy. The additional load from EV charging helps absorb excess PV generation, reducing PV curtailment. Likewise, EVCS curtailment is minimized during the daytime hours due to the availability of solar power, unlike in the EVCS-only case, where charging is entirely grid dependent. However, despite these benefits, EVCS curtailment remains high in the evening when grid limitations prevent full accommodation of charging demand among all cases. Residential demand curtailment follows a similar pattern, remaining low throughout the day but rising sharply in the evening, coinciding with peak EV charging demand. This indicates that while PV generation helps alleviate some curtailment issues, without energy storage, it does not fully resolve challenges associated with high evening demand. When considering the cost-only case, which aims to maximize grid revenue by minimizing residential and EVCS demand curtailment, a distinct operational strategy emerges. This strategy prioritizes residential load delivery, even if it comes at the cost of higher curtailment for PV and increased system losses while maintaining grid stability. As a result, instead of utilizing the full potential of available PV generation, it appears that more power is supplied from the main grid since minimizing PV curtailment was not included as one of the objectives. In addition, EVCS curtailment rises notably, particularly during peak evening demand periods when the grid approaches its capacity limits.
A direct comparison between the PV and EVCS case and the cost-only case reveals several notable differences, as presented in Table 2, while the cost-only scenario introduces notable increases in both PV curtailment and EVCS demand curtailment, it demonstrates a substantial improvement in overall energy delivery. Specifically, unweighted load curtailment is reduced by 43.13%, highlighting the effectiveness of the optimization model in prioritizing total demand satisfaction. However, this gain comes at the expense of increased curtailment in other areas. PV curtailment rises significantly from 0 to 0.0761 p.u., indicating a strong suppression of available renewable generation, primarily due to the absence of PV utilization in the cost optimization strategy. At the same time, EVCS curtailment increases by 40.81%, reflecting a more aggressive limitation on charging demand during periods of network congestion and high residential load, particularly in the evening hours. Moreover, system losses increase by 37.42%, a side effect of the model’s limited utilization of local PV generation. Despite these trade-offs, the net power delivered to end users, measured as unweighted load plus EVCS demand served, improves by 10.22%, indicating that the cost-only model effectively maximizes energy usage within the network constraints, even if it sacrifices some sustainability metrics such as PV utilization.

Table 2.
Comparison of parameters between Average Case 3 (PV and EVCS) and Case 4 (cost-only).
Overall, this study demonstrated that coordinated control of PV and EV resources allows for striking a balance between technical, environmental, and energy justice objectives. The results of the case study clearly show that, with both PV and EV optimally controlled, the proposed model ensures that charging demand is fully met and PV curtailment is maintained close to zero. This indicates not only equitable access to charging energy but also maximized utilization of renewable energy resources, all while maintaining the operational constraints of the power grid.
4.4. Limitations of the Study
There are several limitations associated with the current study. First and foremost, the proposed model was developed and tested under deterministic assumptions. Residential and EVCS demand were assumed known with certainty, and the solar irradiance model ignored the effect of cloud coverage that can change it into a stochastic energy resource. Naturally, a more realistic model should consider uncertainties in EV demand, residential demand, and PV power. This would then require solving the optimization model under uncertainties, for instance using stochastic programming techniques (if the probability distribution functions are known for uncertain parameters) or robust optimization (if the ranges of uncertainties are known, but not their distributions).
Another limitation of the study stems from how EVs were modeled. First, charging stations were represented as an aggregate demand, i.e., not considering individual EVs at the station. This assumption limits the capabilities of the model in reflecting true charging station dynamics by considering the arrival times and charge times of individual vehicles. Further, residential EVs were excluded from the model and assumed to be lumped with the overall residential load. While both EV demand and appliance demand can be viewed as controllable (or demand responsive) loads, they certainly differ in their characteristics, flexibility, and dependence on human behavior. In fact, DR programs designed for residential EVs are different from those targeting individual appliances. Lastly, EVCS demand was assumed relatively flat throughout the day, an assumption that was made for proof of concept purposes. This, however, may not be the case in practice, and the charging station demand may go through non-negligible variations throughout the day, which can affect the dispatch of PV resources and other metrics associated with the grid performance.
5. Conclusions
This study presents a novel VVWC framework that successfully addresses the operational and equity challenges introduced by the high penetration of PV systems and EVs in distribution networks. The proposed solution was formulated as a multi-objective nonlinear mixed-integer optimization model that simultaneously optimizes for energy not served, system losses, PV power curtailment, EV demand curtailment, and system voltage profile. To address equity concerns under constrained grid conditions, DR strategies incorporating energy justice principles were introduced where DR was modeled as voluntary curtailment, but it was applied using criteria from distributional and recognition justice frameworks to ensure that socially vulnerable populations were not disproportionately affected and that the equal distribution of burdens and benefits across the grid were maintained. This addition ensures the proposed solution is not only technically and economically sound but also socially responsible. A realistic approach was adopted in which the distribution grid was modeled by considering asymmetries, unbalanced operation, and the presence of legacy voltage control devices. The results of the case studies demonstrated that optimal coordination between PV and EV resources can enable the utilities to strike a balance between technical, environmental, and energy justice objectives. It was shown that EV charging curtailment can be eliminated while PV curtailment is reduced to almost zero, indicating equitable access to charging demand as well as maximized utilization of renewable energy resources. A comparison was also made between the multi-objective approach proposed here and one in which revenue is the sole criterion. While the latter case improved the total power served and reduced overall load curtailment, it achieved that at the expense of significantly higher PV curtailment and an increase in EVCS unmet demand. Overall, the proposed VVWC approach offers a scalable and socially responsible pathway for managing future distribution grids with high DER integration.
Author Contributions
Both authors have been involved in the various stages of this research. The following details the task assignment. Conceptualization, S.M.; methodology, A.A. and S.M.; software, A.A.; validation, A.A. and S.M.; formal analysis, A.A. and S.M.; investigation, A.A. and S.M.; resources, S.M.; data curation, A.A.; writing—original draft preparation, A.A.; writing—review and editing, S.M.; visualization, A.A.; supervision, S.M.; and project administration, S.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data for this analysis were obtained from publicly available resources.
Conflicts of Interest
The authors declare no conflict of interest.
List of Abbreviations
| Conservation voltage reduction | |
| Demand response | |
| Electric vehicle | |
| Electric vehicle charging station | |
| On-load tap changer | |
| Photovoltaic | |
| Voltage and var control | |
| Voltage, var, and watt control |
Nomenclature
| Indices and Sets | |
| D | Set of nodes. |
| f | Index for objective functions of the multi-objective framework. |
| Indices for buses (nodes). | |
| p | Index for phases. |
| t | Index for time. |
| T | Time horizon of the problem. |
| Parameters | |
| Susceptance of the shunt admittance for bus i connected to phase p. | |
| Susceptance of fixed capacitor for bus i connected to phase p. | |
| Desired energy to be provided to phase p of EVCS at bus i. | |
| Conductance of shunt admittance for bus i connected to phase p. | |
| Conductance of fixed capacitor for bus i connected to phase p. | |
| Maximum current through phase p of the line between nodes i and j. | |
| Rated active power for phase p of EVCS at bus i. | |
| Desired active power for phase p of load at bus i at time t. | |
| Rated active power for phase p of PV at bus i. | |
| Series resistance of the line between phase p of buses i and j. | |
| Maximum apparent power supplied through phase p of the substation (node 1). | |
| Social vulnerability index for demand at bus i. | |
| Target value for objective function f in multi-objective framework. | |
| Binary parameter for existence of a line between phase p of buses i and j. | |
| Binary parameter for presence of a fixed capacitor at phase p of bus i. | |
| Binary parameter for presence of EVCS at phase p of bus i. | |
| Binary parameter for presence of a load at phase p of bus i. | |
| Binary parameter for presence of PV at phase p of bus i. | |
| Binary parameter for presence of a voltage regulator between buses i and j. | |
| Binary parameter for presence of shunt admittance at phase p of bus i. | |
| Series reactance of the line between phase p of buses i and j. | |
| Normalized irradiance level at time t. | |
| Variables | |
| Deficiency variable for objective function f in the multi-objective framework. | |
| Energy provided to phase p of EVCS at bus i over dispatch period. | |
| Magnitude of current in phase p between buses i and j at time t. | |
| Real part of current in phase p between buses i and j at time t. | |
| Imaginary part of current in phase p between buses i and j at time t. | |
| Real part of EVCS current at bus i, phase p, at time t. | |
| Imaginary part of EVCS current at bus i, phase p, at time t. | |
| Real part of demand current at bus i, phase p, at time t. | |
| Imaginary part of demand current at bus i, phase p, at time t. | |
| Real part of PV current injected at bus i, phase p, at time t. | |
| Imaginary part of PV current injected at bus i, phase p, at time t. | |
| Real part of VR primary side current between buses i and j, phase p, at time t. | |
| Imaginary part of VR primary side current between buses i and j, phase p, at time t. | |
| Real part of VR secondary side current between buses i and j, phase p, at time t. | |
| Imaginary part of VR secondary side current between buses i and j, phase p, at time t. | |
| L | Maximum deviation of objective functions from target values. |
| Optimal value of objective function f in the multi-objective framework. | |
| Active power consumed by EVCS at bus i, phase p, at time t. | |
| Active power consumed by demand at bus i, phase p, at time t. | |
| Active power injected by PV at bus i, phase p, at time t. | |
| Reactive power consumed by EVCS at bus i, phase p, at time t. | |
| Reactive power consumed by demand at bus i, phase p, at time t. | |
| Reactive power associated with PV at bus i, phase p, at time t. | |
| Active power supplied by the substation through phase p at time t. | |
| Reactive power supplied by the substation through phase p at time t. | |
| Tap position integer variable for VR between phase p of buses i and j at time t. | |
| Real part of voltage at bus i, phase p, at time t. | |
| Imaginary part of voltage at bus i, phase p, at time t. | |
| Voltage magnitude at bus i, phase p, at time t. | |
References
- Romero Aguero, J.; Khodaei, A. Grid Modernization, DER Integration & Utility Business Models-Trends & Challenges. IEEE Power Energy Mag. 2018, 16, 112–121. [Google Scholar] [CrossRef]
- Mwasilu, F.; Justo, J.J.; Kim, E.K.; Do, T.; Jung, J.W. Electric vehicles and smart grid interaction: A review on vehicle to grid and demand side management. Renew. Sustain. Energy Rev. 2014, 34, 501–516. [Google Scholar] [CrossRef]
- Basu, A.K.; Chowdhury, S.P.; Chowdhury, S.; Paul, S. Microgrids: Energy management by strategic deployment of DERs–A comprehensive survey. Renew. Sustain. Energy Rev. 2011, 15, 4348–4356. [Google Scholar] [CrossRef]
- Verma, R.; Srivastava, S.; Narain, A. Electric Vehicles Challenges, Opportunities, and Future Scope: The Recent Review; Springer: Berlin/Heidelberg, Germany, 2022; pp. 387–396. [Google Scholar] [CrossRef]
- Sanguesa, J.A.; Torres-Sanz, V.; Garrido, P.; Martinez, F.J.; Marquez-Barja, J.M. A Review on Electric Vehicles: Technologies and Challenges. Smart Cities 2021, 4, 372–404. [Google Scholar] [CrossRef]
- Gough, R.; Dickerson, C.; Walsh, C. Vehicle-to-grid feasibility: A techno-economic analysis of EV-based energy storage. Appl. Energy 2017, 192, 12–23. [Google Scholar] [CrossRef]
- Javed, A.H.; Nguyen, P.H.; Morren, J.; Slootweg, J.G.H. Review of operational challenges and solutions for DER integration with distribution networks. In Proceedings of the 2021 56th International Universities Power Engineering Conference (UPEC), Middlesbrough, UK, 31 August–3 September 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Palensky, P.; Dietrich, D. Demand Side Management: Demand Response, Intelligent Energy Systems, and Smart Loads. IEEE Trans. Ind. Inform. 2011, 7, 381–388. [Google Scholar] [CrossRef]
- Albadi, M.; El-Saadany, E. A summary of demand response in electricity markets. Electr. Power Syst. Res. 2008, 78, 1989–1996. [Google Scholar] [CrossRef]
- Siano, P. Demand response and smart grids—A survey. Renew. Sustain. Energy Rev. 2014, 30, 461–478. [Google Scholar] [CrossRef]
- Jenkins, K.; McCauley, D.; Heffron, R.; Stephan, H.; Rehner, R. Energy justice: A conceptual review. Energy Res. Soc. Sci. 2016, 11, 174–182. [Google Scholar] [CrossRef]
- Hernandez, D. Sacrifice along the energy continuum: A call for energy justice. Environ. Justice 2015, 8, 151–156. [Google Scholar] [CrossRef]
- Dugan, J.; Mohagheghi, S. Assessment of Social Vulnerability to Long-Duration Power Outages in the United States. In Proceedings of the 2023 IEEE Green Technologies Conference (GreenTech), Denver, CO, USA, 19–21 April 2023; pp. 123–127. [Google Scholar] [CrossRef]
- Mitra, P.; Heydt, G.; Vittal, V. The impact of distributed photovoltaic generation on residential distribution systems. In Proceedings of the 2012 North American Power Symposium (NAPS), Champaign, IL, USA, 9–11 September 2012; pp. 1–6. [Google Scholar] [CrossRef]
- Alam, M.; Muttaqi, K.; Sutanto, D. A comprehensive assessment tool for solar PV impacts on low voltage three phase distribution networks. In Proceedings of the 2nd International Conference on the Developments in Renewable Energy Technology (ICDRET 2012), Dhaka, Bangladesh, 5–7 January 2012. [Google Scholar]
- Agüero, J.R.; Steffel, S.J. Integration challenges of photovoltaic distributed generation on power distribution systems. In Proceedings of the 2011 IEEE Power and Energy Society General Meeting, Detroit, MI, USA, 24–28 July 2011; pp. 1–6. [Google Scholar] [CrossRef]
- Solanki, S.K.; Ramachandran, V.; Solanki, J. Steady state analysis of high penetration PV on utility distribution feeder. In Proceedings of the PES T&D 2012, Orlando, FL, USA, 7–10 May 2012; pp. 1–6. [Google Scholar] [CrossRef]
- Vlachogiannis, J.G.; Lee, K.Y. Quantum-Inspired Evolutionary Algorithm for Real and Reactive Power Dispatch. IEEE Trans. Power Syst. 2008, 23, 1627–1636. [Google Scholar] [CrossRef]
- Barukčić, M.; Hederić, Ž.; Miklošević, K. Multi objective optimization of energy production of distributed generation in distribution feeder. In Proceedings of the 2014 IEEE International Energy Conference (ENERGYCON), Cavtat, Croatia, 13–16 May 2014; pp. 1325–1333. [Google Scholar] [CrossRef]
- Yu, L.; Czarkowski, D.; de Leon, F. Optimal Distributed Voltage Regulation for Secondary Networks with DGs. IEEE Trans. Smart Grid 2012, 3, 959–967. [Google Scholar] [CrossRef]
- Kulmala, A.; Repo, S.; Järventausta, P. Coordinated Voltage Control in Distribution Networks Including Several Distributed Energy Resources. IEEE Trans. Smart Grid 2014, 5, 2010–2020. [Google Scholar] [CrossRef]
- Falco, M.; Arrigo, F.; Mazza, A.; Bompard, E.; Chicco, G. Agent-based Modelling to Evaluate the Impact of Plug-in Electric Vehicles on Distribution Systems. In Proceedings of the 2019 International Conference on Smart Energy Systems and Technologies (SEST), Porto, Portugal, 9–11 September 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Pieltain Fernández, L.; Gomez San Roman, T.; Cossent, R.; Mateo Domingo, C.; Frías, P. Assessment of the Impact of Plug-in Electric Vehicles on Distribution Networks. IEEE Trans. Power Syst. 2011, 26, 206–213. [Google Scholar] [CrossRef]
- Raouf Mohamed, A.A.; Best, R.; Morrow, D.; Cupples, A.; Bailie, I. Impact of the deployment of solar photovoltaic and electrical vehicle on the low voltage unbalanced networks and the role of battery energy storage systems. J. Energy Storage 2021, 42, 102975. [Google Scholar] [CrossRef]
- Međugorac, M.; Capuder, T.; Skok, M.; Škrlec, D.; Bago, D. On the role and the value of flexibility options in planning of distribution networks with high penetration of electric vehicle charging stations: Case study of Mostar. In Proceedings of the CIRED Porto Workshop 2022: E-Mobility and Power Distribution Systems, Porto, Portugal, 2–3 June 2022; Volume 2022, pp. 414–418. [Google Scholar] [CrossRef]
- Simarro-garcía, A.; Villena-Ruiz, R.; Honrubia-Escribano, A.; Gómez-lázaro, E. Impacts of electric vehicle charging stations on a greek distribution network. In Proceedings of the CIRED Porto Workshop 2022: E-Mobility and Power Distribution Systems, Porto, Portugal, 2–3 June 2022; Volume 2022, pp. 452–456. [Google Scholar] [CrossRef]
- Verzijlbergh, R.A.; Lukszo, Z.; Slootweg, J.G.; Ilic, M.D. The impact of controlled electric vehicle charging on residential low voltage networks. In Proceedings of the 2011 International Conference on Networking, Sensing and Control, Delft, The Netherlands, 11–13 April 2011; pp. 14–19. [Google Scholar] [CrossRef]
- Lopes, J.A.; Soares, F.; Almeida, P.; Moreira da Silva, M. Smart Charging Strategies for Electric Vehicles: Enhancing Grid Performance and Maximizing the Use of Variable Renewable Energy Resources. 2009. Available online: https://repositorio.inesctec.pt/items/31b2cd4a-af96-4b4a-a77f-50dff5cb7052 (accessed on 22 June 2025).
- Pal, A.; Bhattacharya, A.; Chakraborty, A.K. Allocation of EV Fast Charging Station with V2G Facility in Distribution Network. In Proceedings of the 2019 8th International Conference on Power Systems (ICPS), Jaipur, India, 20–22 December 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Boonraksa, T.; Marungsri, B. Optimal Fast Charging Station Location for Public Electric Transportation in Smart Power Distribution Network. In Proceedings of the 2018 International Electrical Engineering Congress (iEECON), Krabi, Thailand, 7–9 March 2018; pp. 1–4. [Google Scholar] [CrossRef]
- Alam, M.S.; Ali Arefifar, S. Optimal Allocation of EV Charging Stations in Distribution Systems Considering Discharging Economy and System Reliability. In Proceedings of the 2021 IEEE International Conference on Electro Information Technology (EIT), Mt. Pleasant, MI, USA, 14–15 May 2021; pp. 1–8. [Google Scholar] [CrossRef]
- Wang, L.; Kwon, J.; Verbas, O.; Rousseau, A.; Zhou, Z. Charging Station Planning to Maximize Extra Load Hosting Capacity in Unbalanced Distribution System. In Proceedings of the 2020 IEEE Power & Energy Society General Meeting (PESGM), Montreal, QC, Canada, 2–6 August 2020; pp. 1–5. [Google Scholar] [CrossRef]
- Ahmad, F.; Iqbal, A.; Ashraf, I.; Marzband, M.; Khan, I. Optimal Siting and Sizing Approach of Plug-in Electric Vehicle Fast Charging Station using a Novel Meta-heuristic Algorithm. In Proceedings of the 2022 2nd International Conference on Emerging Frontiers in Electrical and Electronic Technologies (ICEFEET), Patna, India, 24–25 June 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Tao, Y.; Qiu, J.; Lai, S.; Sun, X.; Zhao, J. Adaptive integrated planning of electricity networks and fast charging stations under electric vehicle diffusion. IEEE Trans. Power Syst. 2023, 38, 499–513. [Google Scholar] [CrossRef]
- Sabillon-Antunez, C.; Melgar-Dominguez, O.D.; Franco, J.F.; Lavorato, M.; Rider, M.J. Volt-VAr Control and Energy Storage Device Operation to Improve the Electric Vehicle Charging Coordination in Unbalanced Distribution Networks. IEEE Trans. Sustain. Energy 2017, 8, 1560–1570. [Google Scholar] [CrossRef]
- Kikusato, H.; Mori, K.; Yoshizawa, S.; Fujimoto, Y.; Asano, H.; Hayashi, Y.; Kawashima, A.; Inagaki, S.; Suzuki, T. Electric Vehicle Charge–Discharge Management for Utilization of Photovoltaic by Coordination Between Home and Grid Energy Management Systems. IEEE Trans. Smart Grid 2019, 10, 3186–3197. [Google Scholar] [CrossRef]
- Wang, L.; Dubey, A.; Gebremedhin, A.H.; Srivastava, A.K.; Schulz, N. MPC-Based Decentralized Voltage Control in Power Distribution Systems with EV and PV Coordination. IEEE Trans. Smart Grid 2022, 13, 2908–2919. [Google Scholar] [CrossRef]
- Dutta, A.; Ganguly, S.; Kumar, C. Coordinated Volt/Var Control of PV and EV Interfaced Active Distribution Networks Based on Dual-Stage Model Predictive Control. IEEE Syst. J. 2022, 16, 4291–4300. [Google Scholar] [CrossRef]
- Ladhiya, H.; C, C. Design of Coordinated Control Method for EV Charging Station and its Impact Mitigation on Power Grid. In Proceedings of the 2024 IEEE International Conference on Interdisciplinary Approaches in Technology and Management for Social Innovation (IATMSI), Gwalior, India, 14–16 March 2024; Volume 2, pp. 1–6. [Google Scholar] [CrossRef]
- Ahmed, M.; Lee, C.; Hassan, M. Optimization-Based Coordinated Charging of EV Fleets and DERs Using Distributed Framework. Energies 2024, 17, 3773. [Google Scholar]
- Lin, J.; Qiu, J.; Tao, Y.; Sun, X. Planning of electric vehicle charging stations with PV and energy storage using a fuzzy inference system. IEEE Trans. Transp. Electrif. 2024, 10, 5894–5909. [Google Scholar] [CrossRef]
- Shi, W.; Li, N.; Xie, X.; Chu, C.C.; Gadh, R. Optimal Residential Demand Response in Distribution Networks. IEEE J. Sel. Areas Commun. 2014, 32, 1441–1450. [Google Scholar] [CrossRef]
- Venkatesan, N.; Solanki, J.; Solanki, S. Residential Demand Response model and impact on voltage profile and losses of an electric distribution network. Appl. Energy 2012, 96, 84–91. [Google Scholar] [CrossRef]
- Hungerford, Z.; Bruce, A.; Macgill, I. The Value of Flexible Load in Power Systems with High Renewable Energy Penetration. Energy 2019, 188, 115960. [Google Scholar] [CrossRef]
- Klaassen, E.; Gerwen, R.; Frunt, J.; Slootweg, J. A methodology to assess demand response benefits from a system perspective: A Dutch case study. Util. Policy 2016, 44, 25–37. [Google Scholar] [CrossRef]
- Roeben, F.; Liu, D.; Reuter, M.; Dahmen, M.; Bardow, A. The demand response potential in copper production. J. Clean. Prod. 2022, 362, 132221. [Google Scholar] [CrossRef]
- Sun, Z.; Li, L. Potential capability estimation for real time electricity demand response of sustainable manufacturing systems using Markov Decision Process. J. Clean. Prod. 2014, 65, 184–193. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).