Abstract
This paper proposes a pipeline leakage detection technology that integrates machine learning algorithms with Dempster–Shafer (DS) evidence theory. By implementing five machine learning algorithms, this study constructs pipeline pressure and flow signal characteristics through wavelet decomposition. The data were normalized and processed using principal component analysis to prepare the algorithm for training. A new method for constructing basic probability functions using a confusion matrix and a simple support function is proposed and compared with the traditional triangular fuzzy number method. The basic probability function of the identification sample is refined by calculating a comprehensive discount factor. Finally, the results from multiple algorithms are fused using DS evidence theory. Experimental results demonstrate that after combining multiple algorithms, the average accuracy improves by 0.1565%, and the precision of the triangular fuzzy number method is enhanced by 0.091%.
1. Introduction
As petroleum and gas pipelines age, their structural integrity deteriorates, which makes pipeline safety a critical concern. Given the flammable and explosive nature of oil and gas products, pipeline leakage incidents can have severe and often irreversible consequences for society. This highlights the importance of effective leakage detection as a fundamental component of pipeline safety management, ensuring the secure and reliable operation of pipeline systems.
Pipeline leakage detection technologies use various techniques to determine whether a leak has occurred by analyzing changes in key parameters. These methods include the negative pressure wave method [1,2], the acoustic method [3,4,5], optical fiber sensing [6], flow modeling [7,8], big data analytics, and machine learning algorithms [9].
Among these, machine learning (ML) algorithms [10,11] have emerged as a highly effective approach for classification and prediction tasks in big data environments. In leakage detection studies, the issue is usually presented as a binary classification task. Several ML algorithms have been widely applied in this domain, including support vector machine (SVM) [12,13,14], logistic regression (LR) [10,11,15], decision tree (Classification and Regression Tree, CART) [16,17], random forest (RF) [18,19,20,21], and backpropagation neural network (BPNN) [22,23,24,25,26]. These algorithms offer high accuracy, ease of implementation, and strong adaptability, making them widely adopted in leakage detection applications. Their continued development has significantly enhanced the precision and efficiency of pipeline leakage detection systems.
In pipeline leakage detection research, single-method approaches are often used to identify leaks, limiting the ability to leverage the advantages of various detection techniques. Moreover, while some systems integrate multiple detection methods, these methods typically operate independently and trigger alarms separately. This results in an excessive number of leakage alarms, creating challenges for operators in managing and verifying alerts. Therefore, there is an urgent need for a unified approach to evaluate leakage alarm information from multiple detection methods, which will enhance the reliability of alarms while reducing false or redundant notifications. In response to these challenges, this study proposes a multi-algorithm fusion framework based on ML and Dempster–Shafer evidence theory (DS) [27,28]. ML algorithms are employed to identify pipeline leakage status. A novel method for constructing basic probability assignment (BPA) functions based on a confusion matrix and a simple support function (SSF) is proposed and compared with the conventional triangular fuzzy number (TFN) method. Furthermore, a discount factor is computed based on the results of multiple algorithms to evaluate the reliability of each algorithm, and the BPA of each sample is adjusted accordingly. Finally, the refined probability assignments are processed using DS evidence fusion theory to generate a unified recognition result, enhancing the precision and reliability of leakage alarms. Therefore, the advantage of this method is that the constructed BPA can be dynamically modified according to the performance of the algorithm, allowing the DS evidence fusion theory to combine the advantages of various algorithms to produce a more reliable BPA and improve the accuracy of the algorithm.
The arrangement of sections and the workflow of this paper are shown in Figure 1. Section 1 provides an overview of the causes of pipeline leakage incidents, their significance, classification, and the development of leakage detection technologies, with a focus on advancements driven by ML algorithms in recent years. Section 2 presents the theoretical foundations and computational processes of ML models. It outlines the calculation process of TFN, the determination of discount factors, and the application of DS evidence fusion theory in pipeline leakage detection systems. Section 3 presents and analyzes the target recognition results obtained using the methods outlined in Section 2. Section 4 presents the main conclusions of this study, summarizing the key innovations, findings, and contributions of the study while discussing future research directions and potential advancements in pipeline leakage detection.
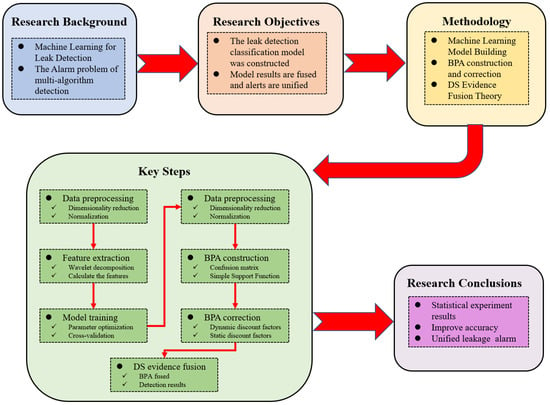
Figure 1.
The workflow chart of the article.
2. Materials and Methods
2.1. Machine Learning Algorithms
2.1.1. Support Vector Machines
The core idea of SVM is to maximize the margin of classification. The basic model is a linear classifier with the maximum margin in the feature space. Using a kernel function transforms it into a nonlinear classifier. It has several advantages, including high efficiency for high dimensional data, strong generalization ability, a kernel function that can adapt to complex nonlinear decision boundaries, and robustness.
The regression function of a nonlinear SVM is expressed as:
where represents the weight vector, is the kernel function, and denotes the bias term, b* = 0.5640. A dataset is considered, where .
An appropriate kernel function and a penalty factor are selected, and initial C = 1. Then, the problem is formulated as a convex quadratic programming optimization, as follows:
Solving this optimization problem yields the optimal solution , .
From this, is selected, with satisfying the condition , with the bias term computed as follows:
For small datasets, the Lagrange operator is introduced to transform the problem into a least squares optimization, ultimately yielding the following function:
where is a kernel function, which is calculated as follows:
where x and z represent the sample points, is the square of the Euclidean distance between two points, and σ is used to control the super parameter of the width of the Gaussian function, with a value of 1.8708.
2.1.2. Logistic Regression
When logistic regression (LR) is used for classification, the primary objective is to minimize the cost function, which quantifies the difference between the predicted results and the actual values. The optimization process yields the optimal model parameters. The advantages include strong interpretability of the model and output, high computational efficiency, suitability for big data, strong ability to model linear relationships, regularization to avoid overfitting, and good robustness to noise and missing data.
The sigmoid function, which maps any input to a probability value between 0 and 1, is depicted in Figure 2.
where x is the normalized input vector, θ are the model coefficients to be solved, , and z is a linear combination of the input features. The hypothesis function for logistic regression is formulated as follows:
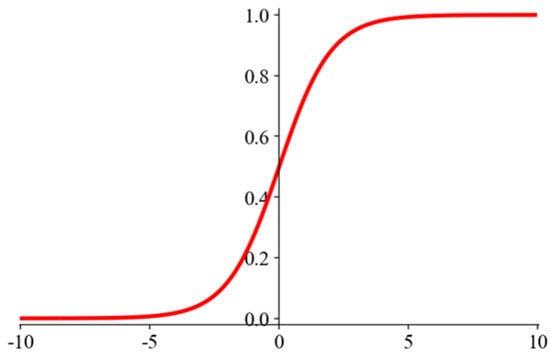
Figure 2.
Sigmoid Function.
The cost function is expressed as follows:
where m is the number of training samples, represents the true label in the data set, is the model predicted value, and is the regularization term to mitigate overfitting. To minimize the cost function, the gradient descent update rule is applied as follows:
where α is the learning rate, initial α = 0.1, λ is the regularization penalty factor, and initial λ = 1.
2.1.3. Decision Tree and Random Forest
Decision trees (Classification and Regression Tree, CART) and random forests (RF) are both tree-based machine learning algorithms. CART starts at the root node, evaluates feature attributes, selects an output branch, and ultimately reaches a leaf node that contains the final decision result. In contrast, random forest is an ensemble learning method that combines multiple decision trees to enhance performance. The final classification result is calculated by averaging the results of multiple decision trees. The advantages of decision trees include high interpretability, low data preprocessing requirements, handling of nonlinear relationships and complex boundaries, high computational efficiency, fast training speed, and in-sensitivity to noise and outliers. The advantages of RF include high prediction accuracy and generalization ability, processing of high-dimensional data and complex nonlinear relationships, evaluation of global feature importance, and parallel calculation.
During the construction of each decision tree, the node-splitting process is guided by a measure of feature purity. Each feature split results in a reduction in information gain. In classification trees, the Gini coefficient is commonly used to evaluate the purity of a node. It is calculated as follows:
where T represents the training set, k is the number of categories, k = 2, and pi represents the probability that a sample in T belongs to category i. The Gini coefficient is calculated for sub-nodes T1 and T2 as follows:
2.1.4. Back Propagation Neural Networks
Back Propagation Neural Networks (BPNN) are a type of feedforward network that utilizes error backpropagation for optimization. The overall structure and functioning of BPNN are illustrated in Figure 3. Its self-learning process involves both information forward propagation and error backpropagation. During forward propagation, the data are passed from the input layer. If the actual output of the output layer does not meet the expectation, error backpropagation is performed, and the weights of each node layer are adjusted according to the error. Because of the ability to adjust for reverse errors, determining the relationship between input and output is easy. Its advantages include strong nonlinear modeling ability, self-learning feature representation, parallel computing ability, and good scalability, which can suppress overfitting and improve generalization performance, as well as suitability for high-dimensional and complex data. The self-learning process of BPNN consists of two main stages: forward propagation of information and backpropagation of errors [26].
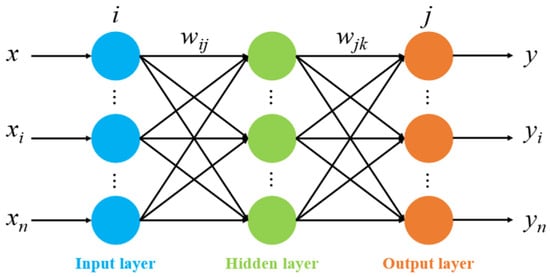
Figure 3.
BPNN structure diagram.
Let each sample be denoted as , where represensts the input features and denotes the target values.
The process begins by using the sample feature to calculate the ai for each node in the hidden layer and the output yi for the output layer. Then, we calculate error for the output layer nodes as follows:
In addition, error for the hidden layer nodes is calculated as follows:
where wki represents the weight between node i and its next layer node k, and denotes the error associated with the output node.
Finally, the weights are updated as follows:
where wji is the weight from node i to node j, η is the learning rate, and η = 0.001. In the initial state, where i = 7, the error , and the weight matrix wji is as shown in Table 1:

Table 1.
The weight calculation result of BPNN when i = 7.
2.2. Triangular Fuzzy Number
For target recognition, the minimum, maximum, and average values of a specific indicator from the sample data can be obtained [28]. A TFN can be constructed based on these values. TFN is especially important in DS evidence fusion theory because it can deal with multi-source heterogeneous data better than other methods in the field of multi-sensor fusion. At the same time, it is an important method to construct BPA functions based on the membership degree of TFN. Its advantage is that the mathematical characteristics of TFN make the operation rules clear, the computational complexity is low, the calculation is efficient and simple to implement, the modeling is intuitive, and the interpretability is strong.
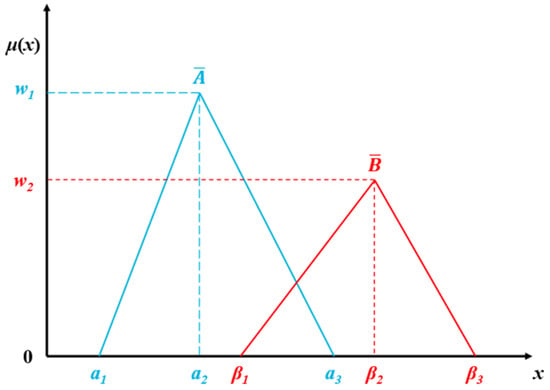
Figure 4.
Schematic diagram of triangle fuzzy numbers.
The membership function for TFN is constructed as follows:
where a, b, and c are the minimum, maximum, and mean, respectively, w is the membership function value when x = b, initial w = 1.0, , and .
Assume the recognition framework for target recognition is . For an observed target , the classifiers S1, …, Sk, …, SK correspond to the K indicators of the recognition category. For each category θi, the recognition result vector of each classifier SK for each training sample is defined as .
Where represents the measure that classifier SK assigns to the sample belonging to the category θi. Assuming θi has MK samples, for indicator k, the following calculations are performed as follows:
The strategy for generating BPA using the TFN representation model can be described as follows:
(1) Case 1: If m = 0, this indicates that the measurement value for indicator k is outside the minimum and maximum range for all categories. The measurement value does not intersect with any TFN representation model, i.e., m(Θ) = 1 or m() = 1.
(2) Case 2: If m = 1, the measurement value V intersects with the TFN representation of a single-element proposition. In this case, the ordinate of the intersection point represents the support of the measurement value V for the single-element proposition.
(3) Case 3: If m > 1, the measurement value V intersects with the TFN representation of multiple propositions. The maximum ordinate of the intersection point is considered the support of the measurement value V for the single-element proposition.
(4) Generating BPA: After obtaining the support for each proposition, the BPA can be generated using the following two methods:
The maximum membership value is subtracted from 1 and is assigned to the whole set Θ. This represents the part of the information considered to be completely unknown, i.e., , and initial = 0.
The support values of each proposition obtained from the above strategy to calculate the BPA for each proposition are normalized as follows:
Then, the calculation formula of W1 is used to normalize the new support and obtain the BPA for each proposition.
2.3. Machine Learning Algorithms in Pipeline Leak Detection
2.3.1. Training Machine Learning Algorithms
- Dataset
This study utilizes Pipeline Studio V4.0.1.0 software to simulate pipeline leakage detection, generating pipeline operation data as input data for ML algorithms. A total of 150 simulated leakage datasets were generated, with each simulation providing both normal operation and leakage data, resulting in a total of 300 datasets. The numerical simulation considers variations in starting pressure, pipeline diameter, and leakage. The simulation parameters are summarized in Table 2.

Table 2.
Parameter selection range for leakage data.
The schematic diagram of the simulated pipeline model is shown in Figure 5.
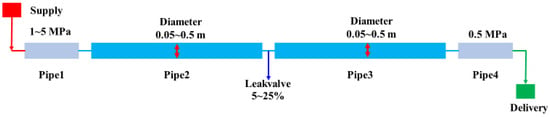
Figure 5.
Schematic diagram of the simulation pipeline model.
- 2.
- Features
For the pipeline leakage detection problem, this study directly selects pressure and flow as the primary features. In many pipeline leakage detection methods, common features include energy and envelope spectrum entropy. In this paper, wavelet packet analysis is employed to construct energy features. The process involves performing wavelet packet analysis on the data using MATLAB R2016a V9.0 software, followed by calculating the energy of the decomposed signal [14].
- 3.
- Data dimensionality reduction
To reduce the dimensionality of the data, the principal component analysis (PCA) algorithm is applied.
- 4.
- Data preprocessing
Data preprocessing refers to the transformation of raw data into a format suitable for model training, aiming to enhance the quality of the input data. In this study, both flow and pressure data are normalized to map them to the [0, 1] range. The normalization process is defined as follows:
- 5.
- Algorithm training
The grid search method is used to train the model, and 5-fold cross-validation is employed to evaluate the model’s performance. This process aims to determine the optimal parameter combination to enhance the algorithm’s efficiency. According to the experience of a large number of experiments, the selection range for the initial values of the model parameters is presented in Table 3.

Table 3.
Selection range of model parameters.
- 6.
- Result evaluation
To evaluate the classification ability of the model, a confusion matrix and overall precision are utilized.
The target classifiers for pipeline leakage detection based on each algorithm were implemented in Python V3.8.5, with the Sklearn library handling all classifier functionalities. The calculation process is depicted in Figure 6. The training process of the algorithm includes obtaining the data set through numerical simulation, constructing the features of the data, and calculating the energy features after the data are decomposed by a wavelet packet. The PCA algorithm is used to reduce the dimensions of the data, which are then normalized. Finally, the machine learning model is trained, and the target is recognized.
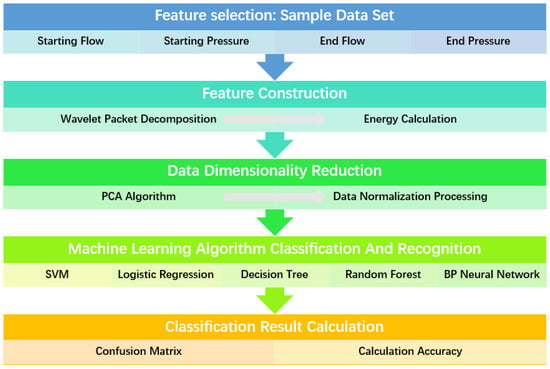
Figure 6.
ML algorithm that classifies sample targets.
2.3.2. Construction of the Basic Probability Assignment (BPA) Function
In the multi-information fusion model proposed in this paper, four pieces of evidence (starting flow, ending flow, starting pressure, and ending pressure) are used, with five algorithm classifiers trained on these respective datasets. The recognition framework is Θ = (leakage, no leakage), where event A represents leakage and event B represents no leakage. The algorithm constructs the BPA, which consists of the following steps:
(1) Method 1: BPA calculation using Xu’s method: For a given classifier, the classification result is expressed by the confusion matrix Ck, which is then normalized. This method was previously proposed in [27].
where , with representing the sample size for a specific category, and is the total sample size for the i-th category, defined as .
Specifically, for the classifier treating output category ωj, the BPA is calculated as follows:
(2) Method 2: BPA calculation using SSF (simple support function). The BPA calculation process based on a SSF was proposed by Xie [28]. The BPA is given as follows:
where .
This paper uses both of the above strategies to calculate the BPA and compares them to explore a more accurate BPA construction method.
2.4. Calculation of Comprehensive Discount Factor
2.4.1. Static Discount Factors α and β
There are two types of static discount factors, α and β, each calculated differently and exhibiting distinct capabilities. This study compares both methods.
where αi represents the static discount factor of the i-th sample, N is the total number of samples, BPAi represents the BPA of the i-th sample, BPA0 denotes the BPA of the actual output for the sample, and DBBA represents the Jousselme distance.
The calculation for the reliability of the classifier is expressed as follows:
The reliability actor is given as follows:
The static discount factor is calculated as follows:
2.4.2. Dynamic Discount Factor γ
To evaluate the mutual support reliability between classifiers, the dynamic discount factor γ is introduced. Its calculation process is as follows:
where mi and mj are the BPA calculated by the i-th and j-th classifiers of the training sample Oi, respectively. ρ represents the correlation coefficient, is the support degree, is the relative support degree, and is the absolute reliability.
2.4.3. Comprehensive Discount Factor
By combining both static discount factors, a comprehensive factor for the k-th classifier is computed using the weighted average, with initial = 0.5.
2.5. Dempster–Shafer Evidence Theory
In Dempster–Shafer (DS) evidence theory [29], the identification framework Θ is defined as a set of n mutually exclusive elements, , where θi (1 ≤ i ≤ n) represents a single subset of Θ that contains all objects. The power set represents the set of all subsets of Θ.
2.5.1. DS Evidence Fusion Rules
Two credibility functions, Bel1 and Bel2 [30], are defined in the same framework Θ, with corresponding assignments m1 and m2. The focal elements of evidence are and . The basic probability assignments for these focal elements are and ). Given that , the basic credibility distribution of the two credibility functions, Bel1 and Bel2, is computed by the following function , expressed as follows:
where φ denotes the empty set, and , considering m1, m2,…, mn.
2.5.2. Application of Multi-Algorithm Fusion in Leak Detection
Discount operations based on the Shafer discount rule are used for identifying target . After obtaining the comprehensive discount factor from the confusion matrix of classifier Sk, the comprehensive reliability factor is calculated. Guided by this approach, the Basic Probability Assignment (BPA) output by classifier Sk for the identification target Oi is adjusted according to its corresponding comprehensive discount factor.
Once the discount factor is determined by evaluating the classifiers’ reliability, it is applied to the output evidence of the local classifier, thereby enabling the discount operation on the respective BPA [31]. This paper employs the classical Shafer discount rule for this purpose. The rule is defined as follows:
where initial = 0.5. By applying the Shafer discount rule, the modified BPA is obtained as . Finally, after applying a betting transformation, the final is derived and used as the input for the Dempster–Shafer (DS) decision algorithm.
The model progression procedure is depicted in Figure 7. The calculation process of the model includes the following steps: first, the confusion matrix is obtained from the classification results of the machine learning algorithm, which is then normalized, and the BPA function is calculated using Methods 1 and 2. Then, the static, dynamic, and comprehensive discount factors (α, β, γ) are calculated, and the BPA is corrected using various combinations of discount factors. Finally, the BPA is combined with DS evidence to produce a unified classification result.

Figure 7.
Process of modifying BPA and fusion.
3. Results
3.1. PCA Calculation Results
The 4-dimensional pressure flow data at both ends of the pipeline is decomposed using wavelet transformation. Each signal is further decomposed into 8-dimensional data, which enables the calculation of the signal’s energy. After performing wavelet analysis on the dataset to construct features, a 32-dimensional dataset is obtained. However, for the selected ML algorithm, the dimensionality of the data is too high, necessitating dimensionality reduction. This study utilizes the PCA algorithm for this purpose. The PCA calculation results are presented in Figure 8 and Table 4.
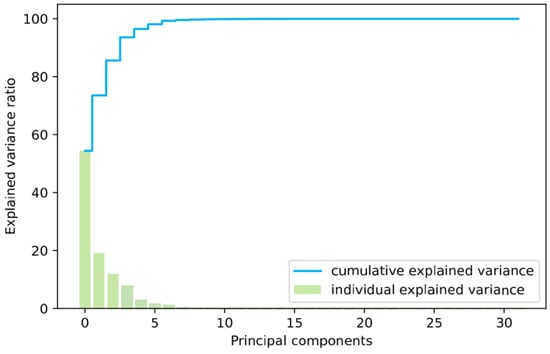
Figure 8.
Explained variance calculation for PCA dimensionality reduction.

Table 4.
Principal component Fk values for PCA dimensionality reduction.
3.2. Classification Results of ML Algorithms
3.2.1. Classification Results
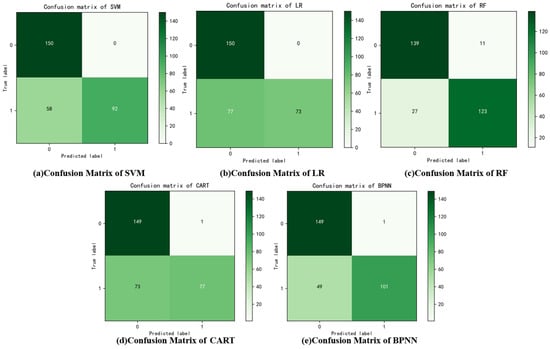
Figure 9.
Classification results of different algorithms.

Table 5.
Comparison of classification accuracy across various algorithms.
3.2.2. Results of Discount Factor
The average dynamic, static, and comprehensive discount factor results are calculated according to the BPA constructed using Method 1, which are shown in Table 6 and Table 7, while the results of Method 2 are shown in Table 8 and Table 9.

Table 6.
Calculation results of different discount factors in Method 1.

Table 7.
Calculation results of comprehensive discount factors using Method 1.

Table 8.
Calculation results of different discount factors in Method 2.

Table 9.
Calculation results of comprehensive discount factors in Method 2.
3.2.3. Calculation Results of DS Evidence Fusion
The classification accuracy of multi-algorithm fusion based on DS evidence theory using different methods is shown in Table 10. The comparison of the classification accuracy of the TFN method using DS fusion is presented in Table 11.

Table 10.
Comparison of DS fusion results for different methods.

Table 11.
Classification accuracy of TFN.
4. Discussion
As shown in Figure 8 and Table 4, the cumulative variance of the first seven principal components exceeds 99%, which is sufficient to capture the main characteristics of the dataset. Consequently, the original dataset is reduced to a 7-dimensional form.
The classification and recognition results of each algorithm are displayed in Figure 9 and Table 5. The classification accuracies for each algorithm are as follows: SVM (0.807%), LR (0.743%), RF (0.873%), CART (0.753%), and BPNN (0.834%). The average accuracy across all algorithms is 0.802%. Among these, the RF algorithm achieves the highest accuracy due to its ensemble nature. The BPNN algorithm follows closely, as its neural network structure, with a large number of neurons, provides a more effective simulation of the data, yielding better classification performance.
Method 1 calculates the average discount factor based on Xu’s method, with the results for α, β, and γ presented in Table 6. It is evident that the LR and CART algorithms exhibit a larger discount for α and β, while the RF algorithm shows a higher discount for γ. The results of the comprehensive discount factor are presented in Table 7. It can be observed that the combination of α + γ yields a larger overall discount, whereas the combination of β + γ results in a smaller discount. Additionally, both combinations lead to greater discounts for the LR and CART algorithms. Furthermore, Method 2 calculates the average discount factor using the SSF method. The results for α, β, and γ are presented in Table 8. It is evident that the average static discount factors α and β exhibit a larger discount for the LR and CART algorithms, whereas the average dynamic discount factor γ indicates a higher discount for the RF algorithm. The calculation results of the comprehensive discount factor are shown in Table 9. It can be observed that the combination of α + γ yields a larger overall discount, while the combination of β + γ results in a smaller discount. Both combinations also lead to larger discounts for the LR and CART algorithms, a trend that is consistent with the results from Method 1.
The calculation results of the multi-algorithm fusion based on DS evidence theory for different methods are presented in Table 10. It is evident that the classification accuracy for the BPA method based on Xu’s study’s findings is 0.983% and 0.947%. For the BPA method using SSF, the classification accuracy is 0.977% and 0.923%. Additionally, the classification accuracy using the comprehensive factor α + γ is higher than that of β + γ, with increases of 0.006% and 0.024%, respectively. Overall, the classification accuracy achieved by the DS evidence fusion algorithm surpasses that of single ML algorithms.
In addition, the accuracy comparison for the TFN method is presented in Table 11. Before the DS evidence fusion, the classification accuracy is 0.814%, 0.785%, 0.823%, and 0.772%, with an average precision of 0.799%. After the DS evidence fusion, the classification accuracy improves to 0.903%, 0.873%, 0.903%, and 0.880%, with an average precision of 0.890%. The classification accuracy of the comprehensive factor-modified BPA method proposed in this paper is significantly higher than the traditional TFN-based BPA method. Moreover, the target recognition and BPA construction method using ML-based approaches outperform the traditional BPA construction method of TFN.
The multi-algorithm fusion method is effective because the DS evidence fusion theory can combine the detection results of each ML algorithm and calculate the comprehensive discount factor of the BPA of each algorithm for the sample, resulting in higher accuracy. Specifically, for samples with conflicting classification results in ML algorithms, considering the difference in recognition ability of each algorithm for different categories and the mutual support between algorithms, the correct classification results in the DS evidence fusion process are increased by the comprehensive discount factor to modify the BPA, and the classification accuracy of pipeline leak detection is improved. In addition, DS evidence fusion will provide a unified detection result, potentially reducing false and repeated alarms in the leak detection system.
On the other hand, the reliability of the performance indicators of the classification algorithm is tested, and the confidence interval of the accuracy quantifies the estimation uncertainty of the model accuracy. Table 12 and Figure 10 show the calculation results for each algorithm’s accuracy and 95% confidence interval. The analysis of the confidence interval reveals that the interval range of each algorithm is large, and its credibility and accuracy are low.

Table 12.
Comparison of 95% confidence intervals for the accuracy of various ML algorithms.
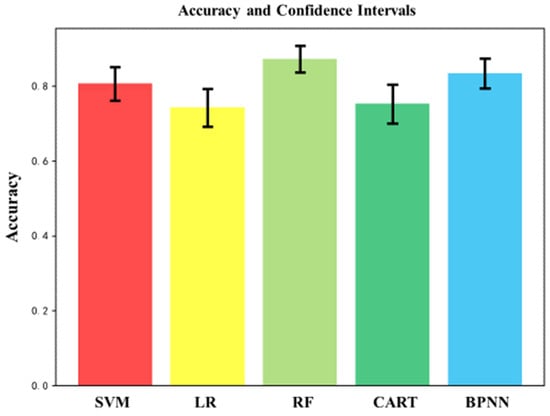
Figure 10.
Comparison of accuracy and confidence intervals for various algorithms.
The accuracy and confidence intervals calculated using the DS fusion method are shown in Table 13 and Figure 11. The analysis of the confidence interval indicates that the interval range of the DS fusion method is smaller, and the calculation accuracy and reliability of the algorithm are greater.

Table 13.
Comparison of DS fusion 95% confidence interval results for different methods.
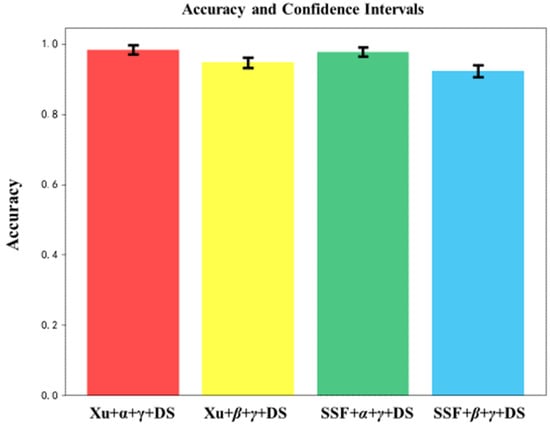
Figure 11.
Comparison of accuracy and 95% confidence intervals of DS fusion results for different methods.
The statistical test determines whether the difference in the performance of the classification algorithm is statistically significant. That is, it determines whether there is a significant difference in performance between two classifiers on the same dataset. The t-test was conducted with the following null hypothesis H0: there is no significant difference between the two models. The significance level is α = 0.05. If the calculated p-value is less than α, the null hypothesis is rejected, indicating a significant difference in performance between the two models. Otherwise, the null hypothesis is accepted, and the model performance difference is insignificant. The significance levels of the machine learning algorithm and the algorithm fused in this paper were compared, and their p-values were calculated as shown in Table 14. We can see that all p-values < 0.05, indicating that the null hypothesis is rejected and that the differences between the algorithms are significant.

Table 14.
Comparison of p-values calculated by machine learning and fusion algorithms.
The fused methods were compared for significance levels, and p-values were calculated, as shown in Table 15. It can be seen that in Xu + α + γ + DS of Method 1 and SSF + α + γ + DS of Method 2, the calculated p-value is 0.23267 > 0.05; thus, the null hypothesis is accepted, and the difference between these two construction methods is not significant. The other p-values < 0.05 reject the null hypothesis and indicate a significant difference between the various algorithms.

Table 15.
The p-value comparison was calculated between the fusion methods.
The robustness of the method proposed in this paper can be addressed through data preprocessing, which uses standardization and normalization methods to process the data. During the feature selection, a single feature is avoided, and flow and pressure data are used for feature extraction. In the model selection and training, the regularization of LR, the dropout parameter in BPNN, and cross-validation in the model training process are used to prevent overfitting and improve the robustness of the method. In addition, the robustness of the method can be further improved by including sensor noise or random disturbance in the data, as well as actual pipeline leakage data, to enrich the dataset.
The limitation of this paper is that only the flow and pressure are considered in the data, and no actual pipeline leakage data are included. In order to apply the algorithm to the detection of actual leakage events, the data sample size should be larger. Only the leakage results from the ML algorithm were fused, but the detection results from the traditional physical model were not. In subsequent research, real leakage data and multi-source sensor data, such as sound, will be considered to build more waveform, time, and frequency domain features, and other BPA construction methods will be investigated for decision fusion and other methods for improvement. At the same time, heuristic optimization methods can be considered to optimize the hyperparameters of the model, while deep learning algorithms, such as the Long Short Term Memory network (LSTM), convolutional neural network (CNN), and other models, can be used for classification and recognition.
5. Conclusions
This paper proposes a multi-algorithm fusion method based on the ML and DS evidence fusion theory. Various machine learning models, such as SVM, LR, CART, RF, and BPNN algorithms, are used to identify pipeline leakage targets. The energy calculation method of wavelet packet analysis is used for feature construction, and the PCA algorithm is used to reduce the dimension of the data, and then the data are normalized. Two BPA construction methods based on Xu and SSF methods are proposed, as well as the comprehensive discount factor that includes both static discount factors (α, β) and dynamic discount factors (γ). A BPA correction scheme based on these comprehensive discount factors is proposed. To achieve uniform recognition results and improve alarm accuracy, this paper proposed a BPA fusion method based on DS evidence fusion. After fusing the two ML algorithms, the average accuracy is increased by 0.1565%, and the average accuracy is increased by 0.091% after fusing the TFN method.
Future research can focus on developing a unified evaluation framework that integrates both prior knowledge-based methods with data-driven analysis. Specifically, for alarm results generated by traditional techniques, such as pressure analysis and leak detection models, it would be valuable to explore how to develop a comprehensive and unified evaluation method that combines multiple algorithms. This approach could then be enhanced with emerging ML algorithms to achieve more cohesive analysis results, ultimately improving the precision and effectiveness of the system.
Author Contributions
Conceptualization, Y.L. and Q.G.; Methodology, Y.L., Q.G. and S.W.; Software, Y.L. and Q.G.; Validation, W.X. and S.W.; Formal analysis, W.X.; Investigation, W.X.; Resources, W.X. and Q.G.; Data curation, Y.L. and W.X.; Writing—original draft, Y.L.; Writing—review & editing, Y.L.; Visualization, Q.G. and S.W.; Supervision, S.W.; Project administration, S.W.; Funding acquisition, S.W. All authors have read and agreed to the published version of the manuscript.
Funding
The authors gratefully acknowledge the financial support from the Natural Science Foundation of Shaanxi Province (No. 2023-JC-YB-597).
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Conflicts of Interest
Author Qiao Guo was employed by the company SUPCON Technology Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Abbreviations
| DS | Dempster–Shafer |
| PCA | Principal Component Analysis |
| ML | Machine Learning |
| SVM | Support Vector Machine |
| LR | Logistic Regression |
| CART | Classification and Regression Tree |
| RF | Random Forest |
| BPNN | Back Propagation Neural Network |
| BPA | Basic Probability Assignment |
| TFN | Triangular Fuzzy Number |
| SSF | Simple Support Function |
| LSTM | Long Short-Term memory network |
| CNN | Convolutional Neural Network |
References
- Aymon, L.; Decaix, J.; Carrino, F.; Mudry, P.-A.; Mugellini, E.; Khaled, O.A.; Baltensperger, R. Leak Detection Using Random Forest and Pressure Simulation. In Proceedings of the 2019 6th Swiss Conference on Data Science (SDS), Bern, Switzerland, 14 June 2019; IEEE: New York, NY, USA, 2019; pp. 109–110. [Google Scholar]
- Cruz, R.P.; da Silva, F.V.; Fileti, A.M.F. Machine Learning and Acoustic Method Applied to Leak Detection and Location in Low-Pressure Gas Pipelines. Clean Technol. Environ. Policy 2020, 22, 627–638. [Google Scholar] [CrossRef]
- Lukonge, A.B.; Cao, X.; Pan, Z. Experimental Study on Leak Detection and Location for Gas Pipelines Based on Acoustic Waves Using Improved Hilbert–Huang Transform. Am. Soc. Civ. Eng. 2021, 12, 4020072. [Google Scholar] [CrossRef]
- Ting, L.L.; Tey, J.Y.; Tan, A.C.; King, Y.J.; Rahman, F.A. Acoustic Emission and Dual-Tree Complex Wavelet Transform with Soft Threshold De-Noising to Enhance Pipeline Leak Detection and Location; Springer: Singapore, 2021; pp. 79–92. [Google Scholar]
- Xie, Y.; Xiao, Y.; Liu, X.; Liu, G.; Jiang, W.; Qin, J. Time-Frequency Distribution Map-Based Convolutional Neural Network (CNN) Model for Underwater Pipeline Leakage Detection Using Acoustic Signals. Sensors 2020, 20, 5040. [Google Scholar] [CrossRef]
- Stajanca, P.; Chruscicki, S.; Homann, T.; Seifert, S.; Schmidt, D.; Habib, A. Detection of Leak-Induced Pipeline Vibrations Using Fiber-Optic Distributed Acoustic Sensing. Sensors 2018, 18, 2841. [Google Scholar] [CrossRef]
- Li, J.; Wu, Y.; Zheng, W.; Lu, C. A Model-Based Bayesian Framework for Pipeline Leakage Enumeration and Location Estimation. Water Resour. Manag. 2021, 35, 4381–4394. [Google Scholar] [CrossRef]
- Chuka, C.E.; Freedom, I.H.; O, U.A. Transient Model-Based Leak Detection and Localization Technique for Crude Oil Pipelines: A Case of N.P.D.C, Olomoro. Saudi J. Eng. Technol. 2016, 1, 37–48. [Google Scholar] [CrossRef]
- Prasad, R.E.J.; Senthil, M.; Yadav, A.; Gupta, P.; Anusha, S.K. A Comparative Study of Machine Learning Algorithms for Gas Leak Detection. In Proceedings of the Inventive Communication and Computational Technologies, Proceedings of ICICCT 2020, Tamil Nadu, India, 28–29 May 2020; Springer: Singapore, 2021; Volume 1, pp. 81–90. [Google Scholar]
- Mashhadi, N.; Shahrour, I.; Attoue, N.; Khattabi, J.E.; Aljer, A. Use of Machine Learning for Leak Detection and Localization in Water Distribution Systems. Smart Cities 2021, 4, 1293–1315. [Google Scholar] [CrossRef]
- Kammoun, M.; Kammoun, A.; Abid, M. Experiments Based Comparative Evaluations of Machine Learning Techniques for Leak Detection in Water Distribution Systems. Water Supply 2021, 22, 628–642. [Google Scholar] [CrossRef]
- Cai, Z.; Dziedzic, R.; Li, S.S. Water Distribution System Leak Detection Using Support Vector Machines. In Proceedings of the Canadian Society of Civil Engineering Annual Conference 2021, Virtual, 26–29 May 2021; CSCE 2021. Springer Nature: Singapore, 2022; Volume 250, pp. 491–499. [Google Scholar]
- Xu, T.; Zeng, Z.; Huang, X.; Li, J.; Feng, H. Pipeline Leak Detection Based on Variational Mode Decomposition and Support Vector Machine Using an Interior Spherical Detector. Process Saf. Environ. Prot. 2021, 153, 167–177. [Google Scholar] [CrossRef]
- Xiao, R.; Hu, Q.; Li, J. Leak Detection of Gas Pipelines Using Acoustic Signals Based on Wavelet Transform and Support Vector Machine. Measurement 2019, 146, 479–489. [Google Scholar] [CrossRef]
- Choudhary, P.; Modi, A.; Botre, B.A.; Akbar, S.A. Leak Detection in Smart Water Distribution Network. In Proceedings of the 4th International Conference on Emerging Technologies, Micro to Nano, 2019: (ETMN 2019), Pune, India, 16–17 December 2019; AIP Publishing: Melville, NY, USA, 2021; Volume 2335, p. 050007. [Google Scholar]
- Shen, Y.; Cheng, W. A Tree-Based Machine Learning Method for Pipeline Leakage Detection. Water 2022, 14, 2833. [Google Scholar] [CrossRef]
- Chen, Z.; Xu, X.; Du, X.; Zhang, J.; Yu, M. Leakage Detection in Pipelines Using Decision Tree and Multi-Support Vector Machine. In Proceedings of the 2017 2nd International Conference on Electrical, Control and Automation Engineering (ECAE 2017), Xiamen, China, 24–25 December 2017; Atlantis Press: Paris, France, 2017; pp. 327–331. [Google Scholar]
- Nguyen, T.-K.; Ahmad, Z.; Kim, J.-M. Leak State Detection and Size Identification for Fluid Pipelines with a Novel Acoustic Emission Intensity Index and Random Forest. Sensors 2023, 23, 9087. [Google Scholar] [CrossRef]
- Chi, Z.; Li, Y.; Wang, W.; Xu, C.; Yuan, R. Detection of Water Pipeline Leakage Based on Random Forest. J. Phys. Conf. Ser. 2021, 1978, 012044. [Google Scholar] [CrossRef]
- Lučin, I.; Lučin, B.; Čarija, Z.; Sikirica, A. Data-Driven Leak Localization in Urban Water Distribution Networks Using Big Data for Random Forest Classifier. Mathematics 2021, 9, 672. [Google Scholar] [CrossRef]
- Ning, F.; Cheng, Z.; Meng, D.; Wei, J. A Framework Combining Acoustic Features Extraction Method and Random Forest Algorithm for Gas Pipeline Leak Detection and Classification. Appl. Acoust. 2021, 182, 108255. [Google Scholar] [CrossRef]
- Zhou, J.; Lin, H.; Li, S.; Jin, H.; Zhao, B.; Liu, S. Leakage Diagnosis and Localization of the Gas Extraction Pipeline Based on SA-PSO BP Neural Network. Reliab. Eng. Amp; Syst. Saf. 2023, 232, 109051. [Google Scholar] [CrossRef]
- Wang, W.; Mao, X.; Liang, H.; Yang, D.; Zhang, J.; Liu, S. Experimental Research on In-Pipe Leaks Detection of Acoustic Signature in Gas Pipelines Based on the Artificial Neural Network. Measurement 2021, 183, 109875. [Google Scholar] [CrossRef]
- Song, Y.; Li, S. Gas Leak Detection in Galvanised Steel Pipe with Internal Flow Noise Using Convolutional Neural Network. Process Saf. Environ. Prot. 2021, 146, 736–744. [Google Scholar] [CrossRef]
- Jia, Z.; Ren, L.; Li, H.; Sun, W. Pipeline Leak Localization Based on FBG Hoop Strain Sensors Combined with BP Neural Network. Appl. Sci. 2018, 8, 146. [Google Scholar] [CrossRef]
- Pérez-Pérez, E.J.; López-Estrada, F.R.; Valencia-Palomo, G.; Torres, L.; Puig, V.; Mina-Antonio, J.D. Leak Diagnosis in Pipelines Using a Combined Artificial Neural Network Approach. Control Eng. Pract. 2021, 107, 104677. [Google Scholar] [CrossRef]
- Chen, X.; Xu, Y.; Guo, H.; Hu, S.; Gu, C.; Hu, J.; Qin, X.; Guo, J. Comprehensive Evaluation of Dam Seepage Safety Combining Deep Learning with Dempster-Shafer Evidence Theory. Measurement 2024, 226, 114172. [Google Scholar] [CrossRef]
- Xie, W.; Liu, Y.; Wang, X.; Wang, J. The Pipeline Leak Detection Algorithm Based on D-S Evidence Theory and Signal Fusion Mechanism. Alex. Eng. J. 2023, 85, 218–235. [Google Scholar] [CrossRef]
- Yannian, W.; Zhuangde, J. Decision Fusion Framework in Diagnostic and Prognostic Assessment of Long-Distance Oil Pipeline Leakage and Damage Based on Dempster–Shafer Theory. J. Phys. Conf. Ser. 2005, 13, 349–352. [Google Scholar] [CrossRef]
- Yaghoubi, V.; Cheng, L.; Paepegem, W.V.; Kersemans, M. A Novel Multi-Classifier Information Fusion Based on Dempster–Shafer Theory: Application to Vibration-Based Fault Detection. Struct. Health Monit. 2021, 21, 596–612. [Google Scholar] [CrossRef]
- Zadkarami, M.; Shahbazian, M.; Salahshoor, K. Pipeline Leak Diagnosis Based on Wavelet and Statistical Features Using Dempster–Shafer Classifier Fusion Technique. Process Saf. Environ. Prot. 2017, 105, 156–163. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).