A Ghost Wave Suppression Method for Towed Cable Data Based on the Hybrid LSMR

Abstract

In marine seismic exploration, ghost waves distort reflection waveforms and narrow the frequency band of seismic records. Traditional deghosting methods are susceptible to practical limitations from sea surface fluctuations and velocity variations. This paper proposes a τ-p domain deghosting method based on the Hybrid Least Squares Residual (HyBR LSMR) algorithm. We first establish a linear forward model in the τ-p domain that describes the relationship between the total wavefield and upgoing wavefield, transforming deghosting into a linear inverse problem. The method then employs the hybrid LSMR algorithm with Tikhonov regularization to address the inherent ill-posedness. A key innovation is the integration of the Generalized Cross Validation (GCV) criterion to adaptively determine regularization parameters and iteration stopping points, effectively avoiding the semi-convergence phenomenon and enhancing solution stability. Applications to both synthetic and field data demonstrate that the proposed method effectively suppresses ghost waves under various acquisition conditions, significantly improves the signal-to-noise ratio and resolution, broadens the effective frequency band, and maintains good computational efficiency, providing a reliable solution for high-precision seismic data processing in complex marine environments.

1. Introduction

Regarding marine seismic exploration, as a core technical means for oil and gas resource development, the quality of its data directly determines the accuracy of geological body imaging and the reliability of resource prediction [1]. In typical marine surveys, the source and receivers are usually placed below the seawater, and the strong reflection interface between seawater and air can lead to the generation of ghost waves [2]. This is an interference signal with an extremely small time difference compared to the primary reflection wave, which not only interferes with the effective wave, causing the frequency band of the seismic record to be compressed, but also may produce false reflection hyperbolas, resulting in false phenomena in offset imaging and seriously affecting seismic resolution [3]. From an industrial application standpoint, the ghost wave issue carries substantial practical implications. Inaccurate removal or suppression of ghost reflections can lead to the misinterpretation of subsurface structures, thereby compromising reservoir characterization and increasing the risk of drilling in non-productive zones. Such inaccuracies not only undermine exploration efficiency but also contribute to significant financial losses due to misguided investments in well placement and field development.

In recent years, as offshore oil and gas exploration has advanced towards deeper waters and complex geological areas, the demand for high-resolution and wide-band seismic data has become increasingly urgent [4,5]. Ghost wave suppression has become one of the core technologies in achieving wide-band processing of offshore seismic data. To suppress ghost wave signals in seismic data and achieve wide-band processing of seismic data, many scholars at home and abroad have developed numerous ghost wave suppression methods. These methods mainly focus on two aspects: one is to weaken the influence of ghost waves through seismic acquisition methods, and the other is to separate ghost waves through seismic data processing methods.

The traditional marine seismic exploration data acquisition method uses a single source to excite and a single cable for receiving. This method is no longer sufficient to meet the current exploration requirements. In recent years, various seismic acquisition technologies that suppress ghost waves have been developed, such as upper-lower dual-cable, dual-receiving cables, inclined cables, and three-dimensional source seismic acquisition [6,7,8]. These acquisition technologies can improve the signal-to-noise ratio and resolution of seismic data to a certain extent, but they also have certain limitations. The upper-lower dual-cable acquisition technology reduces the influence of ghost waves by using different submerged depths of the receivers to correspond to different notch frequencies. However, this technology has strict requirements, not only for controlling the depth of the upper and lower cables, but also for keeping the upper and lower cables in the same vertical plane. In harsh sea conditions, it is prone to data mismatch [9]. The dual-receiving cable is connected in parallel with a vertical velocity receiver (land receiver) beside the pressure receiver (water receiver), using the difference in the response to ghost waves of the two receivers to separate the wave field [10]. After the wide-band data with ghost waves are combined, the ghost waves are significantly suppressed. However, the land receivers are prone to noise interference and require high-precision data processing. The inclined cable acquisition technology designs the tow cable in an inclined state. Due to the different depths of the receivers not being on the same horizontal plane, as the offset distance increases, the ghost waves gradually separate from the effective signals. Compared with the upper-lower dual-cable acquisition technology and the dual-receiving cable acquisition technology, it has better effects. However, this acquisition method has overly strict technical requirements and requires corresponding seismic processing methods, such as mirror offset and joint deconvolution technology, to better suppress ghost waves [11].

To adapt to different acquisition techniques and considering cost issues, relevant scholars have proposed a series of seismic data processing techniques to suppress ghost waves. These mainly include numerous ghost wave suppression methods based on joint deconvolution methods [12], wavefield extension methods [13], Green’s theory [14], and inverse scattering [15]. Among them, the application of the joint deconvolution method is the most widespread, usually carried out in the time–space (t-k) domain, frequency–space (f-x) domain, and frequency–wave number (f-k) domain. However, most of these methods assume a calm sea level [16], while the actual sea surface fluctuates and rises and falls over time. Suppressing ghost waves under the assumption of a flat sea surface will introduce certain errors and make it difficult to ensure the effectiveness of ghost wave suppression and imaging resolution.

In recent years, inversion-based algorithms in the τ-p domain [17] have provided a new solution for suppressing ghost waves. This method decomposes local plane waves into a sparse form, directly obtaining the upgoing wave field without knowing the delay time of the ghost waves, and does not rely on strong assumptions such as the depth of the shot points, detection points, and the speed of the seawater. The dependence on narrow azimuth observation systems is also significantly reduced.

Based on this, this paper proposes a τ-p domain ghost wave suppression method based on the Hybrid Least Squares Residual (HyBR LSMR) algorithm. The core innovation of this method is reflected in three aspects: (1) Based on the theory of plane wave propagation, firstly, a linear equation in the τ-p domain is established between the total wave field observed by the towed cable and the upwelling wave field on the sea surface. By deriving the temporal and spatial relationships between the total wave field, the upwelling ghost wave, and the downwelling ghost wave, the complex wave field separation problem is transformed into the solution of a linear equation system, providing a more accurate mathematical basis for the subsequent inversion. (2) To mitigate the semi-convergence and bias toward erroneous values exhibited by the standard LSMR solver, Tikhonov regularization is embedded, yielding a hybrid LSMR variant. This algorithm dynamically optimizes the regularization parameter during the iteration process, effectively suppressing the solution error caused by matrix ill-conditioning, while retaining the efficient iterative advantage of the LSMR algorithm, achieving stable inversion of the upwelling wave field, and significantly improving the computational efficiency compared to traditional methods. (3) Finally, the Generalized Cross Validation (GCV) function is applied to the parameter selection and iteration termination judgment of the hybrid LSMR algorithm. The GCV function does not require the prior estimation of the noise level and determines the optimal regularization parameter and iteration number adaptively by minimizing the statistical quantity of the prediction error, solving the problem of strong dependence on prior information in traditional regularization methods (such as the bias principle and unbiased prediction risk estimation). The algorithm is tested using synthetic data and actual data, verifying the effectiveness and applicability of this method.

2. Related Work

At present, geophysicists, both at home and abroad, have conducted in-depth research on two aspects: the offshore seismic acquisition method and the seismic data processing method (Figure 1). Firstly, in the field acquisition process, appropriate source combinations, cable shapes, or cable combinations are adopted to reduce the influence of ghost waves; secondly, in the data processing stage, appropriate algorithms are used to eliminate ghost waves from the measured data [18].

Figure 1. Ghost wave’s method of suppression of mainstream approaches.

For the research during the acquisition stage, the main approach is to optimize the observation system and design the system from the perspective of observation time difference to control the distribution of notch points, thereby effectively eliminating the notch points. Haggerty et al. [19] proposed using the upper and lower cable technology to suppress ghost waves in marine seismic data. By placing detectors at different depths and combining their seismic records, an upward traveling wave field without ghost waves at the target depth was obtained, thereby eliminating the influence of ghost waves. Barr et al. [20] proposed the marine dual-detector acquisition technology, adding land detectors (velocity detectors) in addition to water detectors (pressure detectors). The land detectors always remain vertically upward and can detect velocity changes in the vertical direction. By utilizing the differences in phase, amplitude, etc. of different seismic waves, the seismic data from the dual-detector acquisition are combined for wavefield separation to achieve the purpose of ghost wave suppression. Bearnth et al. [21] proposed the oblique cable acquisition technology, with each detector in the cable located at a different depth. Through the minimum–maximum phase, joint deconvolution of the conventional offset and mirror offset results of the oblique cable seismic data is performed to suppress ghost waves. Ferber et al. [22] proposed adding middle cable data and merging the data from the upper, middle, and lower cables. By having different seismic data with different frequency bands and notch characteristics, ghost waves can be eliminated.

For the research on the processing stage, mainly based on the characteristics of the ghost wave signals in the time domain and frequency domain, wave field separation, filtering, and frequency wave number domain methods based on the wave equation theory are used to achieve ghost wave suppression. The ghost wave suppression is carried out on the seismic data with varying depths using the iterative method of the wave equation, and the data after ghost wave suppression is obtained through the nonlinear conjugate gradient inversion algorithm. At the same time, this method can also remove the source ghost waves [23]. Weglein et al. [24] proposed the inverse scattering series method (ISS) as a classic ghost wave data processing method for ghost wave and multiple wave suppression, but ISS is a nonlinear-related processing method and is very prone to errors; Cecconello et al. [25] used the integral method to simulate the source ghost wave effect under time-varying conditions and developed an inversion method for removing the source ghost waves. Kluver et al. [26] proposed to use the migration method to process the double-dip seismic data and extended this method to three dimensions to eliminate the spatial pseudo-frequency phenomenon introduced during the transition from double-dip acquisition technology to three-dimensional technology; Soubaras et al. [12] used the oblique cable acquisition method and the pre-stack-post-stack and mirror migration deconvolution methods to suppress ghost waves and broaden the frequency band of the effective seismic signals. Aytun et al. [27] proposed a ghost wave suppression method in the frequency–wave number domain, eliminating the influence of ghost waves by calculating the delay time of the ghost waves. However, due to the numerous influencing factors, it is difficult to estimate a highly accurate delay time; Wang et al. [28] proposed performing frequency–domain “bootstrap” data processing on the oblique cable data and obtained good ghost wave suppression results. Poole [17] used the method of separating the upgoing and downgoing waves based on the difference in apparent velocities of ghost waves and first reflections in the oblique cable data to separate ghost waves from first reflections. Furthermore, based on the traditional method of eliminating ghost waves, the addition of a virtual source method is adopted. This results in a more stable suppression effect. This method was applied to experiments with air gun arrays and verified good results [29]. These methods have achieved good results in some practical data, but due to the complexity and diversity of the medium and the limited exploration resources, the application scope is still limited. Developing more efficient ghost wave suppression techniques has become an urgent key requirement. Due to the changes in sea water velocity, sea surface undulation, and cable depth errors, the results processed by conventional ghost wave suppression algorithms have noise and ringing. Coates et al. [30] applied the algorithm of separating upgoing and downgoing waves based on the wave equation to the actual data for ghost wave suppression and estimated the cable deployment depth. Grion et al. [31] developed a ghost wave suppression algorithm based on the phase-shift method wave field extension operator for suppressing ghost waves in the case of an undulating sea surface, achieving satisfactory results for ghost wave suppression in cases where the sea surface undulation height is 2 m. Vrolijk et al. [32] added constraints to the ghost wave suppression algorithm to reduce the influence of these factors. Vrolijk et al. [33] further applied deep learning algorithms to the suppression of ghost waves at the source end and achieved good practical results. Zhong et al. [34] proposed a novel MSD-Net deep learning network for suppressing seismic background noise, achieving accurate recovery of weak reflection signals. Bao et al. [35] introduced a secondary convolution kernel and proposed a new secondary convolution attention U-Net for suppressing ghost waves, demonstrating excellent performance in improving the resolution of seismic data and recovering the notch frequency.

3. Method

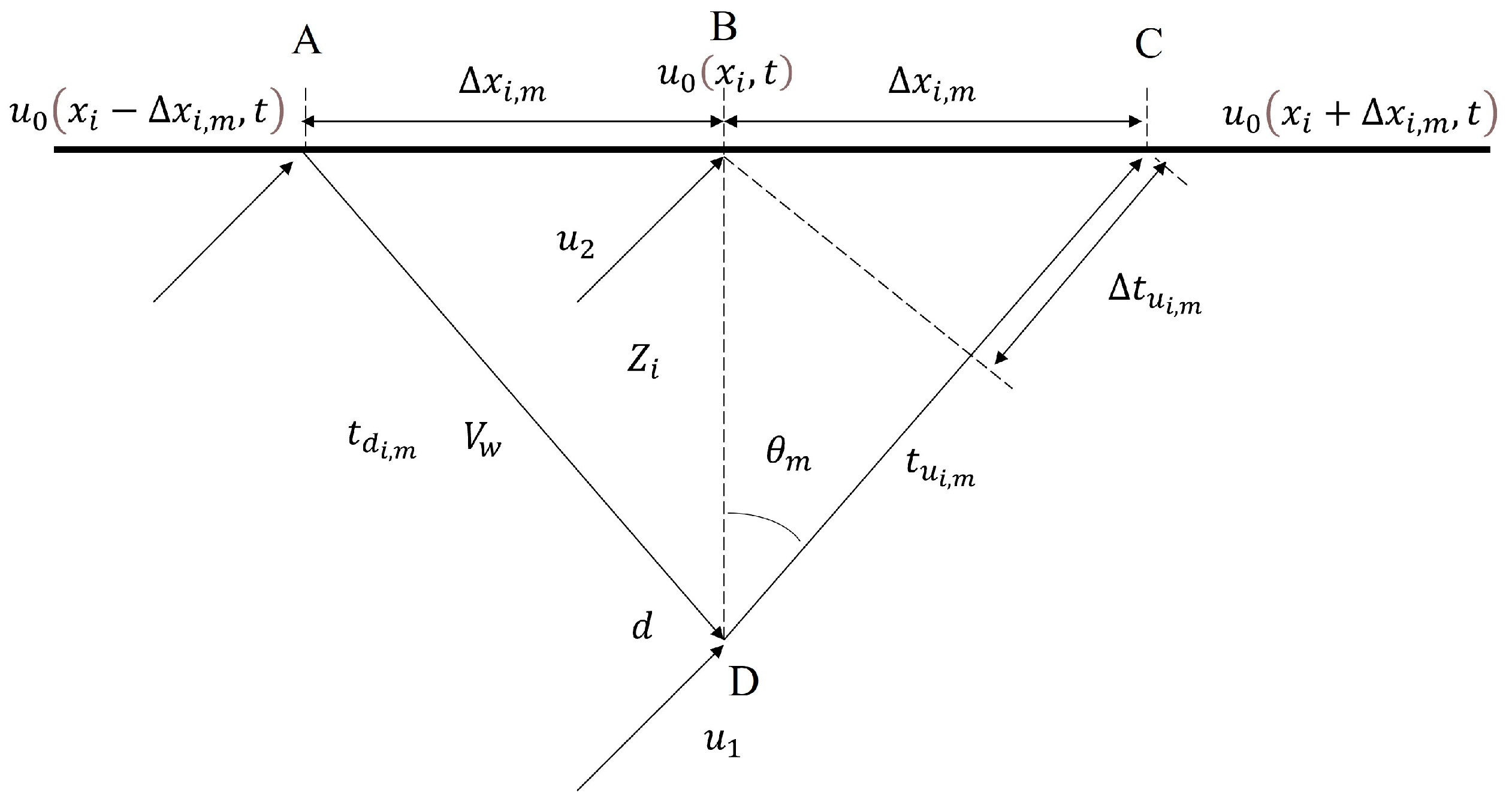
3.1. τ-p Domain Inversion Method

The ghost wave delay time is a function related to the depth of the detection point, the speed of the seawater, and the incident angle of the upstream wave. The τ-p inversion algorithm performs a sparse decomposition of the local plane wave in the τ-p domain to obtain the upstream wave field when the ghost wave delay time is unknown. Its advantage lies in that it does not rely on strong assumptions about the depth of the shot point and detection point, as well as the water speed, and is not strictly constrained by the narrow azimuth assumption.

As shown in Figure 2, disregarding environmental background noise such as ship reflections, the wave field $a\left(x_i,t\right)$ recorded by the marine cable seismic data can be regarded as the sum of the upward reflection wave field $u\left(x_i,t\right)$ from the seabed strata and the downward wave field $d\left(x_i,t\right)$ (ghost wave), which is propagated to the sea surface and then reflected by the sea surface and propagates downward:

$$a\left(x_i,t\right)=u_1\left(x_i,t\right)+d\left(x_i,t\right)$$

(1)

Figure 2. The relationship between the total wavefield recorded by the cable-dragging seismic data and the upward-reflected wavefield of the seabed strata. Point B: A virtual reference point that is located at the sea surface directly above the actual receiver D. The upgoing wavefield at this point, denoted as $u_0\left(x_i,t\right)$, serves as our primary unknown. Point D: The actual receiver location at depth z_i, where the total wavefield $a\left(x_i,t\right)$ is recorded. Point C: A virtual source point for the direct arrival. It is located at the same depth as D, but positioned as such that the ray from C to D represents the path of the upgoing wave arriving at receiver D at time t. The horizontal offset from B to C is ${∆x}_{i,m}$. Point A: A virtual source point for the ghost arrival. It is located at the same depth as D, but positioned as such that the ray from A to D (via reflection at the sea surface above B) represents the path of the ghost wave. The horizontal offset from B to A is ${-∆x}_{i,m}$. $t_{u_{i,m}}$: The travel–time difference for the upgoing wave from point C to point D. $t_{d_{i,m}}$: The travel–time difference for the ghost wave from point A to point D.

In the above equation, $a\left(x_i,t\right)$ represents the total observed wave field or the original data; $u_1\left(x_i,t\right)$ represents an upward-propagating wave field, which is the effective signal.; $d\left(x_i,t\right)$ represents the downwave field, which is also known as the ghost wave.

As shown in Figure 2, at a certain moment, the total wave field p received by point D is the sum of the upward wave field u that the reflected wave propagates to point D, and the downward wave field d that propagates to point A and then is reflected back to point D. The time difference between the arrival of u at point C and the arrival of u at point B is:

$${{∆t}_u}_{i,m}={\displaystyle \frac{z_i{p}_m^{2}v}{\mathit{cos}{\theta }_m}}$$

(2)

In the above equation, ${\theta }_m$ represents the emission angle, $p_m$ represents the parameter of the m-th ray, and $z_i$ represents the submergence depth of the i-th track relative to the sea surface.

The upgoing wave arriving at receiver D at time t can be viewed as originating from virtual source point C. This wave departed from point C at a time $t+t_{u_{i,m}}$. Therefore, the upgoing wavefield $u\left(x_i,t\right)$ recorded at point D equals the wavefield at point C at time $t+t_{u_{i,m}}$, i.e.,

$$u\left(x_i,t\right)=u_0\left(x_i+{∆x}_{i,m},t+t_{u_{i,m}}\right)$$

(3)

Similarly, the ghost wave arriving at receiver D at time t is generated by the upgoing wavefield reflecting at the sea surface point A. This ghost wave originates from virtual source point A departing from point A at time $t-t_{d_{i,m}}$, and after reflection at the sea surface (with reflection coefficient R, typically close to −1), propagates downward to point D. Therefore, the ghost wavefield $d\left(x_i,t\right)$ recorded at point D equals the wavefield at point A at time $t-t_{d_{i,m}}$ multiplied by the reflection coefficient, i.e.,

$$d\left(x_i,t\right)=R·u_0\left(x_i-{∆x}_{i,m},t-t_{d_{i,m}}\right)$$

(4)

Substituting the expressions of these two components into Equation (1), we obtain the preliminary expression for the total wavefield at point D:

$$a\left(x_i,t\right)=u_0\left(x_i+{∆x}_{i,m},t+t_{u_{i,m}}\right)+R·u_0\left(x_i-{∆x}_{i,m},t-t_{d_{i,m}}\right)$$

(5)

In the above equation, a represents the total wave field, $u_0$ represents the upwave, and R represents the reflection coefficient of the seawater.

Assuming that the elastic parameters of the seawater are uniformly and unchanged in the horizontal direction, then the upgoing waves received at points A and C have the following relationship with the upgoing wave received at point B:

$$u_0\left(x_i,t-{∆t}_{u_{i,m}}\right)=u_0\left(x_i+{∆x}_{i,m},t\right)u_0\left(x_i,t+{∆t}_{u_{i,m}}\right)=u_0\left(x_i-{∆x}_{i,m},t\right)$$

(6)

In the above equation, each variable represents the uplink wave $u_0$ at different positions.

Combining (5) and (6) with the frequency–domain linear $\mathsf{\tau }-\mathrm{p}$ inverse transformation, we can obtain:

$$A\left(x_i,t\right)=\sum _{m=1}^{M}V\left(p_m,\omega \right)·exp\left[-j\omega \left(p_m{x}_i+{∆t}_{u_{i,m}}-t_{u_{i,m}}\right)\right]+R·\sum _{m=1}^{M}V\left(p_m,\omega \right)·exp\left[-j\omega \left(p_m{x}_i-{∆t}_{u_{i,m}}+t_{d_{i,m}}\right)\right]$$

(7)

In the above equation, A represents the total wave field observed in the frequency domain, while V denotes the upwave field in the τ–p domain and the frequency domain.

The above equation can be written in matrix form, that is:

$$A=GU$$

Among them:

$$A=\left[\begin{array}{c}A\left(x_1,\omega \right)\\ A\left(x_2,\omega \right)\\ ⋮\\ A\left(x_N,\omega \right)\end{array}\right]G=\left[\begin{array}{}\begin{array}{cccc}{G}_{\mathrm{1,1}}& G_{\mathrm{1,2}}& \dots & G_{1,M}\\ G_{\mathrm{2,1}}& G_{\mathrm{2,2}}& \dots & G_{2,M}\end{array}\\ ⋮\\ \begin{array}{cccc}{G}_{N,1}& G_{N,2}& \dots & G_{N,M}\end{array}\end{array}\right]U=\left[\begin{array}{c}U\left(p_1,\omega \right)\\ U\left(p_2,\omega \right)\\ ⋮\\ U\left(p_N,\omega \right)\end{array}\right]$$

(8)

In the above equation, A represents the observed data, U is the parameter to be determined, and G is the operator.

The traveling wave field U at point B can be obtained by solving the linear equations.

3.2. LSMR Algorithm

This paper employs the hybrid LSMR algorithm to solve the upwelling wave field U. The LSMR algorithm is an iterative algorithm that has emerged in recent years. Both LSQR and LSMR are Krylov subspace methods designed for sparse least squares problems, and they share similar computational costs per iteration. However, LSMR possesses a distinct theoretical advantage: it directly minimizes the norm of the residual of the normal equations at each iteration, whereas LSQR minimizes the residual of the original system. This fundamental difference makes LSMR inherently more suitable for regularizing problems like ours.

For the collected wave field data D, by constructing the linear Laplacian operator G, a linear Laplacian equation GU = D can be established. Using the LSMR algorithm to solve the linear Laplacian equation GU = D is equivalent to solving the linear system b = Ax. By replacing A with the linear Laplacian operator G and b with the wave field data D, the solution x of the linear system corresponds to the upwelling wave field U at the sea surface. For the linear system b = Ax, b is called the data space vector, and x is called the model space vector.

LSMR realizes double diagonalization via the Golub–Kahan recursion: starting with β₁ = ‖b‖, u₁ = b/β₁, α₁v₁ = Aᵀu₁, each step k produces orthogonal vectors u_k+1 and v_k+1 that iteratively reduce (b A) to the upper bidiagonal block (β₁e₁ B_k). The formula is expressed as:

$${\beta }_{k+1}{u}_{k+1}=A{v}_k-{\alpha }_k{u}_k{\alpha }_{k+1}{v}_{k+1}=A^{{\rm T}}{u}_{k+1}-{\beta }_{k+1}{v}_k$$

(9)

After the k steps, we have the matrix:

$v_k=\left(v_1,v_2\dots v_k\right)\in {\mathbb{R}}^{n\times k},u_k=(u_1,u_2\dots u_k)\in {\mathbb{R}}^{m\times k}$, Bidiagonal Matrix:

$$\left(\begin{array}{cc}\begin{array}{c}{\alpha }_1\\ {\beta }_1& {\alpha }_2\end{array}& \\ & \ddots \ddots \\ & & \begin{array}{cc}{\beta }_k& {\alpha }_k\\ & {\beta }_{k+1}\end{array}\end{array}\right)\in {\mathbb{R}}^{\left(k+1\right)\times k}$$

(10)

In each LSMR step, $y_k$ is chosen to minimize ${‖A^{⊺}{r}_k‖}_2$, yielding the iterate $x_k=V_k{y}_k$, so $y_k$ solves the reduced subproblem.

$$\underset{x\in R\left(V_k\right)}{\mathit{min}}{‖A^T\left(Ax-b\right)‖}_2={\underset{y}{\mathit{min}}‖\left(\begin{array}{c}{B}_k^T{B}_k\\ {\overline{\beta }}_{k+1}{e}_k^T\end{array}\right)y-{\overline{\beta }}_1{e}_1‖}_2={\underset{y}{\mathit{min}}‖{\widehat{B}}_{k}y-{\overline{\beta }}_1{e}_1‖}_2$$

(11)

In the above formula: ${\overline{\beta }}_k={\alpha }_k{\beta }_k{\widehat{B}}_k=\left(\begin{array}{c}{B}_k^T{B}_k\\ {\overline{\beta }}_{k+1}{e}_k^T\end{array}\right)$

3.3. Improved Hybrid LSMR Algorithm

Since the conventional LSMR algorithm exhibits semi-convergence behavior, the approximate solution approaches the true solution in the initial stage of the iteration but deviates from the true solution after a certain step. Moreover, ${\widehat{B}}_k$ becomes ill-conditioned in more iterations. Therefore, we propose to use Tikhonov regularization to solve the LSMR subproblem, that is:

$$y_k=\underset{y}{\mathit{argmin}}{‖{\widehat{B}}_{k}y-{\overline{\beta }}_1{e}_1‖}_2^2+{{\lambda }^2‖y‖}_2^2$$

(12)

The scalar λ may be fixed or updated each cycle, giving rise to a hybrid LSMR scheme that stabilizes the iteration history and lessens the danger of premature termination, yielding an inferior solution. Another advantage of the hybrid method is that it can estimate the regularization parameter during the iterative process instead of requiring it a priori. Because ${\widehat{B}}_k$ remains tiny in early iterations, we can afford the heavier cost of a GCV-based rule to pick the regularization parameter at each step. GCV is a method based on predictive statistics and does not require estimating the noise level. It treats the solution derived from the reduced dataset as a reliable predictor for the missing entries, with the GCV criterion expressed as:

$$G_{A,b}\left(\lambda \right)={\displaystyle \frac{n{‖b-A{x}_{\lambda }‖}_2^2}{{\left(trace\right(I-A{A}_{\lambda }^{†}\left)\right)}^2}}$$

(13)

In the above formula: $A=U\sum V^T$ represents the singular values of A.

For the GCV function, at each iteration, ${\lambda }_k$ is selected to minimize the function:

$$U_{{\widehat{B}}_k,{\overline{\beta }}_1{e}_1}\left(\lambda \right)={\displaystyle \frac{1}{k}}{‖\left(I-{\widehat{B}}_k{\widehat{B}}_{k,\lambda }^{†}\right){\overline{\beta }}_1{e}_1‖}_2^2={\displaystyle \frac{2{\sigma }^2}{k}}trace\left({\widehat{B}}_k{\widehat{B}}_{k,\lambda }^{†}\right)-{\sigma }^2$$

(14)

And:

$$G_{{\widehat{B}}_k,{\overline{\beta }}_1{e}_1}\left(\lambda \right)={\displaystyle \frac{k{‖\left(I-{\widehat{B}}_k{\widehat{B}}_{k,\lambda }^{†}\right){\overline{\beta }}_1{e}_1‖}_2^2}{{\left(trace\left(I-{\widehat{B}}_k{\widehat{B}}_{k,\lambda }^{†}\right)\right)}^2}}$$

(15)

Another practical issue is to determine when the GK process should stop iterating. We have proposed a GCV function to determine the iteration stop point k, which can be expressed as:

$$G\left(\lambda \right)={\displaystyle \frac{n{‖\left(I-\widehat{A}{\widehat{A}}_{k,\lambda }^{†}\right)\widehat{b}‖}_2^2}{{\left(trace\left(I-\widehat{A}{\widehat{A}}_{k,\lambda }^{†}\right)\right)}^2}}$$

(16)

The solution for the k-th iteration is given by the following formula:

$$x_k=V_k{y}_k=\underset{{\widehat{A}}_{k,\lambda }^{†}}{\underbrace{V_k{\left({\widehat{B}}_k^T{\widehat{B}}_k+{\lambda }_k^{2}I\right)}^{-1}{\widehat{B}}_k^T{V}_{k+1}^T}}\widehat{b}$$

(17)

If the maximum number of iterations is reached, the GCV function reaches its minimum value, a convergence failure is detected, or the tolerance for residuals is exceeded, then the hybrid LSMR method is terminated.

Based on the aforementioned theory, this paper applies the hybrid LSMR algorithm to suppress ghost waves in tow-cable data. The specific implementation process is as follows: Firstly, the common shot gather set of the original seismic data is transformed to the τ-p domain. A linear system A = GU is constructed, where the observation vector A consists of the total wave field in the τ-p domain, the matrix G is a linear Radon operator constructed based on the ghost wave delay time and ray parameters, and the vector U is the upward-propagating wave field at the sea surface. Subsequently, the hybrid LSMR algorithm is used to iteratively solve this linear system. In each iteration step, the Tikhonov regularization parameter λ is adaptively determined by the generalized cross-validation (GCV) function to dynamically balance the data-fitting degree and the norm constraint of the solution, effectively suppressing the numerical instability caused by the matrix ill-conditionality. The iteration terminates when the minimum value of the GCV function or the preset residual tolerance is reached, ensuring that the inversion process automatically stops before the approximate solution begins to diverge, avoiding the phenomenon of semi-convergence. After the inversion converges, the upward-propagating wave field U in the τ-p domain is reconstructed through inverse Radon transformation to the spatiotemporal domain wave field, and then the wave field extension technique is used to extend it from the sea surface to the actual detector depth, ultimately obtaining the seismic record after ghost wave suppression.

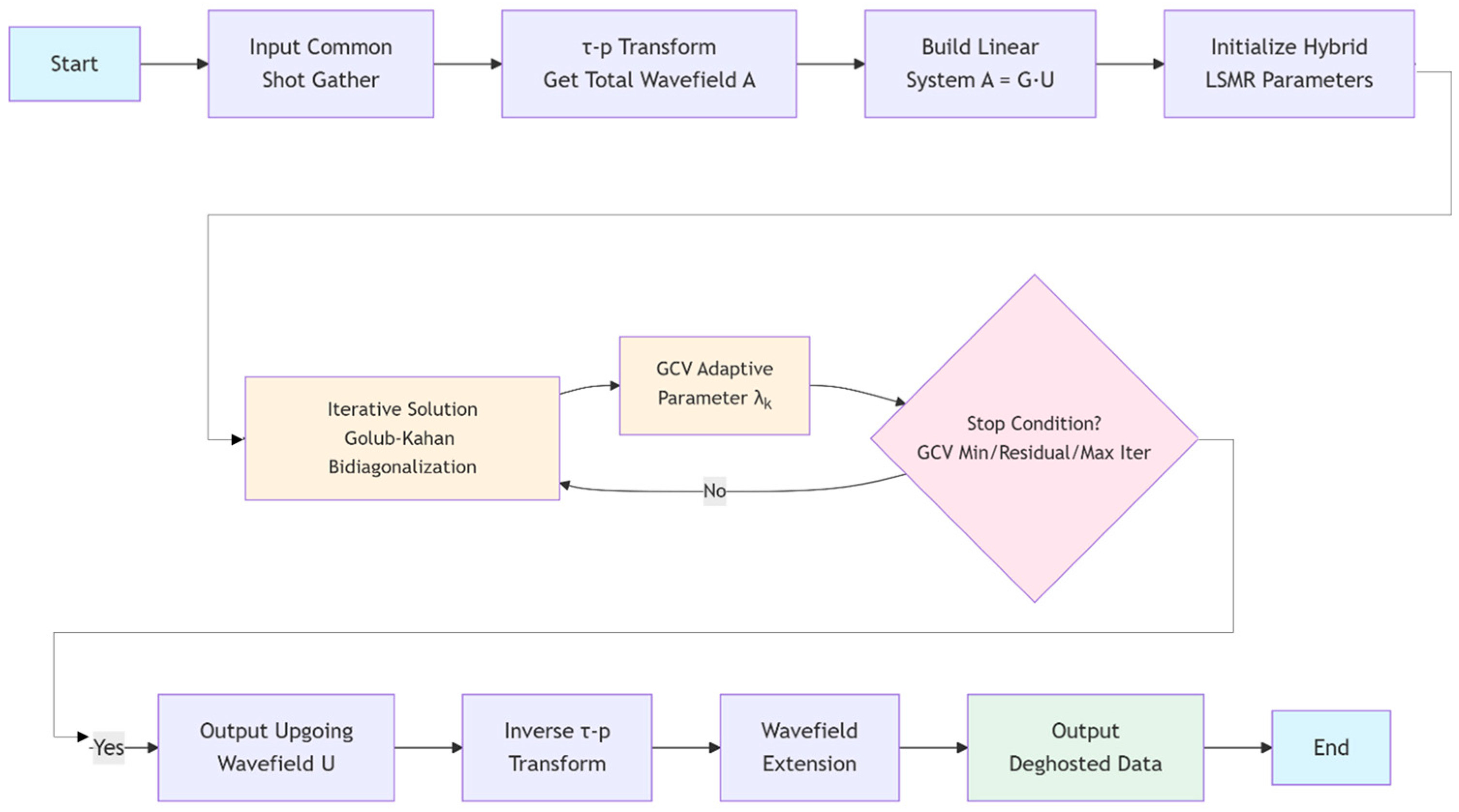
3.4. Algorithm Workflow

To clearly illustrate the implementation process of the proposed hybrid LSMR-based ghost wave suppression method, we present the detailed workflow as follows:

(1)

Input Common Shot Gather: Input the original seismic data in the common shot gather domain.

(2)

τ-p Transform: Transform the seismic data from the time–space (t-x) domain to the τ-p domain to obtain the total wavefield A.

(3)

Construct Linear System: Build the linear system A = GU, where G is the linear Radon operator constructed based on ghost wave delay time and ray parameters, and U is the upgoing wavefield at the sea surface.

(4)

Initialize Hybrid LSMR: Set the initial parameters, including the maximum iteration number, residual tolerance, and initial regularization parameter λ.

(5)

Iterative Solution with GCV: Perform Golub–Kahan bidiagonalization to update the solution subspace. In each iteration, compute the Tikhonov-regularized solution for the subproblem. Use the generalized cross-validation (GCV) function to adaptively determine the optimal regularization parameter λ_k and evaluate the stopping criterion.

(6)

Check Stopping Criteria: Terminate the iteration if one of the following conditions is met: The GCV function reaches its minimum. The residual norm falls below the preset tolerance. The maximum number of iterations is reached.

(7)

Output Upgoing Wavefield in τ-p Domain: Obtain the estimated upgoing wavefield U in the τ-p domain.

(8)

Inverse τ-p Transform: Transform U back to the time–space domain to recover the deghosted seismic wavefield.

(9)

Wavefield Extension (Optional): If needed, extend the wavefield from the sea surface to the actual receiver depth using wavefield continuation techniques.

(10)

Output Deghosted Seismic Record: Output the final ghost-suppressed seismic data.

The workflow is also summarized in the flowchart below for better visualization (Figure 3).

Figure 3. Method flowchart.

4. Data Testing

In order to comprehensively verify the effectiveness and practicability of the ghost wave suppression method based on the hybrid LSMR algorithm, this paper conducts test analyses at two levels: numerical examples and practical data application. The numerical examples construct synthetic seismic records based on typical geological models, systematically comparing the influence of different algorithms and parameter selections on the ghost wave suppression effect; the practical data application selects typical towed cable data from a deepwater area to test the adaptability and stability of the method under complex geological conditions.

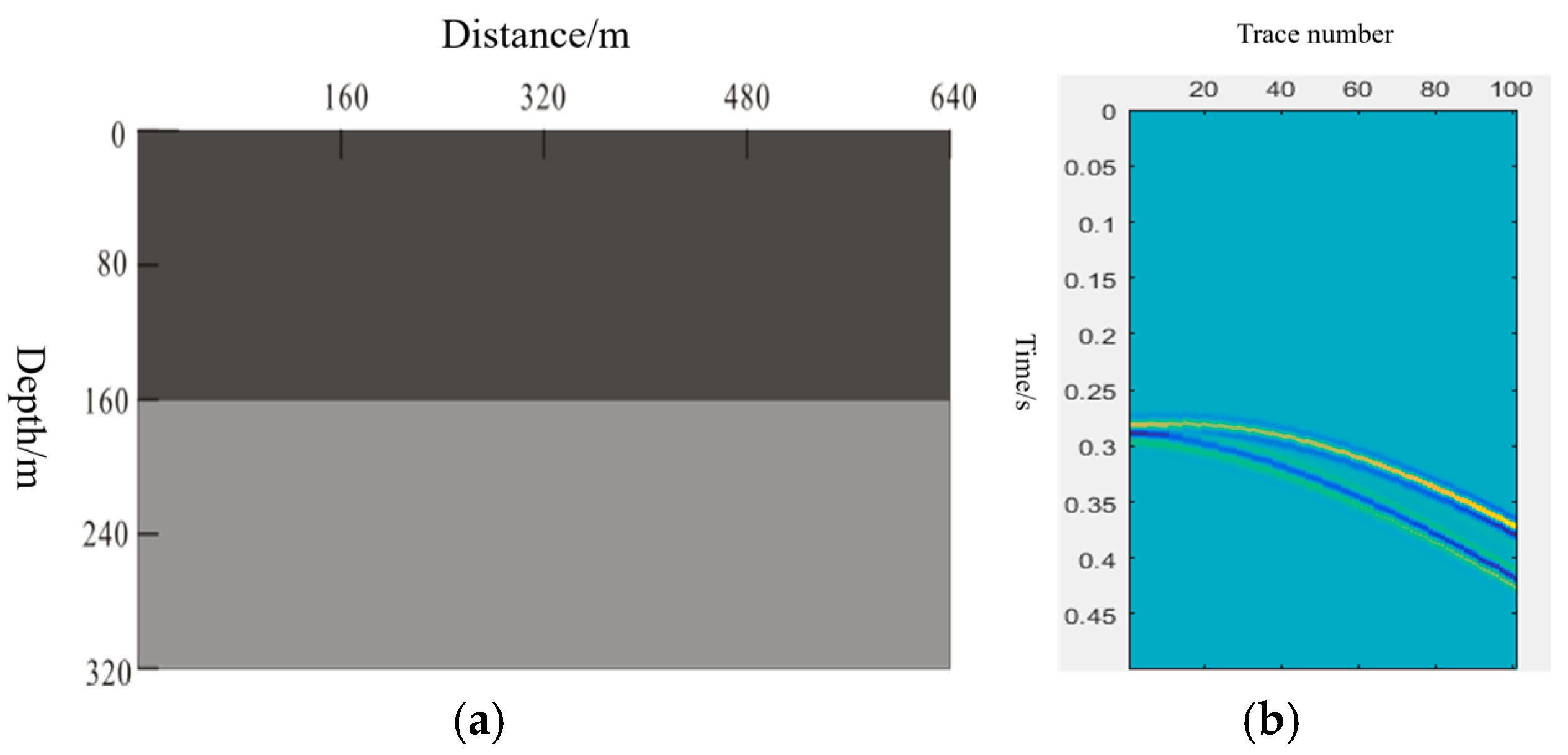
4.1. Numerical Examples

To accurately evaluate the performance of the algorithm, a typical layered velocity–density model (Figure 4a) was designed. This model includes reflection interfaces, with significant differences in layer velocities and densities and is capable of simulating common wave impedance variations in the seabed strata and generating synthetic seismic records with typical ghost wave interference. The forward modeling uses Rayleigh waves with a main frequency of 80 Hz to better simulate the frequency band characteristics of actual seismic waves. The observation system parameters are set as follows: 101 traces, a trace spacing of 4 m, a sampling interval of 0.5 ms, a simulated cable array acquisition method, and a cable depth varying linearly from 6 m to 30 m to simulate the depth variation effect in actual cable acquisition. The forward modeling is carried out using the acoustic finite difference method to accurately simulate the interference effect between the traveling wave and the ghost wave.

Figure 4. Layered model required for forward modeling and simulated single-shot record (The different colors in (a) represent different strata; In figure (b), the variable density map of the seismic reflection is shown. Warm colors represent high amplitude values).

The single-shot record obtained through simulation is shown in Figure 4b. It is clearly observable that there is a reflected wave and its corresponding ghost wave signal. The ghost wave appears as a phase-identical axis immediately following the effective wave, and the time difference varies with the offset distance and cable depth, which is consistent with the theoretical expectation. Such data provide an ideal test sample for the subsequent ghost wave suppression algorithm.

To verify the superiority of the hybrid LSMR algorithm proposed in this paper, the widely used LSQR algorithm and the standard LSMR algorithm were selected as the comparison methods. All the algorithms were executed under the same computing environment to ensure the fairness of the comparison.

The ghost waves were attenuated using the LSQR algorithm, the LSMR algorithm, and the hybrid LSMR algorithm, respectively. The denoising effect was further quantified using the signal-to-noise ratio (SNR). The calculation method is as shown in Equation (18):

$$SNR=10 {\mathit{log}}_{10}\left[{\displaystyle \frac{\sum _{j=1}^{J}x{\left(j\right)}^2}{\sum _{j=1}^J{\left[x\left(j\right)-x_d\left(j\right)\right]}^2}}\right]$$

(18)

In Equation (16), J represents the number of sampling points; x(j) represents the seismic record containing ghost waves; $x_d\left(j\right)$ represents the denoised seismic record. The higher the SNR, the better the denoising effect.

To demonstrate the superiority of the hybrid LSMR method, this paper compares the SNR of the following three denoising methods, as shown in Table 1. The comparison of the denoising results’ SNR of the three algorithms is presented in Table 1. The hybrid LSMR algorithm achieved the highest SNR (4.08), which is significantly superior to the LSQR (2.43) and LSMR (3.11).

Table 1. Comparison of effects of three network structures.

Network	SNR	Recovery Rate (%)
LSQR	2.43	59.4%
LSMR	3.11	65.7%
HyBR LSMR	4.08	73.3%

Note: Recovery rate is calculated as (1 − NRMSE) × 100%, where NRMSE is the Normalized Root Mean Square Error between the deghosted result and the original clean, synthetic primary wavefield. It directly quantifies the amplitude and waveform preservation.

The SNR of the denoising results obtained by HyBR LSMR is superior to the other two methods. The data prove that among the three methods, HyBR LSMR has the best performance and the most effective outcome. It can more effectively suppress the ill-conditioned problems and improve the quality and stability of the solution.

Figure 5 shows the comparison of single-shot records processed by three algorithms. Figure 5a presents the seismic data obtained after suppressing ghost waves using the LSQR method; Figure 5b shows the seismic data obtained after suppressing ghost waves using the standard LSMR method; Figure 5c represents the seismic data obtained after suppressing ghost waves using the method proposed in this paper. In the results of the LSQR algorithm, obvious ghost wave residuals can still be observed, and the amplitude of the effective waves has suffered some loss; the ghost wave suppression effect of the LSMR algorithm has improved, but there are still residual interferences. In the results of the HyBR LSMR algorithm, the ghost waves have been effectively suppressed, the continuity of the effective waves is good, the common phase axis is clear, and there is no significant amplitude distortion.

Figure 5. Comparison of actual data ghost wave suppression effects of different technologies ((a) LSQR; (b) LSMR; (c) HyBR LSMR. The variable density map of the seismic reflection is shown. Warm colors represent high amplitude values).

The selection of regularization parameters significantly affects the solution quality of the inversion problem. To further verify the superiority of the GCV function, this paper compares three methods for selecting the regularization parameters: generalized cross-validation (GCV), bias principle (DP), and unbiased prediction risk estimation (UPRE). All tests are conducted based on the HyBR LSMR algorithm, with only the determination method of the regularization parameters changing.

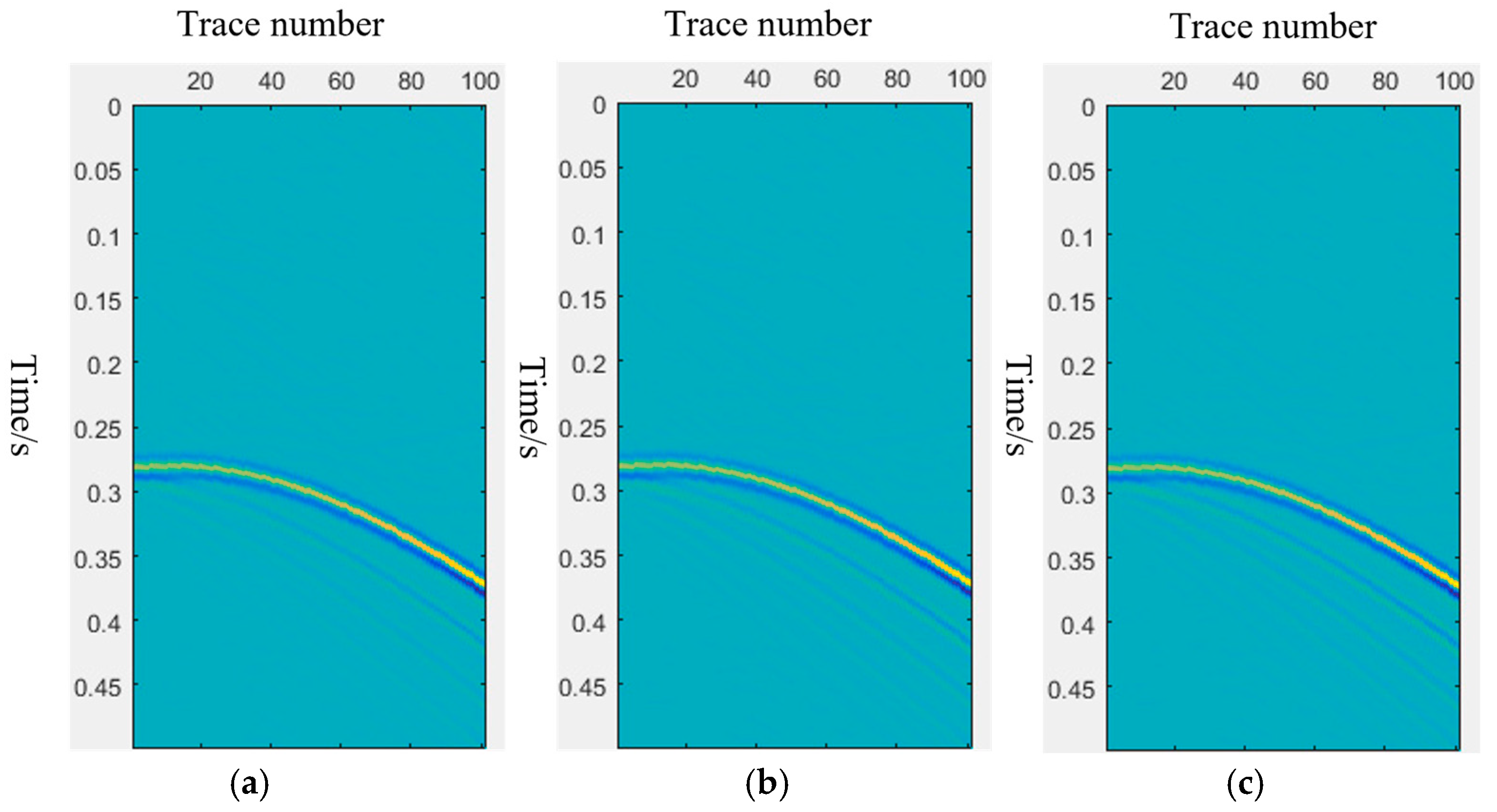
4.1.1. Deviation Principle (DP)

For the noise $‖e‖$ information, its core idea is that the residual ${‖{b-A}_{x_{\lambda }}‖}_2^2$ cannot be less than the error of the right-hand term. That is:

$${‖{b-A}_{x_{\lambda }}‖}_2^2\le ‖e‖$$

(19)

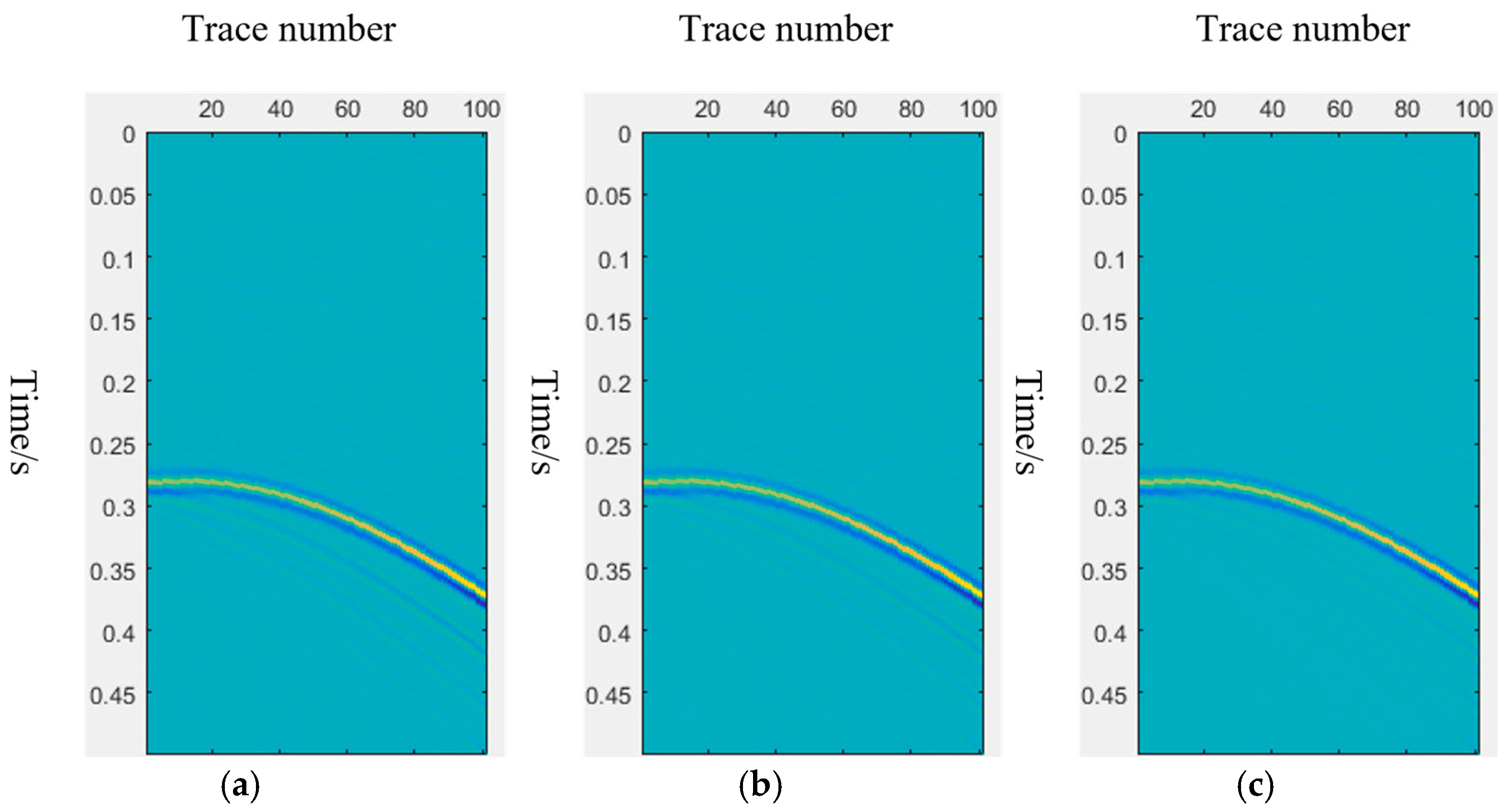
4.1.2. Unbiased Prediction Risk Estimation (UPRE)

UPRE chooses the parameter that minimizes an unbiased estimate of the predicted risk, given by Formula (20).

$$U_{A,b}\left(\lambda \right)={\displaystyle \frac{1}{n}}{‖b-A{x}_{\lambda }‖}_2^2+{\displaystyle \frac{2{\sigma }^2}{n}}trace\left(A{A}_{\lambda }^{†}\right)-{\sigma }^2$$

(20)

Figure 6 examines the influence of different regularization parameters on the suppression effect of ghost waves. Figure 6a shows the seismic data that are obtained after applying the ghost wave suppression method by using the regularization parameters determined based on the deviation principle (DP) method. Figure 6b shows the seismic data that are obtained after applying the ghost wave suppression method by using the regularization parameters determined based on the unbiased prediction risk estimation (UPRE) method. Figure 6c shows the seismic data that are obtained after applying the ghost wave suppression method by using the regularization parameters determined based on the generalized cross-validation (GCV) method. The results of the DP method contain a small amount of residual ghost waves. The results of the UPRE method show significant improvement, but there is still noise locally. The results of the GCV method achieve the most thorough ghost wave suppression, with natural waveforms and high resolution.

Figure 6. Comparison of ghost wave suppression effects for different regularization methods ((a) DP; (b) UPRE; (c) GCV. The variable density map of the seismic reflection is shown. Warm colors represent high amplitude values).

The SNRs of the three denoising methods are compared as shown in Table 2. Through the comparison, it is found that the GCV method achieves the best result (SNR = 4.89), which is superior to the UPRE (4.36) and DP (4.08). Therefore, compared with the bias principle (DP) method and the unbiased prediction risk estimation (UPRE) method, the generalized cross-validation (GCV) method has a better suppression effect on ghost waves, indicating that different regularization parameters play an important role in suppressing ghost waves.

Table 2. Comparison of effects of three different regularization parameters.

Network	SNR	Recovery Rate (%)
DP	4.08	73.4%
UPRE	4.36	76.5%
GCV	4.89	82.3%

4.1.3. Sensitivity Analysis of Cable Depth and Seawater Velocity

A critical consideration for any deghosting method is its robustness to inaccuracies in the acquisition parameters, namely the receiver depth and the seawater velocity. Inaccurate depth readings from depth sensors or errors in the sound velocity profile can potentially degrade the performance. To quantify this, we conducted a sensitivity analysis using the synthetic layered model.

The results in Table 3 demonstrate that the HyBR LSMR algorithm exhibits a notable degree of robustness to errors in both cable depth and water velocity. A 10% error in either parameter leads to a relatively modest degradation in SNR (approximately 0.3–0.4 dB).

Table 3. Sensitivity analysis of cable depth and seawater velocity errors.

Perturbation Type.	Error Magnitude	SNR (dB)	SNR Change (dB)
Cable Depth	5%	4.75	−0.14
	10%	4.52	−0.37
	−5%	4.71	−0.18
	−10%	4.48	−0.41
Water Velocity	+5% (1575 m/s)	4.81	−0.08
	+10% (1650 m/s)	4.66	−0.23
	−5% (1425 m/s)	4.78	−0.11
	−10% (1350 m/s)	4.62	−0.27

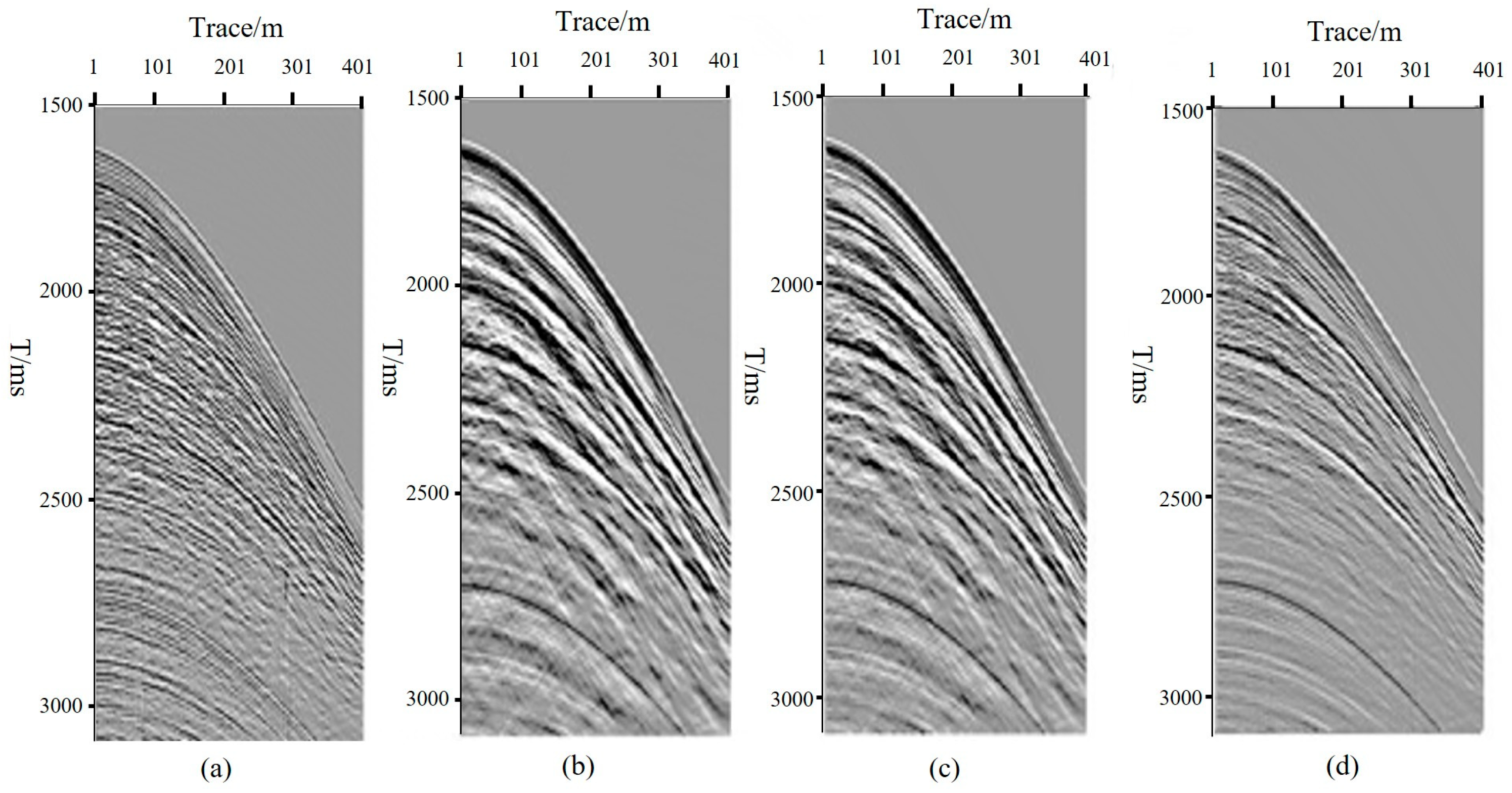
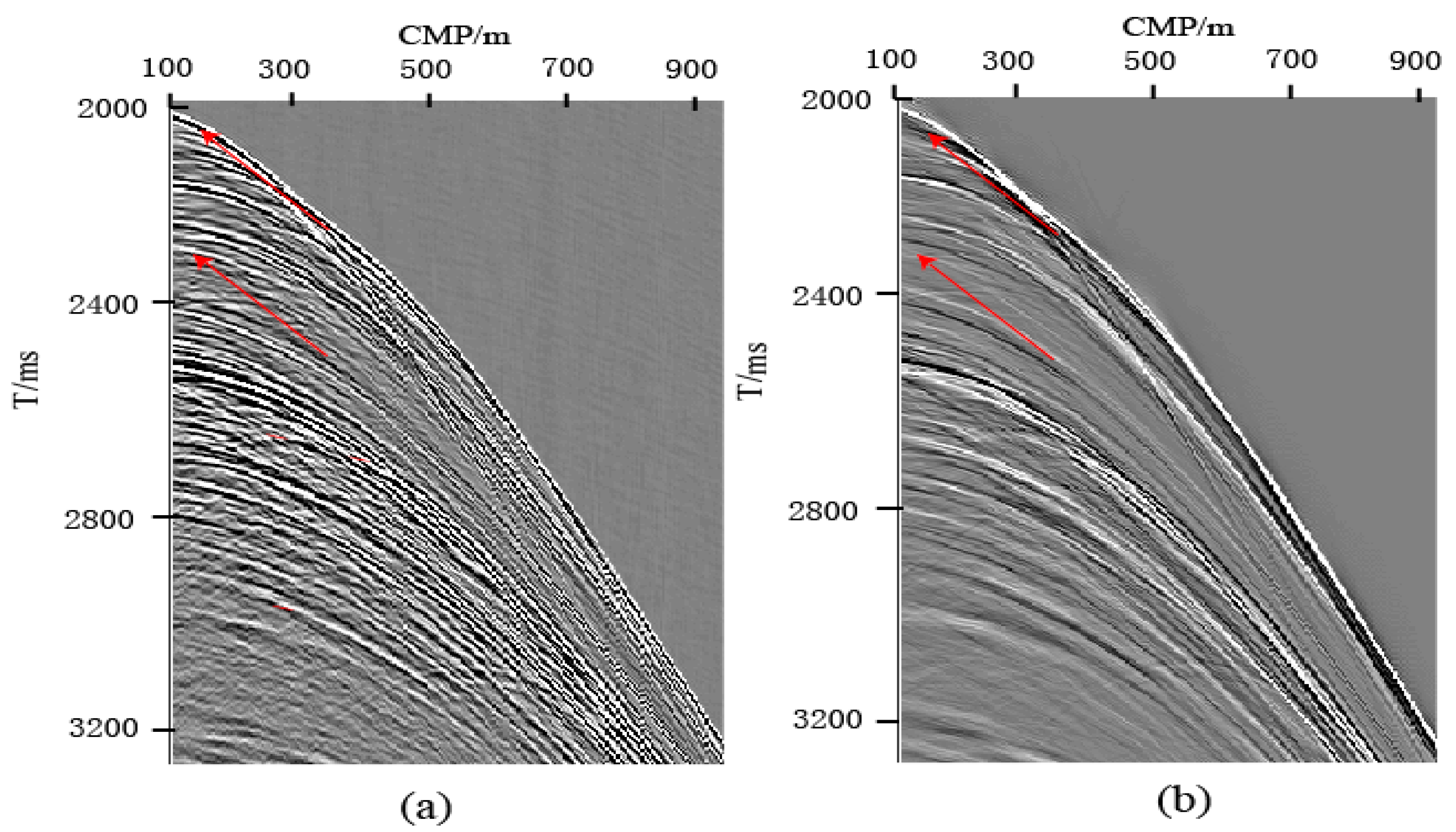
4.2. Application of Actual Data

To verify the effectiveness of the method under actual conditions, data collected by a conventional horizontal cable in a certain deepwater area were selected for testing. The water depth in this area varies between 1000 and 2000 m, and the geological structure is complex. The collected parameters are as follows: the submerged depth of the air gun source is 7 m, the cable depth is 8 m, the channel spacing is 12.5 m, the sampling interval is 2 ms, and the recording length is 8 s. The data contain obvious ghost wave interference, and the effective wave frequency band is limited, which seriously affects the imaging accuracy of the medium and deep layers. The above ghost wave attenuation method was used to suppress the ghost waves in the seismic data.

Figure 7 shows the comparison of single-shot records processed by different algorithms. In the original single-shot record, it can be clearly seen that after each valid reflection wave, there is a wave of opposite polarity immediately following it, presenting the typical “white-black-white” polarity inversion characteristic. This interference severely blurs the original waveform. After being processed by the LSQR algorithm, the energy of the ghost wave has decreased, but the residual can still be seen, and the amplitude of the effective wave has been lost; the improvement in signal-to-noise ratio is limited. The processing effect of the LSMR algorithm is better than that of the LSQR algorithm. The suppression effect of ghost waves in the middle and shallow layers is better, but the energy recovery in the deep layers is insufficient. After being processed by the HyBR LSMR algorithm in this paper, the ghost wave interference is most effectively suppressed. The reflection wave phase tends to be a single, clear “white peak” or “black valley”; the continuity of the common axis and the signal-to-noise ratio are significantly improved, and the wave group characteristics are more realistic and reliable.

Figure 7. Comparison of actual ghost wave suppression effects data of different technologies: (a) before ghost wave suppression, (b) LSQR, (c) LSMR, and (d) HyBR LSMR.

Figure 8 further presents a side-by-side comparison of the single-shot records before ghost wave suppression (a) and after suppression using the method proposed in this paper (b). The comparison shows that the common phase axis of the ghost waves in the processed records has basically disappeared, the energy of the effective waves has been enhanced, and the waveforms have become more focused and crisp. Especially for the reflection signals in the middle and deep layers (below 2 s), they are more continuous and clear, which will greatly improve the accuracy of subsequent structural interpretations and reservoir descriptions.

Figure 8. Comparison of a single gun before ghost wave suppression (a) and after ghost wave suppression (b) (The arrows are used to visually demonstrate the differences).

To quantitatively evaluate the band-broadening effect, we extracted the average amplitude spectra of the single-shot records before and after processing for comparison (Figure 9). The red curve represents the spectrum of the original data, with the effective frequency band ranging from approximately 10 to 80 Hz. The blue curve represents the spectrum after processing using the HyBR LSMR method, showing a significant improvement. The frequency band has been broadened in both directions, with the effective low-frequency components extending robustly to approximately 4 Hz, and the effective high-frequency components expanding to above 90 Hz. The useful frequency band width of the data (usually calculated at the −10 dB point) has significantly increased, with the octave band increasing from approximately 3.0 before processing to 4.4 after processing. This substantial improvement in the spectral structure demonstrates the strong ability of this method to effectively recover the low-frequency and high-frequency components of seismic waves, laying a solid data foundation for subsequent high-resolution migration imaging, full waveform inversion (FWI), and prestack attribute analysis.

Figure 9. Spectrum comparison before and after ghost wave suppression.

Beyond the qualitative and quantitative assessments of deghosting quality, the computational efficiency of the proposed method was analyzed to evaluate its practical applicability. The computational complexity of the HyBR LSMR algorithm remains O(k·m·n), similar to the standard LSMR algorithm, where k is the number of iterations, and m, n are the dimensions of the coefficient matrix. The additional computational overhead introduced by the GCV-based regularization parameter selection is relatively minor, typically adding 20–30% to the total runtime compared to the standard LSMR in our tests. This modest increase is justified by the significant improvement in solution stability and deghosting quality, as demonstrated by the superior SNR and Signal Fidelity results. Given that the τ-p domain inversion naturally handles data in a compressed representation, the overall method maintains competitive computational efficiency that is suitable for industrial-scale processing of 2D lines and can be extended to 3D datasets through parallel processing.

5. Conclusions

This paper addresses the problem of ghost wave interference in marine seismic exploration and proposes a τ-p domain ghost wave suppression method based on the hybrid LSMR algorithm. Through systematic tests and analyses of synthetic data and actual data, the following main conclusions are obtained:

(1)

The τ-p domain linear inversion framework constructed in this paper can effectively describe the wave–field relationship between ghost waves and primary reflection waves, converting the ghost wave suppression problem into a linear equation solving problem. The solver based on the hybrid LSMR algorithm combines the stability of Tikhonov regularization and the efficiency of the LSMR algorithm. The GCV function is used to achieve adaptive selection of regularization parameters and iterative termination, significantly improving the numerical stability and computational efficiency of the inversion process.

(2)

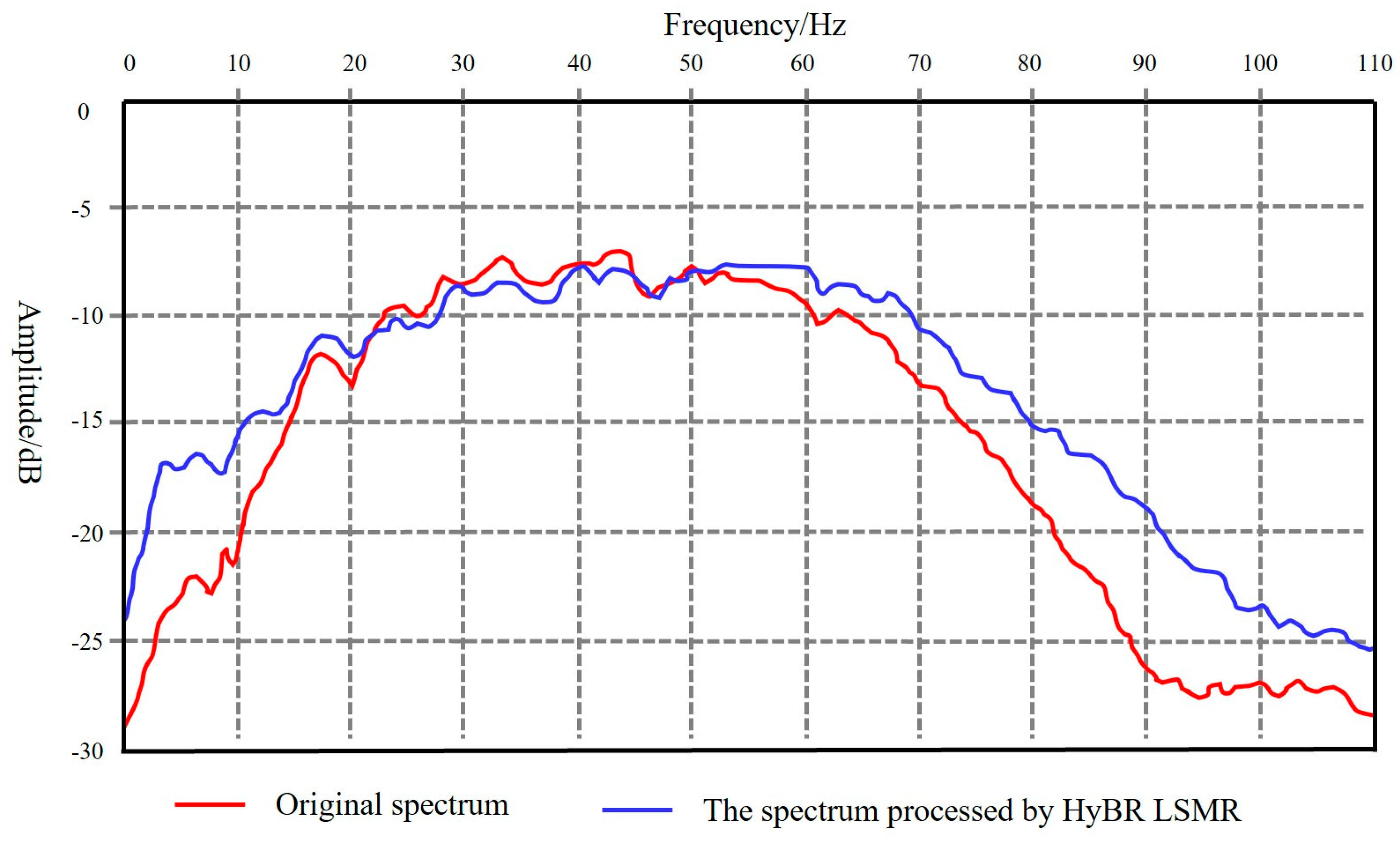
Numerical examples show that compared with traditional LSQR and LSMR algorithms, the HyBR LSMR algorithm performs best in terms of signal-to-noise ratio improvement and ghost wave suppression effects. It can more thoroughly eliminate ghost wave interference and restore the effective reflection wave field. The comparison of different regularization parameter selection methods further verifies the superiority of the GCV function, which can still achieve the best processing effect without relying on prior noise information.

(3)

The processing results of actual data verify the applicability and robustness of this method in complex geological conditions. The ghost wave interference in the processed seismic records is effectively suppressed, the continuity of the same-phase axis, signal-to-noise ratio, and resolution are significantly improved, the spectrum is effectively broadened, and low-frequency and high-frequency information are enhanced.

(4)

The proposed deghosting method holds significant promise for industrial applications, particularly in the context of high-cost and high-risk offshore oil and gas exploration. The ability to obtain high-resolution, broadband seismic data is crucial for accurate reservoir characterization in deepwater and complex geological settings. This method provides a reliable and efficient processing solution that can be directly integrated into conventional marine seismic processing workflows by effectively suppressing ghost waves and broadening the seismic bandwidth without stringent requirements on acquisition parameters.