NN-Based Parallel Model Predictive Control for a Quadrotor UAV

Abstract

A novel neural network (NN)-based parallel model predictive control (PMPC) method is proposed to deal with the tracking problem of the quadrotor unmanned aerial vehicles (Q-UAVs) system in this article. It is well known that the dynamics of Q-UAVs are changeable while the system is operating in some specific environments. In this case, traditional NN-based MPC methods are not applicable because their model networks are pre-trained and kept constant throughout the process. To solve this problem, we propose the PMPC algorithm, which introduces parallel control structure and experience pool replay technology into the MPC method. In this algorithm, an NN-based artificial system runs in parallel with the UAV system to reconstruct its dynamics model. Furthermore, the experience replay technology is used to maintain the accuracy of the reconstructed model, so as to ensure the effectiveness of the model prediction algorithm. Furthermore, a convergence proof of the artificial system is also given in this paper. Finally, numerical results and analysis are given to demonstrate the effectiveness of the PMPC algorithm.

1. Introduction

In the past decade, with the development of sensor and network technologies, Q-UAVs have attracted more and more attention from researchers. Due to the characteristics of efficient deployment and flexible mobility, Q-UAVs are widely used in the fields of nuclear power plant inspections [1,2], forest fire fighting [3,4] and land surveying [5,6]. However, it is challenging to design an effective control for the Q-UAVs system, because of the problems of under-actuating, strong non-linearity, and coupling. Recently, numerous algorithms have been developed by researchers under the framework of traditional control, such as feedback linearization control [7,8], fuzzy logic-based control [9,10], and sliding mode control(SMC) [11,12]. In [13], a non-linear PID controller is designed to deal with the tracking control problem of the Q-UAVs system, where the system energy is considered. A fuzzy-based backstepping SMC algorithm is developed to deal with the tracking problem of the UAVs with parameter uncertainties and external disturbances in [14]. In [15], a second-order SMC algorithm has been introduced to design the Q-UAV controller; however, the optimization characteristics, as an essential part of the control domain, are not considered in the above-mentioned traditional control algorithms.

It is well known, MPC is widely used in many fields as an effective optimal control method, such as the robot control [16,17], autonomous driving [18,19], and energy management [20,21], etc. Under the MPC algorithm scheme, the future system states and behaviors are predicted by the model of the plant, and the control law is optimized based on the analysis and evaluation of the prediction data. Due to obtaining the optimal control by minimizing the performance cost function which is subject to constraints, MPC also has a good performance in the robustness control. Many researchers have also introduced the MPC algorithm into the field of Q-UAV control. In [22], a novel non-linear MPC is proposed to deal with the navigation problem where obstacle avoidance is considered. According to the MPC algorithm scheme, it can be seen that the implementation of the MPC algorithm relies on the accuracy of the prediction model. MPC algorithm is applied to find the optimal paths in the atmosphere with the maximum of the UAV’s energy [23]. In [24], a novel adaptive MPC scheme is established for the angular rate and thrust control of a Q-UAV, where the thrust bound and the disturbances are considered; however, it is difficult to accurately model the dynamics of Q-UAVs due to the high complexity of the system.

Neural networks are widely used to approximate the unknown function for its universal approximation characteristics [25,26,27,28]. Under the MPC scheme, NN technology is introduced to approximate the dynamics model of the Q-UAVs. Many researchers have also made many contributions in this field. In [29], a novel reinforcement learning-based MPC algorithm is developed to deal with the tracking control problem with thrust vectoring capabilities. An offline learning approach is applied to learning the dynamics model of the hybrid Q-UAV in [30]. A Q-UAV controller is designed based on the learning-based MPC algorithm, which is used to provide levels of guarantees about safety, robustness, and convergence in [31]. Alessandro developed an active learning algorithm to deal with the control problem where the model of the Q-UAV is uncertainty-aware [32]. Several novel meta-learning approaches have been developed to approximate the distribution over different “tasks” [33,34]. In the research mentioned above, the NN model is pre-trained before the system runs, and the weight matrices are kept constant during the system operation. However, in some specific environments, such as nuclear radiation and forest fire environments, the dynamics model of the Q-UAVs changes as the system operates. The algorithms mentioned above are unreliable in this case.

Motivated by the above-mentioned problems, we propose a novel NN-based PMPC algorithm. The main contributions are summarized as follows:

(1)

Different from the exiting results [29], the model NN is not only used to approximate the position model of the Q-UAVs but also the whole dynamics model of the Q-UAVs. With our PMPC algorithm, the dynamics model of the Q-UAVs is fully unknown and which will make the optimal problem more difficult to be solved.

(2)

Different from the exiting results [30], the model NN is executed in parallel with the system and is continuously updated with the system runs in the PMPC algorithm. Compared with the unchangeable NN in [30,33,34], our algorithm can be applied in the condition where the dynamics model is changeable during the system running.

(3)

The experiment replay technology is introduced to the PMPC algorithm, which is used to maintain the accuracy of the reconstructed model to ensure the effectiveness of the model prediction algorithm.

The remainder of this article is organized as follows. The problem is formulated in Section 2. In Section 3, the parallel structure and the details of the PMPC algorithm are introduced. Numerical results and analysis are given to demonstrate the effectiveness of the PMPC algorithm in Section 4. Finally, the conclusion is presented in Section 5.

2. Problem Formulation

2.1. Dynamic Models of Q-UAVs

The dynamic models of Q-UAVs have been studied as a system with six degrees of freedom. Under the low speeds assumption, a simple, rigid-body model [35] of Q-UAVs is defined as

$$\begin{array}{cc}\hfill \ddot{x}& =(\cos \varphi \sin \theta \cos \psi +\sin \varphi \sin \psi )\frac{U_1}{m}\hfill \\ \hfill \ddot{y}& =(\cos \varphi \sin \theta \sin \psi -\sin \varphi \cos \psi )\frac{U_1}{m}\hfill \\ \hfill \ddot{z}& =-g+(\cos \varphi \cos \theta )\frac{U_1}{m}\hfill \\ \hfill \ddot{\theta }& =\dot{\varphi }\dot{\psi }\left(\frac{I_z-I_x}{I_y}\right)+\frac{J_R}{I_y}\dot{\varphi }{\mathsf{\Omega }}_R+\frac{L}{I_y}{U}_3\hfill \\ \hfill \ddot{\varphi }& =\dot{\theta }\dot{\psi }\left(\frac{I_y-I_z}{I_x}\right)-\frac{J_R}{I_x}\dot{\theta }{\mathsf{\Omega }}_R+\frac{L}{I_x}{U}_2\hfill \\ \hfill \ddot{\psi }& =\dot{\varphi }\dot{\theta }\left(\frac{I_x-I_y}{I_z}\right)+\frac{1}{I_z}{U}_4\hfill \end{array}$$

(1)

where $\mathbf{S}$$={[x,y,z,\dot{x},\dot{y},\dot{z},\varphi ,\theta ,\psi ,\dot{\varphi },\dot{\theta },\dot{\psi }]}^{\mathrm{T}}$, and $\mathbf{U}={[U_1,U_2,U_3,U_4]}^{\mathrm{T}}$ indicate the state vector and control input of the system, respectively. Furthermore, as shown in Figure 1, $\mathbf{P}=[x,y,z]$, and $\mathsf{\Theta }=[\varphi ,\theta ,\psi ]$ denote the position and Euler angles in the inertial frame ${\mathsf{\Gamma }}_E$, respectively; $\mathbf{V}=[\dot{x},\dot{y},\dot{z}]$ and ${\mathbf{V}}_a=[\dot{\varphi },\dot{\theta },\dot{\psi }]$ denote the velocity of the three axes and the angular velocity of three Euler angles, respectively; $I_x,I_y$, and $I_z$ are the moments of inertia of the Q-UAV around three axes, respectively; and m is the mass of the Q-UAV; L is the length from the rotors to the center of mass; $J_R$ and ${\mathsf{\Omega }}_R$ are the moments of inertia and angular velocity of the propeller blades. Moreover, $U_1,U_2,U_3$, and $U_4$ are the forces generated by the four propellers.

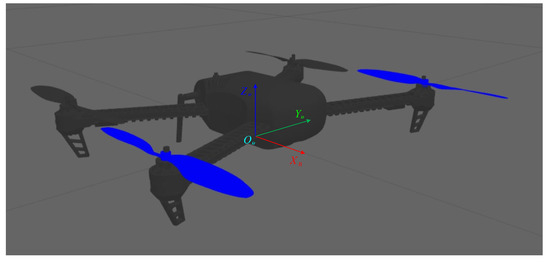
Figure 1. The sketch of Q-UAV with body frame ${\mathcal{O}}_B$.

2.2. Model Predictive Control

Consider a non-linear system defined as

$$\begin{array}{c}\hfill {\mathfrak{x}}_{k+1}=\mathfrak{F}({\mathfrak{x}}_k,{\mathfrak{U}}_k)\end{array}$$

(2)

where ${\mathfrak{x}}_k$ and ${\mathfrak{U}}_k$ are denoted the state and the control input of the system at the time step k, respectively.

Select the $n_p$ as the finite prediction horizon steps, MPC is applied to minimize the performance cost over the $n_p$ steps at each time step k. The optimized control sequence $\mathcal{U}=[{\mathfrak{U}}_k,{\mathfrak{U}}_{k+1},\cdots ,{\mathfrak{U}}_{k+n_p-1}]$ can be obtained by solving the optimal function. The first term in the optimized control sequence is applied in the process and the rest will be applied to solve the optimal control function at the next time step $k+1$, and so on.

2.3. Problem Statement

Under the traditional MPC scheme, the performance of the MPC algorithm is highly dependent on the accuracy of the model. However, the above model is constructed without consideration of the influences of some other sources, such as air drag, the gyroscope effect, and the hub force. To overcome the difficulty of the inaccurate model, a novel NN-based parallel control method is proposed in this paper.

3. Parallel MPC Method

In this section, the PMPC algorithm is introduced to obtain the optimal controller to deal with the tracking control problem for the Q-UAVs with a dynamic dynamics model.

3.1. Algorithm Structure

In the PMPC algorithm, an artificial system is introduced to expand the real problem, which runs in parallel with the real system. The artificial space, between the artificial and real system, is introduced to solve the expanded real problem. The structure of the parallel MPC method can be shown in Figure 2.

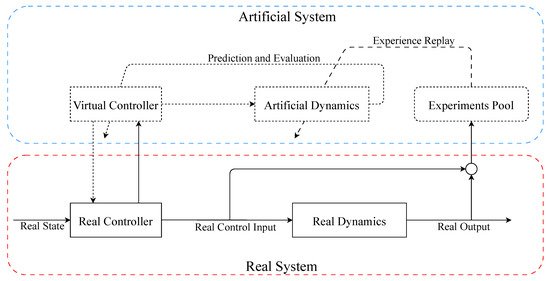
Figure 2. The structure of parallel MPC method.

From Figure 2, the parallel MPC method can be divided into three steps. Firstly, an artificial system is introduced to rebuild the dynamic model of the real system by learning the data observed from the actual system. The artificial system can keep the accuracy of the model with periodic learning of the data in the experiment pool. This is used to ensure the accuracy of the predictive experiments throughout the actual system run. Secondly, based on the artificial system, predictive experiments are performed to analyze the behavior of the Q-UAV system and evaluate the performance of the control laws. Based on the evaluated results, the optimal control law is updated. Thirdly, the appropriate control is applied to the real system with the interactional execution between the artificial and real systems.

3.2. Artificial System

Due to it being difficult to obtain accurate dynamic models of Q-UAVs, an artificial system, based on neural networks, is introduced to rebuild the dynamic model of the real system.

The discrete-time dynamic model of the Q-UAVs can be generally written as [36]

$${\mathbf{S}}_{k+1}=F({\mathbf{S}}_k,{\mathbf{U}}_k)$$

(3)

where ${\mathbf{X}}_k$ and ${\mathbf{U}}_k$ are the system state and control input at k instant.

According to the universal approximation property of the neural network, the ideal neural network representation of the system (3) can be written as

$${\mathbf{S}}_{k+1}={\mathcal{W}}_m^{\ast \mathrm{T}}\mathsf{\Psi }(\mathsf{\Phi }({\mathbf{T}}_k))+{ϵ}_{mk}$$

(4)

where ${\mathbf{T}}_k={[{\mathbf{S}}_k,{\mathbf{U}}_k]}^{\mathrm{T}}$, ${\mathcal{W}}_m^{\ast }$ and ${ϵ}_{mk}$ are the neural network input, the ideal weight matrix, and the reconstruction error, respectively. Furthermore, $\mathsf{\Psi }(·)$ and $\mathsf{\Phi }(·)$ are the activation functions.

The artificial system can be defined as:

$$\begin{array}{c}\hfill {\mathbf{S}}_{k+1}=\mathcal{F}({\mathbf{S}}_k,{\mathbf{U}}_k)\end{array}$$

(5)

which also can be written in the form of a neural network

$${\hat{\mathbf{S}}}_{k+1}={\hat{\mathcal{W}}}_m^{\mathrm{T}}\mathsf{\Psi }(\mathsf{\Phi }({\mathbf{T}}_k))$$

(6)

where ${\hat{\mathcal{W}}}_m$ is the approximation weight matrix of ${\mathcal{W}}_m^{\ast }$. The training process of the artificial system is expressed as Algorithm 1.

Algorithm 1 Neural Networks-Based Artificial System

Initialization:

1: Collect the data set as $${\mathsf{\Omega }}_k=\{{\mathbf{S}}_{k-1},{\mathbf{S}}_{k-2},\cdots ,{\mathbf{S}}_{k-\mathcal{N}}\}$$ (7)    where $\mathcal{N}$ is a large positive integer.

2: Create a neural network as (6).

3: Select the accuracy of modeling $\xi$.

Training:

4: Calculate the training error as $${\tilde{\mathbf{S}}}_k={\hat{\mathbf{S}}}_k-{\mathbf{S}}_k$$ (8)

5: Adjust the weights to minimize the following error $$E_m=\frac{1}{2\mathcal{N}}\sum _{i=1}^{\mathcal{N}}{\tilde{\mathbf{S}}}_{k-i}^T{\tilde{\mathbf{S}}}_{k-i}$$ (9)

6: Update the weight matrix with the following function: $${\hat{\mathcal{W}}}_{m,k}={\hat{\mathcal{W}}}_{m,k-1}-l_m\frac{1}{\mathcal{N}}\sum _{i=1}^{\mathcal{N}}\mathsf{\Psi }(\mathsf{\Phi }({\mathbf{S}}_{k-i-1})){\tilde{\mathbf{S}}}_{k-i}^T$$ (10)    with $l_m$ denoting the learning rate.

7: Until the following function $$\begin{gathered} \parallel ({\hat{\mathcal{W}}}_{m,k-1}-{\hat{\mathcal{W}}}_{m,k}{)}^{\mathrm{T}}({\hat{\mathcal{W}}}_{m,k-1}-{\hat{\mathcal{W}}}_{m,k}) \\ +{\tilde{\mathbf{S}}}_k^{\mathrm{T}}{\tilde{\mathbf{S}}}_k\parallel \le \xi \end{gathered}$$ (11)    is satisfied, return the weight matrix ${\mathcal{W}}_m$.

Next, we will prove the convergence of the artificial system. Before proceeding, the following assumptions are necessary.

Assumption 1.

The reconstruction error ${ϵ}_{mk}$ satisfied the condition as

$${ϵ}_{mk}^{\mathrm{T}}{ϵ}_{mk}\le {\gamma }_m{\tilde{\mathbf{S}}}_k^{\mathrm{T}}{\tilde{\mathbf{S}}}_k$$

(12)

Assumption 2.

The activation function $\mathsf{\Psi }(·)$ and the reconstruction error ${ϵ}_{mk}$ are bounded by the positive constant ${\alpha }_M$ and ${\beta }_M$, respectively.

Theorem 1.

Let the artificial system be defined as (6), and let the weight matrix ${\hat{\mathcal{W}}}_m$ be updated according to (10). If Assumptions 1 and 2 hold, then the system identification error ${\tilde{\mathbf{X}}}_k$ is asymptotically stable and the error matrices ${\tilde{\mathcal{W}}}_m$ and both converge to zero, as $k\to \infty$.

Proof. 

Consider the artificial system (6), and select the Lyapunov function as

$${\mathcal{L}}_m={\tilde{\mathbf{S}}}_k^{\mathrm{T}}{\tilde{\mathbf{S}}}_k+\frac{1}{l_m}tr\{{\tilde{\mathcal{W}}}_{m,k}^T{\tilde{\mathcal{W}}}_{m,k}\}$$

(13)

The difference of (13) can be written as

$$\begin{array}{cc}\hfill \Delta {\mathcal{L}}_m=& {\tilde{\mathbf{S}}}_{k+1}^{\mathrm{T}}{\tilde{\mathbf{S}}}_{k+1}-{\tilde{\mathbf{S}}}_k^{\mathrm{T}}{\tilde{\mathbf{S}}}_k\hfill \\ \hfill & +\frac{1}{l_m}tr\{{\tilde{\mathcal{W}}}_{m,k+1}^T{\tilde{\mathcal{W}}}_{m,k+1}-{\tilde{\mathcal{W}}}_{m,k}^T{\tilde{\mathcal{W}}}_{m,k}\}\hfill \end{array}$$

(14)

Substituting (6) and (10) into (14), we can obtain

$$\begin{array}{cc}\hfill \Delta {\mathcal{L}}_m=& {({\tilde{\mathcal{W}}}_m^{\mathrm{T}}\mathsf{\Psi }(\mathsf{\Phi }({\mathbf{T}}_k)))}^{\mathrm{T}}{\tilde{\mathcal{W}}}_m^{\mathrm{T}}\mathsf{\Psi }(\mathsf{\Phi }({\mathbf{T}}_k))+{ϵ}_{mk}^{\mathrm{T}}{ϵ}_{mk}\hfill \\ \hfill & -2{({\tilde{\mathcal{W}}}_m^{\mathrm{T}}\mathsf{\Psi }(\mathsf{\Phi }({\mathbf{T}}_k)))}^{\mathrm{T}}{ϵ}_{mk}-{\tilde{\mathbf{S}}}_k^{\mathrm{T}}{\tilde{\mathbf{S}}}_k\hfill \\ \hfill & +l_m\mathsf{\Psi }{(\mathsf{\Phi }({\mathbf{T}}_k))}^{\mathrm{T}}\mathsf{\Psi }(\mathsf{\Phi }({\mathbf{T}}_k)){\tilde{\mathbf{X}}}_{k+1}^{\mathrm{T}}{\tilde{\mathbf{X}}}_{k+1}\hfill \end{array}$$

(15)

According to the Cauchy–Schwarz inequality, we have

$$\begin{array}{cc}\hfill \Delta \mathcal{L}\le & {({\tilde{\mathcal{W}}}_m^{\mathrm{T}}\mathsf{\Psi }(\mathsf{\Phi }({\mathbf{T}}_k)))}^{\mathrm{T}}{\tilde{\mathcal{W}}}_m^{\mathrm{T}}\mathsf{\Psi }(\mathsf{\Phi }({\mathbf{T}}_k))+{ϵ}_{mk}^{\mathrm{T}}{ϵ}_{mk}\hfill \\ \hfill & -{\tilde{\mathbf{S}}}_k^{\mathrm{T}}{\tilde{\mathbf{S}}}_k+2l_m\mathsf{\Psi }{(\mathsf{\Phi }({\mathbf{T}}_k))}^{\mathrm{T}}\mathsf{\Psi }(\mathsf{\Phi }({\mathbf{T}}_k))\hfill \\ \hfill & \times ({({\tilde{\mathcal{W}}}_m^{\mathrm{T}}\mathsf{\Psi }(\mathsf{\Phi }({\mathbf{T}}_k)))}^{\mathrm{T}}{\tilde{\mathcal{W}}}_m^{\mathrm{T}}\mathsf{\Psi }(\mathsf{\Phi }({\mathbf{T}}_k))+{ϵ}_{mk}^{\mathrm{T}}{ϵ}_{mk})\hfill \end{array}$$

(16)

Based on the Assumption 2, we can obtain

$$\begin{array}{cc}\hfill \Delta \mathcal{L}\le & -(1-2l_m{\alpha }_M^2)\parallel {\tilde{\mathcal{W}}}_m^{\mathrm{T}}\mathsf{\Psi }(\mathsf{\Phi }({\mathbf{T}}_k))\parallel {}^2\hfill \\ \hfill & -(1-{\gamma }_m-2l_m{\gamma }_m{\alpha }_M^2)\parallel {\tilde{\mathbf{S}}}_k\parallel {}^2\hfill \end{array}$$

(17)

Select $l_m$ to satisfy the condition as

$$\begin{array}{c}\hfill l_m<\min \{\frac{1}{2{\alpha }_M^2},\frac{1-{\gamma }_m}{2{\gamma }_m{\alpha }_M^2}\}\end{array}$$

(18)

Then, we have $\Delta {\mathcal{L}}_m<0$, which means the system identification error ${\tilde{\mathbf{S}}}_k$ is asymptotically stable and the error matrices ${\tilde{\mathcal{W}}}_m$ and both converge to zero, as $k\to \infty$. □

3.3. Predictive Experiments

After reconstructing the actual system, predictive experiments are executed to gain the optimal control of the artificial system (5). In the predictive experiments, the neural networks are applied to predict the state of the artificial system in future N steps. Thus, the system (5) can be rewritten as

$$\begin{array}{c}\hfill {\mathbf{Z}}_{k+1}=\mathcal{F}({\mathbf{Z}}_k,{\mathbf{U}}_k)\end{array}$$

(19)

where ${\mathbf{Z}}_k$ denote the predictive state of the system (5).

Let the control sequence ${\mathcal{U}}_k^{N-1}$ defined as ${\mathcal{U}}_k^{N-1}=\{{\mathbf{U}}_k,{\mathbf{U}}_{k+1},\cdots ,{\mathbf{U}}_{k+N-1}\}$ to be the predictive control in future N steps. Furthermore, the utility function is defined as

$$\begin{array}{c}\hfill \mathsf{\Gamma }({\mathbf{U}}_k,e_k)={\mathbf{U}}_k^{\mathrm{T}}Q{\mathbf{U}}_k+e_k^{\mathrm{T}}R{e}_k\end{array}$$

(20)

where $e_k={\mathbf{S}}_k-{\mathbf{S}}_k^d$ with ${\mathbf{S}}_k^d$ denote the target state at k instant; Q and R are semi-positive definite matrices with suitable dimensions. Thus, the cost function can be defined as

$$\begin{array}{c}\hfill {\mathcal{J}}_k=\sum _{i=0}^{N-1}\mathsf{\Gamma }({\mathbf{U}}_{k+i},e_{k+i})\end{array}$$

(21)

Then, the optimal control sequence can be obtained as

$$\begin{array}{c}\hfill \mathcal{U}=\{\arg \underset{{\mathbf{U}}_i}{\min }\sum _{j=0}^{N-1}\mathsf{\Gamma }({\mathbf{U}}_{i+j},e_{i+j})\}{}_{i=k}^{\infty }\end{array}$$

(22)

However, to maintain the safety and stability of the flight process, the following constraint should be applied in the optimization.

3.3.1. Input Constraint

In the parallel control scheme, the limits of the input of the Q-UAV is considered for the safety of the flight process. The constraint for the Q-UAV can be defined as

$$\begin{array}{c}\hfill {\mathbf{U}}_{min}\le {\mathbf{U}}_k\le {\mathbf{U}}_{max}\end{array}$$

(23)

where the ${\mathbf{U}}_{min}$ and ${\mathbf{U}}_{max}$ denote the minimum and maximum of the input vector at the instant k.

3.3.2. Velocity Constraint

In the algorithm proposed in this article, the velocity of the Q-UAV is limited, which can be defined as

$$\begin{array}{c}\hfill {\dot{x}}_{min}\le \dot{x}\le {\dot{x}}_{max}\\ \hfill {\dot{y}}_{min}\le \dot{y}\le {\dot{y}}_{max}\\ \hfill {\dot{z}}_{min}\le \dot{z}\le {\dot{z}}_{max}\end{array}$$

(24)

where ${\dot{\varsigma }}_{max}$ and ${\dot{\varsigma }}_{min}$ denote the minimum and maximum of the velocity of the Q-UAV in $\varsigma$ axis.

3.3.3. Angle Velocity Constraint

In this article, the limits of the angular velocities are also considered in the proposed algorithm, which can be defined as follows.

$$\begin{array}{c}\hfill {\dot{\varphi }}_{min}\le \dot{\varphi }\le {\dot{\varphi }}_{max}\\ \hfill {\dot{\theta }}_{min}\le \dot{\theta }\le {\dot{\theta }}_{max}\\ \hfill {\dot{\psi }}_{min}\le \dot{\psi }\le {\dot{\psi }}_{max}\end{array}$$

(25)

Similarly to (24), ${\dot{\varphi }}_{min}$, ${\dot{\theta }}_{min}$, and ${\dot{\psi }}_{min}$ denote the minimum angle velocity of three Euler angles, respectively; and ${\dot{\varphi }}_{max}$, ${\dot{\theta }}_{max}$ and ${\dot{\psi }}_{max}$ denote the maximum angle velocity of three Euler angles, respectively.

Then, the parallel predictive experiment method under the constraints can be expressed as Algorithm 2.

Algorithm 2 Parallel Experiment Algorithm

Initialization:

1: Select the semi-positive matrices P and Q to construct the cost function as (21).

2: Select the positive constant N as the control horizon.

Rolling Prediction:

3: Collect data with the artificial system (6) based on current control law.

4: Calculate the cost function by (21).

5: Obtain the optimized control sequence $\mathcal{U}$ according to the function (22) with the constraint (23).

6: Implement the first element of the control sequence into the artificial system (6).

3.4. Parallel Execution

In the above section, the predictive experiments are executed to gain the optimal control of the artificial system (5), which aims to control the discrete-time dynamic model (3) of the Q-UAVs. However, for the real Q-UAV system, it is difficult to rebuild the system dynamics in the whole time horizon by a single artificial system, because the system function is complex and unknown. Thus, to keep the accuracy of the model, the dataset in (7) is updated with time, which means the dataset always stores the latest $\mathcal{N}$ data.

Combining the above sections, the Parallel MPC method can be expressed as Algorithm 3.

Algorithm 3 Parallel MPC algorithm

Initialization:

1: Select the positive integer $\mathcal{N}$ as the maximum length of the experience pool.

2: Select the semi-positive matrices P and Q.

3: Select the positive integer N as the control horizon.

4: Select the computation precision $\zeta$.

5: Select the initial instant $k=0$.

6: Select the positive integer l as the length of the experience pool.

Parallel Predictive Control:

7: if $l<\mathcal{N}$ then

8:    Store the last state ${\mathbf{X}}_{k-1}$, control input ${\mathbf{U}}_{k-1}$ and the system state ${\mathbf{X}}_k$, as a data pair, into the experience pool.

9: else

10:    Remove the first data pair from the experience pool.

11:    Store the newest data pair in the experience pool.

12: end if

13: Training the artificial system with the experience pool until $\parallel {({\hat{\mathcal{W}}}_{m,k-1}-{\hat{\mathcal{W}}}_{m,k})}^{\mathrm{T}}({\hat{\mathcal{W}}}_{m,k-1}-{\hat{\mathcal{W}}}_{m,k})+{\tilde{\mathbf{X}}}_k^{\mathrm{T}}{\tilde{\mathbf{X}}}_k\parallel \le \zeta$ is satisfied.

14: Predict the system state based on the artificial system in the control horizon N.

15: Calculate the cost value based on the function (21) for every predictive instant.

16: Calculate the optimal control based on the cost value.

17: Applying the first optimal control into the actual system.

4. Simulation Results

In this section, to demonstrate the effectiveness of the PMPC algorithm for UAVs, a comparison with traditional MPC is performed. The initial mass of the Q-UAV is chosen as $m=6.98\times {10}^{-2}$ kg; the moment of the inertia of the Q-UAV around the axes are chosen as $I_x=I_y=I_z=3.4\times {10}^{-3}$ kg·m${}^2$, respectively; the moments of inertia of the propeller blades are chosen as $J_R=1.302\times {10}^{-6}$ kg·m${}^2$; the length from the rotors to the center of mass is chosen as $L=1.17\times {10}^{-1}$ m; and the acceleration of gravity is chosen as 9.8 m/s${}^2$.

The parameters in this simulation are chosen as

$$\begin{array}{c}\hfill Q=\left[\begin{array}{cc}10& 0\\ 0& 10\end{array}\right]R=\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right]\end{array}$$

(26)

and the learning rate of the modelNN is chosen as $lr=0.01$, the activation function $\mathsf{\Psi }(·)$ and $\mathsf{\Phi }(·)$ are defined as sigmoid function. To reflect the internal dynamic uncertainties of the UAV dynamic model, 5% parameter inaccuracies are assumed during the model prediction process. Some constraints in this simulation are shown as Figure 3.

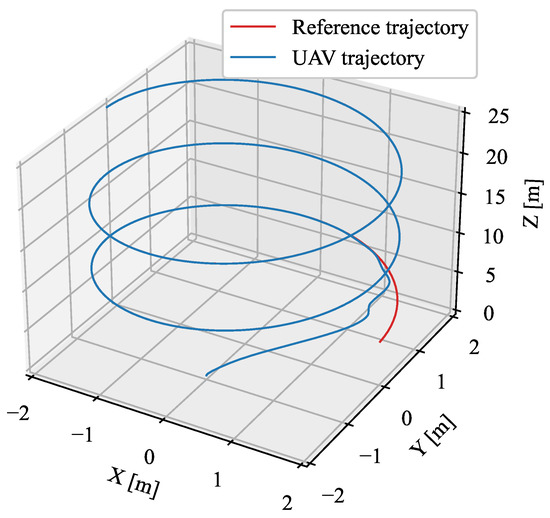
Figure 3. The tracking histories of the UAV.

The target trajectory is chosen as

$$\begin{array}{cc}\hfill x& =2cos(0.05\pi t)\hfill \\ \hfill y& =2sin(0.05\pi t)\hfill \\ \hfill z& =0.2t\hfill \end{array}$$

(27)

It is worth mentioning that the target Euler angles are defined to keep track of the target trajectory in this simulation. Furthermore, the constraints of the position velocity in this simulation are chosen as 1 m/s and the angular velocity is chosen as $\pi /15$ rad/s. The rotating speed of rotors $omega$ is bounded in the range of $[110,860]$ r/s.

As shown in Figure 4, under the PMPC algorithm, the UAV tracked the target trajectory in 15 seconds. However, when it is under traditional MPC control, it cannot follow the target trajectory if the dynamics model is changeable. This means the PMPC algorithm has better performance when dealing with the tracking control problem with a dynamic dynamics model. To demonstrate the robustness of PMPC algorithm, the external disturbances are added at 20 s, and the results are shown in Figure 5. From Figure 5, the system can track the target trajectory in several seconds under the PMPC algorithm.

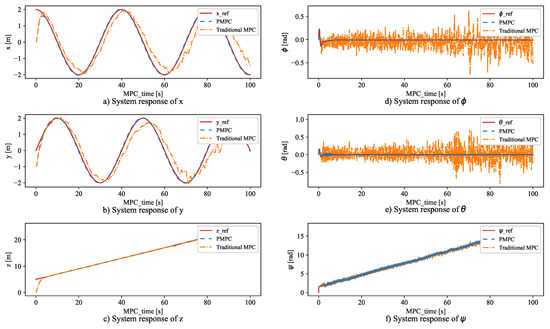
Figure 4. System response of x, y, z, $\varphi$, $\theta$, and $\psi$.

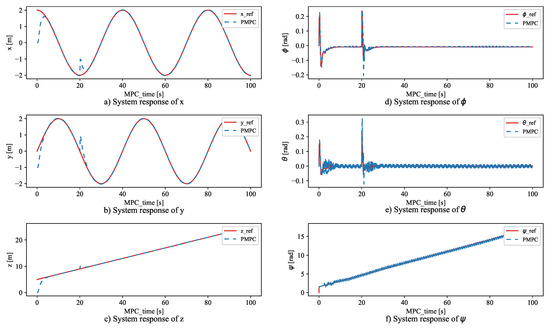
Figure 5. Tracking error of x, y, z, $\varphi$, $\theta$, and $\psi$.

5. Conclusions

In this article, a novel NN-based PMPC optimal tracking control algorithm is proposed for the UAV under a dynamic dynamics model. Due to the dynamics model of the UAV being changeable, which is difficult to deal with for traditional MPC algorithms, a neural network with experiment reply technology is applied to approximate the dynamic model as the system runs. Then, a parallel structure is constituted by the NN-based artificial system and the real system. Under the parallel structure, the MPC algorithm is applied to predict the future states of the artificial system and obtain the optimal control for the tracking control problem. Finally, a simulation is applied to demonstrate the effectiveness of the PMPC algorithm.