Energy-Efficient Bi-Objective Optimization Based on the Moth–Flame Algorithm for Cluster Head Selection in a Wireless Sensor Network

Abstract

Designing an efficient wireless sensor network (WSN) system is considered a challenging problem due to the limited energy supply per sensor node. In this paper, the performance of several bi-objective optimization algorithms in providing energy-efficient clustering solutions that can extend the lifetime of sensor nodes were investigated. Specifically, we considered the use of the Moth–Flame Optimization (MFO) algorithm and the Salp Swarm Algorithm (SSA), as well as the Whale Optimization Algorithm (WOA), in providing efficient cluster-head selection decisions. Compared to a reference scheme using the Low-Energy Adaptive Clustering Hierarchy (LEACH) protocol, the simulation results showed that integrating the MFO, SSA or WOA algorithms into WSN clustering protocols could significantly extend the WSN lifetime, which improved the nodes’ residual energy, the number of alive nodes, the fitness function and the network throughput. The results also revealed that the MFO algorithm outperformed the other algorithms in terms of energy efficiency.

1. Introduction

A wireless sensor network (WSN) is defined as a network with many embedded wireless sensors with various sensing devices [1,2]. It is an infrastructure-based network composed of communication, computing and sensing elements, which makes a sink node capable of reacting to events within a certain context [3,4]. Typically, it is a governmental, civil, industrial or commercial entity, where the environment could be an IT framework, a biological system or the physical world [5]. Usually, a WSN includes thousands of randomly deployed sensors. Theses sensors are battery-powered, and it is difficult to recharge them after deployment [6,7]. Hence, energy efficiency is a significant challenge in WSNs, and different mechanisms have been proposed to deal with this energy efficiency issue [8]. To establish which relaying mode is more energy-efficient and to solve the issue of energy efficiency optimization, a complete analysis of the energy efficiency of full-duplex and half-duplex amplify-and-forward relay-assisted 60 GHz dual-hop indoor wireless systems is presented in [9]. The cluster network topology concept is considered a promising strategy to enhance the energy performance of WSNs. The basic concept of the Low-Energy Adaptive Clustering Hierarchy, which is known as LEACH, is choosing the cluster node within an unsystematic cycle and handing over the entire energy of the network to every node of the sensor, as well as, on average, prolonging the network survival lifetime in addition to reducing energy consumption [10,11,12,13]. For instance, reducing the transmission task of sensor nodes in a WSN can result in extending the service life of the sensor nodes [14]. However, the random technique of choosing the cluster node means that every single node may turn into the cluster node, and there is a chance that a small energy node will turn out to be the cluster node. An additional technique that uses a weighted-objective optimization algorithm is the Moth–Flame Algorithm, which is known as the MFO algorithm and was proposed in [15]. The MFO algorithm has several advantages [16]. The MFO algorithm is popular due to its simple parameters and structure. Furthermore, since the MFO algorithm is efficient, robust and easy to implement within different computer languages, it has been widely used in many optimization applications [17]. The MFO algorithm combines a population-based algorithm and a local search strategy to yield an algorithm capable of global exploration and local exploitation [18]. Like other metaheuristics, the MFO algorithm is simple, flexible and easily implemented; as a result, it can be utilized to solve a wide range of problems [19]. Because of these merits, the MFO algorithm has been successfully applied to various optimization problems, including scheduling [20], the inverse problem and parameter estimation [21,22], classification [23], economics [24], medicine [25], power energy [26] and image processing [27].

Several studies have investigated energy-efficient bi-objective optimization for cluster head selection in wireless sensor networks. For instance, Latiff et al. proposed a novel clustering algorithm based on Particle Swarm Optimization (PSO) called Centralized-PSO (PSO-C); the cluster head (CH) selection process was formulated as a bi-objective optimization problem to find the optimal cluster head set to form one-hop clusters to balance energy consumption. The study considered each sensor node’s residual energy and each cluster head’s closeness to its sensor nodes. The proposed algorithm minimized the objective function to ensure that the sensor nodes with sufficient energy, as well as a minimum distance from their neighbors, were selected as cluster heads [28,29]. Jadhav and Shankar hybridized an energy-efficient CH algorithm based on the Whale Optimization Algorithm (WOA). The proposed WOA-C algorithm contributes to the selection of energy-aware CHs according to a fitness function that considers the node’s residual energy and the sum of the adjacent nodes’ energy. The proposed algorithm was evaluated in terms of energy efficiency, network lifetime, overall stability and throughput. Moreover, the WOA-C algorithm’s performance was evaluated and compared with other standard routing protocols, including the Low-Energy Adaptive Clustering Hierarchy (LEACH) [30]. Honey Bee Optimization (HBO) was proposed by Selvi et al. to minimize energy consumption through finding the optimal path, which is associated with a lower cost. The proposed algorithm showed improvements in the network lifetime and throughput. HBO also showed enhanced performance in terms of scalability and link quality [31]. Syed and Syed developed the Weighted Salp Swarm Algorithm (WSSA) based on the weighted distance position update for improving the convergence rate and performance of the SSA algorithm. The WSSA was validated by many benchmark functions, where it was compared with seven state-of-the-art algorithms. The results showed that the WSSA has an improved convergence rate and performance. In addition, the proposed algorithm was applied to the problem of optimal sensor deployment. The algorithm was applied on a probabilistic sensor model to maximize the coverage, while it was applied on a radio energy model to minimize the energy consumption [32]. Mann and Singh proposed an Improved Artificial Bee Colony (IABC) algorithm for optimal sensor deployment. The proposed algorithm was used for obtaining CHs and improved the energy efficiency. The results showed that the optimal base station position could be obtained by changing the distance to the sensor node number [33].

Hussain and Raziuddin proposed the Completely Informed Artificial Bee Colony (CABC) for optimal CH positions and used a probability sensor model for coverage for a wireless sensor network. The results showed improvements in the coverage rate in a WSN using the proposed algorithm [34]. Li et al. proposed Ant Colony Optimization (ACO) for an energy-efficient wireless sensor network. The algorithm saved on residual energy and the distance of neighbor nodes. According to the pheromone value, the subsequent hop was updated as the distance between nodes was compared. The proposed algorithm showed that a low energy node was not selected as the subsequent hop, which resulted in the efficient load balancing of the network energy [35,36]. Jia et al. studied the maintaining sensing problem coverage by optimizing energy consumption in a WSN. As opposed to the existing consistent sensing model, the authors considered an excess of sensors with a variable sensing radius to be randomly deployed in the monitoring area. A new coverage control format founded on a selective non-dominated sorting genetic algorithm, which is known as (NSGA-II), was implemented within a heterogeneous WSN. The algorithm was applied in a distributed manner by developing a cluster-based architecture [37,38]. Vijayalakshmi and Anandan investigated the choice of the best path within routing that develops a network’s energy efficiency and network lifespan. Different meta-heuristic methods, mainly PSO, have been efficiently utilized that have reduced the problem of local optima. The projected technique was included in the foundation of the algorithms of Tabu as well as PSO search. The results showed the effectiveness of the Tabu PSO that was proposed through the ornamental cluster-shaped number and the percentage of nodes alive, and the decrease in the average continuous delay and the average of the packet loss speed was illustrated [39,40]. Jameii, Faez and Dehghan projected a new algorithm for optimizing the lifetime, connectivity and coverage of a network within wireless sensor networks. NSGA-II was applied to make the best use of the exposure area for presenting the consumption of the balanced energy as well as for reducing the conduction variety of the nodes [41]. Jameii, Faez and Dehghan used NSGA-II to optimize the rate of the coverage of the observing area, the consumption of the balanced energy, and number of active sensor nodes while adaptively mutating the rates and assigning crossover to advance the performance of the algorithm of optimization through learning automata [42]. Bara’a, Khalil and Cosar used NSGA-II to choose mobile sensor locations, offering a long network lifetime as well as a high coverage. The planned system included mobile sensors and a number of targets. The most important idea of the algorithm was making the most of the detected targets number and the network lifetime together [43].

Following an investigation on the best bi-objective optimization algorithm technique for increasing the WSN life span, we found few research that had been conducted on the use of the moth–flame algorithm for cluster head selection in a wireless sensor network. Therefore, this research proposes a bi-objective optimization algorithm based on MFO as a WSN clustering technique by making use of a weighted-sum approach. This study also compared the proposed algorithm with SSA, WOA and LEACH, some of the most well-known hierarchical routing protocols for wireless sensor networks. The adopted algorithm (MFO) demonstrated superior performance regarding efficiency (the speed at which an algorithm finds accurate answers, converges and computes) and effectiveness (an algorithm’s capacity for generating high-quality solutions) in solving wireless sensor optimization problems. This paper is organized as follows. The introduction is presented in Section 1. Related works and background are provided in Section 2. Section 3 is devoted to the WSN energy consumption model as well as the complexity analysis. The simulation results and discussion are addressed in Section 4. Conclusions and further work are covered in Section 5.

2. Related Works and Background

2.1. Selection of the Bi-Objective Optimization Algorithms

It is worth noting that the adopted algorithms (MFO, SSA and WOA) have demonstrated superior performance regarding efficiency (the speed at which an algorithm finds accurate answers, converges and computes) and effectiveness (an algorithm’s capacity for generating high-quality solutions) in solving optimization problems. These metaheuristic optimization algorithms were chosen based mainly on their searching scope and simplicity as well as other critical factors such as time complexity, problem functionality, the number of objectives, output optimality and the number of starting solutions.

From a searching scope point of view, these algorithms look at the entire problem space as a single entity when trying to find the global optimum solutions via a good balance between exploitation and exploration in order to improve the rate of algorithm convergence [44,45]. Exploration entails generating numerous solutions to thoroughly examine the search space on a global basis, whereas exploitation entails focusing the search on a limited region in the knowledge that a currently viable solution exists there. The best solutions are chosen to ensure that they converge to the optimal solution, whereas randomization allows the search to avoid local optima while increasing the diversity of solutions. A successful combination of these two fundamental components almost results in global optimality [46]. In addition, a searching method has a stochastic nature when a set of random variables is employed in extracting a possible solution [47]. Additionally, the progress of the searching process continues iteratively with the same searching procedure until the best potential candidate solution is obtained [48,49]. With respect to simplicity, meta-heuristic algorithms require fewer control parameters to fit the problems under consideration, and they are more appealing and easier to execute since they are based on the use of simpler concepts and the use of establishing parameters that can be altered and tailored to match the problem’s nature [50]. Considering time–growth complexity, it is an important metric in evaluating an algorithm’s run time that is defined according to the algorithm’s implementation and structure. When the quicksort algorithm is used, the computational complexity of the sort is O(n2) and O(nlog(n)) in the worst and best cases, respectively [51]. In terms of functionality and the number of the objective functions, it ensures that the algorithm as well as the corresponding generic implementation code is applicable to a wide variety of issues. Additionally, the emphasis is mostly on the use of algorithms without regard for problem-specific expertise [52]. In addition, the problem in hand has goals with bi-objective functions, which requires incorporation with a weighted average in order to reflect the nature of the existence of the two objectives. As a result, their fitness functions are represented by a multi-parameter vector [53]. Regarding output optimality and the number of starting solutions, the problem of cluster head selection allows for several possible outcomes, all of which are recognized as valid by the solution space, and any of them could be the optimal solution or close to the optimal one [54,55]. Additionally, these meta-heuristic algorithms are population-based approaches, which means that numerous viable solutions work together to overcome local optima traps.

2.2. Moth–Flame Optimization (MFO) Algorithm

The MFO algorithm is a novel meta-heuristic method of optimization. It is a method for travelling an extended distance within a directed path and is inspired by the fact that the moon is distant for a moth [56]. This method ensures that a moth takes off in a directed line during the night. On the other hand, it is also generally found that moths will fly in a spiral pattern around lights. Moths are also deceived by fake lights. To a moth, a man-made light is very similar to the moon; therefore, preserving a similar angle into the source of the light is the reason that moths fly in a spiral pathway [57]. Within the moth–flame algorithm, moths are the confirmer of the answer, where the changeable argument is the position of the moth in the search area. Therefore, moths will take wing in 1-D, 2-D or 3-D spaces; the vector of a moth’s position will vary within the dimensions of the area being searched. The MFO algorithm measures a population as stranded wherever the moths are detected in a matrix form.

The moth simulation is carried out by a spiral function logarithm. The flame points to the moth’s subsequent position around it; this can be observed in the logarithm of a spiral function. The term ‘t’ defines the restriction that chooses the space of every moth throughout the spiral motion; t = −1 represents the immediate or direct space, while t = 1 represents the farthest distance. Moths incessantly change their situations regarding the light up the next spiral pathway. The exploitation as well as exploration of a whole search gap can be definite, as a logarithmic spiral function permits a moth to move around a flame [58,59]. Algorithm 1 demonstrates the pseudocode of the moth–flame algorithm.

Algorithm 1 (MFO) The pseudocode of the moth–flame algorithm

1: Begin 2: initialize the moths position. 3: While(iteration<=Max_iteration) 4: Update the number of flame 5: OM = Fitness Function(M) 6: if iteration equal to 1 7: F = short(M) 8: OF = sort(OM) 9: else 10: F = sort(Mt−1,Mt) 11: OF = sort(Mt−1,Mt) 12: End 13: for i = 1: n 14: for j = 1: d 15: Update t as well as r 16: compute D with regard to the equivalent moth 17: Update M(i,j) with regard to the equivalent 18: End 19: End

2.3. Whale Optimization Algorithm (WOA)

The WOA is a novel nature-inspired meta-heuristic optimization algorithm developed by Mirjalili as well as Lewis (2016) that imitates humpback whales’ social behavior [60]. Whales are known for being extremely clever animals through their movement. The whale optimization algorithm is inspired by specifically humpback whales’ hunting behavior. Generally, humpback whales favor fish or hunt krill that are near the surface of the sea. Humpback whales utilize a particular exclusive hunting technique called bubble net feeding. During bubble net feeding, they swim in the prey area and generate a unique bubble, all along a nine-shaped or circular pathway. Humpback whales can distinguish their prey’s location in addition to surrounding them. For the unknown position of the optimal design in the search area, the existing best-agent-possible solution is the target prey or is near to the optimal solution in the whale optimization algorithm. Once the most excellent search candidate is defined, the next search candidates will thus try to update their positions towards the finest search candidate [61].

2.4. Salp Swarm Algorithm (SSA)

The inspiration for the SSA is the swarming performance of salps when they are foraging, as well as when they are navigating within the ocean. The algorithm contains several mathematical optimization functions to confirm as well as observe efficient behaviors while finding the best possible solutions to optimization problems [62].

2.5. Low-Energy Adaptive Clustering Hierarchy (LEACH)

The LEACH algorithm is a TDMA (Time-Division Multiple Access) fundamental MAC (Medium Access Control) algorithm that was proposed by Heinzelman, Chandrakasan and Balakrishnan (2000). The important goal of this algorithm is to extend the lifetime of WSNs through decreasing the consumption of the energy necessary for maintaining and creating the cluster heads. The process of the LEACH algorithm contains several rounds, with two stages within every round: a steady phase in addition to a setup phase. The steady phase is comparatively longer. The setup mostly relates to the transmission of aggregated information to the base station as well as the aggregation of information at the cluster heads. In the setup phase, the most important aim is to build clusters, as well as choosing cluster heads through choosing a sensor node with the highest remaining energy [63]. Knowing that the dissipation of the energy of the sensors relies on the data size in addition to the transmission distance, LEACH attempts to reduce the number of receptions and transmissions. The main features of LEACH involve the arbitrary rotation of the CH [64]. This study took a different approach by comparing well-known nature-inspired algorithms to the low-energy adaptive clustering hierarchy algorithm, which is a common contemporary routing protocol. Furthermore, the LEACH method is used as a starting point for most cluster head protocols since it is a reliable wireless communication protocol that is both energy efficient and has a low latency.

The MFO algorithm was used in this study because of the following advantages: it guarantees exploration and exploitation. The success of such an algorithm depends on a suitable tradeoff between exploration and exploitation [65] since this impacts the algorithm’s convergence rate. The MFO algorithm tries to optimize the optimization problem and guarantees both exploitation and exploration of the search space by using the logarithmic spiral function, which allows the movement of the moth around the flame and not essentially in the space between the flame and the moth. Moreover, the flame count is gradually lessened during iterations to maintain the balance between exploration and exploitation. In the MFO algorithm, each moth updates its position according to one particular flame. Due to the significance of the WSN-based border protection domain, this study attempted to identify an optimization algorithm that could provide better performance in order to expand the WSN lifetime, increase the number of alive nodes and enhance the throughput and remaining energy.

The MFO algorithm provides a very quick convergence at a very early stage by switching from exploration to exploitation, which increases the MFO algorithm’s efficiency for applications such as classification when a quick solution is required or when energy-efficient cluster head selection is needed in a WSN. However, the MFO algorithm was only considered to be employed for such problems after enhancement was performed in order to solve different kinds of optimization problems. Therefore, this study performed experiments with this algorithm and compared its performance with that of other algorithms. The contributions of this study can be summarized in the following way: it was the first work that compared the MFO algorithm with well-known, nature-inspired algorithms. Moreover, it demonstrated the MFO algorithm’s capability to achieve a very rapid convergence at an early point of the exploration process by moving from exploration to exploitation.

3. Materials and Methods

3.1. The Wireless Network Energy Consumption Model

We investigated a network configuration with the following characteristics: the base station remained intact and was positioned within the sensor network region. Each sensor node was fixed and was capable of sensing. Sensor nodes executed their work and transmitted data to the base station (BS). Each node could operate in cluster head (CH) mode or detecting mode depending on the residual energy level. The wireless energy model states that the transmitted power attenuation decays exponentially as the transmission distance increases.

Firstly, Equation (1) was used to determine the expected number of cluster heads, k.

$$k=\lceil \sqrt{n/2}\rceil$$

(1)

where the ceil-up operator (⌈⌉) was used, and (n) is the number of sensor nodes in the networks, from which k nodes were selected for the initialization of the cluster centers. The wireless energy model for the sensors utilized as a part of the protocol depends on the first-order wireless model that was used as a part of [66,67]. The wireless energy model relies on the consumption of the energy transmission. The energy consumption formula for the transmission from node a to node b, with distance d and packet size K, is given as:

$$E_{Tab}\left(K,d\right)=\left\{\begin{array}{c}K{E}_{elect}+K{\epsilon }_{fs}{d}_{ab}{}^2, d<d_o\\ K{E}_{elect}+K{\epsilon }_{mp}{d}_{ab}{}^4, d\ge d_o\end{array}\right.$$

(2)

where “${\epsilon }_{fs }”$ is the free space fading energy, and “ ${\epsilon }_{mp }$” is the multi-path fading energy. $E_{elect}$ refers to the energy consumed in an electronic circuit to transmit or receive a signal. $d_{ab}$ is the Euclidean distance between nodes a and b. $d_o$ is the constant-threshold estimation of the transmission distance, which is given as:

$$d_o=\sqrt{\frac{{\epsilon }_{fs }}{{\epsilon }_{mp }}}$$

(3)

The appropriate energy consumption model is determined by the threshold distance as a function of the distance (d) between any communication nodes. Since the cluster head’s location determines the distance (d), then (d) changes along with the cluster head. The first part of the mathematical formula (2) represents the free-space path-loss consumed energy, while the second part quantifies the multi-path fading model.

The energy consumption of receiving the data packet, which only depends on the circuit loss, was calculated as

$$E_R\left(K\right)=K*E_{elect}$$

(4)

The energy consumption at the cluster head was calculated as

$$E_c=n{E}_R+E_{TCBS}$$

(5)

where n is related to the number of packets to be sent, and${ \mathrm{E}}_{\mathrm{TCBS}}$ is related to the energy consumption while transmitting from the cluster head to the base station. The energy consumption of transmission from the node to the cluster head within a given cluster was calculated as [68]

$$E_n=n{E}_{Tnc}$$

(6)

The parameters listed in Table 1 are used to determine how much energy is consumed by a wireless sensor network.

Table 1. Energy consumption radio parameters in WSN.

Symbol	Description
$E_{elec}$	Energy consumed in an electronic circuit to transmit or receive a signal
${\epsilon }_{MP}$	Energy consumed by an amplifier to transmit at a shorter distance (multi-path)
${\epsilon }_{FS}$	Energy consumed by an amplifier to transmit at a shorter distance (free space)
${\epsilon }_{DA}$	Data aggregation energy
$d_0$	The threshold estimation of the transmission distance
$E_R$	The energy consumption of receiving the data packet
$E_c$	The energy consumption at the cluster head
$E_n$	The energy consumption at the node
$E_{TCBS}$	The energy consumption of transmission from the cluster head to the base station
$E_{Tnc}$	The energy consumption of transmission from the node to the cluster head

3.2. Weighted-Sum-Based Bi-Objective Optimization

Communication between the CH and the node selected should be modest in terms of both distance and energy consumption. The network must have a massive amount of energy, which means that it must use just a small amount of energy when transmitting data. Thus, one optimized solution will have trade-offs among diverse objectives, and a group of solutions is necessary for characterizing the most efficient solution for every objective [67,68].

The bi-objective function in this study was designed to select the cluster head within every cluster while optimizing two objectives (distance and energy), which are given as

$$f_{obj}=\alpha \times f_1+\left(1-\alpha \right)\times f_2, \alpha =0.5$$

(7)

$$f_1=min\left\{{{\displaystyle \sum }}_{node{ }_i \in C_k}\frac{d\left(node{ }_i, C{H}_k\right)}{\Vert C_k\Vert }\right\}$$

(8)

$$f_2=\frac{{{\displaystyle \sum }}_{i=1}^{N}E\left(nod{e}_i\right)}{{{\displaystyle \sum }}_{j=1}^{k}E\left(C{H}_j\right)}$$

(9)

where f₁ defines the majority great of the Euclidean distance between nodes, node_i∈ cluster C_k, for the cluster heads CH_k, $\Vert C_k\Vert$ is the number of nodes that are managed by cluster C_k within f₂ and N is the number of nodes that are selected as cluster-heads. This ensures the selection of the nodes’ average energy supplies and the best average distance to the nodes from the selected cluster heads. The constant α demonstrates the weight of f₁ and f₂ within the objective f(x). The target function aims to decrease the intra-cluster average distances and improve the energy consumption in the network.

Note that f₁ represents the distance, namely, the distance from every node to the cluster head and the distance from the cluster head to the base station. f₂ represents the ratio of the starting energy of all living nodes in the network (a sensor node is alive when its energy is greater than zero) to the cluster head’s total current energy in the current round. This ensures the selection of a cluster head with high remaining energy. The optimization function reflects a tradeoff between the two objectives. The factor α is a scaling factor that determines the importance of f₁ and f₂, where the factor is selected as 0 ≤ α ≤ 1. The constant factor α is utilized to evaluate the weight of every sub-objective. The fitness function in Equation (7) has the purpose of concurrently reducing the distance between the cluster head and the nodes, while the network energy efficiency optimization is quantified via f₂. This results in weighted-sum-based bi-objective optimization. When α = 0,$f_{obj}=f_2,$ and the fitness function only optimizes the network energy efficiency. When α = 1,$f_{obj}=f_1.$ This only optimizes the distance between the nodes and the cluster heads. When α is equal to 0.5 in Equation (7), both sub-objectives are optimized equally.

3.3. Complexity Analysis

The complexity analysis is an important metric in evaluating an algorithm’s run time that is defined according to the algorithm implementation and structure. The MFO algorithm’s computational complexity depends on the number of moths, the number of variables, the number of maximum iterations and a flame-sorting mechanism in each iteration. As the quicksort algorithm was used, the computational complexity of the sort was in the order of O(n²) and O(nlogn) in the worst- and best-case scenarios, respectively. With the P function, the overall computational complexity can be defined as follows:

$$O\left(MFO\right)=O\left(t\left(O\left(Quick sort\right)+O\left(position update\right)\right)\right)$$

(10)

$$O\left(MFO\right)=O\left(t\left(n^2+n\times d\right)\right)=O\left(t{n}^2+tnd\right)$$

(11)

where n is the number of moths, t is the number of maximum iterations and d is the number of variables. In order to understand how the MFO algorithm can be effective for solving optimization problems theoretically, some observations include:

• The procedure of updating positions allows finding neighboring solutions around the flames, which is a mechanism for typically promoting exploitation.
• As the MFO algorithm uses a population of moths, the local optima avoidance will be high.
• The search space exploration is increased and the local optima stagnation probability is decreased by assigning each moth a flame and then updating the flames sequence within each iteration.
• Taking into consideration current best-obtained solutions up to the present as the number of flames saves promising solutions as moth guides.
• The adaptive flames number balances exploration and exploitation.
• The adaptive convergence constant (r) results in accelerated convergence around the flames on the iterations course.

Such observations make the MFO algorithm able to enhance the initial random solutions as well as the convergence into an enhanced point within the search space.

4. Simulation Results and Discussion

This paper presents a performance evaluation and comparison between three main bi-objective optimization algorithms, namely the whale optimization algorithm (WOA), the salp swarm algorithm (SSA) and the moth–flame optimization (MFO) algorithm in terms of their ability to provide efficient clustering decisions. Some critical metrics for the evaluation process were used, such as the fitness function, the number of alive nodes, the throughput and the residual energy. Then, the algorithm with the best performance was compared with the low-energy adaptive clustering hierarchy (LEACH) protocol.

The proposed algorithms were tested using Matlab R2022. Simulations were carried out on a network with 30 sensor nodes that were deployed in a 100 m $\times$ 100 m field, as shown in Figure 1. A mobile working sensor with a fixed trajectory was used that could be placed at different locations within the deployment area. This could significantly improve the data delivery rate and reduce the energy dissipation of the sensor nodes. The selection of cluster heads was carried out whenever a re-clustering was needed (e.g., when the energy level of the current cluster head fell below a certain threshold). Hence, the selection was not a one-time optimization. The MFO algorithm started creating moths randomly within the solution space, and a random population of sensor nodes were produced through iterations. The nodes were generated after the system reached its statistical foundation, i.e., a steady state status, using the residual analysis. The numbers of generations and search agents were set to 10,000 and 5, respectively. The parameters used in the simulation are shown in Table 2.

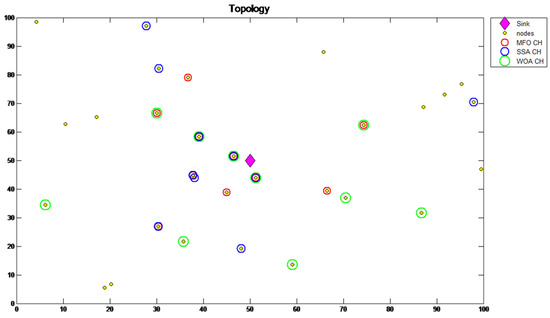
Figure 1. Cluster head selection in WSN via WOA, MFO and SSA.

Table 2. Simulation parameters of the network.

Parameters	Value
Population size	30 sensor nodes
Deployment area	100 $\times$100 m2
The location of the sink	(50, 50)
Initial energy for each node	0.5 J
The energy transmission	50 nJ/bit
The energy receiver	50 nJ/bit
${\epsilon }_{MP}$	0.0013 pJ/bit/m4
${\epsilon }_{FS}$	10 pJ/bit/m2
${\epsilon }_{DA}$	5 nj/bit/packet
$E_{elec}$	50 nJ/bit
Search agents	5
The number of generations	10,000
Size of packet (K)	4096 bits

4.1. First Stage of Analysis

The simulations began by comparing the performance of the WOA, SSA and MFO algorithms in terms of exploration and exploitation, as well as four different metrics (number of alive nodes, network throughput, residual energy and fitness function).

4.1.1. Exploration and Exploitation Process

An effective method for analyzing the exploration and exploitation process is to compare new individuals to the existing population. If a new individual’s similarity to the population is poor, the algorithm will prioritize exploration. The degree of similarity between a new individual and the old population is high during the exploitation process. The following formula was used to determine the similarity of two individuals using the Euclidean distance:

$$\left(x.y\right)=\sqrt{{{\displaystyle \sum }}_{i=1}^n{\left(x_i-y_i\right)}^2}$$

(12)

The new individual’s similarity (S) to the population is determined by the distance between the new individual and its closest neighbor as follows:

$$S\left(in{d}_{new}.P\right)=\underset{ind \in P}{\min }\left(in{d}_{new}. ind\right)$$

(13)

If the similarity value exceeds a threshold value that determines the neighborhood boundary, the procedure is termed exploration; otherwise, it is called exploitation [69]. We defined the threshold value in this study as 1% of the search space. The percentage of individuals exploring the search space for each iteration throughout the optimization process is depicted in Figure 2.

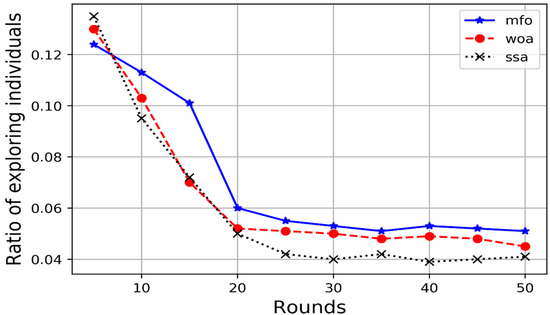
Figure 2. Ratio of individuals exploring the search space.

As illustrated in Figure 2, the number of exploring individuals decreased faster in the WOA and SSA algorithms than in the MFO method. Thus, as compared to the other two algorithms, the MFO method assigned more balanced weights to exploration and exploitation, ensuring sufficient diversity and thus increase the likelihood of converging on the global optima.

4.1.2. Number of Alive Nodes

The number of alive nodes is used to calculate the network lifetime. It is an instantaneous count of all the nodes that have not yet used up all of their energy. Alive nodes are sensor nodes that contain non-zero energy. Figure 3a illustrates a comparison of the performance evaluation between the MFO, SSA and WOA algorithms in terms of the number of alive nodes relative to the number of rounds. A higher number of alive nodes within a network extends the network lifetime. Based on this, the MFO algorithm outperformed the WOA and SSA algorithms. Figure 3b shows the progression of how nodes died using the MFO, WOA and SSA algorithms for 30 sensor nodes over the period (0, 550). The lifetime of the network was increased by using the MFO algorithm, as shown in Figure 3c. For the WOA, MFO, and SSA algorithms, the performance comparison of the number of living nodes vs. the number of rounds was improved. Figure 3 illustrates that there were differences in the performance evaluation between the three algorithms. Considering the timing of the death of the first node for the different protocols, the MFO algorithm had a better performance compared with the SSA and WOA methods. Moreover, the nodes in the MFO and WOA algorithms started to die after 550 rounds. However, the network lifetime of the MFO algorithm was the highest, as the last node died after 2190 rounds, compared to 2130 and 2020 rounds for the SSA and WOA methods, respectively.

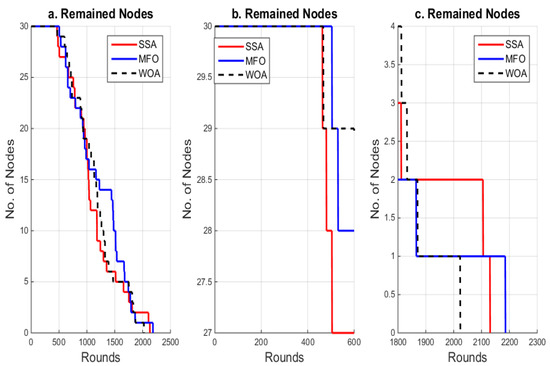
Figure 3. The number of rounds versus the number of alive nodes in MFO, SSA and WOA.

4.1.3. Network Throughput

The network throughput is a significant metric that reflects the performance of a protocol. It represents the number of packets delivered to the base station. Cluster member nodes send the sensed information to the CH in the form of packets. Then, the CH combines the received packets and sends them to the BS. Throughout this phase, if the CH energy is insufficient to transmit, receive or combine the information, the information will be lost, which significantly reduces the network throughput. The throughput performance of the WOA, MFO and SSA algorithms is presented in Figure 4. The MFO algorithm provided the best performance, as shown in Figure 4a, followed by the WOA and SSA methods in the initial interval (0, 700). The MFO algorithm outperformed both the SSA and WOA methods in terms of network throughput during the interval (1850, 2140). However, the MFO algorithm outperformed the SSA and WOA in terms of network throughput during the timeframe (2140, 2200) as shown in Figure 4b.

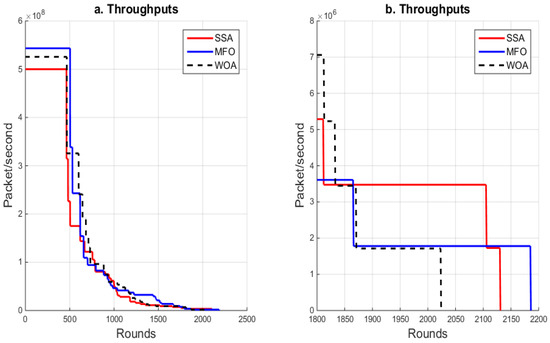
Figure 4. Variation in throughput in MFO, SSA and WOA.

4.1.4. Residual Energy

To ensure the network’s long-term viability, limited resources must be used wisely. When it comes to wireless networks, energy conservation is the most important factor in their design and execution. Having information about the present distribution of residual energy in a network may assist the user in deciding what kind of measures to take. Figure 5 shows the number of rounds versus the residual energy in the MFO, SSA and WOA algorithms. This figure reveals that the MFO algorithm achieved the best energy performance. The number of rounds for the MFO algorithm exceeded that of the SSA and WOA algorithms.

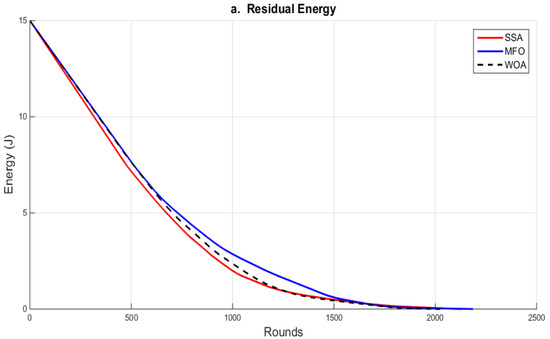
Figure 5. The number of rounds versus residual energy within WOA, MFO and SSA.

4.1.5. Fitness Function

The bi-objective function in this study was designed to select the cluster head within every cluster while optimizing two objectives; the first one minimized the distance from every node to the cluster head and the distance from the cluster head to the base station, while the second one ensured the selection of a cluster head with high remaining energy. Figure 6 displays the quantity of the bi-objective function optimization for all the algorithms, with the MFO protocol outperforming the others because it produced the smallest objective function.

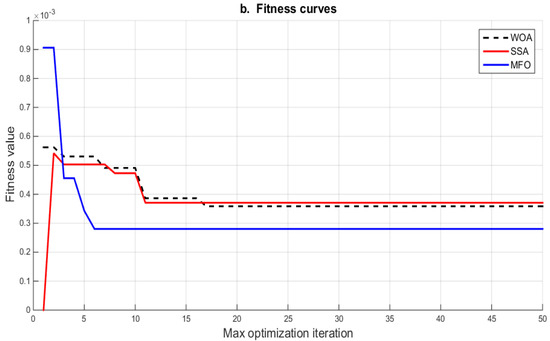
Figure 6. The number of rounds versus fitness function within WOA, MFO and SSA.

In summary, the simulation results revealed that the moth–flame algorithm performed better than the other two algorithms in terms of exploration and exploitation, along with four additional criteria (number of alive nodes, network throughput, residual energy and fitness function).

4.2. Second Stage of Analysis

This stage of the analysis compared the performance of the MFO algorithm with the LEACH algorithm over the wireless network energy consumption model in terms of the number of alive nodes, the network throughput, the residual energy, and the fitness function. The LEACH protocol shares critical characteristics with the MFO algorithm such as purpose and concept, operational structure and process and routing category [70,71,72]. They both aim to rotate sensor nodes as cluster heads so that the high energy dissipation in communicating with the BS is distributed to all the sensor nodes in the network. That is, they maintain a balanced energy usage, responsibility for the CH is rotated and a new cluster is established in each round [73,74]. As an added benefit, the LEACH and MFO methods conduct local data compression, lowering the quantity of data transmitted between clusters and the BS and, as a result, extending the system lifespan and reducing power consumption [75]. Considering their operational structure and process, the MFO and LEACH methods operate in rounds. Each round is divided into two phases: setup and steady state. Clusters are organized during the setup phase, and data transmission occurs during the steady-state phase. Furthermore, both use a simple radio model to describe how energy is dissipated through electronic equipment, such as the transmitter, power amplifier and receiver [76,77,78]. In terms of the routing category, both the MFO and LEACH methods fall in the same category of proactive routing protocols (centralized, source-driven). They both use a link-state routing protocol, where each node determines the channel condition and network topology and forwards it to a centralized location that computes the routing table for all the nodes in the network [79]. In addition, the network can execute dependable operations by adopting hierarchical protocols for data communication, which can save energy for network nodes [80].

In summary, the proposed optimization algorithm’s performance was compared to that of the LEACH method due to the following primary advantages [81,82,83,84,85,86]: (1) The LEACH protocol’s clustering minimizes the amount of energy required for communication between sensor nodes and the BS, allowing the network to last longer. (2) By lowering the linked data locally, the CH’s data aggregation saves a substantial amount of energy. (3) The nodes in the network are placed into sleep mode. As a result, cluster collisions are avoided, and the sensor node’s battery life is increased. (4) In the LEACH protocol, every sensor node has an equal chance of becoming the CH at least once. The network’s longevity is increased by this randomized rotation of the CH. Figure 7 illustrates the performance of the LEACH and MFO algorithms in terms of the number of alive nodes with respect to the number of rounds. The MFO algorithm outperformed LEACH. Figure 7b shows the network’s lifetime for the period (0, 815). Figure 7c illustrates that the nodes survived for approximately 2380 rounds for the MFO algorithm. The performance comparison showed that the MFO algorithm significantly outperformed LEACH. Considering the timing of the death of the first node in the different protocols, the MFO algorithm showed a better performance compared to the LEACH method. Moreover, the last node in the LEACH method died earlier than the last node in the MFO algorithm, as shown in Figure 7b. Moreover, the lifetime of the MFO algorithm was much longer than that of the LEACH method (Figure 7c).

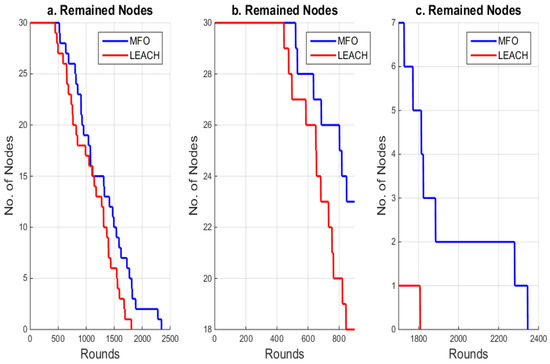
Figure 7. The number of rounds versus the number of alive nodes in MFO and LEACH.

Figure 8 plots the network throughput for the two protocols in terms of the number of rounds. The clustering within the moth–flame algorithm extended the network’s lifetime by preserving the residual energy of the nodes. The MFO algorithm’s throughput was higher than that of the LEACH method, as shown in Figure 8b.

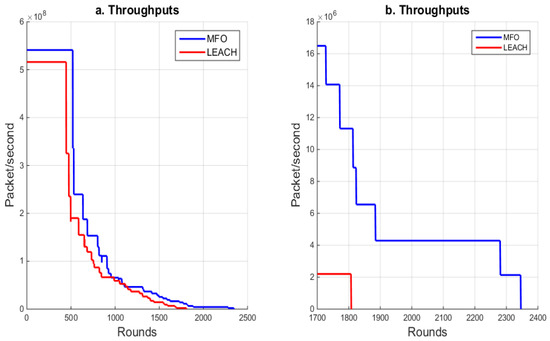
Figure 8. Variation in throughput in MFO and LEACH.

As demonstrated in Figure 9a, the MFO algorithm outperformed the LEACH approach in terms of residual energy. The number of rounds in the MFO algorithm case exceeded 2000 rounds, whereas in the LEACH method case there were about 1800 rounds. Furthermore, Figure 9b shows that the MFO algorithm’s fitness function was significantly lower than that of the LEACH method.

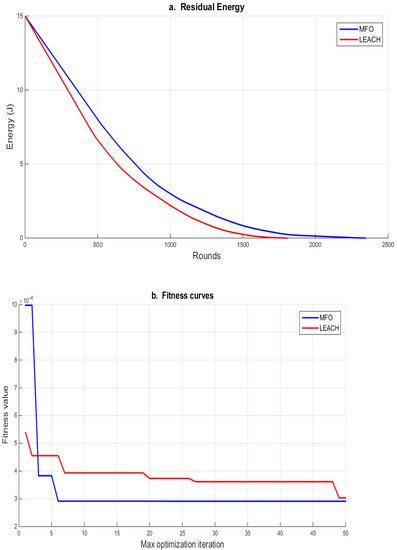
Figure 9. (a) The number of rounds versus the residual energy within MFO and LEACH. (b) The number of rounds versus fitness function for MFO and LEACH.

5. Conclusions and Future Work

In this paper, an MFO-based clustering algorithm for enhancing the network lifetime was proposed and evaluated. The performance of the proposed algorithm was compared with existing clustering protocols (SSA, WOA and LEACH) in terms of four different metrics (fitness function, network lifetime evaluation, energy evaluation and throughput). The MFO algorithm achieved a significant performance improvement with an enhanced energy consumption compared to the SSA and WOA algorithms as well as the LEACH protocol. The proposed algorithm extended the sensor network’s lifetime, preserved the nodes’ energy, extended the network’s lifetime and improved the network throughput. For a future work direction, it is recommended to use specified operators to solve multi-objective algorithms utilizing the MFO algorithm.