Failure Risk Assessment of Coal Gasifier Based on the Integration of Bayesian Network and Trapezoidal Intuitionistic Fuzzy Number-Based Similarity Aggregation Method (TpIFN-SAM)

Abstract

The coal gasifier is the core unit of the coal gasification system. Due to its exposure to high temperatures, high pressures, and aggressive media, it is highly susceptible to serious accidents in the event of failure. Therefore, it is important for the gasifier to perform failure-risk assessment to understand its safety status and provide safety measures. Bayesian networks (BNs) for risk analysis of process systems has received a lot of attention due to its powerful inference capability and its ability to reflect complex relationships between risk factors. However, the acquisition of basic probability data in a Bayesian network is always a great challenge. In this study, an improved Bayesian network integrated with a trapezoidal intuitionistic fuzzy number-based similarity aggregation method (TpIFN-SAM) is proposed for the failure-risk assessment of process systems. This approach used the TpIFN-SAM to collect and aggregate experts’ opinions for obtaining the prior probabilities of the root events in the BN. In the TpIFN-SAM, the intuitionistic fuzzy analytic-hierarchy-process method (IF-AHP) was adopted to assign the expert weights for reducing subjectivity or the bias caused by individual differences. To clarify the suitability of the proposed method, a case study of a coal gasifier was demonstrated, and both prediction and diagnosis analyses of the BN were performed; finally, the weak links of the gasifier were identified.

1. Introduction

The coal-gasification process is an essential part of the “clean coal” technology that can improve overall energy-conversion and -utilization efficiency [1]. This process is carried out in a gasifier (also known as a gasification furnace), in which the combustible parts of coal or coal coke are converted into gases like CO and H₂ by chemical reactions at high temperatures and high pressures. In this condition, the gasifier needs to ensure safe operation. Fire and explosion are unimaginable consequences that may easily occur when equipment fails.

Equipment-failure-risk assessment is a necessary means to clarify the safety status of the equipment and ensure the normal operation of the chemical systems. There are numerous risk-assessment methods available in process systems, one group of which is based on a combination of logical/probabilistic diagrams and deductive reasoning, such as fault-tree analysis (FTA), event-tree analysis (ETA), the bow-tie model (BT), and Bayesian networks (BNs), and are very widely used for risk and reliability analysis due to their intuitiveness, expressiveness, ease of analysis, and reasoning [2,3,4,5]. Of these, BN is suitable for modelling and analyzing complex systems and has gained much attention compared to others, since it can handle the occurrence of multi-state variables, express conditional dependencies among events, and allow for bidirectional reasoning to identify the most failure-prone links of the system better [6,7,8]. As with other approaches, the limitation is that a BN cannot succeed without complete and accurate data (i.e., base-event probabilities and conditional-probability tables), and unfortunately in practice the required data are difficult to obtain. For this reason, a BN is often integrated with data-extraction technologies, particularly expert elicitation.

Currently, the common approaches to data acquisition for a BN include fuzzy set theory [9], rough set theory [10], evidence theory [11], the cloud model [12], and hybrid models [13]. Among them, the combination of fuzzy sets and a BN has been most extensively studied in process-safety engineering since fuzzy set theory is well recognized as a very effective mathematical tool for dealing with uncertain and incomplete information [14]. Kabir et al. [15] developed an O & G pipeline-failure model by assimilating a fuzzy set into a BN. In this model, the prior probability and conditional probability values in the BN can be interpreted according to the linguistic terms corresponding to the trapezoidal fuzzy numbers. Yazdi and Kabir [16] presented a comprehensive framework for risk evaluation of complex process systems through integrating fuzzy set theory with a BN. In this framework, the uncertainty problem of failure data was solved by expert knowledge with improved fuzzy AHP. Zhao et al. [17] also employed fuzzy AHP and BN to assess the domino effects in the coal-gasification process. Yan et al. [18] applied a BN with a fuzzy set to analyze biomass gasification when a gas leakage happens, and they confirmed the missing reliability failure probabilities by using expert judgments obtained based on linguistic terms corresponding to triangular and trapezoidal fuzzy numbers. Subsequently, Mostafa Pouyakian et al. [19] proposed a similar approach to analyze the possible risk factors of storage tanks with a floating roof. Akbar Rostamabadi et al. [20] integrated the fuzzy best–worst method (Fuzzy–BWM) with a BN for safety and reliability analysis of a process system that used Fuzzy–BWM for expert judgment to obtain the required fuzzy probabilities.

These research endeavors have contributed significantly to the successful utilization of BNs in the reliability and risk evaluation of process industries. However, the limitations are that the fuzzy set theory may cause deprivation and deformation of evaluation information because it uses only one membership function to represent the extent to which a particular target pertains to a set [21,22]. In reality, there are often situations where a person may suppose that a target pertains to a set to an extent, but they may not be quite sure about it, which means there may be indecision about the membership extent of the target in the set. For the purpose of resolving the challenge, Atanassov [23] proposed a intuitionistic fuzzy set (IFS) in 1986. In IFS theory there are two different functions, i.e., the membership and non-membership functions, to describe uncertain information. The difference between the two functions is called the degree of hesitation. The IFS theory extends the traditional fuzzy set theory, and it has a stronger ability to express and dispose of uncertainty than fuzzy set theory. In this light, Yu et al. [24] introduced triangular intuitionistic fuzzy numbers (a special case of IFS) to BNs for analysis of the fire damage and blast accident of a crude-oil-storage tank. This attempt showed the potential power of combining IFS with BNs. As far as intuitionistic fuzzy numbers (IFNs) are concerned, trapezoidal IFNs, as an extension of triangular IFNs, better accommodate for the description of non-deterministic information. This inspired us to try to integrate trapezoidal IFNs with BNs to analyze the failure risk of process systems so as to improve the feasibility and flexibility of BNs in engineering applications. Similarly, this is also the motivation for the new approach that is presented next.

When acquiring data using fuzzy set theory or intuitionistic fuzzy set theory, experts often need to be involved. Given the limitations of experts’ own knowledge and experience, certain means are required to deal with experts’ opinions to reduce subjective bias, usually through assigning different weights to the experts and then aggregating the different opinions [25]. Recently, the similarity aggregation method (SAM) [26] as an aggregation strategy for experts’ opinions has been of increasing interest in the safety analysis of process systems like storage tanks for hazardous chemicals [27,28,29] and oil and gas pipelines [30]; this is because it not only conforms to the custom of expert evaluation, but also enables the aggregation result to be more exact and workable [29,31].

The main contributions of this paper are as follows: (1) This study attempts to propose an improved framework integrating intuitionistic fuzzy AHP, trapezoidal intuitionistic fuzzy number-based SAM, and a Bayesian network for failure-risk assessment of a coal gasifier. (2) This framework uses intuitionistic fuzzy AHP to assign the expert weights for reducing subjectivity or the bias caused by individual differences and obtains the likelihood of occurrence of root events in the BN through trapezoidal intuitionistic fuzzy number-based SAM with experts’ judgment. (3) This strategy can more convincingly translate the judgments of all experts into a clear probability value by an intuitionistic fuzzy reasoning approach, thus overcoming the difficulty of obtaining the basic probability data in the BN.

For the remainder, the organization is arranged as follows: Section 2 introduces basic concepts of intuitionistic fuzzy sets, trapezoidal intuitionistic fuzzy numbers, and Bayesian networks. Section 3 presents the improved framework and provides the detailed implementation processes. In Section 4, an example of clarification is provided to demonstrate the specific analysis process and verify the feasibility of the method. Finally, the conclusions are described in Section 5.

2. Preliminaries

2.1. Intuitionistic Fuzzy Set

Definition 1

[23,32]: Let X be a general set, and the intuitionistic fuzzy set (IFS) $\tilde{A}$ is a set in

$$\tilde{A}=\left\{x,{\mu }_{\tilde{A}}\left(x\right),\left.{\nu }_{\tilde{A}}\left(x\right)\right|x\in X\right\}$$

(1)

where ${\mu }_{\tilde{A}}\left(x\right):X\to [0,1]$ and ${\nu }_{\tilde{A}}\left(x\right):X\to [0,1]$ are membership and non-membership, respectively. Furthermore, the following requirements are fulfilled $0\le {\mu }_{\tilde{A}}\left(x\right)+{\nu }_{\tilde{A}}\left(x\right)\le 1$ for all x ∈ X in the $\tilde{A}$. An ordered interval pair consisting of ${\mu }_{\tilde{A}}\left(x\right)$ and ${\nu }_{\tilde{A}}\left(x\right)$ is an intuitionistic fuzzy set, written as $⟨{\mu }_{\tilde{A}}\left(x\right),{\nu }_{\tilde{A}}\left(x\right)⟩$.

For each intuitionistic fuzzy set in X, ${\pi }_{\tilde{A}}\left(x\right)=1-{\mu }_{\tilde{A}}\left(x\right)-{\nu }_{\tilde{A}}\left(x\right)$is the intuitionistic index of x in$\tilde{A}$. This is a measure of the hesitancy of x to$\tilde{A}$. Distinctly, for each x ∈ X, $0\le {\pi }_{\tilde{A}}\left(x\right)\le 1$.

Definition 2

[33]: Let $\tilde{A}$ be an intuitionistic fuzzy number on a real number set R, and its membership and non-membership functions fulfill the following equations:

$${\mu }_{\tilde{A}}\left(x\right)=\left\{\begin{array}{l}{f}_{\tilde{A}}\left(x\right), a<x<b\\ 1,\hspace{1em}\hspace{1em}b\le x\le c\\ g_{\tilde{A}}\left(x\right), c<x<d\\ 0,\hspace{1em}\hspace{1em}\mathrm{otherwise}\end{array}\right., {\nu }_{\tilde{A}}\left(x\right)=\left\{\begin{array}{l}{h}_{\tilde{A}}\left(x\right), a\prime <x<b\\ 0,\hspace{1em}\hspace{1em}b\le x\le c\\ k_{\tilde{A}}\left(x\right), c<x<d\prime \\ 1,\hspace{1em}\hspace{1em}\mathrm{otherwise}\end{array}\right.$$

(2)

respectively, where $0\le {\mu }_{\tilde{A}}\left(x\right)\le 1$, $0\le {\nu }_{\tilde{A}}\left(x\right)\le 1$, and $0\le {\mu }_{\tilde{A}}\left(x\right)+{\nu }_{\tilde{A}}\left(x\right)\le 1$. a′, a, b, c, d, d′ ∈ R, such that $a\prime \le a\le b\le c\le d\le d\prime$ and four functions $f_{\tilde{A}}$, $g_{\tilde{A}}$, $h_{\tilde{A}}$, $k_{\tilde{A}}:R\to \left[0,1\right]$ are known as the sides of intuitionistic fuzzy numbers. In addition, $f_{\tilde{A}}$, $k_{\tilde{A}}$, are non-decreasing continuous functions, and $g_{\tilde{A}}$, $h_{\tilde{A}}$ are non-increasing continuous functions. A set of intuitionistic fuzzy numbers can be defined when the four functions are linear functions, as shown in Definition 3.

Definition 3

[34]: Let ${\tilde{A}}_1$ and ${\tilde{A}}_2$ be two intuitionistic fuzzy numbers ${\tilde{A}}_1=\left({\mu }_{{\tilde{A}}_1},{\nu }_{{\tilde{A}}_1}\right)$, ${\tilde{A}}_2=\left({\mu }_{{\tilde{A}}_2},{\nu }_{{\tilde{A}}_2}\right)$ on a real number set R, then

$${\tilde{A}}_1+{\tilde{A}}_2=\left({\mu }_{{\tilde{A}}_1}+{\mu }_{{\tilde{A}}_2}-{\mu }_{{\tilde{A}}_1}{\mu }_{{\tilde{A}}_2},{\nu }_{{\tilde{A}}_1}{\nu }_{{\tilde{A}}_2}\right)$$

(3)

$${\tilde{A}}_1\times {\tilde{A}}_2=\left({\mu }_{{\tilde{A}}_1}{\mu }_{{\tilde{A}}_2},{\nu }_{{\tilde{A}}_1}+{\nu }_{{\tilde{A}}_2}-{\nu }_{{\tilde{A}}_1}{\nu }_{{\tilde{A}}_2}\right)$$

(4)

$$\lambda {\tilde{A}}_1=\left(1-{\left(1-{\mu }_{{\tilde{A}}_1}\right)}^{\lambda },{\nu }^{\lambda }{}_{{\tilde{A}}_1}\right), \lambda >0$$

(5)

$${\tilde{A}}_1{}^{\lambda }=\left({\mu }^{\lambda }{}_{{\tilde{A}}_1},1-{\left(1-{\nu }_{{\tilde{A}}_1}\right)}^{\lambda }\right), \lambda >0$$

(6)

2.2. Trapezoidal Intuitionistic Fuzzy Number

Definition 4

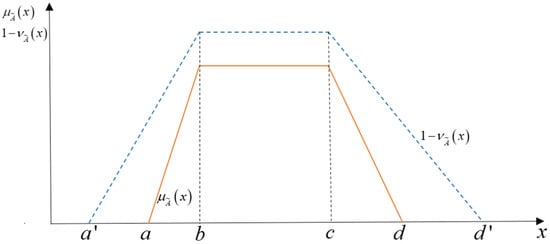
[33]: Let $\tilde{A}$ be a trapezoidal intuitionistic fuzzy number (TpIFN) with parameters $a\prime \le a\le b\le c\le d\le d\prime$ and indicated as $\tilde{A}=\left(a,b,c,d;a\prime ,b,c,d\prime \right)$ on a real number set R, then its membership and non-membership functions satisfy the following equations:

$${\mu }_{\tilde{A}}\left(x\right)=\left\{\begin{array}{l}{\displaystyle \frac{x-a}{b-a}}, a<x<b\\ 1,\hspace{1em}\hspace{1em} b\le x\le c\\ {\displaystyle \frac{d-x}{d-c}}, c<x<d\\ 0,\hspace{1em}\hspace{1em} \mathrm{otherwise}\end{array}\right., {\nu }_{\tilde{A}}\left(x\right)=\left\{\begin{array}{l}{\displaystyle \frac{b-x}{b-a\prime }}, a\prime <x<b\\ 0,\hspace{1em}\hspace{1em} b\le x\le c\\ {\displaystyle \frac{x-c}{d\prime -c}}, c<x<d\prime \\ 1,\hspace{1em}\hspace{1em} \mathrm{otherwise}\end{array}\right.$$

(7)

respectively, where $0\le {\mu }_{\tilde{A}}\left(x\right)\le 1$, $0\le {\nu }_{\tilde{A}}\left(x\right)\le 1$, $0\le {\mu }_{\tilde{A}}\left(x\right)+{\nu }_{\tilde{A}}\left(x\right)\le 1$. Figure 1 shows a general trapezoidal intuitionistic fuzzy number.

Figure 1. A general trapezoidal intuitionistic fuzzy number.

Definition 5

[34]: Let ${\tilde{A}}_1=\left(a_1,b_1,c_1,d_1;a_1\prime ,b_1,c_1,d_1\prime \right)$ and ${\tilde{A}}_2=\left(a_2,b_2,c_2,d_2;a_2\prime ,b_2,c_2,d_2\prime \right)$ be two trapezoidal intuitionistic fuzzy numbers, then

$${\tilde{A}}_1+{\tilde{A}}_2=\left(a_1+a_2,b_1+b_2,c_1+c_2,d_1+d_2;a_1\prime +a_2\prime ,b_1+b_2,c_1+c_2,d_1\prime +d_2\prime \right)$$

(8)

$${\tilde{A}}_1\times {\tilde{A}}_2=\left(a_1{a}_2,b_1{b}_2,c_1{c}_2,d_1{d}_2;a_1\prime a_2\prime ,b_1{b}_2,c_1{c}_2,d_1\prime d_2\prime \right)$$

(9)

$$\lambda {\tilde{A}}_1=\left(\lambda a_1,\lambda b_1,\lambda c_1,\lambda d_1; \lambda a_1\prime ,\lambda b_1,\lambda c_1,\lambda d_1\prime \right)$$

(10)

$${\tilde{A}}_1{}^{\lambda }=\left(a_1{}^{\lambda },b_1{}^{\lambda },c_1{}^{\lambda },d_1{}^{\lambda }; a_1{\prime }^{\lambda },b_1{}^{\lambda },c_1{}^{\lambda },d_1{\prime }^{\lambda }\right)$$

(11)

2.3. The Expectation of a TpIFN

Heilpern [35] defined the expected interval and expected value of a fuzzy number. The expected interval and expected value can be applied to fuzzy-number ranking or comparison problems. The expected value as the center of the expected interval can be regarded as the expected payoff connected to a linguistic term. This can also be generalized for TpIFNs. It is assumed that that $\tilde{A}=\left(a,b,c,d;a\prime ,b,c,d\prime \right)$ is a TpIFN, and EI^μ and EI^ν denote the expected interval matching with membership and non-membership functions, respectively. The center of the expected interval of an intuitionistic fuzzy number is called the expected value of this number, denoted by $EV\left(\tilde{A}\right)$, and EV^μ and EV^ν denote the expected value corresponding to membership and non-membership functions, respectively. Its parametric form are $\mu \left(\alpha \right)$ = $\left(\overline{\mu \left(\alpha \right)},\underset{¯}{\mu \left(\alpha \right)}\right)$ and $\nu \left(\alpha \right)$ = $\left(\overline{\nu \left(\alpha \right)},\underset{¯}{\nu \left(\alpha \right)}\right)$, where μ(α) and ν(α) are the parametric form of a TpIFN corresponding to membership and non-membership functions, respectively, and $\overline{\mu \left(\alpha \right)}=d-\alpha \left(d-c\right)$; $\underset{¯}{\mu \left(\alpha \right)}=a+\alpha \left(b-a\right)$ and $\overline{\nu \left(\alpha \right)}=b-\left(1-\alpha \right)\left(b-a\prime \right)$; $\underset{¯}{\nu \left(\alpha \right)}=c+\left(1-\alpha \right)\left(d\prime -c\right)$ [36].

$$E{V}^{\mu }\left(\tilde{A}\right)=\frac{{\displaystyle \underset{0}{\overset{1}{\int }}\overline{\mu \left(\alpha \right)}}d\alpha +{\displaystyle \underset{0}{\overset{1}{\int }}\underset{¯}{\mu \left(\alpha \right)}d\alpha }}{2}=\frac{a+b+c+d}{4}$$

(12)

$$E{V}^{\nu }\left(\tilde{A}\right)=\frac{{\displaystyle \underset{0}{\overset{1}{\int }}\overline{\nu \left(\alpha \right)}}d\alpha +{\displaystyle \underset{0}{\overset{1}{\int }}\underset{¯}{\nu \left(\alpha \right)}d\alpha }}{2}=\frac{a\prime +b+c+d\prime }{4}$$

(13)

$$EV\left(\tilde{A}\right)=\lambda E{V}^{\mu }\left(\tilde{A}\right)+\left(1-\lambda \right)E{V}^{\nu }\left(\tilde{A}\right)$$

(14)

Let $\lambda =0.5$, then

$$EV\left(\tilde{A}\right)=\frac{1}{2}E{V}^{\mu }\left(\tilde{A}\right)+\frac{1}{2}E{V}^{\nu }\left(\tilde{A}\right)=\frac{a+a\prime +2b+2c+d+d\prime }{8}$$

(15)

See Appendix A for the proof process.

2.4. Bayesian Network

A Bayesian network (BN), known as a probabilistic graphical model, is a directed acyclic graph (DAG) that binds graph theory with probability theory. A BN consists of nodes representing events (i.e., random variables) and oriented lines (from parent nodes to child nodes) connecting these nodes and representing their causal relationships. Each node and its set of parent nodes corresponds to a conditional probability distribution $P(X_i|Parent(X_i))$ that indicates how much influence there is among the parent nodes and the child node. Given that a BN consists of n random variables X₁, X₂,…, X_n, according to the conditional independency and chain laws, the complete united probability distribution can be recorded as [37]

$$P\left(X_1,X_2, \dots ,X_{n-1},X_n\right)={\displaystyle \prod _{i=1}^{n}P\left(X_i|Parent\left(X_i\right)\right)}$$

(16)

Figure 2 shows an illustration of a BN including six nodes. Node X₁ is called the parent node of X₂ and X₃, whereas X₂ and X₃ are called the child nodes of X₁. It is worth mentioning that X₁ is also called the root node because it has no parent node. The complete united probability distribution of this can be expressed by Equation (16):

$$P\left(X_1,X_2,X_3,X_4,X_5,X_6\right)=P\left(\left.X_6\right|X_5\right)P\left(\left.X_5\right|X_3,X_2\right)P\left(\left.X_4\right|X_2,X_1\right)P\left(\left.X_3\right|X_1\right)P\left(\left.X_2\right|X_1\right)P\left(X_1\right)$$

(17)

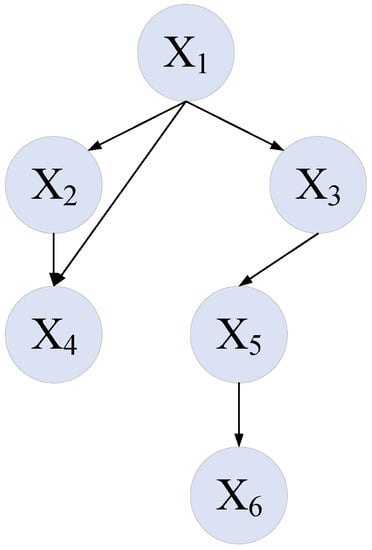
Figure 2. Example of a Bayesian network.

In the BN model, it has a forward (predictive) and backward (diagnostic) ability of inference. The forward inference is the inference from the causes (root nodes) to their effects (leaf nodes). Under the circumstances, new beliefs about this effect are obtained by using information about causes. In contrast, the backward inference is the inference on the contrary side (i.e., from the effect back to the cause). In this inference, the process of obtaining a new belief about causes based on known effects is continuously estimated and upgraded. Bayes’ theorem can be used to advance the diagnosis analysis of the BN model (see Equation (18)) [37].

$$P\left(A|B\right)=\frac{P\left(B|A\right)P\left(A\right)}{P\left(B\right)}$$

(18)

where A and B are two random events; P(A) and P(B) are the prior probability of event A and B, respectively; and P(A|B) is the posterior probability of event A occurring given after the occurrence of B.

2.5. Mapping to Bayesian Network from Fault Tree

The determination of a BN structure is the first step in using it for prediction and diagnosis. There are several ways of constructing BNs: (1) expert knowledge-based [38], (2) data-driven [39], and (3) mapped from other models like the fault-tree, event-tree, or bow-tie models [40,41,42]. The third approach is adopted in this study, where the potential accident scenarios of a system are first determined by a fault tree, which is then mapped into a BN according to the method shown in Figure 3.

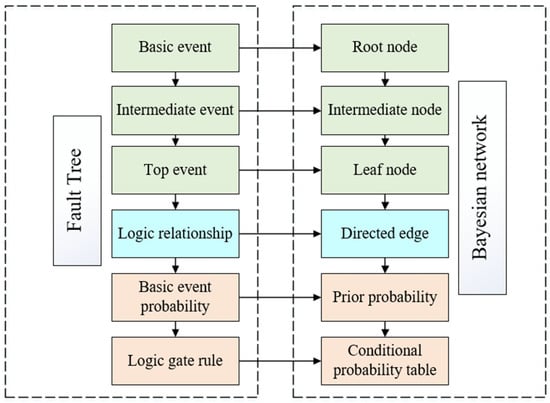
Figure 3. Mapping rules from fault tree to Bayesian network.

The conditional probability table (CPT) is another key component of BNs for implementing inference. During this process, the logical gate of the fault tree (FT) is used to confirm the CPT of each node in the BN. The logic gate rules of the FT describe the fault–logic relationship between parent and child events. Table 1 and Table 2 show the rules of how to obtain a CPT according to the two most critical logic gates of FT: the “AND” gate and the “OR” gate [40].

Table 1. CPT corresponding to the AND gate in FT (Occ: occurred; Non: non-occurred).

X1		Occ				Non
X2		Occ		Non		Occ		Non
X3		Occ	Non	Occ	Non	Occ	Non	Occ	Non
T	Occ	1	0	0	0	0	0	0	0
	Non	0	1	1	1	1	1	1	1

Table 2. CPT corresponding to the OR gate in FT (Occ: occurred; Non: non-occurred).

X1		Occ				Non
X2		Occ		Non		Occ		Non
X3		Occ	Non	Occ	Non	Occ	Non	Occ	Non
T	Occ	1	1	1	1	1	1	1	0
	Non	0	1	1	1	1	1	1	1

3. Proposed Model for Failure-Risk Assessment Based on BN with TpIFN-SAM

3.1. General Framework

The proposed framework is mainly used to analyze the failure probability of process systems, which consists of five core parts—construction of the BN through FT, expert elicitation, aggregation of experts’ opinions by the TpIFN-SAM, the defuzzification process, and BN analysis—and is shown in Figure 4. The specific analysis process is described from Section 3.2, Section 3.3, Section 3.4, Section 3.5, Section 3.6 and Section 3.7.

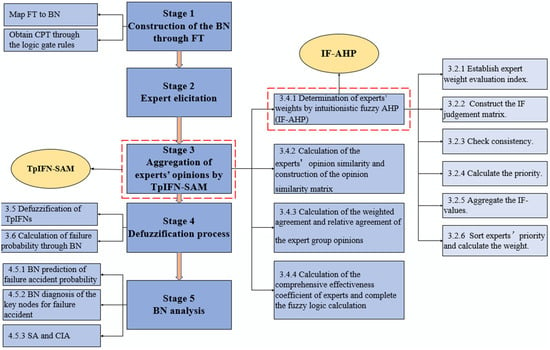
Figure 4. The proposed analysis framework.

3.2. Construction of the BN through FT

The construction of a BN describing system-failure scenarios and paths is the first step in analyzing the probability of possible failures in a process system. Here, the FT is first drawn according to the system’s structural characteristics and associated risk factors, where the top event is generally set as the most undesired event. Then, the FT is mapped into a BN with CPTs using the mapping rules mentioned in Section 2.5.

3.3. Expert Elicitation

In this framework, expert elicitation is put to use for computing the probabilities of root events in the BN when the accurate probabilities of the events are lacking. In generally, the experts cannot give accurate probability values. This study therefore uses a method combining the TpIFNs and expert elicitation to elaborate the failure probabilities of each root node. Experts express their opinions on risk events in linguistic terms based on the practice or standards in the actual situation in this industry. In addition, the natural estimate of human memory capacity is 7 ± 2 grades [28,43]. Thus, 5–9 language terms scored by experts is most appropriate. Furthermore, heterogeneous expert judgment is adopted to reduce the prejudice of expert evaluation.

3.4. Aggregation of Experts’ Opinions by TpIFN-SAM

3.4.1. Determination of Experts’ Weights by Intuitionistic Fuzzy AHP (IF-AHP)

For the purpose of resolving the subjective preferences of experts and the incompleteness of individual knowledge and experience that may lead to biased results, the preference is usually to create an expert group of professionals and the relative importance of each expert’s opinion is represented by assigning weights to each expert. There are several expert-weighting methods, like the method of arithmetic average [22], the Delphi method [44], and AHP [45]. However, these methods are often criticized for failing to sufficiently solve the intrinsic ambiguity and subjectivity. As an extension of AHP, intuitionistic fuzzy AHP (IF-AHP) [46] can enhance the inconsistent intuitive-preference relationship without the involvement of decision-makers, thereby fundamentally solving the above-mentioned problems. As a result, this work employs the IF-AHP method to acquire the expert-weight coefficients. The specific calculation of the expert weights are as follows.

Step 1. Establish the evaluation indices of expert weights.

There are some general deviations in the experts’ judgements on the same event. This situation is affected by their professional position, educational background, and work experience. Therefore, a three-level hierarchical structure diagram of judging expert weights is established, as shown in Figure 5. Professional position, education level, and service time are accommodated as the evaluation indices of expert weights.

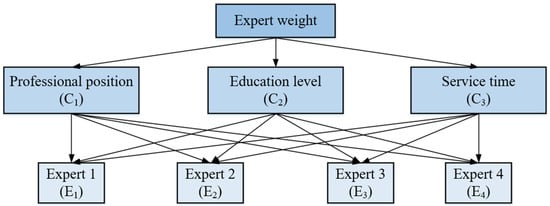
Figure 5. Three-level hierarchical structure of judging expert weights.

Step 2. Construct the IF-judgment matrix.

The intuitionistic fuzzy judgment matrices for the three-level indices are then established. Factors belonging to the same level of each factor of the previous level are matched and compared to build an intuitionistic fuzzy judgment matrix: $R={\left(r_{ij}\right)}_{n\times n}$, with i, j representing the rows and columns of the matrix, respectively, where r_ij = (μ_ij, ν_ij); μ_ij denotes the degree to which an expert prefers i when comparing the importance of factor i and factor j; ν_ij denotes the degree to which an expert prefers j; and π_ij = 1 − μ_ij − ν_ij denotes the hesitation degree. To better identify the intuitionistic preference relationship, an evaluation scale table is constructed, as shown in Table 3.

Table 3. IF-AHP preference scale.

Level	IFNs
i is significantly important than j.	μ = 0.9, ν = 0–0.1
i is much more important than j.	μ = 0.8, ν = 0–0.2
I is more important than j.	μ = 0.7, ν = 0–0.3
i is slightly more important than j.	μ = 0.6, ν = 0–0.4
i is as important as j.	μ = ν

Note: Reciprocal IFNs can be obtained by exchanging μ and ν.

Step 3. Check consistency.

The consistency-test formula shown below is given for distance measurement based on the intuitionistic fuzzy information [46]:

$$d\left(\overline{R},R\right)=\frac{1}{2\left(n-1\right)\left(n-2\right)}{\displaystyle \sum _{i=1}^n}{\displaystyle \sum _{j=1}^n\left(\left|{\overline{\mu }}_{ij}-{\mu }_{ij}\right|+\left|{\overline{\nu }}_{ij}-{\nu }_{ij}\right|+\left|{\overline{\pi }}_{ij}-{\pi }_{ij}\right|\right)}$$

(19)

where $R={\left(r_{ij}\right)}_{n\times n}$ is the intuitionistic fuzzy judgment matrix obtained by pairwise comparison of indices at each layer $R={\left(r_{ij}\right)}_{n\times n}$, $\overline{R}={\left({\overline{r}}_{ij}\right)}_{n\times n}$ is the intuitionistic fuzzy consistency-judgment matrix calculated from the intuitionistic fuzzy judgment matrix, and n represents the number of experts.

Let $\overline{R}=\left({\overline{\mu }}_{ij},{\overline{\nu }}_{ij}\right)$ when j > i + 1, where

$${\overline{\mu }}_{ij}=\frac{\sqrt[j-i-1]{{\displaystyle \prod _{t=i+1}^{j-1}{\mu }_{it}{\mu }_{tj}}}}{\sqrt[j-i-1]{{\displaystyle \prod _{t=i+1}^{j-1}{\mu }_{it}{\mu }_{tj}}}+\sqrt[j-i-1]{{\displaystyle \prod _{t=i+1}^{j-1}\left(1-{\mu }_{it}\right)\left(1-{\mu }_{tj}\right)}}}$$

(20)

$${\overline{\nu }}_{ij}=\frac{\sqrt[j-i-1]{{\displaystyle \prod _{t=i+1}^{j-1}{\nu }_{it}{\nu }_{tj}}}}{\sqrt[j-i-1]{{\displaystyle \prod _{t=i+1}^{j-1}{\nu }_{it}{\nu }_{tj}}}+\sqrt[j-i-1]{{\displaystyle \prod _{t=i+1}^{j-1}\left(1-{\nu }_{it}\right)\left(1-{\nu }_{tj}\right)}}}$$

(21)

Let ${\overline{r}}_{ij}=r_{ij}$ when j = i + 1; let ${\overline{r}}_{ij}=\left({\overline{\nu }}_{ij},{\overline{\mu }}_{ij}\right)$ when j < i + 1.

Substitute ${\overline{\mu }}_{ij}$, ${\overline{\nu }}_{ij}$ into $d\left(\overline{R},R\right)$, if $d\left(\overline{R},R\right)<0.1$, then pass the consistency check; if $d\left(\overline{R},R\right)\ge 0.1$, the parameters σ will be set to iterate—that is, to transform the matrix by regulating the iterative parameters σ until it passes. Given parameters σ (σ ∈ [0, 1]), let

$${\tilde{\overline{\mu }}}_{ij}=\frac{{\left({\mu }_{ij}\right)}^{1-\sigma }{\left({\mu }_{ij}\right)}^{\sigma }}{{\left({\mu }_{ij}\right)}^{1-\sigma }{\left({\overline{\mu }}_{ij}\right)}^{\sigma }+{\left(1-{\mu }_{ij}\right)}^{1-\sigma }{\left(1-{\overline{\mu }}_{ij}\right)}^{\sigma }},i,j=1,2, \dots ,n$$

(22)

$${\tilde{\overline{\nu }}}_{ij}=\frac{{\left({\nu }_{ij}\right)}^{1-\sigma }{\left({\overline{\nu }}_{ij}\right)}^{\sigma }}{{\left({\nu }_{ij}\right)}^{1-\sigma }{\left({\overline{\nu }}_{ij}\right)}^{\sigma }+{\left(1-{\overline{\nu }}_{ij}\right)}^{1-\sigma }{\left(1-{\overline{\nu }}_{ij}\right)}^{\sigma }},i,j=1,2, \dots ,n$$

(23)

Substitute the adjusted matrix into $d\left(\tilde{\overline{R}},R\right)$, and then we can get

$$d\left(\tilde{\overline{R}},R\right)=\frac{1}{2\left(n-1\right)\left(n-2\right)}{\displaystyle \sum _{i=1}^n}{\displaystyle \sum _{j=1}^n\left(\left|{\tilde{\mu }}_{ij}-{\mu }_{ij}\right|+\left|{\tilde{\nu }}_{ij}-{\nu }_{ij}\right|+\left|{\tilde{\pi }}_{ij}-{\pi }_{ij}\right|\right)}$$

(24)

Step 4. Calculate the priority.

After obtaining the intuitionistic fuzzy consistency-judgment matrix, the priority of the indices of the previous layer is calculated by

$${\epsilon }_i=\left(\frac{{\displaystyle \sum _{j=1}^n{\mu }_{ij}}}{{\displaystyle \sum _{i=1}^n}{\displaystyle \sum _{j=1}^n\left(1-{\nu }_{ij}\right)}},1-\frac{{\displaystyle \sum _{j=1}^n\left(1-{\nu }_{ij}\right)}}{{\displaystyle \sum _{i=1}^n}{\displaystyle \sum _{j=1}^n\left(1-{\mu }_{ij}\right)}}\right),i=1,2, \dots ,n$$

(25)

where i denotes the number of experts.

Step 5. Aggregate the IFNs.

According to the priority ԑ_i, the aggregated priority value of each expert W_i can be calculated by

$$W_i=\sum _{j=1}^n\left({\epsilon }_j\times {\epsilon }_{ij}\right),i=1,2,\cdot \cdot \cdot ,n$$

(26)

Step 6. Sort experts’ priority and calculate their weights.

The crisp value of the priority of each expert is obtained by

$$\rho \left(W_i\right)=0.5\left(1+{\pi }_{W_i}\right)\left(1-{\mu }_{W_i}\right)$$

(27)

where a smaller ρ(W_i) represents stronger priority from the expert. The relative weight of each expert can be calculated by

$$w_i=\frac{S\left(W_i\right)}{{\displaystyle \sum _{i=1}^{n}S\left(W_i\right)}}$$

(28)

where

$$S\left(W_i\right)=1-\rho \left(W_i\right)$$

(29)

3.4.2. Calculation of the Experts’ Opinion Similarity and Construction of the Opinion Similarity Matrix

When the weights of all experts in the expert group are determined, the experts will be consulted to give the probability of occurrence of the root events in the BN as regards linguistic terms. These opinions are converted into the corresponding TpIFNs. The experts’ opinion similarity can then be given by Equation (30).

$$S\left({\tilde{E}}_i,{\tilde{E}}_j\right)=\left\{\begin{array}{l}\frac{EV\left({\tilde{E}}_i\right)}{EV\left({\tilde{E}}_j\right)},EV\left({\tilde{E}}_i\right)\le EV\left({\tilde{E}}_j\right)\\ \frac{EV\left({\tilde{E}}_j\right)}{EV\left({\tilde{E}}_i\right)},EV\left({\tilde{E}}_j\right)\le EV\left({\tilde{E}}_i\right)\end{array}\right.$$

(30)

where $EV\left({\tilde{E}}_i\right)$ is the expectation of the TpIFN converted from the ith expert’s linguistic opinion on the probability of a certain root event’s occurrence, and it can be calculated by Equation (10) in Section 2.3. $S\left({\tilde{E}}_i,{\tilde{E}}_j\right)$ is the opinion similarity between the ith expert and the jth expert. If there are m experts in the group, the similarity matrix S_m is

$$S_m=\left[\begin{array}{cccc}1& S_{21}& \cdots & S_{1m}\\ S_{21}& 1& \cdots & S_{2m}\\ ⋮& ⋮& \ddots & ⋮\\ S_{m1}& S_{m2}& \cdots & 1\end{array}\right]$$

(31)

where $S_{ij}=S\left({\tilde{E}}_i,{\tilde{E}}_j\right)$ when i ≠ j, and S_ij = 1 when i = j.

3.4.3. Calculation of the Weighted Agreement and Relative Agreement of Each Expert

The weighted agreement degree of each expert’s opinion can be calculated by

$$WA(E_i)=\frac{{\displaystyle \sum _{\begin{array}{l}j=1\\ j\ne i\end{array}}^{m}w(E_j)\cdot S\left({\tilde{E}}_i,{\tilde{E}}_j\right)}}{{\displaystyle \sum _{\begin{array}{l}j=1\\ j\ne i\end{array}}^{m}w(E_j)}},i=1,2,\dots ,m$$

(32)

where E_i (i = 1,2, …, m) is the ith expert, and then the relative agreement degree of each expert can be obtained by

$$RAD\left(E_i\right)=\frac{WA\left(E_i\right)}{{\displaystyle \sum _{i=1}^{m}WA\left(E_i\right)}},i=1,2,\dots ,m$$

(33)

3.4.4. Calculation of the Consensus Degree Coefficient of Experts and Aggregation of the Opinions

Since the relative importance of experts is variable, each expert has their own weight coefficient w_i. The consensus degree coefficient (CDC_i) of the ith expert can be considered as

$$CD{C}_i=\beta \cdot w_i+\left(1-\beta \right)\cdot RA{D}_i$$

(34)

where β (0 < β < 1) is defined as the relaxation factor, which represents the importance of the average agreement of experts compared to the relative agreement. After that, the $\tilde{R}$, which means the result of aggregation, can be confirmed as

$$\tilde{R}={\displaystyle \sum _{i=1}^n\left(CD{C}_i\left(\cdot \right){\tilde{E}}_i\right)}$$

(35)

where (·) is the multiplication operator of the TpIFNs.

3.5. Defuzzification of TpIFNs

After the occurrence possibility of each root event expressed as a TpIFN is obtained through TpIFN-SAM, the defuzzification process is required in order to gain the clear value of the possibility, which is called the possibility score (PS). In this work, the centroid method (see Equation (36)) is adopted to perform the defuzzification of a TpIFN $\tilde{A}=\left(a,b,c,d;a\prime ,b,c,d\prime \right)$.

$$PS=\frac{\left(d\prime -a\prime \right)\left(b+c-4d\prime -4a\prime \right)+\left(d-a\right)\left(2a+b+c+2d\right)+4\left(d{\prime }^2-a{\prime }^2\right)}{4\left(d\prime -a\prime +d-a\right)}$$

(36)

3.6. Calculation of Failure Probability of the System through BN

For the purpose of launching the analysis of the failure probability of the system using the BN, it is essential here to convert the PSs of the root nodes into conventional failure-probability values (FPs). In general, the formula proposed by Onisawa [47] can be adopted to translate PS into FP. However, this approach is not widely applicable due to the distinction in failure-probability classification standards in different industries, as well as the difference in the definition of linguistic scale for the failure probability [48]. Therefore, a corresponding further calculation method is adopted to convert PS into FP, and the formula is as follows [24]:

$$FP=\left\{\begin{array}{l}{\displaystyle \frac{1}{{10}^K}}, PS\ne 0\\ 0,\hspace{1em} PS=0\end{array}\right.$$

(37)

where

$$K=\left\{\begin{array}{l}-0.72\ln PS+2.839,\hspace{1em}0\le PS<0.2\\ -{\displaystyle \frac{1}{3}}\times \left(10PS-14\right),\hspace{1em} 0.2\le PS\le 0.8\\ {\left[{\displaystyle \frac{\left(1-PS\right)}{PS}}\right]}^{0.445}\times 3.705, 0.8<PS\le 1\end{array}\right.$$

(38)

3.7. Sensitivity Analysis (SA) and Critical Importance Analysis (CIA)

Besides calculating the failure probability of a system using BNs, the identification and analysis of critical events affecting the system failure is also an important task in failure assessment. However, the results may be inaccurate if merely relying on prior or posterior probabilities to identify the most critical events. Therefore, this work presents several analysis methods, such as the ratio of variation (RoV), sensitivity analysis (SA), and criticality-importance analysis. RoV is used to measure the degree of the effect of root events in terms of system failure, and it can be calculated by [24]

$$RoV\left(X_i\right)=\frac{\phi \left(X_i\right)-\varphi \left(X_i\right)}{\varphi \left(X_i\right)}$$

(39)

where $\phi \left(X_i\right)$ and $\varphi \left(X_i\right)$ indicate the posterior and prior probability of the ith event, respectively.

SA can provide a great degree of help in verifying the probabilistic parameters of BN. This is achieved by researching the influence of tiny changes in numerical parameters on the posterior probability. Highly sensitive parameters have a more significant effect on reasoning results. The sensitivity value is the partial derivative of the posterior output result of the hypothesis relative to the likelihood of a particular state of the evidence. From a mathematical perspective, for a hypothesis θ given evidence e as a function of a probabilistic likelihood x, the posterior probability $P\left(\theta \left|e\right.\right)\left(x\right)$ is the sensitivity function f(x) of x. The sensitivity function is as follows [49]:

$$f\left(x\right)=P\left(\theta \left|e\right.\right)\left(x\right)=\frac{P\left(\theta ^e\right)\left(x\right)}{P\left(e\right)\left(e\right)}=\frac{J\cdot x+K}{M\cdot x+N}$$

(40)

where the coefficients J, K, M, and N originate from the original (unvaried) parameters of the BN.

The absolute value of the first derivative of the sensitivity function at the original-likelihood value can be used to express the sensitivity of the likelihood value, which can be represented by the SV (sensitivity value),

$$SV=\left|\frac{J\cdot N-K\cdot M}{{\left(M\cdot x+N\right)}^2}\right|$$

(41)

The influence of the root events can also calculate the criticality importance of the roots in a fault-tree framework [29].

$$I^{CR}(i|t)=\frac{I^P(i|t)P_i(t)}{Q_0(t)}$$

(42)

$$I^P(i|t)=\frac{\partial Q_0(t)}{\partial P_i(t)}=Q_0(1_i,t)-Q_0(0_i,t)$$

(43)

where I^CR(i|t) is the criticality importance of the ith root event when time t is reached. P_i(t) and Q₀(t) are the probabilities when the ith event and the top event occur, respectively. Q₀(0_i,t) is the probability of the top event when the non-occurrence of the ith root event is known, and Q₀(1_i,t) is the probability of top event when the occurrence of ith root event is known.

4. Application for Failure Assessment of a Coal Gasifier

This section demonstrates the specific analysis process of the proposed method by taking a coal gasifier as an example. Figure 6 shows the process of the coal-gasification system. Firstly, the coal–water slurry is broken up, atomized, and sprayed into the gasifier under the action of a high-speed oxygen stream passing through the nozzle. The oxygen and the atomized water–coal slurry are subjected to high temperatures in the gasifier and then rapidly undergo a series of complex processes such as preheating, water evaporation, coal dry distillation, volatile pyrolysis combustion, and carbon gasification to produce wet gas with CO, H₂, CO₂, and water vapor as the main components. Finally, the wet gas, slag, and unreacted carbon leave the reaction zone together and enter the cooling chamber. The molten slag is trapped in the water, falls into the slag tank, and is discharged periodically via the slag-discharge system, whereas the gas and saturated steam go to the next treatment system. In this system the gasifier is the central piece of equipment for the realization of the gasification process.

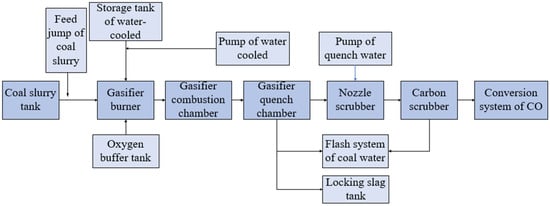
Figure 6. Flow chart of the coal-gasification system.

4.1. Construction of the BN for Analyzing the Failure Risk of the Gasifier

Based on the experts’ suggestions and relevant literature, the FT of the gasifier was instituted. The failure of the gasifier was set as the top event, and it was primarily leaded by the abnormality of gasifier, equipment-corrosion, and human organization factors. Further analysis was executed due to the above sub-top events till all possible root events were considered. The FT of the gasifier and the corresponding event symbols in the FT are shown in Figure 7 and Table 4. The FT of the gasifier was then converted into the corresponding BN through the method presented in Section 2.5. The CPTs were determined for all the intermediate nodes according to the logic-gate rules and the BN model illustrated in Figure 8.

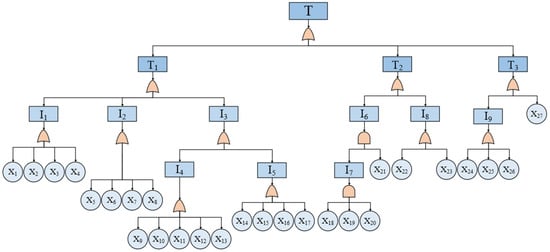
Figure 7. The fault-tree model of the coal gasifier.

Table 4. Description of the events in the fault tree of the coal gasifier.

T/IEs	Description	REs	Description	REs	Description
T	Gasifier failure	X1	Slag opening blocked by large pieces of slag	X14	Low oxygen-flow rate
T1	Gasifier abnormality	X2	Slag opening blocked by molten furnace bricks	X15	High flow rate of coal slurry
T2	Corrosion failure	X3	Low liquid level in quench chamber	X16	High concentration of coal slurry
T3	Human organization factors	X4	Cracking in the quench ring or vertical pipe	X17	Temperature sensor damaged
I1	Pressure fluctuation	X5	Abnormal flow rate of quench water	X18	High H2S content
I2	Abnormal liquid level	X6	Abnormal flow rate of coal water	X19	High CO2 content
I3	Abnormal temperature	X7	Leakage of drain valve of quench water	X20	High H2O content
I4	Too-high temperature	X8	Liquid-level gauge damaged by blockage	X21	High flow rate
I5	Too-low temperature	X9	High oxygen-flow rate	X22	Anti-corrosion layer damaged
I6	Internal corrosion	X10	Low flow rate of coal slurry	X23	Insulation layer damaged
I7	Medium content	X11	Low concentration of coal slurry	X24	Pre-job training is not up to standard
I8	External corrosion	X12	Burner damaged	X25	Improper operation
I9	Unintentional destruction	X13	Temperature sensor damaged	X26	Unattended (unsafe supervision)
				X27	Deliberate destruction

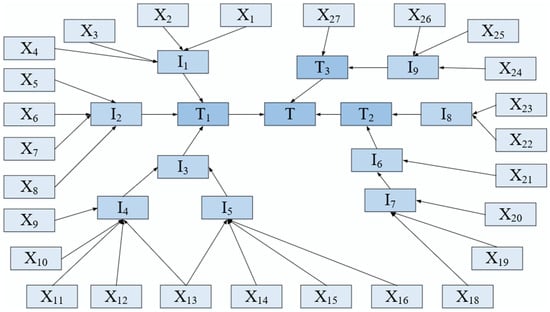
Figure 8. The Bayesian network for the failure of the gasifier mapped from FT.

4.2. Collection of Experts’ Opinions on the Failure of the Coal Gasifier

4.2.1. Definition of the TpIFN–Probabilistic Linguistic Scales

Based on experts’ opinions and relevant literature, this study classified the failure probability of gasifiers into seven levels. Each level corresponds to a range of values for the failure probability of the gasifier, as Table 5 shows.

Table 5. Failure-probability rating of the coal gasifier.

Level	Description	Failure Probability
Quite Low	No expected failures over the entire operating life of the equipment.	<10−5
Low	≥1 accident may occur during the entire operating life of the equipment.	10−5–10−4
Ordinary Low	≥1 accident may occur within 10 years of equipment operation.	10−4–5 × 10−4
Moderate	≥1 accident may occur within 5 years of equipment operation.	5 × 10−4–2 × 10−3
Odinary High	≥1 accident may occur per year of equipment operation.	2 × 10−3–10−2
High	≥1 accident may occur per quarter of equipment operation.	10−2–10−1
Quite High	≥1 accident may occur per month of equipment operation.	>10−1

In linguistic terms, intuitionistic fuzzy membership functions come in many forms to address the uncertainty and inaccuracy of expert judgments. Triangular and trapezoidal intuitionistic fuzzy membership functions are more efficient for risk analysis. Still, a triangle is a particular case of a trapezoid. Therefore, in this study, the membership and non-membership functions of TpIFNs were used to quantitate the probability of gasifier-failure-accident risk. Seven sets of TpIFNs were determined according to the given probability interval in the gasifier-failure-accident risk. Transformation of linguistic variables into corresponding TpIFNs was carried out by mapping relationship of trapezoidal intuitionistic fuzzy sets. The trapezoidal intuitionistic fuzzy sets produced the qualitive failure probabilities of risk events to quantify, as Table 6 shows. The membership and non-membership function curves of TpIFNs matching with seven linguistic variables are illustrated in Figure 9.

Table 6. Trapezoidal intuitionistic fuzzy number corresponding to failure possibility.

Failure Possibility	Trapezoidal Intuitionistic Fuzzy Number
Quite Low	(0, 0, 0.075, 0.1; 0, 0, 0.075, 0.1)
Low	(0.005, 0.12, 0.13, 0.245; 0, 0.12, 0.13, 0.25)
Ordinary Low	(0.15, 0.275, 0.325, 0.45; 0.125, 0.275, 0.325, 0.475)
Moderate	(0.35, 0.45, 0.55, 0.65; 0.3, 0.45, 0.55, 0.7)
Ordinary High	(0.55, 0.675, 0.725, 0.85; 0.525, 0.675, 0.725, 0.875)
High	(0.755, 0.87, 0.88, 0.995; 0.75, 0.87, 0.88, 1)
Quite High	(0.9, 0.925, 1, 1; 0.9, 0.925, 1, 1)

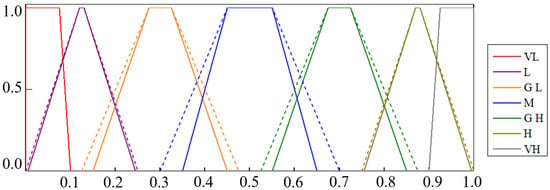
Figure 9. Membership and non-membership functions of probabilistic-language scales.

4.2.2. Expert’s Opinions on Root Events of the BN

Four experts with different professional backgrounds were selected to establish an expert group. To match up to the failure-probability ratings mentioned in Table 5, a seven-level linguistic-term set (QL, LO, OL, MO, OH, HI, QH) was used to express the experts’ opinions on the occurrence possibility of each root event in the BN. Table 7 shows the experts’ judgments of all root nodes.

Table 7. Experts’ opinions on root events of the BN for the gasifier failure.

Event	Linguistic Judgment of Experts				Event	Linguistic Judgment of Experts
	E1	E2	E3	E4		E1	E2	E3	E4
X1	OL	MO	OL	MO	X15	OL	MO	MO	MO
X2	MO	OL	OL	MO	X16	MO	MO	OL	OL
X3	OL	LO	OL	OL	X17	MO	OH	MO	MO
X4	OL	OL	OL	MO	X18	MO	OH	MO	OH
X5	MO	MO	OL	OL	X19	OH	MO	OH	MO
X6	MO	MO	OL	OL	X20	HI	HI	HI	HI
X7	MO	MO	OL	OL	X21	MO	MO	OL	MO
X8	MO	MO	MO	MO	X22	OH	OH	MO	OH
X9	MO	OL	MO	MO	X23	OH	MO	OH	OH
X10	OL	MO	MO	MO	X24	OL	OL	MO	MO
X11	MO	MO	OL	OL	X25	MO	MO	OL	MO
X12	OL	MO	MO	OL	X26	OL	MO	MO	MO
X13	MO	MO	MO	OH	X27	LO	LO	QL	LO
X14	OL	MO	MO	MO

4.3. Aggregation of the TpIFNs for Describing the Failure Probabilities of the Root Nodes

4.3.1. Calculation of the Experts’ Weights

The IF-AHP method mentioned above was used for the computation of the experts’ weights. The personal information of the experts is shown in Table 8.

Table 8. Basic information of the experts.

	Professional Position	Education Level	Service Time
E1	Professor	Doctorate	30
E2	Engineer	Master’s	24
E3	Associate professor	Doctorate	23
E4	Engineer	Bachelor’s	32

The judgment matrix for the three indices of professional position (C₁), education level (C₂), and service time (C₃) is shown in Table 9. The expert group’s intuitionistic-preference relationships for C₁–C₃ are shown in Table 10, Table 11 and Table 12.

Table 9. The intuitionistic-preference relationship for the three indices (C₁–C₃).

R	C1	C2	C3
C1	(0.5, 0.5)	(0.7, 0.2)	(0.6, 0.2)
C2	(0.2, 0.7)	(0.5, 0.5)	(0.2, 0.6)
C3	(0.2, 0.6)	(0.6, 0.2)	(0.5, 0.5)

Table 10. The expert group’s intuitionistic-preference relationship for professional position (C₁).

R1	E1	E2	E3	E4
E1	(0.5, 0.5)	(0.7, 0.2)	(0.6, 0.3)	(0.7, 0.2)
E2	(0.3, 0.6)	(0.5, 0.5)	(0.3, 0.6)	(0.4, 0.4)
E3	(0.3, 0.6)	(0.6, 0.3)	(0.5, 0.5)	(0.6, 0.3)
E4	(0.2, 0.7)	(0.4, 0.4)	(0.3, 0.6)	(0.5, 0.5)

Table 11. The expert group’s intuitionistic-preference relationship for education level (C₂).

R2	E1	E2	E3	E4
E1	(0.5, 0.5)	(0.7, 0.2)	(0.4, 0.4)	(0.7, 0.1)
E2	(0.2, 0.7)	(0.5, 0.5)	(0.7, 0.2)	(0.6, 0.2)
E3	(0.4, 0.4)	(0.2, 0.7)	(0.5, 0.5)	(0.7, 0.1)
E4	(0.1, 0.7)	(0.2, 0.6)	(0.1, 0.7)	(0.5, 0.5)

Table 12. The expert group’s intuitionistic-preference relationship for service time (C₃).

R3	E1	E2	E3	E4
E1	(0.5, 0.5)	(0.6, 0.2)	(0.6, 0.2)	(0.4, 0.4)
E2	(0.2, 0.6)	(0.5, 0.5)	(0.3, 0.3)	(0.2, 0.6)
E3	(0.2, 0.6)	(0.3, 0.3)	(0.5, 0.5)	(0.2, 0.6)
E4	(0.4, 0.4)	(0.6, 0.2)	(0.6, 0.2)	(0.5, 0.5)

A consistency check of the preference relationships was then performed according to Equations (22) and (23). An example illustrated the consistency-test process of the intuitionistic preference relation R.

Through Equations (20) and (21), the intuitionistic fuzzy consistency judgment matrix $\overline{R}={\left({\overline{r}}_{ij}\right)}_{n\times n}$ was calculated according to R.

$$\overline{R}=\left(\begin{array}{ccc}\left(0.5,0.5\right)& \left(0.7,0.2\right)& \left(0.368,0.273\right)\\ \left(0.2,0.7\right)& \left(0.5,0.5\right)& \left(0.2,0.6\right)\\ \left(0.273,0.368\right)& \left(0.6,0.2\right)& \left(0.5,0.5\right)\end{array}\right)$$

(44)

Take ${\overline{r}}_{13}$ as an example:

$${\overline{\mu }}_{13}=\frac{{\mu }_{12}\cdot {\mu }_{23}}{{\mu }_{12}\cdot {\mu }_{23}+\left(1-{\mu }_{12}\right)\left(1-{\mu }_{23}\right)}=\frac{0.7\times 0.2}{0.7\times 0.2+0.3\times 0.8}=0.368$$

(45)

$${\overline{\nu }}_{13}=\frac{{\nu }_{12}\cdot {\nu }_{23}}{{\nu }_{12}\cdot {\nu }_{23}+\left(1-{\nu }_{12}\right)\left(1-{\nu }_{23}\right)}=\frac{0.2\times 0.6}{0.2\times 0.6+0.8\times 0.4}=0.273$$

(46)

The distance between R and $\overline{R}$ calculated by Equation (19) was $d\left(\overline{R},R\right)=0.232>0.1$, indicating that the consistency check failed. We had to adjust the parameters with Equations (22) and (23) until the consistency test was passed. The fused intuitionistic preference relation $\tilde{\overline{R}}$ was obtained.

$$\tilde{\overline{R}}=\left(\begin{array}{ccc}\left(0.5,0.5\right)& \left(0.7,0.2\right)& \left(0.413,0.258\right)\\ \left(0.2,0.7\right)& \left(0.5,0.5\right)& \left(0.2,0.6\right)\\ \left(0.258,0.413\right)& \left(0.6,0.2\right)& \left(0.5,0.5\right)\end{array}\right)$$

(47)

where σ = 0.8. According to Equation (24), the distance between $\tilde{\overline{R}}$ and R $d\left(\tilde{\overline{R}},R\right)=0.0935<0.1$, and the consistency check was passed. The consistency checks for the intuitionistic-preference relationships R_i (i = 1, 2, 3) were also conducted according to the same process.

Next, the priority of each consistent intuitionistic-preference relationship was derived. For example, the priority vector of the $\tilde{\overline{R}}$ was calculated as ε₁ = (0.315, 0.602), ε₂ = (0.176, 0.602), and ε₃ = (0.265, 0.632) with Equation (25). Subsequently, all prioritization vectors were aggregated. Take W₁ as an example:

$$\begin{array}{c}{W}_1={\displaystyle \sum _{j=1}^4}\left({\epsilon }_j\times {\epsilon }_{1j}\right)\\ =(0.315, 0.602) \times (0.284, 0.622)+(0.176, 0.602) \times (0.256, 0.6)+(0.265, 0.632) \times (0.223,\\ 0.591)\\ = (0.182, 0.607)\end{array}$$

(48)

Table 13 shows the aggregated intuitionistic fuzzy priority of C_i.

Table 13. The aggregated intuitionistic fuzzy priority of C_i.

εi	C1	C2	C3	Wj
	(0.315, 0.602)	(0.176, 0.602)	(0.265, 0.632)
E1	(0.284, 0.622)	(0.256, 0.6)	(0.223, 0.591)	(0.182, 0.607)
E2	(0.171, 0.742)	(0.222, 0.657)	(0.128, 0.697)	(0.122, 0.688)
E3	(0.227, 0.689)	(0.2, 0.671)	(0.128, 0.697)	(0.135, 0.677)
E4	(0.159, 0.757)	(0.1, 0.786)	(0.223, 0.591)	(0.122, 0.702)

Per Equations (28) and (29), $S\left(W_1\right)=1-{\displaystyle \frac{\left(1+{\pi }_{W_1}\right)\left(1-{\mu }_{W_1}\right)}{2}}=0.502$. Similarly, S(W₂) = 0.478, and S(W₃) = 0.486, S(W₄) = 0.484. After normalization, the experts’ weights were finally obtained: w = (w₁, w₂, w₃, w₄) = (0.257, 0.245, 0.250, 0.248).

4.3.2. Aggregation of the Experts’ Opinions

After obtaining the experts’ weights and the TpIFNs were converted from the experts’ opinions on the occurrence possibilities of the events, the proposed TpIFN-SAM was used to aggregate the opinions. To elaborate the specific process of the TpIFN-SAM, the root node X₁₈ was treated as an example, and the calculation process is shown in Table 14.

Table 14. Detailed aggregation and FP calculation process of the node X₁₈.

Subject	Data	Subject	Data	Process
${\tilde{E}}_1$	(0.38, 0.46, 0.57, 0.63; 0.32, 0.46, 0.56, 0.68)	$EV\left({\tilde{E}}_1\right)$	0.509	$\begin{array}{l}EV\left(\tilde{E}\right)=\\ {\displaystyle \frac{a_1+b_1+2a_2+2a_3+a_4+b_4}{8}}\end{array}$
${\tilde{E}}_2$	(0.56, 0.68, 0.74, 0.83; 0.53, 0.68, 0.74, 0.85)	$EV\left({\tilde{E}}_2\right)$	0.701	$\begin{array}{l}EV\left({\tilde{E}}_1\right)=\\ {\displaystyle \frac{0.38+0.32+2\times 0.46+2\times 0.57+0.63+0.68}{8}}\end{array}$
${\tilde{E}}_3$	(0.39, 0.47, 0.58, 0.64; 0.33, 0.47, 0.58, 0.69)	$EV\left({\tilde{E}}_3\right)$	0.519
${\tilde{E}}_4$	(0.57, 0.69, 0.75, 0.84; 0.54, 0.69, 0.75, 0.86)	$EV\left({\tilde{E}}_4\right)$	0.711
$S\left({\tilde{E}}_1,{\tilde{E}}_2\right)$	0.726	$S\left({\tilde{E}}_2,{\tilde{E}}_3\right)$	0.740	$S\left({\tilde{E}}_i,{\tilde{E}}_j\right)=\left\{\begin{array}{l}{\displaystyle \frac{EV\left({\tilde{E}}_i\right)}{EV\left({\tilde{E}}_j\right)}},if:EV\left({\tilde{E}}_i\right)\le EV\left({\tilde{E}}_j\right)\\ {\displaystyle \frac{EV\left({\tilde{E}}_j\right)}{EV\left({\tilde{E}}_i\right)}},if:EV\left({\tilde{E}}_j\right)\le EV\left({\tilde{E}}_i\right)\end{array}\right.$
$S\left({\tilde{E}}_1,{\tilde{E}}_3\right)$	0.981	$S\left({\tilde{E}}_2,{\tilde{E}}_4\right)$	0.986
$S\left({\tilde{E}}_1,{\tilde{E}}_4\right)$	0.715	$S\left({\tilde{E}}_3,{\tilde{E}}_4\right)$	0.729	$S\left({\tilde{E}}_1,{\tilde{E}}_2\right)={\displaystyle \frac{EV\left({\tilde{E}}_1\right)}{EV\left({\tilde{E}}_2\right)}}={\displaystyle \frac{0.509}{0.701}}=0.726$
WA (E1)	0.821
WA (E2)	0.825
WA (E3)	0.832
WA (E4)	0.817
RAD (E1)	0.249			$WA(E_i)={\displaystyle \frac{{\displaystyle \sum _{\begin{array}{l}j=1\\ j\ne i\end{array}}^m\omega (E_i)\cdot S\left({\tilde{E}}_i,{\tilde{E}}_j\right)}}{{\displaystyle \sum _{\begin{array}{l}j=1\\ j\ne i\end{array}}^m\omega (E_j)}}},i=1,2,\dots ,m$
RAD (E2)	0.334
RAD (E3)	0.253			$\begin{array}{l}WA(E_1)={\displaystyle \frac{0.257\times \left(0.726+0.981+0.715\right)}{0.245+0.25+0.248}}\\ =0.821\end{array}$
RAD (E4)	0.248
CDC1	0.252			$RAD\left(E_i\right)={\displaystyle \frac{WA\left(E_i\right)}{{\displaystyle \sum _{i=1}^{m}WA\left(E_i\right)}}},i=1,2,\dots ,m$
CDC2	0.298
CDC3	0.252			$\begin{array}{l}RAD\left(E_1\right)={\displaystyle \frac{0.821}{0.821+0.825+0.832+0.817}}\\ =0.249\end{array}$
CDC4	0.248
Aggregation TpIFN	(0.502, 0.608, 0.697, 0.776; 0.456, 0.608, 0.697, 0.812)			CDCi = β·ω + (1 − β)·RADi
PS	0.534
FP	1.30 × 10−³			CDC1 = 0.4 × 0.257 + 0.6 × 0.249 = 0.252

4.4. TpIFN-Defuzzification

4.4.1. Conversion of the TpIFNs into PSs

The aggregated results obtained by the TpIFN-SAM were still TpIFNs, so TpIFN Defuzzification was performed by Equation (36) to further convert the TpIFNs into PSs with crisp values.

4.4.2. Determination of the FPs of All Root Nodes

The PSs of the root nodes were not probability values. In order to implement probabilistic inference with the BN, the PSs were further converted into FPs according to Equations (37) and (38). Table 15 shows all root nodes of the FPs.

Table 15. The aggregated expert opinions and the corresponding failure probabilities of the root events in the BN.

Events	Aggregated TpIFNs	PS	FP
X1	(0.278, 0.361, 0.451, 0.547; 0.235, 0.361, 0.451, 0.599)	0.312	2.36 × 10−4
X2	(0.278, 0, 0.361, 0.451, 0.547; 0.235, 0.361, 0.451, 0.599)	0.312	2.36 × 10−4
X3	(0.111, 0.231, 0.273, 0.389; 0.082; 0.231, 0.273; 0.421)	0.169	7.60 × 10−5
X4	(0.221, 0.323, 0.394, 0.506; 0.184, 0.323, 0.394, 0.556)	0.267	1.67 × 10−4
X5	(0.281, 0.368, 0.437, 0.546; 0.234, 0.368, 0.437, 0.585)	0.312	2.36 × 10−4
X6	(0.257, 0.349, 0.427, 0.530; 0.226, 0.349, 0.427, 0.569)	0.301	2.17 × 10−4
X7	(0.251, 0.343, 0.421, 0.510; 0.240, 0.343, 0.421, 0.559)	0.301	2.16 × 10−4
X8	(0.394, 0.447, 0.551, 0.668; 0.352, 0.447, 0.551, 0.726)	0.407	4.91 × 10−4
X9	(0.415, 0.454, 0.561, 0.676; 0.343, 0.454, 0.561, 0.721)	0.409	4.96 × 10−4
X10	(0.422, 0.459, 0.567, 0.679; 0.349, 0.459, 0.567, 0.712)	0.416	5.26 × 10−4
X11	(0.248, 0.340, 0.417, 0.505; 0.236, 0.340, 0.417, 0.552)	0.298	2.12 × 10−4
X12	(0.401, 0.438, 0.543, 0.661; 0.330, 0.438, 0.543, 0.689)	0.399	4.61 × 10−4
X13	(0.487, 0.542, 0.657, 0.728; 0.399, 0.542, 0.657, 0.760)	0.477	8.39 × 10−4
X14	(0.415, 0.454, 0.561, 0.676; 0.343, 0.454, 0.561, 0.721)	0.409	4.96 × 10−4
X15	(0.422, 0.459, 0.567, 0.679; 0.349, 0.459, 0.567, 0.712)	0.416	5.26 × 10−4
X16	(0.248, 0.340, 0.417, 0.505; 0.236, 0.340, 0.417, 0552)	0.298	2.12 × 10−4
X17	(0.487, 0.542, 0.657, 0.728; 0.399, 0.542, 0.657, 0.760)	0.477	8.39 × 10−4
X18	(0.502, 0.608, 0.697, 0.776; 0.456, 0.608, 0.697, 0.812)	0.534	1.30 × 10−3
X19	(0.484, 0.587, 0.675, 0.755; 0.440, 0.587, 0.675, 0.791)	0.517	1.14 × 10−3
X20	(0.814, 0.867, 0.909, 0.977; 0.768, 0.867, 0.909, 0.992)	0.777	8.35 × 10−3
X21	(0.393, 0.504, 0.603, 0.666; 0.332, 0.504, 0.603, 0.716)	0.428	5.74 × 10−4
X22	(0.561, 0.663, 0.743, 0.828; 0.532, 0.663, 0.743, 0.861)	0.596	2.10 × 10−3
X23	(0.561, 0.663, 0.743, 0.828; 0.532, 0.663, 0.743, 0.861)	0.596	2.10 × 10−3
X24	(0.297, 0.401, 0.488, 0.553; 0.245, 0.401, 0.488, 0.593)	0.337	2.86 × 10−4
X25	(0.401, 0.467, 0.597, 0.669; 0.368, 0.467, 0.597, 0.705)	0.436	6.12 × 10−4
X26	(0.396, 0.461, 0.579, 0.659; 0.357, 0.461, 0.579, 0.697)	0.424	5.59 × 10−4
X27	(0.007, 0.113, 0.123, 0.224; 0.002, 0.113, 0.123, 0.241)	0.061	1.40 × 10−5

4.5. BN Analysis

4.5.1. Prediction of the Failure Probability of the Gasifier

Before the BN performs forward prediction, it is necessary to obtain the CPT of each relevant node. Each CPT in this case was obtained by expert evaluation. Table 16 shows the CPT of the intermediate node I₁. The rest of the CPTs can be found in Appendix B.

Table 16. The CPT of event I₁ in the BN model (Occ: occurred; Non: non-occurred).

X1	X2	X3	X4	I1
				Occ	Non
Occ	Occ	Occ	Occ	1.00	0.00
Occ	Occ	Occ	Non	0.67	0.33
Occ	Occ	Non	Occ	0.69	0.31
Occ	Non	Occ	Occ	0.72	0.28
Occ	Non	Occ	Non	0.62	0.38
Occ	Non	Non	Occ	0.58	0.42
Occ	Occ	Non	Non	0.57	0.43
Occ	Non	Non	Non	0.21	0.79
Non	Occ	Occ	Occ	0.85	0.15
Non	Occ	Occ	Non	0.67	0.33
Non	Occ	Non	Occ	0.68	0.32
Non	Occ	Non	Non	0.31	0.69
Non	Non	Occ	Occ	0.42	0.58
Non	Non	Occ	Non	0.18	0.82
Non	Non	Non	Occ	0.21	0.79
Non	Non	Non	Non	0.00	1.00

The GeNIe software was used to analyze the established BN model of the coal gasifier. Figure 10 shows the prior probability of the failure of the gasifier through the forward inference of the BN. The failure probability of the gasifier (FP_T) was 0.036. To contrast the variations between the FT and the BN, the FP_T was also calculated through FT analysis, and the results show that the FP_T in the FT was 0.013, which is nearly three times higher than that in the BN. This is because the BN takes into account the conditional dependencies between events and can more objectively report the features of the system.

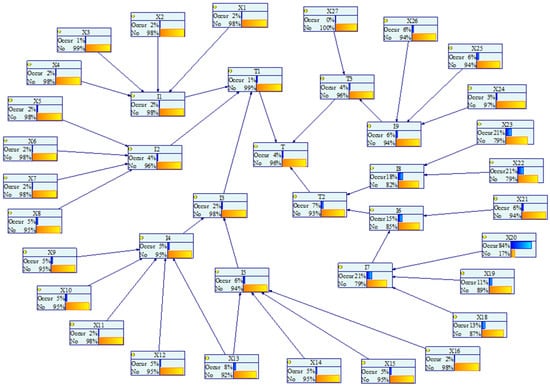
Figure 10. The prior probability of each node in the BN of the coal gasifier.

4.5.2. Diagnosis of the Key Nodes for the Failure of the Coal Gasifier

The backward inference of the BN was executed to update the occurrence probabilities of the root nodes to assess the extent to which the root nodes affect the failure of the gasifier. Figure 11 shows the posterior probability of each root node P (X_i = Occur | T = Occur) obtained by backward inference of the BN. In the case that the leaf node must occur, the posterior probability of the root nodes X₂₀ (High H₂O content), X₂₂ (Anti-corrosion layer damaged), and X₂₃ (Insulation layer damaged) are the most worrying ones. Therefore, the key nodes can be preliminarily determined.

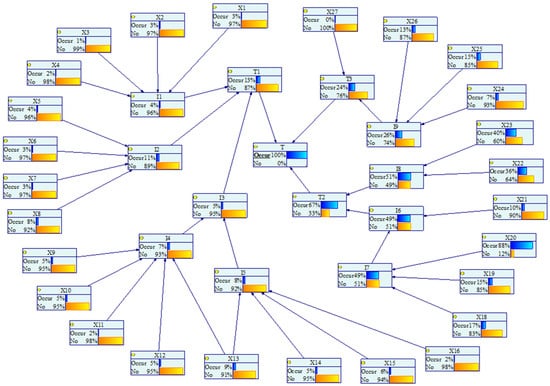
Figure 11. The posterior probability of each node in the BN of the coal gasifier.

By comparing the prior and the posterior probability regarding each root node, as shown in Figure 12, the root nodes with large changes in occurrence probability can be obtained as X₂₂ (Anti-corrosion layer damaged), X₂₃ (Insulation layer damaged) and X₂₅ (Improper operation), indicating that these three root events have a large contribution to the failure probability of the gasifier. The acquisition of the prior and the posterior probability shows the forward-inference (prediction) ability and backward-inference (diagnosis) ability of the BN, respectively, which completely reflects the superiority of the BN’s bidirectional-inference ability. Meanwhile, this ability can be used to provide preliminary judgments and lay the foundation for subsequent analysis and determination of key nodes.

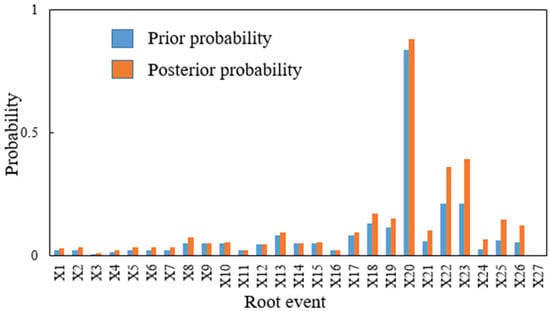
Figure 12. Prior and posterior probabilities of root nodes of the BN model.

4.5.3. SA and CIA

The RoV of each root node was calculated with Equation (39). Figure 13 displays the calculation results of the importance of all basic events. The top six key root nodes were X₂₅ (Improper operation), X₂₄ (Pre-job training is not up to standard), X₂₆ (Unattended/unsafe supervision), X₂₇ (Deliberately damaged), X₂₃ (Insulation layer damaged), and X₂₁ (High flow rate).

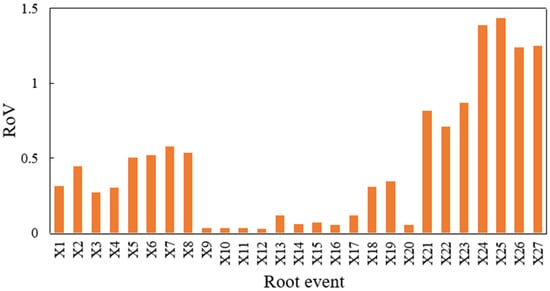
Figure 13. RoV of the root node probability using the BN model for the coal gasifier.

For the purpose of further elucidating the devotion of all root nodes to the occurrence of accidents and identify the critical factors, SA and CIA were performed. Figure 14 shows the sensitivity value and the critical importance of each root node. For the BN, X₂₅ (Improper operation), X₂₄ (Pre-job training is not up to standard), X₂₆ (Unattended/unsafe supervision), X₂₇ (Deliberately damaged), X₂₃ (Insulation layer damaged), and X₂₂ (Anti-corrosion layer damaged) were the top six key events for the gasifier failure. For the FT, the top six key factors included X₂₂ (Anti-corrosion layer damaged), X₂₃ (Insulation layer damaged), X₁₃, X₁₇ (Temperature sensor damaged), X₂₅ (Improper operation), and X₂₁ (High flow rate). The results obtained by the two methods are discrepant. The reason for this is that the BN still considered conditional dependencies between events, whereas the FT did not capture them.

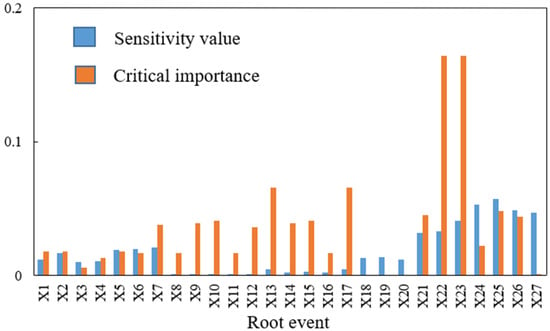
Figure 14. Comparison of sensitivity value and critical importance of the root nodes of the BN model for the coal gasifier.

From the results of the SA and CIA, it can be found that X₂₅ (Improper operation) was considered the most critical factor on the failure of the coal gasifier. In addition, damage to anti-corrosion measures (X₂₂ and X₂₃) was also a very important influencing factor. Therefore, more attention should be allocated to the management and training of operators, and special attention should be paid to regular inspection of the integrity of insulation and anti-corrosion layers to minimize the failure of the gasifier.

5. Conclusions

In this study, a new integration framework was proposed to assess the failure risk of the process system. The improvements of this method compared with the previous method are as follows:

• This framework combined the Bayesian network with the TpIFN-SAM to provide an alternative strategy for obtaining the prior probabilities of the root events in BNs.
• A set of TpIFNs was defined to quantify the linguistic terms for describing the failure possibilities of the events in BNs, which are more general and expressive than TpIFNs.
• The TpIFN-SAM can effectively aggregate the expert opinions on the prior probabilities of the root events in BNs and reduce the uncertain cumulative effect of the aggregation process by taking the effect of individual discrepancies into account for the consistency. The bidirectional reasoning of the BN coupled with sensitivity analysis can accurately calculate the system-failure probability and identify the key influencing factors that may lead to accidents.

Limitations also exist in this work. The basic probabilities of the root events in the BN were assumed to be constant in the proposed framework, but in many cases they are time dependent. Therefore, developing a BN approach for dynamic systems will be covered in future research work.