Exponential Stabilization for a Class of Strict-Feedback Nonlinear Time Delay Systems via State Feedback Control Scheme

Abstract

This paper considers the exponential stabilization problem for a class of strict-feedback nonlinear systems with multiple time-varying delays, whose nonlinear terms satisfy the linear growth condition. The state feedback controller that relies on a positive parameter to be determined is constructed to deal with nonlinear terms. By tactfully introducing the Lyapunov–Krasovskii functional with an exponential function and selecting the applicable parameter to be determined, the implementable state feedback controller can be obtained to guarantee that the closed-loop system is exponentially stable. The proposed state feedback control scheme is finally applied to the control design of two-stage chemical reactor system, which illustrates the effectiveness of the control method.

1. Introduction

Time delay phenomena frequently exist in a large number of practical applications, such as information transfer processes, chemical reaction processes, communication networks and power supply networks, etc. Additionally, the appearance of a time delay is one of the important factors leading to performance deterioration and the instability of a system; hence, the stability analysis of dynamic systems with time delays has become an important theoretical and practical topic. During the past several decades, with the help of different controller design and analysis methods, a great deal of effort has been put into the stabilization problems of nonlinear time delay systems, especially for strict-feedback nonlinear time delay systems. By adopting fuzzy logic systems to identify the unknown nonlinear terms, Refs. [1,2,3] investigated the problems of adaptive fuzzy tracking control for strict-feedback nonlinear time delay systems with an output constraint or full-state constraints. Through introducing the radial basis function neural networks to approximate unknown nonlinear functions and designing the adaptive neural network controller, Refs. [4,5,6,7] considered the adaptive control problems of strict-feedback nonlinear time delay systems. In addition, Refs. [8,9,10,11], respectively, studied the robust adaptive control problems of strict-feedback nonlinear time delay systems with different system structures.

It can be seen from the above-mentioned literatures that almost all controllers are designed to make the closed-loop systems asymptotically stable or bounded. However, the control requirements of many practical systems are not only stable but also have a certain rate of convergence in some circumstances. Due to the fact that the exponential stability has this property, the exponential stabilization problems of nonlinear time delay systems have received much attention and have obtained a series of rich results. Oucheriah [12] addressed the robust exponential stabilization for a class of uncertain dynamic time delay systems with a bounded controller. Hua et al. [13] considered a class of interconnected time delay systems with general nonlinear interconnections and mismatched time delay functions, and a decentralized state feedback controller was systematically designed to ensure that the solutions of the closed-loop system were uniformly ultimately bounded and exponentially convergent towards a ball. Using the Razumikhin theorem, Dong et al. [14] provided the continuous state feedback controller design scheme and established the exponential stabilization criterion based on the solutions of the standard Riccati differential equation for nonlinear systems with uncertainties and time-varying delays. Applying some sufficient conditions in terms of linear matrix inequalities, the problem of the exponential stabilization of memristive neural networks with time delays was investigated in Wu and Zeng [15]. Benabdallah and Echi [16] dealt with the exponential stabilization control problem for a kind of nonlinear systems with a constant time delay. Taking into account the time-varying delays and nonlinear disturbances, Li et al. [17] solved the exponential stabilization for a class of switched time-varying systems, and time-dependent switching signals have been characterized by Metzler matrices such that the closed-loop system is globally exponentially stable. The exponential stabilization problems of memristive neural networks with time delays and different system structures were, respectively, investigated in [18,19,20,21].

Motivated by the above analysis, this paper will further consider the problem of exponential stabilization for a class of strict-feedback nonlinear systems with multiple time-varying delays. Firstly, we propose the state feedback control law, which depends on a determined positive parameter to compensate for nonlinear terms. Secondly, with the construction of the Lyapunov–Krasovskii functional that includes the exponential function and fully considers the influence of time-varying delays, by choosing the applicable parameter, the exponential stability of the closed-loop system is strictly verified via two different ways. Finally, a simulation example is provided to show the effectiveness of the proposed design strategy.

Notations:${\mathbf{R}}_{+}$ denotes the set of all non-negative real numbers, ${\mathbf{R}}^n$ is the real n-dimensional space, $\mathrm{I}$ stands for the unit matrix of the corresponding dimension, $\mathrm{T}$ denotes the transpose, ${\lambda }_{max}(·)$ (or ${\lambda }_{min}(·))$ means the maximum (or minimum) eigenvalue of a symmetric matrix, $|·|$ stands for the Euclidean norm of a vector or the induced Euclidean norm of a matrix and $\mathcal{C}([-\sigma ,0];{\mathbf{R}}^n)$ represents the set of all $R^n$-value continuous functions on $[-\sigma ,0]$ endowed with the norm $\parallel ·\parallel$ defined by $\parallel h\parallel ={max}_{s\in [-\sigma ,0]}\left|h\left(s\right)\right|$ for $h\in \mathcal{C}([-\sigma ,0];R^n)$.

2. Problem Description

Consider the strict-feedback nonlinear system with multiple time-varying delays described by

$$\begin{array}{ccc}\hfill {\dot{x}}_1& =& x_2+f_1({\overline{x}}_1,x_{1,{\sigma }_{1t}}),\hfill \\ \hfill {\dot{x}}_2& =& x_3+f_2({\overline{x}}_2,x_{1,{\sigma }_{1t}},x_{2,{\sigma }_{2t}}),\hfill \\ & ⋮& \hfill \\ \hfill {\dot{x}}_n& =& u+f_n({\overline{x}}_n,x_{1,{\sigma }_{1t}},\cdots ,x_{n,{\sigma }_{nt}}),\hfill \end{array}$$

(1)

where $x={[x_1,\cdots ,x_n]}^{\mathrm{T}}\in {\mathbf{R}}^n$ and $u\in \mathbf{R}$ are the system state and control input, respectively. For $l=1,\cdots ,n$, ${\overline{x}}_l={[x_1,\cdots ,x_l]}^{\mathrm{T}}$, $x_{l,{\sigma }_{lt}}=x_l(t-{\sigma }_{lt})$ is the time-delayed system state, ${\sigma }_{lt}={\sigma }_l\left(t\right):{\mathbf{R}}_{+}\to [0,{\overline{\sigma }}_l]$ is the time-varying delay that satisfies ${\dot{\sigma }}_{lt}\le {\rho }_l<1$, the nonlinear term $f_l:{\mathbf{R}}^l\times {\mathbf{R}}^l\to \mathbf{R}$ satisfies the local Lipschitz condition and vanishes at zero, and the initial condition is $\{x\left(s\right):-\sigma \le s\le 0\}=\psi \in \mathcal{C}([-\sigma ,0];{\mathbf{R}}^n)$ with $\sigma ={max}_{1\le l\le n}\left\{{\overline{\sigma }}_l\right\}$.

The control objective of this paper is to construct the state feedback controller such that the closed-loop system of system (1) with any initial condition $\psi$ is exponentially stable, i.e., there exists a pair of positive constants $\lambda$ and N such that the solution $x(t,\psi )$ of system (1) satisfies

$$\begin{array}{c}\hfill \left|x(t,\psi )\right|\le N\parallel \psi \parallel e^{-\lambda t},\forall t\ge 0,\psi \in \mathcal{C}([-\sigma ,0];{\mathbf{R}}^n).\end{array}$$

(2)

To achieve this purpose, the following assumption is made for system (1).

Assumption 1.

For $l=1,\cdots ,n$, there exist positive constants ${\beta }_{li}$ and ${\overline{\beta }}_{li}$ such that

$$\begin{array}{c}\hfill |f_l|\le {\displaystyle \sum _{i=1}^l}{\beta }_{li}|x_i|+{\displaystyle \sum _{i=1}^l}{\overline{\beta }}_{li}\left|x_{i,{\sigma }_{it}}\right|.\end{array}$$

Remark 1.

The definition of exponential stability (2) for nonlinear time delay systems can be regarded as an extension of the definition of exponential stability for nonlinear systems without a time delay in Khalil [22]. In the case of the time-varying delay ${\sigma }_{lt}\equiv 0(l=1,\cdots ,n)$, inequality (2) will be changed into $\left|x(t,x(0\left)\right)\right|\le N\left|x\left(0\right)\right|e^{-\lambda t}$, which was used in Khalil [22].

Remark 2.

As illustrated in [12,14,15,16,17] and the related works, it can be seen that the linear growth condition in Assumption 1 is a natural condition often adopted to study the exponential stabilization problem of nonlinear time delay systems.

In what follows, the state feedback controller design and stability analysis of system (1) will be given.

3. Controller Design and Stability Analysis

Letting

$$\begin{array}{ccc}\hfill & & A=\left[\begin{array}{cc}{0}_{(n-1)\times 1}& \mathrm{I}\\ 0& 0_{1\times (n-1)}\end{array}\right],B=\left[\begin{array}{c}{0}_{(n-1)\times 1}\\ 1\end{array}\right],F=\left[\begin{array}{c}{f}_1\\ ⋮\\ f_n\end{array}\right],\hfill \end{array}$$

(3)

system (1) can be compactly rewritten as

$$\begin{array}{ccc}\hfill \dot{x}& =& Ax+Bu+F.\hfill \end{array}$$

(4)

Introduce the coordinate transformation

$$\begin{array}{c}\hfill z=\mathsf{\Xi }\left(\kappa \right)x=\mathrm{diag}\{1,\kappa ,\cdots ,{\kappa }^{n-1}\}x,\end{array}$$

(5)

and the state feedback controller

$$\begin{array}{c}\hfill u=\Delta \left(\kappa \right)x=\left[\frac{{\delta }_n}{{\kappa }^n},\cdots ,\frac{{\delta }_1}{\kappa }\right]x,\end{array}$$

(6)

where $z={[z_1,\cdots ,z_n]}^{\mathrm{T}}$, $\kappa$ is a positive parameter to be determined, $\mathrm{diag}\{·\}$ stands for diagonal matrix and $\overline{\Delta }=[{\delta }_n,\cdots ,{\delta }_1]$ is selected such that $A+B\overline{\Delta }$ is Hurwitz. With the help of (5) and (6), using the fact that $\mathsf{\Xi }\left(\kappa \right)(A+B\Delta \left(\kappa \right))={\kappa }^{-1}(A+B\overline{\Delta })\mathsf{\Xi }\left(\kappa \right)$, we obtain the transformed closed-loop system

$$\begin{array}{ccc}\hfill \dot{z}& =& \mathsf{\Xi }\left(\kappa \right)Ax+\mathsf{\Xi }\left(\kappa \right)B\Delta \left(\kappa \right)x+\mathsf{\Xi }\left(\kappa \right)F\hfill \\ & =& \mathsf{\Xi }\left(\kappa \right)(A+B\Delta (\kappa \left)\right)x+\mathsf{\Xi }\left(\kappa \right)F\hfill \\ & =& {\kappa }^{-1}(A+B\overline{\Delta })z+\mathsf{\Xi }\left(\kappa \right)F.\hfill \end{array}$$

(7)

Consider the Lyapunov function

$$\begin{array}{c}\hfill U\left(z\right)=ϵz^{\mathrm{T}}\mathsf{\Phi }z,\end{array}$$

(8)

where $ϵ$ is a positive real number and $\mathsf{\Phi }$ is a positive definite symmetric matrix and satisfies ${(A+B\overline{\Delta })}^{\mathrm{T}}\mathsf{\Phi }+\mathsf{\Phi }(A+B\overline{\Delta })=-\mathrm{I}$. Applying (7) and (8), the derivative of $U\left(z\right)$ is

$$\begin{array}{ccc}\hfill \dot{U}\left(z\right)& =& {\kappa }^{-1}ϵz^{\mathrm{T}}\left[{(A+B\overline{\Delta })}^{\mathrm{T}}\mathsf{\Phi }+\mathsf{\Phi }(A+B\overline{\Delta })\right]z+2ϵz^{\mathrm{T}}\mathsf{\Phi }\mathsf{\Xi }\left(\kappa \right)F\hfill \\ & \le & -\frac{ϵ}{\kappa }{\left|z\right|}^2+2ϵ\left|\mathsf{\Phi }\right|\left|z\right|\left|\mathsf{\Xi }\left(\kappa \right)F\right|.\hfill \end{array}$$

(9)

Using Assumption 1 and (5), one leads to

$$\begin{array}{ccc}\hfill \left|\mathsf{\Xi }\right(\kappa \left)F\right|& \le & \sum _{l=1}^n\sum _{i=l}^n{\kappa }^{i-1}{\beta }_{il}|x_l|+\sum _{l=1}^n\sum _{i=l}^n{\kappa }^{i-1}{\overline{\beta }}_{il}\left|x_{l,{\sigma }_{lt}}\right|\hfill \\ & =& \sum _{l=1}^n\sum _{i=0}^{n-l}{\kappa }^i{\beta }_{il}|z_l|+\sum _{l=1}^n\sum _{i=0}^{n-l}{\kappa }^i{\overline{\beta }}_{il}\left|z_{l,{\sigma }_{lt}}\right|\hfill \\ & \le & \nu \left(\kappa \right)\sum _{l=1}^n|z_l|+\overline{\nu }\left(\kappa \right)\sum _{l=1}^n\left|z_{l,{\sigma }_{lt}}\right|\hfill \\ & \le & \sqrt{n}\nu \left(\kappa \right)\left|z\right|+\overline{\nu }\left(\kappa \right)\sum _{l=1}^n\left|z_{l,{\sigma }_{lt}}\right|,\hfill \end{array}$$

(10)

where

$$\begin{array}{ccc}\hfill z_{l,{\sigma }_{lt}}& =& z_l(t-{\sigma }_{lt}),\nu \left(\kappa \right)=\beta \sum _{i=0}^{n-1}{\kappa }^i,\overline{\nu }\left(\kappa \right)=\overline{\beta }\sum _{i=0}^{n-1}{\kappa }^i,\hfill \\ \hfill \beta & =& \underset{1\le l\le n}{max}\left\{\underset{0\le i\le n-l}{max}\left\{{\beta }_{il}\right\}\right\},\overline{\beta }=\underset{1\le l\le n}{max}\left\{\underset{0\le i\le n-l}{max}\left\{{\overline{\beta }}_{il}\right\}\right\}.\hfill \end{array}$$

Adopting the mean square inequality and (10), there is a positive constant $\varsigma$ such that

$$\begin{array}{ccc}\hfill \dot{U}\left(z\right)& \le & -\frac{ϵ}{\kappa }{\left|z\right|}^2+2ϵ\sqrt{n}{\left|\mathsf{\Phi }\right|\nu \left(\kappa \right)\left|z\right|}^2+2ϵ\left|\mathsf{\Phi }\right|\overline{\nu }\left(\kappa \right)\left|z\right|\sum _{l=1}^n\left|z_{l,{\sigma }_{lt}}\right|\hfill \\ & \le & -\left(\frac{1}{\kappa }-2\sqrt{n}\left|\mathsf{\Phi }\right|\nu \left(\kappa \right)-\frac{ϵ}{\varsigma }n\left|\mathsf{\Phi }\right|\overline{\nu }\left(\kappa \right)\right){ϵ\left|z\right|}^2+\varsigma \left|\mathsf{\Phi }\right|\overline{\nu }\left(\kappa \right)\sum _{l=1}^n{z}_{l,{\sigma }_{lt}}^2.\hfill \end{array}$$

(11)

Then, the main result of this paper is illustrated in the following theorem.

Theorem 1.

For system (1) with Assumption 1, if there exists a positive constant κ such that

$$\begin{array}{c}\hfill \frac{1}{\kappa }-2\sqrt{n}\left|\mathsf{\Phi }\right|\nu \left(\kappa \right)-\frac{ϵ}{\varsigma }n\left|\mathsf{\Phi }\right|\overline{\nu }\left(\kappa \right)-\frac{\varsigma e^{\sigma }}{(1-\rho )ϵ}\left|\mathsf{\Phi }\right|\overline{\nu }\left(\kappa \right)>0,\end{array}$$

(12)

under the state feedback controller (6), then the closed-loop system is exponentially stable, where $\rho ={max}_{1\le l\le n}\left\{{\rho }_l\right\}$.

Proof. 

Choosing the Lyapunov–Krasovskii functional

$$\begin{array}{c}\hfill \overline{U}(t,z)=U\left(z\right)+\varsigma \left|\mathsf{\Phi }\right|\overline{\nu }\left(\kappa \right)\sum _{l=1}^n\frac{e^{-(t-{\overline{\sigma }}_l)}}{1-{\rho }_l}{\int }_{t-{\sigma }_{lt}}^t{e}^s{z}_l^2\left(s\right)ds,\end{array}$$

(13)

according to (11), the derivative of $\overline{U}(t,z)$ is

$$\begin{array}{ccc}\hfill \dot{\overline{U}}(t,z)& \le & -\left(\frac{1}{\kappa }-2\sqrt{n}\left|\mathsf{\Phi }\right|\nu \left(\kappa \right)-\frac{ϵ}{\varsigma }n\left|\mathsf{\Phi }\right|\overline{\nu }\left(\kappa \right)\right){ϵ\left|z\right|}^2+\varsigma \left|\mathsf{\Phi }\right|\overline{\nu }\left(\kappa \right)\sum _{l=1}^n{z}_{l,{\sigma }_{lt}}^2\hfill \\ & & +\varsigma \left|\mathsf{\Phi }\right|\overline{\nu }\left(\kappa \right)\sum _{l=1}^n\frac{e^{-(t-{\overline{\sigma }}_l)}}{1-{\rho }_l}\left[e^t{z}_l^2-(1-{\dot{\sigma }}_{lt})e^{t-{\sigma }_{lt}}{z}_{l,{\sigma }_{lt}}^2\right]\hfill \\ & & -\varsigma \left|\mathsf{\Phi }\right|\overline{\nu }\left(\kappa \right)\sum _{l=1}^n\frac{e^{-(t-{\overline{\sigma }}_l)}}{1-{\rho }_l}{\int }_{t-{\sigma }_{lt}}^t{e}^s{z}_l^2\left(s\right)ds\hfill \\ & \le & -\left(\frac{1}{\kappa }-2\sqrt{n}\left|\mathsf{\Phi }\right|\nu \left(\kappa \right)-\frac{ϵ}{\varsigma }n\left|\mathsf{\Phi }\right|\overline{\nu }\left(\kappa \right)\right){ϵ\left|z\right|}^2+\varsigma \left|\mathsf{\Phi }\right|\overline{\nu }\left(\kappa \right)\sum _{l=1}^n{z}_{l,{\sigma }_{lt}}^2\hfill \\ & & +\varsigma \left|\mathsf{\Phi }\right|\overline{\nu }\left(\kappa \right)\sum _{l=1}^n\frac{e^{{\overline{\sigma }}_l}}{1-{\rho }_l}{z}_l^2-\varsigma \left|\mathsf{\Phi }\right|\overline{\nu }\left(\kappa \right)\sum _{l=1}^n{e}^{{\overline{\sigma }}_l-{\sigma }_{lt}}{z}_{l,{\sigma }_{lt}}^2\hfill \\ & & -\varsigma \left|\mathsf{\Phi }\right|\overline{\nu }\left(\kappa \right)\sum _{l=1}^n\frac{e^{-(t-{\overline{\sigma }}_l)}}{1-{\rho }_l}{\int }_{t-{\sigma }_{lt}}^t{e}^s{z}_l^2\left(s\right)ds\hfill \\ & \le & -\left(\frac{1}{\kappa }-2\sqrt{n}\left|\mathsf{\Phi }\right|\nu \left(\kappa \right)-\frac{ϵ}{\varsigma }n\left|\mathsf{\Phi }\right|\overline{\nu }\left(\kappa \right)-\frac{\varsigma {ϵ}^{-1}{e}^{\sigma }}{1-\rho }\left|\mathsf{\Phi }\right|\overline{\nu }\left(\kappa \right)\right)ϵ{\left|z\right|}^2\hfill \\ & & -\varsigma \left|\mathsf{\Phi }\right|\overline{\nu }\left(\kappa \right)\sum _{l=1}^n\frac{e^{-(t-{\overline{\sigma }}_l)}}{1-{\rho }_l}{\int }_{t-{\sigma }_{lt}}^t{e}^s{z}_l^2\left(s\right)ds.\hfill \end{array}$$

(14)

With the aid of (12), (14) and the denseness of real numbers, there exists a constant $c_1>0$ such that

$$\begin{array}{ccc}\hfill \dot{\overline{U}}(t,z)& \le & -c_1{ϵ\left|z\right|}^2-\varsigma \left|\mathsf{\Phi }\right|\overline{\nu }\left(\kappa \right)\sum _{l=1}^n\frac{e^{-(t-{\overline{\sigma }}_l)}}{1-{\rho }_l}{\int }_{t-{\sigma }_{lt}}^t{e}^s{z}_l^2\left(s\right)ds.\hfill \end{array}$$

(15)

From (8), one can obtain

$$\begin{array}{c}\hfill {ϵ\left|z\right|}^2\ge \frac{1}{{\lambda }_{max}\left(\mathsf{\Phi }\right)}U\left(z\right),\end{array}$$

which, together with (15), implies

$$\begin{array}{ccc}\hfill \dot{\overline{U}}(t,z)& \le & -\frac{c_1}{{\lambda }_{max}\left(\mathsf{\Phi }\right)}U\left(z\right)-\varsigma \left|\mathsf{\Phi }\right|\overline{\nu }\left(\kappa \right)\sum _{l=1}^n\frac{e^{-(t-{\overline{\sigma }}_l)}}{1-{\rho }_l}{\int }_{t-{\sigma }_{lt}}^t{e}^s{z}_l^2\left(s\right)ds.\hfill \end{array}$$

(16)

Taking $c=min\left\{\frac{c_1}{{\lambda }_{max}\left(\mathsf{\Phi }\right)},1\right\}$, by (16), it is easy to deduce that

$$\begin{array}{ccc}\hfill \dot{\overline{U}}(t,z)& \le & -c\overline{U}(t,z),\hfill \end{array}$$

(17)

which means

$$\begin{array}{ccc}\hfill \overline{U}(t,z)& \le & \overline{U}(0,z\left(0\right))e^{-ct}\hfill \\ & \le & \left(ϵ{\lambda }_{max}{\left(\mathsf{\Phi }\right)\left|z\left(0\right)\right|}^2+\frac{\varsigma e^{\sigma }}{1-\rho }\left|\mathsf{\Phi }\right|\overline{\nu }\left(\kappa \right)\sum _{l=1}^n{\int }_{-\sigma }^0{e}^s{z}_l^2\left(s\right)ds\right)e^{-ct}\hfill \\ & \le & \left(ϵ{\lambda }_{max}{\left(\mathsf{\Phi }\right)\left|z\left(0\right)\right|}^2+\frac{\varsigma e^{\sigma }}{1-\rho }\left|\mathsf{\Phi }\right|\overline{\nu }\left(\kappa \right){\parallel z\parallel }^2{\int }_{-\sigma }^0{e}^{s}ds\right)e^{-ct}\hfill \\ & \le & \left(ϵ{\lambda }_{max}\left(\mathsf{\Phi }\right)+\frac{\varsigma e^{\sigma }}{1-\rho }\left|\mathsf{\Phi }\right|\overline{\nu }\left(\kappa \right)\right){\parallel z\parallel }^2{e}^{-ct}.\hfill \end{array}$$

(18)

Furthermore, applying (5), (18) and $\overline{U}(t,z)\ge ϵ{\lambda }_{min}\left(\mathsf{\Phi }\right){\left|z\right|}^2$, one leads to

$$\begin{array}{ccc}\hfill |x|& \le & |{\mathsf{\Xi }}^{-1}\left(\kappa \right)\Vert z|\le |{\mathsf{\Xi }}^{-1}\left(\kappa \right)|{\left(\frac{\overline{U}(t,z)}{ϵ{\lambda }_{min}\left(\mathsf{\Phi }\right)}\right)}^{\frac{1}{2}}\hfill \\ & \le & |{\mathsf{\Xi }}^{-1}\left(\kappa \right)|{\left(\frac{ϵ{\lambda }_{max}\left(\mathsf{\Phi }\right)(1-\rho )+\varsigma e^{\sigma }\left|\mathsf{\Phi }\right|\overline{\nu }\left(\kappa \right)}{ϵ{\lambda }_{min}\left(\mathsf{\Phi }\right)(1-\rho )}\right)}^{\frac{1}{2}}\parallel z\parallel e^{-\frac{c}{2}t}\hfill \\ & \le & |\mathsf{\Xi }\left(\kappa \right)\Vert {\mathsf{\Xi }}^{-1}\left(\kappa \right)|{\left(\frac{ϵ{\lambda }_{max}\left(\mathsf{\Phi }\right)(1-\rho )+\varsigma e^{\sigma }\left|\mathsf{\Phi }\right|\overline{\nu }\left(\kappa \right)}{ϵ{\lambda }_{min}\left(\mathsf{\Phi }\right)(1-\rho )}\right)}^{\frac{1}{2}}\parallel \psi \parallel e^{-\frac{c}{2}t}.\hfill \end{array}$$

(19)

Therefore, according to the inequalities (2) and (19), Theorem 1 holds for $\lambda =\frac{c}{2}$ and $N=\left|\mathsf{\Xi }\left(\kappa \right)\right||{\mathsf{\Xi }}^{-1}\left(\kappa \right)|{\left(\frac{ϵ{\lambda }_{max}\left(\mathsf{\Phi }\right)(1-\rho )+\varsigma e^{\sigma }\left|\mathsf{\Phi }\right|\overline{\nu }\left(\kappa \right)}{ϵ{\lambda }_{min}\left(\mathsf{\Phi }\right)(1-\rho )}\right)}^{\frac{1}{2}}$. □

Remark 3.

It should be pointed out that the positive parameter κ satisfying condition (12) always exists because $\frac{1}{\kappa }$ tends to infinity and the remaining three terms are finite as κ tends to zero.

By selecting another Lyapunov–Krasovskii functional that is different from (13), we can draw another conclusion.

Theorem 2.

For system (1) with Assumption 1, if there exist positive constants κ and α such that

$$\begin{array}{c}\hfill \frac{1}{2\kappa }-2\sqrt{n}\left|\mathsf{\Phi }\right|\nu \left(\kappa \right)-\frac{ϵ}{\varsigma }n\left|\mathsf{\Phi }\right|\overline{\nu }\left(\kappa \right)>0,\end{array}$$

(20)

and

$$\begin{array}{c}\hfill \frac{ϵ}{2\kappa }(1-\rho )e^{-\alpha \sigma }-\varsigma \left|\mathsf{\Phi }\right|\overline{\nu }\left(\kappa \right)>0,\end{array}$$

(21)

then the exponential stabilization of the closed-loop system can also be achieved through the state feedback controller (6).

Proof. 

Considering another Lyapunov–Krasovskii functional

$$\begin{array}{c}\hfill \tilde{U}\left(z\right)=U\left(z\right)+\frac{ϵ}{2\kappa }\sum _{l=1}^n{\int }_{t-{\sigma }_{lt}}^t{e}^{-\alpha (t-s)}{z}_l^2\left(s\right)ds,\end{array}$$

(22)

from (11), one obtains

$$\begin{array}{ccc}\hfill \dot{\tilde{U}}\left(z\right)& \le & -\left(\frac{1}{2\kappa }-2\sqrt{n}\left|\mathsf{\Phi }\right|\nu \left(\kappa \right)-\frac{ϵ}{\varsigma }n\left|\mathsf{\Phi }\right|\overline{\nu }\left(\kappa \right)\right){ϵ\left|z\right|}^2+\varsigma \left|\mathsf{\Phi }\right|\overline{\nu }\left(\kappa \right)\sum _{l=1}^n{z}_{l,{\sigma }_{lt}}^2\hfill \\ & & -\frac{ϵ}{2\kappa }\sum _{l=1}^n(1-{\rho }_l)e^{-\alpha {\sigma }_{lt}}{z}_{l,{\sigma }_{lt}}^2-\frac{ϵ\alpha }{2\kappa }\sum _{l=1}^n{\int }_{t-{\sigma }_{lt}}^t{e}^{-\alpha (t-s)}{z}_l^2\left(s\right)ds\hfill \\ & \le & -\left(\frac{1}{2\kappa }-2\sqrt{n}\left|\mathsf{\Phi }\right|\nu \left(\kappa \right)-\frac{ϵ}{\varsigma }n\left|\mathsf{\Phi }\right|\overline{\nu }\left(\kappa \right)\right)ϵ{\left|z\right|}^2-\frac{ϵ\alpha }{2\kappa }\sum _{l=1}^n{\int }_{t-{\sigma }_{lt}}^t{e}^{-\alpha (t-s)}{z}_l^2\left(s\right)ds\hfill \\ & & -\left(\frac{ϵ}{2\kappa }(1-\rho )e^{-\alpha \sigma }-\varsigma \left|\mathsf{\Phi }\right|\overline{\nu }\left(\kappa \right)\right)\sum _{l=1}^n{z}_{l,{\sigma }_{lt}}^2.\hfill \end{array}$$

(23)

Based on (20), (21) and the denseness of real numbers, (23) is changed into

$$\begin{array}{ccc}\hfill \dot{\tilde{U}}\left(z\right)& \le & -{\tilde{c}}_1ϵ{\left|z\right|}^2-\frac{ϵ\alpha }{2\kappa }\sum _{l=1}^n{\int }_{t-{\sigma }_{lt}}^t{e}^{-\alpha (t-s)}{z}_l^2\left(s\right)ds\hfill \\ & \le & -\frac{{\tilde{c}}_1}{{\lambda }_{max}\left(\mathsf{\Phi }\right)}U\left(z\right)-\frac{ϵ\alpha }{2\kappa }\sum _{l=1}^n{\int }_{t-{\sigma }_{lt}}^t{e}^{-\alpha (t-s)}{z}_l^2\left(s\right)ds\hfill \\ & \le & -\tilde{c}\tilde{U}\left(z\right),\hfill \end{array}$$

(24)

where $\tilde{c}=min\left\{\frac{{\tilde{c}}_1}{{\lambda }_{max}\left(\mathsf{\Phi }\right)},\alpha \right\}$, and ${\tilde{c}}_1$ is a positive constant.

It is easy to deduce from (22) and (24) that

$$\begin{array}{ccc}\hfill {\left|z\right|}^2& \le & \frac{1}{ϵ{\lambda }_{min}\left(\mathsf{\Phi }\right)}\tilde{U}\left(z\right)\le \frac{1}{ϵ{\lambda }_{min}\left(\mathsf{\Phi }\right)}\tilde{U}\left(z\left(0\right)\right)e^{-\tilde{c}t}\hfill \\ & \le & \frac{1}{{\lambda }_{min}\left(\mathsf{\Phi }\right)}\left({\lambda }_{max}\left(\mathsf{\Phi }\right){\left|z\left(0\right)\right|}^2+\frac{1}{2\kappa }\sum _{l=1}^n{\int }_{-\sigma }^0{e}^{\alpha s}{z}_l^2\left(s\right)ds\right)e^{-\tilde{c}t}\hfill \\ & \le & \frac{1}{{\lambda }_{min}\left(\mathsf{\Phi }\right)}\left({\lambda }_{max}{\left(\mathsf{\Phi }\right)\left|z\left(0\right)\right|}^2+\frac{1}{2\kappa \alpha }{\parallel z\parallel }^2\right)e^{-\tilde{c}t}\hfill \\ & \le & \frac{2\kappa \alpha {\lambda }_{max}\left(\mathsf{\Phi }\right)+1}{2\kappa \alpha {\lambda }_{min}\left(\mathsf{\Phi }\right)}{\parallel z\parallel }^2{e}^{-\tilde{c}t}.\hfill \end{array}$$

(25)

By virtue of (5), we further have

$$\begin{array}{c}\hfill \left|x\right|\le |\mathsf{\Xi }\left(\kappa \right)\Vert {\mathsf{\Xi }}^{-1}\left(\kappa \right)|{\left(\frac{2\kappa \alpha {\lambda }_{max}\left(\mathsf{\Phi }\right)+1}{2\kappa \alpha {\lambda }_{min}\left(\mathsf{\Phi }\right)}\right)}^{\frac{1}{2}}\parallel \psi \parallel e^{-\frac{\tilde{c}}{2}t}.\end{array}$$

(26)

Hence, Theorem 2 is satisfied with $N=\left|\mathsf{\Xi }\left(\kappa \right)\right||{\mathsf{\Xi }}^{-1}\left(\kappa \right)|{\left(\frac{2\kappa \alpha {\lambda }_{max}\left(\mathsf{\Phi }\right)+1}{2\kappa \alpha {\lambda }_{min}\left(\mathsf{\Phi }\right)}\right)}^{\frac{1}{2}}$ and $\lambda =\frac{\tilde{c}}{2}$. □

Remark 4.

In this paper, the exponential stabilization problem for a class of strict-feedback nonlinear system (1) with multiple time-varying delays is investigated. By considering the Lyapunov–Krasovskii functional with exponential function (13) or (22), the exponential stability of the closed-loop systems can be proven.

On the basis of Theorem 2, it is possible to further deduce the following property on the exponential stabilization of system (1), which is summarized in Corollary 1.

Corollary 1.

For system (1) with Assumption 1, if there exists $0<\kappa <\overline{\kappa }$ such that condition (20) is satisfied, by selecting

$$\begin{array}{c}\hfill 0<\alpha <\frac{1}{\sigma }ln\left(\frac{(1-\rho )ϵ}{2\varsigma \left|\mathsf{\Phi }\right|\kappa \overline{\nu }\left(\kappa \right)}\right),\end{array}$$

(27)

then the closed-loop system is exponentially stable by adopting the state feedback controller (6), where $\overline{\kappa }$ is a proper positive real number.

Proof. 

We know from Theorem 2 that the closed-loop system is exponentially stable if conditions (20) and (21) hold. Now, we can make condition (21) always true by suitably choosing the positive parameters $\alpha$ and $\kappa$ in the following way.

One can easily see that (21) is satisfied if and only if

$$\begin{array}{c}\hfill -\alpha \sigma >ln\left(\frac{2\varsigma \left|\mathsf{\Phi }\right|\kappa \overline{\nu }\left(\kappa \right)}{(1-\rho )ϵ}\right).\end{array}$$

Additionally, it is noted that $\kappa \overline{\nu }\left(\kappa \right)$ tends to zero as $\kappa$ tends to zero, which implies that there exists $0<\kappa <\overline{\kappa }$ such that

$$\begin{array}{c}\hfill 2\varsigma \left|\mathsf{\Phi }\right|\kappa \overline{\nu }\left(\kappa \right)<(1-\rho )ϵ.\end{array}$$

Therefore, we can take (27) such that condition (21) is always satisfied. □

Remark 5.

For Corollary 1, the positive parameter κ satisfying condition (20) can also be found. Since $\frac{1}{2\kappa }$ tends to infinity and the remaining two terms are finite in (20) as κ tends to zero, there always exists $0<\kappa <\tilde{\kappa }$ such that condition (20) holds. Hence, conditions (20) and (21) can be satisfied simultaneously by choosing $0<\kappa <min\{\overline{\kappa },\tilde{\kappa }\}$ and (27).

4. An Example

To demonstrate the effectiveness of the proposed design scheme, let us consider the two-stage chemical reactor with delayed recycle streams [23,24] shown in Figure 1, which contains two well-mixed isothermal continuous stirred tank reactors 1 and 2. The mass balance equations are

$$\begin{array}{ccc}\hfill {\dot{x}}_1& =& \frac{1-R_2}{V_1}{x}_2-\frac{x_1}{{\mu }_1}-{\gamma }_1{x}_1+{\delta }_1(x_1,x_{1,{\sigma }_{1t}}),\hfill \\ \hfill {\dot{x}}_2& =& \frac{F}{V_2}u-\frac{x_2}{{\mu }_2}-{\gamma }_2{x}_2+\frac{R_1}{V_2}{x}_{1,{\sigma }_{1t}}+\frac{R_2}{V_2}{x}_{2,{\sigma }_{2t}}+{\delta }_2({\overline{x}}_2,x_{1,{\sigma }_{1t}},x_{2,{\sigma }_{2t}}),\hfill \end{array}$$

(28)

where $x_1$ and $x_2$ are the compositions, $V_1$ and $V_2$ are the reactor volumes, F is the feed rate, $R_1$ and $R_2$ are the recycle flow rates, ${\mu }_1$ and ${\mu }_2$ are the reactor residence times, ${\gamma }_1$ and ${\gamma }_2$ are the reaction constants, ${\delta }_1(·)$ and ${\delta }_2(·)$ represent the uncertainties or disturbances and ${\sigma }_{1t}$ and ${\sigma }_{2t}$ are the time-varying delays.

Figure 1. Two-stage chemical reactor with delayed recycle streams.

Taking $V_1=0.6{\mathrm{m}}^3$, $R_1=0.2{\mathrm{m}}^3/\mathrm{s}$, ${\mu }_1=2\mathrm{s}$, ${\gamma }_1=0.2{\mathrm{s}}^{-1}$, ${\delta }_1(·)=0.5x_1+0.12sin{x}_{1,{\sigma }_{1t}}$, ${\sigma }_{1t}=0.15(1+cost)$, $V_2=0.8{\mathrm{m}}^3$, $R_2=0.4{\mathrm{m}}^3/\mathrm{s}$, ${\mu }_2=4\mathrm{s}$, ${\gamma }_2=0.1{\mathrm{s}}^{-1}$, ${\delta }_2(·)=0.1sin{x}_1+0.2x_2-0.1x_{1,{\sigma }_{1t}}-0.4x_{2,{\sigma }_{2t}}$, ${\sigma }_{2t}=0.1(1-sint)$ and $F=0.8{\mathrm{m}}^3/\mathrm{s}$, system (28) is transformed into

$$\begin{array}{ccc}\hfill {\dot{x}}_1& =& x_2-0.2x_1+0.12sin{x}_{1,{\sigma }_{1t}},\hfill \\ \hfill {\dot{x}}_2& =& u+0.1sin{x}_1-0.15x_2+0.15x_{1,{\sigma }_{1t}}+0.1x_{2,{\sigma }_{2t}}.\hfill \end{array}$$

(29)

It is clear that Assumption 1 is satisfied by ${\beta }_{11}=0.2$, ${\overline{\beta }}_{11}=0.12$, ${\beta }_{21}={\overline{\beta }}_{22}=0.1$, ${\beta }_{22}={\overline{\beta }}_{21}=0.15$. Choosing $\overline{\Delta }=[-2,-1]$, $A+B\overline{\Delta }$ is thus Hurwitz. From which, we further obtain the positive definite symmetric matrix $\mathsf{\Phi }=\left[\begin{array}{cc}1.75& 0.25\\ 0.25& 0.75\end{array}\right]$. By constructing the state feedback controller

$$\begin{array}{c}\hfill u=-\frac{2}{{\kappa }^2}{x}_1-\frac{1}{\kappa }{x}_2,\end{array}$$

(30)

and taking $ϵ=\varsigma =1$, $\sigma =0.3$, $\beta =0.2$, $\overline{\beta }=0.15$, $\rho =0.15$, $c_1=0.5$, it is easy to deduce from (12) of Theorem 1 that

$$\begin{array}{c}\hfill \frac{1}{\kappa }-2.4968-1.9968\kappa >0.\end{array}$$

(31)

Figure 2 shows the change curve of $y=\frac{1}{\kappa }-2.4968-1.9968\kappa$, $\kappa \in (0,0.5]$. Therefore, we can take $0<\kappa <0.3191$ such that (31) holds.

Figure 2. The curve of $y=\frac{1}{\kappa }-2.4968-1.9968\kappa$.

In the simulation, selecting the initial data $x_1\left(0\right)=1$ and $x_2\left(0\right)=-1.5$, Figure 3, Figure 4 and Figure 5, respectively, provide the responses of the closed-loop system (29) and (30) with different parameter values $\kappa =0.1,0.2,0.3$.

Figure 3. The trajectories of system state $x_1$.

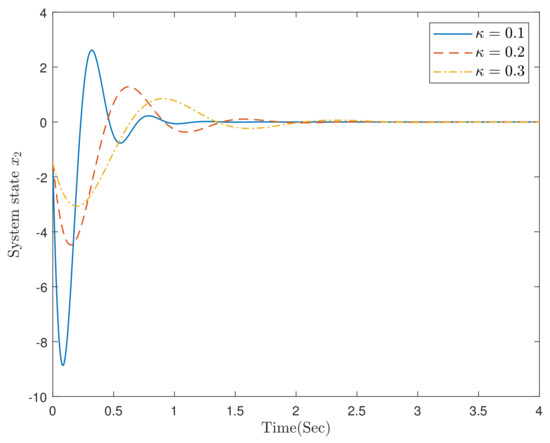
Figure 4. The trajectories of system state $x_2$.

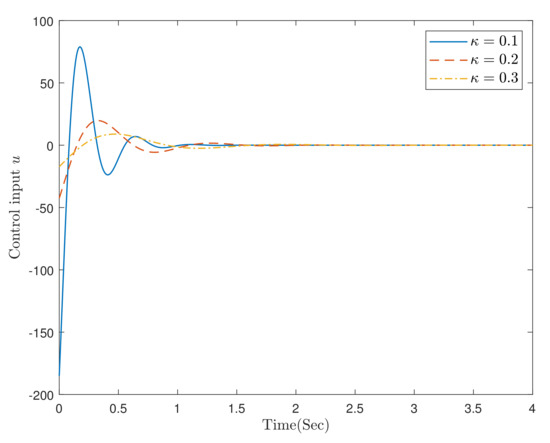
Figure 5. The trajectories of control input u.

Remark 6.

For system (29), applying (20) and (21) of Theorem 2 and choosing ${\tilde{c}}_1=0.25$ leads to

$$\begin{array}{ccc}& & \frac{1}{2\kappa }-1.8159-1.5659\kappa >0,\hfill \end{array}$$

(32)

$$\begin{array}{ccc}& & 0.85e^{-0.3\alpha }-0.5427\kappa (1+\kappa )>0.\hfill \end{array}$$

(33)

Figure 6 gives the change curves of $y_1=\frac{1}{2\kappa }-1.8159-1.5659\kappa$, $\kappa \in (0,0.4]$, $y_2=0.85e^{-0.3\alpha }$, $\alpha \in [0,1.4]$ and $y_3=0.5427\kappa (1+\kappa )$, $\kappa \in [0,1.4]$. From Figure 6, we can select $0<\kappa <0.2298$ and $0<\alpha <0.7283$ such that (32) and (33) are satisfied simultaneously.

Figure 6. The curves of $y_1$, $y_2$ and $y_3$.

5. Conclusions

This paper solves the exponential stabilization problem for a class of strict-feedback nonlinear systems (1) with multiple time-varying delays. By introducing two different Lyapunov–Krasovskii functionals (13) and (22) with an exponential function, two different proof approaches are provided to verify that the presented state feedback controller can guarantee that the closed-loop system is exponentially stable. The simulation results demonstrate the effectiveness of the proposed control method.

There exist some interesting problems to be further investigated. One is to study the finite-time control problem of system (1) as discussed in [25,26]. Another is to consider the fault-tolerant control in Zhang et al. [27] or fault detection control in Jiang and Zhao [28] of system (1).