Research on Profit Distribution of Logistics Alliance Considering Communication Structure and Task Completion Quality

Abstract

A reasonable profit distribution mechanism is the foundation for the formation and stability of the logistics alliance. On the basis of traditional influencing factors such as marginal contribution, resource input efficiency and risk-taking, the influence of communication structure restrictions and task completion quality on the profit distribution of logistics alliance was further considered in this paper. Then, a two-stage profit distribution model for logistics alliance with two types of communication structures was constructed. According to this model, the initial distribution uses the vertical projection method weighting each influencing factor to form the distribution scheme of modified Shapley value and Average Tree solution; the secondary distribution further modifies the initial distribution scheme based on the fuzzy comprehensive evaluation of the logistics task completion quality, and forms the final distribution scheme. The example analysis shows that the profit distribution model established in this paper is more fair and feasible, which can effectively avoid the “hitchhiking” phenomenon, and can motivate members to work hard to complete the logistics task. In addition, the model can provide a method for the distribution of benefits for alliances with limited communication structures.

1. Introduction

Alliance is a common organizational operation form in the logistics industry. In reality, cold chain logistics companies, transportation companies, landing distribution companies, warehousing companies and other logistics companies with different main businesses often form alliances around a specific logistics task to jointly provide logistics services. On the one hand, the logistics industry is a typical industry with a high entry threshold, and the high investment and high risks that a single enterprise cannot afford can be shared in the form of alliances. On the other hand, alliances have significant advantages in reducing transaction costs, better meeting consumer demands, and achieving economies of scale. With the intensification of market competition, the importance of logistics alliance is increasingly more prominent, but it must also be seen that it faces the threat of instability. The logistics enterprises in the alliance are only temporary cooperative relationships formed to obtain excess returns. Looking at each logistics enterprise alone, it is still an independent rational economic entity, and still aims to maximize its own interests. Therefore, when the information is asymmetric, various logistics enterprises of the alliance will be lazy, hitchhiking, and breaking contracts, which will affect the stability and efficiency of the alliance. To sum up, how to reasonably and fairly distribute alliance revenue has become a key issue of coordinating the relationship between logistics enterprises, ensuring the stability of the alliance, and giving full play to the advantages of the alliance.

In response to this problem, the Shapley value method is currently recognized as the basic model of alliance profit distribution. This model distributes profits based on the marginal contribution of each alliance member, embodying the principle of more pay for more work, and effectively avoiding equal division [1]. Some subsequent scholars believe that the profit distribution of logistics alliance should also consider the influence of multiple factors such as risk-taking [2] and resource input [3], and in the determination of the weight of each influencing factor, it should be compared with the analytic hierarchy process (AHP) weighting method [4], the interval analytic hierarchy process (IAHP) weighting method [5], the technique for order preference by similarity to an ideal solution (TOPSIS) weighting method [6], and other methods to establish a modified Shapley value profit distribution model. However, these existing profit distribution models are all based on the assumption that members can form alliances freely, and cannot be applied to the profit distribution of logistics alliance with communication structure restrictions. In fact, constrained by business connections, special resources and technologies, and even political factors, not all logistics enterprises can freely form alliances, and the alliance structure is often restrictive. For example, the logistics alliance formed centered on the logistics enterprises with a regional pass, the logistics alliance formed around the logistics enterprises with cold chain equipment, and the leader-type logistics alliance initiated by a logistics enterprise with sufficient customers; in these alliances, members do not communicate and cooperate directly, but only cooperate with alliance-led enterprises which have special resources. Therefore, it is urgent to study how to design a profit distribution model to make the alliance revenue tilt towards the core of the alliance and the leading enterprises with strong comprehensive strength and great discourse power. In addition, as a derivative service, the completion quality of logistics tasks directly affects the revenue of logistics alliance. Therefore, how to motivate alliance members to improve logistics service quality through profit distribution is also a problem that needs to be explored in depth.

In view of this, this paper intends to continue to consider the factors of communication structure and task completion quality on the basis of the existing profit distribution model, and use the vertical projection method to determine the weight of each influencing factor, and then construct a two-stage profit distribution model based on modified Shapley value and Average Tree Solution (A-T solution), in order to provide a fair and reasonable profit distribution method guidance for logistics alliance.

2. Literature Review

Theoretically, the problem of profit distribution of logistics alliance can be abstracted into the cooperation game solution problem of a multi-player cooperative game. Scholars gave different solutions from different perspectives, such as the Shapley value method [1], the minimum cost-remaining savings (MCRS) method [7], Nash equilibrium method [8], Raiffa solution method [9], and mathematical programming method [10]. Other scholars used the Shapley value method, the minimum core multi-objective programming method, the simplified MCRS method, and the Nash equilibrium method to solve the profit distribution problem in joint distribution, and compared and analyzed the advantages and disadvantages of each method [11]. Among them, the Shapley value method is the most widely used, which distributes profits based on the actual contribution of members to the alliance, and gives the specific distribution value calculation method, which has made a good attempt at fairness.

Based on the particularity of different logistics alliances, many subsequent studies improved the Shapley value method from three directions, and formed an increasingly reasonable profit distribution model. Firstly, as for the research of the influencing factors of logistics alliance profit distribution, Lin et al. additionally considered factors such as the risk, investment, and tasks of logistics enterprises, and combined the Shapley value method to build an optimized profit distribution model for logistics alliance. Yu et al. established a set of profit distribution correction factors including input cost value, risk allocation coefficient, industry leadership, market influence, and willingness to participate [12]. Li introduced the bargaining coefficient to modify the Shapley value method for profit distribution of agricultural product logistics cooperation [13]. Wang et al. designed the profit distribution scheme of the express enterprise alliance under the shared warehousing mode based on factors such as investment ratio, risk ratio, and innovation research contribution [14]. Guajardo et al. modified the Shapley value profit distribution model of the joint distribution alliance according to the delivery time factor [15]. Secondly, as for the optimization of the influencing factors weighting methods, through expert consultation, Yu et al. directly determined the weight coefficients of each revising factor [12]. Xu et al. used the AHP method to determine the weights of the influencing factors of the profit distribution of the joint distribution alliance. In order to avoid the unreliability of subjective weighting due to the influence of expert experience, Du adopted the IAHP method to determine the weight of the influencing factors of the profit distribution in the fourth party logistics cross-border e-commerce logistics alliance [5]; Lin et al. used the TOPSIS fixed weight function method to weight the impact indexes of relevant profit distribution [6]. Thirdly, as for the uncertainty of alliance revenue, with the deepening of research, some scholars found that the revenue of alliance or the contribution of members is not necessarily a certain value, which introduced the fuzzy theory to define the alliance revenue and then carry out the profit distribution. For example, Song assumed that the input and output data of each member enterprise of the reverse logistics alliance is a fuzzy number, and constructed an efficiency measurement model based on fuzzy data envelopment analysis to modify the Shapley value method [16].

It can be seen that the research results of the profit distribution of logistics alliance have been relatively abundant so far, but there some limitations still exist. Firstly, the existing research assumes that members can freely form alliances, and has not considered the communication structure restrictions of logistics alliance. At present, Herings et al. have used cycle-free graphs to represent different structures of alliances, and have given the A-T solution that applies to all graph games [17], but these studies have not been combined with other factors that affect the profit distribution of logistics alliance. Secondly, existing research is based on prior, one-time profit distribution, which seldom considers the dynamic nature of it. In fact, as a service, the quality of logistics task completion has a huge impact on the alliance revenue and efficiency. Therefore, the secondary distribution of alliance revenue should be based on the task completion quality to motivate member enterprises to improve the task effort level. Finally, the currently commonly used TOPSIS weighting method sorts the influencing factors of profit distribution according to the relative Euclidean distance. The results cannot fully reflect the advantages and disadvantages of each factor and need to be further optimized.

In summary, this paper intends to continue to consider the factors of communication structure and task completion quality to improve the Shapley value and the A-T solution model, and use the orthogonal projection method to weight the influencing factors of profit distribution, and finally give a reasonable and feasible profit distribution model of logistics alliance. The remainder of this study is organized as follows: Section 3 analyzes the influencing factors of logistics alliance profit distribution and gives the quantitative method of each influencing factor. Section 4 constructs a two-stage profit distribution model for logistics alliance with two types of communication structures. Section 5 verifies the rationality and feasibility of the logistics alliance profit distribution model designed in this paper through the example analysis. Section 6 summarizes the results and shortcomings of this study.

3. Analysis on Influencing Factors of Logistics Alliance Profit Distribution

Clarifying the influencing factors is the basis and premise of designing the profit distribution model of logistics alliance. According to the literature extraction method and rule analysis method, it is found that marginal contribution, resource input, and risk-taking are the most recognized and widely used elements of alliance profit distribution. On this basis, taking into account the fact that some logistics enterprises are unable to freely form alliances and the importance of service quality to the excess profit of the alliance, the key factors affecting the distribution of profits of logistics alliance are classified into five aspects: marginal contribution, alliance communication structure, resource input efficiency, risk-taking, and logistics task completion quality.

3.1. Marginal Contribution

The distribution of profits according to the contributions made by the members to the alliance conforms to the principle of more pay for more work. Only by linking the contribution level of the alliance members to the profit distribution can their enthusiasm for work and investment be better stimulated, which is recognized as an important factor affecting the profit distribution of alliance. At present, the distribution of profits based on marginal contribution is based on the Shapley value method and is improved in combination with other influencing factors.

3.2. Alliance Communication Structure

As shown in Figure 1, the structure of logistics alliance has various forms. Figure 1a is a fully connected logistics alliance, and all nodes are edge-connected, which represents equality between alliance members and free alliance cooperation between each other. Figure 1b is an alliance with communication structure restrictions (In addition to the star structure represented in Figure 1b, the structural form of the alliance with communication structure restrictions also has a tree structure, incompletely-connected structure, etc., which are not listed here.), and the nodes of Members 2, 3, and 4 are only edge-connected with Member 1, but are not edge-connected with each other, which means that member 1 has a prominent position in the alliance. Obviously, the profit distribution of logistics alliance under the limitation of communication structure must reflect the difference of member status, which can be solved by the A-T solution method.

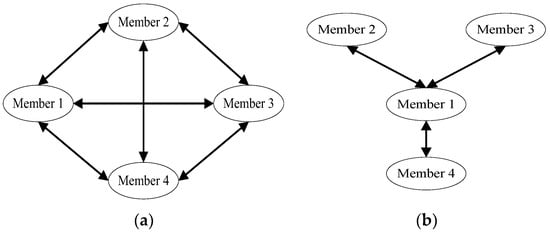
Figure 1. (a) Alliance without communication structure restrictions; (b) alliance with communication structure restrictions.

3.3. Resource Input Efficiency

The logistics industry is a typical resource-intensive industry, which requires a lot of labor, infrastructure, and capital investment. The main goal of logistics alliance is to gather and optimize the allocation of resources behind multiple logistics enterprises. However, due to different divisions of business, each logistics enterprise has different contributions of resource input to the alliance, and the distribution of profits should reflect this difference.

At the same time, in reality, the goals and contents of different logistics alliances are different, and the same investment of members plays different roles in different alliances. Therefore, the profit distribution based on resource input should also consider the scarcity of resources and whether they have made effective contributions to the alliance revenue, that is, whether a certain amount of resource input can obtain effective output in increasing the profit of the alliance, improving the overall service level and market competitiveness of the alliance. In a highly competitive market environment, invalid investment cannot correspond to high profit distribution. In view of this, this paper proposes to distribute profits through the resource input efficiency assessment of alliance members, so as to avoid the drawbacks of only focusing on input quantity and ignoring output quality. Specifically, the measurement of resource input efficiency will learn from the practice of He Xijun [18] and use the data envelopment analysis (DEA) method to analyze the ratio of multiple resource inputs to multiple outputs. The calculation model is:

$$\min \theta -\epsilon ({\displaystyle \sum _{k=1}^l{u}_k{}^{-}+{\displaystyle \sum _{r=1}^t{u}_r^{+}}})$$

(1)

$$\{\begin{array}{l}{\displaystyle \sum _{i=1}^n{r}_i{x}_{ki}+u_k^{-}-\theta x_{ki}=0}\\ {\displaystyle \sum _{i=1}^n{r}_i{y}_{ri}-u_r^{+}=y_{ri}}\\ r_i\ge 0,i=1,2,\dots ,n\\ u_k^{-}\ge 0,u_r^{+}\ge 0\end{array}$$

(2)

where $n$ is the number of logistics enterprises participating in the distribution of profits. The number of input indexes is $l$, and the number of output indexes is $t$, which represent different input resources and output effectiveness, respectively. $x_{ki}$ means the quantity of the $k^{th}$ resource entered by the $i^{th}$ logistics enterprise, $y_{ri}$ means the quantity of the $r^{th}$ output of the $i^{th}$ logistics enterprise, $u_k^{-}$, $u_r^{+}$ are slack variables, $\epsilon$ is the non-Archimedean infinitesimal, and $r_i$, $u_k^{-}$, $u_r^{+}$, $\theta$ are the parameters to be estimated. The value of $\theta$ is generally used as the measurement index of the input–output effect. When ${\theta }^{*}=1$ and $u_k^{-}=u_r^{+}=0$, the decision-making unit DEA is scale-effective and technical-effective. If ${\theta }^{*}<0$ or $u_k^{-}\ne 0$, $u_r^{+}\ne 0$, the decision-making unit DEA is ineffective; if $u_k^{-}=u_r^{+}=0$, it is technical-effective. When $E=1\left|{\theta }^{*}{\displaystyle \sum _{i=1}^n{r}^{*}=1}\right|$, it is scale-effective; when $E<1$, it is increasing returns-to-scale; otherwise, it decreases. The larger the value of $\theta$ of the logistics enterprises, the higher the efficiency of their resource input and the more profits that are distributed.

3.4. Risk-Taking

There are many potential risks in the operation of logistics alliance, such as member moral risk, logistics operation risk, market competition risk, and natural disaster risk. According to utility theory, members who take more risks in alliance activities will demand more compensation in the profit distribution. Thus, the paper uses the loss value brought by the risk to measure the risk of each logistics enterprise, that is, the risk $w$ is a function of the probability $P$ of risk events and the loss $C$ caused by risk events, $w=F(p,c)$.

In addition, since each logistics enterprise in the alliance undertakes risks with all the investment at most, the loss caused by risk events is $c_i={\alpha }_i{I}_i$, where ${\alpha }_i$ is the risk loss rate of logistics enterprise $i$, and $I_i$ is the logistics subtask input of $i$.

Therefore, it can be obtained that the risk undertaken by the logistics enterprise $i$ is $w_i=p_i{\alpha }_i{I}_i$, $i=\left\{0,1,2,\dots ,n\right\}$, and the proportion of the overall risk taking is $W_i=\frac{w_i}{{\displaystyle \sum _1^n{w}_i}}$.

3.5. Logistics Task Completion Quality

As a service industry, the completion quality of logistics tasks directly affects the logistics demand, which is the foundation of the existence of logistics alliance and represents its core competitiveness. Therefore, in order to form incentives for alliance members, the profit distribution of logistics alliance must be based on the quality inspection of logistics task completion. The measurement of logistics task completion quality is usually completed by constructing an evaluation index system, and the specific evaluation indexes include cargo damage and error rate, error processing, and logistics time. Finally, the logistics enterprises with higher evaluation scores get more profits in the alliance.

4. Design of a Two-Stage Profit Distribution Model for Logistics Alliance with Two Types of Communication Structures

As shown in Figure 2, firstly, considering the importance of logistics service quality, a two-stage profit distribution mechanism is designed. That is, before the logistics task starts (at the beginning of the establishment of the alliance), the initial distribution scheme is formulated based on the agreements of multiple logistics enterprises; after the task is completed, the initial distribution scheme is modified by adding the task completion quality evaluation of each logistics enterprise to obtain the final profit distribution scheme. Secondly, in the design of the initial distribution scheme, innovatively considering that the logistics alliance can be divided into two types according to whether the members can form an alliance arbitrarily, the Shapley value method and A-T method are used to design the profit distribution mechanism of the two types of alliance, and the factors such as resource input efficiency and risk-taking are added for improvement.

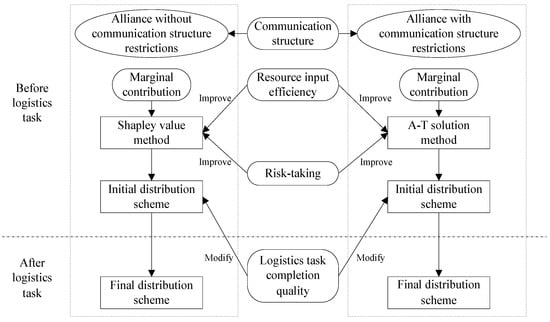
Figure 2. Two-stage profit distribution model for logistics alliance with two types of communication structures.

4.1. Initial Profit Distribution Model for Logistics Alliance Considering Communication Structures

4.1.1. Shapley Value Profit Distribution Model for Alliance without Communication Structure Restrictions

In the cooperative game $G(n,v)$, $\phi (v)=\left\{{\phi }_1(v),{\phi }_2(v),\dots ,{\phi }_n(v)\right\}$ is the classic Shapley allocation, where ${\phi }_i(v)$ means the profit distribution obtained by logistics enterprise $i$ under alliance $n$:

$${\phi }_i(v)={\displaystyle \sum _{i\in S\in n}\frac{(\left|S\right|-1)!(n-\left|S\right|)!}{n!}}(v(S)-v(S/i))$$

(3)

where $n$ is the number of all logistics enterprises, $\left|S\right|$ is the number of logistics enterprises participating in alliance $S$, and $\frac{(\left|S\right|-1)!(n-\left|S\right|)!}{n!}$ is the appearance probability of different alliances; $v(S)$ is the revenue of alliance $S$, $v(S/i)$ is the alliance revenue after logistics enterprise $i$ withdraws from the alliance $S$, and $v(S)-v(S/i)$ represents the revenue difference before and after the participation of logistics enterprise $i$ in alliance $S$, namely the contribution value of logistics enterprise $i$.

4.1.2. A-T Solution Profit Distribution Model for Alliance with Communication Structure Restrictions

Myerson et al. used graph theory, especially the knowledge of undirected connected graphs, to study cooperative game solutions with communication structures [19]. In graph game theory, only those who are directly or indirectly connected can be aligned, thus effectively depicting their restrictive communication relationship. At the same time, Myerson proposed the Myerson value solution, the single-valued solution of the graph game, and demonstrated the branch validity, fairness, and selectivity of the solution. Hering then defined the A-T solution [17] for the cycle-free graph games and extended it to all alliance profit distribution problems with communication structure. The principle of the basic A-T solution is as follows:

The logistics alliance with communication structure restrictions can be represented by triple $(N,v,L)$, $N$ and $v$ are still the set and payoff function of logistics enterprises, and $L\subseteq \left\{\left\{i,j\right\}|i\ne j,i,j\in N\right\}$ is the communication edge set of all logistics enterprises. When $L=\left\{\left\{i,j\right\}|i\ne j,i,j\in N\right\}$, the alliance has a complete communication structure. It is also assumed that the set of mutually cooperative logistics enterprises is $S\in P(N)$ ($P(N)$ is the power set of $N$); at this time, $v(S)$ means the total revenue obtained by the set $S$, and $(S,L(S))$ is the subgraph of the graph $(N,L)$, where $L(S)=\left\{\left\{i,j\right\}\in L|i,j\in S\right\}$. If $S$ cannot form a larger alliance by combining with other logistics enterprises $j\in N\backslash S$, then $S$ is called a connected branch, and all connected branches form a set $C^{L(S)}(S)$.

In a directed graph $(N,D)$, if the directed edge set $D\subseteq \left\{(i,j)\in N\times N|i\ne j\right\}$ satisfies $(i_h,i_{h+1})\in D,\forall h\in \left\{0,1,\dots ,k-1\right\}$, the sequence $(i_1,\dots ,i_k)$ composed of different nodes is called a directed path from node $i_1$ to $i_k$. For a directed graph $(N,T)$, if $T$ is the edge set composed of $n$ directed edges, and the node $i\in N$ has a unique directed path to each node in $N\backslash \left\{i\right\}$, then the graph is called a tree, and $i$ is called a root. Let $(N,L)$ be an undirected graph, and the tree $(N,T)$ is the spanning tree of $(N,L)$, if $(i,j)\in T\Rightarrow (i,j)\in L$, that is, any directed edge in $T$ is an undirected edge in $L$.

Therefore, in the graph game $(N,v,L)$, a sequence $(i_1,\dots ,i_k)$ is composed of different nodes $i_1,\dots ,i_k$, where $k\ge 1$. If it satisfies: $i_k=i_1$; $(i_h,i_{h+1})\in L$, $h=0,1,\dots ,k-1$; $i_1,\dots ,i_k$ are nodes that are different from each other, then $(i_1,\dots ,i_k)$ forms a circle. The graph game without any cycles is called a cycle-free graph game.

In Figure $(N,L)$, the n-tuple $B=(B_1,B_2,\dots ,B_n)$ composed of the subset of set $N$ is called an admissible n-tuple if the following two conditions are satisfied, and all admissible n-tuples constitute the set $B^L$. Condition 1: For all $i\in N$, there is $i\in B_i$, and there exists $j\in N$, such that $B_j=N$. Condition 2: For all $i\in N$ and $S\in C^L(B_i\backslash \left\{i\right\})$, there is $j\in N$, when $\left\{i,j\right\}\in L$, $S=B_j$.

To sum up, the profit distribution of each logistics enterprise in the alliance is determined by the traditional A-T solution method as follows:

$$A{T}_i(N,v,L)=\frac{1}{\left|B^L\right|}{\displaystyle \sum _{B\in B^L}(v(B_i)-{\displaystyle \underset{K\in \stackrel{\wedge }{C^L}(B_i\backslash \left\{i\right\}))}{\sum v(K)}}}$$

(4)

where $B^L$ is the set of all possible alliances, $\left|B^L\right|$ is the number of elements in $B^L$, $i\in N$, and $\frac{1}{\left|B_L\right|}$ is equivalent to weighting factors. $v(B_i)$ is the revenue of the subset $B_i$ of all logistics enterprises, and ${\displaystyle \underset{K\in \stackrel{\wedge }{C^L}(B_i\backslash \left\{i\right\})}{\sum v(K)}}$ is the profit of the alliance after subset $B_i$ removes logistics enterprise $i$. Then, $v(B_i)-{\displaystyle \underset{K\in \stackrel{\wedge }{C^L}(B_i\backslash \left\{i\right\})}{\sum v(K)}}$ represents the marginal contribution of logistics enterprise $i$.

It can be seen from the above principles that the A-T solution is mainly based on the Shapley value solution, and introduces concepts such as connected branch sets, tree diagram, cycle-free graph game, and admissible tuples to describe the relationship of alliance members with communication structure restrictions, and then screen out feasible sub-alliances for profit distribution. When the alliance has a complete communication structure, the A-T solution is the same as the corresponding Shapley value solution. Therefore, the A-T solution only further considers the difference in the importance of alliance members on the basis of the Shapley value solution method, changing the assumption that the status of alliance members is the same, and the combination of each subset of the alliance set is random, so as to distribute the profits with communication structure restrictions. Thhe profit distribution scheme $\left\{A{T}_1(N,v,L),A{T}_2(N,v,L),\dots ,A{T}_n(N,v,L)\right\}$ should also meet the requirements of overall rationality, alliance rationality, and individual rationality.

4.1.3. Improved Shapley Value Solution and Improved A-T Solution Profit Distribution Model Based on a Vertical Projection Method

The Shapley value solution and the A-T solution assume that the resources invested in forming the alliance, the degree of effort to complete the alliance task, and the risk taken by each alliance’ member are equal, which is difficult for reflecting the actual situation. Therefore, it is necessary to improve the Shapely value solution and the A-T solution combined with relevant influencing factors. The key problem of improvement is to determine the weight of each influencing factor. A reasonable weight value can compromise the results of profit distribution under different influencing factors to obtain a comprehensive and fair profit distribution scheme. At present, the TOPSIS fixed weight function method is mainly used for the weighting of influencing factors, but this method sorts the schemes according to the relative Euclidean distance, and the results cannot fully reflect the advantages and disadvantages of each scheme. The orthogonal projection method is a new method obtained by optimizing and improving the TOPSIS method. This method replaces the Euclidean distance with the vertical distance, which can more accurately reflect the satisfaction of the alliance members to different distribution results. Based on the orthogonal projection method, this paper weights different influencing factors of profit distribution, so as to determine the coordinated alliance profit distribution scheme under the comprehensive factors. The specific steps are as follows:

Step 1: Establish a decision matrix. Suppose that there are $n$ members in the logistics alliance, there are $m$ kinds of profit distribution schemes, and the distribution result of the $i^{th}$ profit distribution scheme to alliance member $j$ is $x_{ij}$; then, the decision matrix is expressed as:

$$X=\left(\begin{array}{l}\begin{array}{ccc}{x}_{11}& \dots & x_{1n}\end{array}\\ \begin{array}{ccc}{x}_{21}& \dots & x_{2n}\end{array}\\ \begin{array}{ccc}\dots & \dots & \dots \end{array}\\ \begin{array}{ccc}{x}_{m1}& \dots & x_{mn}\end{array}\end{array}\right)$$

Step 2: Standardize the decision matrix. In order to eliminate the influence of different dimensions of each index on the calculation, the data in the decision matrix are normalized to construct the standard decision matrix $Y={\left(y_{ij}\right)}_{m\times n}$.

Step 3: Construct a weighted decision matrix. Assume the weight vectors of each profit distribution scheme $w=(w_1,w_2,\dots ,w_m)$, ${\displaystyle \sum _{i=1}^m{w}_i=1}$; multiply the standardized decision matrix with each weight to construct the weighted decision matrix $R={\left(r_{ij}\right)}_{m\times n}$, $r_{ij}=y_{ij}\times w_i$.

Step 4: Determine the ideal solution.

The positive ideal solution:

$$S^{+}=\left\{S^{+}|S_j^{+}=\underset{1\le i\le m}{\max }(r_{ij}),j=1,2,\dots ,n\right\}$$

(5)

The negative ideal solution:

$$S^{-}=\left\{S^{-}|S_j^{-}=\underset{1\le i\le m}{\max }(r_{ij}),j=1,2,\dots ,n\right\}$$

(6)

Step 5: Calculate the weight $w_i$. Translate the coordinate origin to the positive ideal solution point and simplify the calculation. The shifted decision matrix becomes $T={\left(t_{ij}\right)}_{m\times h}$, where $t_{ij}=r_{ij}-S_j^{+}$. After the translation, the positive ideal solution becomes $\left\{0,0,\dots ,0\right\}$, and the negative ideal solution becomes $Q^{-}$, $Q^{-}=\left\{q_j^{-}|j=1,2,\dots ,n\right\}$, where $Q^{-}=t_{kj}$ satisfies $\left|t_{kj}\right|\ge \left|t_{ij}\right|,(k=1,2,\dots ,m)$. Assume $p_i=(a-b)•(a-T_i)={\displaystyle \sum _{j=1}^h{t}_{ij}{q}_j^{-}}$, where $p_i$ represents the relative dissatisfaction of alliance member $j$ with the $i^{th}$ profit distribution method. Then, the smaller $p_i$ is, the higher the satisfaction of the alliance member with the $i^{th}$ profit distribution scheme is. Thus, the optimization model can be constructed as follows:

$$\min z={\displaystyle \sum _{i=1}^m{\displaystyle \sum _{j=1}^n{t}_{ij}\times q_j^{-}}}$$

(7)

$$s.t.\{\begin{array}{l}{\displaystyle \sum _{i=1}^m{w}_i=1}\\ 0\le w_i\le 1,i=1,2,\dots ,m\end{array}$$

(8)

where Equation (7) is the objective function, indicating that the scheme closer to the positive ideal solution is better; Equation (8) is the constraint condition, that is, the sum of the weight coefficients of various distribution schemes is 1.

Step 6: Determine the initial profit distribution scheme. The initial profit distribution amount can be obtained by the addition of the products of the weights of different distribution schemes of each logistics enterprise and the corresponding profit distribution amount. The initial profit distribution scheme can be expressed as:

$${\psi }_j={\displaystyle \sum _{i=1}^m(x_{ij}•w_i)}$$

(9)

In Equation (9), ${\psi }_j$ presents the initial distribution amount obtained by the $j^{th}$ logistics enterprise of the alliance.

4.2. Design of Final Profit Distribution Model of Logistics Alliance Considering Task Completion Quality

There are relatively mature research results on the evaluation index system of logistics task completion quality. For example, Parasuraman et al. established the service quality (SERVQUAL) model based on the theory of total quality management in the 1980s [20]; in 1999, Mentzer et al. put forward the logistics service quality (LSQ) model based on the SERVQUAL model in combination with result orientation, including ordering procedures, personnel contact quality, information quality, order accuracy, order condition, and other indexes [21]; in 2009, China also proposed the Chinese national standard GB/T24359-2009 “Quality Requirements for Third-Party Logistics Services”, including indexes such as order on-time completion rate, order processing accuracy rate, cargo damage rate, and cargo error rate [22]. Considering the practicability and simplicity of the evaluation index selection and the recognition of various types of logistics enterprises, on the basis of previous studies, indexes are selected to evaluate the task completion quality of logistics enterprises from the dimensions of efficiency and accuracy of logistics task completion, as well as customer satisfaction. The overall evaluation index system of the logistics task completion quality is shown in Figure 3.

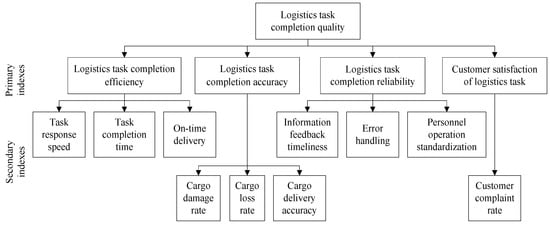
Figure 3. The evaluation index system of logistics task completion quality.

First, the efficiency of logistics task completion can be measured by indicators of task response speed, task completion time, and on-time delivery. The task response speed reflects the time it takes for the logistics company to receive the logistics task and reply to the customer. The task completion time is the time it takes for the logistics company to complete the entire logistics task. The on-time delivery refers to whether the logistics company delivers the goods at the time agreed with the customer in advance. Second, the accuracy of logistics task completion can be measured by indicators of cargo damage rate, cargo loss rate, and cargo delivery accuracy. The cargo damage and loss rate refer to the proportion of goods damaged and lost due to improper operation of logistics enterprises in the logistics process. The cargo delivery accuracy refers to the ability of logistics enterprises to deliver the correct quantity and quality of goods to the correct consignee. Third, the reliability of logistics task completion can be measured by indicators of information feedback timeliness, error handling and personnel operation standardization. The timeliness of information feedback refers to the speed at which the logistics enterprise shares the logistics task process information to the logistics demander. The error handling is mainly used to evaluate the ability of the logistics enterprise to solve problems. The standardization of personnel operations refers to whether the employees of the logistics enterprise complete the work according to the established standards. Fourth, the customer satisfaction of logistics tasks can be measured by the indicator of the customer complaint rate, that is, the proportion of customer complaints.

It can be seen from it that the two-stage distribution of alliance interests pays more attention to the performance level of logistics enterprises in completing logistics tasks, so as to motivate them to make efforts to shorten task completion time, reduce completion cost, improve customer satisfaction, etc., and ultimately ensure the improvement of the overall operation efficiency and efficiency of logistics alliance.

Considering the ambiguity in the evaluation criteria and evaluation process of indexes such as task response speed and error processing, the fuzzy comprehensive evaluation method is used to evaluate the task completion quality of logistics enterprises. This method has the characteristics of clear results and strong systematicity, which can better solve the fuzzy and difficult quantitative problems, and is suitable for the evaluation of various uncertain problems [23]. The main steps are as follows:

Step 1: Set up a comment set. Set the grade set $L=\left\{L_1,L_2,\dots ,L_m\right\}$ of the comprehensive evaluation of logistics subtask performance, where $L_m$ is the comment, indicating the evaluation level of each index, such as excellent, good, medium, poor, and the worst. The five-point scoring method is adopted, let $L_1=5$, which represents the best completion quality, $L_5=1$, which means the worst completion quality, and assign 5-1 points in turn.

Step 2: Establish a fuzzy comprehensive evaluation matrix. Set up an expert group including representatives of various logistics enterprises, and score on the basis of the comment set. Let the $j^{th}$ secondary index of the $i^{th}$ primary index have $b_{ij1}$ number of $L_1$ level comments, $b_{ij2}$ number of $L_2$ level comments, and $b_{ijm}$ number of $L_m$ level comments. Then, the membership degree of the logistics subtask to the comments at all levels is $b_{ijm}^{\prime }=\frac{b_{ijm}}{{\displaystyle \sum _1^m{b}_{ijm}}}$, and the evaluation fuzzy matrix of the four primary indexes, such as logistics task completion efficiency and logistics task completion accuracy, can be expressed as:

$$B_i=\left(\begin{array}{cccc}{b}_{i11}^{\prime }& b_{i12}^{\prime }& \cdots & b_{i1m}^{’}\\ b_{i21}^{’}& b_{i22}^{’}& \cdots & b_{i2m}^{’}\\ \dots & \dots & \dots & \dots \\ b_{ij1}^{’}& b_{ij2}^{’}& \cdots & b_{ijm}^{’}\end{array}\right), i=\left\{1,2,3,4\right\}$$

(10)

Step 3: Use the entropy weight method to determine the evaluation index weight. The calculation formula of entropy is $O_{ij}=-\frac{1}{\log m}{\displaystyle \sum _1^m{b}_{ijm}^{’}\times \log b_{ijm}^{’}}$, and the weights of the secondary index and the primary index are: $W_{ij}\raisebox{1ex}{$E_{ij}$}\!\left/ \!\raisebox{-1ex}{${\displaystyle \sum _{j=1}^n{E}_{ij}}$}\right.$, $W_i=\frac{{\displaystyle \sum _{j=1}^n{E}_{ij}}}{{\displaystyle \sum _{i=1}^m{\displaystyle \sum _{j=1}^n{E}_{ij}}}}$, $E_{ij}=1+\frac{1}{\log m}{\displaystyle \sum _1^m{b}_{ijm}^{’}\times \log b_{ijm}^{’}}$.

Step 4: Conduct fuzzy comprehensive evaluation. That is, use the fuzzy synthesis operator $M=(•,\otimes )$ to synthesize the primary index weight $W_i$ and the fuzzy evaluation matrix c, so as to generate the fuzzy evaluation result vector of logistics task completion quality: $V_i=W_i•B_i=(v_1,v_2,\dots ,v_m), i=\left\{1,2,3,4\right\}$.

Step 5: Calculate the comprehensive score of the task completion quality of the $k^{th}$ logistics enterprise in the alliance $P_k=V•L$.

Step 6: Determine the final profit distribution scheme. The proportion of the final logistics alliance revenue that the $k^{th}$ logistics enterprise can obtain when undertaking the logistics subtasks is: ${\pi }_k=\frac{{\psi }_k{P}_k}{{\displaystyle \sum _{k=0}^n{\psi }_k{P}_k}}$, where ${\psi }_k$ is the initial profit distribution amount; the final profit distribution amount is: ${\psi }_k^{’}={\pi }_k\times Z$, and $Z$ is the total revenue of the alliance.

5. Example Analysis

This section is an example of comparing the various models assuming three logistics enterprises with different main businesses in an established logistics alliance for a certain logistics task. Assumptions include:

-

The revenue of the logistics enterprise operating separately and in alliance can be obtained through accounting;

-

The excess revenue can be obtained under the alliance mode;

-

The input and output of each logistics enterprise for building the alliance can be reliably evaluated;

-

The evaluation results of each logistics enterprise on the logistics task completion quality are unanimous.

5.1. Profit Distribution Based on Marginal Contribution and Communication Structure

Considering that alliances under different logistics tasks can be divided into alliances with and without communication structure restrictions, the Shapley value method and the A-T solution method are used to distribute profits based on the marginal contribution of logistics enterprises.

5.1.1. Alliance Profit Distribution without Communication Structure Restrictions

The revenue parameter values of logistics enterprises under different cooperation situations are shown in Table 1.

Table 1. Revenue parameter values of logistics enterprises under different cooperation situations.

Cooperation Situations	$\left\{1\right\}$	$\left\{2\right\}$	$\left\{3\right\}$	$\left\{1,2\right\}$	$\left\{1,3\right\}$	$\left\{2,3\right\}$	$\left\{1,2,3\right\}$	$\phi$
Revenues	200	600	100	900	400	850	1500	0

As shown in Table 2, according to the Shapley value method, the profit distribution amount of logistics enterprise 1 is ${\phi }_1=383.3$; in the same way, the profit distribution amount of logistics enterprise 2 is ${\phi }_2=808.4$; the profit distribution amount of logistics enterprise 3 is ${\phi }_3=308.3$. Such distribution of profits satisfies that the sum of the three is equal to the total amount of profits achieved by the alliance operation, that is, it satisfies the cumulative nature; and the amount of profits obtained by the three logistics enterprises under the alliance is higher than that of independent operation and other alliance scales, which has certain rationality.

Table 2. Profit distribution of logistics enterprise 1 based on Shapley value method.

$S_1$	$\left\{1\right\}$	$\left\{1,2\right\}$	$\left\{1,3\right\}$	$\left\{1,2,3\right\}$
$v(s)$	200	900	400	1500
$v(s\backslash 1)$	0	600	100	850
$v(s)-v(s\backslash 1)$	200	300	300	650
$\left|s\right|$	1	2	2	3
$(\left|s\right|-1)!(n-\left|s\right|)!/n!$	1\3	1\6	1\6	1\3
$\frac{(\left|s\right|-1)!(n-\left|s\right|)!}{n!}(v(s)-v(s\backslash 1))$	66.7	50	50	216.7

5.1.2. Alliance Profit Distribution with Communication Structure Restrictions

Assuming that logistics enterprise 2 has decisive resources when completing a certain logistics task, logistics enterprises 1 and 3 cannot cooperate directly, and must form an alliance with enterprise 2 as the core. That is, alliance $\left\{1,3\right\}$ does not exist. Thus, $B^L=\left\{(\left\{1,2,3\right\},\left\{2,3\right\},\left\{3\right\}),(\left\{1\right\},\left\{1,2,3\right\},\left\{3\right\}),(\left\{1\right\},\left\{1,2\right\},\left\{1,2,3\right\})\right\}$, $\left|B^L\right|=3$.

$$A{T}_1(N,v,L)=\frac{1}{3}[(v(\left\{1,2,3\right\})-v(\left\{2,3\right\}))+(v(\left\{1\right\})-0)+(v(\left\{1\right\})-0)]=350$$

$$A{T}_2(N,v,L)=\frac{1}{3}[(v(\left\{1,2,3\right\})-v(\left\{1\right\}-v(\left\{3\right\})))+(v(\left\{1,2\right\})-v(\left\{1\right\}))+(v(\left\{2,3\right\})-v(\left\{3\right\}))]=883.3$$

$$A{T}_3(N,v,L)=\frac{1}{3}[(v(\left\{1,2,3\right\})-v(\left\{1,2\right\}))+(v(\left\{3\right\})-0)+(v(\left\{3\right\})-0)]=266.7$$

To sum up, according to the A-T solution, the profit distribution of logistics enterprise 1 is ${\phi }_1=350$; similarly, the profit distribution of logistics enterprise 2 is ${\phi }_2=883.3$; the profit distribution of logistics enterprise 3 is ${\phi }_3=266.7$. Such amount of profit distribution also satisfies the cumulative nature and is also greater than the revenue obtained by the three logistics enterprises operating separately. However, the profit distribution under the A-T solution is more inclined to logistics enterprise 2, that is, more inclined to the alliance-led enterprise, which reflects the importance of enterprise 2 and is more reasonable.

5.2. Profit Distribution Based on Resource Input Efficiency

It is assumed that each logistics enterprise inputs labor and equipment and facilities resources to complete the alliance task, and the output effect of resource input is characterized by the improvement of service ability and market competitiveness. Among them, the improvement of service capacity is mainly the increase in freight volume, and the improvement of market competitiveness is mainly the increase in the volume of logistics orders.

Table 3 sets the specific input–output data of each logistics enterprise, and imports it into DEAP software to calculate the input–output effectiveness of each logistics enterprise. The result $\theta$ is (0.679, 1, 0.8; 0.879, 1, 1). After normalization, the distribution ratio of logistics service providers is calculated, and the alliance revenue distribution is: ${\phi }_1=411$, ${\phi }_2=604.5$, ${\phi }_3=484.5$. Similarly, the distribution in the alliance with communication structure restrictions is: ${\phi }_1=458$, ${\phi }_2=521$, ${\phi }_3=521$. According to such a profit distribution method, the logistics enterprises with high input–output efficiency receive more profits, thus encouraging the logistics enterprises to improve the input effectiveness, thereby promoting the reduction of logistics task cost.

Table 3. Input–output data of each logistics enterprise.

	Labor Force/Person	Equipment and Facilities/Unit	Service Capability/%	Market Competitiveness/%
Alliance without communication structure restrictions	50	20	0.07	0.06
	80	25	0.15	0.13
	30	30	0.08	0.075
Alliance with communication structure restrictions	35	10	0.055	0.05
	75	20	0.13	0.12
	15	15	0.05	0.07

5.3. Profit Distribution Based on Risk-Taking

The input cost value of each logistics enterprise is obtained after asset evaluation, accounting and other financial processing of the resources invested by each logistics enterprise to complete the alliance task. In addition, the parameter values of risk probability and risk loss rate are set according to the specific situation of logistics enterprises undertaking logistics tasks. The details are shown in Table 4.

Table 4. Parameter values of risk-taking in logistics enterprises.

Alliance without Communication Structure Restrictions
Logistics Service Provider	Input Cost	Risk Probability	Risk Loss Rate
1	$I_1=50$	$p_1=0.3$	${\alpha }_1=55\%$
2	$I_2=100$	$p_2=0.4$	${\alpha }_2=65\%$
3	$I_3=80$	$p_3=0.15$	${\alpha }_3=60\%$
Alliance with Communication Structure Restrictions
Logistics Service Provider	Input Cost	Risk Probability	Risk Loss Rate
1	$I_1=20$	$p_1=0.1$	${\alpha }_1=25\%$
2	$I_2=80$	$p_2=0.4$	${\alpha }_2=60\%$
3	$I_3=30$	$p_3=0.35$	${\alpha }_3=70\%$

Thus, it can be obtained that the risk taken by logistics enterprise 1 in the alliance without communication structure restrictions is $w_1=p_1{\alpha }_1{I}_1=0.3\times 55\%\times 50=8.25$, and $\left\{w_1,w_2,w_3\right\}=\left\{8.25,26,7.2\right\}$ is obtained by similar calculation; the proportion of the overall risk-taking is $W_1=0.199$, and similarly, $W_2=0.627$, $W_3=0.174$. In this way, the alliance revenue distribution is: ${\phi }_1=298.5$, ${\phi }_2=940.5$, ${\phi }_3=261$. Similarly, the distribution in the alliance with communication structure restrictions is: ${\phi }_1=27$, ${\phi }_2=1065$, ${\phi }_3=408$. It can be seen that the profit distribution scheme can realize the risk compensation for logistics enterprises.

5.4. Initial Profit Distribution Scheme

The profit distribution schemes under different influencing factors are shown in Table 5. The orthogonal projection method is used to set the weight of each distribution scheme, and then the various distribution schemes are integrated to obtain the initial profit distribution scheme of the logistics alliance. Since alliances are divided into two types according to whether there are communication structure restrictions, there are also two types of profit distribution schemes. The following only takes alliances without communication structure restrictions as an example to illustrate the process of setting the weights of distribution schemes by the orthogonal projection method.

Table 5. Alliance profit distribution amount under different influencing factors.

Alliance without Communication Structure Restrictions
Logistics Enterprise	Marginal Contribution	Resource Input Efficiency	Risk-Taking
1	383.3	411	298.5
2	808.4	604.5	940.5
3	308.3	484.5	261
Alliance with Communication Structure Restrictions
Logistics Enterprise	Marginal Contribution	Resource Input Efficiency	Risk-Taking
1	350	458	27
2	883.3	521	1065
3	266.7	521	408

Step 1: According to Table 5, the decision matrix is $X=\left(\begin{array}{ccc}383.3& 808.4& 308.3\\ 411& 604.5& 484.5\\ 298.5& 940.5& 261\end{array}\right)$.

Step 2: Normalize the decision matrix according to formula $\frac{x_{ij}}{\sqrt{{\displaystyle \sum _{i=1}^m{x}_{ij}^2}}}$ to obtain the standardized decision matrix $Y=\left(\begin{array}{ccc}0.602& 0.586& 0.489\\ 0.646& 0.438& 0.768\\ 0.469& 0.682& 0.414\end{array}\right)$.

Step 3: Construct a weighted decision matrix $R=\left(\begin{array}{c}{w}_1\\ w_2\\ w_3\end{array}\right)•Y=\left(\begin{array}{ccc}0.602w_1& 0.586w_2& 0.489w_3\\ 0.646w_1& 0.438w_2& 0.768w_3\\ 0.469w_1& 0.682w_2& 0.414w_3\end{array}\right)$.

Step 4: Determine the ideal solution $S^{+}=\left\{0.646w_1,0.682w_2,0.768w_3\right\}$, $S^{-}=\left\{0.469w_1,0.438w_2,0.414w_3\right\}$.

Step 5: Solve the weight $w_i$. Translate the coordinate origin to the positive ideal solution point. Then, the shifted decision matrix becomes $T=\left(\begin{array}{ccc}-0.044w_1& -0.096w_2& -0.279w_3\\ 0& -0.244w_2& 0\\ -0.177w_1& 0& -0.354w_3\end{array}\right)$, the positive ideal solution becomes $Q^{+}=\left\{0,0,0\right\}$, and the negative ideal solution becomes $Q^{-}=\left\{-0.177w_1,-0.244w_2,-0.354w_3\right\}$. Thus, the optimization model is constructed:

$$\min Z=0.039w_1^2+0.083w_2^2+0.224w_3^2$$

$$s.t.\{\begin{array}{l}{w}_1+w_2+w_3=1\\ w_1\ge 0,w_2\ge 0,w_3\ge 0\end{array}$$

Apply LINGO software to solve the model and the results are: $w_1=0.431$, $w_2=0.396$, and $w_3=0.173$; then, the initial profit distribution of logistics enterprises 1, 2, and 3 is: ${\psi }_1=379.5988$, ${\psi }_2=750.5089$, ${\psi }_3=369.8923$.

The process of setting the initial distribution scheme of the alliance with communication structure restrictions by the orthogonal projection method will not be repeated, and the obtained weights are: $w_1=0.247$, $w_2=0.442$, $w_3=0.311$; the initial profit distribution amount is: ${\psi }_1=297.283$, ${\psi }_2=779.6721$, and ${\psi }_3=423.0449$.

5.5. Final Profit Distribution Scheme Based on Logistics Task Completion Quality Modification

After the task is completed, representatives of each logistics enterprise, industry expert, and customer will be organized to score and evaluate the task completion quality of each logistics enterprise. Due to space limitations, the following only shows the evaluation process of the task completion quality of logistics enterprise 1 in the alliance without communication structure restrictions.

Firstly, calculate the membership degree $b_{ijm}^{’}=\frac{b_{ijm}}{{\displaystyle \sum _1^m{b}_{ijm}}}$ according to Table 6, so as to obtain the fuzzy relation matrix of the four first-level indexes:

$$\begin{gathered} B_1=\left(\begin{array}{ccccc}0.25& 0.4& 0.15& 0.1& 0.1\\ 0.2& 0.5& 0.25& 0.05& 0\\ 0.25& 0.25& 0.35& 0.1& 0.05\end{array}\right) \\ {B}_2=\left(\begin{array}{ccccc}0.15& 0.25& 0.45& 0.1& 0.05\\ 0.2& 0.25& 0.45& 0.05& 0.05\\ 0.15& 0.3& 0.3& 0.1& 0.15\end{array}\right) \end{gathered}$$

$$\begin{gathered} B_3=\left(\begin{array}{ccccc}0.25& 0.35& 0.4& 0& 0\\ 0.3& 0.25& 0.25& 0.15& 0.05\\ 0.2& 0.4& 0.2& 0.2& 0\end{array}\right) \\ {B}_4=\left(\begin{array}{ccccc}0.2& 0.25& 0.25& 0.15& 0.15\end{array}\right) \end{gathered}$$

Table 6. Score data of logistics task completion quality.

Primary Indexes	No.	SecondaryIndexes	No.	Scores
				Excellent	Good	Medium	Poor	Very Poor
Logistics task completion efficiency	1	Task response speed	1	5	8	3	2	2
		Task completion time	2	4	10	5	1	0
		Delivery on time	3	5	5	7	2	1
Logistics task completion accuracy	2	Cargo damage rate	1	3	5	9	2	1
		Cargo loss rate	2	4	5	9	1	1
		Cargo delivery accuracy	3	3	6	6	2	3
Logistics task completion reliability	3	Information feedback timeliness	1	5	7	8	0	0
		Error processing	2	6	5	5	3	1
		Personnel operation standardization	3	4	8	4	4	0
Customer satisfaction of logistics task	4	Customer compliant rate	1	4	5	5	3	3

Secondly, on the basis of the fuzzy relation matrix, the entropy weight method is used to calculate the weights of the primary and secondary indexes:

$O_1=\left(0.906 0.724 0.896\right)$$O_2=(0.851 0.824 0.946)$$O_3=(0.671 0.926 0.829)$$O_4=\left(0.985\right)$; then $E_1=(0.094 0.276 0.104)$$E_2=(0.149 0.176 0.054)$$E_3=(0.329 0.074 0.171)$$E_4=(0.015)$; and then $w_{11}=\raisebox{1ex}{$0.094$}\!\left/ \!\raisebox{-1ex}{$0.474$}\right.=0.198$, similarly, $w_{12}=0.582$, $w_{13}=0.219$; finally, $W_1=\raisebox{1ex}{$0.474$}\!\left/ \!\raisebox{-1ex}{$1.442$}\right.=0.329$. The calculation process of the weights of other indexes is omitted, and the results are shown in Table 7.

Table 7. The weight of logistics task completion quality evaluation indexes.

Objective	Primary Indexes	Weight	Secondary Indexes	Weight
The evaluation index system of logistics task completion quality	Logistics task completion efficiency	0.329	Task response speed	0.198
			Task completion time	0.582
			Delivery on time	0.219
	Logistics task completion accuracy	0.263	Cargo damage rate	0.393
			Cargo loss rate	0.464
			Cargo delivery accuracy	0.142
	Logistics task completion reliability	0.398	Information feedback timeliness	0.573
			Error processing	0.129
			Personnel operation standardization	0.298
	Customer satisfaction of logistics task	0.01	Customer compliant rate	1

Thirdly, calculate the comprehensive evaluation score of the logistics task completion quality of logistics enterprise 1 in the alliance without communication structure restrictions. That is, calculate $V=\left(\begin{array}{c}{V}_1\\ V_2\\ V_3\\ V_4\end{array}\right)=\left(\begin{array}{ccccc}0.221& 0.425& 0.252& 0.071& 0.031\\ 0.173& 0.257& 0.428& 0.077& 0.064\\ 0.242& 0.352& 0.321& 0.079& 0.006\\ 0.2& 0.25& 0.25& 0.15& 0.15\end{array}\right)$, where $\begin{array}{l}{V}_1=\left(\begin{array}{ccc}{w}_{11}& w_{12}& w_{13}\end{array}\right)•B_1\\ =\left(\begin{array}{ccccc}0.221& 0.425& 0.252& 0.071& 0.031\end{array}\right)\end{array}$, then $P_1=\left(\begin{array}{cccc}0.329& 0.263& 0.398& 0.01\end{array}\right)•V•\left(\begin{array}{c}5\\ 4\\ 3\\ 2\\ 1\end{array}\right)=3.648$.

Thus, in the alliance without communication structure restrictions, the task completion quality evaluation score of logistics enterprise 1 is $P_1=3.648$; the same fuzzy comprehensive evaluation process can obtain the task completion quality evaluation score $P_2=4.005$ of logistics enterprise 2; the task completion quality evaluation score of logistics enterprise 3 is $P_3=2.768$.

Finally, determine the final profit distribution scheme. Calculate the final profit distribution ratios ${\pi }_1=\frac{{\psi }_1{P}_1}{{\displaystyle \sum _{k=1}^3{\psi }_k{P}_k}}=0.256$, ${\pi }_2=0.555$, and ${\pi }_3=0.189$, and then the final profit distribution amount is ${\psi }_1^{\prime }=0.256\times 1500=384$, ${\psi }_2^{\prime }=0.555\times 1500=832.5$, ${\psi }_3^{’}=0.189\times 1500=283.5$. In the same way, the task completion quality evaluation scores of each logistics enterprise in the alliance with communication structure restrictions can be obtained, and then the initial profit distribution scheme can be modified to obtain the final profit distribution scheme.

The summary of the initial and final profit distribution schemes is shown in Table 8. It can be seen from the table that, due to the poor quality of task completion of logistics enterprise 3, its final income is less than the initial income, while logistics enterprises 1 and 2 have high task completion quality, and finally share more alliance revenue. It can be seen that modifying the initial profit distribution scheme considering the quality of logistics task completion can play a role in stimulating logistics service providers to work hard to complete alliance tasks.

Table 8. Summary and comparison of the profit distribution schemes.

Alliance without Communication Structure Restrictions
Logistics Enterprise	Initial Profit Distribution Scheme	Final Profit Distribution Scheme
1	379.5988	384
2	750.5089	832.5
3	369.8923	283.5
Alliance with communication structure restrictions
Logistics enterprise	Initial profit distribution scheme	Final profit distribution scheme
1	297.283	276.2
2	779.6721	925.6
3	423.0449	298.2

6. Conclusions

Based on the Shapley value method and the A-T solution method of the classical alliance profit distribution, this paper introduces multiple influencing factors and the orthogonal projection method to modify them, and constructs a two-stage profit distribution model suitable for logistics alliance with two types of communication structures. The results of example analysis show that the profit distribution model designed in this paper can comprehensively examine the marginal contribution, communication structure restrictions, resource input efficiency, and risk-taking of the logistics enterprises in the alliance in the initial distribution, effectively avoid the “hitchhiking” phenomenon, and solve the problem that the logistics alliance with communication structure restrictions cannot apply the traditional Shapley value method to carry out profit distribution; in the secondary distribution, it can motivate the logistics enterprises to improve the task completion quality, thereby improving the operational efficiency of the logistics alliance, which is more in line with practical needs. In addition, there are still some influencing factors of logistics alliance profit distribution that have not been considered in this paper. For example, this paper only studies the case where the alliance revenue is an exact value, and the distribution problem when the revenue is a fuzzy number needs to be explored in the future.