Abstract
Effective high slope risk assessment plays an important role in the safety management and control of the open-pit coal mining process. Traditional slope stability risk assessment methods rarely consider the time factor or evaluate the dynamic change of high slope in an open-pit mine at a certain time in a sensitivity assessment. This paper develops an interval trapezoidal fuzzy soft set method to achieve the high slope dynamic risk evaluation. The proposed dynamic interval trapezoidal fuzzy soft set method for risk assessment of high slope in an open-pit coal mine is developed by integrating the time points and weights of slope risk factors. The extended interval trapezoidal fuzzy soft set was used to calculate the weights of risk factors at different times, and the Fuzzy Analytical Hierarchy Process (FAHP) method was applied to determine the weights of risk factors. The weight change of different risk factors with time can be easily achieved with the proposed method. As a case study, this approach is implemented into a risk assessment model for the north high slope in Shengli #1 open-pit mine located in Xilinhot, Inner Mongolia. The model complies with three time points and contains 4 primary risk factors (S) and 17 secondary risk factors. The results indicated that the hydrological climate conditions and slope geometry conditions were the high risk factors affecting this open-pit coal mine slope. The reasonability and effectiveness of the evaluation results were verified with in-situ observations and measurements. This dynamic risk assessment method is helpful for improving safety management and control for the high slopes of open-pit mines in the coal mining process.
1. Introduction
In the current process of coal mining, coal mine disasters occur frequently, including landslides, gas explosion, the collapse of the roof, and rock burst, etc., whilst landslides are the dominant disaster type for the open-pit coalmine [1,2,3]. Slope stability directly affects coal mining safety. Especially for the high slope in the open-pit coalmine, where the height is generally over 200 m, a landslide disaster is more likely to occur because of complex geological conditions and multiple risk factors [4]. Accurate assessment and analysis of high slope stability in an open-pit mine is very important for landslide disaster prevention and control [5,6].
Slope stability analysis usually involves various uncertain factors, such as the statistical uncertainty of rock and soil parameters. However, conventional deterministic analyses, which use a factor of safety (FS) as the slope stability criterion, cannot quantitatively and comprehensively consider the influence of these uncertain factors [7,8,9]. Many scholars have tried to use different monitoring technologies to realize slope dynamic early warning, such as displacement information integration [10], synthetic aperture radar interference [11], ground-based synthetic aperture radar technology [12], and multi-technology combination [13], etc. However, these monitoring techniques lack multivariate risk factors analysis. By contrast, risk assessment based on statistics and probability theory can reasonably and comprehensively quantify these uncertainties in slope stability analysis. The most frequently used analytical methods are probability theory [14,15,16,17], interval number theory [18], fuzzy theory [19,20,21,22], rough set theory, etc. [23,24], and direct MonteCarlo simulation (MCS) [25,26,27]. However, these methods cannot accurately solve the complex problem of slope risk assessment in which multiple factors and a large number of field data are involved. In recent years, analytic hierarchy process (AHP) [28,29,30] has been applied to systematically assess the slope stability. Santos et al. [31] proposed a hazard graph and generated the quantitative hazard assessment system to carry out risk analysis for open-pit mine slopes and saw the method as having a high discrimination capacity. Cheng et al. [32] used the random finite difference method (RFDM) to assess the risk of slope failure and concluded that the structure had a dual effect on the stability of the slope. Pinheiro et al. [33] developed slope quality Index and applied it to many real road slopes. Soft set theory also was used to study slope stability affected by multiple risk factors. Yang et al. [34] applied soft set theory to optimize the measures of highway slope treatment, and in their work the weights of affecting factors used in the slope safety evaluation were given by different experts. Fuzzy analytic hierarchy process (FAHP) determines the relative importance of each criterion through pairwise comparison given by domain experts or decision makers and is widely used to calculate standard weights [35,36,37,38]. In addition, Zhang and his co-researchers generalized parametric soft sets to dynamic interval trapezoidal fuzzy soft sets and made comprehensive evaluation decisions. The simultaneous feasibility of the decision-making method is proved by a case study [39]. The dynamic fuzzy soft set is also expanded into dynamic interval-valued fuzzy soft sets by He and his co-authors [40]. The operations and properties of dynamic interval-valued fuzzy soft set are studied, and the dynamic interval-valued fuzzy soft set decision is proposed. Zhu et al. enriched and improved the theory of interval trapezoidal fuzzy soft sets and promoted its practical application [41]. All of these achievements for statistics and probability theory have illustrated its capability and popularity in slope reliability analysis.
However, the studies rarely considered the factor of time in their sensitivity evaluation. Thus, the risk assessment of high slope cannot fully reflect the dynamic change of high slope in an open-pit coal mine during a certain period of time. For a slope in an open-pit coal mine, the change of slope stability at different time points is of great importance in risk management. In this work, an interval trapezoidal fuzzy soft set method is developed to achieve the high slope dynamic risk evaluation. The proposed dynamic interval trapezoidal fuzzy soft set method for risk assessment of high slope is developed by integrating time points and the weights of slope risk factors. More specifically, the time period is firstly clarified when the risk factors affecting the slope stability of open-pit mine are strongly superimposed. Then, the risk evaluation grade of the high slope is determined by the FAHP method, which determines slope risk factors by referring to the relevant specifications of the open-pit mine. The risk evaluation grade of the high slope is determined by the FAHP method. Again, the slope risk factors are quantified by expert scoring, and the weight of each risk factor is calculated by FAHP. The weight is independent of time. Then, the dynamic interval trapezoidal fuzzy soft set method is used to integrate the time and weights of different risk factors, and the entropy matrix is used to calculate the evaluation value of risk factors at different moments. The following, the multi-attribute decision integration and evaluation of all risk factor parameters in all time periods are carried out by the dynamic interval trapezoidal fuzzy soft set method. Finally, the high slope in the Shengli open- pit coal mine was taken as a case study, three time points were selected, and the parameter values of 17 secondary indicators were obtained. The risk factors of the high slope at different time points were evaluated and then verified with the field data monitored.
2. Expansion of Interval Trapezoidal Fuzzy Soft Sets
2.1. Interval Trapezoidal Fuzzy Soft Sets and Their Properties
In this section, we introduced some basic definitions and their properties in interval trapezoidal fuzzy soft set theory [42,43].
Definition 1.
Let U be an initial universe set and E be a set of parameters. A denotes an interval trapezoidal fuzzy soft set over a common universe U. A is a subset of E, and . A pair is called an interval trapezoidal fuzzy soft set over a common universe U, where F is a mapping given by F:.
That is to say, for , we can obtain
where is the interval trapezoidal fuzzy number corresponding to x in .
Definition 2.
Let and be interval trapezoidal fuzzy soft sets over a common universe U. is the intersection of and , where and . For , we can obtain,
where and are the interval trapezoidal fuzzy Numbers corresponding to x in and .
Definition 3.
Let and be interval trapezoidal fuzzy soft sets over a common universe U. The union of and is defined as the soft set , where and . For , we can have
Among them
where and are the interval trapezoidal fuzzy numbers corresponding to x in and , respectively.
If and are two interval trapezoidal fuzzy soft sets over a common universe U, then and is defined as
We can obtain
for , where and are the interval trapezoidal fuzzy numbers of x in the and , respectively.
If and are two interval trapezoidal fuzzy soft sets over a common universe U, or is defined as
We can obtain
where and are the interval trapezoidal fuzzy numbers of x in the and , respectively.
2.2. Correlation Theorem of Interval Trapezoidal Fuzzy Soft Sets
Theorem 1.
If , and are three interval trapezoidal fuzzy soft sets over a common universe U, we can obtain
Theorem 2.
If and are two interval trapezoidal fuzzy soft sets over a common universe U, we can obtain
Theorem 3.
If , and are three interval trapezoidal fuzzy soft sets over a common universe U, we can obtain
Based on the above expansion of interval trapezoidal fuzzy soft sets, the dynamic risk evaluation model of high slope in an open-pit mine are established in the next section.
3. Establishing the Dynamic Risk Evaluation Model of High Slope in Open-Pit Mine
In this section, the following steps are used to integrate the time points and weights of slope risk factors (see Figure 1).
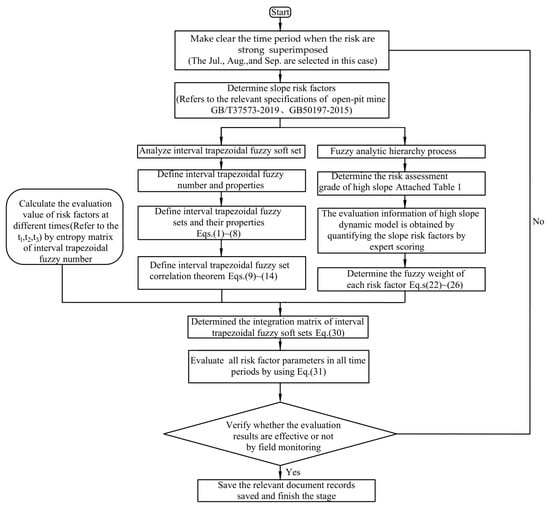
Figure 1.
Intuitionistic trapezoidal fuzzy soft set method for risk assessment of high slopes.
Step 1: Make clear the time period when the risk factors affecting the slope stability of open-pit mine are strong superimposed.
Step 2: Determine slope risk factors by referring to the relevant specifications of open-pit mine. They are technical specification for annual evaluation of the stability of open-pit coal mine slopes (GB/T 37573-2019) and code for the design of open-pit mines in the coal industry (GB 50197-2015). Then, the risk evaluation grade of high slope is determined by the FAHP method.
Step 3: The slope risk factors are quantified by expert scoring, and the weight of each risk factor is determined by FAHP method.
Step 4: The time and weight of risk factors are integrated by dynamic interval trapezoidal fuzzy soft sets, and the evaluation value of risk factors at different moments is calculated by entropy matrix. Finally, the multi-attribute decision integration and evaluation of all risk factor parameters in all time periods are carried out by dynamic interval trapezoidal fuzzy soft sets.
For the dynamic evaluation of high slope risk in open-pit mine, the time point sets of monitoring data are given, which is denoted as
where t is the time point of different risk factors; k is the number of time points.
To determine four primary indexes, we mainly refer to the relevant specifications of open-pit mine, which are technical specification for annual evaluation of the stability of open-pit coal mine slopes (GB/T 37573-2019) and specifications for design of open pit mine of coal industry (GB 50197-2015). To determine 17 primary indexes (see Table A1), we not only refer to the relevant specifications of open pit mine but also add to concern factors for high slope stability by technical and managerial personnel of the open pit mine.
The parameter sets of risk assessment are
where B1 is hydrological-climatic conditions, and B2 is internal geological structure of slope. B3 and B4 are slope geometry and inducing factors of landslide, respectively.
where e11 is weathering and freeze-thaw, and e12 is the state of groundwater. e13 is permeability of rock and soil layer, and e14 is annual rainfall. e21 and e22 are lithology and geological structure, respectively. e23 and e24 are slope structure and internal friction angle, respectively. e25 is cohesion of slope. e31 and e32 are slope angle and slope height, respectively. e33 is relationship between soft surface and slope surface, and e34 is slope morphology. e41 and e42 are human factors and impact of blasting, respectively. e43 and e44 are slope angle of excavation and earthquake intensity, respectively. B1~B4 are primary indicators and e11~e44 are secondary indicators.
The slope risk evaluation result set is
where n is the number of evaluation grades.
3.1. Determining the Weights in Different Time Range
If is the interval trapezoidal fuzzy number, its entropy value is
The entropy matrix of at a different range is obtained by calculating the values of B1, B2, B3 using Equation (22). is the kth evaluation matrix. is the value of attribute cj in the form of interval trapezoidal fuzzy number about evaluation grade ti at time point of tk.
Where i = 1, 2, 3; k = 1, 2…; j = q1, q2…ql; q = 1, 2, 3, 4. ql represents the number of parameters of the index Bq. Then, all the entropy values in the corresponding entropy matrix are added.
The entropy matrix can be obtained
The corresponding weight at the moment tk of Bq
3.2. Determining the Index Weight by FAHP Method
In order to determine the weight of each influencing factor, FAHP [44,45,46] method is used and a fuzzy consistent matrix is firstly constructed, and the matrix satisfies the following conditions:
If A is a fuzzy consistent matrix, the weight can be denoted by
It is worth noting that when , it needs to be modified until is satisfied.
3.3. Integration and Decision Method of Interval Trapezoidal Fuzzy Soft Sets
Let be an initial universe set and be a set of parameters. The matrix of is corresponding to the interval trapezoidal fuzzy soft set of . Where, i = 1, 2, …m; j = 1, 2, …n; k = 1, 2, …K. is the corresponding interval trapezoidal fuzzy number of and , the interval trapezoidal fuzzy soft matrix between the algorithm is given as follows.
If and are interval trapezoidal fuzzy soft matrix, and , we can obtain
If is the interval trapezoidal fuzzy soft matrix and the weight satisfies the conditions of and .
The weighted average operator of the interval trapezoidal fuzzy matrix can be denoted by
We can obtain
The integrated synthetic interval trapezoidal fuzzy soft matrix of is denoted as .
The decision values are used to deal with the decision problems of the interval trapezoidal fuzzy soft sets, and the decision values for in the universe set based on interval trapezoidal fuzzy soft sets in the domain are denoted by
where the corresponding interval trapezoidal fuzzy number of is
3.4. Case Study
3.4.1. Dynamic Risk Assessment Based on Trapezoidal Fuzzy Soft Set in Shengli Open-Pit Mine
- (1)
- Decision-making steps and methods
Based on above interval trapezoidal fuzzy soft set model of high slope in an open-pit coal mine, the dynamic evaluation risk steps of high slope in an open-pit coal mine are divided into four steps:
(1) Determine the times when the risk factors affecting the slope stability of open-pit mine are strong superimposed;
(2) Determine the weight of each parameter using Equations (22)–(26);
(3) Integrate interval trapezoidal fuzzy soft matrix at different times using Equation (30);
(4) Calculate the decision values corresponding to different risks using Equation (31). The multi-attribute decision integration and evaluation of all risk factor parameters in all time periods are carried out by dynamic interval trapezoidal fuzzy soft sets.
- (2)
- Determination of values for dynamic model parameter set
The north end slope of Shengli #1 open-pit mine is taken in this case study (see Figure 2). The slope height and maximum slope angle are, respectively, 200 m and 57°. Three moments were selected, i.e., , t1 is 1 July 2016; t2 is 1 August 2016 and t3 is 1 September 2016. The three time points (July, August and September) selected are the times with strong superposition of risk factors for open-pit mine slope. In this time period, there are many unstable factors inducing landslides. On the one hand, these three months are the rainy season for the open-pit mines in northern China, with a relatively concentrated and large rainfall, and the slope stability is greatly affected by hydrogeological factors. On the other hand, the open-pit mines in northern China can only be mined but not stripped in winter due to weather reasons. In order to leave enough earthwork and coal for winter mining, the blasting frequency during the three months (July, August and September) is relatively large, and the slope stability is greatly affected by mining factors. The risk decision of high slope in open-pit mine is evaluated from four primary risk factors (S), the hydrological and climatic conditions (B1), the slope internal geological structure (B2), the slope geometric conditions (B3), and landslide risk factors (B4). The risk level may be labeled as low, general and high, which are denoted by (x1), (x2), and (x3), respectively. In addition, 17 secondary indicators are selected to carry out risk assessment in four primary indicators. This will be described in the third part later on. The risk grade is divided by considering the influence of comprehensive factors. Low and medium are classified as low decision risk, high as general decision risk, and dangerous and extremely dangerous as high decision risk. The expert evaluation method was used to evaluate the slope risk factors of open-pit mine. Data were collected mainly through questionnaires. A sample of the questionnaire is attached. The data were mainly collected from the production technicians, stripping workers and management personnel of Shengli Open-pit coal mine. It covers all positions of frontline production, management and technology in open-pit coal mines. Among them, 80 questionnaires were sent out by Shengli open-pit coal mine, and 72 questionnaires were effectively recovered. The parameters of slope risk factor B1, B2, B3 and B4 at time t1, t2 and t3 are listed in Table A2, Table A3, Table A4, Table A5, Table A6, Table A7, Table A8, Table A9, Table A10, Table A11 and Table A12 in Appendix A.

Figure 2.
High slopes of Shengli #1 open-pit mine.
- (3)
- Calculation of weights for dynamic model
The values of the four primary risk indicators of B1, B2, B3 and B4 are calculated by Equation (22), subsequently the entropy matrix of corresponding to tk at different moments can be obtained. For example, the calculation results of the entropy matrix of B1 at different times are shown in Table 1, Table 2 and Table 3.

Table 1.
Entropy of each parameter of hydrological and climatic conditions B1 at time t1.

Table 2.
Entropy of each parameter of hydrological and climatic conditions B1 at time t2.

Table 3.
Entropy of each parameter of hydrological and climatic conditions B1 at time t3.
The weight of B1 is calculated by Equations (23) and (24), and the result is
Similarly, the weights of B2, B3 and B4 can be obtained
3.4.2. Risk Evaluation
Based on the above interval valued fuzzy set model, the dynamic risk of the north end slope in Shengli #1 open-pit coalmine is evaluated comprehensively. The above three time points are selected to evaluate the risk from four aspects, i.e., hydro-climatic conditions, slope internal geological structure, slope geometric conditions and induced factors. The risk evaluation of high slope is divided into three levels: low (x1), general (x2) and high (x3). Combined with the above theory, the weights at different times are obtained and then the comprehensive interval trapezoidal fuzzy soft set evaluation information for different parameter sets in all time range can be obtained by Equation (29). That is, the comprehensive evaluation values of influencing factors B1, B2, B3 and B4 in the whole time range subjected to different risks can be obtained as listed in Table A14, Table A15, Table A16 and Table A17 in Appendix A.
Meanwhile, the fuzzy symmetry matrix of each parameter for the risk factors (i.e., hydro-climatic conditions, internal geological structure, geometric conditions and induced factors) are obtained by FAHP theory in Table A18, Table A19, Table A20 and Table A21, as shown in Appendix A. The corresponding weight vectors are calculated as follows
The fuzzy symmetric matrix for primary risk indicators is obtained in Table A22 in Appendix A. The weight value is obtained by Equation (41)
The weights of risk parameters for the risk evaluation system of high slope in open-pit mine are given in Table 4.

Table 4.
Weights of risk parameters for the risk evaluation system.
The interval trapezoidal fuzzy soft set of different parameters are integrated by Equation (30). The integrated evaluation value of different parameters belonging to open-pit slope risk and the integrated value of surface mine slope risk relative to different risk grades are obtained in Table A23 and Table A24 in Appendix A.
The comprehensive evaluation value of the relative risk level, which is either low, general or high, can be obtained. The evaluation value which represents low risk for high slope in Shengli open-pit mine is
The evaluation value which represents general risk for high slope is
The evaluation value which represents high risk for high slope is
Further, the decision value of the high slope risk in the open-pit which is subject to low risk, general risk, and higher risk can be obtained. The integrated evaluation value is calculated according to Equation (28). The results are shown in Table 5.

Table 5.
Different decision factors relative to open-pit slope risk.
As shown in Table 5, for the decision-making results of the high slope in Shengli #1 open-pit mine, the values of B1 and B3 indicate a high risk level, while the values of B2 and B4 indicate a general risk level. Thus, among the many factors affecting the instability of the slope of Shengli #1 open-pit coal mine, hydro-climatic conditions and slope geometric conditions belong to high risk factors. Special attention should be paid to hydrology and slope geometry during slope stability maintenance. For example, slope reinforcement and radar displacement monitoring should be planned and performed during the rainy season. The stability evaluation should be performed when designing the slope angle.
4. Verification with Field Data
In order to verify the rationality of the above-mentioned risk evaluation method, the in-situ monitoring data were analyzed in the north end slope of Shengli #1 coalmine. The anchor monitoring points are arranged to monitor the axial force variation of the anchor cable and the displacement parameters are analyzed in the north end of the slope. Field layout with 4 anchor monitoring points and regional failure of a certain landslide in the north end slope is shown in Figure 3. The correlation laws were obtained by field monitoring results of the slope sliding in the north end slope of the open-pit mine in 2016, the axial force variation of the anchor cable in 2016, the rainfall in 2016 and the displacement of the north slope of the slope. The GPS monitoring displacements before and after the landslide accident are presented in Figure 4. The axial force variation of the anchor cable of the north end slope in 2016 are presented in Figure 5, and the rainfall and the displacement of the north side in 2017 are presented in Figure 6.
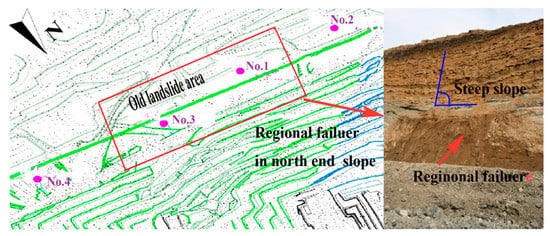
Figure 3.
Field layout with 4 anchor monitoring points and regional landslide in north end slope.
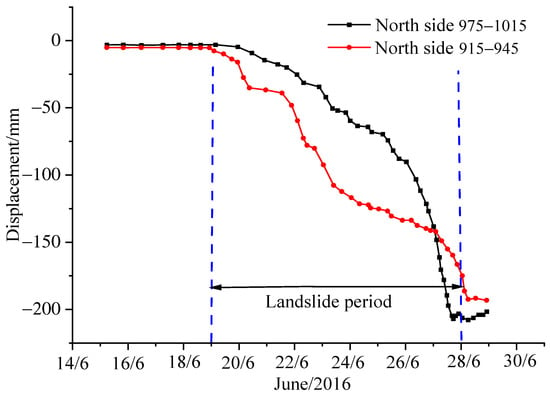
Figure 4.
Displacement curves of the north end slope from 16 June to 29 June 2016.
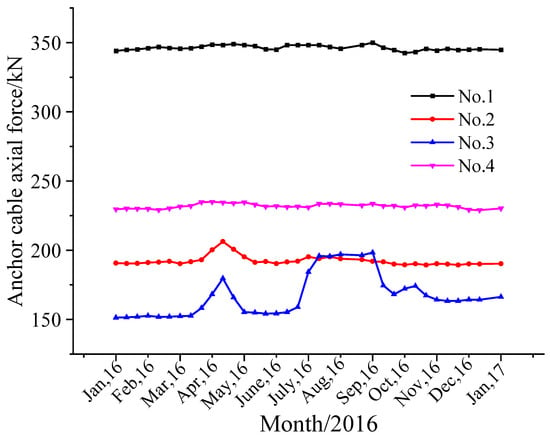
Figure 5.
Axial force variation of anchor cable for the north end slope in 2016.
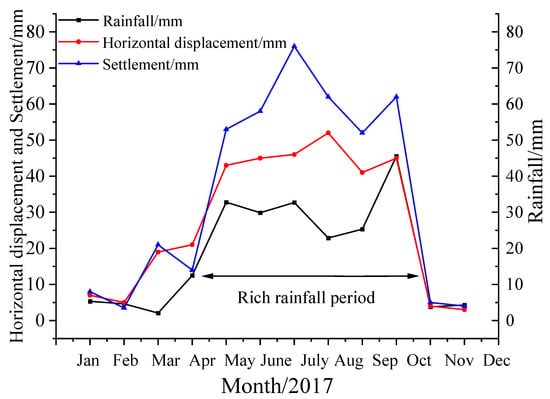
Figure 6.
Rainfall and displacement curves of the north end slope in 2017.
The maximum angles of 975–1015 level and 915–945 level in the north end slope are 45° and 57, respectively. It can be seen from Figure 4, Figure 5 and Figure 6 that the slope of displacement curve started to be relatively flat, then increased first and then decreased, and finally the slope gradually restored stability from June 16 to June 30. The maximum horizontal displacement of 915–945 level is 210 mm and that of 975–1015 level is 190 mm. Meanwhile, the horizontal displacement of 915–945 level (larger angle) is larger than that of 975–1015 level (smaller angle). The average angle of the north slope is larger than that of the southern slope. Historical data show that the frequency of landslides in the north slope is higher than in the southern slope, so the geometric angle of the slope has a greater impact on the stability of the slope. In March and June, 2016, the anchor cable axial force suddenly increased, and the maximum change occurred at the monitoring points of No. 1 and No. 3 which are located in the old landslide area. The above results indicate that the high slope has a potential landslide risk. The horizontal displacement and settlement of the slope in 2016 are much larger in the rainy season than in other months, which indicates that the precipitation conditions have a greater impact on the stability of the slope. The above statistical results are consistent with the risk evaluation results of the interval trapezoidal fuzzy soft set proposed in this work.
5. Conclusions
A dynamic risk assessment method of high slope in open-pit coalmine based on interval trapezoidal fuzzy soft set has been proposed for realizing dynamic early warning of high slope risk in open-pit coalmine. The proposed dynamic interval trapezoidal fuzzy soft set method integrates time points and the weights of slope risk factors. The formulations of the proposed method are derived, along with a detailed introduction to the procedures for implementation. Finally, the method is illustrated by a case study of high slope in Shengli #1 open mine located in Xilinhot, Inner Mongolia to verify the effectiveness of the proposed method. The main conclusions are summarized as follows:
- (1)
- The proposed method can effectively describe dynamic evaluation information of high slope, which makes it clear for the correlation between the influence of various uncertain factors on the slope and the time dimension. Compared with the traditional probabilistic analytical method, the proposed method can integrate time points and the weights of slope risk factors, especially for complex high slopes in open-pit coalmine, which enhances the practicability of interval trapezoidal fuzzy soft set theory in slope reliability analysis;
- (2)
- The risk dynamic evaluation model of high slope in an open-pit coal mine is established based on developed interval trapezoidal fuzzy soft set. In the model, the integration operator of interval trapezoidal fuzzy soft set is calculated and the comprehensive interval trapezoidal fuzzy soft set evaluation information in all time periods for different parameter sets can be obtained. The risk assessment of different factors with time can be easily achieved with the proposed method. This is not achievable by the traditional probabilistic analyses, which greatly facilitate the application of the interval trapezoidal fuzzy soft set method in probabilistic slope stability analysis;
- (3)
- The dynamic risk assessment model established above is applied in a case study for the north end slope of Shengli #1 open-pit mine. In the application of the model, three time points are selected to calculate the parameter values required by the above method, and 17 secondary risk factors of the high slope at different time points are evaluated. The results show that, for the north end slope stability of Shengli #1open-pit coal mine, the risks of hydro-climatic conditions and slope geometric conditions are relatively high, and the risks of internal geological structure and induced factors of slope are general. Meanwhile, the field monitoring parameters of the north end slope at different time ranges are analyzed; the results show that the above-mentioned slope dynamic evaluation model and method are reasonable and effective. In the process of slope reinforcement at the later stage for Shengli #1 open-pit mine, the influence of hydrological and climatic conditions and geometric shapes should be evaluated.
Author Contributions
Conceptualization, Z.W., M.H. and P.Z.; methodology, Z.W. and P.Z.; software, M.H.; validation, X.L. and S.Y.; formal analysis, Z.W.; investigation, P.Z., X.L. and S.Y.; data curation, P.Z.; writing—original draft preparation, Z.W., M.H. and P.Z.; writing—review and editing, Z.W.; funding acquisition, Z.W. and X.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Scientific and Technological Project of Henan Province (222102320060), Strength Improvement Plan of the Advantageous Disciplines of Zhongyuan University of Technology (SD202232), Henan Postgraduate Education Reform and Quality Improvement Project (YIS2022SZ16), Postgraduate Education Reform and Quality Improvement Project of Zhongyuan University of Technology (JG202220).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Table A1.
Risk assessment index system and classification standard for slope of open-pit coal mine.
Table A1.
Risk assessment index system and classification standard for slope of open-pit coal mine.
| Primary Indicator | Secondary Indicators | LEVEL OF RISK | ||||
|---|---|---|---|---|---|---|
| Low | Medium | High | Dangerous | Extremely Dangerous | ||
| Hydro-climatic conditions | Weathering and freeze-thaw | Tiny | Low | Medium | large | strong |
| Groundwater occurrence | Tiny | Low | Medium | large | strong | |
| Water permeability | Tiny | Low | Medium | large | strong | |
| Average annual rainfall | <200 | 200~400 | 400~700 | 700~1100 | >1100 | |
| Geological structure inside the slope | Lithology | Wholly | Slightly weathered | Weakly weathered | Cracked | Granular structures |
| Geological structure | Simple | relatively simple | Generally | Relatively complex | Complex | |
| Slope structure | Overall structure | Blocky structure | Layered structure | Cataclastic structure | Granular Structures | |
| Internal friction | >35 | 35~28 | 28~21 | 21~14 | <14 | |
| Cohesion | >220 | 120~220 | 80~120 | 50~80 | <50 | |
| Slope geometric conditions | Slope angle | <20 | 20~30 | 30~40 | 40~50 | >50 |
| Slope height | <30 | 30~60 | 60~100 | 100~200 | >200 | |
| Relationship between weak surface (fault) and slope | Perpendicular slope | Vertical slope | Transverse slope | Bedding slope | Parallel slope | |
| Slope morphology | Concave slope | Concave and straight mixing | Straight slope | Convex and straight mixing | Convex slope | |
| Induced factors | Human factors | Tiny | Low | Medium | Large | Strong |
| Destructive factor | Tiny | Low | Medium | Large | Strong | |
| Excavation angle | <15 | 15~30 | 30~45 | 45~60 | >60 | |
| Seismic intensity | <3 | 3~5 | 5~7 | 7~8 | >8 | |

Table A2.
The different risk evaluation values subordinated by influencing factors of B1 at time t1.
Table A2.
The different risk evaluation values subordinated by influencing factors of B1 at time t1.
| e11 | e12 | e13 | e14 | |
|---|---|---|---|---|
| x1 | [(0.2,0.3);0.3; 0.4;(0.5,0.6)] | [(0.2,0.3);0.3; 0.4;(0.4,0.5)] | [(0.4,0.5);0.6; 0.7;(0.7,0.8)] | [(0.5,0.6);0.6; 0.7;(0.7,0.8)] |
| x2 | [(0.2,0.3);0.3; 0.4;(0.4,0.5)] | [(0.3,0.4);0.5; 0.6;(0.7,0.8)] | [(0.5,0.7);0.7; 0.7;(0.8,0.9)] | [(0.2,0.3);0.3; 0.4;(0.5,0.6)] |
| x3 | [(0.3,0.5);0.5; 0.6;(0.6,0.7)] | [(0.3,0.4);0.4; 0.4;(0.5,0.6)] | [(0.3,0.5);0.5; 0.6;(0.6,0.7)] | [(0.5,0.6);0.7; 0.7;(0.8,0.9)] |

Table A3.
The different risk evaluation values subordinated by influencing factors of B2 at time t1.
Table A3.
The different risk evaluation values subordinated by influencing factors of B2 at time t1.
| e21 | e22 | e23 | e24 | e25 | |
|---|---|---|---|---|---|
| x1 | [(0.5,0.6);0.7; 0.7;(0.8,0.9)] | [(0.2,0.3);0.4; 0.4;(0.5,0.6)] | [(0.5,0.6);0.7; 0.7;(0.8,0.9)] | [(0.3,0.4);0.4; 0.4;(0.5,0.6)] | [(0.3,0.4);0.4; 0.4;(0.5,0.6)] |
| x2 | [(0.1,0.3);0.3; 0.3;(0.4,0.5)] | [(0.5,0.6);0.7; 0.7;(0.8,0.9)] | [(0.6,0.7);0.7; 0.7;(0.8,0.9)] | [(0.3,0.4);0.5; 0.6;(0.7,0.8)] | [(0.2,0.3);0.3; 0.4;(0.4,0.5)] |
| x3 | [(0.3,0.5);0.5; 0.6;(0.6,0.7)] | [(0.2,0.3);0.4; 0.4;(0.5,0.6)] | [(0.3,0.5);0.5; 0.6;(0.6,0.7)] | [(0.6,0.7);0.7; 0.7;(0.8,0.9)] | [(0.2,0.4);0.4; 0.4;(0.5,0.6)] |

Table A4.
The different risk evaluation values subordinated by influencing factors of B3 at time t1.
Table A4.
The different risk evaluation values subordinated by influencing factors of B3 at time t1.
| e31 | e32 | e33 | e34 | |
|---|---|---|---|---|
| x1 | [(0.4,0.5);0.6; 0.7;(0.7,0.8)] | [(0.5,0.6);0.7; 0.7;(0.8,0.9)] | [(0.2,0.3);0.3; 0.4;(0.4,0.5)] | [(0.1,0.2);0.2; 0.3;(0.3,0.4)] |
| x2 | [(0.2,0.3);0.4; 0.4;(0.5,0.6)] | [(0.3,0.5);0.5; 0.6;(0.6,0.7)] | [(0.5,0.6);0.6; 0.7;(0.8,0.9)] | [(0.1,0.3);0.3; 0.4;(0.4,0.5)] |
| x3 | [(0.1,0.3);0.3; 0.4;(0.4,0.5)] | [(0.2,0.4);0.4; 0.4;(0.5,0.6)] | [(0.4,0.5);0.6; 0.7;(0.7,0.8)] | [(0.5,0.6);0.7; 0.7;(0.8,0.9)] |

Table A5.
The different risk evaluation values subordinated by influencing factors of B4 at time t1.
Table A5.
The different risk evaluation values subordinated by influencing factors of B4 at time t1.
| e41 | e42 | e43 | e44 | |
|---|---|---|---|---|
| x1 | [(0.2,0.3);0.3; 0.4;(0.4,0.5)] | [(0.2,0.4);0.4; 0.4;(0.5,0.6)] | [(0.1,0.2);0.2; 0.3;(0.3,0.4)] | [(0.4,0.5);0.6; 0.7;(0.7,0.8)] |
| x2 | [(0.4,0.6);0.6; 0.7;(0.7,0.8)] | [(0.2,0.3);0.3; 0.4;(0.5,0.6)] | [(0.3,0.4);0.4; 0.4;(0.5,0.6)] | [(0.6,0.7);0.7; 0.8;(0.9,1)] |
| x3 | [(0.1,0.4);0.4; 0.4;(0.5,0.6)] | [(0.1,0.3);0.3; 0.3;(0.4,0.5) | [(0.3,0.5);0.5; 0.6;(0.6,0.7)] | [(0.5,0.7);0.7; 0.7;(0.8,0.9)] |

Table A6.
The different risk evaluation values subordinated by influencing factors of B1 at time t2.
Table A6.
The different risk evaluation values subordinated by influencing factors of B1 at time t2.
| e11 | e12 | e13 | e14 | |
|---|---|---|---|---|
| x1 | [(0.3,0.4);0.4; 0.4;(0.5,0.7)] | [(0.5,0.6);0.7; 0.7;(0.8,0.9)] | [(0.2,0.3);0.3; 0.4;(0.5,0.6)] | [(0.4,0.5);0.5; 0.6;(0.6,0.7)] |
| x2 | [(0.1,0.2);0.2; 0.4;(0.5,0.6)] | [(0.4,0.6);0.6; 0.7;(0.7,0.8)] | [(0.1,0.2);0.2; 0.3;(0.4,0.5)] | [(0.3,0.4);0.4; 0.4;(0.5,0.6)] |
| x3 | [(0.3,0.5);0.5; 0.6;(0.7,0.8)] | [(0.4,0.5);0.5; 0.6;(0.7,0.8)] | [(0.4,0.6);0.6; 0.7;(0.7,0.8)] | [(0.5,0.6);0.7; 0.8;(0.8,0.9)] |

Table A7.
The different risk evaluation values subordinated by influencing factors of B2 at time t2.
Table A7.
The different risk evaluation values subordinated by influencing factors of B2 at time t2.
| e21 | e22 | e23 | e24 | e25 | |
|---|---|---|---|---|---|
| x1 | [(0.2,0.3);0.4; 0.4;(0.5,0.6)] | [(0.1,0.2);0.2; 0.3;(0.4,0.5)] | [(0.3,0.6);0.6; 0.7;(0.8,0.9)] | [(0.4,0.6);0.6; 0.7;(0.8,0.9)] | [(0.3,0.4);0.4; 0.4;(0.6,0.7)] |
| x2 | [(0.3,0.5);0.5; 0.6;(0.7,0.8)] | [(0.1,0.3);0.3; 0.4;(0.4,0.6)] | [(0.5,0.7);0.7; 0.7;(0.8,0.9)] | [(0.1,0.3);0.3; 0.4;(0.5,0.6)] | [(0.2,0.3);0.3; 0.4;(0.4,0.5)] |
| x3 | [(0.4,0.5);0.6; 0.7;(0.7,0.8)] | [(0.2,0.4);0.4; 0.4;(0.5,0.7)] | [(0.3,0.5);0.5; 0.6;(0.7,0.8)] | [(0.5,0.7);0.7; 0.7;(0.8,0.9)] | [(0.4,0.5);0.5; 0.6;(0.6,0.7)] |

Table A8.
The different risk evaluation values subordinated by influencing factors of B3 at time t2.
Table A8.
The different risk evaluation values subordinated by influencing factors of B3 at time t2.
| e31 | e32 | e33 | e34 | |
|---|---|---|---|---|
| x1 | [(0.2,0.4);0.4; 0.4;(0.5,0.6)] | [(0.5,0.6);0.7; 0.7;(0.8,0.9)] | [(0.1,0.2);0.3; 0.4;(0.4,0.5)] | [(0.3,0.5);0.5; 0.6;(0.7,0.8)] |
| x2 | [(0.2,0.3);0.3; 0.4;(0.5,0.6)] | [(0.5,0.6);0.6; 0.7;(0.7,0.8)] | [(0.1,0.2);0.2; 0.3;(0.3,0.4)] | [(0.3,0.4);0.4; 0.4;(0.5,0.6)] |
| x3 | [(0.3,0.5);0.5; 0.6;(0.7,0.8)] | [(0.4,0.5);0.5; 0.6;(0.7,0.8)] | [(0.4,0.6);0.6; 0.7;(0.8,0.9)] | [(0.5,0.6);0.7; 0.8;(0.8,0.9)] |

Table A9.
The different risk evaluation values subordinated by influencing factors of B4 at time t2.
Table A9.
The different risk evaluation values subordinated by influencing factors of B4 at time t2.
| e41 | e42 | e43 | e44 | |
|---|---|---|---|---|
| x1 | [(0.3,0.5);0.5; 0.6;(0.7,0.8)] | [(0.3,0.5);0.6; 0.7;(0.7,0.8)] | [(0.1,0.2);0.2; 0.3;(0.3,0.4)] | [(0.4,0.5);0.5; 0.6;(0.9,1)] |
| x2 | [(0.1,0.3);0.3; 0.4;(0.5,0.6)] | [(0.6,0.7);0.7; 0.8;(0.9,1)] | [(0.2,0.3);0.3; 0.4;(0.5,0.6)] | [(0.4,0.5);0.6; 0.7;(0.8,0.9)] |
| x3 | [(0.2,0.4);0.4; 0.4;(0.6,0.7)] | [(0.1,0.3);0.3; 0.4;(0.4,0.6)] | [(0.1,0.2);0.2; 0.2;(0.3,0.4)] | [(0.1,0.3);0.3; 0.4;(0.5,0.6)] |

Table A10.
The different risk evaluation values subordinated by influencing factors of B1 at time t3.
Table A10.
The different risk evaluation values subordinated by influencing factors of B1 at time t3.
| e11 | e12 | e13 | e14 | |
|---|---|---|---|---|
| x1 | [(0.5,0.7);0.7; 0.7;(0.8,0.9)] | [(0.1,0.2);0.2; 0.2;(0.2,0.5)] | [(0.1,0.4);0.4; 0.4;(0.5,0.6)] | [(0.1,0.6);0.6; 0.7;(0.7,0.8)] |
| x2 | [(0.1,0.4);0.4; 0.4;(0.5,0.6)] | [(0.1,0.6);0.6; 0.7;(0.7,0.8)] | [(0.1,0.2);0.2; 0.2;(0.2,0.4)] | [(0.1,0.3);0.3; 0.4;(0.4,0.5)] |
| x3 | [(0.2,0.3);0.3; 0.4;(0.4,0.5)] | [(0.3,0.4);0.4; 0.4;(0.5,0.6)] | [(0.5,0.6);0.6; 0.7;(0.7,0.8)] | [(0.3,0.4);0.4; 0.4;(0.5,0.6)] |

Table A11.
The different risk evaluation values subordinated by influencing factors of B2 at time t3.
Table A11.
The different risk evaluation values subordinated by influencing factors of B2 at time t3.
| e21 | e22 | e23 | e24 | e25 | |
|---|---|---|---|---|---|
| x1 | [(0.1,0.7);0.7; 0.7;(0.8,0.9)] | [(0.1,0.4);0.4; 0.4;(0.5,0.6)] | [(0.1,0.2);0.2; 0.3;(0.3,0.5)] | [(0.1,0.6);0.6; 0.7;(0.7,0.8)] | [(0.1,0.3);0.3; 0.4;(0.4,0.5)] |
| x2 | [(0.1,0.6);0.6; 0.7;(0.7,0.8)] | [(0.1,0.3);0.3; 0.4;(0.5,0.6)] | [(0.1,0.4);0.4; 0.4;(0.5,0.6)] | [(0.1,0.7);0.7; 0.8;(0.9,1)] | [(0.5,0.6);0.6; 0.7;(0.7,0.8)] |
| x3 | [(0.3,0.4);0.4; 0.4;(0.5,0.6)] | [(0.1,0.2);0.2; 0.3;(0.3,0.4) | [(0.4,0.5);0.5; 0.6;(0.6,0.7)] | [(0.6,0.7);0.7; 0.7;(0.8,0.9)] | [(0.3,0.4);0.4; 0.4;(0.5,0.6)] |

Table A12.
The different risk evaluation values subordinated by influencing factors of B3 at time t3.
Table A12.
The different risk evaluation values subordinated by influencing factors of B3 at time t3.
| e31 | e32 | e33 | e34 | |
|---|---|---|---|---|
| x1 | [(0.1,0.2);0.2; 0.2;(0.2,0.4)] | [(0.2,0.3);0.3; 0.4;(0.4,0.6)] | [(0.2,0.3);0.3; 0.3;(0.3,0.9)] | [(0.1,0.4);0.4; 0.4;(0.5,0.6)] |
| x2 | [(0.1,0.3);0.3; 0.3;(0.3,0.4)] | [(0.1,0.3);0.3; 0.4;(0.4,0.5)] | [(0.1,0.2);0.2; 0.2;(0.2,0.7)] | [(0.1,0.3);0.3; 0.3;(0.3,0.4)] |
| x3 | [(0.3,0.4);0.4; 0.4;(0.5,0.6)] | [(0.1,0.2);0.2; 0.2;(0.2,0.3)] | [(0.3,0.4);0.4; 0.4;(0.5,0.6)] | [(0.2,0.3);0.3; 0.4;(0.4,0.5)] |

Table A13.
The different risk evaluation values subordinated by influencing factors of B4 at time t3.
Table A13.
The different risk evaluation values subordinated by influencing factors of B4 at time t3.
| e41 | e42 | e43 | e44 | |
|---|---|---|---|---|
| x1 | [(0.1,0.3);0.3; 0.4;(0.4,0.5)] | [(0.1,0.2);0.2; 0.2;(0.2,0.7)] | [(0.1,0.5);0.5; 0.6;(0.6,0.7)] | [(0.1,0.3);0.3; 0.3;(0.3,0.4)] |
| x2 | [(0.1,0.2);0.2; 0.2;(0.2,0.4)] | [(0.1,0.4);0.4; 0.4;(0.5,0.6)] | [(0.1,0.3);0.3; 0.3;(0.3,0.4)] | [(0.1,0.3);0.3; 0.4;(0.4,0.5)] |
| x3 | [(0.5,0.6);0.6; 0.7;(0.7,0.8)] | [(0.2,0.3);0.3; 0.4;(0.4,0.5)] | [(0.3,0.4);0.4; 0.4;(0.4,0.5)] | [(0.2,0.3);0.3; 0.3;(0.3,0.4)] |

Table A14.
The influencing factors of B1 in the whole time period belong to the comprehensive evaluation value of different risks.
Table A14.
The influencing factors of B1 in the whole time period belong to the comprehensive evaluation value of different risks.
| e11 | e12 | e13 | e14 | |
|---|---|---|---|---|
| x1 | [(0.37,0.53);0.53; 0.54;(0.65,0.79)] | [(0.30,0.41);0.47; 0.49;(0.57,0.74)] | [(0.21,0.39);0.42; 0.48;(0.55,0.66)] | [(0.33,0.56);0.56; 0.66;(0.66,0.77)] |
| x2 | [(0.12,0.30);0.30; 0.40;(0.48,0.58)] | [(0.27,0.56);0.58; 0.68;(0.70,0.80)] | [(0.21,0.35);0.35; 0.39;(0.47,0.62)] | [(0.21,0.34);0.34; 0.40;(0.46,0.56)] |
| x3 | [(0.26,0.43);0.43; 0.53;(0.58,0.69)] | [(0.34,0.44);0.44; 0.49;(0.59,0.70)] | [(0.42,0.56);0.56; 0.65;(0.66,0.77)] | [(0.43,0.53);0.61; 0.67;(0.72,0.83)] |

Table A15.
The influencing factors of B2 in the whole time period belong to the comprehensive evaluation value of different risks.
Table A15.
The influencing factors of B2 in the whole time period belong to the comprehensive evaluation value of different risks.
| e21 | e22 | e23 | e24 | e25 | |
|---|---|---|---|---|---|
| x1 | [(0.24,0.55);0.61; 0.61;(0.71,0.83)] | [(0.12,0.31);0.33; 0.36;(0.46,0.56)] | [(0.28,0.48);0.51; 0.58;(0.67,0.81)] | [(0.27,0.56);0.56; 0.65;(0.71,0.82)] | [(0.23,0.36);0.36; 0.4;(0.51,0.61)] |
| x2 | [(0.19,0.51);0.51; 0.60;(0.65,0.76)] | [(0.21,0.38);0.42; 0.48;(0.56,0.70)] | [(0.40,0.61);0.61; 0.61;(0.71,0.83)] | [(0.15,0.51);0.53; 0.64;(0.76,1)] | [(0.33,0.44);0.44; 0.54;(0.54,0.65)] |
| x3 | [(0.34,0.46);0.51; 0.58;(0.61,0.71)] | [(0.16,0.31);0.33; 0.36;(0.43,0.58)] | [(0.34,0.5);0.5; 0.6;(0.64,0.74)] | [(0.56,0.7);0.7; 0.7;(0.8,0.9)] | [(0.32,0.44);0.44; 0.49;(0.54,0.64)] |

Table A16.
The influencing factors of B3 in the whole time period belong to the comprehensive evaluation value of different risks.
Table A16.
The influencing factors of B3 in the whole time period belong to the comprehensive evaluation value of different risks.
| e31 | e32 | e33 | e34 | |
|---|---|---|---|---|
| x1 | [(0.22,0.36);0.39; 0.43;(0.47,0.6)] | [(0.4,0.51);0.59; 0.61;(0.7,0.83)] | [(0.16,0.26);0.3; 0.36;(0.36,0.73)] | [(0.18,0.4);0.4; 0.47;(0.56,0.67)] |
| x2 | [(0.16,0.3);0.32; 0.36;(0.43,0.53)] | [(0.33,0.48);0.48; 0.58;(0.58,0.69)] | [(0.21,0.32);0.32; 0.39;(0.45,0.69)] | [(0.18,0.34);0.34; 0.36;(0.41,0.51)] |
| x3 | [(0.26,0.42);0.42; 0.49;(0.57,0.68)] | [(0.25,0.38);0.38; 0.43;(0.51,0.62)] | [(0.36,0.51);0.53; 0.61;(0.69,0.8)] | [(0.4,0.51);0.59; 0.67;(0.7,0.82)] |

Table A17.
The influencing factors of B4 in the whole time period belong to the comprehensive evaluation value of different risks.
Table A17.
The influencing factors of B4 in the whole time period belong to the comprehensive evaluation value of different risks.
| e41 | e42 | e43 | e44 | |
|---|---|---|---|---|
| x1 | [(0.21,0.39);0.39; 0.49;(0.54,0.65)] | [(0.21,0.38);0.43; 0.49;(0.51,0.73)] | [(0.10,0.33);0.33; 0.43;(0.43,0.54)] | [(0.30,0.43);0.46; 0.54;(0.73,1.00)] |
| x2 | [(0.18,0.35);0.35; 0.43;(0.47,0.60)] | [(0.36,0.52);0.52; 0.61;(0.73,1.00)] | [(0.19,0.32);0.32; 0.36;(0.43,0.53)] | [(0.36,0.50);0.54; 0.65;(0.74,1.00)] |
| x3 | [(0.31,0.49);0.49; 0.54;(0.62,0.72)] | [(0.14,0.30);0.30; 0.38;(0.40,0.54)] | [(0.23,0.36);0.36; 0.39;(0.42,0.52)] | [(0.25,0.43);0.43; 0.46;(0.54,0.66)] |

Table A18.
Fuzzy symmetric matrix for influencing factors of hydrology-climate B1.
Table A18.
Fuzzy symmetric matrix for influencing factors of hydrology-climate B1.
| B1 | e11 | e12 | e13 | e14 |
|---|---|---|---|---|
| e11 | 0.5 | 0.4 | 0.3 | 0.7 |
| e12 | 0.6 | 0.5 | 0.6 | 0.3 |
| e13 | 0.7 | 0.4 | 0.5 | 0.4 |
| e14 | 0.3 | 0.7 | 0.6 | 0.5 |

Table A19.
Fuzzy symmetric matrix for influencing factors of geological structure in slope B2.
Table A19.
Fuzzy symmetric matrix for influencing factors of geological structure in slope B2.
| B2 | e21 | e22 | e23 | e24 | e25 |
|---|---|---|---|---|---|
| e21 | 0.5 | 0.4 | 0.3 | 0.7 | 0.4 |
| e22 | 0.6 | 0.5 | 0.6 | 0.3 | 0.8 |
| e23 | 0.7 | 0.4 | 0.5 | 0.4 | 0.6 |
| e24 | 0.3 | 0.7 | 0.6 | 0.5 | 0.3 |
| e25 | 0.6 | 0.2 | 0.4 | 0.7 | 0.5 |

Table A20.
Fuzzy symmetric matrix for influencing factors of slope geometry condition B3.
Table A20.
Fuzzy symmetric matrix for influencing factors of slope geometry condition B3.
| B3 | e31 | e32 | e33 | e34 |
|---|---|---|---|---|
| e31 | 0.5 | 0.4 | 0.3 | 0.4 |
| e32 | 0.6 | 0.5 | 0.6 | 0.3 |
| e33 | 0.7 | 0.4 | 0.5 | 0.4 |
| e34 | 0.6 | 0.7 | 0.6 | 0.5 |

Table A21.
Fuzzy symmetric matrix for inducing factors B4.
Table A21.
Fuzzy symmetric matrix for inducing factors B4.
| B4 | e41 | e42 | e43 | e44 |
|---|---|---|---|---|
| e41 | 0.5 | 0.4 | 0.3 | 0.7 |
| e42 | 0.6 | 0.5 | 0.6 | 0.8 |
| e43 | 0.7 | 0.4 | 0.5 | 0.6 |
| e44 | 0.3 | 0.2 | 0.4 | 0.5 |

Table A22.
Fuzzy symmetric matrix corresponding to first level index.
Table A22.
Fuzzy symmetric matrix corresponding to first level index.
| A | B1 | B2 | B3 | B4 |
|---|---|---|---|---|
| B1 | 0.5 | 0.4 | 0.3 | 0.4 |
| B2 | 0.6 | 0.5 | 0.3 | 0.2 |
| B3 | 0.7 | 0.7 | 0.5 | 0.4 |
| B4 | 0.6 | 0.8 | 0.6 | 0.5 |

Table A23.
The integrated evaluation value of different parameters belonging to open-pit slope risk.
Table A23.
The integrated evaluation value of different parameters belonging to open-pit slope risk.
| B1 | B2 | B3 | B4 | |
|---|---|---|---|---|
| x1 | [(0.302,0.472);0.495; 0.548;(0.608,0.736)] | [(0.223,0.439);0.460; 0.509;(0.603,0.716)] | [(0.239,0.387);0.422; 0.473;(0.531,0.713)] | [(0.183,0.370);0.392; 0.476;(0.516,0.680)] |
| x2 | [(0.205,0.392);0.396; 0.467;(0.529,0.641)] | [(0.258,0.484);0.497; 0.568;(0.641,0.783)] | [(0.224,0.364);0.367; 0.426;(0.466,0.604)] | [(0.269,0.423);0.427; 0.498;(0.584,0.771)] |
| x3 | [(0.368,0.494);0.515; 0.588;(0.642,0.749)] | [(0.331,0.469);0.482; 0.533;(0.593,0.707)] | [(0.334,0.462);0.497; 0.567;(0.631,0.744)] | [(0.216,0.372);0.372; 0.426;(0.471,0.590)] |

Table A24.
Integrated value of surface mine slope risk relative to different risk grades.
Table A24.
Integrated value of surface mine slope risk relative to different risk grades.
| A | |
|---|---|
| x1 | [(0.225,0.401);0.427;0.491;(0.548,0.704)] |
| x2 | [(0.243,0.408);0.414;0.481;(0.546,0.699)] |
| x3 | [(0.295,0.434);0.450;0.512;(0.567,0.681)] |
References
- Whittall, J.R.; McDougall, S.; Eberhardt, E. A risk-based methodology for establishing landslide exclusion zones in operating open pit mines. Int. J. Rock Mech. Min. Sci. 2017, 100, 100–107. [Google Scholar] [CrossRef]
- Zhang, J.X.; Li, B.; Liu, Y.W.; Li, P.; Fu, J.W.; Chen, L.; Ding, P.C. Dynamic multifield coupling model of gas drainage and a new remedy method for borehole leakage. Acta Geotech. 2022, 17, 4699–4715. [Google Scholar] [CrossRef]
- Li, B.; Zhang, J.X.; Liu, Y.W.; Qu, L.N.; Liu, Q.; Sun, Y.X.; Xu, G. Interfacial porosity model and modification mechanism of broken coal grouting: A theoretical and experimental study. Surf. Interfaces 2022, 33, 102286. [Google Scholar] [CrossRef]
- Nie, L.; Li, Z.C.; Zhang, M. Deformation character and stability analysis of the landslide caused by the mining activity: A case study in the west open-pit mine, China. J. Balk. Tribol. Assoc. 2016, 22, 1001–1013. [Google Scholar]
- Huang, S.-Y.; Zhang, S.-H.; Liu, L.-L.; Zhu, W.-Q.; Cheng, Y.-M. Efficient slope reliability analysis and risk assessment based on multiple Kriging metamodels. Comput. Geotech. 2021, 137, 104277. [Google Scholar] [CrossRef]
- Liu, L.L.; Cheng, Y.M. System reliability analysis of soil slopes using an advanced Kriging metamodel and quasi—Monte Carlo simulation. Int. J. Geomech. 2018, 18, 06018019. [Google Scholar] [CrossRef]
- Cheng, Y.M.; Li, L.; Liu, L.L. Simplified approach for locating the critical probabilistic slip surface in limit equilibrium analysis. Nat. Hazards Earth Syst. Sci. 2015, 15, 1061–1112. [Google Scholar] [CrossRef]
- Wang, Z.; Shafieezadeh, A. ESC: An efficient error-based stopping criterion for kriging-based reliability analysis methods. Struct. Multidiscip. Optim. 2019, 59, 1621–1637. [Google Scholar] [CrossRef]
- Azhari, A.; Ozbaya, U. Investigating the effect of earthquakes on open pit mine slopes. Int. J. Rock Mech. Min. Sci. 2017, 100, 218–228. [Google Scholar] [CrossRef]
- Feng, G.; Xia, Y.Y.; Wang, Z.D.; Yan, M. Dynamic early warning method of open-pit mine slopes based on integrated displacement information. China Saf. Sci. J. 2022, 32, 116–122. [Google Scholar]
- Xu, Q.; Dong, X.J.; Li, W.L. Integrated Space-Air-Ground early detect ion, monitoring and warning system for potential catastrophic geoharzards. Geomat. Inf. Sci. Wuhan Univ. 2019, 44, 957–966. [Google Scholar]
- Karunathilake, A.; Zou, L.; Kikuta, K.; Nishimoto, M.; Sato, M. Implementation iand configuration of GB-SAR for landslide monitoring: Case study in Minam i-Aso, Kumamoto. Explor. Geophys. 2019, 50, 210–220. [Google Scholar] [CrossRef]
- Du, Y.; Huang, G.W.; Zhang, Q. Asynchronous RTK method for dletecting the stability of the reference station in GNSS deformation monitoring. Sensors 2020, 20, 1320. [Google Scholar] [CrossRef] [PubMed]
- Basahel, H.; Mitri, H. Probabilistic assessment of rock slopes stability using the response surface approach—A case study. Int. J. Min. Sci. Technol. 2019, 29, 18–31. [Google Scholar] [CrossRef]
- Li, D.Q.; Yang, Z.Y.; Cao, Z.J.; Zhang, L.M. Area failure probability method for slope system failure risk assessment. Comput. Geotech. 2019, 107, 36–44. [Google Scholar] [CrossRef]
- Wang, L.; Wu, C.; Tang, L.; Zhang, W.; Lacasse, S.; Liu, H.; Gao, L. Efficientreliability analysis of earth dam slope stability using extreme gradient boosting method. Acta Geotech. 2020, 15, 313–3150. [Google Scholar] [CrossRef]
- Zhang, W.; Wu, C.; Zhong, H.; Li, Y.; Lin, W. Prediction of undrained shear strength using extreme gradient boosting and random forest based on Bayesian optimization. Geosci. Front. 2021, 12, 469–477. [Google Scholar] [CrossRef]
- Xu, X.H.; Shang, Y.Q.; Wang, Y.C. Global Stability Analysis of slope based on decision-making model of multi-attribute and interval number. Chin. J. Rock Mech. Eng. 2010, 29, 1840–1849. (In Chinese) [Google Scholar]
- Cheng, M.Y.; Roy, A.F.V.; Chen, K.L. Evolutionary risk preference inference model using fuzzy support vector machine for road slope collapse prediction. Expert Syst. Appl. 2012, 39, 1737–1746. [Google Scholar] [CrossRef]
- Hosseini, N.; Gholinejad, M. Investigating the Slope Stability Based on Uncertainty by Using Fuzzy Possibility Theory. Arch. Min. Sci. 2014, 59, 179–188. [Google Scholar] [CrossRef]
- Park, H.J.; Um, J.G.; Woo, I.; Kim, J.W. Application of fuzzy set theory to evaluate the probability of failure in rock slopes. Eng. Geol. 2012, 125, 92–101. [Google Scholar] [CrossRef]
- Liu, B.; Zhang, P.; Zhang, J.W. Analysis on slope stability of open-pit coal mine based on grey support vector machine. Int. J. Smart Home 2016, 10, 169–178. [Google Scholar] [CrossRef]
- Wang, G.Y.; Cui, H.L.; Li, Q. Investigation of method for determining factors weights in evaluating slope stability based on rough set theory. Rock Soil Mech. 2009, 30, 2418–2422. [Google Scholar]
- Li, Y.; Liu, J. Slope instability disaster forecast and its application based on RS-CPM model. J. Cent. South Univ. (Sci. Technol.) 2013, 44, 2971–2976. [Google Scholar]
- Echard, B.; Gayton, N.; Lemaire, M. AK-MCS: An active learning reliability methodcombining Kriging and Monte Carlo Simulation. Struct. Saf. 2011, 33, 145–154. [Google Scholar] [CrossRef]
- Liu, L.L.; Cheng, Y.M.; Wang, X.M. Genetic algorithm optimized Taylor Krigingsurrogate model for system reliability analysis of soil slopes. Landslides 2017, 14, 535–546. [Google Scholar] [CrossRef]
- Kim, J.; Song, J. Probability-Adaptive Kriging in n-Ball (PAK-Bn) for reliability analysis. Struct. Saf. 2020, 85, 101924. [Google Scholar] [CrossRef]
- Zhan, W.; Lin, H.; Li, Z.L. Research on Security Risk Assessment System of Soil Slope Based on AHP. Appl. Mech. Mater. 2015, 744, 570–573. [Google Scholar] [CrossRef]
- Zhang, J.; He, P.; Xiao, J.; Fei, X. Risk assessment model of expansive soil slope stability based on Fuzzy-AHP method and its engineering application. Geomat. Nat. Hazards Risk 2018, 9, 389–402. [Google Scholar] [CrossRef]
- Zhao, C.; Cheng, G.P. Application of AHP in Material Selection in Slope Protection Project in Riverway. Adv. Mater. Res. 2013, 683, 921–924. [Google Scholar] [CrossRef]
- Dos Santos, T.B.; Lana, M.S.; Pereira, T.M.; Canbulat, I. Quantitative hazard assessment system (Has-Q) for open pit mine slopes. Int. J. Min. Sci. Technol. 2019, 29, 419–427. [Google Scholar] [CrossRef]
- Cheng, H.Z.; Chen, J.; Chen, R.P.; Chen, G.; Zhong, Y. Risk assessment of slope failure considering the variability in soil properties. Comput. Geotech. 2018, 103, 61–72. [Google Scholar] [CrossRef]
- Pinheiro, M.; Sanches, S.; Miranda, T.; Neves, A.; Tinoco, J.; Ferreira, A.; Correia, A.G. A new empirical system for rock slope stability analysis in exploitation stage. Int. J. Rock Mech. Min. Sci. 2015, 76, 182–191. [Google Scholar] [CrossRef]
- Yang, Z.P.; Zhou, X.L.; Hu, X. Decision on treatment schemes for highway slopes based on soft set theory. Technol. Highw. Transp. 2016, 32, 22–25. (In Chinese) [Google Scholar]
- Zhou, X.; Sun, Y.; Huang, Z.; Yang, C.; Yen, G.G. Dynamic multi-objective optimization and fuzzy AHP for copper removal process of zinc hydrometallurgy. Appl. Soft Comput. 2022, 129, 109613. [Google Scholar] [CrossRef]
- Qin, D.L.; Zhang, L.; Li, J.H. Risk Assessment Approach for Information Security Based on FAHP. Comput. Eng. 2009, 35, 156–158. [Google Scholar]
- Chen, T.; Lin, Y.C.; Chiu, M.C. Approximating alpha-cut operations approach for effective and efficient fuzzy analytic hierarchy process analysis. Appl. Soft Comput. 2019, 85, 105855. [Google Scholar] [CrossRef]
- Ahmed, F.; Kilic, K. Fuzzy Analytic Hierarchy Process: A performance analysis of various algorithms. Fuzzy Sets Syst. 2019, 362, 110–128. [Google Scholar] [CrossRef]
- Zhang, Y.L.; Xu, H.W.; Liu, W.F. Interval-valued fuzzy parameterized soft sets and its applications in decision making. J. Xihua Univ. Nat. Sci. 2014, 33, 44–52. [Google Scholar]
- He, X.; Du, Y.X.; Liu, W.F. Dynamic interval-valued fuzzy soft sets and their application to decision making. J. Sichuan Univ. Sci. Eng. (Nat. Sci. Ed.) 2015, 28, 92–96. [Google Scholar]
- Zhu, J.; Xu, Y.; Chen, X.G. Interval-valued trapezoid fuzzy soft set and its properties. J. Heilongjiang Univ. Sci. Technol. 2016, 26, 332–335. [Google Scholar]
- Acar, U.; Koyuncu, F.; Tanay, B. Soft sets and soft rings. Comput. Math. Appl. 2010, 59, 3458–3463. [Google Scholar] [CrossRef]
- Maji, P.K.; Biswas, R.; Roy, A.R. Soft set theory. Comput. Math. Appl. 2003, 45, 555–562. [Google Scholar] [CrossRef]
- Buckley, J.J.; Feuring, T.; Hayashi, Y. Fuzzy hierarchical analysis. Fuzzy Sets Syst. 1985, 17, 233–247. [Google Scholar] [CrossRef]
- Chen, S.J.; Chen, S.M. Fuzzy risk analysis based on the ranking of generalized trapezoidal fuzzy numbers. Appl. Intell. 2007, 26, 1–11. [Google Scholar] [CrossRef]
- Laarhoven, P.; Pedrycz, W. A fuzzy extension of Saaty’s priority theory. Fuzzy Sets Syst. 1983, 11, 199–227. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).