Abstract
We introduce a generalization of the one-dimensional accelerated failure time model allowing the covariate effect to be any positive function of the covariate. This function and the baseline hazard rate are estimated nonparametrically via an iterative algorithm. In an application in non-life reserving, the survival time models the settlement delay of a claim and the covariate effect is often called operational time. The accident date of a claim serves as covariate. The estimated hazard rate is a nonparametric continuous-time alternative to chain-ladder development factors in reserving and is used to forecast outstanding liabilities. Hence, we provide an extension of the chain-ladder framework for claim numbers without the assumption of independence between settlement delay and accident date. Our proposed algorithm is an unsupervised learning approach to reserving that detects operational time in the data and adjusts for it in the estimation process. Advantages of the new estimation method are illustrated in a data set consisting of paid claims from a motor insurance business line on which we forecast the number of outstanding claims.
1. Introduction
The parametric accelerated failure time (AFT) model has been well established in medical statistics and other applications (Kalbfleisch and Prentice 2002) for decades. The aim of this paper is to introduce a nonparametric generalization of the one-dimensional AFT model for right-truncated data and apply it to estimate the number of outstanding claims in non-life insurance.
Given a covariate and given no failure has occurred until time t, the AFT specifies that the probability of a failure between time t and equals with for an underlying hazard rate and a deterministic vector . More formally, this model is expressed through the conditional hazard rate
Its interpretation is straightforward, for example, in a medical context where failure time T describes the amount of time for a tumor to reach a critical stage. For each individual i, the value of depends on its covariate (the patient’s medical data). A value of , for instance, means that the development of the tumor happens twice as fast for a patient and means 10% slower development than usual. This is in contrast to the proportional hazard model , where the interpretation of is non-trivial (Cox 1972). For the statistical analysis in the AFT model, one can transform the observed failure times through (if one knows ). The transformed survival time follows the same distribution for all individuals and is independent of the covariate .
The AFT model has been studied by various authors including Buckley and James (1979); Louis (1981); Miller (1976), and Ritov and Wellner (1988). Comprehensive overviews have been given in Cox and Oakes (1984) and Andersen et al. (1993). The model is still widely used and adapted to new problems in medical research. A recent modification of the AFT model has been introduced in Li and Jin (2018) and recent applications include AIDS research (Fulcher et al. 2017) and cancer research (Cho et al. 2018) among many others.
This article focuses on the one-dimensional case and provides a nonparametric generalization of the parametric AFT model above assuming . We estimate nonparametrically and impose no structural assumption. In a finance or insurance context, the unknown function is often called operational time and it can accelerate or slow down the survival time T. However, with our definition, has the same effect as in the AFT model, i.e., the effect is reversed. We can transform observed survival times and covariates via to obtain identically distributed survival times that are independent of their covariates as in the AFT model. In our application of non-life reserving, X is the accident date of an insurance claim and T is its settlement delay which can be affected by calendar effects, seasonal effects or a trend in the speed of claims finalization over time, e.g., due to new organizational structures in the insurance company, more efficient IT systems, or changes in legislation. The latter trends over time are captured by our operational time function . We estimate and the marginal hazard rate of . Together, they yield an estimate of the conditional hazard rate of T given X, which contains full information of the distribution of T given X. This hazard rate is used to estimate outstanding claim numbers through extrapolation with a chain-ladder type algorithm. The proposed algorithm in this article detects the effects of operational time and adjusts for them. If there is no operational time present, the algorithm still estimates smoothed chain-ladder development factors for an optimal bandwidth that is selected through cross-validation.
The concept of operational time was originally developed for stochastic processes in Feller (1971). In actuarial research, it was first used for processes of claim numbers in Bühlmann (1970) and for non-life reserving in Reid (1978) and Taylor (1981, 1982). Comprehensive summaries about operational time in reserving have been provided in Taylor et al. (2008) and Taylor and McGuire (2016). For an overview of its use in mathematical finance, we refer to Swishchuk (2016).
The algorithm in this paper is an alternative to the most widely used algorithm in non-life reserving, the chain-ladder method. The difference is that, in chain-ladder, it is assumed that accident date and settlement delay are independent, and thus chain-ladder does not account for calendar time effects like court rulings, emergence of latent claims, or changes in operational time. The first stochastic model around the chain-ladder method was introduced in Mack (1993). Chain-ladder is still widely used in the insurance industry and as a benchmark for new methods in research as explained in overviews of reserving methods in England and Verrall (2002) and, more recently, Taylor (2019). Based on the idea of chain-ladder, different multiplicative models with independent effects of accident date and settlement delay were introduced in Kremer (1982); Kuang et al. (2009); Renshaw and Verrall (1998), and Verrall (1991).
Aside from these publications, the greater part of the research on claims reserving can be summarized into two streams: a Poisson process approach and a two-dimensional kernel estimation approach for truncated data. The first (older and more extensive) stream of research focuses on Poisson process models in Antonio and Plat (2014); Avanzi et al. (2016); Huang et al. (2015); Jewell (1989, 1990); Larsen (2007), and Norberg (1993, 1999). Extensions that investigate dependent covariates or marked Cox processes include Zhao and Zhou (2010); Zhao et al. (2009), or Badescu et al. (2016), respectively. A semiparametric approach very similar to operational time is given in Crevecoeur et al. (2019), in which the authors allow time on weekends and public holidays to pass faster in order to make up for less claim reports on these days while ensuring a continuous distribution of reporting delay.
The approach in this present paper fits into the second stream of reserving research based on “continuous chain-ladder” (Hiabu et al. (2016); Lee et al. 2015, 2017; Martínez-Miranda et al. (2013)). In a broader statistical context, the problem was introduced as “in-sample forecasting” (Mammen et al. 2015) and said papers applied their results to forecasting problems beyond actuarial research. These articles have in common that no distributional assumptions are made and that kernel estimation is performed under the assumption of a structural model for the joint density or conditional hazard rate. In the operational time model, Lee et al. (2017) assume the nonparametric factor , i.e., , and estimate as well as the two marginal densities of accident year and settlement delay. The latter is the closest approach to this present paper; however, we estimate a conditional hazard rate instead of a multivariate density. The advantage of our approach is that we only estimate two functions ( and ) instead of three, and then extrapolate claim numbers to estimate the number of outstanding claims. This extrapolation is analogous to the algorithm in the chain-ladder method. Since our estimated conditional hazard rates are similar to chain-ladder development factors (Hiabu 2017), we consider it more natural to extrapolate in a hazard framework than to perform extrapolation with density functions. Therefore, we only forecast the effect of the accident date X and do not estimate its distribution. All mentioned continuous chain-ladder publications including this present paper focus on claim numbers instead of payment amounts. Recently, Bischofberger et al. (2019) have shown how to extend the models and estimators for payment amounts. This extension is also feasible for our approach; however, adding extensive additional technicalities is beyond the scope of this paper.
In traditional statistical learning, learning problems are classified as “supervised” and “unsupervised” (Hastie et al. 2008). For supervised learning algorithms, the goal is to predict an outcome measure for a given input. For this purpose, the algorithm trains on paired data consisting of (input, output) and then applies the learned structure to predict an output from a new input. On the other hand, in unsupervised learning, there is no output in the data and the goal of the algorithm is often to find patterns in the data minimizing a loss criterion. Nonparametric kernel estimation is used in both approaches: for nonparametric regression in supervised learning and for kernel density estimation in unsupervised learning (Hastie et al. 2008). The new forecasting procedure in this article can be classified as an unsupervised machine learning technique. Although the goal is to give an estimate of the number of outstanding claims from past data, our algorithm cannot be trained on a data set of input and output (in form of past claims and future claims) and then applied to a new input. The presented algorithm estimates the conditional distribution of settlement delay given the accident date that is specific for the data set it is used on. This estimation involves kernel hazard estimators and the minimization of a loss function.
Very recently, following a trend in applied statistics, various other machine learning approaches to claims reserving that do not belong to any of the previous streams have arisen. Soon these articles may constitute a third big stream of research. Useful machine learning techniques for reserving include regression trees (Baudry and Robert 2019; Wüthrich 2018) and neural networks (Kuo 2019) among others. These approaches also take dependence between accident date and delay into account and are thus more flexible than many of the aforementioned models. In contrast to the algorithm in this article, they are all based on supervised learning. A neural network architecture based on classical chain-ladder literature, into which the over-dispersed Poisson reserving model of Renshaw and Verrall (1998) is embedded, has been introduced in Gabrielli et al. (2019).
This article is structured as follows. The underlying mathematical model is introduced in Section 2. Section 3 explains an algorithm to estimate operational time and the baseline hazard. Section 4 illustrates how to estimate outstanding liabilities from an operational time and a baseline hazard estimate. A data-driven bandwidth selection procedure is introduced in Section 5 and Section 6 containing an illustration for a real data set.
2. Model
We start with a general mathematical model for hazard rates with operational time but without filtering and afterwards adapt it to observations on a run-off triangle in the context of claims reserving. Since this particular triangular data structure can be expressed as truncated data, a counting process survival model lends itself to our cause.
2.1. General Model
Let be a two-dimensional random variable on the square for . Suppose that T can be written as
for a random variable that is independent of X and a function . We call operational time and Equation (1) operational time model. The support of is for some . In the sequel, we define quantities for each realization of with .
In a counting process framework, we identify the survival time with and treat as a one-dimensional covariate. We first define the counting process setting before linking it to the random variable . Suppose we observe a counting process with respect to a suitable filtration (Andersen et al. 1993, p. 60). The intensity of at time t is defined as
To illustrate the effect of operational time on the intensity, we start with a simple model for unfiltered data, denoted by the superscript . We use the notation with superscripts since we will focus on a specific hazard later on, for which we want to reserve the plain notation and N. For illustration, we define the counting process with the adapted filtration . The intensity of given satisfies Aalen’s multiplicative model (Aalen 1980) with
where is the conditional hazard of T given X and is the marginal hazard of . We want to emphasize that the hazard rate of is in particular not conditioned on X because and X are independent. The fact that is a function of just one argument is the advantage of assuming the structural Model (1) because one can now easily derive an estimator for . For unique identification of , we choose the normalization in the sequel.
The advantage of this framework is that we can easily handle certain filtering schemes like right-censoring and left-truncation. If the observations of T are right-censored, we observe where is the censored value of with respect to some censoring time C and is the corresponding censoring variable. Moreover, suppose our observations to be left-truncated. In particular, we assume the special case of left-truncation . Hence, we use the counting process with respect to its adapted filtration and with intensity
for exposure . The conditional hazard has the same structure as in the last case,
The model in Equation (2) has been investigated for nonparametric regression in Linton et al. (2011); however, their model did not allow for right-truncation in run-off triangles. The next chapter introduces the operational time hazard model for right-truncation, which will be used in the sequel.
2.2. Model on the Run-Off Triangle with Right-Truncation
When estimating future claim numbers, reserving departments in the non-life insurance industry work with data of historical claims aggregated in two dimensions: the accident date of the claim and the settlement delay, i.e., the time between accident date and payment to the policy holder. Note that, as in the chain-ladder method, we will not need the number of individuals under risk (the number of underwritten policies) for the estimation of future claim numbers. Therefore, we suppose the data contain only paid claims.
We denote by X the underwriting date of the policy and by T the settlement delay. Hence, adopting the notation from above, we follow the settlement delay as survival time and the accident date as covariate on which we will condition. In Model (1), the operational time function links a non-observable random delay to the observed settlement delay depending on the accident date. The independent delay can be seen as pure delay, cleared of all external factors. A value implies a larger delay T with the heuristic that “time is running slower” and vice versa. This is best explained on the data set that is used in Section 6. The estimator of has values smaller than 1 for accident dates after January 2006 (see Section 6). This phenomenon is most likely due to the improved use of technology in the insurance company and has also been observed on the same data set in Lee et al. (2017). Instead of treating this as a special case, we let time run faster in this period and use the same delay throughout the whole range of accident dates. In particular, this does prevent discontinuities in the distribution of the delay. Since time was running faster for accident dates in 2006 and later, their actual delay effect , cleared of operational time, is larger (and sometimes even beyond the diagonal in the run-off triangle) in Figure 1. The operational time estimate already has a downwards trend for accident dates in 2004 and 2005; however, values in 2004 and and at the end of 2005 are larger than 1. On these dates, time was running slower in our model which is why the independent delay for early accidents is slightly shorter than in the original data.
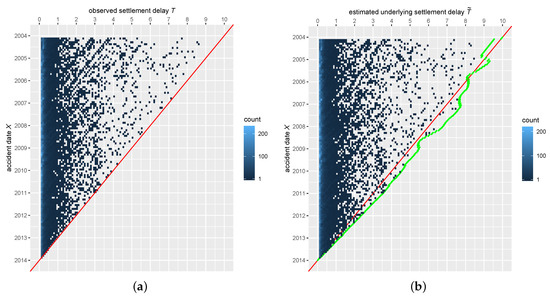
Figure 1.
Original data and data with unobservable delay cleared of operational time. The operational time in (b) is estimated in Section 6. Claim counts are aggregated into monthly bins for visualization, and settlement delay is displayed in years. The red line represents the date of data collection and the green points are the date of data collection cleared of operational time effects (with respect to accident date). (a) original data; (b) data cleared of operational time.
To adapt the operational time hazard Model (2) to the needs of our application, we assume pairs of observations , , on the triangle . Hence, we have right-truncated observations of T because it now holds . To circumvent this difficulty, we invert time and look at observations which are left-truncated in (Ware and DeMets 1976), so we can apply Model (2). Note that our observations only have the same distribution as if conditioned on . We do not assume any censoring in the following.
As before, we focus on a counting process . The intensity of the time-reversed counting process with respect to its natural filtration now equals
where is the conditional hazard of given and . In particular, we get
with the marginal hazard of since and X are independent. We will also refer to as a baseline hazard in the following. The reason for the unintuitive argument of is that operational time is defined for T in “forward time”; however, is the hazard rate in reversed time but cleared of operational time, c.f., Equation (2).
It can be easily derived that our model coincides with the structured model on the joint density f considered in Lee et al. (2017) for the choice and being the marginal densities of , respectively, and . The advantage of our approach is that we only estimate two functions and instead of three because we use the algorithm illustrated in Section 4 to estimate the outstanding reserve. Hence, we only forecast the effect of given underwriting data and do not estimate the distribution of X. For full inference on X, the roles of T and X have to be swapped.
Note that a multivariate extension of the operational time Model (1) for covariates and with is possible and would result in the same hazard Model (3) with analogous baseline hazard if right-truncation is well-defined (for instance with being first component of ). However, the estimation of and explained in the next section would get rather involved including a d-dimensional numerical minimization for the estimation of .
3. Estimation of Baseline Hazard and Operational Time
In this section, we show how to estimate the components and and then combine the estimators into a structured estimator of the conditional hazard. We want to recall that the whole estimation procedure is done in reversed time instead of T for the reporting delay. Hence, the following estimators are defined for and . This technical difficulty is necessary because of the right-truncation described in the last section. However, it does not constitute an issue since, once the components are estimated, we can evaluate all functions at to get the results for t. We also want to remark again that the underwriting date X is always considered in “forward time”. In the following, we see the conditional hazard as a function of two arguments and denote its estimators by . The unstructured hazard estimator in step 1 is analogously denoted by .
The proposed estimation procedure is as follows. The necessary expressions (7) and (10), and the loss criterion (11) will be introduced below:
- Estimate the (unstructured) conditional hazard by through Equation (7).
- Set and .
- Estimate through Equation (10) using .
- Estimate by minimizing the loss in (11) numerically for every x using .
- Repeat steps 3 and 4 for until the convergence criterionis satisfied in iteration .
- Set the final conditional hazard estimator toforThe final estimator in (non-reversed) “forward time” is set to
Note that the first conditional estimator in step 1 is unstructured, which means that, in general, it does not satisfy Equation (3). We also want to remark that the final estimator is used to extrapolate claim numbers in the next section. Despite being more intuitive, it does not occur in a well-defined model because of the right-truncation .
All estimators , , are defined via integrated quadratic loss criteria and the hazard estimators , have closed form representations as local linear kernel estimators.
3.1. Pre-Step: Unstructured Conditional Hazard
We start with the unstructured conditional hazard estimator. Let and to simplify the notation. For convenience, we will also write . For any , the local linear kernel hazard estimator is defined as the first component minimizing the loss function
for . Moreover, we use a two-dimensional kernel K and bandwidth for as well as the common notation . The term is needed to make the expression well-defined. The loss criterion L results in the closed form solution
for occurrence and exposure estimators
where the components of the two-dimensional vector are
and the entries of the -dimensional matrix are given by
The closed form solution has been derived in Nielsen (1998). This paper focusses on the local linear kernel estimator because of its good performance at boundaries. The simpler and more intuitive (Nadaraya–Watson type) local constant hazard estimator is given in Appendix A as an alternative. However, on bounded support, it is known to suffer from bias at boundaries (Nielsen 1998; Nielsen and Tanggaard 2001).
3.2. Estimation of Baseline Hazard Given Operational Time
Starting with the pilot estimator , we calculate the first iteration and then recursively update making use of . For the r-th iteration, we define as the hazard rate minimizing the loss
for operational time and the conditional hazard estimate . The loss function reflects the principle of minimizing a chi-square criterion (Berkson 1980) in which a least squares criterion is weighted by an estimate of the inverse of the asymptotic variance of , here . The function w is a weighting function, which is used to ensure that the resulting hazard estimator is a ratio between an occurrence estimator and an exposure estimator. It will be specified later. The minimization of (9) has the analytic solution
where for . The derivation is analogous to Linton et al. (2011). Now, setting the weighting results in
The transformation adds the effect of operational time to occurrence and exposure estimators that were constructed with respect to . The function is the estimate of in the r-th iteration. Hence, we evaluate and at x but at the value of t that was corrected with the operational time effect.
It is worth pointing out that we do not get two marginal one-dimensional hazard estimator despite X and the cleared delay being independent. This makes the implementation quite involved.
3.3. Estimation of Operational Time Given Baseline Hazard
To estimate in the r-th iteration, we minimize the loss function in Equation (9) in given the baseline hazard and the conditional hazard estimate . Since there is no closed form solution to this problem (Linton et al. 2011), one has to minimize it numerically point-wise in x. Moreover, we set with the last estimator of as above. Hence, for every , we minimize
numerically for values . The values have to be chosen manually. We define to be the function minimizing (11) point-wise in x. For unique identification of and , we set the normalization .
Since there is no closed form solution of and the occurrence and exposure estimators and in Equation (10) depend on both t and x, asymptotic theory of our results is not straightforward and thus beyond the scope of this present paper. These difficulties arise due to the time-reversion that was necessary to derive estimators for right-truncated data. Asymptotic properties for analogous estimators on observations that are not right-truncated have been derived in Linton et al. (2011) in a non-parametric regression context. The fact that we cope with both right-truncation as present in run-off triangles and operational time distinguishes this present paper from preceding work. For a straightforward derivation of asymptotic properties of with standard counting process arguments as in Andersen et al. (1993), one would have to make further assumptions. A feasible approach would be to assume that can be estimated at a parametric -rate, which is possible for instance in a finite parametrization. Being against the distribution-free nature of this paper (and its benchmark the chain-ladder method), we decided against this simplification.
A modification of the proposed hazard estimator that has been proved efficient for large sample sizes would be a two-step multiplicative bias correction, which has been introduced for local linear kernel hazard estimators in Nielsen and Tanggaard (2001). Since this paper aims at explaining a new model and estimation procedure, and a bias correction method would add a lot of notation and complexity that might distract from our new idea, such an extension is left for future research.
4. Estimating Outstanding Claim Amounts
We use our hazard estimator to forecast outstanding claim amounts in a similar way development factors are used in the chain-ladder method. In chain-ladder with yearly aggregated data, the j-th development factor is effectively the ratio between claims whose payments are up to years delayed and those whose payments are up to j years delayed. For each claim, this yields an estimate of the probability that the payment will be years delayed given it has not been made within the first j years. Certainly, for more granular data, the time periods are shorter, but the principle stays the same.
In order to formally define development factors, one must first introduce the way data are aggregated in run-off triangles (England and Verrall 2002). The data are given as , , for the triangle . The accident date is given in days from the beginning of data collection and settlement delay is given in days. The last day of data collection is also expressed in days since day 0, and it is implicitly assumed to be the largest possible delay. The last assumption is commonly made in industry for data sets covering large enough time periods (usually if years or years). It is then said that the triangle is “fully run off”.
We adopt the notation of England and Verrall (2002) to introduce development factors. Suppose our data have been aggregated into bins with edge length . In the -matrix C, we count the number of observations per bin. Its entries are defined as the number of claims i for which is in bin j and is in bin k. In another matrix D, the cumulative numbers of events with respect to T are given by for . The triangle represents the future and therefore contains no claim counts. This is the part we want to forecast. Now, the development factors are defined as
For the calculation of , the last available entry with claims that were delayed years ( in row ) is omitted, which can be seen as scaling by exposure. In the chain-ladder method, the development factors are then used to extrapolate the claim numbers in the cumulative matrix D into the future via
and for . The total number of outstanding claims is then given by the last column of the estimated cumulative aggregated data
We now link development factors to hazard estimation. Hiabu (2017) has proved the asymptotic relationship
for being a histogram-type hazard estimator of the delay in reversed time, the j-th bin of the aggregated data, and the bin width that satisfies for . However, this relationship was introduced under the assumption that accident date and settlement delay are independent. As an alternative for our Model (1), we define granular time-dependent development factors as
where is the j-th bin for the delay and the k-th one for accident date for . Then, we use our time-dependent development factors to forecasts reserves from a granular cumulative triangle D via
and for . The difference to chain-ladder is that our development factors additionally depend on the row k and that we calculate them on a finer grid, i.e., smaller , larger m, and more granular matrices C and D. In the application in Section 6, we use monthly aggregated data for the operational time hazard estimator and quarterly aggregated data for chain-ladder. Ideally, daily or even more granular data should be used for the proposed hazard estimator; however, this was practically computationally infeasible in our application. Analogously to chain-ladder, our final estimate for the number of outstanding payments is the last column in the estimated cumulative triangle .
Figure 2 illustrates how development factors are used for extrapolation. The cumulated data is given in black, forecasts are in red and all development factors are given in blue. Our proposed time-dependent development factors can be used like traditional development factors but vary for different rows of the cumulative triangle. The illustration in Figure 2 does not show the fact that our time-dependent development factors are computed on a finer scale than for chain-ladder. Moreover, the shift x-direction through operational time cannot be seen in the illustration.
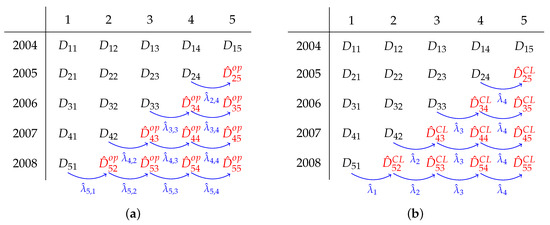
Figure 2.
Forecasting outstanding claim numbers with time-dependent development factors and chain-ladder development factors. Illustrative example with five accident years and maximum settlement delay of five years. (a) forecasting with time-dependent development factors via Equation (13); (b) forecasting with chain-ladder development factors via Equation (12).
5. Bandwidth Selection
For computational reasons, bandwidth selection is done via K-fold cross-validation (Lee et al. 2017) for . The set of observations is randomly split into K disjoint parts of equal size via . To find the optimal bandwidth, we minimize the score function
for partial validation scores
The estimator is the estimator defined in Equation (4) with bandwidth b, but computed for observations only. It is being validated against the observations . Being asymptotically equivalent, the estimate is a proxy to the first two terms of the validation score
that occur after solving the quadratic expression in the integral, in which the true hazard is unknown (Gámiz et al. 2013; Nielsen and Linton 1995). The preferred alternative, leave-one-out cross-validation, is practically unfeasible since the algorithm in Section 3 is too computationally expensive.
6. Application: Estimation of Outstanding Liabilities
We apply our estimation procedure on a data set from a Cypriot motor insurance business line. This data set contains n = 51,216 paid claims that were recorded between 1 January 2004 and 31 December 2013. First, we estimate operational time and the baseline hazard on the data set. Making use of the resulting structured conditional hazard estimate , we estimate outstanding liabilities through the approach with time-dependent development factors illustrated in Section 4.
For each claim , the data set contains the accident date and the payment date. Instead of the settlement date, we define the settlement delay as the difference between payment date and accident date. Afterwards, we normalize the data such that the accident date and settlement delay take values in . Now, the data are arranged on a triangular shaped support for days with accident date x and settlement delay t as described in Section 2.2. For computational reasons, the data are aggregated into a monthly run-off triangle
on which and are estimated. As the kernel function, we choose a multiplicative kernel with k being the Epanechnikov kernel . The data-driven bandwidth selection procedure in Section 5 leads to the optimal bandwidths months and months for delay and accident date, respectively. For the estimation of , we minimize the loss functions (11) in the interval for every in every iteration of the algorithm.
The estimated baseline hazard and operational time are shown in Figure 3. For the operational time estimate in Figure 3a, the settlement delay at 1 January 2004 is used as benchmark and claim settlement for most accident dates between February 2004 and December 2005 is slightly slower than this benchmark. In November 2004, the operational time estimator catches a trend towards faster settlement of claims despite short declines in 2005 and 2009. This phenomenon is most likely due to the improved use of technology in the insurance company and has also been observed on the same data set in Lee et al. (2017). The decrease of speed in claims finalization at the end of 2005 and 2009 could be due to new employees in the reserving department who are training in their first months. The average accident that happened after January 2006 was settled faster than our benchmark with the value of the operational time estimate being below 1 for this period. After 2010, our model shows the fastest processing and payments of claims. Due to high variation in the estimation of in the lower corner of the run-off triangle, we recommend to set to the value of the previous month for the last five months (about the last of the support of ). Note that this adjustment is still in the spirit of our approach to improve in the estimation by chain-ladder (and even multiplicative nonparametric methods as in Martínez-Miranda et al. (2013) and Hiabu et al. (2016)) because a constant operational time value corresponds to the case where T and X are independent and we still allow for dependency through operational time for of the accident dates. We want to remark that this issue does not occur if un-truncated data (on a squared support instead of a triangular one) is given. The baseline hazard estimate of the payment delay (in forward time) in Figure 3b has the expected shape with a steep decrease for short delays and a value close to zero for delays larger than 1.5 years. This shape indicates that the vast majority of the claims in this data set were paid off within the first year as can be seen in Figure 1.
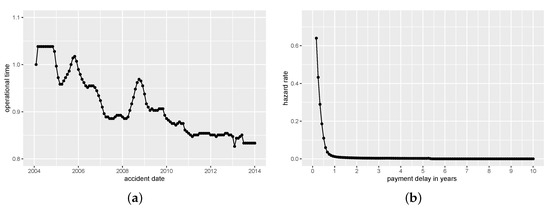
Figure 3.
Estimated components of hazard rate of the payment delay T: (a) operational time estimate with optimal bandwidths; (b) baseline hazard estimate of payment delay (in forward time) with optimal bandwidths.
The estimated outstanding liabilities by accident year and by payment year are given in Table 1. The results from the chain-ladder method with quarterly aggregated data are used as a benchmark. The shift through operational time yields less claims than chain-ladder for all payment years except for 2016. Since the value of the operational time estimate (Figure 3a) is below the benchmark 1 for all claims with accident year later than 2005, these claims were settled faster than older claims. These claims constitute the majority of outstanding claims since most claims are estimated to be settled within one and a half years (Figure 3b). Hence, most claims are expected to be paid out earlier than estimated through average payment delay in the chain-ladder method. The same effect can be seen with respect to accident years. On 31 December 2013, the date of data collection, our operational time estimator forecasts old claims from accidents before 2009 to be paid off since their settlement delay is expected to be shorter than average settlement. On the other hand, chain-ladder still estimates a few claims from accidents between 2005 and 2008. In total, for this data set, the estimated number of outstanding payments by operational time is lower (1054) than the reserve estimate by quarterly chain-ladder (1414).

Table 1.
Estimated number of outstanding claims through hazard with operational time (op. time) and quarterly chain-ladder (CL) by accident year and payment year.
Although the comparison might seem unfair at first due to different levels of aggregation, more granular aggregation for chain-ladder would not improve the quality of its estimates. As shown in a simulation study in Baudry and Robert (2019), even when enough data are available for monthly aggregation, chain-ladder reserve estimates based on monthly data show very high variance, making them effectively unreliable in practice; however, monthly data are necessary for chain-ladder if one is interested, for instance, in the estimation of monthly cash-flows. This phenomenon has been confirmed in a simulation in Bischofberger et al. (2019), in which kernel estimators picked larger bandwidths while still being able to yield monthly cash-flow predictions. Furthermore, chain-ladder is typically used on at least quarterly aggregated data to prevent columns that contain only zeros in the run-off triangle. Where the chain-ladder algorithm cannot handle this issue, our operational time hazard estimator can cope with it.
In an independence test based on Conditional Kendall’s tau for truncated data (Austin and Betensky 2014; Martin and Betensky 2005), the hypothesis of independent settlement delay T and accident date X was rejected. Hence, the assumptions of the chain-ladder model of Mack (1993) are violated (Hiabu 2017) and one cannot rely on its estimate in this data set. Since the chain-ladder model with independent variables is nested within our prosed operational time Model (1), we recommend our model—although inference for our operational time structure has not been carried out. With the hazard Model (3) being rather involved, the theory for a hypothesis test for the operational time structure is beyond the scope of this article.
Choices of bandwidths with higher validation scores can lead to unrealistic reserve estimates that differ from the chain-ladder estimate by up to 100%. On the one hand, the operational time hazard estimator is sensitive to the choice of bandwidth. On the other hand, the result obtained through cross-validation is stable with four bandwidth choices close to the optimal validation score resulting in very similar estimates of the number of outstanding claims.
7. Conclusions
We introduced a new hazard model that allows for operational time in right-truncated data as present in run-off triangles. In a structured hazard model, the conditional hazard rate of the settlement delay given the accident date is expressed through operational time (a function of the accident date) and the baseline hazard of the settlement delay (cleared of effects from accident date). Minimizing an integrated squared loss, we define nonparametric estimators of operational time and the baseline hazard. These estimators are calculated through an iterative algorithm that updates the estimates of operational time and the baseline hazard in each iteration until it converges. If no right-truncation is present, our hazard model is a nonparametric extension of the accelerated failure model with a one-dimensional covariate.
Our estimation procedure detects operational time in the data and corrects for it in the estimation process. Therefore, it can be classified as an unsupervised machine learning technique. Since operational time is a common source of dependence between accident date and settlement date in the data, we recommend the approach illustrated here if one cannot prove independent covariates in the date through hypothesis testing (and other structural dependencies like seasonal effects can be ruled out). Even if the accident date and settlement are independent, our estimator works and estimates operational time . However, in the latter case or if independence is not rejected by a statistical test, estimation via chain-ladder tends to be more stable than our operational time hazard estimates and should be considered.
In an application in a real data set of paid claims, we forecast the number of outstanding claims for a motor insurance business line. For this purpose, we suggested to transform our operational time and baseline hazard estimators into time-dependent development factors. These are then used to extrapolate the claim numbers in the data set analogously to what is done in the chain-ladder method.
The downsides of the approach illustrated here are computational complexity and numerical instability of the operational time estimator on the data in the last 5–10% of accident dates, i.e., in the lower corner of the run-off triangle. The latter issue also arises in many other approaches to non-life claims reserving. Our suggested way to deal with it in our model is to set the value of operational time to the last stable value for the affected dates, which corresponds to the assumption of independent accident date and settlement delay on the most recent accident dates. Therefore, our approach still corrects for operational time on more than 90–95% of the data and in the remaining data it is as good as kernel hazard methods that assume independent variables.
Funding
This work was supported by the Deutsche Forschungsgemeinschaft (DFG) through the Research Training Group RTG 1953.
Acknowledgments
The author would like to thank Munir Hiabu and Enno Mammen for valuable advice.
Conflicts of Interest
The author declares no conflict of interest.
Appendix A. Alternative Local Constant Estimators
As an alternative to the local linear estimator of in Equation (7), one could use the local constant estimator
with
It is defined through the integrated squared loss minimization
for and as before. The term is again needed to make the expression well-defined.
References
- Aalen, Odd O. 1980. A model for nonparametric regression analysis of counting processes. In Mathematical Statistics and Probability Theory. Lecture Notes in Statistics. Edited by Witold Klonecki, Andrzej Kozek and Jan Rosiński. New York: Springer, vol. 2, pp. 1–25. [Google Scholar]
- Andersen, Per K., Ørnulf Borgan, Richard D. Gill, and Niels Keiding. 1993. Statistical Models Based on Counting Processes. New York: Springer. [Google Scholar]
- Antonio, Katrien, and Richard Plat. 2014. Micro-level stochastic loss reserving for general insurance. Scandinavian Actuarial Journal 2014: 649–69. [Google Scholar] [CrossRef]
- Austin, Matthew D., and Rebecca A. Betensky. 2014. Eliminating bias due to censoring in kendall’s tau estimators for quasi-independence of truncation and failure. Computational Statistics & Data Analysis 73: 16–26. [Google Scholar]
- Avanzi, Benjamin, Bernard Wong, and Xinda Yang. 2016. A micro-level claim count model with overdispersion and reporting delays. Insurance: Mathematics and Economics 71: 1–14. [Google Scholar] [CrossRef][Green Version]
- Badescu, Andrei L., X. Sheldon Lin, and Dameng Tang. 2016. A marked Cox model for the number of IBNR claims: Theory. Insurance: Mathematics and Economics 69: 29–37. [Google Scholar] [CrossRef]
- Baudry, Maximilien, and Christian Y. Robert. 2019. A machine learning approach for individual claims reserving in insurance. Applied Stochastic Models in Business and Industry 35: 1127–55. [Google Scholar] [CrossRef]
- Berkson, Joseph. 1980. Minimum chi-square, not maximum likelihood! The Annals of Statistics 8: 457–87. [Google Scholar] [CrossRef]
- Bischofberger, Stephan M., Munir Hiabu, and Alex Isakson. 2019. Continuous chain-ladder with paid data. Scandinavian Actuarial Journal. [Google Scholar] [CrossRef]
- Buckley, Jonathan, and Ian James. 1979. Linear regression with censored data. Biometrika 66: 429–36. [Google Scholar] [CrossRef]
- Bühlmann, Hans. 1970. Mathematical Methods in Risk Theory. Berlin: Springer. [Google Scholar]
- Cho, Youngjoo, Chen Hu, and Debashis Ghosh. 2018. Covariate adjustment using propensity scores for dependent censoring problems in the accelerated failure time model. Statistics in Medicine 37: 390–404. [Google Scholar] [CrossRef]
- Cox, David R. 1972. Regression models and life tables. Journal of the Royal Statistical Society: Series B 34: 187–220. [Google Scholar]
- Cox, David R., and David Oakes. 1984. Analysis of Survival Data, 1st ed. Boca Raton: Chapman & Hall/CRC. [Google Scholar]
- Crevecoeur, Jonas, Katrien Antonio, and Roel Verbelen. 2019. Modeling the number of hidden events subject to observation delay. European Journal of Operational Research 277: 930–44. [Google Scholar] [CrossRef]
- England, Peter D., and Richard J. Verrall. 2002. Stochastic claims reserving in general insurance. British Actuarial Journal 8: 443–544. [Google Scholar] [CrossRef]
- Feller, William. 1971. An Introduction to Probability Theory and Its Applications. New York: John Wiley & Sons, vol. 2. [Google Scholar]
- Fulcher, Isabel R., Eric Tchetgen Tchetgen, and Paige L. Williams. 2017. Mediation analysis for censored survival data under an accelerated failure time model. Epidemiology 28: 660–66. [Google Scholar] [CrossRef] [PubMed]
- Gabrielli, Andrea, Ronald Richman, and Mario V. Wüthrich. 2019. Neural network embedding of the over-dispersed Poisson reserving model. Scandinavian Actuarial Journal. [Google Scholar] [CrossRef]
- Gámiz, María Luz, Lena Janys, María Dolores Martínez-Miranda, and Jens Perch Nielsen. 2013. Bandwidth selection in marker dependent kernel hazard estimation. Computational Statistics & Data Analysis 68: 155–69. [Google Scholar]
- Hastie, Trevor, Robert Tibshirani, and Jerome Friedman. 2008. The Elements of Statistical Learning: Data Mining, Inference and Prediction. New York: Springer. [Google Scholar]
- Hiabu, Munir. 2017. On the relationship between classical chain ladder and granular reserving. Scandinavian Actuarial Journal 2017: 708–29. [Google Scholar] [CrossRef]
- Hiabu, Munir, Enno Mammen, María Dolores Martínez-Miranda, and Jens Perch Nielsen. 2016. In-sample forecasting with local linear survival densities. Biometrika 103: 843–59. [Google Scholar] [CrossRef]
- Huang, Jinlong, Chunjuan Qiu, Xianyi Wu, and Xian Zhou. 2015. An individual loss reserving model with independent reporting and settlement. Insurance: Mathematics and Economics 64: 232–45. [Google Scholar] [CrossRef]
- Jewell, William S. 1989. Predicting IBNYR events and delays I. Continuous time. ASTIN Bulletin 19: 25–55. [Google Scholar] [CrossRef]
- Jewell, William S. 1990. Predicting IBNYR events and delays II. Discrete time. ASTIN Bulletin 20: 93–111. [Google Scholar] [CrossRef]
- Kalbfleisch, John D., and Ross L. Prentice. 2002. The Statistical Analysis of Failure Time Data, 2nd ed. Wiley Series in Probability and Statistics; Hoboken: John Wiley & Sons. [Google Scholar]
- Kremer, Erhard. 1982. IBNR-claims and the two-way model of ANOVA. Scandinavian Actuarial Journal 1982: 47–55. [Google Scholar] [CrossRef]
- Kuang, Di, Bent Nielsen, and Jens Perch Nielsen. 2009. Chain-ladder as maximum likelihood revisited. Annals of Actuarial Science 4: 105–21. [Google Scholar] [CrossRef]
- Kuo, Kevin. 2019. Deeptriangle: A deep learning approach to loss reserving. Risks 7: 97. [Google Scholar] [CrossRef]
- Larsen, Christian Roholte. 2007. An individual claims reserving model. ASTIN Bulletin 37: 113–32. [Google Scholar] [CrossRef]
- Lee, Young K., Enno Mammen, Jens Perch Nielsen, and Byeong U. Park. 2015. Asymptotics for in-sample density forecasting. The Annals of Statistics 43: 620–51. [Google Scholar] [CrossRef]
- Lee, Young K., Enno Mammen, Jens Perch Nielsen, and Byeong U. Park. 2017. Operational time and in-sample density forecasting. The Annals of Statistics 45: 1312–41. [Google Scholar] [CrossRef][Green Version]
- Li, Jialiang, and Baisuo Jin. 2018. Multi-threshold accelerated failure time model. The Annals of Statistics 46: 2657–82. [Google Scholar] [CrossRef]
- Linton, Oliver B., Enno Mammen, Jens Perch Nielsen, and Ingrid Van Keilegom. 2011. Nonparametric regression with filtered data. Bernoulli 17: 60–87. [Google Scholar] [CrossRef]
- Louis, Thomas A. 1981. Nonparametric analysis of an accelerated failure time model. Biometrika 68: 381–90. [Google Scholar] [CrossRef]
- Mack, Thomas. 1993. Distribution-free calculation of the standard error of chain ladder reserve estimates. ASTIN Bulletin 23: 213–25. [Google Scholar] [CrossRef]
- Mammen, Enno, María Dolores Martínez-Miranda, and Jens Perch Nielsen. 2015. In-sample forecasting applied to reserving and mesothelioma. Insurance: Mathematics and Economics 61: 76–86. [Google Scholar] [CrossRef]
- Martin, Emily C., and Rebecca A. Betensky. 2005. Testing quasi-independence of failure and truncation times via conditional Kendall’s tau. Journal of the American Statistical Association 100: 484–92. [Google Scholar] [CrossRef]
- Martínez-Miranda, María Dolores, Jens Perch Nielsen, Stefan Sperlich, and Richard J. Verrall. 2013. Continuous chain ladder: Reformulating and generalising a classical insurance problem. Expert Systems with Applications 40: 5588–603. [Google Scholar] [CrossRef]
- Miller, Rupert G. 1976. Least squares regression with censored data. Biometrika 63: 449–64. [Google Scholar] [CrossRef]
- Nielsen, Jens Perch. 1998. Marker dependent kernel hazard estimation from local linear estimation. Scandinavian Actuarial Journal 1998: 113–24. [Google Scholar] [CrossRef]
- Nielsen, Jens Perch, and Oliver B. Linton. 1995. Kernel estimation in a non-parametric marker dependent hazard model. The Annals of Statistics 23: 1735–48. [Google Scholar] [CrossRef]
- Nielsen, Jens Perch, and Carsten Tanggaard. 2001. Boundary and bias correction in kernel hazard estimation. Scandinavian Journal of Statistics 28: 675–98. [Google Scholar] [CrossRef]
- Norberg, Ragnar. 1993. Prediction of outstanding liabilities in non-life insurance. ASTIN Bulletin 23: 95–115. [Google Scholar] [CrossRef]
- Norberg, Ragnar. 1999. Prediction of outstanding liabilities II. Model variations and extensions. ASTIN Bulletin 29: 5–25. [Google Scholar] [CrossRef]
- Reid, D. H. 1978. Claim reserves in general insurance. Journal of the Institute of Actuaries 105: 211–315. [Google Scholar] [CrossRef]
- Renshaw, Arthur E., and Richard J. Verrall. 1998. A stochastic model underlying the chain-ladder technique. British Actuarial Journal 4: 903–23. [Google Scholar] [CrossRef]
- Ritov, Ya’acov, and Jon A. Wellner. 1988. Censoring, martingales, and the cox model. Contemporary Mathematics 80: 191–219. [Google Scholar]
- Swishchuk, Anatoliy. 2016. Change of Time Methods in Quantitative Finance. New York: Springer. [Google Scholar]
- Taylor, Greg. 2019. Loss reserving models: Granular and machine learning forms. Risks 7: 82. [Google Scholar] [CrossRef]
- Taylor, Greg, and Gráinne McGuire. 2016. Stochastic Loss Reserving Using Generalized Linear Models. Arlington: Casualty Actuarial Society. CAS Monograph Series; Number 3. [Google Scholar]
- Taylor, Greg, Gráinne McGuire, and James Sullivan. 2008. Individual claim loss reserving conditioned by case estimates. Annals of Actuarial Science 3: 215–56. [Google Scholar] [CrossRef]
- Taylor, Greg. 1981. Speed of finalization of claims and claims runoff analysis. ASTIN Bulletin 12: 81–100. [Google Scholar] [CrossRef][Green Version]
- Taylor, Greg. 1982. Zehnwirth’s comments on the see-saw method: A reply. Insurance: Mathematics and Economics 1: 105–108. [Google Scholar] [CrossRef]
- Verrall, Richard J. 1991. Chain ladder and maximum likelihood. Journal of the Institute of Actuaries 118: 489–99. [Google Scholar] [CrossRef]
- Ware, James H., and David L. DeMets. 1976. Reanalysis of some baboon descent data. Biometrics 32: 459–63. [Google Scholar] [CrossRef]
- Wüthrich, Mario V. 2018. Machine learning in individual claims reserving. Scandinavian Actuarial Journal 2018: 465–80. [Google Scholar] [CrossRef]
- Zhao, Xiao Bing, and Xian Zhou. 2010. Applying copula models to individual claim loss reserving methods. Insurance: Mathematics and Economics 46: 290–99. [Google Scholar] [CrossRef]
- Zhao, Xiao Bing, Xian Zhou, and Jing Long Wang. 2009. Semiparametric model for prediction of individual claim loss reserving. Insurance: Mathematics and Economics 45: 1–8. [Google Scholar] [CrossRef]
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).