Abstract
This study examines the out-of-sample predictability of expected skewness of oil price returns, which serves as a metric for global future risks, as we show statistically through the association with crises of different nature, for stock returns of 10 (8 advanced plus two emerging) countries using long-range monthly data of over a century for each country. Using a distributed lag predictive econometric model, which controls for endogeneity, persistence, and conditional heteroscedasticity, we provide evidence of the strong statistical significance of the predictive impact of the third moment of oil price returns for equity returns for all the countries across various forecast horizons and the length of out-of-sample periods. These findings also hold for the shorter sample periods of 3 other emerging markets: Brazil, China, and Russia. Our findings have important implications for academics, investors, and policymakers.
1. Introduction
The existing connection between oil and stock markets is unlikely to weaken in the foreseeable future. Oil remains a critical input that significantly affects corporate earnings and, consequently, stock market behavior. Additionally, fluctuations in oil prices directly impact consumer income, which, in turn, influences the demand for goods and services produced by the listed companies in the stock exchange markets. Other key factors, such as geopolitical and climate-related risks—including the Russia–Ukraine War, the Palestine–Israel conflict, and wildfires in the US and Australia, etc.—have further shaped the relationship between oil and stock markets (; ). For instance, the recent Russia–Ukraine conflict highlighted this dynamic, as it contributed to a decline in global aggregate demand ().
The international literature associating oil prices and/or returns to the predictability of stock prices and/or returns, as well as the equity-premium, is enormous, to say the least, with the reader referred to (), () and () for detailed reviews. Within these studies, recent works (see, for example, ; ; ; ) have highlighted the role of asymmetric oil price/and or returns in predicting stock returns, to the extent that (), (), and () have shown the importance of the skewness of oil price returns in forecasting stock returns. Recall that skewness is a measurement of the distortion of symmetrical distribution or a measure of asymmetry in a dataset. Therefore, skewness (in oil returns) can be quantified as a representation of the extent to which a given distribution deviates from the normal distribution (of oil market returns) and, hence, can act as a metric of the evolution of unbalanced (relative to a baseline) future risks ().
Theoretically, the predictability of stock returns based on the skewness of oil price returns can be explained through the impact on cash flows, discount factors, interest rates, and inflation (), as well as through the recent process of financialization observed around the turn of the century, and especially after the Global Financial Crisis (). More elaborately, oil prices can directly and indirectly influence stock market returns, primarily through their impact on cash flows. The effect of oil price fluctuations on the economic fundamentals of various countries largely depends on their status as oil importers or exporters. This dynamic is well captured by the income transfer theory, which posits that rising oil prices result in income transfer from net oil-importing countries to net oil-exporting countries. Consequently, oil price shocks are likely to produce differential impacts on the stock markets of these two groups of countries.
Moreover, the predictability of oil prices for stock market returns may be attributed to the financialization of oil markets. This phenomenon allows market participants to diversify their portfolios by incorporating oil-related derivatives, thereby improving their ability to hedge against risk (; ). Furthermore, the predictability of oil for stock returns arises from oil price changes affecting key economic factors, such as the discount rate, interest rates, and inflation (), which indirectly contribute to variations in excess returns. In addition, the skewness of oil price returns has also been shown to contain leading information for not only oil price returns (; ) but also its volatility (), which then (indirectly) feeds into movements in stock returns (; ).
Meanwhile, previous studies have largely focused on the first- and second-moment predictability of crude oil for stock returns while overlooking the higher moments. This study, therefore, contributes to the line of literature addressing this gap by examining the out-of-sample predictability of oil return skewness for stock returns in both developed economies (G7 plus Switzerland) and emerging markets (BRICS), enhancing our findings’ generalizability.
Against this backdrop, the objective of our paper is to extend the works of (), () and () on forecastability of aggregate and industry-level stock returns of China and the United States (US), due to expected skewness of oil returns spanning three decades of recent data, to as many as 10 (8 developed and two emerging) international stock markets covering over a century of data in each case. In fact, for the US and the United Kingdom (UK), our analysis covers the complete modern era of the petroleum industry with the drilling of the first oil well in the US at Titusville, Pennsylvania, in 1859, due to the availability of corresponding equity price data even before this period. For the rest of the countries, i.e., Canada, France, Germany, India, Italy, Japan, South Africa, and Switzerland, we are able to cover their entire history of stock returns movement in relation to oil price returns skewness.
Utilizing the longest possible data samples prevents the so-called “sample selection bias”. In the process, we capture various positive and negative oil shocks associated with, for example, the US Civil War, the two World Wars, the West Coast gas famine, the Great Depression, the Korean conflict, the Suez Crisis, the OPEC oil embargo, the Iranian revolution, the Iran–Iraq War, the Gulf War, the Global Financial Crisis, the outbreak of the Coronavirus pandemic in 2020, and, of course, more recently ongoing Russia–Ukraine War.1
Note that, as indicated by (, ), the best test of any predictive model (with regards to the econometric methods used and in terms of the predictors employed) is in its out-of-sample forecasting performance rather than in-sample predictability. Given this, econometrically speaking, for our forecasting exercise, we adopt the (, )-type distributed lag model framework, which accommodates salient data characteristics, such as endogeneity, persistence, and conditional heteroscedasticity that are commonly found in historical equity and oil markets datasets (, ; ). To the best of our knowledge, ours is the first work to forecast international stock returns spanning over 100 years of monthly data based on the information content of skewness of oil price returns, and in the process also adds to the voluminous literature on forecasting equity returns of developed and emerging countries (see ; ; for comprehensive reviews) by relying on a new-metric, i.e., skewness, associated with the (third moment) of oil price returns, which inherently incorporates information of the first and second moments, utilized primarily thus far in this area of stock and oil nexus.
2. Variables and Methodology
2.1. Data
The dataset consists of the market indexes of 8 advanced economies, which include the G7, with the name of the stock index, and sample periods of the corresponding log-returns noted in parenthesis: Canada (S&P TSX 300 Composite Index; 1915:02–2023:09), France (CAC All-Tradable Index; 1898:01–2023:09), Germany (CDAX Composite Index; 1870:01–2023:09), Italy (Banca Commerciale Italiana Index; 1905:02–2023:09), Japan (Nikkei 225 Index; 1914:08–2023:09), the UK (FTSE All Share Index; 1859:10–2023:09), the US (S&P500 Index; 1859:10–2023:09), plus Switzerland (All Share Stock Index; 1916:02–2023:09).2 The two emerging markets considered are India (Bombay Stock Exchange Index; 1920:08–2023:09), and South Africa (Johannesburg All Share Stock Index; 1910:2023:09). The crude oil price is represented by the West Texas Intermediate (WTI; 1859:10–2023:09), the expected skewness of which is computed from its log-returns. The coverage of the sample periods is purely driven by data availability, with all the variables sourced from the Global Financial Data.3
Building on the foregoing, the descriptive statistics of our variables (oil and stock returns) are presented, alongside figures illustrating the co-movement between oil return (and skewness) and stock returns across the G7 plus Switzerland, and the entire BRICS countries (see Table A1 and Figure A1 in Appendix A of the paper). The figures provide evidence that both positive and negative oil returns (skewness) exhibit predictive potential for stock returns in these countries, as the latter tends to portray a mean-reverting tendency regardless of fluctuations in the former. Furthermore, we have also partitioned the descriptive statistics into distinct sub-sample periods, including the Great Depression, World Wars, OPEC emergence, COVID-19 period, and Russia–Ukraine War. Importantly, the summary statistics provided additional nuances to the illustrated trends.
2.2. Econometric Model
As pointed out above, we utilize the WN-type distributed lag model framework, which accommodates salient long data characteristics, such as endogeneity, persistence, and conditional heteroscedasticity. The model tackles endogeneity and persistence through the inclusion of a differencing term while addressing heteroscedasticity involves pre-weighting the model variables using the inverse of the standard deviation of the residuals from the conventional Generalized Autoregressive Conditional Heteroskedasticity (GARCH(1,1)) model. Formally, the WN-type distributed lag model can be described as follows:
where is the log-returns of the stock price computed as , and is oil price returns skewness. denotes the constant; denotes the slope coefficients associated with the incorporated predictor; represents the endogeneity/persistence adjustment terms in Equation (1), for with being the autoregressive coefficient of the predictor variable, indicating the corresponding degree of persistence; is the non-linear trend of the stock returns, which is obtained from the () filter; while is the residual term that follows a white noise process.
rstkt = α + β1skoilt−1 + β2Δskoilt + β3ntrend + εt
In order to obtain a time-varying measure of the expected skewness of oil returns (roilt), we estimate the following asymmetric version of the Conditional Autoregressive Value at Risk by Regression Quantiles (CaViaR) model, as developed by (), with τ depicting the quantile as follows:
Using the estimated model parameters from this quantile regression, and assuming that Equation (2) is used to form expectations, we compute the one-step-ahead, expected or predicted, well-established Kelley skewness () as follows:
We simplify the notation by setting to skoilt.
Skewness captures future risks in the oil market, and can result from variations in expected skewness, which likely originates from extreme directed changes in aggregate demand and supply, geopolitical acts and threats, rare disaster events, including pandemics, and even financial market spillovers. (). Given this, we identified various types of crises and geopolitical events in Table A2 in Appendix A of the paper; we defined a dummy variable equal to 1 for the months corresponding to such years of events and used 0 for anything otherwise. When we regressed skoilt on the dummy, we found a positive coefficient of 0.074, with a standard error of 0.015, and a t-statistic of 4.978, implying statistical significance at the 1% level, with a p-value of 0.000. This confirms that our measure of skewness can be associated with global risks, and hence, is likely to serve as a predictor for stock returns, based on the channels discussed in the introduction.
The baseline model (Model 1) is the historical average model, which is a subset of the model specification in Equation (1), when the comprising slope coefficients are set to zero. Model 2, as specified in Equation (1), assesses the predictability of oil price returns skewness for stock returns after controlling for the existent persistence and non-linear trend.
We employ the () test to formally compare Model 2, with the historical average, i.e., Model 1, given that the latter is nested in the former. The CW metric works effectively for nested models, examining whether the difference in forecast errors of the competing models is negligible. The estimation equation for the CW test statistic is provided in Equation (4):
where denotes the forecast horizon; and denote the squared residuals from the restricted and unrestricted model variants, respectively, of our WN-type distributed lag model; while represents an adjusted squared residual that is peculiar to the CW test and incorporated as a corrective measure for the noisy forecasts of the larger model. The term, is defined as , where , , and represents the number of averaged forecast points. The evaluation relies on regressing on a constant and determining whether paired forecast errors from competing models are equal or not, using the t-statistic of the estimated constant. A significant t-statistic suggests that our unrestricted predictive model performs better than the restricted benchmark model.
3. Forecasting Results
In this section, we present the CW test results of the forecasting performance of the model with the expected skewness of oil price returns, which nests the benchmark of the historical average of stock returns, i.e., without our predictor of concern. Table 1 reports the CW test statistics for h = 1, 3, and 64, with a 50% in- and out-of-sample split (following the extant literature and, in particular, ()), whereby the stock returns were cumulated for the multi-steps-ahead horizons based on the rolling window approach. We observe that the incorporation of expected oil returns skewness provides vital information that improved the stock prediction across all the countries, as depicted by the significance of the CW forecast comparison test statistics at the 1% level.

Table 1.
Forecast evaluation result using the () test statistics [50:50 data split].
For further robustness check, the case of a longer in-sample, and hence shorter out-of-sample, with a 75–25% split is also examined (see Table 2), to allow us to conduct a forecasting analysis over the most recent periods in line with the recent works of (), () and (). We find similar stances under the CW test comparison, i.e., significance at the 1% level, as with the 50–split case. This indicates that the improvement of the precision of our predictive model variant with expected skewness of oil returns over the benchmark historical average model transcends the data sample and, hence, is robust to the choice of out-of-sample periods. Our findings are consistent with the established literature highlighting the predictability of oil returns for stock returns (e.g., ; ; ; ; ; ). For example, () provide evidence that forecasts of stock market returns, derived from the skewness of oil price returns, are statistically and economically significant in out-of-sample performance.

Table 2.
Forecast evaluation result using the () test statistics [75:25 data split].
While we do not have over a century of data for Brazil (Brazil Bolsa de Valores de Sao Paulo (BOVESPA) Stock Index), China (Shanghai Stock Exchange (SSE) Composite Index), and Russia (MOEX Russia Composite Index), with our sample periods for the log-returns starting in 1954:02, 1993:01, and 1995:01, respectively, we consider these three countries to produce results for the entire BRICS bloc, just as the G7 (refer to Table 3). This is primarily in light of their importance in the global financial system in terms of their ability to provide portfolio diversification benefits relative to advanced markets (). Also, this allows us to compare our findings with the work of (), wherein the authors dealt specifically with China, with the works of () and () devoted to the US. As mentioned, all data are sourced from the Global Financial Data and ends in 2023:09. As with the 10 international stock returns with over a century of data, our results tend to carry over for the three additional emerging markets, which have relatively shorter data samples, consistently across alternative forecast horizons and in- and out-of-sample-splits. In other words, we continue to confirm the strong statistical importance (at the 1% level) of the expected skewness of oil price returns for the future path of stock returns of Brazil, China, and Russia.

Table 3.
Forecast evaluation result using the () test statistics.
As an alternative representation of our findings, we present in Figure A25 in Appendix A, the cumulative sum of squared errors for the benchmark model and the extended model with skewness over time, following (). As can be seen clearly, this metric is consistently lower for the model with skewness compared to the model without it, thus confirming graphically our statistical findings of out-of-sample forecasting reported in Table 1, Table 2 and Table 3.
In sum, in line with the existing literature, we provide evidence of the historical importance of the expected skewness of oil price returns in forecasting stock returns of both developed and emerging countries.
4. Conclusions
In this paper, we conduct an out-of-sample forecasting analysis of 10 international stock returns based on the information content of expected skewness of oil price returns, which serves as a metric of global risks, spanning over a century of data in each case. Based on a distributed lag predictive econometric framework, which controls for endogeneity, persistence, and conditional heteroscedasticity, we provide evidence of strong statistical significance of the third moment of oil price returns for equity returns of the eight developed and two emerging markets, with the result being robust to multi-steps-ahead forecast horizons and choices of the length of the out-of-sample periods. These findings also continue to hold for three other emerging markets, Brazil, China, and Russia, but with shorter sample periods.
On the one hand, finance practitioners require stock return forecasts for asset allocation. On the other hand, academics are interested in stock return forecasts since they have important implications for producing robust market efficiency measures, which, in turn, help to produce more realistic asset pricing models. Understandably, our results have important multi-layer implications. First, investors would need to account for the expected skewness of oil price returns in their portfolio decisions, which are based on accurate forecasts of stock returns. Second, from the perspective of academicians, our results suggest that stock markets are at least weakly inefficient, and the role of global risks, as captured by the third moment of oil returns, must be incorporated into asset pricing models. Finally, with stock market movements being a predictor of the real economy (), policy authorities would need to closely monitor the expected skewness of oil price returns to understand the future movements in output and inflation and accordingly design policy responses.
As part of future research, extending our analysis to forecasting stock return volatility would be interesting due to the expected skewness of oil price returns. Future research could explore whether the predictive power of oil price return skewness for stock return volatility varies across sectors, such as energy and technology, and how this relationship behaves, particularly during periods of economic crises, geopolitical tensions, or shifts in energy policy.
Author Contributions
Conceptualization, R.G.; methodology, A.A.S.; software, A.A.S.; validation, R.G.; formal analysis, A.A.S.; investigation, R.G. and A.A.S.; resources, R.G. and A.A.S.; data curation, R.G.; writing—original draft preparation, R.G. and A.A.S.; writing—review and editing, R.G. and A.A.S.; visualization, R.G. and A.A.S.; project administration, R.G.; supervision, A.A.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data will be made available upon request.
Acknowledgments
We would like to thank editor and the four anonymous referees, and the Editor of the Special Issue, for many helpful comments. Any remaining errors are solely ours.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Table A1.
Descriptive statistics of oil and stock returns across various periods.
Table A1.
Descriptive statistics of oil and stock returns across various periods.
| Full Sample | Ward War I [1914–1918]6 | Great Depression [1929–1941]7 | Ward War II [1939–1945]8 | OPEC Formation [September 1960–Present]9 | COVID-19 [December 2019–December 2023]10 | Invasion of Ukraine by Russia [February 2022–Present]11 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| G7 Countries + Switzerland | Oil Return | Stock Return | Oil Return | Stock Return | Oil Return | Stock Return | Oil Return | Stock Return | Oil Return | Stock Return | Oil Return | Stock Return | Oil Return | Stock Return |
| Canada (1915:01–2023:09) | 0.31 (7.00) | 0.40 (4.47) | 2.11 (4.26) | 0.18 (2.25) | −0.26 (5.75) | −0.67 (7.02) | 0.47 (3.42) | 0.33 (4.19) | 0.45 (8.00) | 0.49 (4.36) | 0.98 (16.91) | 0.37 (4.60) | 0.36 (8.44) | −0.28 (3.09) |
| France (1898:01–2023:09) | 0.33 (6.72) | 0.54 (5.1) | 0.78 (5.40) | 0.36 (3.59) | −0.26 (5.75) | 0.30 (6.64) | 0.47 (3.42) | 1.58 (7.15) | 0.45 (8.00) | 0.43 (5.21) | 0.98 (16.91) | 0.37 (5.51) | 0.36 (8.44) | −0.03 (3.89) |
| Japan (1914:08–2023:09) | 0.3 (7.0) | 0.55 (6.03) | 1.56 (4.68) | 1.15 (5.69) | −0.26 (5.75) | 0.32 (4.61) | 0.47 (3.42) | 0.09 (3.17) | 0.45 (8.00) | 0.43 (5.31) | 0.98 (16.91) | 0.74 (4.01) | 0.36 (8.44) | 0.98 (2.49) |
| Germany (1870:01–2023:09) | 0.15 (7.63) | 0.22 (7.03) | 0.78 (5.40) | −0.40 (6.40) | −0.26 (5.75) | −0.01 (4.04) | 0.47 (3.42) | 0.51 (1.61) | 0.45 (8.00) | 0.30 (5.07) | 0.98 (16.91) | 0.00 (5.61) | 0.36 (8.44) | −0.65 (4.40) |
| Italy (1905:02–2023:09) | 0.29 (6.80) | 0.42 (6.70) | 0.78 (5.40) | 0.18 (5.00) | −0.26 (5.75) | 0.23 (5.21) | 0.47 (3.42) | 1.97 (11.32) | 0.45 (8.00) | 0.25 (6.23) | 0.98 (16.91) | 0.42 (6.05) | 0.36 (8.44) | 0.01 (4.58) |
| UK (1859:10–2023:09) | 0.08 (9.28) | 0.28 (3.80) | 0.78 (5.40) | −0.21 (1.90) | −0.26 (5.75) | −0.18 (4.67) | 0.47 (3.42) | 0.50 (4.57) | 0.45 (8.00) | 0.48 (5.07) | 0.98 (16.91) | 0.07 (4.44) | 0.36 (8.44) | 0.05 (2.71) |
| USA (1859:10–2023:09) | 0.08 (9.28) | 0.41 (4.09) | 0.78 (5.40) | −0.03 (3.18) | −0.26 (5.75) | −0.62 (8.19) | 0.47 (3.42) | 0.37 (4.05) | 0.45 (8.00) | 0.58 (3.61) | 0.98 (16.91) | 0.76 (4.66) | 0.36 (8.44) | −0.18 (3.94) |
| Switzerland (1916:07–2023:09) | 0.27 (7.02) | 0.29 (4.30) | 1.44 (3.65) | −0.32 (2.00) | −0.26 (5.75) | −0.10 (5.20) | 0.47 (3.42) | 0.07 (3.06) | 0.45 (8.00) | 0.32 (4.51) | 0.98 (16.91) | 0.07 (3.87) | 0.36 (8.44) | −0.75 (3.12) |
| BRICS | ||||||||||||||
| Brazil (1954:02–2023:09) | 0.41 (7.62) | 5.19 (19.86) | - - | - - | - - | - - | - - | - - | 0.45 (8.00) | 5.47 (20.78) | 0.98 (16.91) | 0.18 (6.97) | 0.36 (8.44) | 0.45 (4.58) |
| Russia (1997:10–2023:09) | 0.48 (10.28) | 1.71 (10.45) | - - | - - | - - | - - | - - | - - | 0.48 (10.28) | 1.71 (10.45) | 0.98 (16.91) | 0.47 (7.85) | 0.36 (8.44) | −0.04 (10.15) |
| India (1921:07–2023:09) | 0.28 (6.98) | 0.48 (5.17) | - - | - - | −0.26 (5.75) | 0.20 (3.74) | 0.47 (3.42) | 0.92 (3.96) | 0.45 (8.00) | 0.79 (6.01) | 0.98 (16.91) | 1.08 (5.10) | 0.36 (8.44) | 0.56 (3.32) |
| China (1991:01–2023:09) | 0.32 (9.56) | 1.58 (14.76) | - | - | - | - | - | - | 0.32 (9.56) | 1.58 (14.76) | 0.98 (16.91) | 0.26 (4.27) | 0.36 (8.44) | −0.29 (4.49) |
| South Africa (1910:02–2024:05) | 0.30 (6.92) | 0.60 (4.46) | 0.78 (5.40) | 0.20 (2.48) | −0.26 (5.75) | 0.41 (3.88) | 0.47 (3.42) | 0.88 (2.69) | 0.45 (8.00) | 0.87 (5.38) | 0.98 (16.91) | 0.58 (4.79) | 0.36 (8.44) | −0.05 (3.55) |
Note: The mean and standard deviation (shown in parentheses) are reported. Due to variations in data scope, some countries are missing out from certain sub-sample periods. The oil return for some sample periods including OPEC emergence, COVID-19 and invasion of Ukraine by Russia have the same start and end dates across the countries (barring Russia and China which have shorter period for OPEC emergence), hence, their uniform values for both mean and standard deviation.
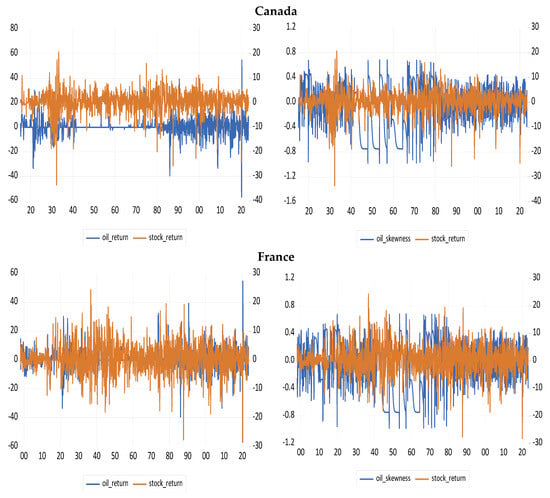
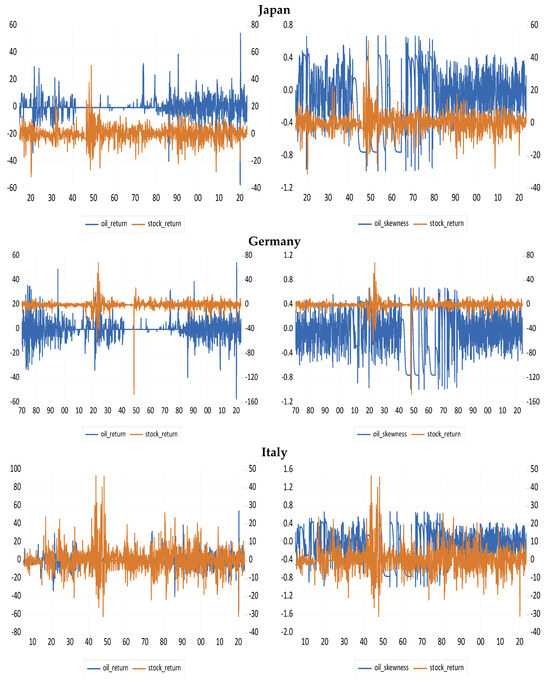
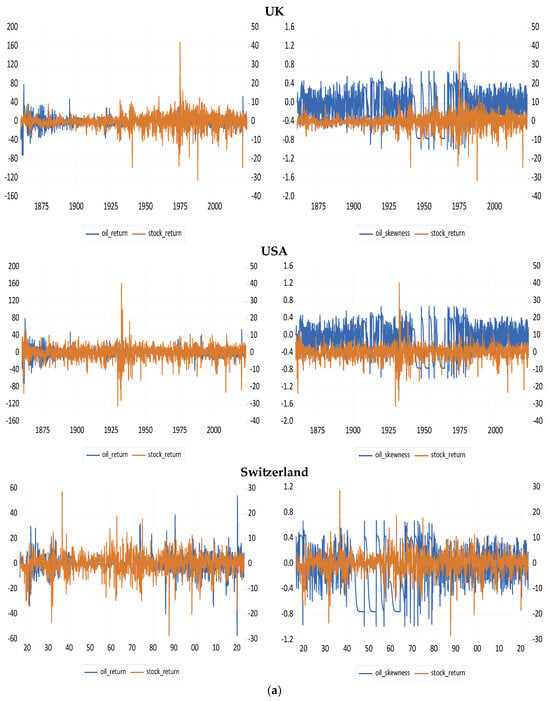
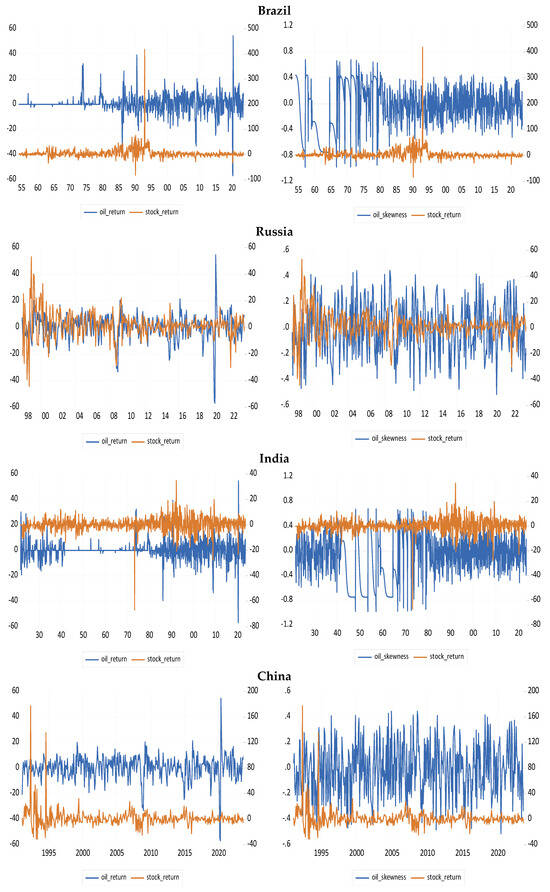
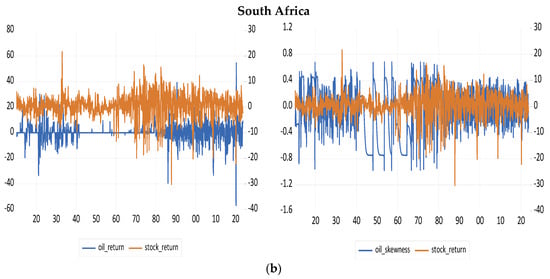
Figure A1.
Data Plots. (a): Oil return (skewness)—stock return nexus in the G7 plus Switzerland. (b): Oil return (skewness)—stock return nexus in BRICS—Brazil, Russia, India, China, and South Africa.

Table A2.
List of global crises and geopolitical events.
Table A2.
List of global crises and geopolitical events.
| Crises | Date |
|---|---|
| Panic of 1866 | 1866 |
| Great Depression of British Agriculture | 1873–1896 |
| Long Depression | 1873–1896 |
| Panic of 1901 | 1901 |
| Panic of 1907 | 1907 |
| World War I | 1914–1918 |
| Depression of 1920–21 | 1920–1921 |
| Wall Street Crash of 1929 and Great Depression | 1929–1939 |
| World War II | 1939–1945 |
| OPEC oil price shock | 1973 |
| Energy crisis | 1979 |
| Secondary banking crisis | 1973–1975 |
| Early 1980s Recession | 1981–1982 |
| Latin American debt crisis | 1982 |
| Bank stock crisis | 1983 |
| Japanese asset price bubble | 1986–1992 |
| Black Monday | 1987 |
| Savings and loan crisis | 1986–1995 |
| Special Period in Cuba | 1990–1994 |
| India economic crisis | 1991 |
| Finnish banking crisis | 1991–1993 |
| Swedish banking crisis | 1990 |
| Economic crisis in Mexico | 1994 |
| Asian financial crisis | 1997 |
| Russian financial crisis | 1998 |
| Ecuador financial crisis | 1998–1999 |
| Argentine economic crisis | 1999–2002 |
| Samba effect | 1999 |
| Dot-com bubble | 2000-2002 |
| Turkish economic crisis | 2001 |
| Uruguay banking crisis | 2002 |
| Venezuelan general strike | 2002–2003 |
| Financial Crisis | 2007–2009 |
| 2000s energy crisis | 2003–2009 |
| Subprime mortgage crisis | 2007–2010 |
| United States housing bubble and United States housing market correction | 2003–2011 |
| Automotive industry crisis | 2008–2010 |
| Icelandic financial crisis | 2008–2012 |
| Irish banking crisis | 2008–2010 |
| Russian financial crisis | 2008–2009 |
| Latvian financial crisis | 2008 |
| Venezuelan banking crisis | 2009–2010 |
| Spanish financial crisis | 2008–2016 |
| European sovereign debt crisis | 2009–2018, and ongoing |
| Portuguese financial crisis | 2010–2014 |
| Crisis in Venezuela | 2012–2018, and ongoing |
| Ukrainian crisis | 2013–2014 |
| Russian financial crisis | 2014 |
| Brazilian economic crisis | 2014–2017 |
| Chinese stock market crash | 2015 |
| Turkish currency and debt crisis | 2018 |
| Debt crisis in India | 1993–2018, and ongoing |
| COVID-19 Pandemic | 2020 |
| Russia–Ukraine War | 2022, and ongoing |
| Israel–Hamas War | 2023 |
Sources: (), (), and (, ), with data beyond 2010 derived from the list of major economic crises available online at: https://en.wikipedia.org/wiki/List_of_economic_crises (accessed on 1 June 2023).
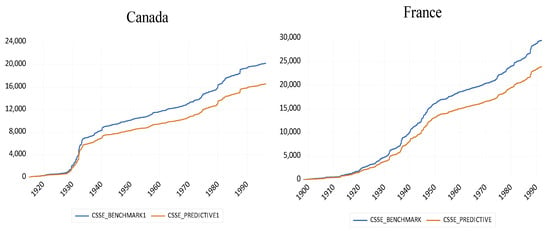
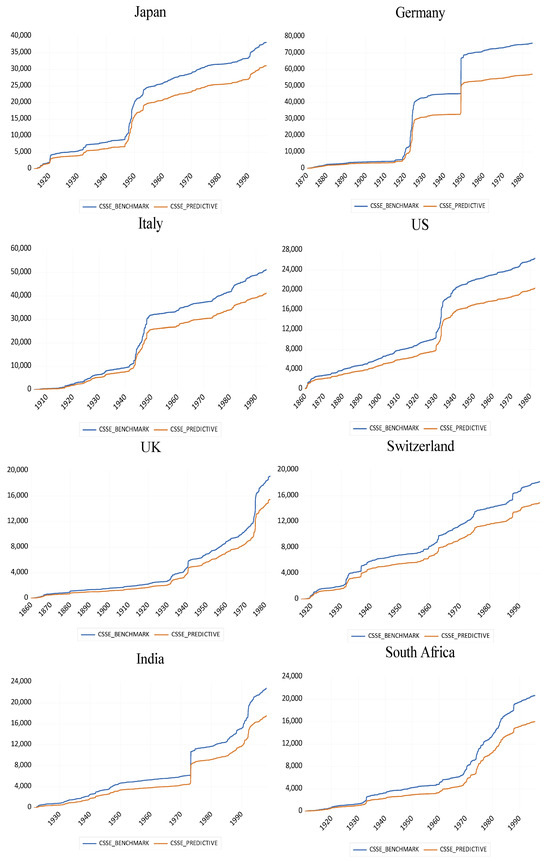
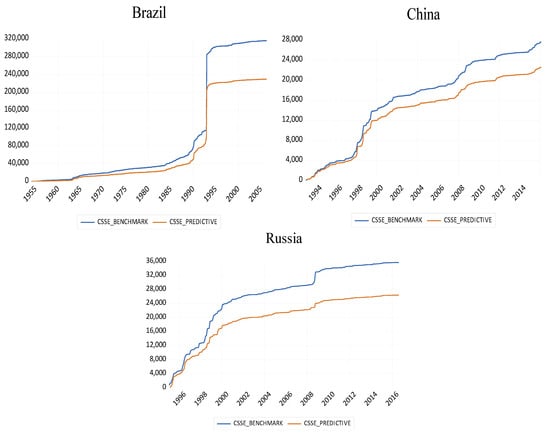
Figure A2.
Cumulative sum of squares comparison between the benchmark model and our predictive model.
Notes
| 1 | The reader is referred to () for a detailed discussion of historical oil shocks from 1859 to 2009. |
| 2 | Stock price data for the UK and the US in fact starts from 1693:01 and 1791:08, respectively. |
| 3 | https://globalfinancialdata.com/ (accessed on 1 June 2023). |
| 4 | The rationale for multiple forecast horizons is to ensure robustness while capturing short-, medium-, and longer-term effects, and providing a comprehensive understanding of how oil price skewness influences stock return over varying time scales. |
| 5 | The plots are based on a one-month ahead rolling window framework. The other forecast horizons (h = 3 and h = 6) follow the same pattern and are therefore suppressed for brevity. |
| 6 | See History.com via https://www.history.com/topics/world-war-i. Accessed on 1 June 2023. |
| 7 | According to Federal Reserve (see https://www.federalreservehistory.org/essays/great-depression#). Accessed on 1 June 2023. |
| 8 | See History.com via https://www.history.com/topics/world-war-ii. Accessed on 1 June 2023. |
| 9 | https://www.opec.org/opec_web/en/about_us/24.htm#. Accessed on 1 June 2023. |
| 10 | https://www.cdc.gov/museum/timeline/covid19.html. Accessed on 1 June 2023. |
| 11 | https://commonslibrary.parliament.uk/research-briefings/cbp-9847/. Accessed on 1 June 2023. |
References
- Balcilar, Mehmet, Rangan Gupta, and Christian Pierdzioch. 2022. Oil-price uncertainty and international stock returns: Dissecting quantile-based predictability and spillover effects using more than a century of data. Energies 15: 8436. [Google Scholar] [CrossRef]
- Balcilar, Mehmet, Rangan Gupta, and Mark E. Wohar. 2017. Common cycles and common trends in the stock and oil markets: Evidence from more than 150 years of data. Energy Economics 61: 72–86. [Google Scholar] [CrossRef]
- Balcilar, Mehmet, Rıza Demirer, and Shawkat Hammoudeh. 2019. Quantile relationship between oil and stock returns: Evidence from emerging and frontier stock markets. Energy Policy 134: 110931. [Google Scholar] [CrossRef]
- Balcilar, Mehmet, Rangan Gupta, and Stephen M. Miller. 2015. Regime switching model of US crude oil and stock market prices: 1859 to 2013. Energy Economics 49: 317–27. [Google Scholar] [CrossRef]
- Basher, Syed Abul, Alfred A. Haug, and Perry Sadorsky. 2018. The impact of oil-market shocks on stock returns in major oil-exporting countries. Journal of International Money and Finance 86: 264–80. [Google Scholar] [CrossRef]
- Bernanke, Ben. 2016. The relationship between stocks and oil prices. Ben Bernanke’s Blog on Brookings, February 19. [Google Scholar]
- Clark, Todd E., and Kenneth D. West. 2007. Approximately normal tests for equal predictive accuracy in nested models. Journal of Econometrics 138: 291–311. [Google Scholar] [CrossRef]
- Dai, Zhifeng, Huiting Zhou, Jie Kang, and Fenghua Wen. 2021. The skewness of oil price returns and equity premium predictability. Energy Economics 94: 105069. [Google Scholar] [CrossRef]
- Degiannakis, Stavros, George Filis, and Vipin Arora. 2018. Oil Prices and Stock Markets: A Review of the Theory and Empirical Evidence. The Energy Journal 39: 85–130. [Google Scholar] [CrossRef]
- Ebrahimi, Nima, and Craig Pirrong. 2018. The Risk of Skewness and Kurtosis in Oil Market and the Cross-Section of Stock Returns. Available online: https://ssrn.com/abstract=3168191 (accessed on 1 June 2023). [CrossRef]
- Engle, Robert F., and Simone Manganelli. 2004. CAViaR: Conditional Autoregressive Value at Risk by Regression Quantiles. Journal of Business & Economic Statistics 22: 367–81. [Google Scholar]
- Fernandez-Perez, Adrian, Bart Frijns, Ana-Maria Fuertes, and Joëlle Miffre. 2018. The Skewness of commodity futures returns. Journal of Banking and Finance 86: 143–58. [Google Scholar] [CrossRef]
- Galbraith, John Kenneth. 1990. A Short History of Financial Euphoria. New York: Penguin Books. [Google Scholar]
- Gupta, Rangan, and Mark Wohar. 2017. Forecasting oil and stock returns with a Qual VAR using over 150 years of data. Energy Economics 62: 181–86. [Google Scholar] [CrossRef]
- Gupta, Rangan, Florian Huber, and Philipp Piribauer. 2020. Predicting international equity returns: Evidence from time-varying parameter vector autoregressive models. International Review of Financial Analysis 68: 101456. [Google Scholar] [CrossRef]
- Gupta, Rangan, Qiang Ji, Christian Pierdzioch, and Vasilios Plakandaras. 2023. Forecasting the conditional distribution of realized volatility of oil price returns: The role of skewness over 1859 to 2023. Finance Research Letters 58: 104501. [Google Scholar] [CrossRef]
- Hamilton, James D. 2013. Historical Oil Shocks. In Routledge Handbook of Major Events in Economic History. Edited by Randall E. Parker and Robert Whaples. New York: Routledge Taylor and Francis Group, pp. 239–65. [Google Scholar]
- Hashmi, Shabir Mohsin, Bisharat Hussain Chang, and Niaz Ahmed Bhutto. 2021. Asymmetric effect of oil prices on stock market prices: New evidence from oil-exporting and oil-importing countries. Resources Policy 70: 101946. [Google Scholar] [CrossRef]
- Hodrick, Robert, and Edward C. Prescott. 1997. Postwar U.S. Business Cycles: An Empirical Investigation. Journal of Money, Credit, and Banking 29: 1–16. [Google Scholar]
- Ji, Qiang, Bing-Yue Liu, and Ying Fan. 2019. Risk dependence of CoVaR and structural change between oil international stock markets. Energy Economics 38: 136–45. [Google Scholar]
- Kelley, Truman L. 1947. Fundamentals of Statistics. Harvard: Harvard University Press. [Google Scholar]
- Kilian, Lutz, and Cheolbeom Park. 2009. The impact of oil price shocks on the US stock market. International Economic Review 50: 1267–87. [Google Scholar] [CrossRef]
- Ma, Yan-Ran, Dayong Zhang, Qiang Ji, and Jiaofeng Pan. 2019. Spillovers between oil and stock returns in the US energy sector: Does idiosyncratic information matter? Energy Economics 81: 536–44. [Google Scholar] [CrossRef]
- Mo, Xuan, Zhi Su, and Libo Yin. 2019. Can the skewness of oil returns affect stock returns? Evidence from China’s A-Share markets. North American Journal of Economics and Finance 50: 101042. [Google Scholar] [CrossRef]
- Narayan, Paresh Kumar, and Rangan Gupta. 2015. Has oil price predicted stock returns for over a century? Energy Economics 48: 18–23. [Google Scholar] [CrossRef]
- Pan, Lei, and Vinod Mishra. 2022. International portfolio diversification possibilities: Can BRICS become a destination for US investors? Applied Economics 54: 2302–19. [Google Scholar] [CrossRef]
- Rapach, David, and Guofu Zhou. 2013. Forecasting stock returns. In Handbook of Economic Forecasting. Edited by Graham Elliott and Allan Timmermann. Amsterdam: Elsevier, vol. 2 (Part A), pp. 328–83. [Google Scholar]
- Rapach, David, and Guofu Zhou. 2022. Asset Pricing: Time-Series Predictability. Oxford Research Encyclopedia of Economics and Finance. Available online: https://oxfordre.com/economics (accessed on 1 June 2023).
- Reinhart, Carmen M., and Kenneth S. Rogoff. 2009. This Time Is Different: Eight Centuries of Financial Folly. Princeton: Princeton University Press. [Google Scholar]
- Reinhart, Carmen M., and Kenneth S. Rogoff. 2011. From Financial Crash to Debt Crisis. American Economic Review 101: 1676–706. [Google Scholar] [CrossRef]
- Reinhart, Carmen M., and Vincent R. Reinhart. 2010. After the fall. Paper presented at the Economic Policy Symposium, Jackson Hole, Federal Reserve Bank of Kansas City, Jackson Hole, WY, USA, August 26–28; pp. 17–60. [Google Scholar]
- Salisu, Afees A., Abeeb O. Olaniran, and Xuan Vinh Vo. 2023. Tail risks and forecastability of stock returns of advanced economies: Evidence from centuries of data. The European Journal of Finance 29: 466–81. [Google Scholar] [CrossRef]
- Salisu, Afees A., Abeeb O. Olaniran, and Xuan Vinh Vo. 2025. Geopolitical Risk, Climate Risk and Financial Innovation in the Energy Market. Energy 2025: 134365. [Google Scholar] [CrossRef]
- Salisu, Afees A., and Rangan Gupta. 2022. Commodity Prices and Forecastability of International Stock Returns over a Century: Sentiments versus Fundamentals with Focus on South Africa. Emerging Markets Finance and Trade 58: 2620–36. [Google Scholar] [CrossRef]
- Salisu, Afees A., Rangan Gupta, and Riza Demirer. 2022. Oil Price Uncertainty Shocks and Global Equity Markets: Evidence from a GVAR Model. Journal of Risk and Financial Management 15: 355. [Google Scholar] [CrossRef]
- Sheng, Xin, Rangan Gupta, and Qiang Ji. 2023. The Effects of Disaggregate Oil Shocks on Aggregate Expected Skewness of the United States. Risks 11: 186. [Google Scholar] [CrossRef]
- Smyth, Russell, and Paresh Kumar Narayan. 2018. What do we know about oil prices and stock returns? International Review of Financial Analysis 57: 148–56. [Google Scholar] [CrossRef]
- Stock, James H., and Mark W. Watson. 2003. Forecasting Output and Inflation: The Role of Asset Prices. Journal of Economic Literature 41: 788–829. [Google Scholar] [CrossRef]
- Tavor, Tchai. 2024. Assessing the financial impacts of significant wildfires on US capital markets: Sectoral analysis. Empirical Economics 67: 1115–48. [Google Scholar] [CrossRef]
- Wang, Yudong, Zhiyuan Pan, Li Liu, and Chongfeng Wu. 2019. Oil price increases and the predictability of equity premium. Journal of Banking and Finance 102: 43–58. [Google Scholar] [CrossRef]
- Welch, Ivo, and Amit Goyal. 2008. A comprehensive look at the empirical performance of equity premium prediction. The Review of Financial Studies 21: 1455–508. [Google Scholar] [CrossRef]
- Westerlund, Joakim, and Paresh Kumar Narayan. 2012. Does the choice of estimator matter when forecasting returns? Journal of Banking & Finance 36: 2632–40. [Google Scholar]
- Westerlund, Joakim, and Paresh Kumar Narayan. 2015. Testing for predictability in conditionally heteroscedastic stock returns. Journal of Financial Econometrics 13: 342–75. [Google Scholar] [CrossRef]
- Yin, Libo, and Yang Wang. 2019. Forecasting the oil prices: What is the role of skewness risk? Physica A: Statistical Mechanics and Its Applications 534: 120600. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).