Abstract
How to consider the a priori risks in experience-rating models has been questioned in the actuarial community for a long time. Classic past-claim-rating models, such as the Buhlmann–Straub credibility model, normalize the past experience of each insured before applying claim penalties. On the other hand, classic Bonus–Malus Scales (BMS) models generate the same surcharges and the same discounts for all insureds because the transition rules within the class system do not depend on the a priori risk. Despite the quality of prediction of the BMS models, this experience-rating model could appear unfair to many insureds and regulators because it does not recognize the initial risk of the insured. In this paper, we propose the creation of different BMSs for each type of insured using recursive partitioning methods. We apply this approach to real data for the farm insurance product of a major Canadian insurance company with widely varying sizes of insureds. Because the a priori risk can change over time, a study of the possible transitions between different BMS models is also performed.
1. Introduction
An experience ratemaking model uses past claims experience to update the basic premium computed with the risk characteristics of the insureds. To avoid penalizing the risky insureds twice, insurers must find a way to consider the a priori risks in experience-rating models. Indeed, because risky policyholders already have higher basic premiums than less risky policyholders, they are expected to also claim more often than less risky policyholders. Consequently, they should also be expected to be penalized less for a claim than less risky policyholders. Similarly, risky insureds should be rewarded much more than lower-risk insureds if they do not claim.
This problem of treating insureds differently in experience-rating models has long been known in the actuarial community. Indeed, even classic past-claim-rating models normalize the past experience of each insured i before applying claim penalties. For example, by designating a measure of the a priori risk, for contract t of insured i, a normalized past experience is used in the Buhlmann–Straub credibility model instead of , which is used in the Bühlmann (1967) credibility model.
Instead on focusing on credibility premiums, other approaches developed joint distributions of all contracts of the same insured to find predictive premiums for claims frequency. For example:
- Models allowing a dynamic time dependence between contracts of the same insured: models based on series of correlated random effects (Bolancé et al. 2007; Abdallah et al. 2016), jitter models (Shi and Valdez 2014), time series for count data (Gourieroux and Jasiak 2004; Bermúdez et al. 2018; Bermúdez and Karlis 2021 or Pinquet 2020).
- Longitudinal models allowing for dependence structures between many type of claims (Abdallah et al. 2016; Pechon et al. 2019, 2021; Gómez-Déniz and Calderín-Ojeda 2018).
- Longitudinal models allowing dependence between claim frequency and claim severity (Shi et al. 2016; Oh et al. 2020; Jeong and Valdez 2020).
On the other hand, a Bonus–Malus Scales (BMS) model is an experience-rating model that has been used in practice for a long time (see Lemaire 2012 or Denuit et al. 2007 for classic textbooks, or Frangos and Vrontos 2001; Mehmet and Saykan 2005 or Ágoston and Gyetvai 2020 for research papers on BMS scales). The BMS model is a class system with a finite number of levels, where a relativity is assigned to each level. Depending on the transition rules of the BMS, insureds usually move down by a level if they do not claim during their contract, and move up a specific number of levels for each claim they make. The insured’s new level at the end of the year is then used to compute the next annual premium. To account for the differences in a priori risk in automobile insurance, Denuit et al. (2007) uses one BMS model for young drivers and another BMS model for older drivers. However, this approach does not take advantage of the data structure that is now available from insurers. Indeed, to find the relativity of each BMS level, Denuit et al. (2007) uses the classic BMS theory, which is based on aggregate data.
Recently, Boucher and Inoussa (2014) explained how classic BMS theory could be generalized for granular data, where each insured is observed for many contracts. Verschuren (2021) generalizes the BMS approach for multiproducts and adds more flexible estimation methods by using the generalized additive model (GAM) theory. Finally, Boucher (2022) shows how BMS models are linked with simple GLM models that have covariates associated with the past claims experience.
Those recent BMS models generate the same surcharges and the same discounts for all insureds because the transition rules within the class system do not depend on the a priori risk. Despite the quality of prediction of the BMS models, this experience-rating model could appear unfair to many insureds and regulators because it does not recognize the initial risk of the insured. In this paper, based on the new BMS theory, we show how insurers can create different BMSs to account for the differences in a priori risk.
The paper has the following structure. In Section 2, we carefully explain the recent BMS theory that uses granular data. As an illustration, the BMS model is applied to a farm insurance product. The results are discussed, and the problem related to the a priori risk is highlighted. We show that when a single BMS is used on the entire insurance portfolio, higher BMS levels are filled with bigger farms, and similarly, we show that bigger farms have a higher average BMS level than smaller farms. In Section 3, we show how to group farms of similar size to create distinct and independent BMS models. This more equitably rates the farms, and better rewards and penalizes them, because their size is directly taken into account for past claims rating. To find the best groups to form among the farms, similar to what is conducted with classification trees, we use a recursive partitioning algorithm (see Diao and Weng 2019 for a recent use of classification trees in a credibility theory situation). Because the size of the farm, which is defined by the number of insured items, can change at any time, a study of the transitions between different BMS models is also performed. The last section concludes.
2. Review of the BMS Model
2.1. Summary of the Past-Claims-Rating Model
Boucher (2022) defines two kinds of variables to use in experience rating:
- The variable to model, named the target variable;
- The information used to define what we consider the past claim experience, named the scope variable.
For this paper, we model the number of claims (i.e., the target variable) based only on the number of past claims (i.e., the scope variable). In other words, the idea of the experience-rating model of this paper is to predict the number of claims of insured i, for contract of period T, by taking into account all the past number of claims, from contract to contract . A new insured with is someone without any past insurance experience. Formally, we are looking to compute the conditional expected value of , which is the number of claims of insured i for contract of period T, defined as:
where is a vector of all number of claims of each contract between time 1 and time for insured i, and is a vector containing covariates used in the ratemaking for contract T. This usually corresponds to information about the age of the insured, the marital status of the insured, etc.
2.2. The Bonus–Malus Scale Models
To model the number of claims of insured i, for contract T, the Poisson distribution of mean is usually the starting point, but other count distributions can easily be used (see Denuit et al. 2007 for a review of using count distributions to model the number of claims, or Cameron and Trivedi 2013 for an exhaustive review of count distributions). For this paper, for the sake of simplify, we only use the Poisson distribution.
For experience rating, to differentiate between new insureds and insureds with experience, past-claims-rating models use both the number of past claims and the number of contracts without claims, defined as . In such situations, the mean parameter of the Poisson distribution can be expressed as:
where, for insured i, corresponds to the insured’s total number of past claims, and is the sum of policy periods without a claim. The same mean parameter can be expressed as:
with:
where is the Relativity parameter, and is the Jump parameter. The new variable , based on and , summarizes all past claim experience and is called a claim score. This approach is called the Kappa-N model (Boucher 2022), and because it is defined by the mean parameter, it can easily be used with many count distributions. The Kappa-N model can be interpreted as follows:
- For an insured i without insurance experience, we have and , which means that a new insured without experience has a claim score of 100, i.e., an entry level of 100.
- Each year without a claim decreases the claim score by 1;
- Each claim increases the claim score by .
- The impact of a single claim on the premium is equal to years without claims.
- The penalty for a claim is %.
- Each year without a claim decreases the premium by %.
Boucher (2022) showed that the prediction quality of the Kappa-N model is significantly better than standard count models that do not use any covariates linked to experience rating. However, the Kappa-N model has some major flaws. The model does not limit the claim score to minimum or maximum values. In some situations, it can also lead to extreme surcharges for insureds who claimed frequently. Moreover, because it is based on and , the Kappa-N model does not allow for any forgiveness and the model does not weight past claims by their age (Bolancé et al. 2007).
Numerical Example
Suppose that we have the insureds from Table 1, where the insurance experience is shown for three insureds. Suppose a Kappa-N model was fitted, resulting in a rating structure that implies a decrease of one level for each year without a claim. The estimated jump-parameter is 4, meaning that each claim penalizes the insured with an increase of 4 to the claim score. If we start at level 100 in 2011, because of the values of and (also shown in Table 1), insureds would, respectively, be at levels 90, 118 and 121 in 2021. The graph on the left of Figure 1 shows another way to see how the level , for insured , are computed.

Table 1.
Insureds with claims experience.
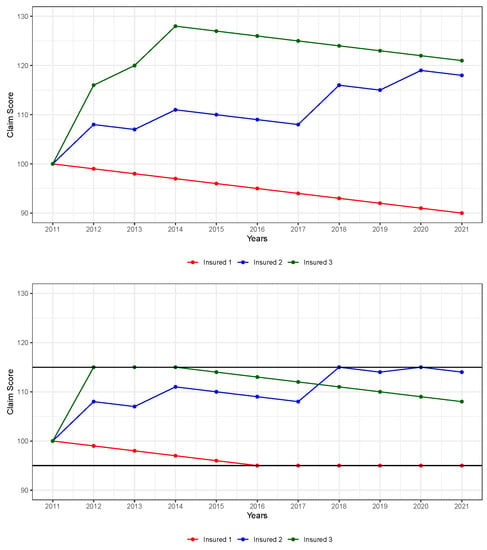
Figure 1.
Insureds with claim experience, with and without limits .
If we want to weight claims by their age and introduce some form of forgiveness to the rating model, a solution is to limit the value of all claim scores, for all past insurance contracts. For illustration, we suppose that 115 is the maximum value of the claim score, i.e., , and the minimum value is 95, i.e., . To compute premiums in 2021, we apply these two limits to all past claim scores. Figure 1 shows how the limits applied to past contracts impact the claim score in 2021 for all three insureds. With this approach, we see that many of the problems mentioned earlier are at least partially solved: past claims can ultimately be forgiven, and the model introduces a form of time weighting for past claims.
By adding maximum and minimum claim-score values for past contracts, the Kappa-N approach developed so far has been transformed into what is usually called a Bonus–Malus Scale system (BMS), where the claim score can be seen as a BMS level, or simply a BMS score. More formally, the BMS is a class system with a finite number of levels (when is an integer), where a relativity is assigned to each level. For this BMS model, the transition rule is simple: an insured moves down by one level if there is no claim over the course of the contract and moves up by levels for each claim.
BMS models can be defined using four structural parameters: the entry level , the jump parameter , the maximum level of the system and the minimum level of the system . For a specific insured, the BMS level is defined as:
where the level is always between and for all .
For the Kappa-N model, estimating the parameters by maximum likelihood is simple. However, for BMS models, because the model needs to recompute the claim-score path of each insured from their first contract, finding the best values for structural parameters , and is not that easy. To estimate the structural parameters, a grid search for all structural parameters can be performed. That means that all values are tried, and we select the BMS model with the biggest log-likelihood. By limiting the possible values of , and , this approach is not difficult, nor is it too time consuming.
2.3. Summary of the Numerical Illustration
2.3.1. Data Used
We used a sample of the farm insurance data from a major insurance company in Canada, using contracts between 2010 and 2020. The general form of the data used is shown in Table 2, where each line in the database corresponds to a specific coverage in an annual contract. For each observation, we have information about the insured, the contract and the items covered, but we also see the date of the first insurance contract with the insurer. Information about claims that happened during that period of time is also available.

Table 2.
Fictive Data Sample-Contract Level.
Unlike with automobile insurance in Canada, where insureds frequently move from one insurer to another, farm insurance has relatively stable insureds. In our dataset, the average number of years with the insurer is , and the maximum observed years is close to 601. The maximum available years of past claims experience for all insureds is 15 years, and only insurance experience with the insurer is available. We considered the first year of insurance of any insured to be the first year with the insurer. In other words, if a farm is first seen in the database in 2003, this farm is considered a new insured without any prior experience in 2003.
For the farm insurance product, an item corresponds to a specific tractor or combine for which specific information is available. With a total of approximately 700,000 insured items insured for more than 120,000 contracts, the average number of items insured per contract is around 6. The distribution of the number of items insured per contract can be seen in Figure 2. Almost 50% of all farms only have one insured items, while approximately 10% of farms have more than 20 insured items. More precisely, 40 farms have more than 100 insured items, with a maximum of more than 200 insured items for a single contract. As we see in the next sections, the difference between small farms and larger farms is important for BMS models.
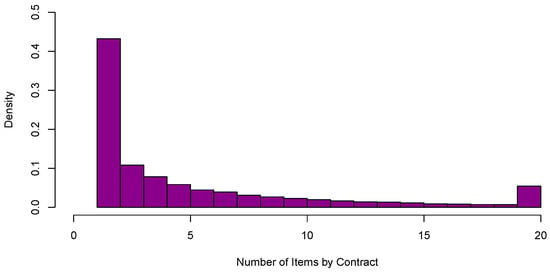
Figure 2.
Distribution of the number of items by contract.
2.3.2. Estimated Parameters of the BMS Model
The estimated parameters of the Poisson BMS model are shown in Table 3. The log-likelihood value is shown. For the test dataset, the logarithmic score defined as was used (see Roel et al. 2018 for details or descriptions of other scores) to define the prediction quality. To better understand the results obtained for the Poisson BMS model, we can compute the discounts and surcharges of the model based on the number of past claims. More concretely, we then have:

Table 3.
Results of the Poisson BMS model.
- The jump parameter is equal to 6, meaning that each claim increases the BMS level by 6. After a claim, an insured would need 6 years without a claim to return to the original premium (before the claim);
- The value of is . That means that the penalty for a claim is equal to , and each year without claim decreases the premium by ;
- The maximum BMS level is , meaning that the maximum surcharge, compared with level 100, is ;
- The minimum BMS level is , meaning that the minimum surcharge, compared with level 100, is .
As we can see, these basic results are found and computed easily. This method of computing the surcharges and discounts would clearly be useful to any insureds, brokers or administrators. It is simple to explain to insureds how large their penalties for a claim will be and how long they will be penalized for that claim. Another interesting result of the BMS model is that all insureds have a premium located between and times the basic premium for a new insured at level 100. This narrowly limits the range of premiums.
2.3.3. Problems with the Size of Farms
By comparing the predicted and the observed claims frequency on the training and test datasets, Boucher (2022) showed that the BMS model seems to fit the data well. We see that classifying insureds by their claim score (or BMS level) works well as the insureds with higher levels has worse claims experience than insureds with lower levels.
However, the size of each farm in the insurance portfolio is different, and size has a direct impact of the past rating model. Figure 2 showed the distribution of the number of insured machinery (called items) per farm. The BMS model used here generates the same surcharges and the same discounts for all insureds. However, because large farms are expected to have more claim than smaller ones, they should normally also be expected to be penalized less for a claim. Similarly, a large farm should be rewarded much more for a year without claim. An experience-rating system that does not recognize this type of situations may appear to penalize larger farms twice.
That means that the connection between BMS levels and the size of the farm is noteworthy. To more clearly see the impact of the number of insured items on each farm, using the BMS model from Table 3, we compute the BMS level of each contract in the database. For each BMS level, we compute the average number of insured items on each farm for that level. Similarly, we computed the average BMS level based on the number of insured items. Figure 3 illustrates the result. As we expect, the higher BMS levels are filled with bigger farms, and bigger farms have an average BMS level much higher than smaller farms.
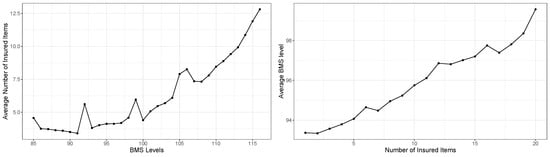
Figure 3.
Average number of insured items by BMS level (left) and average BMS level by number of insured items (right).
Despite the prediction quality of the BMS model, the BMS model could seem unfair to many insureds and regulators because it does not recognize the initial risk of the insured. To correct this situation and promote the use of the BMS in practice, the BMS model should be generalized to include the a priori risks in the rating structure.
3. Partitioning the Portfolio
As proposed by Denuit et al. (2007) for young drivers in Belgium, a way to deal with farms of different sizes would be to divide the portfolio into groups. Indeed, groups of farms of similar sizes could be created, and each group would have their own experience-rating model, with its own a priori rating parameters and its own structural BMS parameters. Farms could then be more equitably rated, and more correctly rewarded and penalized, as their size would be directly taken into account when performing past claims rating.
To find the best groups to form among the farms, similar to what is carried out with classification trees, we perform a recursive partitioning of the portfolio (see Diao and Weng 2019 for more details but also for an application to compute more accurate credibility premiums). Because we expect the risk to be proportional to the number of insured items in each contract, we need to find a division point based on the number of items from which we create two groups: insureds with a smaller (or equal) number of items than the point division and another group with more items than the division point.
We use an algorithm to test each possible subgroup of our insurance portfolio by cross-validation. We split the training dataset into five folds, from which four of the five are used to estimate the parameters of a Poisson BMS model, and the remaining fold is used to compute predictive statistics. To evaluate the prediction quality on the test fold, because we are working with count data, the logarithmic score defined earlier was used. For each item value from 1 to 212 (the maximum number of items observed in a single contract), we are looking for the value where the sum of the logarithmic score of the two groups is maximized. Then, for each of the two subgroups created, we create two more new groups that generate a better total logarithmic score. We repeat this until the sum of all scores cannot be improved, or when a group is composed only of farms with the same number of insured items.
The resulting classification tree of the number of items is shown in Figure 4, where the percentage shown corresponds to the proportion of contracts that belong to that interval of the training dataset. We can see from the algorithm that:
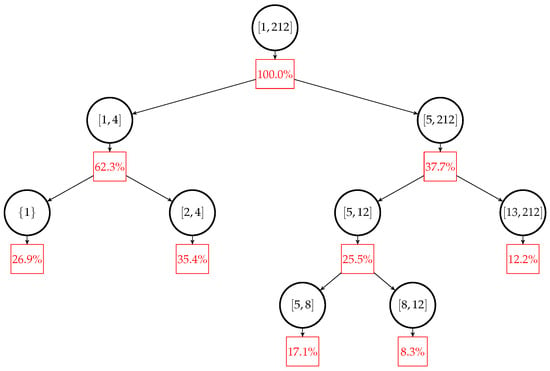
Figure 4.
Recursive partitioning by the number of insured items.
- The first iteration divides the insureds into two groups: insured with four or fewer than four insured items, which represents 62.3% of all insureds, and insureds with more than four items, which represents 37.7% of the insureds.
- The first group of insureds is then divided again into two groups: farms with one insured item (26.9%) and farms with between two and four insured items (35.4%). The second group is also divided into two more groups: between 5 and 12 items (31.0%) and insureds with more than 12 items (6.7%).
- Finally, only the group with between 5 and 12 items can be divided again: groups with between 5 and 8, and between 9 and 12 items, are created.
3.1. Analyzing Each Group of Farms
To better understand the division of the portfolio into groups, Table 4 shows a descriptive summary of each group of farms from division step 0, 1, 2 and 3. For each division, we observe major differences between each group of farms. For example, the average claims frequency of the portfolio is 2.36%, but it is 0.36% for insureds with only one insured item and is slightly under 10% for farms with more than 13 insured items. Past claims experience, summarized by variables and , also shows the difference between groups: on average, small farms have fewer reported claims (0.49) than the larger farms (1.68). The number of years without a claim, expressed by , is much closer for each group, except for the smaller farms with only one insured item. It is also interesting to see that larger farms have more insurance experience, noted , than small ones. Generally, the larger the farm is, the longer it stays with the insurer.

Table 4.
Descriptive summary of each group of farms.
Covariates based on the characteristics of the farm were used in the claim count model. More specifically, by referring to Equation (2), is a vector, with six covariates and an intercept. For privacy reasons, but also because this is not the focus on the paper, covariates are simply labeled as and their meaning is not explained. Figure 5 shows the mean of each covariate used in all count models for all five groups, with the dashed line representing the average for the whole portfolio. Major differences between groups can be observed for covariates and . This is not surprising because those covariates are directly linked to the number of insured items per farm. Covariates , , and , on the other hand, do not vary depending on the group.
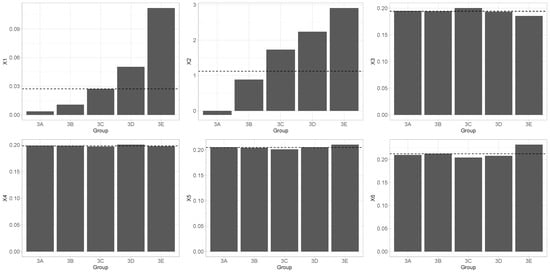
Figure 5.
Mean of all covariates used by groups (dashed line for the mean of the whole portfolio).
Figure 6 shows the distribution of each group of farms of division 3 across all BMS levels for the original BMS models summarized in Table 3. The conclusion of that figure is similar to what we saw with Figure 3: the proportion of larger farms in the highest levels of the BMS is greater than the proportion seen in the lower BMS levels. We see, for example, that the proportion of contracts from groups 3A and 3B is smaller in level 115 than in level 85. The opposite is observed for group 3E. However, the proportion of insureds from groups 3C and 3D seems to be stable across all BMS levels.
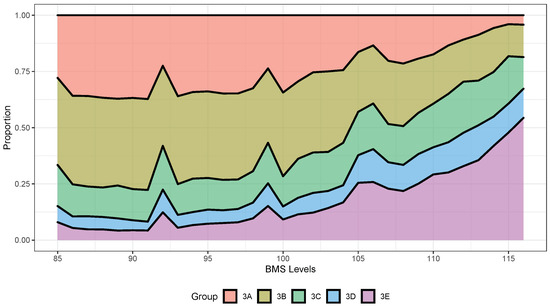
Figure 6.
Proportion of each group within BMS levels for the BMS model.
3.2. Different BMS Models versus the Original BMS Model
By dividing the portfolio into groups based on the number of insured items, we also obtained five different BMS models for each group of farms. Results of the estimation of each BMS model are shown in Table 5. A comparison with the original BMS, which has been fitted to the whole portfolio, is also shown, where the log-likelihood statistics and logarithmic scores of the original BMS model are divided by group.

Table 5.
Comparison of the original BMS and the BMS by group model.
Because it generalizes the original BMS model, a specific BMS model for each group obviously improves the log-likelihood of each group and the total log-likelihood ( vs. , almost 80 points for 33 additional parameters). Improving the log-likelihood that much could be a sign of overfitting. However, this is not the case because, interestingly, the total logarithmic score used on the test dataset also improved ( vs. ), and we can see that the logarithmic score of each group improved, except for group 3B. This is an indication that an experience-rating model that uses the size of the insured should be considered in farm insurance.
We can also see that the estimators of the structural parameters , and are very different from one group to another. This can be interpreted in many ways. Using the estimated value of , we can see how many years it takes to forgive one claim for each group. Another place we can see the impact of the BMS parameters is on the spectrum of possible premiums, which is very different for each group. For example, the maximum/minimum BMS levels for group 3A are 156/99 (57 levels), while the maximum/minimum BMS levels for group 3E are 107/85 (22 levels).
Using the structural parameters of the BMS also allows us to compute various discounts and surcharges, as shown in Table 6. The table shows the impact of a year without a claim and the surcharge for each claim. There are only two possibilities for the insured: to claim or not to claim; thus, we have to compare relativities between a scenario where the insured claims and a scenario where the insured does not claim. This is shown in the Claim Impact column. Finally, based on the estimated values of and , the maximum surcharge and the maximum discount for each BMS model is also shown. Several observations can be made about these tables:

Table 6.
Discounts and surcharges for each group.
- Group 3A, which is composed of farms with only one insured item, seems very different than the other farms. Perhaps these small insureds are family farms, while the farms in the other groups are more industrial.
- Group 3A generates extreme surcharge values for insureds who claim too much: they are more than 53 times the basic premium for insureds at the top of the Bonus–Malus Scale. Even if this BMS model seems to be better than the original BMS model for group 3A (when looking at the logarithmic score), this is not realistic and cannot be applied in practice. On the other hand, groups 3B, 3C and 3D have similar maximum surcharges ranging from 0.780 to 0.920, which can also be seen as an indication that small farms with one insured item seem very different than the other farms. The maximum surcharge for larger farms is limited to an increase of 35.2% compared with the basic level (100).
- The maximum discounts are similar for each group, except group 3A. Compared with a new insured at level 100, insureds from group 3A can expect a maximum discount of only around 7%, but other insureds can obtain discounts ranging from 31.1% to 47.1%.
- The surcharge for each claim is very different from one group to another. We see that for group 3A and 3B the impact of a claim is similar, while the impacts are similar for groups 3C, 3D and 3E.
To more clearly understand the difference between having five different BMS models, one for each group, and a single BMS model that is applied directly to the whole portfolio, the left graph of Figure 7 shows the distribution of the BMS relativities for all groups with the single BMS model when it is applied to the whole portfolio. As seen in Table 6, the maximum relativity of the original BMS model is , and the minimum is (1–37.5%), but the figure also shows how the contracts are spread across all levels for each group. The graph on the right of the same figure shows the same result but for five different BMS models. Group 3A includes extreme cases where the BMS relativites are much higher than 2.5.
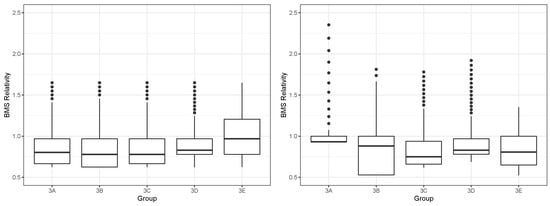
Figure 7.
Distribution of the BMS relativities for each group (left: original BMS, right: BMS by group).
Finally, an analysis was also performed of the estimated a priori parameters related the covariates used in the models. Table 7 shows some similarities between the values of the parameters but also large differences between groups.

Table 7.
Estimated parameters for BMS models applied to each group.
The results obtained by dividing the farm insurance portfolio into subgroups to take into consideration the size of the farms is an interesting way to deal with the size of the insureds when conducting experience rating. Indeed, even if the final model is much more complex, and has many structural parameters that result in a cumbersome approach to estimating all parameters, the final results improve prediction capacity compared with the standard BMS model (also known as the original BMS model). Dividing farms by the number of insured items is an interesting way to evaluate the impact of the size of a farm. Other variables or covariates can be used instead of the number of insured items to evaluate the insured’s a priori risk. In automobile insurance, the driver’s age could be used to divide the insureds into subgroups. For other products, dividing insureds into groups might work if we can find heterogeneous groups of insureds in the portfolio.
3.3. Limits of the Approach
Longitudinal count models, such as those seen in Abdallah et al. (2016) or Pechon et al. (2021), can directly use the number of farms as the exposition basis. Consequently, those models allow for the computation predictive premiums that consider the a priori risk while using much fewer parameters than the classification tree BMS model proposed here. However, as mentioned by Boucher (2022), these longitudinal models are often difficult for insurers to implement, and BMS solutions are often required.
The classification tree BMS model divides the portfolio and independently estimates all the BMS parameters of each group. That means that we consider each group to be fundamentally different, which is not the case. They all have something in common: small farms might be a little bit different than bigger farms, but ultimately, the same types of machinery are covered and they face the same kinds of perils (thefts, hail, fire, etc.). A way to correct this flaw could be to allow the sharing of some parameters between each group. This solution reduces the number of parameters of the model, which often leads to a reduction in overfitting. This could be an idea for future research because it needs developing another estimating algorithm.
A Study of Transition Rules
Dividing the portfolio into different groups causes a bigger problem. Indeed, nothing is preventing a farm from buying or selling items (tractors) at any moment in time. That means that, for example, a farm in group 3B could transition to group 3A simply by removing a tractor in its insurance contract. Because we do not have access to past risk characteristics (in other words the number of items insured in the past), the past claims experience of that farm are then used with a BMS structure with instead of . Transitioning to other groups has obviously not been considered in the modeling, and it leads to illogical results, where, for example, the insured receives a new surcharge for past claims even if no new claim was reported.
To see the potential impact of such a transition, we used the whole portfolio and analyzed insureds with a number of items on the boundary of each group 3A, …, 3E. Our objective is to measure the impact of a small variation in the number of insured items on the premium calculated by the BMS models. Table 8 shows the 8 possibilities studied. Of course, it would be possible for a farm to add or remove two or more items from its policy in the same year. In these situations, it would be possible for a farm to transition from group 3A to 3C (by adding between 4 and 7 items in the same year), from group 3B to 3D (by adding at least 5 items) and from group 3C to 3E (by adding at least 5 items). Similarly, a farm of group 3E can transition to group 3C by removing at least 5 items, and so on. We do not show the impact of those transitions, but they could be analyzed easily following the same procedure.

Table 8.
List of farms analyzed for the transition study.
For each possibility, we analyze the impact of the transition from one group to another one by computing the ratio of BMS relativities. The result is shown for each transition in Figure 8. Transitioning from group 3A or to group 3A generates extreme situations (the right graph of the figure is limited because the maximum value is around 27). For other transitions, even if the impact is not as big, we can see that changing groups could have a serious impact. Receiving a new past claims surcharge without making a new claim is not something that could be applied in practice.
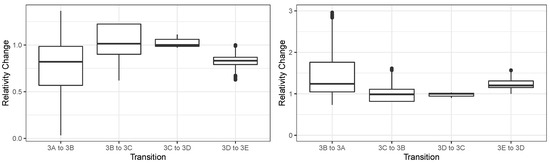
Figure 8.
Relativity impact of the transition from one group to another.
Creating distinct BMS models for young and older drivers, as in Denuit et al. (2007), is more logical and simpler. Firstly, because the BMS model to use depends on the age of the driver, which the insured does not control. Secondly, because the transition from the first BMS (for young drivers) to the second BMS only happens once and in one direction. Consequently, the insurer knows when the transition will happen. However, knowing the time of the transition has another advantage. Indeed, the insured’s past risk characteristics, i.e., for , are usually not used in ratemaking and are often not even available to the insurer. If the insurer knows the age at which the insured moves from the first BMS model to the second one, which we can call a, it allows the insurer to know that an insured of a or years old has just made a BMS transition. Without knowing the insured’s past characteristics, the insurer knows that it should apply transition rules, which could limit the variation in surcharges or discounts.
If the insurer uses the number of insured items to create distinct BMSs, it is not automatically possible to know if an insured has moved from one BMS to another. It then becomes very difficult to propose a method to mitigate the effect of the transitions, such as the ones seen in Figure 8, unless the insurer collects the history of the number of insured items or heavily transforms the BMS pricing model.
4. Conclusions
As mentioned in Boucher (2022), using the BMS model instead of complex longitudinal distributions or advanced credibility approaches simplifies the understanding of the ratemaking structure of an insurer. Indeed, by its simplicity, the BMS system can be explained to the legislative authorities that regulate pricing, as well as to the various administrators of insurance companies and policyholders. However, despite the quality of prediction of the BMS models, the BMS often appears unfair because it does not consider the initial risk of the insured in the penalty structure.
In order to respond to this criticism of policyholders who might complain about being penalized twice, first by the a priori ratemaking and then by the predictive ratemaking, we proposed to modify the BMS approach. Using a recursive division algorithm such as the one used by Diao and Weng (2019), we created several groups of insureds and applied a separate BMS model for each group. In our numerical application, we used the farm insurance product, and the a priori risk was defined as the number of insured items. By using a recursive partitioning algorithm on the farm portfolio, we show that the fit statistics and the predictive scores were greatly improved compared with a unique BMS applied on the whole portfolio. Moreover, we show that partitioning makes it easier to identify groups of insureds that have different loss experience than other groups. Indeed, the approach allows us to see that farms with only one insured item had a very different loss experience than other types of farms.
The approach generates excellent fit statistics and provides very good prediction quality and could easily be applied to many insurance products such as automobile insurance. However, when used with the number of insured items, it also has flaws. The main flaw is related to possible overfitting but also the possibility of a transition from one BMS to another. Indeed, because the BMS used for a farm is based on the number of insured items, a farm could quickly move to another BMS simply by adding or removing an item from its policy. As we have seen in our numerical application, this leads to situations where an insured’s premium can rise or fall sharply simply because the applicable structural parameters change too drastically from one BMS to the next.
A direct way to correct this approach could be to allow the sharing of some structural parameters (, and ) or some between each group. For example, in Table 5 and Table 7, we saw some similarities between parameters. This approach can save parameters to the model, which often reduces overfitting. This is an interesting idea that could work. However, creating an algorithm to estimate the parameters of such a model could be far more complex than what we used here and would need to be developed.
We instead believe that it is the step of dividing the portfolio into clear groups that should be generalized. By analogy, using a model that necessitates partitioning of the portfolio is similar to a piecewise regression, where a different regression model is used for each segment of the variable to model. We think that it makes more sense to develop a unique BMS model for all farms where, to follow the analogy, a smoothing function might be used to consider the size, or the a priori risk, of each farm. Indeed, because there might be some similarities between contracts or policyholders from different groups, a more holistic approach might be worth considering. This model could then consider the size of the insured as a characteristic of the risk to be included, for example, in the penalty structure of the past claims algorithm.
Funding
This research received no external funding. The author gratefully ackowledges The Co-operators throught the Co-operators Chair in Actuarial Risk Analysis.
Conflicts of Interest
The author declares no conflict of interest.
Note
| 1 | Farms are sometimes passed from generation to generation. Insurance experience would not be reset in such a case. |
References
- Abdallah, Anas, Jean-Philippe Boucher, and Hélène Cossette. 2016. Sarmanov family of multivariate distributions for bivariate dynamic claim counts model. Insurance: Mathematics and Economics 68: 120–33. [Google Scholar] [CrossRef] [Green Version]
- Ágoston, Kolos Csaba, and Márton Gyetvai. 2020. Joint optimization of transition rules and the premium scale in a bonus-malus system. ASTIN Bulletin: The Journal of the IAA 50: 743–76. [Google Scholar] [CrossRef]
- Bermúdez, Lluís, and Dimitris Karlis. 2021. Multivariate inar (1) regression models based on the sarmanov distribution. Mathematics 9: 505. [Google Scholar] [CrossRef]
- Bermúdez, Lluís, Montserrat Guillén, and Dimitris Karlis. 2018. Allowing for time and cross dependence assumptions between claim counts in ratemaking models. Insurance: Mathematics and Economics 83: 161–69. [Google Scholar] [CrossRef]
- Bolancé, Catalina, Michel Denuit, Montserrat Guillén, and Philippe Lambert. 2007. Greatest accuracy credibility with dynamic heterogeneity: The harvey-fernandes model. Belgian Actuarial Bulletin 7: 14–18. [Google Scholar]
- Boucher, Jean-Philippe. 2022. Bonus-malus scale models: Creating artificial past claims history. Annals of Actuarial Science. Available online: https://archipel.uqam.ca/14973/ (accessed on 26 July 2022).
- Boucher, Jean-Philippe, and Rofick Inoussa. 2014. A posteriori ratemaking with panel data. ASTIN Bulletin: The Journal of the IAA 44: 587–612. [Google Scholar] [CrossRef]
- Bühlmann, Hans. 1967. Experience rating and credibility. ASTIN Bulletin: The Journal of the IAA 4: 199–207. [Google Scholar] [CrossRef] [Green Version]
- Cameron, A. Colin Cameron, and Pravin K. Trivedi Trivedi. 2013. Regression Analysis of Count Data. Cambridge: Cambridge University Press, vol. 53. [Google Scholar]
- Denuit, Michel, Xavier Maréchal, Sandra Pitrebois, and Jean-François Walhin. 2007. Actuarial Modelling of Claim Counts: Risk Classification, Credibility and Bonus-Malus Systems. Hoboken: John Wiley & Sons. [Google Scholar]
- Diao, Liqun, and Chengguo Weng. 2019. Regression tree credibility model. North American Actuarial Journal 23: 169–96. [Google Scholar] [CrossRef]
- Frangos, Nicholas E., and Spyridon D. Vrontos. 2001. Design of optimal bonus-malus systems with a frequency and a severity component on an individual basis in automobile insurance. ASTIN Bulletin: The Journal of the IAA 31: 1–22. [Google Scholar] [CrossRef] [Green Version]
- Gómez-Déniz, Emilio, and Enrique Calderín-Ojeda. 2018. Multivariate credibility in bonus-malus systems distinguishing between different types of claims. Risks 6: 34. [Google Scholar] [CrossRef] [Green Version]
- Gourieroux, Christian, and Joann Jasiak. 2004. Heterogeneous inar (1) model with application to car insurance. Insurance: Mathematics and Economics 34: 177–92. [Google Scholar] [CrossRef]
- Jeong, Himchan, and Emiliano A. Valdez. 2020. Predictive compound risk models with dependence. Insurance: Mathematics and Economics 94: 182–95. [Google Scholar] [CrossRef]
- Lemaire, Jean. 2012. Bonus-Malus Systems in Automobile Insurance. New York: Springer Science & Business Media, vol. 19. [Google Scholar]
- Mehmet, Mert, and Yasemin Saykan. 2005. On a bonus-malus system where the claim frequency distribution is geometric and the claim severity distribution is pareto. Hacettepe Journal of Mathematics and Statistics 34: 75–81. [Google Scholar]
- Oh, Rosy, Peng Shi, and Jae Youn Ahn. 2020. Bonus-malus premiums under the dependent frequency-severity modeling. Scandinavian Actuarial Journal 2020: 172–95. [Google Scholar] [CrossRef]
- Pechon, Florian, Michel Denuit, and Julien Trufin. 2019. Multivariate modelling of multiple guarantees in motor insurance of a household. European Actuarial Journal 9: 575–602. [Google Scholar] [CrossRef] [Green Version]
- Pechon, Florian, Michel Denuit, and Julien Trufin. 2021. Home and motor insurance joined at a household level using multivariate credibility. Annals of Actuarial Science 15: 82–114. [Google Scholar] [CrossRef]
- Pinquet, Jean. 2020. Positivity properties of the arfima (0, d, 0) specifications and credibility analysis of frequency risks. Insurance: Mathematics and Economics 95: 159–65. [Google Scholar] [CrossRef]
- Roel, Verbelen, Katrien Antonio, and Gerda Claeskens. 2018. Unraveling the Predictive Power of Telematics Data in Car Insurance Pricing. Journal of the Royal Statistical Society: Series C (Applied Statistics) 67: 1275–1304. [Google Scholar] [CrossRef] [Green Version]
- Shi, Peng, and Emiliano A. Valdez. 2014. Longitudinal modeling of insurance claim counts using jitters. Scandinavian Actuarial Journal 2014: 159–79. [Google Scholar] [CrossRef]
- Shi, Peng, Xiaoping Feng, and Jean-Philippe Boucher. 2016. Multilevel modeling of insurance claims using copulas. The Annals of Applied Statistics 10: 834–63. [Google Scholar] [CrossRef]
- Verschuren, Robert Matthijs. 2021. Predictive claim scores for dynamic multi-product risk classification in insurance. ASTIN Bulletin: The Journal of the IAA 51: 1–25. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).