Abstract
China’s bond market has been ranked third globally; however, China’s corporate bonds are significantly less liquid than its stocks. Liquidity risk is an important component in China’s corporate bond spreads. In this paper, we propose a stochastic liquidity discount factor model to evaluate the liquidity risk premium and its term structure in China’s corporate bond market. The Monte Carlo simulation technique is used to quantify the impact on the liquidity premium of various liquidity factors: the liquidity level, liquidity volatility, liquidity shock, and the liquidity elasticity. Our findings conclude that the liquidity level is the most significant component of a liquidity premium. The impact on the liquidity premium of other liquidity factors is all conditional on the liquidity level. In addition, the impact of liquidity shocks and volatility is also subject to the market’s equilibrium mechanism. Further, the term of a bond affects the premium both directly and indirectly through its influence on a bond’s liquidity.
1. Introduction
The study of the liquidity effect in corporate bonds originates from the study of the credit spread puzzle. Although tax, systematic risk, and default event risk explain the credit spread puzzle to a large extent, liquidity has been recognized as an important component of a credit spread (Driessen 2005; Elton et al. 2001; Longstaff 2005). Various empirical studies have shown that the liquidity premium is a nontrivial component of a corporate bond yield (Acharya 2013; Bai 2019; Chen 2018, 2007; Houweling 2005; Lin 2011). However, Richardson and Palhares (2018) examined U.S. corporate bonds and concluded that there was no evidence of a liquidity premium in credit markets. This motivated us to explore whether a liquidity premium exists in Chinese corporate bonds.
According to the Morningstar news, the Chinese bond market was the world’s second largest at the end 2020. The total value of Chinese bonds reached about USD19 trillion, representing 15% of the global bond market. However China’s corporate bonds are significantly less liquid than its stocks. Wu (2022) showed that the liquidity premiums were the main aspects of the spreads in China’s corporate bonds, using a regression model between the spreads and various observed liquidity-related variables. Although their research is concurrent with ours, it would be meaningful to investigate the liquidity premium in Chinese corporate bonds from different liquidity perspectives to provide an insight into the liquidity premium in Chinese corporate bonds.
The data for our research were the corporate bond trade data from the China Stock Market and Accounting Research (CSMAR) database1 and the corporate bond information data from the RESSET Database2, which is a professional financial data provider. The data we used were from 2007 to 2013, which were appropriate to investigate the liquidity risk, because the time period included the liquidity shock during the 2008 financial crisis. As pointed out by Pastor and Stambaugh (2019), the market liquidity estimation is more precise over a period that includes a financial crisis rather than normal times.
For our research, we propose a stochastic liquidity discount model by incorporating a stochastic liquidity discount factor into the Merton (1974), the first structural credit risk model, which has served as the foundation for all other structural models. Credit risk models are usually used to evaluate the liquidity premiums in corporate bonds, including structural credit risk models and reduced form credit risk models. In a reduced form credit risk model, the liquidity is a latent factor with an ambiguous economic meaning. Duffie (1999) made the first attempt to use a reduced form credit risk model to study the liquidity effect on corporate bond prices by proposing a new concept of a default and liquidity-adjusted short-term interest rate. Jarrow (2001) introduced liquidity risk to a reduced form risk model and interpreted the liquidity premium as a “convenient yield”. Driessen (2005) and Longstaff (2005) explicitly modeled the liquidity effect by assuming liquidity followed a specific stochastic process.
In contrast, in a structural credit risk model, liquidity has a clear economic meaning, although it is usually assumed to be a constant or following a deterministic distribution. For example, Tychon (2005) and Zheng (2006) assumed liquidity was a constant. Ericsson (2006) assumed that bondholders were subject to exogenous liquidity shocks, under which bonds are sold immediately at a discounted price in a perfectly liquid market, and the discount factor was uniformly distributed between 0 and 1. Fu (2012) assumed that exogenous liquidity shocks followed a Poisson process, and the discount factor was a constant.
Following Ericsson (2006) and Fu (2012), we assume that bondholders in an imperfect market have to sell bonds immediately at a fraction of their price in a perfectly liquid market and assume the fraction follows a stochastic process. Li (2021) used a similar idea and defined illiquidity as the value that bondholders must give up for bond liquidation, and they assumed credit risk and liquidity risk events followed a deterministic joint distribution. Our proposed model is based on the Merton model and incorporates a stochastic liquidity discount process into it with the following features. First, the proposed stochastic liquidity discount process evolves within a reasonable range subject to an upper bound and a lower bound. Second, the liquidity level, liquidity risk, and liquidity elasticity are specifically parameterized in the model in order to investigate their individual impact on the price of a corporate bond. To be more specific, the liquidity level is defined as the long-term value of the liquidity with an upper and lower limit; the liquidity risk is represented by the liquidity shock intensity and liquidity volatility; and the mean reversion speed of the liquidity process denotes the liquidity elasticity.
Based on the Monte Carlo simulations and our data, there exists a significant liquidity premium in China’s corporate bond prices. Our research not only confirms the conclusions of Dick-Nielsen (2012) that liquidity premiums will increase dramatically in a liquidity crisis, but it also finds that the liquidity level is the most critical factor determining the liquidity premium. The influence of the liquidity shock, liquidity volatility, liquidity elasticity, and a bond’s term on the liquidity premium is conditional on the liquidity level. The effect of the liquidity volatility is significant while the liquidity volatility is relatively high at a normal liquidity level; otherwise, it is negligible at an abnormal liquidity level. This result is consistent with the empirical result of Bongaerts (2017) based on U.S. corporate bonds that liquidity risk carries an economically negligible risk premium. In addition, the effect of the liquidity shocks and liquidity elasticity are constrained by the liquidity market’s balancing mechanism.
We also explore the impact of the term on China’s corporate bonds’ liquidity premium. The term of a bond has a twofold effect on the liquidity premium. On the one hand, the term of a bond determines the length of time in which a bond is subject to liquidity shocks. This is called the direct effect. On the other hand, the term of a bond also changes its liquidity profile in terms of the liquidity level, liquidity volatility, and liquidity intensity and, therefore, indirectly affects the liquidity premium. This is called the indirect effect of a bond’s term. In terms of the direct effect, we found the term structure of a liquidity yield spread to be convex and monotonically decreasing, and the liquidity premium dominated the yield spread of a short-term corporate bond, which was consistent with the results of (Zheng 2006; Ericsson 2006; Fu 2012). In addition, the ratio of the liquidity yield spread to the gross yield spread also had a convex and monotonically decreasing term structure, while the term structure of the liquidity price spread was concave and monotonically increasing. When considering the comprehensive effect of the term of a bond, the liquidity premium of a short-term bond significantly decreased, and the liquidity premium of a long-term bond dramatically increased.
The rest of paper is organized as follows. In Section 2, we introduce a bond price model with a liquidity effect. Then we incorporate a stochastic liquidity discount process into the model in Section 3. Section 4 describes the Monte Carlo simulation algorithm. Section 5 explains the parameter specifications and presents the calibrated parameter values. Numerical analysis results are presented in Section 6 and Section 7 concludes the paper.
2. The Bond Price Model with Liquidity Effect
Structural credit risk models date back to (Merton 1974) who first proposed a structural model to price corporate bonds based on the Black–Scholes model (see Black 1973). In the Merton model, a corporate capital structure is composed of equity and zero-coupon bonds, the capital market is perfect and complete, corporate assets can be traded continuously, and their values follow a stochastic process in a risk-neutral probability measure expressed as
where is the value of corporate assets, r is the constant risk-free interest rate, is the volatility of corporate assets, and is a standard Brownian motion in measure. From the aforementioned assumptions, a corporate bond is a portfolio consisting of a long position of a risk-free bond and a short position of a European put option based on the corporate assets. The price of the corporate bond is given by
where F is the face value of a zero coupon corporate bond, T is the maturity of a zero-coupon corporate bond, is the cumulative distribution function of a standard Gaussian distribution, and .
In the Merton model, the corporate bond market is liquid, and there is no liquidity risk premium in corporate bond prices. However, the realistic corporate bond market is imperfect. In an imperfect market, when the bondholders do not encounter any liquidity shock during the entire lifetime of their bonds, and the corporate assets exceed the face value of the bonds, then, the bonds will not default, and the bonds’ cash flow at maturity will be given by
where is an indicator function, is a default time, and is a liquidity shock time. When the bondholders do not encounter a liquidity shock, but the corporate asset value is less than the face value of the bonds, then, the bonds will default, and the cash flow of the bond at maturity will be
However, if the bondholders encounter a liquidity shock during the life of their bonds, then, the bondholders are assumed to sell their bonds immediately at a fraction of the price of the bonds if sold in a perfect liquid market, and the cash flow of the bonds will become
where is the bond price in a perfect market at the time of a liquidity shock, and is the fraction. The bond prices in an imperfect market are less than their prices in a perfect market, because the bondholders obtain liquidity at a cost in an imperfect market. With this said, we have .
Using the principle of risk-neutral valuation, the price of corporate bonds in an imperfect liquid market is:
where is the filtration comprised of both the default and liquidity information, and is the expectation under measure.
To investigate the liquidity effect on the price of a corporate bond, we made two additional assumptions: (1) a liquidity shock is independent of credit risk; and (2) a liquidity shock follows an exponential distribution with liquidity intensity . Then, the price of a corporate bond in an imperfect market is expressed as
It is clear that the fraction, , is a critical factor in understanding the liquidity effect on the price of a corporate bond in an imperfect market.
3. Stochastic Liquidity Discount Process
Bondholders might encounter a liquidity shock before the maturity of their purchased corporate bonds for many reasons, including portfolio rebalancing, risk management, and/or other unexpected liquidity demands. In a perfect market, a liquidity shock has no impact on bond prices. No matter when bondholders encounter liquidity shocks, they are able to sell their bonds at , the price in a perfect market. However in an imperfect market, bondholders subject to liquidity shocks bear a liquidity cost, which can be measured by at time t, for . In a sense, the value of should reflect the liquidity demand and supply. When bondholders encounter a liquidity shock, their demand for liquidity will increase. Under this circumstance, bondholders are willing to sell their bonds at a reasonable cost to meet their liquidity demand, which implies might decrease. In other words, does reflect the liquidity demander’s cost of realizing the liquidity and liquidity provider’s revenue of providing the liquidity.
We propose a stochastic process for , because economic factors, which cause liquidity shocks and, therein, increase the bondholders’ opportunity cost of holding bonds and change the structure of the liquidity supply, are dynamic in nature. In addition, it is reasonable to assume that there exists a market rebalancing mechanism between the liquidity demand and supply that leads to a long-term equilibrium level of liquidity. When the liquidity is above the long-term level, a decease in liquidity demand and increase in liquidity supply will exert a downward-pulling force toward the long-term level; while, when the liquidity is below the long-term level, an increase in the liquidity demand and a decrease in the liquidity supply will pull the process up toward the long-term value. Therefore, the dynamics of can be expressed by a mean-reversion stochastic differential Equation (SDE) with an upper bound and a lower bound in , as shown in the following equation:
where is the mean reversion speed that reflects the liquidity elasticity, is the volatility of the liquidity, is the upper bound of , is the lower bound of , and is the long-term equilibrium level of the liquidity. The upper and lower bounds depend on the bond market environment and bond characteristics. When is equal to either the upper or lower bound, , and the evolution of is completely controlled by the deterministic term in which the mean reversion ensures that never exceeds either the upper or lower bound. is a standard Brownian motion in the real-world probability measure. From Equation (8), we can see that measures the uncertainty of the change in . When , the random change in , liquidity level, and liquidity risk together contribute to the liquidity effect. When , there is only a deterministic change in , and the liquidity effect is driven by the deterministic liquidity change.
It is certain that is a variable that cannot be directly observed in the market; therefore, we propose using bid-ask spreads to derive . The usual bid-ask quotes posted by dealers in the corporate bond market are limited; moreover, they are only valid for a limited period of time (see Jankowitsch 2011). Therefore, an estimate of the bid-ask spread in (Roll 1984) can be used instead. Let denote one half of the bid-ask spread at time t and be estimated by
where is the covariance function of two random variables x and y, and is the difference of the logarithm in the consecutive bond prices. As proven by Hasbrouck (2007), there is a relationship between the bond price and the middle price of the bid and ask prices at time t as follows:
Using the middle price as a proxy for the bond price in a perfect market, the price in an imperfect market is given by
which implies that
4. Monte Carlo Simulation
Considering the complexity of the SDE in Equation (8) for , the formula for pricing corporate bond with liquidity effect in Equation (7) does not have an analytic solution. Therefore, corporate bond prices are computed using the Monte Carlo simulation technique. Let
The Monte Carlo simulation algorithm for is as follows.
- (1)
- Simulate a liquidity shock time using .
- (2)
- Simulate a random variable using , and calculate the corporate asset value at the time of liquidity shock as . Then is calculated by Equation (2).
- (3)
- Simulate the path of for , using the Milstein Schemewhere , , and . We choose to be a week and the initial value of to be . Based on the simulated path, is simulated as , where is the largest integer function.
- (4)
- Compute X using Equation (13).
- (5)
- Repeat steps for n times and obtain a sample with size n of X, denoted by . is estimated by the sample mean , which isand the two-sided confidence interval of with a degree of confidence is given bywhere is percentile of distribution with degree of freedom , and is the sample standard deviation given byGiven an allowed error in the Monte Carlo simulation , the number of samples in the Monte Carlo simulation, n, should satisfy the condition:
For the Monte Carlo simulation, we need to specify the values of a series of parameters, including the risk-free interest rate r, corporate asset value at time t, volatility of the corporate asset , liquidity shock intensity , and the parameters in the SDE for . The next section outlines in detail how to obtain these parameters and their descriptive statistics.
5. Parameter Specification
5.1. The Data
The parameters of the model were estimated using Chinese financial market data. The data used for numerical analysis included interest rates, corporate liabilities, corporate market values, daily stock returns, corporate bond information, corporate bond daily trades, and the tick data of corporate bond trades. The data of the interest rates, corporate liabilities, corporate market values, daily stock returns, and corporate bond daily trades were from Wind3. The interest rates included the Interbank Overnight Repo Rate (IORR) and the Shanghai Interbank Overnight Offered Rate (SHIBOR). The former is the trade volume weighted daily, and the latter is quoted daily. The corporate liabilities were the book values of the current liabilities and long-term liabilities obtained from quarterly financial reports. The tick data of corporate bond trades were from CSMAR. The corporate bond information from RESSET included the bond code, the stock code of the bond issuer, bond maturity, bond issue date, bond issue term, and the bond issue amount. The period of the data was from 12 October 2007 to 31 December 2013.
5.2. Risk-Free Interest Rate
In financial practice, short-term interest rates with low credit risk are normally used as the risk-free interest rate. In the Chinese financial market, both the IORR and SHIBOR can be used as the risk-free interest rate. The difference between these two rates is usually small. The SHIBOR is not a collateralized rate, while the IORR is collateralized by government bonds and has a smaller credit risk premium; thus, the IORR is usually lower than the SHIBOR. In addition, the SHIBOR is quoted by members, while the IORR is determined by actual market trades that more accurately reflect real fund costs in the market. Therefore, we used the IORR as a proxy for the risk-free interest rate. Table 1 displays the descriptive statistics4 of the IORR during the same period as our corporate bond trade data.

Table 1.
Statistics of the IORR.
5.3. Corporate Asset Value
Given the face value F of a corporate bond, its corresponding corporate asset value at time t (denoted by ) is determined by the asset–liability ratio
where is the corporate asset–liability ratio at time t, which is estimated by the ratio of the total corporate debt to the total corporate asset value at that time. Usually the total corporate asset value can be calculated either by summing up the market value of equity and debt or by summing up the book value of equity and debt. Following (Eom 2004), we used the book value of debt and corporate capitalization to calculate the value of the corporate assets, and the quarterly asset–liability ratios per company were calculated. The mean and the cross section statistics of the computed ratios are shown in Table 2.

Table 2.
Statistics of the corporate asset–liability ratio.
5.4. Volatility of Corporate Assets
The volatility of a corporate asset cannot be directly observed. Jones (1984) used the volatility of a corporate stock to calculate the volatility of a corporate asset by the following ratio between them:
where is the volatility of a corporate asset, is the volatility of a corporate stock, E is the corporate capitalization, and is the derivative of the corporate capitalization with respect to the corporate asset value, calculated based on the model in (Merton 1974) as follows:
where T is the term of the corporate debt and is calculated as the weighted average of the current liabilities and long-term liabilities. The term of the current liabilities is assumed to be 0.5 year. Table 3 lists the term, amount, and number of issues of various corporate bonds. Based on Table 3, the issue amount weighted term of China’s corporate bonds was 6.23 years during the period of the available data. The term of a corporate debt T was, therefore, calculated as
where CL and LL are that company’s outstanding amount of current liabilities and long-term liabilities, respectively.

Table 3.
Terms of corporate bonds.
The calculation of is based on the daily yields, expressed as
where m is the number of daily yields in a quarter, and is the daily yields approximated by
where is the stock close price on trade day i.
Because in Equation (20) cannot be solved explicitly, the Newton–Raphson iteration method was used to approximate it. In the process of iteration, the initial value of was set to be multiplied by the leverage ratio, the risk-free interest rate in Equation (21) was set to be the mean value of the IORR , and the convergence tolerance was set to . The mean of the quarterly volatilities per company was calculated; then, the cross-section statistics were obtained and are shown in Table 4, based on the computed mean values.

Table 4.
Statistics of volatility.
5.5. Liquidity Shock Intensity
Liquidity shocks are assumed to be exogenous and to follow an exponential distribution with parameter . The mean of the time to a liquidity shock is equal to . At the same time, the time to a liquidity shock is equal to the holding period of bonds. This indicates that the liquidity shock intensity is equal to the reciprocal of the mean of the holding periods of the bonds (see He 2014). The holding period of the bonds is measured by the reciprocal of the bonds’ yearly turnover. Therefore, the liquidity shock intensity is obtained using the time series of the bonds’ yearly turnover. The estimated liquidity shock intensity is in the physical probability measure.
The liquidity shock intensity used for pricing a corporate bond with the liquidity effect in Equation (7) should be measured in the risk-neutral probability measure. A simple way to estimate the liquidity shock intensity in the risk-neutral probability measure is to assume that the ratio of liquidity shock intensities in two probability measures is equal to the ratio of credit risk intensities in two probability measures. Driessen (2005) used 104 U.S. firms’ bond prices and default rates between 1991 and 2000 and estimated that the ratio of credit risk intensities under two probability measures for AA-, A-, and BBB- rated firms were approximately 1.83, 2.61, and 2.37, respectively. Giesecke (2011) used value weighted default rates for U.S. nonfinancial bonds from 1866 to 2008 and estimated that the mean of the ratio was equal to 2.04. They also claimed that the pricing of credit risk by the financial markets was remarkably consistent over time. Following their research results, in this paper we assumed that the ratio of the liquidity shock intensity under Q measure and P measure was equal to 2.00. Based on this assumption, the statistics of liquidity shock intensities under the risk-neutral probability measure were obtained and are shown in Table 5. We can see that the mean is much greater than the median, and the liquidity shock intensity is therefore right-skewed.

Table 5.
Statistics of the liquidity shock intensity in the risk-neutral measure.
5.6. Parameter Calibration
The generalized moment method (GMM) was used to estimate the parameters , , and in the SDE for , which was discretized by the Euler Scheme as
where follows a standard normal distribution. Following (Chan 1992), the approximate moment conditions based on the Euler Scheme are
The weekly time series of were obtained using Equation (12), in which the weekly half bid-ask spreads were estimated by Equation (9) following the method in (Roll 1984) and using the tick data of the corporate bond trades, which included at least two pairs of prices in a week. is the maximum of during the sample period, and is the minimum. The descriptive statistics of the five parameters were calculated and are shown in Table 6. We can see that the values of parameters , , and do not change much above the 10th percentile, while the values of and have a large standard deviation and are right skewed.

Table 6.
Statistics of the parameters in the SDE of .
6. Numerical Analysis
Based on the Monte Carlo simulation algorithm in Section 4, we used different percentiles of the parameter values specified in Section 5 as different scenarios to compute bond prices and analyze the effect of different liquidity profiles on the bond prices.
6.1. Existence of a Liquidity Premium
A liquidity premium can be expressed as a liquidity price spread and a liquidity yield spread. A liquidity price spread (LPS) is the difference between the bond prices with and without the liquidity effect. A liquidity yield spread (LYS) is the difference between two yields with and without the liquidity effect. In the Monte Carlo simulation, the number of simulations was determined by setting and for the face value of a bond equal to 100. The bond term was set to 6.23 years, which is the issue amount weighted average term of long-term corporate bonds in China’s market. The other parameters in the model were either the sample mean value (Case 1) or the median value (Case 2).
In Case 1, the corporate bond price was equal to 80.51 without the liquidity effect and 80.06 with the liquidity effect, and the corresponding yield rate was 3.48% and 3.57%, respectively. Therefore, the liquidity premium was 0.45 in the price spread and 0.09% in the yield spread. In the Merton Model, without the liquidity effect, the credit yield spread (which is the difference between the bond yields with and without credit risk) was 1.07%. The sum of the liquidity yield spread and the credit yield spread gave the gross yield spread of 1.16%. The credit yield spread accounted for 92.24% of the bond’s gross yield spread, and the liquidity effect accounted for 7.76%.
In Case 2, the median of the interest rate was 2.27%, the corporate bond price was equal to 81.74 without the liquidity effect and 81.55 with the liquidity effect, and the corresponding yields were 3.24% and 3.27%, respectively. Therefore, the liquidity premium was 0.19 in the price spread and 0.03% in the yield spread. The credit yield spread was 0.97%; together with the liquidity yield spread of 0.03%, the bond gross yield spread was 1.00%. The percentage of the credit yield spread in the bond gross yield spread was 97.00%, and the percentage of the liquidity yield spread was 3.00%.
In both cases, the liquidity premium was much higher than the simulation error 0.01, which means that the liquidity premium was not caused by the simulation error. It can be concluded that there exists an economically and statistically significant liquidity premium in the corporate bond market in China. In addition, the difference between the liquidity premiums in Case 1 and Case 2 shows that the liquidity premium might be subject to the market environment and the bonds’ characteristics.
6.2. The Effect of Liquidity Level, Risk, and Elasticity
The liquidity effect can be attributed to the liquidity level, liquidity risk, and liquidity elasticity. The liquidity level is represented by the long-term value , the upper limit , and the lower limit . The liquidity risk comes from uncertainties of the liquidity shocks and random changes in the liquidity level, reflected by the liquidity intensity and liquidity volatility , respectively. The mean reversion speed reflects the liquidity elasticity. Since the liquidity risk and elasticity are constrained by the liquidity level in the liquidity SDE in Equation (8), we decomposed the liquidity premium by first analyzing the liquidity level effect and then analyzing the effect of the liquidity risk and elasticity at different liquidity levels.
To analyze the effect of a liquidity level, the long-term value , upper limit , and lower limit were set as different percentiles (such as 0%, 10%, 30%, 50%, 70%, 90%, and 100%) as listed in Table 6. The bond term was 6.23 years, and the other parameters were set at their mean value. Table 7 shows that when the liquidity level was very high (represented by the 100th percentile), the liquidity premium was too small to be considered. The liquidity premium increased when the liquidity level decreased. When the liquidity level changed from the 100th to the 10th percentile, the liquidity premium increased slowly; however, when the liquidity level changed from the tenth to the zero percentile, the liquidity premium increased sharply. This is explained by the fact that the long-term value, upper limit, and lower limit above the tenth percentile did not change significantly, as shown in Table 6. In addition, if the zero percentile of the liquidity level indicates a liquidity crisis, then the simulation result verifies the empirical research by (Dick-Nielsen 2012) that the liquidity premium increases sharply in a liquidity crisis. Table 7 also reveals that the percentage of the liquidity yield spread in the bond gross yield spread, denoted as LYSR, was normally less than 20% but exceeded 50% in a liquidity crisis.

Table 7.
The effect of the liquidity level on liquidity premium.
The liquidity risks include the uncertainties of the liquidity demand and the liquidity level, indicated by the liquidity intensity and the liquidity volatility , respectively. The larger the , the more frequent the liquidity shock, and the stronger the liquidity demand of the bondholders. When a liquidity shock occurs, the bondholders sell bonds to meet their liquidity demand. The fluctuation in the liquidity level at the time of selling the bonds, determined by the liquidity volatility , leads to a liquidity risk for bondholders. Table 8 summarizes our numerical analysis results.

Table 8.
The effect of the liquidity risk on the liquidity premium.
From Table 8, we can see that the effect of both the liquidity intensity and the liquidity volatility on the liquidity premium was minimal when the liquidity level was very high, represented by the 90th to 100th percentiles. The effect of the liquidity risks on the liquidity premium depended on the liquidity level. In this sense, the liquidity levels have a first-order effect on the liquidity premium, and the liquidity risks have a second-order effect on the liquidity premium.
Table 8 also reveals that the effect of the liquidity shocks on the liquidity premium at a given a liquidity level will not monotonically increase with the increase in the liquidity intensity, and the effect reached its maximum when the liquidity intensity was at the 90th percentile. This might be the mean-reversion property and the upper bound and lower bound of liquidity set in the model, to take into account the bond market’s ability to maintain the equilibrium of liquidity demand and supply. When the liquidity demand of the bondholders increases, the liquidity supply will increase for an increased liquidity premium. The increase in liquidity supply restrains the continuous increase in the liquidity premium.
To be more specific, when the liquidity level was greater than the zero percentile, the effect of the liquidity volatility on the liquidity premium increased when the liquidity volatility increased. Specifically, when the percentile of the liquidity volatility was between zero and the fiftieth, the effect was small. In contrast, when the liquidity volatility exceeded its 50th percentile, then the liquidity volatility began to strongly affect the liquidity premium. The extent of the effect even doubled when the liquidity volatility exceeded its 90th percentile. On the other hand, when a liquidity level was at the zero percentile, the liquidity volatilities at different percentiles had a similar impact on the liquidity premium. Therefore, it can be concluded that the effect of the liquidity volatility on the liquidity premium occurs when a liquidity level is not abnormal, and the liquidity volatility is high. This result provides more information than the empirical finding by (Bongaerts 2017) that the risk premium caused by the liquidity risk of a corporate bond is insignificant.
The liquidity elasticity, which is the ability to revert to the long-term value, is reflected by a mean reversion speed. The higher the mean reversion speed, the larger the liquidity elasticity. Table 9 shows the effect of the liquidity elasticity on the liquidity premium at different liquidity levels. Similar to the effect of the liquidity volatility, the effect of the liquidity elasticity also depended on the liquidity level. When the liquidity level was either high or low, the effect of the liquidity elasticity was weak. Interestingly, the effect of the liquidity elasticity was U-shaped. When the mean reversion speed was either low or high, its effect on the liquidity premium was significant.

Table 9.
The effect of the liquidity elasticity on the liquidity premium.
6.3. Term Structure of the Liquidity Premium
In this section, we examine whether the term of a bond affects the liquidity premium. Theoretically, a bond’s term might have a twofold effect on the liquidity premium. First, a bond’s term determines the length of time in which a bond is subject to liquidity shocks. We call this the direct effect. Second, the term of a bond also changes its liquidity profiles, which affect the liquidity premium. We call this the comprehensive effect of a bond’s term.
At the pricing time t, the time to maturity is , and the expected number of liquidity shocks is . The longer the bond term, the higher the number of expected liquidity shocks. To examine the direct effect, we set all other parameters at their mean value, and the liquidity premium was computed with various bond terms. Figure 1 shows the term structure of the liquidity premium.
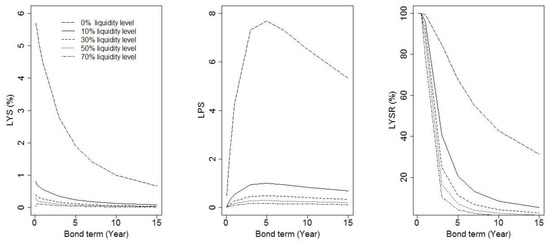
Figure 1.
The direct effect of the bond term on the liquidity premium.
Firstly, the term structure of the liquidity premium was conditional on the liquidity level. The effect of the bond terms on the liquidity premium increased when the liquidity level decreased. When a liquidity level changed from the tenth to the zero percentile, the term structure curve of the liquidity premium dramatically shifted upward. When a liquidity level exceeded its 70th percentile, the effect of the term on the liquidity premium was very minimal and, therefore, not shown in Figure 1.
Secondly, the term structure of the liquidity yield spreads was decreasing and convex, as shown in the left panel of Figure 1. This is consistent with the findings of (Driessen 2005) and of (Ericsson 2006). The percentage of the liquidity yield spread in the gross yield spread of a short-term bond was very high, as presented in the right panel in Figure 1. This indicates that liquidity instead of credit risk dominates the yield spread of a short-term bond. This result is consistent with the conclusion of (Zheng 2006; Fu 2012). In addition, the term structure of the percentage of the liquidity yield spread in the gross yield spread was also decreasing and convex.
At last, in contrast to the term structure of the liquidity yield spread, the term structure of the liquidity price spreads in the middle panel was concave with the strongest effect occurring when a bond term was at approximately five years. In addition, the lower the liquidity level, the more concave and the stronger the effect of the bond term on the liquidity price spread.
To examine the comprehensive effect of the term of a bond on its liquidity premium, we used six one-factor linear regressions to model the change in liquidity profiles as the bond’s term changed. The one-factor linear regression is
where y is the liquidity shock intensity , long term value , upper limit , lower limit , liquidity volatility , or mean reversion speed . Table 10 lists the values of c and for each of y. We can see that the term of a bond significantly affected its liquidity shock intensity, long-term value, liquidity volatility, and lower limit.

Table 10.
The effect of the bond term on the liquidity premiums.
In particular, the significant negative effect of a bond’s term on liquidity intensities indicates that, the longer the term, the smaller the liquidity shock intensity. This result coincides with our intuition that a long-term bond is usually bought and held to maturity. The significant negative effect of the term of a bond on its long-term value and lower limit confirms the negative correlation between a bond’s term and liquidity, as concluded by (Tychon 2005; He 2014). In addition, the term of a bond positively and significantly affected the liquidity volatility.
Based on the one-factor linear regression models for the four liquidity parameters that changed significantly with a bond’s different terms, we calculated the bond term-adjusted liquidity shock intensity, long-term value, liquidity volatility, and lower limit. The term structure of the liquidity premium was constructed with these four bond term-adjusted parameters, and the other parameters were set as their mean value. The structure of the liquidity premium with all parameters set at their mean value is also depicted for comparison, as shown in Figure 2.
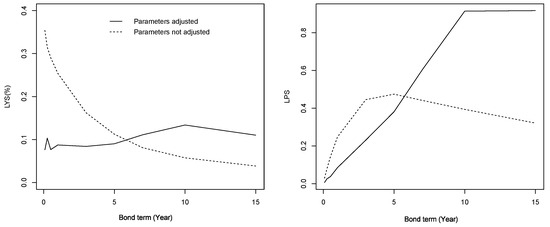
Figure 2.
The effect of bond term on liquidity premium.
It can be seen that the term structure of the liquidity yield spreads became irregular after considering the comprehensive effect of the bond terms on the liquidity premium. Generally speaking, the term structure of the liquidity price spreads was exaggerated after considering the comprehensive effect of bond terms.
In addition, the liquidity premium of a bond with a term of less than five years decreased after considering the comprehensive effect, represented by the solid line staying below the dashed line in both the liquidity yield spread plot and the liquidity price spread plot. The liquidity premium of a bond with a term of longer than five years increased after considering the comprehensive effect; in other words, the solid line is above the dashed line when the bond term is greater than five years. This might be explained by the practice that long-term bonds are usually put into buy and hold portfolios, and the direct effect of the term of a bond on the liquidity premium is therefore marginal. The comprehensive effect takes into account a bond term’s negative effect on the liquidity, and the liquidity premium of a long-term bond, therefore, increases.
7. Conclusions
This paper investigated the magnitude of the liquidity premium and the impact of various liquidity factors on the liquidity premium in China’s corporate bond market, based on China’s corporate bond trade data and the corporate bond information data from 2007 to 2013. For these research goals, we incorporated a stochastic liquidity discount process into the Merton model and built a corporate bond pricing model in an imperfect liquidity market.
In the proposed model, three main liquidity risk factors (liquidity level, liquidity risk, and liquidity elasticity) were defined and parameterized. Their impact on the liquidity premium was investigated one by one. Our research confirmed that there exists a significant liquidity premium in China’s corporate bond market. Among the three liquidity risk factors, the liquidity level played the most important role in determining the liquidity premium.
The effect of the liquidity risk (in terms of liquidity shocks and liquidity volatilities), liquidity elasticity, and the bond term was conditional on a bond’s liquidity level. The effect of the liquidity shocks was subject to the liquidity level and the market’s equilibrium mechanism in the liquidity demand and supply. The effect of the liquidity volatility was significant when the liquidity volatility was relatively high at a normal liquidity level and was trivial at an otherwise abnormal liquidity level because of the dominating effect of an abnormal liquidity level. Especially in a liquidity crisis, the liquidity level will cause a dramatically increased liquidity premium. In addition, the effect of the liquidity elasticity on the liquidity premium appeared to be U-shaped because of the market’s equilibrium.
The bond terms had a twofold effect on the liquidity premium, namely, a direct effect and a comprehensive effect. The direct effect considers the fact that the term of a bond directly determines the number of liquidity shocks the bond is exposed to, while the comprehensive effect takes into account the changes in the liquidity profiles caused by different bond terms. The direct effect led to a convex and decreasing term structure curve of the liquidity yield spreads. The term structure of the liquidity yield spread as a percentage of the gross yield spread was also convex and decreasing. In addition, the liquidity yield spreads dominated the gross yield spread of a short-term bond. When using term-adjusted parameters to consider the comprehensive effect of the term, the liquidity premium of a short-term bond became smaller, while the liquidity premium of a long-term bond became dramatically higher.
To summarize, our research makes three main contributions to the current literature. First, by incorporating a stochastic liquidity process into the Merton model, this paper proposed a feasible method to price corporate bonds in an imperfect liquidity market. We also acknowledge the limitation of the proposed approach. There is no closed form solution, and we resorted to the Monte Carlo simulation. We leave this issue to a future work and will continue to explore stochastic liquidity dynamics for pricing corporate bonds with liquidity risk.
Second, in addition to confirming the existence of a liquidity premium in China’s corporate bond market, our analysis provided a deep understanding of the liquidity premium from different perspectives of liquidity. Our findings, based on the data containing a liquidity shock during the subprime mortgage crisis from 2007 to 2010, have important implications for the liquidity premium during the current pandemic-induced liquidity shock period. Dienemann (2021) estimated that the pandemic-induced shock to market-wide liquidity has a magnitude of about six standard deviations. It is worth considering the corporate bond liquidity under such a stressed condition in the future.
Third, the term structure of the liquidity effect was studied. The direct and indirect impacts on the liquidity premium of the term of a bond were quantified. Although we acknowledge that our results were based on China’s corporate bond data and should be interpreted with caution, they provide indicative information to companies in need of direct financing, especially in the post-pandemic period with a pandemic-induced liquidity shock.
Author Contributions
Conceptualization, X.M.; methodology, X.M.; software, X.M.; validation, X.M.; formal analysis, X.M.; investigation, X.M.; resources, X.M.; data curation, X.M.; writing—original draft preparation, M.J.; writing—review and editing, M.J.; visualization, X.M. and M.J.; supervision, M.J.; project administration, X.M.; funding acquisition, X.M. All authors have read and agreed to the published version of the manuscript.
Funding
The authors acknowledge the financial support from the National Natural Science Foundation of China (Grant No. 71161012) and Jiangxi Provincial Visiting Scholar Program for Young University Researchers.
Data Availability Statement
Not applicable.
Conflicts of Interest
The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
Notes
| 1 | Retrieved from http://www.gtarsc.com/ (accessed on 8 May 2022). |
| 2 | Retrieved from http://www.resset.com/ (accessed on 8 May 2022). |
| 3 | Retrieved from http://www.wind.com.cn/ (accessed on 19 May 2022). |
| 4 | The tables in the paper use three important descriptive statistics: Mean, Standard Deviation (SD), and Percentiles. |
References
- Acharya, Viral V., Yakov Amihud, and Sreedhar T. Bharath. 2013. Liquidity Risk of Corporate Bond Returns: Conditional Approach. Journal of Financial Economics 110: 358–86. [Google Scholar] [CrossRef]
- Bai, Jennie, Turan G. Bali, and Quan Wen. 2019. Common risk factors in the cross-section of corporate bond returns. Journal of Financial Economics 131: 619–42. [Google Scholar] [CrossRef]
- Black, Fischer, and Myron Scholes. 1973. The Pricing of Options and Corporate Liabilities. Journal of Political Economy 81: 637–54. [Google Scholar] [CrossRef] [Green Version]
- Bongaerts, Dion, Frank De Jong, and Joost Driessen. 2017. An Asset Pricing Approach to Liquidity Effects in Corporate Bond Markets. The Review of Financial Studies 30: 1229–69. [Google Scholar] [CrossRef]
- Chan, Kalok C., G. Andrew Karolyi, Francis A. Longstaff, and Anthony B. Sanders. 1992. An Empirical Comparison of Alternative Models of the Short-term Interest Rate. The Journal of Finance 47: 1209–27. [Google Scholar] [CrossRef]
- Chen, Hui, Rui Cui, Zhiguo He, and Konstantin Milbradt. 2018. Quantifying liquidity and default risks of corporate bonds over the business cycle. The Review of Financial Studies 31: 852–97. [Google Scholar] [CrossRef]
- Chen, Long, David A. Lesmond, and Jason Wei. 2007. Corporate Yield Spreads and Bond Liquidity. The Journal of Finance 62: 119–49. [Google Scholar] [CrossRef]
- Dick-Nielsen, Jens, Peter Feldhütter, and David Lando. 2012. Corporate Bond Liquidity Before and After the Onset of the Subprime Crisis. Journal of Financial Economics 103: 471–92. [Google Scholar] [CrossRef] [Green Version]
- Dienemann, Fabian. 2021. A New Perspective on the Corporate Bond Liquidity Factor. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3887421 (accessed on 8 May 2022).
- Driessen, Joost. 2005. Is Default Event Risk Priced in Corporate Bonds? The Review of Financial Studies 18: 165–95. [Google Scholar] [CrossRef]
- Duffie, Darrell, and Kenneth J. Singleton. 1999. Modeling Term Structures of Defaultable Bonds. The Review of Financial Studies 12: 687–20. [Google Scholar] [CrossRef] [Green Version]
- Elton, Edwin J., Martin J. Gruber, Deepak Agrawal, and Christopher Mann. 2001. Explaining the Rate Spread on Corporate Bonds. The Journal of Finance 56: 247–77. [Google Scholar] [CrossRef]
- Eom, Young Ho, Jean Helwege, and Jing-zhi Huang. 2004. Structural Models of Corporate Bond Pricing: An Empirical Analysis. The Review of Financial Studies 17: 499–544. [Google Scholar] [CrossRef]
- Ericsson, Jan, and Olivier Renault. 2006. Liquidity and Credit Risk. The Journal of Finance 61: 2219–50. [Google Scholar] [CrossRef]
- Fu, Jianping, Xingchun Wang, and Yongjin Wang. 2012. Credit spreads, endogenous bankruptcy and liquidity risk. Computational Management Science 9: 515–30. [Google Scholar] [CrossRef]
- Giesecke, Kay, Francis A. Longstaff, Stephen Schaefer, and Ilya Strebulaev. 2011. Corporate Bond Default Risk: A 150-year Perspective. Journal of Financial Economics 102: 233–50. [Google Scholar] [CrossRef]
- He, Zhiguo, and Konstantin Milbradt. 2014. Endogenous Liquidity and Defaultable Bonds. Econometrica 82: 1443–508. [Google Scholar]
- Houweling, Patrick, Albert Mentink, and Ton Vorst. 2005. Comparing Possible Proxies of Corporate Bond Liquidity. Journal of Banking and Finance 29: 1331–58. [Google Scholar] [CrossRef] [Green Version]
- Jankowitsch, Rainer, Amrut Nashikkar, and Marti G. Subrahmanyam. 2011. Price Dispersion in OTC Markets: A New Measure of Liquidity. Journal of Banking and Finance 35: 343–57. [Google Scholar] [CrossRef] [Green Version]
- Jarrow, Robert. 2001. Default Parameter Estimation using Market Prices. Financial Analysts Journal 57: 75–92. [Google Scholar] [CrossRef] [Green Version]
- Jones, E. Philip, Scott P. Mason, and Eric Rosenfeld. 1984. Contingent Claims Analysis of Corporate Capital Structures: An Empirical Investigation. The Journal of Finance 39: 611–25. [Google Scholar] [CrossRef]
- Li, Xinting, Baochen Yang, Yunpeng Su, and Yunbi An. 2021. Pricing Corporate Bonds with Credit Risk, Liquidity Risk, and Their Correlation. Discrete Dynamics in Nature and Society 2021: 6681035. [Google Scholar] [CrossRef]
- Lin, Hai, Junbo Wang, and Chunchi Wu. 2011. Liquidity Risk and Expected Corporate Bond Returns. Journal of Financial Economics 99: 628–50. [Google Scholar] [CrossRef]
- Longstaff, Francis A., Sanjay Mithal, and Eric Neis. 2005. Corporate Yield Spreads: Default Risk or Liquidity? New Evidence from the Credit Default Swap Market. The Journal of Finance 60: 2213–53. [Google Scholar] [CrossRef] [Green Version]
- Merton, Robert C. 1974. On the Pricing of Corporate Debt: The Risk Structure of Interest Rates. The Journal of Finance 29: 449–70. [Google Scholar]
- Pastor, Lubos, and Robert F. Stambaugh. 2019. Liquidity Risk after 20 Years. (No. w25774). Cambridge: National Bureau of Economic Research. [Google Scholar]
- Richardson, Scott, and Diogo Palhares. 2018. (Il) liquidity premium in credit markets: A myth? The Journal of Fixed Income 28: 5–23. [Google Scholar] [CrossRef]
- Roll, Richard. 1984. A Simple Implicit Measure of the Effective Bid-ask Spread in an Efficient Market. The Journal of Finance 39: 1127–39. [Google Scholar] [CrossRef]
- Tychon, Pierre, and Vincent Vannetelbosch. 2005. A Model of Corporate Bond Pricing with Liquidity and Marketability Risk. Journal of Credit Risk 1: 3–35. [Google Scholar] [CrossRef]
- Wu, Zijian, Baochen Yang, and Yunpeng Su. 2022. Liquidity, Credit Risk, and Their Interaction on the Spreads in China’s Corporate Bond Market. Discrete Dynamics in Nature and Society 2022: 2996704. [Google Scholar] [CrossRef]
- Zheng, Harry. 2006. Interaction of Credit and Liquidity Risks: Modelling and Valuation. Journal of Banking and Finance 30: 391–407. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).