1. Introduction
Archimedean copulas, which in two dimensions are of the form
where
is the one-dimensional generator, have become a popular mode of modelling dependence in both finance and insurance. Several ways of constructing copula families are given in Chapter 3 of
Joe (
2015). The interpretation of the generator as the Williamson transform of a radial random variable has given rise to new Archimedean families; see
McNeil and Nešlehová (
2009,
2010). Archimedean copulas are a flexible class due to the ease with which new Archimedean copulas with an enriched parameter space can be constructed from existing ones using transformations. For the bivariate case, five of such transformations, namely, left composition, right composition, scaling, exponentiation, and the linear combination of the (inverse) generator, were introduced in the literature by
Genest et al. (
1998). They were reviewed by
Michiels and De Schepper (
2012), and in more detail in
Michiels and De Schepper (
2009), with the focus on the so-called
function (which is the ratio of the inverse generator to its derivative). For the latter, see also
Michiels et al. (
2011).
In the literature, several generalized families were constructed that contain the Archimedean class as a special case, e.g., the Archimax family in
Capéraà et al. (
2000) (which includes extreme value copulas as another special case). The background risk model where one random variable (“systemic risk”) acts multiplicatively on a series of other random variables (“idiosyncratic risks”) is the basis of generalization of Archimedean copulas in several ways, as demonstrated in
Côté and Genest (
2019) and
Marri and Moutanabbir (
2022).
Commonly used families typically feature a generator being completely monotonic and thereby the Laplace transform of a mixing random variable. Common examples include Clayton and Frank (as far as dependence is positive), Gumbel–Hougaard, and Joe. This subfamily of Archimedean copulas, also known as shared frailty models, has the advantage of being valid in any dimension. Recent applications regarding shared frailty models involve the aforementioned background risk model; see (
Albrecher et al. 2011;
Furman et al. 2021;
Sarabia et al. 2018).
The Gumbel–Hougaard copula is a good fit to the well-known dataset of loss vs. Allocated Loss Adjustment Expenses (ALAE), which is the object of statistical inference in several publications, starting with
Genest et al. (
1998). For extensive analysis, consult
Joe (
2015). Probably there are several other case studies of dependence in insurance where the use of shared frailty models is appropriate.
Shared frailty dependency models have the property of being conditionally increasing (CI) and multivariate totally positive of order 2 (MTP
), as shown in
Müller and Scarsini (
2005). In the specific case of two dimensions, this is known as TP
, implying stochastically increasing (SI), which in turn implies both left tail decreasing (LTD) and right tail increasing (RTI). If the two involved marginal random variables are remaining lifetimes, LTD/RTI implies that the hazard rate of the one upon hazard (e.g., death or default) of the other goes up. The stronger condition SI implies that the hazard rate of the one given the hazard of the other (e.g., death or default) at time
t decreases as
t goes up. This was noted in
Spreeuw (
2006). The underlying assumption of SI may work out well in reliability theory. Consider two printers available to office staff. When one fails, the other one, pending the repair of the first, is used more intensively and thereby exposed to greater strain. It is sensible to assume that the longer the first printer is out of order, the higher the failure rate of the remaining machine would be.
For coupled lives, however, it is not so clear-cut. On the one hand, the event of the death of one life usually triggers an elevated mortality of the surviving life, so the assumption of LTD/RTI seems sensible. In addition, such lives are exposed to common risks due to permanently living together and due to a similar background (“birds of a feather flock together”, the so called long-term dependence according to
Hougaard (
2000)). On the other hand, however, there is also the phenomenon of the event of the one life dying leading to the mortality of the remaining life temporarily going up, which is the so-called broken-heart syndrome (short-term dependence, also attributed to
Hougaard (
2000)). Similar nonstandard features may apply to other cases in insurance (and finance as well). In short, there is a case for constructing copula families allowing for flexibility in terms of type of dependence, such as LTD/RTI but not necessarily SI.
In this paper, we introduce a new Archimedean copula family that is based on a link between Archimedean generators and utility functions; see
Spreeuw (
2010) for more details. Unlike mainstream copulas, this family has the property of being LTD/RTI, but not necessarily SI, the latter being clearly indicated by the sign of one of the parameters.
The outline of the paper is as follows.
Section 2 gives the basic definitions of Archimedean copula, and the dependence concepts of LTD/RTI and SI.
Section 3 introduces the new family and analyzes its basic properties.
Section 4 fits the new Archimedean family to the section of censored remaining lifetime data of coupled lives, as in
Luciano et al. (
2008).
Section 5 sets out a conclusion.
2. Basic Definitions
Define
as the generator of a 2-dimensional Archimedean copula, being strictly continuous, strictly decreasing, convex, with
and
. The copula itself is then specified as
where
each take values between 0 and 1.
Next are definitions of the tail concepts of left tail decreasing (LTD), right tail increasing (RTI) and stochastically increasing (SI), based on two random variables
X and
Y, and their copula
C. They can all be found in Chapter 5 of
Nelsen (
2006).
Definition 1. Y is LTD in X (notation LTD ) is nonincreasing in x for all y. For an exchangeable copula C (i.e., for ) of random variables X and Y, LTD and LTD are equivalent.
Definition 2. Y is RTI in X (notation RTI ) is nondecreasing in x for all y. For an exchangeable copula C (i.e., for ) of random variables X and Y, RTI and RTI are equivalent.
Definition 3. Y is SI in X (notation SI ) is nonincreasing in x for all
Proposition 1. If C is Archimedean with generator ψ, LTD or LTD if and only if ψ is logconvex. Likewise, if , the rotated copula (also known as survival copula) of C (so for ) is Archimedean with generator is RTI or RTI if and only if is logconvex.
Proposition 2. If C is Archimedean with differentiable generator ψ, SI or SI if and only if is logconvex.
3. SAHARA Family
The SAHARA copula family is derived from the Symmetric Asymptotic Hyperbolic Absolute Risk Aversion (SAHARA) utility function introduced in
Chen et al. (
2011). This utility function is specified below.
As shown in
Spreeuw (
2010), a strict Archimedean generator can be obtained from a utility function
if
. For SAHARA, this is the case when
. Then, applying the formula
leads to the Archimedean generator
Remark 1. This approach of obtaining an Archimedean generator from a utility function is not to be confused with the method of obtaining the inverse
of an Archimedean generator from a utility function. For the latter, consult Spreeuw (2014). The SAHARA utility function was inspired by nonmonotone risk aversion coefficient
which, unlike common utility functions, is not monotone in its argument. It is rather increasing for
attaining a maximum for
, and decreasing for
. The SAHARA utility function found applications in both finance and insurance (
Bernard et al. 2021;
Bernard and Kwak 2016;
Brachetta and Schmidli 2020;
Chen et al. 2021;
Chen and Vellekoop 2017;
Li and Ma 2018;
Schumacher 2018). As shown in
Spreeuw (
2010), a risk aversion monotone decreasing (increasing) on the positive real line in general implies that the corresponding Archimedean copula is stochastic increasing (stochastic decreasing) in two dimensions. The former property applies to the vast majority of commonly applied copula families (including all those whose generator is a completely monotonic function). For
the copula is neither stochastic increasing nor stochastic decreasing. To the best of our knowledge, there are hardly any copula families that share this property.
For
, the condition imposed on
can be somewhat relaxed to
,
corresponding to the Clayton copula with parameter
. Due to scaling, for some real-valued
and
,
gives exactly the same Archimedean copula as
. To see this, we divide in (
3) both numerator and denominator by
. This gives:
Now, being real-valued implies that is real-valued as well. In addition, it is well-known that a generator is only defined up to a multiple constant. In other words, for , and generate the same Archimedean copula. is equivalent to . Hence, without loss of generality, we take from now on bearing in mind that, for , the Clayton copula with parameter is obtained as a limiting case. For , the Clayton copula is again obtained as a limiting case, although now with parameter .
It can be numerically shown that this copula (a) for a fixed decreases in concordance with increasing ; (b) for negative fixed , it increases in concordance with increasing ; and (c) for a positive fixed , it first decreases and then increases in concordance in terms of . For any finite , and lead to independence and comonotonicity, respectively.
According to Theorem 4.3 of
Joe (
1997), p. 91, for Archimedean copulas with a strict generator, the population version of Kendall’s tau can be written as:
Using software system
Wolfram Mathematica (see
Wolfram Research Inc. (
2017)) this gives the expression:
for
considerably reducing to
. Taking the limit for
, keeping
constant, gives
. This is the well-known formula of Kendall’s tau for the Clayton copula, and therefore not very surprising. Taking the limit
, keeping
constant, gives
. This implies that, for increasing
, the range of values taken by
increases. So, the lowest possible value of
for this family is
. For fixed nonpositive
,
is monotone increasing in
from 0 to 1. For fixed and finite positive
,
as a function of
first decreases until a certain negative minimum that is greater than
, and increases afterwards. The greater the value of
is, the greater the value of
for which the minimum is reached and the smaller the minimal value. The difference between Kendall’s tau for
and
is
which is zero for
increasing until
(which for
and
gives values of Kendall’s tau of
and
, respectively), then decreasing for increasing
and ultimately vanishing. There is no upper tail dependence, while the lower tail dependence coefficient is
.
Another interesting feature of this family concerns the conditional survival copula, that is, if the copula of the conditional joint survival function
. If the joint survival function
has an Archimedean copula with generator
, the conditional joint survival function
also has an Archimedean copula with generator
where
. (Usually the conditional copula is rather given in terms of the inverse generator
, see (
Charpentier 2003;
Spreeuw 2006;
Sungur 2002)) Applying (
4) to the SAHARA family gives
so the conditional copula is again SAHARA with parameters
and
. It follows that dependence increases over time, and the copula converges to Clayton with parameter
. Again, this is unlike most other copula families where the limiting dependence is either none (independence) or perfect positive.
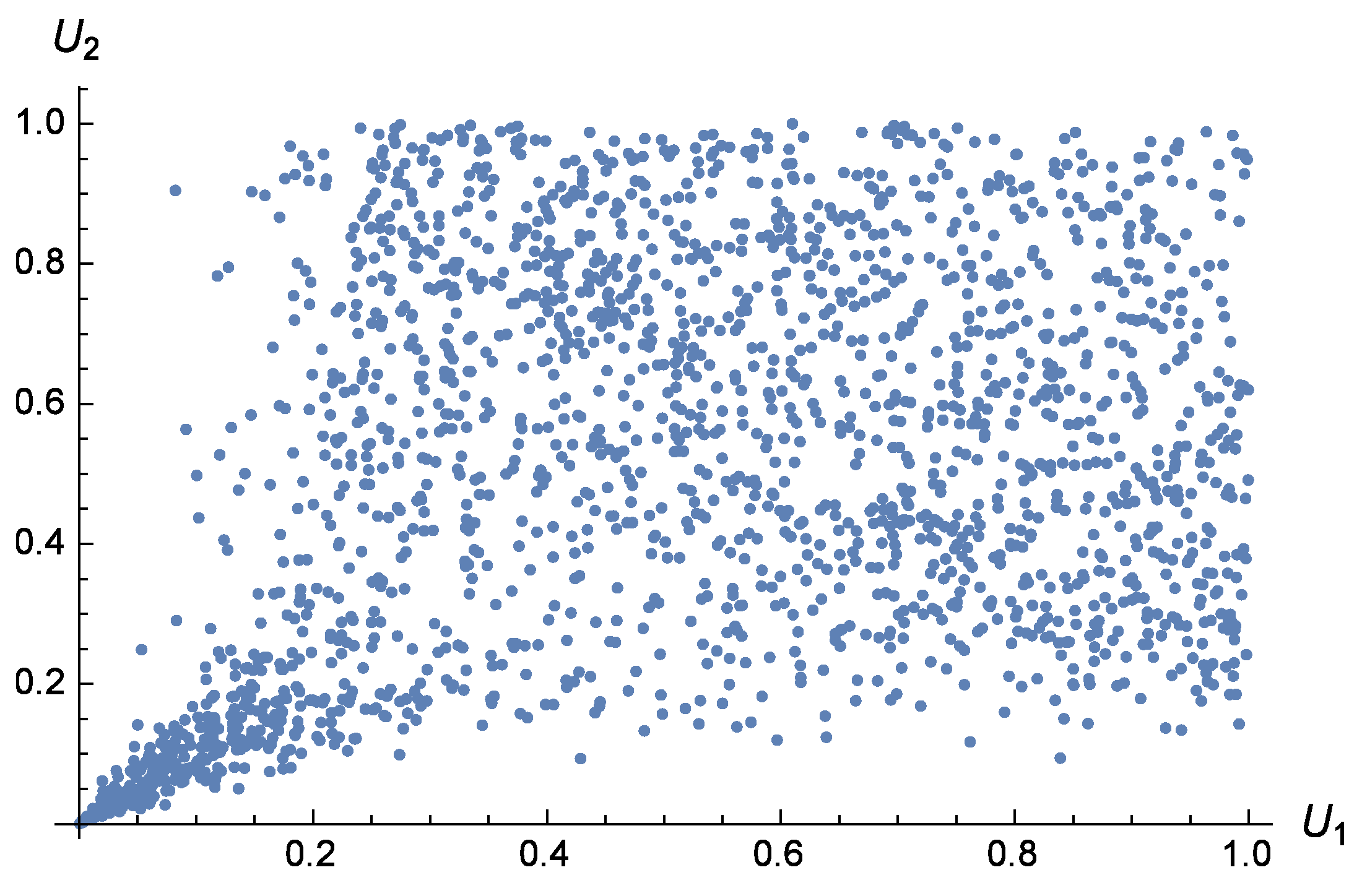
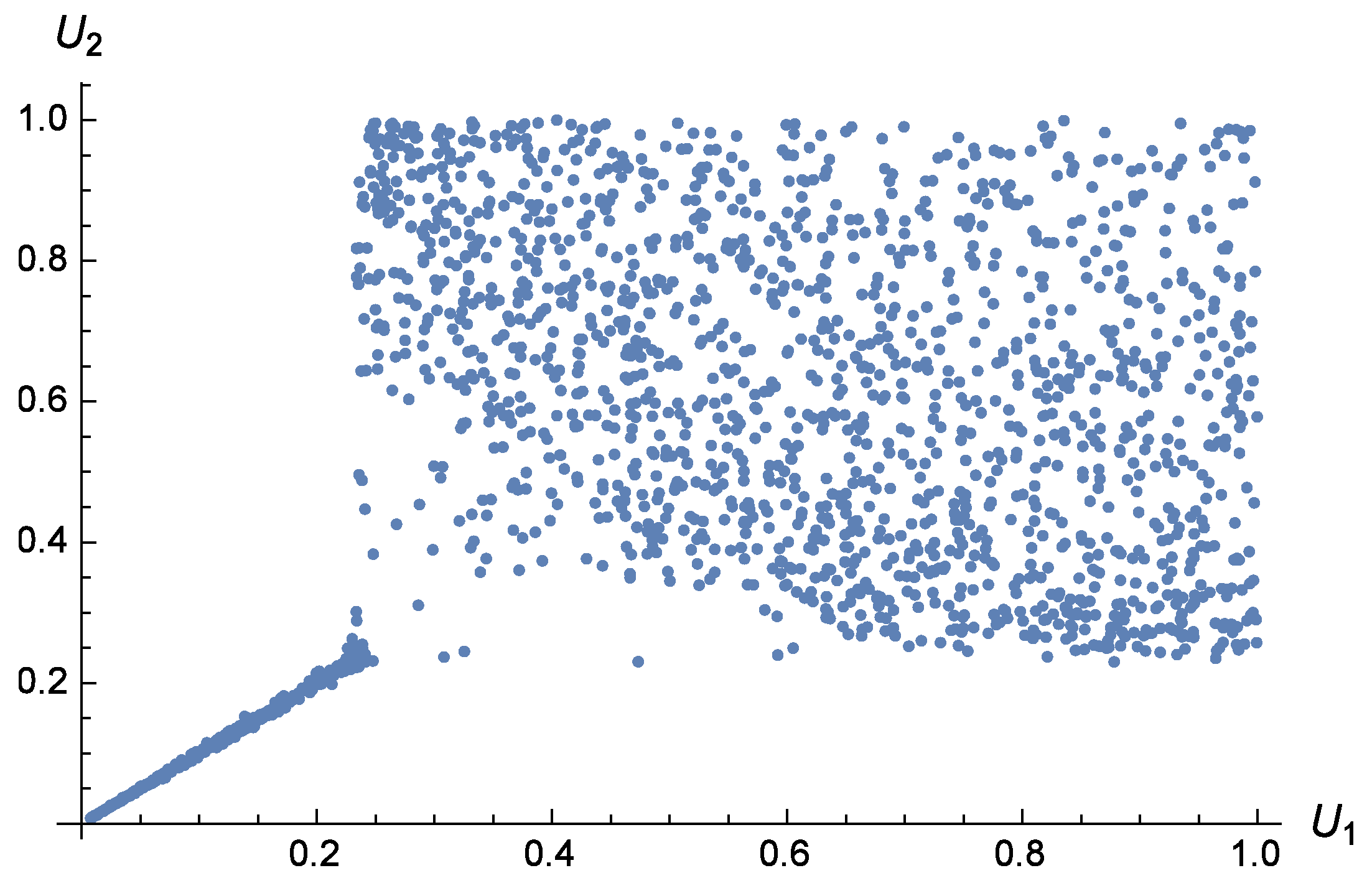
Some scatterplots follow in
Figure 1,
Figure 2 and
Figure 3, for Kendall’s tau fixed at
and varying values for
and
. As
went up, we encountered on the one hand increasingly positive dependence in the bottom left part, and increasingly negative dependence in the top right half. Such families could be considered when data feature strongly positive dependence for small values, and weakly positive, no, or even negative dependence for large values.
The SAHARA copula is clearly flexible and versatile. A drawback is that the inverse of the generator is not available in closed form, like some families introduced in
McNeil and Nešlehová (
2010);
Hua and Joe (
2011) and
Hua (
2015), rendering computations more complicated.
4. Application
For the numerical application in this section, we use the example about modelling dependence of coupled lives in
Luciano et al. (
2008) and
Spreeuw (
2014). The two publications used different data, although they both concern samples specified as generations from the same large dataset of annuitants from a Canadian insurer. In this section, copula families are fitted into the data from
Luciano et al. (
2008) rather than those from
Spreeuw (
2010). We follow the same procedure of modelling and calibration as that in
Luciano et al. (
2008) and
Spreeuw (
2014). Some elaboration on deriving the empirical generator is in order to render this paper self-contained.
The joint survival function of two remaining lifetimes
(male, age
x at the start of the observation) and
(female, age
y at the start of the observation) is given in terms of a survival copula
as
In this setup, the lives are coupled at the time when they are observed (rather than at birth, as in, e.g.,
Frees et al. (
1996)), just like in
Carriere (
2000). Using a modified version of the procedure by
Wang and Wells (
2000), the performance of a candidate Archimedean copula is judged on the basis of distance between the empirical Kendall function, denoted by
, and the theoretical Kendall function, denoted by
, where
is the inverse generator of the copula concerned, with
being the parameter vector estimate minimizing the distance between
and
. For single parameter copulas,
=
, while for families with two parameters,
. The distance or error is defined under the
norm (so, in the usual quadratic sense). Therefore,
with
Given that the data were right censored, the lower bound
was greater than zero. In this example, it is taken to be the smallest value for which
is positive:
The empirical Kendall function, denoted by
, was derived from Dabrowska’s nonparametric estimator of the joint survival function (see
Dabrowska (
1988)). Given that the data were right censored, with many observations being doubly censored,
is zero between 0 and a certain value
, at which point it jumps. In this case,
. The pseudo-maximum likelihood (PML) procedure uses as input rescaled Kaplan–Meier estimates of the marginal survival functions in order to accommodate censoring.
Luciano et al. (
2008) fit the data to Clayton, Gumbel-Hougaard, Frank, entry 20 of Table 4.2 in
Nelsen (
2006) (“4.2.20 Nelsen”) and the so-called Special copula. For convenience, the last two are listed below with their generators:
4.2.20 Nelsen:.
Special:.
Luciano et al. (
2008) concluded that 4.2.20 Nelsen fit the data best. In this section, we compare its performance with that of SAHARA and the best contender of common two-parameter families from
Joe (
1997,
2015), i.e., BB2. Its generator is:
The 4.2.20 Nelsen is a special case of BB2 arising for
.
Results are given in
Table 1. The positive estimate for
indicates the absence of SI.
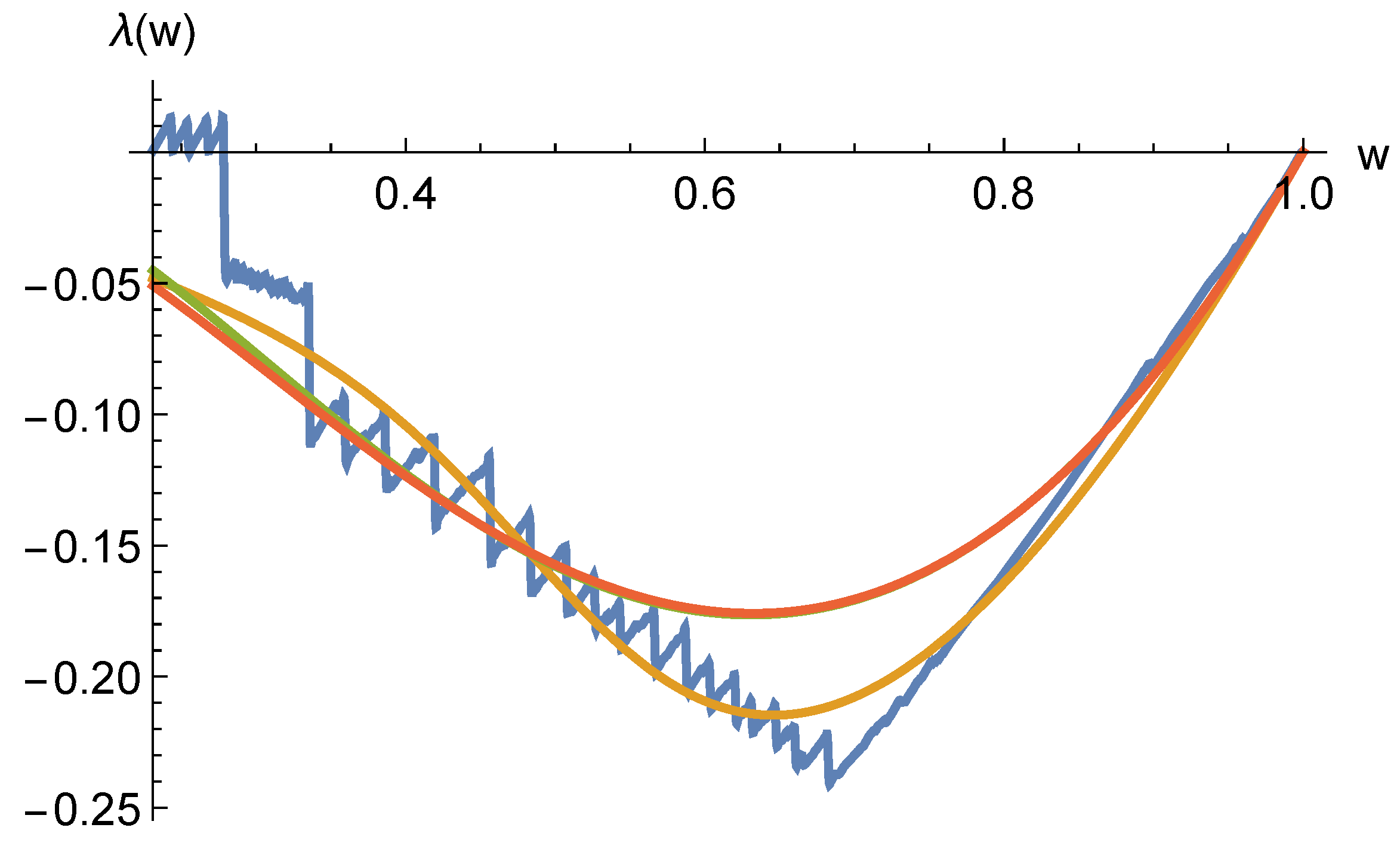
As in
Luciano et al. (
2008), we performed a graphical comparison between the theoretical and the empirical K functions through transformation
for
. The result can be found in
Figure 4. SAHARA achieved a significant improvement to the fit compared to the other families.
Now consider the notion of SI in more detail. For two random variables
and
,
being SI in
is equivalent to
being nondecreasing in
for all
. Related to this is the notion of long-term dependence as introduced in
Hougaard (
2000). If we define
as the conditional force of mortality of life
at duration
t given
(
dies at duration
), then the dependence between
and
is of the long-term type if
is constant or decreasing as a function of
, while dependence is short-term if
is increasing as a function of
. To understand this, it is important to that, as indicated before, for Archimedean copulas, stochastic increasing (SI) is equivalent to
being logconvex.
Spreeuw (
2006) showed that this property of the generator also applies to long-term dependence, implying that SI and long-term dependence are actually equivalent. On the other hand, however, for the SAHARA family, we have:
which is monotone increasing in
s across the board for negative
. For positive values of
, however, the expression decreases in
s for
, so the SI property does not hold. The positive parameter estimate for
suggests that short-term rather than long-term dependence may prevail between the coupled lives. To investigate this further, we analysed the data in the same vein as in
Spreeuw and Owadally (
2013), who devise an augmented Markov model to allow for short-term dependence for the entire dataset. Results are reported in
Table 2.
In this table,
e denotes the time in which an integer number of years that have elapsed since the death of the partner. So, e.g.,
concerns the lives that were bereaved less than a year ago. For each possible value of
e (noting that each life was observed for 5 years or less), we calculate number of deaths reported, the risk exposure, and the overall mortality rate being the ratio of the values in the second and third column. So, for instance, the risk exposure of lives who lost their partner less than a year ago is
, and there were 69 lives that died within one year after their partner. Now, long-term dependence implies that the mortality rate in the last column should be increasing as a function of
e, but the results in
Table 2 show that this is not the case, and that short-term dependence may be present even though the aggregate mortality rate for
is higher than for
e equal to
or 3.
Ideally, one such table should be shown for each gender. However, due to the small number of observed deaths in the dataset, in particular for higher values of
e caused by heavy censoring, males and females were combined. Results in
Table 2 should thus be interpreted as an indication of possible short-term dependence, rather than firm evidence.