Supervised Machine Learning Classification for Short Straddles on the S&P500
Abstract
1. Introduction
2. Machine Learning Framework
- Problem definition: describes the concrete problem we are trying to solve, which, in our case, is a description of the trading strategy and the corresponding workflow
- Data: describes the available data
- Evaluation: describes measures to assess the quality of our approaches, and what would constitute a successful model
- Features: describes the features we are modeling and which data we use for this
- Modeling: which models we are assessing and how we compare them
- Experiments: based on our previous findings, we can decide which of the previous steps we want to adapt and which new approaches to try
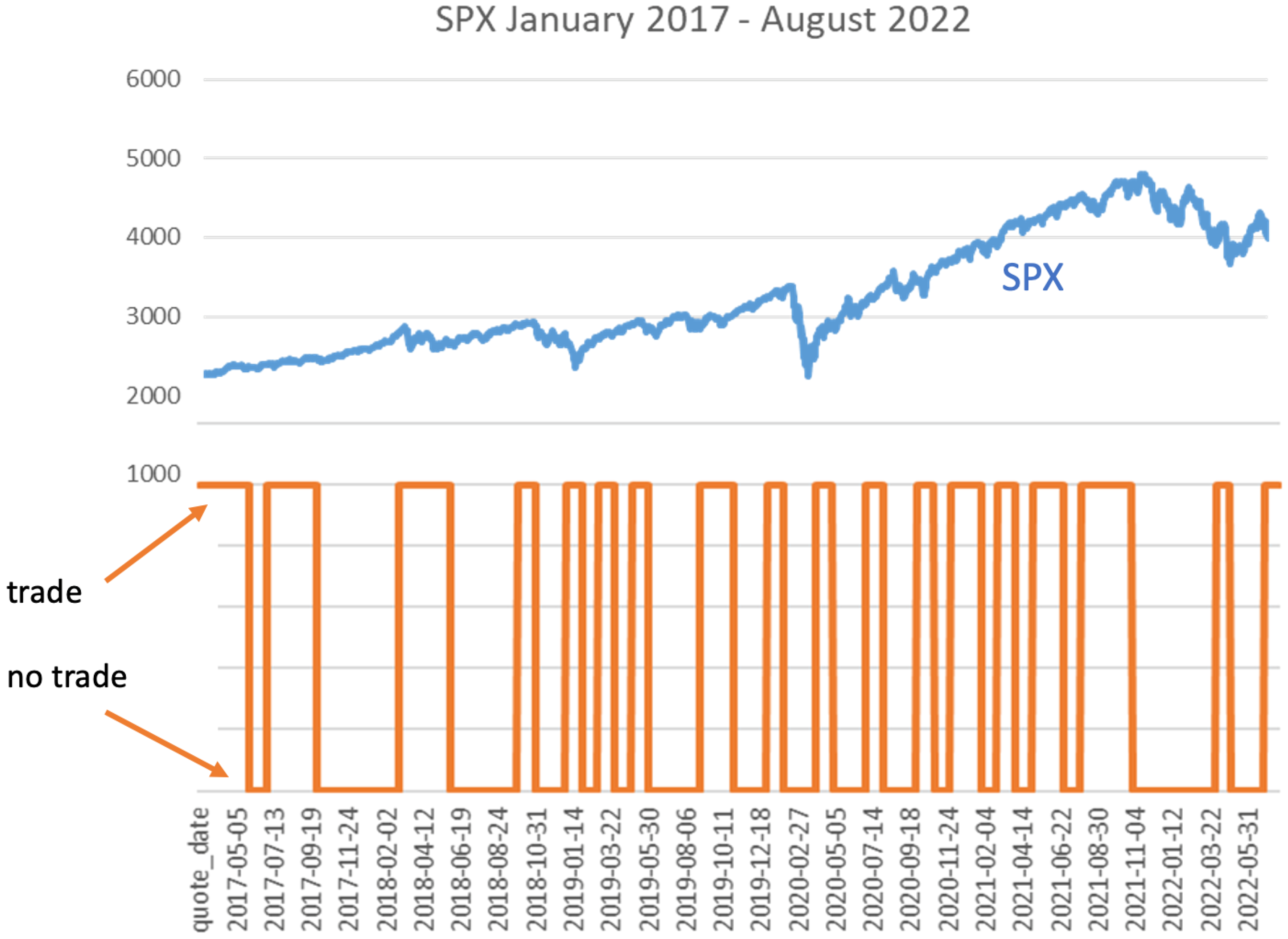
2.1. Description of the Trading Strategy and the Work Flow
- -
- We choose a fixed time period of length T (e.g., two months, one month, one week, two trading days, …). For our simplified setting, we exclusively consider options with a remaining lifetime of one week.
- -
- For a given day t, we trade SPX options with remaining time to expiration T (or with the shortest possible time to expiration larger than or equal to T). We always initiate the trade at the closing time of the trading day t.
- -
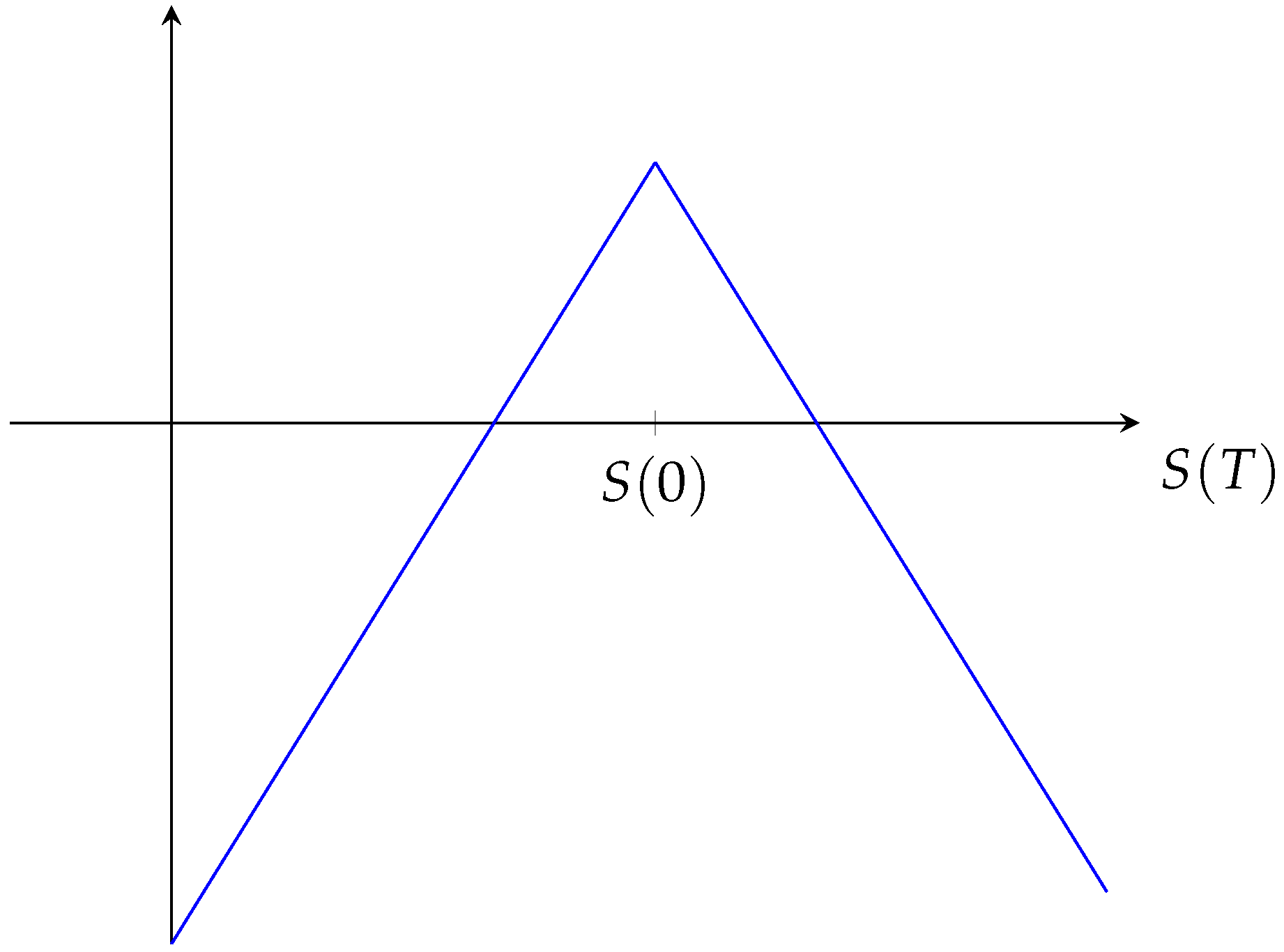
- We always go short on the same quantity of call- and put-options with the same time to expiration (approximately) T and strike as close at-the-money as possible (i.e., with a strike as close as possible to the current value of the S&P500).
- -
- In the basic variant, we hold the option contracts until expiration.
- -
- Possible variant: In the case in which we aim to limit losses, we go long on the same quantity of put options with the same expiration and with a strike , and/or we go long on the same quantity of call options with the same expiration and with a strike . The strikes and/or of the long positions are chosen on the basis of various parameters (depending on what variant we are looking at). They will always depend on the current value of the S&P500 (at the trading date); in some cases they will also depend on the value of the S&P500-volatility index VIX or on a certain historical volatility, while, in other cases, they will depend on the prices of the put and/or call options in question.
- -
- Thus, upon entering the trade, we receive a positive premium of M USD, which is given by the price of the short positions (minus the price of the possible long positions).
- -
- Our reference currency in all cases is the U.S. dollar (USD).
- -
- For training our machine learning models, we always trade exactly one contract of options. In reality, when executing these trades, one would decide on the number of options to be traded by determining the required margin and calculate the possible number of contracts with the available capital.
- -
- Possible variant: Some variants of the strategy are equipped with an exit strategy, which means that all contracts are closed as soon as the losses/or gains from the call and put positions (since the last trading day) exceed a certain pre-defined level.
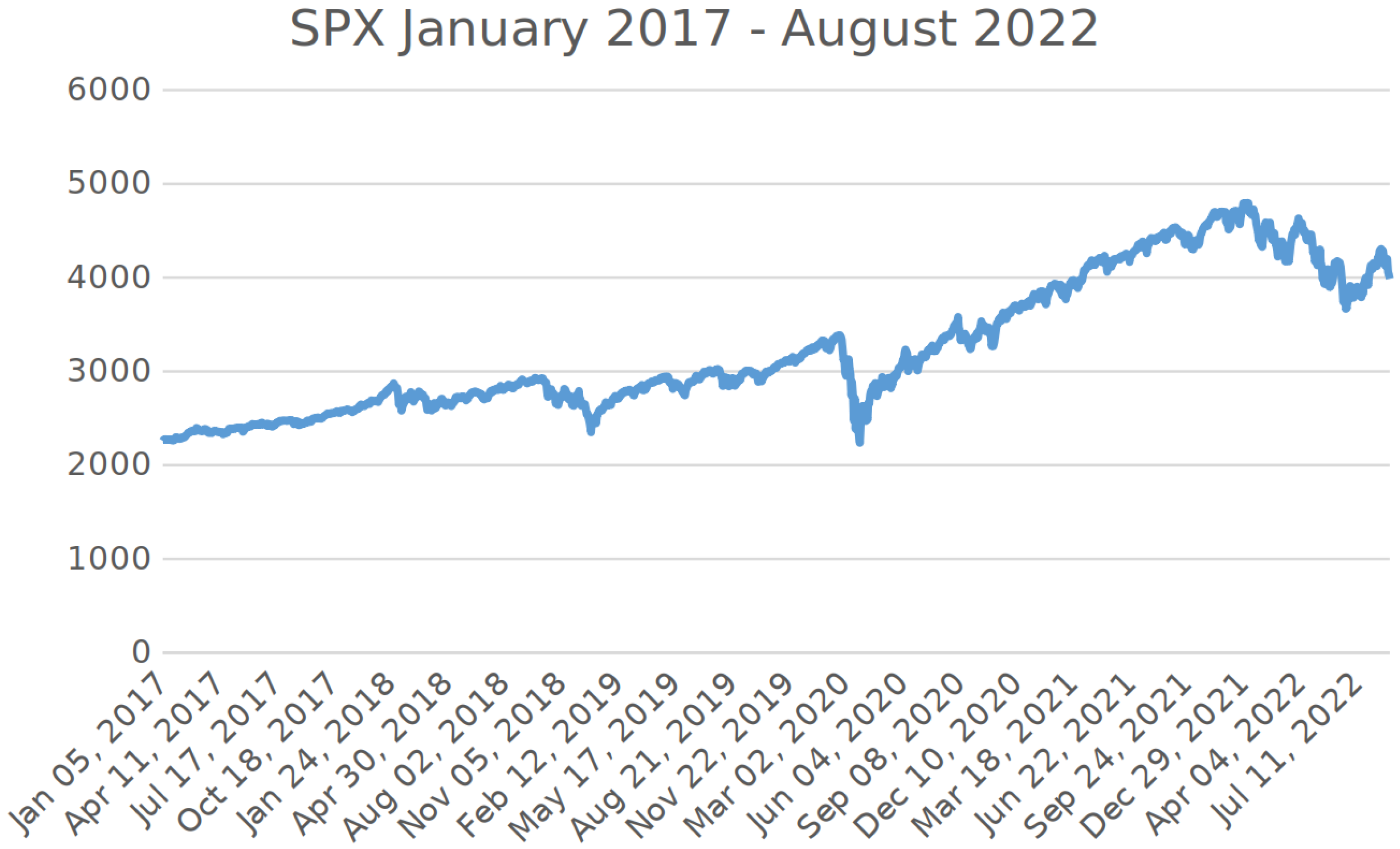
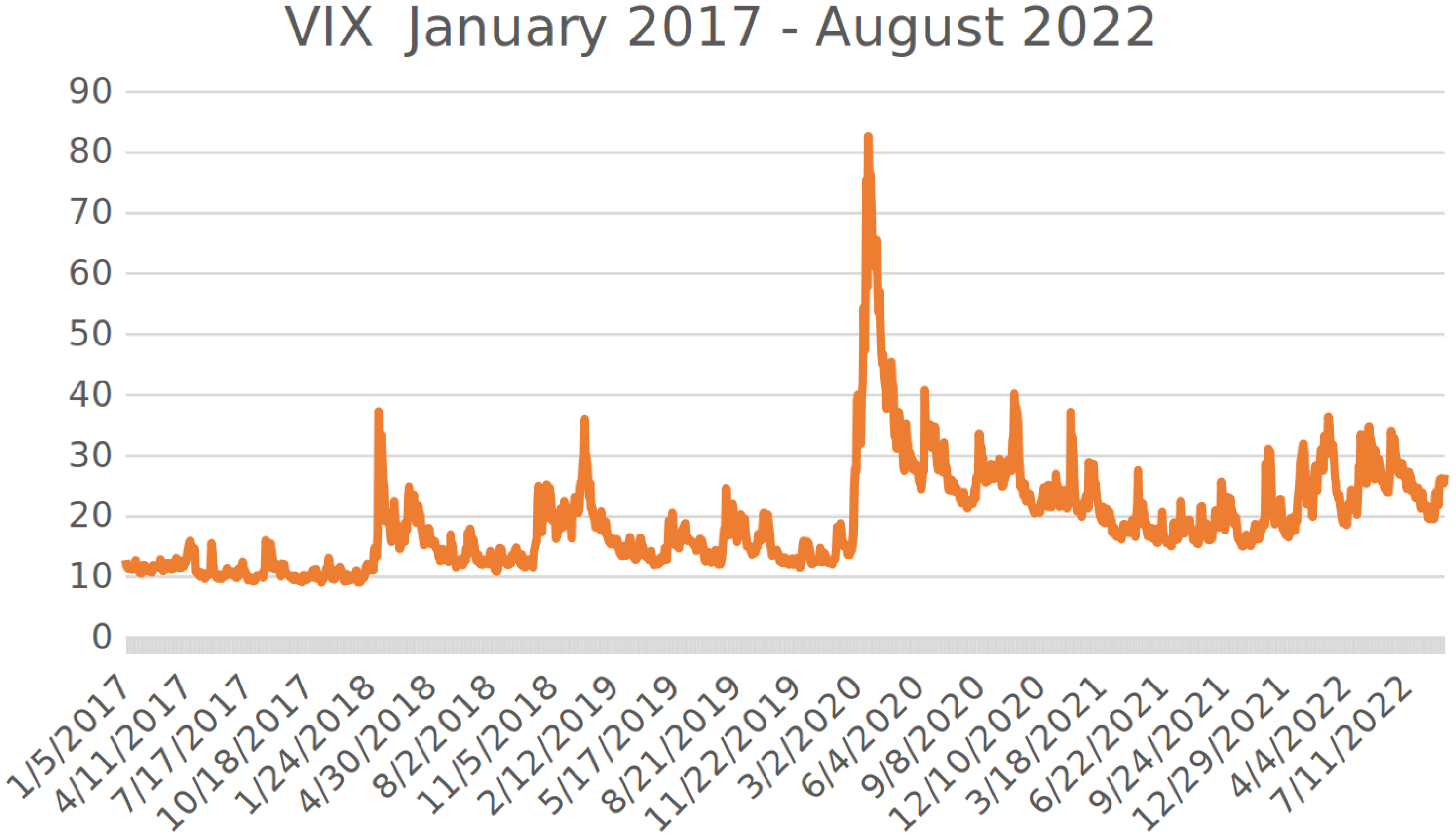
2.2. Data
- daily historical put- and call-option price data1, which, amongst others, includes:
- -
- last ask and bid prices for any available strikes and expiry date
- -
- open, close, high and low prices per day
- -
- traded volume and open interest
- daily publicly available market data, such as
- -
- close, open, high and low of the underlying
- -
- close, open, high and low of the S&P500 volatility index VIX
- -
- USD-Libor rates
2.3. Evaluation Criteria
2.3.1. Classification Metrics
- -
- accuracy: computes the accuracy (default is fraction) of correct predictions
- -
- recall: recall describes the quality of a classifier in finding all positive samples and is given by the ratiowhere are the true positives and are the false negatives
- -
- balanced accuracy: gives the accuracy of a classifier, adjusted by the probability of the outcome of each class. More precisely, it is defined as the average recall obtained for each class.
- -
- precision: describes the ability of the classifier to avoid false positives () and is calculated by the ratio
- -
- average precision: precision and recall are two measures which cannot be improved without worsening the other; it is always necessary to make trade-offs in the optimization of these two metrics. For this reason, the precision-recall curve is a very interesting visualization. The average precision metric provides a summary of the precision-recall curve in one single metric as the weighted mean of precisions at given thresholds , where the weights are given by the increase in the recall metric from the previous threshold :
- -
- negative average precision: the same as average precision above, but with both inverted targets and inverted predictions as parameters.
- -
- average fraction of positives (i.e., average fraction of trades): is calculated by taking the mean of all , which gives the number of executed trades as a fraction.
- -
- PRC: the precision recall curve gives the precision-recall pairs for varying thresholds.
- -
- PRC (auc): collects information of the PRC in one metric by calculating the area under the curve.
- -
- F1 score: again a combined measure of precision and recall, which can be interpreted as the harmonic mean of these two metrics.
- -
- Brier score loss: measures the mean squared difference between the predicted probability and the actual outcome
- -
- cross-entropy loss (or negative log loss): the loss function used in logistic regression for a classifier which gives a prediction probability to an actual outcome y. In the binary case (with and p the probability of ), this leads to:
- -
- ROC curve: the ROC (receiver operating characteristic) curve is determined by plotting the fraction of true positives to the fraction of false positives for the varying threshold.
- -
- ROC (auc): collects information on the ROC curve in one metric by calculating the area under the curve.
- -
- Pearson correlation coefficient: a measure of the linear relationship between two datasets. It tests the null hypothesis that the distributions of the sets are uncorrelated and normally distributed.
- -
- Spearman correlation coefficient: measures the monotonicity of the relationship between two datasets. It is non-parametric and, in contrast to the Pearson correlation, does not assume both datasets to be normally distributed. As with other correlation coefficients, the Pearson and Spearman coefficients have values between −1 and +1 where 0 means no correlation.
- -
- Pearson/Spearman correlation coefficient p-value: represents the approximate probability that an uncorrelated system will produce datasets that have a Pearson/Spearman correlation at least as extreme as the one computed from these datasets.
2.3.2. Profit Metrics
- -
- total profit: for given predictions and given profits , we calculate the total profit by simply calculating the sum:
- -
- long-and-short total profit: essentially the same as the total profit above, but instead of 0 (do not trade), we use −1, therefore shorting the strategy in those cases instead of not trading at all.
- -
- average profit: is determined by taking the mean in an analogous way to the total profit above:
- -
- average profit per trade: is determined by taking the mean as above, but only where is not 0.
- -
- standard deviation of profit per trade: is determined by taking the standard deviation of the profits where is not 0.
- -
- downside deviation of profit per trade: is determined by taking the standard deviation of the profits where is not 0 and .
- -
- maximum drawdown: maximum loss from a peak to a subsequent trough before a new peak is reached in the timeline of the cumulated profits, i.e.,:
- -
- Sharpe ratio: the ratio between the average excess return of the predicted strategy executions over a risk-free asset and its standard deviation. As a risk free asset, we use the six-month USD Libor. For computing the return of each strategy execution, we assume a margin of USD 100,000 to be deposited at the quote date of each short straddle and that each strategy portfolio consists of one contract (100 pieces) call- and one contract put-option. The return for a given prediction y and given profit p is then:
- -
- Sortino ratio: very similar to the Sharpe ratio above, but using the downside deviation instead of the standard deviation that is used for the Sharpe ratio.
2.4. Features
- -
- put price: we use the average of the last bid and ask price and reduce it by USD 0.1 for our sell price
- -
- call price: is determined analogously to the put price
- -
- strike: current strike price, which is the closest strike price to the current S&P500 value
- -
- days to expiry: the number of days to expiration of the options
- -
- S&P500 close of last 20 trading days: the absolute closing price of the S&P500
- -
- S&P500 close of last 20 trading days relative to the S&P500 value on the previous day
- -
- S&P500 high: the highest value of the S&P500 on the current day
- -
- S&P500 low: the lowest value of the S&P500 on the current day
- -
- VIX close of trading day and the previous 20 trading days
- -
- VIX high: the highest value of the VIX on the current day
- -
- VIX low: the lowest value of the VIX on the current day
- -
- 1-month USD Libor: the current value of the one-month US-Dollar London Inter-Bank Offered Rate
- -
- six-month USD Libor: the current value of the six-month US-Dollar London Inter-Bank Offered Rate
- -
- pm-settled: indicates whether, for the settlement of the currently considered options, the closing (pm-settled) or the opening value of the S&P500 is relevant (i.e., whether the option is of SPXW-type or of SPX-type)
2.5. Modeling
2.5.1. Decision Trees
- -
- A bare decision tree classifier relying on an instance of a simple classical decision tree.
- -
- The random forest classifier is an averaging algorithm based on randomized decision trees. It is a perturb-and-combine technique specifically designed for trees. In this sense, a diverse set of classifiers is created by introducing randomness in the classifier construction. The prediction of the ensemble is given as the averaged prediction of the individual classifiers. Each tree in the ensemble is built from a sample drawn with replacement from the training set. Furthermore, when splitting each node during the construction of a tree, the best split, in our case, is determined from all the input features. These two sources of randomness are introduced to decrease the variance of the forest estimator. The scikit-learn implementation combines classifiers by averaging their probabilistic prediction instead of letting each classifier vote for a single class.
- -
- The extremely randomized trees classifier (extra_trees) is very similar to the random forest classifier and also represents an averaging algorithm based on randomized decision trees. The main difference is that, instead of looking for the most discriminative thresholds, multiple thresholds are drawn randomly for each possible feature and the best of these randomly generated thresholds is chosen as the splitting rule.
2.5.2. Logistic Regression with SGD Training
2.5.3. k Nearest Neighbors (kNN) Classifier
- -
- Uniform: All points in each neighborhood are weighted equally.
- -
- Distance: Points are weighted by the inverse of their distance. In this case, closer neighbors of a query point will have a greater influence than neighbors which are further away.
2.5.4. Multi-Layer Perceptron Classifier
2.5.5. AdaBoost Classifier
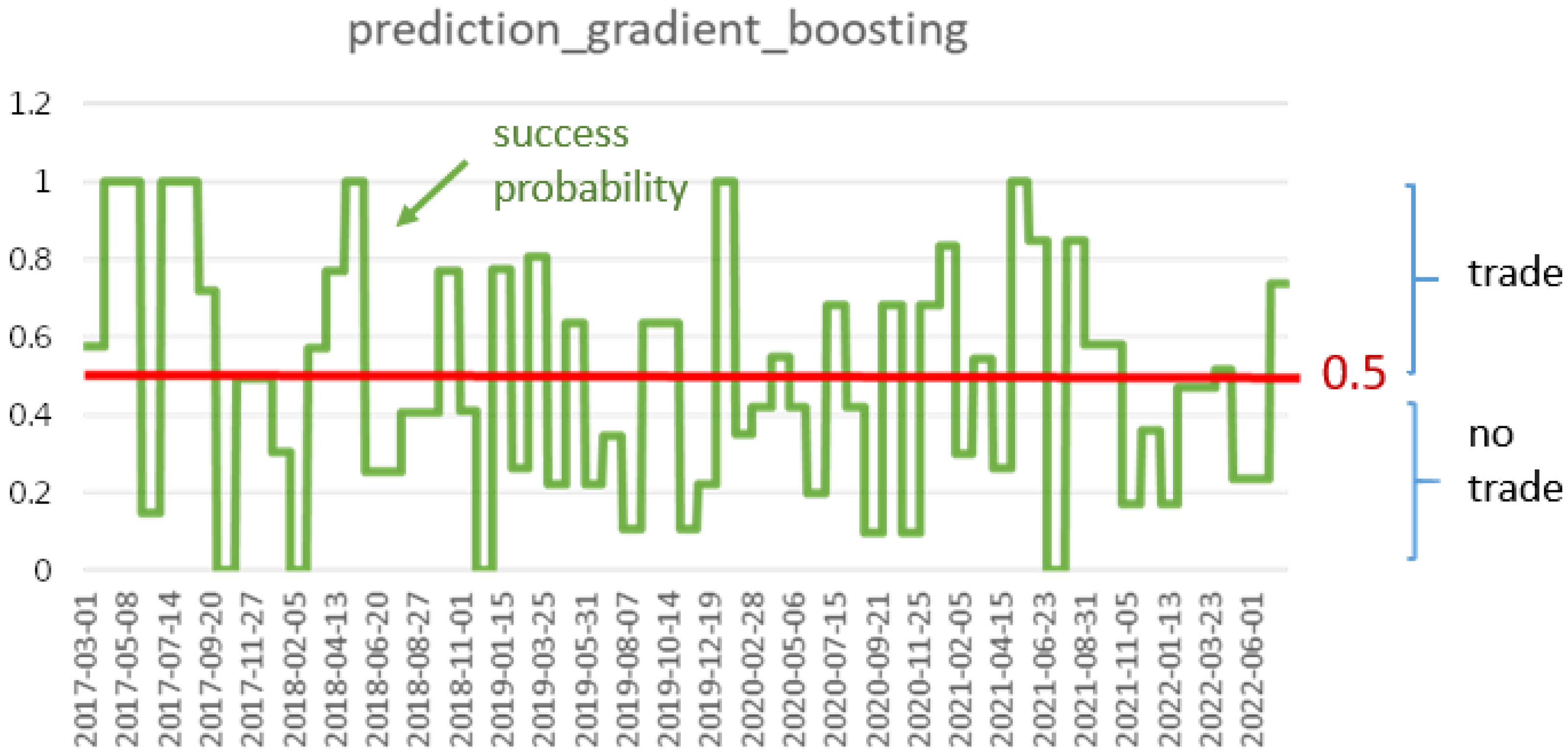
2.5.6. Gradient-Boosting Classifier
2.5.7. C-Support Vector Classification
2.5.8. Other Classifiers
- -
- ensemble: represents a combination of the other classifiers that tries to improve generalizability or robustness over a single estimator. It is determined in the course of the hyperparameter search.
- -
- Strat: randomly samples one-hot vectors from a multinomial distribution parametrized by the empirical class prior probabilities.
- -
- All: a “dummy classifier” that represents the trade-always strategy for comparison.
2.5.9. Hyperparameters
2.6. Experiments
Experiment Parameters
- -
- Feature columns: we use all features listed in Section 2.5 above.
- -
- Prequential split frequency: 1 month
- -
- Start date for test sets: Jan 2017
- -
- Start date of training set: 2011
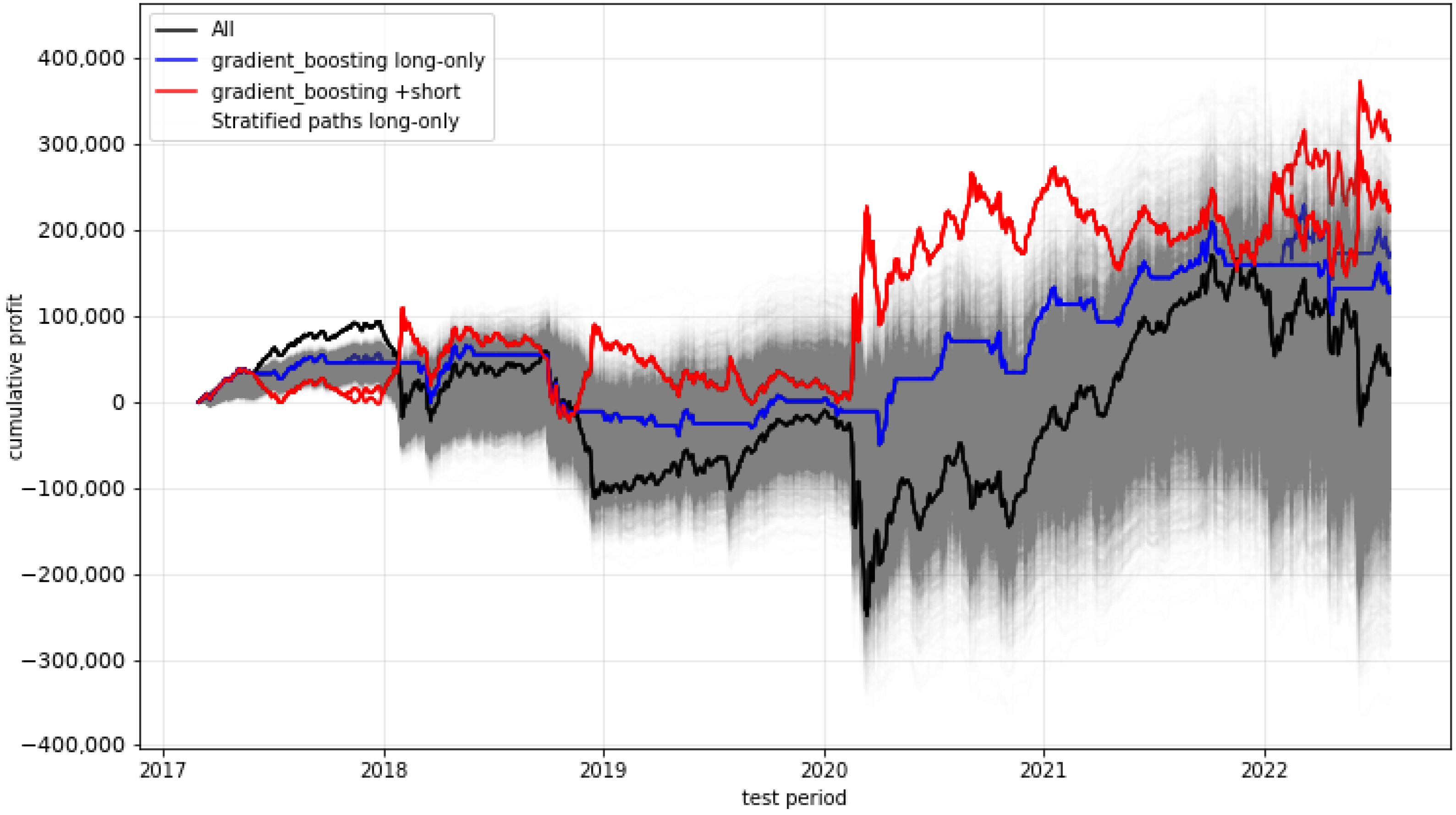
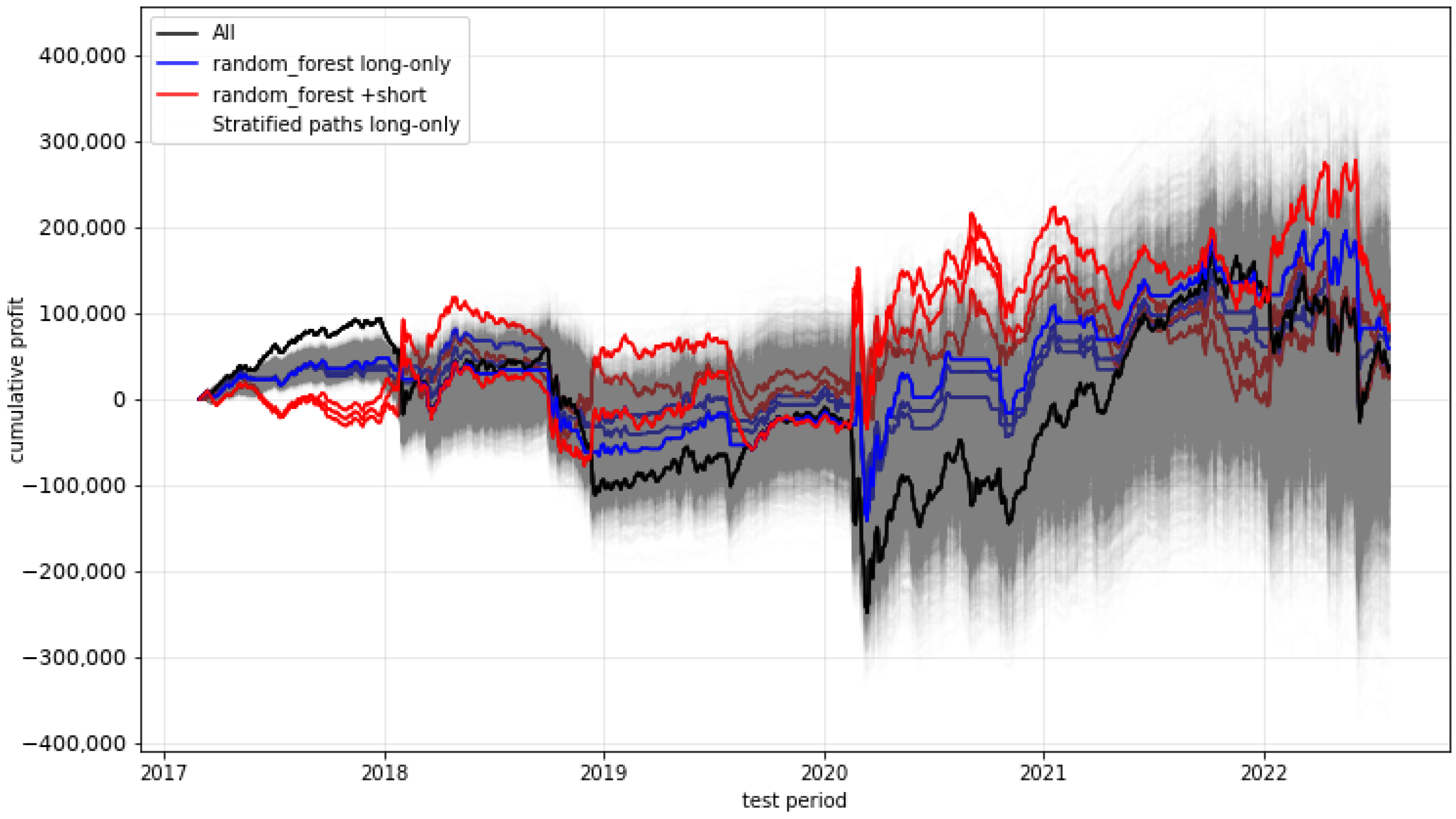
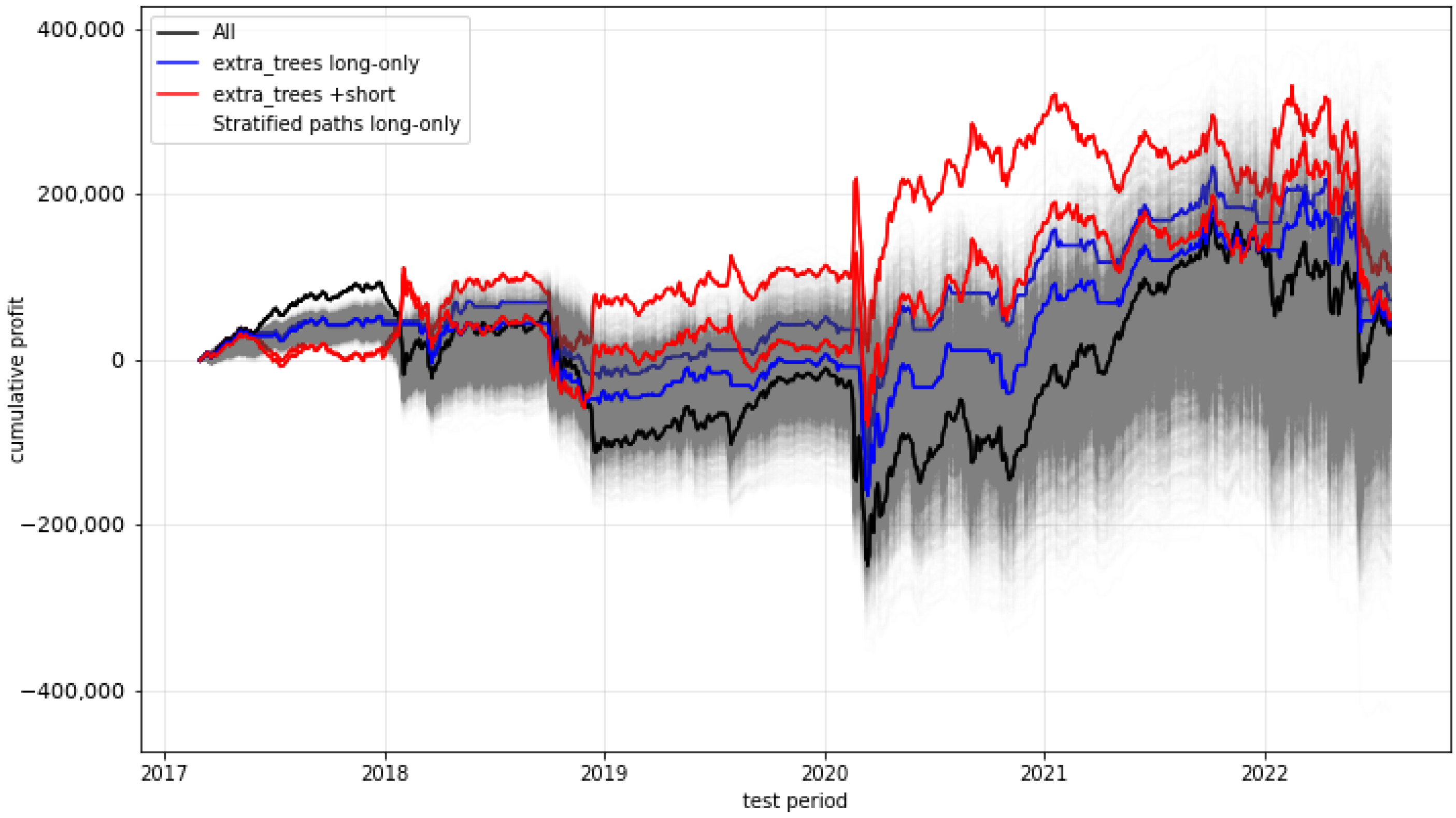
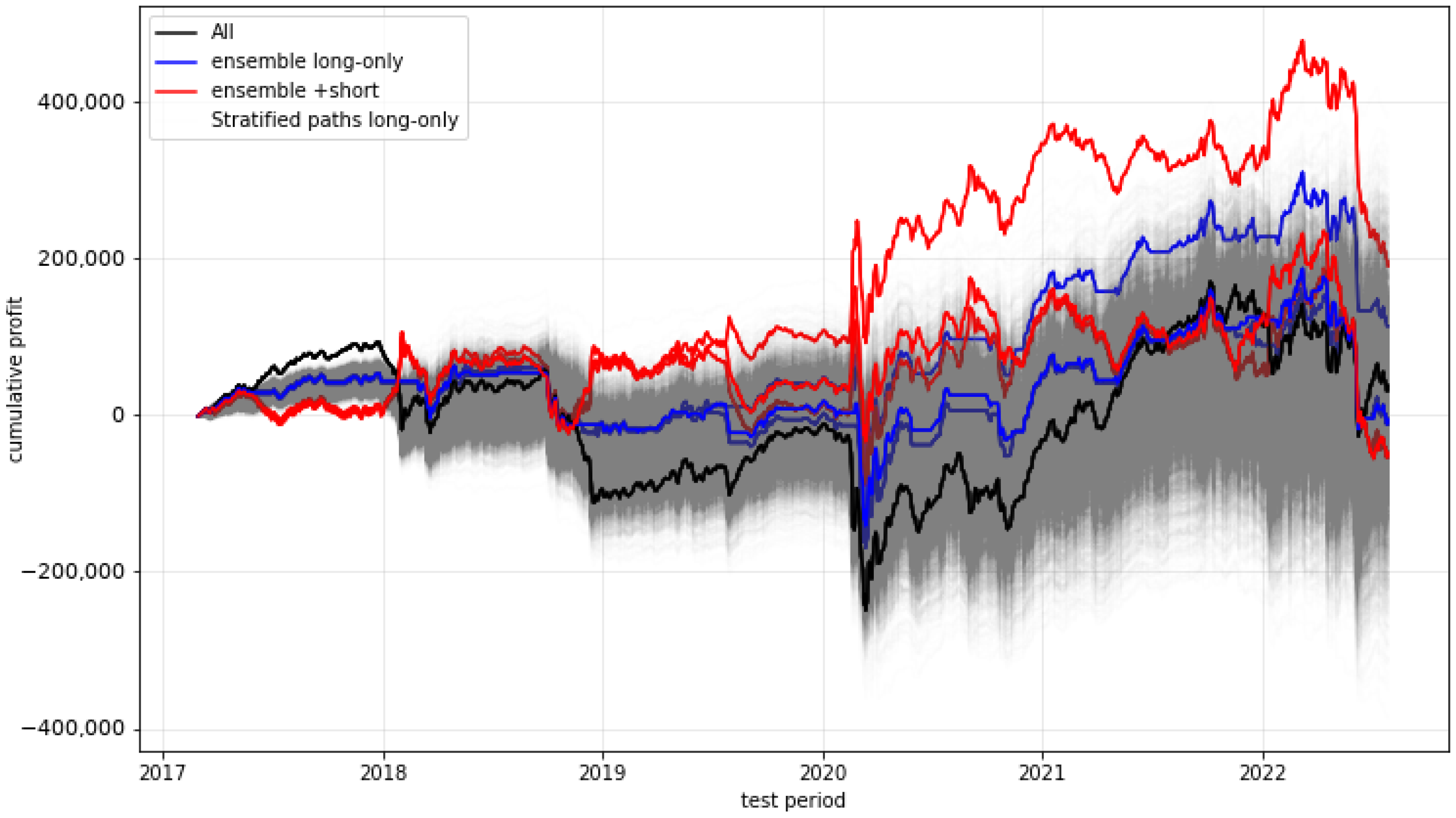
2.7. Result Overview
3. Conclusions and Next Steps for Further Research
- -
- : trading naked short positions at and hold until expiration
- -
- : trading naked short positions and close if a certain loss or gain threshold is reached (losses/gains with respect to the opening of the positions)
- -
- : trading short positions at and, additionally, a long put position at a certain predefined strike
- -
- : trading short positions at and, additionally, a long call at a certain predefined strike
- -
- : trading short positions at and, additionally, long positions at and , respectively
- -
- : trading short positions at and use futures to cover for losses when a certain underlying threshold is reached
- -
- : do not trade at all
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Detailed Metrics
- -
- Looking at the mean balanced accuracy (which is a central measure in machine learning) over all test sets of each of the model variants, we see that the SGD and SVM are slightly superior:Table A1. Models with significantly better mean balanced accuracy.
Model Mean Balanced_Accuracy p-Value (t-Test) sgd (42) 0.52251 ≤0.1 libsvm_svc (42) 0.50830 ≤0.05 All 0.50000 - -
- A similar picture is observed when taking the unbalanced accuracy into account, though the difference is more marginal here and SGD does not get close to significance:Table A2. Models with significantly better mean accuracy.
Model Mean Accuracy p-Value (t-Test) libsvm_svc (42) 0.58875 ≤0.05 All 0.58386 - -
- We observe that a quite large number of our models shows a significantly better ability to avoid false positives, which can be explained by the choice of the trade-always strategy as the baseline:Table A3. Models with significantly better mean average precision.
Model Mean Average_Precision p-Value (t-Test) mlp (42) 0.67053 ≤0.00001 sgd (42) 0.66340 ≤0.00001 random_forest (43) 0.64447 ≤0.001 extra_trees (45) 0.64397 ≤0.001 ensemble (43) 0.64156 ≤0.001 libsvm_svc (45) 0.64134 ≤0.00001 decision_tree (45) 0.63985 ≤0.0001 adaboost (42) 0.61464 ≤0.05 All 0.58386 - -
- This trend is even clearer when taking into account the average precision weighted with respect to the corresponding profit:Table A4. Models with significantly better mean average precision weighted.
Model Mean Average_Precision_Weighted p-Value (t-Test) mlp (42) 0.67519 ≤0.00001 sgd (42) 0.65945 ≤0.00001 extra_trees (45) 0.64731 ≤0.001 libsvm_svc (45) 0.64382 ≤0.00001 random_forest (43) 0.64247 ≤0.0001 ensemble (42) 0.64226 ≤0.001 decision_tree (42) 0.64217 ≤0.0001 adaboost (42) 0.60115 ≤0.05 All 0.56093 - -
- When looking at the inverse, we witness a similar situation with respect to the negative average precision:Table A5. Models with significantly better mean negative average precision.
Model Mean Neg_Average_Precision p-Value (t-Test) random_forest (42) 0.52796 ≤0.00001 mlp (45) 0.52677 ≤0.00001 ensemble (42) 0.51780 ≤0.00001 extra_trees (43) 0.51600 ≤0.00001 sgd (42) 0.50775 ≤0.00001 libsvm_svc (45) 0.50510 ≤0.00001 decision_tree (45) 0.50178 ≤0.0001 adaboost (42) 0.47823 ≤0.0001 All 0.41614 - -
- And, for the profit-weighted variant thereof:Table A6. Models with significantly better mean negative average precision weighted.
Model Mean Neg_Average_Precision_Weighted p-Value (t-Test) random_forest (43) 0.55610 ≤0.00001 mlp (45) 0.55530 ≤0.00001 extra_trees (43) 0.55048 ≤0.00001 ensemble (42) 0.54799 ≤0.00001 libsvm_svc (45) 0.54725 ≤0.0001 decision_tree (45) 0.53705 ≤0.0001 sgd (42) 0.52875 ≤0.00001 adaboost (42) 0.49263 ≤0.01 All 0.43907 - -
- In terms of the “naked” (i.e., not adapted for recall) precision, only the SVM shows a significant outperformance, which is, however, very slim:Table A7. Models with significantly better mean precision.
Model Mean Precision p-Value (t-Test) libsvm_svc (42) 0.58747 ≤0.05 All 0.58386 - -
- -
- If we want to take into account all possible classification thresholds, the ROC (auc) is a suitable metric. In this respect, the SGD is clearly superior to “All”, and even the MLP gets close to significance:Table A9. Models with significantly better mean ROC (auc).
Model Mean roc_auc p-Value (t-Test) sgd (42) 0.53519 ≤0.05 mlp (42) 0.52932 ≤0.1 All 0.50000 - -
- -
- The harmonic mean of the precision and recall; the F1 score shows the SVM to be close to performing significantly better, however, only marginally:Table A11. Models with significantly better mean F1.
Model Mean f1 p-Value (t-Test) libsvm_svc (42) 0.72545 ≤0.1 All 0.72386 - -
- The log loss is an expressive measure in logistic regression and serves as our error function. Here, almost all our models (except kNN) significantly, and by far, outperform the trade-always strategy:Table A12. Models with significantly better mean log loss.
Model Mean Neg_Log_Loss p-Value (t-Test) libsvm_svc (42) 0.68048 ≤0.00001 sgd (42) 0.68843 ≤0.00001 adaboost (43) 0.73816 ≤0.00001 mlp (43) 0.76562 ≤0.00001 decision_tree (45) 0.78851 ≤0.00001 extra_trees (45) 0.79962 ≤0.00001 ensemble (43) 0.80476 ≤0.00001 random_forest (45) 0.85737 ≤0.00001 gradient_boosting (43) 1.40729 ≤0.00001 All 14.37345 - -
- This result is slightly more pronounced when weighting the errors with the profits:Table A13. Models with significantly better mean log loss weighted.
Model Mean Neg_Log_Loss_Weighted p-Value (t-Test) libsvm_svc (42) 0.68513 ≤0.00001 sgd (42) 0.69036 ≤0.00001 adaboost (43) 0.73716 ≤0.00001 mlp (43) 0.76759 ≤0.00001 decision_tree (45) 0.78563 ≤0.00001 extra_trees (45) 0.80820 ≤0.00001 ensemble (42) 0.81221 ≤0.00001 random_forest (45) 0.86108 ≤0.00001 gradient_boosting (43) 1.39735 ≤0.00001 All 15.16521 - -
- Our second central loss metric, the Brier score loss, presents a similar picture, although the difference is much slimmer:Table A14. Models with significantly better mean Brier score loss.
Model Mean Neg_Brier_Score p-Value (t-Test) libsvm_svc (42) 0.24369 ≤0.00001 sgd (42) 0.24764 ≤0.00001 adaboost (43) 0.27132 ≤0.00001 mlp (43) 0.27656 ≤0.00001 extra_trees (45) 0.28776 ≤0.00001 decision_tree (45) 0.29016 ≤0.00001 ensemble (43) 0.29039 ≤0.00001 random_forest (42) 0.30013 ≤0.0001 gradient_boosting (43) 0.33770 ≤0.01 All 0.41614 - -
- Analogously, the profit-weighted variants are as follows:Table A15. Models with significantly better mean Brier score loss weighted.
Model Mean Neg_Brier_Score_Weighted p-Value (t-Test) libsvm_svc (42) 0.24601 ≤0.00001 sgd (42) 0.24861 ≤0.00001 adaboost (43) 0.27087 ≤0.00001 mlp (43) 0.27785 ≤0.00001 decision_tree (45) 0.28856 ≤0.00001 extra_trees (45) 0.29083 ≤0.00001 ensemble (42) 0.29355 ≤0.0001 random_forest (42) 0.30253 ≤0.0001 gradient_boosting (43) 0.33765 ≤0.01 All 0.43907 - -
- Last, but not least, the only purely profit-related metric for which we could find a statistically significant outperformance over the trade-always strategy is the maximum drawdown. Here again, almost all our models (except SVM) show a drastic improvement. This leads us to suspect that the models performed well in learning to detect and avoid potential large losses:Table A16. Models with significantly better mean maximum drawdown.
Model Mean Mdd p-Value (t-Test) gradient_boosting (42) 8759.10894 ≤0.0001 sgd (43) 11896.23051 ≤0.00001 k_nearest_neighbors (42) 12281.32476 ≤0.0001 adaboost (43) 12281.32476 ≤0.0001 random_forest (43) 13309.35616 ≤0.0001 decision_tree (43) 13492.23228 ≤0.0001 mlp (45) 14515.37226 ≤0.0001 extra_trees (43) 14996.15541 ≤0.001 ensemble (42) 16223.32536 ≤0.01 All 25375.40132
Appendix B. Box Plots
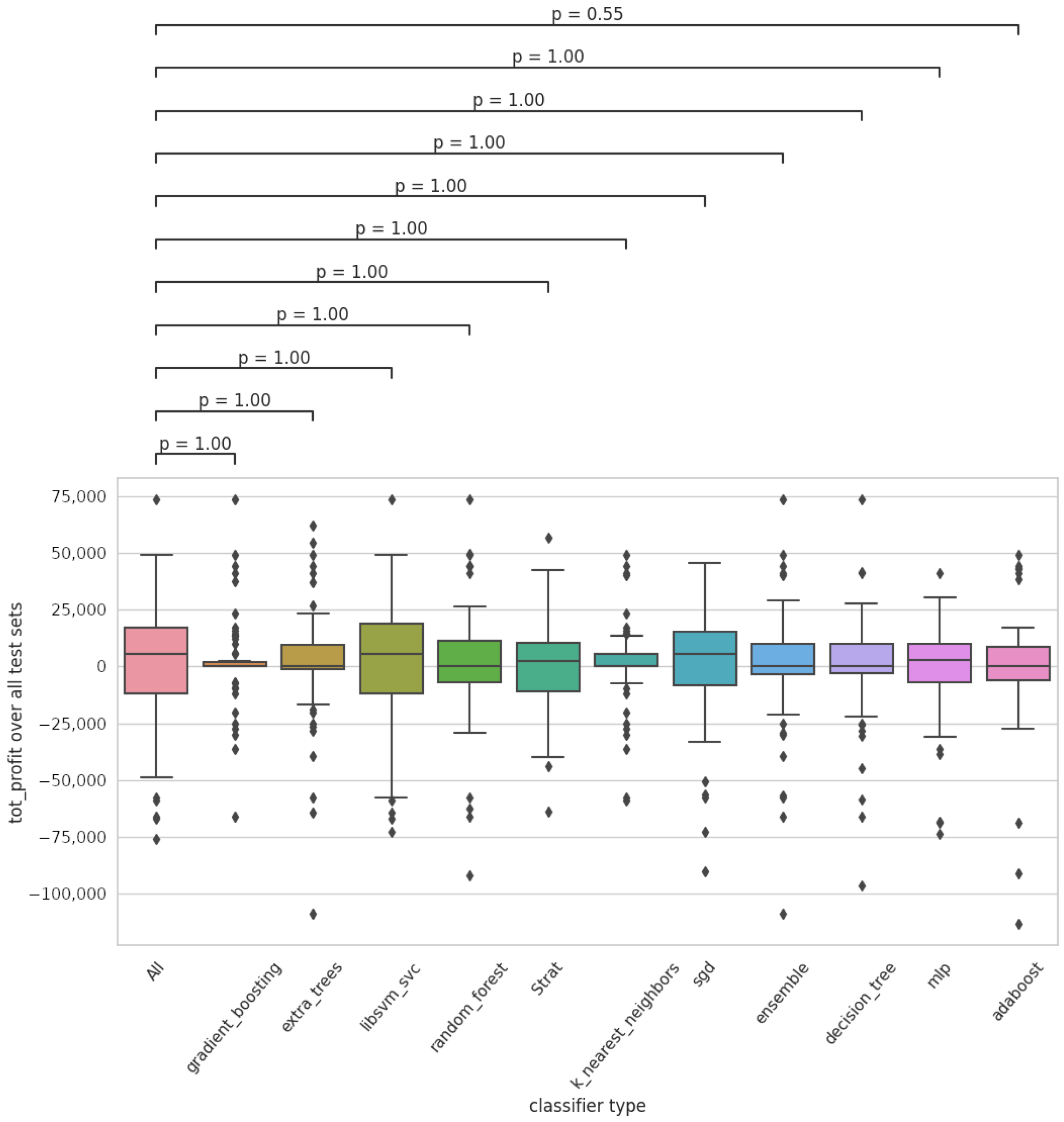

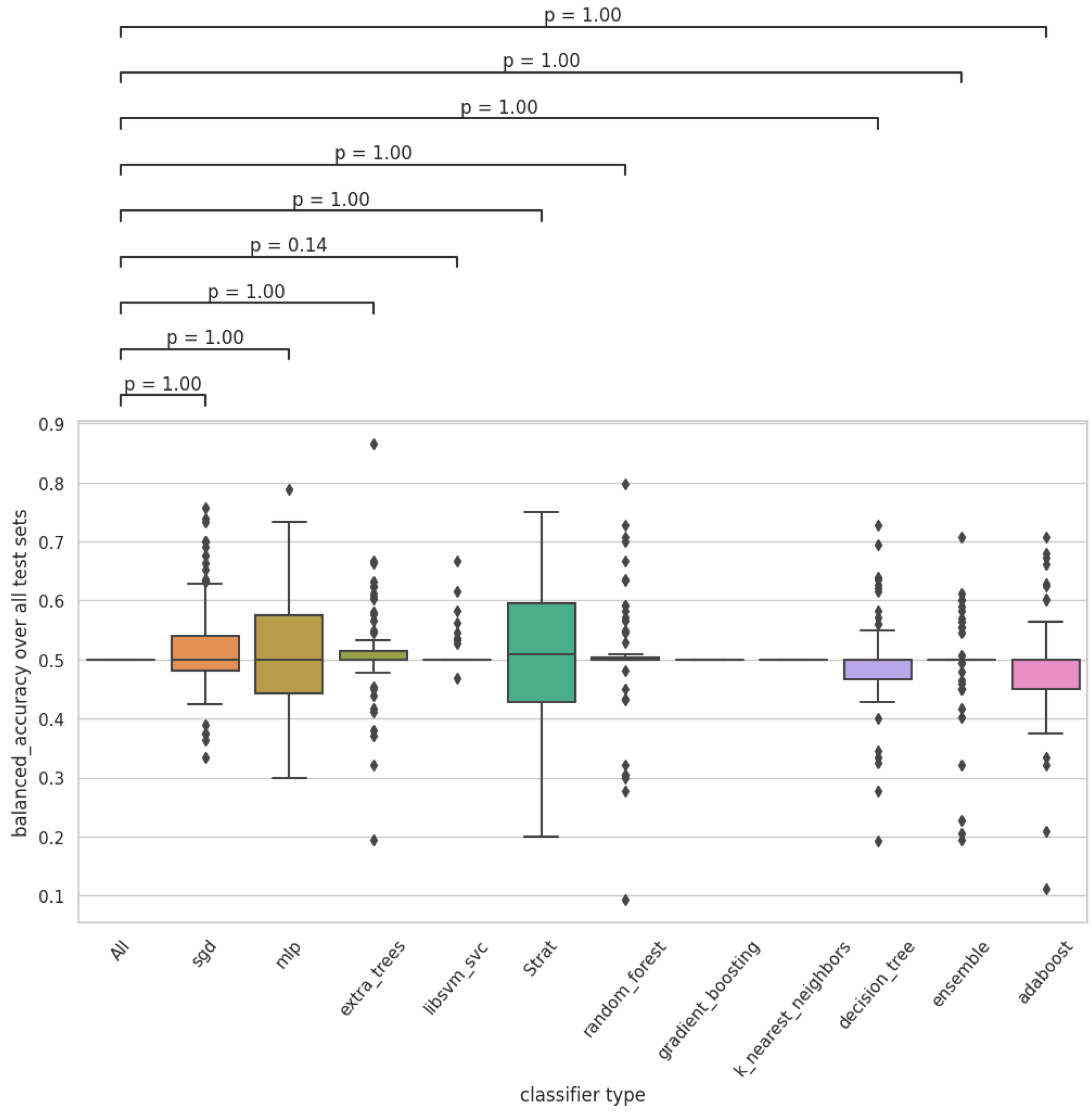
| 1 | These are from the CBOE data shop (https://datashop.cboe.com/ accessed on 14 August 2022). |
| 2 | https://github.com/automl/auto-sklearn/tree/master/autosklearn/pipeline/components/classification (accessed on 18 October 2022). |
References
- Auto-Sklearn Documentation. 2022. Available online: https://automl.github.io/auto-sklearn/master/ (accessed on 3 September 2022).
- Babenko, Vitalina, Andriy Panchyshyn, L. Zomchak, M. Nehrey, Z. Artym-Drohomyretska, and Taras Lahotskyi. 2021. Classical machine learning methods in economics research: Macro and micro level example. WSEAS Transactions on Business and Economics 18: 209–17. [Google Scholar] [CrossRef]
- Bourke, Daniel. 2020a. A 6 Step Field Guide for Building Machine Learning Projects. Available online: https://towardsdatascience.com/a-6-step-field-guide-for-building-machine-learning-projects-6e4554f6e3a1 (accessed on 30 March 2022).
- Bourke, Daniel. 2020b. A 6 Step Framework for Approaching Machine Learning Projects. Available online: https://github.com/mrdbourke/zero-to-mastery-ml/blob/master/section-1-getting-ready-for-machine-learning/a-6-step-framework-for-approaching-machine-learning-projects.md (accessed on 30 March 2022).
- Brunhuemer, Alexander, Gerhard Larcher, and Lukas Larcher. 2021. Analysis of option trading strategies based on the relation of implied and realized S&P500 volatilities. ACRN Journal of Finance and Risk Perspectives, Special Issue 18th FRAP Conference 10: 106–203. [Google Scholar]
- Carr, Peter, Liuren Wu, and Zhibai Zhang. 2020. Using machine learning to predict realized variance. Journal of Investment Management 18: 1–16. [Google Scholar]
- Chiang, Thomas C. 2020. Risk and policy uncertainty on stock-bond return correlations: Evidence from the us markets. Risks 8: 58. [Google Scholar] [CrossRef]
- Cohen, Gil. 2022. Algorithmic trading and financial forecasting using advanced artificial intelligence methodologies. Mathematics 10: 3302. [Google Scholar] [CrossRef]
- Day, Theodore E., and Craig M. Lewis. 1997. Initial margin policy and stochastic volatility in the crude oil futures market. The Review of Financial Studies 10: 303–32. [Google Scholar] [CrossRef]
- Del Chicca, Lucia, and Gerhard Larcher. 2012. A comparison of different families of put-write option strategies. ACRN Journal of Finance and Risk Perspectives 1: 1–14. [Google Scholar]
- Feurer, Matthias, Katharina Eggensperger, Stefan Falkner, Marius Lindauer, and Frank Hutter. 2020. Auto-sklearn 2.0: Hands-free automl via meta-learning. arXiv arXiv:2007.04074. [Google Scholar]
- Feurer, Matthias, Aaron Klein, Katharina Eggensperger, Jost Springenberg, Manuel Blum, and Frank Hutter. 2015. Efficient and robust automated machine learning. Advances in Neural Information Processing Systems 28: 2962–970. [Google Scholar]
- Gama, João, Raquel Sebastião, and Pedro Pereira Rodrigues. 2013. On evaluating stream learning algorithms. Machine Learning 90: 317–46. [Google Scholar] [CrossRef]
- Lacoste, Alexandre, Mario Marchand, François Laviolette, and Hugo Larochelle. 2014. Agnostic bayesian learning of ensembles. Papar presented at International Conference on Machine Learning (PMLR), Bejing, China, June 22–24; pp. 611–19. [Google Scholar]
- Larcher, Gerhard, Lucia Del Chicca, and Michaela Szölgyenyi. 2013. Modeling and performance of certain put-write strategies. The Journal of Alternative Investments 15: 74–86. [Google Scholar] [CrossRef]
- Lindauer, Marius, Katharina Eggensperger, Matthias Feurer, André Biedenkapp, Difan Deng, Carolin Benjamins, Tim Ruhopf, René Sass, and Frank Hutter. 2021. Smac3: A versatile bayesian optimization package for hyperparameter optimization. Journal of Machine Learning Research 23: 54–54. [Google Scholar] [CrossRef]
- Nagula, Pavan Kumar, and Christos Alexakis. 2022. A new hybrid machine learning model for predicting the bitcoin (BTC-USD) price. Journal of Behavioral and Experimental Finance 36: 100741. [Google Scholar] [CrossRef]
- Oktoviany, Prilly, Robert Knobloch, and Ralf Korn. 2021. A machine learning-based price state prediction model for agricultural commodities using external factors. Decisions in Economics and Finance 44: 1063–85. [Google Scholar] [CrossRef]
- Osterrieder, Joerg, Daniel Kucharczyk, Silas Rudolf, and Daniel Wittwer. 2020. Neural networks and arbitrage in the VIX. Digital Finance 2: 97–115. [Google Scholar] [CrossRef]
- Ramsauer, Hubert, Bernhard Schäfl, Johannes Lehner, Philipp Seidl, Michael Widrich, Thomas Adler, Lukas Gruber, Markus Holzleitner, Milena Pavlović, Geir Kjetil Sandve, and et al. 2020. Hopfield networks is all you need. arXiv arXiv:2008.02217. [Google Scholar]
- Santa-Clara, Pedro, and Alessio Saretto. 2009. Option strategies: Good deals and margin calls. Journal of Financial Markets 12: 391–417. [Google Scholar] [CrossRef]
- SciKit-Learn Documentation. 2022. Available online: https://scikit-learn.org/stable/ (accessed on 25 August 2022).
- Scipy-Stats Documentation. 2022. Available online: https://docs.scipy.org/doc/scipy/reference/stats.html (accessed on 3 September 2022).
- Sheng, Yankai, and Ding Ma. 2022. Stock index spot-futures arbitrage prediction using machine learning models. Entropy 24: 1462. [Google Scholar] [CrossRef]
- Tino, Peter, Christian Schittenkopf, and Georg Dorffner. 2001. Financial volatility trading using recurrent neural networks. IEEE Transactions on Neural Networks 12: 865–74. [Google Scholar] [CrossRef]
- Ungar, Jason, and Matthew T. Moran. 2009. The cash-secured put-write strategy and performance of related benchmark indexes. The Journal of Alternative Investments 11: 43–56. [Google Scholar] [CrossRef]
- Wen, Wen, Yuyu Yuan, and Jincui Yang. 2021. Reinforcement learning for options trading. Applied Sciences 11: 11208. [Google Scholar] [CrossRef]
- Wiese, Magnus, Robert Knobloch, Ralf Korn, and Peter Kretschmer. 2020. Quant GANs: Deep generation of financial time series. Quantitative Finance 20: 1419–440. [Google Scholar] [CrossRef]

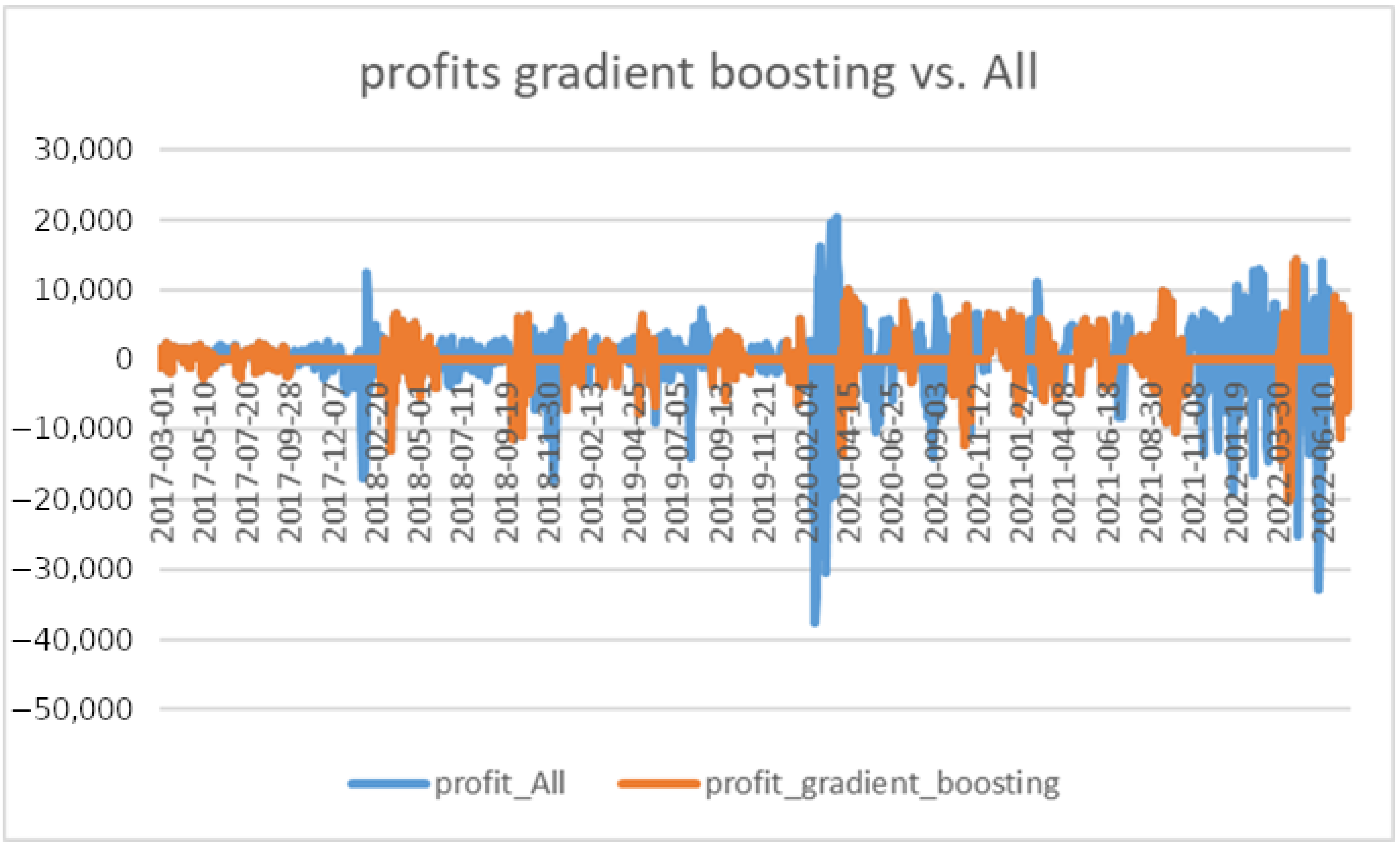
| Gradient_Boosting | All | |||
|---|---|---|---|---|
| Mean | std | Mean | std | |
| accuracy | 0.49536 | 0.18367 | 0.58386 | 0.16314 |
| balanced_accuracy | 0.50000 | 0.00000 | 0.50000 | 0.00000 |
| average_precision | 0.58386 | 0.16314 | 0.58386 | 0.16314 |
| neg_average_precision | 0.41614 | 0.16314 | 0.41614 | 0.16314 |
| neg_brier_score | 0.34217 | 0.14704 | 0.41614 | 0.16314 |
| f1 | 0.32455 | 0.37499 | 0.72386 | 0.13355 |
| neg_log_loss | 1.42258 | 1.47060 | 14.37345 | 5.63480 |
| precision | 0.26268 | 0.31561 | 0.58386 | 0.16314 |
| recall | 0.44615 | 0.50096 | 1.00000 | 0.00000 |
| roc_auc | 0.50000 | 0.00000 | 0.50000 | 0.00000 |
| prc_auc | 0.20807 | 0.08157 | 0.20807 | 0.08157 |
| accuracy_weighted | 0.50053 | 0.22299 | 0.56093 | 0.21437 |
| balanced_accuracy_weighted | 0.50000 | 0.00000 | 0.50000 | 0.00000 |
| average_precision_weighted | 0.56093 | 0.21437 | 0.56093 | 0.21437 |
| neg_average_precision_weighted | 0.43907 | 0.21437 | 0.43907 | 0.21437 |
| neg_brier_score_weighted | 0.34062 | 0.16345 | 0.43907 | 0.21437 |
| f1_weighted | 0.31416 | 0.36962 | 0.69437 | 0.18283 |
| neg_log_loss_weighted | 1.40911 | 1.50248 | 15.16521 | 7.40419 |
| precision_weighted | 0.25381 | 0.31599 | 0.56093 | 0.21437 |
| recall_weighted | 0.44615 | 0.50096 | 1.00000 | 0.00000 |
| roc_auc_weighted | 0.50000 | 0.00000 | 0.50000 | 0.00000 |
| prc_auc_weighted | 0.20807 | 0.08157 | 0.20807 | 0.08157 |
| avg_profit_weighted | 100 | 891 | 28 | 1472 |
| tot_profit_weighted | 2029 | 19,154 | 569 | 30,599 |
| losh_tot_profit_weighted | 3489 | 30,402 | 569 | 30,599 |
| avg_trading_profit_weighted | 224 | 1336 | 28 | 1472 |
| std_trading_profit_weighted | 3323 | 2098 | 4047 | 3218 |
| downt_std_trading_profit_weighted | 1958 | 1686 | 2672 | 2553 |
| mdd_weighted | 8759 | 15,607 | 25,375 | 29,953 |
| avg_trades_weighted | 0.44615 | 0.50096 | 1.00000 | 0.00000 |
| avg_profit_norm_weighted | 0.00000 | 0.00000 | −0.00000 | 0.00000 |
| tot_profit_norm_weighted | 0.00000 | 0.00000 | 0.00000 | 0.00000 |
| avg_trading_profit_norm_weighted | 0.00000 | 0.00000 | −0.00000 | 0.00000 |
| sharpe | 0.364 | −0.006 | ||
| sortino | 0.317 | −0.006 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brunhuemer, A.; Larcher, L.; Seidl, P.; Desmettre, S.; Kofler, J.; Larcher, G. Supervised Machine Learning Classification for Short Straddles on the S&P500. Risks 2022, 10, 235. https://doi.org/10.3390/risks10120235
Brunhuemer A, Larcher L, Seidl P, Desmettre S, Kofler J, Larcher G. Supervised Machine Learning Classification for Short Straddles on the S&P500. Risks. 2022; 10(12):235. https://doi.org/10.3390/risks10120235
Chicago/Turabian StyleBrunhuemer, Alexander, Lukas Larcher, Philipp Seidl, Sascha Desmettre, Johannes Kofler, and Gerhard Larcher. 2022. "Supervised Machine Learning Classification for Short Straddles on the S&P500" Risks 10, no. 12: 235. https://doi.org/10.3390/risks10120235
APA StyleBrunhuemer, A., Larcher, L., Seidl, P., Desmettre, S., Kofler, J., & Larcher, G. (2022). Supervised Machine Learning Classification for Short Straddles on the S&P500. Risks, 10(12), 235. https://doi.org/10.3390/risks10120235







