Abstract
This study introduces a simple, sensitive, efficient, and low-cost gas detection method in the terahertz range. A mode-adjustable Fabry–Pérot cavity is proposed to enhance detection by tuning the cavity length to match the cavity’s resonant frequency with the gas absorption peak. Terahertz frequency domain spectroscopy (THz-FDS), offering MHz-level resolution, provides stronger applicability than other spectral systems. Carbon monoxide (CO) is used as the test gas, with its 465 GHz absorption peak validating the coupling enhancement. The experiment measures CO absorption spectra from 0.02 to 1.5 THz, achieving a detection limit of 7%. Using a vacuum cavity to eliminate water vapor interference, low concentrations are detected, with a mode number of m = 10 yielding a detection limit of 3500 ppm, 20 times better than previous results. The impact of different modes on coupling was analyzed, showing more effective coupling when the Q-value of the resonant peak closely matches that of the gas absorption peak. This method demonstrates high sensitivity and applicability for detecting low concentrations of toxic and harmful gases.
1. Introduction
Detecting gases, especially toxic and hazardous ones, is essential for ensuring safety and facilitating production processes. This detection is vital across various domains, such as monitoring greenhouse gases in the environment [1], assessing indoor air quality [2], controlling vehicle exhaust emissions [3], and overseeing industrial production [4]. To achieve high sensitivity in detection, traditional feature recognition methods predominantly depend on the electrical or chemical characteristics of the gases involved [5]. By inducing a chemical reaction between the gas and a designated substance or material, it is possible to identify the gas type by observing changes in specific parameters, including color [4], as well as current and voltage readings [6]. Although the electrochemical method is relatively mature, due to its working principles, it inevitably faces issues such as complex structures, poor stability, and temperature drift.
Another prevalent method for gas detection is optical gas detection, which utilizes the absorption spectrum characteristics of gases [7]. This technique has demonstrated significant potential owing to its rapid response time, minimal time drift, and overall insensitivity to variations in temperature [8]. Its basic principle can be explained by the Lambert–Beer law [9]:
where I is the light intensity at the absorption peak, I0 is the initial light intensity, α is the absorption coefficient, C is the gas concentration, and L is the path length of the light. Since gas molecules absorb energy at specific frequencies due to rotational transitions, characteristic absorption peaks are generated in the spectrum, which can be used as criteria for gas detection. However, in practical situations, the absorption peaks are often not very pronounced due to limitations in path length or gas concentration. Due to the fact that most terahertz sources operate at power levels in the milliwatt or even microwatt range, they are more susceptible to random noise interference, especially when the gas absorption peaks are not distinct. Therefore, this effect is more pronounced for terahertz gases [10].
To detect gases at low concentrations, it is essential to extend the optical path length to enhance sensitivity, which can be achieved using methods such as the white cell technique [11,12]. As another optical path length extension technique, cavity-enhanced absorption spectroscopy (CEAS) is an ultra-sensitive spectroscopic method based on high-finesse optical resonators. By placing the sample inside the resonant cavity and utilizing multiple reflections between cavity mirrors, it significantly increases the effective optical path length (up to kilometer-scale), enabling trace detection with limits reaching ppt levels [13]. Depending on light excitation methods and signal detection principles, CEAS primarily divides into pulsed cavity ring-down spectroscopy (CRDS) and continuous-wave cavity-enhanced spectroscopy (CW-CEAS) [14]. CRDS employs pulsed or modulated continuous-wave lasers, determining absorption coefficients by measuring the exponential decay time (τ) of intracavity light intensity. This method’s results are independent of initial light intensity, offering strong interference resistance, particularly suitable for transient free radicals (e.g., OH) or weakly absorbing species [15]. CW-CEAS uses continuous-wave lasers, extracting absorption signals either through direct transmitted intensity measurement or combined phase modulation techniques (e.g., phase-shift CEAS). While providing high stability and enabling high-resolution molecular fingerprint scanning when coupled with narrow-linewidth lasers, it requires precise calibration for source fluctuations [16]. Further technical variants include broadband CEAS (BBCEAS) [17] and off-axis integrated cavity output spectroscopy (OA-ICOS) [18]. Compared to traditional long-path absorption spectroscopy (e.g., white cells), CEAS achieves longer effective path lengths in compact setups through passive resonator gain mechanisms, with reduced sensitivity to mirror contamination [19]. However, CEAS critically depends on high-reflectivity cavity mirrors for path length extension and electro-optic modulators for laser “chopping,” increasing system complexity and cost. More critically, as laser fluctuations significantly impact detection, high-power laser sources are required for stable operation—a challenging requirement in certain bands like the terahertz range. Consequently, terahertz applications typically employ CRDS for stable single-frequency detection, inherently sacrificing terahertz’s broadband advantage [20].
In recent decades, the idea of modes that are strongly coupled through vibrations has emerged [21]. This effect is manifested in optics as a strong interaction between the light field and molecules, which can lead to changes in excited states and energy transfer, thereby forming a mixed excitation known as “vibrational polariton” [22]. It also introduces a novel approach for material detection by artificially modifying the resonator’s resonant frequency to align with the absorption peaks of the material, thus enhancing the detection limit. Ran Damari investigated the strong coupling of organic molecular materials within the terahertz spectrum. By adjusting the cavity modes to interact with the vibrational modes of α-lactose molecules, coherent Rabi oscillations at 0.53 THz were observed [23]. Xiaomei Shi suggested employing a multi-stage resonant cavity design to detect gases at lower concentrations and successfully achieved simulation results for low-concentration hydrogen cyanide gas [24]. However, previous studies faced limitations due to frequency resolution, confining gas detection in the terahertz range to simulation findings only. In our earlier research, we addressed this challenge by utilizing terahertz frequency domain spectroscopy (THz-FDS) to attain high-frequency resolution [25]. By designing a Fabry–Pérot (FP) cavity system, we were able to couple the central resonant frequency with the vapor’s absorption peak at 560 GHz, marking the first experimental demonstration of the coupling between the FP cavity and gas absorption peaks in the terahertz domain. Additionally, the cavity’s mode can be adjusted, making it adaptable for various gases and substances. However, due to experimental constraints, the detection limit was restricted to only 10%.
Building on prior research [25], this paper presents a high-sensitivity gas detection technique utilizing the FP cavity in conjunction with THz-FDS. By modifying the optical path and constructing a vacuum cavity, the absorption of terahertz waves by vapor can be minimized, allowing for the detection of low gas concentrations. Carbon monoxide (CO) gas is selected as the experimental subject. The experiment measures 16 absorption peaks of CO in the range of 0.02–1.5 THz. Furthermore, the detection limit of our experiment employing THz-FDS without the FP cavity is 7%. By varying the cavity length, we can adjust the cavity’s resonant frequency to align with the gas absorption frequency, thereby enhancing the ability to discriminate between different gases. Successful coupling of the absorption peak of CO at approximately 460 GHz is demonstrated. By controlling the volume concentration of CO in the chamber with a gas flow meter, the detection limit of CO after using the FP cavity is measured to be 3500 ppm, which is a 20-times improvement compared to direct measurements. Additionally, the effects of the modes on the system’s performance are discussed by comparing the low mode (m = 10) and the high mode (m = 20). The choice of mode significantly impacts the interference effects and sensitivity of the optical path, thereby further optimizing the detection performance. In the terahertz frequency range, achieving high-sensitivity gas detection has remained a significant challenge due to the limited power of existing systems. Taking carbon monoxide—the subject of this study—as an example, direct detection using terahertz spectroscopic systems yields a relatively high detection limit, typically on the order of percentage levels [26,27,28,29]. Patrick et al. employed THz-TDS to directly measure the free induction decay (FID) signal of CO molecules in the time domain and applied a linear dispersion model to fit the temporal waveform, thereby extracting both rotational constants and gas parameters. Their estimated detection limit reached approximately 7900 ppm [30]. Chuxuan Zhao et al. utilized a multi-pass cell to extend the optical path length and applied multi-line fitting to infer gas concentration, enabling the discrimination of combustion mixtures with a CO detection limit of 250 ppm [31]. The use of multi-pass cells to enhance detection sensitivity through extended optical paths has long been a classical approach in optical gas sensing [8,11]. Xiaonan Liu et al. combined a multi-pass cell for increased reflections with light-induced thermoelastic spectroscopy (LITES), achieving a detection limit as low as 96 ppm through the synergistic amplification of both techniques [32]. It is evident that existing methods largely rely on either optical path extension via multi-pass cells or numerical fitting operations to improve detection limits. In contrast, the FP cavity used in this work offers a structurally simple solution that enhances the detection limit of terahertz gas spectroscopy without significantly increasing optical complexity or data processing demands. The enhancement effect provided by the cavity on absorption peaks significantly aids in the identification of various substances, including greenhouse gases, toxic gases, and explosives.
2. Materials and Methods
2.1. Terahertz Wave Generation and Detection System
The terahertz (THz) spectroscopy system encompasses various technical solutions, among which the most common is the terahertz time-domain spectroscopy (THz-TDS) system. This system, which uses femtosecond laser pulses to excite and detect THz waves, has been widely utilized, and features high signal-to-noise ratios and broad bandwidths [33]. Another technical solution is the terahertz frequency-domain spectroscopy (THz-FDS) system, which offers high-frequency resolution up to the MHz range as compared to the GHz level achievable by THz-TDS [34]. Therefore, for gases with sharp absorption peaks, THz-FDS demonstrates better performance in identification, providing more precise spectral information.
Figure 1a shows the schematic diagram of THz-FDS system in this study, which consists of a laser photo mixing coupling unit, THz emitter and receiver, and THz optical path, along with a control system and a computer. The THz-FDS experimental system features THz generation and measurement components from TOPTICA Photonics, specifically the TeraScan 780, with the system controller being the DLC Smart. This device not only controls the laser source but also provides the bias voltage and measures the amplified signals. The photo-mixing laser source in the system is driven by two distributed feedback lasers (DFB lasers) with wavelengths of approximately 783 nm and 785 nm, producing continuous wave laser output. The operating frequencies of both lasers are precisely adjusted through thermal control to achieve accurate control of the frequency of the THz wave. The two laser beams are transmitted via optical fibers to a laser coupler to generate the photo-mixing signal, which is divided into two beams with an average power of 36 mW and approximately the same phase. One of these signals is used to excite a low-temperature grown gallium arsenide (LT-GaAs) photoconductive antenna to generate THz waves. The THz waves emitted from the transmitting antenna are directed towards an off-axis parabolic mirror L1 for collimation, producing parallel light. The parallel light then passes through lens L2 for focusing. After passing through the sample to be tested, the light is focused again by lenses L3 and L4 before being received by the receiving antenna. All off-axis parabolic mirrors have a focal length of 4 inches. Additionally, an amplifier is responsible for amplifying the nano ampere photoconductive current signal, which is then input into the DLC Smart controller for signal processing, with the final data being transmitted to a computer for analysis and utilization.
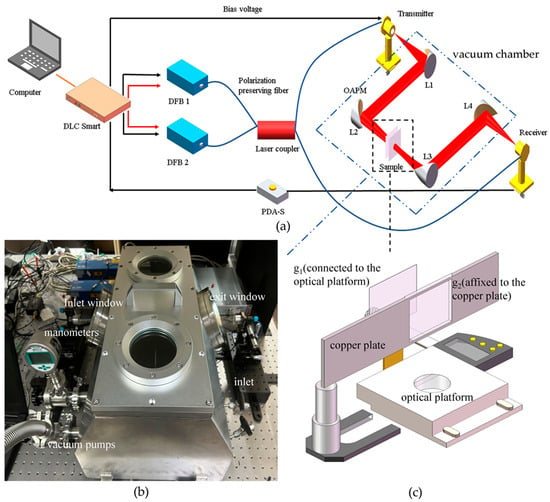
Figure 1.
(a) Schematic diagram of transmission terahertz frequency domain spectroscopy system, The red and black lines represent two types of connections between the DLC controller and the DFB: electrical wires and optical fibers. (b) vacuum chamber c Model diagram of the FP cavity (c) Schematic diagram of the Fabry-Perot cavity.
In previous studies, the terahertz optical path was directly exposed to the atmosphere [25]. However, water vapor in the atmosphere has a strong absorption effect on terahertz waves, which poses significant interference with gas detection research [35]. Therefore, based on the original system, we place the terahertz optical path in a sealed vacuum chamber to eliminate the interference of water vapor, while also facilitating the control of gas detection.
2.2. Vacuum Gas Chamber Construction and Optical Path Modification
As shown in Figure 1b, the final vacuum chamber setup consists of several components: transmitting and receiving antennas, the vacuum chamber body, the optical path inside the gas chamber, a pressure gauge, and a vacuum pump. The vacuum chamber body can be further divided into the main body, the top cover, the vacuum pump connection port, and the gas inlet. Since the laser used in this system is transmitted through optical fibers, it is not possible to place the entire system inside a vacuum system; instead, only the terahertz optical path from the transmitting antenna to the receiving antenna is placed inside the vacuum chamber. The effects of the portion of the terahertz optical path exposed to the atmosphere on the signal will be discussed later. The vacuum chamber body is made of 304 stainless steel, with a volume of 40 L and a wall thickness of 5 mm.
To minimize light intensity loss at the incident and exit windows, we chose polytetrafluoroethylene (PTFE) material after research, as it has a transmittance of approximately 90% in the terahertz frequency range [36]. After adjusting the optical path, the light intensity should be as close as possible to 80% of that before the adjustment. Additionally, to reduce FP interference caused by the windows, we tilted them at a 45° angle. The final incident and exit windows are circular with a radius of 55 mm and a thickness of 10 mm. For observation convenience, two quartz glass observation windows with a radius of 50 mm and a thickness of 10 mm are opened at the front and back of the top cover. The pressure gauge and vacuum pump are connected to the chamber via a KF25 interface, with the pressure gauge measuring a range of −100 kPa to 0 Pa, allowing real-time display of the current pressure inside the chamber during measurement. Due to the small size of the chamber, we selected a TRP-6 vacuum pump with a pumping speed of 1.5 L/s and a limit pressure of 4 × 10−1 Pa.
In the optical path before adjustment, L1, L2, L3, and L4 are all off-axis parabolic mirrors with a focal length of 4 inches. However, due to physical structural limitations, we were unable to position the transmitting and receiving antennas at the focal points of off-axis parabolic mirrors L1 and L4 during the adjustment process. The distance between the antennas and mirrors L1 and L4 could only be reduced to approximately 12 cm and could not be further minimized. Since the optical paths between L1 and L2, and L3 and L4 are collimated, it is necessary to ensure that the transmitting and receiving antennas are at the focal points of L1 and L4, with the distance between L2 and L3 being twice the focal length. After analysis, we replaced L1 and L4 with off-axis parabolic mirrors with a focal length of 6 inches. The resulting optical signal after adjustment is shown in Figure 2. It can be observed that after the optical path adjustment, the light intensity is approximately 80% of that before the adjustment, which is consistent with expectations, indicating that the optical path adjustment was successful.
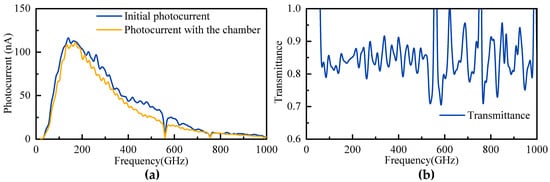
Figure 2.
Before and after optical path adjustment (a) comparison of photocurrent signal amplitude (b) transmittance.
Due to the limitations of the physical structure, the transmitting and receiving antennas cannot be positioned close to the incident window, resulting in a gap of 20 mm for each. Therefore, the optical path of the terahertz signal exposed to the atmosphere is 40 mm. It is necessary to investigate the impact of this portion on the overall interference caused by vapor. The overall optical path of the terahertz system is 1017 mm, meaning that the portion exposed to the atmosphere is approximately 1/25 of the total optical path. According to Equation (1), since the optical path exposed to the atmosphere is extremely short compared to the total optical path, simple calculations show that in a vacuum chamber, even at 50% relative humidity, the final effect is equivalent to placing the entire optical path in an atmosphere with less than 2% relative humidity. This has a minimal impact on the overall results.
With theoretical calculations in hand, we conducted experimental validation of this calculation. First, we opened the top cover of the chamber to expose the entire optical path to an atmosphere with 34% relative humidity and measured the absorption spectrum at that time. Next, we sealed the chamber and operated the vacuum pump for 1 h, reducing the relative humidity to below 0.5%, and measured the absorption spectrum again. Chamber pressure ≤ 0.1 Pa after pumping. The results are shown in Figure 3.
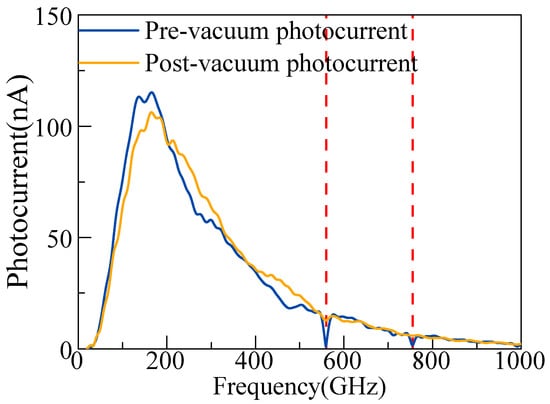
Figure 3.
The amplitude of the photogenerated current before and after vacuum pumping. Red dashed lines: absorption peaks of water vapor at ~560 GHz and ~710 GHz.
It can be observed that there are no significant absorption peaks after evacuating the chamber at the original water vapor absorption peak positions around ~560 GHz and ~755 GHz. Therefore, it can be concluded that the portion exposed to the atmosphere does not significantly interfere with the experiment.
2.3. The Design of the Fabry–Pérot Resonator
The Fabry–Pérot (FP) cavity is an important instrument capable of achieving multi-beam interference. It has long been an effective tool for length measurement and the study of the ultra-fine structure of spectra. Additionally, it serves as a fundamental configuration for laser resonators and provides a theoretical basis for the study of interference filters [37]. A uniform plane wave propagates along the axial direction in the FP cavity for numerous round trips. When the wavelength of the incident light aligns with the resonant wavelength of the cavity, the reflection and interference effects of the light within the cavity lead to a substantial increase in light intensity. The intensity formula for multiple-beam interference transmission is [38,39]:
where IR(δ) is the intensity of the reflected light, I0 is the incident light intensity, R is the square of the cavity reflectivity, and δ is the phase difference increment factor. The definition of δ is [40]:
where λ is the wavelength of the incident light, n is the refractive index of the cavity, d is the length of the cavity and is the angle of incidence. The light intensity reflectance R influences the resonator finesse in the intensity curve; a higher R results in a sharper peak. The frequency gap between adjacent transmission peaks in the transmittance spectrum is referred to as the free spectral range (FSR), represented by Equation (4) [41,42]:
where c represents the speed of light. The relationship between the full width at half maximum (FWHM) of the cavity resonance peak and the FSR is given by Equation (5), where F represents the cavity finesse, defined as . The finesse characterizes the spectral resolution capability of the resonant cavity [43].
Since the FSR varies with the cavity length while the finesse depends solely on the intensity reflectivity of the cavity mirrors, the FWHM of the resonance peaks can be effectively controlled by adjusting the cavity length. The center frequency of the resonant cavity is defined by the cavity length, following the relation , where m indicates the resonance modes. By modifying the cavity length, the central resonance frequency of the FP cavity can be adjusted to align with the absorption peak, thus amplifying the gas absorption peak.
Figure 1b illustrates the diagram of the FP cavity structure utilized in the study. We selected quartz glass for the flat plates of the cavity, which are square with dimensions of 50 mm by 50 mm. These glasses possess a reflectivity of 8% within the terahertz frequency range. Initially, the thickness of the glass plate was chosen to be 300 μm, and the frequency response of the cavity is shown as the blue line in Figure 4. However, the inherent resonant period of the 300 μm thickness interfered with the observation of the coupling. Therefore, we adjusted the thickness of the glass plate to 100 μm to provide a wider frequency observation window. The radius of the terahertz beam is 5 mm. During the experiment, we ensure that the Fabry–Pérot cavity is positioned at the center of the optical path to prevent light intensity loss caused by the incident beam not being fully accommodated by the entrance window, which could lead to errors in the transmission spectrum. The adjustment of the cavity length is performed using an electronically controlled optical platform (Chuanglai Optoelectronics, Dezhou, China), which offers a precision of 1 μm. One piece of quartz glass is directly mounted on the platform, while the other is secured to a 3 mm thick copper plate. Initially, the two quartz glass pieces are placed in close contact, and the distance between them is then adjusted with the optical platform.
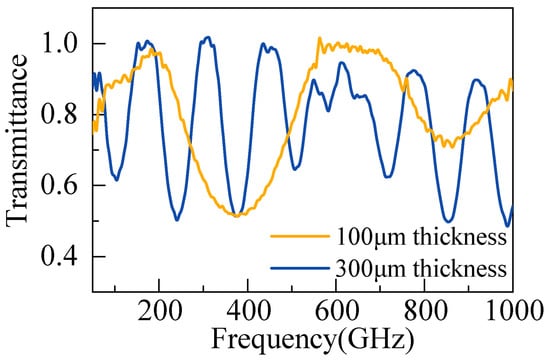
Figure 4.
The cavity response of 100 μm-thick quartz glasses (yellow) and 300 μm-thick quartz glasses (blue).
During the experiment, the FP cavity is oriented vertically within the terahertz optical path. Care is taken to ensure that the center of the terahertz light spot is aligned with the center of the cavity to prevent any potential loss of light intensity. Additionally, given that the cavity material is quartz glass, it can be inferred from Formula (2) that the resonator finesse of the resonance peak is relatively low. Consequently, to match the quality factor Q of the gas absorption peak, a higher-order mode is employed during the experiment.
3. Experimental Details
3.1. Modulation of Gaseous Concentration
CO was selected as the target gas for this study due to its relevance in environmental monitoring and industrial safety applications. The experiments were conducted in a custom-designed vacuum chamber with a total volume of 40 L, providing a controlled environment for gas concentration measurements. Initially, an EIDEX gas analyzer was utilized to monitor the gas concentration within the chamber. However, it was observed that the sensitivity of the THz-FDS instrument was insufficient to reliably detect CO concentrations, even at the maximum detection limit of 1000 ppm. This limitation necessitated the development of an alternative approach to ensure accurate and reproducible results.
A two-step procedure was implemented to address this challenge. First, the chamber was evacuated using a high-performance vacuum pump for 1 h before each experiment to reduce the relative humidity to below 0.1%, thereby minimizing potential interference from water vapor during measurements. This step was critical to ensure that the THz-FDS instrument could operate under optimal conditions. Second, a precision mass flow controller was employed to regulate the gas flow rate into the chamber at a constant rate of 0.4 L/min. By combining the known chamber volume with the controlled flow rate, the gas concentration inside the chamber could be calculated with reasonable accuracy. This method allowed for the precise introduction of CO at desired concentrations, enabling systematic evaluation of the THz-FDS system’s performance.
While this approach introduced some degree of uncertainty in the concentration measurements, primarily due to minor fluctuations in flow rate and potential gas adsorption on chamber walls, the resulting error was deemed negligible for the purposes of this study. This is because the experimental results focused on concentration levels in the thousands of ppm, where such uncertainties represent only a small fraction of the total concentration. Furthermore, the consistency of the flow control system and the stability of the chamber environment ensured that the measurements were reproducible and reliable.
3.2. Data Processing Methods
The final data obtained in this study were in the form of transmission spectra, which were derived by comparing the measured signals in a CO-filled environment to those in a vacuum reference (with humidity below 0.1%). This approach allowed us to generate transmission spectra in the frequency range of 0–1.5 THz. To achieve this, the amplitude of the received signal was first extracted from the complex signal captured by the receiver, which contained both amplitude and phase information. The Hilbert transform, as shown in Equation (6), was applied to the signal to separate its amplitude and phase components [44].
where H is the Hilbert transform, indicates the complex photocurrent signal. Before applying the Hilbert transform, the frequency-domain signal was converted to the time domain using an inverse Fourier transform. This step was critical to address the issue of echo interference, which can significantly distort the results. To mitigate this, a windowing function was applied to the time-domain signal, and the echo regions were selectively zeroed out. This preprocessing step effectively minimized the impact of echoes, ensuring a cleaner signal for subsequent analysis.
The transmission spectrum was then calculated using Equation (7), which relates the amplitude of the transmitted signal in the CO environment to that in the vacuum reference.
where T indicates the transmission spectrum, |Specref| is the reference signal amplitude, and |Specsam| is the sample signal amplitude. This normalized spectrum provides a clear representation of the interaction between the THz waves and the CO molecules, revealing characteristic absorption features within the 0–1.5 THz range. The use of the vacuum reference as a baseline ensures that any external influences, such as residual humidity or chamber effects, are accounted for, thereby enhancing the accuracy and reliability of the results.
During actual experiments, THz-FDS is susceptible to various sources of noise that introduce errors in the data. Among these, the most significant interference arises from FP effects caused by reflections at multiple interfaces within the system. Notably, these oscillations are not random; they remain consistent as long as the optical paths and interface properties of the system remain unchanged.
To eliminate such interference, the most straightforward approach is to construct a mathematical model of the entire system using the transfer matrix method, treating the sample’s refractive index and extinction coefficient as unknown variables, and then solve the equations to obtain the results [40]. However, applying this method presents significant challenges in modeling. First, the material properties of the terahertz photoconductive antenna are difficult to characterize. It is unclear how much electromagnetic energy is absorbed or reflected during the signal reflection process by the photoconductive antenna. Furthermore, changes in the frequency or polarization state of the terahertz wave make these parameters even more uncertain. Additionally, the substrate of the terahertz photoconductive antenna is gallium arsenide (GaAs) semiconductor, whose absorption and reflection properties under laser-induced carrier excitation remain unknown. Second, precise measurement is unattainable. Due to the extremely short wavelength of terahertz waves, it is challenging to accurately measure the spatial optical path dimensions with sufficient precision.
Another common approach involves using filtering techniques to eliminate oscillatory noise with fixed periods from the signal. However, conventional filters are not well-suited for application in THz-FDS systems due to two main challenges: Firstly, in broadband scenarios, the refractive index dispersion of materials within the system causes the characteristics of interference to vary with frequency. As a result, filter parameters must be continuously adjusted across the frequency range, complicating their practical implementation. Secondly, filters tend to remove useful information along with noise. If the absorption spectrum contains frequency components coinciding with those targeted by the filter, meaningful data will be unavoidably lost, leading to reduced accuracy in the final results [41].
Based on this, we adopted an alternative frequency-time transformation method that offers a simpler and more effective approach to suppressing echo interference [42]. As shown in the thumbnail of Figure 5b, the signal exhibits multiple echoes in addition to the strongest main peak. From fundamental optical principles, it is known that each reflection introduces a time delay of 2nd/c to the main signal, where n is the refractive index of the medium (approximately 1 for air in this case), and d is the propagation distance. When the optical path length is sufficiently long, the time separation between the main signal and the reflected signals exceeds the duration of the main pulse. This allows us to effectively suppress FP interference using time-domain zeroing. Given that the terahertz main pulse width is on the order of picoseconds, this method is particularly well-suited for terahertz signals.
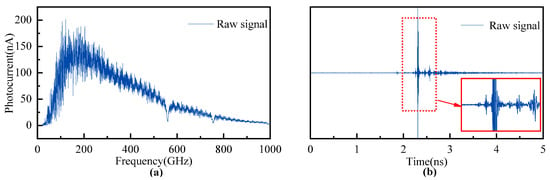
Figure 5.
(a) Signal amplitude before denoising (b) Time-domain signal.
We first converted the Hilbert-transformed frequency-domain signal into the time domain via inverse Fourier transform. After obtaining the time-domain signal, we retained only the main pulse by applying a time-domain zeroing operation to all components outside the main peak. The processed signal was then converted back to the frequency domain using the fast Fourier transform to achieve noise reduction. The original signal shown in Figure 1 was denoised using a selected window range of 2.28–2.35 ns. A comparison of the signals before and after denoising is presented in Figure 6. As can be observed, the noise is significantly reduced after FP interference suppression.
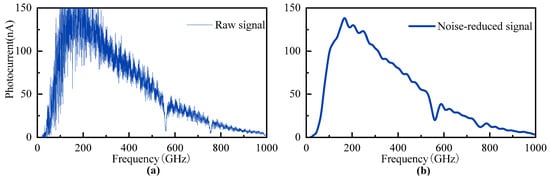
Figure 6.
(a) Signal amplitude before denoising (b) Noise-reduced signal.
Although this approach partially diminishes the advantage of high frequency resolution in THz-FDS, the inherently low power of terahertz spectroscopic systems makes them particularly susceptible to systemic noise and echo interference. Therefore, the frequency-time transformation method effectively enhances signal quality while preserving signal integrity to the greatest extent possible.
3.3. Center Frequency Adjustment and Coupling Mode Selection
The enhancement of gas detection sensitivity in this study was achieved by optimizing the coupling between the gas absorption peaks and the resonant frequencies of the FP cavity. To accomplish this, we first conduct preliminary experiments on the gas to be detected to identify its absorption peak within the system signal range. We select the most suitable absorption peak position based on several indicators, including absorption intensity, signal-to-noise ratio, and interference from neighboring absorption peaks. Subsequently, we adjust the cavity length so that the resonant frequency of the cavity at a specific mode matches the gas absorption peak for coupling. Based on the coupling mechanism, two distinct modes were identified: (1) the peak-valley coupling mode, where the absorption peak aligns with the transmission spectrum peak, and (2) the valley-valley coupling mode, where the absorption peak aligns with the transmission spectrum valley. Previous studies have demonstrated that the peak-valley coupling mode is more suitable for detecting low gas concentrations, as it provides higher sensitivity [25].
Following the acquisition of baseline data without the FP cavity, the cavity was introduced into the system. By varying the length of the FP cavity, the central resonant frequency can be aligned with the absorption peak of the gas. The chamber was then sealed and evacuated to reduce the relative humidity to below 0.1%, ensuring minimal interference from water vapor. Subsequently, CO was introduced at varying concentrations to obtain the experimental results with the FP cavity.
The selection of the modes (m) was based on prior investigations into the impact of different modes on detection performance. It was found that the experimental results are optimal when the quality factor (Q-value) of the cavity transmission spectrum closely matches that of the gas absorption peak. Through systematic testing, the mode order m = 10 was selected for this study, as it provided the best alignment of Q-values and thus the highest sensitivity. Detailed results and discussions regarding the performance of different mode orders will be presented in later sections.
4. Results and Discussion
4.1. CO Absorption Spectrum and Absorption Peak Selection
CO has extensive applications in fields such as chemistry [45], metallurgy [29], and fuel [46]. However, if its concentration is not properly controlled, it can pose significant risks to human health and equipment as a toxic and hazardous gas. Therefore, it is essential to detect low concentrations of CO. We initially measured the absorption peaks of CO gas directly using THz-FDS to select suitable absorption peaks for coupling. First, we measured dry air with a relative humidity of less than 0.1% as a reference. Then, we gradually increased the concentration of carbon monoxide in the chamber using a gas cylinder and a flow meter. It was not until the CO concentration in the chamber reached 7% that we obtained a relatively distinct absorption peak of CO in the low-frequency range, as shown in Figure 5. This also represents the detection limit of CO gas when using THz-FDS directly.
From Figure 7, we can identify 10 absorption peaks of CO gas within the 0–1.5 THz range used in our study, located at approximately 0.345 THz, 0.460 THz, 0.576 THz, 0.692 THz, 0.808 THz, 0.921 THz, 1.037 THz, 1.153 THz, 1.269 THz, and 1.381 THz. These results are consistent with previously reported experimental findings [47]. We compared the measured experimental data with the HITRAN database, and the results are shown in Table 1. In our system, the frequency resolution is set to 20 MHz. Using the uniform distribution uncertainty calculation method, the resulting uncertainty is approximately 11.55 MHz [48]. Ultimately, we selected the absorption peak at approximately 0.46 THz as the target for coupling. This choice was made because its absorption intensity is moderate, and its frequency is relatively low, resulting in a better signal-to-noise ratio than higher frequencies, thereby effectively reducing errors. Additionally, although we minimized humidity to an extremely low level during the experiment, we still avoided selecting CO absorption peaks too close to water vapor absorption peaks to prevent potential interference and enhance the accuracy of the experiment. At this frequency, a mode number of m = 1 corresponds to a cavity length of 0.326 mm.
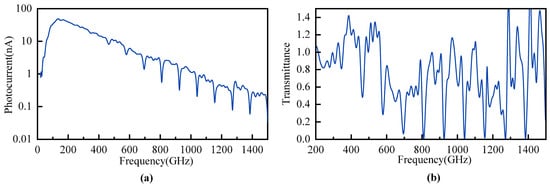
Figure 7.
The 0.02–1.5 THz range of CO: (a) Photocurrent signal amplitude (b) transmission spectrum.

Table 1.
Comparison of experimental results with HITRAN database results.
4.2. Mode Selection
The selection of the m was based on prior investigations into the impact of different modes on detection performance. The Q-value of gas absorption peaks was calculated using the FWHM method. It is defined by Equation (8) [49]:
where f0 represents the central resonant frequency. In our system, the energy loss of the FP cavity is predominantly governed by mirror losses, and the cavity materials exhibit negligible dispersion within the operational frequency range. Consequently, the intrinsic Q-factor of the cavity can be considered independent of the mode number variation [48]. However, when we focus on a single resonance peak at the gas absorption frequency, we can approximate its equivalent Q-factor using the gas absorption peak’s Q-value as reference. Our previous research demonstrated that optimal coupling observation is achieved when the equivalent Q-value of the cavity resonance peak approaches the Q-value of the gas absorption peak.
To determine the mode order for the experiment, we first analyzed the Q-value of the CO absorption peak at ~0.465 THz. As illustrated in Figure 8a, the CO absorption peak exhibits an FWHM of approximately 22 GHz, corresponding to a Q-value of ~21. This value is a benchmark for selecting the appropriate modes of the FP cavity, as the alignment of the cavity’s equivalent Q-value with the gas absorption peak is crucial for achieving high detection sensitivity.
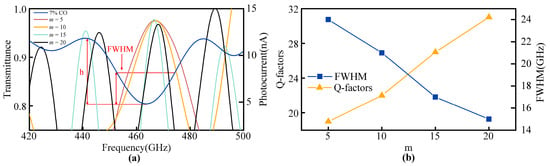
Figure 8.
(a) CO absorption peak and transmission spectra of different modes (b) FWHM and equivalent Q-factors of different modes cavity.
Next, we systematically evaluated the transmission spectra of the FP cavity in the absence of CO for four different mode orders (m = 5, 10, 15, and 20). The cavity lengths corresponding to the four mode numbers are 1.630 mm, 3.260 mm, 4.890 mm, and 6.520 mm, respectively. For each mode, the FWHM and corresponding equivalent Q-value were calculated, as summarized in Figure 8b. Among the tested modes, m = 10 demonstrated an FWHM of ~21 GHz and a Q-value of ~22, which closely matched the Q-value of the CO absorption peak. The selection of m = 10 was further justified by its ability to have sharp resonance and experimental feasibility. While higher modes (e.g., m = 15 or 20) could theoretically provide sharper resonances, they are also more susceptible to environmental noise. Conversely, lower modes (e.g., m = 5) exhibit broader resonances, which reduce the sensitivity of the detection system. Thus, m = 10 represents an optimal mode, offering both high sensitivity and robust performance under experimental conditions.
4.3. Cavity Enhancement Effect and Detection Limit
After selecting the modes, we attempted to observe the enhancement effect of the FP cavity on the absorption peak. In the initial experiment, we first measured the transmission spectra of 5000 ppm CO without the cavity and compared it with the transmission spectra of the same CO concentration using the FP cavity at the m = 10 (d = 3.260 mm). The results are shown in Figure 9. Additionally, to quantify the enhancement effect, we introduced a gain factor F, defined as [24]:
where ∆Tcavity and ∆Tref represent the difference between the transmission spectrum value at the frequency of the absorption peak and the initial transmittance. Under ideal conditions, the transmission spectrum without the cavity should appear as a horizontal line with a constant value of 1, except in the vicinity of the absorption peak (indicated by the red line in Figure 9). However, as can be observed in Figure 9, the yellow line exhibits irregular oscillations, indicating deviations from the ideal transmission spectrum. The oscillations originate from multipath interference, where terahertz waves reflect repeatedly at interfaces such as the vacuum chamber’s input/output windows and off-axis parabolic mirrors. The reflected signals remain embedded in the main signal and cannot be isolated in the time domain [49]. At this stage, the absorption effect of 5000 ppm CO measured directly by THz-FDS is significantly weaker than the observed oscillations (as previously determined, the detection limit for direct measurement is 7%). As a result, the gain factor F calculated under these conditions is inaccurate. To address this issue, we introduced a new reference: the transmission spectrum of 0 ppm CO under the same mode (m = 10). This reference spectrum was used to replace ∆Tref in the gain factor formula. After this substitution, the results are shown in Figure 10. The recalculated gain factor F is approximately 1100%, demonstrating a substantial enhancement effect when the FP cavity is utilized. This approach not only resolves the inaccuracy caused by the weak absorption signal but also provides a more reliable metric for evaluating the performance of the cavity-enhanced detection system.
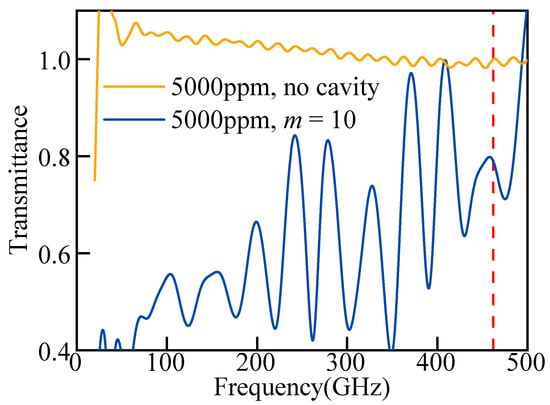
Figure 9.
5000 ppm CO transmittance (yellow), 5000 ppm CO, modes 10 transmittance (blue). Red dashed line: absorption peak of carbon monoxide at ~460 GHz.
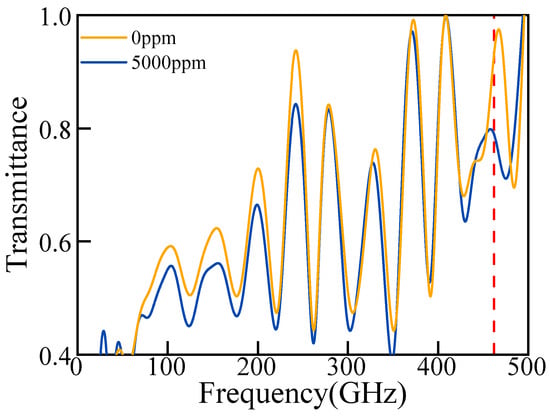
Figure 10.
0 ppm CO, modes 10 transmittance (yellow), 5000 ppm CO, modes 10 transmittance (blue).
After confirming the enhancement effect of the FP cavity on the CO absorption peak, we proceeded to investigate the detection limit of the system under this configuration. Using the transmission spectrum of 0 ppm CO at m = 10 as the reference, we conducted ten repeated measurements to establish a baseline with error bars. A concentration was considered detectable if its absorption peak fell outside the error bar range of the reference spectrum.
Starting from 3000 ppm, we measured CO concentrations in increments of 500 ppm, ultimately obtaining six data points ranging from 3000 ppm to 5500 ppm, as shown in Figure 11a. To ensure statistical rigor, each concentration was tested ten times, and the average value was used as the final result. Due to the collision broadening effect between gas molecules, as the concentration of carbon monoxide increases, the average distance between molecules decreases and the collision frequency rises. Collision-induced inter-molecular electric field disturbances cause the ground state energy levels to rise or the excited state energy levels to fall, resulting in a reduction in the transition energy [50]. This is reflected in Figure 11a as a redshift of the carbon monoxide absorption peaks and a decrease in the sharpness of the coupling position of the cavity resonance peaks. The results demonstrate that the system achieves a detection limit of 3500 ppm, representing a 14-fold improvement compared to the detection limit without the FP cavity. As shown, even at lower gas concentrations, the FP cavity produces significant absorption effects. This occurs because the cavity’s transmittance is highly sensitive to intracavity material losses. By adjusting the cavity length to couple the FP cavity’s resonance peak with the gas absorption peak, the transmitted intensity becomes extremely responsive to gas concentration changes, enabling detection through the decrease in transmittance at the resonance point. This enhancement is equivalent to extending the effective optical path length from the original 1017 mm to approximately 14 m, highlighting the system’s exceptional sensitivity. We extracted the maximum transmittance values of the cavity under different carbon monoxide concentrations, as shown in Figure 11b. The results demonstrate a strong linear correlation between transmittance and CO concentration above 3500 ppm.
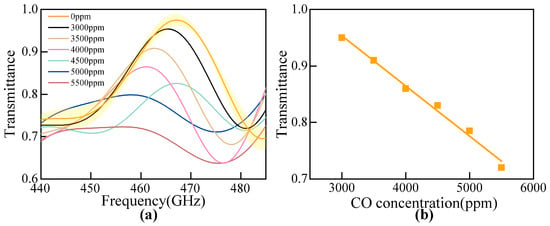
Figure 11.
(a) Comparison of different concentrations at the same modes. (b) Transmittance of the cavity at different CO concentrations.
5. Conclusions
This study presents a highly sensitive gas detection method based on the FP cavity utilizing the THz-FDS system. By precisely adjusting the cavity length to align the resonant frequency with the gas absorption peak, we achieved a significant enhancement of the absorption signal. Using a modified gas chamber, we identified ten absorption peaks of CO within the 0–1.5 THz range and selected m = 10 for its optimal Q-value matching. The system demonstrated remarkable performance, with a gain factor F of up to 1100% for the CO absorption peak at 0.465 THz at a concentration of 5000 ppm. Furthermore, the detection limit for CO was improved to 3500 ppm, a 20-times enhancement over direct measurement, equivalent to extending the optical path length to approximately 20 m. These results validate the high sensitivity and practical potential of our FP cavity-enhanced approach, offering a promising solution for advanced gas sensing applications. Meanwhile, this method exhibits excellent versatility. By adjusting the length of the FP cavity, its resonant center frequency can be coupled with the absorption peaks of other gases. It is anticipated that combining this method with high-power terahertz sources will achieve superior gas detection performance.
Author Contributions
Conceptualization, Y.W., K.C. and C.R.; Data curation, Y.W. and L.H.; Formal analysis, Y.W., K.C. and A.K.F.; Funding acquisition, C.R.; Investigation, Y.W., K.C. and C.R.; Methodology, Y.W., K.C. and L.H.; Project administration, Y.W., K.C. and C.R.; Resources, K.C. and L.H.; Supervision, C.R.; Writing—original draft, Y.W.; Writing—review and editing, K.C., A.K.F., L.H. and C.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China, grant number 61222110, 61831001.
Data Availability Statement
Data underlying the results presented in this paper are not publicly available at this time but may be obtained from the authors upon reasonable request.
Acknowledgments
The authors have reviewed and edited the output and take full responsibility for the content of this publication. The authors gratefully acknowledge the support from the National Natural Science Foundation of China. We also extend our sincere appreciation to Xiaoping Zheng of Tsinghua University and Haoran Wang for their insightful discussions and valuable contributions to this work.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| THz | Terahertz |
| THz-FDS | Terahertz Frequency Domain Spectrometer |
| FP | Fabry–Pérot |
References
- Fine, G.F.; Cavanagh, L.M.; Afonja, A.; Binions, R. Metal Oxide Semi-Conductor Gas Sensors in Environmental Monitoring. Sensors 2010, 10, 5469–5502. [Google Scholar] [CrossRef]
- Kim, S.-J.; Hwang, I.-S.; Kang, Y.C.; Lee, J.-H. Design of Selective Gas Sensors Using Additive-Loaded In2O3 Hollow Spheres Prepared by Combinatorial Hydrothermal Reactions. Sensors 2011, 11, 10603–10614. [Google Scholar] [CrossRef] [PubMed]
- Pijolat, C.; Pupier, C.; Sauvan, M.; Tournier, G.; Lalauze, R. Gas detection for automotive pollution control. Sens. Actuators B Chem. 1999, 59, 195–202. [Google Scholar] [CrossRef]
- Hou, C.; Li, J.; Huo, D.; Luo, X.; Dong, J.; Yang, M.; Shi, X. A portable embedded toxic gas detection device based on a cross-responsive sensor array. Sens. Actuators B Chem. 2012, 161, 244–250. [Google Scholar] [CrossRef]
- Lu, G.; Ocola, L.E.; Chen, J. Gas detection using low-temperature reduced graphene oxide sheets. Appl. Phys. Lett. 2009, 94, 083111. [Google Scholar] [CrossRef]
- Sauli, F. GEM: A new concept for electron amplification in gas detectors. Nucl. Instrum. Methods Phys. Res. Sect. Accel. Spectrometers Detect. Assoc. Equip. 1997, 386, 531–534. [Google Scholar] [CrossRef]
- Arunajatesan, V.; Subramaniam, B.; Hutchenson, K.W.; Herkes, F.E. In situ FTIR investigations of reverse water gas shift reaction activity at supercritical conditions. Chem. Eng. Sci. 2007, 62, 5062–5069. [Google Scholar] [CrossRef]
- Hodgkinson, J.; Tatam, R.P. Optical gas sensing: A review. Meas. Sci. Technol. 2013, 24, 012004. [Google Scholar] [CrossRef]
- Ingle, J.D., Jr.; Stanley, R.C. Spectrochemical Analysis; Prentice Hall: Saddle River, NJ, USA, 1988. [Google Scholar]
- Cao, C.; Zhang, X.H.; Zhao, X.Y.; Zhang, H. Review of terahertz time domain and frequency domain spectroscopy. Spectrosc. Spectr. Anal. 2018, 38, 2688–2699. [Google Scholar]
- White, J.U. Long Optical Paths of Large Aperture. J. Opt. Soc. Am. 1942, 32, 285–288. [Google Scholar] [CrossRef]
- Grassi, L.; Guzzi, R. Theoretical and practical consideration of the construction of a zero-geometric-loss multiple-pass cell based on the use of monolithic multiple-face retroreflectors. Appl. Opt. 2001, 40, 6062–6071. [Google Scholar] [CrossRef] [PubMed]
- Ni, Z.; Shao, J.; Zhou, H.; Wang, K. Research on trace gas measurement by ICOS with WMS. In Proceedings of the SPIE/COS Photonics Asia, Beijing, China, 12–14 October 2016; Zhang, C., Zhang, X.-C., Tani, M., Eds.; p. 1003028. [Google Scholar] [CrossRef]
- Safronova, M.S.; Johnson, W.R. All-order methods for relativistic atomic structure calculations. Can. J. Phys. 2005, 83, 309–324. [Google Scholar]
- Melinger, J.S.; Yang, Y.; Mandehgar, M.; Grischkowsky, D. THz detection of small molecule vapors in the atmospheric transmission windows. Opt. Express 2012, 20, 6788–6807. [Google Scholar] [CrossRef]
- Meinen, J.; Thieser, J.; Platt, U.; Leisner, T. Technical Note: Using a high finesse optical resonator to provide a long light path for differential optical absorption spectroscopy: CE-DOAS. Atmos. Chem. Phys. 2010, 10, 3901–3914. [Google Scholar] [CrossRef]
- Platt, U.; Meinen, J.; Pohler, D.; Leisner, T. Broadband Cavity Enhanced Differential Optical Absorption Spectroscopy (CE-DOAS)—Applicability and corrections. Atmos. Meas. Tech. 2009, 2, 713–723. [Google Scholar] [CrossRef]
- Zheng, K.; Zheng, C.; Zhang, H.; Guan, G.; Zhang, Y.; Wang, Y.; Tittel, F.K. A novel gas sensing scheme using near-infrared multi-input multi-output off-axis integrated cavity output spectroscopy (MIMO-OA-ICOS). Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2021, 256, 119745. [Google Scholar] [CrossRef]
- Ji, X.; Li, W.; Song, J.; Wei, L.; Liu, X.S. CEAS: Cis-regulatory element annotation system. Nucleic Acids Res. 2006, 34, W551–W554. [Google Scholar] [CrossRef]
- Hindle, F.; Bocquet, R.; Pienkina, A.; Cuisset, A.; Mouret, G. Terahertz gas phase spectroscopy using a high-finesse Fabry–Pérot cavity. Optica 2019, 6, 1449–1454. [Google Scholar] [CrossRef]
- Long, J.P.; Simpkins, B.S. Coherent Coupling between a Molecular Vibration and Fabry–Perot Optical Cavity to Give Hybridized States in the Strong Coupling Limit. ACS Photonics 2015, 2, 130–136. [Google Scholar] [CrossRef]
- Shalabney, A.; George, J.; Hutchison, J.; Pupillo, G.; Genet, C.; Ebbesen, T.W. Coherent coupling of molecular resonators with a microcavity mode. Nat. Commun. 2015, 6, 5981. [Google Scholar] [CrossRef] [PubMed]
- Damari, R.; Weinberg, O.; Krotkov, D.; Demina, N.; Akulov, K.; Golombek, A.; Schwartz, T.; Fleischer, S. Strong coupling of collective intermolecular vibrations in organic materials at terahertz frequencies. Nat. Commun. 2019, 10, 3248. [Google Scholar] [CrossRef] [PubMed]
- Shi, X.; Zhao, Z.; Han, Z. Highly sensitive and selective gas sensing using the defect mode of a compact terahertz photonic crystal cavity. Sens. Actuators B Chem. 2018, 274, 188–193. [Google Scholar] [CrossRef]
- Wu, Y.; Chen, K.; Fahad, A.K.; Wang, H.; Zheng, X.; Ruan, C. The enhancement detection method based on the Fabry–Pérot cavity using terahertz frequency-domain spectroscopy. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2025, 327, 125293. [Google Scholar] [CrossRef] [PubMed]
- Ying, H.; Wang, X.H.; Guo, L.T.; Zhang, C.L. Terahertz time-domain spectroscopy study of carbon monoxide. Spectrosc. Spectr. Anal. 2006, 26, 1008–1011. [Google Scholar]
- Shimizu, N.; Matsuyama, K.; Hosako, I. Absorption spectra of hydrogen chloride and carbon monoxide in smoke. In Proceedings of the 2012 37th International Conference on Infrared, Millimeter, and Terahertz Waves, Wollongong, NSW, Australia, 23–28 September 2012; IEEE: New York, NY, USA; pp. 1–2. [Google Scholar] [CrossRef]
- Su, Y.; Zheng, X.; Deng, X. Terahertz Spectrum Analysis Based on Empirical Mode Decomposition. J. Infrared Milli. Terahz. Waves 2017, 38, 972–979. [Google Scholar] [CrossRef]
- Pinheiro, P.; Schouler, M.C.; Gadelle, P.; Mermoux, M.; Dooryhée, E. Effect of hydrogen on the orientation of carbon layers in deposits from the carbon monoxide disproportionation reaction over Co/Al2O3 catalysts. Carbon 2000, 38, 1469–1479. [Google Scholar] [CrossRef]
- Kilcullen, P.; Hartley, I.D.; Jensen, E.T.; Reid, M. Terahertz Time Domain Gas-phase Spectroscopy of Carbon Monoxide. J. Infrared Milli. Terahz. Waves 2015, 36, 380–389. [Google Scholar] [CrossRef]
- Zhao, C.; Wang, W.; Zhu, N.; Song, Z.; Chao, X. Quantitative, multi-species gas sensing using broadband terahertz time-domain spectroscopy. Meas. Sci. Technol. 2024, 35, 045503. [Google Scholar] [CrossRef]
- Liu, X.; Ma, Y. Sensitive carbon monoxide detection based on light-induced thermoelastic spectroscopy with a fiber-coupled multipass cell [Invited]. Chin. Opt. Lett. 2022, 20, 031201. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, Z.; Yang, Y.; Chen, T.; Zhang, C. Identification terahertz spectra for the dyestuffs based on principal component analysis and Savitzky-Golay filter. Optik 2018, 172, 668–673. [Google Scholar] [CrossRef]
- Duvillaret, L.; Garet, F.; Coutaz, J.-L. Highly precise determination of optical constants and sample thickness in terahertz time-domain spectroscopy. Appl. Opt. 1999, 38, 409–415. [Google Scholar] [CrossRef]
- Ruan, C.; Kong, D.; Dai, J.; Chen, K.; Guo, S.; Wu, X. High-resolution frequency-domain spectroscopy for water vapor with coherent and continuous terahertz wave. Chin. Opt. Lett. 2019, 17, 073001. [Google Scholar]
- Wietzke, S.; Jansen, C.; Reuter, M.; Jung, T.; Hehl, J.; Kraft, D.; Chatterjee, S.; Greiner, A.; Koch, M. Thermomorphological study of the terahertz lattice modes in polyvinylidene fluoride and high-density polyethylene. Appl. Phys. Lett. 2010, 97, 022901. [Google Scholar] [CrossRef]
- Egan, P.; Stone, J.A. Absolute refractometry of dry gas to ±3 parts in 109. Appl. Opt. 2011, 50, 3076–3086. [Google Scholar] [CrossRef] [PubMed]
- Zhong, X.H. Modern Fundamentals of Optics; Peking University Press: Beijing, China, 2003. [Google Scholar]
- Hernandez, G. Fabry–Pérot Interferometers; Cambridge University Press: Cambridge, UK, 1986; ISBN 0521322383. [Google Scholar]
- Chilwell, J.; Hodgkinson, I. Thin-films field-transfer matrix theory of planar multilayer waveguides and reflection from prism-loaded waveguides. J. Opt. Soc. Am. A 1984, 1, 742–753. [Google Scholar] [CrossRef]
- Born, M.; Wolf, E. Principles of Optics: Electromagnetic Theory of Propagation, Interference and Diffraction of Light, 7th ed.; Publishing House of Electronics Industry: Beijing, China, 2016; pp. 49–63. [Google Scholar]
- Xiong, Q.X.; Liu, F.; Chang, Q. Signals and Systems; Higher Education Press: Beijing, China, 2011; pp. 105–121. [Google Scholar]
- Liu, S.; Dong, X.; Sun, J.; Shum, P. Free-spectral range tunable Fabry–Perot filter with superimposed fiber Bragg gratings. Opt. Commun. 2009, 282, 4729–4732. [Google Scholar]
- Levitzki, A.; Mishani, E. Tyrphostins and Other Tyrosine Kinase Inhibitors. Annu. Rev. Biochem. 2006, 75, 93–109. [Google Scholar] [CrossRef]
- Delogu, F.; Mulas, G.; Garroni, S. Hydrogenation of carbon monoxide under mechanical activation conditions. Appl. Catal. A Gen. 2009, 366, 201–205. [Google Scholar] [CrossRef]
- Shen, F.; Shi, J.; Chen, T.-Y.; Shi, F.; Li, Q.-Y.; Zhen, J.-Z.; Li, Y.-F.; Dai, Y.-N.; Yang, B.; Qu, T. Electrochemical reduction of CO2 to CO over Zn in propylene carbonate/tetrabutylammonium perchlorate. J. Power Sources 2018, 378, 555–561. [Google Scholar] [CrossRef]
- Araki, M.; Tabata, Y.; Shimizu, N.; Matsuyama, K. Terahertz spectroscopy of CO and NO: The first step toward temperature and concentration detection for combustion gases in fire environments. J. Mol. Spectrosc. 2019, 361, 34–39. [Google Scholar] [CrossRef]
- Withayachumnankul, W.; Fischer, B.M.; Lin, H.; Abbott, D. Uncertainty in terahertz time-domain spectroscopy measurement. J. Opt. Soc. Am. B 2008, 25, 1059–1072. [Google Scholar] [CrossRef]
- Kong, D.-Y.; Wu, X.-J.; Wang, B.; Gao, Y.; Dai, J.; Wang, L.; Ruan, C.-J.; Miao, J.-G. High resolution continuous wave terahertz spectroscopy on solid-state samples with coherent detection. Opt. Express 2018, 26, 17964–17976. [Google Scholar] [CrossRef] [PubMed]
- Lyons, J.R.; Herde, H.; Stark, G.; Blackie, D.S.; Pickering, J.C.; De Oliveira, N. VUV pressure-broadening in sulfur dioxide. J. Quant. Spectrosc. Radiat. Transf. 2018, 210, 156–164. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).