Development of a Calibration Transfer Methodology and Experimental Setup for Urine Headspace Analysis

Abstract

Electronic noses (E-Noses) equipped with metal-oxide semiconductor (MOS) sensors are promising tools for non-invasive medical diagnostics. Their adoption in clinical practice, however, is limited—among others—by sensor variability across devices, which makes individual calibration necessary. This study presents an approach for the development of a calibration transfer (CT) methodology for urine headspace analysis, involving the design and realization of a dedicated experimental setup and protocol. Partial least squares-discriminant analysis (PLS-DA) models were trained on human urine samples enriched with selected biomarkers to simulate pathological states. Models from a reference (“master”) device were transferred to other (“slave”) units in multiple master–slave configurations using Direct Standardization (DS). To overcome the variability of human urine, synthetic urine recipes were formulated to mimic sensor responses and serve as reproducible transfer samples. Several strategies for selecting transfer samples were evaluated, including the Kennard–Stone algorithm, a DBSCAN-based approach, and random selection. Without CT, classification accuracy on slave devices decreased markedly (37–55%) compared to the master’s performance (79%), whereas applying DS with synthetic standards restored accuracy to 75–80%. These results demonstrate that combining reproducible synthetic standards with DS enables effective model transfer across E-Noses, reducing calibration requirements and supporting their broader applicability in medical diagnostics.

1. Introduction

Gas sensors, particularly Metal Oxide Semiconductor (MOS) sensors, which are widely used in Electronic Noses (E-Noses), are nominally identical at a macroscopic scale, but they exhibit intrinsic non-reproducibility due to microscopic variations in active site distribution from manufacturing [1]. This inherent variability poses significant challenges to the broad adoption of E-Noses.

E-Noses are sensitive to volatile organic compounds (VOCs) present in the gas phase. Similarly to the human olfactory system, E-Noses need a preliminary exposure to different odors to “learn” and recognize them. This calibration process is commonly referred to as “training”. During this phase, sensors’ resistance changes in response to calibration compounds are recorded. These data are then used to develop classification or regression models via machine learning algorithms [2]. This calibration step is complex and time-consuming, involving sample collection, sensor measurements, data preprocessing, feature extraction, and model training. The volume of data and computational demands can make this process even more challenging.

As a result of the gas sensors’ lack of reproducibility, a calibration model developed for one E-Nose (“master”) often performs poorly when applied to another device (“slave”), even though they are both equipped with identical sensor types [3]. These limitations hinder the large-scale adoption of E-Noses in industrial and clinical applications.

In the field of medical diagnostics, E-Noses have been used to analyze bodily fluids such as urine, containing VOC biomarkers that are indicative of various physiological and pathological states. Analytical methods such as gas chromatography-mass spectrometry (GC-MS) [4] and selected ion flow tube mass spectrometry (SIFT-MS) [5] have proven effective in detecting individual VOC biomarkers linked to conditions like diabetes, cancer, and metabolic disorders. However, these techniques are expensive, time-consuming, and the association between single biomarkers and specific diseases remains unclear [6]. The advantage of E-Noses lies in their ability to analyze the VOC mixture as a whole, thereby acting as a black box, which captures the global odor profile without needing to identify individual compounds. This holistic approach allows E-Noses to detect patterns that may be indicative of specific diseases, without requiring a detailed understanding of the exact chemical composition of the analysed gas mixture. Studies have demonstrated the potential of E-Noses in diagnosing diseases through the analysis of breath, urine, and other biological fluids. E-Noses have been employed to diagnose early-stage lung cancer [7], prostate cancer [8], tuberculosis [9], diabetes [10], kidney disease [11] and other conditions. Despite these encouraging results, most studies remain at the proof-of-concept stage, lacking the robustness and scalability required for real-world application.

In recent years, the study and development of advanced sensing materials has succeeded in improving sensor response stability [12]. Despite such advancements, long-term drift and the lack of reproducibility of sensor responses across devices remain unsolved challenges, and the major limitation to the adoption of E-Noses in clinical practice, entailing the need for frequent recalibration and restricting the generalizability of findings. To address these issues, several Calibration Transfer (CT) techniques have been developed and reported in the literature. These include Direct Standardization (DS), Piecewise Direct Standardization (PDS), Orthogonal Signal Correction (OSC), Multiplicative Signal Correction (MSC), Generalized Least Squares Weighting (GLSW), and Slope and Bias Correction (SBC), among others [12]. In general, these approaches aim to reduce both calibration time and cost, enabling the transfer of models between instruments without the need for full recalibration. Moreover, CT methods can also be periodically applied to the same device to correct for signal drift and maintain model performance over time.

Most of these CT strategies rely on the use of “transfer samples”, which are used for transferring calibration across devices (or on the same device that has changed its behavior over time). When applying this type of strategy, the choice of suitable transfer samples becomes crucial for successful CT. In this context, the intrinsic variability of real samples poses another significant challenge, adding to the instrument variability and complicating CT. For instance, considering urine, the composition differs between individuals and fluctuates within the same individual over time due to factors such as diet and hydration, making it an unreliable calibration standard. To overcome this limitation, one novel aspect of this study is the introduction of synthetic standard mixtures designed to reproduce urine sensor responses while offering reproducibility and scalability.

In this study, the application of E-Noses to disease diagnostics is simulated through the analysis of real urine mixtures: pure urine and urine spiked with biomarkers (acetone and 4-heptanone) [13].

Among the available Calibration Transfer (CT) techniques, Direct Standardization (DS) was selected for its straightforward implementation. The main contribution of this study lies not in the CT algorithm itself, but in the development of a systematic methodology that includes the preparation of synthetic urine calibration standards, the design of transfer sample selection strategies, and the application of DS.

By introducing synthetic mixtures as calibration standards in combination with Direct Standardization, this work provides a practical route to overcome one of the main barriers to the broader adoption of E-Noses, particularly in diagnostics but also in other application domains.

2. Materials and Methods

2.1. Design of the Experimental Setup for Calibration Transfer

2.1.1. Sampling System

Figure 1 illustrates the sampling system developed within this study to realize a gaseous headspace from liquid samples for subsequent analysis with E-Noses. It includes the following components:

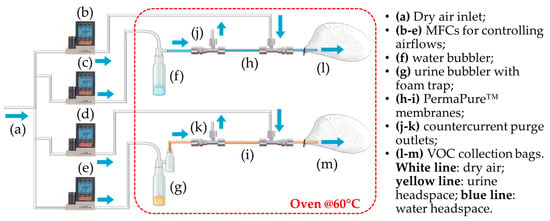
Figure 1. Diagram of the sampling setup. (a) Dry air inlet; (b–e) MFCs for controlling airflows; (f) water bubbler; (g) urine bubbler with foam trap; (h,i) PermaPure™ membranes; (j,k) countercurrent purge outlets; (l,m) VOC collection bags.

• A compressed air line supplying filtered air;
• Two glass bubblers, one containing the liquid urine sample and the other containing distilled water to be used as reference for sensor baseline;
• A foam trap in the urine line to prevent foam from entering the sample bag;
• Two Nafion™ membranes to reduce the humidity content of the gaseous samples (PermaPure™, Inc., model MD-050-72S-1; Lakewood, NJ, USA);
• Disposable Nalophan™ bags used for VOCs collection, in compliance with the European Standard EN13725:2022 [14] for dynamic olfactometry;
• Four mass flow controllers (MFC) from Alicat Scientific (Tucson, AZ, USA) to regulate the flow rate of the air streams;
• Teflon™ tubing for system connections;
• A forced-air oven set at 60 °C, equipped with temperature control and inlet/outlet ports for gas tubing;
• Heating wires with thermocouples and insulation to maintain gas line temperature.

This study was carried out using MATLAB R2020a (The MathWorks Inc., Natick, MA, USA). The MATLAB-controlled setup consists of two parallel lines: one for generating urine headspace and another for producing a reference air bag. Both operate inside a ventilated oven at 60 °C. This temperature was selected based on prior research work aimed at optimizing the experimental protocol for prostate cancer diagnosis via urinary VOC analysis [15]. That study identified 60 °C as the optimal temperature for maximizing urinary VOC concentration for E-Nose detection while preventing sample degradation. Each bubbler is filled with 20 mL of liquid: urine or distilled water. Compressed air is bubbled through each liquid at 400 mL/min for 15 min for the urine line and for 25 min for the air line. The resulting vapors pass through gas dryers (Nafion™ dryers by PermaPure™, Inc., model MD-050-72S-1; Lakewood, NJ, USA) to remove excess humidity. PermaPure™ gas dryers allow water vapor molecules to permeate through Nafion™ membranes and be swept away by a dry counter-current carrier gas at 1.2 L/min. Headspaces, rich in VOCs, are collected in 6 L (urine) and 10 L (air) Nalophan™ bags. After each sampling, the system is cleaned by emptying and refilling bubblers with 20 mL distilled water. The sampling time for cleaning process was set at 10 min.

2.1.2. E-Noses Setup for Calibration Transfer

The experimental setup for studying CT between E-Noses (Figure 2) consists of three custom-made PEEK (polyether ether ketone) chambers. PEEK is selected for its chemical stability and confirmed inertness on MOS sensors [16]. The three chambers (A, B, and C) operate in parallel and are placed inside a temperature-controlled oven at 60 °C.

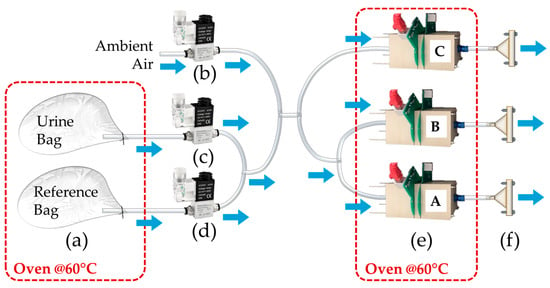
Figure 2. PEEK chambers setup. It represents the urine and reference bags (a), the valves that control the ambient air (b), urine sample (c) and reference air (d) lines, the E-Nose PEEK chambers A, B and C (e), and the vacuum pumps connected to them (f).

The setup consists of three lines: one for ambient air, and two for drawing reference air and urine headspace from the respective bags prepared using the sampling system shown in Figure 1.

During the E-Nose analysis, the sample bags are kept in the same temperature-controlled oven used for the sampling at 60 °C.

Three electro valves by Heschen (Foshan, China) control the different phases of the analysis:

• Before phase (4 min): at the start of the analysis, the electro valve system switches from ambient air to the reference air bag line, allowing the sensors to establish a baseline;
• During phase (3 min): the system then switches to the sample air bag line, enabling the sensors to analyze the sample;
• After phase (4 min): once the sample analysis is complete, the system reopens the reference air bag line to restore the baseline;
• Cleaning phase: at the end of the process, the system switches back to the ambient air line.

The ON/OFF electro valves are controlled by a microcontroller connected to a LabVIEW–based control system. This system ensures the precise activation or blocking of different flow rates as required during the experiment.

Each chamber has an internal volume of approximately 300 mL, and the three pumps operate at a flow rate of 300 mL/min. To ensure optimal sensor performance and reliable measurements, the aforementioned analysis times are chosen to allow adequate full gas exchange per chamber during the analysis. A custom electronic system with a LabVIEW GUI manages simultaneous data acquisition at a rate of 20 Hz, logging, PID flow control, and valve operation.

Each PEEK chamber houses eight MOS sensors of six types (TGS2602, TGS2603, TGS2610, TGS2611, TGS2620, and TGS2600, Figaro Engineering Inc., Osaka, Japan), with two sensor types duplicated per chamber. Four virtual chambers (V1–V4) are generated by removing duplicates from physical chambers A, B, and C (V1, V2, V3), and grouping duplicates together (V4), producing four nominally identical sensor arrays (Table 1) for CT experiments.

Table 1. Number and type of MOS sensors installed in three real chambers (A, B and C) and in the four “virtual” chambers (V1, V2, V3 and V4). V4 is formed by grouping the duplicates of chambers A, B and C. The virtual chambers are nominally identical: they contain the same number and type of sensors.

	Number of Sensors
Chamber	TGS2602	TGS2603	TGS2610	TGS2620	TGS2611	TGS2600
A	1×	1×	2×	1×	1×	2×
B	1×	1×	1×	2×	2×	1×
C	2×	2×	1×	1×	1×	1×
V1	1×	1×	1×	1×	1×	1×
V2	1×	1×	1×	1×	1×	1×
V3	1×	1×	1×	1×	1×	1×
V4	1×	1×	1×	1×	1×	1×

2.2. Sample Preparation

2.2.1. Human Urine Mixtures for E-Nose Classification Model Development

In this study, calibration transfer techniques using synthetic urine were investigated. The goal was to transfer classification models between nominally identical E–Noses. These models were developed to distinguish between different classes of human urine samples. Multiple samples of human urine were collected anonymously from different individuals to prepare six distinct batches, exhibiting natural variability. Each batch was created by pooling approximately samples from 15 different individuals, for a total volume of about 2 L per batch. Because the samples composing a batch came from different people, the chemical composition and concentrations of compounds vary, making the batches completely distinct from one another. Each of these six batches was then divided into three classes to be classified. A portion was kept unaltered (pure urine); in the two other portions 4-heptanone (0.625 μL/Lurine) and acetone (3.25 μL/Lurine) were added, respectively, in quantities that are in the range of those naturally found in human urine [17]. The purpose of this study was not to reproduce the full complexity of disease-related VOC profiles, but to mimic the varying levels of VOC biomarkers found in urine as indicators of various pathologies while keeping the experimental design relatively simple and well-controlled to focus on the methodological development. In this context, the choice of 4-heptanone and acetone was based on prior findings demonstrating a correlation between their varying concentrations with prostate cancer [13].

To prepare the enriched mixtures, individual urine samples were first combined in a single flask and homogenized using a magnetic stirrer. The mixture was then divided into three portions. Using a micropipette with disposable tips, the designated quantities of 4-heptanone and acetone were added to two portions, while the third remained unaltered. Each mixture was then thoroughly mixed again to ensure uniform distribution of the biomarkers. Aliquots of 20 mL (sufficient for a single analysis) were dispensed into plastic containers and stored at −18 °C. The entire preparation process is illustrated in Figure 3. Table 2 provides an overview of the batch (B1–B6) and class partitions.

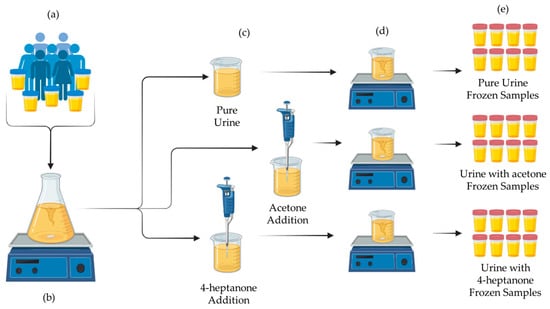
Figure 3. Schematic of the preparation steps. (a) Urine collection; (b) pooling and homogenization; (c) division and spiking; (d) final mixing; (e) aliquoting and freezing.

Table 2. Overview of the samples prepared from the six distinct urine batches (B1–B6). For each batch, three portions were created: pure urine, urine spiked with acetone, and urine spiked with 4-heptanone. The “ID” column indicates the specific class and batch for each sample.

Portion	Class	ID
1	Pure Urine	B1 pure
2		B2 pure
3		B3 pure
4		B4 pure
5		B5 pure
6		B6 pure
7	Urine spiked with acetone	B1 + acetone
8		B2 + acetone
9		B3 + acetone
10		B4 + acetone
11		B5 + acetone
12		B6 + acetone
13	Urine spiked with 4-heptanone	B1 + 4-heptanone
14		B2 + 4-heptanone
15		B3 + 4-heptanone
16		B4 + 4-heptanone
17		B5 + 4-heptanone
18		B6 + 4-heptanone

A key aspect of this study design was to capture variability both among the three biomarker conditions, representing distinct physio-pathological states, and across the six urine batches. This approach aimed to reflect real-world inter-patient variability, ensuring that the calibration model could differentiate biomarker classes while remaining robust to natural fluctuations in urine composition.

2.2.2. Synthetic Urine Mixtures as E-Nose Calibrants

The formulation of synthetic urine calibrants followed a systematic approach that integrated literature data on real urine with experimental validation. Seventy Scopus-indexed articles using keywords including “VOC”, “composition”, “urine”, and “metabolites” were analyzed. This comprehensive review aimed to identify the compounds typically present in urine. From all reported compounds, only a subset was retained. Selection criteria included high concentration levels, recurrence across multiple studies, and reported association with disease biomarkers. When a compound was detected but not quantified, its concentration was taken from the Human Metabolome Database [4].

Based on a preliminary screening, 17 compounds were initially selected: 4-heptanone, trimethylamine, phenol, p-cresol, ethanol, methanol, formaldehyde, acetaldehyde, phenylacetic acid, butyric acid, 2-butanone, acetone, acetic acid, isobutyric acid, propionic acid, benzoic acid, 2-pentanone, and 2-heptanone.

Urinary VOC concentrations were expressed in μmol per mmol of creatinine, which serves as an internal reference due to its role as a metabolic byproduct of muscle activity and its relatively constant daily excretion. The odor types and corresponding concentrations of the screened compounds are reported in the Supplementary Materials (Table S1).

Although 24-h urine collection is the gold standard to reduce dilution-related variability, it is time-consuming and inconvenient. Spot urine samples normalized to creatinine provide a practical alternative [18], reducing variability due to hydration differences, minimizing measurement errors, and enabling more reliable comparisons.

Using the average creatinine concentration in healthy adult males (${\mathrm{C}}_{\mathrm{av},\mathrm{creatinine}}$ = 1.26 g/L [19]) and the molecular weight of creatinine (${\mathrm{MW}}_{\mathrm{creatinine}}$ = 113.12 mg/mmol), the mass concentrations (${\mathrm{C}}_{\mathrm{i}}^{\mathrm{massive}}$) of all compounds were calculated Equation (1) from their average creatinine-normalized concentrations (${\mathrm{C}}_{\mathrm{av},\mathrm{i}}$) and molecular weights (${\mathrm{MW}}_{\mathrm{i}}$).

$${\mathrm{C}}_{\mathrm{i}}^{\mathrm{massive}}={\displaystyle \frac{{\mathrm{C}}_{\mathrm{av},\mathrm{i}}{\mathrm{MW}}_{\mathrm{i}}}{{\mathrm{MW}}_{\mathrm{creatinine}}}}{\mathrm{C}}_{\mathrm{av},\mathrm{creatinine}}$$

(1)

A simplified thermodynamic approach was applied to estimate headspace composition from liquid-phase concentrations. This approximation was deemed sufficient for the purposes of the present study, enabling the selection of a representative subset of compounds. Henry’s Law [20] was applied, assuming that each compound forms a binary mixture with water. The molar fraction of each compound in the liquid phase was calculated from its mass fraction and molecular weights. These molar fractions ranged between 10⁻⁶ and 10⁻¹⁰, indicating infinitely dilute solutions.

Temperature adjustments for the operational conditions (60 °C) were incorporated through the Van’t Hoff Equation (2).

$${\displaystyle \frac{\mathrm{d}\ln {\mathrm{H}}_{\mathrm{s}}}{\mathrm{d}\left(\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\mathrm{T}$}\right.\right)}}={\displaystyle \frac{-\Delta \mathrm{sol}\mathrm{H}}{\mathrm{R}}}$$

(2)

Henry’s constants at temperatures of 25 °C and 60 °C and the value of ${\displaystyle \frac{∆\mathrm{s}\mathrm{o}\mathrm{l}\mathrm{H}}{\mathrm{R}}}$, along with references from which they were extracted, are listed in the Supplementary Materials (Table S2).

Once Henry’s constants were calculated at the temperatures of interest (25 °C and 60 °C), assuming gas-phase ideality and atmospheric pressure, Henry’s Law was finally applied to estimate the corresponding concentration in the gas phase,

$${\mathrm{ppm}}_{\mathrm{i}}={\displaystyle \frac{{\mathrm{C}}_{\mathrm{i}}^{\mathrm{molar}}}{{\mathrm{H}}_{\mathrm{s},\mathrm{i}}\mathrm{P}}}\times {10}^{-6}$$

(3)

where ${\mathrm{C}}_{\mathrm{i}}^{\mathrm{molar}}$ is the molar concentration of compound i in the liquid phase (mol/L) obtained by dividing the mass concentration of each species by its molecular weight, ${\mathrm{H}}_{\mathrm{s},\mathrm{i}}$ is the Henry’s constant at the specified temperature (mol/(L·atm)), and P is the atmospheric pressure (1 atm). From these, the obtained concentration of the whole headspace was equal to 265 ppm at 25 °C and 72 ppm at 60 °C. Concentration of synthetic urine compounds in the headspace in ppm, gas phase molar fractions, and the values of ${\mathrm{C}}_{\mathrm{i}}^{\mathrm{molar}}$ are reported in Supplementary Materials (Table S3).

Based on these gas-phase concentrations, the ten most abundant VOCs were selected in order to design a realistic reference mixture for calibration purposes.

From the molar concentrations in urine, the corresponding volumetric concentrations to be dosed in the liquid phase were calculated,

$${\mathrm{C}}_{\mathrm{i}}^{\mathrm{vol}}={\displaystyle \frac{{\mathrm{C}}_{\mathrm{i}}^{\mathrm{molar}}\times {\mathrm{MW}}_{\mathrm{i}}}{{\mathrm{\rho }}_{\mathrm{i}}}}$$

(4)

where ${\mathrm{C}}_{\mathrm{i}}^{\mathrm{molar}}$ is the molar concentration, ${\mathrm{MW}}_{\mathrm{i}}$ is the molecular weight, and ${\mathrm{\rho }}_{\mathrm{i}}$ is the density of each compound.

Based on these calculations, the ten most abundant compounds were identified and considered as the basis of the Synthetic Urine Reference Recipe (Table 3), calculated from the average concentration values (in μmol per mmol of creatinine) reported in the literature.

Table 3. Synthetic Urine Reference Recipe.

VOCs	Concentration ($\mathbf{m}{\mathbf{L}}_{\mathbf{i}}/{\mathbf{L}}_{{\mathbf{H}}_2\mathbf{O}}$)
4-Heptanone	1.56 × 10−4
Trimethylamine	2.46 × 10−3
p-Cresol	5.38 × 10−2
Methanol	1.67 × 10−2
Acetaldehyde	1.62 × 10−3
2-Butanone	5.49 × 10−3
Acetone	3.22 × 10−3
Acetic acid	8.28 × 10−3
Isobutyric acid	3.54 × 10−3
Propionic acid	2.47 × 10−3

After the formulation of this first synthetic urine recipe, further experiments were carried out with the purpose of refining and optimising the initial recipe by formulating other recipes.

In this process, we decided to add ammonia to the compounds included in the initial formulation, because it is well-known to be one of the main components of urine headspace [21], and also because it represents the volatile fraction derived from urea, which is one of the most abundant compounds in liquid urine. Indeed, while the first formulation of synthetic urine was focused on urinary biomarkers potentially associated with specific pathological conditions, the experimental design was extended to more comprehensively replicate the overall composition of real urine. This broader approach aimed to better mimic the complex volatile compound profile of natural urine, beyond disease-related markers alone. Ammonia was thus included because of its high abundance in urine [21] and its role as a key volatile compound, substantially affecting both the chemical composition of urine headspace, its odour profile, and its potential effect on E-Nose sensor responses.

Refinements were guided by comparative analyses of synthetic versus real urine using E-Nose responses, PCA clustering, and PID sensor measurements.

Synthetic urine was prepared in a 1 L glass flask under controlled conditions to minimize volatile losses (an ice bath was used throughout preparation). Distilled water (950 mL) served as the base. Liquid compounds, including 4-heptanone, methanol, 2-butanone, acetone, acetic acid, isobutyric acid, propionic acid, and ammonia, were added with precooled pipette tips to reduce evaporation. Special handling procedures were applied to trimethylamine (chilled to favor pipette adhesion), p-cresol (dissolved in 5 mL of distilled water and heated below its flash point to liquefy before addition), and acetaldehyde (kept refrigerated, diluted in 5 mL of distilled water, and rapidly transferred to avoid evaporation due to its low boiling point).

Final volume was adjusted to 1 L, with thorough homogenization via magnetic stirring (~5 min). To prevent photodegradation, the flask was wrapped in aluminum foil and sealed. Aliquots (100 mL) were stored at −18 °C and thawed at ≤60 °C (~5 min) prior to analysis to minimize VOC loss.

2.3. E-Nose Classification Models

Data processing was performed using RStudio, specifically R version 4.4.0 (R Core Team, 2024), including preprocessing, feature extraction and selection, and classification model development.

2.3.1. Data Preprocessing

Raw resistance values (R) were normalized via R−R0 [22]. R0 (baseline resistance) was calculated as the average resistance during the stable “before” phase plateau (190–215 s). A 20-point moving average filter was applied to smooth the signal, balancing noise reduction and data integrity.

2.3.2. Feature Extraction

Features were extracted from the preprocessed resistance signals recorded during the “during” phase to reduce data dimensionality while preserving the most informative content. Extracted features included resistance ratios and differences at specific times, areas under the curve, single-point resistance values, resistance difference ratios, and exponential moving averages (EMA). Additional features came from the phase space (dR/dt vs. R), including phase integral, local minima, derivative and curvatures. Details are in the Supplementary Materials (Tables S4 and S5).

2.3.3. Feature Selection and Classification Models Development

The classification models were developed for each of the seven previously described chambers: chambers A, B, C (the “physical” chambers), V1, V2, V3, and V4 (the nominally identical “virtual” chambers with no sensor duplicates). Additional classification models were built by pairing the sensors of the virtual chambers (e.g., V1 with V2, etc.) to investigate how classification and CT performance vary under different configurations, particularly by duplicating each of the installed sensors. This created 6 additional coupled chambers (V1 + V2, V1 + V3, V1 + V4, V2 + V3, V2 + V4, and V3 + V4).

Outliers detected via T² and Q residuals were removed; analyses with hardware issues were excluded. After this, ~70 samples per configuration (7 single chambers and 6 pairs of chambers) constituted the whole dataset for that configuration. These samples include at least 3 replicates of samples with the same ID (see Table 2). The data processing is schematized in Figure 4.

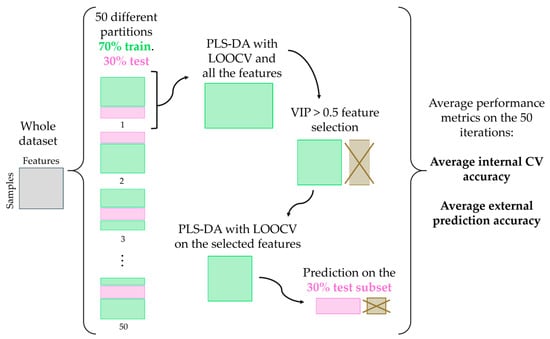
Figure 4. Pipeline for the development of classification models.

For each case, the dataset was partitioned into 50 different train–test splits (70% training, 30% testing), resulting in 50 distinct classification models, ensuring that the distribution of samples across different classes is balanced. This splitting is useful to avoid bias towards more frequent classes.

For each partition, PLS-DA [23] was applied to the scaled and centered training set, using leave-one-out cross-validation (LOOCV) [24,25,26]. Models with 1 to 10 latent variables (LVs) were evaluated, selecting the number maximizing cross-validation (CV) accuracy [27]. Accuracy was used as a figure of merit for the classification performance [28]. The VIP (Variable Importance in Projection) score was calculated for each feature, and features with VIP ≥ 0.5 were selected [29].

A final PLS-DA model was developed with the selected features and then tested on the 30% independent test set, obtaining the external prediction accuracy. Average CV accuracy values and test accuracy values were calculated on the various train/test splits. The purpose of partitioning the dataset into 50 splits and computing average accuracies was to evaluate the consistency and homogeneity of the dataset.

2.4. Calibration Transfer and Selection of Transfer Samples

Direct Standardization (DS) was selected as the CT technique due to its widespread use [30] and its suitability for synthetic samples, as it directly aligns responses between master and slave instruments using shared Transfer Samples. The novelty is the implementation of custom-made calibrant mixtures as Transfer Samples.

DS is based on the idea that the relationship between the master and slave sensor responses (${\mathrm{S}}_{\mathrm{M}}$ and ${\mathrm{S}}_{\mathrm{S}}$, respectively) can be described by a transformation matrix, F. The general relationship is expressed by Equation (5).

$${\mathrm{S}}_{\mathrm{M}}={\mathrm{S}}_{\mathrm{S}}\mathrm{F}$$

(5)

F is estimated with the so-called Transfer Samples (TS) analyzed on both instruments, by relating the matrix of responses of the slave instrument (${{\mathrm{S}}_{\mathrm{M}}}_{\mathrm{T}\mathrm{S}}$) to the matrix of responses of the master instrument (${{\mathrm{S}}_{\mathrm{S}}}_{\mathrm{T}\mathrm{S}}$), through the use of the pseudo-inverse (${\mathrm{S}}_{\mathrm{s}}^{+}$) [31] Equation (6).

$$\mathrm{F}={\mathrm{S}}_{{\mathrm{s}}_{\mathrm{TS}}}^{+}{\mathrm{S}}_{{\mathrm{M}}_{\mathrm{TS}}}$$

(6)

The new analyses performed with the slave are corrected with the transformation matrix, before prediction with the master’s model. All chamber combinations were tested; however, to illustrate the developed methodology, four master–slave configurations are discussed in detail: V1 → V2, V1 → V3, V1 → V4, V1 + V2 → V3 + V4.

Three synthetic urine recipes, chosen for their similarity to real urine sensor responses (see Section 3.2), were tested as Transfer Sample candidates. Various selection algorithms were used to determine which and how many Transfer Samples to employ (Table 4). Random selection was also performed to assess the benefit of algorithm-based selection.

Table 4. Methods employed for Transfer Samples selection.

Method	Inputs	Description	Advantages/Limitations
Kennard–Stone Algorithm (Mahalanobis distance)	Selected features	Samples ordered based on Mahalanobis distance, to homogeneously cover the analysis space.	Advantages: homogeneous coverage of the space; reproducible. Limitations: samples located at the edges of the space may represent atypical behaviours and reduce the representativeness of the main data distribution.
	2 PCs scores
	3 PCs scores
Extremes + Densest Cluster (DBSCAN)	2 PCs scores	Selection of extremes and central points from the densest cluster using DBSCAN	Advantages: balances diversity and density. Limitations: when few Transfer Samples are used, the selected set may overrepresent uncommon behaviours.
	3 PCs scores
Random Selection	Selected features	Random selection of Transfer Samples.	Advantages: provides baseline comparison; simple and unbiased towards feature distribution. Limitations: non–reproducible; typically lower and more unstable accuracy.

Transfer Sample selection was explored under four scenarios: (i) all synthetic mixtures combined, and (ii–iv) each of the three recipes individually. For each algorithm and scenario, Direct Standardization was applied iteratively with increasing numbers of Transfer Samples to compute the standardization matrix, adjust the slave data, and predict using the master model. Classification accuracy and the number of Transfer Samples were recorded at each step. The number of TS was chosen based on the maximum accuracy value.

2.4.1. Kennard–Stone (KS) Algorithm

Based on Mahalanobis distance [32], the KS algorithm selects representative Transfer Samples by uniformly covering the feature space. This method is schematized in Figure 5.

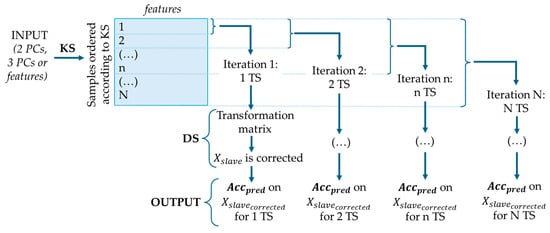
Figure 5. KS and DS procedure, where $X_{slav{e}_{corrected}}$ is the corrected dataset and $Ac{c}_{pred}$ is the accuracy of prediction.

Three input types were tested: selected features and PCA scores with 2 or 3 components. Samples were ordered to maximize spatial separation, starting from those farthest from the centroid. DS was applied iteratively, beginning with one Transfer Sample and progressively adding more according to the KS order. At each iteration, the corrected slave dataset was predicted using the master model, and both prediction accuracy and the number of Transfer Samples were recorded.

2.4.2. The Extremes + Densest Cluster Method

The Extremes + Densest Cluster method (Figure 6) was designed to select Transfer Samples that capture both the boundaries and the central, most representative region of the sample space.

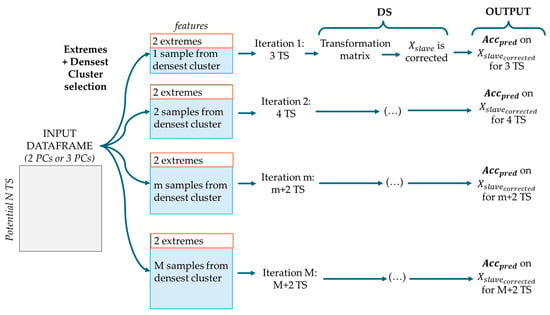
Figure 6. Extremes + Densest Cluster and DS procedure, where $X_{slav{e}_{corrected}}$ is the corrected dataset and $Ac{c}_{pred}$ is the accuracy of prediction, M is the total number of eligible samples from the densest cluster.

Two extreme points were selected: the one farthest from the origin and the one farthest from the previous (using Euclidean distance). The densest cluster was then identified via Density Based Spatial Clustering of Applications with Noise (DBSCAN) [33] based on PCA scores (2 or 3 components). At each iteration, the two extremes were fixed while samples from the densest cluster were considered at an incremental number, starting from the most central. DS correction was applied at each iteration, and prediction accuracy was recorded to evaluate performance and identify the optimal number of Transfer Samples.

2.4.3. Random Selection

In this method, Transfer Samples were selected randomly (Figure 7). Transfer Samples were randomly ordered based on five different seeds. DS correction was applied at each iteration, starting with one Transfer Sample and progressively adding more according to the random order, and prediction accuracy was recorded to evaluate performance and identify the optimal number of Transfer Samples.

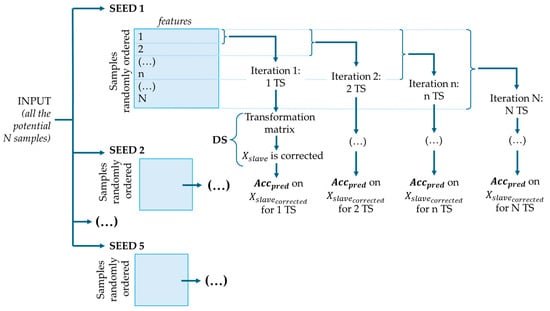
Figure 7. Random selection and DS procedure, where $X_{slav{e}_{corrected}}$ is the corrected dataset and $Ac{c}_{pred}$ is the accuracy of prediction.

3. Results

3.1. Development of E-Nose Classification Models

To illustrate the distribution of samples across classes and batches, PCA was performed on the data from one representative chamber. Figure 8 shows, for one of the chambers as example, the distribution of samples along the first two principal components: (a) labeled by class to highlight class separability, and (b) labeled by batch (B1–B6) to illustrate the distribution between batches.

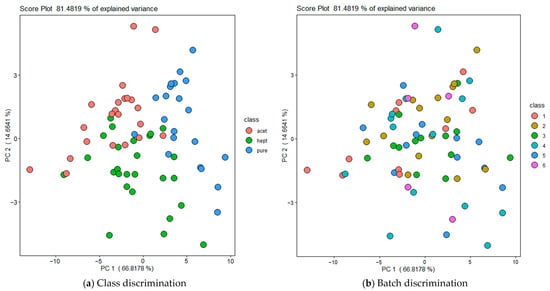
Figure 8. Principal Component Analysis (PCA) of all urine samples along the first two principal components. (a) Samples labeled by class (Pure, Acetone, 4-heptanone) to illustrate class separability. (b) Samples labeled by batch (B1–B6) to highlight natural variability between batches. Data shown correspond to one representative chamber; similar distributions were observed for the other chambers.

It should be highlighted that the PCA shown in Figure 8 was obtained using features selected to maximize discrimination among classes rather than discrimination among batches. However, it can be observed that the analyses of samples belonging to the same class and batch are not overlapping in the PCA space, indicating that sensors have responded differently to samples from the same batch. These differences can be explained considering that the measurements have been carried out over a prolonged time period (i.e., approximately six months from June to November 2024) and also other experimental factors such as minor variations in manual sample thawing and handling conditions, compressed air background composition, different aging of the PermaPure membranes between the reference air and urine lines, small fluctuations in pump flow rate, and possible minor changes in sensor baseline and sensitivity due to drift. This intra-batch variability justifies the adoption of a random data-splitting strategy, as samples from the same batch are sufficiently different from each other to be included in both training and test sets. As proof thereof, “leave-one-batch-out” cross validations produce comparable results in terms of classification accuracy.

PLS-DA models with VIP feature selection were developed using different configurations. For each configuration, the average internal cross-validation and external prediction accuracies (Table 5) were calculated on the 50 train-test partitions (70% train, 30% test) of the dataset (~70 samples). Feature selection was performed independently within each of the 50 train–test partitions, for each of the 13 configurations. Consequently, the number and identity of the selected features differed significantly from model to model.

Table 5. Results of the classification models in terms of averaged internal CV accuracy and external prediction accuracy for all the configurations evaluated in the study.

Chamber(s) Configuration	Average Internal Accuracy [%]	Internal Accuracy Range [%]	Average Prediction Accuracy [%]	Prediction Accuracy Range [%]
A	79.6	(78.5–80.7)	76.1	(73.3–78.8)
B	81.6	(80.6–82.5)	78.4	(75.9–80.9)
C	77.4	(76.1–78.7)	75.5	(72.6–78.4)
V1	80.6	(79.5–81.7)	74.8	(72.2–77.5)
V2	79.6	(78.5–80.6)	76.9	(74.6–79.3)
V3	77.3	(76–78.6)	73.5	(70.5–76.4)
V4	76.9	(75.8–78.1)	73.5	(70.8–76.1)
V1 + V2	82.8	(81.7–83.9)	81.3	(78.7–83.8)
V1 + V3	79.6	(78.3–80.8)	78.4	(75.6–81.2)
V1 + V4	80	(79–81)	77.3	(74.5–80)
V2 + V3	81.9	(80.8–83.1)	78.4	(75.9–80.9)
V2 + V4	82.5	(81.2–83.7)	81.4	(78.6–84.1)
V3 + V4	78.8	(77.7–80.1)	73.2	(70.2–76.1)

Overall, the results indicate that the PLS-DA classification models achieved solid performance across all configurations, with average internal and external accuracies ranging from 73% to 83%, even if the classification task was made more challenging by the natural variability between urine batches used for training and testing.

Moreover, the narrow intervals observed across performance metrics point out the homogeneity of the dataset and the robustness of the results.

Comparing physical chambers (A, B, C) with their virtual counterparts (V1, V2, V3) revealed no consistent performance trend. Similarly, models developed using paired combinations of virtual chambers (e.g., V1 + V2, V1 + V3, V2 + V4), which involved complete sensor duplication, did not yield significant improvements in classification accuracy. However, sensor duplication contributes to greater system stability and model robustness towards transfer learning, as it reduces the influence of individual sensor variability [34].

3.2. Synthetic Urine Mixtures

The main goal of this investigation was to determine whether the synthetic mixtures formulated within this study elicit sensor responses comparable to real urine samples, thereby enabling the identification of the most representative and suitable formulations. Several synthetic urine formulations were prepared with different concentrations. Details of each formulation, including concentration adjustments, are provided in the Supplementary Materials.

All recipes were tested using E-Nose and PID. First, raw sensor curves were observed, indicating the potential of some of the synthetic mixtures to be used as calibrant mixtures for the instruments. The same features extracted to build the classification models were extracted from the sensor responses obtained when exposed to synthetic urine mixtures. The sensor data from synthetic urine samples analyses were projected onto the PCA score plot constructed with the features extracted from the sensors’ responses exposed to the three real urine classes (Figure 9).

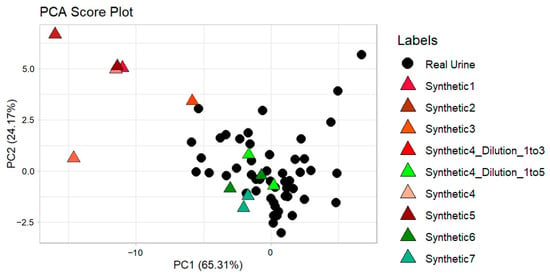
Figure 9. Synthetic urine samples from all the tested recipes projected onto the PCA score plot of the real urine data (pure urine, urine with 4-heptanone, and urine with acetone).

The PCA clearly identified the synthetic mixtures that best overlap with real urine samples and thus are considered to be most suitable to be used as Transfer Samples for CT. Specifically, Synthetic #4 (1:5 dilution), Synthetic #6, and Synthetic #7 (present in duplicates on the PCA score plot) show overlap with the real urine clusters. Also, multiple measurements were carried out with the PID analyzer. The results obtained confirmed the conclusion based on the E-Nose data: the average values of the PID analyzer in mV for synthetic urine mixtures #4 1:5, #6 and #7 are comparable to the mV average readings of real urine (Table 6).

Table 6. PID results for real urine and synthetic recipes.

	Synthetic #4 1:5 [mV]	Synthetic #6 [mV]	Synthetic #7 [mV]	Real Urine [mV]
AVERAGE:	110.6	164.6	103.8	107.0
STDEV:	15.25	18.42	8.71	14.37

The information obtained from the exploratory analysis of the data obtained from the E-Nose sensors analyses was coupled with the PID analyses. Based on this, the synthetic urine mixtures #4 1:5, #6 and #7 were considered as potential calibrants for the CT approach here developed. Their composition is reported in Table 7.

Table 7. Synthetic urine recipes selected for CT.

	#4 1:5	#6	#7
Liquid Species:	μL/Lwater	μL/Lwater	μL/Lwater
4-heptanone	0.10	0.10	0.02
Acetone	0.27	0.66	0.66
Trimethylamine	2.05	2.05	0.29
Acetaldehyde	0.27	0.50	0.50
2-butanone	0.92	0.92	0
Methanol	1.84	4.52	4.52
Acetic acid	1.38	1.59	1.59
Isobutyric acid	1.68	1.68	1.24
Propionic acid	0.41	0.41	0.17
Ammonia	24.50	24.50	24.50
Solid Species	mg/Lwater	mg/Lwater	mg/Lwater
P-cresol	9.23	9.23	1.45

3.3. Calibration Transfer Results

3.3.1. Transfer of Calibration Models Without Correction

Classification models trained on individual virtual chambers (V1–V4) and on paired combinations (e.g., V1 + V2, V2 + V4) were transferred to other configurations without applying correction methods. For each configuration (individual or paired chambers), the 50 models trained were tested on the entire dataset from each target configuration. Average prediction accuracies without Direct Standardization correction ranged between 38% and 52% across all chamber combinations. Full results for each model and prediction pair are provided in the Supplementary Materials (Table S6). As expected, all transfers resulted in a significant drop in performance, highlighting the necessity of applying CT techniques to align the target (slave) sensor data with that of the source (master).

3.3.2. Transfer Samples Selection and Direct Standardization Correction

Direct standardization (DS) was implemented to correct the slave data of each configuration before the transferring of the classification model of the corresponding master chamber(s). The DS results obtained for the following four configurations are presented: V1→V2; V1→V3; V1→V4; V1 + V2→V3 + V4. One of the 50 models developed with the virtual chamber V1 (master) was used to predict analyses performed with V2, V3, and V4 (slaves), after applying Direct Standardization to correct the slave data. A single model was chosen among the 50 because it would be computationally too expensive to test the transfer for every model and for every master–slave pair. The selected model represents the average predictive accuracy, i.e., its performance is close to the mean accuracy values across all models. Then, one of the 50 models developed with the pair V1 + V2 (master) was chosen with the same criteria and used to predict analyses performed with the pair V3 + V4 (slave), again corrected with Direct Standardization. As already mentioned, studying the transfer between coupled chambers (V1 + V2→V3 + V4) is done to analyze the effect of having all sensors duplicated on the CT performance in respect to the single chamber cases.

The PLS-DA classification model of the V1 master was developed with 7 latent variables achieving an internal accuracy of 88.2% (CI_95%: 76.2–94.4%) and an external prediction accuracy of 79% (CI_95%: 60.2–91.2%). The PLS-DA classification model of the V1 + V2 master was developed with 8 latent variables reaching an internal accuracy of 83% (CI_95%: 73.5–92.5%) and an external prediction accuracy of 79% (CI_95%: 60.2–91.2%). Thus, for both master configurations the target accuracy was 79%.

Prior to applying DS correction, the master model predicted the slave data for each of the four aforementioned transfers with accuracies of 37.14%, 40.85%, 54.93%, and 54.93%, respectively: performance levels that were consistently low, as anticipated.

The results of CT for the different configurations tested after DS implementation are reported in Table 8, Table 9, Table 10 and Table 11. The tables show the external prediction accuracy, obtained by applying the model calibrated on the master instrument to predict the overall dataset measured by the slave instrument. The corresponding number of Transfer Samples (TS) is also shown for each Transfer Sample selection algorithm and for each combination of synthetic urine mixtures to be used as TS.

Table 8. Calibration Transfer results for V1→V2. Accuracies above 70% are shown in bold.

V1→V2	Method	Input	All Synthetic Samples Together (from #4 1:5, #6, #7)	Samples of #6	Samples of #4 1:5	Samples of #7
	Kennard–Stone (Mahalanobis distance)	PC1 and PC2	57.1% 21 TS	70% 5 TS	54.3% 3 TS	62.8% 3 TS
		PC1, PC2 and PC3	67.1% 20 TS	55.7% 8 TS	50% 3 TS	62.9% 6 TS
		Features	51.4% 2 TS	60% 3 TS	51.4% 3 TS	55.7% 13 TS
	Extremes + Dense cluster (DBSCAN)	PC1 and PC2	57.1% 21 TS	74.3% 5 TS	54.3% 7 TS	68.6% 4 TS
		PC1, PC2 and PC3	80% 15 TS	74.3% 5 TS	52.8% 5 TS	75.7% 6 TS
	Random selection		74.3% 10 TS	62.8% 8 TS	50% 10 TS	52.8% 2 TS

Table 9. Calibration Transfer results for V1→V3. Accuracies above 70% are shown in bold.

V1→V3	Method	Input	All Synthetic Samples Together (from #4 1:5, #6, #7)	Samples of #6	Samples of #4 1:5	Samples of #7
	Kennard–Stone (Mahalanobis distance)	PC1 and PC2	73.2% 29 TS	61.9% 2 TS	43.6% 6 TS	56.3% 14 TS
		PC1, PC2 and PC3	77.5% 19 TS	66.2% 9 TS	56.3% 2 TS	57.8% 13 TS
		Features	71.8% 28 TS	59.2% 2 TS	52.1% 7 TS	50.7% 14 TS
	Extremes + Dense cluster (DBSCAN)	PC1 and PC2	71.8% 32 TS	50.7% 9 TS	47.9% 13 TS	53.5% 3 TS
		PC1, PC2 and PC3	71.8% 32 TS	50.7% 8 TS	46.5% 11 TS	64.8% 7 TS
	Random selection		66.2% 23 TS	47.9% 9 TS	42.3% 10 TS	63.4% 5 TS

Table 10. Calibration Transfer results for V1→V4. Accuracies above 70% are shown in bold.

V1→V4	Method	Input	All Synthetic Samples Together (from #4 1:5, #6, #7)	Samples of #6	Samples of #4 1:5	Samples of #7
	Kennard–Stone (Mahalanobis distance)	PC1 and PC2	75.4% 12 TS	47.7% 10 TS	63.1% 14 TS	53.9% 2 TS
		PC1, PC2 and PC3	64.6% 26 TS	63.1% 5 TS	63.1% 14 TS	53.9% 3 TS
		Features	69.2% 23 TS	53.9% 10 TS	63.1% 14 TS	64.6% 4 TS
	Extremes + Dense cluster (DBSCAN)	PC1 and PC2	64.6% 12 TS	61.5% 3 TS	56.9% 3 TS	70.8% 5 TS
		PC1, PC2 and PC3	70.8% 22 TS	61.5% 3 TS	56.9% 3 TS	70.8% 5 TS
	Random selection		67.7% 13 TS	63.1% 4 TS	56.9% 3 TS	64.6% 4 TS

Table 11. Calibration Transfer results for V1 + V2→V3 + V4. Accuracies above 70% are shown in bold.

V1 + V2 → V3 + V4	Method	Input	All Synthetic Samples Together (from #4 1:5, #6, #7)	Samples of #6	Samples of #4 1:5	Samples of #7
	Kennard–Stone (Mahalanobis distance)	PC1 and PC2	76.9% 8 TS	67.8% 6 TS	53.9% 7 TS	69.2% 12 TS
		PC1, PC2 and PC3	76.9% 11 TS	58.5% 7 TS	73.9% 9 TS	69.2% 12 TS
		Features	73.2% 8 TS	55.4% 3 TS	63.1% 8 TS	69.2% 12 TS
	Extremes + Dense cluster (DBSCAN)	PC1 and PC2	73.2% 30 TS	61.5% 5 TS	50.8% 3 TS	69.2% 12 TS
		PC1, PC2 and PC3	70.4% 8 TS	47.7% 11 TS	47.7% 11 TS	64.6% 8 TS
	Random selection		67.7% 8 TS	58.5% 3 TS	63.1% 7 TS	63.1% 9 TS

Random selection rarely achieved accuracies above 70%, succeeding in only 1 of 16 scenarios (V1→V2 with all mixtures), and even in that case it was outperformed by non-random strategies. This confirms that the Kennard–Stone (KS) and DBSCAN methods are effective and superior approaches for Transfer Sample selection in CT applications.

The four transfer scenarios yielded variable outcomes.

• V1→V2: Satisfactory prediction accuracies were achieved using all three synthetic mixtures combined, as well as with mixtures #6 and #7 individually. Mixture #6 performed best with a limited number of Transfer Samples (5 TS), while mixture #4 1:5 underperformed. The DBSCAN method with 3 PCs achieved the highest accuracy of 80% (CI_95%: 61.4–92.9%) using all mixtures combined with 15 TS.
• V1→V3: Only the combined use of all synthetic mixtures resulted in prediction accuracy values exceeding 70%. While most non-random methods performed well, the number of required TS was relatively high (19–32) also when algorithms for Transfer Samples selection were implemented. The best performance was achieved with the Kennard–Stone method with 3 PCs (77.5% accuracy, CI_95%: 60.2–90.3%, with 19 TS).
• V1→V4: performed well using all mixtures or mixture #7. The DBSCAN method with three PCs performed reliably, although the highest accuracy (i.e., 75.4% with CI_95%: 58.8–88.6%) was obtained using the KS method with 2 PCs.
• V1 + V2→V3 + V4: This configuration showed strong transferability, particularly with all mixtures used together. Fewer TS were required compared to V1→V3 and V1→V4 to achieve comparable accuracies. Using KS or DBSCAN (with 3 PCs), accuracies of up to 76.9% (CI_95%: 59.2–89.5%) were achieved with as few as 8 TS. This contrasts with V1→V3 and V1→V4, which required 19 and 12 TS, respectively, to achieve comparable results. These findings indicate that paired-chamber models, with duplicated sensors, enhance both robustness and transferability, ultimately reducing the number of TS necessary. Even mixture #4 (1:5), which had previously shown limited effectiveness, performed well under these conditions when combined with the KS method and 3 PCs.

Across all scenarios, the reported results reflect a balance between maximizing accuracy and minimizing the number of TS, highlighting the efficiency and practical value of the proposed CT strategies.

4. Discussion and Conclusions

In biomedical applications, where reproducibility, reliability, and regulatory compliance are of paramount importance, transfer learning can enhance the robustness of E-Nose systems by mitigating instrument-specific biases and reducing inter-device variability. This study presents a methodology for CT that bridges laboratory findings with real-world application. It allows predictive models to adapt from a source to a target device with minimal retraining and limited need for new labeled data. This is a major advantage in clinical settings where sample availability is constrained.

Direct Standardization (DS) using ad hoc formulated synthetic mixtures as Transfer Samples was tested and proved effective, especially where collecting many real human samples is challenging. The proposed CT approach significantly improved prediction accuracy in all master–slave configurations, as summarized in Table 12. Results comparable to the reference accuracy of 79% on the master device were achieved.

Table 12. Accuracy improvements for each of the four master–slave transfer when applying DS, number of Transfer Samples employed, and method/mixture(s) used.

Master–Slave	Prediction Accuracy Without DS Correction	Prediction Accuracy with DS Correction and No. of Transfer Samples (TS)	Method and Synthetic Mixture(s) Used
V1→V2	37.1% (CI95%: 20.2–58%)	80%–15 TS (CI95%: 61.4–92.9%)	Extremes + Dense Cluster (DBSCAN), 3 PCs. 3 mixtures together.
V1→V3	40.9% (CI95%: 23.6–62.5%)	77.5%–19 TS (CI95%: 60.2–90.3%)	KS, 3 PCs. 3 mixtures together.
V1→V4	54.9% CI95%: 36.2–75.4%)	75.4%–12 TS (CI95%: 58.8–88.6%)	KS, 2 PCs. 3 mixtures together.
V1 + V2 →V3 + V4	54.9% (CI95%: 36.2–75.4%)	76.9%–8 TS (CI95%: 59.2–89.5%)	KS, 2 PCs. 3 mixtures together.

Structured sample selection methods like Kennard–Stone (KS) and DBSCAN outperformed random selection: these findings confirm that the logic behind those ordered sample selection algorithms is well-suited for CT. Using PC scores instead of VIP-based features generally produced better results. The optimal number of PCs to be used depends on the variance distribution of the specific dataset. KS was more effective with evenly distributed data in PCA space, while DBSCAN excelled when a dense central cluster and peripheral outliers were present. Using three PCs with DBSCAN produced the highest number of successful transfers.

The combined use of all three formulations of synthetic mixtures resulted as the most effective. It captured both physiological (e.g., hydration, diet) and pathological (e.g., biomarker fluctuations) variability, thus improving model generalization, although some residual variability inherent to human real samples may still limit predictive performance.

If only one mixture can be used (due to resource constraints, time limitations, or logistical challenges), #6 and #7 are preferable to #4 1:5, which reached high accuracy in only one of 24 transfers. Mixtures #6 and #7 performed similarly well as individual transfer standards when paired with an appropriate sample selection method.

These findings apply to the other CT configurations tested using V2, V3, V4, and V3 + V4 as master datasets: except for V3 → V4, accuracies above 70% were achieved with 4–30 Transfer Samples, generally using all three mixtures. The worst performance was achieved for V4 probably because this “virtual” chamber consists of sensors placed in different physical chambers, underlying the presence of potential differences among the environments of the physical chambers A, B and C.

In general, considering that the training of an E-Nose typically requires hundreds of urine samples collected under precise and costly clinical protocols, a calibration transfer procedure based on a limited number of synthetic and therefore highly reproducible samples represents a potentially powerful strategy. It could be assumed that, as a further optimization of the proposed methodology for adoption in the clinical practice for calibration purposes, the realization of synthetic transfer mixtures could be to some extent be automatized, making the analysis relatively simple and fast. Such an approach could not only facilitate the transfer of training from one device to another but also enable the periodic re-calibration of a single device, effectively addressing the issue of sensor drift over time. Future developments should investigate alternative data processing pipelines using the dataset generated in this study, including diverse feature engineering strategies and modelling approaches. This could enhance the predictive accuracy and robustness of the master device model. Improving the performance of the initial model could strengthen its generalizability and yield better outcomes in CT applications.

Additionally, efforts should focus on optimizing sensor arrangements and exploring new synthetic formulations to further boost CT performance and overcome remaining challenges in standardizing E-Nose–based diagnostic tools. Refining the CT setup will also be essential to improve the repeatability of gas analyses over time and across different E–Nose chambers.

The decision of working with spiked urine samples allowed us to develop and optimize a robust methodology while minimizing the influence of typical confounding factors that arise when analysing samples from patients with different real pathologies. By controlling the sample composition, we could focus on the methodological aspects without the complexity introduced by disease-related biochemical differences. Future studies should aim to evaluate the applicability of the proposed approach to real patient cohorts, focusing on specific diseases (e.g., prostate cancer), to assess its performance in clinically relevant settings.

On the other hand, the proposed methodology could potentially be extended to other biological fluids containing biomarkers (e.g., breath, saliva), although this would require the development of suitable synthetic calibrants. Once appropriate synthetic mixtures are formulated to reproduce the characteristic VOC profiles of each biofluid, the same DS-based transfer procedure could potentially be applied. In the case of breath analysis, the formulation of a gaseous synthetic mixture would be necessary, which represents a more complex task.