Mixture of Species Sampling Models

Abstract

We introduce mixtures of species sampling sequences (mSSS) and discuss how these sequences are related to various types of Bayesian models. As a particular case, we recover species sampling sequences with general (not necessarily diffuse) base measures. These models include some “spike-and-slab” non-parametric priors recently introduced to provide sparsity. Furthermore, we show how mSSS arise while considering hierarchical species sampling random probabilities (e.g., the hierarchical Dirichlet process). Extending previous results, we prove that mSSS are obtained by assigning the values of an exchangeable sequence to the classes of a latent exchangeable random partition. Using this representation, we give an explicit expression of the Exchangeable Partition Probability Function of the partition generated by an mSSS. Some special cases are discussed in detail—in particular, species sampling sequences with general base measures and a mixture of species sampling sequences with Gibbs-type latent partition. Finally, we give explicit expressions of the predictive distributions of an mSSS.

1. Introduction

Discrete random measures have been widely used in Bayesian nonparametrics. Noteworthy examples of such random measures are the Dirichlet process [1], the Pitman–Yor process [2,3], (homogeneous) normalized random measures with independent increments (see, e.g., [4,5,6,7]), Poisson–Kingman random measures [8] and stick-breaking priors [9]. All the previous random measures are of the form

$$P=\sum _{j\ge 1}{p}_j^{\downarrow }{\delta }_{Z_j},$$

(1)

where ${\left(Z_j\right)}_{j\ge 1}$ are i.i.d. random variables taking values in a Polish space $(\mathbb{X},\mathcal{X})$ with common distribution H, and ${\left(p_j^{\downarrow }\right)}_{j\ge 1}$ are random positive weights in $[0,1]$, independent of ${\left(Z_j\right)}_{j\ge 1}$, such that $p_1^{\downarrow }\ge p_2^{\downarrow }\ge p_3^{\downarrow }\ge \dots$.

With a few exceptions—see, e.g., [1,4,10,11,12,13,14]—the base measure H of a random measure P in (1) is usually assumed to be diffuse, since this simplifies the derivation of various analytical results.

The diffuseness of H is assumed also to define the so-called species sampling sequences [15], exchangeable sequences whose directing measure is a discrete random probability of type (1). In this case, the diffuseness of H is motivated by the interpretation of species sampling sequences as sequences describing a sampling mechanism in discovering species from an unknown population. In this context, the $Z_j$s are the possible infinite different species, and the diffuseness of H ensures that there is no redundancy in this description.

On the other hand, from a Bayesian point of view, the diffuseness of H is not always reasonable and there are situations in which a discrete (or mixed) H is indeed natural. For example, recent interest in species sampling models with a spike-and-slab base measure emerged in [16,17,18,19,20,21] in order to induce sparsity and facilitate variable selection. Other models, which are implicitly related to species sampling sequences with non-diffused base measures, are mixtures of Dirichlet processes [10] and hierarchical random measures; see, e.g., [22,23,24,25].

The combinatorial structure of species sampling sequences derived from random measure (1) with general H have been recently studied in [14].

In this paper, we discuss some relevant properties of species sampling sequences with general base measures, as well as some further generalizations, namely mixtures of species sampling sequences with general base measures (mSSS).

An mSSS is an exchangeable sequence whose directing random measure is of type (1), where ${\left(Z_n\right)}_{n\ge 1}$ is a sequence of exchangeable random variables and ${\left(p_n^{\downarrow }\right)}_{n\ge 1}$ are random positive weights in $[0,1]$ with $p_1^{\downarrow }\ge p_2^{\downarrow }\ge p_3^{\downarrow }\ge \dots$, independent of ${\left(Z_n\right)}_{n\ge 1}$.

The core of the results that we prove in this paper is that all the mSSS can be obtained by assigning the values of an exchangeable sequence to the classes of a latent exchangeable random partition. We summarize the results of Section 3 in the next statement.

The following are equivalent:

• $\xi ={\left({\xi }_n\right)}_{n\ge 1}$ is an mSSS;
• with probability one ${\left({\xi }_n\right)}_{n\ge 1}={\left(Z_{I_n}\right)}_{n\ge 1}$, where ${\left(I_n\right)}_{n\ge 1}$ is a sequence of integer-valued random variables independent of the Zs such that, conditionally on $p^{\downarrow }:=(p_1^{\downarrow },p_2^{\downarrow },\dots )$, the $I_n$ are independent and $\mathbb{P}\{I_n=i|p^{\downarrow }\}=p_i^{\downarrow }$.
• with probability one ${\left({\xi }_n\right)}_{n\ge 1}:={\left(Z_{{\mathcal{C}}_n(\Pi )}^{\prime }\right)}_{n\ge 1}$, where ${\left(Z_n^{\prime }\right)}_{n\ge 1}$ is an exchangeable sequence with the same law of ${\left(Z_n\right)}_{n\ge 1}$, Π is an exchangeable partition, independent of ${\left(Z_n^{\prime }\right)}_{n\ge 1}$, obtained by sampling from ${\left(p_n^{\downarrow }\right)}_{n\ge 1}$, and ${\mathcal{C}}_n(\Pi )$ is the index of the block in Π containing n.

The partition $\Pi$ obtained from $p^{\downarrow }=(p_1^{\downarrow },p_2^{\downarrow },\dots )$ is the so-called paint-box process associated with $p^{\downarrow }$. In general, this partition, called the latent partition, does not coincide with the partition induced by the ${\left({\xi }_n\right)}_{n\ge 1}$. Note that also the sequence ${\left(Z_n^{\prime }\right)}_{n\ge 1}$ is latent, in the sense that it cannot be obtained if only ${\left({\xi }_n\right)}_{n\ge 1}$ is known. On the other hand, combining the information contained in ${\left(Z_n^{\prime }\right)}_{n\ge 1}$ and in $\Pi$, one obtains complete knowledge of ${\left({\xi }_n\right)}_{n\ge 1}$, and, in particular, of its clustering behavior. This last observation is essential for the development of all the other results presented in our paper.

The rest of the paper is organized as follows. Section 2 reviews some important results on species sampling models and exchangeable random partitions. Section 3 introduces mixtures of species sampling sequences and discusses how these sequences are related to various types of Bayesian models. In the same section, the stochastic representations for mixtures of species sampling sequences sketched above are proven. In Section 4, we provide an explicit expression of the Exchangeable Partition Probability Function (EPPF) of the partition generated by such sequences. This result is achieved considering two EPPFs arising from a suitable latent partition structure. Some special cases are further detailed. Finally, Section 5 deals with the predictive distributions of mixtures of species sampling sequences.

2. Background Materials

In this section, we briefly review some basic notions of exchangeable random partitions and species sampling models.

2.1. Exchangeable Random Partitions

A partition ${\pi }_n$ of $\left[n\right]:=\{1,\dots ,n\}$ is an unordered collection $\{{\pi }_{1,n},\dots ,{\pi }_{k,n}\}$ of disjoint non-empty subsets (blocks) of $\{1,\dots ,n\}$ such that ${\cup }_{j=1}^k{\pi }_{j,n}=\left[n\right]$. A partition ${\pi }_n=\{{\pi }_{1,n},{\pi }_{2,n},\dots ,{\pi }_{k,n}\}$ has $|{\pi }_n|:=k$ blocks (with $1\le |{\pi }_n|\le n$) and $|{\pi }_{c,n}|$, with $c=1,\dots ,k$, is the number of elements of the block c. We denote by ${\mathcal{P}}_n$ the collection of all partitions of $\left[n\right]$ and, given a partition, we list its blocks in ascending order of their smallest element, i.e., in order of their appearance. For instance, we write $\left[\right(1,3),(2,4),(5\left)\right]$ and not $\left[\right(2,4),(3,1),(5\left)\right]$.

A sequence of random partitions, $\Pi ={\left({\Pi }_n\right)}_{n\ge 1}$, defined on a common probability space, is called a random partition of $\mathbb{N}$ if, for each n, the random variable ${\Pi }_n$ takes values in ${\mathcal{P}}_n$ and, for $m<n$, the restriction of ${\Pi }_n$ to ${\mathcal{P}}_m$ is ${\Pi }_m$ (consistency property).

In order to define an exchangeable random partition, given a permutation $\rho$ of $\left[n\right]$ and a partition ${\pi }_n$ in ${\mathcal{P}}_n$, we denote by $\rho \left({\pi }_n\right)$ the partition with blocks $\{\rho \left(j\right):j\in {\pi }_{i,n}\}$ for $i=1,\dots ,|{\pi }_n|$. A random partition of $\mathbb{N}$ is said to be exchangeable if ${\Pi }_n$ has the same distribution of $\rho \left({\Pi }_n\right)$ for every n and every permutation $\rho$ of $\left[n\right]$. In other words, its law is invariant under the action of all permutations (acting on ${\Pi }_n$ in the natural way).

The law of any exchangeable random partition on $\mathbb{N}$ is completely characterized by its Exchangeable Partition Probability Function (EPPF); in other words, there exists a unique symmetric function $\mathfrak{q}$ on the integers such that, for any partition ${\pi }_n$ in ${\mathcal{P}}_n$,

$$\mathbb{P}\{{\Pi }_n={\pi }_n\}=\mathfrak{q}\left(|{\pi }_{1,n}|,\dots ,|{\pi }_{k,n}|\right)$$

(2)

where k is the number of blocks in ${\pi }_n$. In the following, we shall write $\Pi \sim \mathfrak{q}$ to denote an exchangeable partition of $\mathbb{N}$ with EPPF $\mathfrak{q}$. Note that an EPPF is indeed a family of symmetric functions ${\mathfrak{q}}_k^n(·)$ defined on ${\mathcal{C}}_{n,k}=\{(n_1,\dots ,n_k)\in {\mathbb{N}}^k:{\sum }_{i=1}^k{n}_i=n\}$. To simplify the notation, we write $\mathfrak{q}$ instead of ${\mathfrak{q}}_k^n$. Alternatively, one can assume that $\mathfrak{q}$ is a function on ${\cup }_{n\in \mathbb{N}}{\cup }_{k=1}^n{\mathcal{C}}_{n,k}$. See [26].

Given a sequence of random variables $X={\left(X_j\right)}_{j\ge 1}$ taking values in some measurable space, the random partition ${\Pi }^{*}\left(X\right)$ induced by X is defined as the random partition obtained by the equivalence classes under the random equivalence relation $i\left(\omega \right)\sim j\left(\omega \right)$ if and only if $X_i\left(\omega \right)=X_j\left(\omega \right)$. One can check that a partition induced by an exchangeable random sequence is an exchangeable random partition.

Recall that, by de Finetti’s theorem, a sequence $X={\left(X_n\right)}_{n\ge 1}$ taking values in a Polish space $(\mathbb{X},\mathcal{X})$ is exchangeable if and only if the $X_n$s, given some random probability measure Q on $\mathcal{X}$, are conditionally independent with common distribution Q. Moreover, the random probability Q, known as the directing random measure of X, is the almost sure limit (with respect to weak convergence) of the empirical process $\frac{1}{n}{\sum }_{i=1}^n{\delta }_{X_i}$.

Based on de Finetti’s theorem, Kingman’s correspondence theorem sets up a one-to-one map between the law of an exchangeable random partition on $\mathbb{N}$ (i.e., its EPPF) and the law of random ranked weights $p^{\downarrow }={\left(p_j^{\downarrow }\right)}_{j\ge 1}$ satisfying $1\ge p_1^{\downarrow }\ge p_2^{\downarrow }\ge \cdots \ge 0$ and ${\sum }_j{p}_j^{\downarrow }\le 1$ (with probability one). To state the theorem, recall that a partition $\Pi$ is said to be generated by a (possibly random) $p^{\downarrow }$, if it is generated by a sequence ${\left(I_n\right)}_{n\ge 1}$ of integer-valued random variables that are conditionally independent given $p^{\downarrow }$ with conditional distribution

$$\mathbb{P}\{I_n=i|p^{\downarrow }\}:=\left\{\begin{array}{cc}1-\sum _{j\ge 1}{p}_j^{\downarrow }\hfill & \mathrm{if}i=-n\hfill \\ p_i^{\downarrow }\hfill & \mathrm{if}i\ge 1,\hfill \end{array}\right.$$

(3)

Note that $1-{\sum }_{j\ge 1}{p}_j^{\downarrow }$ is the magnitude of the so-called “dust” component; indeed, each $I_n$ sampled from this part, i.e., $I_n=-n$, contributes to a singleton n in the partition $\Pi$. A consequence is that if ${\sum }_{j\ge 1}{p}_j^{\downarrow }=1$ a.s., the partition $\Pi$ has no singleton. The partition ${\Pi }^{*}\left(I\right)$ is sometimes referred to as the $p^{\downarrow }$-paintbox process; see [27].

Let $\nabla :=\{p_j^{\downarrow }\in [0,1]:p_1^{\downarrow }\ge p_2^{\downarrow }\ge \dots ,{\sum }_{j\ge 1}{p}_j^{\downarrow }\le 1\}$. We are now ready to state Kingman’s theorem.

Theorem 1

([28]). Given any exchangeable random partition Π with EPPF $\mathfrak{q}$, denote by ${\Pi }_{j,n}^{\downarrow }$ the blocks of the partition rearranged in decreasing order with respect to the number of elements in the blocks of ${\Pi }_n$. Then,

$$\underset{n}{lim}{\left(\frac{|{\Pi }_{j,n}^{\downarrow }|}{n}\right)}_{j\ge 1}={\left(p_j^{\downarrow }\right)}_{j\ge 1}a.s.$$

(4)

for some random $p^{\downarrow }={\left(p_j^{\downarrow }\right)}_{j\ge 1}$ taking values in ∇. Moreover, on a possibly enlarged probability space, there is a sequence of integer-valued random variables $I={\left(I_n\right)}_{n\ge 1}$, conditionally independent given $p^{\downarrow }$, such that (3) holds and the partition induced by I is equal to Π a.s.

Kingman’s theorem is usually stated in a slightly weaker form (see, e.g., Theorem 2.2 in [26]) and the equality between ${\Pi }^{*}\left(I\right)$ and $\Pi$ is given in law. The previous “almost sure” version can be easily derived by inspecting the proof of Kingman’s theorem given in [29].

A consequence of the previous theorem is that $\mathfrak{q}\mapsto \mathrm{Law}\left(p^{\downarrow }\right)$ for $p^{\downarrow }$ in (4) defines a bijection from the set of the EPPF and the laws on ∇.

If $p^{\downarrow }$ is proper, i.e., ${\sum }_{j\ge 1}{p}_j^{\downarrow }=1$ a.s., then Kingman’s correspondence between $p^{\downarrow }$ and the EPPF $\mathfrak{q}$ can be made explicit by

$$\mathfrak{q}(n_1,\dots ,n_k)=\sum _{(j_1,\dots ,j_k)\in {\mathbb{N}}_k}\mathbb{E}\left[\prod _{i=1}^k{\left(p_{j_i}^{\downarrow }\right)}^{n_i}\right].$$

(5)

where ${\mathbb{N}}_k$ is the set of all ordered k-tuples of distinct positive integers. See Chapter 2 [26].

Given an EPPF $\mathfrak{q}$, one deduces the corresponding sequence of predictive distributions, which is the sequence of conditional distributions

$$P\{{\Pi }_{n+1}={\pi }_{n+1}|{\Pi }_n={\pi }_n\}$$

when $\Pi \sim \mathfrak{q}$. Starting with ${\Pi }_1=\left\{1\right\}$, given ${\Pi }_n={\pi }_n$ (with $|{\pi }_n|=k$), the conditional probability of adding a new block (containing $n+1$) to ${\Pi }_n$ is

$${\nu }_n\left({\pi }_n\right)={\nu }_n\left(\right|{\pi }_{1,n}|,\dots ,|{\pi }_{k,n}\left|\right):=\frac{\mathfrak{q}\left(\right|{\pi }_{1,n}|,\dots ,|{\pi }_{k,n}|,1)}{\mathfrak{q}\left(\right|{\pi }_{1,n}|,\dots ,|{\pi }_{k,n}\left|\right)};$$

(6)

while the conditional probability of adding $n+1$ to the ℓ-th block of ${\Pi }_n$ (for $\ell =1,\dots ,k$) is

$${\omega }_{n,\ell }\left({\pi }_n\right)={\omega }_{n,\ell }\left(\right|{\pi }_{1,n}|,\dots ,|{\pi }_{k,n}\left|\right):=\frac{\mathfrak{q}\left(\right|{\pi }_{1,n}|,\dots ,|{\pi }_{\ell ,n}|+1,\dots ,|{\pi }_{k,n}\left|\right)}{\mathfrak{q}\left(\right|{\pi }_{1,n}|,\dots ,|{\pi }_{k,n}\left|\right)}.$$

(7)

2.2. Species Sampling Models

A species sampling random probability (SSrp) is a random probability of the form

$$P=\sum _{j\ge 1}{p}_j{\delta }_{Z_j}+(1-\sum _{j\ge 1}{p}_j)H$$

(8)

where ${\left(Z_j\right)}_{j\ge 1}$ are i.i.d. random variables taking values in a Polish space $(\mathbb{X},\mathcal{X})$ with common distribution H, and ${\left(p_j\right)}_{j\ge 1}$ are random positive weights in $[0,1]$, independent of ${\left(Z_j\right)}_{j\ge 1}$, such that ${\sum }_{j\ge 1}{p}_j\le 1$ with probability one. These random probability measures are also known as Type III random probability measures; see [30].

Given the SSrp in (8), let ${\left(p_j^{\downarrow }\right)}_{j\ge 1}$ be the ranked sequence obtained from ${\left(p_j\right)}_{j\ge 1}$ rearranging the $p_j$s in decreasing order. One can always write

$$P=\sum _{j\ge 1}{p}_j^{\downarrow }{\delta }_{{\tilde{Z}}_j}+(1-\sum _{j\ge 1}{p}_j^{\downarrow })H$$

(9)

where ${\left({\tilde{Z}}_j\right)}_{j\ge 1}$ is a suitable random reordering of the original sequence ${\left(Z_j\right)}_{j\ge 1}$. It is easy to check that ${\left({\tilde{Z}}_j\right)}_{j\ge 1}$ are i.i.d. random variables with law H independent of ${\left(p_j^{\downarrow }\right)}_{j\ge 1}$. Hence, H and the EPPF $\mathfrak{q}$ associated via Kingman’s correspondence with ${\left(p_j^{\downarrow }\right)}_{j\ge 1}$ completely characterize the law of P, from now on denoted by $SSrp(\mathfrak{q},H)$.

$SSrp$ with H diffuse are also characterized as directing random measures of a particular type of exchangeable sequences, known as species sampling sequences. Let $\mathfrak{q}$ be an EPPF and H a diffuse probability measure on a Polish space $\mathbb{X}$. An exchangeable sequence $\xi :={\left({\xi }_n\right)}_n$ taking values in $\mathbb{X}$ is a species sampling sequence, $SSS(\mathfrak{q},H)$, if the law of ${\left({\xi }_n\right)}_n$ is characterized by the predictive system:

• (PS1) $\mathbb{P}\{{\xi }_1\in dx\}=H\left(dx\right)$;
• (PS2) the conditional distribution of ${\xi }_{n+1}$ given $({\xi }_1,\dots ,{\xi }_n)$ is

  $$\mathbb{P}\left\{{\xi }_{n+1}\in dx|{\xi }_1,\dots ,{\xi }_n\right\}=\sum _{c=1}^K{\omega }_{n,c}{\delta }_{{\xi }_c^{*}}\left(dx\right)+{\nu }_{n}H\left(dx\right),$$

  where $({\xi }_1^{*},\dots ,{\xi }_K^{*})$ is the sequence of distinct observations in order of appearance, ${\omega }_{n,c}={\omega }_{n,c}\left(\right|{\Pi }_{1,n}|,\dots ,|{\Pi }_{K,n}\left|\right)$, ${\nu }_n={\nu }_n\left(\right|{\Pi }_{1,n}|,\dots ,|{\Pi }_{K,n}\left|\right)$, $K=|{\Pi }_n|$, ${\Pi }_n$ is the random partition induced by $({\xi }_1,\dots ,{\xi }_n)$ and ${\omega }_{n,c}$ and ${\nu }_n$ are related to the $\mathfrak{q}$ by (6) and (7).

We summarize here some results proven in [15].

Proposition 1

([15]). Let H be a diffuse probability measure; then, an exchangeable sequence ${\left({\xi }_n\right)}_n$ is characterized by (PS1)–(PS2) if and only if its directing random measure is an $SSrp(\mathfrak{q},H)$.

As noted in [29], the partition induced by any exchangeable sequence taking values in $\mathbb{X}$ with directing measure $\tilde{\mu }$ depends only on the sequence $\tilde{\mu }\left({\tilde{x}}_j\right)$, where ${\tilde{x}}_j$ are the random atoms forming the discrete component of $\tilde{\mu }$ and ordered in such a way that $\tilde{\mu }\left({\tilde{x}}_1\right)\ge \tilde{\mu }\left({\tilde{x}}_2\right)\ge \dots$. Combining this observation with the previous proposition, one can see that, when H is diffuse and $\xi$ is an $SSS(\mathfrak{q},H)$, the partition ${\Pi }^{*}\left(\xi \right)$ is equal (a.s.) to ${\Pi }^{*}\left(I\right)$ (where I is defined as in Kingman’s theorem) and ${\Pi }^{*}\left(\xi \right)$ has EPPF $\mathfrak{q}$. Note that [29] defines the $p^{\downarrow }$-paintbox process as any random partition ${\Pi }^{*}\left(\xi \right)$ where $\xi$ is an exchangeable sequence with directing random measure (9) and H is a diffuse measure.

One can show (see the proof of Proposition 13 in [15]) that an $SSS(\mathfrak{q},H)$ can be obtained by assigning the values of an i.i.d. sequence ${\left(Z_n\right)}_n$ with distribution H to the classes of an independent exchangeable random partition with EPPF $\mathfrak{q}$. More formally, for a random partition $\Pi$, let ${\mathcal{C}}_n(\Pi )$ be the random index denoting the block containing n, i.e.,

$${\mathcal{C}}_n(\Pi )=c\mathrm{if}n\in {\Pi }_{c,n}$$

or equivalently if $n\in {\Pi }_{c,j}$ for some (and hence all) $j\ge n$. If $Z^{\prime }={\left(Z_n^{\prime }\right)}_n$ is an i.i.d. sequence with law H (diffuse), $\Pi$ is an exchangeable partition with $\Pi \sim \mathfrak{q}$, and $Z^{\prime }$ and $\Pi$ are stochastically independent, then

$${\left({\xi }_n\right)}_{n\ge 1}:={\left(Z_{{\mathcal{C}}_n(\Pi )}^{\prime }\right)}_{n\ge 1}$$

(10)

is an $SSS(\mathfrak{q},H)$. Note that the $Z_n^{\prime }$s appearing in (10) are not the same $Z_n$s of (8), although they have the same law.

It is worth mentioning that the original characterization given in [15] of species sampling sequences is stronger than the one summarized here. Indeed, the original definition of SSS is given using a slightly weaker predictive assumption. For details, see Proposition 13 and the discussion following Proposition 11 in [15].

In summary, when H is diffuse, one can build a species sampling sequence ${\left({\xi }_n\right)}_n$ by one of the following equivalent constructions:

• using the system of predictive distributions (PS1)–(PS2);
• sampling (conditionally) i.i.d. variables from (8);
• combining an i.i.d. sequence from H with an exchangeable random partition by (10).

3. Mixture of Species Sampling Models

We now discuss some possible generalizations of the notion of species sampling sequences and we show that the three constructions presented above are no more equivalent in this setting.

3.1. Definitions and Relation to Other Models

Exchangeable sequences sampled from an $SSrm$ with a general base measure, also known as generalized species sampling sequences ($gSSS$), have been introduced and studied in [14,25].

Definition 1

($gSSS(\mathfrak{q},H)$). ${\left({\xi }_n\right)}_{n\ge 1}$ is a $gSSS(\mathfrak{q},H)$ if it is an exchangeable sequence with directing random measure P, where $P\sim SSrp(\mathfrak{q},H)$, H being any measure on $(\mathbb{X},\mathcal{X})$ (not necessarily diffuse).

Clearly, a $gSSS(\mathfrak{q},H)$ with H diffuse is an $SSS(\mathfrak{q},H)$. On the contrary, if $\xi$ is a $gSSS(\mathfrak{q},H)$ with H non-diffuse, (PS1)–(PS2) are no longer true. Moreover, the EPPF of the random partition induced by $\xi$ with H non-diffuse is not $\mathfrak{q}$. The relation between the partition induced by $\xi$ and $\mathfrak{q}$ has been studied in [14].

In [25], the definition of $gSSS(\mathfrak{q},H)$ with H not necessarily diffuse was motivated by an interest in defining the class of the so-called hierarchical species sampling models. If ${\xi }_1,{\xi }_2,\dots$ are exchangeable random variables with a directing random measure of hierarchical type, one has that

$$\begin{array}{cc}\hfill {\xi }_n|P_1,P_0& \stackrel{i.i.d.}{\sim }{P}_{1}n\ge 1\hfill \\ \hfill P_1|P_0& \sim SSrp(\mathfrak{q},P_0)\hfill \\ \hfill P_0& \sim SSrp({\mathfrak{q}}_0,H_0).\hfill \end{array}$$

In order to understand why the general definition of $gSSS(\mathfrak{q},H)$ is useful in this context, note that, even if $H_0$ is diffuse and ${\mathfrak{q}}_0$ is proper (i.e., the $p^{\downarrow }$ associated with ${\mathfrak{q}}_0$ by Kingman’s correspondence are proper), the conditional distribution of ${\left[{\xi }_n\right]}_{n\ge 1}$ given $P_0$ is not an $SSS$, since $P_0$ is a.s. a purely atomic probability measure on $\mathcal{X}$. Moreover, assuming that $\mathfrak{q}$ is proper, we can write

$$P_1=\sum _j{p}_{j1}{\delta }_{Z_j}$$

where $Z_j$ are conditionally i.i.d. with common distribution $P_0$, given $P_0$, and ${\left(p_{j1}\right)}_j$ are associated by Kingman’s correspondence with the EPPF $\mathfrak{q}$. In other words, in this case, ${\left({\xi }_n\right)}_{n\ge 1}$ are exchangeable with directing random measure $P_1={\sum }_j{p}_{j1}{\delta }_{Z_j}$, where ${\left(p_{j1}\right)}_j$ and ${\left(Z_j\right)}_j$ are independent and ${\left(Z_j\right)}_j$ are exchangeable with directing measure $P_0\sim SSrp({\mathfrak{q}}_0,H_0)$.

The previous observation suggests a further generalization of species sampling sequences.

Definition 2

($mSSS$). We say that ${\left({\xi }_n\right)}_{n\ge 1}$ is a mixture of species sampling sequences ($mSSS$) if it is an exchangeable sequence with directing random measure

$$P=\sum _{j\ge 1}{p}_j^{\downarrow }{\delta }_{Z_j}+(1-\sum _{j\ge 1}{p}_j^{\downarrow })\tilde{H}$$

(11)

where $Z:={\left(Z_n\right)}_{n\ge 1}$ is an exchangeable sequence with directing random measure $\tilde{H}$, $p^{\downarrow }$ a sequence of random weight in ∇ with EPPF $\mathfrak{q}$ such that $P\{{\sum }_{j\ge 1}{p}_j^{\downarrow }>0\}>0$, $(Z,\tilde{H})$ and $p^{\downarrow }$ are stochastically independent.

First of all, note that $gSSS(\mathfrak{q},H)$ is a particular case of Definition 2, obtained from a deterministic $\tilde{H}=H$. Moreover, Definition 2 can be seen as a mixture of $gSSS$. Indeed, if $\xi ={\left({\xi }_n\right)}_{n\ge 1}$ is as in Definition 2 and $\tilde{H}$ is the directing random measure of ${\left(Z_n\right)}_n$, then the conditional distribution of $\xi$ given $\tilde{H}$ is a $gSSS(\mathfrak{q},\tilde{H})$. This motivates the name “mixture of species sampling sequences”.

It is worth noticing that one can also consider more general mixtures of SSS. The most general mixture one can take into consideration leads to a random probability measure of the form (11), where $Z:={\left(Z_n\right)}_{n\ge 1}$ are exchangeable random variables with directing random measure $\tilde{H}$, $p^{\downarrow }$ is a sequence of random weight in ∇ such that $P\{{\sum }_{j\ge 1}{p}_j^{\downarrow }>0\}>0$, where $[Z,\tilde{H}]$, and $p^{\downarrow }$ are not necessarily stochastically independent.

As an example of this more general situation, we describe the so-called mixtures of Dirichlet processes as defined in [10]. Recall that a Dirichlet process $P\sim \mathcal{D}ir\left(\alpha \right)$ is defined as a random probability measure characterized by the system of finite n-dimensional distributions

$$\mathbb{P}\{(P\left(A_1\right),\dots ,P\left(A_n\right))\in ·\}=Dir\left(·;\alpha \left(A_1\right),\dots ,\alpha \left(A_n\right)\right)\forall n\ge 1,\forall A_i\in \mathcal{X}$$

where $Dir(·;a_1,\dots ,a_n)$ is the Dirichlet measure (on the $n-1$ simplex) of parameters $a_1,\dots ,a_n$ and $\alpha$ is a finite $\sigma$-additive measure on $\mathcal{X}$. It is well known that a Dirichlet process is an $SSrp(\mathfrak{q},H)$ for $H(·)=\alpha (·)/\alpha \left(\mathbb{X}\right)$ and

$$\mathfrak{q}(n_1,\dots ,n_k)=\frac{\alpha {\left(\mathbb{X}\right)}^k}{{\left(\alpha \left(\mathbb{X}\right)\right)}_n}\prod _{c=1}^k(n_c-1)!,$$

(12)

where ${\left(x\right)}_n=x(x+1)\dots (x+n-1)$ is the rising factorial (or Pochhammer polynomial); see [2,31]. A mixture of Dirichlet processes is defined in [10] as a random probability measure P characterized by the n-dimensional distributions

$$\mathbb{P}\{(P\left(A_1\right),\dots ,P\left(A_n\right))\in ·\}={\int }_{U}Dir\left(·;{\alpha }_u\left(A_1\right),\dots ,{\alpha }_u\left(A_n\right)\right)Q\left(du\right)$$

(13)

where, now, $(u,A)\mapsto {\alpha }_u\left(A\right)$ is a kernel measure on $U\times \mathcal{X}$ (in particular, $A\mapsto {\alpha }_u\left(A\right)$ is a finte $\sigma$-additive measure on $\mathcal{X}$ for every $u\in U$), $(U,\mathcal{U})$ is a (Borel) regular space (e.g., a Polish space) and Q is a probability measure on $\mathcal{U}$.

Using the fact that a Dirichlet process is the $SSrp$ described above, one can prove that any mixture of Dirichlet processes has a representation of the form (11), where $\left({\left(Z_n\right)}_{n\ge 1}\tilde{H}\right)$ and $p^{\downarrow }$ are stochastically dependent. More precisely, the joint law of $(\tilde{H},{\left(Z_n\right)}_{n\ge 1},p^{\downarrow })$ is characterized by the law of the (augmented) random element

$$(\tilde{H},{\left(Z_n\right)}_{n\ge 1},p^{\downarrow },\tilde{u})$$

given by the following:

• $\tilde{u}$ is a random variable taking values in U with law Q;
• $\tilde{H}(·):={\alpha }_{\tilde{u}}(·)/{\alpha }_{\tilde{u}}\left(\mathbb{X}\right)$;
• ${\left(Z_n\right)}_{n\ge 1}$ are exchangeable random variables with directing random measure $\tilde{H}$;
• $p^{\downarrow }$ is sequence of random weight in ∇ such that $P\{{\sum }_{j\ge 1}{p}_j^{\downarrow }=1\}=1$ and the conditional distribution of $p^{\downarrow }$ given $\tilde{u}$ depends only on ${\alpha }_{\tilde{u}}\left(\mathbb{X}\right)$. In particular, the (conditional) EPPF associated with the law of $p^{\downarrow }$ given $\tilde{u}$ has the form

  $$\mathfrak{q}(n_1,\dots ,n_k|\tilde{u}):=\frac{{\alpha }_{\tilde{u}}{\left(\mathbb{X}\right)}^k}{{\left({\alpha }_{\tilde{u}}\left(\mathbb{X}\right)\right)}_n}\prod _{c=1}^k(n_c-1)!$$

  (14)

Note that the marginal EPPF of the $p^{\downarrow }$, obtained by integrating (14) with respect to the law of $\tilde{u}$, is

$$\mathfrak{q}(n_1,\dots ,n_k)=\prod _{c=1}^k(n_c-1)!{\int }_U\frac{{\alpha }_u{\left(\mathbb{X}\right)}^k}{{\left({\alpha }_u\left(\mathbb{X}\right)\right)}_n}Q\left(du\right).$$

(15)

Without further assumptions, a mixture of Dirichlet processes is a mixture of SSrp with $p^{\downarrow }$ and $\tilde{H}(·)$ possibly dependent. Nevertheless, with this representation at hand, one can easily deduce that if ${\left({\xi }_n\right)}_{n\ge 1}$ is sampled from a mixture of Dirichlet processes under the additional hypothesis that Q is such that ${\alpha }_{\tilde{u}}\left(\mathbb{X}\right)$ and ${\alpha }_{\tilde{u}}(·)/{\alpha }_{\tilde{u}}\left(\mathbb{X}\right)$ are independent, then ${\left({\xi }_n\right)}_{n\ge 1}$ satisfies Definition 2, with $\tilde{H}={\alpha }_{\tilde{u}}(·)/{\alpha }_{\tilde{u}}\left(\mathbb{X}\right)$ and $\mathfrak{q}$ given by (15).

In the rest of the paper, we focus our attention on mSSS for which $[Z,\tilde{H}]$ and $p^{\downarrow }$ are independent.

3.2. Representation Theorems for mSSS

In this section, we give two alternative representations for exchangeable sequences as in Definition 2, which generalize Proposition 1 in [14].

Proposition 2.

An exchangeable sequence $\xi ={\left({\xi }_n\right)}_{n\ge 1}$ is an $mSSS$ as in Definition 2 if and only if

$${\xi }_n=Z_{I_n}a.s.$$

where $Z^{+}={\left(Z_n\right)}_{n\ge 1}$, $\tilde{H}$ and $p^{\downarrow }$ are as in Definition 2 , $Z^{-}={\left(Z_n\right)}_{n\le -1}$ are further conditionally (given $\tilde{H}$) i.i.d. random variables with conditional distribution $\tilde{H}$, and ${\left(I_n\right)}_{n\ge 1}$ is a sequence of integer-valued random variables independent of the Zs and $\tilde{H}$, such that, conditionally on $p^{\downarrow }$, the $I_n$ are independent and (3) holds. All the random elements are defined on a possibly enlarged probability space.

Proof. 

Let ${\sigma }_2=[Z^{+},\tilde{H},p^{\downarrow }]$, where $Z^{+}$, $\tilde{H}$, $p^{\downarrow }$ are defined as in Definition 2 (mSSS). Set $\alpha =1-{\sum }_{j\ge 1}{p}_j^{\downarrow }$. On a possibly enlarged probability space, let ${\left(Z^{\prime }\right)}^{-}={\left(Z_n^{\prime }\right)}_{n\le -1}$ be a sequence of random variables conditionally i.i.d. given $\tilde{H}$ with conditional distribution $\tilde{H}$ and let $I^{\prime }={\left(I_n^{\prime }\right)}_{n\ge 1}$ be a sequence of integer-valued random variables conditionally independent given $p^{\downarrow }$ with conditional distribution (3) with $I_n^{\prime }$ in place of $I_n$. One can also assume that $I^{\prime }$ and $Z=[Z^{+},{\left(Z^{\prime }\right)}^{-}]$ are independent given $[p^{\downarrow },\tilde{H}]$; see Lemma A1 in the Appendix A. Set ${\tau }_1=[I^{\prime },{\left(Z^{\prime }\right)}^{-}]$ and define

$${\left({\xi }_n^{\prime }\right)}_{n\ge 1}=\varphi ({\tau }_1,{\sigma }_2):={(Z_{I_n^{\prime }}\mathbf{1}\{I_n^{\prime }\ge 1\}+Z_{-n}^{\prime }\mathbf{1}\{I_n^{\prime }=-n\})}_{n\ge 1}.$$

Let us show that the law of ${\xi }^{\prime }:={\left({\xi }_n^{\prime }\right)}_{n\ge 1}$ given ${\sigma }_2$ is the same as the law of $\xi$ given ${\sigma }_2$. Take n Borel sets $A_1,\dots ,A_n$ and non-zero integer numbers $i_1,\dots ,i_n$. One has

$$\begin{array}{cc}& \mathbb{P}\left\{{\xi }_1^{\prime }\in A_1,\dots ,{\xi }_n^{\prime }\in A_n,I_1^{\prime }=i_1,\dots ,I_n^{\prime }=i_n|\tilde{H},p^{\downarrow },Z\right\}\hfill \\ & =\prod _{j=1}^n\left[{\delta }_{Z_{i_j}}\left(A_j\right)p_{i_j}^{\downarrow }\mathbf{1}\{i_j>0\}+\alpha {\delta }_{Z_{-j}^{\prime }}\left(A_j\right)\mathbf{1}\{i_j=-j\}\right].\hfill \end{array}$$

Conditionally on $\tilde{H}$, the ${\left(Z_n^{\prime }\right)}_{n\le -1}$ are i.i.d. with law $\tilde{H}$ so that

$$\begin{array}{cc}& \mathbb{P}\left\{{\xi }_1^{\prime }\in A_1,\dots ,{\xi }_n^{\prime }\in A_n,I_1^{\prime }=i_1,\dots ,I_n^{\prime }=i_n|\tilde{H},p^{\downarrow },Z^{+}\right\}\hfill \\ & =\mathbb{E}\left[\mathbb{P}\left\{{\xi }_1^{\prime }\in A_1,\dots ,{\xi }_n^{\prime }\in A_n,I_1^{\prime }=i_1,\dots ,I_n^{\prime }=i_n|\tilde{H},p^{\downarrow },Z\right\}|\tilde{H},p^{\downarrow },Z^{+}\right]\hfill \\ & =\mathbb{E}[\prod _{j=1}^n\left[{\delta }_{Z_{i_j}}\left(A_j\right)p_{i_j}^{\downarrow }\mathbf{1}\{i_j>0\}+\alpha {\delta }_{Z_{-j}^{\prime }}\left(A_j\right)\mathbf{1}\{i_j=-j\}\right]\left|\tilde{H},p^{\downarrow },Z^{+}\right]\hfill \\ & =\prod _{j=1}^n\mathbb{E}[{\delta }_{Z_{i_j}}\left(A_j\right)p_{i_j}^{\downarrow }\mathbf{1}\{i_j>0\}+\alpha {\delta }_{Z_{-j}^{\prime }}\left(A_j\right)\mathbf{1}\{i_j=-j\}\left|\tilde{H},p^{\downarrow },Z^{+}\right]\hfill \\ & =\prod _{j=1}^n\left[{\delta }_{Z_{i_j}}\left(A_j\right)p_{i_j}^{\downarrow }\mathbf{1}\{i_j>0\}+\alpha \tilde{H}\left(A_j\right)\mathbf{1}\{i_j=-j\}\right].\hfill \end{array}$$

Marginalizing with respect to $i_1,\dots ,i_n$,

$$\mathbb{P}\left\{{\xi }_1^{\prime }\in A_1,\dots ,{\xi }_n^{\prime }\in A_n|\tilde{H},p^{\downarrow },Z^{+}\right\}=\prod _{j=1}^{n}P\left(A_j\right).$$

Recalling that $P={\sum }_{j\ge 1}{p}_j^{\downarrow }{\delta }_{Z_j}+\alpha \tilde{H}$,

$$\mathbb{P}\left\{{\xi }_1^{\prime }\in A_1,\dots ,{\xi }_n^{\prime }\in A_n|P\right\}=\prod _{j=1}^{n}P\left(A_j\right)$$

almost surely. Since $\mathbb{X}$ is Polish, we have proven that, given P, ${\left({\xi }_n^{\prime }\right)}_{n\ge 1}$ are i.i.d. with common distribution P. In particular, we have proven that ${\xi }^{\prime }:={\left({\xi }_n^{\prime }\right)}_{n\ge 1}$ given ${\sigma }_2$ is the same as the law of $\xi$ given ${\sigma }_2$. This concludes the proof of the “if part”, since, by the previous argument, any sequence of the form $\left({\xi }^{\prime }\right)$ is of type (mSSS). To complete the proof, it remains to conclude the “only if part”. Setting ${\sigma }_1=\xi$, we have proven that the conditional distribution of ${\sigma }_1$ given ${\sigma }_2$ is the same as the conditional distribution of $\varphi ({\tau }_1,{\sigma }_2)$ given ${\sigma }_2$. At this stage, Lemma A3 in the Appendix A yields that there is $\tau =[{\left(I_n\right)}_{n\ge 1},{\left(Z_n\right)}_{n\le -1}]$ such that ${\left({\xi }_n\right)}_n=\varphi (\tau ,{\sigma }_2)$ a.s., i.e., ${\left({\xi }_n\right)}_n={\left(Z_{I_n}\right)}_n$ a.s. In addition, $\mathcal{L}(\tau ,{\sigma }_2)=\mathcal{L}({\tau }_1,{\sigma }_2)$; hence, the ${\left(Z_n\right)}_{n\le -1}$ are conditionally i.i.d. given $\tilde{H}$ and the $I_n$s are conditionally independent given $[Z^{+},Z^{-},\tilde{H},p^{\downarrow }]$ with the conditional distribution defined by (3). □

Proposition 3.

An exchangeable sequence $\xi ={\left({\xi }_n\right)}_{n\ge 1}$ is an $mSSS$ as defined in Definition 2 if and only if

$${\left({\xi }_n\right)}_{n\ge 1}:={\left(Z_{{\mathcal{C}}_n(\Pi )}^{\prime }\right)}_{n\ge 1}a.s.$$

(16)

where $Z^{\prime }:={\left(Z_n^{\prime }\right)}_{n\ge 1}$ is an exchangeable sequence with the same law of Z, Π is an exchangeable partition with EPPF $\mathfrak{q}$ and Π and $Z^{\prime }$ are independent.

Remark 1.

Note that the $Z_n^{\prime }$s appearing in (16) are not the same $Z_n$s appearing in Definition 2, although they have the same law.

Proof of Proposition 3.

If $\xi$ is mSSS, then, by Proposition 2, we know that $\xi ={\left(Z_{I_n}\right)}_{n\ge 1}$. Let $\Pi ={\Pi }^{*}\left(I\right)$ be the partition induced by ${\left(I_n\right)}_{n\ge 1}$; then, $\Pi$ has EPPF $\mathfrak{q}$ by Kingman’s theorem 1. Denote by $I_1^{*}=I_1,I_2^{*},\dots ,I_K^{*}$ (with $K\le +\infty$) the distinct values of ${\left(I_n\right)}_{n\ge 1}$ in order of appearance, and set

$$Z_n^{\prime }=Z_{I_n^{*}}n=1,\dots ,K.$$

When $K<+\infty$, set $I_{K+j}^{*}=D+j$, where $D=max\{i:i=I_n^{*}\mathrm{for}n\le K\}$, and define the remaining $Z_m^{\prime }$ for $m>K$ accordingly as $Z_m^{\prime }=Z_{I_m^{*}}$. Let $\{i_1,\dots ,i_M\}$ be integers in $\mathbb{Z}\backslash \left\{0\right\}$, and denote the distinct values in $(i_1,\dots ,i_M)$ in order of appearance by $(i_1^{*},\dots ,i_m^{*})$. Let $A_1,\dots ,A_n$ be measurable sets in $\mathcal{X}$, if $n>m$, then

$$\begin{array}{cc}\hfill \mathbb{P}\{& Z_1^{\prime }\in A_1,\dots ,Z_n^{\prime }\in A_n,I_1=i_1,\dots ,I_M=i_M\}\hfill \\ & =\sum _{{\ell }_1,\dots ,{\ell }_{n-m}}\mathbb{P}\{Z_{i_1^{*}}\in A_1,\dots ,Z_{i_m^{*}}\in A_m,Z_{{\ell }_1}\in A_{m+1}\dots ,\hfill \\ & Z_{{\ell }_{n-m}}\in A_n,I_1=i_1,\dots ,I_M=i_M,I_{m+1}^{*}={\ell }_1,\dots ,I_n^{*}={\ell }_{n-m}\}\hfill \end{array}$$

where the sum runs over all the non-zero distinct integers ${\ell }_1,\dots ,{\ell }_{n-m}$ different from $i_1^{*},\dots ,i_m^{*}$. Since $I^{*}$ is a function of I and I and Z are independent, it follows that

$$\begin{array}{cc}\hfill \mathbb{P}\{& Z_{i_1^{*}}\in A_1,\dots ,Z_{i_m^{*}}\in A_m,Z_{{\ell }_1}\in A_{m+1}\dots ,\hfill \\ & Z_{{\ell }_{n-m}}\in A_n,I_1=i_1,\dots ,I_M=i_M,I_{m+1}^{*}={\ell }_1,\dots ,I_n^{*}={\ell }_{n-m}\}\hfill \\ & =\mathbb{P}\{Z_{i_1^{*}}\in A_1,\dots ,Z_{i_m^{*}}\in A_m,Z_{{\ell }_1}\in A_{m+1},\dots ,Z_{{\ell }_{n-m}}\in A_n\}\hfill \\ & \mathbb{P}\{I_1=i_1,\dots ,I_M=i_M,I_{m+1}^{*}={\ell }_1,\dots ,I_n^{*}={\ell }_{n-m}\}\hfill \\ & =\mathbb{P}\{Z_1\in A_1,\dots ,Z_n\in A_n\}\mathbb{P}\{I_1=i_1,\dots ,I_M=i_M,I_{m+1}^{*}={\ell }_1,\dots ,I_n^{*}={\ell }_{n-m}\}\hfill \end{array}$$

where the second equality follows by exchangeability. Summing in ℓ, one obtains

$$\begin{array}{cc}\hfill \mathbb{P}\{Z_1^{\prime }\in A_1,& \dots ,Z_n^{\prime }\in A_n,I_1=i_1,\dots ,I_M=i_M\}\hfill \\ & =\mathbb{P}\{Z_1\in A_1,\dots ,Z_n\in A\}\mathbb{P}\{I_1=i_1,\dots ,I_M=i_M\}.\hfill \end{array}$$

For $m\ge n$, the sum is not needed and the same result follows. This shows that ${\left(Z_n^{\prime }\right)}_n$ is an exchangeable sequence with the same law of Z, and ${\left(Z_n^{\prime }\right)}_n$ and ${\left(I_n\right)}_{n\ge 1}$ are independent. To conclude, note that, with probability one, ${\displaystyle I_{{\mathcal{C}}_n(\Pi )}^{*}=I_n}$, and hence

$${\xi }_n=Z_{I_n}=Z_{I_{{\mathcal{C}}_n(\Pi )}^{*}}=Z_{{\mathcal{C}}_n(\Pi )}^{\prime }.$$

Conversely, let us assume that ${\xi }_n=Z_{{\mathcal{C}}_n(\Pi )}^{\prime }$ and let ${\left(p_j^{\downarrow }\right)}_{j\ge 1}$ be the weights obtained from $\Pi$ by (4). Let $I_1,I_2,\dots$ be the integer-valued random variables appearing in Theorem 1 such that $\Pi ={\Pi }^{*}\left(I\right)$ a.s. It follows that ${\displaystyle {\mathcal{C}}_n(\Pi )={\mathcal{C}}_n\left({\Pi }^{*}\left(I\right)\right)}$ and ${\displaystyle I_{{\mathcal{C}}_n(\Pi )}^{*}=I_n}$, where the $I_n^{*}$ are defined as above for $n\le K$. Setting

$$Z_m:=\left\{\begin{array}{cc}{Z}_k^{\prime }\hfill & \mathrm{if}{I}_k^{*}=m\hfill \\ Z_m^{″}\hfill & \mathrm{if}{I}_k^{*}\ne m\forall k,\hfill \end{array}\right.$$

with $Z_m^{″},m\in \mathbb{Z}$ conditionally i.i.d. given $\tilde{H}$ with law $\tilde{H}$, independent of everything else. Arguing as above, one can check that the ${\left(Z_m\right)}_{m\in \mathbb{Z},m\ne 0}$ are exchangeable random variables with the same law of $Z^{\prime }$ independent of $(I,p^{\downarrow })$. To conclude, note that, in particular,

$$Z_{I_n}=Z_{I_{{\mathcal{C}}_n(\Pi )}^{*}}=Z_{{\mathcal{C}}_n(\Pi )}^{\prime }a.s..$$

The conclusion follows by Proposition 2. □

A simple consequence of the previous proposition is the following.

Corollary 1.

Let ${\left({\xi }_n\right)}_{n\ge 1}$ be an $mSSS$ as defined in Definition 2. For every $A_1,\dots ,A_n$ Borel set in $\mathbb{X}$,

$$\mathbb{P}\left\{{\xi }_1\in A_1,\dots ,{\xi }_n\in A_n\right\}=\sum _{{\pi }_n\in {\mathcal{P}}_n}\mathfrak{q}\left(\right|{\pi }_{1,n}|,\dots ,|{\pi }_{k,n}\left|\right)\mathbb{E}\left[\prod _{c=1}^{|{\pi }_n|}\tilde{H}\left({\cap }_{j\in {\pi }_{c,n}}{A}_j\right)\right].$$

4. Random Partitions Induced by mSSS

Let $\tilde{\Pi }={\Pi }^{*}\left(\xi \right)$ be the random partition induced by an exchangeable sequence $\xi$ defined as in Definition 2, and let ${\Pi }^{\left(0\right)}:={\Pi }^{*}\left(Z^{\prime }\right)$ be the partition induced by the corresponding exchangeable sequence ${\left(Z_n^{\prime }\right)}_n$ (see Proposition 3). Finally, let $\Pi$ be the partition with EPPF $\mathfrak{q}$ appearing in Proposition 3. As already observed, if $Z^{\prime }$ is an i.i.d. sequence from a diffuse H, then ${\Pi }^{\left(0\right)}=[\left(1\right),\left(2\right),\left(3\right),\dots ]$ a.s. and hence ${\Pi }^{*}\left(\xi \right)=\Pi$. The same result follows if $Z^{\prime }$ is exchangeable without ties (see Corollary 2). When ${\Pi }^{\left(0\right)}$ is not the trivial partition, it is clear by construction that different blocks in $\Pi$ can merge in the final clustering configuration (i.e., ${\Pi }^{*}\left(\xi \right)$). In other words, two observations can share the same value because either they belong to the same block in the latent partition $\Pi$ or they are in different blocks but they share the same value (from $Z^{\prime }$). This simple observation leads us to write the EPPF of the random partition ${\Pi }^{*}\left(\xi \right)$ using the EPPF of ${\Pi }^{\left(0\right)}$ and of $\Pi$.

4.1. Explicit Expression of the EPPF

If ${\tilde{\pi }}_n=\{{\tilde{\pi }}_{1,n}\dots ,{\tilde{\pi }}_{k,n}\}$ is a partition of $\left[n\right]$ with $|{\tilde{\pi }}_{i,n}|=n_i$ ($i=1,\dots ,k$) and $\mathit{n}=(n_1,\dots ,n_k)$, we can easily describe all the partitions ${\pi }_n$ more finely than ${\tilde{\pi }}_n$, which are compatible with ${\tilde{\pi }}_n$ in the merging process described above. To do this, first of all, note that any block ${\tilde{\pi }}_{i,n}$ can arise from the union of $1\le m_i\le n_i$ blocks in the latent partition. Hence, given $\mathit{n}=(n_1,\dots ,n_k)$, where $n={\sum }_{i=1}^k{n}_i$, we define the set

$$\mathcal{M}\left(\mathit{n}\right)=\left\{\mathit{m}=(m_1,\dots ,m_k)\in {\mathbb{N}}^k:1\le m_i\le n_i\right\}.$$

See Figure 1 for an example. Once a specific configuration $\mathit{m}$ in $\mathcal{M}\left(\mathit{n}\right)$ is considered, the $m_i$ blocks of the latent partition contributing to the block ${\tilde{\pi }}_{i,n}$, are characterized by the sufficient statistics ${\mathit{\lambda }}_i=({\lambda }_{i1},\dots ,{\lambda }_{i{n}_i})\in {\mathbb{N}}^{n_i}$, where ${\lambda }_{ij}$ is the number of blocks of j elements among the $m_i$ blocks above. This leads, for $\mathit{m}$ in $\mathcal{M}\left(\mathit{n}\right)$, to the definition of

$$\Lambda (\mathit{n},\mathit{m}):=\left\{\begin{array}{cc}& \mathit{\lambda }=[{\mathit{\lambda }}_1,\dots ,{\mathit{\lambda }}_k]\mathrm{where}{\mathit{\lambda }}_i=({\lambda }_{i1},\dots ,{\lambda }_{i{n}_i})\in {\mathbb{N}}^{n_i}:\hfill \\ & \sum _{j=1}^{n_i}j{\lambda }_{ij}=n_i,\sum _{j=1}^{n_i}{\lambda }_{ij}=m_i\mathrm{for}i=1,\dots ,k\hfill \end{array}\right\}.$$

In summary, the set of partitions ${\tilde{\pi }}_n$, which are compatible with ${\tilde{\pi }}_n$ in the merging process described above, can be written as

$${\mathcal{P}}_{{\tilde{\pi }}_n}:={\cup }_{\mathit{m}\in \mathcal{M}\left(\mathit{n}\right)}{\cup }_{\lambda \in \Lambda (\mathit{n},\mathit{m})}{\mathcal{P}}_{{\tilde{\pi }}_n}\left(\lambda \right)$$

(17)

where ${\mathcal{P}}_{{\tilde{\pi }}_n}\left(\mathit{\lambda }\right)$ is the set of all the partitions in ${\mathcal{P}}_n$ with $m_1+\dots +m_k=:\left|\mathit{m}\right|$ blocks such that

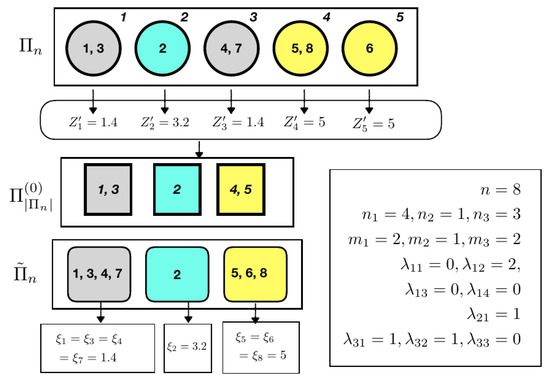
Figure 1. Pictorial representation of the latent partition structure of an mSSS. In the example, the partition induced by $({\xi }_1,\dots ,{\xi }_n)$ for $n=8$ is ${\tilde{\Pi }}_n=\{[1,3,4,7],\left[2\right],[5,6,8]\}$, and it is represented using rounded squares (left bottom). Circles at the top left represent a compatible latent partition, namely ${\Pi }_n=\{[1,3],\left[2\right],[4,7],[5,8],\left[6\right]\}$. The partition on $\{1,\dots ,5\}$ induced by the latent $Z_n^{\prime }$, i.e., ${\Pi }_{|{\Pi }_n|}^{\left(0\right)}=\{[1,3],\left[2\right],[4,5]\}$, is represented with squares in the middle of the figure. Combining ${\Pi }_n$ and ${\Pi }_{|{\Pi }_n|}^{\left(0\right)}$, one obtains ${\tilde{\Pi }}_n$. The statistics $\mathit{n}$, $\mathit{m}$ and $\lambda$ corresponding to this particular configuration are shown in the box at the bottom right.

• it is possible to determine k subset containing $m_1,\dots ,m_k$ of these blocks;
• the union of the blocks in the i-th subset coincides with the i-th block of ${\tilde{\pi }}_n$ for $i=1,\dots ,k$;
• in the i-th block, there are ${\lambda }_{ij}$ blocks with j elements, for $j=1,\dots ,n_i$.

Given the EPPF $\mathfrak{q}$, let

$$\overline{\mathfrak{q}}\left(\mathit{\lambda }\right):=\mathfrak{q}(n_{11},\dots ,n_{1m_1},n_{21},\dots ,n_{k{m}_k}),$$

where $(n_{11},\dots ,n_{1m_1},\dots ,n_{k{m}_k})$ is any sequence of integer numbers such that ${\sum }_{c=1}^{m_i}{n}_{ic}={\sum }_{j}j{\lambda }_{ij}$ for every i and $\#\{c:n_{ic}=j\}={\lambda }_{ij}$ for every i and j. Note that since the value of $\mathfrak{q}(n_{11},\dots ,n_{1m_1},n_{21},\dots ,n_{k{m}_k})$ depends only on the statistics $\mathit{\lambda }$, $\overline{\mathfrak{q}}\left(\mathit{\lambda }\right)$ is well-defined. See, e.g., [26].

Finally, recall that the cardinality of ${\mathcal{P}}_{{\tilde{\pi }}_n}\left(\mathit{\lambda }\right)$ is

$$\mathit{c}\left(\mathit{\lambda }\right):=\prod _{i=1}^k\frac{\left({\sum }_{j}j{\lambda }_{ij}\right)!}{{\prod }_{j=1}^{n_i}{\lambda }_{ij}!{(j!)}^{{\lambda }_{ij}}}=\prod _{i=1}^k\frac{n_i!}{{\prod }_{j=1}^{n_i}{\lambda }_{ij}!{(j!)}^{{\lambda }_{ij}}},$$

See Equation (39) in [15].

Proposition 4.

Let $\xi ={\left({\xi }_n\right)}_{n\ge 1}$ be an $\left(mSSS\right)$. Denote by $\tilde{\Pi }={\Pi }^{*}\left(\xi \right)$ the random partition induced by ξ and by ${\mathfrak{q}}^{\left(0\right)}$ the EPPF of the partition induced by ${\left(Z_n^{\prime }\right)}_{n\ge 1}$. If ${\tilde{\pi }}_n=\{{\tilde{\pi }}_{1,n}\dots ,{\tilde{\pi }}_{k,n}\}$ is a partition of $\left[n\right]$ with $|{\tilde{\pi }}_{i,n}|=n_i$ $(i=1,\dots ,k)$ and $\mathit{n}=(n_1,\dots ,n_k)$, then

$$\mathbb{P}\{{\tilde{\Pi }}_n={\tilde{\pi }}_n\}=\sum _{\mathit{m}\in \mathcal{M}\left(\mathit{n}\right)}{\mathfrak{q}}^{\left(0\right)}\left(\mathit{m}\right)\sum _{\mathit{\lambda }\in \Lambda (\mathit{n},\mathit{m})}\mathit{c}\left(\mathit{\lambda }\right)\overline{\mathfrak{q}}\left(\mathit{\lambda }\right).$$

(18)

Proof. 

Start by writing

$$\mathbb{P}\{{\tilde{\Pi }}_n={\tilde{\pi }}_n\}=\mathbb{P}\left({\cup }_{\mathit{m}\in \mathcal{M}\left(\mathit{n}\right)}{\cup }_{\mathit{\lambda }\in \Lambda (\mathit{n},\mathit{m})}{\cup }_{{\pi }_n\in {\mathcal{P}}_{{\tilde{\pi }}_n}\left(\mathit{\lambda }\right)}\{{\Pi }_n={\pi }_n,{\tilde{\Pi }}_n={\tilde{\pi }}_n\}\right),$$

(19)

which gives

$$\mathbb{P}\{{\tilde{\Pi }}_n={\tilde{\pi }}_n\}=\sum _{\mathit{m}\in \mathcal{M}\left(\mathit{n}\right)}\sum _{\mathit{\lambda }\in \Lambda (\mathit{n},\mathit{m})}\sum _{{\pi }_n\in {\mathcal{P}}_{{\tilde{\pi }}_n}\left(\mathit{\lambda }\right)}\mathbb{P}\{{\tilde{\Pi }}_n={\tilde{\pi }}_n|{\Pi }_n={\pi }_n\}P\{{\Pi }_n={\pi }_n\}$$

(20)

Whenever ${\pi }_n\in {\mathcal{P}}_{{\tilde{\pi }}_n}\left(\mathit{\lambda }\right)$,

$$\mathbb{P}\{{\Pi }_n={\pi }_n\}=\overline{\mathfrak{q}}\left(\mathit{\lambda }\right).$$

Therefore, we can write (20) as

$$\mathbb{P}\{{\tilde{\Pi }}_n={\tilde{\pi }}_n\}=\sum _{\mathit{m}\in \mathcal{M}\left(\mathit{n}\right)}\sum _{\mathit{\lambda }\in \Lambda (\mathit{n},\mathit{m})}\sum _{{\pi }_n\in {\mathcal{P}}_{{\tilde{\pi }}_n}\left(\mathit{\lambda }\right)}P\{{\tilde{\Pi }}_n={\tilde{\pi }}_n|{\Pi }_n={\pi }_n\}\overline{\mathfrak{q}}\left(\mathit{\lambda }\right).$$

(21)

Define now the function $M_{{\tilde{\pi }}_n,{\pi }_n}:\{1,\dots ,|\mathit{m}\left|\right\}\to \{1,\dots ,|{\tilde{\pi }}_n\left|\right\}$ as $M\left(j\right)=i$ if ${\pi }_{j,n}$ is in the i-th subset of blocks, i.e., if ${\pi }_{j,n}\subset {\tilde{\pi }}_{i,n}$. Recalling that k is the number of blocks in ${\tilde{\pi }}_n$, define now a partition $\pi \left(M_{{\tilde{\pi }}_n,{\pi }_n}\right)$ on $\{1,\dots ,|\mathit{m}\left|\right\}$ with k block where the i-th block is

$$\{j:M_{{\tilde{\pi }}_n,{\pi }_n}\left(j\right)=i\}.$$

Recalling that ${\Pi }^{\left(0\right)}$ is the partition induced by the $Z^{\prime }$s, one has

$$\{{\tilde{\Pi }}_n={\tilde{\pi }}_n,{\Pi }_n={\pi }_n\}=\{{\Pi }_{\left|\mathit{m}\right|}^{\left(0\right)}=\pi \left(M_{{\tilde{\pi }}_n,{\pi }_n}\right),{\Pi }_n={\pi }_n\}$$

which gives

$$\begin{array}{cc}\hfill P\{{\tilde{\Pi }}_n={\tilde{\pi }}_n|{\Pi }_n={\pi }_n\}& =P\{{\Pi }_{\left|\mathit{m}\right|}^{\left(0\right)}=\pi \left(M_{{\tilde{\Pi }}_n,{\pi }_n}\right)|{\Pi }_n={\pi }_n\}\hfill \\ & =\mathbb{P}\{{\Pi }_{\left|\mathit{m}\right|}^{\left(0\right)}=\pi \left(M_{{\tilde{\Pi }}_n,{\pi }_n}\right)\}\hfill \end{array}$$

since ${\Pi }^{\left(0\right)}$ and $\Pi$ are independent. To conclude, note that the vector of the cardinalities of the blocks in $\pi \left(M_{{\tilde{\pi }}_n,{\pi }_n}\right)$ is $\mathit{m}$; hence, if ${\mathfrak{q}}^{\left(0\right)}$ is the EPPF of ${\Pi }^{\left(0\right)}$, one has $P\{{\Pi }_{\left|\mathit{m}\right|}^{\left(0\right)}=\pi \left(M_{{\tilde{\pi }}_n,{\pi }_n}\right)\}={\mathfrak{q}}^{\left(0\right)}\left(\mathit{m}\right)$. Since the cardinality of ${\mathcal{P}}_{{\tilde{\pi }}_n}\left(\mathit{\lambda }\right)$ is $\mathit{c}\left(\mathit{\lambda }\right)$, one obtains the thesis. □

Corollary 2.

Let $\xi ={\left({\xi }_n\right)}_n$ be defined according to (mSSS). If $\mathbb{P}\{Z_1^{\prime }=Z_2^{\prime }\}=0$, then ${\Pi }^{*}\left(\xi \right)=\Pi$ with probability one.

Proof. 

If $\mathbb{P}\{Z_1^{\prime }=Z_2^{\prime }\}=0$, by exchangeability, $\mathbb{P}\{Z_{i_1}^{\prime }=Z_{i_2}^{\prime }=\cdots =Z_{i_k}^{\prime }\}\le \mathbb{P}\{Z_1^{\prime }=Z_2^{\prime }\}=0$. Hence, the $Z_i^{\prime }$s are distinct with probability one. Since $({\xi }_1,\dots ,{\xi }_n)=(Z_{{\mathcal{C}}_1(\Pi )}^{\prime },$ $\dots ,Z_{{\mathcal{C}}_n(\Pi )}^{\prime })$ by Proposition 3, it follows that ${\tilde{\Pi }}_n={\Pi }_n$. □

Remark 2.

Note that, as a special case, we recover the fact that if ξ is a $gSSS(\mathfrak{q},H)$ with H diffuse (i.e., it is a $SSS(\mathfrak{q},H)$), then the random partition induced by ξ is a.s. Π.

Remark 3.

The fact that the EPPF of ${\tilde{\Pi }}_n$ is $\mathfrak{q}$ when $\mathbb{P}\{Z_1^{\prime }=Z_2^{\prime }\}=0$ can be deduced from (18). Indeed, if $\mathbb{P}\{Z_1^{\prime }=Z_2^{\prime }\}=0$, then the partition induced by $Z^{\prime }$ is a.s. the trivial partition $\left[\right(1),(2),(3),\dots ]$, so that ${\mathfrak{q}}^{\left(0\right)}\left(\mathit{m}\right)=0$ for every $\mathit{m}\ne (1,1,\dots ,1)$. For $\mathit{m}=(1,1,\dots ,1)$, ${\tilde{\pi }}_n=\{{\tilde{\pi }}_{1,n}\dots ,{\tilde{\pi }}_{k,n}\}$ with $|{\tilde{\pi }}_{i,n}|=n_i$ $(i=1,\dots ,k)$, and $\mathit{n}=(n_1,\dots ,n_k)$, the set $\Lambda (\mathit{n},\mathit{m})$ reduces to the singleton ${\mathit{\lambda }}^{\left(1\right)}:=[{\mathit{\lambda }}_1,\dots ,{\mathit{\lambda }}_k]$, where ${\mathit{\lambda }}_i=(0,0,\dots ,1)$ with ${\mathit{\lambda }}_i$ of length $n_i$. Hence, $\overline{\mathfrak{q}}\left({\mathit{\lambda }}^{\left(1\right)}\right)=\mathfrak{q}\left(\mathit{n}\right)$ and (18) gives $\mathbb{P}\{{\tilde{\Pi }}_n={\tilde{\pi }}_n\}=\overline{\mathfrak{q}}\left({\mathit{\lambda }}^{\left(1\right)}\right)=\mathfrak{q}\left(\mathit{n}\right)$.

4.2. EPPF When $\Pi$ Is of Gibbs Type

An important class of exchangeable random partitions is that of Gibbs-type partitions, introduced in [32] and characterized by the EPPF

$$\mathfrak{q}(n_1,\dots ,n_k):=V_{n,k}\prod _{j=1}^k{(1-\sigma )}_{n_j-1},$$

(22)

where ${\left(x\right)}_n=x(x+1)\dots (x+n-1)$, $\sigma <1$ and $V_{n,k}$ are positive real numbers such that $V_{1,1}=1$ and

$$(n-\sigma k)V_{n+1,k}+V_{n+1,k+1}=V_{n,k},n\ge 1,1\le k\le n.$$

A noteworthy example of Gibbs-type EPPF is the so-called Pitman–Yor two-parameter family. It is defined by

$$\mathfrak{q}(n_1,\dots ,n_k):=\frac{{\prod }_{i=1}^{k-1}(\theta +i\sigma )}{{(\theta +1)}_{n-1}}\prod _{c=1}^k{(1-\sigma )}_{n_c-1},$$

(23)

where $0\le \sigma <1$ and $\theta >-\sigma$; or $\sigma <0$ and $\theta =\left|\sigma \right|m$ for some integer m; see [2,31].

In order to state the next result, we recall that

$$\sum _{\begin{array}{c}({\lambda }_1,\dots ,{\lambda }_n)\\ {\sum }_{j=1}^{n}j{\lambda }_j=n,{\sum }_{j=1}^n{\lambda }_j=k\end{array}}\prod _{j=1}^n{\left[{(1-\sigma )}_{j-1}\right]}^{{\lambda }_j}\frac{n!}{{\prod }_{j=1}^n{\lambda }_i!{(j!)}^{{\lambda }_j}}=S_{\sigma }(n,k)$$

(24)

where $S_{\sigma }(n,k)$ is the generalized Stirling number of the first kind; see (3.12) in [26]. In the same book, various equivalent definitions of generalized Stirling numbers are presented.

Corollary 3.

Let $\tilde{\Pi }={\Pi }^{*}\left(\xi \right)$ be defined as in Proposition 4 with $\mathfrak{q}$ of Gibbs type defined in (22). If ${\tilde{\pi }}_n=\{{\tilde{\pi }}_{1,n}\dots ,{\tilde{\pi }}_{k,n}\}$ is a partition of $\left[n\right]$ with $|{\tilde{\pi }}_{i,n}|=n_i$ ($i=1,\dots ,k$) and $\mathit{n}=(n_1,\dots ,n_k)$, then

$$\mathbb{P}\{{\tilde{\Pi }}_n={\tilde{\pi }}_n\}=\sum _{\mathit{m}\in \mathcal{M}\left(\mathit{n}\right)}{\mathfrak{q}}^{\left(0\right)}\left(\mathit{m}\right)V_{n,\left|\mathit{m}\right|}\prod _{i=1}^k{S}_{\sigma }(n_i,m_i).$$

Proof. 

Combining Proposition 4 with (22), one obtains

$$\begin{array}{cc}\hfill \mathbb{P}\{{\tilde{\Pi }}_n={\tilde{\pi }}_n\}& =\sum _{\mathit{m}\in \mathcal{M}\left(\mathit{n}\right)}{\mathfrak{q}}^{\left(0\right)}\left(\mathit{m}\right)V_{n,\left|\mathit{m}\right|}\sum _{\mathit{\lambda }\in \Lambda (\mathit{n},\mathit{m})}\prod _{i=1}^k\prod _{j=1}^{n_i}{\left[{(1-\sigma )}_{j-1}\right]}^{{\lambda }_{i,j}}\frac{n_i!}{{\prod }_{j=1}^{n_i}{\lambda }_{ij}!{(j!)}^{{\lambda }_{ij}}}\hfill \\ & =\sum _{\mathit{m}\in \mathcal{M}\left(\mathit{n}\right)}{\mathfrak{q}}^{\left(0\right)}\left(\mathit{m}\right)V_{n,\left|\mathit{m}\right|}\hfill \\ & \times \prod _{i=1}^k\sum _{\begin{array}{c}({\lambda }_{i1},\dots ,{\lambda }_{i{n}_i})\\ {\sum }_{j=1}^{n_i}j{\lambda }_{ij}=n_i,{\sum }_{j=1}^{n_i}{\lambda }_{ij}=m_i\end{array}}\prod _{j=1}^{n_i}{\left[{(1-\sigma )}_{j-1}\right]}^{{\lambda }_{i,j}}\frac{n_i!}{{\prod }_{j=1}^{n_i}{\lambda }_{ij}!{(j!)}^{{\lambda }_{ij}}}\hfill \\ & =\sum _{\mathit{m}\in \mathcal{M}\left(\mathit{n}\right)}{\mathfrak{q}}^{\left(0\right)}\left(\mathit{m}\right)V_{n,\left|\mathit{m}\right|}\prod _{i=1}^k{S}_{\sigma }(n_i,m_i).\hfill \end{array}$$

 □

4.3. The EPPF of a $gSSS(\mathfrak{q},H)$

As a special case, we now consider the partition induced by a $gSSS(\mathfrak{q},H)$ with general base measure H. For the rest of the section, it is useful to decompose H as

$$H\left(dx\right)=\sum _{i\ge 1}{a}_i{\delta }_{{\overline{x}}_i}\left(dx\right)+(1-a)H^c\left(dx\right)$$

(25)

where ${\mathbb{X}}_0:=\{{\overline{x}}_1,{\overline{x}}_2,\dots \}$ is the collection of points with positive H probability, $a_i=H\left({\overline{x}}_i\right)$, $a=H\left({\mathbb{X}}_0\right)\in [0,1]$ and $H^c(·)=H(·\cap {\mathbb{X}}_0^c)/H\left({\mathbb{X}}_0^c\right)$ is a diffuse probability measure on $\mathbb{X}$. The sum is assumed taken over $i\in \{1,\dots ,|{\mathbb{X}}_0\left|\right\}$.

We now describe ${\mathfrak{q}}^{\left(0\right)}$, i.e., the EPPF of the partition induced by ${\left(Z_n^{\prime }\right)}_{n\ge 1}$. Let $\mathit{m}$ in $\mathcal{M}\left(\mathit{n}\right)$, where $\mathit{n}=(n_1,\dots ,n_k)$, and assume that the realization of ${\Pi }_{\left|\mathit{m}\right|}^{\left(0\right)}$ has k blocks of cardinality $m_1,\dots ,m_k$. Set $z_i=0$ if the $Z_n^{\prime }$ corresponding to the i-th block of ${\Pi }_{\left|\mathit{m}\right|}^{\left(0\right)}$ comes from the diffuse component $H^c$, while $z_k=\ell$ if it is equal to ${\overline{x}}_{\ell }$. Since the blocks in ${\Pi }^{\left(0\right)}$ need to be associated with different values of the $Z_n^{\prime }$, one has that necessarily $z_i=z_j=0$ if $z_i=z_j$ for $i\ne j$. In this case, the block is a singleton, which is $m_i=m_j=1$. On the other hand, if $m_i\ge 2$, i.e., a merging occurred, necessarily, $z_i>0$. Note that it is also possible that $m_i=1$ but $z_i>0$. This motivates the definition of the set

$$\begin{array}{cc}\hfill \mathcal{Z}\left(\mathit{m}\right):& =\{(z_1,\dots ,z_k)\in \{0,1,\dots ,|{\mathbb{X}}_0{\left|\right\}}^k:\mathrm{if}{z}_i=z_j\mathrm{for}i\ne j\mathrm{then}{z}_i=z_j=0\hfill \\ & \mathrm{and}{m}_i=m_j=1;\mathrm{if}{m}_i\ge 2\mathrm{then}{z}_i>0\}\hfill \end{array}$$

for $\mathit{m}$ in $\mathcal{M}\left(\mathit{n}\right)$ where $\mathit{n}=(n_1,\dots ,n_k)$. The probability of obtaining, in an i.i.d. sample of length $\left|\mathit{m}\right|$ from H, exactly k ordered blocks with cardinality $m_1,\dots ,m_k$, such that observations in each block are equal and observations in distinct blocks are different, is

$$H^{\#}\left(\mathit{m}\right):=\sum _{(z_1,\dots ,z_k)\in \mathcal{Z}\left(\mathit{m}\right)}{(1-a)}^{\#\{j:z_j=0\}}\prod _{j:z_j>0}{a}_{z_j}^{m_j}.$$

By exchangeability, $H^{\#}\left(\mathit{m}\right)$ turns out to be ${\mathfrak{q}}^{\left(0\right)}\left(\mathit{m}\right)$. Note also that if $a=1$, $H^{\#}\left(\mathit{m}\right)$ reduces to

$$\sum _{(z_1,\dots ,z_k)}\prod _{j=1}^k{a}_{z_j}^{m_j}$$

where $z_1,\dots ,z_k$ runs over all distinct positive integers (less than or equal to $|{\mathbb{X}}_0|$ if ${\mathbb{X}}_0$ is finite), which is nothing else (5) for deterministic weights.

To rewrite $H^{\#}\left(\mathit{m}\right)$ in a different way, given $\mathit{m}=(m_1,\dots ,m_k)$ in $\mathcal{M}\left(\mathit{n}\right)$, let ${\mathit{m}}^{*}$ be the vector containing all the elements $m_i>1$ and let r be its length, with possibly $r=0$ if $\mathit{m}=(1,1,\dots ,1)$, and define for $\ell \ge 0$

$$A_{\mathit{m},\ell }=\sum _{j_1\ne \dots \ne j_{r+\ell }}{a}_{j_1}^{m_1^{*}}\dots a_{j_r}^{m_r^{*}}{a}_{j_{r+1}}\dots a_{j_{r+\ell }}$$

with the convention that $A_{\mathit{m},0}=1$ when $r=0$. A simple combinatorial argument shows that

$$H^{\#}\left(\mathit{m}\right)=\sum _{\ell =0}^{k-r}{(1-a)}^{k-\ell -r}\left(\genfrac{}{}{0pt}{}{k-r}{\ell }\right)A_{\mathit{m},\ell }.$$

Proposition 4 gives immediately the next proposition.

Proposition 5.

Let ξ be a $gSSS(\mathfrak{q},H)$ and let $\tilde{\Pi }={\Pi }^{*}\left(\xi \right)$ be the random partition induced by ξ. If ${\tilde{\pi }}_n=[{\tilde{\pi }}_{1,n}\dots ,{\tilde{\pi }}_{k,n}]$ is a partition of $\left[n\right]$ with $|{\tilde{\pi }}_{i,n}|=n_i$ $(i=1,\dots ,k)$ and $\mathit{n}=(n_1,\dots ,n_k)$, then

$$\mathbb{P}\{{\tilde{\Pi }}_n={\tilde{\pi }}_n\}=\sum _{\mathit{m}\in \mathcal{M}\left(\mathit{n}\right)}{H}^{\#}\left(\mathit{m}\right)\sum _{\mathit{\lambda }\in \Lambda (\mathit{n},\mathit{m})}\mathit{c}\left(\mathit{\lambda }\right)\overline{\mathfrak{q}}\left(\mathit{\lambda }\right).$$

Remark 4.

Once again, if H is diffuse, then $H^{\#}\left(\mathit{m}\right)=0$ for every $\mathit{m}\ne (1,1,\dots ,1)$. Hence, the above formula reduces to the familiar

$$\mathbb{P}\{{\tilde{\Pi }}_n={\tilde{\pi }}_n\}=\mathfrak{q}\left(\right|{\tilde{\pi }}_{n,1}|,\dots ,|{\tilde{\pi }}_{n,k}\left|\right)=\mathbb{P}\{{\Pi }_n={\tilde{\pi }}_n\}.$$

4.4. EPPF for $gSSS$ with Spike-and-Slab Base Measure

We now consider the special case of $gSSS$ with a spike-and-slab base measure. A spike-and-slab measure is defined as

$$H\left(dx\right)=a{\delta }_{x_0}\left(dx\right)+(1-a)H^c\left(dx\right)$$

(26)

where $a\in (0,1)$, $x_0$ is a point of $\mathbb{X}$ and $H^c$ is a diffuse measure on $\mathbb{X}$. This type of measure has been used as a base measure in the Dirichlet process by [16,17,18,19,20] and in the Pitman–Yor process by [21].

Here, we deduce by Proposition 5 the explicit form of the EPPF of the random partition induced by a sequence sampled from a species sampling random probability with such a base measure.

Proposition 6.

Let H be as in (26), $\tilde{\Pi }$ be the random partition induced by a $gSSS(\mathfrak{q},H)$ and Π be an exchangeable random partition with EPPF $\mathfrak{q}$. If ${\pi }_n=\{{\pi }_{1,n}\dots ,{\pi }_{k,n}\}$ is a partition of $\left[n\right]$ with $|{\pi }_{i,n}|=n_i$ ($i=1,\dots ,k$), then

$$\begin{array}{cc}\hfill \mathbb{P}\{& {\tilde{\Pi }}_n={\pi }_n{\}=(1-a)}^k\mathfrak{q}(n_1,\dots ,n_k)\hfill \\ \hfill & +{(1-a)}^{k-1}\sum _{i=1}^k\mathfrak{q}(n_1,\dots ,n_{i-1},n_{i+1},\dots ,n_k)\sum _{r=1}^{n_i}{a}^r{q}_n\left(r\right|n_1,\dots ,n_{i-1},n_{i+1},\dots ,n_k)\hfill \end{array}$$

(27)

where, conditionally on the fact that ${\Pi }_{n-n_i}$ has $k-1$ blocks with sizes $n_1,\dots ,n_{i-1},n_{i+1},\dots ,n_k$, the probability that ${\Pi }_n$ has $k-1+r$ blocks is denoted by $q_n\left(r\right|n_1,\dots ,n_{i-1},n_{i+1},\dots ,n_k)$. If, in addition, $\mathfrak{q}$ is of Gibbs type (22), then

$$\begin{array}{cc}\hfill \mathbb{P}\{{\tilde{\Pi }}_n={\pi }_n\}& ={(1-a)}^k{V}_{n,k}\prod _{j=1}^k{(1-\sigma )}_{n_j-1}\hfill \\ & +{(1-a)}^{k-1}\sum _{i=1}^k\prod _{j=1,j\ne i}^k{(1-\sigma )}_{n_j-1}\sum _{r=1}^{n_i}{a}^r{V}_{n,k-1+r}{S}_{\sigma }(n_i,r).\hfill \end{array}$$

Proof. 

In this case, $H^{\#}\left(\mathit{m}\right)=0$ if $m_i\ge 2$ and $m_j\ge 2$ for some $i\ne j$ because H has only one atom. Moreover, $H^{\#}\left(\mathit{m}\right)$ is clearly symmetric and

$$H^{\#}(1,1,1,\dots ,1)={(1-a)}^k+k{(1-a)}^{k-1}a$$

$$H^{\#}(m,1,\dots ,1)=a^m{(1-a)}^{k-1}\mathrm{for}m>1.$$

By Proposition 5,

$$\begin{array}{cc}\hfill \mathbb{P}\{{\tilde{\Pi }}_n={\pi }_n\}& =[{(1-a)}^k+k{(1-a)}^{k-1}a]\mathfrak{q}(n_1,\dots ,n_k)\hfill \\ & +{(1-a)}^{k-1}\sum _{i=1}^k\sum _{m_i=2}^{n_i}{a}^{m_i}\sum _{\mathit{\lambda }\in \Lambda \left(\mathit{m}\right)}c\left(\mathit{\lambda }\right)\overline{\mathfrak{q}}\left(\mathit{\lambda }\right)\hfill \\ & =[{(1-a)}^k+k{(1-a)}^{k-1}]\mathfrak{q}(n_1,\dots ,n_k)+\hfill \\ & +{(1-a)}^{k-1}\sum _{i=1}^k\sum _{r=2}^{n_i}{a}^r\sum _{\begin{array}{c}\mathit{\lambda }\in \Lambda \left(\mathit{m}\right)\mathrm{for}\mathit{m}:\\ m_i=r,m_j=1,j\ne i\end{array}}c\left(\mathit{\lambda }\right)\mathfrak{q}(n_1,\dots ,n_{i-1},{\mathbf{n}}_r^{\left(i\right)},n_{i+1},\dots ,n_k)\hfill \\ & ={(1-a)}^k\mathfrak{q}(n_1,\dots ,n_k)\hfill \\ & +{(1-a)}^{k-1}\sum _{i=1}^k\sum _{r=1}^{n_i}{a}^r\sum _{\begin{array}{c}\mathit{\lambda }\in \Lambda \left(\mathit{m}\right)\mathrm{for}\mathit{m}:\\ m_i=r,m_j=1,j\ne i\end{array}}c\left(\mathit{\lambda }\right)\mathfrak{q}(n_1,\dots ,n_{i-1},{\mathbf{n}}_r^{\left(i\right)},n_{i+1},\dots ,n_k)\hfill \end{array}$$

where ${\mathbf{n}}_r^{\left(i\right)}$ is any vector of r positive integers with sum $n_i$ such that ${\lambda }_{ij}$ of them are equal to j. In view of the definition of $c\left(\mathit{\lambda }\right)$, formula (27) is immediately obtained.

If $\mathfrak{q}$ is of Gibbs type, taking into account (24), then

$$q_n\left(r\right|n_1,\dots ,n_{i-1},n_{i+1},\dots ,n_k)=\frac{V_{n,k-1+r}}{V_{n-n_i,k-1}}{S}_{\sigma }(n_i,r)$$

and the second part of the thesis follows by simple algebra. □

Applying Proposition 6 to the Pitman–Yor EPPF defined in (23), one immediately recovers the results stated in Theorem 1 and Corollary 1 of [21].

5. Predictive Distributions

In this section, we provide some expressions for the predictive distributions of mixtures of species sampling sequences.

5.1. Some General Results

Let $\xi$ be as in Definition 2 and let ${\left(Z_n^{\prime }\right)}_n$ and ${\Pi }_n$ be the sequence of exchangeable random variables and the exchangeable random partition appearing in Proposition 3. Let

$${\mathcal{G}}_n=\sigma (Z_1^{\prime },\dots ,Z_{|{\Pi }_n|}^{\prime },{\Pi }_n)$$

be the $\sigma$-field generated by $(Z_1^{\prime },\dots ,Z_{|{\Pi }_n|}^{\prime },{\Pi }_n)$. By Proposition 3, one has ${\xi }_n=Z_{{\mathcal{C}}_n(\Pi )}^{\prime }$ a.s.; hence, ${\xi }_n$ is ${\mathcal{G}}_n$ measurable. Note that, in general, $\sigma ({\xi }_1,\dots ,{\xi }_n)$ can be strictly contained in ${\mathcal{G}}_n$. Set ${\Xi }_n:=\left|{\Pi }_n\right|$ and, for any $k\ge 1$, let ${\mathcal{K}}_{k+1}(·|·)$ be a kernel corresponding to the conditional distribution of $Z_{k+1}^{\prime }$ given $Z_1^{\prime },\dots ,Z_k^{\prime }$ (i.e., the $k+1$-predictive distribution of the exchangeable sequence $Z^{\prime }$). Finally, recall that $\tilde{\Pi }={\Pi }^{*}\left(\xi \right)$ is the partition induced by $\xi$ and define ${\xi }_{1:{\tilde{K}}_n}^{*}=({\xi }_1^{*},\dots ,{\xi }_{{\tilde{K}}_n}^{*})$ as the distinct values in order of appearance of ${\xi }_{1:n}:=({\xi }_1,\dots ,{\xi }_n)$ with ${\tilde{K}}_n=\left|{\tilde{\Pi }}_n\right|$.

Proposition 7.

Let ξ as in Definition 2. Then,

$$\mathbb{P}\{{\xi }_{n+1}\in ·|{\mathcal{G}}_n\}=\sum _{\ell =1}^{{\Xi }_n}{\omega }_{n,\ell }\left({\Pi }_n\right){\delta }_{Z_{\ell }^{\prime }}(·)+{\nu }_n\left({\Pi }_n\right){\mathcal{K}}_{{\Xi }_n+1}(·|Z_1^{\prime },\dots ,Z_{{\Xi }_n}^{\prime })$$

(28)

where ${\nu }_n$ and ${\omega }_{n,\ell }$ are defined by (6) and (7). If $P\{Z_1^{\prime }=Z_2^{\prime }\}=0$, then

$$\begin{array}{cc}\hfill \mathbb{P}\{{\xi }_{n+1}\in ·|{\xi }_1,\dots ,{\xi }_n\}& =\mathbb{P}\{{\xi }_{n+1}\in ·|{\xi }_1^{*},\dots ,{\xi }_{{\tilde{K}}_n}^{*},{\tilde{\Pi }}_n\}\hfill \\ \hfill & =\sum _{\ell =1}^{{\tilde{K}}_n}{\omega }_{n,\ell }\left({\tilde{\Pi }}_n\right){\delta }_{{\xi }_{\ell }^{*}}(·)+{\nu }_n\left({\tilde{\Pi }}_n\right){\mathcal{K}}_{{\tilde{K}}_n+1}(·|{\xi }_1^{*},\dots ,{\xi }_{{\tilde{K}}_n}^{*}).\hfill \end{array}$$

(29)

Proof. 

Set

$$E_{new}^{*}=\{{\Xi }_{n+1}={\Xi }_n+1\}.$$

Since ${\xi }_n=Z_{{\mathcal{C}}_n(\Pi )}^{\prime }$, one can write

$$\begin{array}{cc}\hfill \mathbb{P}\{{\xi }_{n+1}\in A|{\mathcal{G}}_n\}& =\sum _{\ell =1}^{{\Xi }_n}\mathbb{P}\{{\xi }_{n+1}\in A,n+1\in {\Pi }_{\ell ,n}|{\mathcal{G}}_n\}+\mathbb{P}\{{\xi }_{n+1}\in A,E_{new}^{*}|{\mathcal{G}}_n\}\hfill \\ & =\sum _{\ell =1}^{{\Xi }_n}\mathbb{P}\{Z_{\ell }^{\prime }\in A,n+1\in {\Pi }_{\ell ,n}|{\mathcal{G}}_n\}+\mathbb{P}\{Z_{{\Xi }_{n+1}}^{\prime }\in A,E_{new}^{*}|{\mathcal{G}}_n\}\hfill \\ & =\sum _{\ell =1}^{{\Xi }_n}{\delta }_{Z_{\ell }^{\prime }}\left(A\right)\mathbb{P}\{n+1\in {\Pi }_{\ell ,n}|{\mathcal{G}}_n\}+\mathbb{P}\{Z_{{\Xi }_n+1}^{\prime }\in A,E_{new}^{*}|{\mathcal{G}}_n\}\hfill \end{array}$$

Now, since $\Pi$ and ${\left(Z_n^{\prime }\right)}_n$ are independent, it follows that $\mathbb{P}\{n+1\in {\Pi }_{\ell ,n}|{\mathcal{G}}_n\}=\mathbb{P}\{n+1\in {\Pi }_{\ell ,n}|{\Pi }_n\}={\omega }_{n,\ell }\left({\Pi }_n\right)$ and also

$$\begin{array}{cc}\hfill \mathbb{P}\{Z_{{\Xi }_n+1}^{\prime }& \in A,E_{new}^{*}|{\mathcal{G}}_n\}\hfill \\ & =\mathbb{P}\{Z_{{\Xi }_n+1}^{\prime }\in A|Z_1^{\prime },\dots ,Z_{{\Xi }_n}^{\prime }\}\mathbb{P}\left\{E_{new}^{*}\right|{\Pi }_n\}\hfill \\ & ={\mathcal{K}}_{{\Xi }_n+1}\left(A\right|Z_1^{\prime },\dots ,Z_{{\Xi }_n}^{\prime }){\nu }_n\left({\Pi }_n\right).\hfill \end{array}$$

Combining all the claims, one obtains (28). The second part of the proof follows since, if $P\{Z_1^{\prime }=Z_2^{\prime }\}=0$, the $Z_i^{\prime }$s are distinct with probability one. Since $({\xi }_1,\dots ,{\xi }_n)=(Z_{{\mathcal{C}}_1(\Pi )}^{\prime },\dots ,Z_{{\mathcal{C}}_n(\Pi )}^{\prime })$, it follows that ${\tilde{\Pi }}_n={\Pi }_n$, ${\Xi }_n={\tilde{K}}_n$ and $({\xi }_1^{*},\dots ,{\xi }_{{\tilde{K}}_n}^{*})=(Z_1^{\prime },\dots ,Z_{{\Xi }_n}^{\prime })$ with probability one and ${\mathcal{G}}_n=\sigma ({\xi }_1,\dots ,{\xi }_n)$. Hence, (29) follows from (28). □

Remark 5.

Note that (29) can be also derived as follows. $\mathbb{P}\{Z_1^{\prime }=Z_2^{\prime }\}=0$ is equivalent to the fact that $\tilde{H}$ is almost sure diffuse. Hence, conditionally on $\tilde{H}$, we have a $SSS(\mathfrak{q},\tilde{H})$; then, by (PS2) in Section 2.2, one has

$$\begin{array}{cc}\hfill \mathbb{P}\{{\xi }_{n+1}\in ·|{\xi }_1,\dots ,{\xi }_n,\tilde{H}\}& =\sum _{\ell =1}^{{\tilde{K}}_n}{\omega }_{n,\ell }\left({\tilde{\Pi }}_n\right){\delta }_{{\xi }_{\ell }^{*}}(·)+{\nu }_n\left({\tilde{\Pi }}_n\right)\tilde{H}\left(dx\right).\hfill \end{array}$$

(30)

Taking the conditional expectation of the previous equation, given ${\xi }_1,\dots ,{\xi }_n$, we obtain

$$\begin{array}{cc}\hfill \mathbb{P}\{{\xi }_{n+1}\in A|{\xi }_1,\dots ,{\xi }_n\}& =\sum _{\ell =1}^{{\tilde{K}}_n}{\omega }_{n,\ell }\left({\tilde{\Pi }}_n\right){\delta }_{{\xi }_{\ell }^{*}}\left(A\right)+{\nu }_n\left({\tilde{\Pi }}_n\right)\mathbb{E}\left[\tilde{H}\left(A\right)\right|{\xi }_1,\dots ,{\xi }_n]\hfill \end{array}$$

(31)

and the thesis follows since one can check (arguing as in the proof of the proposition) that

$$\mathbb{E}\left[\tilde{H}\left(A\right)\right|{\xi }_1,\dots ,{\xi }_n]=\mathbb{E}\left[\tilde{H}\left(A\right)\right|Z_1^{\prime },\dots ,Z_{{\tilde{K}}_n}^{\prime }]={\mathcal{K}}_{{\tilde{K}}_n+1}\left(A\right|Z_1^{\prime },\dots ,Z_{{\tilde{K}}_n}^{\prime }).$$

Assume now that the random variables $Z_j^{\prime }$ are defined on $\mathbb{X}$ by a Bayesian model with likelihood $f\left(z_j\right|u)$ and prior $Q\left(u\right)$, where f is a density with respect to a dominating measure $\lambda$ and Q is a probability measure defined on a Polish space U (the space of parameters). In other words,

$$\mathbb{P}\{Z_1^{\prime }\in A_1,\dots ,Z_k^{\prime }\in A_k\}={\int }_U\left({\int }_{A_1\times A_2\cdots \times A_k}\prod _{j=1}^{k}f\left(z_j\right|u)\lambda \left(d{z}_1\right)\dots \lambda \left(d{z}_k\right)\right)Q\left(du\right).$$

Note that this means that $\tilde{H}\left(A\right)={\int }_{A}f\left(z\right|\tilde{u})\lambda \left(dz\right)$, where $\tilde{u}\sim Q$. Bayes’ theorem (see, e.g., Theorem 1.31 in [33]) gives

$$\mathbb{P}\{Z_{k+1}^{\prime }\in d{z}_{k+1}|Z_1^{\prime },\dots ,Z_k^{\prime }\}=\left({\int }_{U}f\left(z_{k+1}\right|u)Q\left(du\right|Z_1^{\prime },\dots ,Z_k^{\prime })\right)\lambda \left(d{z}_{k+1}\right)$$

where $Q\left(du\right|Z_1,\dots ,Z_k)$ is the usual posterior distribution, which is

$$Q\left(du\right|Z_1^{\prime },\dots ,Z_k^{\prime }):=\frac{{\prod }_{j=1}^{k}f\left(Z_j^{\prime }\right|u)Q\left(du\right)}{{\int }_U{\prod }_{j=1}^{k}f\left(Z_j^{\prime }\right|v)Q\left(dv\right)}.$$

If $\lambda$ is a diffuse measure, one obtains $\mathbb{P}\{Z_1^{\prime }=Z_2^{\prime }\}=0$. Hence, (29) in Proposition 7 applies and one has

$$\begin{array}{cc}\hfill \mathbb{P}\{{\xi }_{n+1}\in dx|{\xi }_1,\dots ,{\xi }_n\}=& \sum _{\ell =1}^{{\tilde{K}}_n}{\omega }_{n,\ell }\left({\tilde{\Pi }}_n\right){\delta }_{{\xi }_{\ell }^{*}}\left(dx\right)\hfill \\ \hfill & +{\nu }_n\left({\tilde{\Pi }}_n\right)\left({\int }_{U}f\left(x\right|u)Q\left(du\right|{\xi }_1^{*},\dots ,{\xi }_{{\tilde{K}}_n}^{*})\right)dx.\hfill \end{array}$$

(32)

For example, one can apply this result to a mixture of Dirichlet processes in the sense of [10], as briefly described at the end of Section 3.1. Assume that ${\alpha }_{\tilde{u}}\left(\mathbb{X}\right)$ and $\tilde{H}(·)={\alpha }_{\tilde{u}}(·)/{\alpha }_{\tilde{u}}\left(\mathbb{X}\right)$ are independent and that ${\alpha }_u\left(A\right)/{\alpha }_u\left(\mathbb{X}\right)={\int }_{Z}f\left(z\right|u)\lambda \left(dz\right)$ for a suitable dominating diffuse measure $\lambda$.

Under these hypotheses, a sample ${\left({\xi }_n\right)}_{n\ge 1}$ from a mixture of Dirichlet processes is an mSSS with $\mathfrak{q}$ described in (15) and, in addition, $\mathbb{P}\{Z_1^{\prime }=Z_2^{\prime }\}=0$. Combining (15) with (6) and (7), one obtains

$${\omega }_{n,\ell }\left({\tilde{\Pi }}_n\right)=\left|{\tilde{\Pi }}_{n,\ell }\right|\frac{{\int }_U\frac{{\alpha }_u{\left(\mathbb{X}\right)}^{{\tilde{K}}_n}}{{\left({\alpha }_u\left(\mathbb{X}\right)\right)}_{n+1}}Q\left(du\right)}{{\int }_U\frac{{\alpha }_u{\left(\mathbb{X}\right)}^{{\tilde{K}}_n}}{{\left({\alpha }_u\left(\mathbb{X}\right)\right)}_n}Q\left(du\right)}$$

and

$${\nu }_n\left({\tilde{\Pi }}_n\right)=\frac{{\int }_U\frac{{\alpha }_u{\left(\mathbb{X}\right)}^{{\tilde{K}}_n+1}}{{\left({\alpha }_u\left(\mathbb{X}\right)\right)}_{n+1}}Q\left(du\right)}{{\int }_U\frac{{\alpha }_u{\left(\mathbb{X}\right)}^{{\tilde{K}}_n}}{{\left({\alpha }_u\left(\mathbb{X}\right)\right)}_n}Q\left(du\right)}$$

Hence, the predictive distribution of ${\xi }_{n+1}$ given $({\xi }_1,\dots ,{\xi }_n)$ is (33) for ${\omega }_{n,\ell }\left({\tilde{\Pi }}_n\right)$ and ${\nu }_n\left({\tilde{\Pi }}_n\right)$ given above.

Note that the same result can be deduced by combining Lemma 1 and Corollary 3.2’ in [10].

Example 1

(Species Sampling NIG). Let $Z_n^{\prime }$ be defined as a mixture of normal random variables with Normal-Inverse-Gamma prior. In other words, given ${\mu }_0\in \mathbb{R}$, $k_0>0,{\alpha }_0>0,{\beta }_0>0$,

$$\begin{array}{cc}& Z_n|\tilde{\mu },{\tilde{\sigma }}^2\stackrel{i.i.d.}{\sim }\mathcal{N}(\tilde{\mu },{\tilde{\sigma }}^2)\hfill \\ & \tilde{\mu }|{\tilde{\sigma }}^2\sim \mathcal{N}({\mu }_0,{\tilde{\sigma }}^2/k_0)\hfill \\ & {\tilde{\sigma }}^2\sim \mathrm{In}\Gamma ({\alpha }_0,{\beta }_0)\hfill \end{array}$$

where $\mathcal{N}(\mu ,{\sigma }^2)$ denotes a normal distribution of mean μ and variance ${\sigma }^2$ and $\mathrm{In}\Gamma (\alpha ,\beta )$ is the inverse gamma distribution with shape α and scale β. Let ${\mathcal{T}}_{\nu }(·|\mu ,{\sigma }^2)$ be the density of a Student-T distribution with ν degrees of freedom and $(\mu ,\sigma )$ position/scale parameters, i.e.,

$${\mathcal{T}}_{\nu }\left(x\right|\mu ,{\sigma }^2):=\frac{1}{\sqrt{{\sigma }^2}}\frac{\Gamma \left(\frac{\nu +1}{2}\right)}{\sqrt{\nu \pi }\Gamma \left(\frac{\nu }{2}\right)}{\left(1+\frac{1}{\nu {\sigma }^2}{\left(x-\mu \right)}^2\right)}^{\frac{-\nu +1}{2}}.$$

It is well known that, under these assumptions, ${\mathcal{K}}_{k+1}\left(A\right|z_1,\dots ,z_k)$ has density ${\mathcal{T}}_{2{\alpha }_k}\left(z\right|{\mu }_k,{\sigma }_k^2)$, where the parameters are updated

$$\begin{array}{cc}\hfill {\mu }_k& =\frac{k_0{\mu }_0+k{\overline{z}}_n}{k_0+n}{\overline{z}}_k=\frac{1}{k}\sum _{j=1}^k{z}_j{\alpha }_k={\alpha }_0+k/2,\hfill \\ \hfill {\sigma }_k^2& =\frac{\left({\beta }_0+\frac{1}{2}{\sum }_{j=1}^k{(z_j-{\overline{z}}_k)}^2+\frac{k{k}_0{({\overline{z}}_k-{\mu }_0)}^2}{2(n+k_0)}\right)(k_0+k+1)}{({\alpha }_0+k/2)(k_0+k)}\hfill \end{array}$$

Thus, in this case, if $z_1,\dots ,z_k$ are distinct real numbers and ${\pi }_n=[{\pi }_{1,n},\dots ,{\pi }_{k,n}]$, one has

$$\begin{array}{cc}\hfill \mathbb{P}\{{\xi }_{n+1}\in dx|{\xi }_1^{*}=z_1,\dots ,{\xi }_k^{*}=z_k,{\Pi }^{*}\left(\xi \right)={\pi }_n\}& =\sum _{\ell =1}^k{\omega }_{n,\ell }\left({\pi }_n\right){\delta }_{{\xi }_{\ell }^{*}}\left(dx\right)\hfill \\ \hfill & +{\nu }_n\left({\pi }_n\right){\mathcal{T}}_{2{\alpha }_k}\left(x\right|{\mu }_n,{\sigma }_k^2)dx.\hfill \end{array}$$

(33)

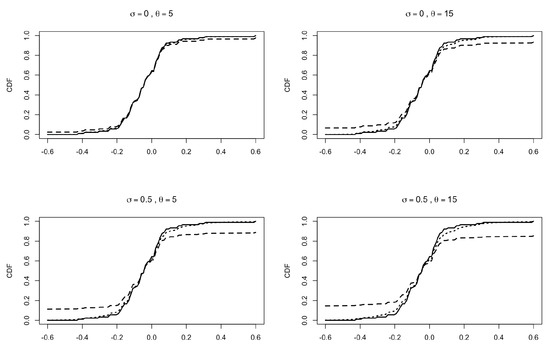
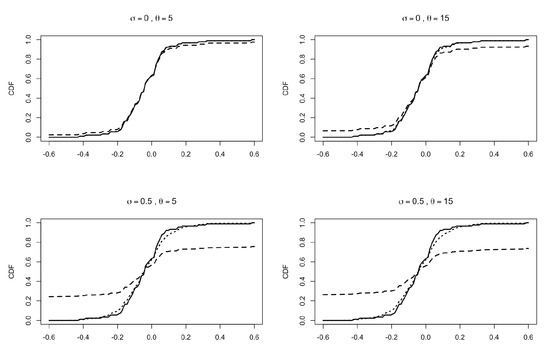
We show an application of (33) to a true dataset by choosing ${\omega }_{n,\ell }$ and ${\nu }_n$ according to a Pitman–Yor two-parameter family; see (23). The data are the relative changes in reported larcenies between 1991 and 1995 (relative to 1991) for the 90 most populous US counties, taken from Section 2.1 of [34]. We apply our models to both the raw data and the rounded data (approximated to the second digit) in order to obtain ties in the ξs. In the evaluation of the predictive CDFs, we fix ${\mu }_0=0$, ${\alpha }_0=0.1$, ${\beta }_0=0.1$ and $k_0=0.1$. In Figure 2, we report the empirical CDF of the rounded data (solid line), the predictive CDF obtained from (33) (dotted line) and the predictive CDF of a Pitman–Yor species sampling sequence (see PS2) with $H={\mathcal{T}}_{2{\alpha }_0}(·|{\mu }_0,{\sigma }_0^2)$, ${\sigma }_0^2={\beta }_0(k_0+1)/{\alpha }_0{k}_0$ (dashed line). Similar plots are reported in Figure 3, with raw data in place of the rounded data. Note that in all the various settings, the influence of the hyper-parameters $(\theta ,\sigma )$ is stronger in the CDF of the simple Pitman–Yor species sampling model with respect to the corresponding predictive CDF derived from (33).

Figure 2. Predictive CDFs for the relative changes in larcenies between 1991 and 1995 (relative to 1991) for the 90 most populous US counties; data taken from Section 2.1 of [34]. Data have been rounded to the second decimal. Here, $n=90$ and $k=36$. Solid line: empirical CDF. Dotted line: predictive CDF from (33). Dashed line: predictive CDF from PS2 with $H={\mathcal{T}}_{2{\alpha }_0}(·|{\mu }_0,{\sigma }_0^2)$, ${\sigma }_0^2={\beta }_0(k_0+1)/{\alpha }_0{k}_0$. Different plots correspond to different values of $\theta$ and $\sigma$. In all the plots, the predictive CDFs are evaluated with ${\mu }_0=0$, ${\alpha }_0=0.1$, ${\beta }_0=0.1$ and $k_0=0.1$.

Figure 3. Predictive CDFs for the relative changes in larcenies between 1991 and 1995 (relative to 1991) for the 90 most populous US counties; data taken from Section 2.1 of [34]. Raw data, without rounding. Here, $n=90$ and $k=36$. Solid line: empirical CDF. Dotted line: predictive CDF from (33). Dashed line: predictive CDF from PS2 with $H={\mathcal{T}}_{2{\alpha }_0}(·|{\mu }_0,{\sigma }_0^2)$, ${\sigma }_0^2={\beta }_0(k_0+1)/{\alpha }_0{k}_0$. Different plots correspond to different values of $\theta$ and $\sigma$. In all the plots, the predictive CDFs are evaluated with ${\mu }_0=0$, ${\alpha }_0=0.1$, ${\beta }_0=0.1$ and $k_0=0.1$.

5.2. Predictive Distributions for $gSSS$

We now deduce an explicit form for the predictive distribution of a $gSSS$ with general base measure H given in (25).

Recall that we denote by ${\tilde{\Pi }}_n$ the partition induced by ${\xi }_{1:n}$, with ${\tilde{K}}_n=\left|{\tilde{\Pi }}_n\right|$, and by ${\Pi }_n$ the latent partition appearing in Proposition 3. We also set

$${\zeta }_i=\left\{\begin{array}{cc}\ell \hfill & \mathrm{if}{\xi }_i^{*}={\overline{x}}_{\ell }\hfill \\ 0\hfill & \mathrm{if}{\xi }_i^{*}\in {\mathbb{X}}_0^c.\hfill \end{array}\right.$$

The variable ${\zeta }_i$ is a discrete random variable that takes value 0 if ${\xi }_i^{*}$ comes from the diffuse component of H.

Let ${\mathcal{P}}_{{\tilde{\pi }}_n,z_{1:k}}\subset {\mathcal{P}}_{{\tilde{\pi }}_n}$ be the set of all the possible configurations of ${\Pi }_n$ that are compatible with the observed partition ${\tilde{\Pi }}_n={\tilde{\pi }}_n$ and the additional information given by ${\zeta }_{1:{\tilde{K}}_n}=z_{1:k}$, ${\tilde{K}}_n=k$. In order to describe this set, observe that if $z_i>0$, then the block ${\tilde{\pi }}_{i,n}$ may arise from the union of more blocks in ${\pi }_n$, while, if $z_i=0$, then ${\tilde{\pi }}_{i,n}={\pi }_{\varphi \left(i\right),n}$ for some $\varphi$. Note that it may happen that $\varphi \left(i\right)\ne i$.

Recalling that the elements in $\mathit{m}=(m_1,\dots ,m_k)$ in (17) are used to describe the numbers of sub-blocks into which the blocks of ${\tilde{\pi }}_n$ have been divided to form the latent partition ${\pi }_n$, it turns out that the set ${\mathcal{P}}_{{\tilde{\pi }}_n,z_{1:k}}$ has the additional constraint $m_i=1$ whenever $z_i=0$. These considerations yield that, starting from ${\tilde{\pi }}_n$ and $z_{1:k}$, the set of admissible $\mathit{m}$ can also be described by resorting to the definition of $\mathcal{Z}\left(\mathit{m}\right)$ as follows:

$$\begin{array}{cc}\hfill \mathcal{M}(\mathit{n},z_{1:k})& :=\left\{\mathit{m}\in \mathcal{M}\left(\mathit{n}\right):z_{1:k}\in \mathcal{Z}\left(\mathit{m}\right)\right\}\hfill \\ & =\left\{\mathit{m}\in {\mathbb{N}}^k:m_i=1\mathrm{if}{z}_i=0,1\le m_i\le n_i\mathrm{if}{z}_i>0\right\}.\hfill \end{array}$$

With this position, one has

$$\begin{array}{cc}\hfill {\mathcal{P}}_{{\tilde{\pi }}_n,z_{1:k}}& ={\cup }_{\mathit{m}\in \mathcal{M}\left(\mathit{n}\right):z_{1:k}\in \mathcal{Z}\left(\mathit{m}\right)}{\cup }_{\mathit{\lambda }\in \Lambda (\mathit{n},\mathit{m})}{\mathcal{P}}_{{\tilde{\pi }}_n}\left(\mathit{\lambda }\right)\hfill \\ \hfill & ={\cup }_{\mathit{m}\in \mathcal{M}(\mathit{n},z_{1:k})}{\cup }_{\mathit{\lambda }\in \Lambda (\mathit{n},\mathit{m})}{\mathcal{P}}_{{\tilde{\pi }}_n}\left(\mathit{\lambda }\right),\hfill \end{array}$$

(34)

where $\Lambda (\mathit{n},\mathit{m})$ and ${\mathcal{P}}_{{\tilde{\pi }}_n}\left(\mathit{\lambda }\right)$ have been defined in Section 4.1.

For any $\mathit{m}$ in $\mathcal{M}(\mathit{n},z_{1:k})$ and any $\mathit{\lambda }$ in $\Lambda (\mathit{n},\mathit{m})$, we define

$${\mathit{\lambda }}^{new}:=[{\mathit{\lambda }}_1,\dots ,{\mathit{\lambda }}_k,1].$$

In other words, ${\mathit{\lambda }}^{new}$ corresponds to the configuration obtained from $\mathit{\lambda }$ by adding one new element as a new block. In the following, let $\tilde{\mathbf{N}}=\left(\right|{\tilde{\Pi }}_{1,n}|,\dots ,|{\tilde{\Pi }}_{{\tilde{K}}_n,n}\left|\right)$, and let ${\tilde{\mathbf{N}}}^{i+}$ be obtained from $\tilde{\mathbf{N}}$ by adding 1 to its i-th component.

Proposition 8.

Let ${\left({\xi }_n\right)}_{n\ge 1}$ be a $gSSS(\mathfrak{q},H)$. Then, for any A in $\mathcal{X}$,

$$P\{{\xi }_{n+1}\in A|{\xi }_{1:n}\}=\frac{1}{{\mathcal{Z}}_n}\left(\sum _{i=1}^{{\tilde{K}}_n}{w}_i{\delta }_{{\xi }_i^{*}}\left(A\right)+w_0{\overline{H}}_n\left(A\right)\right)a.s.$$

where

$$\begin{array}{cc}& {\overline{H}}_n\left(A\right):=\left[\sum _{\ell :{\overline{x}}_{\ell }\notin {\xi }_{1:{\tilde{K}}_n}^{*}}{a}_{\ell }{\delta }_{{\overline{x}}_{\ell }}\left(A\right)+(1-a)H^c\left(A\right)\right]{H(\mathbb{X}\backslash {\xi }_{1:{\tilde{K}}_n}^{*})}^{-1},\hfill \\ & w_i:=\sum _{\mathit{m}\in \mathcal{M}({\tilde{\mathbf{N}}}^{i+},{\zeta }_{1:{\tilde{K}}_n})}\prod _{j:{\zeta }_j>0}{a}_{{\zeta }_j}^{m_j}\sum _{\mathit{\lambda }\in \Lambda \left({\tilde{\mathbf{N}}}^{i+},\mathit{m}\right)}\mathit{c}\left(\mathit{\lambda }\right)\overline{\mathfrak{q}}\left(\mathit{\lambda }\right),\hfill \\ & w_0:=H(\mathbb{X}\backslash {\xi }_{1:{\tilde{K}}_n}^{*})\sum _{\mathit{m}\in \mathcal{M}(\tilde{\mathbf{N}},{\zeta }_{1:{\tilde{K}}_n})}\prod _{j:{\zeta }_j>0}{a}_{{\zeta }_j}^{m_j}\sum _{\mathit{\lambda }\in \Lambda \left(\tilde{\mathbf{N}},\mathit{m}\right)}\mathit{c}\left(\mathit{\lambda }\right)\overline{\mathfrak{q}}\left({\mathit{\lambda }}^{new}\right),\hfill \\ & {\mathcal{Z}}_n:=\sum _{\mathit{m}\in \mathcal{M}(\tilde{\mathbf{N}},{\zeta }_{1:{\tilde{K}}_n})}\prod _{j:{\zeta }_j>0}{a}_{{\zeta }_j}^{m_j}\sum _{\mathit{\lambda }\in \Lambda \left(\tilde{\mathbf{N}},\mathit{m}\right)}\mathit{c}\left(\mathit{\lambda }\right)\overline{\mathfrak{q}}\left(\mathit{\lambda }\right).\hfill \end{array}$$

Proof. 

We start by defining the following events for $i=1,\dots ,{\tilde{K}}_n$:

$$E_i=\{{\xi }_{n+1}={\xi }_i^{*}\},E_{new}=\{{\xi }_{n+1}\notin {\xi }_{1:{\tilde{K}}_n}^{*}\}.$$

Since conditioning on ${\xi }_{1:n}$ is equivalent to the condition on $[{\xi }_{1:{\tilde{K}}_n}^{*},{\tilde{\Pi }}_n]$, one can write

$$P\{{\xi }_{n+1}\in A|{\xi }_{1:n}\}=\sum _{i=1}^{{\tilde{K}}_n}P\{{\xi }_{n+1}\in A,E_i|{\xi }_{1:{\tilde{K}}_n}^{*},{\tilde{\Pi }}_n\}+P\{{\xi }_{n+1}\in A,E_{new}|{\xi }_{1:{\tilde{K}}_n}^{*},{\tilde{\Pi }}_n\}$$

Now, set

$$E_{new}^{*}:=\{{\mathcal{C}}_{n+1}(\Pi )=|{\Pi }_n|+1\}$$

and

$$E_i^{*}=\left\{\right|{\mathcal{C}}_{n+1}(\Pi )|\le |{\Pi }_n|\mathrm{and}{\Pi }_{{\mathcal{C}}_{n+1}(\Pi ),n}\subset {\tilde{\Pi }}_{i,n}\}.$$

On ${\zeta }_i=0$, one has (up to zero probability sets)

$$\{{\xi }_{n+1}\in A\}\cap E_i=\{{\xi }_i^{*}\in A\}\cap E_i^{*}$$

while, on ${\zeta }_i>0$ (up to zero probability sets),

$$\{{\xi }_{n+1}\in A\}\cap E_i=\left(\{{\xi }_i^{*}\in A\}\cap E_i^{*}\right)\cup \left(\{{\xi }_i^{*}\in A\}\cap \{Z_{|{\Pi }_n|+1}^{\prime }={\overline{x}}_{{\zeta }_i}\}\cap E_{new}^{*}\right).$$

Note that (up to zero probability sets)

$$\{Z_{|{\Pi }_n|+1}^{\prime }={\overline{x}}_{{\zeta }_i}\}\cap E_{new}^{*}\cap \{{\zeta }_i=0\}=\varnothing .$$

Hence,

$$\begin{array}{cc}\hfill \mathbb{P}\{{\xi }_{n+1}\in A,E_i& |{\xi }_{1:{\tilde{K}}_n}^{*},{\tilde{\Pi }}_n\}\hfill \\ \hfill & ={\delta }_{{\xi }_i^{*}}\left(A\right)\mathbb{P}\{E_i^{*}\cup (\{Z_{|{\Pi }_n|+1}^{\prime }={\overline{x}}_{{\zeta }_i}\}\cap E_{new}^{*})|{\tilde{\Pi }}_n,{\xi }_{1:{\tilde{K}}_n}^{*}\}.\hfill \end{array}$$

(35)

Similarly, using that $E_{new}\subset E_{new}^{*}$, one obtains

$$\begin{array}{cc}\hfill \mathbb{P}\{{\xi }_{n+1}\in A,E_{new}|{\xi }_{1:n}\}& =\mathbb{P}\{{\xi }_{n+1}\in A,E_{new},E_{new}^{*}|{\tilde{\Pi }}_n,{\xi }_{1:{\tilde{K}}_n}^{*}\}\hfill \\ \hfill & =\mathbb{P}\{{\xi }_{n+1}\in A,E_{new}|{\xi }_{1:{\tilde{K}}_n}^{*},E_{new}^{*}\}\mathbb{P}\left\{E_{new}^{*}\right|{\tilde{\Pi }}_n,{\xi }_{1:{\tilde{K}}_n}^{*}\}\hfill \\ \hfill & =H_n\left(A\right)\mathbb{P}\left\{E_{new}^{*}\right|{\tilde{\Pi }}_n,{\xi }_{1:{\tilde{K}}_n}^{*}\}\hfill \end{array}$$

(36)

where

$$H_n\left(A\right)=\sum _{\ell :{\overline{x}}_{\ell }\notin {\xi }_{1:{\tilde{K}}_n}^{*}}{\overline{a}}_{\ell }{\delta }_{{\overline{x}}_{\ell }}\left(A\right)+(1-a)H^c\left(A\right).$$

At this stage, note that, by construction,

$$\mathcal{L}\left({\xi }_{1:{\tilde{K}}_n}^{*}\right|{\Pi }_n,Z_{|{\Pi }_n|+1}^{\prime },{\zeta }_{1:{\tilde{K}}_n},{\tilde{\Pi }}_n,{\Pi }_{n+1})=\mathcal{L}\left({\xi }_{1:{\tilde{K}}_n}^{*}\right|{\zeta }_{1:{\tilde{K}}_n})$$

where $\mathcal{L}\left({\xi }_{1:{\tilde{K}}_n}^{*}\right|{\zeta }_{1:{\tilde{K}}_n})$ is characterized by

$$P({\xi }_1^{*}\in A_1,\dots ,{\xi }_{{\tilde{K}}_n}^{*}\in A_{{\tilde{K}}_n}|{\zeta }_{1:{\tilde{K}}_n})=\prod _{i=1}^{{\tilde{K}}_n}\left(H^c\left(A_i\right)\mathbf{1}\{{\zeta }_i=0\}+{\delta }_{{\overline{x}}_{{\zeta }_i}}\left(A_i\right)\mathbf{1}\{{\zeta }_i>0\}\right),$$

and then

$$\mathcal{L}(Z_{|{\Pi }_n|+1}^{\prime },{\zeta }_{1:{\tilde{K}}_n},{\tilde{\Pi }}_n,{\Pi }_{n+1},{\xi }_{1:{\tilde{K}}_n}^{*}|{\Pi }_n)=\mathcal{L}(Z_{|{\Pi }_n|+1}^{\prime },{\zeta }_{1:{\tilde{K}}_n},{\tilde{\Pi }}_n,{\Pi }_{n+1}|{\Pi }_n)\mathcal{L}\left({\xi }_{1:{\tilde{K}}_n}^{*}\right|{\zeta }_{1:{\tilde{K}}_n}).$$

Hence,

$$\begin{array}{cc}\hfill \mathcal{L}({\Pi }_n,{\Pi }_{n+1},Z_{|{\Pi }_n|+1}^{\prime },& {\xi }_{1:{\tilde{K}}_n}^{*},{\zeta }_{1:{\tilde{K}}_n},{\tilde{\Pi }}_n)\hfill \\ \hfill & =\mathcal{L}\left({\Pi }_n\right)\mathcal{L}(Z_{|{\Pi }_n|+1}^{\prime },{\zeta }_{1:{\tilde{K}}_n},{\tilde{\Pi }}_n,{\Pi }_{n+1}|{\Pi }_n)\mathcal{L}\left({\xi }_{1:{\tilde{K}}_n}^{*}\right|{\zeta }_{1:{\tilde{K}}_n})\hfill \end{array}$$

(37)

which shows, in particular, that $[{\Pi }_n,{\Pi }_{n+1},Z_{|{\Pi }_n|+1}^{\prime },{\tilde{\Pi }}_n]$ and ${\xi }_{1:{\tilde{K}}_n}^{*}$ are conditionally independent given ${\zeta }_{1:{\tilde{K}}_n}$. Since $E_i^{*}$, $E_{new}^{*}$ and $\{Z_{|{\Pi }_n|+1}^{\prime }={\overline{x}}_{{\zeta }_i}\}\cap E_{new}^{*}$ depend logically only on ${\Pi }_{n+1},Z_{|{\Pi }_n|+1}^{\prime },{\tilde{\Pi }}_n,{\zeta }_{1:{\tilde{K}}_n}$, one obtains

$$\begin{array}{cc}\hfill & \mathbb{P}\left\{E_i^{*}\right|{\tilde{\Pi }}_n,{\xi }_{1:{\tilde{K}}_n}^{*}\}=\mathbb{P}\left\{E_i^{*}\right|{\tilde{\Pi }}_n,{\zeta }_{1:{\tilde{K}}_n}\},\hfill \\ \hfill & \mathbb{P}\{(Z_{|{\Pi }_n|+1}^{\prime }={\overline{x}}_{{\zeta }_i})\cap E_{new}^{*}|{\tilde{\Pi }}_n,{\xi }_{1:{\tilde{K}}_n}^{*}\}=\mathbb{P}\{(Z_{|{\Pi }_n|+1}^{\prime }={\overline{x}}_{{\zeta }_i})\cap E_{new}^{*}|{\tilde{\Pi }}_n,{\zeta }_{1:{\tilde{K}}_n}\}\hfill \end{array}$$

(38)

and, finally,

$$\mathbb{P}\left\{E_{new}^{*}\right|{\tilde{\Pi }}_n,{\xi }_{1:{\tilde{K}}_n}^{*}\}=\mathbb{P}\left\{E_{new}^{*}\right|{\tilde{\Pi }}_n,{\zeta }_{1:{\tilde{K}}_n}\}.$$

(39)

Since $[{\tilde{\Pi }}_n,{\zeta }_{1:{\tilde{K}}_n},{\tilde{K}}_n]$ are discrete random variables, we use the elementary definition of the conditional probability of events to evaluate the conditional distributions (38) and (39). Specifically, assume that ${\tilde{K}}_n=k$, $[{\tilde{\Pi }}_n,{\zeta }_{1:{\tilde{K}}_n}]=[{\tilde{\pi }}_n,z_{1:k}]$, $\tilde{\mathbf{N}}=\mathit{n}$, and, for a given event E, write

$$\mathbb{P}\left\{E\right|{\tilde{\Pi }}_n={\tilde{\pi }}_n,{\zeta }_{1:{\tilde{K}}_n}=z_{1:k}\}=\frac{\mathbb{P}\{E,{\tilde{\Pi }}_n={\tilde{\pi }}_n,{\zeta }_{1:{\tilde{K}}_n}=z_{1:k}\}}{\mathbb{P}\{{\tilde{\Pi }}_n={\tilde{\pi }}_n,{\zeta }_{1:{\tilde{K}}_n}=z_{1:k}\}}.$$

(40)

As for the denominator in (40), letting ${\mathcal{M}}_n^{*}=\mathcal{M}(\mathit{n},z_{1:k})$ and $J=\#\{i:z_i>0\}$, using (34), one obtains

$$\begin{array}{cc}\hfill \mathbb{P}\{{\tilde{\Pi }}_n=& {\tilde{\pi }}_n,{\zeta }_{1:{\tilde{K}}_n}=z_{1:k}\}\hfill \\ & =\sum _{{\pi }_n\in {\mathcal{P}}_{{\tilde{\pi }}_n,z_{1:k}}}\mathbb{P}\{{\tilde{\Pi }}_n={\tilde{\pi }}_n,{\zeta }_{1:{\tilde{K}}_n}=z_{1:k},{\Pi }_n={\pi }_n\}\hfill \\ & =\sum _{\mathit{m}\in {\mathcal{M}}_n^{*}}\sum _{\mathit{\lambda }\in \Lambda (\mathit{n},\mathit{m})}\sum _{{\pi }_n\in {\mathcal{P}}_{{\tilde{\pi }}_n}\left(\mathit{\lambda }\right)}\mathbb{P}\{{\tilde{\Pi }}_n={\tilde{\pi }}_n,{\zeta }_{1:n}=z_{1:k},{\Pi }_n={\pi }_n\}\hfill \\ & ={(1-a)}^{k-J}\sum _{\mathit{m}\in {\mathcal{M}}_n^{*}}\prod _{j:z_j>0}{a}_{z_j}^{m_j}\sum _{\mathit{\lambda }\in \Lambda (\mathit{n},\mathit{m})}\sum _{{\pi }_n\in {\mathcal{P}}_{{\tilde{\pi }}_n}\left(\mathit{\lambda }\right)}\overline{\mathfrak{q}}\left(\mathit{\lambda }\right)\hfill \\ & ={(1-a)}^{k-J}\sum _{\mathit{m}\in {\mathcal{M}}_n^{*}}\prod _{j:z_j>0}{a}_{z_j}^{m_j}\sum _{\mathit{\lambda }\in \Lambda (\mathit{n},\mathit{m})}\mathit{c}\left(\mathit{\lambda }\right)\overline{\mathfrak{q}}\left(\mathit{\lambda }\right).\hfill \end{array}$$

As for the numerators in (40), when $E=E_{new}^{*}$, we start from

$$\begin{array}{cc}& P\{E_{new}^{*},{\tilde{\Pi }}_n={\tilde{\pi }}_n,{\zeta }_{1:{\tilde{K}}_n}=z_{1:k},{\Pi }_n={\pi }_n\}\hfill \\ & =P\left\{E_{new}^{*}\right|{\Pi }_n={\pi }_n\}P\{{\tilde{\Pi }}_n={\tilde{\pi }}_n,{\zeta }_{1:{\tilde{K}}_n}=z_{1:k},{\Pi }_n={\pi }_n\}\hfill \\ & =P\left\{E_{new}^{*}\right|{\Pi }_n={\pi }_n\}{(1-a)}^{k-J}\prod _{j:z_j>0}{a}_{z_j}^{m_j}\overline{\mathfrak{q}}\left(\mathit{\lambda }\right)\hfill \\ & ={(1-a)}^{k-J}\prod _{j:z_j>0}{a}_{z_j}^{m_j}\overline{\mathfrak{q}}\left({\mathit{\lambda }}^{new}\right).\hfill \end{array}$$

where, in the last equality, we used that for ${\pi }_n\in {\mathcal{P}}_{{\tilde{\pi }}_n}\left(\mathit{\lambda }\right)$, one has

$$P\left\{E_{new}^{*}\right|{\Pi }_n={\pi }_n\}=\frac{\overline{\mathfrak{q}}\left({\mathit{\lambda }}^{new}\right)}{\overline{\mathfrak{q}}\left(\mathit{\lambda }\right)}.$$

Taking the sum over ${\mathcal{P}}_{{\tilde{\pi }}_n,z_{1:k}}$ gives

$$P\{E_{new}^{*},{\tilde{\Pi }}_n={\tilde{\pi }}_n,{\zeta }_{1:{\tilde{K}}_n}=z_{1:k}\}={(1-a)}^{k-J}\sum _{\mathit{m}\in {\mathcal{M}}_n^{*}}\prod _{j:z_j>0}{a}_{z_j}^{m_j}\sum _{\mathit{\lambda }\in \Lambda \left(\mathit{n},\mathit{m}\right)}\mathit{c}\left(\mathit{\lambda }\right)\overline{\mathfrak{q}}\left({\mathit{\lambda }}^{new}\right).$$

Combining these with (39) and (40) and recalling that ${\mathcal{M}}_n^{*}=\mathcal{M}(\mathit{n},z_{1:k})$, one obtains

$$\mathbb{P}\left\{E_{new}^{*}\right|{\tilde{\Pi }}_n,{\xi }_{1:{\tilde{K}}_n}^{*}\}=\frac{{\sum }_{\mathit{m}\in \mathcal{M}(\mathit{n},z_{1:k})}{\prod }_{j:z_j>0}{a}_{z_j}^{m_j}{\sum }_{\mathit{\lambda }\in \Lambda \left(\mathit{n},\mathit{m}\right)}\mathit{c}\left(\mathit{\lambda }\right)\overline{\mathfrak{q}}\left({\mathit{\lambda }}^{new}\right)}{{\sum }_{\mathit{m}\in \mathcal{M}(\mathit{n},z_{1:k})}{\prod }_{j:z_j>0}{a}_{z_j}^{m_j}{\sum }_{\mathit{\lambda }\in \Lambda \left(\mathit{n},\mathit{m}\right)}\mathit{c}\left(\mathit{\lambda }\right)\overline{\mathfrak{q}}\left(\mathit{\lambda }\right)}.$$

Finally, it remains to consider (40) when $E=E_i^{*}\cup (\{Z_{|{\Pi }_n|+1}^{\prime }={\overline{x}}_{{\zeta }_i}\}\cap E_{new}^{*})$. Now, observe that

$$\begin{array}{cc}\hfill (E_i^{*}& \cup (\{Z_{|{\Pi }_n|+1}^{\prime }={\overline{x}}_{{\zeta }_i}\}\cap E_{new}^{*}))\cap \{{\tilde{\Pi }}_n={\tilde{\pi }}_n,{\zeta }_{1:{\tilde{K}}_n}=z_{1:k}\}\hfill \\ & =\{{\tilde{\Pi }}_{n+1}={\tilde{\pi }}_n^{i+},{\zeta }_{1:{\tilde{K}}_n}=z_{1:k}\}=\{{\tilde{\Pi }}_{n+1}={\tilde{\pi }}_n^{i+},{\zeta }_{1:{\tilde{K}}_{n+1}}=z_{1:k}\}\hfill \end{array}$$

where ${\tilde{\pi }}_n^{i+}$ denote the partition in ${\mathcal{P}}_{n+1}$ obtained from ${\tilde{\pi }}_n$ by adding $n+1$ to the i-th block of ${\tilde{\pi }}_n$. Note that, for the second equality, we used that, on ${\tilde{\Pi }}_{n+1}={\tilde{\pi }}_n^{i+}$, one has ${\tilde{K}}_{n+1}={\tilde{K}}_n=k$.

Hence, using (34) with ${\tilde{\pi }}_n^{i+}$ in place of ${\tilde{\pi }}_n$, one concludes that

$$\begin{array}{cc}& \mathbb{P}\{{\tilde{\Pi }}_{n+1}={\tilde{\pi }}_n^{i+},{\zeta }_{1:{\tilde{K}}_{n+1}}=z_{1:k}\}\hfill \\ & =\sum _{\begin{array}{c}\mathit{m}\in \mathcal{M}({\mathit{n}}^{i+},z_{1:k})\\ \mathit{\lambda }\in \Lambda (\mathit{n},\mathit{m})\end{array}}\sum _{{\pi }_{n+1}\in {\mathcal{P}}_{{\tilde{\pi }}_{n+1}}\left(\mathit{\lambda }\right)}P\{{\tilde{\Pi }}_{n+1}={\tilde{\pi }}_n^{i+},{\Pi }_{n+1}={\pi }_{n+1},{\zeta }_{1:{\tilde{K}}_{n+1}}=z_{1:k}\}\hfill \\ & ={(1-a)}^{k-J}\sum _{\mathit{m}\in \mathcal{M}({\mathit{n}}^{i+},z_{1:k})}\prod _{j:z_j>0}{a}_{z_j}^{m_j}\sum _{\mathit{\lambda }\in \Lambda \left(\mathit{n},\mathit{m}\right)}\mathit{c}\left(\mathit{\lambda }\right)\overline{\mathfrak{q}}\left(\mathit{\lambda }\right)\hfill \end{array}$$

where ${\mathit{n}}^{i+}=(n_1,\dots ,n_i+1,\dots ,n_k)$. Hence, by (38)–(40), one can write

$$\begin{array}{cc}\hfill \mathbb{P}\{E_i^{*}& \cup (\{Z_{|{\Pi }_n|+1}^{\prime }={\overline{x}}_{{\zeta }_i}\}\cap E_{new}^{*})|{\tilde{\Pi }}_n,{\xi }_{1:{\tilde{K}}_n}^{*}\}\hfill \\ & =\frac{{\sum }_{\mathit{m}\in \mathcal{M}({\mathit{n}}^{i+},z_{1:k})}{\prod }_{j:z_j>0}{a}_{z_j}^{m_j}{\sum }_{\mathit{\lambda }\in \Lambda \left(\mathit{n},\mathit{m}\right)}\mathit{c}\left(\mathit{\lambda }\right)\overline{\mathfrak{q}}\left(\mathit{\lambda }\right)}{{\sum }_{\mathit{m}\in \mathcal{M}(\mathit{n},z_{1:k})}{\prod }_{j:z_j>0}{a}_{z_j}^{m_j}{\sum }_{\mathit{\lambda }\in \Lambda \left(\mathit{n},\mathit{m}\right)}\mathit{c}\left(\mathit{\lambda }\right)\overline{\mathfrak{q}}\left(\mathit{\lambda }\right)}.\hfill \end{array}$$

Combining these results, one obtains the thesis. □

6. Conclusions and Discussion

We have defined a new class of exchangeable sequences, called mixtures of species sampling sequences (mSSS). We have shown that these sequences include various well-known Bayesian nonparametric models. In particular, the observations of many nonparametric hierarchical models (e.g., hierarchical Dirichlet process, hierarchical Pitman–Yor process and, more generally, hierarchical species sampling models [22,23,24,25]) are mSSS. We have shown that also observations sampled from a mixture of Dirichlet processes [10] are mSSS, under some additional assumptions. Our general class also includes species sampling sequences with a general (not necessarily diffuse) base measure, which have been used in various applications, e.g., in the case of “spike-and-slab”-type nonparametric priors [16,17,18,19,20,21].

We believe that our general framework sheds light on the common structure of all the above-mentioned models, leading to a possible unified treatment of some of their important features. Our techniques provides unified proofs for various results that, up to now, have been proven with ad hoc methods.

We have proven that all the mSSS are obtained by assigning the values of an exchangeable sequence to the classes of a latent exchangeable random partition. This representation is proven in the strong sense of an almost sure equality (see Section 3) and leads to the simple and clear derivation of an explicit expression for the EPPF of an mSSS. We believe that our general proof simplifies the derivation of the EPPF of many of the above-mentioned particular cases. Moreover, our results show that the clustering and the predictive structure of various well-known models do not depend on the relation between these models and completely random measures, but are essentially a consequence of the simple combinatorial structure of these sequences. Many important differences between well-known models (such as mixtures of Dirichlet and hierarchical Dirichlet) can be explained easily by simple differences in the latent partition and the corresponding latent exchangeable sequence.

We stress that a clear understanding of the clustering structure of mSSS is fundamental for practical purposes, since these models are typically used to cluster observations. Moreover, we hope that the explicit expression for EPPFs in our general framework can lead to the development of new MCMC algorithms for sampling from the posterior distribution.

Finally, we believe that some of the results we have proven here for mSSS can be extended to the more general case of partially exchangeable arrays. In this direction, for future works, a possible generalization of mSSS is to consider partially exchangeable arrays with a mixture of species sampling random probability measures as directing measures.