On the Quasi-Total Roman Domination Number of Graphs

Abstract

Domination theory is a well-established topic in graph theory, as well as one of the most active research areas. Interest in this area is partly explained by its diversity of applications to real-world problems, such as facility location problems, computer and social networks, monitoring communication, coding theory, and algorithm design, among others. In the last two decades, the functions defined on graphs have attracted the attention of several researchers. The Roman-dominating functions and their variants are one of the main attractions. This paper is a contribution to the Roman domination theory in graphs. In particular, we provide some interesting properties and relationships between one of its variants: the quasi-total Roman domination in graphs.

1. Introduction

Domination in graphs was first defined as a graph-theoretical concept in 1958. This area has attracted the attention of many researchers due to its diversity of applications to real-world problems, such as problems with the location of facilities, computing and social networks, communication monitoring, coding theory, and algorithm design, among others. In that regard, this topic has experienced rapid growth, resulting in over 5000 papers being published. We refer to [1,2] for theoretical results and practical applications.

Given a graph G, a dominating set is a subset $D\subseteq V\left(G\right)$ of vertices, such that every vertex not in D is adjacent to at least one vertex in D. The minimum cardinality among all dominating sets of G is called the domination number of G. The number of works, results and open problems that exist on this parameter and its variants provide a very wide range of work directions to consider, which come from their very theoretical aspects to a significant number of practical applications, passing through a large number of relationships and connections between some invariants of graph theory itself.

In the last two decades, the interest in research concerning dominating functions in graphs has increased. One of the reasons for this is that dominating functions generalize the concept of dominating sets. In particular, the Roman dominating functions (defined in [3], due to historical reasons arising from the ancient Roman Empire and described in [4,5]), and their variants, are one of the main attractions. At present, more than 300 papers have been published on this topic.

In 2019, Cabrera García et al. [6] defined and began the study of an interesting variant of Roman-dominating functions: the quasi-total Roman-dominating functions. This paper deals precisely with this style of domination, and our goal is to continue with the study of this novel parameter in graphs.

Definitions, Notation and Organization of the Paper

We begin this subsection by stating the main basic terminology which will be used in the whole work. Let $G=\left(V\right(G),E(G\left)\right)$ be a simple graph with no isolated vertex. Given a vertex $v\in V\left(G\right)$, $N\left(v\right)=\{x\in V(G):xv\in E(G\left)\right\}$ and $N\left[v\right]=N\left(v\right)\cup \left\{v\right\}$. A vertex $v\in V\left(G\right)$ is called a leaf vertex if $\left|N\right(v\left)\right|=1$. Given a set $D\subseteq V\left(G\right)$, $N\left(D\right)={\cup }_{v\in D}N\left(v\right)$, $N\left[D\right]=N\left(D\right)\cup D$ and $\partial \left(D\right)=N\left(D\right)\backslash D$. Moreover, given a set $D\subseteq V\left(G\right)$ and a vertex $v\in D$, $epn(v,D)=\{u\in V(G)\backslash D:N(u)\cap D=\{v\left\}\right\}$. Also, and as is commonly defined, $G-D$ denotes the graph obtained from G such that $V(G-D)=V\left(G\right)\backslash D$ and $E(G-D)=E\left(G\right)\backslash \{uv\in E(G):u\in Dorv\in D\}$. Moreover, the subgraph of G induced by $D\subseteq V\left(G\right)$ will be denoted by $G\left[D\right]$.

We say that G is F-free if it contains no copy of F as an induced subgraph. A set $D\subseteq V\left(G\right)$ is a 2-packing if $N\left[x\right]\cap N\left[y\right]\ne ⌀$ for every pair $x,y\in D$. The 2-packing number of G, denoted by $\rho \left(G\right)$, is defined as $max\left\{\right|D|:D\mathrm{is}\mathrm{a}\mathrm{2-packing}\mathrm{of}G\}$. A 2-packing of cardinality $\rho \left(G\right)$ is called a $\rho \left(G\right)$-set. We will assume an analogous correspondence when referring to the optimal sets or functions derived from other parameters used in the article.

Let $f:V\left(G\right)\to \{0,1,2\}$ be a function on G. Observe that f generates three sets $V_0$, $V_1$ and $V_2$, where $V_i=\{v\in V\left(G\right):f\left(v\right)=i\}$ for $i\in \{0,1,2\}$. In this sense, we will write $f(V_0,V_1,V_2)$ to refer to the function f. Given a set $D\subseteq V\left(G\right)$, $f\left(D\right)={\sum }_{v\in D}f\left(v\right)$. The weight of f is defined as $\omega \left(f\right)=f\left(V\left(G\right)\right)=|V_1|+2|V_2|$. We shall also use the following notations: $V_{1,2}=\{v\in V_1:N\left(v\right)\cap V_2\ne ⌀\}$, $V_{1,0}=\{v\in V_1:N\left(v\right)\subseteq V_0\}$ and $V_{1,1}=V_1\backslash (V_{1,2}\cup V_{1,0})$. A function $f(V_0,V_1,V_2)$ on G is a dominating function if $N\left(v\right)\cap (V_1\cup V_2)\ne ⌀$ for every vertex $v\in V_0$. Moreover, f is a total dominating function (TDF) if $N\left(v\right)\cap (V_1\cup V_2)\ne ⌀$ for every vertex $v\in V\left(G\right)$. Next, we highlight some particular cases of known domination parameters, which we define here in terms of (total) dominating functions.

• A set $D\subseteq V\left(G\right)$ is a (total) dominating set of G if there exists a (total) dominating function $f(V_0,V_1,V_2)$ such that $f\left(x\right)>0$ if, and only if, $x\in D$. The (total) domination number of G, denoted by (${\gamma }_t\left(G\right)$) $\gamma \left(G\right)$, is the minimum cardinality among all (total) dominating sets of G. For more information on domination and total domination see the books [1,2,7], the survey [8] and the recent works [9,10,11].
• A function $f(V_0,V_1,V_2)$ is a Roman-dominating function if $N\left(v\right)\cap V_2\ne ⌀$ for every $v\in V_0$. The Roman domination number of G, denoted by ${\gamma }_R\left(G\right)$, is the minimum weight among all Roman-dominating functions on G. For more information on Roman domination and its varieties, see the articles [3,12].
• A TDF $f(V_0,V_1,V_2)$ is a total Roman-dominating function (TRDF) on a graph G without isolated vertices if $N\left(v\right)\cap V_2\ne ⌀$ for every vertex $v\in V_0$. The total Roman domination number, denoted by ${\gamma }_{tR}\left(G\right)$, is the minimum weight among all TRDFs on G. For recent results on the total Roman domination in graphs we cite [13,14,15,16,17,18,19,20].
• A quasi-total Roman-dominating function (QTRDF) on a graph G is a dominating function $f(V_0,V_1,V_2)$ such that $N\left(x\right)\cap V_2\ne ⌀$ for every $x\in V_0$; and $N\left(y\right)\cap (V_1\cup V_2)\ne ⌀$ for every $y\in V_2$. The minimum weight among all QTRDFs on G is called the quasi-total Roman domination number, and is denoted by ${\gamma }_{qtR}\left(G\right)$. This parameter was introduced by Cabrera Martínez et al. [6].

As consequence of the above definitions and the well-known inequalities $\rho \left(G\right)\le \gamma \left(G\right)$ (see [1]), ${\gamma }_t\left(G\right)\le {\gamma }_R\left(G\right)$ (see [21]) and ${\gamma }_{tR}\left(G\right)\le {\gamma }_R\left(G\right)+\gamma \left(G\right)$ (see [14]), we establish an inequality chain involving the previous parameters.

Theorem 1.

If G is a graph with no isolated vertex, then

$$\rho \left(G\right)\le \gamma \left(G\right)\le {\gamma }_t\left(G\right)\le {\gamma }_R\left(G\right)\le {\gamma }_{qtR}\left(G\right)\le {\gamma }_{tR}\left(G\right)\le {\gamma }_R\left(G\right)+\gamma \left(G\right).$$

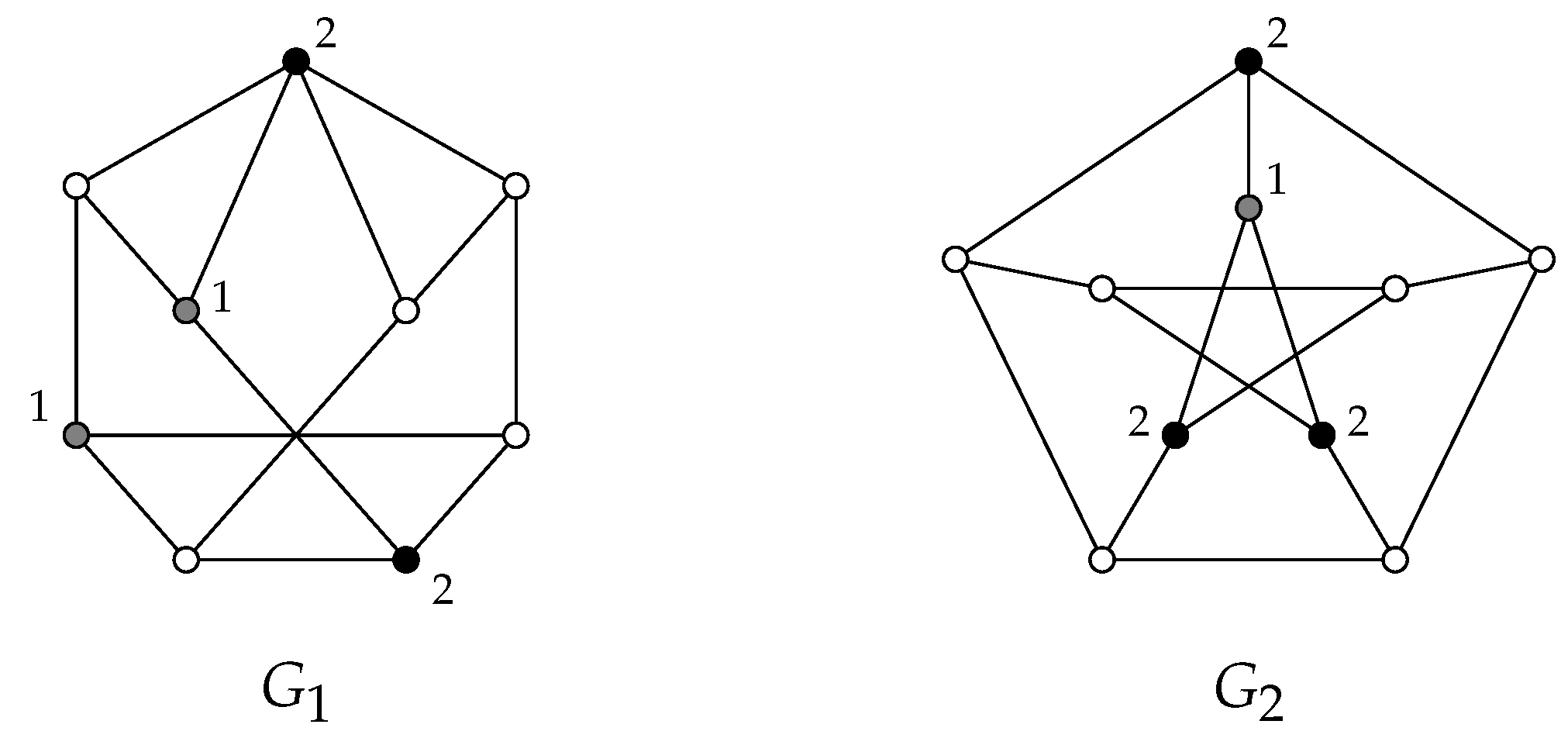
For instance, for the graphs $G_1$ and $G_2$ given in Figure 1 we deduce the next inequality chains. In that regard, the labels of (gray and black) coloured vertices describe the positive weights of a ${\gamma }_{qtR}\left(G_i\right)$-function, for $i\in \{1,2\}$.

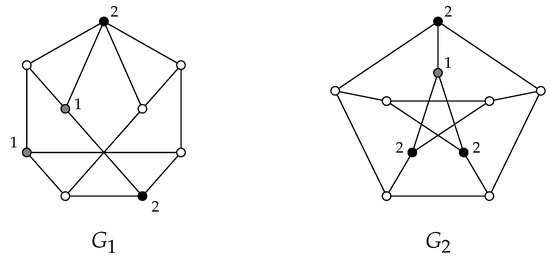
Figure 1. The labels of (gray and black) coloured vertices describe the positive weights of a ${\gamma }_{qtR}\left(G_i\right)$-function, for $i\in \{1,2\}$.

• $\rho \left(G_1\right)=1<3=\gamma \left(G_1\right)<4={\gamma }_t\left(G_1\right)<5={\gamma }_R\left(G_1\right)<6={\gamma }_{qtR}\left(G_1\right)<7={\gamma }_{tR}\left(G_1\right).$
• $\rho \left(G_2\right)=1<3=\gamma \left(G_2\right)<4={\gamma }_t\left(G_2\right)<6={\gamma }_R\left(G_2\right)<7={\gamma }_{qtR}\left(G_2\right)={\gamma }_{tR}\left(G_2\right).$

As mentioned before, the goal of this work is continue the study of the quasi-total Roman domination number of graphs. In that regard, the paper is organized as follows. First, we obtain new, tight bounds for this parameter. Such bounds can also be seen as relationships between this novel parameter and several other classical domination parameters such as the (total) domination and (total) Roman domination numbers. Finally, and as a consequence of this previous study, we derive new results on the total Roman domination number of a graph.

2. Bounds and Relationships with Other Parameters

Let G be a disconnected graph and let $G_1,\dots ,G_r$ ($r\ge 2$) be the components of G. Observe that any QTRDF $f(V_0,V_1,V_2)$ on G satisfies that f restricted to $V\left(G_j\right)$ is a QTRDF on $G_j$, for every $j\in \{1,\dots ,r\}$. Therefore, the following result is obtained for the case of disconnected graphs.

Remark 1

([6]). Let $G_1,\dots ,G_r$ ($r\ge 2$) be the components of a disconnected graph G. Then

$${\gamma }_{qtR}\left(G\right)=\sum _{i=1}^r{\gamma }_{qtR}\left(G_i\right).$$

As a consequence of the above remark, throughout this paper, we only consider nontrivial connected graphs. Next, we give two useful lemmas, which provide some tools to deduce some of the results.

Lemma 1. 

Let G be a nontrivial connected graph. If $f(V_0,V_1,V_2)$ is a ${\gamma }_{qtR}\left(G\right)$-function, then the following statements hold.

(i)

$f^{\prime }(V_0^{\prime }=V_0,V_1^{\prime }=V_1\backslash V_{1,0},V_2^{\prime }=V_2)$ is a ${\gamma }_{tR}(G-V_{1,0})$-function.

(ii)

$epn(v,V_2)\cap V_0\ne ⌀$, for every $v\in V_2$.

(iii)

If ${\gamma }_{qtR}\left(G\right)={\gamma }_R\left(G\right)$, then $V_{1,2}=⌀$.

Proof. 

Let $f(V_0,V_1,V_2)$ be a ${\gamma }_{qtR}\left(G\right)$-function. First, we proceed to prove (i). Notice that $G-V_{1,0}$ has no isolated vertex. Hence, the function $f^{\prime }(V_0^{\prime },V_1^{\prime },V_2^{\prime })$, defined by $V_0^{\prime }=V_0$, $V_1^{\prime }=V_1\backslash V_{1,0}$ and $V_2^{\prime }=V_2$, is a TRDF on $G-V_{1,0}$. Hence, ${\gamma }_{tR}(G-V_{1,0})\le \omega \left(f^{\prime }\right)$. Now, if ${\gamma }_{tR}(G-V_{1,0})<\omega \left(f^{\prime }\right)$, then from any ${\gamma }_{tR}(G-V_{1,0})$-function and the set $V_{1,0}$, we can construct a QTRDF on G of weight less than $\omega \left(f\right)={\gamma }_{qtR}\left(G\right)$, which is a contradiction. Therefore, the function $f^{\prime }$ is a ${\gamma }_{tR}(G-V_{1,0})$-function, as required.

Now, we proceed to prove (ii). Let $v\in V_2$. Obviously, $N\left(v\right)\cap V_0\ne ⌀$. If $epn(v,V_2)\cap V_0=⌀$, then the function $f^{\prime }(V_0^{\prime },V_1^{\prime },V_2^{\prime })$, defined by $V_1^{\prime }=V_1\cup \left\{v\right\}$, $V_2^{\prime }=V_2\backslash \left\{v\right\}$ and $V_0^{\prime }=V_0$, is a QTRDF on G of weight $\omega \left(f^{\prime }\right)<\omega \left(f\right)={\gamma }_{qtR}\left(G\right)$, which is a contradiction. Therefore, $epn(v,V_2)\cap V_0\ne ⌀$, which completes the proof of (ii).

Finally, we proceed to prove (iii). Assume that ${\gamma }_{qtR}\left(G\right)={\gamma }_R\left(G\right)$. First, suppose that $V_{1,2}\ne ⌀$. It is easy to see that the function $f^{\prime }(V_0^{\prime },V_1^{\prime },V_2^{\prime })$, defined by $V_1^{\prime }=V_1\backslash V_{1,2}$, $V_2^{\prime }=V_2$ and $V_0^{\prime }=V_0\cup V_{1,2}$, is a Roman-dominating function on G. Hence, ${\gamma }_R\left(G\right)\le \omega \left(f^{\prime }\right)<\omega \left(f\right)={\gamma }_{qtR}\left(G\right)$, which is a contradiction. Therefore, $V_{1,2}=⌀$, which completes the proof of (iii). □

Lemma 2.

Let G be a nontrivial connected graph. If $f(V_0,V_1,V_2)$ is a ${\gamma }_{qtR}\left(G\right)$-function such that $|V_1|$ is minimum, then one of the following conditions holds.

(i) 

$V_{1,0}=⌀$.

(ii) 

$V_{1,0}$ is a 2-packing of G.

Proof. 

Let $f(V_0,V_1,V_2)$ be a ${\gamma }_{qtR}\left(G\right)$-function, such that $|V_1|$ is minimal. Assume that $V_{1,0}\ne ⌀$. It is clear by definition that $V_{1,0}$ is an independent set. Now, suppose that $V_{1,0}$ is not a 2-packing of G. Therefore, two vertices $u,v\in V_{1,0}$ exist at distance two. Let $w\in N\left(u\right)\cap N\left(v\right)$. Notice that $w\in V_0$ and $N\left(w\right)\cap V_2\ne ⌀$. With these conditions in mind, observe that the function $f^{\prime }(V_0^{\prime },V_1^{\prime },V_2^{\prime })$, defined by $V_1^{\prime }=V_1\backslash \{u,v\}$, $V_2^{\prime }=V_2\cup \left\{w\right\}$ and $V_0^{\prime }=V\left(G\right)\backslash (V_1^{\prime }\cup V_2^{\prime })$, is a QTRDF on G of weight $\omega \left(f^{\prime }\right)=\omega \left(f\right)$ and $|V_1^{\prime }|<|V_1|$, which is a contradiction. Therefore, $V_{1,0}$ is a 2-packing of G, which completes the proof. □

We continue with one of the main results of this paper.

Theorem 2.

If G is a nontrivial connected graph, then at least one of the following statements holds.

(i) 

${\gamma }_{qtR}\left(G\right)={\gamma }_{tR}\left(G\right)$.

(ii) 

${\gamma }_{qtR}\left(G\right)=min\{{\gamma }_{tR}(G-S)+\left|S\right|:S is a \mathrm{2-}packing of G\}.$

Proof. 

Let $f(V_0,V_1,V_2)$ be a ${\gamma }_{qtR}\left(G\right)$-function such that $|V_1|$ is minimum. If $V_{1,0}=⌀$, then by Lemma 1-(i) we deduce that f is also a ${\gamma }_{tR}\left(G\right)$-function, which implies that ${\gamma }_{qtR}\left(G\right)={\gamma }_{tR}\left(G\right)$. Hence, from now on, we assume that $V_{1,0}\ne ⌀$. By Lemma 2, it follows that $V_{1,0}$ is a 2-packing of G. Moreover, by Lemma 1-(i) we have the function $f^{\prime }(V_0^{\prime }=V_0,V_1^{\prime }=V_1\backslash V_{1,0},V_2^{\prime }=V_2)$ is a ${\gamma }_{tR}(G-V_{1,0})$-function. Therefore, ${\gamma }_{qtR}\left(G\right)={\gamma }_{tR}(G-V_{1,0})+|V_{1,0}|\ge min\{{\gamma }_{tR}(G-S)+\left|S\right|:S \mathrm{is} \text{a} \mathrm{2-packing} \mathrm{of} G\}$. We only need to prove that ${\gamma }_{qtR}\left(G\right)\le min\{{\gamma }_{tR}(G-S)+\left|S\right|:S \mathrm{is} \text{a} \mathrm{2-packing} \mathrm{of} G\}$. In such a sense, let S be a 2-packing of G for which ${\gamma }_{tR}(G-S)+\left|S\right|$ is minimum, and let $g^{\prime }(W_0^{\prime },W_1^{\prime },W_2^{\prime })$ be a ${\gamma }_{tR}(G-S)$-function. Observe that the function $g(W_0,W_1,W_2)$, defined by $W_0=W_0^{\prime }$, $W_1=W_1^{\prime }\cup S$ and $W_2=W_2^{\prime }$, is a QTRDF on G. Therefore, ${\gamma }_{qtR}\left(G\right)\le \omega \left(g\right)=min\{{\gamma }_{tR}(G-S)+\left|S\right|:S\mathrm{is} \text{a} \mathrm{2-packing} \mathrm{of} G\}$, which completes the proof. □

The next proposition is a direct consequence of Theorem 2.

Proposition 1.

If G is a nontrivial connected graph, then

$${\gamma }_{qtR}\left(G\right)\ge {\gamma }_{tR}\left(G\right)-\rho \left(G\right).$$

Proof. 

If ${\gamma }_{qtR}\left(G\right)={\gamma }_{tR}\left(G\right)$, then the inequality holds. Assume that ${\gamma }_{qtR}\left(G\right)<{\gamma }_{tR}\left(G\right)$. By Theorem 2 there exists a 2-packing S of G such that ${\gamma }_{qtR}\left(G\right)={\gamma }_{tR}(G-S)+\left|S\right|$. Let $f^{\prime }(V_0^{\prime },V_1^{\prime },V_2^{\prime })$ be a ${\gamma }_{tR}(G-S)$-function and let $S^{\prime }\subseteq N\left(S\right)$ be a set of cardinality $\left|S\right|$ such that $N\left(x\right)\cap S^{\prime }\ne ⌀$ for every vertex $x\in S$. Observe that the function $f(V_0,V_1,V_2)$, defined by $V_2=V_2^{\prime },V_1=V_1^{\prime }\cup S\cup (S^{\prime }\backslash V_2^{\prime })$ and $V_0=V\left(G\right)\backslash (V_1\cup V_2)$, is a TRDF on G. Therefore, ${\gamma }_{tR}\left(G\right)\le \omega \left(f\right)\le \omega \left(f^{\prime }\right)+\left|S\right|+|S^{\prime }|={\gamma }_{tR}(G-S)+2\left|S\right|={\gamma }_{qtR}\left(G\right)+\left|S\right|\le {\gamma }_{qtR}\left(G\right)+\rho \left(G\right)$, which completes the proof. □

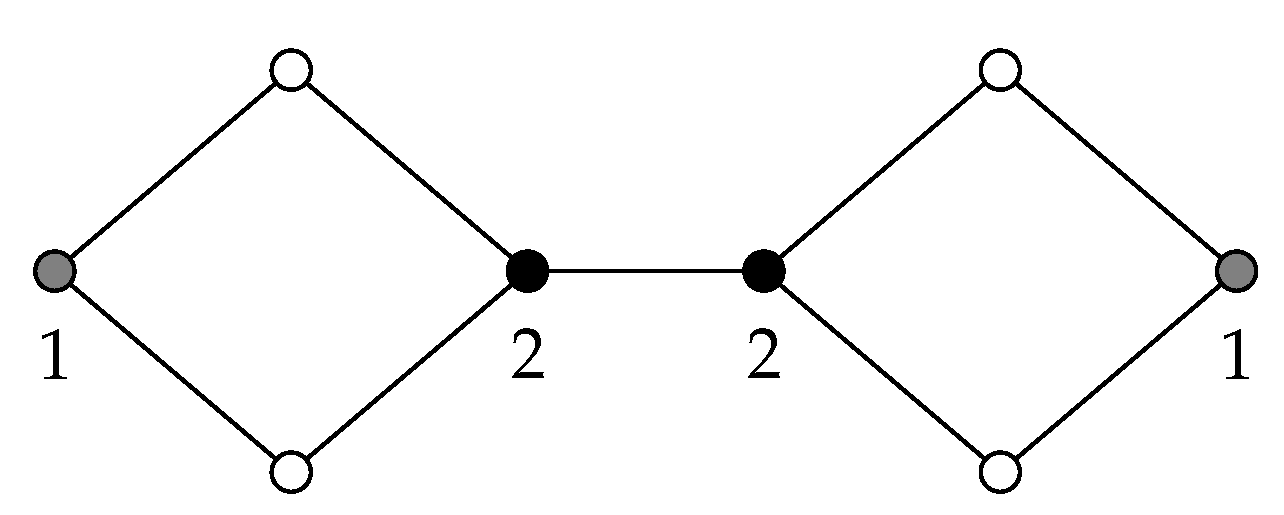
The bound above is tight. For instance, it is achieved for the graph G given in the Figure 2. Notice that this figure describes the positive weights of a ${\gamma }_{qtR}\left(G\right)$-function. In addition, it is easy to see that $\rho \left(G\right)=2$ and ${\gamma }_{tR}\left(G\right)=8$. Hence, ${\gamma }_{qtR}\left(G\right)=6={\gamma }_{tR}\left(G\right)-\rho \left(G\right)$, as required.

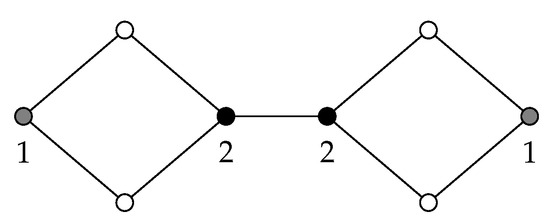
Figure 2. The labels of (gray and black) coloured vertices describe the positive weights of a ${\gamma }_{qtR}\left(G\right)$-function.

It is well-known that ${\gamma }_{tR}\left(G\right)\ge 2\gamma \left(G\right)\ge {\gamma }_R\left(G\right)$ for any graph G with no isolated vertex (see [3,15]). From this inequality chain, we deduce the following result.

Theorem 3.

For any nontrivial connected graph G,

$$2\gamma \left(G\right)-\rho \left(G\right)\le {\gamma }_{qtR}\left(G\right)\le 3\gamma \left(G\right).$$

Proof. 

By combining the bound ${\gamma }_{tR}\left(G\right)\ge 2\gamma \left(G\right)$ and the bound given in Proposition 1, we deduce that ${\gamma }_{qtR}\left(G\right)\ge 2\gamma \left(G\right)-\rho \left(G\right)$.

Now, from the bound ${\gamma }_R\left(G\right)\le 2\gamma \left(G\right)$ and the inequality ${\gamma }_{qtR}\left(G\right)\le {\gamma }_R\left(G\right)+\gamma \left(G\right)$ given in Theorem 1 we obtain ${\gamma }_{qtR}\left(G\right)\le {\gamma }_R\left(G\right)+\gamma \left(G\right)\le 3\gamma \left(G\right)$, as desired. □

The lower bounds given in the two previous results are tight. We will show later that, as a consequence of Lemma 3, the graphs $G_{a,0}\in \mathcal{G}$ satisfy the equality established in Proposition 1, while the graph $G_{2,0}$ satisfies the equality given in Theorem 3.

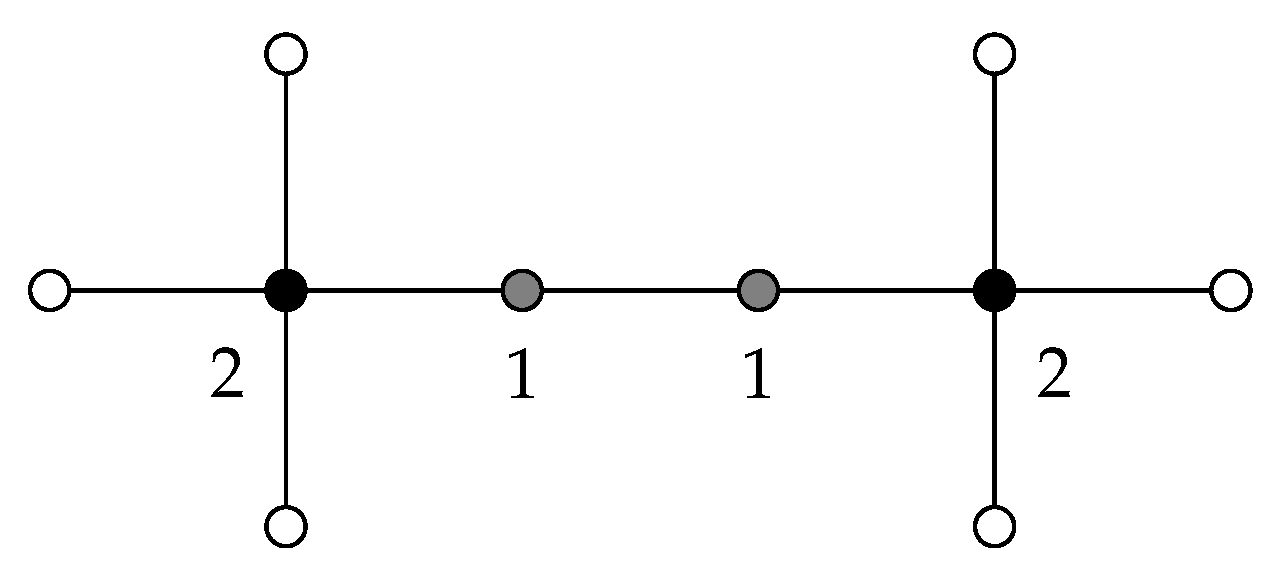
With respect to the equality in the bound ${\gamma }_{qtR}\left(G\right)\le 3\gamma \left(G\right)$ above, we can see that this bound is tight. For instance, it is achieved for the graph G given in the Figure 3. Notice that this figure describes the positive weights of a ${\gamma }_{qtR}\left(G\right)$-function, and as a consequence, we deduce that ${\gamma }_{qtR}\left(G\right)=6=3\gamma \left(G\right)$, as required.

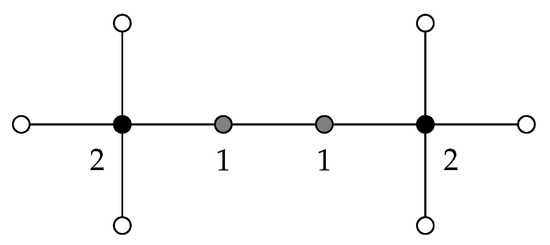
Figure 3. The labels of (gray and black) coloured vertices describe the positive weights of a ${\gamma }_{qtR}\left(G\right)$-function.

In addition, we can deduce the following connection. To this end, we need to say that a graph G is called a Roman graph if ${\gamma }_R\left(G\right)=2\gamma \left(G\right)$.

Proposition 2.

If G is a graph such that ${\gamma }_{qtR}\left(G\right)=3\gamma \left(G\right)$, then G is a Roman graph.

Proof. 

From the proof of Theorem 3, we have that $3\gamma \left(G\right)={\gamma }_{qtR}\left(G\right)\le {\gamma }_R\left(G\right)+\gamma \left(G\right)\le 3\gamma \left(G\right)$. Thus, we have equalities in the inequality chain above. In particular, ${\gamma }_R\left(G\right)=2\gamma \left(G\right)$, which completes the proof. □

Notice that the opposed to the proposition above is not necessarily true. For instance, the graph $G_2$ given in Figure 1 is a Roman graph, but it does not satisfy the equality ${\gamma }_{qtR}\left(G_2\right)=3\gamma \left(G_2\right)$.

The following result gives a lower bound for the quasi-total Roman domination number and characterizes the class of connected graphs for which ${\gamma }_{qtR}\left(G\right)\in \{\gamma \left(G\right)+1,\gamma \left(G\right)+2\}$.

Theorem 4.

For any nontrivial connected graph G of order n,

$${\gamma }_{qtR}\left(G\right)\ge \gamma \left(G\right)+1.$$

Furthermore,

(i) 

${\gamma }_{qtR}\left(G\right)=\gamma \left(G\right)+1$ if and only if $G\cong P_2$.

(ii) 

${\gamma }_{qtR}\left(G\right)=\gamma \left(G\right)+2$ if and only if one of the following conditions holds.

(a)

$G\ncong P_2$ has a vertex of degree $n-\gamma \left(G\right)$.

(b)

G has two adjacent vertices $u,v$ such that $|\partial (\{u,v\}\left)\right|=n-\gamma \left(G\right)$.

Proof. 

If $G\cong P_2$, then it is clear that ${\gamma }_{qtR}\left(G\right)=\gamma \left(G\right)+1$. From now on, assume that $G\ncong P_2$. Let $f(V_0,V_1,V_2)$ be a ${\gamma }_{qtR}\left(G\right)$-function, such that $|V_1|$ is minimum. Note that $(V_1\backslash V_{1,2})\cup V_2$ is a dominating set of G, and $|V_2|\ge 1$. Hence, ${\gamma }_{qtR}\left(G\right)=2|V_2|+|V_1|\ge (|V_2|+|V_1\backslash V_{1,2}\left|\right)+|V_2|\ge \gamma \left(G\right)+1$, and the lower bound follows.

Now, suppose that ${\gamma }_{qtR}\left(G\right)=\gamma \left(G\right)+1$. So, we have equalities in the inequality chain above. In particular, $V_{1,2}=⌀$ and $|V_2|=1$, which is a contradiction. Therefore, if $G\ncong P_2$, then ${\gamma }_{qtR}\left(G\right)\ge \gamma \left(G\right)+2$, and, as a consequence, (i) follows.

We next proceed to prove (ii). First, suppose that ${\gamma }_{qtR}\left(G\right)=\gamma \left(G\right)+2$. Notice that,

$$\gamma \left(G\right)+2=\omega \left(f\right)\ge \left(\right|V_2|+|V_1\backslash V_{1,2}\left|\right)+|V_2|\ge \gamma \left(G\right)+|V_2|.$$

This implies that $|V_2|\in \{1,2\}$, and, in such a case, we consider the following two cases.

Case 1. $|V_2|=1$. In this case, we have that $|V_1|=\gamma \left(G\right)$. Let $V_2=\left\{v\right\}$. Now, as $|N\left(v\right)\cap V_1|=1$ and $V_0\subseteq N\left(v\right)$, we deduce that $\left|N\left(v\right)\right|=|V_0|+1=(n-|V_1|-|V_2\left|\right)+1=n-\gamma \left(G\right)$, which implies that condition (a) follows.

Case 2. $|V_2|=2$. Let $V_2=\{u,v\}$. In this case we have that $|V_1|=\gamma \left(G\right)-2$, and we have equalities in the inequality chain above. As a consequence, $V_{1,2}=⌀$, which implies that u and v are adjacent vertices. Hence, $\partial \left(\{u,v\}\right)=V_0$ and, therefore, $|\partial \left(\{u,v\}\right)|=|V_0|=n-|V_1|-|V_2|=n-\gamma \left(G\right)$. Therefore, condition (b) follows.

On the other hand, suppose that one of the conditions (a) and (b) holds. In such a sense, we consider the next two cases. Recall that ${\gamma }_{qtR}\left(G\right)\ge \gamma \left(G\right)+2$ since $G\ncong P_2$.

Case 1. Suppose that (a) holds. Let $v\in V\left(G\right)$ such that $\left|N\right(v\left)\right|=n-\gamma \left(G\right)$ and $w\in N\left(v\right)$. Notice that the function $f^{\prime }(V_0^{\prime },V_1^{\prime },V_2^{\prime })$, defined by $V_2^{\prime }=\left\{v\right\}$, $V_0^{\prime }=N\left(v\right)\backslash \left\{w\right\}$ and $V_1^{\prime }=V\left(G\right)\backslash (V_0^{\prime }\cup V_2^{\prime })$, is a QTRDF on G. Hence, ${\gamma }_{qtR}\left(G\right)\le \omega \left(f^{\prime }\right)=2|V_2^{\prime }|+|V_1^{\prime }|=2+\gamma \left(G\right)$, which implies that ${\gamma }_{qtR}\left(G\right)=\gamma \left(G\right)+2$, as required.

Case 2. Suppose that (b) holds. Let $u,v$ be two adjacent vertices such that $|\partial (\{u,v\}\left)\right|=n-\gamma \left(G\right)$. Observe that the function $f^{″}(V_0^{″},V_1^{″},V_2^{″})$, defined by $V_2^{″}=\{u,v\}$, $V_0^{″}=\partial \left(\{u,v\}\right)$ and $V_1^{″}=V\left(G\right)\backslash (V_0^{″}\cup V_2^{″})$, is a QTRDF on G. Hence, ${\gamma }_{qtR}\left(G\right)\le \omega \left(f^{″}\right)=2|V_2^{″}|+|V_1^{″}|=4+(\gamma \left(G\right)-2)=\gamma \left(G\right)+2$, which implies that ${\gamma }_{qtR}\left(G\right)=\gamma \left(G\right)+2$, as required.

Therefore, the proof is complete. □

Cabrera Martínez et al. [6] in 2019, established that ${\gamma }_{qtR}\left(G\right)\le n-\rho \left(G\right)(\delta \left(G\right)-2)$ for any nontrivial graph G of order n and minimum degree $\delta \left(G\right)$. The following bounds for the total Roman domination number and the domination number, respectively, are direct consequences of the previous inequality, Proposition 1 and Theorem 3.

Theorem 5.

The following statements hold for any nontrivial connected graph G of order n and $\delta \left(G\right)\ge 4$.

(i) 

${\gamma }_{tR}\left(G\right)\le n-\rho \left(G\right)(\delta \left(G\right)-3).$

(ii) 

$\gamma \left(G\right)\le \frac{n-\rho \left(G\right)\left(\delta \right(G)-3)}{2}.$

From Proposition 1 and Theorem 1, we obtain the following useful inequality chain.

$${\gamma }_{tR}\left(G\right)-\rho \left(G\right)\le {\gamma }_{qtR}\left(G\right)\le {\gamma }_{tR}\left(G\right).$$

(1)

An interesting question that arises from the inequality chain above is the following. Can the differences ${\gamma }_{qtR}\left(G\right)-({\gamma }_{tR}\left(G\right)-\rho \left(G\right))$ and ${\gamma }_{tR}\left(G\right)-{\gamma }_{qtR}\left(G\right)$ be as large as possible? Next, we provide an affirmative answer to the previous question. For this purpose, we need to introduce the following family of graphs. Given two integers $a,b\ge 0$ ($a+b\ge 2$), a graph $G_{a,b}\in \mathcal{G}$ is defined as follows.

• We begin with a nontrivial connected graph G of order $\left|V\right(G\left)\right|=a+b$ with vertex set $V\left(G\right)=\{u_1,\dots ,u_a,v_1,\dots ,v_b\}$.
• Attach a path $P_4=x_1{x}_2{x}_3{x}_4$ to every $u_i\in V\left(G\right)$, $i\in \{1,\dots ,a\}$, by adding an edge between $u_i$ and every vertex in $\{x_1,x_2,x_4\}$.
• Attach a double star $S_{1,2}$ to every $v_j\in V\left(G\right)$, $j\in \{1,\dots ,b\}$, by adding an edge between $v_j$ and every leaf vertex of $S_{1,2}$.

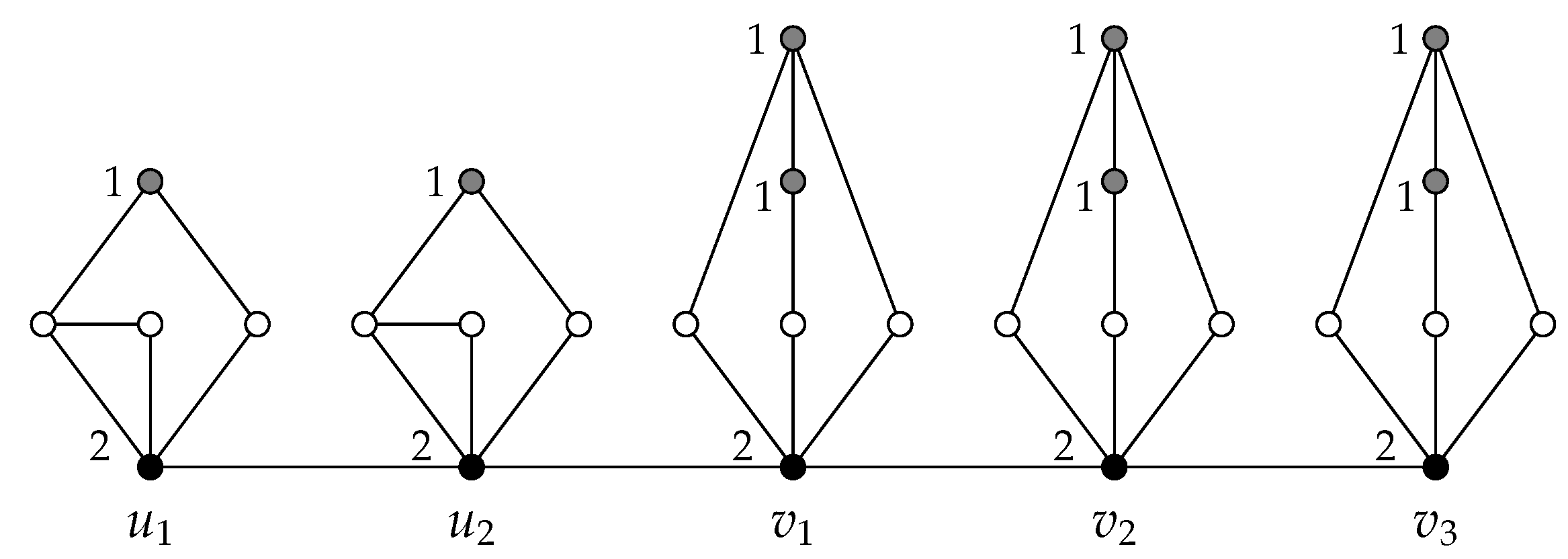
The Figure 4 shows the graph $G_{2,3}$ by taking $G\cong P_5$. We next give exact formulas for the total Roman domination number, the quasi-total Roman domination number and the packing number of the graphs of the family $\mathcal{G}$. These results are almost straightforward to deduce and, according to this fact, the proofs are left to the reader.

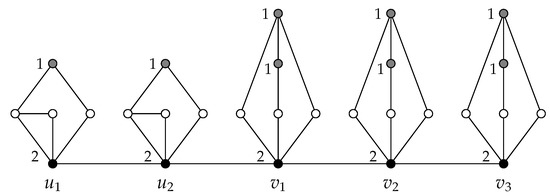
Figure 4. The graph $G_{2,3}$ by taking G as the path graph $P_5$. The labels of (gray and black) coloured vertices describe the positive weights of a ${\gamma }_{qtR}\left(G_{2,3}\right)$-function.

Lemma 3.

Let $a,b\ge 0$ be two integers, such that $a+b\ge 2$. If G is a connected graph such that $\left|V\right(G\left)\right|=a+b$, then the following equalities hold.

(i) 

${\gamma }_{tR}\left(G_{a,b}\right)=4a+4b$.

(ii) 

${\gamma }_{qtR}\left(G_{a,b}\right)=3a+4b$.

(iii) 

$\rho \left(G_{a,b}\right)=a+b$.

According to the lemma above, for any integers $a,b\ge 0$ ($a+b\ge 2$), we obtain that any graph $G_{a,b}\in \mathcal{G}$ satisfies

${\gamma }_{qtR}\left(G_{a,b}\right)-({\gamma }_{tR}\left(G_{a,b}\right)-\rho \left(G_{a,b}\right))=b$ and ${\gamma }_{tR}\left(G_{a,b}\right)-{\gamma }_{qtR}\left(G_{a,b}\right)=a$,

which provides the answer to our previous question. In addition, and as a consequence of Lemma 3, we deduce that the lower and upper bounds given in Inequality chain (1) are tight. For instance, any graph $G_{a,0}\in \mathcal{G}$ satisfies that ${\gamma }_{qtR}\left(G_{a,0}\right)={\gamma }_{tR}\left(G_{a,0}\right)-\rho \left(G_{a,0}\right)$, while any graph $G_{0,b}\in \mathcal{G}$ satisfies that ${\gamma }_{qtR}\left(G_{0,b}\right)={\gamma }_{tR}\left(G_{0,b}\right)$.

It is well known that $\rho \left(G\right)=1$ for every graph G with a diameter of, at most, two. In this sense, and as direct consequence of the Inequality chain (1), we have that ${\gamma }_{qtR}\left(G\right)\in \{{\gamma }_{tR}\left(G\right)-1,{\gamma }_{tR}\left(G\right)\}$ for every graph G with diameter of, at most, two. We next show some subclasses which satisfy the equality ${\gamma }_{qtR}\left(G\right)={\gamma }_{tR}\left(G\right)$. For this, we need to cite the following result.

Theorem 6

([6]). The following statements hold for any nontrivial graph G.

(i) 

${\gamma }_{qtR}\left(G\right)=2$ if and only if $G\cong P_2$.

(ii) 

${\gamma }_{qtR}\left(G\right)=3$ if and only if $G\ncong P_2$ and $\gamma \left(G\right)=1$.

(iii) 

${\gamma }_{qtR}\left(G\right)=4$ if and only if ${\gamma }_t\left(G\right)=\gamma \left(G\right)=2$.

The join of two graphs $G_1$ and $G_2$, denoted by $G_1+G_2$, is the graph obtained from $G_1$ and $G_2$ with vertex set $V(G_1+G_2)=V\left(G_1\right)\cup V\left(G_2\right)$ and edge set $E(G_1+G_2)=E\left(G_1\right)\cup E\left(G_2\right)\cup \{uv:u\in V\left(G_1\right),v\in V\left(G_2\right)\}$. Observe that $diam(G_1+G_2)\le 2$ by definition. The following result, which is a consequence of Theorem 6, shows that ${\gamma }_{tR}(G_1+G_2)={\gamma }_{qtR}(G_1+G_2)$.

Theorem 7.

For any nontrivial graphs $G_1$ and $G_2$,

$${\gamma }_{qtR}(G_1+G_2)={\gamma }_{tR}(G_1+G_2)=\left\{\begin{array}{cc}3,\hfill & ifmin\{\gamma \left(G_1\right),\gamma \left(G_2\right)\}=1;\hfill \\ 4,\hfill & otherwise.\hfill \end{array}\right.$$

We continue analysing other subclasses of graphs with a diameter of two. The following results consider the planar graphs with a diameter of two.

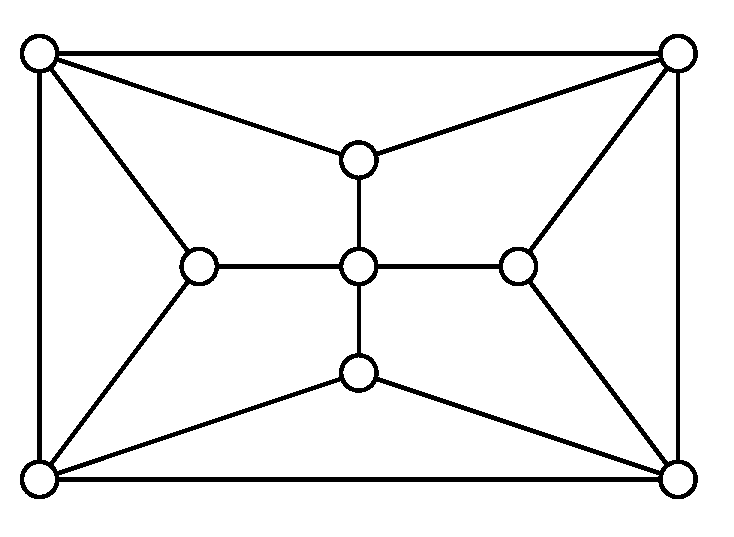
Theorem 8

([22]). If G is a planar graph with $diam\left(G\right)=2$, then the following statements hold.

(i)

$\gamma \left(G\right)\le 2$ or $G=G_9$, where $G_9$ is the graph given in Figure 5.

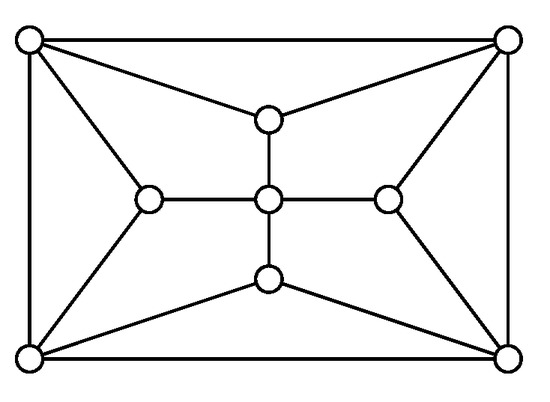Figure 5. The planar graph $G_9$ with $diam\left(G_9\right)=2$ and ${\gamma }_t\left(G_9\right)=\gamma \left(G_9\right)=3$.

(ii)

${\gamma }_t\left(G\right)\le 3$.

Theorem 9.

For any planar graph G with $diam\left(G\right)=2$,

$${\gamma }_{qtR}\left(G\right)={\gamma }_{tR}\left(G\right)=\left\{\begin{array}{cc}3,\hfill & if\gamma \left(G\right)=1;\hfill \\ 4,\hfill & if\gamma \left(G\right)={\gamma }_t\left(G\right)=2;\hfill \\ 5,\hfill & if{\gamma }_t\left(G\right)=\gamma \left(G\right)+1=3;\hfill \\ 6,\hfill & ifG=G_9.\hfill \end{array}\right.$$

Proof. 

If $G=G_9$, then it is easy to check that ${\gamma }_{qtR}\left(G\right)={\gamma }_{tR}\left(G\right)=6$. From now on, let $G\ne G_9$ be a planar graph with $diam\left(G\right)=2$. It is straightforward that ${\gamma }_{qtR}\left(G\right)={\gamma }_{tR}\left(G\right)=3$ if and only if $\gamma \left(G\right)=1$. Hence, assume that $\gamma \left(G\right)\ge 2$. By Theorem 8, it follows that $\gamma \left(G\right)=2$ and ${\gamma }_t\left(G\right)\in \{2,3\}$. Next, we analyse these two cases.

Case 1. ${\gamma }_t\left(G\right)=2$. By Theorems 6 and 1 and the well-known bound ${\gamma }_{tR}\left(G\right)\le 2{\gamma }_t\left(G\right)$ (see [15]) we obtain that $4={\gamma }_{qtR}\left(G\right)\le {\gamma }_{tR}\left(G\right)\le 2{\gamma }_t\left(G\right)=4$. Thus, ${\gamma }_{qtR}\left(G\right)={\gamma }_{tR}\left(G\right)=4$.

Case 2. ${\gamma }_t\left(G\right)=3$. As a consequence of the Theorem 6 we have that ${\gamma }_{qtR}\left(G\right)\ge 5$. Let $\{u,v\}$ be a $\gamma \left(G\right)$-set. Since ${\gamma }_t\left(G\right)=3$ and $diam\left(G\right)=2$, it follows that u and v are at distance two. Let $w\in N\left(u\right)\cap N\left(v\right)$. Notice that the function f, defined by $f\left(u\right)=f\left(v\right)=2$, $f\left(w\right)=1$ and $f\left(x\right)=0$ for every $x\in V\left(G\right)\backslash \{u,v,w\}$, is a TRDF on G, which implies that ${\gamma }_{tR}\left(G\right)\le \omega \left(f\right)=5$. Hence, by the fact that ${\gamma }_{qtR}\left(G\right)\le {\gamma }_{tR}\left(G\right)$ we deduce that ${\gamma }_{qtR}\left(G\right)={\gamma }_{tR}\left(G\right)=5$.

Therefore, the proof is complete. □

However, for the case of non-planar graphs with a diameter of two, there are graphs that satisfy ${\gamma }_{qtR}\left(G\right)={\gamma }_{tR}\left(G\right)$ or ${\gamma }_{qtR}\left(G\right)={\gamma }_{tR}\left(G\right)-1$. For instance, for the graphs $G_1$ and $G_2$ given in Figure 1 we have that ${\gamma }_{qtR}\left(G_1\right)=6={\gamma }_{tR}\left(G_1\right)-1$ and ${\gamma }_{qtR}\left(G_2\right)=7={\gamma }_{tR}\left(G_2\right)$. In connection with this fact, we pose the following open problem.

Problem 1.

Characterize the families of non-planar graphs G with diameter two for which ${\gamma }_{qtR}\left(G\right)={\gamma }_{tR}\left(G\right)$ or ${\gamma }_{qtR}\left(G\right)={\gamma }_{tR}\left(G\right)-1$.

Notice that, as consequence of the Inequality chain (1), any new result for the total Roman domination number gives us a new result for the quasi-total Roman domination number and vice versa. In such a sense, we continue with two new bounds for the total Roman domination number. Before this, we need to introduce the following definition. A set S of vertices of a graph G is a vertex cover if every edge of G is incident with at least one vertex in S. The vertex cover number of G, denoted by $\beta \left(G\right)$, is the minimum cardinality among all vertex covers of G.

Theorem 10.

For any $K_{1,3}$-free graph G with $\delta \left(G\right)\ge 3$,

$${\gamma }_{tR}\left(G\right)\le \beta \left(G\right)+\gamma \left(G\right).$$

Proof. 

Let D be a $\gamma \left(G\right)$-set and S a $\beta \left(G\right)$-set. Let $f(V_0,V_1,V_2)$ be a function defined by $V_0=V\left(G\right)\backslash (D\cup S)$, $V_1=(D\cup S)\backslash (D\cap S)$ and $V_2=D\cap S$. Now, we proceed to prove that f is a TRDF on G. We first note that S is a total dominating set because G is $K_{1,3}$-free. Hence, $V_1\cup V_2=D\cup S$ is a total dominating set of G. Let $v\in V_0=V\left(G\right)\backslash (D\cup S)$. So, $N\left(v\right)\subseteq S$ and $N\left(v\right)\cap D\ne ⌀$. Hence $N\left(v\right)\cap D\cap S\ne ⌀$, i.e., $N\left(v\right)\cap V_2\ne ⌀$. Therefore, f is a TRDF on G, as desired. Thus, ${\gamma }_{tR}\left(G\right)\le \omega \left(f\right)\le |(D\cup S)\backslash (D\cap S)|+2|D\cap S|=\beta \left(G\right)+\gamma \left(G\right)$, which completes the proof. □

Lemma 4

([15]). If G is a graph with no isolated vertex, then there exists a ${\gamma }_{tR}\left(G\right)$-function $f(V_0,V_1,V_2)$ such that either $V_2$ is a dominating set of G, or the set S of vertices not dominated by $V_2$ satisfies $G\left[S\right]=k{K}_2$ for some $k\ge 1$, where $S\subseteq V_1$ and $\partial \left(S\right)\subseteq V_0$.

Theorem 11.

If G is a $\{K_{1,3},K_{1,3}+e\}$-free graph such that $\delta \left(G\right)\ge 3$, then there exists a ${\gamma }_{tR}\left(G\right)$-function $f(V_0,V_1,V_2)$ such that $V_2$ is a dominating set of G, and, as a consequence,

$${\gamma }_{tR}\left(G\right)\ge {\gamma }_t\left(G\right)+\gamma \left(G\right).$$

Proof. 

Suppose that there is no ${\gamma }_{tR}\left(G\right)$-function $f(V_0^{\prime },V_1^{\prime },V_2^{\prime })$ such that $V_2^{\prime }$ is a dominating set of G. By Lemma 4, there exists a ${\gamma }_{tR}\left(G\right)$-function $f(V_0,V_1,V_2)$ such that $V_{1,1}$ satisfies that $G\left[V_{1,1}\right]=k{K}_2$ for some $k\ge 1$ and $\partial \left(V_{1,1}\right)\subseteq V_0$. We can assume that $|V_1|$ is minimum among all ${\gamma }_{tR}\left(G\right)$-functions because it is a requirement for the existence of the function f (see the proof of Lemma 4). Let $u,v\in V_{1,1}$ be two adjacent vertices. Hence, $\partial \left(\{u,v\}\right)\subseteq V_0$. Since $\delta \left(G\right)\ge 3$, there are two vertices $w_1,w_2\in N\left(v\right)\cap V_0$, and as G is a $\{K_{1,3},K_{1,3}+e\}$-free graph, we deduce that at least one of these vertices is also adjacent to u. Hence, and without loss of generality, assume that $\{u,v\}\subseteq N\left(w_1\right)$. Observe that the function $g(W_0,W_1,W_2)$, defined by $W_2=V_2\cup \left\{w_1\right\},W_1=V_1\backslash \{u,v\}$ and $W_0=V\left(G\right)\backslash (W_1\cup W_2)$, is a TRDF on G of weight $\omega \left(g\right)=\omega \left(f\right)$ and $|W_1|<|V_1|$, which is a contradiction. Therefore, there exists a ${\gamma }_{tR}\left(G\right)$-function $f(V_0,V_1,V_2)$ such that $V_2$ is a dominating set of G. Since $V_1\cup V_2$ is a total dominating set of G, we deduce that ${\gamma }_t\left(G\right)+\gamma \left(G\right)\le |V_1\cup V_2|+|V_2|=2|V_2|+|V_1|={\gamma }_{tR}\left(G\right)$, which completes the proof. □

Observe that, if G is a $\{K_{1,3},K_{1,3}+e\}$-free graph of minimum degree at least three with $\beta \left(G\right)={\gamma }_t\left(G\right)$, then the bounds given in the two previous theorems are achieved. Moreover, let G be a $(n-2)$-regular graph obtained from the complete graph $K_n$ (n even) by deleting the edges of a perfect matching. Notice that G is $\{K_{1,3},K_{1,3}+e\}$-free and satisfies that ${\gamma }_{tR}\left(G\right)=4={\gamma }_t\left(G\right)+\gamma \left(G\right).$

Theorem 12.

If G is a connected $\{K_{1,3},K_{1,3}+e\}$-free graph such that $\delta \left(G\right)\ge 3$, then the following statements hold.

(i) 

${\gamma }_t\left(G\right)+\gamma \left(G\right)-\rho \left(G\right)\le {\gamma }_{qtR}\left(G\right)\le \beta \left(G\right)+\gamma \left(G\right).$

(ii) 

If ${\gamma }_{tR}\left(G\right)={\gamma }_R\left(G\right)$, then ${\gamma }_{qtR}\left(G\right)=2{\gamma }_t\left(G\right).$

Proof. 

Statement (i) is a direct consequence of combining Inequality chain (1) and Theorems 10 and 11. Finally, we proceed to prove (ii). By Theorem 11 there exists a ${\gamma }_{tR}\left(G\right)$-function $f(V_0,V_1,V_2)$ such that $V_2$ is a dominating set of G. Hence, $V_{1,1}=⌀$. Moreover, as ${\gamma }_{tR}\left(G\right)={\gamma }_R\left(G\right)$, we deduce that f is also a ${\gamma }_{qtR}\left(G\right)$-function and Lemma 1 (iii)-(a) leads to $V_{1,2}=⌀$. Therefore $V_1=⌀$, which implies that $V_2$ is a total dominating set of G. Hence, $2{\gamma }_t\left(G\right)\le 2\left|V_2\right|={\gamma }_{qtR}={\gamma }_{tR}\le 2{\gamma }_t\left(G\right)$. Therefore, ${\gamma }_{qtR}=2{\gamma }_t\left(G\right)$, as required. □

3. Conclusions and Open Problems

This paper is a contribution to the graph domination theory. We have studied the quasi-total Roman domination in graphs. For instance, we have shown the close relationship that exists between this novel parameter and other invariants, such as (total) domination number, (total) Roman domination number and 2-packing number.

We conclude by proposing some open problems.

• Settle Problem 1.
• Characterize the graphs that satisfy the following equalities.

  -

  ${\gamma }_{qtR}\left(G\right)={\gamma }_{tR}\left(G\right)$.

  -

  ${\gamma }_{qtR}\left(G\right)={\gamma }_{tR}\left(G\right)-\rho \left(G\right)$.

  -

  ${\gamma }_{qtR}\left(G\right)=3\gamma \left(G\right)$.

• We have shown that if G is a $\{K_{1,3},K_{1,3}+e\}$-free graph with minimum degree $\delta \left(G\right)\ge 3$, then ${\gamma }_{qtR}\left(G\right)\ge {\gamma }_t\left(G\right)+\gamma \left(G\right)-\rho \left(G\right)$. We conjecture that the previous bound holds for any graph with no isolated vertex.