Abstract
We are proposing Tulczyjew’s triple for contact dynamics. The most important ingredients of the triple, namely symplectic diffeomorphisms, special symplectic manifolds, and Morse families, are generalized to the contact framework. These geometries permit us to determine so-called generating family (obtained by merging a special contact manifold and a Morse family) for a Legendrian submanifold. Contact Hamiltonian and Lagrangian Dynamics are recast as Legendrian submanifolds of the tangent contact manifold. In this picture, the Legendre transformation is determined to be a passage between two different generators of the same Legendrian submanifold. A variant of contact Tulczyjew’s triple is constructed for evolution contact dynamics.
1. Introduction
Lagrangian dynamics are generated by a Lagrangian function defined on the tangent bundle of the configuration space of a physical system, whereas Hamiltonian dynamics are governed by a Hamiltonian function on the cotangent bundle , which is canonically symplectic [1,2,3,4]. If a Lagrangian function is regular, that is, if it satisfies the Hessian condition, then the fiber derivative becomes a fibered local diffeomorphism from the tangent bundle to the cotangent bundle. In this case, the fiber derivative turns out to be the Legendre transformation linking the Lagrangian and the Hamiltonian realizations of the physical system.
If a Lagrangian function happens to be degenerate, then the fiber derivative fails to be a local diffeomorphism since its image space turns out only to be, in the best of cases, a proper submanifold of the cotangent bundle . That is, one only arrives at a presymplectic picture determined by some constraint functions. To deal with these constraints, Dirac proposed an algorithm, nowadays called the Dirac–Bergmann algorithm [5,6]. This algorithm proposes a method to arrive at a submanifold (possibly smaller than the image space of the Legendre transformation) of the cotangent bundle where the Hamilton’s equations becomes well-defined. In the final stage of the algorithm, one obtains the so-called Dirac bracket. There also exists a more geometric version of this approach called the Gotay–Nester–Hinds algorithm [7]. Inspired the tools introduced in [7], the Skinner–Rusk unified theory [8] is establishing a unification of Lagrangian and Hamiltonian formalisms on the Whitney sum of tangent and cotangent bundles. In this paper, we shall focus on the Tulczyjew approach for the Legendre transformations of singular Lagrangians.
The Classical Tulczyjew’s Triple. Tulczyjew’s triple is a commutative diagram linking three symplectic bundles, namely, , and via symplectic diffeomorphisms [9]. This geometrization enables one to recast Lagrangian and Hamiltonian dynamical equations as Lagrangian submanifolds of the Tulczyjew symplectic space [10]. Referring to this geometry, the Legendre transformation is defined as a passage between two different generators of the same Lagrangian submanifold [11,12]. This definition is free from the non-degeneracy requirement that is the Hessian condition. Evidently, this approach is in harmony with the creed by Weinstein “everything is a Lagrangian submanifold” [13]. We reserve Section 2 for a brief summary of the Tulczyjew’s triple and the Legendre transformation in this picture.
Tulczyjew’s triple is modified for many physical systems and it is carried to several geometric frameworks. For higher order Lagrangian dynamics, the triple is upgraded in [14,15]. For physical theories where the configuration space is a Lie group, the triple is examined in a series of works [16,17,18,19]. The triple is examined for principal fiber bundles in [20,21]. It is written for the vector bundle of n-vectors in [22]. For the case of the field theories, we refer to an extensive, but incomplete list [23,24,25,26,27,28,29,30,31,32], and for the higher order field theories see, for example, [33].
Contact Hamiltonian Dynamics. A symplectic manifold must be even dimensional. An odd dimensional generalization of symplectic geometry is contact geometry [34]. Hamiltonian dynamics are available on this generalization as well [35,36,37,38]. In the present work, as a generic model of contact manifold, we consider the extended cotangent bundle
with the contact one-form . Here, z is the real variable, and is the pull-back of the canonical one-form on the cotangent bundle . In a coordinate free formulation, contact Hamiltonian dynamics generated by a Hamiltonian function H are defined as
where is the Reeb field associated with the contact form , and is the interior product. In Darboux’ coordinates , the contact Hamilton’s equations are computed to be
Contact Hamiltonian dynamics have different features from classical Hamiltonian dynamics. One interesting characteristic of contact Hamiltonian dynamics is the loss of conservation of Hamiltonian function along the motion [39,40]. Even, the canonical contact volume form is not preserved under the action of the contact Hamiltonian dynamics (see [41]). The dissipative nature of contact Hamiltonian dynamics makes them proper for dissipative dynamical systems. We present here an incomplete list of some recent works along this direction: [37,39,40,42]. Additionally, we can argue that contact framework looks proper for thermodynamics, see, for example, the following incomplete list: [35,43,44,45]. Accordingly, we also wish to cite [46,47,48,49] for the use of contact geometry for qualitative analysis of reversible–irreversible dynamics under GENERIC (an acronym for General Equation for Non-equilibrium Reversible-Irreversible Coupling) formalism. At the end of this paper, we shall provide some applications of our results on thermodynamics. We cite [50,51] for some recent studies on variational aspects of contact Hamiltonian dynamics.
There is evolution contact Hamiltonian formalism on the extended cotangent bundle. In this case, for a Hamiltonian function H, evolution contact Hamilton’s equation is defined to be
Here, is the Lie derivative. According to the Cartan’s formula, it is computed to be . In Darboux’s coordinates, the local picture of the evolution contact Hamilton’s Equation (4) is computed to be
Note that if 0 is a regular value of H, then the evolutionary vector field is tangent to the hypersurface and, thus, to every Legendrian submanifold contained in . Therefore, the integral curves of may be interpreted as thermodynamical processes for a system with thermodynamical phase space in the extended cotangent bundle. This fact was used in [52] to discuss the relation between evolution contact dynamics and simple thermodynamical systems with friction.
Contact Lagrangian Dynamics. Corresponding Lagrangian formalism for contact Hamiltonian dynamics is also available in the literature under the name of Herglotz (or generalized Euler–Lagrange) formalism [53]. See also [38]. In this paper, as the geometric framework, we consider the extended tangent bundle
A Lagrangian function on determines the Herglotz (generalized Euler–Lagrange) equations as
Here, z is the real variable appearing in . Evidently, if the Lagrangian function L is independent of z, then Equation (7) reduces to the classical Euler–Lagrange equations. If the Lagrangian function L is non-degenerate, that is, if the rank of the Hessian matrix
is maximum, then the fiber derivative
turns out to be a local diffeomorphism. In this case, a direct calculation shows that the fiber derivative (9) maps the Herglotz equations in (7) to the contact Hamilton’s Equation (3) once the Hamiltonian function is taken to be
If a Lagrangian function fails to be non-degenerate then, as in the symplectic case, the transformation (9) fails to be a local isomorphism. Then the image space of can only be, in the best of the cases, a proper submanifold of the extended cotangent bundle. One way to deal with the constraints defining the image space is to employ a version of Dirac algorithm. This is recently studied in [54]. Another way is to generalize the unified formalism for contact dynamics as presented in a recent study [55]. In this paper, our interest is to study the Legendre transformation for contact dynamics following the understanding of Tulczyjew.
Goal of the Present Work. The aim of this work is to define Legendre transformation between the Herglotz Equation (7) and the contact Hamilton’s Equation (3) by properly constructing a Tulczyjew’s triple for the case of contact manifolds. We shall call this as contact Tulczyjew’s triple. Such an attempt involves modifications of the ingredients of the classical Tulczyjew’s triple to the contact geometry. Here, in the contact case, the role of Tulczyjew’s symplectic space will be played by the extended tangent bundle of the extended cotangent bundle. Accordingly, Tulczyjew’s triple will consist of the iterated extended bundles , , as well as contact transformation between them. Maybe, the most vital object in this picture is the introduction of the notion of special contact manifolds. This novel framework permits one to recast both the contact Lagrangian and the contact Hamiltonian dynamics as a Legendrian submanifold of . This enables us to realize that Lagrangian and Hamiltonian functions as generating objects of the same Legendrian submanifold. Thus, by merging special contact geometry with Morse family theory, the Legendre transformation for contact dynamics is defined to be a passage between two different generators of the same Legendrian submanifold. In addition, there is an (evolution) Hamiltonian flow on contact geometry preserving the energy, but not the kernel of the contact form. There is also Lagrangian counterpart of this theory called evolution Herglotz equations. By properly modifying contact Tulczyjew’s triple, the Legendre transformation for the evolution Herglotz equations and the evolution contact Hamilton’s equations are obtained. In this theory, contact manifolds and Legendrian submanifolds are replaced by symplectic manifolds and Legendrian submanifolds, respectively. We call this geometry the evolution contact Tulczyjew’s triple.
The content of this work is as follows. The main body of the paper consists of three sections. In Section 2, for the sake of the completeness of the manuscript and in order to fix the notation, a brief summary of classical Tulczyjew’s triple is given. Section 3 is reserved for the basics on contact dynamics in both Hamiltonian and Lagrangian formulations. Section 4 is the one containing the novel results of the paper where the Tulczyjew’s triple is constructed for the contact and evolution contact dynamics.
2. The Classical Tulczyjew’s Triple
2.1. (Special) Symplectic Manifolds
A manifold is said to be symplectic if it is equipped with a non-degenerate closed two-form [1,3,56]. In this case, is called a symplectic two-form. A diffeomorphism between two symplectic manifold is called a symplectic diffeomorphism if it respects the symplectic two-forms.
Submanifolds. Let be a symplectic manifold, and be a submanifold of . We define the symplectic orthogonal complement of as the vector subbundle of
The rank of the tangent bundle is the sum of the ranks of the tangent bundle and its symplectic orthogonal complement . We list some of the important cases.
- is called an isotropic submanifold if . In this case, the dimension of is less or equal to the half of the dimension of .
- is called a coisotropic submanifold if . In this case, the dimension of is greater or equal to the half of the dimension of .
- is called a Lagrangian submanifold if . In this case, the dimension of is equal to the half of the dimension of .
Under a symplectic diffeomorphism, the image of a Lagrangian (isotropic, coisotropic) submanifold is a Lagrangian (resp. isotropic, coisotropic) submanifold.
The Cotangent Bundle. The generic examples of symplectic manifolds are cotangent bundles. To see this, consider a manifold , and its cotangent bundle . The canonical (Liouville) one-form on is defined, on a vector X over as
Here, is the projection from the tangent bundle to its base manifold , whereas is the tangent lift of the cotangent projection . To be more precise, we present the following commutative diagram,
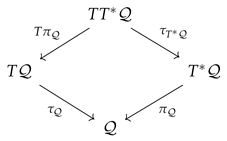

Minus of the exterior derivative of the canonical one-form , that is, , is the canonical symplectic two-form on the cotangent bundle .
Hamiltonian Vector Fields. Let X be a vector field on the symplectic manifold . It is called a local Hamiltonian vector field if it preserves the symplectic two-form
Poincaré Lemma assures us the existence of a local function H satisfying the so-called Hamilton’s equation
Notice that, in this realization, we denote the Hamiltonian vector field by . If there exists a global Hamiltonian function H then is called a (global) Hamiltonian vector field.
If the dimension of is n then the cotangent bundle turns out to be a dimensional manifold. In this case, the n-th power of the symplectic two-form is a non-vanishing top-form on . So that, it determines a volume form, the so-called symplectic volume. The identity (14) gives that a Hamiltonian vector field preserves the symplectic volume. Further, the skew-symmetry of the symplectic two-form manifests the conservation of the Hamiltonian function H. If H is the total energy, then this is called the conservation of energy.
A set of natural bundle coordinates on are Darboux coordinates, meaning that the canonical one-form and the symplectic two-form are written as
respectively. In this realization, the Hamilton’s Equation (15) is computed to be
Special Symplectic Structures. Let be a symplectic manifold carrying an exact symplectic two-form , with is being a potential one-form. Assume also that, is the total space of a fiber bundle . Here, is the base space, and is the projection. A special symplectic structure is a quintuple
where is a fiber preserving symplectic diffeomorphism from to the cotangent bundle (see [57,58]). The symplectic diffeomorphism relating canonical symplectic two-form on and the symplectic two-form satisfies both
Here, is the canonical one-form defined in (12). Accordingly, the symplectic diffeomorphism can be characterized by the following pairing
for a vector field X on , for any point x in . To see this definition, simply evaluate X with the pull-back one form that is,
where we have employed the definition (12) of the canonical one-form in the second line whereas the identities and in the third line. We exhibit a special symplectic manifold with the following commutative diagram
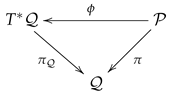

The two-tuple is called underlying symplectic manifold of the special symplectic structure.
2.2. Morse Families
First of all, we will review the definition of a special kind of Lagrangian submanifolds of a cotangent bundle endowed with the canonical symplectic structure (for more details, see [4,59]). Let be a submanifold of a smooth manifold and be a closed one-form defined on . Then, we can consider a Lagrangian submanifold of given by
where is the canonical inclusion. Note that for every point q in , there exists an open subset including q, and a real valued smooth function such that . In this case, is called the (local) generating function of . Next, we will review the definition of Morse families and the Lagrangian submanifolds associated with them.
Consider a fiber bundle where is the total space of dimension , whereas is the base manifold of dimension n. Here, is the bundle projection. The vertical bundle over the manifold is a vector sub-bundle of containing vectors that belong to the kernel of the tangent mapping that is,
The co-normal bundle is the space of co-vectors in annihilating vectors in the vertical bundle . A real-valued function E on the total space of a fiber bundle is called Morse family (or generating family) [4,58] if
for all in the intersection .
Generating Lagrangian Submanifolds. A Morse family E defined on generates an immersed Lagrangian submanifold of the cotangent bundle as
The inverse of this statement is also true. Thus, we state the following theorem, which is generalizing the well-known Poincaré Lemma for non-horizontal Lagrangian submanifolds. Accordingly, it is called as generalized Poincaré Lemma or Maslov-Hörmander Theorem [4,60,61].
Theorem 1.
For a Lagrangian submanifold of a cotangent bundle , there always exists, at least locally, a Morse family E generating .
We picture the Lagrangian submanifold generated by a Morse family E on as follows.

Given a Lagrangian submanifold, its Morse family generator is far from being unique. For example, one may find a Morse family with less number of fiber variables generating the same Lagrangian submanifold. This procedure is called reduction of Morse family. See [60] for further discussions on this subject.
We merge a Morse family E defined on and a special symplectic structure depicted diagrammaticality in (22). This permits us to define a Lagrangian submanifold of the symplectic manifold [9]. Here is the diagram,

Here, is the Lagrangian submanifold of given in (26), and the inverse of the symplectic diffeomorphism maps to a Lagrangian submanifold of . That is, .
Local Picture. Now, we present local realization of these discussions. Let be local coordinates on and we consider the induced local coordinates on the the total space . In this image, a function E is called a Morse family if the rank of the following matrix
is equal to K. In this case, the Lagrangian submanifold (26) generated by E is viewed locally as
Note that the dimension of the submanifold is half of the dimension of the cotangent bundle and the canonical symplectic two-form vanishes on .
2.3. Merging Two Special Symplectic Structures
Let be an exact symplectic manifold. Assume that admits two different fiber bundle structures denoted by and . Further, let these fibrations lead to two special symplectic symplectic structures denoted by and , respectively. We merge these two special symplectic structures in one diagram as follows:
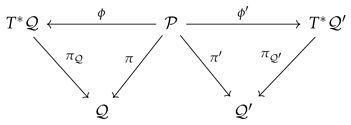

This is the most abstract realization of classical Tulczyjew’s triple. Notice that, in this geometry, the symplectic two-form on admits two different potential one forms and so that
Further, by employing the canonical symplectic two-forms and over the corresponding cotangent bundles and , the following properties hold
Consider the product manifold and let and be the maps defined in (31). Assume that the image space of
is an embedded submanifold of . Further, we assume that the map is a surjective submersion. The equalities (32) show that the difference is a closed one-form. Using Poincaré Lemma, we have that for every point p in there exists an open subset containing p and a smooth function on such that
The vertical bundle with respect to the fibration is precisely the intersection of the vertical bundles with respect to and , that is, . Notice that is a -basic one-form. In fact, due to the fiber preserving character of the symplectic diffeomorphisms and , the potential one-forms and are taking values in the co-normal bundles and , respectively. We deduce that the difference of potential one-forms takes values in the co-normal bundle since
where is the fibration in (34). So, there exists a unique closed one-form such that . In fact, given in (35) is a -basic function and, therefore, there exists a smooth function on satisfying . The following diagram illustrates the above situation.
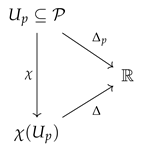

Next, we consider the following Lagrangian submanifold of the canonical symplectic manifold given by
Consider the symplectic diffeomorphism
where is the canonical form on the cotangent bundle, whereas
Referring to (39), we map the Lagrangian submanifold in (38) to a Lagrangian submanifold of . Then, we will prove the following result.
Theorem 2.
The of the symplectic diffeomorphism
pictured in (31) is an open subset of the Lagrangian submanifold .
Proof.
Evidently, is a Lagrangian submanifold of so that it is enough to show that is a subset of . In fact, we will see that
which implies the result. Suppose that be an element of , then we have that is precisely . Assume that in so that . This gives
However, since
we conclude that
Conversely, suppose that in and , . If , we will see that , which implies that in . We see that which gives . On the other hand,
Thus, as , we conclude that
□
To illustrate the Legendre transformation in this geometry, we present the following discussion. Assume the existence of the triple in (31). Start with the left wing of the triple by considering a real valued function F on . This determines a Lagrangian submanifold of . By employing the inverse of the symplectic diffeomorphism to , one arrives at a Lagrangian submanifold of the symplectic manifold . This submanifold can also be defined in terms of the potential one-form as
The Legendre transformation in terms of Tulczyjew [9,12] is to determine a generating family for referring to the right wing of the triple (31). To have that, first map to a Lagrangian submanifold of by means of the symplectic diffeomorphism . As a manifestation of the generalized Poincaré lemma, there exits a Morse family on a fiber bundle generating .
2.4. The Classical Tulczyjew’s Triple
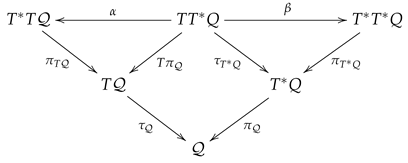
In this subsection, we draw Tulczyjew’s triple for classical dynamics assuming a configuration manifold . This is to construct the triple (31) by replacing with the tangent bundle , whereas replacing with the cotangent bundle . On the upper level of (31), this results with the iterated bundles , and in order. See that, being cotangent bundles, both and are symplectic. We now establish the symplectic structure on admitting two potential one forms.
Symplectic structure on . Consider the canonical symplectic manifold equipped with the exact symplectic two-form . The derivation takes the symplectic two-form on to a one-form on as
for any tangent vector Y on . Here, is the tangent bundle projection to whereas is the tangent mapping of the bundle projection . We define two one-forms on as
where the derivation is the commutator . The exterior derivatives of these one-forms results with a symplectic two-form on defined to be
We record this in the following theorem [12].
Theorem 3.
Consider the Darboux’s coordinates on the cotangent bundle . In terms of the induced local coordinate chart on the tangent bundle , the potential one-forms in (48) are computed to be
Notice that, in this case, the symplectic two-form turns out to be
Note that, the value is an exact one-form. Actually, it is the exterior derivative of coupling function .
One can arrive at the tangent bundle symplectic two-form on as the complete lift of the canonical symplectic two-form on . To have this, from [3,62] we recall the definition of the complete lift of a differential form. The complete lift of the canonical one-form is computed to be
Complete lift of forms commutes with exterior derivative. Thus, we compute
As manifested in the display, we conclude that .
By recalling Diagram (13), notice that admits two bundle structures. It is a vector bundle over with respect to the vector bundle projection , and it is a vector bundle over with vector bundle projection . Thus, we can consider the projection
from to the Whitney sum . The function is -basic and it induces a smooth function on , which is just the coupling function
In addition, is a submanifold of the product manifold . Thus, we can consider the Lagrangian submanifold induced by the exact one-form as in Section 2.2. Moreover, using the construction presented in Section 2.3, we deduce that is the graph of a symplectic diffeomorphism between and . In terms of the Darboux’ coordinates on , it is computed to be
The canonical involution on . The iterated tangent bundle is a tangent bundle with the base manifold along with the tangent bundle projection . It is possible to show that can be written as a vector bundle over apart from the canonical tangent bundle fibration. This fibration is achieved by the tangent mapping of the projection . To manifest this, we plot here the double vector bundle structure of the iterated tangent bundle in the following commutative diagram
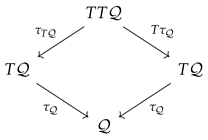

Referring to this double bundle structure [1,63,64], consider a differential mapping from an open domain of to . The differential of with respect to t, at , results with a curve lying in the tangent bundle depending on the free variable s. If one further takes the differential of the curve with respect to s, at , then arrives at a vector in . Accordingly, the canonical involution on is defined by changing the order of differentiations
An observation gives that the involution is changing the order of the fibrations
Pairing between and . We now establish a pairing between an element Z in and an element W in such that and that . Recall that, there is a curve in so that and, there is a curve in so that . In this framework, the pairing is defined as
Here, the pairing on the right hand side is the one between and .
In the induced coordinates on the iterated tangent bundle , the fibration in (57) read
whereas the canonical involution in (59) is computed to be
Coordinate expression of the pairing (60) is as follows. Let us choose coordinates on as , and coordinates on then,
Now, we define two special symplectic structures for the symplectic manifold . One is to and the other is to . We assume that, being cotangent bundles, and are equipped with the canonical symplectic forms and , respectively.
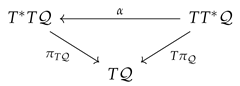
Left Wing of the Tulczyjew’s triple. Start with defining the vector fibration morphism
where is the canonical involution defined in (59), whereas the pairing on the right hand side is the one given in (60). Here, the pairing of the left hand side is the canonical pairing between and . Locally, one has that
See that, is a symplectic diffeomorphism by satisfying . Here, is the canonical symplectic two-form on , and is the lifted symplectic two-form (49) on . So that we arrive at a special symplectic structure
where is the one-form in (50), and is the tangent lift of the cotangent bundle projection . We include this in the following diagram for future reference

Right Wing of the Tulczyjew’s triple. The nondegeneracy of the canonical symplectic two-form leads to the existence of a (musical) diffeomorphism
Locally, one has that
Note that, is a symplectomorphism by satisfying . Here, is the canonical symplectic two-form on . So that we arrive at the following special symplectic structure
Here, is the potential one-form in (48) and that is the tangent bundle projection. The diagram is for the future reference.
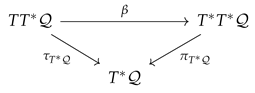

The Tulczyjew’s triple for classical mechanics is the following commutative diagram merging the two special symplectic structures (65) and (69) in one picture
 where and are symplectomorphisms such that
where and are symplectomorphisms such that

By employing the composition of two symplectic diffeomorphisms and , we arrive at a symplectic diffeomorphism . This is exactly the one in (56).
2.5. The Legendre Transformation
Let us now realized Euler–Lagrange equations generated by a Lagrangian function L on the tangent as a Lagrangian submanifold of using the left side of Tulczyjew’s triple (70). The image space of the exterior derivative is a Lagrangian submanifold of the manifold . By employing the inverse of , we transfer this Lagrangian submanifold to a Lagrangian submanifold of the manifold . In terms of the local coordinates on , is computed to be
Dynamics determined by the Lagrangian submanifold is computed simply by taking the time derivatives of the base coordinates and equate them to the fiber coordinates given by , respectively. By this, we arrive at the Euler–Lagrange equations
Notice that, for this realization, we have not asked any regularity conditions for the Lagrangian function. That is, this theory is valid for singular Lagrangians as well.
The Legendre Transformation of Euler–Lagrange Equations. We now generate the Lagrangian submanifold given in (71) referring to the right wing of the Tulczyjew’s triple (70). Let us remark once more that this is the Legendre transformation in the understanding of Tulczyjew. To have that, at first consider the Morse family over the Pontryagin bundle as
where is the canonical pairing between and . In coordinates, we write the Morse family as
We remark that the matrix
has maximal rank. For the choice of sign conventions, we consider the minus of the Morse family, that is, . So, according to the definition in (30), the minus of the Morse family generates a Lagrangian submanifold of the cotangent bundle as
In order to transfer this Lagrangian submanifold to , we merge the Pontryagin bundle with the right wing of the Tulczyjew’s triple (70) as follows
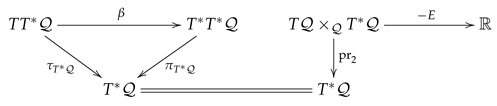

This permits us to arrive at the following Lagrangian submanifold of
A direct computation proves that the Lagrangian submanifold in (78) and the Lagrangian submanifold in (71) are the same. So that the Legendre transformation is achieved. If the Lagrangian function is non-degenerate, then from the equation
one can explicitly determine the velocity in terms of the momenta . In other words, for a non-degenerate Lagrangian function the fiber derivative
is a local diffeomorphism. In this case, the Morse family E can be reduced to a well-defined Hamiltonian function
on .
Inverse Legendre Transformation. The inverse Legendre transformation is also possible in a similar way. This time, one starts with a Hamiltonian system where H is a Hamiltonian function. See that, in this notation Hamiltonian vector field defined in (15) is determined through
Notice that the Lagrangian submanifold determined by the equality (82) is written in coordinates as
Evidently, this Lagrangian submanifold is precisely determining the Hamilton’s Equation (17). In the present picture, the inverse Legendre transformation is to generate the Lagrangian submanifold (83) by referring to the right wing of the triple. If the Hamiltonian function is not regular then one needs to employ a Morse family
So, if we consider the Pontryagin bundle over and we proceed as in the previous subsection, we will obtain the inverse Legendre transformation.
3. Contact Dynamics
3.1. Contact Manifolds
A —dimensional manifold is called contact manifold if it is equipped with a contact one-form satisfying [4,34]. We denote a contact manifold by a two-tuple . The Reeb vector field is the unique vector field satisfying
At each point of the manifold , the kernel of the contact form determines the contact structure . The complement of this structure, denoted by , is determined by the kernel of the exact two-form . These give the following decomposition of the tangent bundle
Here, is a vector sub-bundle of rank . The restriction of to is non-degenerate so that is a symplectic vector bundle over . The rank of is 1, and it is generated by the Reeb field .
Contactization. It is possible to arrive at a contact manifold starting from a symplectic manifold. To have this, consider a symplectic manifold admitting an integer symplectic two form . Introduce the principal circle (quantization) bundle
The contact one-form on is the connection one-form associated with a principal connection on the principal -bundle with curvature . This procedure is called contactization.
Another example of a contact manifold can be obtained from an exact symplectic manifold as follows. Consider a trivial line bundle over a manifold given by . The first jet bundle, denoted by is diffeomorphic to the product space that is,
We call this space the extended cotangent bundle. There exist two projections
where is the cotangent bundle projection whereas z is the standard coordinate on . Referring to the fibration defined by , we have the following globally trivial contactization of the canonical symplectic manifold
Here, the contact one-form on the jet bundle is defined to be
where is the canonical one-form (12) on the cotangent bundle . Notice that, we have employed abuse of notation by identifying z and with their pull-backs on the total space . The previous construction also works if we replace by an arbitrary exact symplectic manifold and, in such a case, we obtain a contact structure on the product manifold . There exist Darboux’ coordinates on , where i is running from 1 to n. In these coordinates, the contact one-form and the Reeb vector field are computed to be
respectively. Notice that, in this realization, the horizontal bundle is generated by the vector fields
It is important to note that these generators are not closed under the Jacobi–Lie bracket that is,
where stands for the Kronecker delta. The Darboux’s theorem manifests that local picture presented in this subsection is generic for all contact manifolds of dimension .
Musical Mappings. For a contact manifold , there is a musical isomorphism ♭ from the tangent bundle to the cotangent bundle defined to be
This mapping takes the Reeb field to the contact one-form . We denote the inverse of this mapping by ♯. Referring to this, we define a bi-vector field on as
The couple induces a Jacobi structure [59,65,66]. This is a manifestation of the equalities
where the bracket is the Schouten–Nijenhuis bracket. We cite [4,66,67,68] for more details on the Jacobi structure associated with a contact one-form. Referring to the bi-vector field we introduce the following musical mapping
Evidently, the mapping fails to be an isomorphism. Notice that the kernel is spanned by the contact one-form . So that, the image space of is precisely the horizontal bundle exhibited in (93).
In terms of the Darboux coordinates , we compute the image of a one-form in by as
Symplectization. The symplectization of a contact manifold is the symplectic manifold , where t denotes the standard coordinate on factor. In this case, is said to be the symplectification of . The inverse of this assertion is also true. That is, if is a symplectic manifold, then turns out to be contact.
3.2. Submanifolds of Contact Manifolds
Let be a contact manifold. Recall the associated bi-vector field defined in (96). Consider a linear subbundle of the tangent bundle (that is, a distribution on ). We define the contact complement of as
where the sharp map on the right hand side is the one in (98) and is the annihilator of . Let be a submanifold of . We say that is:
- Isotropic if .
- Coisotropic if .
- Legendrian if .
Assume that a submanifold of a contact manifold is defined to be the zero level set of k real smooth functions . We determine k vector fields . The image space of these vector fields are spanning the contact complement
In this geometry, is coisotropic if and only if, for all . According to the local computation in (99), we have that is co-isotropic if and only if
Referring to this local observation, one can easily prove that a submanifold of is Legendrian if and only if it is a maximal integral manifold of . In this case, the dimension of must be n (see [4,37,69]).
Generating Functions. Consider the first order jet bundle endowed with the contact structure given in (91). Let F be a real valued function on the base manifold . Its first prolongation is a section of the bundle displayed in (89) that is,
The image space of the first prolongation is a Legendrian submanifold of . The converse of this assertion is also true, that is, if the image space of a section of is a Legendrian submanifold, then it is the first prolongation of a function F. Evidently, this is not the only way to obtain a Legendrian submanifold.
Consider, for example, a Morse family E defined on a smooth bundle according to Section 2.2. Then, referring to the definition (26), we define a Lagrangian submanifold of the cotangent bundle . In the light of the first jet prolongation in (103), we lift this Lagrangian submanifold to a Legendrian submanifold of the contact manifold . To see this, consider a local system of coordinates on the base manifold , and the induced coordinates on the total space . Then, referring to the Darboux’s coordinates on , the Legendrian submanifold generated by a Morse family is computed to be
On the other hand, the lift of a Legendrian submanifold to the symplectification is a Lagrangian submanifold. In fact, is a Legendrian submanifold of a contact manifold if and only if is a Lagrangian submanifold of the symplectic manifold , see [70].
3.3. Contact Diffeomorphisms and Contact Hamiltonian Systems
Let and be two contact manifolds. A diffeomorphism from to is said to be a contact diffeomorphism (or contactomorphism) if it preserves the contact structures that is, . In terms of the contact forms, a contact diffeomorphism is the one satisfying
where is a non-zero conformal factor. To manifest the existence of this conformal factor, a mapping satisfying (105) is also called as conformal contact diffeomorphism. In this understanding, the contact mapping is denoted by a two-tuple .
For a contact manifold , we denote the group of contact diffeomorphisms [71] by
Here, is standing for the group of all diffeomorphism on . A vector field on the contact manifold is a contact vector field (called also as infinitesimal conformal contactomorphism) if it generates one-parameter group of contact diffeomorphisms. We have that the space of contact vector fields is given by
Sometimes a contact vector field is denoted by a two-tuple in order to manifest the existence of the conformal factor . In order to discuss the geometry of , we perform the following observation. This permits us to introduce Hamiltonian dynamics on the present framework as well (for more details, see [35,36,37,72]).
(Contact) Hamiltonian Vector Fields. For a real valued function H on a contact manifold , there is a corresponding contact vector field , defined as follows:
where is the Reeb vector field. Here, H is called the (contact) Hamiltonian function and is called the (contact) Hamiltonian vector field. We denote a contact Hamiltonian system as a three-tuple where is a contact manifold and H is a smooth real function on M. A direct computation determines the conformal factor for a given Hamiltonian vector fields as
That is, .
In this realization, the contact Jacobi bracket of two smooth functions on is defined by
where and are Hamiltonian vectors fields determined through (108). Here, is the Lie bracket of vector fields. Then, the identity
establishes the isomorphism
between the Lie algebras of real smooth functions and contact vector fields.
According to (109), the flow of a contact Hamiltonian system preserves the contact structure, but it does not preserve neither the contact one-form nor the Hamiltonian function. Instead, we obtain
Being a non-vanishing top-form we can consider as a volume form on . Hamiltonian motion does not preserve the volume form since
However, it is immediate to see that, for a nowhere vanishing Hamiltonian function H, the quantity is preserved along the motion (see [41]).
Referring to the Darboux’s coordinates , for a Hamiltonian function H, the Hamiltonian vector field, determined in (108), is computed to be
whereas the contact Jacobi bracket (110) is
Thus, we obtain that the Hamilton’s equations for H as
Evolution vector fields Another vector field can be defined from a Hamiltonian function H on a contact manifold : the evolution vector field of H [52], denoted as , which is the one that satisfies
In local coordinates, it is given by
so that the integral curves satisfy the evolution equations
The evolution and Hamiltonian vector fields are related by
Quantomorphisms. By asking the conformal factor in the definition (105) to be the unity, one arrives the conservation of the contact forms
We call such a mapping as a strict contact diffeomorphism (or quantomorphism). For a contact manifold we denote the space of all strict contact transformations as
The Lie algebra of this group is consisting of the infinitesimal quantomorphisms
If the contact vector field is determined through a smooth function H as in (108), then falls into the subspace if and only if . This reads that, to generate an infinitesimal quantomorphism, a function H must not depend on the fiber variable z.
Now, consider the canonical contact manifold . For two functions, those that are not dependent on the fiber variable z, the contact Jacobi bracket in (116) locally turns out to be equal to the canonical Poisson bracket on , therefore we find that
where is the infinitesimal quantomorphism generated by H. Accordingly, one arrives at an isomorphism
from the Lie algebra of Hamiltonian vector fields into the canonical cotangent bundle to the Lie algebra of infinitesimal quantomorphisms on the extended cotangent bundle.
3.4. Contact Lagrangian Dynamics
Once more, we consider the extended configuration space , but this time take it as the total space of the standard fibration from to . In this bundle structure, the base manifold is and the fibration is simply the projection to the second factor. The first jet manifold is diffeomorphic to
We call this space the extended tangent bundle.
Suppose that is a Lagrangian function. In order to arrive at the dynamical equations governed by such a Lagrangian function, one needs to employ the Herglotz principle, which is defined by an action functional [38,53,73].
The value of the functional attains its extremum if is a solution of the Herglotz equations (also known as the generalized Euler–Lagrange equations):
and z is a solution of the Cauchy problem
It is important to notice that (128) represents a family of differential equations, since for each function , a different differential equation arises, hence depends on . Without the explicit dependence of z, this problem reduces to a problem of the classical calculus of variations. If the functional z defined in (129) is invariant with respect to translation in time, then the quantity
is conserved on solutions of the Herglotz equations for regular Lagrangians.
For a regular Lagrangian function L, the fiber derivative determines a diffeomorphism from the extended tangent bundle to the extended cotangent bundle as
A direct calculation shows that the Legendre transformation (131) maps the Herglotz equations in (128) to the contact Hamilton’s equations (117) if the Hamiltonian function is defined to be
The evolution-Herglotz equations. One can obtain the Lagrangian formalism for the evolution vector field by using a nonlinear nonholonomic action principle, as shown in [74]. The resulting equations are the evolution Herglotz equations
4. Tulczyjew’s triple for Contact Geometry
4.1. Special Contact Structures
Let be a contact manifold and the total space of a fibre bundle . We introduce a special contact structure as a quintuple
where is a fiber preserving contact diffeomorphism from to the canonical contact manifold . The two-tuple is said to be the underlying contact manifold of the special contact structure. Here, we have a diagram exhibiting a special contact structure in a pictorial way
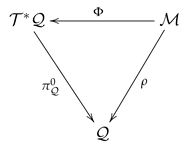 where is the fibration given in (89).
where is the fibration given in (89).

It is possible to define a special contact space starting with a special symplectic space defined in Section 2.1. For this, suppose that is an exact symplectic manifold and in the product manifold we consider the standard contact structure (that is, the contactization of the exact symplectic structure ). Assume also that admits a special symplectic structure as pictured in (22). Then, admits a special contact structure , where , and the following diagram
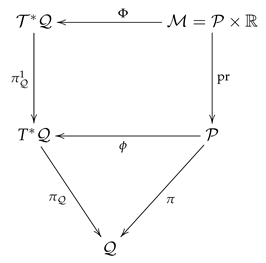 is commutative, with the fibration given in (89). Here, it is considered that . This construction is the contactization of the special symplectic structure.
is commutative, with the fibration given in (89). Here, it is considered that . This construction is the contactization of the special symplectic structure.

We now merge a Morse family E defined on a fiber bundle and a special contact space in order to arrive at a Legendrian submanifold of . For this, consider the following commutative diagram
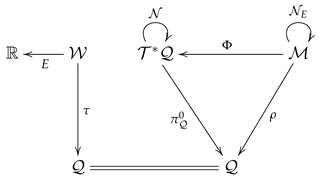

Referring to the definition in (104), we obtain a Legendrian submanifold of the jet bundle . Then, by employing the inverse of the contact diffeomorphism , we arrive at a Legendrian submanifold of . Referring to this realization, we shall exhibit both the contact Hamiltonian and contact Lagrangian dynamics as Legendrian submanifolds of the same contact manifold in the following subsection.
4.2. Tangent Contact Manifold
We start by lifting a contact structure on a contact manifold a contact structure on the extended tangent bundle . This lifting is in introduced in [70] to characterize the contact vector fields on (in particular, the Hamiltonian vector fields in ) in terms of Legendrian submanifolds of the contact manifold . In fact, more later, in this direction, we shall use some other results those available in [70].
Theorem 4.
For a contact manifold , the extended tangen bundle is a contact manifold by admitting a contact one-form
where u is coordinate on whereas and are the complete and vertical lifts of η, respectively.
The one-form is said to be the tangent contact structure and we will denote the tangent contact manifold as a two-tuple
Contact Hamiltonian Dynamics as a Legendrian Submanifold. Let be a contact manifold. Consider a vector field X, a real valued function on , hence a section
of the fibration . We plot the following commutative diagram to see this
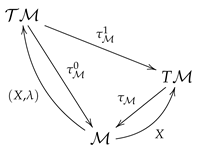

Using Theorem 3.13 in [70] and the comments at the beginning of this subsection, we deduce that the pair is a contact vector field (an infinitesimal conformal contactomorphism), that is, an element of in (107) if and only if the image space of is a Legendrian submanifold of the tangent contact manifold . This result states that the image of a contact Hamiltonian vector field , after suitably included in the contactified tangent bundle, turns out to be a Legendrian submanifold. As discussed in the previous section, the conformal factor in the present case is . So that, the image of the mapping
is a Legendrian submanifold of the tangent contact manifold . To see this more clearly, let us discuss this geometry in the realm of special contact spaces.
Consider a contact manifold . Its extended tangent bundle is a contact manifold endowed with the contact structure given by (139) and , as an extended cotangent bundle, is also a contact manifold. Between these two extended spaces, we introduce a fiber preserving contact diffeomorphism as follows
where is the contact one-form on . It is a direct computation to see that
where is the contact one-form on the canonical contact manifold and is the lifted contact one-form on given in (138). This observation permits us to determine a special contact space and following the order given in (134), we write this special contact manifold as
Accordingly, following the picture in (135), we plot the following diagram
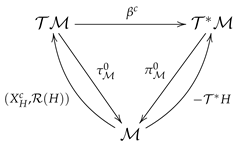 where we have employed the projections and . This diagram also manifests how one can transfer the Legendrian submanifolds one onto the other. If H is a Hamiltonian function on the contact manifold , then the image space of , as defined in (103), is a Legendrian submanifold of . Thus, since is a contact diffeomorphism, by pulling back the image space of , we arrive at a Legendrian submanifold of the tangent contact manifold . However, using (143), we have that
where we have employed the projections and . This diagram also manifests how one can transfer the Legendrian submanifolds one onto the other. If H is a Hamiltonian function on the contact manifold , then the image space of , as defined in (103), is a Legendrian submanifold of . Thus, since is a contact diffeomorphism, by pulling back the image space of , we arrive at a Legendrian submanifold of the tangent contact manifold . However, using (143), we have that

This is the contact version of the identity (82). Notice that, this observation can be considered as an indirect proof of the assertion that the image space of a contact vector field is a Legendrian submanifold.
Local Picture. Consider Darboux’s coordinates on then we assume the induced coordinates on as . In this local realization, the lifted contact one-form defined in (138) is computed to be
and the Reeb vector field is . In this realization, the contact mapping in (143) turns out to be
The fact that is a contactomorphism, that is the identity (144), follows from a direct calculation in coordinates. Observe that,
Consider now a Hamiltonian function H on the contact manifold . Minus of its first prolongation defines a Legendrian submanifold of given by
Referring to the inverse of the contact diffeomorphism we compute a Legendrian submanifold of as
It is immediate to see that the Legendrian submanifold can be alternatively obtained by
So, the contact Hamiltonian dynamics are determined by the Legendrian submanifold as follows. Let be a smooth curve on and consider the lift of to defined by
where is the tangent lift to . Then, is a solution of the contact Hamilton’s equations for H if and only if its lift to is contained in the Legendrian submanifold . In fact, if the local expression of is
then, from (152), it follows that for every , if and only if satisfies the following equations
They are precisely the contact Hamilton’s equations in (117).
4.3. Contact Tulczyjew’s Triple
Classical Tulczyjew’s triple is obtained by properly merging two special symplectic structures. Following the same understanding, we introduce Tulczyjew’s triple for contact dynamics by properly merging two special contact structures.
Contact Lift of Diffeomorphism in (56). Recall the symplectic diffeomorphism , defined in (56), from the cotangent bundle to the cotangent bundle . We extend this mapping to the level of contact manifolds
by assuming that extension is the identity on and it vanishes on the zero section. Accordingly, we recall the mapping in (56), consider a local chart on then we have an arbitrary extension
To determine w, we compute
where and are the canonical contact one-forms on and , respectively. Hence, is a contact mapping if and only if . Since we ask w to vanish on the zero section, necessarily . Therefore, the unique extension is, locally, computed to be
Next, we will present an intrinsic definition of . For this purpose, we will use the following identifications
Then, we have that
where is the canonical pairing between and .
The Left Wing of the triple. Now, using the contact mapping in (159), we define a contact diffeomorphism
Indeed, it is immediate to show that
where is the lifted contact one-form on given in (148). Then, we define the following special contact structure
which is diagrammatically given by
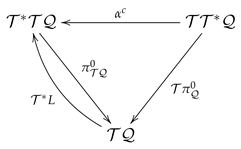 with the projections
with the projections

Here, we have employed the following global trivialization in .
Generalized Euler–Lagrange Equations as a Lagrangian Submanifold. Consider a Lagrangian function L on . The image space of its first prolongation, that is, , is a Legendrian submanifold of computed to be
Referring to the left wing of the contact triple (176), that is by applying the inverse of the mapping , we arrive at a Legendrian submanifold of as
The Lagrangian dynamics are determined by the Legendrian submanifold as follows. First of all, we consider the transformation induced by L given by
with defined by
Then, a smooth curve is a solution of the dynamics if and only if the lift of the curve given by
is contained in the Legendrian submanifold . In fact, if the local expression of c is
then, using (168), it follows that , , if and only if c satisfies
where the first two equations are the Herglotz equations in (128) and the latter is the Herglotz’s differential principle in (129). We remark that this theory does not require any regularity conditions on the Lagrangian function.
The Right Wing of the triple. To have the right wing, we simply replace the arbitrary contact manifold with the canonical contact manifold in the special contact manifold (145). In this case, the total spaces become and with the fibrations
We denote this special contact manifold as
Since Darboux’s coordinates are employed in Section 4.2, all the local formulations available in that subsection hold also in the present case.
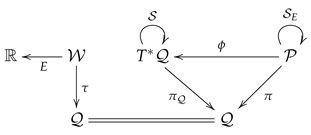
Contact triple. We now merge the special contact spaces (164) and (175) in order to construct a Tulzyjew’s triple for the contact geometry. Accordingly, we couple the commutative diagrams in (146) and (165) and arrive at the following diagram
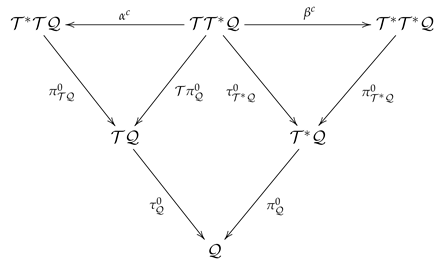 where the contact diffeomorphisms and are those defined in (143) and (162), respectively. Here, the projections and (respectively and ) are given by (174) (respectively, (166)).
where the contact diffeomorphisms and are those defined in (143) and (162), respectively. Here, the projections and (respectively and ) are given by (174) (respectively, (166)).

4.4. Evolution Contact Tulczyjew’s Triple
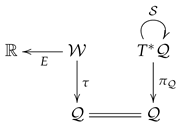
We will analyze how the Tulczyjew’s triple can be used to understand the evolution dynamics. First of all, we notice that there is not, a natural way, to describe an evolution vector field on a contact manifold as a Legendrian submanifold of . However, we will see that such a vector field may be considered as a Lagrangian submanifold of an exact symplectic submanifold of .
Consider a contact manifold . In (86), we have realized the kernel of the contact one-form as a symplectic vector bundle of the tangent bundle . Consider now the inclusion mapping
where i is the inclusion of into . Consider now the one-form on , and the two-form . In the following proposition, we state that is a symplectic two-form on
Proposition 1.
The exact two-form induces a symplectic structure on .
Proof.
Let be the Darboux’s coordinates on , so that are the induced coordinates for . In the light of the inclusion (177), we can employ as a local coordinate chart on since
In other words,
Thus, the Reeb vector field of the contact manifold is transverse to the manifold of codimension one . This implies that the exact two-form induces a symplectic structure on .
□
Lagrangian submanifolds and evolution vector fields. Given a vector field X on and a real smooth function , one can construct a section of the extended tangent bundle .
Theorem 5.
Let be a contact manifold. The map defines a Lagrangian submanifold of the exact symplectic manifold if and only if and is closed.
Proof.
First of all, note that the image of X lies on if and only if . For the second condition, we use well-known properties of complete and vertical lifts (see [62]);
Thus, the image of is Lagrangian if and only if
□
Looking at the definition of the evolution vector field (118), we obtain the following result.
Corollary 1.
The map defines a Lagrangian submanifold of the exact symplectic manifold if and only if, locally, and for a (local) smooth function .
Proof.
Since the evolution vector field satisfies
one arrives that is closed. Conversely, if and is closed, in a local chart U, one has that
for a local smooth function H. By contracting the equality with the Reeb vector field, we obtain that . Thus, . □
We start by presenting the following commutative diagram:
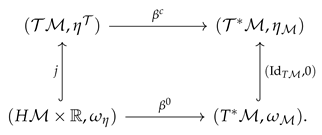

Here, is the contact mapping in (143), the mapping is the canonical inclusion of the cotangent bundle into the extended cotangent bundle as a zero section and the smooth map is given by
In coordinates,
Now, we are ready to plot the right wing of Tulczyjew’s triple for the evolution contact dynamics. For this, we replace the contact manifold with the extended cotangent bundle . Note that, in this case, we have
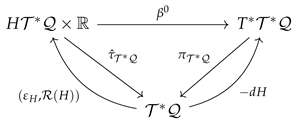 where is the projection taking a two-tuple mapping to , that is,
using that is a vector subbundle of . In order to see that the triangle commutes, we compute that
where we have used (118) and the Cartan’s formula. Following notation presented in (18), we write that the quintuple
determines a special symplectic structure. Since is a symplectic diffeomorphism, we can realize one more time that the image space as a Lagrangian submanifold of . Moreover, if is a smooth curve on and we consider the lift of the curve given by (154), then one may prove that is a solution of the contact evolution equations for H if and only if , for every .
where is the projection taking a two-tuple mapping to , that is,
using that is a vector subbundle of . In order to see that the triangle commutes, we compute that
where we have used (118) and the Cartan’s formula. Following notation presented in (18), we write that the quintuple
determines a special symplectic structure. Since is a symplectic diffeomorphism, we can realize one more time that the image space as a Lagrangian submanifold of . Moreover, if is a smooth curve on and we consider the lift of the curve given by (154), then one may prove that is a solution of the contact evolution equations for H if and only if , for every .

Recall the mapping given in (162). Consider the following commutative diagram
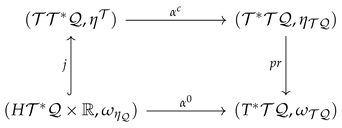 where j is the inclusion mapping in (178), is the natural projection from the extended cotangent bundle to the first factor that is the cotangent bundle . Using (162) and (178), we deduce that the local expression of is
where j is the inclusion mapping in (178), is the natural projection from the extended cotangent bundle to the first factor that is the cotangent bundle . Using (162) and (178), we deduce that the local expression of is
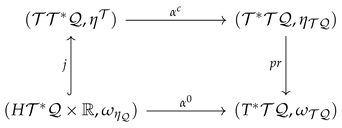
A direct calculation proves that that is is a symplectic diffeomorphism. Further, we can determine another potential one-form for the symplectic two-form given in (180) as follows
where is the canonical one-form on the cotangent bundle . We now construct the left wing of evolution contact Tulczyjew’s triple as follows
 where is the projection defined by . The local expression of is
where is the projection defined by . The local expression of is

Note that, following the notation in (18), we have that the quintuple
is a special symplectic structure.
For a given Lagrangian function , pulls the Lagrangian submanifold to a Lagrangian submanifold of the symplectic manifold . This Lagrangian submanifold is the realization of the evolution Herglotz equations. In fact,
Thus, a curve is a solution of the evolution Herglotz equations for L if and only if , for every , where is the lift of the curve given by (154).
We merge the right and left wings of triple given in (188) and (195), respectively. Thus, we have the evolution contact Tulczyjew’s triple:
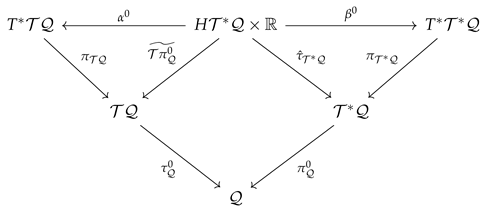

Note that this triple is consisting of two special symplectic structures.
4.5. The Legendre Transformation
At first we introduce the following Whitney product
over the extended manifold . This is an dimensional manifold which we call extended Pontryagin bundle. We introduce the local coordinates on . We now generate the Legendrian submanifold on given in (168) referring to the right wing of the contact Tulczyjew’s triple (176). This is the Legendre transformation in the understanding of Tulczyjew. To have that, define the following Morse family
To represent the minus of the Morse family , we are drawing the right side of the Tulczyjew’s triple (176) by equipping it with the Whitney product (200) as follows
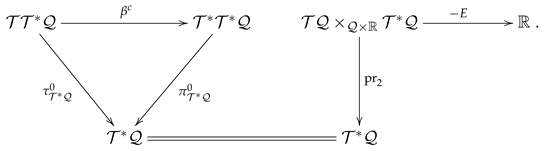
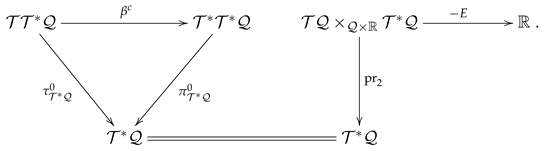
This geometry fits well in the general picture in (137). Recalling (104), a direct computation determines the Legendrian submanifold of generated by minus of the Morse family as
Using the inverse of the contact diffeomorphism , we map the Legendrian submanifold to a Legendrian submanifold of the contact manifold as
See that, this Legendrian submanifold is exactly the Legendrian submanifold in (168) realizing the Herglotz Equations (128) and (129). This completes the Legendre transformation of the Herglotz equations to the contact Hamiltonian formalism.
If, further, the Lagrangian function is non-degenerate, then from the equation
one can explicitly determine the velocity in terms of . This gives
as a local diffeomorphism relating and . In this case, the Morse family E can be reduced to a well-defined contact Hamiltonian function
on .
It is possible to perform the inverse Legendre transformation of the contact Hamiltonian dynamics as well. This time, one needs to generate the Legendrian submanifold in (152) realizing the contact Hamilton’s equations (156) referring to the left wing of the contact triple (176).
The Legendre Transformation for Evolution Dynamics. Recall the Tulczyjew’s triple (199) exhibited for the case of evolution contact dynamics. We consider the Lagrangian submanifold of generated by a Lagrangian on referring to the left wing (195) of the triple. Once more, consider the total space given in (200), and the energy function E given in (201). In this evolution case, we plot the following diagram merging the right wing (188) of the evolution Tulczyjew’s triple and the Morse family determined by that is
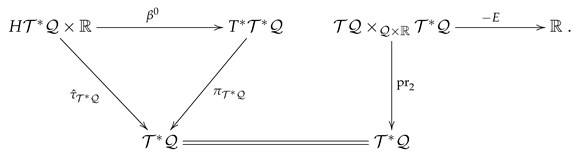

From (30), we deduce that the Lagrangian submanifold of the cotangent bundle generated by is computed to be
Using the inverse of the symplectic diffeomorphism , we transfer the Lagrangian submanifold to a Lagrangian submanifold of as follows
This is exactly the Lagrangian submanifold realizing the evolution Herglotz equations. In a similar way, one may obtain the inverse Legendre transformation of the contact evolution dynamics for a Hamiltonian function .
5. Example: The Ideal Gas
5.1. A Quantomorphism on the Euclidean Space
Thermodynamics have been studied extensively in the framework of contact geometry. For some recent work directly related with the present discussions, we cite [35,43,44,45]. In this section, we shall be applying the theoretical results obtained in the previous sections to some thermodynamical models.
We start this subsection by providing the following theorem realizing a strict contact diffeomorphism (quantomorphism) on the extended cotangent bundle of the Euclidean space, see also [43]. The proof follows by a direct calculation.
Theorem 6.
Consider a disjoint partition of the set of indices so that the coordinates on is given as , where and . Then the following mapping
preserves the canonical contact one-form . Here, are the Darboux’s coordinates on the extended cotangent bundle .
In Section 3.2, we have stated that the image of the first prolongation of a smooth function on the base manifold is a Legendrian submanifold of the extended cotangent bundle. Accordingly, consider a smooth function on so that its first prolongation to the extended cotangent bundle turns out to be a Legendrian submanifold of as given in (103). Under the quantomorphism in (210), we have a Legendrian submanifold on the image space as
This alternative realization of the Legendrian submanifold is important for geometric characterization of reversible thermodynamics.
5.2. Equilibrium Thermodynamics
Obeying the geometry exhibited in the previous section, we take with coordinates . Here, S stands for the entropy, V is the volume, and N is the mole number of classical ideal gas. The conjugate variables are the temperature, the pressure, and the chemical potential, respectively. By employing the internal energy U as the fiber coordinate, we complete the following realization of the extended cotangent bundle . Consider the contact one-form
As a particular instance, we choose the internal energy
as a function depending on the base coordinates . Here, is a positive constant, c is the heat capacity and R is the universal gas constant. The first prolongation is a Legendrian submanifold of the contact manifold . By considering that the temperature and the pressure , we have the following set of equations
those realizing .
The Legendre Transformations. In the light of Theorem 6, and the transformation (211), we now present the Legendre transformation between the internal energy, the enthalpy, the Helmholtz function, and the Gibbs function. For a similar discussion, but in the framework of symplectic geometry, see [12]. We start with the Legendrian submanifold determined by the internal energy U in (213).
(1) We decompose the base variables as and V and apply Theorem 6 to the volume variable. This results with a quantomorphism computed to be
Note that, on the image space, the fiber component is the enthalpy function . If we solve the pressure from the equation , the enthalpy function can be written as a function of the new base variables , that is
where is a constant defined to be . So that, the enthalpy function is another generator of the same Legendrian submanifold. Indeed, the first prolongation of is given the system of equations in (214) so that .
(2) We start once more with the internal energy, but this time we perform the transformation to the entropy variable S. For this case, we have the quantomorphism
In this case, the fiber term is the Helmholtz function. Using the identity , we write the Helmholtz function as a function of the base components of the image space, that is
Thus, F is another generator of the same Legendrian submanifold determined by the equations (214), that is .
(3) This time, we consider the Helmholtz function F in (218) and apply the transformation given in Theorem 6 to the volume variable, that is
The fiber term is the Gibbs function. By taking , we write the Gibbs function as a function of the base variables, that is
We have that is the Legendrian submanifold determined by Equation (214). Evidently, by iteratively applying in (217) and in (219), one can define a quantomorphism from the internal energy setting to the Gibbs function setting. In this case, the quantomorphism is determined as
This gives a direct passage from the internal energy to the Gibbs function.
(4) To complete the Legendre transformations, we consider the Gibbs function in (220) and define the quantomorphism to the chemical potential variable , that is
The fiber variable determines a new generator of the Legendrian submanifold depending on the base variables of the image space. In this case, we have that
Composing the quantomorphism in (221) with in (222), one can derive a Legendre transformation from the internal energy U setting to W as
This is the full Legendre transformation of the ideal gas. If we insist that the dynamics of the gas stays in the Legendrian submanifold determined through the equations (214), we can consider the fiber variable for an arbitrary internal energy U as a Hamiltonian function of the dynamics for the ideal case. Let us discuss this motion in the following subsection.
5.3. Hamiltonian Flow and Its Legendrian Realization
We consider the quantomorphism in (224), but instead of a specific internal energy, we let U be an independent variable. Consider the Hamiltonian function
on the extended cotangent bundle . Note that we determine the Hamiltonian function (225) by substituting the ideal gas equation (that is the second equation in (214)) into the minus of the generator function of the quantomorphism. The minus sign is to fit physical intuition, for example, to be sure that the entropy S is increasing along the motion. In fact, while computing the Hamiltonian dynamics, the minus sign will be compensated with the minus sign appearing in the formulation given in (147). According to (151), the image space of the first prolongation of the Hamiltonian function (225)
is a Legendrian submanifold of the iterated extended cotangent bundle . On the other hand, the contact Hamiltonian vector field associated with the Hamiltonian function (225) is
Notice that, the coefficients of and are zero. This gives that the Hamiltonian dynamics is isothermal and isochoric.
We consider the induced coordinates on the extended tangent bundle as follows. For the base manifold we use , for the fibers of the tangent bundle we refer and for the extension we use u as the standard coordinate on . Accordingly, for the present case, the lifted contact one-form (148) is computed to be
The Reeb field on is , and the directional derivative of the Hamiltonian function (225) is . The image space of the coupling of the Hamiltonian vector field and determines a Legendrian submanifold, of the extended tangent bundle , given by
Evidently, the Legendrian submanifolds in (226) and (229) are related with the contactomorphism by satisfying the relation as we have proven in (147).
Now, we wish to generate the Legendrian submanifold in (229) referring to the left wing of the contact Tulczyjew’s triple (176), that is to generate it via a Lagrangian function (probably as a Morse family) defined on the extended tangent bundle . In the light of Section 4.5, we now apply the inverse Legendre transformation. The first step is to apply in (162) to the Legendrian submanifold in (229). The image space is
which is a Legendrian submanifold of .
We assume the coordinates on the extended tangent bundle and define the Whitney sum of the extended tangent and the extended cotangent bundles with coordinates . Note that, in the Whitney sum, we fix the base coordinates in and the extension U in . The subscript in the notation of Whitney sum manifests these choices. A calculation gives that the Legendrian submanifold in (230) is generated by a Morse family on . In other words, the Lagrangian function
can be understood as defined on the extended tangent bundle , but depending on the auxiliary variables . By merging the Lagrangian function with the left wing of the contact Tulzyjew’s triple (176), we get the following diagram:
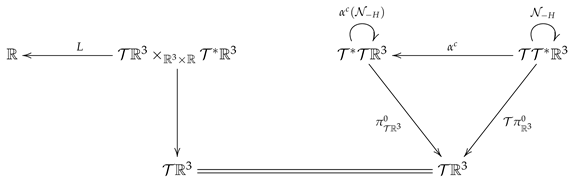

According to the local realization of the generating family in (104), it is a direct calculation to show that the Legendrian submanifold is generated by the Morse family L in (231).
We remark that in this formalism of thermodynamics, Hamiltonians are usually singular, as in the case above, so there is no Lagrangian formulation in the classical sense. Hence, we think that Tulcyzjew triples might be a useful tool in this situation.
5.4. Evolutionary Flow and Its Lagrangian Realization
We once more consider the Hamiltonian function H exhibited in (225) and defined on the extended cotangent bundle . The evolutionary vector field is defined in (119). A direct calculation determines the evolutionary vector field for the Hamiltonian function (225) as
on . By referring to Corollary 1, we establish that the image space
turns out to be a Lagrangian submanifold of defined in (179). Via in (193), we map the Lagrangian submanifold (234) to a Lagrangian submanifold
in the cotangent bundle . According to (30), it is immediate to see that the Lagrangian function L given in (231) defined on the Whitney sum of the extended tangent and the extended cotangent bundles generates the Lagrangian submanifold in (235). In order to visualize the Lagrangian submanifold, we draw the following diagram by merging the Morse family (231) and the left wing of the evolution contact Tulczyjew’s triple (199)
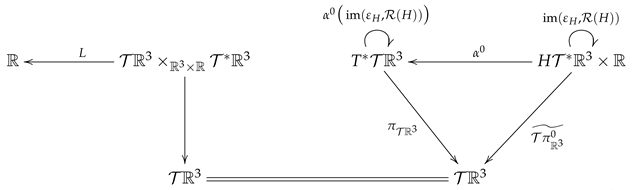 where is the mapping given in (196).
where is the mapping given in (196).

6. Discussion
In this paper, we have used the tangent contact structure, on the extended tangent bundle , which was introduced in [70]. Referring to this, and by introducing the notion of special contact structure, we have constructed a Tulcyzjew’s triple for contact manifolds, see Diagram (176). This permits us to describe both the contact Lagrangian and the contact Hamiltonian dynamics as Legendrian submanifolds of . In this formulation, the Legendre transformation is defined as a passage between two generators of the same Legendrian submanifold. Note that, this approach is free from the Hessian condition. That means, it is applicable for degenerate theories as well. We, further, present Tulcyzjew’s triple for evolutionary dynamics, see Diagram (199). Instead of contact structures, the evolution triple (199) consists of special symplectic structures. In this construction, the contact manifold is substituted by the extended horizontal bundle , which is symplectic. We have concluded the paper by applications of the theoretical results to geometrical foundations of some thermodynamical models.
Here are some further questions we wish to pursue:
- In Section 4.2, we have established that the image space of a contact Hamiltonian vector field is a Legendrian submanifold of the tangent contact manifold. Evidently, not all Legendrian submanifolds determine explicit dynamical equations. This observation motivates us to define the notion of an implicit Hamiltonian Contact Dynamics as a non-horizontal Legendrian submanifold of the tangent contact manifold. We refer to [75] for a similar discussion done for the case of symplectic dynamics and integrability of the non-horizontal Lagrangian submanifolds. We find it interesting to elaborate the integrability of implicit Hamiltonian contact dynamics.
- Following, the first question raised in this section, we plan to write a Hamilton–Jacobi theory for implicit Hamiltonian contact dynamics. Hamilton–Jacobi theory for (explicit) Hamiltonian contact dynamics is recently examined in [72,76]. Hamilton–Jacobi theory for implicit symplectic dynamics is discussed in [77,78].
- In the literature, Tulczyjew’s triple for higher order classical dynamical systems is already available [14,15]. Higher order contact dynamics is studied in [79]. As a future work, we plan to extend the geometry presented in the present paper to higher order contact framework.
Author Contributions
Writing—original draft, O.E., M.L.V., M.d.L. and J.C.M. All authors have contributed equally. All authors have read and agreed to the published version of the manuscript.
Funding
M. de León and M. Lainz acknowledge the partial finantial support from MICINN Grant PID2019-106715GB-C21 and the ICMAT Severo Ochoa project CEX2019-000904-S. M. Lainz wishes to thank MICINN and ICMAT for a FPI-Severo Ochoa predoctoral contract PRE2018-083203. J.C. Marrero acknowledges the partial support from European Union (Feder) grant PGC2018-098265-B-C32.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Abraham, R.; Marsden, J.E. Foundations of Mechanics; Benjamin/Cummings Publishing: Reading, MA, USA, 1978. [Google Scholar]
- Holm, D.D.; Schmah, T.; Stoica, C. Geometric Mechanics and Symmetry: From Finite to Infinite Dimensions; Oxford University Press: Oxford, UK, 2009; Volume 12. [Google Scholar]
- de León, M.; Rodrigues, P.R. Methods of Differential Geometry in Analytical Mechanics; North-Holland Mathematics Studies; North-Holland Publishing Co.: Amsterdam, The Netherlands, 1989; Volume 158, p. x+483. [Google Scholar]
- Libermann, P.; Marle, C.M. Symplectic Geometry and Analytical Mechanics; Mathematics and Its Applications; D. Reidel Publishing Co.: Dordrecht, The Netherlands, 1987; Volume 35, p. xvi+526. [Google Scholar]
- Dirac, P.A.M. Generalized Hamiltonian dynamics. Proc. R. Soc. Lond. Ser. A 1958, 246, 326–332. [Google Scholar] [CrossRef]
- Dirac, P.A.M. Lectures on Quantum Mechanics; Belfer Graduate School of Science Monographs Series; Belfer Graduate School of Science, New York; Produced and Distributed by Academic Press, Inc.: New York, NY, USA, 1967; Volume 2, p. v+87. [Google Scholar]
- Gotay, M.; Nester, J.M.; Hinds, G. Presymplectic manifolds and the Dirac-Bergmann theory of constraints. J. Math. Phys. 1978, 19, 2388–2399. [Google Scholar] [CrossRef]
- Skinner, R.; Rusk, R. Generalized Hamiltonian dynamics. I. Formulation on T*Q ⊕ TQ. J. Math. Phys. 1983, 24, 2589–2594. [Google Scholar] [CrossRef]
- Tulczyjew, W.M.; Urbański, P. A Slow and Careful Legendre Transformation for Singular Lagrangians. The Infeld Centennial Meeting (Warsaw, 1998). Acta Phys. Pol. 1999, 10, 2909–2978. [Google Scholar]
- Tulczyjew, W.M. Les sous-variétés Lagrangiennes et la dynamique Hamiltonienne. Comptes Rendus Acad. Sci. Paris Ser. AB 1976, 283, A15–A18. [Google Scholar]
- Tulczyjew, W.M. Hamiltonian Systems, Lagrangian Systems and the Legendre Transformation. In Symposia Mathematica; Academic Press: London, UK, 1974; Volume XIV (Convegno di Geometria Simplettica e Fisica Matematica, INDAM, Rome, 1973), pp. 247–258. [Google Scholar]
- Tulczyjew, W.M. The Legendre transformation. Ann. Inst. H. Poincaré Sect. A (N.S.) 1977, 27, 101–114. [Google Scholar]
- Weinstein, A. The symplectic “category”. In Differential Geometric Methods in Mathematical Physics; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 1982; pp. 45–51. [Google Scholar]
- de León, M.; Lacomba, E.A. Lagrangian submanifolds and higher-order mechanical systems. J. Phys. A 1989, 22, 3809–3820. [Google Scholar] [CrossRef]
- Esen, O.; Guha, P. On the geometry of the Schmidt-Legendre transformation. J. Geom. Mech. 2018, 10, 251. [Google Scholar] [CrossRef]
- Esen, O.; Gümral, H. Tulczyjew’s triplet for Lie groups I: Trivializations and reductions. J. Lie Theory 2014, 24, 1115–1160. [Google Scholar]
- Esen, O.; Gümral, H. Tulczyjew’s triplet for Lie groups II: Dynamics. J. Lie Theory 2017, 27, 329–356. [Google Scholar]
- Esen, O.; Gümral, H.; Sütlü, S. Tulczyew triplets for Lie groups III: Higher order dynamics and reductions for iterated bundles. arXiv 2021, arXiv:2102.10807. [Google Scholar]
- Grabowska, K.; Zając, M. The Tulczyjew triple in mechanics on a Lie group. J. Geom. Mech. 2016, 8, 413–435. [Google Scholar] [CrossRef]
- García-Toraño Andrés, E.; Guzmán, E.; Marrero, J.C.; Mestdag, T. Reduced dynamics and Lagrangian submanifolds of symplectic manifolds. J. Phys. A 2014, 47, 225203. [Google Scholar] [CrossRef]
- Esen, O.; Kudeyt, M.; Sütlü, S. Tulczyjew’s Triplet with an Ehresmann connection I: Trivialization and Reduction. arXiv 2020, arXiv:2007.11662. [Google Scholar]
- Grabowski, J.; Grabowska, K.; Urbański, P. Geometry of Lagrangian and Hamiltonian formalisms in the dynamics of strings. J. Geom. Mech. 2014, 6, 503–526. [Google Scholar] [CrossRef][Green Version]
- Campos, C.M.; Guzmán, E.; Marrero, J.C. Classical field theories of first order and Lagrangian submanifolds of premultisymplectic manifolds. J. Geom. Mech. 2012, 4, 1–26. [Google Scholar] [CrossRef]
- Cantrijn, F.; Ibort, A.; de León, M. On the geometry of multisymplectic manifolds. J. Aust. Math. Soc. (Ser. A) 1999, 66, 303–330. [Google Scholar] [CrossRef]
- de León, M.; de Diego, D.M.; Santamarıa-Merino, A. Tulczyjew’s triples and Lagrangian submanifolds in classical field theory. In Applied Differential Geometry and Mechanics; Academia Press: Ghent, Belgium, 2003; p. 189. [Google Scholar]
- de León, M.; Lacomba, E.A.; Rodrigues, P.R. Special presymplectic manifolds, Lagrangian submanifolds and the Lagrangian-Hamiltonian systems on jet bundles. In Proceedings of the First “Dr. Antonio A. R. Monteiro” Congress on Mathematics (Spanish) (Bahía Blanca, 1991), Bahía Blanca, Argentina, 7–9 August 1991; pp. 103–122. [Google Scholar]
- de León, M.; Salgado, M.; Vilariño, S. Methods of Differential Geometry in Classical Field Theories; World Scientific Publishing Co. Pte. Ltd.: Hackensack, NJ, USA, 2016; p. xiii+207. [Google Scholar]
- de León, M.; Vilariño, S. Lagrangian submanifolds in k-symplectic settings. Monatsh. Math. 2013, 170, 381–404. [Google Scholar] [CrossRef]
- Echeverria-Enriquez, A.; Munoz-Lecanda, M.C.; Roman-Roy, N. Geometry of multisymplectic Hamiltonian first-order field theories. J. Math. Phys. 2000, 41, 7402–7444. [Google Scholar] [CrossRef]
- Grabowska, K. A Tulczyjew triple for classical fields. J. Phys. A 2012, 45, 145207. [Google Scholar] [CrossRef]
- Grabowska, K.; Grabowski, J. Tulczyjew triples: From statics to field theory. J. Geom. Mech. 2013, 5, 445–472. [Google Scholar] [CrossRef][Green Version]
- Román-Roy, N.; Rey, A.M.; Salgado, M.; Vilariño, S. On the k-symplectic, k-cosymplectic and multisymplectic formalisms of classical field theories. J. Geom. Mech. 2011, 3, 113–137. [Google Scholar] [CrossRef]
- Grabowska, K.; Vitagliano, L. Tulczyjew triples in higher derivative field theory. J. Geom. Mech. 2015, 7, 1–33. [Google Scholar] [CrossRef][Green Version]
- Arnold, V.I. Mathematical Methods of Classical Mechanics; Mathematical Methods of Classical Mechanics; Springer: New York, NY, USA, 1989. [Google Scholar]
- Bravetti, A. Contact Hamiltonian dynamics: The concept and its use. Entropy 2017, 19, 535. [Google Scholar] [CrossRef]
- Bravetti, A.; Cruz, H.; Tapias, D. Contact Hamiltonian mechanics. Ann. Phys. 2017, 376, 17–39. [Google Scholar] [CrossRef]
- de León, M.; Lainz Valcázar, M. Contact Hamiltonian systems. J. Math. Phys. 2019, 60, 102902. [Google Scholar] [CrossRef]
- de León, M.; Lainz Valcázar, M. A review on contact Hamiltonian and Lagrangian systems. Rev. Acad. Canaria Cienc. 2019, XXXI, 1–46. [Google Scholar]
- Gaset, J.; Gracia, X.; Munoz-Lecanda, M.C.; Rivas, X.; Román-Roy, N. New contributions to the Hamiltonian and Lagrangian contact formalisms for dissipative mechanical systems and their symmetries. Int. J. Geom. Methods Mod. Phys. 2020, 17, 2050090. [Google Scholar] [CrossRef]
- de León, M.; Sardón, C. Cosymplectic and contact structures for time-dependent and dissipative Hamiltonian systems. J. Phys. A 2017, 50, 255205. [Google Scholar] [CrossRef]
- Bravetti, A.; de León, M.; Marrero, J.C.; Padrón, E. Invariant measures for contact Hamiltonian systems: Symplectic sandwiches with contact bread. J. Phys. A 2020, 53, 455205. [Google Scholar] [CrossRef]
- Ciaglia, F.M.; Cruz, H.; Marmo, G. Contact manifolds and dissipation, classical and quantum. Ann. Phys. 2018, 398, 159–179. [Google Scholar] [CrossRef]
- Bravetti, A. Contact geometry and thermodynamics. Int. J. Geom. Methods Mod. Phys. 2019, 16, 1940003. [Google Scholar] [CrossRef]
- Ghosh, A.; Bhamidipati, C. Contact geometry and thermodynamics of black holes in AdS spacetimes. Phys. Rev. D 2019, 100, 126020. [Google Scholar] [CrossRef]
- Mrugala, R.; Nulton, J.D.; Schön, J.C.; Salamon, P. Contact structure in thermodynamic theory. Rep. Math. Phys. 1991, 29, 109–121. [Google Scholar] [CrossRef]
- Grmela, M. Contact geometry of mesoscopic thermodynamics and dynamics. Entropy 2014, 16, 1652–1686. [Google Scholar] [CrossRef]
- Grmela, M. Multiscale Thermodynamics. Entropy 2021, 23, 165. [Google Scholar] [CrossRef]
- Grmela, M.; Öttinger, H.C. Dynamics and thermodynamics of complex fluids. I. Development of a general formalism. Phys. Rev. E 1997, 56, 6620. [Google Scholar] [CrossRef]
- Pavelka, M.; Klika, V.; Grmela, M. Multiscale Thermo-Dynamics; de Gruyter: Berlin, Germany, 2018. [Google Scholar]
- Wang, K.; Wang, L.; Yan, J. Implicit variational principle for contact Hamiltonian systems. Nonlinearity 2017, 30, 492–515. [Google Scholar] [CrossRef]
- Wang, K.; Wang, L.; Yan, J. Variational principle for contact Hamiltonian systems and its applications. J. Math. Pures Appl. 2019, 123, 167–200. [Google Scholar] [CrossRef]
- Simoes, A.A.; de León, M.; Lainz Valcázar, M.; Martín de Diego, D. Contact geometry for simple thermodynamical systems with friction. Proc. R. Soc. A 2020, 476, 20200244. [Google Scholar] [CrossRef]
- Herglotz, G. Berührungstransformationen, Lectures at the University of Göttingen; University of Göttingen: Göttingen, Germany, 1930. [Google Scholar]
- de León, M.; Lainz Valcázar, M. Singular Lagrangians and precontact Hamiltonian systems. Int. J. Geom. Methods Mod. Phys. 2019, 16, 1950158. [Google Scholar] [CrossRef]
- de León, M.; Gaset, J.; Lainz Valcázar, M.; Rivas, X.; Román-Roy, N. Unified Lagrangian-Hamiltonian formalism for contact systems. Fortschr. Phys. 2020, 68, 2000045. [Google Scholar] [CrossRef]
- Cannas da Silva, A. Lectures on Symplectic Geometry; Lecture Notes in Mathematics; Springer: Berlin/Heidelberg, Germany, 2001; Volume 1764. [Google Scholar] [CrossRef]
- Lawruk, B.; Śniatycki, J.; Tulczyjew, W.M. Special symplectic spaces. J. Differ. Equ. 1975, 17, 477–497. [Google Scholar] [CrossRef]
- Śniatycki, J.; Tulczyjew, W.M. Generating forms of Lagrangian submanifolds. Indiana Univ. Math. J. 1972, 22, 267–275. [Google Scholar] [CrossRef]
- Marle, C.M. On Jacobi manifolds and Jacobi bundles. In Symplectic Geometry, Groupoids, and Integrable Systems (Berkeley, CA, 1989); Springer: New York, NY, USA, 1991; Volume 20, pp. 227–246. [Google Scholar]
- Benenti, S. Hamiltonian Structures and Generating Families; Universitext; Springer: New York, NY, USA, 2011; p. xiv+258. [Google Scholar]
- Weinstein, A. Lectures on Symplectic Manifolds; American Mathematical Society: Providence, RI, USA, 1977; p. iv+48. [Google Scholar]
- Yano, K.; Ishihara, S. Tangent and Cotangent Bundles: Differential Geometry; Pure and Applied Mathematics, No. 16; Marcel Dekker, Inc.: New York, NY, USA, 1973; p. ix+423. [Google Scholar]
- Godbillon, C. Géométrie Différentielle et Mécanique Analytique; Hermann: Paris, Fance, 1969; p. 183. [Google Scholar]
- Urbański, P. Double Vector Bundles in Classical Mechanics. Rend. Semin. Mat. 1996, 54, 405–421. [Google Scholar]
- Kirillov, A.A. Local Lie algebras. Uspehi Mat. Nauk 1976, 31, 57–76. [Google Scholar] [CrossRef]
- Lichnerowicz, A. Les variétés de Jacobi et leurs algèbres de Lie associées. J. Math. Pures Appl. 1978, 57, 453–488. [Google Scholar]
- Bruce, A.J.; Grabowska, K.; Grabowski, J. Remarks on contact and Jacobi geometry. SIGMA Symmetry Integr. Geom. Methods Appl. 2017, 13, 059. [Google Scholar] [CrossRef][Green Version]
- de León, M.; Marrero, J.C.; Padrón, E. Lichnerowicz-Jacobi cohomology of Jacobi manifolds. C. R. Acad. Sci. Paris Sér. I Math. 1997, 324, 71–76. [Google Scholar] [CrossRef]
- de León, M.; Lainz Valcázar, M. Infinitesimal symmetries in contact Hamiltonian systems. J. Geom. Phys. 2020, 153, 103651. [Google Scholar] [CrossRef]
- Ibáñez, R.; de León, M.; Marrero, J.C.; Martín de Diego, D. Co-isotropic and Legendre-Lagrangian submanifolds and conformal Jacobi morphisms. J. Phys. A 1997, 30, 5427–5444. [Google Scholar] [CrossRef][Green Version]
- Banyaga, A. The Structure of Classical Diffeomorphism Groups; Mathematics and its Applications; Kluwer Academic Publishers Group: Dordrecht, The Netherlands, 1997; Volume 400, p. xii+197. [Google Scholar]
- de León, M.; Lainz Valcázar, M.; Muñiz Brea, A. The Hamilton–Jacobi theory for contact Hamiltonian systems. arXiv 2021, arXiv:2103.17017. [Google Scholar]
- Guenther, R.B.; Schwerdtfeger, H.; Herglotz, G.; Guenther, C.; Gottsch, J. The Herglotz Lectures on Contact Transformations and Hamiltonian Systems; Juliusz Schauder Center for Nonlinear Studies; Nicholas Copernicus University: Toruń, Poland, 1996. [Google Scholar]
- Simoes, A.A.; Martín de Diego, D.; Lainz Valcázar, M.; de León, M. The geometry of some thermodynamic systems. arXiv 2020, arXiv:2012.07404. [Google Scholar]
- Mendella, G.; Marmo, G.; Tulczyjew, W.M. Integrability of implicit differential equations. J. Phys. A 1995, 28, 149–163. [Google Scholar] [CrossRef]
- Grillo, S.; Padrón, E. Extended Hamilton-Jacobi theory, contact manifolds, and integrability by quadratures. J. Math. Phys. 2020, 61, 012901. [Google Scholar] [CrossRef]
- Esen, O.; de León, M.; Sardón, C. A Hamilton-Jacobi theory for implicit differential systems. J. Math. Phys. 2018, 59, 022902. [Google Scholar] [CrossRef]
- Esen, O.; de León, M.; Sardón, C. A Hamilton-Jacobi formalism for higher order implicit Lagrangians. J. Phys. A 2020, 53, 075204. [Google Scholar] [CrossRef]
- de León, M.; Gaset, J.; Laínz, M.; Muñoz Lecanda, M.C.; Román-Roy, N. Higher-order contact mechanics. Ann. Phys. 2021, 425, 168396. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).