Performance of a Novel Chaotic Firefly Algorithm with Enhanced Exploration for Tackling Global Optimization Problems: Application for Dropout Regularization
Abstract
:1. Introduction
- A novel modified FA algorithm was implemented by specifically targeting the known flaws of the basic implementation of the FA approach;
- The devised algorithm was later utilized to help establish the proper dropout value and enhancing the CNN accuracy;
- Other well-known swarm intelligence metaheuristics for CNN dropout regularization challenge were further investigated.
2. Preliminaries and Related Works
3. Proposed Method
3.1. The Original Firefly Algorithm
3.2. Motivation for Improvements
3.3. Novel FA Metaheuristics
- Explicit exploration mechanism based on the solution’s exhaustiveness;
- gBest chaotic local search (CLS) strategy.
3.3.1. Explicit Exploration Mechanism
3.3.2. The gBest CLS Strategy
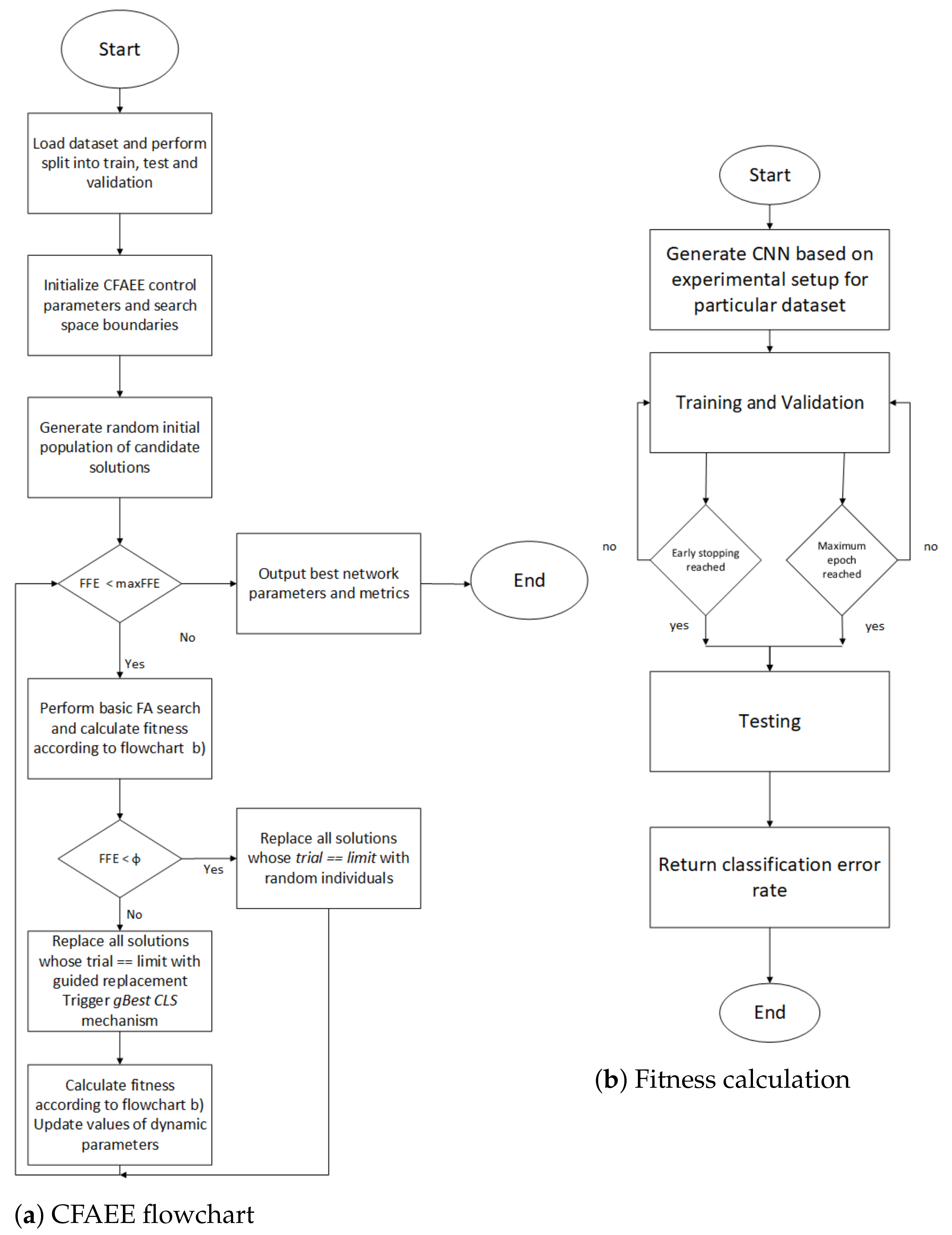
3.3.3. Chaotic FA with Enhanced Exploration Pseudo-Code
| Algorithm 1 The CFAEE pseudo-code |
| Initialize main metaheuristics control parameters N and T |
| Initialize search space parameters D, and |
| Initialize CFAEE control parameters , , , , K and |
| Generate initial random population using Equation (15) in the search space |
| whiledo |
| for to N do |
| for to i do |
| if then |
| Move solution z in the direction of individual i in D dimensions (Equation (12)) |
| Attractiveness changes with distance r as exp[] (Equation (10)) |
| Evaluate new solution, replace the worse individual with better one and update intensity of light (fitness) |
| end if |
| end for |
| end for |
| if then |
| Replace all solutions for which with random ones using Equation (15) |
| else |
| Replace all solutions for which with guided replacement using Equation (16) |
| for to K do |
| Perform gBest CLS around the using Equations (17)–(19) and generate |
| Retain better solution between and |
| end for |
| end if |
| Update and according to Equations (14) and (20), respectively |
| end while |
| Return the best individual from the population |
| Post-process results and perform visualization |
3.3.4. The CFAEE Complexity and Drawbacks
4. Bound-Constrained Benchmark Simulations
4.1. Experimental Setup
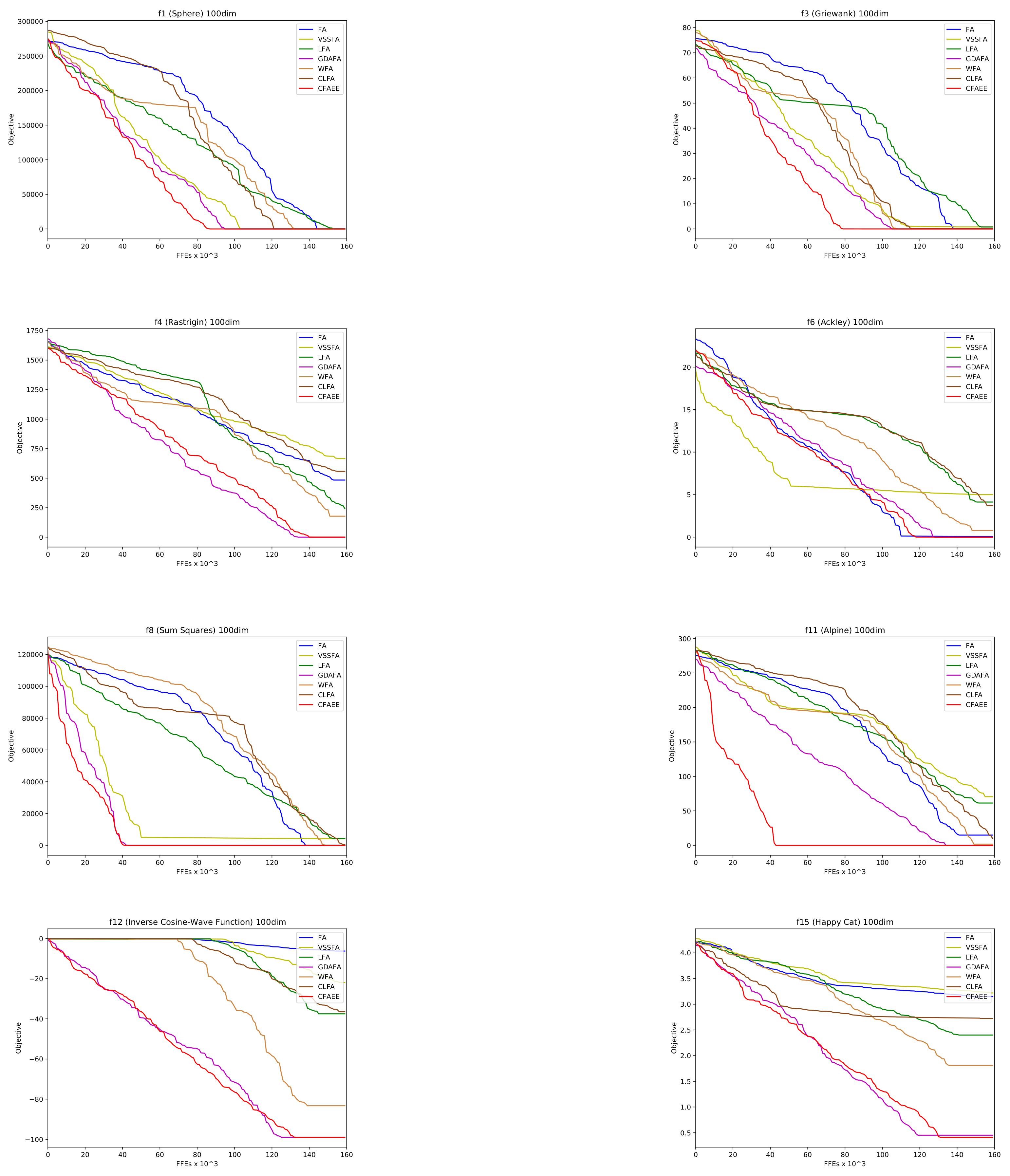
4.2. Benchmark Problem Set 1
4.3. Benchmark Problem Set 2
5. Dropout Estimation Simulations
5.1. Basic Experimental Setup
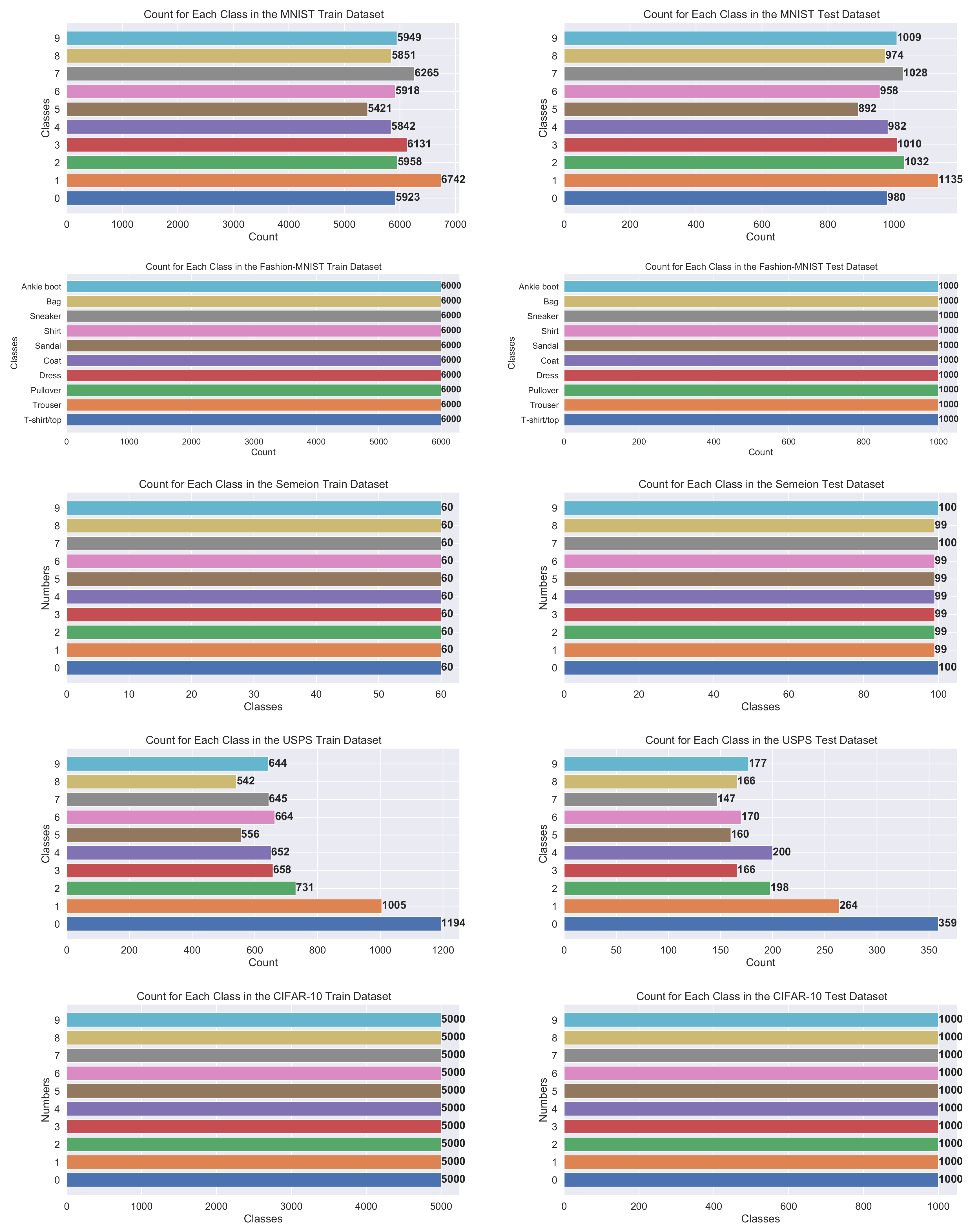
- MNIST—consists of images of handwritten digits “0–9”; it is divided into 60,000 training and 10,000 testing observations; image size pixels gray-scale (http://yann.lecun.com/exdb/mnist/, accessed on 10 October 2021);
- Fashion-MNIST—dataset of Zalando’s article images; it is comprised of different clothing images divided into 10 classes; it is split into 60,000 and 10,000 images used for training and testing, respectively; image size pixels (https://github.com/zalandoresearch/fashion-mnist, accessed on 10 October 2021);
- Semeion—includes a total of 1593 handwritten digits “0–9” images collected from 80 persons; digits are written accurately (normal way) and inaccurately (fast way); the original dataset is not split into training and testing; image size grayscale and each pixel is binarized (https://archive.ics.uci.edu/ml/datasets/Semeion+Handwritten+Digit, accessed on 10 October 2021);
- USPS—contains handwritten digits “0–9” images obtained from the envelopes of the United States Postal Service; dataset is split into 7291 training and 2007 testing images; image size gray-scale (http://statweb.stanford.edu/tibs/ElemStatLearn/datasets/zip.info.txt, accessed on 10 October 2021);
- CIFAR-10—consists of various images from 10 classes; subset of 80 million tiny images retrieved and collected by Alex Krizhevsky, Vinod Nair, and Geoffrey Hinton; divided into 50,000 images for training and 10,000 images for testing; image size color-scale (http://www.cs.toronto.edu/kriz/cifar.html, accessed on 10 October 2021).
5.2. Results, Comparative Analysis, and Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Yang, X.S. Firefly Algorithms for Multimodal Optimization. In Stochastic Algorithms: Foundations and Applications; Watanabe, O., Zeugmann, T., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 169–178. [Google Scholar]
- Bezdan, T.; Cvetnic, D.; Gajic, L.; Zivkovic, M.; Strumberger, I.; Bacanin, N. Feature Selection by Firefly Algorithm with Improved Initialization Strategy. In Proceedings of the 7th Conference on the Engineering of Computer Based Systems, Novi Sad, Serbia, 26–27 May 2021; pp. 1–8. [Google Scholar]
- Bacanin, N.; Bezdan, T.; Venkatachalam, K.; Al-Turjman, F. Optimized convolutional neural network by firefly algorithm for magnetic resonance image classification of glioma brain tumor grade. J. Real Time Image Process. 2021, 18, 1085–1098. [Google Scholar] [CrossRef]
- Kumar, V.; Kumar, D. A systematic review on firefly algorithm: Past, present, and future. Arch. Comput. Methods Eng. 2021, 28, 3269–3291. [Google Scholar] [CrossRef]
- de Rosa, G.; Papa, J.; Yang, X.S. Handling Dropout Probability Estimation in Convolution Neural Networks Using Metaheuristics. Soft Comput. 2018, 22, 6147–6156. [Google Scholar] [CrossRef] [Green Version]
- Zivkovic, M.; Bacanin, N.; Venkatachalam, K.; Nayyar, A.; Djordjevic, A.; Strumberger, I.; Al-Turjman, F. COVID-19 cases prediction by using hybrid machine learning and beetle antennae search approach. Sustain. Cities Soc. 2021, 66, 102669. [Google Scholar] [CrossRef] [PubMed]
- Wainer, J.; Fonseca, P. How to tune the RBF SVM hyperparameters? An empirical evaluation of 18 search algorithms. Artif. Intell. Rev. 2021, 54, 4771–4797. [Google Scholar] [CrossRef]
- Basha, J.; Bacanin, N.; Vukobrat, N.; Zivkovic, M.; Venkatachalam, K.; Hubálovskỳ, S.; Trojovskỳ, P. Chaotic Harris Hawks Optimization with Quasi-Reflection-Based Learning: An Application to Enhance CNN Design. Sensors 2021, 21, 6654. [Google Scholar] [CrossRef]
- Beni, G. Swarm intelligence. Complex Soc. Behav. Syst. Game Theory Agent Based Model. 2020, 791–818. [Google Scholar] [CrossRef]
- Abraham, A.; Guo, H.; Liu, H. Swarm intelligence: Foundations, perspectives and applications. In Swarm Intelligent Systems; Springer: Berlin/Heidelberg, Germany, 2006; pp. 3–25. [Google Scholar]
- Li, M.W.; Wang, Y.T.; Geng, J.; Hong, W.C. Chaos cloud quantum bat hybrid optimization algorithm. Nonlinear Dyn. 2021, 103, 1167–1193. [Google Scholar] [CrossRef]
- Zivkovic, M.; Bacanin, N.; Tuba, E.; Strumberger, I.; Bezdan, T.; Tuba, M. Wireless Sensor Networks Life Time Optimization Based on the Improved Firefly Algorithm. In Proceedings of the 2020 International Wireless Communications and Mobile Computing (IWCMC), Limassol, Cyprus, 15–19 June 2020; pp. 1176–1181. [Google Scholar]
- Zivkovic, M.; Bacanin, N.; Zivkovic, T.; Strumberger, I.; Tuba, E.; Tuba, M. Enhanced Grey Wolf Algorithm for Energy Efficient Wireless Sensor Networks. In Proceedings of the 2020 Zooming Innovation in Consumer Technologies Conference (ZINC), Online, 26–27 May 2020; pp. 87–92. [Google Scholar]
- Bacanin, N.; Tuba, E.; Zivkovic, M.; Strumberger, I.; Tuba, M. Whale Optimization Algorithm with Exploratory Move for Wireless Sensor Networks Localization. In Proceedings of the International Conference on Hybrid Intelligent Systems, Sehore, India, 10–12 December 2019; Springer: Berlin/Heidelberg, Germany, 2019; pp. 328–338. [Google Scholar]
- Zivkovic, M.; Zivkovic, T.; Venkatachalam, K.; Bacanin, N. Enhanced Dragonfly Algorithm Adapted for Wireless Sensor Network Lifetime Optimization. In Data Intelligence and Cognitive Informatics; Springer: Berlin/Heidelberg, Germany, 2021; pp. 803–817. [Google Scholar]
- Bacanin, N.; Bezdan, T.; Tuba, E.; Strumberger, I.; Tuba, M.; Zivkovic, M. Task scheduling in cloud computing environment by grey wolf optimizer. In Proceedings of the 2019 27th Telecommunications Forum (TELFOR), Belgrade, Serbia, 26–27 November 2019; pp. 1–4. [Google Scholar]
- Strumberger, I.; Bacanin, N.; Tuba, M.; Tuba, E. Resource scheduling in cloud computing based on a hybridized whale optimization algorithm. Appl. Sci. 2019, 9, 4893. [Google Scholar] [CrossRef] [Green Version]
- Bezdan, T.; Zivkovic, M.; Tuba, E.; Strumberger, I.; Bacanin, N.; Tuba, M. Glioma Brain Tumor Grade Classification from MRI Using Convolutional Neural Networks Designed by Modified FA. In Proceedings of the International Conference on Intelligent and Fuzzy Systems, Istanbul, Turkey, 21–23 July 2020; Springer: Berlin/Heidelberg, Germany, 2020; pp. 955–963. [Google Scholar]
- Bacanin, N.; Bezdan, T.; Tuba, E.; Strumberger, I.; Tuba, M. Monarch butterfly optimization based convolutional neural network design. Mathematics 2020, 8, 936. [Google Scholar] [CrossRef]
- Zivkovic, M.; Venkatachalam, K.; Bacanin, N.; Djordjevic, A.; Antonijevic, M.; Strumberger, I.; Rashid, T.A. Hybrid Genetic Algorithm and Machine Learning Method for COVID-19 Cases Prediction. In Proceedings of the International Conference on Sustainable Expert Systems: ICSES 2020, Nepal, South Asia, 17–18 September 2020; Springer: Berlin/Heidelberg, Germany, 2021; Volume 176, p. 169. [Google Scholar]
- Milosevic, S.; Bezdan, T.; Zivkovic, M.; Bacanin, N.; Strumberger, I.; Tuba, M. Feed-Forward Neural Network Training by Hybrid Bat Algorithm. In Proceedings of the Modelling and Development of Intelligent Systems: 7th International Conference, MDIS 2020, Sibiu, Romania, 22–24 October 2020; Revised Selected Papers 7. Springer: Berlin/Heidelberg, Germany, 2021; pp. 52–66. [Google Scholar]
- Gajic, L.; Cvetnic, D.; Zivkovic, M.; Bezdan, T.; Bacanin, N.; Milosevic, S. Multi-layer Perceptron Training Using Hybridized Bat Algorithm. In Computational Vision and Bio-Inspired Computing; Springer: Berlin/Heidelberg, Germany, 2021; pp. 689–705. [Google Scholar]
- Hongtao, L.; Qinchuan, Z. Applications of deep convolutional neural network in computer vision. J. Data Acquis. Process. 2016, 31, 1–17. [Google Scholar]
- Xiao, T.; Xu, Y.; Yang, K.; Zhang, J.; Peng, Y.; Zhang, Z. The application of two-level attention models in deep convolutional neural network for fine-grained image classification. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 842–850. [Google Scholar]
- Zhang, Y.; Zhao, D.; Sun, J.; Zou, G.; Li, W. Adaptive convolutional neural network and its application in face recognition. Neural Process. Lett. 2016, 43, 389–399. [Google Scholar] [CrossRef]
- Lawrence, S.; Giles, C.L.; Tsoi, A.C.; Back, A.D. Face recognition: A convolutional neural-network approach. IEEE Trans. Neural Netw. 1997, 8, 98–113. [Google Scholar] [CrossRef] [Green Version]
- Ranjan, R.; Sankaranarayanan, S.; Castillo, C.D.; Chellappa, R. An all-in-one convolutional neural network for face analysis. In Proceedings of the 2017 12th IEEE International Conference on Automatic Face & Gesture Recognition (FG 2017), Washington, DC, USA, 30 May–3 June 2017; pp. 17–24. [Google Scholar]
- Matsugu, M.; Mori, K.; Mitari, Y.; Kaneda, Y. Subject independent facial expression recognition with robust face detection using a convolutional neural network. Neural Netw. 2003, 16, 555–559. [Google Scholar] [CrossRef]
- Ramaiah, N.P.; Ijjina, E.P.; Mohan, C.K. Illumination invariant face recognition using convolutional neural networks. In Proceedings of the 2015 IEEE International Conference on Signal Processing, Informatics, Communication and Energy Systems (SPICES), Kozhikode, India, 19–21 February 2015; pp. 1–4. [Google Scholar]
- Simard, P.Y.; Steinkraus, D.; Platt, J.C. Best practices for convolutional neural networks applied to visual document analysis. In Proceedings of the ICDAR, Edinburgh, UK, 3–6 August 2003; Volume 3. [Google Scholar]
- Afzal, M.Z.; Capobianco, S.; Malik, M.I.; Marinai, S.; Breuel, T.M.; Dengel, A.; Liwicki, M. Deepdocclassifier: Document classification with deep convolutional neural network. In Proceedings of the 2015 13th International Conference on Document Analysis and Recognition (ICDAR), Tunis, Tunisia, 23–26 August 2015; pp. 1111–1115. [Google Scholar]
- Stoean, C.; Lichtblau, D. Author Identification Using Chaos Game Representation and Deep Learning. Mathematics 2020, 8, 1933. [Google Scholar] [CrossRef]
- Špetlík, R.; Franc, V.; Matas, J. Visual heart rate estimation with convolutional neural network. In Proceedings of the British Machine Vision Conference, Newcastle, UK, 3–6 September 2018; pp. 3–6. [Google Scholar]
- Li, Q.; Cai, W.; Wang, X.; Zhou, Y.; Feng, D.D.; Chen, M. Medical image classification with convolutional neural network. In Proceedings of the 2014 13th International Conference on Control Automation Robotics & Vision (ICARCV), Singapore, 10–12 December 2014; pp. 844–848. [Google Scholar]
- Ting, F.F.; Tan, Y.J.; Sim, K.S. Convolutional neural network improvement for breast cancer classification. Expert Syst. Appl. 2019, 120, 103–115. [Google Scholar] [CrossRef]
- Liu, Y.; Racah, E.; Correa, J.; Khosrowshahi, A.; Lavers, D.; Kunkel, K.; Wehner, M.; Collins, W. Application of deep convolutional neural networks for detecting extreme weather in climate datasets. arXiv 2016, arXiv:1605.01156. [Google Scholar]
- Chattopadhyay, A.; Hassanzadeh, P.; Pasha, S. Predicting clustered weather patterns: A test case for applications of convolutional neural networks to spatio-temporal climate data. Sci. Rep. 2020, 10, 1317. [Google Scholar] [CrossRef]
- Yang, X.S.; Xingshi, H. Firefly Algorithm: Recent Advances and Applications. Int. J. Swarm Intell. 2013, 1, 36–50. [Google Scholar] [CrossRef] [Green Version]
- Strumberger, I.; Tuba, E.; Bacanin, N.; Zivkovic, M.; Beko, M.; Tuba, M. Designing convolutional neural network architecture by the firefly algorithm. In Proceedings of the 2019 International Young Engineers Forum (YEF-ECE), Caparica, Portugal, 10 May 2019; pp. 59–65. [Google Scholar]
- Strumberger, I.; Bacanin, N.; Tuba, M. Enhanced Firefly Algorithm for Constrained Numerical Optimization, IEEE Congress on Evolutionary Computation. In Proceedings of the IEEE International Congress on Evolutionary Computation (CEC 2017), Donostia, Spain, 5–8 June 2017; pp. 2120–2127. [Google Scholar]
- Xu, G.H.; Zhang, T.W.; Lai, Q. A new firefly algorithm with mean condition partial attraction. Appl. Intell. 2021, 1–14. [Google Scholar] [CrossRef]
- Bacanin, N.; Tuba, M. Firefly Algorithm for Cardinality Constrained Mean-Variance Portfolio Optimization Problem with Entropy Diversity Constraint. Sci. World J. Spec. Issue Comput. Intell. Metaheuristic Algorithms Appl. 2014, 2014, 721521. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Zhou, X.; Sun, H.; Yu, X.; Zhao, J.; Zhang, H.; Cui, L. Firefly algorithm with adaptive control parameters. Soft Comput. 2017, 3, 5091–5102. [Google Scholar] [CrossRef]
- Karaboga, D.; Basturk, B. On the performance of artificial bee colony (ABC) algorithm. Appl. Soft Comput. 2008, 8, 687–697. [Google Scholar] [CrossRef]
- Moradi, P.; Imanian, N.; Qader, N.N.; Jalili, M. Improving exploration property of velocity-based artificial bee colony algorithm using chaotic systems. Inf. Sci. 2018, 465, 130–143. [Google Scholar] [CrossRef]
- Alatas, B. Chaotic bee colony algorithms for global numerical optimization. Expert Syst. Appl. 2010, 37, 5682–5687. [Google Scholar] [CrossRef]
- dos Santos Coelho, L.; Mariani, V.C. Use of chaotic sequences in a biologically inspired algorithm for engineering design optimization. Expert Syst. Appl. 2008, 34, 1905–1913. [Google Scholar] [CrossRef]
- Li, C.; Zhou, J.; Xiao, J.; Xiao, H. Parameters identification of chaotic system by chaotic gravitational search algorithm. Chaos Solitons Fractals 2012, 45, 539–547. [Google Scholar] [CrossRef]
- Chen, H.; Xu, Y.; Wang, M.; Zhao, X. A balanced whale optimization algorithm for constrained engineering design problems. Appl. Math. Model. 2019, 71, 45–59. [Google Scholar] [CrossRef]
- Liang, X.; Cai, Z.; Wang, M.; Zhao, X.; Chen, H.; Li, C. Chaotic oppositional sine–cosine method for solving global optimization problems. Eng. Comput. 2020, 1–17. [Google Scholar] [CrossRef]
- Mirjalili, S. SCA: A sine cosine algorithm for solving optimization problems. Knowl. Based Syst. 2016, 96, 120–133. [Google Scholar] [CrossRef]
- Mirjalili, S.Z.; Mirjalili, S.; Saremi, S.; Faris, H.; Aljarah, I. Grasshopper optimization algorithm for multi-objective optimization problems. Appl. Intell. 2018, 48, 805–820. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The whale optimization algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Liu, J.; Mao, Y.; Liu, X.; Li, Y. A dynamic adaptive firefly algorithm with globally orientation. Math. Comput. Simul. 2020, 174, 76–101. [Google Scholar] [CrossRef]
- Zhu, Q.; Xiao, Y.; Chen, W.; Ni, C.; Chen, Y. Research on the improved mobile robot localization approach based on firefly algorithm. Chin. J. Sci. Instrum. 2016, 37, 323–329. [Google Scholar]
- Kaveh, A.; Javadi, S. Chaos-based firefly algorithms for optimization of cyclically large-size braced steel domes with multiple frequency constraints. Comput. Struct. 2019, 214, 28–39. [Google Scholar] [CrossRef]
- Yang, X.S. Firefly Algorithm, Lévy Flights and Global Optimization. In Research and Development in Intelligent Systems XXVI; Bramer, M., Ellis, R., Petridis, M., Eds.; Springer: London, UK, 2010; pp. 209–218. [Google Scholar]
- Yu, S.; Zhu, S.; Ma, Y.; Mao, D. A variable step size firefly algorithm for numerical optimization. Appl. Math. Comput. 2015, 263, 214–220. [Google Scholar] [CrossRef]
- Awad, N.; Ali, M.; Liang, J.; Qu, B.; Suganthan, P.; Definitions, P. Evaluation criteria for the CEC 2017 special session and competition on single objective real-parameter numerical optimization. Technol. Rep. 2016. Available online: http://home.elka.pw.edu.pl/ (accessed on 4 October 2021).
- Gupta, S.; Deep, K. Improved sine cosine algorithm with crossover scheme for global optimization. Knowl. Based Syst. 2019, 165, 374–406. [Google Scholar] [CrossRef]
- Hussien, A.G.; Amin, M. A self-adaptive Harris Hawks optimization algorithm with opposition-based learning and chaotic local search strategy for global optimization and feature selection. Int. J. Mach. Learn. Cybern. 2021, 1–28. [Google Scholar] [CrossRef]
- Friedman, M. The use of ranks to avoid the assumption of normality implicit in the analysis of variance. J. Am. Stat. Assoc. 1937, 32, 675–701. [Google Scholar] [CrossRef]
- Friedman, M. A comparison of alternative tests of significance for the problem of m rankings. Ann. Math. Stat. 1940, 11, 86–92. [Google Scholar] [CrossRef]
- Iman, R.L.; Davenport, J.M. Approximations of the critical region of the fbietkan statistic. Commun. Stat. Theory Methods 1980, 9, 571–595. [Google Scholar] [CrossRef]
- Sheskin, D.J. Handbook of Parametric and Nonparametric Statistical Procedures; Chapman and Hall/CRC: Boca Raton, FL, USA, 2020. [Google Scholar]
- Jia, Y.; Shelhamer, E.; Donahue, J.; Karayev, S.; Long, J.; Girshick, R.; Guadarrama, S.; Darrell, T. Caffe: Convolutional architecture for fast feature embedding. In Proceedings of the 22nd ACM International Conference on Multimedia, Orlando, FL, USA, 3–7 November 2014; pp. 675–678. [Google Scholar]
- Yang, X.S.; Hossein Gandomi, A. Bat algorithm: A novel approach for global engineering optimization. Eng. Comput. 2012, 29, 464–483. [Google Scholar] [CrossRef] [Green Version]
- Gandomi, A.H.; Yang, X.S.; Alavi, A.H. Cuckoo search algorithm: A metaheuristic approach to solve structural optimization problems. Eng. Comput. 2013, 29, 17–35. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Wang, G.G.; Deb, S.; Gao, X.Z.; Coelho, L.D.S. A new metaheuristic optimisation algorithm motivated by elephant herding behaviour. Int. J. Bio-Inspired Comput. 2016, 8, 394–409. [Google Scholar] [CrossRef]
- Simon, D. Biogeography-based optimization. IEEE Trans. Evol. Comput. 2008, 12, 702–713. [Google Scholar] [CrossRef] [Green Version]
- Mirjalili, S.; Gandomi, A.H.; Mirjalili, S.Z.; Saremi, S.; Faris, H.; Mirjalili, S.M. Salp Swarm Algorithm: A bio-inspired optimizer for engineering design problems. Adv. Eng. Softw. 2017, 114, 163–191. [Google Scholar] [CrossRef]
- Stoean, R. Analysis on the potential of an EA–surrogate modelling tandem for deep learning parametrization: An example for cancer classification from medical images. Neural Comput. Appl. 2018, 32, 313–322. [Google Scholar] [CrossRef]



| Parameter and Notation | Value |
|---|---|
| Number of solution N | 20 (benchmark1), 30 (benchmark2) |
| Maximum number of () | 160,000 (benchmark1), 15,030 (benchmark2) |
| Absorption coefficient | 1.0 |
| Attractiveness at | 1.0 |
| Randomization (step) | changes according to Equation (14) |
| Initial value of step | 0.5 |
| Minimum value of step | 0.1 |
| Solutions’ exhaustiveness | |
| CLS strategy step number K | 4 |
| CLS strategy | changes according to Equation (20) |
| Parameter |
| ID | Name | Search Range | Formulation | Optimum |
|---|---|---|---|---|
| f1 | Sphere | min | 0 | |
| f2 | Moved Axis Function | min | 0 | |
| f3 | Griewank | min | 0 | |
| f4 | Rastrigin | min | 0 | |
| f5 | The Schwefel’s Problem 1.2 | min | 0 | |
| f6 | Ackley | min , where | 0 | |
| f7 | Powell Sum | min | 0 | |
| f8 | Sum Squares | min | 0 | |
| f9 | Schwefel 2.22 | min | 0 | |
| f10 | Powell Singular | min | 0 | |
| f11 | Alpine | min | 0 | |
| f12 | Inverse Cosine-Wave Function | min | −D+1 | |
| f13 | Pathological | min | 0 | |
| f14 | Discus | min | 0 | |
| f15 | Happy Cat | min , where | 0 | |
| f16 | Drop-Wave Function | min | −1 | |
| f17 | Schaffer 2 | min | 0 | |
| f18 | Camel Function-Three Hump | min | 0 |
| Function | Algorithm | Best Value | Worst Value | Mean Value | Function | Algorithm | Best Value | Worst Value | Mean Value |
|---|---|---|---|---|---|---|---|---|---|
| FA VSSFA LFA GDAFA WFA CLFA CFAEE | 0 0 0 0 0 0 | 0 0.531452 0 0.116521 0 0 | 0 0.151967 0 0.067858 0 0 | FA VSSFA LFA GDAFA WFA CLFA CFAEE | 0 0 0 0 0 0 | 0 0.735625 0 0.79956 0 0 | 0 0.327158 0 0.431151 0 0 | ||
| FA VSSFA LFA GDAFA WFA CLFA CFAEE | 0 0 0 0 0 0 | 0 5.74765 0 4.005821 0 0 | 0 1.32645 0 1.003456 0 0 | FA VSSFA LFA GDAFA WFA CLFA CFAEE | 0 0 0 0 0 | 0 14.95923 0 9.18410 0 0 | 0 2.736795 0 3.381069 0 0 | ||
| FA VSSFA LFA GDAFA WFA CLFA CFAEE | 0 0 0 0 0 | 0 0 0 0 | 0 0 0 0 | FA VSSFA LFA GDAFA WFA CLFA CFAEE | 0 0 0 0 0 0 | 0 0.451043 0 0.224532 0 0 | 0 0.145892 0 0.131779 0 0 | ||
| FA VSSFA LFA GDAFA WFA CLFA CFAEE | 5.969720 1.12073 0 0 2.537912 2.142703 0 | 5.969720 16.96541 4.352192 0 22.243001 27.135292 0 | 5.969720 7.962931 2.160021 0 10.984211 11.528380 0 | FA VSSFA LFA GDAFA WFA CLFA CFAEE | −3.007700 −7.416352 −9 −9 −9 −7.982860 −9 | −3.007700 −6.100051 −8.154811 −9 −6.738521 −5.318621 −9 | −3.007740 −6.821470 −8.837092 −9 −7.182860 −6.730021 −9 | ||
| FA VSSFA LFA GDAFA WFA CLFA CFAEE | 0 0 0 0 0 0 | 0 1.216521 0 0.668310 0 0 | 0 0.371654 0 0.315237 0 0 | FA VSSFA LFA GDAFA WFA CLFA CFAEE | 0.502000 0 0 0 | 0.502000 0 0 | 0.502000 0 0 | ||
| FA VSSFA LFA GDAFA WFA CLFA CFAEE | 1.156728 1.197652 | 0.363197 0.569403 | FA VSSFA LFA GDAFA WFA CLFA CFAEE | 643.025312 0 0 0 0 0 | 697.974622 0 0.634750 0 0.177280 0 0 | 644.124100 0 0 0 0 | |||
| FA VSSFA LFA GDAFA WFA CLFA CFAEE | 0 0 0 0 0 | 0 0 0 0 | 0 0 0 0 | FA VSSFA LFA GDAFA WFA CLFA CFAEE | 1.753800 0 0 0 0.622315 0 0 | 1.753800 0.432198 0.453921 0 0.978813 0.635291 0 | 1.753800 0.168663 0 0.860170 0.160825 0 | ||
| FA VSSFA LFA GDAFA WFA CLFA CFAEE | 0 0 0 0 0 0 | 0 1.413521 0 0.727350 0 0 | 0 0.237733 0 0.355913 0 0 |
| Function | Algorithm | Best Value | Worst Value | Mean Value | Function | Algorithm | Best Value | Worst Value | Mean Value |
|---|---|---|---|---|---|---|---|---|---|
| FA VSSFA LFA GDAFA WFA CLFA CFAEE | 0 13.62752 9.542603 0 0.143725 0 | 20.168334 17.455290 0.329325 0.335712 6.25 | 17.05007 14.08179 0.237264 0.194190 1.41 | FA VSSFA LFA GDAFA WFA CLFA CFAEE | 0 15.668320 7.896512 0 0.759455 0.663490 0 | 18.532451 13.652705 4.84 1.652710 2.0693 | 17.168332 11.634482 1.444582 1.444582 6.09 | ||
| FA VSSFA LFA GDAFA WFA CLFA CFAEE | 0 952.735293 495.234239 0 9.0823 8.458129 0 | 1292.759201 932.959210 27.288553 35.736666 3.52 | 1151.53123 831.976505 15.382611 19.345189 4.52 | FA VSSFA LFA GDAFA WFA CLFA CFAEE | 740.533299 1297.755023 0 3.545252 5.3022 0 | 4352.542059 3675.442951 33.82541 28.982541 1.13 | 2953.135592 2626.920051 23.710392 17.315642 4.44 | ||
| FA VSSFA LFA GDAFA WFA CLFA CFAEE | 0.453243 0.331970 0 0 | 0.573032 0.511440 1.84 | 0.516954 0.446482 2.33 | FA VSSFA LFA GDAFA WFA CLFA CFAEE | 13.115620 6.718345 0 0.245052 0.133675 0 | 16.344592 13.539203 0.731462 0.475093 8.54 | 14.957239 10.529380 0.417792 0.312399 1.03 | ||
| FA VSSFA LFA GDAFA WFA CLFA CFAEE | 53.728352 91.368000 26.842502 0 10.562432 48.503233 0 | 53.728352 145.032962 47.888361 0.293775 70.887502 118.455291 0.163325 | 53.728352 131.851977 37.948270 52.398675 89.757932 2.31 | FA VSSFA LFA GDAFA WFA CLFA CFAEE | −2.745302 −14.281512 −19.773059 −29 −27.135292 −19.932444 −29 | −2.738143 −10.236442 −14.387294 −28.981153 −23.462555 −13.572562 −28.975432 | −2.741055 −12.601748 −17.381692 −28.995732 −25.463931 −16.488942 −28.997240 | ||
| FA VSSFA LFA GDAFA WFA CLFA CFAEE | 0 188.932905 175.893044 0 1.363823 1.167251 0 | 249.742592 248.643292 5.757921 7.374155 7.35 | 229.451399 218.334752 3.464743 3.888032 5.65 | FA VSSFA LFA GDAFA WFA CLFA CFAEE | 4.821110 4.34 | 4.854329 0.135155 0.131320 3.13 | 4.831800 7.09 | ||
| FA VSSFA LFA GDAFA WFA CLFA CFAEE | 4.340823 3.011800 0.433632 0.447690 | 4.530665 3.725154 0.855143 2.853752 1.05 | 4.493832 3.383214 2.87 0.688177 1.1317517 | FA VSSFA LFA GDAFA WFA CLFA CFAEE | 16.331 12.645 0 0.10623 0 | 22.498 20.226 0.50956 0.42646 1.15 | 19.8985 16.6886 0.261277 0.244281 2.29 | ||
| FA VSSFA LFA GDAFA WFA CLFA CFAEE | 6.16e-05 123.295565 21.954921 0 4.57E-11 3.52e-08 0 | 6.18e-05 1158.432456 4319.824940 3.17e-38 1.38e-03 9.83e-03 4.91 | 541.478399 1345.324915 3.12 | FA VSSFA LFA GDAFA WFA CLFA CFAEE | 2.3302 2.262251 0.723335 0 1.175841 1.307425 0 | 2.3302 2.348725 1.466781 0.637052 1.371513 1.743721 0.592563 | 2.3302 2.305134 1.060788 9.92 1.294690 1.524977 | ||
| FA VSSFA LFA GDAFA WFA CLFA CFAEE | 0 152.832522 103.285692 0 1.534341 1.561 0 | 3.17e-04 275.964302 214.365219 4.781903 5.175238 2.22 | 235.952315 173.448925 3.255770 3.270697 9.29 |
| Function | Algorithm | Best Value | Worst Value | Mean Value | Function | Algorithm | Best Value | Worst Value | Mean Value |
|---|---|---|---|---|---|---|---|---|---|
| FA VSSFA LFA GDAFA WFA CLFA CFAEE | 0 86.457552 84.743562 0 0.776975 6.0074 0 | 94.965352 101.550299 1.343821 9.086351 3.35 | 91.851742 95.331892 1.123621 7.397248 2.12 | FA VSSFA LFA GDAFA WFA CLFA CFAEE | 7.270000 75.261423 61.271532 0 4.667233 19.453222 0 | 7.345340 79.183492 69.287492 0.282980 7.217744 29.786432 0.253300 | 7.272472 76.237822 65.957970 6.75 5.953690 24.393170 | ||
| FA VSSFA LFA GDAFA WFA CLFA CFAEE | 20,155.732954 20,134.629495 0 183.584823 1439.319025 0 | 0.861329 23,097.569290 23,511.452949 2.732509 326.044592 2483.724942 0.525656 | 0.296353 21,435.685432 22,061.730052 0.263728 246.343291 1955.372492 0.255429 | FA VSSFA LFA GDAFA WFA CLFA CFAEE | 0.113550 24,876.459003 24,626.324592 0 95.657422 688.787853 0 | 0.754291 29,942.359392 33,338.728942 0.769235 143.859235 1431.750099 0.621509 | 0.212700 27,295.176529 29,210.135929 116.538544 1058.681232 5.31 | ||
| FA VSSFA LFA GDAFA WFA CLFA CFAEE | 0.783852 0.746025 0 0.167315 0 | 0.354451 0.850443 0.837694 1.25 0.186983 | 0.195824 0.811365 0.799866 0.166489 2.13 | FA VSSFA LFA GDAFA WFA CLFA CFAEE | 14.775500 68.413502 58.357421 0 1.295332 7.397541 0 | 15.145392 73.163592 65.772001 2.27 2.282315 11.648522 | 14.950132 70.657632 61.465342 1.686960 9.200357 3.02 | ||
| FA VSSFA LFA GDAFA WFA CLFA CFAEE | 436.882200 638.513205 223.195002 0 113.543829 476.735252 0 | 551.395213 706.697495 263.465402 1.653533 213.352932 613.530234 1.293298 | 484.606492 668.543402 243.792502 0.589842 178.416452 558.464329 0.539520 | FA VSSFA LFA GDAFA WFA CLFA CFAEE | -4.445052 −23.0423521 −44.356992 −99 −87.920501 −40.345210 −99 | −8.728848 −19.167452 −34.123586 −98.835492 −79.465202 −27.446501 −98.872555 | −6.178500 −21.911352 −37.588482 −98.947900 −83.891430 −36.452653 −98.962902 | ||
| FA VSSFA LFA GDAFA WFA CLFA CFAEE | 2428.940492 4012.652903 3888.542030 0 33.682005 293.459724 0 | 2592.352049 4633.727049 4683.634029 0.418092 72.436405 518.965567 0.435304 | 2433.183441 4315.743555 4365.895902 53.696570 385.652334 4.67 | FA VSSFA LFA GDAFA WFA CLFA CFAEE | 20.651103 0.162015 0.147652 0.142465 0.117900 3.65 | 20.770492 0.187683 0.191543 0.186110 0.169890 3.33 | 20.659945 0.169435 0.175026 0.163519 0.154551 9.66 | ||
| FA VSSFA LFA GDAFA WFA CLFA CFAEE | 4.924155 4.140800 0.635644 3.269543 | 5.442632 4.543301 1.108742 4.236500 2.75 | 5.032945 4.412393 1.03 0.845798 3.732709 | FA VSSFA LFA GDAFA WFA CLFA CFAEE | 93.691550 95.931103 0 0.880193 8.075650 0 | 105.629021 109.031902 1.358399 14.832029 2.83 | 100.355603 103.562900 6.53 1.099707 11.357613 | ||
| FA VSSFA LFA GDAFA WFA CLFA CFAEE | 0 21978.054329 0 | 3.45 | 6.65 | FA VSSFA LFA GDAFA WFA CLFA CFAEE | 3.158222 3.186900 2.271819 0 1.756300 2.569432 0 | 3.158339 3.256833 2.492549 0.786523 1.896942 2.835301 0.725431 | 3.158275 3.225253 2.405293 0.451663 1.8131570 2.704312 0.417902 | ||
| FA VSSFA LFA GDAFA WFA CLFA CFAEE | 0.185455 0 36.945444 293.842003 0 | 0.499821 0.567650 73.345992 486.513050 0.475325 | 0.289011 53.455374 375.451515 3.19 |
| Function | Algorithm | Best Value | Worst Value | Mean Value | Function | Algorithm | Best Value | Worst Value | Mean Value |
|---|---|---|---|---|---|---|---|---|---|
| FA VSSFA LFA GDAFA WFA CLFA CFAEE | −1 −1 −1 −1 −1 −1 −1 | −1 −1 −1 −1 −0.95357 −1 −1 | −1 −1 −1 −1 −0.997534 −1 −1 | FA VSSFA LFA GDAFA WFA CLFA CFAEE | 0 0 0 0 0 0 0 | 0 0 0 0 0 0 | 0 0 0 0 0 0 | ||
| FA VSSFA LFA GDAFA WFA CLFA CFAEE | 0 0 0 0 0 0 0 | 0 0 0 0 0 | 0 0 0 0 0 |
| FA | VSSFA | LFA | WFA | CLFA | GDAFA | CFAEE | |
|---|---|---|---|---|---|---|---|
| Best 10 dim | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Mean 10 dim | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Worst 10 dim | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Total 10 dim | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Best 30 dim | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| Mean 30 dim | 0 | 0 | 0 | 0 | 0 | 2 | 13 |
| Worst 30 dim | 0 | 0 | 0 | 0 | 0 | 3 | 12 |
| Total 30 dim | 0 | 0 | 0 | 0 | 0 | 5 | 26 |
| Best 100 dim | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| Mean 100 dim | 0 | 0 | 0 | 0 | 0 | 3 | 12 |
| Worst 100 dim | 0 | 0 | 0 | 0 | 0 | 3 | 12 |
| Total 100 dim | 0 | 0 | 0 | 0 | 0 | 6 | 25 |
| GRAND TOTAL | 0 | 0 | 0 | 0 | 0 | 11 | 51 |
| Function | CFAEE | GDAFA | FA | VSSFA | LFA | WFA | CLFA |
|---|---|---|---|---|---|---|---|
| f1 | 1.02 | 7.50 | |||||
| f2 | |||||||
| f3 | |||||||
| f4 | |||||||
| f5 | |||||||
| f6 | 5.05 | 4.41 | 3.61 | ||||
| f7 | |||||||
| f8 | |||||||
| f9 | 7.27 | 5.95 | |||||
| f10 | |||||||
| f11 | 1.68 | 9.20 | |||||
| f12 | − | − | −6.18 | − | − | − | − |
| f13 | |||||||
| f14 | 1.10 | ||||||
| f15 | 3.16 | 3.22 | 2.41 | 1.81 | 2.71 | ||
| p-value | 3.125 | 4.39 | 2.13 | 3.05 | 3.05 | 3.05 | 3.05 |
| ID | Name of the function | Class | Search Range | Optimum |
|---|---|---|---|---|
| F1 | Shifted and Rotated Bent Cigar Function | Unimodal | [−100, 100] | 100 |
| F2 | Shifted and Rotated Sum of Different Power Function | Unimodal | [−100, 100] | 200 |
| F3 | Shifted and Rotated Zakharov Function | Unimodal | [−100, 100] | 300 |
| F4 | Shifted and Rotated Rosenbrock’s Function | Multimodal | [−100, 100] | 400 |
| F5 | Shifted and Rotated Rastrigin’s Function | Multimodal | [−100, 100] | 500 |
| F6 | Shifted and Rotated Expanded Scaffer’s Function | Multimodal | [−100, 100] | 600 |
| F7 | Shifted and Rotated Lunacek Bi-Rastrigin Function | Multimodal | [−100, 100] | 700 |
| F8 | Shifted and Rotated Non-Continuous Rastrigin’s Function | Multimodal | [−100, 100] | 800 |
| F9 | Shifted and Rotated Lévy Function | Multimodal | [−100, 100] | 900 |
| F10 | Shifted and Rotated Schwefel’s Function | Multimodal | [−100, 100] | 1000 |
| F11 | Hybrid Function 1 (N = 3) | Hybrid | [−100, 100] | 1100 |
| F12 | Hybrid Function 2 (N = 3) | Hybrid | [−100, 100] | 1200 |
| F13 | Hybrid Function 3 (N = 3) | Hybrid | [−100, 100] | 1300 |
| F14 | Hybrid Function 4 (N = 4) | Hybrid | [−100, 100] | 1400 |
| F15 | Hybrid Function 5 (N = 4) | Hybrid | [−100, 100] | 1500 |
| F16 | Hybrid Function 6 (N = 4) | Hybrid | [−100, 100] | 1600 |
| F17 | Hybrid Function 6 (N = 5) | Hybrid | [−100, 100] | 1700 |
| F18 | Hybrid Function 6 (N = 5) | Hybrid | [−100, 100] | 1800 |
| F19 | Hybrid Function 6 (N = 5) | Hybrid | [−100, 100] | 1900 |
| F20 | Hybrid Function 6 (N = 6) | Hybrid | [−100, 100] | 2000 |
| F21 | Composition Function 1 (N = 3) | Composition | [−100, 100] | 2100 |
| F22 | Composition Function 2 (N = 3) | Composition | [−100, 100] | 2200 |
| F23 | Composition Function 3 (N = 4) | Composition | [−100, 100] | 2300 |
| F24 | Composition Function 4 (N = 4) | Composition | [−100, 100] | 2400 |
| F25 | Composition Function 5 (N = 5) | Composition | [−100, 100] | 2500 |
| F26 | Composition Function 6 (N = 5) | Composition | [−100, 100] | 2600 |
| F27 | Composition Function 7 (N = 6) | Composition | [−100, 100] | 2700 |
| F28 | Composition Function 8 (N = 6) | Composition | [−100, 100] | 2800 |
| F29 | Composition Function 9 (N = 3) | Composition | [−100, 100] | 2900 |
| F30 | Composition Function 10 (N = 3) | Composition | [−100, 100] | 3000 |
| Algorithm | F1 | F2 | F3 | F4 | F5 | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Mean | STD | Mean | STD | Mean | STD | Mean | STD | Mean | STD | |
| IHHO | 26.921 | n/a | n/a | 3.02 | 52.152 | 4.03 | 2.607 | 3.251 | ||
| HHO | n/a | n/a | 53.631 | 24.927 | ||||||
| DE | n/a | n/a | 8.530 | 6.232 | ||||||
| GOA | n/a | n/a | 61.300 | 19.48 | 16.803 | |||||
| GWO | n/a | n/a | 10.705 | 8.543 | ||||||
| MFO | n/a | n/a | 27.727 | 12.860 | ||||||
| MVO | n/a | n/a | 46.451 | 1.392 | 9.888 | |||||
| PSO | n/a | n/a | 65.409 | 10.318 | 7.305 | |||||
| WOA | n/a | n/a | 69.033 | 17.46 | ||||||
| SCA | n/a | n/a | 47.271 | 9.352 | ||||||
| FA | n/a | n/a | 54.991 | 18.858 | 19.302 | |||||
| CFAEE | 1.31 | 14.353 | n/a | n/a | 3.02 | 28.131 | 2.372 | 5.01 | 3.285 | |
| Algorithm | F6 | F7 | F8 | F9 | F10 | |||||
| Mean | STD | Mean | STD | Mean | STD | Mean | STD | Mean | STD | |
| IHHO | 6.00 | 0.082 | 10.041 | 6.526 | 85.42 | |||||
| HHO | 12.320 | 18.921 | 5.700 | |||||||
| DE | 4.744 | 10.373 | 6.873 | |||||||
| GOA | 10.295 | 11.375 | 14.512 | 93.212 | ||||||
| GWO | 1.909 | 16.343 | 5.053 | 12.11 | ||||||
| MFO | 2.411 | 22.655 | 13.786 | |||||||
| MVO | 4.365 | 11.278 | 12.216 | 9.00 | 0.012 | |||||
| PSO | 3.539 | 9.008 | 5.982 | 9.00 | 0.003 | 1.50 | ||||
| WOA | 13.695 | 23.692 | 17.470 | |||||||
| SCA | 4.105 | 13.299 | 7.577 | 85.98 | ||||||
| FA | 11.393 | 11.55 | 13.914 | 81.44 | ||||||
| CFAEE | 6.00 | 0.051 | 7.23 | 11.391 | 8.08 | 5.422 | 42.11 | 1.25 | ||
| Algorithm | F11 | F12 | F13 | F14 | F15 | |||||
| Mean | STD | Mean | STD | Mean | STD | Mean | STD | Mean | STD | |
| IHHO | 13.523 | 1.42 | 1.651 | |||||||
| HHO | 45.729 | |||||||||
| DE | 36.317 | 1.35 | 78.355 | 11.826 | 1.51 | 18.454 | ||||
| GOA | 58.009 | |||||||||
| GWO | 183.524 | |||||||||
| MFO | 107.133 | |||||||||
| MVO | 27.331 | |||||||||
| PSO | 1.10 | 3.727 | 88.291 | |||||||
| WOA | 82.415 | |||||||||
| SCA | 96.535 | |||||||||
| FA | 39.705 | |||||||||
| CFAEE | 1.10 | 1.503 | 3.18 | 2.29 | 1.35 | 20.499 | 21.350 | 1.51 | 10.217 | |
| Algorithm | F16 | F17 | F18 | F19 | F20 | |||||
| Mean | STD | Mean | STD | Mean | STD | Mean | STD | Mean | STD | |
| IHHO | 59.44 | 7.519 | 1.90 | 6.993 | 19.561 | |||||
| HHO | 65.751 | 86.017 | ||||||||
| DE | 41.15 | 19.514 | 1.84 | 23.298 | 23.711 | |||||
| GOA | 74.824 | |||||||||
| GWO | 38.759 | 73.994 | ||||||||
| MFO | 65.311 | 72.321 | ||||||||
| MVO | 46.126 | 86.303 | ||||||||
| PSO | 1.65 | 65.364 | 16.123 | 35.410 | ||||||
| WOA | 73.459 | |||||||||
| SCA | 95.425 | 46.855 | ||||||||
| FA | 71.303 | |||||||||
| CFAEE | 86.359 | 1.71 | 8.442 | 21.565 | 1.90 | 8.717 | 2.01 | 9.443 | ||
| Algorithm | F21 | F22 | F23 | F24 | F25 | |||||
| Mean | STD | Mean | STD | Mean | STD | Mean | STD | Mean | STD | |
| IHHO | 2.20 | 4.615 | 17.820 | 14.213 | 85.338 | |||||
| HHO | 53.711 | 25.234 | 35.522 | 93.623 | 49.573 | |||||
| DE | 78.104 | 17.513 | 15.163 | 2.66 | 69.502 | 15.543 | ||||
| GOA | 56.877 | 23.536 | 57.833 | 32.598 | ||||||
| GWO | 32.884 | 57.573 | 13.862 | 25.132 | 28.256 | |||||
| MFO | 29.255 | 93.557 | 11.327 | 76.435 | 37.776 | |||||
| MVO | 11.839 | 10.445 | 18.246 | 84.256 | ||||||
| PSO | 49.783 | 72.300 | 76.143 | 33.735 | ||||||
| WOA | 60.021 | 29.838 | 85.902 | |||||||
| SCA | 65.229 | 66.636 | 45.449 | 11.548 | 37.291 | |||||
| FA | 34.701 | 17.452 | 47.019 | |||||||
| CFAEE | 2.20 | 48.552 | 2.26 | 13.040 | 2.55 | 21.929 | 2.81 | 95.429 | ||
| Algorithm | F26 | F27 | F28 | F29 | F30 | |||||
| Mean | STD | Mean | STD | Mean | STD | Mean | STD | Mean | STD | |
| IHHO | 33.657 | 48.694 | 3.20 | 28.982 | ||||||
| HHO | 51.306 | 85.653 | ||||||||
| DE | 95.929 | 3.07 | 2.558 | 27.035 | 35.216 | |||||
| GOA | 25.326 | 75.411 | ||||||||
| GWO | 13.541 | 49.822 | ||||||||
| MFO | 5.722 | 93.459 | 55.593 | |||||||
| MVO | 21.875 | 75.139 | ||||||||
| PSO | 31.830 | 62.374 | ||||||||
| WOA | 48.124 | |||||||||
| SCA | 13.152 | 89.259 | 48.339 | |||||||
| FA | 27.015 | 31.117 | ||||||||
| CFAEE | 2.86 | 48.690 | 3.13 | 3.20 | 27.914 | 2.22 | 1.44 | |||
| Function | IHHO | HHO | DE | GOA | GWO | MFO | MVO | PSO | WOA | SCA | FA | CFAEE |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| F1 | 2 | 7 | 11 | 5 | 9 | 8 | 3 | 4 | 10 | 12 | 6 | 1 |
| F3 | 1.5 | 7 | 10 | 3.5 | 8 | 12 | 3.5 | 6 | 11 | 9 | 5 | 1.5 |
| F4 | 1 | 10 | 9 | 6 | 5 | 8 | 3 | 4 | 11 | 12 | 7 | 2 |
| F5 | 2 | 9 | 11 | 5 | 4 | 8 | 3 | 6 | 10 | 12 | 7 | 1 |
| F6 | 1.5 | 11 | 9 | 6 | 3 | 4 | 5 | 7 | 10 | 8 | 12 | 1.5 |
| F7 | 8 | 11 | 12 | 4 | 5.5 | 7 | 3 | 2 | 9 | 10 | 5.5 | 1 |
| F8 | 2 | 6.5 | 12 | 8 | 3 | 6.5 | 5 | 4 | 10 | 11 | 9 | 1 |
| F9 | 8 | 10 | 12 | 5.5 | 3 | 9 | 1.5 | 1.5 | 11 | 7 | 5.5 | 4 |
| F10 | 3 | 9 | 10 | 7 | 4 | 8 | 5 | 1 | 11 | 12 | 6 | 2 |
| F11 | 3 | 6.5 | 4.5 | 8 | 12 | 10 | 4.5 | 1.5 | 9 | 11 | 6.5 | 1.5 |
| F12 | 4 | 10 | 3 | 8 | 5 | 7 | 6 | 2 | 11 | 12 | 9 | 1 |
| F13 | 3 | 11 | 1.5 | 10 | 7 | 9 | 4 | 5 | 8 | 12 | 6 | 1.5 |
| F14 | 1 | 5 | 3 | 9 | 10 | 12 | 8 | 4 | 11 | 7 | 6 | 2 |
| F15 | 4 | 10 | 1.5 | 9 | 8 | 11 | 7 | 3 | 12 | 5 | 6 | 1.5 |
| F16 | 5.5 | 11 | 3 | 1 | 7.5 | 10 | 9 | 2 | 12 | 5.5 | 7.5 | 4 |
| F17 | 3 | 7 | 4.5 | 12 | 4.5 | 6 | 8.5 | 2 | 10.5 | 8.5 | 10.5 | 1 |
| F18 | 3 | 7 | 1 | 5 | 11 | 10 | 8 | 4 | 9 | 12 | 6 | 2 |
| F19 | 1.5 | 10 | 3 | 6 | 11 | 8 | 7 | 4 | 12 | 9 | 5 | 1.5 |
| F20 | 2 | 12 | 3 | 10 | 5 | 8 | 6.5 | 4 | 11 | 9 | 6.5 | 1 |
| F21 | 1.5 | 12 | 3 | 7.5 | 7.5 | 9.5 | 9.5 | 4 | 11 | 5.5 | 5.5 | 1.5 |
| F22 | 2 | 5 | 3 | 10 | 4 | 8 | 6.5 | 6.5 | 12 | 11 | 9 | 1 |
| F23 | 2 | 12 | 6.5 | 8 | 4.5 | 6.5 | 9 | 3 | 10 | 11 | 4.5 | 1 |
| F24 | 3 | 12 | 1 | 6 | 7.5 | 9 | 7.5 | 4 | 10 | 11 | 5 | 2 |
| F25 | 2 | 9 | 4 | 6.5 | 8 | 10 | 5 | 3 | 11.5 | 11.5 | 6.5 | 1 |
| F26 | 2 | 12 | 3.5 | 5 | 10 | 7 | 8.5 | 3.5 | 11 | 8.5 | 6 | 1 |
| F27 | 12 | 11 | 1 | 7 | 5 | 3 | 5 | 8 | 10 | 9 | 5 | 2 |
| F28 | 4 | 10 | 3 | 5 | 11 | 2 | 8 | 6.5 | 12 | 9 | 6.5 | 1 |
| F29 | 1.5 | 11 | 3.5 | 10 | 5 | 8 | 8 | 3.5 | 12 | 6 | 8 | 1.5 |
| F30 | 2 | 11 | 3 | 6 | 7 | 8 | 4 | 9 | 10 | 12 | 5 | 1 |
| Average Ranking | 3.138 | 9.483 | 5.362 | 6.862 | 6.724 | 8.017 | 5.914 | 4.069 | 10.621 | 9.603 | 6.655 | 1.552 |
| Rank | 2 | 10 | 4 | 8 | 7 | 9 | 5 | 3 | 12 | 11 | 6 | 1 |
| Function | IHHO | HHO | DE | GOA | GWO | MFO | MVO | PSO | WOA | SCA | FA | CFAEE |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| F1 | 2 | 7 | 347 | 5 | 9 | 8 | 3 | 4 | 346 | 348 | 6 | 1 |
| F3 | 56.5 | 63 | 327 | 58.5 | 323 | 334 | 58.5 | 61 | 328 | 326 | 60 | 56.5 |
| F4 | 144 | 226 | 211 | 177 | 164 | 192 | 152 | 157 | 255 | 278 | 183 | 146 |
| F5 | 138 | 213 | 242 | 194 | 174 | 206 | 169 | 196 | 241 | 245 | 197 | 135 |
| F6 | 153.5 | 235 | 218 | 173 | 158 | 161 | 165 | 180 | 232 | 212 | 270 | 153.5 |
| F7 | 193 | 264 | 266 | 145 | 155.5 | 184 | 140 | 136 | 244 | 246 | 155.5 | 131 |
| F8 | 151 | 198.5 | 251 | 204 | 167 | 198.5 | 191 | 172 | 229 | 231 | 207 | 143 |
| F9 | 141 | 310 | 318 | 89.5 | 80 | 285 | 78.5 | 78.5 | 313 | 91 | 89.5 | 87 |
| F10 | 81 | 293 | 301 | 257 | 88 | 290 | 95 | 74 | 309 | 317 | 216 | 75 |
| F11 | 114 | 159.5 | 127.5 | 185 | 300 | 271 | 127.5 | 103.5 | 265 | 280 | 159.5 | 103.5 |
| F12 | 13 | 19 | 12 | 17 | 14 | 16 | 15 | 11 | 344 | 345 | 18 | 10 |
| F13 | 43 | 331 | 39.5 | 324 | 54 | 321 | 45 | 46 | 314 | 337 | 53 | 39.5 |
| F14 | 66 | 70 | 68 | 311 | 316 | 333 | 73 | 69 | 320 | 72 | 71 | 67 |
| F15 | 52 | 329 | 48.5 | 322 | 303 | 335 | 65 | 51 | 336 | 55 | 62 | 48.5 |
| F16 | 291.5 | 308 | 276 | 64 | 298.5 | 305 | 302 | 233 | 312 | 291.5 | 298.5 | 282 |
| F17 | 122 | 225 | 181.5 | 269 | 181.5 | 205 | 239.5 | 113 | 262.5 | 239.5 | 262.5 | 107 |
| F18 | 38 | 76 | 35 | 47 | 332 | 325 | 82 | 41 | 319 | 338 | 50 | 36 |
| F19 | 28.5 | 44 | 30 | 33 | 330 | 37 | 34 | 31 | 339 | 42 | 32 | 28.5 |
| F20 | 98 | 294 | 112 | 260.5 | 150 | 237.5 | 223 | 121 | 286 | 247.5 | 223 | 96 |
| F21 | 99.5 | 281 | 129 | 227.5 | 227.5 | 252.5 | 252.5 | 162.5 | 272 | 209 | 209 | 99.5 |
| F22 | 110 | 142 | 118 | 258 | 130 | 217 | 170.5 | 170.5 | 297 | 283 | 234 | 101 |
| F23 | 126 | 279 | 202.5 | 223 | 178.5 | 202.5 | 237.5 | 134 | 247.5 | 260.5 | 178.5 | 102 |
| F24 | 119.5 | 288 | 105 | 200.5 | 220 | 236 | 220 | 132.5 | 259 | 267.5 | 175.5 | 111 |
| F25 | 117 | 243 | 168 | 214.5 | 230 | 256 | 195 | 139 | 274.5 | 274.5 | 214.5 | 93 |
| F26 | 84 | 315 | 85.5 | 94 | 306 | 106 | 249.5 | 85.5 | 307 | 249.5 | 97 | 77 |
| F27 | 284 | 277 | 119.5 | 175.5 | 148 | 132.5 | 148 | 200.5 | 267.5 | 220 | 148 | 125 |
| F28 | 137 | 287 | 124 | 166 | 289 | 92 | 254 | 189.5 | 296 | 273 | 189.5 | 83 |
| F29 | 108.5 | 295 | 115.5 | 209 | 123 | 187 | 187 | 115.5 | 304 | 162.5 | 187 | 108.5 |
| F30 | 21 | 342 | 22 | 25 | 26 | 27 | 23 | 340 | 341 | 343 | 24 | 20 |
| Average Ranking | 108.017 | 221.172 | 158.621 | 169.948 | 188.810 | 205.259 | 144.655 | 122.328 | 291.724 | 244.276 | 147.259 | 91.931 |
| Rank | 2 | 10 | 6 | 7 | 8 | 9 | 4 | 3 | 12 | 11 | 5 | 1 |
| Friedman Value | Critical Value | p-Value | Iman–Davenport Value | F Critical Value |
|---|---|---|---|---|
| 1.820 |
| Comparison | p_VALUES | Ranking | alpha = 0.05 | alpha = 0.1 | H1 | H2 |
|---|---|---|---|---|---|---|
| CFAEE vs. HHO | 0 | 0 | 0.00455 | 0.00909 | TRUE | TRUE |
| CFAEE vs. WOA | 0 | 1 | 0.00500 | 0.01000 | TRUE | TRUE |
| CFAEE vs. SCA | 0 | 2 | 0.00556 | 0.01111 | TRUE | TRUE |
| CFAEE vs. MFO | 3 | 0.00625 | 0.01250 | TRUE | TRUE | |
| CFAEE vs. GOA | 4 | 0.00714 | 0.01429 | TRUE | TRUE | |
| CFAEE vs. GWO | 5 | 0.00833 | 0.01667 | TRUE | TRUE | |
| CFAEE vs. FA | 6 | 0.01000 | 0.02000 | TRUE | TRUE | |
| CFAEE vs. MVO | 7 | 0.01250 | 0.02500 | TRUE | TRUE | |
| CFAEE vs. DE | 8 | 0.01667 | 0.03333 | TRUE | TRUE | |
| CFAEE vs. PSO | 9 | 0.02500 | 0.05000 | TRUE | TRUE | |
| CFAEE vs. IHHO | 10 | 0.05000 | 0.10000 | FALSE | FALSE |
| Dataset | Train Set | Validation Set | Testing Set |
|---|---|---|---|
| MNIST | 20.000 (64) | 40.000 (100) | 10.000 (100) |
| Fashion-MNIST | 20.000 (64) | 40.000 (100) | 10.000 (100) |
| Semeion | 200 (2) | 400 (400) | 993 (993) |
| USPS | 2.406 (32) | 4.885 (977) | 2.007 (2.007) |
| CIFAR-10 | 20.000 (100) | 30.000 (100) | 10.000 (100) |
| Dataset | Epochs | ||||
|---|---|---|---|---|---|
| MNIST | 0.01 | 0.9 | 0.0005 | [0, 1] | 10.000 |
| Fashion-MNIST | 0.01 | 0.9 | 0.0005 | [0, 1] | 10.000 |
| Semeion | 0.001 | 0,9 | 0.0005 | [0, 1] | 10.000 |
| USPS | 0.01 | 0.9 | 0.0005 | [0, 1] | 10.000 |
| CIFAR-10 | 0.001 | 0.9 | 0.004 | [0, 1] | 4.000 |
| Algorithm | Parameters |
|---|---|
| BA [67] | , , , |
| CS [68] | , , |
| PSO [69] | , , |
| EHO [70] | , , , |
| WOA [53] | linearly decreasing from 2 to 0, linearly decreasing from −1 to −2, b=1 |
| SCA [51] | , linearly decreasing from 2 to 0 |
| SSA [72] | non-linearly decreasing from 2 to 0, and rand from [0, 1] |
| GOA [52] | c linearly decreasing from 1 to 0 |
| BBO [71] | , , |
| FA [1] | , , |
| Method | MNIST | Fashion-MNIST | Semeion | USPS | CIFAR-10 | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| acc. | acc. | acc. | acc. | acc. | ||||||
| Caffe | 99.07 | 0 | 91.71 | 0 | 97.62 | 0 | 95.80 | 0 | 71.47 | 0 |
| Dropout Caffe | 99.18 | 0.5 | 92.53 | 0.5 | 98.14 | 0.5 | 96.21 | 0.5 | 72.08 | 0.5 |
| BA | 99.14 | 0.491 | 92.56 | 0.505 | 98.35 | 0.692 | 96.45 | 0.762 | 71.49 | 0.633 |
| CS | 99.14 | 0.489 | 92.41 | 0.491 | 98.21 | 0.544 | 96.31 | 0.715 | 71.21 | 0.669 |
| PSO | 99.16 | 0.493 | 92.38 | 0.481 | 97.79 | 0.371 | 96.33 | 0.725 | 71.51 | 0.621 |
| EHO | 99.13 | 0.475 | 92.36 | 0.470 | 98.11 | 0.481 | 96.24 | 0.682 | 71.15 | 0.705 |
| WOA | 99.15 | 0.489 | 92.43 | 0.493 | 98.23 | 0.561 | 96.32 | 0.722 | 71.23 | 0.685 |
| SCA | 99.17 | 0.496 | 92.53 | 0.501 | 98.25 | 0.580 | 96.29 | 0.705 | 71.54 | 0.597 |
| SSA | 99.19 | 0.499 | 92.63 | 0.527 | 98.31 | 0.642 | 96.41 | 0.753 | 71.58 | 0.529 |
| GOA | 99.16 | 0.492 | 92.44 | 0.494 | 98.15 | 0.513 | 96.15 | 0.481 | 70.95 | 0.849 |
| BBO | 99.13 | 0.474 | 92.35 | 0.468 | 98.16 | 0.515 | 96.17 | 0.483 | 71.08 | 0.768 |
| FA | 99.18 | 0.495 | 92.58 | 0.511 | 98.29 | 0.619 | 96.42 | 0.758 | 71.55 | 0.583 |
| CFAEE | 99.26 | 0.529 | 92.73 | 0.570 | 98.46 | 0.719 | 96.88 | 0.845 | 72.32 | 0.388 |
| Function | CFAEE | Caffe | DropoutCaffe | BA | CS | PSO | EHO | WOA | SCA | SSA | GOA | BBO | FA |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MNIST | 0.74 | 0.9 | 0.82 | 0.86 | 0.86 | 0.8 | 0.87 | 0.85 | 0.83 | 0.81 | 0.84 | 0.87 | 0.82 |
| Fashion-MNIST | 7.27 | 8.29 | 7.47 | 7.44 | 7.59 | 7.62 | 7.64 | 7.57 | 7.47 | 7.37 | 7.56 | 7.65 | 7.42 |
| Semeion | 1.54 | 2.38 | 1.86 | 1.65 | 1.79 | 2.21 | 1.89 | 1.77 | 1.75 | 1.69 | 1.85 | 1.84 | 1.71 |
| USPS | 3.12 | 4.2 | 3.79 | 3.55 | 3.69 | 3.67 | 3.76 | 3.68 | 3.71 | 3.59 | 3.85 | 3.83 | 3.58 |
| CIFAR-10 | 27.68 | 28.53 | 27.92 | 28.51 | 28.79 | 28.5 | 28.85 | 28.77 | 28.46 | 28.42 | 29.05 | 28.92 | 28.45 |
| p-value | 3.125 | 3.125 | 3.125 | 3.125 | 3.125 | 3.125 | 3.125 | 3.125 | 3.125 | 3.125 | 3.125 | 3.125 | 3.125 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bacanin, N.; Stoean, R.; Zivkovic, M.; Petrovic, A.; Rashid, T.A.; Bezdan, T. Performance of a Novel Chaotic Firefly Algorithm with Enhanced Exploration for Tackling Global Optimization Problems: Application for Dropout Regularization. Mathematics 2021, 9, 2705. https://doi.org/10.3390/math9212705
Bacanin N, Stoean R, Zivkovic M, Petrovic A, Rashid TA, Bezdan T. Performance of a Novel Chaotic Firefly Algorithm with Enhanced Exploration for Tackling Global Optimization Problems: Application for Dropout Regularization. Mathematics. 2021; 9(21):2705. https://doi.org/10.3390/math9212705
Chicago/Turabian StyleBacanin, Nebojsa, Ruxandra Stoean, Miodrag Zivkovic, Aleksandar Petrovic, Tarik A. Rashid, and Timea Bezdan. 2021. "Performance of a Novel Chaotic Firefly Algorithm with Enhanced Exploration for Tackling Global Optimization Problems: Application for Dropout Regularization" Mathematics 9, no. 21: 2705. https://doi.org/10.3390/math9212705
APA StyleBacanin, N., Stoean, R., Zivkovic, M., Petrovic, A., Rashid, T. A., & Bezdan, T. (2021). Performance of a Novel Chaotic Firefly Algorithm with Enhanced Exploration for Tackling Global Optimization Problems: Application for Dropout Regularization. Mathematics, 9(21), 2705. https://doi.org/10.3390/math9212705











