Removing Symmetry in Circulant Graphs and Point-Block Incidence Graphs

Abstract

An automorphism of a graph is a mapping of the vertices onto themselves such that connections between respective edges are preserved. A vertex v in a graph G is fixed if it is mapped to itself under every automorphism of G. The fixing number of a graph G is the minimum number of vertices, when fixed, fixes all of the vertices in G. The determination of fixing numbers is important as it can be useful in determining the group of automorphisms of a graph-a famous and difficult problem. Fixing numbers were introduced and initially studied by Gibbons and Laison, Erwin and Harary and Boutin. In this paper, we investigate fixing numbers for graphs with an underlying cyclic structure, which provides an inherent presence of symmetry. We first determine fixing numbers for circulant graphs, showing in many cases the fixing number is 2. However, we also show that circulant graphs with twins, which are pairs of vertices with the same neighbourhoods, have considerably higher fixing numbers. This is the first paper that investigates fixing numbers of point-block incidence graphs, which lie at the intersection of graph theory and combinatorial design theory. We also present a surprising result-identifying infinite families of graphs in which fixing any vertex fixes every vertex, thus removing all symmetries from the graph.

1. Introduction

If you look closely at a QR-code you will see that three of the corners are marked with small nested squares. Marking these corners gives the QR-code a fixed orientation (where the original, and rotations of 90, 180 and 270 degrees are all different). The marked corner adjacent to two other marked corners is placed in the upper left. With this fixed orientation a smart phone can read it and know how it should be oriented accordingly. QR-codes are designed in black and white; however, if they included an additional colour, say blue, we would only need to mark two adjacent corners, one with a blue nested square and one with a black nested square. The blue square could correspond to the upper left corner and the black square could correspond to the upper right corner. We note that it is possible to fix two corners in black and white if the nested squares are drawn differently. This QR-code example shows that the fixing number of $C_4$ is 2.

In this paper, we consider the problem of removing symmetry from a graph by fixing vertices. We say that a vertex v in a graph G is fixed if it is mapped to itself under every automorphism of G. The fixing number of a graph G is the minimum number of vertices, when fixed, fixes all of the vertices in G, and as a result all symmetries of the graph are removed. The determination of fixing numbers are important as they provide insight into the famous problem of determining the automorphism group of a graph. Fixing numbers were introduced by Gibbons and Laison [1], and independently by Erwin and Harary [2]. Fixing numbers have also been called determining numbers by Boutin [3]. Fixing/determining numbers have been investigated for many families of graphs including complete graphs, paths, cycles [2], Cayley graphs and Frucht graphs [1], Cartesian products [4] and Kneser graphs [5]. Recently fixing numbers were determined for cographs and unit interval graphs [6]. We also note a concrete application as the removing of symmetry from graphs is related to a problem in robotic manipulation where the goal is to determine the orientation of a marked sphere from a single visual image [7].

In this paper, we investigate circulant graphs and point-block incidence graphs which arise from combinatorial designs. In both families, the graphs are regular and their circular structures are closely tied to modular arithmetic. We will use $fix(G)$ to denote the fixing number of a graph G. We will refer to a vertex $v\in V(G)$ as distinguishable if it is fixed under every automorphism of G. Following the definition from in [8] two vertices u and v are twins if they have the same open neighbourhoods or the same closed neighbourhoods. For any undefined notation, please see the text by West [9].

In this paper, we determine fixing numbers for multiple families of graphs. In Section 2, we identify the fixing number for powers of paths, which motivates the results in Section 3, including a similar result for powers of cycles. This leads us to an investigation of fixing numbers of circulant graphs. In Section 4, we investigate fixing numbers for point-block incidence graphs. This includes presentation of infinite families of graphs where fixing any vertex fixes every vertex, thus removing all symmetries from the graph. In the Conclusion section we pose ideas for future study.

2. Powers of Paths

We begin by determining the fixing number of powers of paths. The graph $P_n^m$ ($m\le n$) is the graph with $v_1,v_2,...,v_n$ as its set of vertices and $\{v_i{v}_j:|i-j|\le m\}$ as its set of edges. A small example is shown in Figure 1.

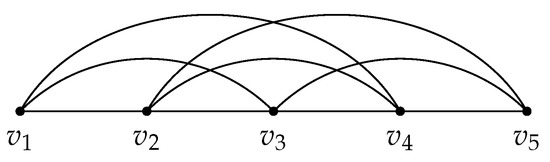
Figure 1. The graph $P_5^3$.

To obtain the fixing number, we first need to examine the degrees of the vertices in a power of a path. A vertex that is adjacent to all other vertices will be called a spanning vertex. We note that a graph with no non-trivial automorphisms can have at most one spanning vertex. A graph with two spanning vertices will have an automorphism that transposes the two spanning vertices.

Lemma 1.

If $m\ge \frac{n}{2}$, then $P_n^m$ has $2m-n+2$ spanning vertices. Furthermore, for every i where $1\le i\le n-m-1$, there exist exactly two vertices with degree $n-1-i$.

Proof. 

Following the definition, we notice that the vertices $v_i$ where $i\in [n-m,m+1]$ have the property that $|i-j|\le m$ for every $j\in [1,n]$. By definition, this implies that these vertices have degree $n-1$. Thus, there are $m+1-(n-m)+1=2m-n+2$ spanning vertices. Notice that $v_{n-m-1}$ and $v_{m+2}$ have degree $n-2$. Similarly, $v_{n-m-2}$ and $v_{m+3}$ have degree $n-3$. In general, $v_{n-m-i}$ and $v_{m+1+i}$ have degree $n-1-i$, thus completing the proof. □

Theorem 1.

Let n and m be integers such that$n>m$.

1.

If $m=n-1$, then $fix(P_n^m)=n-1$.

2.

If $n-2\ge m\ge \frac{n}{2}$, then $fix(P_n^m)=2m-n+2$

3.

If $\frac{n}{2}>m$, then $fix(P_n^m)=1$.

Proof. 

The first case is a complete graph, therefore $fix(K_n)=n-1$.

We now prove the second case. As $m\ge \frac{n}{2}$, then there exists $2m-n+2$ spanning vertices in $P_n^m$. We must distinguish $2m-n+2-1$ of them (all but one). Let $V_i=\{v_i,v_{n-i+1}\}$ for each $i\in [1,n-m-1]$. Notice that as automorphisms preserve degrees, every automorphism maps $V_i$ to itself for each i. We break these symmetries by fixing $v_1$. Then, $v_n$ is fixed and of the non-spanning vertices, half of the vertices $v_i$ will be adjacent to $v_1$ and the other half $v_{n-i}$ will not be adjacent to $v_1$. Therefore, there is no automorphism that will swap $v_i$ with $v_{n-i}$. It follows that the only automorphism is the trivial one. As we removed all symmetries by fixing only one non-spanning vertex, we conclude the fixing number is $n-2k+2-1+1=n-2k+2$.

For the third case we note the graph has only one non-trivial automorphism, where $v_i$ is swapped with $v_{n-i+1}$ for all $1\le i\le ⌊\frac{n}{2}⌋$. When n is even we can fix any vertex and remove this automorphism, when n is odd we can fix any vertex other than the centre vertex and remove this automorphism. □

3. Fixing Numbers of Circulant Graphs

The circulant graph $C_{n}A$, where $A\subseteq [n]$, is the graph with set of vertices equal to ${\mathbb{Z}}_n$ and set of edges equal to $\{ij:(i-j)modn\in A\mathrm{or}(j-i)modn\in A\}$. The numbers in A are called the generators of A. We start our study of circulant graphs with a particular type, the power of cycles. We note that aside from the degenerate case of $P_2$ all circulant graphs have a fixing number that is greater than 1. The reason is that if you fix any vertex v in a circulant graph with at least 3 vertices, there is a non-trivial automorphism (reflection) that fixes v.

3.1. Cycle Powers

The kth power of $C_n$, denoted by $C_n^k$, is the circulant graph where $A=[k]$. In our first two theorems, we determine the fixing numbers for cycle powers.

Theorem 2.

If $n=2k$, then $fix(C_n^{k-1})=k$.

Proof. 

Two vertices—p and q—in $C_n^{m-1}$ are not adjacent if and only if $p\equiv q+kmodn$. Thus, $\overline{C_n^{k-1}}$ is a disconnected graph with k components each isomorphic to $P_2$. If we fix one vertex in each component, we will have eliminated all symmetries, and if we fix less than k vertices, then there must be at least one component with no vertices fixed. We conclude that $fix(C_n^{k-1})=fix(\overline{C_n^{k-1}})=k$. □

Theorem 3.

If $n>2k$, then $fix(C_n^{k-1})=2$.

Proof. 

We start by fixing vertices 1 and 2. We claim that this is enough to break all symmetries. As $k+1$ is the only vertex adjacent to 2 but not to 1, the vertex $k+1$ is fixed. By a similar argument, $n-k+2$ is fixed, and as $n>2k$, $n-k+2\ne k+1$. Let $V_1=\{i:3\le i\le k\}$ and $V_2=\{i:n-k+3\le i\le n\}$. The vertices in $V_1$ are adjacent to $k+1$, while the vertices in $V_2$ are not; thus, we cannot swap a vertex in $V_1$ with a vertex in $V_2$. Notice also that every vertex in $V_1$ is adjacent to a different number of vertices in $V_2$. For instance, 3 is adjacent to every vertex i where $n-k+4\le i\le n$, while k is adjacent to no vertex in $V_2$. Thus, each vertex in $V_1$ is distinguishable. The same argument applies to vertices in $V_2$. We then have a collection of $2k$ fixed vertices. This is enough to fix all of the other vertices in the graph as i is the only vertex adjacent to $i-1,i-2,i-3$ and $i-4$ for all $k+2\le i\le n-k+1$. □

At first glance it seems that the cases where $\frac{n}{2}<k\le n$ have not been covered, but they are covered by the fact that in the cases $C_n^k\cong K_n$, where $K_n$ is the complete graph on n vertices.

3.2. The Twin Property and Circulant Graphs

We continue our study of circulant graphs by considering a relation on the set of vertices.

Definition 1.

A pair of vertices v and u are twins if $N(v)-\{u\}=N(u)-\{v\}$.

This topic is particularly interesting because if u and v are twins, then there exists an automorphism $\varphi$ such that $\varphi (u)=v$, $\varphi (v)=u$, and $\varphi$ is the identity function for every other vertex. Twins carry symmetry as is, but the presence of twins in circulant graphs is particularly special because we can calculate the fixing number of any circulant graph where such a structure is present. To achieve this goal, we need to investigate the properties of twins in circulant graphs. It is noted in [6] that the twin property is an equivalence relation. We restate the result for regular graphs as it will be useful in some of our proofs.

Theorem 4.

The twin property is an equivalence relation in regular graphs.

Proof. 

Let u∼v denote that vertices u and v are twins. Next, let $u,v$ and w be vertices. It is clear that $u\sim v$ implies $v\sim u$. For transitivity, assume that $u\sim v$ and $v\sim w$. We will prove that $u\in N(v)$ if and only if $w\in N(v)$ by contradiction. Assume without loss of generality that $u\in N(v)$ and $w\notin N(v)$, and set $N=N(u)-\{u,v,w\}$. Notice that $N=N(v)-\{u,v,w\}=N(w)-\{u,v,w\}$. If $u\in N(w)$, then $|N(u)|=\left|N\right|+2$ and $|N(v)|=\left|N\right|+1$, which is a contradiction with the fact that G is regular. If $u\notin N(w)$, then $|N(w)|=\left|N\right|$ and $|N(v)|=\left|N\right|+1$ which again is a contradiction. For the proof that $u\sim w$, we proceed with two cases.

Case 1: Assume $uv$ is not an edge. Then, $N(u)=N(u)-\{v\}=N(v)-\{u\}=N(v)$. By the claim we proved above, we have that $vw$ is not an edge. Thus, $N(v)=N(v)-\{w\}=N(w)-\{v\}=N(w)$, and so $N(u)=N(w)$. Finally, it is easy to see that this implies that $N(u)-\{w\}=N(w)-\{u\}$, i.e., $u\sim w$.

Case 2: Assume $uv$ is an edge. Let $p\in N(u)-\{w\}$, so $p\ne u$ and $p\ne w$. If $p=v$, then $p\in N(w)-\{u\}$ as $vw$ is an edge. Assume then that $p\ne v$. Then, $p\in N(u)-\{v\}$, so $p\in N(v)-\{u\}$, so $p\in N(v)-\{w\}$, so $p\in N(w)-\{v\}$, and so $p\in N(w)-\{u\}$. Thus $N(u)-\{w\}\subset N(w)-\{u\}$. Through a similar argument, $N(w)-\{u\}\subset N(u)-\{w\}$, i.e., $u\sim w$. □

Definition 2.

The maximal family of v, denoted by $[v]$, as the set of all vertices that are twins with v. Further, call any such set a maximal family and let $\left|v\right|=|[v]|$.

In circulant graphs, the set $[v]$ can also be thought as the equivalence class that contains v. This is a consequence of Theorem 4 and the fact that circulant graphs are regular.

Theorem 5.

Let $C_{n}A$ be a connected circulant graph. If $i\in [i+m]$, then $i\in [i+2m]$.

Proof. 

Notice that if i and j are twins, then $i+1$ and $j+1$ are twins too. Thus, by this claim $v_{i+m}$ is a twin of $v_{i+2m}$. Since the twin property is an equivalence relation, we have that i is a twin of $i+2m$, i.e. $i\in [i+2m]$. □

Theorem 6.

In $C_{n}A$, if m is the smallest integer such that i is a twin of $i+m$, then $[i]=\{i+pm:p\in \mathbb{N}\}$. Further, m divides n.

Proof. 

We will prove this by contradiction. Assume that there exists a vertex j that is a twin of i such that $i+pm<j<i+(p+1)m$ for some p. This implies that $i+j-pm$ is a twin of i. By the definition of m, i is not a twin of $i+1,\cdots ,i+m-1$. However, one of these vertices is $i+j-pm$ which is a contradiction. As for the second part, we will prove that it is the case when $i=0$ which will be enough for every i. If m does not divide n, then set $n=pm+r$ where $0<r<m$. Notice that 0 is a twin of $pm$, so it is a twin of $(p+1)m$ too, but $(p+1)mmodn$ is less than m, which contradicts the assumption that m was the smallest such integer. □

The above result hints at why twins are so special in circulant graphs. The fact that a generator set, A, exists allows us to completely characterize the equivalence class that contains any vertex v.

Theorem 7.

For any $v\in V(C_{n}A)$, $C_{n}A$ has exactly $\frac{n}{\left|v\right|}$ different maximal families.

Proof. 

First, let $v=0$. Let m be the smallest integer such that 0 and m are twins, and notice that $\left|v\right|=\frac{n}{m}$. As $[0],[1],\cdots ,[m-1]$ are all different maximal families in $C_{n}A$, we have exactly $m=\frac{n}{\left|v\right|}$ maximal families. If $v\ne 0$, we can repeat the proof by shifting the index. □

Theorem 8.

If u and v are twins and ϕ is an automorphism, then $\varphi (u)$ and $\varphi (v)$ are twins too.

Proof. 

As automorphisms preserve adjacency, it must be that $N(\varphi (u))-\{\varphi (v)\}=\varphi (N(u)-\{v\})=\varphi (N(v)-\{u\})=N(\varphi (v))-\{\varphi (u)\}.$ □

We need one final observation before the main result of the section. Since $\left|v\right|=\left|u\right|$ for every pair of vertices $v,u\in V(C_{n}A)$, a graph having twins implies that every vertex v has $\left|v\right|>1$. We now have everything we need to calculate the fixing number of any graph with twins.

Theorem 9.

If $\left|v\right|>1$ for some vertex in $C_{n}A$, then $fix(C_{n}A)=n-\frac{n}{\left|v\right|}$.

Proof. 

Notice that $\left|v\right|=\left|u\right|$ for any two vertices. As we observed before, if v and u are twins, then there exists an automorphism such that $\varphi (u)=v$ and $\varphi (v)=u$ and is the identity for other vertices. Thus, we must fix at least $\left|v\right|-1$ vertices for every maximal family. This would fix $\frac{n}{\left|v\right|}(|v|-1)=n-\frac{n}{\left|v\right|}$ vertices. We only need to show that there are no more automorphisms left. We will prove this by contradiction. Let $\varphi$ be an automorphism that is not the identity. It follows that there exist vertices u and v that have not been fixed such that $\varphi (v)=u$. Further, it must be that u is not a twin with v because every element of $[u]$ is fixed but u. Let $v^{\prime }\in [v]$ such that $v^{\prime }\ne v$. By Theorem 8, the vertices $\varphi (v)$ is a twin of $\varphi (v^{\prime })$. However, this implies that u is a twin of $v^{\prime }$ as $v^{\prime }$ is fixed. This is a contradiction as the twin relationship is transitive, so $u\in [v^{\prime }]$ implies that $u\in [v]$. Thus, every remaining vertex in the graph is fixed. □

Theorem 10.

For every integer m, there exists a connected circulant graph $C_{n}A$ such that $\left|v\right|=m$ for every $v\in V(C_{n}A).$

Although we have calculated the fixing number of every circulant graph with twins, there is the open question of being able to identify circulant graphs which have twins. To answer that question we need to investigate the connection between circulant graphs and their generators.

In the following section, we will point out circulant graphs where $\left|v\right|=2$. In a complete graph, any two vertices are twins. As complete graphs are circulant graphs, it follows that both $\left|v\right|=2$ and $\left|v\right|=n-1$, the two extremes of circulant graphs with twins, are possible.

3.3. Fixing Numbers and Generators

To facilitate our study of circulant graphs and their generators, it will be convenient to restate elementary properties of circulant graphs.

Theorem 11.

Let $m=\frac{n}{2}$, and let $\{A,B\}$ be a partition of $\{1,\cdots ,m\}$. Then, $\overline{C_{n}A}=C_{n}B$.

Proof. 

It is enough to see that two vertices are adjacent in $C_{n}A$ if and only if those two vertices are not adjacent in $C_{n}B$. Let i and j be adjacent in $C_{n}A$. This happens if and only if $(i-j)=k\in A$ or $(j-i)=k^{\prime }\in A$. Further, $k\in A$ or $k^{\prime }\in A$ if and only if $k\notin B$ or $k^{\prime }\notin B$. Finally, $k\notin B$ or $k^{\prime }\notin B$ if and only if i is not adjacent to j in $C_{n}B$. □

Theorem 12.

For a given set A where $maxA\le n$, let $m=gcd(A)$ and let $k=\frac{n}{gcd(m,n)}$. If $\frac{A}{m}=\{\frac{a}{m}:a\in A\}$, then $C_{n}A\cong gcd(m,n)C_k\frac{A}{m}$.

Proof. 

Assume first that $gcd(m,n)>1$. Let $V_i=\{i,i+m,i+2m,\cdots \}$. Notice that $|V_i|=\frac{n}{gcd(m,n)}=k$. Furthermore, from the definition of $C_{n}A$, $1+im$ is adjacent to u if and only if $u=1+(i+j)m$ or $u=1+(i-j)m$ where $j\in \frac{A}{m}$. Thus, $1+im$ is adjacent to u if and only if $u\in V_1$. This proves that $C_{n}A$ is disconnected, it has a component whose vertices are those in $V_1$, and that this component is isomorphic to $C_k\frac{A}{m}$. By using the same arguments for each i, we see that the vertices of $V_i$ corresponds to a component of $C_{n}A$ and each of these components is isomorphic to $C_k\frac{A}{m}$. Furthermore, notice that ${\mathbb{Z}}_n/m\mathbb{Z}$ has order $gcd(m,n)$, so $C_{n}A$ has $gcd(m,n)$ components and each is isomorphic to $C_k\frac{A}{m}$, thus giving us the result. When $gcd(m,n)=1$, m is a generator of the group $({\mathbb{Z}}_n,{+}_n)$, implying that $V_1=V(C_{n}A)$. Thus, the same arguments of adjacency apply with the exception that the graph is not disconnected. □

Theorem 13.

$C_{n}A$ is connected if and only if $gcd(A,n)=1$. Furthermore, $C_{n}A$ has$gcd(A,n)$ components.

Proof. 

If $C_{n}A$ is connected, then by Theorem 12$gcd(A,n)=1$. For the other direction, assume that $gcd(A,n)=1$. Set $A=\{m_1,\cdots ,m_k\}$ and $m=gcd(A)$. Theorem 12 implies that $C_{n}A\cong C_n\frac{A}{m}$. It is enough to see that $C_n\frac{A}{m}$ is connected. Set $m_i^{\prime }=\frac{m_i}{m}$ for every i and notice that $gcd(m_1^{\prime },\cdots ,m_k^{\prime })=gcd(\frac{A}{m})=1$. Thus, there is a path from 0 to any vertex, and so the graph is connected. The number of components is an easy consequence of Theorem 12 and the result we just proved. □

The following fact is left without proof.

Fact 1.

$C_{n}A\cong C_n\{n-a:a\in A\}$.

This fact has the handy consequence that we can always assume the set of generators has at most $\frac{n}{2}$ elements. We can make the additionally strong assumption that $A\subseteq [\frac{n}{2}]$. With these observations, we start the calculation of fixing numbers by noting a very special case that outcomes directly from a result due to Boutin and the fact that $C_{st}\{s,t\}\cong C_s\times C_t$ whenever $gcd(s,t)=1$, which was proven in [8]. We next restate a result from [4].

Theorem 14.

If $G=G_1^{k_1}\times \cdots \times G_m^{k_m}$ such that $G_i$ is prime, then $fix(G)=max\{fix(G_i^{k_i})\}$.

Corollary 1.

If $gcd(s,t)=1$ and $st\ge 3$, then $fix(C_{st}\{s,t\})=2$.

Our first major result characterizes the fixing number of any circulant graph with only one generator.

Theorem 15.

If $n>m>3$, then

$$fix(C_n\{m\})=\left\{\begin{array}{cc}2gcd(n,m)\hfill & ifm\ne \frac{n}{2}\hfill \\ m\hfill & ifm=\frac{n}{2}.\hfill \end{array}\right.$$

Proof. 

If $m=\frac{n}{2}$, then $C_n\{m\}\cong m{K}_2$, so we must use m vertices to fix the graph. For the other case, by Theorem 12 $C_n\{m\}\cong gcd(m,n)C_k$ where $k=\frac{n}{gcd(m,n)}$. Thus, $fix(C_n\{m\})=gcd(m,n)fix(C_k)=2gcd(m,n)$. □

As we study circulant graphs, we will notice that twins are present. When there are two generators, we can identify these graphs easily.

Theorem 16.

In the graph $C_n\{k_1,k_2\}$, if $n=2m$ and $k_1+k_2=m$, then $N(i)=N(i+m).$

Proof. 

We do so with a chain of double implications. $u\in N(i)-\{i+m\}$ if and only if $u=i\pm k_1$ or $u=i\pm k_2$ if and only if $u\in N(i+m)$. The last double implication is due to the fact that $n=2m$. For instance, if $u=i-k_1$, then u is adjacent to $i-k_1-k_2=i-m=i+m$. □

Corollary 2.

If $n=2m$ and $k_1+k_2=m$, then $fix(C_n\{k_1,k_2\})=m$.

Proof. 

The previous result implies that $\left|v\right|=2$ for every v in a circulant graph. Combining this with Theorem 9 gives the desired result. □

If it happens that fixing vertices 0 and 1 causes the vertex 2 to be fixed as well, then fixing i and $i+1$ causes $i+2$ to be fixed. Thus, fixing 0 and 1 causes 2 to be fixed, so 1 and 2 causes 3 to be fixed, and so on. By repeatedly applying this method, we see that every vertex in the graph is fixed. In other words, we have proven the following fact.

Fact 2.

If fixing vertices 0 and 1 fixes vertex 2 as well, then the only available automorphism is the identity one.

The following result gives the fixing number of any circulant graph with two generators where 1 is one of the generators.

Theorem 17.

If $3<k\le \frac{n}{2}$, then

$$fix(C_n\{1,k\})=\left\{\begin{array}{cc}k+1\hfill & ifn=2(k+1)\hfill \\ 2\hfill & otherwise\hfill \end{array}\right.$$

Proof. 

The case where $n=2k+2$ is covered by Corollary 2 since $n=2(k+1)$. Assume then that $n\ne 2k+2$ and fix 0 and 1. Notice that $8\le 2k\le n$. These two assumptions give the following.

$$\begin{array}{cc}\hfill \{1\}& =N(2)\cap N(0)\hfill \end{array}$$

(1)

$$\begin{array}{cc}\hfill \{-k,1\}& \subset N(1-k)\cap N(0)\hfill \end{array}$$

(2)

$$\begin{array}{cc}\hfill \{k,1\}& \subset N(1+k)\cap N(0).\hfill \end{array}$$

(3)

As the size of these intersections is preserved under automorphisms, 2 cannot be mapped to either $1-k$ or $1+k$. These vertices belong to $N(1)$. As this set must be mapped to itself and 0 is fixed, we conclude 2 is fixed too. Thus, by Fact 2 every vertex in the graph is fixed. □

From Fact 1, we can assume that $k\le \frac{n}{2}$, so indeed it covers every single case where there are two generators and 1 is one of them. A side consequence of Theorem 17 is the following. The fixing number of circulant graphs with two generators where 1 is one of them is equal to 2 if and only if the graph does not have twins. As we will see later, the same happens when there are two generators and 2 is one of the generators.

Theorem 17 covers a surprising amount of cases. For each set of generators, there are many other sets of generators that produce the same circulant graph. The case where $1\in A$ is particularly strong because of the two following results.

Theorem 18.

Assume that $gcd(m_1,n)=1$, $m_1\ne m_2$ and $m_1\ne n-m_2$. If there exists an integer $k<n$ such that $m_2\equiv m_{1}kmodn$, then $C_n\{m_1,m_2\}\cong C_n\{1,k\}$.

Proof. 

As $gcd(m_1,n)=1$, then $m_1$ is a generator of the additive group ${\mathbb{Z}}_n$. Vertices $0,m_1,2m_1,\cdots ,-m_1$ are the vertices of a cycle $C_n$. Let $v_i^{\prime }=i{m}_1$. We see that $v_i^{\prime }$ is adjacent to $v_{i-1}^{\prime }$ and $v_{i+1}^{\prime }$. From the hypothesis, we know that $C_n\{m_1,m_2\}$ is 4-regular, so all we have to do is to prove that $v_i^{\prime }$ is adjacent to $v_{i-k}^{\prime }$ and $v_{i+k}^{\prime }$. Note that $i{m}_1$ is adjacent to $i{m}_1-m_2$ and $i{m}_1+m_2$, so by our hypothesis, $i{m}_1$ is adjacent to $i{m}_1-k{m}_1$ and $i{m}_1+k{m}_1$, thus $v_i^{\prime }$ is adjacent to $v_{i-k}^{\prime }$ and $v_{i+k}^{\prime }$. □

Theorem 19.

If there exists an integer $m\in A$ such that $gcd(m,n)=1$, then there exists a set $A^{\prime }$ where $1\in A^{\prime }$ such that $C_{n}A\cong C_n{A}^{\prime }$.

Proof. 

Let $A=\{m_1,\cdots ,m_p\}$ where $m_1=m$. As $m_1$ is a generator of $(Z_n,{+}_n)$, then there exists integers $k_i$ such that $m_i\cong k_i{m}_1$$modn$. Thus, we can use the same technique as in Theorem 18 to show that we can construct a circulant graph $C_n{A}^{\prime }$ isomorphic to $C_{n}A$ where $A^{\prime }=\{1,k_2,\cdots ,k_p\}$. □

The following two facts about automorphisms will come in handy as we prove more results.

Fact 3.

For every i, $|N(0)\cap N(2)|=|N(i)\cap N(i+2)|$.

Fact 4.

If ϕ is an automorphism that fixes u and v, then ϕ maps $N(u)-N(v)$ to $N(\varphi (u))-N(\varphi (v))$.

Many circulant graphs can be re-expressed such that 1 is one of the generators. This is why the study of circulant graphs with 1 as a generator can be far-reaching. Having 1 as a generator allows for many more arguments regarding the neighbourhoods. These are presented in the following two results.

Theorem 20.

Let $m\ge \frac{n}{2}$ and $k_i$ be integers such that $1<k_1<\cdots <k_m\le \frac{n}{2}$. If $|N(2)\cap N(0)|=1$, then $fix(C_n\{1,k_1,\cdots ,k_m\})=2$.

Proof. 

We begin by fixing 0 and 1. We will show that, under the above conditions, 2 must be fixed. This will suffice as $|N(2)\cap N(0)|=|N(i+2)\cap N(i)|$, so Fact 3 would give the result.

Notice that

$$N(1)=\{0,2,1\pm k_1,\cdots ,1\pm k_m\}.$$

As $\{1,k_i\}\subset N(1+k_i)\cap N(0)$ and $\{1,-k_i\}\subset N(1-k_i)\cap N(0)$ for every i, then it follows that $|N(v)\cap N(0)|\ge 2$ for every $v\in N(1)$ but possibly 0 and 2. Note that the size of intersections is preserved under intersections, so since $|N(2)\cap N(0)|=1$, 2 cannot be mapped to $1\pm k_i$ for every i. However, $N(1)$ is fixed so 2 must be mapped to itself. □

Corollary 3.

Let $k_i$ be integers such that $1<k_1<\cdots <k_m$ and set $A=\{1,k_1,\cdots ,k_m\}$. If $n>2+2k_m$ and $|a-b|\ne 2$ for every $a,b\in A$, then $fix(C_{n}A)=2$.

Proof. 

By Theorem 20, we only need to show that $|N(2)\cap N(0)|=1$. As 1 is in the intersection, we only need to verify that no other vertex is in the intersection. We will prove that every member of $N(2)$ except for 1 cannot be in $N(0)$. From our choice of n, it follows that $3\notin N(0)$. Consider $2+k_i$ for some i. For $2+k_i$ to be in $N(0)$, there must be a j such that $\pm k_j\in N(v_0)$ and $2+k_i\equiv \pm k_j$$modn$. By our hypothesis, $2+k_i-k_j\ne 0$. It cannot be that $2+k_i\equiv -k_{j}modn$ since $n>2+2k_m\ge 2+k_i+k_j$, and equally it cannot be that $2+k_i\equiv k_{j}modn$ since $n>|2+k_i-k_j|$. Thus, $2+k_i\notin N(0)$ and so the only vertex in $N(0)\cap N(2)$ is 1, thus completing the proof. □

We conclude this subsection, and with it our study on circulant graphs, by calculating the fixing number of any circulant graph that has 2 as a generator. The statement assumes that k is odd and n is even, but notice that if these are false, then we can restate the circulant graph so that 1 becomes a generator of A, which is a case we have covered. Thus, the result below covers those cases that have not been addressed.

Theorem 21.

If $k\le \frac{n}{2}$, n is even and $k>1$ is odd, then

$$fix(C_n\{2,k\})=\left\{\begin{array}{cc}k+2\hfill & ifn=2(k+2)\hfill \\ 2\hfill & otherwise\hfill \end{array}\right.$$

Proof. 

We will consider the cases of $k=3$, $k=5$ and $k>5$. For $k=3$, we will consider the cases of $n<10,n=10$ and $n>10$. When $k=3$ and $n<10$, we only have the cases of $C_6\{2,3\}$ and $C_8\{2,3\}$. It is easy to verify manually that the fixing number is 2 in both of these cases. When $k=3$ and $n=10$, we have that $n=2(2+k)$, so by Corollary 2 the fixing number is indeed $2+k$. The rest of the paragraph will be the proof of the case where $k=3$ and $n>10$. Fix 0 and 1. We claim 2 is fixed. Notice that $N(0)-N(1)=\{2,-3\}$ must be mapped to itself by Fact 4, and by similar arguments $\{-1,4\}$ maps to itself too. Notice however that $\{-1,4\}\subset N(2)$ and $\{-1,4\}\not\subset N(-3)$. As $\{-1,4\}$ is fixed, it follows that 2 cannot be mapped to $-3$, so 2 must be fixed, and so by Fact 2 every vertex is fixed.

For $k=5$, the cases where $n\le 14$ can be covered in the same way that $k=3$ and $n\le 10$ were covered. So assume that $k=5$ and $n>14$. Fix 0 and 1. We claim 2 is fixed. It can be seen that the path $1,6,4,2$ is a shortest path from 1 to 2, so $d(1,2)=3$. Similarly, the path $1,-1,-3,-5$ is a shortest path from 1 to −5. Thus, $d(1,2)=d(1,-5)=3$. By similar arguments, we can see that $d(1,5)=2=d(1,-2)$. As automorphisms preserve distance and $N(0)$ gets mapped to itself, we see that $\{2,-5\}$ and $\{-2,5\}$ both get mapped to themselves. Now if there exists an automorphism that maps 2 to $-5$, then $\{d(2,-2),d(2,5)\}=\{d(-5,-2),d(-5,5)\}$, but it can be seen that these sets are not equal to each other for the chosen n. Thus, 2 is fixed, so by Fact 2 every vertex is fixed.

The last case of possible values of k is when $k>5$. The subcases where $n=2k+4$ and $n=4k$ are special, so we will treat them separately. When $k>5$ and $n=2k+4$, the fixing number is given by Corollary 2 as $n=2(k+2)$. When $k>5$ and $n=4k$, fix 0 and 1. Notice that there are exactly two paths from 0 to $2k$: $0,k,2k$ and $0,-k,2k$. As these paths are preserved under automorphisms, then $\{k,-k\}$ is mapped to itself. Thus, as $N(0)$ is mapped to itself, $\{2,-2\}$ is also mapped to itself. Additionally, $d(2,1)=d(1,0)<d(3,0)=d(2,-1)$, and since distance is preserved under automorphisms, then 2 cannot be mapped to −2. We conclude 2 is fixed. By Fact 2, every vertex is fixed.

Finally, assume that $k>5$, $n\ne 4k$ and $n\ne 2k+4$. Fix 0 and 2. We start by proving that this fixes 4 from which we conclude that every vertex with an even index is fixed. The set $N(2)=\{0,4,2-k,2+k\}$ must be mapped to itself. By our choice of n and k we can prove by exhaustion that the first line in the equations below is true. The others follow easily.

$$\begin{array}{cc}\hfill \{2\}& =N(4)\cap N(0)\hfill \\ \hfill \{2,-k\}& \subset N(2-p)\cap N(0)\hfill \\ \hfill \{2,k\}& \subset N(2+k)\cap N(0).\hfill \end{array}$$

As the size of these intersections is preserved, 4 cannot be mapped to $2-k$ or $2+k$ so 4 is fixed. Thus, every vertex with an even index is mapped to itself. We will now prove that the neighbourhood of every even index is fixed too, and as every odd vertex is adjacent to an even vertex, it would follow that every vertex is fixed. We prove the case for $N(0)$; other cases follow by a change in index. The only two vertices not yet fixed in $N(0)$ are k and $-k$. If $n=2k$, then these are equal and so it must be fixed. Thus, assume that $n>2k$. These vertices are adjacent to $2k$ and $-2k$ correspondingly, and as these vertices are fixed, we only need to show that $2k\ne -2k$. Notice that $2k$ is equal to $-2k$ if and only if $n|4k$. If $n>4k$ or $2k<n<4k$, then this is impossible. As these two are the only possibilities left, we are done. □

Again, note that the fixing number of $C_{n}A$, where $\left|A\right|=2$ and $2\in A$, is equal to 2 if and only if $C_{n}A$ does not have twins. The natural question, and one way in which the study of circulant graphs can be furthered, is if this always holds. We state this as a conjecture.

Conjecture 1.

If A is a set such that $\left|A\right|=2$ and $C_{n}A$ is connected, then $fix(C_{n}A)=2$ if and only if $C_{n}A$ does not have twins.

The family of graphs $C_{5t}(5,t)$ where $t\ge 2$ does not have twins and has a fixing number of $2t$. In addition, the circulant graph $C_{24}\{2,4,5,6,7,10\}$ does not have twins. Yet, by exhaustion it can also be verified that its fixing number is higher than 2. Thus, these are circulant graphs without twins whose fixing number is not 2, so this conjecture does not generalize to all circulant graphs.

4. Point-Block Incidence Graphs

In this section, we investigate point-block incidence graphs which have similar circular/modular properties of circulant graphs. In fact, there is an overlap between the two families which we present in Theorem 22.

A point-block incidence graph is a bipartite graph $G=(P,B)$ with a set of point vertices $P=\{p_1,p_2,\cdots ,p_r\}$ and a set of blocks $B=\{B_1,B_2,\cdots ,B_s\}$ where $p_i\in P$ is adjacent to $B_j\in B$ if and only if $p_i\in B_j$.

In this section, we will consider point-block incidence graphs where the blocks have size 3 and are generated by a single triple with computations performed mod k. We will use $G_n[a_r,a_s,a_t]$ to denote a point-block incidence graph on $n=2k$ vertices with a starter block $[a_r,a_s,a_t]$, where the points are $a_1,a_2,...,a_k$ and the blocks are $[\left(a_{r+i}\right) modk,\left(a_{s+i}\right) modk,\left(a_{t+i}\right) modk]$ for all $0\le i\le k-1$. Despite the simplicity of this construction, point-block incidence graphs can differ in their respective automorphism groups and fixing numbers.

The main goals of this section are to

(i)

Determine the fixing numbers of 3-regular point block incidence graphs.

(ii)

Determine the conditions when $G_n[u,v,w]\cong G_n[x,y,z]$.

In our next theorem, we present a connection between circulant graphs and point-block incidence graphs.

Theorem 22.

Let $k\ge 6$. Then $G_{4k+2}[0,1,2]\cong C_{4k+2}[1,2k+1]$.

Proof. 

We will show that both graphs are Möbius ladders with $4k+2$ vertices. For the point-block incidence graph generated by the block $[0,1,2]$ with computations performed mod k, for $0\le i\le \frac{k}{2}-1$ we label the vertices with either points or blocks. We begin by constructing the graph $P_2\times P_k$ with $P_2$ and $P_k$ where $V(P_2)$$=\{u_0,u_1\}$ and $V(P_k)=\{v_0,v_1,\cdots ,v_{k-1}\}$. Then, $V(P_2\times P_k)=\{u_0{v}_0,u_0{v}_1,\dots ,u_0{v}_{k-1},u_1{v}_0,u_1{v}_1,\dots ,u_1{v}_{k-1}\}$. We will use $u_0{v}_i$ and $u_1{v}_i$ to denote the i-$th$ vertex on the left and right sides of the circular ladder, respectively. Later, we will add connecting edges to from a Möbius ladder.

$u_0{v}_{2i}=2i$

$u_1{v}_{2i+1}=2i+1$

$u_0{v}_{2i+1}=[2i,2i+1,2i+2]$

$u_1{v}_{2i}=[2i-1,2i,2i+1]$

For the point-block incidence graph generated by the block $[0,1,2]$ with computations performed mod k, for $0\le i\le \frac{k+1}{2}-1$ we label the vertices as in the previous case. Then edges are added between vertices $u_0{v}_{k-1}$ and $u_1{v}_0$ and between vertices $u_1{v}_{k-1}$ and $u_0{v}_0$. This will create a Möbius Ladder Graph with $2k$ vertices.

Label the vertices of the circulant graph with $w_0,w_2,\dots ,w_{4k+1}$ where $w_i$ is adjacent to $w_{i-1}$, $w_{i+1}$, and $w_{i+2k+1}$ with arithmetic performed modulo $4k+1$. Then, we can define an isomorphism from the circulant to the point-block incidence graph:

$$f\left(w_i\right)=\left\{\begin{array}{cc}{u}_0{v}_i\hfill & \mathrm{if}0\le i\le 2k\hfill \\ u_1{v}_i\hfill & \mathrm{if}2k+1\le i\le 4k+1.\hfill \end{array}\right.$$

□

We continue with two elementary lemmas that show that point-block incidence graphs generated by a single block are invariant under arithmetic shifts and negation.

Lemma 2.

Let $k\ge 6$. Then, we have the following.

(1)

$G_{2k}[0,a,b]\cong G_{2k}[i,a+i,b+i]$ for any $0\le i\le k-1$.

(2)

$G_n[0,a,b]\cong G_n[0,ta,tb]$ for all $1\le t\le k$ where $gcd(n,t)=1$.

where all computations are performed modulo k.

Proof. 

For for the first condition we will prove that the mapping $\varphi :i\to (a+i)modk$ between points is an isomorphism. It is clear that this mapping is bijective. We will show next that the neighbours of a vertex a, map to the neighbours of $a+i$. The blocks adjacent to a are $[0,a,b]$, $[a,2a,b+a]$ and $[a-b,2a-b,a]$, and the blocks adjacent to $a+i$ are $[0,a+i,b+i]$, $[a+i,2a+i,b+a+i]$ and $[a-b+i,2a-b+i,a+i]$.

For the second condition we will prove that the mapping $\psi :a\to ta$ between points is an isomorphism. This mapping is also bijective. We will show that the neighbours of a vertex a, map to the neighbours of $ta$. The blocks adjacent to a are $[0,a,b]$, $[a,2a,b+a]$ and $[a-b,2a-b,a]$, and the blocks adjacent to $ta$ are $[0,ta,tb]$, $[ta,2ta,t\left(b+a\right)]$ and $[t(a-b),t(2a-b),ta]$. □

Lemma 3.

For any $k\ge 6$, $G_{2k}[0,a,b]\cong G_{2k}[0,b-a,b]$ where computations are performed modulo k.

Proof. 

We will prove that the mapping $\psi :i\to -i$ between points is an isomorphism. It is clear that this mapping is bijective. We will show next that the neighbours of a vertex a, map to the neighbours of $-a$. The blocks adjacent to a are $[0,a,b]$, $[a,2a,b+a]$, and $[a-b,2a-b,a]$, and the blocks adjacent to $-a$ are $[0,-a,-b]$, $[-a,-2a,-b-a]$, and $[b-a,-2a+b,-a]$. □

The two previous lemmas allow us to identify starter blocks where the resulting point-block incidence graphs are isomorphic. Our goal is to minimize the set of starter blocks for a given $m\ge 6$.

In the next theorem, we start with the block families of triples and remove duplicates that arise by the two previous lemmas to obtain a family of starter blocks for each $m\ge 6$.

Lemma 4.

Let $ms\ge 3$. Then, $G_{2ms}[0,ma,mb]\cong m{G}_{2s}[0,a,b]$.

Proof. 

For each $0\le i\le 2s-1$ there exists an isomorphism of the block $G_{2s}[i,a+i,b+i]$ to $G_{2ms}[mi,m\left(a+i\right),m\left(b+i\right)]$ where point a is mapped to $ma$. □

Next, we give an example of family of point-block incidence graphs which have a fixing number of 1, and furthermore the fixing of any point or block vertex removes all non-trivial automorphisms.

Lemma 5.

If any vertex in a point-block incidence graph is fixed then any automorphism maps points to points and blocks to blocks.

Proof. 

Let $G=(P,B)$. Suppose a point vertex $p\in P$ is fixed. Then, all of the point vertices have an even distance from p and all block vertices have an odd distance from p. These different parities force points to be mapped to points and blocks to be mapped to blocks. □

Theorem 23.

The point-block incidence graph generated with single block $[0,1,3]$ with computations done mod k when k ≥ 9, has a fixing number of 1. Furthermore, fixing any vertex fixes all other vertices.

Proof. 

The graph contains the point vertices $0,1,\cdots ,k-1$ and the block vertices $[0,1,3]$, $[1,2,4]$, ..., $[k-3,k-2,0]$ and $[k-1,0,2]$. We show that fixing any point vertex fixes all vertices in the graph (including both point and block vertices). We begin by fixing the vertex 0, which permutes its neighbouring blocks $[0,1,3]$, $[k-3,k-2,0]$ and $[k-1,0,2]$. We have to consider all of the possible cases of 0, 1, or 3 fixed blocks. For the sake of completeness we include the details. We include the first subcases of the case of 0 and 1 fixed blocks. The remaining subcases can be found in the Supplementary Materials section.

• 0 Fixed blocks
  $[0,1,3]\to [k-3,k-2,0]\to [k-1,0,2]\to [0,1,3]$. We note that we do not need to check the reverse direction as applying the given direction twice gives the reverse direction. This implies that $1\to \{k-3,k-2\}$, $3\to \{k-3,k-2\}$, $k-3\to \{k-1,2\}$, $k-2\to \{k-1,2\}$, $k-1\to \{1,3\}$, $2\to \{1,3\}$. We then consider the block $[2,3,5]$. It would have to be mapped to a block with either a 1 or 3 and either a $k-3$ or $k-2$. We consider the four following cases:
  • $2\to 1$, $3\to k-3$
    In this case, the block $[2,3,5]$ has to be mapped to a block with a 1 and a $k-3$. This does not exist.
  • $2\to 1$, $3\to k-2$
    In this case, $[2,3,5]$ has to be mapped to a block with a 1 and a $k-2$. This would be the block $[k-2,k-1,1]$, implying that $5\to k-1$ and also that $k-1\to 3$ and $1\to k-3$. In that case, the block $[1,2,4]$ must be mapped to a block with a 1 and a $k-3$, which does not exist.
  • $2\to 3$, $3\to k-3$
    In this case, the block $[2,3,5]$ would have to be mapped to a block with a 3 and $k-3$. For all other cases when k> 9, we are done because no such block exists. For the mod 9 case, $[2,3,5]$ would be mapped to $[3,4,6]$, implying $5\to 4$, and also that $k-1\to 1$ and $1\to k-2$. Then, the block $[7,8,1]$ would have to be mapped to a block with a 1 and a 7. However, the only block with this property is itself, which would contradict our assumption that we have 0 fixed blocks.
  • $2\to 3$, $3\to k-2$
    For this case, the block $[2,3,5]$ would have to be mapped to a block with a 3 and a $k-2$. Such block does not exist.
• 1 fixed block - first possibility
  $[0,1,3]\to [0,1,3]$, $[k-3,k-2,0]\to [k-1,0,2]$, $[k-1,0,2]\to [k-3,k-2,0]$
  This implies that $1\to \{1,3\}$, $3\to \{1,3\}$, $k-3\to \{k-1,2\}$, $k-2\to \{k-1,2\}$, $k-1\to \{k-3,k-2\}$ and $2\to \{k-3,k-2\}$.
  We then consider the block $[2,3,5]$. It has to be mapped to a block with a 1 or a 3 and either a $k-3$ or $k-2$. We consider the four following cases:
  • $3\to 1$, $2\to k-3$
    If this is the case, then block $[2,3,5]$ must be mapped to a block with a 1 and a $k-3$. Such block does not exist.
  • $3\to 1$, $2\to k-2$
    In this case, block $[2,3,5]$ must be mapped to a block with a 1 and a $k-2$. This would be the block $[k-2,k-1,1]$, implying that $5\to k-1$. This is a contradiction because only $k-3$ or $k-2$ can be mapped to a $k-1$.
  • $3\to 3$, $2\to k-3$
    If this is the case, then block $[2,3,5]$ has to be mapped to a block with a 3 and a $k-3$. No such block exists for all mod k cases where k > 9. For mod 9, $[2,3,5]$ has to be mapped to the block $[3,4,6]$, implying that $5\to 4$, $1\to 1$ and $k-1\to k-2$. Then, the block $[7,8,1]$ must be mapped to a block with a 1 and a 7 which does not exist.
  • $3\to 3$, $2\to k-2$
    In this case, the block $[2,3,5]$ has to be mapped to a block with a 3 and a $k-2$. Such block does not exist.
• 3 Fixed blocks
  $[0,1,3]\to [0,1,3]$, $[k-3,k-2,0]\to [k-3,k-2,0]$, $[k-1,0,2]\to [k-1,0,2]$
  This implies that $1\to \{1,3\}$, $3\to \{1,3\}$, $k-3\to \{k-3,k-2\}$, $k-2\to \{k-3,k-2\}$$k-1\to \{k-1,2\}$, $2\to \{k-1,2\}$.
  We then consider the block $[2,3,5]$. It must be mapped to a block with a $k-1$ or 2 and either a 1 or 3.
  • $2\to 2$, $3\to 3$
    In this case, $[2,3,5]$ would be mapped to itself, implying $5\to 5$, $k-1\to k-1$ and $1\to 1$. Then, the block $[k-2,k-1,1]$ would be mapped to a itself, implying that $k-2\to k-2$. Then, the block $[k-3,k-2,0]$ would be mapped to itself, further implying that $k-3\to k-3$, Then the vertices 0, ..., $k-1$ are now fixed and because the other vertices are adjacent to distinct triples of these vertices, they are now fixed as well.
  • $2\to 2$, $3\to 1$
    In this case, the block $[2,3,5]$ would be mapped to $[1,2,4]$, implying that $5\to 4$, $1\to 3$ and $k-1\to k-1$. In that case, the block $[k-2,k-1,1]$ would be mapped to a block with a $k-1$ and a 3, which does not exist.
  • $2\to k-1$, $3\to 3$
    In this case, the block $[2,3,5]$ has to be mapped to a block with a $k-1$ and a 3. Such block does not exist.
  • $2\to k-1$, $3\to 1$
    In this case, the block $[2,3,5]$ must be mapped to a block with a $[k-2,k-1,1]$, implying that $5\to k-2$. This is a contradiction because only $k-3$ or $k-2$ can be mapped to $k-2$.
    Suppose we fix the block $[1,2,4]$, then the vertices 1, 2 and 4 have either 0, 1 or 3 fixed points.
  This completes the proof.

□

In the next theorem, we consider point-block incidence graphs generated by the block $[0,1,2]$. We will show these graphs are either the Cartesian product of $P_2$ and a cycle, or a Möbius Ladder Graph with $2k$ vertices. These graphs have a fixing number of 2.

Theorem 24.

Let $G_{2k}[0,1,2]$ be the point-block incidence graph generated by the block $[0,1,2]$ with computations performed mod $k\ge 6$. Then

$$G_{2k}[0,1,2]\cong \left\{\begin{array}{cc}{P}_2\times C_k\hfill & ifk\mathrm{is}even\hfill \\ M_{2k}\hfill & ifkisodd.\hfill \end{array}\right.$$

Furthermore, the fixing numbers of each of these graphs is 2.

Proof. 

We begin by constructing the graph $P_2\times P_k$ with $P_2$ and $P_k$ where $V(P_2)$$=\{u_0,u_1\}$ and $V(P_k)=\{v_0,v_1,\cdots ,v_{k-1}\}$. Then, $V(P_2\times P_k)=\{u_0{v}_0,u_0{v}_1,\cdots ,u_0{v}_{k-1},u_1{v}_0,u_1{v}_1,\cdots ,u_1{v}_{k-1}\}$.

We first consider the case where k is even. For the point-block incidence graph generated by the block $[0,1,2]$ with computations performed mod k, for $0\le i\le \frac{k}{2}-1$ we label the vertices with either points or blocks.

• $u_0{v}_{2i}=2i$
• $u_1{v}_{2i+1}=2i+1$
• $u_0{v}_{2i+1}=[2i,2i+1,2i+2]$
• $u_1{v}_{2i}=[2i-1,2i,2i+1]$

Then edges are added between vertices $u_0{v}_{k-1}$ and $u_0{v}_0$ and between vertices $u_1{v}_{k-1}$ and $u_1{v}_0$. This will create a graph of the form $C_2\times P_k$.

Next, we consider the case where k is odd. For the point-block incidence graph generated by the block $[0,1,2]$ with computations performed mod k, for $0\le i\le \frac{k+1}{2}-1$ we label the vertices as in the previous case. Then, edges are added between vertices $u_0{v}_{k-1}$ and $u_1{v}_0$ and between vertices $u_1{v}_{k-1}$ and $u_0{v}_0$. This will create a Möbius ladder graph with $2k$ vertices.

These graphs have a fixing number of 2. We first note that fixing only one vertex still leaves a non-trivial reflection automorphism. If two vertices u and v are fixed then all remaining vertices w correspond to a unique pair $\left(d(u,w),d(v,w)\right)$. Therefore, the fixing number of these graphs is 2. □

In our next two theorems we give examples of graph families which have considerably larger fixing numbers.

Theorem 25.

(triplets) Let k be divisible by 3. Then, fix$(G_{\frac{k^2}{3}}[0,\frac{k}{3},\frac{2k}{3}])=\frac{2k}{3}$.

Proof. 

This follows as a consequence of Lemma 4.3, where $m=\frac{k}{3}$. □

Next, we present a family of connected graphs where the fixing number is $\frac{n}{4}$. An example is shown in Figure 2.

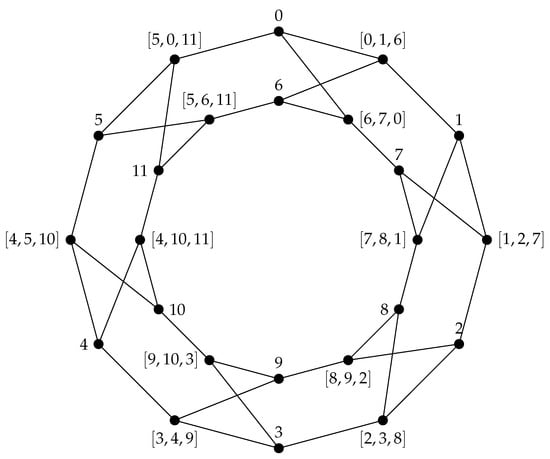
Figure 2. A half-step graph $G_{24}[0,1,6]$.

Theorem 26.

(half-steps) $fix\left(G_{4k}[0,1,k]\right)=k$.

Proof. 

It may be helpful to refer to Figure 2. The graph $G_{4k}[0,1,k]$ consists of k copies of $C_4$ which are connected by pairs of edges. The vertices in each $C_4$ are $\{i,[i,i+1,k+i],k+i,[k+i,k+i+1,i]\}$ for all $0\le i\le k-1$. As there exists an automorphism that transposes $[i,i+1,k+i]$ and $[k+i,k+i+1,i]$ along with $i+1$ and $k+i+1$, one of these four vertices must be fixed to remove this automorphism. Therefore, the fixing number of $G_{4k}[0,1,k]$ is at least k. For the other bound we assume that point vertices $0,1,\cdots ,k-1$ are all fixed. Then, the block vertices $[0,1,k]$, $[1,2,k+1],\dots ,[k-1,0,2k-1]$ are all fixed as they are each adjacent to a different pair of fixed point vertices. Then, all of the block vertices $[k,k+1,0]$, $[k+1,k+2,1],\dots$, $[k-1,k,2k-1]$ are all fixed as they are each adjacent to a different vertex that was fixed in our first step. Then, the vertices $k,k+1,\dots ,2k-1$ are all fixed since they are each adjacent to a different triple of already fixed vertices. Therefore, $fix(G_{4k}[0,1,k])=k.$ □

5. Conclusions

There are two main approaches to studying the fixing number of circulant graphs that our paper uses, and each one has its own advantages. The first approach is by considering the generators of the circulant graph. This technique has the advantage of giving a concrete description of the neighbourhood of every vertex. As neighbourhoods are preserved in isomorphisms, this route is effective when proving that the fixing number is 2. Most of our results concerning this technique are an outcome of fixing 2 vertices and proving by examining the neighbourhoods that all other vertices are fixed. For the case with arbitrary generators, there needs to be more understanding as to which generators cause the fixing number to be higher than 2. In the cases we covered, those scenarios where the fixing number is not 2 are exactly the cases where twins occur but there are circulant graphs that do not have twins that still have a fixing number higher than 2. This leads to the second approach for investigating fixing numbers: studying structures such as twins. These structures which generate symmetry are key to understanding when the fixing number is larger than 2. A development of both of these techniques would result in a concrete understanding of when the fixing number is 2 and when it is not, thus hopefully leading to a general formula that gives the fixing number of any circulant graph.

On the other topic of point-block incidence graphs, Lemmas 2 and 3 were useful for investigating when $G_n[u,v,w]\cong G_n[x,y,z]$. However, the second part of Lemma 3 depends on the modulus where the arithmetic is being performed. For example, the point-block incidence graphs when arithmetic is being performed mod 11, all point-block incidence graphs are isomorphic to either $G_{22}[0,1,2]$, or $G_{22}[0,1,3]$. We investigated the cases for even values of n, $8\le n\le 32$ and the results are found in the Supplementary Materials section, but we note the problem gets increasingly more complex, particularly in cases where $\frac{n}{2}$ is highly composite.