Interior Elastic Scattering by a Non-Penetrable Partially Coated Obstacle and Its Shape Recovering

Abstract

In this paper, the interior elastic direct and inverse scattering problem of time-harmonic waves for a non-penetrable partially coated obstacle placed in a homogeneous and isotropic medium is studied. The scattering problem is formulated via the Navier equation, considering incident circular waves due to point-source fields, where the corresponding scattered data are measured on a closed curve inside the obstacle. Our model, from the mathematical point of view, is described by a mixed boundary value problem in which the scattered field satisfies mixed Dirichlet-Robin boundary conditions on the Lipschitz boundary of the obstacle. Using a variational equation method in an appropriate Sobolev space setting, uniqueness and existence results as well as stability ones are established. The corresponding inverse problem is also studied, and using some specific auxiliary integral operators an appropriate modified factorisation method is given. In addition, an inversion algorithm for shape recovering of the partially coated obstacle is presented and proved. Last but not least, useful remarks and conclusions concerning the direct scattering problem and its linchpin with the corresponding inverse one are given.

1. Introduction

Mathematical and modelling techniques for wave scattering theory have played an essential role in recent decades and are widely used in real-world problems. Broadly speaking, classic scattering theory is concerned with the effect a bounded obstacle has on a time-harmonic incident wave, which is known as a scattering problem. A lot of scientific work has been done for direct scattering problems as well as for the inverse ones [1,2,3,4,5,6]. The first problems have the following interpretation: If the total field is the superposition of an incident field ${\mathbf{u}}^{inc}$ and the scattered field ${\mathbf{u}}^{sct}$, then the direct scattering problem is to determine the scattered field from the knowledge of the incident wave field and the governing differential equation of the wave motion. On the other hand, we have the inverse scattering problems, where the determination of physical or/and geometrical properties of the inhomogeneity from the knowledge of the incident and scattered field is considered.

At this point we mention that some scientific research works deal with inverse problems for elasticity using methods for hyperbolic equations and not methods applicable to elliptic ones, e.g., [7,8]. Hence, these problems in elastodynamics are time-dependent, and they constitute a scientific extension for the reader in time-dependent inverse problems.

In this work, the elastic direct scattering problem of time-harmonic waves by a bounded non-penetrable partially coated obstacle will be studied. In particular, our partially coated obstacle will be referred to as the scatterer, which consists of an inhomogeneity to the propagation of a given time-harmonic elastic wave field; our incident wave is a point-source field located at a point inside the scatterer (see later p. 2, Figure 1). Hence, knowing the governing Navier differential equation of the total wave field, the geometrical and physical properties of the scatterer, and the incident field, the scattered field will be determined. Further, the corresponding inverse problem and shape identification of the obstacle will be considered and studied. In contrast to traditional approaches applied in inverse scattering theory, which deal with iterative techniques such as regularised Newton methods [9,10,11] or conjugate gradient methods, our study focuses on a non-iterative method. The latter is known as factorization method (FM); here we exploit a modified factorization method (MFD) which avoids the need of solving the corresponding direct scattering problem. The MFD belongs to a wide class of methods, known as qualitative methods, and is a different technique for solving inverse scattering problems compared to an iterative one. These methods require less a priori information, and for an excellent source we refer the reader to [4].

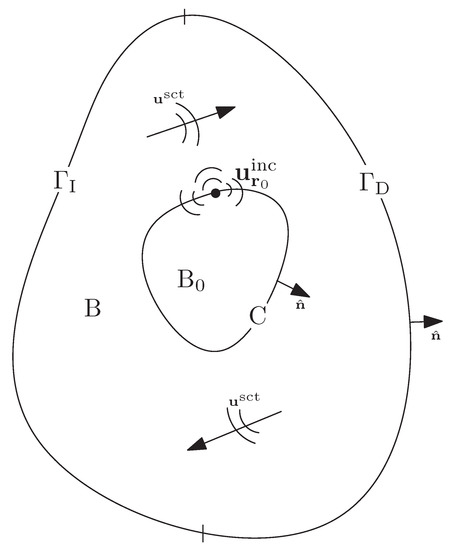
Figure 1. The mixed scattering configuration.

Our scattering problem will be mathematically modelled by a mixed boundary value problem, and emphasis on its well-posedness using a variational method will be given. We will extend the results from the acoustic case proposed in [12] to the more complicated elastic one. We consider as incident elastic wave ${\mathbf{u}}_{r_0}^{inc}$, a source located at a point with position vector ${\mathbf{r}}_0$ [13], i.e.,

$$\begin{array}{ccc}\hfill {\mathbf{u}}_{r_0}^{inc}\left(\mathbf{r}\right)& =& \frac{i}{4}\{-\frac{1}{\rho {\omega }^2}{\nabla }_r\otimes {\nabla }_r[H_0^{\left(1\right)}(k^p|\mathbf{r}-{\mathbf{r}}_0|)-H_0^{\left(1\right)}(k^s|\mathbf{r}-{\mathbf{r}}_0|)]\hfill \\ \hfill \\ & & +\frac{1}{\mu }\tilde{\mathbf{I}}{H}_0^{\left(1\right)}(k^s|\mathbf{r}-{\mathbf{r}}_0|)\},\mathbf{r}\ne {\mathbf{r}}_0\hfill \end{array}$$

(1)

where $\tilde{\mathbf{I}}$ is the identity dyadic, $H_0^{\left(1\right)}\left(z\right)$ is the Hankel function of first kind and zero order, $\rho$ denotes the mass density, $\omega >0$ is the angular frequency and $k^p$ and $k^s$ are the wave numbers of longitudinal and shear waves respectively. This is actually similar to the fundamental solution in two dimensional elasticity with a singularity at the point ${\mathbf{r}}_0$ which satisfies the following Navier equation

$$\left({\Delta }^{*}+\rho {\omega }^2\right)\tilde{\mathsf{\Gamma }}(\mathbf{r}-{\mathbf{r}}^{\prime })=-\tilde{\mathbf{I}}\delta (\mathbf{r}-{\mathbf{r}}^{\prime }),\mathbf{r},{\mathbf{r}}^{\prime }\in {\mathbb{R}}^2$$

(2)

where ${\Delta }^{*}=\mu \Delta +(\lambda +\mu )\nabla (\nabla ·)$ stands for the Kupradze’s differential operator, $\lambda ,\mu$ are the Lamé constants of the elastic medium and $\delta (\mathbf{r}-{\mathbf{r}}^{\prime })$ represents the Dirac measure concentrated at the point $\mathbf{r}$. For the Lamé constants, strong ellipticity conditions $\mu >0$ and $\lambda +2\mu >0$ hold, in order for the medium to sustain longitudinal as well as transverse waves.

The paper at hand deals with an interior scattering problem where both incident point-sources and scattered wave fields inside our obstacle are considered. For our problem, Dirichlet-Robin type boundary conditions will be considered, a Sobolev space setting will be presented and the appropriate mixed boundary value problem will be studied. In elasticity, the Dirichlet boundary condition has the meaning of a rigid body where the displacement vector is given, whereas the Robin type or impedance boundary condition is applied on the coated part of the elastic obstacle. The latter partially coating part of our boundary is due to a constant surface impedance c (see Equation (5)), and the mathematical relation upon this part is a combination of the displacement and surface-stress vector, simultaneously [14].

Applications regarding elastic materials and environments, especially for the coated obstacle case, are very extensive and there a lot of examples from real-world problems in the following areas: engineering mechanics, medical imaging, non-destructive testing and evaluation, geophysics material science, etc. (for details see [15] and references therein). The present results concerning elastic direct scattering problems are used in the study of corresponding inverse problems for partially coated obstacles buried-or-non in elastic layered background media. The latter research direction is also investigated in this paper and useful results are given.

Our paper is organised as follows. In Section 2, the direct scattering problem for a partially coated obstacle irradiated by an elastic incident point-source field is considered. We formulate our problem in a suitable functional space setting, which is described by a specific mixed boundary value problem for the Navier equation. We consider the case where our point-source field is located on some curve C inside the scatterer. The latter is crucial, since our future goal is the shape reconstruction of the obstacle via the scattering data measured on the above curve. In Section 3, uniqueness and existence of the direct mixed scattering problem via the variational method is established, and using Riesz-Fredholm theory, stability of solutions is also proved. In Section 4, we study the corresponding inverse scattering problem and using the factorization method due to some specific auxiliary operators, determination of the shape of the partially coated obstacle from the knowledge of near-field data is achieved. Finally, in Section 5 we end up with fruitful conclusions and remarks for partially coated obstacles in elastic media.

2. Setting up the Scattering Problem

Let $B\subset {\mathbb{R}}^2$ denote a closed bounded and simply connected domain with Lipschitz boundary $\partial B\equiv \mathsf{\Gamma }:={\mathsf{\Gamma }}_D\cup \Pi \cup {\mathsf{\Gamma }}_I$, where ${\mathsf{\Gamma }}_D$ ($D:$ stands for the Dirichlet boundary condition) and ${\mathsf{\Gamma }}_I$ (I: stands for the Robin boundary condition) are disjoint, relatively open subsets of $\mathsf{\Gamma }$ having $\Pi$ as their common boundary in $\mathsf{\Gamma }$. Moreover, the Dirichlet and impedance type of boundary conditions are specified on ${\mathsf{\Gamma }}_D$ and ${\mathsf{\Gamma }}_I$, respectively.

We state the direct scattering problem which is described by the following mixed boundary value problem: For a given elastic incident point-source ${\mathbf{u}}_{r_0}^{inc}$, find the total elastic wave field ${\mathbf{u}}^{tot}={\mathbf{u}}^{sct}+{\mathbf{u}}_{r_0}^{inc}$, such that

$$\begin{array}{ccc}& & ({\Delta }^{*}+\rho \left(\mathbf{r}\right){\omega }^2){\mathbf{u}}^{tot}\left(\mathbf{r}\right)=\mathbf{0},\mathbf{r}\in B\hfill \\ \hfill \end{array}$$

(3)

$$\begin{array}{ccc}& & {\mathbf{u}}^{tot}\left(\mathbf{r}\right)=\mathbf{0},\mathbf{r}\in {\mathsf{\Gamma }}_D\hfill \\ \hfill \end{array}$$

(4)

$$\begin{array}{ccc}& & T{\mathbf{u}}^{tot}\left(\mathbf{r}\right)+i\omega c{\mathbf{u}}^{tot}\left(\mathbf{r}\right)=\mathbf{0},\mathbf{r}\in {\mathsf{\Gamma }}_I\hfill \end{array}$$

(5)

where ${\Delta }^{*}$ is Kupradze’s differential operator (see p. 2), and T is the physical stress vector, given by

$$T^{\left(r\right)}=2\mu {\widehat{\mathbf{n}}}_r·\nabla +\lambda {\widehat{\mathbf{n}}}_r\nabla ·+\mu \widehat{\mathbf{n}}\times \nabla \times ,$$

(6)

where ${\mathbf{n}}_r$ stands for the outward unit normal vector define almost everywhere on $\partial B$ at the point $\mathbf{r}$. The superscript (which will be omitted from now on) denotes the action of the differential operator on the indicated variable. Throughout this paper $c>0$ is the surface impedance being a constant, $\lambda ,\mu$, are the Lamé coefficients as before and $\rho \left(\mathbf{r}\right)$ denotes the mass density, given by

$$\rho \left(\mathbf{r}\right)=\left\{\begin{array}{c}{\rho }_0,\mathbf{r}\in {\mathbb{R}}^2⧹\overline{B}\\ \\ {\rho }_1,\mathbf{r}\in B.\end{array}\right.$$

(7)

In what follows in this paper, we assume C to be a Lipschitz closed curve inside B and $B_0$ to be the interior domain enclosed by C. We also assume as incident wave a point-source ${\mathbf{u}}_{r_0}^{inc}\left(\mathbf{r}\right)$ given by ${\mathbf{u}}_{r_0}^{inc}\left(\mathbf{r}\right)\equiv \tilde{\mathsf{\Gamma }}(\mathbf{r},{\mathbf{r}}_0),\mathbf{r}\in {\mathbb{R}}^2$ and ${\mathbf{r}}_0\in C$ where $\tilde{\mathsf{\Gamma }}(\mathbf{r},{\mathbf{r}}_0)$ is the fundamental solution of the Navier Equation (2), given by (1); the mixed scattering configuration is shown in Figure 1.

We need the following Sobolev space setting. Let ${\mathsf{\Gamma }}_0$ be a partial boundary of $\mathsf{\Gamma }$, then we define

$$\begin{array}{ccc}& & H^{1/2}\left({\mathsf{\Gamma }}_0\right)=\{\mathbf{u}{|}_{{\mathsf{\Gamma }}_0}:\mathbf{u}\in H^{1/2}\left(\mathsf{\Gamma }\right)\},\hfill \\ \hfill \\ & & {\tilde{H}}^{1/2}\left({\mathsf{\Gamma }}_0\right)=\{\mathbf{u}\in H^{1/2}\left(\mathsf{\Gamma }\right):supp\left(\mathbf{u}\right)\subseteq {\overline{\mathsf{\Gamma }}}_0\},\hfill \\ \hfill \\ & & H^{-1/2}\left({\mathsf{\Gamma }}_0\right)={({\tilde{H}}^{1/2})}^{\prime }\mathrm{the}\mathrm{dual}\mathrm{space}\mathrm{of}{\tilde{H}}^{1/2}\left({\mathsf{\Gamma }}_0\right),\hfill \\ \hfill \\ & & {\tilde{H}}^{-1/2}\left({\mathsf{\Gamma }}_0\right)={(H^{1/2}({\mathsf{\Gamma }}_0))}^{\prime }\mathrm{the}\mathrm{dual}\mathrm{space}\mathrm{of}{H}^{1/2}\left({\mathsf{\Gamma }}_0\right),\hfill \\ \hfill \\ & & H_0^1(B,{\mathsf{\Gamma }}_D)=\{\mathbf{u}\in H^1\left(B\right):\mathbf{u}=\mathbf{0},on{\mathsf{\Gamma }}_D\},\hfill \end{array}$$

where $H^1\left(B\right)$ and $H_{loc}^1({\mathbb{R}}^2⧹\overline{B})$ are the usual Sobolev spaces, $H^{1/2}\left(\mathsf{\Gamma }\right)$ is the trace space and $H_0^1(B,{\mathsf{\Gamma }}_D)$ is equipped with the norm induced from $H^1\left(B\right)$, i.e.,

$${\parallel \mathbf{u}\parallel }_{H^1\left(B\right)}^2={\parallel \mathbf{u}\parallel }_{L^2\left(B\right)}^2+{\parallel \nabla \mathbf{u}\parallel }_{L^2\left(B\right)}^2.$$

(8)

We now define the following interior mixed boundary value problem (IMBVP):

$$\begin{array}{ccc}& & ({\Delta }^{*}+{\rho }_1{\omega }^2){\mathbf{u}}^{sct}\left(\mathbf{r}\right)=\mathbf{0},\mathbf{r}\in B\hfill \\ \hfill \end{array}$$

(9)

$$\begin{array}{ccc}& & {\mathbf{u}}^{sct}\left(\mathbf{r}\right)=\mathbf{f},\mathbf{r}\in {\mathsf{\Gamma }}_D\hfill \\ \hfill \end{array}$$

(10)

$$\begin{array}{ccc}& & T{\mathbf{u}}^{sct}+i\omega c{\mathbf{u}}^{sct}=\mathbf{h},\mathbf{r}\in {\mathsf{\Gamma }}_I.\hfill \end{array}$$

(11)

If we assume ${\mathbf{u}}^{tot}={\mathbf{u}}^{sct},\mathbf{f}=-{\mathbf{u}}_{r_0}^{inc}\in H^{\frac{1}{2}}\left({\mathsf{\Gamma }}_D\right)$, $\mathbf{h}=-(T{\mathbf{u}}_{r_0}^{inc}\left(\mathbf{r}\right)+i\omega c{\mathbf{u}}_{r_0}^{inc}\left(\mathbf{r}\right))\in H^{-\frac{1}{2}}\left({\mathsf{\Gamma }}_I\right)$, then the problem (9)–(11) is a special case of (3)–(5). The above IMBVP will be expressed in a variational sense and its well-posedness will be exploited.

3. Variational Formulation and Its Linchpin with Well-Posedness

In this section a variational formulation of the problem will be presented, and an equivalent integral form of the scattering problem (9)–(11) will be established.

Let $\mathbf{\varphi }\in H_0^1(B,{\mathsf{\Gamma }}_D)$ be a vector test function; we multiply each one of the Equations (9)–(11) with function $\overline{\mathbf{\varphi }}\in H_0^1(B,{\mathsf{\Gamma }}_D)$ (where overline $``-"$ denotes the conjugate), and applying the first generalised Betti’s formula [16] for functions ${\mathbf{u}}^{sct}$ and $\overline{\mathbf{\varphi }}$ we get

$${\int }_B\overline{\mathbf{\varphi }}·{\Delta }^{*}{\mathbf{u}}^{sct}d\upsilon ={\int }_{\partial B}\overline{\mathbf{\varphi }}·T{\mathbf{u}}^{sct}ds-{\int }_B\mathcal{E}(\overline{\mathbf{\varphi }},{\mathbf{u}}^{sct})d\upsilon ,$$

(12)

where

$$\begin{array}{ccc}\hfill \mathcal{E}(\mathbf{v},\mathbf{w})& =& (\mu +2\lambda )\left(\frac{\partial v_1}{\partial x_1}\frac{\partial w_1}{\partial x_1}+\frac{\partial v_2}{\partial x_2}\frac{\partial w_2}{\partial x_2}\right)\hfill \\ \hfill \\ & & +\mu \left(\frac{\partial v_1}{\partial x_2}\frac{\partial v_2}{\partial x_2}+\frac{\partial v_2}{\partial x_1}\frac{\partial w_2}{\partial x_1}\right)\hfill \\ \hfill \\ & & +\lambda \left(\frac{\partial v_1}{\partial x_1}\frac{\partial w_2}{\partial x_2}+\frac{\partial v_2}{\partial x_2}\frac{\partial w_1}{\partial x_1}\right)\hfill \\ \hfill \\ & & +\mu \left(\frac{\partial v_1}{\partial x_2}\frac{\partial w_2}{\partial x_1}+\frac{\partial v_2}{\partial x_1}\frac{\partial w_1}{\partial x_2}\right)\hfill \end{array}$$

(13)

with $\mathbf{v}=(v_1,v_2)$ and $\mathbf{w}=(w_1,w_2)$ is a specific energy functional in 2D-linear elasticity and expresses the energy disseminated through the point of the material being shifted. Using now Equation (9) and the notation $\partial B\equiv \mathsf{\Gamma }:={\mathsf{\Gamma }}_D\cup \Pi \cup {\mathsf{\Gamma }}_I$, from (12) we take

$$\begin{array}{ccc}\hfill {\int }_B(-{\rho }_1{\omega }^2)\overline{\mathbf{\varphi }}·{\mathbf{u}}^{sct}d\upsilon & =& {\int }_{{\mathsf{\Gamma }}_I}\overline{\mathbf{\varphi }}·T{\mathbf{u}}^{sct}ds+{\int }_{{\mathsf{\Gamma }}_D}\overline{\mathbf{\varphi }}·T{\mathbf{u}}^{sct}ds\hfill \\ \hfill \\ & & -{\int }_B\mathcal{E}(\overline{\mathbf{\varphi }},{\mathbf{u}}^{sct})d\upsilon .\hfill \end{array}$$

(14)

The latter with the aid of (11) yields to

$$\begin{array}{ccc}& & {\int }_B\left(\mathcal{E}(\overline{\mathbf{\varphi }},{\mathbf{u}}^{sct})-{\rho }_1{\omega }^2\overline{\mathbf{\varphi }}·{\mathbf{u}}^{sct}\right)d\upsilon +i\omega c{\int }_{{\mathsf{\Gamma }}_I}\overline{\mathbf{\varphi }}·{\mathbf{u}}^{sct}ds\hfill \\ \hfill \\ & =& {\int }_{{\mathsf{\Gamma }}_I}\mathbf{h}·\overline{\mathbf{\varphi }}ds+{\int }_{{\mathsf{\Gamma }}_D}\overline{\mathbf{\varphi }}·T{\mathbf{u}}^{sct}ds,\hfill \end{array}$$

(15)

and having in mind that $\mathbf{\varphi }\in H_0^1(B,{\mathsf{\Gamma }}_D)$, we easily take

$${\int }_B\left(\mathcal{E}(\overline{\mathbf{\varphi }},{\mathbf{u}}^{sct})-{\rho }_1{\omega }^2\overline{\mathbf{\varphi }}·{\mathbf{u}}^{sct}\right)d\upsilon +i\omega c{\int }_{{\mathsf{\Gamma }}_I}\overline{\mathbf{\varphi }}·{\mathbf{u}}^{sct}ds={\int }_{{\mathsf{\Gamma }}_I}\mathbf{h}·\overline{\mathbf{\varphi }}ds.$$

(16)

In the variational sense, the problem (9)–(11) is equivalent by finding a function ${\mathbf{u}}^{sct}\in H^1\left(B\right)$ which satisfies:

$${\int }_B\left(\mathcal{E}(\overline{\mathbf{\varphi }},{\mathbf{u}}^{sct})-{\rho }_1{\omega }^2\overline{\mathbf{\varphi }}·{\mathbf{u}}^{sct}\right)d\upsilon +i\omega c{\int }_{{\mathsf{\Gamma }}_I}\overline{\mathbf{\varphi }}·{\mathbf{u}}^{sct}ds=<\mathbf{h},\mathbf{\varphi }>,$$

(17)

where ${\int }_{{\mathsf{\Gamma }}_I}\mathbf{h}·\overline{\mathbf{\varphi }}ds=<\mathbf{h},\mathbf{\varphi }>$. For the latter, we consider that for any $m\in \mathbb{C},\mathbf{k},\mathbf{g}\in H^{-\frac{1}{2}}\left({\mathsf{\Gamma }}_I\right)$ and $\mathbf{\varphi }\in H_0^1(B,{\mathsf{\Gamma }}_D)$ a test function, we can get

$$<\mathbf{k},\mathbf{k}>={\int }_{{\mathsf{\Gamma }}_I}\mathbf{k}·\overline{\mathbf{k}}ds={\int }_{{\mathsf{\Gamma }}_I}{|\mathbf{k}|}^{2}ds\ge 0,for\mathbf{k}\in H^{-\frac{1}{2}}\left({\mathsf{\Gamma }}_I\right)\cap H_0^1(B,{\mathsf{\Gamma }}_D).$$

(18)

It easily follows that for $<\mathbf{k},\mathbf{k}>=0$ we can arrive at ${\int }_{{\mathsf{\Gamma }}_I}{|\mathbf{k}|}^{2}ds=0$ and hence $\mathbf{k}=\mathbf{0}$.

Further, we easily get $<\mathbf{k},\mathbf{\varphi }>=\overline{<\mathbf{\varphi },\mathbf{k}>}$, $<m\mathbf{k},\mathbf{\varphi }>=m<\mathbf{k},\mathbf{\varphi }>$ as well as $<\mathbf{k}+\mathbf{g},\mathbf{\varphi }>=<\mathbf{k},\mathbf{\varphi }>+<\mathbf{g},\mathbf{\varphi }>$; therefore, $<\mathbf{k},\mathbf{\varphi }>$ is an inner product.

In what follows, we prove continuous dependence of the solution of our IMBVP due to the boundary data, and therefore the following uniqueness-existence theorem holds.

Theorem 1.

The interior mixed boundary value problem (IMBVP) (9)–(11), has a unique weak solution ${\mathbf{u}}^{sct}\in H^1\left(B\right)$ satisfying (17), and furthermore

$$\parallel {\mathbf{u}}^{sct}{\parallel }_{H^1\left(B\right)}\le C\left({\parallel \mathbf{f}\parallel }_{H^{\frac{1}{2}}\left({\mathsf{\Gamma }}_D\right)}+{\parallel \mathbf{h}\parallel }_{H^{-\frac{1}{2}}\left({\mathsf{\Gamma }}_I\right)}\right)$$

(19)

for some positive constant C.

Proof. 

Let us first deal with the uniqueness by showing that the homogeneous problem of (9)–(11) $\left(\mathbf{f}=\mathbf{h}=0\right)$, has only the trivial solution, i.e., ${\mathbf{u}}^{sct}=\mathbf{0}$ in B. We consider the variational Equation (17), by letting $\mathbf{\varphi }={\mathbf{u}}^{\mathbf{sct}}$, and therefore

$${\int }_B\left(\mathcal{E}(\overline{{\mathbf{u}}^{sct}},{\mathbf{u}}^{sct})-{\rho }_1{\omega }^2\overline{{\mathbf{u}}^{sct}}·{\mathbf{u}}^{sct}\right)d\upsilon +i\omega c{\int }_{{\mathsf{\Gamma }}_I}{\mathbf{u}}^{sct}·\overline{{\mathbf{u}}^{sct}}ds=<\mathbf{h},{\mathbf{u}}^{sct}>.$$

(20)

Since $\mathbf{h}=\mathbf{0}$, we get

$${\int }_B\left(\mathcal{E}(\overline{{\mathbf{u}}^{sct}},{\mathbf{u}}^{sct})-{\rho }_1{\omega }^2{|{\mathbf{u}}^{sct}|}^2\right)d\upsilon +i\omega c{\int }_{{\mathsf{\Gamma }}_I}{|{\mathbf{u}}^{sct}|}^{2}ds=0.$$

(21)

By taking the imaginary part in the latter relation, we have

$$Im\left({\int }_B\left(\mathcal{E}(\overline{{\mathbf{u}}^{sct}},{\mathbf{u}}^{sct})-{\rho }_1{\omega }^2|{\mathbf{u}}^{sct}|\right)d\upsilon +i\omega c{\int }_{{\mathsf{\Gamma }}_I}{|{\mathbf{u}}^{sct}|}^{2}ds\right)=0,$$

(22)

and using (13) and the fact ${\rho }_1{\omega }^2{|{\mathbf{u}}^{sct}|}^2\in \mathbb{R}$, we get

$$\omega c{\int }_{{\mathsf{\Gamma }}_I}{|{\mathbf{u}}^{sct}|}^{2}ds=0.$$

(23)

Having in mind that $\omega ,c$ are positive real numbers, we take ${\mathbf{u}}^{sct}=\mathbf{0},on{\mathsf{\Gamma }}_I$. We can also get by the boundary condition (11) that $T{\mathbf{u}}^{sct}\left(\mathbf{r}\right)=\mathbf{0}$, on ${\mathsf{\Gamma }}_I$. By Holmgren’s uniqueness theorem [17] we conclude that ${\mathbf{u}}^{sct}=\mathbf{0}$ in B, and hence uniqueness is secured.

We continue our well-posedness analysis with the existence of solutions of the problem (9)–(11). Let a vector function ${\mathbf{u}}_0\in H^1\left(B\right)$ being a solution of the static Navier equation ${\Delta }^{*}\mathbf{u}=\mathbf{0}$ in B with ${\mathbf{u}}_0={\mathbf{f}}_{ext}$ on $\mathsf{\Gamma }$, where

$${\mathbf{f}}_{ext}{|}_{\mathsf{\Gamma }}=\left\{\begin{array}{c}\mathbf{f},\mathrm{on}{\mathsf{\Gamma }}_D\\ \\ \mathbf{0},\mathrm{otherwise}\end{array}\right.$$

(24)

i.e., ${\mathbf{f}}_{ext}$ is the continuous by zero extension of $\mathbf{f}$ on $\mathsf{\Gamma }$. Using the property $\parallel {\mathbf{f}}_{ext}{\parallel }_{H^{\frac{1}{2}}\left(\mathsf{\Gamma }\right)}\le C_1{\parallel \mathbf{f}\parallel }_{H^{\frac{1}{2}}\left({\mathsf{\Gamma }}_D\right)}$ we can obtain $\parallel {\mathbf{u}}_0{\parallel }_{H^1\left(B\right)}\le C_1\parallel {\mathbf{f}}_{ext}{\parallel }_{H^{\frac{1}{2}}\left(\mathsf{\Gamma }\right)}\le C_2{\parallel \mathbf{f}\parallel }_{H^{\frac{1}{2}}\left({\mathsf{\Gamma }}_D\right)}$, where $C_1$, $C_2$ are positive constants. If we now denote by $\mathbf{w}$ the difference ${\mathbf{u}}^{sct}-{\mathbf{u}}_0$ we take,

$$\left({\Delta }^{*}+{\rho }_1{\omega }^2\right)\mathbf{w}\left(\mathbf{r}\right)={\Delta }^{*}{\mathbf{u}}^{sct}-{\Delta }^{*}{\mathbf{u}}_0+{\rho }_1{\omega }^2{\mathbf{u}}^{sct}-{\rho }_1{\omega }^2{\mathbf{u}}_0$$

(25)

and with the aid of ${\Delta }^{*}{\mathbf{u}}_0=\mathbf{0}inB$ and (9) we arrive at

$$\left({\Delta }^{*}+{\rho }_1{\omega }^2\right)\mathbf{w}\left(\mathbf{r}\right)=-{\rho }_1{\omega }^2{\mathbf{u}}_{0}inB.$$

(26)

After some manipulations, we also have the following boundary condition

$$T\mathbf{w}+i\omega \mathbf{w}=\mathbf{h}-\left(T{\mathbf{u}}_0+i\omega c{\mathbf{u}}_0\right),on{\mathsf{\Gamma }}_I$$

(27)

as well as the boundary condition

$$\mathbf{w}=\mathbf{0}on{\mathsf{\Gamma }}_D.$$

(28)

We mention here that relations (26)–(28) will be used for proving the stability of solution of our IMBVP (see later, p. 10).

In the sequel, our proof moves on with stability-existence results. Having in mind that $\mathbf{w}={\mathbf{u}}^{sct}-{\mathbf{u}}_0$, we will prove the following alternative form of the Equation (17)

$$\begin{array}{ccc}& & {\int }_B\left[\mathcal{E}(\overline{\mathbf{\varphi }},\mathbf{w})-{\rho }_1{\omega }^2\overline{\mathbf{\varphi }}·\mathbf{w}\right]d\upsilon +i\omega c{\int }_{{\mathsf{\Gamma }}_I}\overline{\mathbf{\varphi }}·\mathbf{w}ds\hfill \\ \hfill \\ & =& <\mathbf{h},\mathbf{\varphi }>-{\int }_{{\mathsf{\Gamma }}_I}\overline{\mathbf{\varphi }}·\left(T{\mathbf{u}}_0+i\omega c{\mathbf{u}}_0\right)ds\hfill \\ & & +{\int }_B{\rho }_1{\omega }^2\overline{\mathbf{\varphi }}·{\mathbf{u}}_{0}d\upsilon .\hfill \end{array}$$

(29)

Indeed, we make use of the following first generalised Betti’s formula:

$${\int }_B\overline{\mathbf{\varphi }}·{\Delta }^{*}{\mathbf{u}}_{0}d\upsilon ={\int }_{\partial B}\overline{\mathbf{\varphi }}·\mathbf{P}{\mathbf{u}}_{0}ds-{\int }_B\mathcal{E}(\overline{\mathbf{\varphi }},{\mathbf{u}}_0)d\upsilon$$

(30)

where ${\mathbf{Pu}}_0$ is the generalised stress vector on the boundary $\partial B$ defined, by [18]

$$\mathbf{P}{\mathbf{u}}_0=(\mu +\tilde{\alpha })\frac{\partial {\mathbf{u}}_0}{\partial \mathbf{n}}+\tilde{\beta }\widehat{\mathbf{n}}div{\mathbf{u}}_0-\tilde{\alpha }{\widehat{\mathbf{n}}}^{\perp }di{v}^{\perp }{\mathbf{u}}_0$$

(31)

with the differential operator $di{v}^{\perp }$ given as [18]

$$di{v}^{\perp }\mathbf{u}:=\frac{\partial u_1}{\partial r_2}-\frac{\partial u_2}{\partial r_1},\mathbf{u}\left(\mathbf{r}\right)\equiv (u_1\left(\mathbf{r}\right),u_2\left(\mathbf{r}\right)),\mathbf{r}=(r_1,r_2).$$

(32)

We point out that if we set $\tilde{\alpha }=\mu$ and $\tilde{\beta }=\lambda$, our surface stress vector $\mathbf{P}{\mathbf{u}}_0$ will be transformed to the physical stress vector $T{\mathbf{u}}_0=2\mu \frac{\partial {\mathbf{u}}_0}{\partial \widehat{\mathbf{n}}}+\lambda \widehat{\mathbf{n}}div{\mathbf{u}}_0-\mu {\widehat{\mathbf{n}}}^{\perp }di{v}^{\perp }{\mathbf{u}}_0$. Hence relation (30), via ${\Delta }^{*}{\mathbf{u}}_0=\mathbf{0}inB$, can be written as

$${\int }_B\mathcal{E}(\overline{\mathbf{\varphi }},{\mathbf{u}}_0)d\upsilon ={\int }_{{\mathsf{\Gamma }}_I\cup \Pi \cup {\mathsf{\Gamma }}_D}\left(2\mu \frac{\partial {\mathbf{u}}_0}{\partial \widehat{\mathbf{n}}}+\lambda \widehat{\mathbf{n}}div{\mathbf{u}}_0-\mu {\widehat{\mathbf{n}}}^{\perp }di{v}^{\perp }{\mathbf{u}}_0\right)·\overline{\mathbf{\varphi }}ds.$$

(33)

Taking into account that $\mathbf{\varphi }\in H_0^1(B,{\mathsf{\Gamma }}_I)$, the latter yields to

$${\int }_B\mathcal{E}(\overline{\mathbf{\varphi }},{\mathbf{u}}_0)d\upsilon ={\int }_{{\mathsf{\Gamma }}_I}\left(2\mu \frac{\partial {\mathbf{u}}_0}{\partial \mathbf{n}}+\lambda \widehat{\mathbf{n}}div{\mathbf{u}}_0-\mu {\widehat{\mathbf{n}}}^{\perp }di{v}^{\perp }{\mathbf{u}}_0\right)·\overline{\mathbf{\varphi }}ds.$$

(34)

The variational Equation (17), via (34) gives

$$\begin{array}{ccc}& & {\int }_B\left(\mathcal{E}(\overline{\mathbf{\varphi }},\mathbf{w})-{\rho }_1{\omega }^2\mathbf{w}·\overline{\mathbf{\varphi }}\right)d\upsilon +i\omega c{\int }_{{\mathsf{\Gamma }}_I}\mathbf{w}·\overline{\mathbf{\varphi }}ds\hfill \\ \hfill \\ & =& <\mathbf{h},\mathbf{\varphi }>-{\int }_{{\mathsf{\Gamma }}_I}(2\mu \frac{\partial {\mathbf{u}}_0}{\partial \mathbf{n}}+\lambda \mathbf{n}\nabla {\mathbf{u}}_0-\mu {\mathbf{n}}^{\perp }{\nabla }^{\perp }{\mathbf{u}}_0)·\overline{\mathbf{\varphi }}ds\hfill \\ \hfill \\ & & +{\int }_B{\rho }_1{\omega }^2{\mathbf{u}}_0·\overline{\mathbf{\varphi }}d\upsilon -i\omega c{\int }_{{\mathsf{\Gamma }}_I}{\mathbf{u}}_0·\overline{\mathbf{\varphi }}ds,\hfill \end{array}$$

(35)

where relation ${\mathbf{u}}^{sct}=\mathbf{w}+{\mathbf{u}}_0$ has been taken into account. Hence,

$$\begin{array}{ccc}& & {\int }_B\left(\mathcal{E}(\overline{\mathbf{\varphi }},\mathbf{w})-{\rho }_1{\omega }^2\mathbf{w}·\overline{\mathbf{\varphi }}\right)d\upsilon +i\omega c{\int }_{{\mathsf{\Gamma }}_I}\mathbf{w}·\overline{\mathbf{\varphi }}ds\hfill \\ \hfill \\ & =& <\mathbf{h},\mathbf{\varphi }>-{\int }_{{\mathsf{\Gamma }}_I}(T{\mathbf{u}}_0+i\omega c{\mathbf{u}}_0)·\overline{\mathbf{\varphi }}ds\hfill \\ & & +{\int }_B{\rho }_1{\omega }^2{\mathbf{u}}_0·\overline{\mathbf{\varphi }}d\upsilon .\hfill \end{array}$$

(36)

If we now define the following auxiliary operators:

$$\alpha (\mathbf{w},\mathbf{\varphi })={\int }_B\left(\mathcal{E}(\overline{\mathbf{\varphi }},\mathbf{w})-{\rho }_1{\omega }^2\mathbf{w}·\overline{\mathbf{\varphi }}\right)d\upsilon +i\omega c{\int }_{{\mathsf{\Gamma }}_I}\mathbf{w}·\overline{\mathbf{\varphi }}ds,$$

(37)

$$\ell \left(\mathbf{\varphi }\right)=<\mathbf{h},\mathbf{\varphi }>-\left({\int }_{{\mathsf{\Gamma }}_I}\left(T{\mathbf{u}}_0+i\omega c{\mathbf{u}}_0\right)·\overline{\mathbf{\varphi }}ds-{\int }_B{\rho }_1{\omega }^2{\mathbf{u}}_0·\overline{\mathbf{\varphi }}d\upsilon \right),$$

(38)

$${\alpha }_1(\mathbf{w},\mathbf{\varphi })={\int }_B\left(\mathcal{E}(\overline{\mathbf{\varphi }},\mathbf{w})+\mathbf{w}·\overline{\mathbf{\varphi }}\right)d\upsilon +i\omega c{\int }_{{\mathsf{\Gamma }}_I}\mathbf{w}·\overline{\mathbf{\varphi }}ds$$

(39)

and

$${\alpha }_2(\mathbf{w},\mathbf{\varphi })={\int }_B(-{\rho }_1{\omega }^2-1)\mathbf{w}·\overline{\mathbf{\varphi }}ds,$$

(40)

then, it can easily be seen that (36) arrives at:

$$\alpha (\mathbf{w},\mathbf{\varphi })={\alpha }_1(\mathbf{w},\mathbf{\varphi })+{\alpha }_2(\mathbf{w},\mathbf{\varphi }).$$

(41)

Via (37) and (38), it is obvious that

$$\alpha (\mathbf{w},\mathbf{\varphi })=\ell \left(\mathbf{\varphi }\right),$$

(42)

with $\ell \left(\mathbf{\varphi }\right)$ being a linear bounded conjugate function, and therefore

$${\alpha }_1(\mathbf{w},\mathbf{\varphi })+{\alpha }_2(\mathbf{w},\mathbf{\varphi })=\ell \left(\mathbf{\varphi }\right).$$

(43)

We also mention that although we have to deal with the complicated nature of $\mathcal{E}$ (given in (13)), we can easily prove that $\alpha (\mathbf{w},\mathbf{\varphi })$ is a sesquilinear form.

Following now similar steps as those in [19], we deal with the integral operator ${\alpha }_1(\mathbf{w},\mathbf{\varphi })$ given by (39), which for $\mathbf{\varphi }=\mathbf{w}$ arrives at

$${\alpha }_1(\mathbf{w},\mathbf{w})={\int }_B\left(\mathcal{E}(\overline{\mathbf{w}},\mathbf{w})+\mathbf{w}·\overline{\mathbf{w}}\right)d\upsilon +i\omega c{\int }_{{\mathsf{\Gamma }}_I}\mathbf{w}·\overline{\mathbf{w}}d\upsilon .$$

(44)

After some calculations, for $\mathbf{w}=(w_1,w_2)$ we can rewrite $\mathcal{E}(\mathbf{w},\mathbf{w})$ as

$$\begin{array}{c}\hfill \mathcal{E}(\mathbf{w},\mathbf{w})={\lambda |\nabla ·\mathbf{w}|}^2+\mu {\left(\frac{\partial w_1}{\partial x_1}\right)}^2+(\lambda +\mu )\left[{\left(\frac{\partial w_1}{\partial x_1}\right)}^2+{\left(\frac{\partial w_2}{\partial x_2}\right)}^2\right].\end{array}$$

(45)

From the latter, $\mathcal{E}(\mathbf{w},\mathbf{w})$ is non-negative and using (44) we arrive at

$$|{\alpha }_1(\mathbf{w},\mathbf{w})|=|{\int }_B\left({\lambda |\nabla ·\mathbf{w}|}^2+{|\mathbf{w}|}^2\right)d\upsilon +M+{i\omega c\parallel \mathbf{w}\parallel }_{L^2\left({\mathsf{\Gamma }}_I\right)}^2|,$$

(46)

where

$$M={\int }_B\left(\mu {\left(\frac{\partial w_1}{\partial x_2}+\frac{\partial w_2}{\partial x_1}\right)}^2+(\lambda +\mu )\left[{\left(\frac{\partial w_1}{\partial x_1}\right)}^2+{\left(\frac{\partial w_2}{\partial x_2}\right)}^2\right]\right)d\upsilon .$$

(47)

After some manipulations in (46), we also have the following

$$|{\alpha }_1(\mathbf{w},\mathbf{w})|\ge \lambda {\int }_B{|\nabla ·\mathbf{w}|}^{2}d\upsilon +{\int }_B{|\mathbf{w}|}^{2}d\upsilon .$$

(48)

We denote as a constant $c^{\prime }=min\{\lambda ,1\}$ (which is a positive constant) and hence,

$$|{\alpha }_1(\mathbf{w},\mathbf{w})|\ge c^{\prime }{\{\parallel \nabla \mathbf{w}\parallel }_{L^2\left(B\right)}^2+{\parallel \mathbf{w}\parallel }_{L^2\left(B\right)}^2\}.$$

(49)

From the latter inequality we get

$$|{\alpha }_1(\mathbf{w},\mathbf{w})|\ge c^{\prime }{\parallel \mathbf{w}\parallel }_{H^1\left(B\right)}^2,$$

(50)

and therefore, the functional ${\alpha }_1$ is strictly coercive.

Next we deal with the boundedness of the functional $\ell \left(\mathbf{\varphi }\right)$. Using (38) we have

$$|\ell \left(\mathbf{\varphi }\right)|=|<\mathbf{h},\mathbf{\varphi }>-\left({\int }_{{\mathsf{\Gamma }}_I}\left(T{\mathbf{u}}_0+i\omega c{\mathbf{u}}_0\right)·\overline{\mathbf{\varphi }}ds-{\int }_B{\rho }_1{\omega }^2{\mathbf{u}}_0·\overline{\mathbf{\varphi }}d\upsilon \right)|.$$

(51)

If we now consider in (51) the Cauchy–Schwartz inequality and some calculations, we arrive at

$$\begin{array}{ccc}\hfill |\ell (\mathbf{\varphi })|& \le & {\parallel \mathbf{h}\parallel }_{H^{\frac{1}{2}}\left(\mathsf{\Gamma }\right)}{\parallel \mathbf{\varphi }\parallel }_{H^{\frac{1}{2}}\left(\mathsf{\Gamma }\right)}+\parallel T{\mathbf{u}}_0{\parallel }_{H^{\frac{1}{2}}\left(\mathsf{\Gamma }\right)}{\parallel \mathbf{\varphi }\parallel }_{H^{\frac{1}{2}}\left(\mathsf{\Gamma }\right)}\hfill \\ \hfill \\ & & +|i\omega c|\parallel {\mathbf{u}}_0{\parallel }_{H^{\frac{1}{2}}\left(\mathsf{\Gamma }\right)}{\parallel \mathbf{\varphi }\parallel }_{H^{\frac{1}{2}}\left(\mathsf{\Gamma }\right)}\hfill \\ \hfill \\ & & +|{\rho }_1{\omega }^2|\parallel {\mathbf{u}}_0{\parallel }_{H^1\left(B\right)}{\parallel \mathbf{\varphi }\parallel }_{H^1\left(B\right)}.\hfill \end{array}$$

(52)

Hence, from the fact that T is bounded, i.e., there exists a positive constant $\tilde{c}$ such that $\parallel T{\mathbf{u}}_0{\parallel }_{H^{\frac{1}{2}}\left(\mathsf{\Gamma }\right)}\le \tilde{c}{\parallel {\mathbf{u}}_0\parallel }_{H^{\frac{1}{2}}\left(\mathsf{\Gamma }\right)}$, we can get

$$\begin{array}{ccc}\hfill |\ell (\mathbf{\varphi })|& \le & {\parallel \mathbf{h}\parallel }_{H^{\frac{1}{2}}\left(\mathsf{\Gamma }\right)}{\parallel \mathbf{\varphi }\parallel }_{H^{\frac{1}{2}}\left(\mathsf{\Gamma }\right)}+\tilde{c}\parallel {\mathbf{u}}_0{\parallel }_{H^{\frac{1}{2}}\left(\mathsf{\Gamma }\right)}{\parallel \mathbf{\varphi }\parallel }_{H^{\frac{1}{2}}\left(\mathsf{\Gamma }\right)}\hfill \\ \hfill \\ & & +|i\omega c|\parallel {\mathbf{u}}_0{\parallel }_{H^{\frac{1}{2}}\left(\mathsf{\Gamma }\right)}{\parallel \mathbf{\varphi }\parallel }_{H^{\frac{1}{2}}\left(\mathsf{\Gamma }\right)}\hfill \\ \hfill \\ & & +|{\rho }_1{\omega }^2|\parallel {\mathbf{u}}_0{\parallel }_{H^1\left(B\right)}{\parallel \mathbf{\varphi }\parallel }_{H^1\left(B\right)},\hfill \end{array}$$

(53)

and finally,

$$\begin{array}{ccc}\hfill |\ell (\mathbf{\varphi })|& \le & {\parallel \mathbf{h}\parallel }_{H^{\frac{1}{2}}\left(\mathsf{\Gamma }\right)}{\parallel \mathbf{\varphi }\parallel }_{H^{\frac{1}{2}}\left(\mathsf{\Gamma }\right)}+(\tilde{c}+|i\omega c|)\parallel {\mathbf{u}}_0{\parallel }_{H^{\frac{1}{2}}\left(\mathsf{\Gamma }\right)}{\parallel \mathbf{\varphi }\parallel }_{H^{\frac{1}{2}}\left(\mathsf{\Gamma }\right)}\hfill \\ \hfill \\ & & +|{\rho }_1{\omega }^2|\parallel {\mathbf{u}}_0{\parallel }_{H^1\left(B\right)}{\parallel \mathbf{\varphi }\parallel }_{H^1\left(B\right)}.\hfill \end{array}$$

(54)

Therefore, there exist positive constants $c_1,c_2,c_3$ such that

$$\begin{array}{ccc}\hfill |\ell (\mathbf{\varphi })|& \le & c_1{\parallel \mathbf{h}\parallel }_{H^{-\frac{1}{2}}\left({\mathsf{\Gamma }}_I\right)}{\parallel \mathbf{\varphi }\parallel }_{{\tilde{H}}^{\frac{1}{2}}\left({\mathsf{\Gamma }}_I\right)}+c_2\parallel {\mathbf{u}}_0{\parallel }_{H^{\frac{1}{2}}\left({\mathsf{\Gamma }}_I\right)}{\parallel \mathbf{\varphi }\parallel }_{{\tilde{H}}^{\frac{1}{2}}\left({\mathsf{\Gamma }}_I\right)}\hfill \\ \hfill \\ & & +c_3\parallel {\mathbf{u}}_0{\parallel }_{H^{\frac{1}{2}}\left({\mathsf{\Gamma }}_D\right)}{\parallel \mathbf{\varphi }\parallel }_{H^1\left(B\right)}.\hfill \end{array}$$

(55)

After some calculations, we arrive at

$${\parallel \ell \left(\mathbf{\varphi }\right)\parallel }_{H^1\left(B\right)}\le C^{\prime }{(\parallel \mathbf{h}\parallel }_{H^{-\frac{1}{2}}\left({\mathsf{\Gamma }}_I\right)}+{\parallel \mathbf{f}\parallel }_{H^{\frac{1}{2}}\left({\mathsf{\Gamma }}_D\right)}{)\parallel \mathbf{\varphi }\parallel }_{H^1\left(B\right)},$$

(56)

for some positive constant $C^{\prime }$ and therefore ℓ is bounded. Having in mind that $\alpha =\ell$ (see (42)), we have that

$${\parallel \alpha \parallel }_{H^1\left(B\right)}\le C^{\prime }{(\parallel \mathbf{h}\parallel }_{H^{-\frac{1}{2}}\left({\mathsf{\Gamma }}_I\right)}+{\parallel \mathbf{f}\parallel }_{H^{\frac{1}{2}}\left({\mathsf{\Gamma }}_D\right)}),$$

(57)

and applying the Riesz representation theorem, we get

$${\parallel \mathbf{w}\parallel }_{H^1\left(B\right)}\le C^{\prime }{(\parallel \mathbf{h}\parallel }_{H^{-\frac{1}{2}}\left({\mathsf{\Gamma }}_I\right)}+{\parallel \mathbf{f}\parallel }_{H^{\frac{1}{2}}\left({\mathsf{\Gamma }}_D\right)}).$$

(58)

Since now ${\mathbf{u}}^{sct}=\mathbf{w}+{\mathbf{u}}_0$, we take

$$\parallel {\mathbf{u}}^{sct}{\parallel }_{H^1\left(B\right)}\le {\parallel \mathbf{w}\parallel }_{H^1\left(B\right)}+{\parallel {\mathbf{u}}_0\parallel }_{H^1\left(B\right)},$$

(59)

and the latter via (58), gives

$$\parallel {\mathbf{u}}^{sct}{\parallel }_{H^1\left(B\right)}\le {\tilde{c}}_1\left({\parallel \mathbf{h}\parallel }_{H^{-\frac{1}{2}}\left({\mathsf{\Gamma }}_I\right)}+{\parallel \mathbf{f}\parallel }_{H^{\frac{1}{2}}\left({\mathsf{\Gamma }}_D\right)}+{\parallel {\mathbf{u}}_0\parallel }_{H^1\left(B\right)}\right)$$

(60)

for some positive constant ${\tilde{c}}_1$. Using now the trace theorem [20], there exists a positive constant C such that

$$\parallel {\mathbf{u}}^{sct}{\parallel }_{H^1\left(B\right)}\le {C(\parallel \mathbf{h}\parallel }_{H^{-\frac{1}{2}}\left({\mathsf{\Gamma }}_I\right)}+{\parallel \mathbf{f}\parallel }_{H^{\frac{1}{2}}\left({\mathsf{\Gamma }}_D\right)}).$$

(61)

Finally, combining the previous results with the above inequality and using the Lax–Milgram theorem [4] our proof is completed. □

4. The Inverse Problem

In this section we address the inverse scattering problem concerning partially coated obstacles which are bounded and simply connected domains in ${\mathbb{R}}^2$. Our aim is to recover the shape of the partially coated scatterer B from the knowledge of the near field data ${\mathbf{u}}^{sct}\left(\mathbf{r}\right),\mathbf{r}\in C$ due to the point source ${\mathbf{u}}_{r_0}^{inc}\left(\mathbf{r}\right)\equiv \tilde{\mathsf{\Gamma }}(·,{\mathbf{r}}_0),{\mathbf{r}}_0\in C$ (see (1)).

The latter is mathematically modelled by the following interior mixed boundary value problem:

$$\begin{array}{ccc}& & ({\Delta }^{*}+{\rho }_1{\omega }^2){\mathbf{u}}^{tot}\left(\mathbf{r}\right)=\mathbf{0},\mathbf{r}\in B\hfill \\ \hfill \end{array}$$

(62)

$$\begin{array}{ccc}& & {\mathbf{u}}^{tot}\left(\mathbf{r}\right)=\mathbf{0},\mathbf{r}\in {\mathsf{\Gamma }}_D\hfill \\ \hfill \end{array}$$

(63)

$$\begin{array}{ccc}& & T{\mathbf{u}}^{tot}\left(\mathbf{r}\right)+i\omega c{\mathbf{u}}^{tot}\left(\mathbf{r}\right)=\mathbf{0},\mathbf{r}\in {\mathsf{\Gamma }}_I,\hfill \end{array}$$

(64)

where ${\mathbf{u}}^{tot}\left(\mathbf{r}\right)={\mathbf{u}}_{r_0}^{inc}\left(\mathbf{r}\right)+{\mathbf{u}}^{sct}\left(\mathbf{r}\right)$, ${\rho }_1$ is the mass density in B and $c>0$ the surface impedance. The problem (62)–(64) is actually the problem (9)–(11)written this time in terms of the total displacement field ${\mathbf{u}}^{tot}$. The mixed partially coated obstacle B and its boundary $\mathsf{\Gamma }$ can be uniquely determined; the proof is omitted for brevity since it can be exploited if we consider minor modifications as those used in [15].

The Modified Factorization Method

In the sequel, we will follow the basic ideas arising from the factorization method, in order to recover the boundary of the non-penetrable partially coated obstacle B. These ideas have been used widely, mostly in various inverse-acoustic and electromagnetic scattering problems [4,21]. For inverse elastic scattering problems, factorization method has also been employed [15,22], and in this work we will exploit a modification of the factorization method concerning the shape recovering of the scatterer B.

Initially, we introduce the near−field operator $\mathcal{N}:{\left[L^2\left(C\right)\right]}^2\to \left[L^2\left(C\right)\right]$ defined as:

$$\left(\mathcal{N}\mathbf{b}\right)\left(\mathbf{r}\right)={\int }_C{\mathbf{u}}^{sct}\left(\mathbf{r}\right)·\mathbf{b}\left({\mathbf{r}}_0\right)ds\left({\mathbf{r}}_0\right),\mathbf{r}\in C.$$

(65)

The factorization method requires the following decomposition

$$\mathcal{N}={\tilde{\mathcal{H}}}^{*}\mathcal{M}\tilde{\mathcal{H}},$$

(66)

where the operator $\tilde{\mathcal{H}}={({\mathbf{H}}_{\mathbf{1}},{\mathbf{H}}_{\mathbf{2}})}^{\top }:{\left[L^2\left(C\right)\right]}^2\to {\left[H^{\frac{1}{2}}\left({\mathsf{\Gamma }}_D\right)\right]}^2\times {\left[H^{-\frac{1}{2}}\left({\mathsf{\Gamma }}_I\right)\right]}^2$ is given by

$${\mathbf{H}}_{\mathbf{1}}\mathbf{b}={\mathbf{\upsilon }}_{\mathbf{b}}{{|}_{{\mathsf{\Gamma }}_D},{\mathbf{H}}_{\mathbf{2}}\mathbf{b}=(T+i\omega c){\mathbf{\upsilon }}_{\mathbf{b}}|}_{{\mathsf{\Gamma }}_I},$$

(67)

${\mathbf{\upsilon }}_{\mathbf{b}}$ is a single-layer potential of the form

$${\mathbf{\upsilon }}_{\mathbf{b}}={\int }_C\tilde{\mathsf{\Gamma }}(\mathbf{r},{\mathbf{r}}_0)\mathbf{b}\left({\mathbf{r}}_0\right)ds\left({\mathbf{r}}_0\right),$$

(68)

($\mathbf{b}\in {\left[L^2\left(C\right)\right]}^2$ the density function), and ${\tilde{\mathcal{H}}}^{*}$ is the adjoint operator of $\tilde{\mathcal{H}}$ (operator $\mathcal{M}$ will be given shortly (see p. 13)). For the decomposition of $\mathcal{N}$, we also need to define a boundary data-to-near filed data operator:

$$\mathbf{G}:{\left[H^{\frac{1}{2}}\left({\mathsf{\Gamma }}_D\right)\right]}^2\times {\left[H^{-\frac{1}{2}}\left({\mathsf{\Gamma }}_I\right)\right]}^2\to {\left[L^2\left(C\right)\right]}^2,$$

(69)

such that

$$\mathbf{G}\left(\mathbf{f}\left(\mathbf{r}\right),\mathbf{h}\left(\mathbf{r}\right)\right)={\mathbf{u}}^{sct}\left(\mathbf{r}\right){\mid }_C.$$

(70)

Taking into account operator $\tilde{\mathcal{H}}$, we now get

$$\mathbf{G}\left(\tilde{\mathcal{H}}\mathbf{b}\right)=\mathbf{G}({\mathbf{\upsilon }}_{\mathbf{b}}{|}_{{\mathsf{\Gamma }}_D},(T+i\omega c){\mathbf{\upsilon }}_{\mathbf{b}}{|}_{{\mathsf{\Gamma }}_I}).$$

(71)

Using the single layer potential and the relation

$$\tilde{\mathsf{\Gamma }}(\mathbf{r},{\mathbf{r}}_0)\equiv {\mathbf{u}}_{r_0}^{inc}\left(\mathbf{r}\right)={\mathbf{u}}^{tot}(\mathbf{r},{\mathbf{r}}_0)-{\mathbf{u}}^{sct}\left(\mathbf{r}\right),$$

(72)

we take

$$\begin{array}{ccc}\hfill -\mathbf{G}\left(\tilde{\mathcal{H}}\mathbf{b}\right)\left(\mathbf{r}\right)& =& -\mathbf{G}({\mathbf{H}}_{\mathbf{1}}\mathbf{b},{\mathbf{H}}_{\mathbf{2}}\mathbf{b})\hfill \\ \hfill \\ & =& -\mathbf{G}\left({\int }_C\tilde{\mathsf{\Gamma }}(\mathbf{r},{\mathbf{r}}_0)\mathbf{b}\left({\mathbf{r}}_0\right)ds\left({\mathbf{r}}_0\right),(T+i\omega c){\int }_C\tilde{\mathsf{\Gamma }}(\mathbf{r},{\mathbf{r}}_0)\mathbf{b}\left({\mathbf{r}}_0\right)ds\left({\mathbf{r}}_0\right)\right)\hfill \\ \hfill \\ & =& -\mathbf{G}\left(-{\int }_C\mathbf{f}\left(\mathbf{r}\right)·\mathbf{b}\left({\mathbf{r}}_0\right)ds\left({\mathbf{r}}_0\right){\mid }_{{\mathsf{\Gamma }}_D},-{\int }_C\mathbf{h}\left(\mathbf{r}\right)·\mathbf{b}\left({\mathbf{r}}_0\right)ds\left({\mathbf{r}}_0\right){\mid }_{{\mathsf{\Gamma }}_I}\right),\hfill \end{array}$$

(73)

and therefore

$$-\mathbf{G}\tilde{\mathcal{H}}\mathbf{b}\left(\mathbf{r}\right)=-\mathbf{G}\left(-{\int }_C\mathbf{f}\left(\mathbf{r}\right)·\mathbf{b}\left({\mathbf{r}}_0\right)ds\left({\mathbf{r}}_0\right){\mid }_{{\mathsf{\Gamma }}_D},-{\int }_C\mathbf{h}\left(\mathbf{r}\right)·\mathbf{b}\left({\mathbf{r}}_0\right)ds\left({\mathbf{r}}_0\right){\mid }_{{\mathsf{\Gamma }}_I}\right).$$

(74)

We now consider the continuous by zero expansion ${\mathbf{f}}_{ext},{\mathbf{h}}_{ext}$ of $\mathbf{f}$ and $\mathbf{h}$, respectively, upon $\mathsf{\Gamma }$, i.e.,

$${\mathbf{f}}_{ext}\left(\mathbf{r}\right){\mid }_{{\mathsf{\Gamma }}_D}=\mathbf{f}\left(\mathbf{r}\right),{\mathbf{h}}_{ext}\left(\mathbf{r}\right){\mid }_{{\mathsf{\Gamma }}_I}=\mathbf{h}\left(\mathbf{r}\right)$$

(75)

and by (74) we have

$$-\mathbf{G}\tilde{\mathcal{H}}\mathbf{b}\left(\mathbf{r}\right)=-\mathbf{G}\left({\int }_C{\mathbf{f}}_{ext}\left(\mathbf{r}\right)·\mathbf{b}\left({\mathbf{r}}_0\right)ds\left({\mathbf{r}}_0\right){{|}_{\partial B},-{\int }_C{\mathbf{h}}_{ext}\left(\mathbf{r}\right)·\mathbf{b}\left({\mathbf{r}}_0\right)ds\left({\mathbf{r}}_0\right)|}_{\partial B}\right),$$

(76)

hence,

$$-\left(\mathbf{G}\tilde{\mathcal{H}}\right)\mathbf{b}\left(\mathbf{r}\right)={\int }_C{\mathbf{u}}^{sct}\left(\mathbf{r}\right)·\mathbf{b}\left({\mathbf{r}}_0\right)ds\left({\mathbf{r}}_0\right).$$

(77)

Combining (65) and (77) the following factorization for near-field operator $\mathcal{N}$ holds:

$$\left(\mathcal{N}\mathbf{b}\right)\left(\mathbf{r}\right)=-\left(\mathbf{G}\tilde{\mathcal{H}}\mathbf{b}\right)\left(\mathbf{r}\right),$$

(78)

or, in equivalent form

$$\mathcal{N}=-\mathbf{G}\tilde{\mathcal{H}}.$$

(79)

In the sequel, we will calculate and find the adjoint operator of $\tilde{\mathcal{H}}$. Let $(\mathbf{p}\left(\mathbf{r}\right),\mathbf{q}\left(\mathbf{r}\right))\in {[{\tilde{H}}^{-\frac{1}{2}}\left({\mathsf{\Gamma }}_D\right)]}^2\times {[{\tilde{H}}^{\frac{1}{2}}\left({\mathsf{\Gamma }}_I\right)]}^2$ and $\mathbf{b}\left(\mathbf{r}\right)\in {\left[L^2\left(C\right)\right]}^2$. Then

$$\begin{array}{ccc}\hfill <\tilde{\mathcal{H}}\mathbf{b},(\mathbf{p},\mathbf{q})>& =& {\int }_C\mathbf{b}\left(\mathbf{r}\right)·{\int }_{{\mathsf{\Gamma }}_D}\mathbf{p}\left(\mathbf{r}\right)\overline{\tilde{\mathsf{\Gamma }}(\mathbf{r},{\mathbf{r}}_0)}ds\left(\mathbf{r}\right)ds\left({\mathbf{r}}_0\right)\hfill \\ \hfill \\ \hfill & & +{\int }_C\mathbf{b}\left(\mathbf{r}\right)·{\int }_{{\mathsf{\Gamma }}_I}\mathbf{q}\left(\mathbf{r}\right)(T-i\omega c)\overline{\tilde{\mathsf{\Gamma }}(\mathbf{r},{\mathbf{r}}_0)}ds\left(\mathbf{r}\right)ds\left({\mathbf{r}}_0\right)\hfill \\ \hfill \\ & =& <\mathbf{b},{\tilde{\mathcal{H}}}^{*}(\mathbf{p},\mathbf{q})>.\hfill \end{array}$$

(80)

After some calculations we end up with adjoint operator ${\tilde{\mathcal{H}}}^{*}$, given by

$${\tilde{\mathcal{H}}}^{*}(\mathbf{p},\mathbf{q})\left(\mathbf{r}\right)={\int }_{{\mathsf{\Gamma }}_D}\mathbf{p}\left(\mathbf{r}\right)\overline{\tilde{\mathsf{\Gamma }}(\mathbf{r},{\mathbf{r}}_0)}ds\left({\mathbf{r}}_0\right)+{\int }_{{\mathsf{\Gamma }}_I}\mathbf{q}\left(\mathbf{r}\right)(T-i\omega c)\overline{\tilde{\mathsf{\Gamma }}(\mathbf{r},{\mathbf{r}}_0)}ds\left({\mathbf{r}}_0\right).$$

(81)

In addition, we define a combination of single and double layer potential $\mathbf{V}$, written as:

$$\mathbf{V}\left(\mathbf{r}\right):={\int }_{\mathsf{\Gamma }}{\mathbf{p}}_{ext}\left({\mathbf{r}}_0\right)\overline{\tilde{\mathsf{\Gamma }}(\mathbf{r},{\mathbf{r}}_0)}ds\left({\mathbf{r}}_0\right)+{\int }_{\mathsf{\Gamma }}{\mathbf{q}}_{ext}\left({\mathbf{r}}_0\right)(T-i\omega c)\overline{\tilde{\mathsf{\Gamma }}(\mathbf{r},{\mathbf{r}}_0)}ds\left({\mathbf{r}}_0\right),$$

(82)

where $({\mathbf{p}}_{ext},{\mathbf{q}}_{ext})\in {[H^{-\frac{1}{2}}\left(\mathsf{\Gamma }\right)]}^2\times {[H^{\frac{1}{2}}\left(\mathsf{\Gamma }\right)]}^2$. We now want to find the jump relation of $\mathbf{V}\left(\mathbf{r}\right)$ when $\mathbf{r}$ approaches the boundary $\mathsf{\Gamma }$ from the inside of the domain B. Using the jump relation of the single and double layer potential [18], we arrive at

$$\begin{array}{ccc}\hfill {\mathbf{V}\left(\mathbf{r}\right)|}_{{\mathbf{r}}^{-}\to \mathsf{\Gamma }}& =& {\int }_{\mathsf{\Gamma }}{\mathbf{p}}_{ext}\left({\mathbf{r}}_0\right)\overline{\tilde{\mathsf{\Gamma }}(\mathbf{r},{\mathbf{r}}_0)}ds\left({\mathbf{r}}_0\right)\hfill \\ \hfill \\ & & +{\int }_{\mathsf{\Gamma }}{\mathbf{q}}_{ext}\left({\mathbf{r}}_0\right)(T-i\omega c)\overline{\tilde{\mathsf{\Gamma }}(\mathbf{r},{\mathbf{r}}_0)}ds\left({\mathbf{r}}_0\right)-{\mathbf{q}}_{ext}\left(\mathbf{r}\right).\hfill \end{array}$$

(83)

In a similar way, we can get the jump relation for ${(T+i\omega c)\mathbf{V}\left(\mathbf{r}\right)|}_{{\mathbf{r}}^{-}\to \mathsf{\Gamma }}$ in the form

$$\begin{array}{ccc}\hfill & & {(T+i\omega c)\mathbf{V}\left(\mathbf{r}\right)|}_{{\mathbf{r}}^{-}\to \mathsf{\Gamma }}\hfill \\ \hfill \\ & =& T\left[{\int }_{\mathsf{\Gamma }}{\mathbf{p}}_{ext}\left({\mathbf{r}}_0\right)\overline{\tilde{\mathsf{\Gamma }}(\mathbf{r},{\mathbf{r}}_0)}ds\left({\mathbf{r}}_0\right)+{\int }_{\mathsf{\Gamma }}{\mathbf{q}}_{ext}\left({\mathbf{r}}_0\right)(T-i\omega c)\overline{\tilde{\mathsf{\Gamma }}(\mathbf{r},{\mathbf{r}}_0)}ds\left({\mathbf{r}}_0\right)\right]\hfill \\ & & +i\omega c\left[{\mathbf{p}}_{ext}\left({\mathbf{r}}_0\right)\overline{\tilde{\mathsf{\Gamma }}(\mathbf{r},{\mathbf{r}}_0)}ds\left({\mathbf{r}}_0\right)+{\int }_{\mathsf{\Gamma }}{\mathbf{q}}_{ext}\left({\mathbf{r}}_0\right)(T-i\omega c)\overline{\tilde{\mathsf{\Gamma }}(\mathbf{r},{\mathbf{r}}_0)}ds\left({\mathbf{r}}_0\right)\right]\hfill \\ \hfill \\ & & +{\mathbf{p}}_{ext}\left(\mathbf{r}\right)-2i\omega c{\mathbf{q}}_{ext}\left(\mathbf{r}\right).\hfill \end{array}$$

(84)

For our decomposition analysis, it is necessary to define the following boundary integral operators $S,K,K^{\prime }$ and $\mathsf{\Lambda }$ as (their properties and details can be found in [23]):

$$\begin{array}{ccc}& & S\mathbf{g}\left(\mathbf{r}\right):={\int }_{\mathsf{\Gamma }}\overline{\tilde{\mathsf{\Gamma }}(\mathbf{r},{\mathbf{r}}_0;\mathit{p})}·\mathbf{g}\left({\mathbf{r}}_0\right)ds\left({\mathbf{r}}_0\right),\mathbf{r}\in \mathsf{\Gamma }\hfill \end{array}$$

(85)

$$\begin{array}{ccc}& & K\mathbf{g}\left(\mathbf{r}\right):={\int }_{\mathsf{\Gamma }}{T}^{\left({\mathbf{r}}_0\right)}\overline{\tilde{\mathsf{\Gamma }}(\mathbf{r},{\mathbf{r}}_0;\mathit{p})}·\mathbf{g}\left({\mathbf{r}}_0\right)ds\left({\mathbf{r}}_0\right),\mathbf{r}\in \mathsf{\Gamma }\hfill \end{array}$$

(86)

$$\begin{array}{ccc}& & K^{\prime }\mathbf{g}\left(\mathbf{r}\right):={\int }_{\mathsf{\Gamma }}{T}^{\left(\mathbf{r}\right)}\overline{\tilde{\mathsf{\Gamma }}(\mathbf{r},{\mathbf{r}}_0;\mathit{p})}·\mathbf{g}\left({\mathbf{r}}_0\right)ds\left({\mathbf{r}}_0\right),\mathbf{r}\in \mathsf{\Gamma }\hfill \end{array}$$

(87)

$$\begin{array}{ccc}& & \mathsf{\Lambda }\mathbf{g}\left(\mathbf{r}\right):=T^{\left(\mathbf{r}\right)}{\int }_{\mathsf{\Gamma }}{T}^{\left({\mathbf{r}}_0\right)}\overline{\tilde{\mathsf{\Gamma }}(\mathbf{r},{\mathbf{r}}_0;\mathit{p})}·\mathbf{g}\left({\mathbf{r}}_0\right)ds\left({\mathbf{r}}_0\right),\mathbf{r}\in \mathsf{\Gamma }\hfill \end{array}$$

(88)

where $\mathit{p}\in S^1=\{\mathbf{d}\in {\mathbb{R}}^2:|\mathbf{d}|=1\}$ denotes the polarization vector of an elastic point source at any ${\mathbf{r}}_0\in {\mathbb{R}}^2$ (see (1)), and in particular we consider ${\mathbf{u}}_{r_0}^{inc}\left(\mathbf{r}\right)=\tilde{\mathsf{\Gamma }}(\mathbf{r},{\mathbf{r}}_0)·\mathit{p}\equiv \tilde{\mathsf{\Gamma }}(\mathbf{r},{\mathbf{r}}_0;\mathit{p}).$ In this way we avoid the dyadic nature of the fundamental solution, and in relations (85)–(88) the vector $\mathit{p}$ plays the role of an argument rather than a variable.

We can now consider (83) and (84) restricted on ${\mathsf{\Gamma }}_D$ and ${\mathsf{\Gamma }}_I$ respectively, due to the following matrix integral form (recall that ${\mathbf{p}}_{ext}{{|}_{{\mathsf{\Gamma }}_I}=\mathbf{0},{\mathbf{q}}_{ext}|}_{{\mathsf{\Gamma }}_D}=\mathbf{0}$)

$$\left(\begin{array}{c}{\mathbf{V}|}_{{\mathbf{r}}^{-}\to {\mathsf{\Gamma }}_D}\\ \\ (T^{\left(\mathbf{r}\right)}+i\omega c){\mathbf{V}|}_{{\mathbf{r}}^{-}\to {\mathsf{\Gamma }}_I}\end{array}\right)=\mathcal{M}\left(\begin{array}{c}\mathbf{p}\\ \\ \mathbf{q}\end{array}\right).$$

(89)

In (89), and after some computational effort, the integral operator $\mathcal{M}$ is found to be

$$\mathcal{M}=\left(\begin{array}{cc}{S}_{{\mathsf{\Gamma }}_D}{|}_{{\mathsf{\Gamma }}_D}& {(K-i\omega cS)}_{{\mathsf{\Gamma }}_I}{|}_{{\mathsf{\Gamma }}_D}\\ \\ {(K^{\prime }+i\omega cS)}_{{\mathsf{\Gamma }}_D}{|}_{{\mathsf{\Gamma }}_I}& {(\mathsf{\Lambda }-i\omega c{K}^{\prime }+i\omega cK+{\omega }^2{c}^{2}S-2i\omega I)}_{{\mathsf{\Gamma }}_I}{|}_{{\mathsf{\Gamma }}_I}\end{array}\right).$$

(90)

The latter in combination with (70) and (81) lead to

$$\mathbf{G}\mathcal{M}\left(\begin{array}{c}\mathbf{p}\\ \\ \mathbf{q}\end{array}\right)={\tilde{\mathcal{H}}}^{*}(\mathbf{p},\mathbf{q}).$$

(91)

In the sequel, we prove the following.

Theorem 2.

Assume that ${\omega }^2$ is not an eigenvalue of $-{\Delta }^{*}$ in $B_0$, then

(i) 

For the integral operator $\mathcal{M}$ we have

$$Im\{<\mathcal{M}(\mathbf{p},\mathbf{q}),(\mathbf{p},\mathbf{q})>\}<0,$$

(92)

for any $(\mathbf{p},\mathbf{q})\in {\left[H^{-\frac{1}{2}}\left({\mathsf{\Gamma }}_D\right)\right]}^2\times {\left[{\tilde{H}}^{\frac{1}{2}}\left({\mathsf{\Gamma }}_I\right)\right]}^2$ and $(\mathbf{p},\mathbf{q})\ne (\mathbf{0},\mathbf{0})$.

(ii) 

The bilinear matrix operator $\mathcal{M}$ is invertible.

Proof. 

(i)

Using the integral operator $\mathcal{M}$ and its linchpin with matrix Equation (89) we have:

$$<\mathcal{M}(\mathbf{p},\mathbf{q}),(\mathbf{p},\mathbf{q})>={\int }_{{\mathsf{\Gamma }}_D}{\mathbf{V}}^{-}·\overline{\mathbf{p}}ds\left({\mathbf{r}}_0\right)+{\int }_{{\mathsf{\Gamma }}_I}(T^{\left(\mathbf{r}\right)}+i\omega c){\mathbf{V}}^{-}·\overline{\mathbf{q}}ds\left({\mathbf{r}}_0\right).$$

(93)

From expressions (83) and (84), taking into account (82) and after some calculations we find

$$\begin{array}{ccc}& & \mathbf{p}=-\frac{1}{2}(T{\mathbf{V}}^{+}-T{\mathbf{V}}^{-}){|}_{{\mathsf{\Gamma }}_D}\hfill \\ \hfill \end{array}$$

(94)

$$\begin{array}{ccc}& & \mathbf{q}=\frac{1}{2}({\mathbf{V}}^{+}-{\mathbf{V}}^{-}){|}_{{\mathsf{\Gamma }}_I}\hfill \end{array}$$

(95)

and

$$\begin{array}{ccc}& & ({\mathbf{V}}^{+}-{\mathbf{V}}^{-}){|}_{{\mathsf{\Gamma }}_D}=\mathbf{0}\hfill \\ \hfill \end{array}$$

(96)

$$\begin{array}{ccc}& & 2i\omega c\mathbf{q}=(T{\mathbf{V}}^{+}-T{\mathbf{V}}^{-}){|}_{{\mathsf{\Gamma }}_I}.\hfill \end{array}$$

(97)

Taking into account (93) we have

$$\begin{array}{ccc}& & <\mathcal{M}(\mathbf{p},\mathbf{q}),(\mathbf{p},\mathbf{q})>\hfill \\ \hfill \\ & =& -\frac{1}{2}{\int }_{{\mathsf{\Gamma }}_D}{\mathbf{V}}^{-}·(T^{\left(\mathbf{r}\right)}\overline{{\mathbf{V}}^{+}}-T^{\left(\mathbf{r}\right)}\overline{{\mathbf{V}}^{-}})ds\left({\mathbf{r}}_0\right)\hfill \\ \hfill \\ & & +\frac{1}{2}{\int }_{{\mathsf{\Gamma }}_I}(\overline{{\mathbf{V}}^{+}}-\overline{{\mathbf{V}}^{-}})·(T^{\left(\mathbf{r}\right)}{\mathbf{V}}^{-}+i\omega c{\mathbf{V}}^{-})ds\left({\mathbf{r}}_0\right)\hfill \\ \hfill \\ & =& -\frac{1}{2}{\int }_{{\mathsf{\Gamma }}_D}({\mathbf{V}}^{+}·T^{\left(\mathbf{r}\right)}\overline{{\mathbf{V}}^{+}}-{\mathbf{V}}^{-}·T^{\left(\mathbf{r}\right)}\overline{{\mathbf{V}}^{-}})ds\left({\mathbf{r}}_0\right)\hfill \\ \\ & & +\frac{1}{2}{\int }_{{\mathsf{\Gamma }}_I}[\overline{{\mathbf{V}}^{+}}·T^{\left(\mathbf{r}\right)}{\mathbf{V}}^{-}-\overline{{\mathbf{V}}^{-}}·T^{\left(\mathbf{r}\right)}{\mathbf{V}}^{-}+\overline{({\mathbf{V}}^{+}-{\mathbf{V}}^{-})}·i\omega c{\mathbf{V}}^{-}]ds\left({\mathbf{r}}_0\right)\hfill \\ \hfill \\ & =& -\frac{1}{2}{\int }_{{\mathsf{\Gamma }}_D}({\mathbf{V}}^{+}·T^{\left(\mathbf{r}\right)}\overline{{\mathbf{V}}^{+}}-{\mathbf{V}}^{-}·T^{\left(\mathbf{r}\right)}\overline{{\mathbf{V}}^{-}})ds\left({\mathbf{r}}_0\right)\hfill \\ \hfill \\ & & +\frac{1}{2}{\int }_{{\mathsf{\Gamma }}_I}[\overline{{\mathbf{V}}^{+}}·T^{\left(\mathbf{r}\right)}{\mathbf{V}}^{-}-\overline{{\mathbf{V}}^{-}}·T^{\left(\mathbf{r}\right)}{\mathbf{V}}^{-}-\overline{({\mathbf{V}}^{+}}-{\mathbf{V}}^{-})·i\omega c{\mathbf{V}}^{-}]ds\left({\mathbf{r}}_0\right).\hfill \end{array}$$

(98)

Hence, we get

$$\begin{array}{ccc}\hfill & & <\mathcal{M}(\mathbf{p},\mathbf{q}),(\mathbf{p},\mathbf{q})>\hfill \\ \hfill \\ & =& \frac{1}{2}{\int }_{{\mathsf{\Gamma }}_D}({\mathbf{V}}^{-}·T^{\left(\mathbf{r}\right)}\overline{{\mathbf{V}}^{-}}-{\mathbf{V}}^{+}·T^{\left(\mathbf{r}\right)}\overline{{\mathbf{V}}^{+}})ds\left({\mathbf{r}}_0\right)\hfill \\ \\ \hfill & & +\frac{1}{2}{\int }_{{\mathsf{\Gamma }}_I}(\overline{{\mathbf{V}}^{+}}·T^{\left(\mathbf{r}\right)}{\mathbf{V}}^{+}-\overline{{\mathbf{V}}^{-}}·T^{\left(\mathbf{r}\right)}{\mathbf{V}}^{-})ds\left({\mathbf{r}}_0\right)\hfill \\ \hfill \\ & & +\frac{1}{2}{\int }_{{\mathsf{\Gamma }}_I}[-i\omega c({\mathbf{V}}^{+}-{\mathbf{V}}^{-})·\overline{{\mathbf{V}}^{+}}+i\omega c\overline{({\mathbf{V}}^{+}-{\mathbf{V}}^{-})}·{\mathbf{V}}^{-}]ds\left({\mathbf{r}}_0\right).\hfill \end{array}$$

(99)

Taking the imaginary part of (99), we have

$$\begin{array}{ccc}& & Im\{<\mathcal{M}(\mathbf{p},\mathbf{q}),(\mathbf{p},\mathbf{q})>\}\hfill \\ \hfill \\ & =& \frac{1}{2}Im\left\{{\int }_{{\mathsf{\Gamma }}_D}({\mathbf{V}}^{-}·T^{\left(\mathbf{r}\right)}\overline{{\mathbf{V}}^{-}}-{\mathbf{V}}^{+}·T^{\left(\mathbf{r}\right)}\overline{{\mathbf{V}}^{+}})ds\left({\mathbf{r}}_0\right)\right\}\hfill \\ \hfill \\ & & +\frac{1}{2}Im\left\{{\int }_{{\mathsf{\Gamma }}_I}(\overline{{\mathbf{V}}^{+}}·T^{\left(\mathbf{r}\right)}{\mathbf{V}}^{+}-\overline{{\mathbf{V}}^{-}}·T^{\left(\mathbf{r}\right)}{\mathbf{V}}^{-})ds\left({\mathbf{r}}_0\right)\right\}\hfill \\ \hfill \\ & & +\frac{1}{2}Im\left\{{\int }_{{\mathsf{\Gamma }}_I}[-i\omega c({\mathbf{V}}^{+}-{\mathbf{V}}^{-})·\overline{{\mathbf{V}}^{+}}+i\omega c\overline{({\mathbf{V}}^{+}-{\mathbf{V}}^{-})}·\overline{{\mathbf{V}}^{-}}]ds\left({\mathbf{r}}_0\right)\right\}\hfill \\ \hfill \\ & =& \frac{1}{2}Im\left\{{\int }_{{\mathsf{\Gamma }}_D}({\mathbf{V}}^{-}·T^{\left(\mathbf{r}\right)}\overline{{\mathbf{V}}^{-}}-{\mathbf{V}}^{+}·T^{\left(\mathbf{r}\right)}\overline{{\mathbf{V}}^{+}})ds\left({\mathbf{r}}_0\right)\right\}\hfill \\ \hfill \\ & & +\frac{1}{2}Im\left\{{\int }_{{\mathsf{\Gamma }}_I}({\mathbf{V}}^{-}·T^{\left(\mathbf{r}\right)}\overline{{\mathbf{V}}^{-}}-{\mathbf{V}}^{+}·T^{\left(\mathbf{r}\right)}\overline{{\mathbf{V}}^{+}})ds\left({\mathbf{r}}_0\right)\right\}\hfill \\ \hfill \\ & & +\frac{1}{2}Im\left\{{\int }_{{\mathsf{\Gamma }}_I}[-i\omega c\overline{({\mathbf{V}}^{+}-{\mathbf{V}}^{-})}·{\mathbf{V}}^{+}+i\omega c\overline{({\mathbf{V}}^{+}-{\mathbf{V}}^{-})}·{\mathbf{V}}^{-}]ds\left({\mathbf{r}}_0\right)\right\},\hfill \end{array}$$

and therefore we can arrive at

$$\begin{array}{ccc}& & Im\{<\mathcal{M}(\mathbf{p},\mathbf{q}),(\mathbf{p},\mathbf{q})>\}\hfill \\ \\ & =& \frac{1}{2}Im\left\{{\int }_{{\mathsf{\Gamma }}_D}({\mathbf{V}}^{-}·T^{\left(\mathbf{r}\right)}\overline{{\mathbf{V}}^{-}}-{\mathbf{V}}^{+}·T^{\left(\mathbf{r}\right)}\overline{{\mathbf{V}}^{+}})ds\right\}-\omega c{\int }_{{\mathsf{\Gamma }}_I}|{\mathbf{V}}^{+}-{\mathbf{V}}^{-}{|}^{2}ds.\hfill \end{array}$$

(100)

We now consider $B_R=C_R⧹B$, with $C_R$ being a circle with large enough radius R. From the latter and after some calculations, we have

$$\begin{array}{ccc}\hfill & & Im\{<M(\mathbf{p},\mathbf{q}),(\mathbf{p},\mathbf{q})>\}\hfill \\ \hfill \\ & =& Im\{-\rho {\omega }^2{\int }_{B_R\cup B}|\mathbf{V}{|}^{2}d\upsilon -{\int }_{|\mathbf{r}|=R}\mathbf{V}·T\overline{\mathbf{V}}ds-{\int }_{B_R\cup B}\mathcal{E}(\mathbf{V},\overline{\mathbf{V}})d\upsilon \}\hfill \\ \\ & & -\omega c{\int }_{{\mathsf{\Gamma }}_I}|{\mathbf{V}}^{+}-{\mathbf{V}}^{-}|ds,\hfill \end{array}$$

(101)

where $\mathcal{E}(\mathbf{V},\overline{\mathbf{V}})$ is the analogous functional as it is given in (13) if we substitute $\mathbf{v}=\mathbf{V}$ and $\mathbf{w}=\overline{\mathbf{V}}$. Using now Betti’s formula in (101), we get

$$Im\{<\mathcal{M}(\mathbf{p},\mathbf{q}),(\mathbf{p},\mathbf{q})>\}=-Im\left\{{\int }_{|\mathbf{r}|=R}\mathbf{V}·T\overline{\mathbf{V}}ds\right\}-\omega c{\int }_{{\mathsf{\Gamma }}_I}{|{\mathbf{V}}^{+}-{\mathbf{V}}^{-}|}^{2}ds.$$

(102)

Using the radiation conditions [16]

$$T{\mathbf{V}}^p\left(\mathbf{r}\right)-i{k}_p(\lambda +2\mu ){\mathbf{V}}^p\left(\mathbf{r}\right)=O\left(r^{-2}\right),r:=|\mathbf{r}|\to \infty$$

(103)

and

$$T{\mathbf{V}}^s\left(\mathbf{r}\right)-i{k}_s\mu {\mathbf{V}}^s\left(\mathbf{r}\right)=O\left(r^{-2}\right),r:=|\mathbf{r}|\to \infty ,$$

(104)

hold uniformly for all directions $\widehat{\mathbf{r}}=\frac{\mathbf{r}}{r}$, relation (102) arrives at

$$\begin{array}{ccc}\hfill Im\{<\mathcal{M}(\mathbf{p},\mathbf{q}),(\mathbf{p},\mathbf{q})>\}& \le & -\zeta {\int }_{|\mathbf{r}|=R}{|\mathbf{V}|}^{2}ds\hfill \\ \hfill & & -\omega c{\int }_{{\mathsf{\Gamma }}_I}{|{\mathbf{V}}^{+}-{\mathbf{V}}^{-}|}^{2}ds+O\left(R^{-1}\right),\hfill \end{array}$$

where $\zeta =max\{k_p(\lambda +2\mu ),k_s\mu \}\in \mathbb{R}$. We now let $R\to \infty$ and since $\zeta >0,\omega c>0$, we take

$$Im\{<\mathcal{M}(\mathbf{p},\mathbf{q}),(\mathbf{p},\mathbf{q})>\}\le 0$$

(105)

with $(\mathbf{p},\mathbf{q})\in {\left[{\tilde{H}}^{-\frac{1}{2}}\left({\mathsf{\Gamma }}_D\right)\right]}^2\times {\left[{\tilde{H}}^{\frac{1}{2}}\left({\mathsf{\Gamma }}_I\right)\right]}^2$. If we now assume for (105) that equality holds, then both terms ${\int }_{|\mathbf{r}|=R}{|\mathbf{V}|}^{2}ds$ and ${\int }_{{\mathsf{\Gamma }}_I}{|{\mathbf{V}}^{+}-{\mathbf{V}}^{-}|}^{2}ds$ are vanishing. Using Rellich’s Lemma and unique continuation principle [5,20], we get

$$\mathbf{V}=\mathbf{0}in{\mathbb{R}}^2⧹\overline{B},{\mathbf{V}}^{-}{{|}_{{\mathsf{\Gamma }}_I}={\mathbf{V}}^{+}|}_{{\mathsf{\Gamma }}_I}=\mathbf{0},$$

(106)

and since $\mathbf{V}$ satisfies the Navier Equation (62) in B, by Holmgren’s theorem [24] we take $\mathbf{V}=\mathbf{0}$ in B. From (94)–(97) we can now conclude that

$$\mathbf{p}\left(\mathbf{r}\right)=\mathbf{q}\left(\mathbf{r}\right)=\mathbf{0}=2i\omega c\mathbf{q}\left(\mathbf{r}\right).$$

(107)

Taking into account the above arguments, we can see that indeed the imaginary part of the integral operator $\mathcal{M}$ is strictly negative, i.e., relation (92) holds.

(ii)

We now want to show that $\mathcal{M}$ is invertible. Concerning the injectivity of $\mathcal{M}$, let us assume that $\mathcal{M}(\mathbf{p},\mathbf{q})=\mathbf{0}$. Hence $Im\{<\mathcal{M}(\mathbf{p},\mathbf{q}),(\mathbf{p},\mathbf{q})>\}$ is vanishing too, and using previous argument (see (107)) we have $\mathbf{p}=\mathbf{q}=\mathbf{0}$, and now injectivity of $\mathcal{M}$ is secured.

In what follows, we consider the matrix−integral operator

$$\begin{array}{c}\hfill \tilde{\mathcal{M}}=\left(\begin{array}{cc}{S}_{{\mathsf{\Gamma }}_D}{|}_{{\mathsf{\Gamma }}_D}& (K_{{\mathsf{\Gamma }}_I}-i\omega c{S}_{{\mathsf{\Gamma }}_I}){|}_{{\mathsf{\Gamma }}_D}\\ (-K_{{\mathsf{\Gamma }}_D}^{\prime }-i\omega c{S}_{{\mathsf{\Gamma }}_D}){|}_{{\mathsf{\Gamma }}_I}& (-{\mathsf{\Lambda }}_{{\mathsf{\Gamma }}_I}-i\omega c{K}_{{\mathsf{\Gamma }}_I}^{\prime }-{\omega }^{2}c{S}_{{\mathsf{\Gamma }}_I}+2i\omega I){|}_{{\mathsf{\Gamma }}_I}\end{array}\right)\end{array}$$

(108)

and therefore the following decomposition for $\mathcal{M}$ holds

$$\mathcal{M}\left(\begin{array}{c}\mathbf{p}\\ \mathbf{q}\end{array}\right)=\left(\begin{array}{cc}1& 0\\ 0& -1\end{array}\right)\tilde{\mathcal{M}}\left(\begin{array}{c}\mathbf{p}\\ \mathbf{q}\end{array}\right).$$

(109)

The latter implies that invertibility of $\mathcal{M}$ and $\tilde{\mathcal{M}}$ is an equivalent argument and since injectivity of $\mathcal{M}$ is proved, the injectivity of $\tilde{\mathcal{M}}$ is secured as well. In addition and due to Fredholm theory, if we combine the above injectivity showing that $\tilde{\mathcal{M}}$ is a Fredholm operator with index zero, then operators $\mathcal{M}$ and $\tilde{\mathcal{M}}$ are bounded and invertible.

□

We state the following lemma; its proof follows analogous arguments and minor modifications as those in [12,25], and here it is omitted for brevity.

Lemma 1.

Let $S_0,K_0,K_0^{\prime },{\mathsf{\Lambda }}_0$ be operators corresponding to the operators (85)–(88), with kernel

$${\tilde{\mathsf{\Gamma }}}_0(\mathbf{r},{\mathbf{r}}^{\prime })=\frac{3\mu +\lambda }{4\pi \mu (2\mu +\lambda )}log\frac{1}{|\mathbf{r}-{\mathbf{r}}^{\prime }|}\tilde{\mathbf{I}}+\frac{\mu +\lambda }{4\pi \mu (2\mu +\lambda )}\mathbf{J}(\mathbf{r}-{\mathbf{r}}^{\prime }),$$

(110)

where $\mathbf{r},{\mathbf{r}}^{\prime }\in {\mathbb{R}}^2,\mathbf{r}\ne {\mathbf{r}}^{\prime }$, $\mathbf{J}\left(\mathbf{r}\right):=\frac{\mathbf{r}{\mathbf{r}}^{\top }}{{|\mathbf{r}|}^2}$ and ${\tilde{\mathsf{\Gamma }}}_0(\mathbf{r},{\mathbf{r}}^{\prime })$ corresponds to the elasto-static case i.e., ($\omega =0$). If we assume the differences $S-S_0,K-K_0,K^{\prime }-K_0$ and $\mathsf{\Lambda }-{\mathsf{\Lambda }}_0$, then:

(i) 

The operators $S-S_0,K-K_0,K^{\prime }-K_0$ and $\mathsf{\Lambda }-{\mathsf{\Lambda }}_0$ are compact.

(ii) 

The operators $K_0$ and $K_0^{\prime }$ are adjoint operators.

(iii) 

The operator $S_0$ is self-adjoint operator.

(iv) 

The operators $S_0$ and $-{\mathsf{\Lambda }}_0$ are coercive.

We also give and prove the following result.

Theorem 3.

The near field operator

$$\mathcal{N}:{\left[L^2\left(C\right)\right]}^2\to L^2\left(C\right)$$

(111)

given by (65) can be written as:

$$\mathcal{N}=-{\tilde{\mathcal{H}}}^{*}{\mathcal{M}}^{-1}\tilde{\mathcal{H}},$$

(112)

with operator ${\tilde{\mathcal{H}}}^{*}$ being compact and has dense range in ${\left[L^2\left(C\right)\right]}^2$.

Proof. 

Let us recall that

$$\mathcal{N}=-\mathbf{G}\tilde{\mathcal{H}}.$$

The latter in combination with (91), the fact that $\mathcal{M}$ is invertible and ${\mathcal{M}}^{-1}$ is bounded, gives:

$$\mathcal{N}=-{\tilde{\mathcal{H}}}^{*}{\mathcal{M}}^{-1}\tilde{\mathcal{H}}.$$

(113)

Compactness of ${\tilde{\mathcal{H}}}^{*}$ now is secured, by the fact that ${\mathbf{u}|}_{B_0}\in H^1\left(B_0\right)$ ($B_0$ is the interior domain enclosed by C) and ${\mathbf{u}|}_C\in H^{\frac{1}{2}}\left(C\right)$; therefore, the operator $\mathbf{G}:{\left[H^{\frac{1}{2}}\left({\mathsf{\Gamma }}_D\right)\right]}^2\times {\left[H^{-\frac{1}{2}}\left({\mathsf{\Gamma }}_I\right)\right]}^2\to {\left[L^2\left(C\right)\right]}^2$ is compact.

Last but not least, we will prove that ${\tilde{\mathcal{H}}}^{*}$ has dense range. Assume that $\tilde{\mathcal{H}}\mathbf{b}=\mathbf{0}$. From the definition of $\tilde{\mathcal{H}}$ (see (67)), we have

$${\mathbf{\upsilon }}_{\mathbf{b}}{|}_{{\mathsf{\Gamma }}_D}=\mathbf{0}\mathrm{and}(T+i\omega c){\mathbf{\upsilon }}_{\mathbf{b}}=\mathbf{0}.$$

(114)

Hence ${\mathbf{\upsilon }}_{\mathbf{b}}$ solves the following exterior mixed boundary value problem:

$$\begin{array}{ccc}& & ({\Delta }^{*}+{\rho }_1{\omega }^2)\mathbf{\upsilon }=\mathbf{0},\mathrm{in}{\mathbb{R}}^2⧹\overline{B}\hfill \\ \hfill \end{array}$$

(115)

$$\begin{array}{ccc}& & \mathbf{\upsilon }=\mathbf{0},\mathrm{on}{\mathsf{\Gamma }}_D\hfill \\ \hfill \end{array}$$

(116)

$$\begin{array}{ccc}& & T\mathbf{\upsilon }+i\omega c\mathbf{\upsilon }=\mathbf{0},\mathrm{on}{\mathsf{\Gamma }}_I\hfill \\ \hfill \end{array}$$

(117)

$$\begin{array}{ccc}& & T{\mathbf{\upsilon }}^{\left(p\right)}-i{k}_p(\lambda +2\mu ){\mathbf{\upsilon }}^{\left(p\right)}=O\left(r^{-2}\right)\hfill \\ \hfill \end{array}$$

(118)

$$\begin{array}{ccc}& & T{\mathbf{\upsilon }}^{\left(s\right)}-i{k}_s\mu {\mathbf{\upsilon }}^{\left(s\right)}=O\left(r^{-2}\right)\hfill \end{array}$$

(119)

with $r:=|\mathbf{r}|\to +\infty$. The problem (115)–(119) has a unique solution [26], and we can easily get ${\mathbf{\upsilon }}_{\mathbf{b}}=0$ in ${\mathbb{R}}^2⧹\overline{B}$. From the analytic continuation argument we take ${\mathbf{\upsilon }}_{\mathbf{b}}=0$ in ${\mathbb{R}}^2⧹{\overline{B}}_0$, and therefore ${\mathbf{\upsilon }}_{\mathbf{b}}^{+}{{|}_C={\mathbf{\upsilon }}_{\mathbf{b}}^{-}|}_C=0$. Using the fact that ${\omega }^2$ is not an eigenvalue of $-{\Delta }^{*}$ in $B_0$, we arrive at ${\mathbf{\upsilon }}_{\mathbf{b}}=0$ in $B_0$. We also have $T{\mathbf{\upsilon }}_{\mathbf{b}}^{+}-T{\mathbf{\upsilon }}_{\mathbf{b}}^{-}=0$ on C, and finally $\mathbf{b}=\mathbf{0}$. The above argument yields to injectivity of $\tilde{\mathcal{H}}$ and therefore ${\tilde{\mathcal{H}}}^{*}$ has dense range. □

In the sequel, we make use of an essential theorem (see [25], p. 57) which is very helpful in the suggested modified factorization method due to the introduction of some proposed key auxiliary operators. For the convenience of the reader, we state it here.

Theorem 4.

Let $X\subset U\subset X^{*}$ be a Gelfand triple with a Hilbert space U and a reflexive Banach space X such that the embedding is dense. Furthermore, let Y be a second Hilbert space and let $N:Y\to Y,G:X\to Y$ and $\mathsf{\Lambda }:X^{*}\to X$ be linear bounded operators such that

$$N=G\mathsf{\Lambda }{G}^{*}.$$

If we assume that:

(i) 

G is a compact operator,

(ii) 

There exists $t\in [0,2\pi ]$ such that $Re\left[e^{it}\mathsf{\Lambda }\right]=C+K$ with some compact operator K and some self-adjoint and coercive operator $C:X^{*}\to X$, i.e., there is constant ${\gamma }_0>0$ with $<\varphi ,C\varphi >\ge {\gamma }_0{\parallel \varphi \parallel }^2$, for all $\varphi \in X^{*}$,

(iii) 

$Im\left[\mathsf{\Lambda }\right]$ is non−negative or non−positive on $X^{*}$, i.e., $<\varphi ,Im\left(\mathsf{\Lambda }\right)>\ge 0$ or $<\varphi ,Im\left(\mathsf{\Lambda }\right)>\le 0$, for all $\varphi \in \overline{R\left(G^{*}\right)}$ and $\varphi \ne 0$, and

(iv) 

$Re\left[e^{it}\mathsf{\Lambda }\right]$ is one−to−one or $Im\left(\mathsf{\Lambda }\right)$ is strictly positive or strictly negative, for all $\varphi \in \overline{R\left(G^{*}\right)}$ and $\varphi \ne 0$,

then the operator $N_{♯}=|Re\left[e^{it}N\right]|+|Im\left(N\right)|$ is positive, and the range of G coincides with the range of $N_{♯}^{\frac{1}{2}}$.

Remark 1.

The above analysis deals with the matrix−integral operator $\mathcal{M}$, for which the essential theorem introduced by Kirsh and Grinberg [25] cannot be applied. In particular, the decomposition of the real part of the matrix operator $\mathcal{M}$ into a compact operator and a coercive one is not valid, and hence we have to modify our functional analysis technique by considering some suitable auxiliary operators.

In what follows, we define new operators ${\mathcal{N}}_{\mathcal{D}},{\mathcal{N}}_{\mathcal{I}}$ related with $\mathcal{N}$ as follows:

$${\mathcal{N}}_{\mathcal{D}}=\mathcal{N}-{\xi }_1{\mathbf{U}}^{*}\mathbf{U},{\mathcal{N}}_{\mathcal{I}}=\mathcal{N}+{\xi }_2{\mathbf{U}}^{*}\mathbf{U},$$

(120)

where ${\xi }_1,{\xi }_2\in \mathbb{C}$ with $Im{\xi }_1<0,Im{\xi }_2>0$ and $\mathbf{U}:{\left[L^2\left(C\right)\right]}^2\to {\left[L^2\left(C\right)\right]}^2$ is given as

$$\left(\mathbf{U}\mathbf{b}\right)\left(\mathbf{r}\right)={\int }_C\tilde{\mathsf{\Gamma }}(\mathbf{r},{\mathbf{r}}_0)\mathbf{b}\left({\mathbf{r}}_0\right)ds\left({\mathbf{r}}_0\right),\mathbf{r}\in \partial D.$$

(121)

In (121) $\partial D$ is the smooth boundary of a known domain D which is open, bounded with $\overline{D}\subset B$, ${\overline{B}}_0\subset D$ and $\partial D\cap C=\varnothing$. The following theorem holds.

Theorem 5.

We assume that ${\omega }^2$ is not an interior Dirichlet eigenvalue of ${\Delta }^{*}$ in both D and $B_0$. Then the following decompositions hold:

$${\mathcal{N}}_{\mathcal{D}}=-{\left(\begin{array}{c}{\mathbf{H}}_{\mathbf{1}}\\ \mathbf{U}\end{array}\right)}^{*}{\mathcal{M}}_1\left(\begin{array}{c}{\mathbf{H}}_{\mathbf{1}}\\ \mathbf{U}\end{array}\right),$$

(122)

and

$${\mathcal{N}}_{\mathcal{I}}=-{\left(\begin{array}{c}\mathbf{U}\\ {\mathbf{H}}_{\mathbf{2}}\end{array}\right)}^{*}{\mathcal{M}}_2\left(\begin{array}{c}\mathbf{U}\\ {\mathbf{H}}_{\mathbf{2}}\end{array}\right),$$

(123)

with

$${\mathcal{M}}_1={\mathcal{M}}_{1O}+{\mathcal{M}}_{1C}$$

(124)

and

$${\mathcal{M}}_2={\mathcal{M}}_{2O}+{\mathcal{M}}_{2C},$$

(125)

In addition, the operators ${\mathcal{M}}_{1O},{\mathcal{M}}_{2O}$ are coercive and ${\mathcal{M}}_{1C},{\mathcal{M}}_{2C}$ are compact.

Proof. 

Let us consider the following exterior boundary value problem:

$$\begin{array}{ccc}& & ({\Delta }^{*}+{\rho }_0{\omega }^2)\mathbf{w}=\mathbf{0}in{\mathbb{R}}^2⧹\overline{D}\hfill \\ \hfill \end{array}$$

(126)

$$\begin{array}{ccc}& & \mathbf{w}={\mathbf{g}}_{1}on\partial D\hfill \\ \hfill \end{array}$$

(127)

$$\begin{array}{ccc}& & T{\mathbf{w}}^{\left(p\right)}-i{k}_p(\lambda +2\mu ){\mathbf{w}}^{\left(p\right)}=O\left(r^{-2}\right),\hfill \\ \hfill \end{array}$$

(128)

$$\begin{array}{ccc}& & T{\mathbf{w}}^{\left(s\right)}-i{k}_s\mu {\mathbf{w}}^{\left(s\right)}=O\left(r^{-2}\right),\hfill \end{array}$$

(129)

for $r:=|\mathbf{r}|\to \infty$ and ${\mathbf{g}}_1\in {\left[L^2(\partial D)\right]}^2$. We also define the operator

$$\tilde{\mathcal{Q}}=({\mathbf{Q}}_{\mathbf{1}},{\mathbf{Q}}_{\mathbf{2}}):{\left[L^2(\partial D)\right]}^2\to {\left[H^{\frac{1}{2}}\left({\mathsf{\Gamma }}_D\right)\right]}^2\times {\left[H^{-\frac{1}{2}}\left({\mathsf{\Gamma }}_I\right)\right]}^2$$

(130)

given by

$${\mathbf{Q}}_{\mathbf{1}}{\mathbf{g}}_{\mathbf{1}}{=\mathbf{w}|}_{{\mathsf{\Gamma }}_D}and{\mathbf{Q}}_{\mathbf{2}}{\mathbf{g}}_{\mathbf{1}}{=(T\mathbf{w}+i\omega c\mathbf{w})|}_{{\mathsf{\Gamma }}_I},$$

(131)

with $\mathbf{w}$ being a solution of (126)–(129). The exterior boundary value problem (126)–(129) has a solution with boundary data $\mathbf{g}\in {\left[L^2(\partial D)\right]}^2$ [15,26] and its regularity properties yield to compactness of the operator $\mathcal{Q}$. Using relation (68) it is easy to prove that ${\mathbf{\upsilon }}_{\mathbf{b}}$ solves problem (126)–(129), with ${\mathbf{g}}_{\mathbf{1}}{{|}_{\partial D}={\mathbf{\upsilon }}_{\mathbf{g}}|}_{\partial D}$, and via (121)

$${\mathbf{g}}_{\mathbf{1}}{{|}_{\partial D}={\mathbf{\upsilon }}_{\mathbf{g}}|}_{\partial D}=\mathbf{U}\mathbf{g}.$$

(132)

In addition, from definitions of $\tilde{\mathcal{H}}$ and $\tilde{\mathcal{Q}}$ (see (67) and (131)), we get

$${\mathbf{H}}_{\mathbf{1}}={\mathbf{Q}}_{\mathbf{1}}\mathbf{U}.$$

(133)

and using a similar consideration, the following relation

$${\mathbf{H}}_{\mathbf{2}}={\mathbf{Q}}_{\mathbf{2}}\mathbf{U}$$

(134)

also holds. From (120) and the factorization relation (113) we have

$$\begin{array}{ccc}\hfill {\mathcal{N}}_D& =& \mathcal{N}-{\xi }_1{\mathbf{U}}^{*}\mathbf{U}\hfill \\ \hfill \\ & =& -{\tilde{\mathcal{H}}}^{*}{\mathcal{M}}^{-1}\tilde{\mathcal{H}}-{\xi }_1{\mathbf{U}}^{*}\mathbf{U}\hfill \\ & =& -{\left(\begin{array}{c}{\mathbf{H}}_{\mathbf{1}}\\ \mathbf{U}\end{array}\right)}^{*}\left(\begin{array}{cc}I& 0\\ 0& {{\mathbf{Q}}_{\mathbf{2}}}^{*}\end{array}\right){\mathcal{M}}^{-1}\left(\begin{array}{cc}I& 0\\ 0& {\mathbf{Q}}_{\mathbf{2}}\end{array}\right)\left(\begin{array}{c}{\mathbf{H}}_{\mathbf{1}}\\ \mathbf{U}\end{array}\right)-{\xi }_1{\mathbf{U}}^{*}\mathbf{U}\hfill \\ & =& -{\left(\begin{array}{c}{\mathbf{H}}_{\mathbf{1}}\\ \mathbf{U}\end{array}\right)}^{*}\left[\left(\begin{array}{cc}I& 0\\ 0& {{\mathbf{Q}}_{\mathbf{2}}}^{*}\end{array}\right){\mathcal{M}}^{-1}\left(\begin{array}{cc}I& 0\\ 0& {\mathbf{Q}}_{\mathbf{2}}\end{array}\right)+\left(\begin{array}{cc}0& 0\\ 0& {\xi }_{1}I\end{array}\right)\right]\left(\begin{array}{c}{\mathbf{H}}_{\mathbf{1}}\\ \mathbf{U}\end{array}\right).\hfill \end{array}$$

(135)

If we use the notation

$${\mathcal{M}}_1:=\left(\begin{array}{cc}I& 0\\ 0& {{\mathbf{Q}}_{\mathbf{2}}}^{*}\end{array}\right){\mathcal{M}}^{-1}\left(\begin{array}{cc}I& 0\\ 0& {\mathbf{Q}}_{\mathbf{2}}\end{array}\right)+\left(\begin{array}{cc}0& 0\\ 0& {\xi }_{1}I\end{array}\right),$$

(136)

then (122) is secured. In what follows and since ${\mathcal{M}}^{-1}$ is bounded, we can write

$${\mathcal{M}}^{-1}=\left(\begin{array}{cc}{S}_0^{-1}& 0\\ 0& {\mathsf{\Lambda }}_0^{-1}\end{array}\right)-{\mathcal{M}}^{-1}{\mathcal{M}}^c\left(\begin{array}{cc}{S}_0^{-1}& 0\\ 0& {\mathsf{\Lambda }}_0^{-1}\end{array}\right),$$

(137)

where

$${\mathcal{M}}^c=\mathcal{M}-\left(\begin{array}{cc}{S}_0& 0\\ 0& {\mathsf{\Lambda }}_0\end{array}\right).$$

(138)

Then (137) via (136) is written as

$$\begin{array}{ccc}\hfill {\mathcal{M}}_1& =& \left(\begin{array}{cc}{S}_0^{-1}& 0\\ 0& {\xi }_{1}I\end{array}\right)+\left(\begin{array}{cc}0& 0\\ 0& {{\mathbf{Q}}_{\mathbf{2}}}^{*}{\mathsf{\Lambda }}_0^{-1}{\mathbf{Q}}_{\mathbf{2}}\end{array}\right)\hfill \\ \hfill \\ & & -\left(\begin{array}{cc}I& 0\\ 0& {\mathbf{Q}}_{\mathbf{2}}\end{array}\right){\mathcal{M}}^{-1}{\mathcal{M}}^c\left(\begin{array}{cc}{S}_0^{-1}& 0\\ 0& {\mathsf{\Lambda }}_0^{-1}\end{array}\right)\left(\begin{array}{cc}I& 0\\ 0& {\mathbf{Q}}_{\mathbf{2}}\end{array}\right)\hfill \end{array}$$

(139)

and if we set

$${\mathcal{M}}_{1O}:=\left(\begin{array}{cc}{S}_0^{-1}& 0\\ 0& {\xi }_{1}I\end{array}\right),$$

(140)

and

$$\begin{array}{c}{\mathcal{M}}_{1C}\\ :=\left(\begin{array}{cc}0& 0\\ 0& {{\mathbf{Q}}_{\mathbf{2}}}^{*}{\mathsf{\Lambda }}_0^{-1}{\mathbf{Q}}_{\mathbf{2}}\end{array}\right)-\left(\begin{array}{cc}I& 0\\ 0& {{\mathbf{Q}}_{\mathbf{2}}}^{*}\end{array}\right){\mathcal{M}}^{-1}{\mathcal{M}}^c\left(\begin{array}{cc}{S}_0^{-1}& 0\\ 0& {\mathsf{\Lambda }}_0^{-1}\end{array}\right)\left(\begin{array}{cc}I& 0\\ 0& {\mathbf{Q}}_{\mathbf{2}}\end{array}\right),\end{array}$$

(141)

then ${\mathcal{M}}_{10}$ is a coercive operator and ${\mathcal{M}}_{1c}$ a compact one. Here we have taken into account the compactness of ${\mathbf{Q}}_{\mathbf{2}}$ and ${\mathcal{M}}^c$ as well as that $Re{\xi }_1>0$.

Following a similar analysis as before for ${\mathcal{N}}_D$, we can also prove relation (123). We now use the notation

$${\mathcal{M}}_{2O}:=\left(\begin{array}{cc}-{\xi }_{2}I& 0\\ 0& {\mathsf{\Lambda }}_0^{-1}\end{array}\right)$$

(142)

and

$${\mathcal{M}}_{2C}:=\left(\begin{array}{cc}{{\mathbf{Q}}_{\mathbf{1}}}^{*}{S}_0^{-1}& 0\\ 0& 0\end{array}\right)-\left(\begin{array}{cc}{{\mathbf{Q}}_{\mathbf{1}}}^{*}& 0\\ 0& I\end{array}\right){\mathcal{M}}^{-1}{\mathcal{M}}^c\left(\begin{array}{cc}{S}_0^{-1}& 0\\ 0& {\mathsf{\Lambda }}_0^{-1}\end{array}\right)\left(\begin{array}{cc}{\mathbf{Q}}_{\mathbf{1}}& 0\\ 0& I\end{array}\right)$$

(143)

If we assume that $Re{\xi }_2<0$ we conclude that ${\mathcal{M}}_{20}$ is coercive and since the operators ${\mathbf{Q}}_{\mathbf{1}}$ and ${\mathcal{M}}^c$ are compact, ${\mathcal{M}}_{2c}$ is also compact. □

We also state the following theorem.

Theorem 6.

Assume that ${\omega }^2$ is neither a Dirichlet eigenvalue of $-{\Delta }^{*}$ in D, nor in $B_0$, then

(i) 

The operators $Im\left\{{\mathcal{M}}_1\right\}$ and $Im\left\{{\mathcal{M}}_2\right\}$ are strictly negative.

(ii) 

The operators $({{\mathbf{H}}_{\mathbf{1}}}^{*},{\mathbf{U}}^{*})={\left(\begin{array}{c}{\mathbf{H}}_{\mathbf{1}}\\ \mathbf{U}\end{array}\right)}^{*}$ and $({\mathbf{U}}^{*},{{\mathbf{H}}_{\mathbf{2}}}^{*})={\left(\begin{array}{c}{\mathbf{U}}^{*}\\ {\mathbf{H}}_{\mathbf{2}}\end{array}\right)}^{*}$ are compact and have dense ranges in $L^2\left(C\right)$.

Proof. 

(i)

Let us consider an arbitrary $\tilde{\mathbf{l}}=({\mathbf{l}}_{\mathbf{1}},{\mathbf{l}}_{\mathbf{2}})\in {\left[H^{\frac{1}{2}}\left({\mathsf{\Gamma }}_D\right)\right]}^2\times {\left[L^2(\partial D)\right]}^2$ and assume $Im{\xi }_1<0$. We have the following analysis:

$$\begin{array}{ccc}& & Im\{<{\mathcal{M}}_1\mathbf{l},\mathbf{l}>\}\hfill \\ \hfill \\ & =& Im\{<\left(\begin{array}{cc}I& 0\\ 0& {{\mathbf{Q}}_{\mathbf{2}}}^{*}\end{array}\right){\mathcal{M}}^{-1}\left(\begin{array}{cc}I& 0\\ 0& {\mathbf{Q}}_{\mathbf{2}}\end{array}\right)\mathbf{l},\mathbf{l}>\}+Im\{<{\xi }_1{\mathbf{l}}_{\mathbf{2}},{\mathbf{l}}_{\mathbf{2}}>\}\hfill \\ \\ & =& Im\{<\widehat{\mathbf{l}},\mathcal{M}\widehat{\mathbf{l}}>\}+Im\left\{{\xi }_1\right\}{\parallel {\mathbf{l}}_{\mathbf{2}}\parallel }^2\hfill \\ \hfill \\ & =& -Im\{<\mathcal{M}\widehat{\mathbf{l}},\widehat{\mathbf{l}}>\}+Im\left\{{\xi }_1\right\}{\parallel {\mathbf{l}}_{\mathbf{2}}\parallel }^2\hfill \end{array}$$

(144)

where

$$\widehat{\mathbf{l}}={\mathcal{M}}^{-1}\left(\begin{array}{cc}I& 0\\ 0& {\mathbf{Q}}_{\mathbf{2}}\end{array}\right)={\mathcal{M}}^{-1}\left(\begin{array}{c}{\mathbf{l}}_{\mathbf{1}}\\ {\mathbf{Q}}_{\mathbf{2}}{\mathbf{l}}_{\mathbf{2}}\end{array}\right).$$

(145)

Taking into account that $Im\{<\mathcal{M}\widehat{\mathbf{l}},\widehat{\mathbf{l}}>\}\ge 0$, from (145) we end up with

$$Im\{<{\mathcal{M}}_1\mathbf{l},\mathbf{l}>\}\le 0.$$

(146)

Concerning now the vanishing of (146), if we assume $Im\{<{\mathcal{M}}_1\mathbf{l},\mathbf{l}>\}=0$, then via (145) we can arrive at $Im\{<\mathcal{M}\widehat{\mathbf{l}},\widehat{\mathbf{l}}>\}=Im{\xi }_1{\parallel {\mathbf{l}}_{\mathbf{2}}\parallel }^2=0$ and therefore by (145), we get:

$$\left(\begin{array}{c}{\mathbf{l}}_{\mathbf{1}}\\ {\mathbf{Q}}_{\mathbf{2}}{\mathbf{l}}_{\mathbf{2}}\end{array}\right)=\left(\begin{array}{c}\mathbf{0}\\ \mathbf{0}\end{array}\right)\mathrm{and}{\mathbf{l}}_{\mathbf{2}}=\mathbf{0}.$$

(147)

Hence $\tilde{\mathbf{l}}=\mathbf{0}$, and operator $Im\left\{{\mathcal{M}}_1\right\}$ is strictly negative. Following similar arguments as above, and considering $Im{\xi }_2>0$, the operator $Im\left\{{\mathcal{M}}_2\right\}$ is also strictly negative.

(ii)

From relation (121) we can see that

$$\left({\mathbf{U}}^{*}\mathbf{b}\right)\left(\mathbf{r}\right)={\int }_C\overline{\tilde{\mathsf{\Gamma }}(\mathbf{r},{\mathbf{r}}_0)}\mathbf{b}\left({\mathbf{r}}_0\right)ds\left({\mathbf{r}}_0\right),\mathbf{r}\in C,$$

(148)

hence, compactness of ${\mathbf{U}}^{*}$ is secured since the integral operator ${\mathbf{U}}^{*}$ has a weakly singular kernel. We assume now that $\mathbf{U}\mathbf{b}\left(\mathbf{r}\right)=\mathbf{0},\mathbf{r}\in \partial D$, which is written as

$${\int }_C\tilde{\mathsf{\Gamma }}(\mathbf{r},{\mathbf{r}}_0)\mathbf{b}\left({\mathbf{r}}_0\right)ds\left({\mathbf{r}}_0\right)=0,\mathbf{r}\in \partial D.$$

(149)

The single layer potential in the left hand side of (149) satisfies the Navier equation for $\mathbf{r}\in D$, with

$${\int }_C\tilde{\mathsf{\Gamma }}(\mathbf{r},{\mathbf{r}}_0)·\mathbf{b}\left({\mathbf{r}}_0\right)ds\left({\mathbf{r}}_0\right){|}_{\partial D}=0,$$

(150)

and since ${\omega }^2$ is not a Dirichlet eigenvalue of $-{\Delta }^{*}$ in D we arrive at ${\int }_C\tilde{\mathsf{\Gamma }}(\mathbf{r},{\mathbf{r}}_0)\mathbf{b}\left({\mathbf{r}}_0\right)ds\left({\mathbf{r}}_0\right)=0$ for $\mathbf{r}\in D$, which also vanishes in ${\mathbb{R}}^2$; therefore, $\mathbf{b}=\mathbf{0}$. The injectivity now of ${\mathbf{U}}^{*}$ is proved.

□

In view of Theorems 5 and 6 it is obvious that operator ${\mathcal{N}}_D$ satisfies all the conditions of Theorem 4, and hence

$$Range\left[{\left({\mathcal{N}}_D^{\#}\right)}^{\frac{1}{2}}\right]=Range\left[({{\mathbf{H}}_{\mathbf{1}}}^{*},{\mathbf{U}}^{*})\right],$$

(151)

where

$${\mathcal{N}}_D^{\#}=|Re\left\{{\mathcal{N}}_D\right\}|+|Im\left\{{\mathcal{N}}_D\right\}|.$$

(152)

For $\tilde{\mathbf{\varphi }}=({\mathbf{\varphi }}_1,{\mathbf{\varphi }}_2)\in {[{\tilde{H}}^{-\frac{1}{2}}\left({\mathsf{\Gamma }}_D\right)]}^2\times {\left[L^2(\partial D)\right]}^2$, we have that

$$({{\mathbf{H}}_{\mathbf{1}}}^{*},{\mathbf{U}}^{*})\tilde{\mathbf{\varphi }}\left(\mathbf{r}\right)={\int }_{{\mathsf{\Gamma }}_D}{\mathbf{\varphi }}_1\left({\mathbf{r}}_0\right)\overline{\tilde{\mathsf{\Gamma }}(\mathbf{r},{\mathbf{r}}_0)}ds\left({\mathbf{r}}_0\right)+{\int }_{\partial D}{\mathbf{\varphi }}_2\left({\mathbf{r}}_0\right)\overline{\tilde{\mathsf{\Gamma }}(\mathbf{r},{\mathbf{r}}_0)}ds\left({\mathbf{r}}_0\right).$$

(153)

The operator ${\mathcal{N}}_I$ also satisfies the conditions of Theorem 3, hence

$$Range\left[{\left({\mathcal{N}}_I^{\#}\right)}^{\frac{1}{2}}\right]=Range\left[({\mathbf{U}}^{*},{\mathbf{H}}_2^{*})\right],$$

(154)

where

$${\mathcal{N}}_I^{\#}=|Re\left\{{\mathcal{N}}_I\right\}|+|Im\left\{{\mathcal{N}}_I\right\}|.$$

(155)

Again, for every $\tilde{\mathbf{\varphi }}=({\mathbf{\varphi }}_1,{\mathbf{\varphi }}_2)\in {\left[L^2(\partial D)\right]}^2\times {[{\tilde{H}}^{\frac{1}{2}}\left({\mathsf{\Gamma }}_I\right)]}^2$, we have

$$({\mathbf{U}}^{*},{\mathbf{H}}_2^{*})\tilde{\mathbf{\varphi }}\left(\mathbf{r}\right)={\int }_{\partial D}{\mathbf{\varphi }}_1\left({\mathbf{r}}_0\right)\overline{\tilde{\mathsf{\Gamma }}(\mathbf{r},{\mathbf{r}}_0)}ds\left({\mathbf{r}}_0\right)+{\int }_{{\mathsf{\Gamma }}_I}{\mathbf{\varphi }}_2\left({\mathbf{r}}_0\right)(T+i\omega c)\overline{\tilde{\mathsf{\Gamma }}(\mathbf{r},{\mathbf{r}}_0)}ds\left({\mathbf{r}}_0\right).$$

(156)

Proposition 1.

Assume that ${\omega }^2$ is neither a Dirichlet eigenvalue of $-{\Delta }^{*}$ in both D and $B_0$. If we take any given nonitersecting arc L, which is smooth piecewise and without cups, defined by

$${\mathsf{\Phi }}_L^1\left(\mathbf{r}\right)={\int }_L{\mathbf{\varphi }}_1\left({\mathbf{r}}_0\right)\overline{\tilde{\mathsf{\Gamma }}(\mathbf{r},{\mathbf{r}}_0)}ds\left({\mathbf{r}}_0\right)+{\int }_{\partial D}{\mathbf{\varphi }}_2\left({\mathbf{r}}_0\right)\overline{\tilde{\mathsf{\Gamma }}(\mathbf{r},{\mathbf{r}}_0)}ds\left({\mathbf{r}}_0\right),$$

(157)

for any $\tilde{\mathbf{\varphi }}=({\mathbf{\varphi }}_1,{\mathbf{\varphi }}_2)\in {[{\tilde{H}}^{-\frac{1}{2}}\left(L\right)]}^2\times {\left[L^2(\partial D)\right]}^2$ with ${\mathbf{\varphi }}_1\left(\mathbf{r}\right)\ne \mathbf{0}$ for all $\mathbf{r}\in L$, we have that:

$$L\subseteq {\mathsf{\Gamma }}_D\iff {\mathsf{\Phi }}_L^1\in Range\left[(H_1^{*},{\mathbf{U}}^{*})\right].$$

(158)

Proof. 

Let us first consider that $L\subseteq {\mathsf{\Gamma }}_D$. Then from ${\tilde{H}}^{-\frac{1}{2}}\left(L\right)\subset {\tilde{H}}^{-\frac{1}{2}}\left({\mathsf{\Gamma }}_D\right)$, and taking into account (153), we easily get

$${\mathsf{\Phi }}_L^1\in Range({\mathbf{H}}_1^{*},{\mathbf{U}}^{*}).$$

(159)

On the contrary and using the abduction method, let us assume that L is not a subset of ${\mathsf{\Gamma }}_D$ and

$${\mathsf{\Phi }}_L^1\in Range(H_1^{*},{\mathbf{U}}^{*})$$

(160)

simultaneously. Therefore, there exists $\tilde{\mathbf{\beta }}=({\mathbf{\beta }}_1,{\mathbf{\beta }}_2)\in {[{\tilde{H}}^{-\frac{1}{2}}\left({\mathsf{\Gamma }}_D\right)]}^2\times [L^2{(\partial D)]}^2$ for which the following relation holds:

$${\mathsf{\Phi }}_L^1\left(\mathbf{r}\right)={\int }_{{\mathsf{\Gamma }}_D}{\mathbf{\beta }}_1\left({\mathbf{r}}_0\right)\overline{\tilde{\mathsf{\Gamma }}(\mathbf{r},{\mathbf{r}}_0)}ds\left({\mathbf{r}}_0\right)+{\int }_{\partial D}{\mathbf{\beta }}_2\left({\mathbf{r}}_0\right)\overline{\tilde{\mathsf{\Gamma }}(\mathbf{r},{\mathbf{r}}_0)}ds\left({\mathbf{r}}_0\right).$$

(161)

If we now take a fixed point $\mathbf{r}\equiv {\mathbf{z}}_0$, such that ${\mathbf{z}}_0\notin {\mathsf{\Gamma }}_D$, but ${\mathbf{z}}_0\in L$, then a singularity for ${\mathsf{\Phi }}_L^1\left(\mathbf{r}\right)$ at $\mathbf{r}={\mathbf{z}}_0$ occurs, whereas the right hand side of (161) has not. The assertion easily follows by contradiction. □

Taking into account Theorems 4–6 and Proposition 1, we are ready now to state the following essential theorem of this paper.

Theorem 7.

Assume that ${\omega }^2$ is neither a Dirichlet eigenvalue of $-{\Delta }^{*}$ in D nor a Dirichlet eigenvalue of $-{\Delta }^{*}$ in $B_0$. Then

$$L\subseteq {\mathsf{\Gamma }}_D\iff {\mathsf{\Phi }}_L^1\in Range\left[({{\mathbf{H}}_{\mathbf{1}}}^{*},{\mathbf{U}}^{*})\right]$$

(162)

and

$$L\subseteq {\mathsf{\Gamma }}_D\iff \sum _{j=1}^{\infty }\frac{|<{\mathsf{\Phi }}_L^1,{\mathbf{\psi }}_j{>}_{L^2\left(C\right)}{|}^2}{|{\lambda }_j|}<\infty .$$

(163)

Here $({\lambda }_j,{\mathbf{\psi }}_j)$ is an eigenvalue system of ${\mathcal{N}}_D^{\#}$, where ${\mathcal{N}}_D^{\#}$ is given in (152).

Using the same steps as before, the shape reconstruction of ${\mathsf{\Gamma }}_I$ can be treated in a similar way. Indeed, if we again assume that ${\omega }^2$ is neither a Dirichlet eigenvalue of $-{\Delta }^{*}$ in D nor a Dirichlet eigenvalue in $B_0$ as well, then the following relations

$$L\subseteq {\mathsf{\Gamma }}_I\iff {\mathsf{\Phi }}_L^2\in Range\left[({\mathbf{U}}^{*},{{\mathbf{H}}_{\mathbf{2}}}^{*})\right],$$

(164)

and

$$L\subseteq {\mathsf{\Gamma }}_I\iff \sum _{j=1}^{\infty }\frac{|<{\mathsf{\Phi }}_L^2,{\mathbf{\psi }}_j{>}_{L^2\left(C\right)}{|}^2}{|{\lambda }_j|}<\infty .$$

(165)

hold, where

$${\mathsf{\Phi }}_L^2:={\int }_{\partial D}{\mathbf{\varphi }}_1\left({\mathbf{r}}_0\right)\overline{\tilde{\mathsf{\Gamma }}(\mathbf{r},{\mathbf{r}}_0)}ds\left({\mathbf{r}}_0\right)+{\int }_L{\mathbf{\varphi }}_2\left({\mathbf{r}}_0\right)(T-i\omega c)\overline{\tilde{\mathsf{\Gamma }}(\mathbf{r},{\mathbf{r}}_0)}ds\left({\mathbf{r}}_0\right),$$

(166)

with $\tilde{\mathbf{\varphi }}=({\mathbf{\varphi }}_1,{\mathbf{\varphi }}_2)\in {\left[L^2(\partial D)\right]}^2\times {[{\tilde{H}}^{\frac{1}{2}}\left(L\right)]}^2$ and ${\mathbf{\varphi }}_2\left(\mathbf{r}\right)\ne \mathbf{0}$ for all $\mathbf{r}\in L$, and here as before $({\lambda }_j,{\mathbf{\psi }}_j)$ is an eigenvalue system of ${\mathcal{N}}_I^{\#}$, recall ${\mathcal{N}}_I^{\#}=|Re\left\{{\mathcal{N}}_I\right\}|+|Im\left\{{\mathcal{N}}_I\right\}|$.

5. Conclusions

In this paper an elastic mixed scattering problem in two dimensional linear elasticity for a non-penetrable obstacle was studied. The direct scattering problem as well as the corresponding inverse one were addressed. We mention that our problem is not a typical one, since it concerns a point-source field placed inside the scatterer, i.e., inside a Lipschitz closed curve into the partially coated obstacle (see Figure 1). We make the following remarks:

(i)

On the boundary of the scatterer, a Dirichlet and an impedance type of boundary condition is imposed, specified by ${\mathsf{\Gamma }}_D$ and ${\mathsf{\Gamma }}_I$, respectively. Our method can be expanded and is still valid, for the case where our boundary is divided into more than two disjoint, relatively open subsets of $\mathsf{\Gamma }$.

(ii)

Solvability of the direct problem is an essential one, since the measurements (data) of the scattered waves inside the partially coated scatterer are used for the corresponding inverse problem.

(iii)

Concerning the corresponding inverse scattering problem, a modified factorisation method in order to retrieve the shape reconstruction of a partially coated obstacle was presented.

(iv)

Basic auxiliary operators were introduced, since from the mathematical point of view the basic Theorem 4 (page 17) could not be applied. The key idea was to factorise these new auxiliary operators and prove some essential properties, in order to apply the above theorem and recover the shape reconstruction of the obstacle.

(v)

An inversion algorithm via Proposition 1 and Theorem 7 were established. Concerning numerical examples, and to the best of our knowledge, in elasticity there are no numerical results for partially coated obstacles which deal with a Dirichlet boundary condition and an impedance one. However, this is beyond the aim of this paper; our analytical method contributes to the understanding of the physical background, and its usefulness lies in checking the credibility of the corresponding numerical technique. We hope to provide examples in the future, and numerical results showing the applicability of the method are also welcomed.