New Improved Results for Oscillation of Fourth-Order Neutral Differential Equations

Abstract

In this study, a new oscillation criterion for the fourth-order neutral delay differential equation ${\left(r\left(u\right){\left({\left(x\left(u\right)+p\left(u\right)x\left(\delta \left(u\right)\right)\right)}^{‴}\right)}^{\alpha }\right)}^{\prime }+q\left(u\right)x^{\beta }\left(\varphi \left(u\right)\right)=0,u\ge u_0$ is established. By introducing a Riccati substitution, we obtain a new criterion for oscillation without requiring the existence of the unknown function. Furthermore, the new criterion improves and complements the previous results in the literature. The results obtained are illustrated by an example.

1. Introduction

The behavior of solutions of functional differential/difference equations is a very fertile area for study and investigation, as it has great importance in various applied sciences; see [1,2,3,4,5]. Delay differential equations (DDEs) of neutral type arise in various phenomena; see Hale’s monograph [3]. Oscillation theory, as one of the branches of qualitative theory, has gained much attention in recent times. Agarwal et al. [6,7], Baculikova and Dzurina [8], Bohner et al. [9,10], Chatzarakis et al. [11], and Moaaz et al [12,13] extended and improved several techniques for studying the oscillation of second-order DDEs. On the other hand, odd-order DDEs have received interest in studies [14,15,16,17]. The development of the study of equations of the second order is reflected in the equations of the even order, and this can be observed in the works [18,19,20,21,22,23,24].

In this study, we establish a new criterion for oscillation of the fourth-order neutral DDE

$${\left(r\left(u\right){\left(w^{‴}\left(u\right)\right)}^{\alpha }\right)}^{\prime }+q\left(u\right)x^{\beta }\left(\varphi \left(u\right)\right)=0,$$

(1)

where $u\ge u_0$ and $w\left(u\right)=x\left(u\right)+p\left(u\right)x\left(\delta \left(u\right)\right)$. Throughout this study, we suppose $\alpha$ and $\beta$ are ratios of odd positive integers and $\beta \ge \alpha ,$$r,\delta \in C^1\left[u_0,\infty \right),$$p,q,\varphi \in C\left[u_0,\infty \right),$$r\left(u\right)>0,$$r^{\prime }\left(u\right)\ge 0,$$q\left(u\right)>0,$$0\le p\left(u\right)<p_0<\infty ,$${\delta }^{\prime }\left(u\right)\ge {\delta }_0>0,$$\varphi \circ \delta =\delta \circ \varphi ,$$\varphi \left(u\right)\le \delta \left(u\right)\le u,$${lim}_{u\to \infty }\delta \left(u\right)={lim}_{u\to \infty }\varphi \left(u\right)=\infty$, and

$${\int }_{u_0}^{\infty }\frac{1}{r^{1/\alpha }\left(\varsigma \right)}\mathrm{d}\varsigma =\infty .$$

Via a solution of (1), we obtain the function x$\in C^3[u_x,\infty ),u_x\ge u_0,$which has the property $r{\left(w^{‴}\right)}^{\alpha }\in C^1[u_x,\infty ),$and satisfies (1) on $[u_x,\infty )$. We consider only those solutions x of (1) that satisfy $sup\{\left|x\left(u\right)\right|:u\ge u\}>0,$for all $u\ge u_x$. A solution of (1) is called oscillatory if it has arbitrarily large zeros on $[u_x,\infty )$ for some $u_x\ge u_0$; otherwise, it is called non-oscillatory.

Many works have dealt with sufficient conditions for oscillation of solutions of the DDE

$$w^{\left(2n\right)}\left(u\right)+q\left(u\right)x\left(\varphi \left(u\right)\right)=0,\mathrm{for}n\ge 2,$$

(2)

and special cases thereof; see [18,20,21,23]. The advantage of these works over others is that they took into account all of the positive values of $p\left(u\right)$. Agarwal et al. [18] studied oscillation of an even-order equation, Equation (2). They concluded a new relationship between the solution x and the corresponding function w as

$$x\left(u\right)\ge w\left(u\right)\frac{1}{p\left({\delta }^{-1}\left(u\right)\right)}\left(1-\frac{1}{p\left({\delta }^{-1}\left({\delta }^{-1}\left(u\right)\right)\right)}{\left(\frac{{\delta }^{-1}\left({\delta }^{-1}\left(u\right)\right)}{{\delta }^{-1}\left(u\right)}\right)}^{n-1}\right),$$

and used a Riccati substitution to obtain the following results:

Theorem 1.

Suppose that

$$p_{*}\left(u\right):=\frac{1}{p\left({\delta }^{-1}\left(u\right)\right)}\left(1-\frac{{\left({\delta }^{-1}\left({\delta }^{-1}\left(u\right)\right)\right)}^{n-1}}{{\left({\delta }^{-1}\left(u\right)\right)}^{n-1}p\left({\delta }^{-1}\left({\delta }^{-1}\left(u\right)\right)\right)}\right)>0.$$

If there exist two functions $\rho ,\varkappa \in C^1\left(\left[u_0,\infty \right),\left(0,\infty \right)\right)$ such that, for some ${\lambda }_0\in \left(0,1\right),$

$${\int }^{\infty }\left(\rho \left(u\right)q\left(u\right)p_{*}\left(\varphi \left(u\right)\right)\frac{{\left({\delta }^{-1}\left(\varphi \left(u\right)\right)\right)}^{n-1}}{u^{n-1}}-\frac{\left(n-2\right)!{\left({\rho }_{+}^{\prime }\left(u\right)\right)}^2}{4{\lambda }_0{u}^{n-2}\rho \left(u\right)}\right)\mathrm{d}u=\infty$$

and

$${\int }^{\infty }\left(\frac{\varkappa \left(u\right)}{\left(n-3\right)!}{\int }_u^{\infty }{\left(\zeta -u\right)}^{n-3}q\left(\zeta \right)p^{*}\left(\varphi \left(\zeta \right)\right)\frac{{\delta }^{-1}\left(\varphi \left(\zeta \right)\right)}{\zeta }\mathrm{d}\zeta -\frac{{\left({\varkappa }_{+}^{\prime }\left(u\right)\right)}^2}{4\varkappa \left(u\right)}\right)\mathrm{d}u=\infty ,$$

then (2) is oscillatory.

By using a different technique (comparison with the first-order delay equation), Baculikova et al. [20] and Xing et al. [23] studied the sufficient conditions for oscillation of (2).

Theorem 2.

(Corollary 2.8, Corollary 2.14 [20,23]). If ϕ is invertible, ${\varphi }^{-1}\in C^1([u_0,\infty ),R),$${\left({\varphi }^{-1}\left(u\right)\right)}^{\prime }\ge {\varphi }_0>0$ and

$$\frac{{\delta }_0{\varphi }_0}{\left({\delta }_0+p_0\right)\left(n-1\right)!}\underset{u\to \infty }{liminf}{\int }_{{\delta }^{-1}\left(\varphi \left(u\right)\right)}^u\tilde{Q}\left(\varsigma \right){\varsigma }^{n-1}\mathrm{d}\varsigma >\frac{1}{\mathrm{e}},$$

then (2) is oscillatory, where $\tilde{Q}\left(u\right)=min\{q\left({\varphi }^{-1}\left(u\right)\right),q\left({\varphi }^{-1}\left(\delta \left(u\right)\right)\right)\}$.

Moreover, Baculikova et al. [20] introduced a new Riccati substitution to obtain one condition that guarantees oscillation for (2).

Theorem 3.

Assume that ${\left({\varphi }^{-1}\left(u\right)\right)}^{\prime }\ge {\varphi }_0>0$. If there exists a function $\kappa \left(u\right)\in C^1\left(\left[u_0,\infty \right),\left(0,\infty \right)\right)$ such that

$$\underset{u\to \infty }{limsup}{\int }_{u_0}^u\left(\frac{1}{2^{\beta -1}}\kappa \left(\varsigma \right)\tilde{Q}\left(\varsigma \right)-\frac{\left(\frac{1}{{\varphi }_0}+\frac{p_0^{\alpha }}{{\varphi }_0{\delta }_0}\right){\left({\kappa }_{+}^{\prime }\left(\varsigma \right)\right)}^{\alpha +1}}{{\left(\alpha +1\right)}^{\left(\alpha +1\right)}{\left(ϵM{\varsigma }^{n-2}\rho \left(\varsigma \right)\right)}^{\alpha }}\right)\mathrm{d}\varsigma =\infty ,$$

(3)

holds for some $ϵ\in \left(0,1\right)$ and for all $M>0$, then (2) is oscillatory.

It can be clearly observed that the previous theorem is not sufficient for application to a high number of examples due to the necessity to fulfill Condition (3) for all positive values of M.

In 2016, Li and Rogovchenko [21] improved the results in [18,20,23]. They used an approach similar to that used in [18] but based on a comparison with the first-order delay equation.

Theorem 4.

Assume that there exist functions $\varrho \in C\left[u_0,\infty \right)$ and $\xi \in C^1\left[u_0,\infty \right)$ satisfying

$$\varrho \left(u\right)\le \varphi \left(u\right),\varrho \left(u\right)<\delta \left(u\right),\xi \left(u\right)\le \varphi \left(u\right),\xi \left(u\right)<\delta \left(u\right),{\xi }^{\prime }\left(u\right)\ge 0$$

and

$$\underset{u\to \infty }{lim}\varrho \left(u\right)=\underset{u\to \infty }{lim}\xi \left(u\right)=\infty .$$

If

$$\frac{1}{\left(n-1\right)!}\underset{u\to \infty }{liminf}{\int }_{{\delta }^{-1}\left(\varrho \left(u\right)\right)}^{u}q\left(\varsigma \right)p_{*}\left(\varphi \left(\varsigma \right)\right){\left({\delta }^{-1}\left(\varrho \left(\varsigma \right)\right)\right)}^{n-1}\mathrm{d}\varsigma >\frac{1}{\mathrm{e}}$$

and

$$\frac{1}{\left(n-3\right)!}\underset{u\to \infty }{liminf}{\int }_{{\delta }^{-1}\left(\xi \left(u\right)\right)}^u\left({\int }_{\varsigma }^{\infty }{\left(\nu -\varsigma \right)}^{n-3}q\left(\nu \right)p^{*}\left(\varphi \left(\nu \right)\right)\mathrm{d}\nu \right){\delta }^{-1}\left(\xi \left(\varsigma \right)\right)\mathrm{d}\varsigma >\frac{1}{\mathrm{e}},$$

then (2) is oscillatory, where

$$p^{*}\left(u\right)=\frac{1}{p\left({\delta }^{-1}\left(u\right)\right)}\left(1-\frac{{\delta }^{-1}\left({\delta }^{-1}\left(u\right)\right)}{{\delta }^{-1}\left(u\right)p\left({\delta }^{-1}\left({\delta }^{-1}\left(u\right)\right)\right)}\right).$$

Since there is no general rule as to how to choose functions $\varrho$ and $\xi$ satisfying the imposed conditions, an interesting problem is how an improved result can be established without requiring the existence of the unknown function $\varrho$ and $\xi$.

In this paper, we are interested in studying the oscillatory behavior of solutions to a class of DDEs of neutral type. The technique used is based on introducing two Riccati substitutes, such as that used in Theorem 3. However, in the case where $\alpha =\beta$, we present conditions that do not need to be satisfied for all positive values of M. Moreover, the technique used (Riccati substitution) is distinguished from that used in [21,23] in that it does not require the assumption of unknown functions. Using the example most often mentioned in the literature, we compare our results with previous results.

In order to discuss our main results, we need the following lemmas:

Lemma 1

([8]). Let $A,B\ge 0$. Then

$${\left(A+B\right)}^{\beta }\le 2^{\beta -1}\left(A^{\beta }+B^{\beta }\right),\mathrm{for}\beta \ge 1$$

and

$${\left(A+B\right)}^{\beta }\le \left(A^{\beta }+B^{\beta }\right),\mathrm{for}\beta \le 1.$$

Lemma 2

([24]). Let α bea ratios of two odd positive integers. Then

$$Kv-u{v}^{{}^{\left(\alpha +1\right)/\alpha }}\le \frac{{\alpha }^{\alpha }}{{(\alpha +1)}^{\alpha +1}}\frac{K^{\alpha +1}}{u^{\alpha }},u>0.$$

Lemma 3

([25]). Let $\mathsf{\Omega }\in C^n\left(\left[u_0,\infty \right),\left(0,\infty \right)\right).$ Suppose that ${\mathsf{\Omega }}^{\left(n\right)}\left(u\right)\ne 0$ is of fixed sign on $\left[u_0,\infty \right)$ and ${\mathsf{\Omega }}^{\left(n-1\right)}\left(u\right){\mathsf{\Omega }}^{\left(n\right)}\left(u\right)\le 0$ for all $u\ge u_1\ge u_0$. If ${lim}_{u\to \infty }\mathsf{\Omega }\left(u\right)\ne 0,$ then there exists $u_{\mu }\ge u_1$ such that

$$\mathsf{\Omega }\left(u\right)\ge \frac{\mu }{\left(n-1\right)!}{u}^{n-1}\left|{\mathsf{\Omega }}^{\left(n-1\right)}\left(u\right)\right|,$$

for all $u\ge u_{\mu }$ and $\mu \in \left(0,1\right)$.

Lemma 4

([26]). Assume that z satisfies $z^{\left(k\right)}\left(u\right)>0,$$k=0,1,...,n,$ and $z^{\left(k+1\right)}\left(u\right)<0,$ then

$$z\left(u\right)\ge \frac{\lambda }{k}u{z}^{\prime }\left(u\right),$$

for all values of $\lambda$in $\left(0,1\right)$ eventually.

2. Main Results

In the sequel, we adopt the following notation:

$${\eta }_1\left(u,u_1\right)={\int }_{u_1}^u\frac{1}{r^{1/\alpha }\left(\varsigma \right)}\mathrm{d}\varsigma ,$$

$${\eta }_{k+1}\left(u,u_1\right)={\int }_{u_1}^u{\eta }_k\left(\nu ,u_1\right)\mathrm{d}\nu ,k=1,2$$

and

$$Q\left(u\right)=min\left\{q\left(u\right),q\left(\delta \left(u\right)\right)\right\}.$$

Lemma 5.

Let $x$be a positive solution of (1). Then, ${\left(r\left(u\right){\left(w^{‴}\left(u\right)\right)}^{\alpha }\right)}^{\prime }<0$ and there are two possible cases eventually:

$$\begin{array}{ccc}\hfill \left({\mathbf{C}}_1\right)w\left(u\right)& >& 0,w^{\prime }\left(u\right)>0,w^{″}\left(u\right)>0,w^{‴}\left(u\right)>0,w^{\left(4\right)}\left(u\right)<0;\hfill \\ \hfill \left({\mathbf{C}}_2\right)w\left(u\right)& >& 0,w^{\prime }\left(u\right)>0,w^{″}\left(u\right)<0,w^{‴}\left(u\right)>0.\hfill \end{array}$$

Proof. 

Assume that x is a positive solution of (1). From (1), we obtain ${\left(r\left(u\right){\left(w^{‴}\left(u\right)\right)}^{\alpha }\right)}^{\prime }\le 0$. Thus, using Lemma 2.2.1 in [25], we obtain the cases $\left({\mathbf{C}}_1\right)$ and $\left({\mathbf{C}}_2\right)$ for the function w and its derivatives. □

Theorem 5.

Let $\beta \ge 1$,

$$\varphi \left(u\right)\in C^1\left(\left[u_0,\infty \right)\right),{\varphi }^{\prime }>0\mathrm{and}\varphi \left(u\right)\le \delta \left(u\right).$$

Assume that there exist functions $\rho ,$$\vartheta \in C^1\left(\left[u_0,\infty \right),\left(0,\infty \right)\right)$ such that

$$\underset{u\to \infty }{limsup}{\int }_{u_0}^u\left(M^{\beta -\alpha }\rho \left(\varsigma \right)\frac{Q\left(\varsigma \right)}{2^{\beta -1}}-\left(1+\frac{p_0^{\beta }}{{\delta }_0}\right)\frac{{\left(\alpha +1\right)}^{-\left(\alpha +1\right)}{\left({\rho }_{+}^{\prime }\left(\varsigma \right)\right)}^{\alpha +1}}{{\left(\rho \left(\varsigma \right){\eta }_2\left(\varphi \left(\varsigma \right),u_1\right){\varphi }^{\prime }\left(\varsigma \right)\right)}^{\alpha }}\right)\mathrm{d}\varsigma =\infty$$

(4)

and

$$\underset{u\to \infty }{limsup}{\int }_{u_0}^u\left(M^{\left(\beta /\alpha \right)-1}\vartheta \left(v\right){\left(\frac{{\delta }_0}{{\delta }_0+p_0^{\beta }}\right)}^{1/\alpha }{\int }_v^{\infty }{\left(\frac{1}{r\left(\nu \right)}\mathsf{\Phi }\left(\nu \right)\right)}^{1/\alpha }\mathrm{d}\nu -\frac{{\left({\vartheta }_{+}^{\prime }\left(v\right)\right)}^2}{4\vartheta \left(v\right)}\right)\mathrm{d}v=\infty ,$$

(5)

for all $M>0$ and some $\lambda \in \left(0,1\right)$, where

$$\mathsf{\Phi }\left(\nu \right)={\int }_{{\delta }^{-1}\left(\nu \right)}^{\infty }\frac{Q\left(\varsigma \right)}{2^{\beta -1}}{\left(\frac{\varphi \left(\varsigma \right)}{\varsigma }\right)}^{\beta /\lambda }\mathrm{d}\varsigma ,$$

${\rho }_{+}^{\prime }\left(u\right)=max\left\{0,{\rho }^{\prime }\left(u\right)\right\}$ and ${\vartheta }_{+}^{\prime }\left(u\right)=max\left\{0,{\vartheta }^{\prime }\left(u\right)\right\}$. Thus, (1) is oscillatory.

Proof. 

Assume that x is a positive solution of (1). It follows from Lemma 5 that there exist two possible cases: $\left(C_1\right)$ and $\left(C_2\right).$ Let $\left(C_1\right)$ hold. Since ${\left(r\left(u\right){\left(w^{‴}\left(u\right)\right)}^{\alpha }\right)}^{\prime }\le 0$, we obtain

$$\begin{array}{ccc}\hfill w^{″}\left(u\right)& \ge & w^{″}\left(u\right)-w^{″}\left(u_1\right)={\int }_{u_1}^u\frac{{\left(r\left(\varsigma \right){\left(w^{‴}\left(\varsigma \right)\right)}^{\alpha }\right)}^{1/\alpha }}{r^{1/\alpha }\left(\varsigma \right)}\mathrm{d}\varsigma \hfill \\ & \ge & r^{1/\alpha }\left(u\right)w^{‴}\left(u\right){\eta }_1\left(u,u_1\right),\hfill \end{array}$$

integrating the above inequality from $u_1$ to $u,$ we have

$$w^{\prime }\left(u\right)\ge r^{1/\alpha }\left(u\right)w^{‴}\left(u\right){\eta }_2\left(u,u_1\right),$$

(6)

integrating (6) from $u_1$ to $u,$ we obtain

$$w\left(u\right)\ge r^{1/\alpha }\left(u\right)w^{‴}\left(u\right){\eta }_3\left(u,u_1\right).$$

(7)

Now, from (1), we obtain

$$\begin{array}{ccc}\hfill 0& \ge & {\left(r\left(u\right){\left(w^{‴}\left(u\right)\right)}^{\alpha }\right)}^{\prime }+\frac{p_0^{\beta }}{{\delta }_0}{\left(r\left(\delta \left(u\right)\right){\left(w^{‴}\left(\delta \left(u\right)\right)\right)}^{\alpha }\right)}^{\prime }+q\left(u\right)x^{\beta }\left(\varphi \left(u\right)\right)\hfill \\ & & +p_0^{\beta }q\left(\delta \left(u\right)\right)x^{\beta }\left(\varphi \left(\delta \left(u\right)\right)\right),\hfill \end{array}$$

which follows from Lemma 1 and $\varphi o\delta =\delta o\varphi$ that

$${\left(r\left(u\right){\left(w^{‴}\left(u\right)\right)}^{\alpha }\right)}^{\prime }+\frac{p_0^{\beta }}{{\delta }_0}{\left(r\left(\delta \left(u\right)\right){\left(w^{‴}\left(\delta \left(u\right)\right)\right)}^{\alpha }\right)}^{\prime }+\frac{Q\left(u\right)}{2^{\beta -1}}{w}^{\beta }\left(\varphi \left(u\right)\right)\le 0.$$

(8)

Next, defining the function $\omega \left(u\right)$ as

$$\omega \left(u\right)=\rho \left(u\right)\frac{r\left(u\right){\left(w^{‴}\left(u\right)\right)}^{\alpha }}{w^{\alpha }\left(\varphi \left(u\right)\right)},$$

(9)

then $\omega \left(u\right)>0.$ Differentiating (9) with respect to u, we have

$${\omega }^{\prime }\left(u\right)=\frac{{\rho }^{\prime }\left(u\right)}{\rho \left(u\right)}\omega \left(u\right)+\rho \left(u\right)\frac{{\left(r\left(u\right){\left(w^{‴}\left(u\right)\right)}^{\alpha }\right)}^{\prime }}{w^{\alpha }\left(\varphi \left(u\right)\right)}-\rho \left(u\right)\frac{\alpha r\left(u\right){\left(w^{‴}\left(u\right)\right)}^{\alpha }{w}^{\prime }\left(\varphi \left(u\right)\right){\varphi }^{\prime }\left(u\right)}{w^{\alpha +1}\left(\varphi \left(u\right)\right)},$$

(10)

from (6) and $\varphi \left(u\right)<u,$ we obtain

$$w^{\prime }\left(\varphi \left(u\right)\right)\ge r^{1/\alpha }\left(\varphi \left(u\right)\right)w^{‴}\left(\varphi \left(u\right)\right){\eta }_2\left(\varphi \left(u\right),u_1\right)\ge r^{1/\alpha }\left(u\right)w^{‴}\left(u\right){\eta }_2\left(\varphi \left(u\right),u_1\right),$$

(11)

and, thus, (10) can be written as

$${\omega }^{\prime }\left(u\right)\le \frac{{\rho }^{\prime }\left(u\right)}{\rho \left(u\right)}\omega \left(u\right)+\rho \left(u\right)\frac{{\left(r\left(u\right){\left(w^{‴}\left(u\right)\right)}^{\alpha }\right)}^{\prime }}{w^{\alpha }\left(\varphi \left(u\right)\right)}-\frac{\alpha {\left(w^{‴}\left(u\right)\right)}^{\alpha +1}{\eta }_2\left(\varphi \left(u\right),u_1\right){\varphi }^{\prime }\left(u\right)}{{\rho }^{-1}\left(u\right)r^{-\left(\alpha +1\right)/\alpha }\left(u\right)w^{\alpha +1}\left(\varphi \left(u\right)\right)}.$$

(12)

It follows from (9) and (12) that

$${\omega }^{\prime }\left(u\right)\le \frac{{\rho }^{\prime }\left(u\right)}{\rho \left(u\right)}\omega \left(u\right)+\rho \left(u\right)\frac{{\left(r\left(u\right){\left(w^{‴}\left(u\right)\right)}^{\alpha }\right)}^{\prime }}{w^{\alpha }\left(\varphi \left(u\right)\right)}-\frac{\alpha {\eta }_2\left(\varphi \left(u\right),u_1\right){\varphi }^{\prime }\left(u\right)}{{\rho }^{1/\alpha }\left(u\right)}{\omega }^{\left(\alpha +1\right)/\alpha }\left(u\right).$$

(13)

Similarly, defining another function $\psi$ by

$$\psi \left(u\right)=\rho \left(u\right)\frac{r\left(\delta \left(u\right)\right){\left(w^{‴}\left(\delta \left(u\right)\right)\right)}^{\alpha }}{w^{\alpha }\left(\varphi \left(u\right)\right)},$$

(14)

then $\psi \left(u\right)>0.$ Differentiating (14) with respect to u, we have

$${\psi }^{\prime }\left(u\right)=\frac{{\rho }^{\prime }\left(u\right)}{\rho \left(u\right)}\psi \left(u\right)+\rho \left(u\right)\frac{{\left(r\left(\delta \left(u\right)\right){\left(w^{‴}\left(\delta \left(u\right)\right)\right)}^{\alpha }\right)}^{\prime }}{w^{\alpha }\left(\varphi \left(u\right)\right)}-\frac{\alpha {\left(w^{‴}\left(\delta \left(u\right)\right)\right)}^{\alpha }{w}^{\prime }\left(\varphi \left(u\right)\right){\varphi }^{\prime }\left(u\right)}{{\rho }^{-1}\left(u\right)r^{-1}\left(\delta \left(u\right)\right)w^{\alpha +1}\left(\varphi \left(u\right)\right)},$$

(15)

from (6) and $\varphi \left(u\right)<\delta \left(u\right),$ we obtain

$$w^{\prime }\left(\varphi \left(u\right)\right)\ge r^{1/\alpha }\left(\varphi \left(u\right)\right)w^{‴}\left(\varphi \left(u\right)\right){\eta }_2\left(\varphi \left(u\right),u_1\right)\ge r^{1/\alpha }\left(\delta \left(u\right)\right)w^{‴}\left(\delta \left(u\right)\right){\eta }_2\left(\varphi \left(u\right),u_1\right),$$

(16)

and, thus, (15) can be written as

$${\psi }^{\prime }\left(u\right)\le \frac{{\rho }^{\prime }\left(u\right)}{\rho \left(u\right)}\psi \left(u\right)+\rho \left(u\right)\frac{{\left(r\left(\delta \left(u\right)\right){\left(w^{‴}\left(\delta \left(u\right)\right)\right)}^{\alpha }\right)}^{\prime }}{w^{\alpha }\left(\varphi \left(u\right)\right)}-\frac{\alpha {\left(w^{‴}\left(\delta \left(u\right)\right)\right)}^{\alpha +1}{\eta }_2\left(\varphi \left(u\right),u_1\right){\varphi }^{\prime }\left(u\right)}{{\rho }^{-1}\left(u\right)r^{-\left(1+\alpha \right)/\alpha }\left(\delta \left(u\right)\right)w^{\alpha +1}\left(\varphi \left(u\right)\right)}.$$

(17)

It follows from (14) and (17) that

$${\psi }^{\prime }\left(u\right)\le \frac{{\rho }^{\prime }\left(u\right)}{\rho \left(u\right)}\psi \left(u\right)+\rho \left(u\right)\frac{{\left(r\left(\delta \left(u\right)\right){\left(w^{‴}\left(\delta \left(u\right)\right)\right)}^{\alpha }\right)}^{\prime }}{w^{\alpha }\left(\varphi \left(u\right)\right)}-\frac{\alpha {\eta }_2\left(\varphi \left(u\right),u_1\right){\varphi }^{\prime }\left(u\right)}{{\rho }^{1/\alpha }\left(u\right)}{\psi }^{\left(1+\alpha \right)/\alpha }\left(u\right).$$

(18)

Multiplying (18) by $p_0^{\beta }/{\delta }_0$ and combining it with (13), we obtain

$$\begin{array}{ccc}\hfill {\omega }^{\prime }\left(u\right)+\frac{p_0^{\beta }}{{\delta }_0}{\psi }^{\prime }\left(u\right)& \le & \rho \left(u\right)\left(\frac{{\left(r\left(u\right){\left(w^{‴}\left(u\right)\right)}^{\alpha }\right)}^{\prime }}{w^{\alpha }\left(\varphi \left(u\right)\right)}+\frac{p_0^{\beta }}{{\delta }_0}\frac{{\left(r\left(\delta \left(u\right)\right){\left(w^{‴}\left(\delta \left(u\right)\right)\right)}^{\alpha }\right)}^{\prime }}{w^{\alpha }\left(\varphi \left(u\right)\right)}\right)\hfill \\ & & +\frac{{\rho }_{+}^{\prime }\left(u\right)}{\rho \left(u\right)}\omega \left(u\right)-\frac{\alpha {\eta }_2\left(\varphi \left(u\right),u_1\right){\varphi }^{\prime }\left(u\right)}{{\rho }^{1/\alpha }\left(u\right)}{\omega }^{\left(\alpha +1\right)/\alpha }\left(u\right)\hfill \\ & & +\frac{p_0^{\beta }}{{\delta }_0}\left(\frac{{\rho }_{+}^{\prime }\left(u\right)}{\rho \left(u\right)}\psi \left(u\right)-\frac{\alpha {\eta }_2\left(\varphi \left(u\right),u_1\right){\varphi }^{\prime }\left(u\right)}{{\rho }^{1/\alpha }\left(u\right)}{\psi }^{\left(1+\alpha \right)/\alpha }\left(u\right)\right).\hfill \end{array}$$

From (8), we obtain

$$\begin{array}{ccc}\hfill {\omega }^{\prime }\left(u\right)+\frac{p_0^{\beta }}{{\delta }_0}{\psi }^{\prime }\left(u\right)& \le & -\rho \left(u\right)\frac{Q\left(u\right)}{2^{\beta -1}}\frac{w^{\beta }\left(\varphi \left(u\right)\right)}{w^{\alpha }\left(\varphi \left(u\right)\right)}-\frac{\alpha {\eta }_2\left(\varphi \left(u\right),u_1\right){\varphi }^{\prime }\left(u\right)}{{\rho }^{1/\alpha }\left(u\right)}{\omega }^{\left(\alpha +1\right)/\alpha }\left(u\right)\hfill \\ & & +\frac{p_0^{\beta }}{{\delta }_0}\left(\frac{{\rho }_{+}^{\prime }\left(u\right)}{\rho \left(u\right)}\psi \left(u\right)-\frac{\alpha {\eta }_2\left(\varphi \left(u\right),u_1\right){\varphi }^{\prime }\left(u\right)}{{\rho }^{1/\alpha }\left(u\right)}{\psi }^{\left(1+\alpha \right)/\alpha }\left(u\right)\right)\hfill \\ & & +\frac{{\rho }_{+}^{\prime }\left(u\right)}{\rho \left(u\right)}\omega \left(u\right).\hfill \end{array}$$

(19)

From Lemma 2, (20), becomes

$$\begin{array}{ccc}\hfill {\omega }^{\prime }\left(u\right)+\frac{p_0^{\beta }}{{\delta }_0}{\psi }^{\prime }\left(u\right)& \le & -\rho \left(u\right)\frac{Q\left(u\right)}{2^{\beta -1}}{w}^{\beta -\alpha }\left(\varphi \left(u\right)\right)+\frac{1}{{\left(\alpha +1\right)}^{\alpha +1}}\frac{{\left({\rho }_{+}^{\prime }\left(u\right)\right)}^{\alpha +1}}{{\left(\rho \left(u\right){\eta }_2\left(\varphi \left(u\right),u_1\right){\varphi }^{\prime }\left(u\right)\right)}^{\alpha }}\hfill \\ & & +\frac{p_0^{\beta }}{{\delta }_0}\frac{1}{{\left(\alpha +1\right)}^{\alpha +1}}\frac{{\left({\rho }_{+}^{\prime }\left(u\right)\right)}^{\alpha +1}}{{\left(\rho \left(u\right){\eta }_2\left(\varphi \left(u\right),u_1\right){\varphi }^{\prime }\left(u\right)\right)}^{\alpha }}.\hfill \end{array}$$

(20)

Since $w^{\prime }\left(u\right)>0$, there exist a $u_2\ge u_1$ and a constant $M>0$ such that

$$w\left(u\right)>M,\mathrm{for}\mathrm{all}u\ge u_2,$$

(21)

by using (21) and integrating (20) from $u_2$$\left(u_2\ge u_1\right)$ to u, we obtain

$$\begin{array}{ccc}\hfill {\int }_{u_2}^u\left(\rho \left(\varsigma \right)\frac{Q\left(\varsigma \right)}{2^{\beta -1}}{M}^{\beta -\alpha }-\left(1+\frac{p_0^{\beta }}{{\delta }_0}\right)\frac{{\left(\alpha +1\right)}^{-\left(\alpha +1\right)}{\left({\rho }_{+}^{\prime }\left(\varsigma \right)\right)}^{\alpha +1}}{{\left(\rho \left(\varsigma \right){\eta }_2\left(\varphi \left(\varsigma \right),u_1\right){\varphi }^{\prime }\left(\varsigma \right)\right)}^{\alpha }}\right)\mathrm{d}\varsigma & \le & \omega \left(u_2\right)\hfill \\ & & +\frac{p_0^{\beta }}{{\delta }_0}\psi \left(u_2\right),\hfill \end{array}$$

which contradicts (4).

Let $\left(C_2\right)$ hold. We define a function $\phi \left(u\right)$ by

$$\phi \left(u\right)=\vartheta \left(u\right)\frac{w^{\prime }\left(u\right)}{w\left(u\right)},$$

(22)

then $\omega \left(u\right)>0.$ Differentiating (22), we have

$${\phi }^{\prime }\left(u\right)=\frac{{\vartheta }^{\prime }\left(u\right)}{\vartheta \left(u\right)}\phi \left(u\right)+\vartheta \left(u\right)\frac{w^{″}\left(u\right)}{w\left(u\right)}-\vartheta \left(u\right)\frac{{\left(w^{\prime }\left(u\right)\right)}^2}{w^2\left(u\right)},$$

(23)

from (22) and (23), we have

$${\phi }^{\prime }\left(u\right)=\frac{{\vartheta }^{\prime }\left(u\right)}{\vartheta \left(u\right)}\phi \left(u\right)+\vartheta \left(u\right)\frac{w^{″}\left(u\right)}{w\left(u\right)}-\frac{1}{\vartheta \left(u\right)}{\phi }^2\left(u\right).$$

(24)

Integrating (8) from u to ∞ and using ${\left(r\left(u\right){\left(w^{‴}\left(u\right)\right)}^{\alpha }\right)}^{\prime }\le 0,$ we obtain

$$-r\left(u\right){\left(w^{‴}\left(u\right)\right)}^{\alpha }-\frac{p_0^{\beta }}{{\delta }_0}r\left(\delta \left(u\right)\right){\left(w^{‴}\left(\delta \left(u\right)\right)\right)}^{\alpha }\le -{\int }_u^{\infty }\frac{Q\left(\varsigma \right)}{2^{\beta -1}}{w}^{\beta }\left(\varphi \left(\varsigma \right)\right)\mathrm{d}\varsigma .$$

(25)

From Lemma 4 and (25), we have

$$-r\left(u\right){\left(w^{‴}\left(u\right)\right)}^{\alpha }-\frac{p_0^{\beta }}{{\delta }_0}r\left(\delta \left(u\right)\right){\left(w^{‴}\left(\delta \left(u\right)\right)\right)}^{\alpha }\le -{\int }_u^{\infty }\frac{Q\left(\varsigma \right)}{2^{\beta -1}}{\left(\frac{\varphi \left(\varsigma \right)}{\varsigma }\right)}^{\beta /\lambda }{w}^{\beta }\left(\varsigma \right)\mathrm{d}\varsigma ,$$

that is,

$$r\left(u\right){\left(w^{‴}\left(u\right)\right)}^{\alpha }+\frac{p_0^{\beta }}{{\delta }_0}r\left(\delta \left(u\right)\right){\left(w^{‴}\left(\delta \left(u\right)\right)\right)}^{\alpha }\ge w^{\beta }\left(u\right){\int }_u^{\infty }\frac{Q\left(\varsigma \right)}{2^{\beta -1}}{\left(\frac{\varphi \left(\varsigma \right)}{\varsigma }\right)}^{\beta /\lambda }\mathrm{d}\varsigma ,$$

since $\delta \left(u\right)\le u$ and ${\left(r\left(u\right){\left(w^{‴}\left(u\right)\right)}^{\alpha }\right)}^{\prime }\le 0$, we have

$$r\left(\delta \left(u\right)\right){\left(w^{‴}\left(\delta \left(u\right)\right)\right)}^{\alpha }+\frac{p_0^{\beta }}{{\delta }_0}r\left(\delta \left(u\right)\right){\left(w^{‴}\left(\delta \left(u\right)\right)\right)}^{\alpha }\ge w^{\beta }\left(u\right){\int }_u^{\infty }\frac{Q\left(\varsigma \right)}{2^{\beta -1}}{\left(\frac{\varphi \left(\varsigma \right)}{\varsigma }\right)}^{\beta /\lambda }\mathrm{d}\varsigma ,$$

that is,

$$r\left(\delta \left(u\right)\right){\left(w^{‴}\left(\delta \left(u\right)\right)\right)}^{\alpha }\ge \left(\frac{{\delta }_0}{{\delta }_0+p_0^{\beta }}\right)w^{\beta }\left(u\right){\int }_u^{\infty }\frac{Q\left(\varsigma \right)}{2^{\beta -1}}{\left(\frac{\varphi \left(\varsigma \right)}{\varsigma }\right)}^{\beta /\lambda }\mathrm{d}\varsigma$$

(26)

or

$$r\left(u\right){\left(w^{‴}\left(u\right)\right)}^{\alpha }\ge \left(\frac{{\delta }_0}{{\delta }_0+p_0^{\beta }}\right)w^{\beta }\left({\delta }^{-1}\left(u\right)\right){\int }_{{\delta }^{-1}\left(u\right)}^{\infty }\frac{Q\left(\varsigma \right)}{2^{\beta -1}}{\left(\frac{\varphi \left(\varsigma \right)}{\varsigma }\right)}^{\beta /\lambda }\mathrm{d}\varsigma ,$$

since ${\delta }^{-1}\left(u\right)>u$, then $w\left({\delta }^{-1}\left(u\right)\right)>w\left(u\right).$ From the above inequality, we have

$$r\left(u\right){\left(w^{‴}\left(u\right)\right)}^{\alpha }\ge \left(\frac{{\delta }_0}{{\delta }_0+p_0^{\beta }}\right)w^{\beta }\left(u\right){\int }_{{\delta }^{-1}\left(u\right)}^{\infty }\frac{Q\left(\varsigma \right)}{2^{\beta -1}}{\left(\frac{\varphi \left(\varsigma \right)}{\varsigma }\right)}^{\beta /\lambda }\mathrm{d}\varsigma .$$

Integrating the above inequality from u to $\infty ,$ we obtain

$$w^{″}\left(u\right)\le -{\left(\frac{{\delta }_0}{{\delta }_0+p_0^{\beta }}\right)}^{1/\alpha }{w}^{\beta /\alpha }\left(u\right){\int }_u^{\infty }{\left(\frac{1}{r\left(\nu \right)}{\int }_{{\delta }^{-1}\left(\nu \right)}^{\infty }\frac{Q\left(\varsigma \right)}{2^{\beta -1}}{\left(\frac{\varphi \left(\varsigma \right)}{\varsigma }\right)}^{\beta /\lambda }\mathrm{d}\varsigma \right)}^{1/\alpha }\mathrm{d}\nu ,$$

(27)

from (27) and (24), we have

$$\begin{array}{ccc}\hfill {\phi }^{\prime }\left(u\right)& \le & -\vartheta \left(u\right){\left(\frac{{\delta }_0}{{\delta }_0+p_0^{\beta }}\right)}^{1/\alpha }{w}^{\left(\beta /\alpha \right)-1}\left(u\right){\int }_u^{\infty }{\left(\frac{1}{r\left(\nu \right)}\mathsf{\Phi }\left(\nu \right)\right)}^{1/\alpha }\mathrm{d}\nu \hfill \\ & & +\frac{{\vartheta }^{\prime }\left(u\right)}{\vartheta \left(u\right)}\phi \left(u\right)-\frac{1}{\vartheta \left(u\right)}{\phi }^2\left(u\right).\hfill \end{array}$$

Thus, we obtain

$${\phi }^{\prime }\left(u\right)\le -\vartheta \left(u\right){\left(\frac{{\delta }_0}{{\delta }_0+p_0^{\beta }}\right)}^{1/\alpha }{w}^{\left(\beta /\alpha \right)-1}\left(u\right){\int }_u^{\infty }{\left(\frac{1}{r\left(\nu \right)}\mathsf{\Phi }\left(\nu \right)\right)}^{1/\alpha }\mathrm{d}\nu +\frac{{\left({\vartheta }_{+}^{\prime }\left(u\right)\right)}^2}{4\vartheta \left(u\right)},$$

(28)

by using (21) and integrating (28) from $u_1$ to u, we obtain

$$\phi \left(u_1\right)\ge {\int }_{u_1}^u\left(\vartheta \left(v\right){\left(\frac{{\delta }_0}{{\delta }_0+p_0^{\beta }}\right)}^{1/\alpha }{M}^{\left(\beta /\alpha \right)-1}{\int }_v^{\infty }{\left(\frac{1}{r\left(\nu \right)}\mathsf{\Phi }\left(\nu \right)\right)}^{1/\alpha }\mathrm{d}\nu -\frac{{\left({\vartheta }_{+}^{\prime }\left(v\right)\right)}^2}{4\vartheta \left(v\right)}\right)\mathrm{d}v,$$

which contradicts (5). This completes the proof. □

Example 1.

Consider the fourth-order neutral differential equation

$${\left(x\left(u\right)+p_{0}x\left(au\right)\right)}^{\left(4\right)}+\frac{q_0}{u^4}x\left(bu\right)=0,$$

(29)

where $a,b\in \left(0,1\right),$$a>b,$ and $q_0>0$. We note that $p\left(u\right)=p_0,$$\delta \left(u\right)=au,$$\varphi \left(u\right)=bu,$ and $q\left(u\right)=q_0/u^4$. It can be easily verified that

$$\begin{array}{ccc}\hfill Q\left(u\right)& =& \frac{q_0}{u^4},\hfill \\ \hfill \mathsf{\Phi }\left(u\right)& =& q_0{b}^{1/\lambda }{a}^3\frac{1}{3u^3}\hfill \end{array}$$

and

$${\eta }_2\left(\varphi \left(u\right),u_1\right)=\frac{1}{2}{\left(bu-u_1\right)}^2.$$

By choosing $\rho \left(u\right)=u^3$ and $\vartheta \left(u\right)=u,$ we obtain

$$\begin{array}{ccc}& & \underset{u\to \infty }{limsup}{\int }_{u_2}^u\left(\rho \left(\varsigma \right)\frac{Q\left(\varsigma \right)}{2^{\beta -1}}{M}^{\beta -\alpha }-\frac{\left(1+\frac{p_0^{\beta }}{{\delta }_0}\right)}{{\left(\alpha +1\right)}^{\alpha +1}}\frac{{\left({\rho }_{+}^{\prime }\left(\varsigma \right)\right)}^{\alpha +1}}{{\left(\rho \left(\varsigma \right){\eta }_2\left(\varphi \left(\varsigma \right),u_1\right){\varphi }^{\prime }\left(\varsigma \right)\right)}^{\alpha }}\right)\mathrm{d}\varsigma \hfill \\ & & =\underset{u\to \infty }{limsup}{\int }_{u_2}^u\left({\varsigma }^3\frac{q_0}{{\varsigma }^4}-\frac{\left(1+\frac{p_0}{a}\right)}{{\left(2\right)}^2}\frac{{\left(3{\varsigma }^2\right)}^2}{{\varsigma }^3\frac{{\left(b\varsigma -u_1\right)}^2}{2}b}\right)\mathrm{d}\varsigma \hfill \\ & & =\left(q_0-\frac{9}{2b^3}\left(1+\frac{p_0}{a}\right)\right)\left(+\infty \right)\hfill \end{array}$$

and

$$\begin{array}{ccc}& & \underset{u\to \infty }{limsup}{\int }_{u_1}^u\left(\vartheta \left(v\right){\left(\frac{{\delta }_0}{{\delta }_0+p_0^{\beta }}\right)}^{1/\alpha }{M}^{\left(\beta /\alpha \right)-1}{\int }_v^{\infty }{\left(\frac{1}{r\left(\nu \right)}\mathsf{\Phi }\left(\nu \right)\right)}^{1/\alpha }\mathrm{d}\nu -\frac{{\left({\vartheta }_{+}^{\prime }\left(v\right)\right)}^2}{4\vartheta \left(v\right)}\right)\mathrm{d}v\hfill \\ & & =\underset{u\to \infty }{limsup}{\int }_{u_1}^u\left(v\left(\frac{a}{a+p_0}\right){\int }_v^{\infty }\left({\int }_{\frac{\nu }{a}}^{\infty }\frac{q_0}{{\varsigma }^4}{\left(\frac{b\varsigma }{\varsigma }\right)}^{1/\lambda }\mathrm{d}\varsigma \right)\mathrm{d}\nu -\frac{1}{4v}\right)\mathrm{d}v\hfill \\ & & =\underset{u\to \infty }{limsup}{\int }_{u_1}^u\left(v\left(\frac{a}{a+p_0}\right)\left(\frac{q_0}{6{\left(\frac{1}{a}\right)}^3{v}^2}{b}^{1/\lambda }\right)-\frac{1}{4v}\right)\mathrm{d}v\hfill \\ & & =\left(\left(\frac{a}{a+p_0}\right)\left(\frac{q_0}{6}{a}^3{b}^{1/\lambda }\right)-\frac{1}{4}\right)\left(+\infty \right).\hfill \end{array}$$

Thus, the Conditions (4) and (5) are satisfied if

$$q_0>\frac{9\left(a+p_0\right)}{2a{b}^3}$$

(30)

and

$$q_0>\frac{3\left(a+p_0\right)}{2a^4{b}^{1/\lambda }}$$

(31)

respectively. Therefore, we see that (29) is oscillatory if

$$q_0>max\left\{\frac{9\left(a+p_0\right)}{2a{b}^3},\frac{3\left(a+p_0\right)}{2a^4{b}^{1/\lambda }}\right\}.$$

(32)

Remark 1.

From Theorem 2, we see that (29) is oscillatory if

$$q_0>\frac{9\left(a+p_0\right)}{a{b}^3\mathrm{e}ln\left(a/b\right)}.$$

(33)

Using Theorem 4, if we choose $\eta \left(u\right)=bu,$ then (29) is oscillatory if

$$q_0>\frac{9a^6{p}_0^2}{\left(a^3{p}_0-1\right)b^3\mathrm{e}ln\left(a/b\right)}.$$

(34)

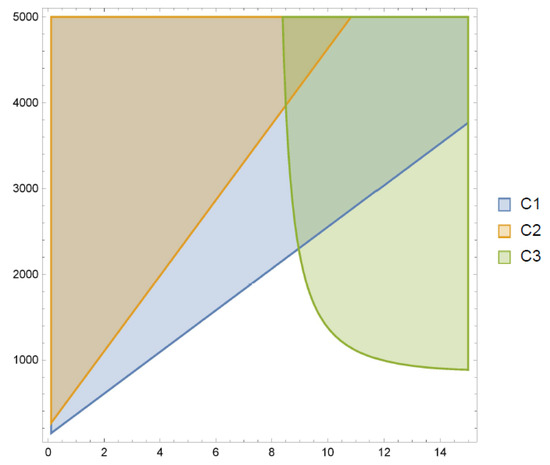
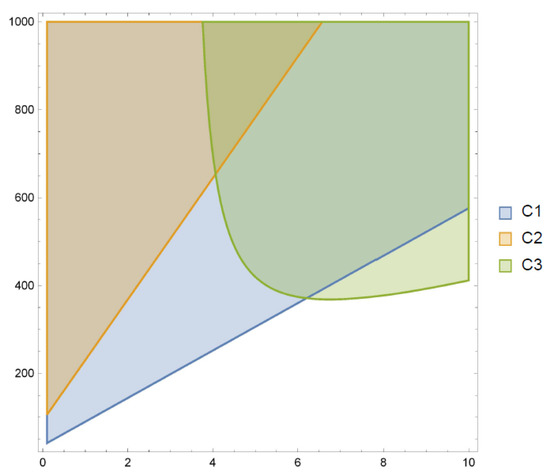
Figure 1 and Figure 2 illustrate the efficiency of the Conditions (32)–(34) in studying the oscillation of the solutions of (29). It can be easily observed that Condition (31) supports the most efficient condition for values of $p\in \left(0,1/a^3\right)$, and Condition (34) supports the most efficient condition for values of $p>\left(1/a^3\right)$. Therefore, our results improve the results in [20,23] and complement the results in [21].

Figure 1. Regions for which Conditions (32)–(34) are satisfied when $a=1/2$ and $b=1/3$.

Figure 2. Regions for which Conditions (32)–(34) are satisfied when $a=2/3$ and $b=1/2$.

3. Conclusions

In this study, we established new criteria for oscillation of solutions of neutral delay differential equation of fourth order (1). By imposing two Riccati substitutions in each case of the derivatives of the corresponding function, we obtained criteria that ensure that all solutions oscillate. To the best of our knowledge, the sharp results that addressed the oscillation of (1) are presented in the works [18,20,21,23]. Li and Rogovchenko [21] improved the results in [18,20,23], but they used Lemma 4 with $\lambda =1$ ( this is inaccurate); see Remark 12 in [14]. Thus, the results in [21] may be somewhat inaccurate. By applying our results to an example, it was shown that our results improve the previous results in the literature.