New Improved Results for Oscillation of Fourth-Order Neutral Differential Equations
Abstract
1. Introduction
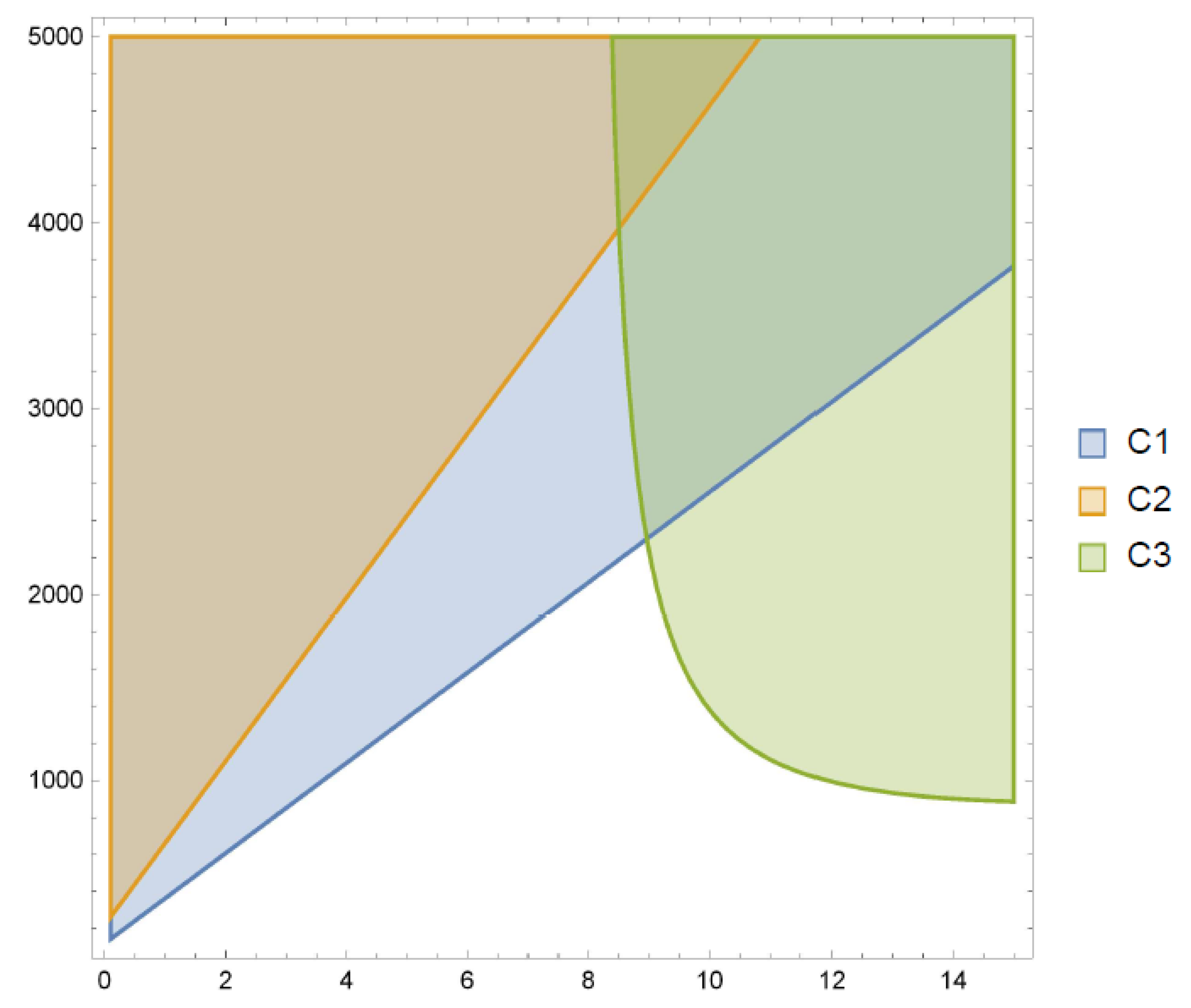
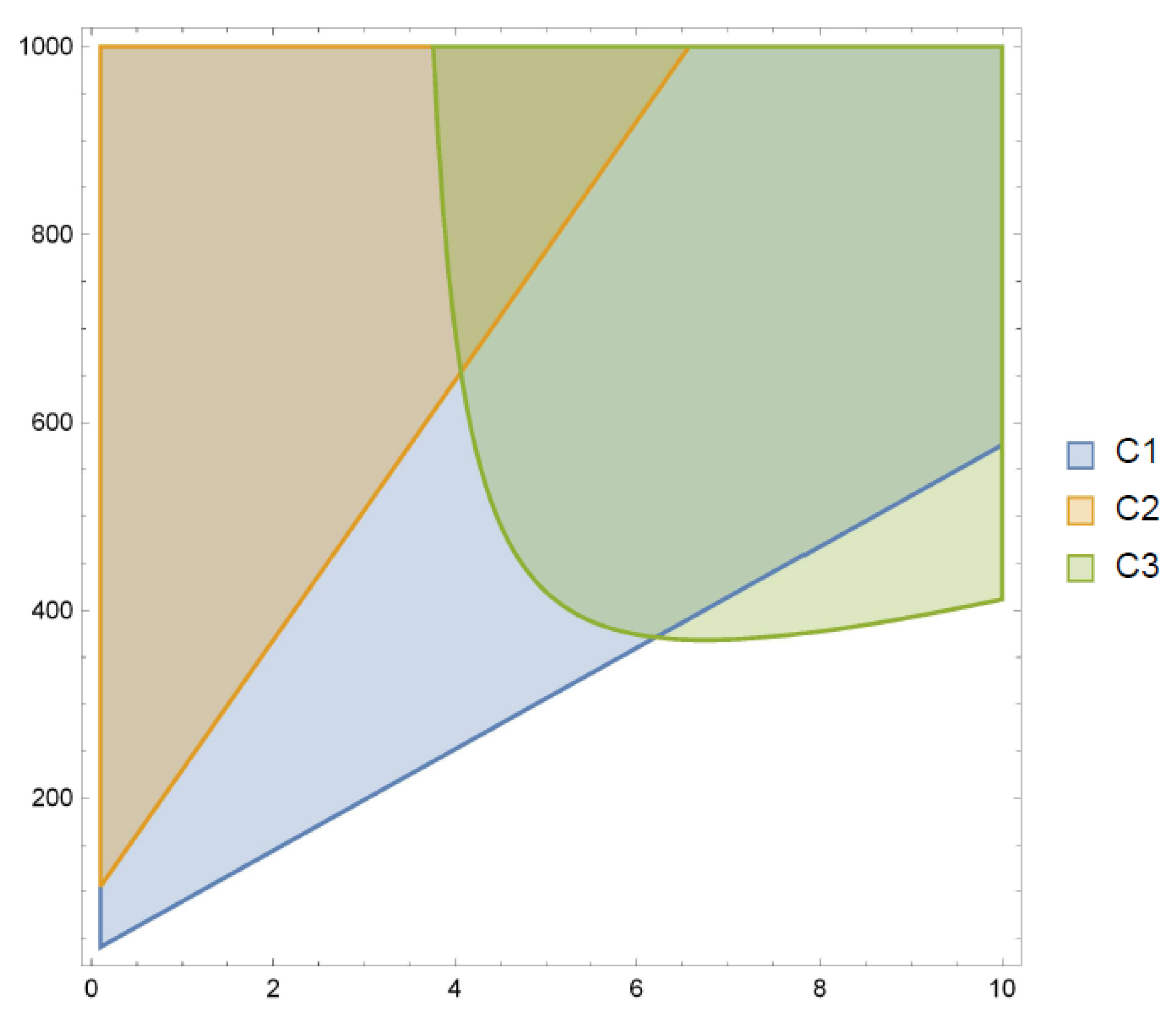
2. Main Results
3. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ahmed, E.; Hegazi, A.S.; Elgazzar, A.S. On difference equations motivated by modelling the heart. Nonlinear Dyn. 2006, 46, 49–60. [Google Scholar] [CrossRef][Green Version]
- Awrejcewicz, J.; Krysko, V. Nonclassic Thermoelastic Problems in Nonlinear Dynamics of Shells; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Hale, J.K. Functional Differential Equations; Springer: New York, NY, USA, 1977. [Google Scholar]
- MacDonald, N. Biological Delay Systems: Linear Stability Theory; Cambridge University Press: Cambridge, UK, 1989. [Google Scholar]
- Moaaz, O.; Chalishajar, D.; Bazighifan, O. Some qualitative behavior of solutions of general class of difference equations. Mathematics 2019, 7, 585. [Google Scholar] [CrossRef]
- Agarwal, R.P.; Bohner, M.; Li, T.; Zhang, C. Oscillation of second-order Emden–Fowler neutral delay differential equations. Ann. Mat. Pura Appl. 2014, 4, 1861–1875. [Google Scholar] [CrossRef]
- Agarwal, R.P.; Zhang, C.; Li, T. Some remarks on oscillation of second order neutral differential equations. Appl. Math. Comput. 2016, 274, 178–181. [Google Scholar] [CrossRef]
- Baculikova, B.; Dzurina, J. Oscillation theorems for second-order nonlinear neutral differential equations. Comput. Math.Appl. 2011, 62, 4472–4478. [Google Scholar] [CrossRef]
- Bohner, M.; Grace, S.R.; Jadlovska, I. Oscillation criteria for second-order neutral delay differential equations. Electron. J.Qual. Theory Differ. Equ. 2017, 60, 1–12. [Google Scholar] [CrossRef]
- Bohner, M.; Grace, S.R.; Jadlovska, I. Sharp oscillation criteria for second-order neutral delay differential equations. Math. Methods Appl. Sci. 2020, 43, 1–13. [Google Scholar] [CrossRef]
- Chatzarakis, G.E.; Moaaz, O.; Li, T.; Qaraad, B. Some oscillation theorems for nonlinear second-order differential equations with an advanced argument. Adv. Differ. Equ. 2020, 2020, 160. [Google Scholar] [CrossRef]
- Moaaz, O.; Anis, M.; Baleanu, D.; Muhib, A. More effective criteria for oscillation of second-order differential equations with neutral arguments. Mathematics 2020, 8, 986. [Google Scholar] [CrossRef]
- Moaaz, O.; Elabbasy, E.M.; Qaraad, B. An improved approach for studying oscillation of generalized Emden–Fowler neutral differential equation. J. Ineq. Appl. 2020, 2020, 69. [Google Scholar] [CrossRef]
- Chatzarakis, G.E.; Grace, S.R.; Jadlovská, I.; Li, T.; Tunç, E. Oscillation criteria for third-order Emden–Fowler differential equations with unbounded neutral coefficients. Complexity 2019, 2019, 7p. [Google Scholar] [CrossRef]
- Jadlovská, I.; Chatzarakis, G.E.; Džurina, J.; Grace, S.R. On Sharp Oscillation Criteria for General Third-Order Delay Differential Equations. Mathematics 2021, 9, 1675. [Google Scholar] [CrossRef]
- Moaaz, O.; Elabbasy, E.M.; Shaaban, E. Oscillation criteria for a class of third order damped differential equations. Arab J. Math. Sci. 2018, 24, 16–30. [Google Scholar] [CrossRef]
- Moaaz, O.; Baleanu, D.; Muhib, A. New aspects for non-existence of kneser solutions of neutral differential equations with odd-order. Mathematics 2020, 8, 494. [Google Scholar] [CrossRef]
- Agarwal, R.P.; Bohner, M.; Li, T.; Zhang, C. A new approach in the study of oscillatory behavior of even-order neutral delay differential equations. Appl. Math. Comput. 2013, 225, 787–794. [Google Scholar] [CrossRef]
- Alsharari, F.; Bazighifan, O.; Nofal, T.A.; Khedher, K.M.; Raffoul, Y.N. Oscillatory Solutions to Neutral Delay Differential Equations. Mathematics 2021, 9, 714. [Google Scholar] [CrossRef]
- Baculikova, B.; Dzurina, J.; Li, T. Oscillation results for even-order quasilinear neutral functional differential equations. Electronic J. Diff. Equ. 2011, 2011, 1–9. [Google Scholar]
- Li, T.; Rogovchenko, Y.V. Oscillation criteria for even-order neutral differential equations. Appl. Math. Lett. 2016, 61, 35–41. [Google Scholar] [CrossRef]
- Moaaz, O.; El-Nabulsi, R.A.; Bazighifan, O. Oscillatory behavior of fourth-order differential equations with neutral delay. Symmetry 2020, 12, 371. [Google Scholar] [CrossRef]
- Xing, G.; Li, T.; Zhang, C. Oscillation of higher-order quasi-linear neutral differential equations. Adv. Difference Equ. 2011, 2011, 1–10. [Google Scholar] [CrossRef]
- Zhang, C.; Agarwal, R.P.; Bohner, M.; Li, T. New results for oscillatory behavior of even-order half-linear delay differential equations. Appl. Math. Lett. 2013, 26, 179–183. [Google Scholar] [CrossRef]
- Agarwal, R.P.; Grace, R.S.; O’Regan, D. Oscillation Theory for Difference and Functional Differential Equations; Kluwer Acad. Publ.: Dordrecht, The Netherlands, 2000. [Google Scholar]
- Kiguradze, I.T.; Chanturiya, T.A. Asymptotic Properties of Solutions of Nonautonomous Ordinary Differential Equations; Kluwer Acad. Publ.: Dordrecht, The Netherlands, 1993. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moaaz, O.; El-Nabulsi, R.A.; Muhib, A.; Elagan, S.K.; Zakarya, M. New Improved Results for Oscillation of Fourth-Order Neutral Differential Equations. Mathematics 2021, 9, 2388. https://doi.org/10.3390/math9192388
Moaaz O, El-Nabulsi RA, Muhib A, Elagan SK, Zakarya M. New Improved Results for Oscillation of Fourth-Order Neutral Differential Equations. Mathematics. 2021; 9(19):2388. https://doi.org/10.3390/math9192388
Chicago/Turabian StyleMoaaz, Osama, Rami Ahmad El-Nabulsi, Ali Muhib, Sayed K. Elagan, and Mohammed Zakarya. 2021. "New Improved Results for Oscillation of Fourth-Order Neutral Differential Equations" Mathematics 9, no. 19: 2388. https://doi.org/10.3390/math9192388
APA StyleMoaaz, O., El-Nabulsi, R. A., Muhib, A., Elagan, S. K., & Zakarya, M. (2021). New Improved Results for Oscillation of Fourth-Order Neutral Differential Equations. Mathematics, 9(19), 2388. https://doi.org/10.3390/math9192388








