Optimal Pricing and Ordering Strategies with a Flexible Return Strategy under Uncertainty

Abstract

To coordinate the supply chain risk caused by demand uncertainty, this paper proposed a flexible return strategy under demand uncertainty, in which the retailer can choose return quantity independently by put option after the selling season, while the return quantity is usually determined by the supplier in the classical return strategy. In our novel return strategy, the exercise price is not fixed, and we developed the base model of this strategy, named the selective buyback contracts model. We have solved the optimal pricing and ordering strategies of supply chain members. Numerical studies demonstrated that the contracts can coordinate a supply chain with one retailer and one supplier, and the supplier can adjust the profit distribution of the supply chain by adjusting the option exercise price. Compared with other return strategies, the selective buyback contracts give the retailer more power of choice, and the supplier receives risk compensation from the put options.

1. Introduction

A supply chain is composed of different independent members, which are the interested parties. Supply chain members make a decision based on maximizing their expected profit, while an independent decision usually damages the interests of the integrated supply chain. Especially in perishable products’ supply chains (e.g., fast fashion, consumer electronics, fresh products, holiday products), products are characterized by a short sales season, high demand uncertainty, and low salvage value. In this context, retailers try to place an order cautiously to decrease the loss from inventory risk. The harm of excess inventory to retailers is (1) storage space occupation, (2) funds’ occupation, and (3) asset impairment. However, suppliers strive to encourage retailers to order as much as possible. How to coordinate the contradiction between suppliers and retailers has become an important subject of supply chain risk management.

Many solutions have been proposed by people in theoretical research and management practice to coordinate the contradiction caused by demand uncertainty. For example, Uniqlo, a Japanese clothing retailer, reduces demand uncertainty by postponement manufacturing technology. They delay the cutting of the length of trousers to the terminal retail stage [1]. A postponement manufacturing strategy is suitable for a supply chain with a strong leader who can control both production and sales. More often, suppliers provide a supply chain contract to retailers to coordinate the supply chain. Among them, the buyback contract is the most widely used [2].

The motive to use a buyback contract is that suppliers want to prevent the discount promotion from damaging the brand value, and suppliers usually have more channels to handle excess inventory [3]. However, the quantity returned to suppliers from retailers after the sales season is decided by the supplier in a traditional buyback contract, and retailers have little decision-making right. The effect of the traditional buyback contract is to encourage retailers to order more rather than to order more accurately. To encourage retailers to place orders more accurately, we proposed a flexible return strategy. We introduce put option contracts in traditional buyback contracts, and named it the selective buyback contract, which can transfer the right of return quantity decision from suppliers to retailers. Through such a flexible buyback contract, the retailer can buy options contracts when he places an order and decide whether or not to exercise them at the end of the sales season. This means the retailer can return the excess product to the supplier at the exercise price. The supplier can also receive risk compensation from the sales of options contracts. In addition, we calculate the optimal decisions of suppliers and retailers when the supply chain reaches coordination.

The selective buyback contract improves the flexibility of the supply chain by introducing put option contracts. In the existing literature, some researchers also introduced put option contracts in supply chain contracts to improve the flexibility of the supply chain [4]. However, as shown in Figure 1, the put option contracts are exercised before the sales season in this contract, meaning that products are returned before the sales season. So, this kind of contract is a kind of quantity flexibility contract rather than a buyback contract, as it is named in much of the literature. This difference is not pointed out in the existing literature.

Figure 1. Products returned during different sales periods.

This paper is structured into six sections. Section 2 reviews the relevant literature. In Section 3, the background of the model is described and assumed, and the meanings of the related parameters are explained. We construct, solve, and analyze a selective buyback contracts model with put option and return policies. Section 4 compares the difference between the classical return strategy and the flexible return strategy. Section 5 performs a numerical analysis of the model. The last part contains the discussion, research limitations, and future research prospects.

2. Literature Review

Our work brings together streams of supply chain risk management, supply chain contract, and option contracts. Although much work has been done in each of these areas, studies that combine the three aspects are relatively rare. In what follows, we review the closely related literature in the three areas, and then summarize the differences between our work and the current literature, and highlight our contributions.

Supply chain risk is an important subject of supply chain management, and the risk caused by uncertain demand is the main source of supply chain risk among various of risk factors [5]. Especially for perishable products, the rapid and substantial depreciation of products caused by over-demand causes huge economic losses for retailers [6]. Therefore, how to coordinate the risks brought by uncertain demand has become an important challenge for improving the performance of the supply chain [7]. Mather first proposed a delayed product differentiation (DPD) strategy to reduce the risk of demand uncertainty [8]. The Japanese fast fashion company, Uniqlo, applies the DPD strategy to pants products, that is, to postpone some processing procedures from the production stage to the terminal retail stage [9]. However, this strategy is not feasible in all supply chains. Its effective execution requires a strong supply chain leader who can control all links from design, production, to retail, so that other members of the supply chain will implement the plan of this strong leader. Among these contracts, buyback contracts are widely used in perishable products’ supply chains because they can reduce the retailers’ inventory risk.

Another tool for supply chain risk management is the supply chain contract. Jeuland and Shugan first proposed the concept of the supply chain contract [10]. He pointed out that the use of the buyback strategy can achieve coordination between retailers and suppliers, but it did not abstract this buyback strategy as a mathematical model. It was not until Pasternack studied the optimal ordering strategy and pricing strategy for perishable products that the repurchase strategy was modeled [11]. Since then, supply chain contracts have been widely used in supply chain coordination, and more forms of supply chain contracts have been innovated. For example, wholesale price contracts [12], quantity flexibility contracts [13], revenue sharing contracts [14], and so on. Generally speaking, there are actually two models of repurchase contracts: one is that the retailer’s remaining inventory is not returned to the supplier, and the supplier only subsidizes this part of the inventory [15]; the other is that the retailer returns the remaining inventory to the supplier, and the supplier pays a certain return subsidy [16]. The latter type of buyback contract is the most commonly used. The reasons are as follows: (1) the buyback contract is simple and easy to implement; (2) to prevent retailers from discounting sales and damaging brand value; and (3) suppliers have more inventory processing channels. However, the classic buyback contract lacks flexibility, and the retailer only passively accepts it, lacking options. Therefore, how to improve the flexibility of the contract has always been an important direction of supply chain contract research.

As a risk management tool in the financial sector, options can hedge losses caused by future uncertainty [17]. It has been shown that an option contract can provide suppliers and retailers with flexibility to share risks caused by uncertain demand, and then improve supply chain performance. Barnes et al. were the first to introduce options into supply chain management research. They prove that the supply coordination with correlated demand is achievable in the presence of an options contract when the exercise price is restricted to being linear [18]. Wu et al. study the capacity option contract, which is used to share supply chain risk between retailers and suppliers, as well as to stimulate high-tech manufacturers to expand capacity [19]. Chen et al. introduce bidirectional option contracts in a service supply chain. They find that the maximum expected profit of the retailer is non-increasing in the service requirement, while that of the supplier is non-decreasing in the service requirement, either with or without bidirectional option contracts [20]. Chen et al. introduce both unilateral and bidirectional option contracts into the container planning problem. They study the application strategies of different option contracts in different practical scenarios [21]. Zhao et al. also propose a bidirectional option contract, which may be exercised as either a call option or a put option, to coordinate a supply chain. They calculate the retailer’s optimal order quantity and the conditions under which supply chain coordination is achieved [22].

The above-mentioned supply chain contracts containing options are usually called buyback contracts, but their essence is a kind of flexible quantity contract, because the execution of the option occurs in the ordering stage before the sale, rather than after the sales season. At this time, the option coordinated is the risk brought by the order quantity, not the risk brought by the remaining inventory. That is to say, the point of this kind of option is actually to prevent the occurrence of excess demand, rather than to coordinate the risk when the excess demand has actually occurred. In addition, the coordination effect of options is closely related to the accuracy of demand forecasting. The closer the demand forecast is to the sales season, the more accurately the effect will be reflected.

In order to resolve the problem mentioned above, to improve the flexibility of traditional repurchase contracts, retailers are allowed to choose the return quantity based on their own forecasts, instead of passively accepting the return quantity determined by the supplier. Combining the advantages of traditional return strategies and put options, we propose a new return strategy called a selective flexible return strategy. Different from other strategies where the option execution occurs in the ordering stage before the sales season, in the selective flexible return strategy, the option execution occurs at the end of the sales season, and the amount of repurchase is determined by the retailer.

3. Model

3.1. Assumption and Notations

Consider a supply chain with one retailer and one supplier. The retailer purchases $Q$ quantities of commodities from the supplier before the selling season. The production cost of the supplier is at the price of $c$ per unit. The retailer will sell commodities to the customer at the price of $p$ per unit during the selling season, where $p$ is fixed in a perfectly competitive market. After the selling season, unsold commodities have a salvage value of $v$ per unit. A penalty for the shortage is considered in other literature, but shortage does not necessarily have a negative impact, as it may cause consumers to have a stronger desire to buy (hunger marketing), so we do not consider out of stock penalties in this paper. The market demand $D$ is a random variable with density $f\left(·\right)$ and distribution $F\left(·\right)$. The parameters that will be used in this paper and their meanings are shown in Table 1.

Table 1. Parameters and meanings.

Parameter	Meaning
$c$	supplier’s unit cost
$w$	price per unit charged by the supplier to the retailer
$v$	per unit salvage value
$p$	retailer’s unit selling price
$s$	price of per option contract
$r$	exercise price of per option contract
$q$	option contracts ordered by the retailer from the supplier
$Q$	amount ordered by the retailer from the supplier
$D$	customer demand
$f\left(·\right)$	probability density function of demand
$F\left(·\right)$	the distribution function of demand
$\overline{F}\left(·\right)$	$1-F\left(·\right)$

To prevent retailers from making profits directly from the wholesale stage, the parameters above conform to the following constraint:

$$p>w>c>v.$$

3.2. The Base Model

Consider the base model; there are no flexible policies in the supply chain, the retailer can only order before the selling season, and per unit is supplied to the retailer at the price of $w$, the retailer sells per unit to the customer at a price of $p$ and per unit that has not been sold is retained at the salvage value of $v$ after the selling season. The retailer decides on its order quantity $Q$ such that its expected profit $\mathsf{\Pi }$ is maximized:

$${\Pi }_R\left(Q\right)=pE\left[min\left(Q,D\right)\right]+vE{\left(Q-D\right)}^{+}-wQ.$$

(1)

The optimal order quantity $Q^{*}$ can be obtained from Equation (1):

$$Q^{*}{F}^{-1}\left(\frac{p-w}{p-v}\right).$$

(2)

With $Q^{*}$, we can now model the supplier’s expected profit:

$${\Pi }_S\left(w\right)=\left(w-c\right)Q^{*}.$$

(3)

3.3. Integrated Supply Chain

In this case, where the supplier and retailer can be seen as a community of interests, the leader of the community makes decisions to maximize the overall supply chain profit, rather than individual profit. The system expected profit can be modeled as follows:

$${\Pi }_{SC}\left(Q\right)=pE\left[min\left(Q,D\right)\right]+vE{\left(Q-D\right)}^{+}-cQ.$$

(4)

The optimal system $Q_{SC}$ is as follows:

$$Q_{SC}=F^{-1}\left(\frac{p-c}{p-v}\right).$$

(5)

Comparing Equation (2) with Equation (5), because $p>w>\mathrm{c}>v$, we can deduce the following:

$$\frac{p-w}{p-v}<\frac{p-c}{p-v}.$$

$F\left(·\right)$ is a monotone increasing function and its inverse function $F^{-1}\left(·\right)$ has the same monotonicity. There is the relationship $Q^{*}<Q_{SC}$, which means that, if no coordination measures are taken in the supply chain and each member makes independent decisions, the overall profit of the supply chain will not reach the optimal level.

3.4. Selective Buy-Back Contracts

3.4.1. Flexible Return Strategy

The flexible return strategy with put options works as shown in Figure 2. Before the selling season, the retailer can order quantity $Q$ at the price of $w$ per unit. Besides, the retailer can purchase $q$ put option contracts at the price of $s$ per contract. The put option contracts give the retailer the right to return unsold products to the supplier after the selling season at the exercise price of $r$ per unit. The portion of the unsold products that exceeds the quantity of put option contracts will be retained by the retailer itself.

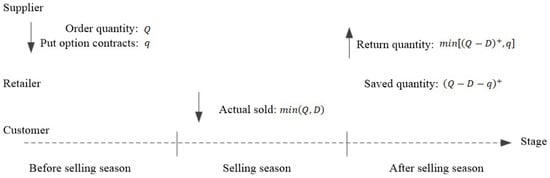
Figure 2. Flexible return strategy with the put option.

3.4.2. Retailer’s Order Decision

The retailer’s decision variables are $Q$ and $q$. Decision making is based on maximizing his expected profit:

$${\mathsf{\Pi }}_R\left(Q,q\right)=pE\left[min\left(Q,D\right)\right]+rE\left[min\left({\left(Q-D\right)}^{+},q\right)\right]+vE{\left(Q^{*}-D-q\right)}^{+}-wQ-sq$$

(6)

Taking partial derivatives on the objective function in Equation (6) concerning $Q$ and $q$ and setting them to zero, the following equations can be obtained:

$$\left(p-w\right)-\left(p-r\right)F\left(Q\right)-\left(r-v\right)F\left(Q-q\right)=0.$$

$$-s+\left(r-v\right)F\left(Q-q\right)=0.$$

Solving the above two equations, we obtain the retailer’s optimal decision:

$$Q=F^{-1}\left(\frac{p-w-s}{p-r}\right).$$

(7)

$$q=Q-F^{-1}\left(\frac{s}{r-v}\right)=Q-\overline{Q}.$$

(8)

For the above to be well-defined, we need to have $Q\ge q$. We meet the following inequality:

$$\frac{p-w-s}{p-r}\ge \frac{s}{r-v}.$$

which reduces to the following:

$$\left(p-w\right)r-\left(p-v\right)s\ge \left(p-w\right)v.$$

(9)

Proposition 1.

The retailer’s optimal decisions on$Q$and$q$ are as follows:

(1) If Equation (9) holds as a strict inequality, then the optimal$Q$and$q$follow Equations (7) and (8), respectively;

(2) If Equation (9) holds as an equality, then the optimal$Q=Q^{*}$in Equation (2) and$q=0$.

Proof. 

As $Q$ and $q$ are the solutions of Equation (6), $p>w>c>v$, as assumed. In case (1), $Q$ and $q$ are well defined by Equations (7) and (8), respectively. In case (2), $\left(p-w\right)r-\left(p-v\right)s=\left(p-w\right)v$ means $q=0$, and $\left(p-w\right)r-\left(p-v\right)s=\left(p-w\right)v$ is substituted into Equation (7) to obtain $Q=Q^{*}$. Case (2) is equivalent to not adopting any coordination strategy, and the expected profits of the supplier and retailer are the same as in the base model. □

Proposition 2.

The retailer’s optimal decisions on$Q$and$q$ are characterized by the following:

(1) The retailer’s optimal order quantity$Q$is a decreasing function of the price of the put option contract$s$; it is an increasing function of the exercise price of$r$.

(2) The retailer’s optimal option contracts quantity$q$is a decreasing function of the price of the put option contract$s$; it is an increasing function of the exercise price of$r$.

Proof. 

Taking partial derivatives on $\frac{p-w-s}{p-r}$ concerning $s$, we can obtain $\frac{\partial \left(\frac{p-w-s}{p-r}\right)}{\partial s}=-\frac{s}{p-r}<0$. Because $F\left(·\right)$ is an increasing function and its inverse function $F^{-1}\left(·\right)$ has the same monotonicity as $F\left(·\right)$, the composite function $F^{-1}\left(\frac{p-w-s}{p-r}\right)$ is a decreasing function of $s$. Therefore, $Q$ is a decreasing function of $s$. In the same way, it can also be proven that $Q$ is an increasing function of $r$, and that $q$ is a decreasing function of $s$ and an increasing function of $r$. □

3.4.3. Supplier’s Pricing Decision

The supplier’s decision variables are $s$ and $r$, and decision making is based on maximizing the following objective functions:

$${\mathsf{\Pi }}_S\left(s,r\right)=\left(w-c\right)Q+sq-\left(r-v\right)E\left[min\left({\left(Q-D\right)}^{+},q\right)\right].$$

(10)

The supplier’s expected profit function simplifies to the following:

$${\mathsf{\Pi }}_S\left(s,r\right)=\left(w+s-c\right)Q-s\overline{Q}-\left(r-v\right){{\displaystyle \int }}_{\overline{Q}}^{Q}F\left(x\right)dx.$$

(11)

Taking partial derivatives upon the objective function with respect to $s$ and $r$, we have the following:

$$\frac{\partial {\mathsf{\Pi }}_S}{\partial s}=q+\left[\left(w+s-c\right)-\left(r-v\right)F\left(Q\right)\right]Q_s^{\prime }-\left[s-\left(r-v\right)F\left(\overline{Q}\right)\right]{\overline{Q}}_s^{\prime },$$

(12)

$$\frac{\partial {\mathsf{\Pi }}_S}{\partial r}=q+\left[\left(w+s-c\right)-\left(r-v\right)F\left(Q\right)\right]Q_r^{\prime }-\left[s-\left(r-v\right)F\left(\overline{Q}\right)\right]{\overline{Q}}_r^{\prime }-{{\displaystyle \int }}_{\overline{Q}}^{Q}F\left(x\right)dx.$$

(13)

where $Q_s^{\prime }$, ${\overline{Q}}_s^{\prime }$, $Q_r^{\prime }$, and ${\overline{Q}}_r^{\prime }$ denote the partial derivatives of $Q$ and $\overline{Q}$ with respect to $s$ and $r$. From Equations (7) and (8), we have the following:

$$Q_s^{\prime }=-{\left[\left(p-r\right)f\left(Q\right)\right]}^{-1},$$

$${\overline{Q}}_s^{\prime }={\left[\left(r-v\right)f\left(\overline{Q}\right)\right]}^{-1},$$

$$Q_r^{\prime }=-Q_s^{\prime }F\left(Q\right),$$

$${\overline{Q}}_r^{\prime }=-{\overline{Q}}_s^{\prime }F\left(\overline{Q}\right),$$

Substituting the last two equations into Equation (13), we have the following:

$$\frac{\partial {\mathsf{\Pi }}_S}{\partial r}=q-\left[\left(w+s-c\right)-\left(r-v\right)F\left(Q\right)\right]Q_s^{\prime }F\left(Q\right)+\left[s-\left(r-v\right)F\left(\overline{Q}\right)\right]{\overline{Q}}_s^{\prime }F\left(\overline{Q}\right)-{{\displaystyle \int }}_{\overline{Q}}^{Q}F\left(x\right)dx.$$

(14)

Because $\frac{\partial {\mathsf{\Pi }}_s}{\partial \mathrm{s}}=0$, this implies the following:

$$\left[s-\left(r-v\right)F\left(\overline{Q}\right)\right]{\overline{Q}}_s^{\prime }=q+\left[\left(w+s-c\right)-\left(r-v\right)F\left(Q\right)\right]Q_s^{\prime }.$$

(15)

We have the following:

$$\frac{\partial {\mathsf{\Pi }}_S}{\partial r}=q+qF\left(\overline{Q}\right)+\left[\left(w+s-c\right)-\left(r-v\right)F\left(Q\right)\right]\left[F\left(\overline{Q}\right)-F\left(Q\right)\right]Q_s^{\prime }-{{\displaystyle \int }}_{\overline{Q}}^{Q}F\left(x\right)dx.$$

Furthermore, from (7), we have the following:

$$p-c-\left(p-v\right)F\left(Q\right)=\left(w+s-c\right)-\left(r-v\right)F\left(Q\right).$$

Hence, $\frac{\partial {\mathsf{\Pi }}_S}{\partial r}=0$ takes the following form:

$$q+qF\left(\overline{Q}\right)+\left[p-c-\left(p-v\right)F\left(Q\right)\right]\left[F\left(\overline{Q}\right)-F\left(Q\right)\right]Q_s^{\prime }-{{\displaystyle \int }}_{\overline{Q}}^{Q}F\left(x\right)dx=0.$$

4. Flexible Return Strategy Compared with the Classical Return Strategy

Pasternack proposed a classical return strategy to coordinate the supply chain. Per unit that has not been sold can be all returned to the supplier at the price of $b$ after the selling season [11]. The retailer’s expected profit can be modeled as follows:

$${\mathsf{\Pi }}_R\left(Q\right)=pE\left[min\left(Q,D\right)\right]+bE{\left(Q-D\right)}^{+}-wQ.$$

(16)

The optimal order quantity ${\mathrm{Q}}^{*}$ can be obtained from Equation (1):

$$Q_b^{*}=F^{-1}\left(\frac{P-W}{P-b}\right).$$

(17)

With $Q_b^{*}$, we can now model the supplier’s expected profit:

$${\mathsf{\Pi }}_S\left(w\right)=\left(w-c\right)Q_b^{*}+\left(v-b\right)E{\left(Q_b^{*}-D\right)}^{+}.$$

(18)

Hold:

$$p>w>c,$$

$$w>b>v.$$

Compared with the classic return strategy, we can see in Table 2 that the retailer’s and the supplier’s decision variables both increase under the flexible return strategy, but the retailer has more right to choose the return quantity. When the option exercise price $r$ of the flexible return strategy is equivalent to the buyback price $b$ of the classical return strategy, and when the option contract price $s=0$, $Q=Q_b^{*}$ and $q=Q$ can be obtained from Equations (7) and (17). This means that the flexible return strategy is equivalent to the classic return strategy.

Table 2. Flexible return strategy compared with the classical return strategy.

Compare Items	Classical Return Strategy	Flexible Return Strategy
Retailer’s decision	$Q$	$\left(Q,q\right)$
Supplier’s decision	$b$	$\left(s,r\right)$
Optimal order quantity	$Q_b^{*}=F^{-1}\left(\frac{p-w}{p-b}\right)$	$Q=F^{-1}\left(\frac{p-w-s}{p-r}\right)$ $q=Q-F^{-1}\left(\frac{s}{r-v}\right)$
Coordination status	partial credit and all return	choose flexibly by retailer

5. Numerical Studies

To start with, consider an example with the following data:

$$p=100, c=30, w=50, v=10, D~N\left(100, 20\right)$$

5.1. Independent Decision

When retailers make independent decisions, their decision making is based on maximizing their expected profit. The decision variables are ordered quantity $Q$ and options contract quantity $q$. We let the option contract price $s$ vary from 0.01 to 1, and the option exercise price $r$ varies from 10 to 50. Through Equations (7) and (8), we can obtain the relationship between the retailer’s decision variables $\left(Q,q\right)$ and $\left(s,r\right)$, respectively, as shown in Figure 3.

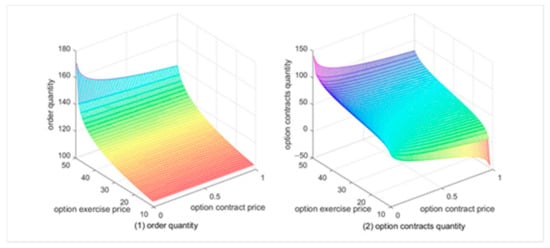
Figure 3. Retailer’s independent decision.

We can observe from Figure 3 that the order quantity and options contract quantity increase as the option exercise price increases, and decrease as the option contract price decreases. This also proves the correctness of proposition 1.

5.2. Integrated Decision

When the flexible return strategy means that the supply chain is coordinated, the retailer’s optimal order quantity $Q$ is equal to the order quantity of the integrated supply chain $Q_{SC}$. Because $Q=Q_{SC}$, we can obtain the following:

$$r=p-\frac{\left(p-w-s\right)\left(p-v\right)}{p-c}.$$

The above equation is substituted into Equation (8). We obtain the relationship between the put option contract quantity, put option contract price, and put option exercise price, respectively, as shown in Figure 4.

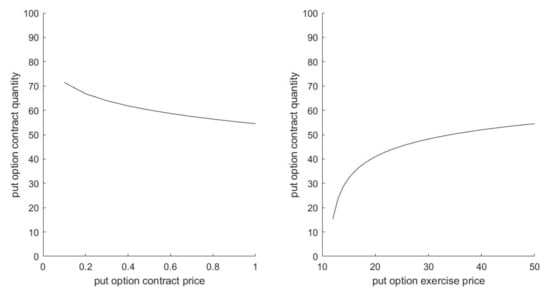
Figure 4. Sensitive to put option contract quantity.

We can observe from Figure 2 that the put option contract quantity decreases as the option contract price increases, and increases as the option exercise price increases. The practical significance is that, the higher the option price, the higher the cost the retailer needs to pay, which will reduce the retailer’s desire to buy options. The higher exercise price of the option means that the retailer’s inventory backlog loss is smaller, which will encourage the retailer to buy more options.

5.3. Expected Profit

The Pareto improvement of the profits of each supply chain member is the basis for the supply chain members to accept the coordination strategy. Otherwise, the coordination strategy will be difficult to implement. We discussed the relationship between expected profit and options contract exercise price at different wholesale prices, with other parameters unchanged. The result is shown in Figure 5.

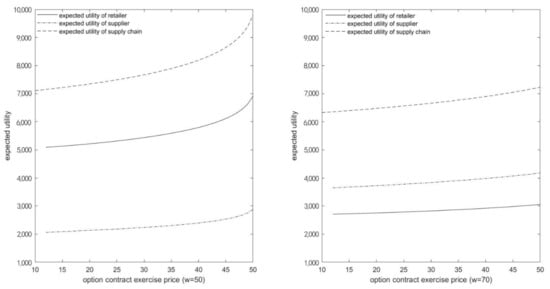
Figure 5. Comparison of expected profit under different wholesale prices.

We can observe from Figure 5 that the member’s expected profit of the supply chain is increasing in the exercise price of the options contract. This implies that increasing the option contracts exercise price can increase the expected profit of each member. The retailer’s expected profit at the wholesale price $w=70$ is lower than at $w=50$, and the supplier’s expected profit at the wholesale price $w=70$ is higher than at $w=50$. This implies that the supplier can adjust the profit distribution by adjusting the wholesale price.

6. Discussion and Conclusions

In this paper, we proposed a flexible return strategy with a put option, in order to coordinate the supply chain risk caused by demand uncertainty. The option can transfer the risk from the retailer to the supplier, and the supplier can receive risk compensation from the retailer. In the novel return strategy, the supplier’s decision variables are put option price and exercise price, whereas the retailer’s decision variables are commodity quantity and option quantity. We developed and solved the mathematical model of the novel return strategy, and numerical studies of the model show the following: (1) the retailer’s optimal commodity quantity ordering is a decreasing function of the supplier’s optimal option pricing, whereas it is an increasing function of the supplier’s optimal option exercise pricing; (2) the retailer’s optimal option quantity ordering is a decreasing function of the supplier’s optimal option pricing, whereas it is an increasing function of the supplier’s optimal option exercise pricing; and (3) the novel return strategy can coordinate a supply chain with one retailer and one supplier, as the profit of all supply chain members has been Pareto improved. Compared with the classical return strategy, the return quantity is not equal to all unsold commodities, and the price of the returned commodities is not equal to the wholesale price. Therefore, the flexible return strategy enables the retailer to have more flexibility in choice, and its scope of application is also wider.

Our results indicate that the selective buyback contract is a very effective contract. It can coordinate a supply chain with one supplier and one retailer. When the supply chain achieved coordination, the option ordering quantity should either be equal to zero or constrained with Formula (7) and Formula (8). The former situation is actually a classic buyback contract, while the widely studied classical buyback contract of Pasternack is a special case of the selective buyback contract we proposed. This indicates that the selective buyback contract has a wide scope of application. Our results also indicate that the expected profits of the supplier and the retailer are increased with the supply chain coordination, and the supplier can adjust the distribution of the overall profit of the supply chain by adjusting the wholesale price. Usually, a strong supplier will set a higher wholesale price, so that more profits in the supply chain will be obtained by the supplier.

Our research has important practical significance. In reality, excess inventory places tremendous pressure on retailers. It not only occupies the retailer’s inventory space, but also causes asset impairment losses. Although the supplier allows the retailer to return the remaining commodities after the sales season in the classical buyback contract, the return quantity is determined by the supplier rather than the retailer. However, retailers are the closest to the demand of end consumers, and it is more reasonable for retailers to determine the return quantity. The selective buyback contract we proposed in this paper gives the decision-making power to the retailer, so that the retailer can determine the return quantity based on its own judgment of the market. In addition, our research has certain theoretical significance. It applies financial risk control tools to supply chain risk management and provides a new idea for supply chain risk management.

There are still some limitations in our study, which can become our research direction in the future. Firstly, we have not addressed the bounded rational related to the two members of the supply chain. For example, although we have calculated the optimal decision, the improvement is in terms of expected profit. Meanwhile, if the decision maker is risk-averse, his decision will not match the optimal decision. Hence, it is important to consider the bounded rational related to the decision maker. This can take several forms, such as risk preference or over-confidence. These will be the subject of our further studies. Secondly, we have not considered the logistic cost of return. Owing to the salvage of the unsold commodities being very low, when the salvage is lower than the logistic cost, it is not wise to continue choosing to return. Therefore, for the selective return contract to be well executed, the logistic cost of the return must be considered. These also will be the subjects of our further studies.